Vibration analysis of variable thickness functionally graded toroidal shell segments

Abstract

In this paper, for the first time, the nonlinear vibration response of toroidal shell segments with varying thickness subjected to external pressure is investigated analytically using Reddy’s third-order shear deformation shell theory. The variable thickness shells are made of functionally graded material (FGM) that is created from ceramic and metal constituents. The material properties of FGM shells are assumed to be gradually graded in the thickness direction according to a simple power-law distribution in terms of volume fractions of constituents. Equations of motion of variable thickness FGM toroidal shell segments are established based on Reddy’s third-order shear deformation shell theory with von Kármán nonlinearity. The Galerkin method and the Runge–Kutta method are used to solve the governing system of partial differential equations of motion, and then the nonlinear vibration response of variable thickness FGM toroidal shell segment is analyzed. A numerical analysis is also performed to show the effects of material and geometrical parameters on the nonlinear vibration response of variable thickness FGM toroidal shell segments.

1 Introduction

In recent years, the study on the stability and vibration of thin structural components with variable thickness has attracted many researchers' interests. Irie et al. [1] and Efraim and Eisenberger [2] studied vibration of variable thickness annular plate and variable thickness thick FGM plates, respectively. Based on classical shell theory, Koiter et al. [3] studied the buckling of cylindrical shells with small periodic axisymmetric thickness variations under axial compression using the energy criterion and a modified shooting method. The buckling of a cylindrical shell with small thickness variations subjected to external pressure has been studied by Nguyen et al. [4] making use of the perturbation technique and the Bubnov–Galerkin method. Li et al. [5] investigated the effect of thickness variation on the stability of composite cylindrical shells subjected to axial compressive load using the perturbation technique and weighted residuals method based on classical shell theory. Also, based on classical shell theory, buckling of a cylindrical shell with variable thickness under axial compression is investigated by Brar et al. [6] making use of the finite difference method. Chen et al. [7] and Feng et al. [8] made use of the perturbation technique, the Galerkin method, and classical shell theory to investigate the buckling of cylindrical shells with arbitrary axisymmetric variable thickness under axial compression and the buckling of pressure loaded cylindrical shells with arbitrary circumferential thickness variations, respectively. Zhou et al. [9] studied the buckling of a cylindrical shell with stepwise variable thickness under external pressure using the hybrid perturbation-Galerkin method. Free vibration characteristics of rotating cylindrical shells with variable thickness is studied by Taati et al. [10] using Galerkin method. Duan and Koh [11] used an analytical approach to investigate free vibration of variable thickness cylindrical shells. A semi-analytical finite clement approach is used by Ganesan and Sivadas [12], and Sivadas and Ganesan [13] to investigate the free vibration behaviour of isotropic circular cylindrical shells and cantilever isotropic circular cylindrical shells with thickness varied in the axial direction, respectively. Using wittrick williams algorithm, El-Kaabazi and Kennedy [14] studied free vibration of variable thickness cylindrical shell. Viswanathan et al. [15] made use of the Spline Function approximation and a point collocation method to study free vibration of layered circular cylindrical with variable thickness. Based on classical shell theory, Aksogan and Sofiyev [16] used the Galerkin method and the Ritz method to investigate the dynamic buckling of a cylindrical shell with variable thickness loaded by a uniform external pressure. Jia-chu et al. [17], and Xin-zhi et al. [18] studied stability, and natural frequency of variable thickness conical shells, respectively.

All the above-mentioned studies are based on classical thin shell theory, usually used for static and dynamic analysis of thin-shell structures. Higher order shear deformation theory has been used for investigating the static and dynamic behaviour of thicker structures with variable thicknesses. Kalbaran and Kurtaran [19] based on the first-order shear deformation shell theory to study the nonlinear static response of laminated composite elliptic panels having variable thickness using the generalized differential quadrature method and Newton–Raphson method. Also, based on the first-order shear deformation shell theory, Nasrekani and Eipakchi [20], and Eipakchi and Nasrekani [21] investigated the displacements of isotropic cylindrical shells and auxetic composite cylindrical shells with variable thickness under external pressure and axial compressive load using the perturbation technique, respectively. Duc et al. [22] made use of the first-order shear deformation shell theory to investigate vibration and dynamic response of sandwich panel with variable thickness.

Functionally graded materials (FGMs) are known as advanced materials usually composed of metal and ceramic constituents, in which material properties gradually vary from one interface to the other. In recent years, static and dynamic behaviours of FGM structures, especially variable thickness FGM structures, have received attention. Shariyat and Alipour [23] presented an analytical approach to investigate the bending and stress of FGM auxetic conical/cylindrical shells with variable thickness based on the first-order shear deformation shell theory. Khoshgoftar [24] and Khoshgoftar et al. [25] used the total potential energy approach and perturbation method to analyze the static behaviour of cylindrical shells with variable thickness based on the first-order shear deformation shell theory and the second-order shear deformation shell theory, respectively. Based on the first-order shear deformation shell theory and perturbation technique, Parhizkar Yaghoobi and Ghannad [26] studied static behaviour of variable thickness FGM cylindrical shell under thermal load. Kashkoli et al. [27] made use of multi-layer method to study static response of FGM cylindrical shell with variable thickness loaded by thermo-mechanical loads. Saeedi et al. [28] investigated static response of long FGM cylindrical shell under thermomechanical loading using the differential quadrature method. Also, using the differential quadrature method, Behravan Rad and Shariyat [29] static response of variable thickness annular plates subjected to magnetic, thermal, and mechanical loads.

Hayati and Atai [30] based on a third-order shear deformation shell theory to study multiobjective mechanical buckling optimization FGM cylindrical shell with thickness variation and initial imperfection, making use of energy approach and finite element modes. Also, using finite element model, Minh and Duc [31] studied the effects of cracks on the stability of variable thickness FGM plates based on the phase-field theory and the new third-order shear deformation plate theory. Using the differential quadrature method, Akbari Alashti and Ahmadi [32] studied buckling of variable thickness FGM cylindrical shell loaded by axial compression and external pressure.

Kim et al. [33] based on the first-order shear deformation shell theory to investigate vibration of FGM doubly curved shell of revolution by using a semi-analytical method. Phu et al. [34] studied nonlinear dynamics responses of variable thickness FGM cylinder shell based on classical thin shell theory. Quoc et al. [35] based on the first-order shear deformation shell theory and Galerkin method investigated vibration of rotating FGM cylindrical shell with variable thickness. Miao et al. [36] investigated free vibration of variable thickness 2D-FGMs cylindrical shell making use of the Sanders’ shell theory, Chebyshev polynomials and the Rayleigh–Ritz method. Ahlawat and Saini [37] studied vibration and buckling of 2D-FGM circular plates with variable thickness using Hamilton’s principle and the Harmonic differential quadrature method. Based on the first-order shear deformation shell theory, Kurpa et al. [38] investigated vibration of variable thickness FGM shallow shells making used of R-functions method.

Toroidal shell segments are special structures and have found applications in practical. Studies on the buckling, postbuckling, and vibration of toroidal shell segments in general, and toroidal shell segments with thickness variation, in particular, have attracted the attention of many authors. Based on classical shell theory, Stein and McElman [39] studied the buckling of isotropic toroidal shell segments under mechanical loads. Oyesanya [40] utilized an analytical approach to investigate the buckling of initial imperfection toroidal shell segments based on Donnell shell theory. Weingarten et al. [41] presented an investigation on finite element shell-buckling of thin isotropic toroidal shell segments using classical thin shell theory. Recently, there has been some research on buckling and post-buckling of the FGM toroidal shell segment. Ninh and Bich [42] investigated nonlinear vibration of simply supported FGM toroidal shell segment under mechanical load based on classical thin shell theory. Based on Reddy’s third-order shear deformation shell theory, Duc and Vuong [43] investigated the vibration behaviour of simply supported FGM toroidal shell segment with constant thickness under mechanical load. Long and Tung [44] studied buckling of FGM toroidal shell segment making use of Reddy’s higher order shear deformation shell theory. Thinh et al. [45] utilized the Galerkin method and the improved Donnell shell theory to investigate nonlinear buckling and postbuckling of FGM toroidal shell segments with thickness variation. In the above studies on isotropic and FGM toroidal shell segments, except for Thinh et al. [45], the main attention is focused on toroidal shell segments with constant thickness. Thinh et al. [45] utilized improved Donnell shell theory usually used for thin shells.

To the best of our knowledge, there are very rare studies focused on the variable thickness shell, and no works focused on the vibration of the thicker variable thickness FGM toroidal shell segment. Toroidal shell segment has been applied in practical fields such as oxygen tanks, rocket fuel tanks, underwater toroidal pressure hull, and satellite support structures. These structures may be made of FGM and have variable thickness. The study of vibration of variable thickness functionally graded toroidal shell segments is necessary and has practical significance. Thus, in this paper, for the first time, the nonlinear vibration response of toroidal shell segments with varying thickness subjected to external pressure is studied. The governing equations are derived based on Reddy’s third-order shear deformation shell theory with von Kármán nonlinearity. Galerkin method and Runge–Kutta method are used to solve the governing equations, and then the nonlinear vibration response of variable thickness FGM toroidal shell segment is analyzed.

2 Governing equations

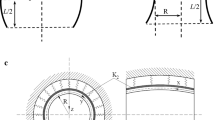
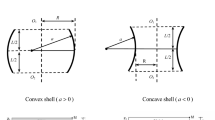
A configuration of FGM toroidal shell segments of variable thickness $h\left( x \right)$ and length $L$ used in the present study is depicted in Fig. 1. The middle surface of the shell is formed by rotation of a plane circular arc of radius $a$ about an axis in the plane of the curve. If $a$ is positive, the shell is convex. If $a$ is negative, the shell is concave. If $a \to \infty$, the toroidal shell segment becomes a cylindrical shell. The $x$ coordinate of the shell is taken along the longitudinal direction, $y$ coordinate along the circumferential direction and $z$ along the thickness direction.

Fig. 1

Geometry and coordinate system of variable thickness toroidal shell segments

Suppose that the inner surface of the FGM shell is ceramic-rich and the outer surface is metal-rich, and the material composition of the shell varies smoothly along the thickness direction according to a simple power-law in terms of the volume fractions of the constituents as Ninh and Bich [42]

$$E\left( {x,z} \right) = E_{m} + \left( {E_{c} - E_{m} } \right)\left( {\frac{2z + h\left( x \right)}{{2h\left( x \right)}}} \right)^{k}$$

(1)

$$\rho \left( {x,z} \right) = \rho_{m} + \left( {\rho_{c} - \rho_{m} } \right)\left( {\frac{2z + h\left( x \right)}{{2h\left( x \right)}}} \right)^{k} ,$$

(2)

where $m$ and $c$ denote metal and ceramic, respectively. $E_{m} ,\rho_{m} ,E_{c} ,\rho_{c}$ are Young modulus and mass density of metal and ceramic constituents, respectively. $E\left( {x,z} \right)$ and $\rho \left( {x,z} \right)$ indicate the effective properties of FGM. The non-negative number $k$ is the volume fraction index defining the distribution of material constituents in FGM. The Poisson’s ratio of material constituents is assumed to be equal and to be constant, i.e. $\nu_{c} = \nu_{m} = const$ Ninh and Bich [42].

In the present study, Reddy’s third-order shear deformation shell theory developed by Reddy and Liu [46] is used to investigate the nonlinear vibration of variable thickness FGM toroidal shell segments subjected to mechanical loads. According to this theory, the displacement components $\left( {u,v,w} \right)$ can be written as

$$\begin{gathered} u\left( {x,y,z,t} \right) = u_{0} \left( {x,y,t} \right)\left( {1 - \frac{z}{a}} \right) + \left[ {z - z^{3} \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}} \right]\phi_{x} \left( {x,y,t} \right) - z^{3} \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}\frac{{\partial w_{0} }}{\partial x} \hfill \\ v\left( {x,y,z,t} \right) = v_{0} \left( {x,y,t} \right)\left( {1 - \frac{z}{R}} \right) + \left[ {z - z^{3} \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}} \right]\phi_{y} \left( {x,y,t} \right) - z^{3} \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}\frac{{\partial w_{0} }}{\partial y} \hfill \\ w\left( {x,y,z,t} \right) = w_{0} \left( {x,y,t} \right), \hfill \\ \end{gathered}$$

(3)

where $t$ is time, $\left( {u_{0} ,v_{0} ,w_{0} } \right)$ are displacements of a point on the mid-surface, and $\phi_{x} ,\phi_{y}$ are the rotations of normal to the middle surface with respect to y- and x-axes, respectively. $R$ is radius of equator.

Based on Reddy’s third-order shear deformation shell theory taking von Kármán nonlinearity into consideration, the normal strains ($\varepsilon_{x} ,\varepsilon_{y}$), in-plane shear strain ($\gamma_{xy}$), and transverse shear strains ($\gamma_{xz} ,\gamma_{yz}$) are expressed as Reddy and Liu [46]

$$\begin{gathered} \varepsilon_{x} = \frac{\partial u}{{\partial x}} - \frac{1}{a}w + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} ,\varepsilon_{y} = \frac{\partial v}{{\partial y}} - \frac{1}{R}w + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} . \hfill \\ \gamma_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}},\gamma_{xz} = \frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial z}} + \frac{1}{a}u,\gamma_{yz} = \frac{\partial w}{{\partial y}} + \frac{\partial v}{{\partial z}} + \frac{1}{R}v. \hfill \\ \end{gathered}$$

(4)

Substituting Eq. (3) into Eq. (4) and ignoring higher order terms on the assumption that $1 - \frac{z}{a} \approx 1,1 - \frac{z}{R} \approx 1$ leads to strain–displacement relations as:

$$\begin{gathered} \left( \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \varepsilon_{x}^{0} \hfill \\ \varepsilon_{y}^{0} \hfill \\ \gamma_{xy}^{0} \hfill \\ \end{gathered} \right) + z\left( \begin{gathered} k_{x}^{\left( 1 \right)} \hfill \\ k_{y}^{\left( 1 \right)} \hfill \\ k_{xy}^{\left( 1 \right)} \hfill \\ \end{gathered} \right) + z^{3} \left( \begin{gathered} k_{x}^{\left( 3 \right)} \hfill \\ k_{y}^{\left( 3 \right)} \hfill \\ k_{xy}^{\left( 3 \right)} \hfill \\ \end{gathered} \right) + \frac{{8z^{3} \frac{\partial h\left( x \right)}{{\partial x}}}}{{3\left( {h\left( x \right)} \right)^{3} }}\left( \begin{gathered} \phi_{x} + \frac{{\partial w_{0} }}{\partial x} \hfill \\ 0 \hfill \\ \phi_{y} + \frac{{\partial w_{0} }}{\partial y} \hfill \\ \end{gathered} \right), \hfill \\ \,\,\left( \begin{gathered} \gamma_{xz} \hfill \\ \gamma_{yz} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \gamma_{xz}^{0} \hfill \\ \gamma_{yz}^{0} \hfill \\ \end{gathered} \right) + z^{2} \left( \begin{gathered} k_{xz}^{\left( 2 \right)} \hfill \\ k_{yz}^{\left( 2 \right)} \hfill \\ \end{gathered} \right), \hfill \\ \end{gathered}$$

(5)

where

$$\begin{gathered} \left( \begin{gathered} \varepsilon_{x}^{0} \hfill \\ \varepsilon_{y}^{0} \hfill \\ \gamma_{xy}^{0} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \frac{{\partial u_{0} }}{\partial x} - \frac{{w_{0} }}{a} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \\ \frac{{\partial v_{0} }}{\partial y} - \frac{{w_{0} }}{R} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} \\ \frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x} + \frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y} \\ \end{gathered} \right){,}\,\left( \begin{gathered} k_{x}^{\left( 1 \right)} \hfill \\ k_{y}^{\left( 1 \right)} \hfill \\ k_{xy}^{\left( 1 \right)} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \frac{{\partial \phi_{x} }}{\partial x} \\ \frac{{\partial \phi_{y} }}{\partial y} \\ \frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} \\ \end{gathered} \right),\,\,\,\left( \begin{gathered} k_{xz}^{\left( 2 \right)} \hfill \\ k_{yz}^{\left( 2 \right)} \hfill \\ \end{gathered} \right) = - \frac{4}{{\left( {h\left( x \right)} \right)^{2} }}\left( \begin{gathered} \phi_{x} + \frac{{\partial w_{0} }}{\partial x} \hfill \\ \phi_{y} + \frac{{\partial w_{0} }}{\partial y} \hfill \\ \end{gathered} \right) \hfill \\ \left( \begin{gathered} k_{x}^{\left( 3 \right)} \hfill \\ k_{y}^{\left( 3 \right)} \hfill \\ k_{xy}^{\left( 3 \right)} \hfill \\ \end{gathered} \right) = - \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}\left( \begin{gathered} \frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} \\ \frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} \\ \frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w_{0} }}{\partial x\partial y} \\ \end{gathered} \right),\,\,\left( \begin{gathered} \gamma_{xz}^{0} \hfill \\ \gamma_{yz}^{0} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \phi_{x} + \frac{{\partial w_{0} }}{\partial x} \hfill \\ \phi_{y} + \frac{{\partial w_{0} }}{\partial y} \hfill \\ \end{gathered} \right). \hfill \\ \end{gathered}$$

(6)

The strain–displacement relations taking von Kármán nonlinearity for variable thickness shell presented in Eq. (5) is a novelty of the present study.

The stress–strain relations for variable thickness FGM toroidal shell segments using Hooke’s law are

$$\begin{gathered} \sigma_{x} = \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} }}\left( {\varepsilon_{x} + \nu \varepsilon_{y} } \right),\sigma_{y} = \frac{{E\left( {x,z} \right)}}{{1 - \nu^{2} }}\left( {\varepsilon_{y} + \nu \varepsilon_{x} } \right) \hfill \\ \sigma_{xy} = \frac{{E\left( {x,z} \right)}}{{2\left( {1 + \nu } \right)}}\gamma_{xy} ,\sigma_{xz} = \frac{{E\left( {x,z} \right)}}{{2\left( {1 + \nu } \right)}}\gamma_{xz} ,\sigma_{yz} = \frac{{E\left( {x,z} \right)}}{{2\left( {1 + \nu } \right)}}\gamma_{yz} \hfill \\ \end{gathered}$$

(7)

where $\nu$ is Poisson’s ratio, $\left( {\sigma_{x} ,\sigma_{y} } \right)$ are normal stresses, $\sigma_{xy}$ is in-plane shear stress, $\left( {\sigma_{xz} ,\sigma_{yz} } \right)$ are transverse shear stresses.

The force and moment resultants of variable thickness FGM toroidal shell segment are defined as

$$\begin{gathered} \left( {N_{i} ,M_{i} ,P_{i} } \right) = \int\limits_{ - h\left( x \right)/2}^{h\left( x \right)/2} {\sigma_{i} \left( {1,z,z^{3} } \right)dz} \,,\left( {i = x;y;xy} \right) \hfill \\ \left( {Q_{j} ,R_{j} } \right) = \int\limits_{ - h\left( x \right)/2}^{h\left( x \right)/2} {\sigma_{jz} \left( {1,z^{2} } \right)dz} ,\,\,\,\left( {j = x;y} \right) \hfill \\ \end{gathered}$$

(8)

Setting Eq. (1), Eq. (5), and Eq. (6) into Eq. (7) and then putting the results into Eq. (8) yields

$$\begin{gathered} \left( {\begin{array}{*{20}c} {N_{x} } & {N_{y} } & {N_{xy} } \\ {M_{x} } & {M_{y} } & {M_{xy} } \\ {P_{x} } & {P_{y} } & {P_{xy} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\Phi_{11} \left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right)} & {\Phi_{12} \left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right)} & {\Phi_{13} \left( {\phi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right)} \\ {\Phi_{21} \left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right)} & {\Phi_{22} \left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right)} & {\Phi_{23} \left( {\phi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right)} \\ {\Phi_{31} \left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right)} & {\Phi_{32} \left( {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right)} & {\Phi_{33} \left( {\phi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right)} \\ \end{array} } \right) \hfill \\ + \left( {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {Q_{13} } \\ {Q_{21} } & {Q_{22} } & {Q_{23} } \\ {Q_{31} } & {Q_{32} } & {Q_{33} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varepsilon_{x}^{0} + \nu \varepsilon_{y}^{0} } & {\varepsilon_{y}^{0} + \nu \varepsilon_{x}^{0} } & {0.5\left( {1 - \nu } \right)\gamma_{xy}^{0} } \\ {k_{x}^{\left( 1 \right)} + \nu k_{y}^{\left( 1 \right)} } & {k_{y}^{\left( 1 \right)} + \nu k_{x}^{\left( 1 \right)} } & {0.5\left( {1 - \nu } \right)k_{xy}^{\left( 1 \right)} } \\ {k_{x}^{\left( 3 \right)} + \nu k_{y}^{\left( 3 \right)} } & {k_{y}^{\left( 3 \right)} + \nu k_{x}^{\left( 3 \right)} } & {0.5\left( {1 - \nu } \right)k_{xy}^{\left( 3 \right)} } \\ \end{array} } \right) \hfill \\ \end{gathered}$$

(9)

$$\left( {\begin{array}{*{20}c} {Q_{x} } & {Q_{y} } \\ {R_{x} } & {R_{y} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {Q_{41} } & {Q_{42} } \\ {Q_{51} } & {Q_{52} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\gamma_{xz}^{0} } & {\gamma_{yz}^{0} } \\ {k_{xz}^{\left( 2 \right)} } & {k_{yz}^{\left( 2 \right)} } \\ \end{array} } \right),$$

(10)

where coefficients $\Phi_{ij} \left( {i = 1 - 3;j = 1 - 3} \right)$, $Q_{ij} \left( {i = 1 - 3;j = 1 - 3} \right),\,Q_{41} ,Q_{42} ,Q_{51} ,Q_{52}$ are determined in Appendix A.

The equations of motion of the toroidal shell segment subjected to uniformly distributed external pressure $q\left( {{\text{N/m}}^{{2}} } \right)$ are given by Reddy and Liu [46]

$$\frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = \overline{{I_{1} }} \ddot{u}_{0} + \overline{{I_{2} }} \ddot{\phi }_{x} - \overline{{I_{3} }} \frac{{\partial \ddot{w}_{0} }}{\partial x}$$

(11)

$$\frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = \overline{{I_{1}^{/} }} \ddot{v}_{0} + \overline{{I_{2}^{/} }} \ddot{\phi }_{y} - \overline{{I_{3}^{/} }} \frac{{\partial \ddot{w}_{0} }}{\partial y}$$

(12)

$$\begin{gathered} \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} - \frac{4}{{\left( {h\left( x \right)} \right)^{2} }}\left( {\frac{{\partial R_{x} }}{\partial x} + \frac{{\partial R_{y} }}{\partial y}} \right) + \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}\left( {\frac{{\partial^{2} P_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} P_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} P_{y} }}{{\partial y^{2} }}} \right) \hfill \\ + \frac{1}{R}N_{y} + \frac{1}{a}N_{x} + N_{x} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + 2N_{xy} \frac{{\partial^{2} w_{0} }}{\partial x\partial y} + N_{y} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + q \hfill \\ = I_{1} \ddot{w}_{0} + \overline{{I_{3} }} \frac{{\partial \ddot{u}_{0} }}{\partial x} + \overline{{I_{5} }} \frac{{\partial \ddot{\phi }_{x} }}{\partial x}\, + \overline{{I_{3}^{/} }} \frac{{\partial \ddot{v}_{0} }}{\partial y} + \overline{{I_{5}^{/} }} \frac{{\partial \ddot{\phi }_{y} }}{\partial y} - \frac{16}{{9\left( {h\left( x \right)} \right)^{4} }}I_{7} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right) \hfill \\ \end{gathered}$$

(13)

$$\frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} + \frac{4}{{\left( {h\left( x \right)} \right)^{2} }}R_{x} - \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}\left( {\frac{{\partial P_{x} }}{\partial x} + \frac{{\partial P_{xy} }}{\partial y}} \right) = \overline{{I_{2} }} \ddot{u}_{0} + \overline{{I_{4} }} \ddot{\phi }_{x} - \overline{{I_{5} }} \frac{{\partial \ddot{w}_{0} }}{\partial x}\,$$

(14)

$$\frac{{\partial M_{y} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x} - Q_{y} + \frac{4}{{\left( {h\left( x \right)} \right)^{2} }}R_{y} - \frac{4}{{3\left( {h\left( x \right)} \right)^{2} }}\left( {\frac{{\partial P_{y} }}{\partial y} + \frac{{\partial P_{xy} }}{\partial x}} \right) = \overline{{I_{2}^{/} }} \ddot{v}_{0} + \overline{{I_{4}^{/} }} \ddot{\phi }_{y} - \overline{{I_{5}^{/} }} \frac{{\partial \ddot{w}_{0} }}{\partial y}$$

(15)

The coefficients $I_{i} ,\widehat{{I_{i} }}\,{\text{and}}\,\widehat{{I_{i}^{/} }}$ are determined in Appendix B. Substituting Eq. (9) and Eq. (10) into Eqs. (11) to (15) with the aid of Eq. (6) yields

$$H_{11} \left( {u_{0} } \right) + H_{12} \left( {v_{0} } \right) + H_{13} \left( {w_{0} } \right) + H_{14} \left( {\phi_{x} } \right) + H_{15} \left( {\phi_{y} } \right) = \overline{{I_{1} }} \ddot{u}_{0} + \overline{{I_{2} }} \ddot{\phi }_{x} - \overline{{I_{3} }} \frac{{\partial \ddot{w}_{0} }}{\partial x}$$

(16)

$$H_{21} \left( {u_{0} } \right) + H_{22} \left( {v_{0} } \right) + H_{23} \left( {w_{0} } \right) + H_{24} \left( {\phi_{x} } \right) + H_{25} \left( {\phi_{y} } \right) = \overline{{I_{1}^{/} }} \ddot{v}_{0} + \overline{{I_{2}^{/} }} \ddot{\phi }_{y} - \overline{{I_{3}^{/} }} \frac{{\partial \ddot{w}_{0} }}{\partial y}$$

(17)

$$\begin{gathered} H_{31} \left( {u_{0} } \right) + H_{32} \left( {v_{0} } \right) + H_{33} \left( {w_{0} } \right) + H_{34} \left( {\phi_{x} } \right) + H_{35} \left( {\phi_{y} } \right) + H_{36} \left( {u_{0} ,w_{0} } \right) \hfill \\ + H_{37} \left( {v_{0} ,w_{0} } \right) + H_{38} \left( {\phi_{x} ,w_{0} } \right) + H_{39} \left( {\phi_{y} ,w_{0} } \right) + q = I_{1} \ddot{w}_{0} + \overline{{I_{3} }} \frac{{\partial \ddot{u}_{0} }}{\partial x}\, \hfill \\ + \overline{{I_{3}^{/} }} \frac{{\partial \ddot{v}_{0} }}{\partial y} + \overline{{I_{5} }} \frac{{\partial \ddot{\phi }_{x} }}{\partial x} + \overline{{I_{5}^{/} }} \frac{{\partial \ddot{\phi }_{y} }}{\partial y} - \frac{16}{{9\left( {h\left( x \right)} \right)^{4} }}I_{7} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right) \hfill \\ \end{gathered}$$

(18)

$$H_{41} \left( {u_{0} } \right) + H_{42} \left( {v_{0} } \right) + H_{43} \left( {w_{0} } \right) + H_{44} \left( {\phi_{x} } \right) + H_{45} \left( {\phi_{y} } \right) = \overline{{I_{2} }} \ddot{u}_{0} + \overline{{I_{4} }} \ddot{\phi }_{x} - \overline{{I_{5} }} \frac{{\partial \ddot{w}_{0} }}{\partial x}\,\,$$

(19)

$$H_{51} \left( {u_{0} } \right) + H_{52} \left( {v_{0} } \right) + H_{53} \left( {w_{0} } \right) + H_{54} \left( {\phi_{x} } \right) + H_{55} \left( {\phi_{y} } \right) = \overline{{I_{2}^{/} }} \ddot{v}_{0} + \overline{{I_{4}^{/} }} \ddot{\phi }_{y} - \overline{{I_{5}^{/} }} \frac{{\partial \ddot{w}_{0} }}{\partial y}$$

(20)

in which operators $H_{1i} ,H_{2i} ,H_{4i} ,H_{5i} \left( {i = 1 - 5} \right)$; $H_{3i} \left( {i = 1 - 9} \right)$ are defined in Appendix C.

Equations (16) to (20) are five governing equations in terms of five variables $u_{0} \left( {x,y,t} \right)$, $v_{0} \left( {x,y,t} \right)$, $w_{0} \left( {x,y,t} \right)$, $\phi_{x} \left( {x,y,t} \right)$, and $\phi_{y} \left( {x,y,t} \right)$. They are used to study the nonlinear vibration of variable thickness FGM toroidal shell segments based on Reddy’s third-order shear deformation shell theory.

3 Galerkin procedure

In this study, variable thickness FGM toroidal shell segments are assumed to be simply supported at two butt-ends and subjected to external harmonic excitation. Thus, the associated boundary condition is

$$w_{0} = 0,\,\,v_{0} = 0,\phi_{y} = 0,M_{x} = 0,\,\,P_{x} = 0,N_{xy} = 0\,,\,N_{x} = 0\,\,{\text{at}}\,\,x = 0\,\,{\text{and}}\,\,x = L$$

(21)

The approximate solutions are chosen as

$$\begin{gathered} u_{0} \left( {x,y,t} \right) = U\left( t \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R} \hfill \\ v_{0} \left( {x,y,t} \right) = V\left( t \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R} \hfill \\ w_{0} \left( {x,y,t} \right) = W\left( t \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R} \hfill \\ \phi_{x} \left( {x,y,t} \right) = \Phi_{x} \left( t \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R} \hfill \\ \phi_{y} \left( {x,y,t} \right) = \Phi_{y} \left( t \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R} \hfill \\ \end{gathered}$$

(22)

where $U\left( t \right),V\left( t \right),W\left( t \right),\Phi_{x} \left( t \right),\Phi_{y} \left( t \right)$ are unknown time-dependent functions, $m$ and $n$ are the numbers of half-waves in $x$ and $y$ directions, respectively. The boundary conditions $w_{0} = 0,\,\,v_{0} = 0$, and $\phi_{y} = 0$ are satisfied at $x = 0$ and $x = L$. The boundary conditions $M_{x} = 0,\,\,P_{x} = 0,N_{xy} = 0\,,\,N_{x} = 0\,\,{\text{at}}\,\,x = 0\,\,{\text{and}}\,\,x = L$ are satisfied in average sense $\frac{1}{2\pi R}\int\nolimits_{0}^{2\pi R} {M_{x} } dy = 0,\,\frac{1}{2\pi R}\int\nolimits_{0}^{2\pi R} {P_{x} } dy = 0,\frac{1}{2\pi R}\int\nolimits_{0}^{2\pi R} {N_{x} } dy = 0$, and $\frac{1}{2\pi R}\int\nolimits_{0}^{2\pi R} {N_{xy} } dy = 0$ at $x = 0$ and $x = L$.

Substituting Eq. (22) into Eqs. (16) to (20) then applying the Galerkin method leads to

$$l_{11} U + l_{12} V + l_{13} W + l_{14} \Phi_{x} + l_{15} \Phi_{y} + l_{16} W^{2} = l_{17} \ddot{U} + l_{18} \ddot{\Phi }_{x} + l_{19} \ddot{W}$$

(23)

$$l_{21} U + l_{22} V + l_{23} W + l_{24} \Phi_{x} + l_{25} \Phi_{y} + l_{26} W^{2} = l_{27} \ddot{V} + l_{28} \ddot{\Phi }_{y} + l_{29} \ddot{W}$$

(24)

$$\begin{gathered} l_{31} U + l_{32} V + l_{33} W + l_{34} \Phi_{x} + l_{35} \Phi_{y} + l_{36} W^{2} + l_{37} UW + l_{38} VW + l_{39} \Phi_{x} W + l_{310} \Phi_{y} W \hfill \\ + l_{311} W^{3} + l_{312} q = l_{313} \ddot{U} + l_{314} \ddot{V} + l_{315} \ddot{\Phi }_{x} \, + l_{316} \ddot{\Phi }_{y} + l_{317} \ddot{W} \hfill \\ \end{gathered}$$

(25)

$$l_{41} U + l_{42} V + l_{43} W + l_{44} \Phi_{x} + l_{45} \Phi_{y} + l_{46} W^{2} = l_{47} \ddot{U} + l_{48} \ddot{\Phi }_{x} + l_{49} \ddot{W}$$

(26)

$$l_{51} U + l_{52} V + l_{53} W + l_{54} \Phi_{x} + l_{55} \Phi_{y} + l_{56} W^{2} = l_{57} \ddot{V} + l_{58} \ddot{\Phi }_{y} + l_{59} \ddot{W},$$

(27)

where coefficients $l_{1i} ,l_{2i} ,l_{4i} ,l_{5i} \left( {i = 1 - 9} \right)$; $l_{3i} \left( {i = 1 - 17} \right)$ are demonstrated in Appendix D.

On the whole, transverse nonlinear vibration is a primary motion for the FGM variable thickness toroidal shell segments, thereby, we can suppose that the four right sides of the four Eqs. (23), (24), (26) and (27) to be equal to zero. With this assumption, the system of five Eqs. (23)–(27) can be converted into the following equation:

$$\left( {1 + D_{1} W} \right)\ddot{W} + D_{2} W + D_{3} W^{2} + D_{4} W^{3} + D_{5} q = 0,$$

(28)

where coefficients $D_{i} \left( {i = 1 - 6} \right)$ are determined in Appendix E.

3.1 Natural frequency

The natural frequencies of FGM variable thickness toroidal shell segments with subscripts $m$ and $n$ are the mode shapes in the x and y directions, respectively, can be determined from Eq. (28) as

$$\omega_{mn} = \sqrt {D_{2} } .$$

(29)

3.2 Nonlinear forced vibrations

Consider FGM variable thickness toroidal shell segments subjected to external harmonic excitation $q = Q\sin \Omega t$. $Q$ and $\Omega$ are assumed to be time independent. Substituting $q = Q\sin \Omega t$ into Eq. (28) and using the Runge–Kutta method, the nonlinear forced vibration of variable thickness FGM toroidal shell segments is calculated and analyzed.

4 Numerical analysis

4.1 Comparisons

This part shows three comparisons to verify the accuracy of the present approach. Firstly, consider an isotropic cylindrical shell with linear asymmetric variation thickness along the axial direction. Material parameters are taken as Sivadas and Ganesan [13] $E = 2.035 \times 10^{11} {\text{Pa,}}$ $\,\nu = 0.285,$ $\rho = 7846\,\,{\text{kg/m}}^{{3}}$. The average thickness, equator radius, and length of the shell is chosen as Sivadas and Ganesan [13] $h_{av} = 0.508\,{\text{mm,}}$$R = 100h_{av} ,$ $L = 0.5R$, respectively. The thickness of the shell linearly varies from the value $h_{\min }$ to the value $h_{\max }$. Thereby, the thickness is defined as $h\left( x \right) = \frac{{2h_{av} }}{1 + \beta }\left( {\beta - \frac{\beta - 1}{L}x} \right)$, in which $\beta = \frac{{h_{\max } }}{{h_{\min } }}$. Using Eq. (29) ($a \to \infty$), the lowest natural frequencies (minimize the function $\frac{{\omega_{mn} }}{2\pi }$ with respect to $m$ and $n$) are calculated and shown in Table 1 in comparison with the results given by Sivadas and Ganesan [13] using Love’s first approximation shell theory and semi-analytical finite element approach. As can be seen, a good agreement is obtained in this comparison.

Table 1 Comparison of lowest natural frequencies for material isotropic, linear symmetric variation cylindrical shell

Secondly, consider an FGM cylindrical shell with linear asymmetric variation thickness along the axial direction. The material parameters are chosen as Phu et al. [34] $E_{m} = 70\,{\text{GPa}}$, $\rho_{m} = 2702\,{\text{kg/m}}^{{3}}$, $E_{c} = 380\,{\text{GPa}}$, $\rho_{c} = 3800\,{\text{kg/m}}^{{3}}$, $\nu_{m} = \nu_{c} = 0.3$. The thickness of FGM shell varies linearly along the axial direction from a value $h_{\min } = 0.004\,{\text{m}}$ to a value $h_{\max } = 0.006\,{\text{m}}$. The radius and length of shell are chosen as $R = 200h_{\min }$, $L = 2R$. The natural frequencies are calculated and compared with the results reported by Phu et al. [34] in Table 2 using classical thin shell theory and Galerikin method. Again, a good agreement is obtained.

Table 2 Comparison of natural frequencies for variable thickness FGM cylindrical shell

Thirdly, an FGM toroidal shell segment is considered with material and geometrical parameters as Ninh and Bich [42]: $E_{m} = 70 \times 10^{9} {\text{Pa,}}$$\rho_{m} = 2702\,\,{\text{kg/m}}^{{3}} ,$$E_{c} = 380 \times 10^{9} {\text{Pa,}}$$\rho_{c} = 3800\,\,{\text{kg/m}}^{{3}} ,$$\,\nu_{m} = \nu_{c} = 0.3,$$h = 0.01\,{\text{m,}}$$a{/}R = 10,$$L{/}R = 0.5$, $k = 5$. The external harmonic excitation is choosen as $q = 1000\sin 6000t\,\,{\text{Pa}}$. The lowest natural frequencies are calculated by minimizing the function $\frac{{\omega_{mn} }}{2\pi }$ with respect to $m$ and $n$ of the present study and compared with those calculated by Eq. (21) of Ninh and Bich [42]. The results are listed in Table 3. The vibration response is compared on Fig. 2. Obviously, a good agreement is obtained in this comparison. Moreover, the lowest natural frequencies of FGM toroidal shell segment calculated in the present study using the Reddy’s third-order shear deformation shell theory ($f^{TSDT}$) are smaller than corresponding values calculated by Eq. (21) of Ninh and Bich [42] using the classical thin shell theory ($f^{CST}$). The error $\left( {\frac{{f^{CST} - f^{TSDT} }}{{f^{CST} }}.100\% } \right)$ decreases as the $R{/}h$ ratio increases. The information in Fig. 2 reveals that the difference between two amplitudes is $\frac{4.0273e - 8 - 3.837e - 8}{{4.0273e - 8}} \simeq 4.7\%$.

Table 3 Comparison of the lowest natural frequencies for FGM toroidal shell segment

Fig. 2

Comparison of forced vibration response of FGM toroidal shell segment

4.2 Nonlinear vibration analysis of FGM variable thickness toroidal shell segments

This section considers FGM variable thickness toroidal shell segments with the material properties are as $E_{m} = 105.6960\,\,{\text{GPa}}$, $E_{c} = 154.3211\,\,{\text{GPa}}$, $\nu = 0.2980$, $\rho_{m} = 4429\,\,{\text{kg/m}}^{{3}}$,$\rho_{c} = 5700\,\,{\text{kg/m}}^{{3}}$. The thickness of the shell is assumed to be linearly varied along the axial direction from the value $h_{\min }$ to the value $h_{\max }$, and defined as $h\left( x \right) = \frac{{2h_{av} }}{1 + \beta }\left( {\beta - \frac{\beta - 1}{L}x} \right)$, in which $h_{av}$ is average thickness, and $\beta = \frac{{h_{\max } }}{{h_{\min } }}$ is variation parameter. Using the Runge–Kutta method to solve Eq. (28), the effects of variation parameter, volume fraction index, and geometrical parameters on natural frequencies and nonlinear vibration response are investigated.

4.2.1 Natural frequencies

Effect of variation parameter $\beta$ on natural frequencies of FGM variable thickness toroidal shell segments is illustrated in Table 4. Parameters are chosen as $h_{av} = 0.02\,\,{\text{m}}$, $R{/}h_{av} = 100$, $L{/}R = 1$, $a{/}R = 10$, $k = 2$. It can be seen that with the same mode numbers, the shell with a constant thickness corresponding to $\beta = \frac{{h_{\max } }}{{h_{\min } }} = 1$ has the lowest frequency in comparison with variable thickness shells. In addition, the natural frequency slightly increases as the variation parameter increases. For example, as variation parameter increases from value $\beta = 1$ to the value $\beta = 5$, the natural frequency increases by 1.4%, 2.8%, 4.7%, 6.5%, 7.9%, and 8.7% corresponding to mode numbers $\left( {m,n} \right) = \left( {1,5} \right)$, (1,6), (1,7), (1,8), (1,9), and (1,10), respectively.

Table 4 Natural frequencies of FGM toroidal shell segment with different variation parameter ($h_{av} = 0.02\,\,{\text{m}}$, $R{/}h_{av} = 100$, $L{/}R = 1$, $a{/}R = 10$, $k = 2$)

Effects of the volume fraction index and $L{/}R$ ratio on natural frequencies of FGM variable thickness toroidal shell segments are shown in Table 5. Parameters are taken as $h_{av} = 0.02\,\,{\text{m}}$, $R = 100h_{av}$, $a = 10R$, $\beta = 2$, $k = 1$, $\left( {m,n} \right) = \left( {1,1} \right)$. It can be seen that for all cases of $L{/}R$ ratio, there is a decreasing trend of natural frequencies as the volume fraction index $k$ increases. This can be explained by the fact that as the volume fraction index $k$ increases, the percentage of ceramic in FGM decreases, and the shell will be softer, leading to the decrease of natural frequency. Numerical values in Table 5 also show that there is also a decreasing trend of natural frequencies as the $L{/}R$ ratio increases. For example, as the $L{/}R$ ratio increases from 0.5 to 1, the natural frequency decreases by 8.85%, 8.86%, and 8.87% corresponding to $k = 0$, $k = 0.1$, and $k = 0.2,$ respectively.

Table 5 Natural frequencies of FGM toroidal shell segment with different volume fraction index and different $L{/}R$ ratio ($h_{av} = 0.02\,\,{\text{m}}$, $R = 100h_{av}$, $a = 10R$, $\beta = 2$, $\left( {m,n} \right) = \left( {1,1} \right)$)

Table 6 depicts how the values of $a{/}L$ and $R{/}h_{av}$ ratios affect the natural frequency of FGM variable thickness toroidal shell segment. It is seen from the table that for all cases of convex shells and concave shells, there is a decreasing trend of natural frequencies as the $R{/}h_{av}$ ratio increases. For example, in the case of convex shells and $a{/}L = 5$, as the $R{/}h_{av}$ ratio increases from 50 to 100, 150, 200, and 500 the natural frequency of the shell decreases by 1.33%, 1.59%, 1.68%, and 1.78%, respectively. In the case of concave shells and $a{/}L = - 5$, the natural frequency of the shell decreases by 2.66%, 3.16%, 3.34%, and 3.53%, respectively, as the $R{/}h_{av}$ ratio increases from 50 to 100, 150, 200, and 500. The result in Table 6 also shows that in the case of convex shells, as the $a{/}L$ ratio increases the natural frequency of FGM variable thickness toroidal shell segments decreases. However, there is a trend in the opposite direction for the case of the concave shell. The natural frequency of the concave shell decreases as the $a{/}L$ ratio decreases. For example, in the case of convex shells and $R{/}h_{av} = 50$, the natural frequency decreases by 7.6%, 10.14%, 11.41%, and 15.22%, respectively, as the $a{/}L$ ratio increases from 5 to 10, 15, 20, and $\infty$. In the case of concave shells and $R{/}h_{av} = 50$, as the $a{/}L$ ratio increases from − 5 to − 10, − 15, and − 20 the natural frequency increases by 10.85%, 14.48%, and 16.3%, respectively. In addition, the natural frequencies of convex shells are greater than the ones of concave shells.

Table 6 Natural frequencies of convex and concave shells with different $a{/}L$ and $L{/}R$ ratios ($R = 2\,{\text{m}}$, $L = 2\,{\text{m}}$, $\beta = 2$, $k = 1$, $\left( {m,n} \right) = \left( {1,3} \right)$)

4.2.2 Nonlinear vibration responses

Figures 3, 4 and 5 depict the nonlinear vibration responses of FGM variable thickness toroidal shell segments corresponding to mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$, $\left( {m,n} \right) = \left( {1,3} \right)$, and $\left( {m,n} \right) = \left( {3,3} \right)$, respectively. In each figure, four cases of $L{/}R$ ratio ($L{/}R = 0.5,1,1.5\,{\text{and}}\,\,2$) are considered. Other parameters are indicated in the figures. It can be seen from these figures that for all cases of mode numbers $\left( {m,n} \right)$, the vibration amplitude of FGM variable thickness toroidal shell segment increases as the $L{/}R$ ratio increases. This indicates that a longer shell has greater vibration amplitude than that of a shorter one.

Fig. 3

The effect of $L{/}R$ ratio on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$

Fig. 4

The effect of $L{/}R$ ratio on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {1,3} \right)$

Fig. 5

The effect of $L{/}R$ ratio on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {3,3} \right)$

The effect of $R{/}h_{av}$ ratio on vibration response of FGM variable thickness toroidal shell segment is illustrated in Figs. 6, 7 and 8 corresponding to mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$, $\left( {m,n} \right) = \left( {1,3} \right)$, and $\left( {m,n} \right) = \left( {3,3} \right)$, respectively. Each figure draws four curves of vibration response corresponding to $R{/}h_{av} = 50$, $R{/}h_{av} = 100$, $R{/}h_{av} = 150$, and $R{/}h_{av} = 200$. Other parameters are indicated in each figure. The result in these figures shows that the vibration amplitude of FGM variable thickness toroidal shell segments decreases significantly as the $R{/}h_{av}$ ratio decreases for all three cases of mode numbers. It means that the vibration response of FGM variable thickness toroidal shell segment is very sensitive to the change of the $R{/}h_{av}$ ratio.

Fig. 6

The effect of $R{/}h_{av}$ ratio on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$

Fig. 7

The effect of $R{/}h_{av}$ ratio on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {1,3} \right)$

Fig. 8

The effect of $R{/}h_{av}$ ratio on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {3,3} \right)$

The volume fraction index $k$ is a parameter that defines the contribution of material constituents in FGM. It can be seen from Eq. (1) that as the volume fraction index $k$ increase, the volume fraction of ceramic constituent decreases, and the volume fraction of metal constituent increases in FGM. Therefore, the volume fraction index $k$ affects effective Young modulus and effective mass density of FGM, leading to the effect on vibration response of FGM variable thickness toroidal shell segment. This effect is illustrated in Figs. 9, 10, 11 and 12 corresponding to mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$, $\left( {m,n} \right) = \left( {1,3} \right)$, $\left( {m,n} \right) = \left( {3,1} \right)$, and $\left( {m,n} \right) = \left( {3,3} \right)$, respectively. In each figure, three cases ($k = 0.1$, $k = 1$, and $k = 10$) are considered. It can be seen that the metal-rich shell ($k = 10$) has a larger vibration amplitude in comparison with that of the other cases.

Fig. 9

The effect of volume fraction index on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {1,1} \right)$

Fig. 10

The effect of volume fraction index on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {1,3} \right)$

Fig. 11

The effect of volume fraction index on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {3,1} \right)$

Fig. 12

The effect of volume fraction index on nonlinear vibration responses of FGM variable thickness toroidal shell segments with mode numbers $\left( {m,n} \right) = \left( {3,3} \right)$

5 Conclusions

An analytical investigation of the vibration of the FGM variable thickness toroidal shell segment is presented in this study. Firstly, based on Reddy’s third-order shear deformation shell theory, the governing partial differential equations of motion of FGM variable thickness toroidal shell segment are obtained. Secondly, the Galerkin method is used to convert the system of partial differential equations into nonlinear differential equations. Lastly, the Runge–Kutta method is used to solve the nonlinear differential equation of motion, and then the vibration response is studied. The effects of geometric, material, and variation parameters on natural frequency and vibration response are analyzed and discussed. It is revealed that shell with a constant thickness has the lowest frequency in comparison with variable thickness shells. The natural frequency increases as the volume fraction index decreases. Geometrical parameters have significant effect on natural frequency and vibration response of variable thickness toroidal shell segment.

Appendices

Appendix A

$$\begin{gathered} \Phi_{11} = \frac{{8E_{4} }}{{3\left( {1 - \nu^{2} } \right)}}h\left( x \right)h{\prime} \left( x \right),\,\Phi_{12} = \frac{{8\nu E_{4} }}{{3\left( {1 - \nu^{2} } \right)}}h\left( x \right)h{\prime} \left( x \right),\,\Phi_{13} = \frac{{4E_{4} }}{{3\left( {1 + \nu } \right)}}h\left( x \right)h{\prime} \left( x \right) \hfill \\ \Phi_{21} = \frac{{8E_{5} }}{{3\left( {1 - \nu^{2} } \right)}}\left( {h\left( x \right)} \right)^{2} h{\prime} \left( x \right),\,\Phi_{22} = \frac{{8\nu E_{5} }}{{3\left( {1 - \nu^{2} } \right)}}\left( {h\left( x \right)} \right)^{2} h{\prime} \left( x \right),\,\Phi_{23} = \frac{{4E_{5} }}{{3\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{2} h{\prime} \left( x \right) \hfill \\ \Phi_{31} = \frac{{8E_{7} }}{{3\left( {1 - \nu^{2} } \right)}}\left( {h\left( x \right)} \right)^{4} h{\prime} \left( x \right),\,\Phi_{32} = \frac{{8\nu E_{7} }}{{3\left( {1 - \nu^{2} } \right)}}\left( {h\left( x \right)} \right)^{4} h{\prime} \left( x \right), \hfill \\ \,\Phi_{33} = \frac{{4E_{7} }}{{3\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{4} h{\prime} \left( x \right),\,Q_{11} = \frac{{E_{1} }}{{1 - \nu^{2} }}h\left( x \right),\,Q_{12} = \frac{{E_{2} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} ,\,Q_{13} = \frac{{E_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} ,\, \hfill \\ Q_{21} = \frac{{E_{2} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} ,\,Q_{22} = \frac{{E_{3} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{3} ,\,Q_{23} = \frac{{E_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} ,\,Q_{31} = \frac{{E_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} ,\, \hfill \\ Q_{32} = \frac{{E_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} Q_{33} = \frac{{E_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{7} ,\,Q_{41} = \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}h\left( x \right),\,Q_{42} = \frac{{E_{3} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} ,\, \hfill \\ Q_{51} = \frac{{E_{3} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} ,\,Q_{52} = \frac{{E_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{5} , \hfill \\ \end{gathered}$$

with

$$E_{1} = E_{m} + \frac{{E_{cm} }}{k + 1},\,E_{2} = \frac{{E_{cm} k}}{{2\left( {k + 1} \right)\left( {k + 2} \right)}},\,E_{3} = \frac{{E_{m} }}{12} + E_{cm} \left[ {\frac{1}{k + 3} - \frac{1}{k + 2} + \frac{1}{{4\left( {k + 1} \right)}}} \right],$$

$$E_{4} = E_{cm} \left[ {\frac{1}{k + 4} - \frac{3}{{2\left( {k + 3} \right)}} + \frac{3}{{4\left( {k + 2} \right)}} - \frac{1}{{8\left( {k + 1} \right)}}} \right],$$

$$E_{5} = \frac{{E_{m} }}{80} + E_{cm} \left[ {\frac{1}{k + 5} - \frac{2}{k + 4} + \frac{3}{{2\left( {k + 3} \right)}} - \frac{1}{{2\left( {k + 2} \right)}} + \frac{1}{{16\left( {k + 1} \right)}}} \right],$$

$$E_{7} = \frac{{E_{m} }}{448} + E_{cm} \left[ \begin{gathered} \frac{1}{k + 7} - \frac{3}{k + 6} + \frac{15}{{4\left( {k + 5} \right)}} - \frac{5}{{2\left( {k + 4} \right)}} \hfill \\ + \frac{15}{{16\left( {k + 3} \right)}} - \frac{3}{{16\left( {k + 2} \right)}} + \frac{1}{{64\left( {k + 1} \right)}} \hfill \\ \end{gathered} \right].$$

Appendix B

$\overline{{I_{1} }} = I_{1} h\left( x \right) + \frac{{2I_{2} }}{a}\left( {h\left( x \right)} \right)^{2} ,$$\overline{{I_{1}^{/} }} = I_{1} h\left( x \right) + \frac{{2I_{2} }}{R}\left( {h\left( x \right)} \right)^{2} ,$$\overline{{I_{2} }} = \left( {I_{2} - \frac{4}{3}I_{4} } \right)\left( {h\left( x \right)} \right)^{2}$$+ \left( {I_{3} - \frac{4}{3}I_{5} } \right)\frac{{\left( {h\left( x \right)} \right)^{3} }}{a}$, $\overline{{I_{2}^{/} }} = \left( {I_{2} - \frac{4}{3}I_{4} } \right)\left( {h\left( x \right)} \right)^{2} + \left( {I_{3} - \frac{4}{3}I_{5} } \right)\frac{{\left( {h\left( x \right)} \right)^{3} }}{R}$, $\overline{{I_{3} }} = \frac{{4I_{4} }}{3}\left( {h\left( x \right)} \right)^{2}$$+ \frac{{4I_{5} }}{3a}\left( {h\left( x \right)} \right)^{3} ,$$\overline{{I_{3}^{/} }} = \frac{{4I_{4} }}{3}\left( {h\left( x \right)} \right)^{2} + \frac{{4I_{5} }}{3R}\left( {h\left( x \right)} \right)^{3} ,$$\overline{{I_{4} }} = \overline{{I_{4}^{/} }} = \left( {I_{3} - \frac{{8I_{5} }}{3} + \frac{16}{9}I_{7} } \right)\left( {h\left( x \right)} \right)^{3} ,$$\overline{{I_{5} }} = \overline{{I_{5}^{/} }} = \left( {\frac{{4I_{5} }}{3} - \frac{16}{9}I_{7} } \right)\left( {h\left( x \right)} \right)^{3} ,$$I_{i} = \frac{1}{{h^{i} \left( x \right)}}.\int\limits_{ - h\left( x \right)/2}^{h\left( x \right)/2} {\rho \left( z \right)z^{i - 1} dz} ,\,\left( {i = 1,2,3,4,5,7} \right).$

Appendix C

$$H_{11} \left( {u_{0} } \right) = \frac{{E_{1} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {h\left( x \right)\frac{{\partial u_{0} }}{\partial x}} \right]}}{\partial x} + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}h\left( x \right)\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}.$$

$$H_{12} \left( {v_{0} } \right) = \frac{{E_{1} \nu }}{{1 - \nu^{2} }}\frac{{\partial \left[ {h\left( x \right)\frac{{\partial v_{0} }}{\partial y}} \right]}}{\partial x} + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}h\left( x \right)\frac{{\partial^{2} v_{0} }}{\partial x\partial y}.$$

$$H_{13} \left( {w_{0} } \right) = H_{13a} \left( {w_{0} } \right) + H_{13b} \left( {w_{0} } \right).$$

$$\begin{aligned} H_{13a} \left( {w_{0} } \right) = & \frac{{ - E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial \left[ {h\left( x \right)w_{0} } \right]}}{\partial x} + \frac{{2cE_{4} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial x}} \right]}}{\partial x} \\ & - \frac{{cE_{4} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right)} \right]}}{\partial x} + \frac{{cE_{4} }}{1 + \nu }h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} - \frac{{cE_{4} }}{1 + \nu }\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }}. \\ \end{aligned}$$

$$H_{13b} \left( {w_{0} } \right) = \frac{{E_{1} }}{{2\left( {1 - \nu^{2} } \right)}}\frac{{\partial \left[ {h\left( x \right)\left( {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right)} \right]}}{\partial x} + \frac{{E_{1} h\left( x \right)}}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left( {\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right)}}{\partial y}.$$

$$H_{14} \left( {\phi_{x} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{x} }}{\partial x}} \right]}}{\partial x} + \frac{{2cE_{4} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\phi_{x} } \right]}}{\partial x} + \frac{{E_{2} - cE_{4} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }}.$$

$$H_{15} \left( {\phi_{y} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\nu \frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{y} }}{\partial y}} \right]}}{\partial x} + \frac{{E_{2} - cE_{4} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} \phi_{y} }}{\partial x\partial y} + \frac{{cE_{4} }}{1 + \nu }h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial \phi_{y} }}{\partial y},$$

$$H_{21} \left( {u_{0} } \right) = \frac{{E_{1} \nu }}{{1 - \nu^{2} }}h\left( x \right)\frac{{\partial^{2} u_{0} }}{\partial x\partial y} + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {h\left( x \right)\frac{{\partial u_{0} }}{\partial y}} \right]}}{\partial x}.$$

$$H_{22} \left( {v_{0} } \right) = \frac{{E_{1} }}{{1 - \nu^{2} }}h\left( x \right)\frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {h\left( x \right)\frac{{\partial v_{0} }}{\partial x}} \right]}}{\partial x}.$$

$$H_{23} \left( {w_{0} } \right) = H_{23a} \left( {w_{0} } \right) + H_{23b} \left( {w_{0} } \right).$$

$$\begin{aligned} H_{23a} \left( {w_{0} } \right) = & - \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)h\left( x \right)\frac{{\partial w_{0} }}{\partial y} - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} + \nu \frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & - \frac{{cE_{4} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right]}}{\partial x} + \frac{{2cE_{4} \nu }}{{1 - \nu^{2} }}h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{\partial x\partial y} + \frac{{cE_{4} }}{1 + \nu }\frac{{\partial \left[ {h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial y}} \right]}}{\partial x}. \\ \end{aligned}$$

$$H_{23b} \left( {w_{0} } \right) = \frac{{E_{1} }}{{1 - \nu^{2} }}h\left( x \right)\left( {\frac{{\partial w_{0} }}{\partial y}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \nu \frac{{\partial w_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right) + \frac{{E_{1} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {h\left( x \right)\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right]}}{\partial x}.$$

$$H_{24} \left( {\phi_{x} } \right) = \frac{{\left( {E_{2} - cE_{4} } \right)\nu }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} \phi_{x} }}{\partial x\partial y} + \frac{{E_{2} - cE_{4} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{x} }}{\partial y}} \right]}}{\partial x} + \frac{{2cE_{4} \nu }}{{1 - \nu^{2} }}h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial \phi_{x} }}{\partial y}.$$

$$H_{25} \left( {\phi_{y} } \right) = \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} + \frac{{E_{2} - cE_{4} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{y} }}{\partial x}} \right]}}{\partial x} + \frac{{cE_{4} }}{1 + \nu }\frac{{\partial \left[ {h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\phi_{y} } \right]}}{\partial x}.$$

$$\begin{aligned} H_{31} \left( {u_{0} } \right) = & \frac{{E_{1} h\left( x \right)}}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial u_{0} }}{\partial x} + \frac{{cE_{4} }}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial u_{0} }}{\partial x}} \right]}}{{\partial x^{2} }} + \frac{{cE_{4} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}} \right]}}{\partial x} \\ & + \frac{{cE_{4} \nu }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{3} u_{0} }}{{\partial x\partial y^{2} }}. \\ \end{aligned}$$

$$\begin{aligned} H_{32} \left( {v_{0} } \right) = & \frac{{E_{1} h\left( x \right)}}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial v_{0} }}{\partial y} + \frac{{cE_{4} \nu }}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial v_{0} }}{\partial y}} \right]}}{{\partial x^{2} }} + \frac{{cE_{4} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} v_{0} }}{\partial x\partial y}} \right]}}{\partial x} \\ & + \frac{{cE_{4} \nu }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }}. \\ \end{aligned}$$

$H_{33} \left( {w_{0} } \right) = H_{33a} \left( {w_{0} } \right) + H_{33b} \left( {w_{0} } \right) + H_{33c} \left( {w_{0} } \right).$

$$\begin{aligned} H_{33a} \left( {w_{0} } \right) = & \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}\left\{ {\frac{{\partial \left[ {h\left( x \right)\frac{{\partial w_{0} }}{\partial x}} \right]}}{\partial x} + h\left( x \right)\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right\} \\ & - 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\left\{ {\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \frac{{\partial w_{0} }}{\partial x}} \right]}}{\partial x} + \left( {h\left( x \right)} \right)^{3} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right\} - \frac{{E_{1} }}{{1 - \nu^{2} }}\left( {\frac{1}{{R^{2} }} + \frac{2\nu }{{Ra}} + \frac{1}{{a^{2} }}} \right)h\left( x \right)w_{0} \\ & - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \left[ {\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right] - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{4} w_{0} } \right]}}{{\partial x^{2} }} \\ & - \frac{{c^{2} E_{7} }}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{5} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right)} \right]}}{{\partial x^{2} }} - \frac{{c^{2} E_{7} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }}} \right]}}{\partial x} \\ & - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} - \frac{{c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} \left( {\frac{{\partial^{4} w_{0} }}{{\partial y^{4} }} + \nu \frac{{\partial^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }}} \right) \\ & + \frac{{2c^{2} E_{7} }}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial x}} \right]}}{{\partial x^{2} }} + \frac{{2c^{2} \nu E_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} \\ & + \frac{{2c^{2} E_{7} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right]}}{\partial x}. \\ \end{aligned}$$

$$\begin{aligned} H_{33b} \left( {w_{0} } \right) = & \frac{{E_{1} h\left( x \right)}}{{2\left( {1 - \nu^{2} } \right)}}\left[ {\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right] \\ & + \frac{{cE_{4} }}{{2\left( {1 - \nu^{2} } \right)}}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{4} \left( {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right)} \right]}}{{\partial x^{2} }} \\ & + \frac{{cE_{4} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \left( {\frac{{\partial w_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right)} \right]}}{\partial x} + \frac{{cE_{4} }}{{2\left( {1 - \nu^{2} } \right)}}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} \left( {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right)}}{{\partial y^{2} }} \\ & - \frac{{E_{1} h\left( x \right)w_{0} }}{{1 - \nu^{2} }}\left[ {\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \left( {\frac{1}{R} + \frac{\nu }{a}} \right)\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right] \\ & - \frac{{cE_{4} \left( {h\left( x \right)} \right)^{2} }}{{1 - \nu^{2} }}\left( {\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)^{2} + 2\nu \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right)^{2} } \right) + \frac{{2cE_{4} }}{1 + \nu }\left( {h\left( x \right)} \right)^{2} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x\partial y^{2} }}} \right)^{2} \\ & + \frac{{2cE_{4} }}{{1 - \nu^{2} }}h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial x}\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) + \frac{{2cE_{4} }}{1 + \nu }h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{33c} \left( {w_{0} } \right) = & \frac{{E_{1} h\left( x \right)}}{{2\left( {1 - \nu^{2} } \right)}}\left[ {\left( {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \left( {\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right] \\ & + \frac{{E_{1} h\left( x \right)}}{1 + \nu }\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{34} \left( {\phi_{x} } \right) = & \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{x} }}{\partial x} + \frac{{c\left( {E_{5} - cE_{7} } \right)}}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial \phi_{x} }}{\partial x}} \right]}}{{\partial x^{2} }} \\ & \frac{{c\left( {E_{5} - cE_{7} } \right)}}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }}} \right]}}{\partial x} + \frac{{c\nu \left( {E_{5} - cE_{7} } \right)}}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} + \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {h\left( x \right)\phi_{x} } \right]}}{\partial x} \\ & - 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \phi_{x} } \right]}}{\partial x} + \frac{{2c\nu E_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{1}{R}} \right)h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\phi_{x} \\ & + \frac{{2c^{2} E_{7} }}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\phi_{x} } \right]}}{{\partial x^{2} }} + \frac{{2c^{2} \nu E_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }}. \\ \end{aligned}$$

$$\begin{aligned} H_{35} \left( {\phi_{y} } \right) = & \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{y} }}{\partial y} + \frac{{c\nu \left( {E_{5} - cE_{7} } \right)}}{{1 - \nu^{2} }}\frac{{\partial^{2} \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial \phi_{y} }}{\partial y}} \right]}}{{\partial x^{2} }} \\ & \frac{{c\left( {E_{5} - cE_{7} } \right)}}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{2} \phi_{y} }}{\partial x\partial y}} \right]}}{\partial x} + \frac{{c\nu \left( {E_{5} - cE_{7} } \right)}}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{3} \phi_{y} }}{{\partial y^{3} }} + \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}h\left( x \right)\frac{{\partial \phi_{y} }}{\partial y} \\ & - 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} \frac{{\partial \phi_{y} }}{\partial y} + \frac{{2c^{2} E_{7} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial \phi_{y} }}{\partial y}} \right]}}{\partial x}. \\ \end{aligned}$$

$$H_{36} \left( {u_{0} ,w_{0} } \right) = \frac{{E_{1} h\left( x \right)}}{{1 - \nu^{2} }}\frac{{\partial u_{0} }}{\partial x}\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) - \frac{{2cE_{7} }}{1 + \nu }h\left( x \right)\frac{{\partial u_{0} }}{\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}.$$

$$H_{37} \left( {v_{0} ,w_{0} } \right) = \frac{{E_{1} h\left( x \right)}}{{1 - \nu^{2} }}\frac{{\partial v_{0} }}{\partial y}\left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) - \frac{{2cE_{7} }}{1 + \nu }h\left( x \right)\frac{{\partial v_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}.$$

$$\begin{aligned} H_{38} \left( {\phi_{x} ,w_{0} } \right) = & \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{x} }}{\partial x}\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right) + \frac{{E_{2} - cE_{4} }}{1 + \nu }\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{x} }}{\partial y}\frac{{\partial^{2} w_{0} }}{\partial x\partial y} \\ & + \frac{{2cE_{4} }}{{1 - \nu^{2} }}h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\phi_{x} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right). \\ \end{aligned}$$

$$\begin{aligned} H_{39} \left( {\phi_{y} ,w_{0} } \right) = & \frac{{E_{2} - cE_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{y} }}{\partial y}\left( {\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) + \frac{{E_{2} - cE_{4} }}{1 + \nu }\left( {h\left( x \right)} \right)^{2} \frac{{\partial \phi_{y} }}{\partial x}\frac{{\partial^{2} w_{0} }}{\partial x\partial y} \\ & + \frac{{2cE_{4} }}{1 + \nu }h\left( x \right)\frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}\phi_{y} . \\ \end{aligned}$$

$$\begin{aligned} H_{41} \left( {u_{0} } \right) = & \frac{{E_{2} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial u_{0} }}{\partial x}} \right]}}{\partial x} + \frac{{E_{2} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} - \frac{{cE_{4} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial u_{0} }}{\partial x}} \right]}}{\partial x} \\ & - \frac{{cE_{4} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}. \\ \end{aligned}$$

$$\begin{aligned} H_{42} \left( {v_{0} } \right) = & \frac{{\nu E_{2} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial v_{0} }}{\partial y}} \right]}}{\partial x} + \frac{{E_{2} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} v_{0} }}{\partial x\partial y} - \frac{{c\nu E_{4} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial v_{0} }}{\partial y}} \right]}}{\partial x} \\ & - \frac{{cE_{4} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} v_{0} }}{\partial x\partial y}. \\ \end{aligned}$$

$H_{43} \left( {w_{0} } \right) = H_{43a} \left( {w_{0} } \right) + H_{43b} \left( {w_{0} } \right).$

$$\begin{aligned} H_{43a} \left( {w_{0} } \right) = & \frac{{ - E_{2} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} w_{0} } \right]}}{\partial x} - \frac{{cE_{5} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right)} \right]}}{\partial x} \\ & - \frac{{cE_{5} }}{1 + \nu }\left( {h\left( x \right)} \right)^{3} \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} + \left[ { - \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}h\left( x \right) + 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} } \right]\frac{{\partial w_{0} }}{\partial x} \\ & + \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{a} + \frac{\nu }{R}} \right)\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} w_{0} } \right]}}{\partial x} + \frac{{c^{2} E_{7} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}} \right)} \right]}}{\partial x} \\ & + \frac{{c^{2} E_{7} }}{1 + \nu }\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} + \frac{{2cE_{5} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial x}} \right]}}{\partial x} + \frac{{cE_{5} }}{1 + \nu }\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} \\ & - \frac{{2c^{2} E_{7} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial x}} \right]}}{\partial x} - \frac{{c^{2} E_{7} }}{1 + \nu }\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{{\partial y^{2} }}. \\ \end{aligned}$$

$$\begin{aligned} H_{43b} \left( {w_{0} } \right) = & \frac{{E_{2} h\left( x \right)}}{{2\left( {1 - \nu^{2} } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \left( {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right)} \right]}}{\partial x} + \frac{{E_{2} \left( {h\left( x \right)} \right)^{2} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left( {\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right)}}{\partial y} \\ & - \frac{{cE_{4} }}{{2\left( {1 - \nu^{2} } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \left( {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} } \right)} \right]}}{\partial x} - \frac{{cE_{4} \left( {h\left( x \right)} \right)^{4} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left( {\frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right)}}{\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{44} \left( {\phi_{x} } \right) = & \frac{{E_{3} - cE_{5} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \frac{{\partial \phi_{x} }}{\partial x}} \right]}}{\partial x} + \frac{{E_{3} - cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }} \\ & + \left[ { - \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}h\left( x \right) + 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} } \right]\phi_{x} - c\frac{{E_{5} - cE_{7} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial \phi_{x} }}{\partial x}} \right]}}{\partial x} \\ & - c\frac{{E_{5} - cE_{7} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }} + \frac{{2cE_{5} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\phi_{x} } \right]}}{\partial x} - \frac{{2c^{2} E_{7} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\phi_{x} } \right]}}{\partial x}. \\ \end{aligned}$$

$$\begin{aligned} H_{45} \left( {\phi_{y} } \right) = & \nu \frac{{E_{3} - cE_{5} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \frac{{\partial \phi_{y} }}{\partial y}} \right]}}{\partial x} + \frac{{E_{3} - cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} \frac{{\partial^{2} \phi_{y} }}{\partial x\partial y} \\ & - c\nu \frac{{E_{5} - cE_{7} }}{{1 - \nu^{2} }}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial \phi_{y} }}{\partial y}} \right]}}{\partial x} + \frac{{cE_{5} }}{1 + \nu }\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial \phi_{y} }}{\partial y} - \frac{{c^{2} E_{7} }}{1 + \nu }\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial \phi_{y} }}{\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{51} \left( {u_{0} } \right) = & \frac{{E_{2} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial u_{0} }}{\partial y}} \right]}}{\partial x} + \frac{{\nu E_{2} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} u_{0} }}{\partial x\partial y} - \frac{{cE_{4} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial u_{0} }}{\partial y}} \right]}}{\partial x} \\ & - \frac{{c\nu E_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} u_{0} }}{\partial x\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{52} \left( {v_{0} } \right) = & \frac{{E_{2} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial v_{0} }}{\partial x}} \right]}}{\partial x} + \frac{{E_{2} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} - \frac{{cE_{4} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{{\partial v_{0} }}{\partial x}} \right]}}{\partial x} \\ & - \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }}H_{53} \left( {w_{0} } \right) = H_{53a} \left( {w_{0} } \right) + H_{53b} \left( {w_{0} } \right). \\ \end{aligned}$$

$$\begin{aligned} H_{53a} \left( {w_{0} } \right) = & - \frac{{cE_{5} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right]}}{\partial x} - \frac{{E_{2} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\left( {h\left( x \right)} \right)^{2} \frac{{\partial w_{0} }}{\partial y} \\ & - \frac{{cE_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{3} \left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} + \nu \frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) + \left[ { - \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}h\left( x \right) + 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} } \right]\frac{{\partial w_{0} }}{\partial y} \\ & + \frac{{c^{2} E_{7} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{2} w_{0} }}{\partial x\partial y}} \right]}}{\partial x} + \frac{{cE_{4} }}{{1 - \nu^{2} }}\left( {\frac{1}{R} + \frac{\nu }{a}} \right)\left( {h\left( x \right)} \right)^{4} \frac{{\partial w_{0} }}{\partial y} + \frac{{c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} \left( {\frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} + \nu \frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & + \frac{{cE_{5} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial y}} \right]}}{\partial x} + \frac{{2c\nu E_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{\partial x\partial y} \\ & - \frac{{c^{2} E_{7} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial w_{0} }}{\partial y}} \right]}}{\partial x} - \frac{{2\nu c^{2} E_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial^{2} w_{0} }}{\partial x\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{53b} \left( {w_{0} } \right) = & \frac{{E_{2} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial y}} \right]}}{\partial x} + \frac{{E_{2} \left( {h\left( x \right)} \right)^{2} }}{{2\left( {1 - \nu^{2} } \right)}}\frac{{\partial \left( {\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)}}{\partial y} \\ & - \frac{{cE_{4} \left( {h\left( x \right)} \right)^{4} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left( {\left( {\frac{{\partial w_{0} }}{\partial y}} \right)^{2} + \nu \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)}}{\partial y},\,\,H_{54} \left( {\phi_{x} } \right) = \frac{{E_{3} - cE_{5} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \frac{{\partial \phi_{x} }}{\partial y}} \right]}}{\partial x} \\ & + \nu \frac{{E_{3} - cE_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{3} \frac{{\partial^{2} \phi_{x} }}{\partial x\partial y} - c\frac{{E_{5} - cE_{7} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial \phi_{x} }}{\partial y}} \right]}}{\partial x} - c\nu \frac{{E_{5} - cE_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{2} \phi_{x} }}{\partial x\partial y} \\ & + \frac{{2\nu cE_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\frac{{\partial \phi_{x} }}{\partial y}. \\ \end{aligned}$$

$$\begin{aligned} H_{55} \left( {\phi_{y} } \right) = & \frac{{E_{3} - cE_{5} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{3} \frac{{\partial \phi_{y} }}{\partial x}} \right]}}{\partial x} + \frac{{E_{3} - cE_{5} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{3} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} \\ & + \left[ { - \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}}h\left( x \right) + 3c\frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}\left( {h\left( x \right)} \right)^{3} } \right]\phi_{y} - c\frac{{E_{5} - cE_{7} }}{{2\left( {1 + \nu } \right)}}\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{5} \frac{{\partial \phi_{y} }}{\partial x}} \right]}}{\partial x} \\ & + \frac{{cE_{5} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{2} \frac{\partial h\left( x \right)}{{\partial x}}\phi_{y} } \right]}}{\partial x} - c\frac{{E_{5} - cE_{7} }}{{1 - \nu^{2} }}\left( {h\left( x \right)} \right)^{5} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }} - \frac{{c^{2} E_{7} }}{1 + \nu }\frac{{\partial \left[ {\left( {h\left( x \right)} \right)^{4} \frac{\partial h\left( x \right)}{{\partial x}}\phi_{y} } \right]}}{\partial x}.\,c = \frac{4}{3}. \\ \end{aligned}$$

Appendix D

$l_{11} U = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{11} \left( {u_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{12} V = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{12} \left( {v_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{13} W = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{13a} \left( {w_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{14} \Phi_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{14} \left( {\phi_{x} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{15} \Phi_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{15} \left( {\phi_{y} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{16} W^{2} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{13b} \left( {w_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{17} \ddot{U} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{1} }} \ddot{u}\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{18} \ddot{\Phi }_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{2} }} \ddot{\phi }_{x} \cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{19} \ddot{W} = - \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{3} }} \frac{{\partial \ddot{w}_{0} }}{\partial x}\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{21} U = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{21} \left( {u_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{22} V = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{22} \left( {v_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{23} W = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{23a} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{24} \Phi_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{24} \left( {\phi_{x} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{25} \Phi_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{25} \left( {\phi_{y} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{26} W^{2} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{23b} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{27} \ddot{V} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{1}^{/} }} \ddot{v}_{0} \sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{28} \ddot{\Phi }_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{2}^{/} }} \ddot{\phi }_{y} \sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{29} \ddot{W} = - \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{3}^{/} }} \frac{{\partial \ddot{w}_{0} }}{\partial y}\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{31} U = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{31} \left( {u_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{32} V = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{32} \left( {v_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{33} W = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{33a} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{34} \Phi_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{34} \left( {\phi_{x} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{35} \Phi_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{35} \left( {\phi_{y} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{36} UW = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{36} \left( {u_{0} ,w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{37} VW = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{37} \left( {v_{0} ,w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{38} \Phi_{x} W = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{38} \left( {\phi_{x} ,w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{39} \Phi_{y} W = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{39} \left( {\phi_{y} ,w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{310} W^{2} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{33b} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{311} W^{3} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {H_{33c} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{312} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$$l_{313} \ddot{U} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {\overline{{I_{3} }} \frac{{\partial \ddot{u}_{0} }}{\partial x}\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{314} \ddot{V} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {\overline{{I_{3}^{/} }} \frac{{\partial \ddot{v}_{0} }}{\partial y}\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{315} \ddot{\Phi }_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {\overline{{I_{5} }} \frac{{\partial \ddot{\phi }_{x} }}{\partial x}\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{316} \ddot{\Phi }_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {\overline{{I_{5}^{/} }} \frac{{\partial \ddot{\phi }_{y} }}{\partial y}\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{317} \ddot{W} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {\left[ {I_{1} h\left( x \right)\ddot{w}_{0} - \frac{{16h^{3} \left( x \right)}}{9}I_{7} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right)} \right]\sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{318} \dot{W} = \int\limits_{0}^{L} {\int\limits_{0}^{\pi R} {2\varepsilon I_{1} h\left( x \right)\dot{w}_{0} \sin \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{41} U = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{41} \left( {u_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{42} V = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{42} \left( {v_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{43} W = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{43a} \left( {w_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{44} \Phi_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{44} \left( {\phi_{x} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{45} \Phi_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{45} \left( {\phi_{y} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{46} W^{2} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{43b} \left( {w_{0} } \right)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{47} \ddot{U} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{2} }} \ddot{u}_{0} \cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{48} \ddot{\Phi }_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{4} }} \ddot{\phi }_{x} \cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{49} \ddot{W} = - \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{5} }} \frac{{\partial \ddot{w}_{0} }}{\partial x}\cos \frac{m\pi x}{L}\sin \frac{ny}{R}dxdy} }$, $l_{51} U = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{51} \left( {u_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{52} V = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{52} \left( {v_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{53} W = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{53a} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{54} \Phi_{x} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{54} \left( {\phi_{x} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{55} \Phi_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{55} \left( {\phi_{y} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{56} W^{2} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {H_{53b} \left( {w_{0} } \right)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{57} \ddot{V} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{2}^{/} }} \ddot{v}_{0} \sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{58} \ddot{\Phi }_{y} = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{4}^{/} }} \ddot{\phi }_{y} \sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$, $l_{59} \ddot{W} = - \int\limits_{0}^{L} {\int\limits_{0}^{2\pi R} {\overline{{I_{5}^{/} }} \frac{{\partial \ddot{w}_{0} }}{\partial y}\sin \frac{m\pi x}{L}\cos \frac{ny}{R}dxdy} }$.

Appendix E

$$D_{1} = \frac{{l_{37} H_{13} + l_{38} H_{23} + l_{39} H_{33} + l_{310} H_{43} }}{{l_{31} H_{13} + l_{32} H_{23} + l_{34} H_{33} + l_{35} H_{43} - l_{317} }},$$

$$D_{2} = \frac{{l_{31} H_{11} + l_{32} H_{21} + l_{33} + l_{34} H_{31} + l_{35} H_{41} }}{{l_{31} H_{13} + l_{32} H_{23} + l_{34} H_{33} + l_{35} H_{43} - l_{317} }},$$

$$D_{3} = \frac{{l_{31} H_{12} + l_{32} H_{22} + l_{34} H_{32} + l_{35} H_{42} + l_{37} H_{11} + l_{38} H_{21} + l_{39} H_{31} + l_{310} H_{41} }}{{l_{31} H_{13} + l_{32} H_{23} + l_{34} H_{33} + l_{35} H_{43} - l_{317} }},$$

$$D_{4} = \frac{{l_{37} H_{12} + l_{38} H_{22} + l_{39} H_{32} + l_{310} H_{42} + l_{311} }}{{l_{31} H_{13} + l_{32} H_{23} + l_{34} H_{33} + l_{35} H_{43} - l_{317} }},$$

$$D_{5} = \frac{{l_{312} }}{{l_{31} H_{13} + l_{32} H_{23} + l_{34} H_{33} + l_{35} H_{43} - l_{317} }},$$

in which

$H_{11} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{13} } & {l_{12} } & {l_{14} } & {l_{15} } \\ {l_{23} } & {l_{22} } & {l_{24} } & {l_{25} } \\ {l_{43} } & {l_{42} } & {l_{44} } & {l_{45} } \\ {l_{53} } & {l_{52} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{12} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{16} } & {l_{12} } & {l_{14} } & {l_{15} } \\ {l_{26} } & {l_{22} } & {l_{24} } & {l_{25} } \\ {l_{46} } & {l_{42} } & {l_{44} } & {l_{45} } \\ {l_{56} } & {l_{52} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{13} = \frac{{\det \left( {\begin{array}{*{20}c} {l_{19} } & {l_{12} } & {l_{14} } & {l_{15} } \\ {l_{29} } & {l_{22} } & {l_{24} } & {l_{25} } \\ {l_{49} } & {l_{42} } & {l_{44} } & {l_{45} } \\ {l_{59} } & {l_{52} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{21} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{13} } & {l_{14} } & {l_{15} } \\ {l_{21} } & {l_{23} } & {l_{24} } & {l_{25} } \\ {l_{41} } & {l_{43} } & {l_{44} } & {l_{45} } \\ {l_{51} } & {l_{53} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{22} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{16} } & {l_{14} } & {l_{15} } \\ {l_{21} } & {l_{26} } & {l_{24} } & {l_{25} } \\ {l_{41} } & {l_{46} } & {l_{44} } & {l_{45} } \\ {l_{51} } & {l_{56} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{23} = \frac{{\det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{19} } & {l_{14} } & {l_{15} } \\ {l_{21} } & {l_{29} } & {l_{24} } & {l_{25} } \\ {l_{41} } & {l_{49} } & {l_{44} } & {l_{45} } \\ {l_{51} } & {l_{59} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{31} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{13} } & {l_{15} } \\ {l_{21} } & {l_{22} } & {l_{23} } & {l_{25} } \\ {l_{41} } & {l_{42} } & {l_{43} } & {l_{45} } \\ {l_{51} } & {l_{52} } & {l_{53} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{32} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{16} } & {l_{15} } \\ {l_{21} } & {l_{22} } & {l_{26} } & {l_{25} } \\ {l_{41} } & {l_{42} } & {l_{46} } & {l_{45} } \\ {l_{51} } & {l_{52} } & {l_{56} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{33} = \frac{{\det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{19} } & {l_{15} } \\ {l_{21} } & {l_{22} } & {l_{29} } & {l_{25} } \\ {l_{41} } & {l_{42} } & {l_{49} } & {l_{45} } \\ {l_{51} } & {l_{52} } & {l_{59} } & {l_{55} } \\ \end{array} } \right)}}{\Delta }$, $H_{41} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{14} } & {l_{13} } \\ {l_{21} } & {l_{22} } & {l_{24} } & {l_{23} } \\ {l_{41} } & {l_{42} } & {l_{44} } & {l_{43} } \\ {l_{51} } & {l_{52} } & {l_{54} } & {l_{53} } \\ \end{array} } \right)}}{\Delta }$, $H_{42} = \frac{{ - \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{14} } & {l_{16} } \\ {l_{21} } & {l_{22} } & {l_{24} } & {l_{26} } \\ {l_{41} } & {l_{42} } & {l_{44} } & {l_{46} } \\ {l_{51} } & {l_{52} } & {l_{54} } & {l_{56} } \\ \end{array} } \right)}}{\Delta }$, $H_{43} = \frac{{\det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{14} } & {l_{19} } \\ {l_{21} } & {l_{22} } & {l_{24} } & {l_{29} } \\ {l_{41} } & {l_{42} } & {l_{44} } & {l_{49} } \\ {l_{51} } & {l_{52} } & {l_{54} } & {l_{59} } \\ \end{array} } \right)}}{\Delta }$.

$\Delta = \det \left( {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{14} } & {l_{15} } \\ {l_{21} } & {l_{22} } & {l_{24} } & {l_{25} } \\ {l_{41} } & {l_{42} } & {l_{44} } & {l_{45} } \\ {l_{51} } & {l_{52} } & {l_{54} } & {l_{55} } \\ \end{array} } \right)$.