Nonlinear vibration of FGM moderately thick toroidal shell segment within the framework of Reddy’s third order-shear deformation shell theory

Abstract

Nonlinear vibration and dynamic response of functionally graded moderately thick toroidal shell segments resting on Pasternak type elastic foundation are investigated in this paper. Functionally graded materials are made from ceramic and metal, and the volume fraction of constituents are assumed to vary through the thickness direction according to a power law function. Reddy’s third order shear deformation, von Karman nonlinearity, Airy stress function method and analytical solutions are used to derive the governing equations. Galerkin method is used to convert the governing equation into nonlinear differential equation, then the explicit expressions of natural frequencies and nonlinear frequency–amplitude relations are obtained. Using Runge–Kutta method, the nonlinear differential equation of motion is solved, and then nonlinear vibration and dynamic response of shells are analyzed. The effects of temperature, material and geometrical properties, and foundation parameters on nonlinear vibration and dynamic characteristics are investigated and discussed in detail.

1 Introduction

Functionally graded material (FGM) is a modern composite material usually created from metal and ceramic constituents. The FGM is both highly heat-resistant like the ceramic and good resilience just like metal. Today, FGMs have been used in several of industries such as aviation, space and nuclear power. The knowledge of the buckling, post-buckling and vibration of FGM structures plays an important role in the design of these structures.

The vibration and dynamic response of shell structures is the important problem that obtained considerable intention of researchers. Alijani et al. (2011) based on Donnell’s nonlinear shallow shell theory, Galerkin method and multiple scales method studied the nonlinear forced vibration of simply supported FGM doubly curved shallow shell. The characteristics of resonance of shells are investigated in cases of excitation frequency near the fundamental frequency and near two times the fundamental frequency. Using Hamiltonian dynamic formulation and Donnell’s shell theory, Du and Li (2014) investigated the effects of material property and temperature environment on resonance condition and bifurcation behavior of functionally graded cylindrical shell. The free vibration behavior of simply supported FGM cylindrical shell subjected to non-uniform internal pressure is studied by Golpayegani and Ghorbani (2016) making use of Rayleigh–Ritz method based on Sander’s thin shells theory. Hadi et al. (2017) using Donnell’s shell theory in conjunctions with Galerkin method and Runge–Kutta method investigated the nonlinear dynamic responses of FGM cylindrical shell resting on nonlinear elastic foundation subjected to axial compressive and lateral loads. Using acoustic wave equation, wave propagation method and based on Flügge shell theory, Han et al. (2018) presented an analytical investigation on free vibration and elastic buckling of FGM cylindrical shell loaded by internal pressure fluid. Also, based on Flügge classical thin shell theory and wave propagation approach, the free vibration of circular cylindrical shell has been investigated by Li (2008). Using Donnell’s shell theory, Ng et al. (2001) investigated dynamic stability of simply supported FGM cylindrical shell subjected to combined static and periodic axial compressive loads. Authors used Bolotin’s method to find out the regions of unstable solutions, and the analyze the effects of material properties on that instability regions. Duc et al. (2017) making use of classical shell theory, Airy stress function, Galerkin method and Runge–Kutta method studied the vibration and nonlinear dynamic responses of FGM elliptical cylindrical shells resting on elastic foundation in thermal environment. The dynamic responses of simply supported FGM cylindrical shell under axial compressive and external pressure loads is studied by Bich and Nguyen (2012) making use of improved Donnell’s shell theory. In this work, the shallowness of shell is ignored. Dung and Thiem (2016) presented an analytical approach to investigate the free vibration of rotating FGM truncated conical shells based on Donnell’s shell theory. The shells are reinforced by FGM stringers and rings. Leckhnisky smeared stiffeners technique is used to investigate the effects of stringers and rings. Based on Donnell’s shell theory in conjunctions with Galerkin method, Sofiyev and Schnack (2012) studied vibration characteristics of simply supported FGM truncated conical shells resting on Pasternak type elastic foundation.

Higher-order shear deformation theory, though complex, was used by researchers for investigating static and dynamic behavior of thicker structures. Kitipornchai et al. (2004) presented a semi-analytical approach to investigate the nonlinear vibration behaviors of imperfect laminated FGM plates using Reddy’s third-order shear deformation plate theory in conjunction with differential quadrature method and Galerkin method. An analytical solution for investigating effects of embedded magnetostrictive layers on vibration suppression of simply supported FGM shell are presented by Pradhan (2005) using the first-order shear deformation shell theory. Bhimaraddi (1984) using higher-order displacement model and Flügge theory studied the free undamped vibration of isotropic circular cylindrical shell. The effects of nine different boundary conditions on the free vibration characteristics for a multi-layered cylindrical shell has been studied by Lam and Loy (1995) using Ritz procedure and Love’s first approximation theory. Tornabene (2009) using the first-order shear deformation theory and generalized differential quadrature method investigated free vibration characteristics of moderately thick FGM conical, cylindrical shells and plates. Using Sander’s first order shear deformation theory and the element-free $kp$-Ritz method, Zhao et al. (2009) studied the static and free vibration responses of FGM cylindrical shell under thermal and mechanical loadings. Shen (2012), Shen and Wang (2014) making use of higher-order shear deformation theory and two-step perturbation technique investigated the large amplitude vibration of FGM cylindrical shell, and FGM cylindrical panel supported by Pasternak elastic foundation exported to thermal environment, respectively. In works reported by Shen (2012) and Shen and Wang (2014), authors considered Voigt model and Mori–Tanaka model of micromechanics and they show that two models have the same reliability for predicting the vibration characteristics of shells and panels. Based on the first-order shear deformation theory in conjunctions with modified Fourier-Ritz method, Jin et al. (2015) analyzed vibration characteristics of laminate functionally graded shallow shell. The authors considered four types of sandwich shell and used spring model to describe the general boundary condition. Punera and Kant (2017) studied free vibration of FGM open cylindrical shells using a set of higher-order shear deformation theories and Navier method. In this work authors used the extended thickness criterion $\left( {h /R} \right)^{2} \ll 1$ for moderately thick shell. Based on shear deformation theory considering von Karman nonlinearity in conjunctions with Galerkin method and homotopic perturbation method, Sofiyev (2016) investigated nonlinear free vibration of orthotropic functionally graded cylindrical shells. Based on first-order shear deformation, Quan et al. (2015) investigated the nonlinear dynamic and vibration of imperfect stiffened functionally grade cylindrical panels under mechanical loading. The dynamic response and nonlinear vibration of imperfect functionally graded thick double-curved shallow resting on elastic foundations are investigated by Quan and Duc (2016) making use of Reddy’s third-order shear deformation shell theory. A unified approach to studied vibration characteristics of FGM moderately thick doubly curved shells, FG sandwich doubly curved shells and panels of revolution with general boundary condition are presented by Wang et al. (2017a, b) making used of the first-order shear deformation theory, modified Fourier series expression and Ritz-variational energy method. Using modified couple stress theory and Navier procedure and based on the first-order shear deformation theory, Beni et al. (2015) examined free vibration behavior of simply supported FGM cylindrical nanoshells. An investigation on nonlinear dynamic behavior of clamped FGM cylindrical shell subjected to external pressure in thermal environment is performed by Zhang et al. (2012) using the first-order shear deformation theory, Hamilton’s principle and Galerkin method. Asanjarani et al. (2014) studied free vibration of FGM truncated conical shell resting on two-parameters elastic foundation using the first-order shear deformation theory and differential quadrature method. Su et al. (2014) presented an investigation on three-dimensional vibration of thick FGM conical, cylindrical shell and plate with elastic boundary condition. Using modified Fourier series and variational principle, authors have obtained the exact solution.

Toroidal shell segment has found applications in satellite support structures, rocket fuel tanks and fusion reactor vessels. Basing on classical shell theory, the nonlinear vibration and dynamic buckling behavior of thin FGM toroidal shell segments have been investigated by Bich et al. (2016) and Ninh and Bich (2016). To the best of the author’s knowledge, investigations on FGM toroidal shell segments are limited in number and most of them are based on classical shell theory only suitable for thin shells. For thicker shells, higher-order shear deformation shell theory should be used to analyze static and dynamic behavior of them for better results. There is no investigation on nonlinear dynamic response of moderately thick toroidal shell segment based on higher-order shear deformation shell theory.

This paper extends previous work reported by Vuong and Duc (2018) and works reported by Bich et al. (2016) and Ninh and Bich (2016). To investigate the nonlinear vibration and dynamic response of moderately thick toroidal shell segments resting on elastic foundations, subjected to axial compressive and external pressure, and exposed to thermal environment. The governing equations are established within the framework of Reddy’s third-order shear deformation shell theory. Galerkin method is used to convert the governing equation into nonlinear differential equation, then the explicit expression of natural frequencies and nonlinear frequency–amplitude relations are obtained. Numerical method using second-order Runge–Kutta are used to solve nonlinear differential equation of motion, and then nonlinear vibration and dynamic response of shells are analyzed.

2 Governing equations

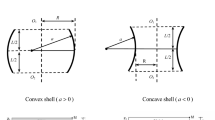
Consider a toroidal shell segment with radius of equator $R$, longitudinal curvature radius $a$ thickness $h$ and length $L$ surrounded by Pasternak type elastic foundation as shown in Fig. 1. The shell is defined in a coordinate system ($x,y,z$) whose origin is located at the end on the middle surface of shell, $x$ and $y$ are in the axial and circumferential directions, respectively, $z$ is perpendicular to surface and pointed inwards.

Fig. 1

Geometry and coordinate system of an FGM toroidal shell segment

The shell is made from functionally graded material which composed of ceramics and metals with effective material properties are assumed to be graded in the thickness direction according to a simple power law distribution in term of the volume fractions of the constituents. The Young modulus $E$, mass density $\rho$ and thermal expansion coefficient $\alpha$ can be expressed in the form (Bich et al. 2016; Vuong and Duc 2018)

$$\left\{ \begin{aligned} E\left( z \right) = E_{m} + \left( {E_{c} - E_{m} } \right)\left( {\frac{2z + h}{2h}} \right)^{k} , \\ \rho \left( z \right) = \rho_{m} + \left( {\rho_{c} - \rho_{m} } \right)\left( {\frac{2z + h}{2h}} \right)^{k} , \\ \alpha \left( z \right) = \alpha_{m} + \left( {\alpha_{c} - \alpha_{m} } \right)\left( {\frac{2z + h}{2h}} \right)^{k} , \\ \end{aligned} \right.$$

(1)

where $\left( {E_{m} ,\rho_{m} ,\alpha_{m} } \right)$ and $\left( {E_{c} ,\rho_{c} ,\alpha_{c} } \right)$ are properties of metal and ceramic constituent, respectively, $k$ is nonnegative number, referred to as the volume fraction index that defines the material distribution. The Poisson’s ratio $\nu$ is assumed to be constant. It is clear from Eq. (1) that, the outer surface of the shell ($z = - \frac{h}{2}$) is metal-rich and the inner surface ($z = \frac{h}{2}$) is ceramic-rich.

In this study, the governing equations are derived within the framework of Reddy’s third-order shear deformation shell theory (Reddy and Liu 1985) considering von Kármán nonlinearity. The strain components across the shell thickness at a distance $z$ from the middle surface are

$$\left( \begin{array}{c} \varepsilon_{x} \\ \varepsilon_{y} \\ \gamma_{xy} \\ \end{array} \right) = \left( \begin{array}{c} \varepsilon_{x}^{0} \\ \varepsilon_{y}^{0} \\ \gamma_{xy}^{0} \\ \end{array}\right) + z\left( \begin{array}{c}k_{x}^{\left( 1 \right)} \\ k_{y}^{\left( 1 \right)} \\ k_{xy}^{\left( 1 \right)} \\ \end{array} \right) + z^{3} \left( \begin{array}{c} k_{x}^{\left( 3 \right)} \\ k_{y}^{\left( 3 \right)} \\ k_{xy}^{\left( 3 \right)} \\ \end{array} \right),\,\,\left( \begin{array}{c} \gamma_{xz} \\ \gamma_{yz} \\ \end{array} \right) = \left( \begin{array}{c} \gamma_{xz}^{0} \\ \gamma_{yz}^{0} \\ \end{array} \right) + z^{2} \left( \begin{array}{c} k_{xz}^{\left( 2 \right)} \\ k_{yz}^{\left( 2 \right)} \\ \end{array} \right),$$

(2)

where

$$\begin{aligned} & \left( \begin{array}{c} \varepsilon_{x}^{0} \\ \varepsilon_{y}^{0} \\ \gamma_{xy}^{0} \\ \end{array} \right) = \left( \begin{array}{c} u_{,x} - \frac{w}{a} + w_{,x}^{2} /2 \\ v_{,y} - \frac{w}{R} + w_{,y}^{2} /2 \\ u_{,y} + v_{,x} + w_{,x} w_{,y} \\ \end{array} \right),\left( \begin{array}{c} k_{x}^{\left( 1 \right)} \\ k_{y}^{\left( 1 \right)} \\ k_{xy}^{\left( 1 \right)} \\ \end{array} \right) = \left( \begin{array}{c} \phi_{x,x} \\ \phi_{y,y} \\ \phi_{x,y} + \phi_{y,x} \\ \end{array} \right),\,\,\,\left( \begin{array}{c} k_{xz}^{\left( 2 \right)} \\ k_{yz}^{\left( 2 \right)} \\ \end{array} \right) = - 3c\left( \begin{array}{c} \phi_{x} + w_{,x} \\ \phi_{y} + w_{,y} \\ \end{array} \right), \\ & \left( \begin{array}{c} k_{x}^{\left( 3 \right)} \\ k_{y}^{\left( 3 \right)} \\ k_{xy}^{\left( 3 \right)} \\ \end{array} \right) = - c\left( \begin{array}{c} \phi_{x,x} + w_{,xx} \\ \phi_{y,y} + w_{,yy} \\ \phi_{x,y} + \phi_{y,x} + 2w_{,xy} \\ \end{array} \right),\,\,\left( \begin{array}{c} \gamma_{xz}^{0} \\ \gamma_{yz}^{0} \\ \end{array} \right) = \left( \begin{array}{c} \phi_{x} + w_{,x} \\ \phi_{y} + w_{,y} \\ \end{array} \right),\,c = \frac{4}{{3h^{2} }}, \\ \end{aligned}$$

(3)

in which $\varepsilon_{x} ,\varepsilon_{y}$ are normal trains, $\gamma_{xy}$ is the in-plane shear train, and $\gamma_{xz} ,\gamma_{yz}$ are the transverse shear trains. Also, $u,v$ are displacement components along $x,y$ directions, respectively, $w$ is the deflection of shell, and $\phi_{x} ,\phi_{y}$ are the slop rotations of normal to the middle surface of shell with respect to $y$ and $x$ axes.

The geometrical compatibility equation for a toroidal shell segment is obtained from Eq. (3) as

$$\varepsilon_{x,yy}^{0} + \varepsilon_{y,xx}^{0} - \gamma_{xy,xy}^{0} = - \frac{1}{R}w_{,xx} - \frac{1}{a}w_{,yy} + \left( {w_{,xy} } \right)^{2} - w_{,xx} w_{,yy} .$$

(4)

Using Hooke’s law for shear deformable shell exposed to thermal environment, the constitutive stress–strain equations are given

$$\left( \begin{array}{c} \sigma_{x} \\ \sigma_{y} \\ \end{array} \right) = \frac{E\left( z \right)}{{1 - \nu^{2} }}\left( \begin{array}{c} \varepsilon_{x} + \nu \varepsilon_{y} - \left( {1 + \nu } \right)\alpha \left( z \right)\Delta T \\ \varepsilon_{y} + \nu \varepsilon_{x} - \left( {1 + \nu } \right)\alpha \left( z \right)\Delta T \\ \end{array} \right),\,\,\left( \begin{array}{c} \sigma_{xy} \\ \sigma_{xz} \\ \sigma_{yz} \\ \end{array} \right) = \frac{E\left( z \right)}{{2\left( {1 + \nu } \right)}}\left( \begin{array}{c} \gamma_{xy} \\ \gamma_{xz} \\ \gamma_{yz} \\ \end{array} \right),$$

(5)

where $\Delta T$ is temperature rise from stress free initial state. In this study $\Delta T$ is assumed to be independent of coordinates $x,y$ and $z$. The components of force and moment resultants are defined as follows

$$\left( {N_{i} ,M_{i} ,P_{i} } \right) = \int\limits_{ - h/2}^{h/2} {\sigma_{i} \left( {1,z,z^{3} } \right)dz} ,\,\,\,i = x,\,y,xy\,,\left( {Q_{j} ,R_{j} } \right) = \int\limits_{ - h/2}^{h/2} {\sigma_{iz} \left( {1,z^{2} } \right)dz} ,\,i = x,\,y.$$

(6)

By virtue of Eqs. (2) and (5), the force and moment resultants are expressed as

$$\begin{aligned} & \left( \begin{array}{c} N_{x} \\ M_{x} \\ P_{x} \\ \end{array} \right) = \frac{{\varepsilon_{x}^{0} + \nu \varepsilon_{y}^{0} }}{{1 - \nu^{2} }}\left( \begin{array}{c} E_{1} \\ E_{2} \\ E_{4} \\ \end{array} \right) + \frac{{k_{x}^{1} + \nu k_{y}^{1} }}{{1 - \nu^{2} }}\left( \begin{array}{c} E_{2} \\ E_{3} \\ E_{5} \\ \end{array} \right) + \frac{{k_{x}^{3} + \nu k_{y}^{3} }}{{1 - \nu^{2} }}\left( \begin{array}{c} E_{4} \\ E_{5} \\ E_{7} \\ \end{array} \right) - \frac{1}{1 - \nu }\left( \begin{array}{c} \Upphi_{1} \\ \Upphi_{2} \\ \Upphi_{3} \\ \end{array} \right), \\ & \left( \begin{array}{c} N_{y} \\ M_{y} \\ P_{y} \\ \end{array} \right) = \frac{{\varepsilon_{y}^{0} + \nu \varepsilon_{x}^{0} }}{{1 - \nu^{2} }}\left( \begin{array}{c} E_{1} \\ E_{2} \\ E_{4} \\ \end{array} \right) + \frac{{k_{y}^{1} + \nu k_{x}^{1} }}{{1 - \nu^{2} }}\left( \begin{array}{c} E_{2} \\ E_{3} \\ E_{5} \\ \end{array} \right) + \frac{{k_{y}^{3} + \nu k_{x}^{3} }}{{1 - \nu^{2} }}\left( \begin{array}{c} E_{4} \\ E_{5} \\ E_{7} \\ \end{array} \right) - \frac{1}{1 - \nu }\left( \begin{array}{c} \Upphi_{1} \\ \Upphi_{2} \\ \Upphi_{3} \\ \end{array} \right), \\ & \left( \begin{array}{c} N_{xy} \\ M_{xy} \\ P_{xy} \\ \end{array} \right) = \frac{{\gamma_{xy}^{0} }}{{2\left( {1 + \nu } \right)}}\left( \begin{array}{c} E_{1} \\ E_{2} \\ E_{4} \\ \end{array} \right) + \frac{{k_{xy}^{1} }}{{2\left( {1 + \nu } \right)}}\left( \begin{array}{c} E_{2} \\ E_{3} \\ E_{5} \\ \end{array} \right) + \frac{{k_{xy}^{3} }}{{2\left( {1 + \nu } \right)}}\left( \begin{array}{c} E_{4} \\ E_{5} \\ E_{7} \\ \end{array} \right), \\ & \left( \begin{array}{c} Q_{i} \\ R_{i} \\ \end{array} \right) = \frac{{\gamma_{iz}^{0} }}{{2\left( {1 + \nu } \right)}}\left( \begin{array}{c} E_{1} \\ E_{3} \\ \end{array} \right) + \frac{{k_{iz}^{2} }}{{2\left( {1 + \nu } \right)}}\left( \begin{array}{c} E_{3} \\ E_{5} \\ \end{array} \right),\,i = x,y, \\ \end{aligned}$$

(7)

where

$$\left( {E_{1} ,E_{2} ,E_{3} ,E_{4} ,E_{5} ,E_{7} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,z^{2} ,z^{3} ,z^{4} ,z^{6} } \right)E\left( z \right)} dz,$$

$$\left( {\Upphi_{1} ,\Upphi_{2} ,\Upphi_{4} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,z^{3} } \right)E\left( z \right)} \alpha \left( z \right)\Delta T\left( z \right)dz.$$

(8)

In the present study, Reddy’s third-order shear deformation theory is used to establish governing equations for a toroidal shell segment exposed to thermal environment, surrounded by Pasternak type elastic foundation and subjected to uniformly distributed external pressure of intensity $q\left( {{\text{N/m}}^{ 2} } \right)$. The nonlinear motion equations are given (Reddy and Liu 1985)

$$N_{x,x} + N_{xy,y} = \overline{{I_{1} }} \frac{{\partial^{2} u}}{{\partial t^{2} }} + \overline{{I_{2} }} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \overline{{I_{3} }} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}\,,$$

(9)

$$N_{xy,x} + N_{y,y} = \overline{{I_{1}^{*} }} \frac{{\partial^{2} v}}{{\partial t^{2} }} + \overline{{I_{2}^{*} }} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{{I_{3}^{*} }} \frac{{\partial^{3} w}}{{\partial y\partial t^{2} }},$$

(10)

$$\begin{aligned} & Q_{x,x} + Q_{y,y} - 3c\left( {R_{x,x} + R_{y,y} } \right) + \frac{1}{R}N_{y} + \frac{1}{a}N_{x} + c\left( {P_{x,xx} + 2P_{xy,xy} + P_{y,yy} } \right) \\ & \quad + N_{x} w_{,xx} + 2N_{xy} w_{,xy} + N_{y} w_{,yy} + q - K_{1} w + K_{2} \left( {w_{,xx} + w_{,yy} } \right) = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} \\ & \quad + \overline{{I_{3} }} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} + \overline{{I_{5} }} \frac{{\partial^{3} \phi_{x} }}{{\partial t^{2} \partial x}}\, + \overline{{I_{3}^{*} }} \frac{{\partial^{3} v}}{{\partial t^{2} \partial y}} + \overline{{I_{5}^{*} }} \frac{{\partial^{3} \phi_{y} }}{{\partial t^{2} \partial y}} - c^{2} I_{7} \left( {\frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}} \right), \\ \end{aligned}$$

(11)

$$M_{x,x} + M_{xy,y} - Q_{x} + 3cR_{x} - c\left( {P_{x,x} + P_{xy,y} } \right) = \overline{{I_{2} }} \frac{{\partial^{2} u}}{{\partial t^{2} }} + \overline{{I_{4} }} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \overline{{I_{5} }} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}\,,$$

(12)

$$M_{y,y} + M_{xy,x} - Q_{y} + 3cR_{y} - c\left( {P_{y,y} + P_{xy,x} } \right) = \overline{{I_{2}^{*} }} \frac{{\partial^{2} v}}{{\partial t^{2} }} + \overline{{I_{4}^{*} }} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{{I_{5}^{*} }} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}\,,$$

(13)

where $K_{1} \left( {{\text{N/m}}^{ 3} } \right)$ is stiffness of Winkler foundation, $K_{2} \left( {\text{N/m}} \right)$ is the shear modulus of Pasternak model, $\varepsilon$ is damping coefficient, and

$$\begin{aligned} & I_{i} = \int\limits_{ - h/2}^{h/2} {\rho \left( z \right)z^{i - 1} dz} ,\,i = \left( {1 - 5,7} \right), \\ & \overline{{I_{1} }} = I_{1} + \frac{{2I_{2} }}{R},\quad \overline{{I_{1}^{*} }} = I_{1} + \frac{{2I_{2} }}{a},\quad \overline{{I_{2} }} = I_{2} + \frac{{I_{3} }}{R} - cI_{4} - \frac{{cI_{5} }}{R},\quad \overline{{I_{2}^{*} }} = I_{2} + \frac{{I_{3} }}{a} - cI_{4} - \frac{{cI_{5} }}{a}, \\ & \overline{{I_{3} }} = cI_{4} + \frac{{cI_{5} }}{R},\quad \overline{{I_{3}^{*} }} = cI_{4} + \frac{{cI_{5} }}{a},\quad \overline{{I_{4} }} = \overline{{I_{4}^{*} }} = I_{3} - 2cI_{5} + c^{2} I_{7} ,\quad \overline{{I_{5} }} = \overline{{I_{5}^{*} }} = cI_{5} - c^{2} I_{7} . \\ \end{aligned}$$

(14)

With the introduction of stress function $F\left( {x,y,t} \right)$ defined as

$$N_{x} = F_{,yy} ,\,\,N_{y} = F_{,xx} ,\,N_{xy} = - F_{,xy} ,$$

(15)

Equations (9) and (10) are rewritten as

$$\frac{{\partial^{2} u}}{{\partial t^{2} }} = - \frac{{\overline{{I_{2} }} }}{{\overline{{I_{1} }} }}\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\overline{{I_{3} }} }}{{\overline{{I_{1} }} }}\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }},\quad \frac{{\partial^{2} v}}{{\partial t^{2} }} = - \frac{{\overline{{I_{2}^{*} }} }}{{\overline{{I_{1}^{*} }} }}\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\overline{{I_{3}^{*} }} }}{{\overline{{I_{1}^{*} }} }}\frac{{\partial^{3} w}}{{\partial y\partial t^{2} }}.$$

(16)

By virtue of Eqs. (7) and (15) one can write

$$\begin{aligned} & \left( {\varepsilon_{x}^{0} ,\varepsilon_{y}^{0} } \right) = \frac{1}{{E_{1} }}\left[ {\left( {F_{,yy} ,F_{,xx} } \right) - \nu \left( {F_{,xx} ,F_{,yy} } \right) - E_{2} \left( {k_{x}^{1} ,k_{y}^{1} } \right) - E_{4} \left( {k_{x}^{3} ,k_{y}^{3} } \right) + \Upphi_{1} \left( {1,1} \right)} \right], \\ & \gamma_{xy}^{0} = \frac{{ - 2\left( {1 + \nu } \right)}}{{E_{1} }}F_{,xy} - \frac{{E_{2} }}{{E_{1} }}k_{xy}^{1} - \frac{{E_{4} }}{{E_{1} }}k_{xy}^{3} . \\ \end{aligned}$$

(17)

Substituting Eq. (17) into Eq. (7), and then substituting the results and Eq. (3) into Eqs. (11)–(13) with the aid of Eq. (16) yields

$$\begin{aligned} & L_{11} \left( w \right) + L_{12} \left( {\phi_{x} } \right) + L_{13} \left( {\phi_{y} } \right) + S\left( {w,F} \right) + q \\ & = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} + \overline{\overline{{I_{5} }}} \frac{{\partial^{3} \phi_{x} }}{{\partial t^{2} \partial x}} + \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} \phi_{y} }}{{\partial t^{2} \partial y}} + \overline{\overline{{I_{7} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \overline{\overline{{I_{7}^{*} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}, \\ \end{aligned} .$$

(18)

$$L_{21} \left( w \right) + L_{22} \left( {\phi_{x} } \right) + L_{23} \left( {\phi_{y} } \right) = \overline{\overline{{I_{3} }}} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \overline{\overline{{I_{5} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}},$$

(19)

$$L_{31} \left( w \right) + L_{32} \left( {\phi_{x} } \right) + L_{33} \left( {\phi_{y} } \right) = \overline{\overline{{I_{3}^{*} }}} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}},$$

(20)

where

$$\begin{aligned} & L_{11} \left( w \right) = - K_{1} w + \left( {A_{7} - 3cA_{8} + K_{2} } \right)\left( {w_{,xx} + w_{,yy} } \right) + cA_{6} \left( {w_{,xxxx} + 2w_{,xxyy} + w_{,yyyy} } \right), \\ & L_{12} \left( w \right) = \left( {A_{7} - 3cA_{8} } \right)\phi_{x,x} + cA_{5} \left( {\phi_{x,xxx} + \phi_{x,xyy} } \right), \\ & L_{13} \left( w \right) = \left( {A_{7} - 3cA_{8} } \right)\phi_{y,y} + cA_{5} \left( {\phi_{y,yyy} + \phi_{y,yxx} } \right), \\ & S\left( {w,F} \right) = \frac{1}{R}F_{,xx} + \frac{1}{a}F_{,yy} + F_{,yy} w_{,xx} - 2F_{,xy} w_{,xy} + F_{,xx} w_{,yy} , \\ & L_{21} \left( w \right) = \left( {3cA_{8} - A_{7} } \right)w_{,x} + \left( {A_{3} - cA_{6} } \right)\left( {w_{,xxx} + w_{,xyy} } \right), \\ & L_{22} \left( {\phi_{x} } \right) = \left( {3cA_{8} - A_{7} } \right)\phi_{x} + \left( {A_{2} - cA_{5} } \right)\left( {\phi_{x,xx} + \frac{1 - \nu }{2}\phi_{x,yy} } \right), \\ & L_{23} \left( {\phi_{y} } \right) = \left( {A_{2} - cA_{5} } \right)\frac{1 + \nu }{2}\phi_{y,xy} , \\ & L_{31} \left( w \right) = \left( {3cA_{8} - A_{7} } \right)w_{,y} + \left( {A_{3} - cA_{6} } \right)\left( {w_{,yyy} + w_{,yxx} } \right). \\ & L_{32} \left( {\phi_{x} } \right) = \left( {A_{2} - cA_{5} } \right)\frac{1 + \nu }{2}\phi_{x,xy} , \\ & L_{33} \left( {\phi_{y} } \right) = \left( {3cA_{8} - A_{7} } \right)\phi_{y} + \left( {A_{2} - cA_{5} } \right)\left( {\phi_{y,yy} + \frac{1 - \nu }{2}\phi_{y,xx} } \right), \\ \end{aligned}$$

(21)

in which

$$\begin{aligned} & A_{1} = \frac{{E_{2} }}{{E_{1} }},\quad A_{2} = \frac{{E_{1} E_{3} - E_{2}^{2} + c\left( {E_{2} E_{4} - E_{1} E_{5} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}},\quad A_{3} = \frac{{c\left( {E_{2} E_{4} - E_{1} E_{5} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}}, \\ & A_{4} = \frac{{E_{4} }}{{E_{1} }},\quad A_{5} = \frac{{E_{1} E_{5} - E_{2} E_{4} + c\left( {E_{4}^{2} - E_{1} E_{7} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}},\quad A_{6} = \frac{{c\left( {E_{4}^{2} - E_{1} E_{7} } \right)}}{{E_{1} \left( {1 - \nu^{2} } \right)}}, \\ & A_{7} = \frac{{E_{1} - 3cE_{3} }}{{2\left( {1 + \nu } \right)}},\,A_{8} = \frac{{E_{3} - 3cE_{5} }}{{2\left( {1 + \nu } \right)}}, \\ & \overline{\overline{{I_{3} }}} = \overline{{I_{4} }} - \left( {\overline{{I_{2} }} } \right)^{2} /\overline{{I_{1} }} ,\quad \overline{\overline{{I_{3}^{*} }}} = \overline{{I_{4}^{*} }} - \left( {\overline{{I_{2}^{*} }} } \right)^{2} /\overline{{I_{1}^{*} }} ,\quad \overline{\overline{{I_{5} }}} = \overline{{I_{5} }} - \overline{{I_{2} }} \overline{{I_{3} }} /\overline{{I_{1} }} ,\quad \overline{\overline{{I_{5}^{*} }}} = \overline{{I_{5}^{*} }} - \overline{{I_{2}^{*} }} \overline{{I_{3}^{*} }} /\overline{{I_{1}^{*} }} , \\ & \overline{\overline{{I_{7} }}} = \left( {\overline{{I_{3} }} } \right)^{2} /\overline{{I_{1} }} - \lambda^{2} I_{7} ,\quad \overline{\overline{{I_{7}^{*} }}} = \left( {\overline{{I_{3}^{*} }} } \right)^{2} /\overline{{I_{1}^{*} }} - \lambda^{2} I_{7} . \\ \end{aligned}$$

(22)

we assumed that the inertial forces caused by $\phi_{x}$ and $\phi_{y}$ are small and they can be ignored. The Eqs. (18)–(20) are rewritten as

$$L_{11} \left( w \right) + L_{12} \left( {\phi_{x} } \right) + L_{13} \left( {\phi_{y} } \right) + S\left( {w,F} \right) + q = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} + \overline{\overline{{I_{7} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \overline{\overline{{I_{7}^{*} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }},$$

(23)

$$L_{21} \left( w \right) + L_{22} \left( {\phi_{x} } \right) + L_{23} \left( {\phi_{y} } \right) = - \overline{\overline{{I_{5} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}},$$

(24)

$$L_{31} \left( w \right) + L_{32} \left( {\phi_{x} } \right) + L_{33} \left( {\phi_{y} } \right) = - \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}.$$

(25)

Substitution of Eqs. (17) into the compatibility Eq. (4) leads to

$$\frac{\Delta \Delta F}{{A_{1} }} = \left( {w_{,xy} } \right)^{2} - w_{,xx} w_{,yy} - \frac{1}{R}w_{,xx} - \frac{1}{a}w_{,yy} .$$

(26)

Equations (23)–(26) are governing equations in term of four variables $w\left( {x,y,t} \right)$, $F\left( {x,y,t} \right)$, $\phi_{x} \left( {x,y,t} \right)$ and $\phi_{y} \left( {x,y,t} \right)$ used to analyze the nonlinear vibration behavior of moderately thick toroidal shell segments subjected to mechanical loading, surrounded by Pasternak type elastic foundations in thermal environment.

3 Solution of governing equations

In this study, the shell is assumed to be simply supported and subjected to uniformly distributed pressure of intensity q and pre-axial compressive load of intensity $P$. Thus, the boundary conditions are

$$w = \phi_{y} = 0,N_{x} = - Ph,N_{xy} = 0,M_{x} = 0,P_{x} = 0\quad {\text{at}}\quad x = 0,x = L.$$

(27)

The approximate solution of governing equations, satisfying the simply supported boundary conditions in average sense may be assumed as

$$w = f\left( t \right)\sin Mx\sin Ny,$$

(28)

$$F = F_{1} \sin Mx\sin Ny + F_{2} \cos 2Mx + F_{3} \cos 2Ny + \frac{1}{2}N_{0y} x^{2} - \frac{1}{2}Phy^{2} ,$$

(29)

$$\phi_{x} = C_{1} \cos Mx\sin Ny,\phi_{y} = C_{2} \sin Mx\cos Ny,$$

(30)

where $M = \frac{m\pi }{L},N = \frac{n}{R},f$ is the time dependent amplitude and $m,n$ are the numbers of half waves in the $x,y$ directions, respectively. Coefficients $F_{1} ,F_{2} ,F_{3}$ are determined by putting Eq. (28) into Eq. (26) as

$$F_{1} = F_{11} f,\quad F_{2} = F_{21} f^{2} ,\quad F_{3} = F_{31} f^{2} ,$$

(31)

where

$$F_{11} = \frac{{E_{1} }}{{\left( {M^{2} + N^{2} } \right)^{2} }}\left( {\frac{{M^{2} }}{R} + \frac{{N^{2} }}{a}} \right),F_{21} = \frac{{E_{1} N^{2} }}{{32M^{2} }},\quad F_{31} = \frac{{E_{1} M^{2} }}{{32N^{2} }}.$$

Next, substituting Eqs. (28)–(29) into Eqs. (24)–(25), coefficients $C_{1} ,C_{2}$ are determined as

$$C_{1} = C_{11} f + C_{12} \dot{f},\quad C_{2} = C_{21} f + C_{22} \dot{f},$$

(32)

where

$$C_{11} = \frac{{v_{13} v_{22} - v_{12} v_{23} }}{{v_{11} v_{22} - v_{12} v_{21} }},C_{12} = \frac{{v_{14} v_{22} - v_{12} v_{24} }}{{v_{11} v_{22} - v_{12} v_{21} }},\quad C_{21} = \frac{{v_{11} v_{23} - v_{21} v_{13} }}{{v_{11} v_{22} - v_{12} v_{21} }},\quad C_{22} = \frac{{v_{11} v_{24} - v_{21} v_{14} }}{{v_{11} v_{22} - v_{12} v_{21} }},$$

(33)

in which$v_{11} = \left( {3cA_{8} - A_{7} } \right) - \left( {A_{2} - cA_{5} } \right)\left( {M^{2} - \frac{1 - \nu }{2}N^{2} } \right),v_{12} = - \frac{1 + \nu }{2}\left( {A_{2} - cA_{5} } \right)MN$,$v_{13} = \left( {A_{3} - cA_{6} } \right)\left( {M^{3} + MN^{2} } \right) + \left( {A_{7} - 3cA_{8} } \right)M,v_{14} = - \overline{\overline{{I_{5} }}} M$,$v_{21} = - \frac{1 + \nu }{2}\left( {A_{2} - cA_{5} } \right)MN,v_{22} = \left( {3cA_{8} - A_{7} } \right) - \left( {A_{2} - cA_{5} } \right)\left( {N^{2} - \frac{1 - \nu }{2}M^{2} } \right)$,

$$v_{23} = \left( {A_{3} - cA_{6} } \right)\left( {N^{3} + NM^{2} } \right) + \left( {A_{7} - 3cA_{8} } \right)N,v_{24} = - \overline{\overline{{I_{5}^{*} }}} N.$$

(34)

Substituting Eqs. (28)–(30) into Eq. (23) and applying Galerkin method for resulting equation, after some calculations, we have

$$B_{1} \ddot{f} + B_{2} \dot{f} + B_{3} f + B_{4} f^{2} + B_{5} f^{3} + \frac{{4\delta_{m} \delta_{n} }}{MNL\pi R}\left[ { - q + \frac{{\Upphi_{1} }}{R} + \left( {\frac{\nu }{R} + \frac{1}{a}} \right)Ph} \right] = 0,$$

(35)

where

$$\begin{aligned} B_{1} & = I_{1} - \left[ {A_{3} - A_{2} \left( {M^{2} + N^{2} } \right)} \right]\left( {C_{12} M + C_{22} N} \right) - A_{6} \left( {M^{2} + N^{2} } \right),B_{2} = 2\varepsilon I_{1} , \\ B_{3} & = - \left[ {A_{3} - A_{2} \left( {M^{2} + N^{2} } \right)} \right]\left( {C_{11} M + C_{21} N} \right) - A_{3} \left( {M^{2} + N^{2} } \right) + A_{5} \left( {M^{2} + N^{2} } \right)^{2} \\ & \quad + F_{11} \left( {\frac{{M^{2} }}{R} + \frac{{N^{2} }}{a}} \right) + k_{1} + k_{2} \left( {M^{2} + N^{2} } \right) - N^{2} \Upphi_{1} - \left( {M^{2} + \nu N^{2} } \right)Ph, \\ B_{4} & = \frac{{ - 16\delta_{m} \delta_{n} }}{3MNL\pi R}\left( {\frac{{M^{2} F_{21} }}{R} + \frac{{N^{2} F_{31} }}{a} + M^{2} N^{2} F_{11} } \right) - \frac{{E_{1} N\delta_{m} \delta_{n} }}{{2ML\pi R^{2} }}, \\ B_{5} & = 2M^{2} N^{2} \left( {F_{21} + F_{31} } \right) + 0.125E_{1} N^{4} , \\ \end{aligned}$$

(36)

in which

$$\delta_{m} = \left( { - 1} \right)^{m} - 1,\delta_{n} = \left( { - 1} \right)^{n} - 1.$$

3.1 Natural frequency

From Eq. (35), the natural frequency of the toroidal shell segment is determined as

$$\omega_{mn} = \sqrt {B_{3} /B_{1} } .$$

(37)

From Eq. (36), the coefficient $B_{3}$ may be rewritten as

$$B_{3} = B_{3}^{*} + K_{1} + K_{2} \left( {M^{2} + N^{2} } \right) - N^{2} \Upphi_{1} - \left( {M^{2} + \nu N^{2} } \right)Ph ,$$

(38)

where

$$B_{3}^{*} = \left[ {A_{2} \left( {M^{2} + N^{2} } \right) - A_{3} } \right]\left( {C_{11} M + C_{21} N} \right) - A_{3} \left( {M^{2} + N^{2} } \right) + A_{5} \left( {M^{2} + N^{2} } \right)^{2} + F_{11} \left( {\frac{{M^{2} }}{R} + \frac{{N^{2} }}{a}} \right).$$

In this study, the toroidal shell segments are assumed to be exposed to uniformly raised thermal environment, and the temperature change $\Delta T$ is independent of coordinate variables $\left( {x,y,z} \right)$. In this case, from Eq. (8), the thermal parameter $\Upphi_{1}$ are expressed as

$$\Upphi_{1} = \Upphi_{10} \Delta T,$$

(39)

where $\Upphi_{10} = \frac{h\Delta T}{1 - \nu }\left( {E_{m} \alpha_{m} + \frac{{E_{m} \alpha_{cm} + E_{cm} \alpha_{m} }}{k + 1} + \frac{{E_{cm} \alpha_{cm} }}{2k + 1}} \right)$.

Introduction of Eqs. (38) and (39) into Eq. (37) yields

$$\omega_{mn} = \sqrt {\frac{{B_{3}^{*} + K_{1} + K_{2} \left( {M^{2} + N^{2} } \right) - N^{2} \Upphi_{10} \Delta T - \left( {M^{2} + \nu N^{2} } \right)Ph}}{{B_{1} }}} .$$

(40)

Equation (40) is used to investigate the natural frequencies of simply supported toroidal shell segments resting on Pasternak type elastic foundation, exposed to thermal environments, and subjected to axial compressive load.

3.2 Nonlinear forced vibration

Consider an FGM toroidal shell segment subjected to external pressure of intensity $q = Q\sin \Upomega t$ and pre-compressive load of intensity P, in which $Q,P$ are time independent constants. In this case, Eq. (35) may be rewritten in the form

$$B_{1} \ddot{f} + B_{2} \dot{f} + B_{3} f + B_{4} f^{2} + B_{5} f^{3} + \frac{{4\delta_{m} \delta_{n} }}{MNL\pi R}\left[ { - Q\sin \Upomega t + \frac{{\Upphi_{1} }}{R} + \left( {\frac{\nu }{R} + \frac{1}{a}} \right)Ph} \right] = 0.$$

(41)

Equation (41) is used to study characteristics of nonlinear forced vibration of shells.

3.3 Nonlinear frequency–amplitude relation

To establish the frequency–amplitude relation of toroidal shell segment, first, we introduce $f = A\sin \Upomega t$ into Eq. (41) and then integrating the result equation over a quarter of vibration period. As the result, the nonlinear frequency–amplitude relation is obtained as follows

$$\gamma^{2} - c_{1} \gamma = 1 + c_{2} A + c_{3} A^{2} + \left( { - c_{4} Q + c_{5} P + c_{6} \Upphi_{1} } \right)\frac{1}{A}$$

(42)

where $\gamma$ is frequency ratio defined as $\gamma = \frac{\Upomega }{{\omega_{mn} }}$, and

$$c_{1} = \frac{{2B_{2} }}{{\pi \sqrt {B_{1} B_{3} } }},c_{2} = \frac{{8B_{4} }}{{3\pi B_{3} }},c_{3} = \frac{{3B_{5} }}{{4B_{3} }},c_{4} = \frac{{4\delta_{m} \delta_{n} }}{{B_{3} MNL\pi R}},c_{5} = \frac{{16\delta_{m} \delta_{n} h}}{{B_{3} MNL\pi^{2} R}}\left( {\frac{\nu }{R} + \frac{1}{a}} \right),c_{6} = \frac{{16\delta_{m} \delta_{n} }}{{B_{3} MNL\pi^{2} R^{2} }}.$$

(43)

Equations (40), (41) and (42) are used to study characteristics of nonlinear vibration of simple supported FGM toroidal shell segments exposed to thermal environment, surrounded by Pasternak type elastic foundation within the framework of Reddy’s third-order shear deformation shell theory.

4 Numerical results and discussions

4.1 Validation of the present study

To validate the accuracy of formulations and the reliability of proposed approach, in the present study, this section will give two numerical examples. Since as longitudinal curvature radius $a \to \infty$, toroidal shell becomes cylindrical shell, in the first comparison, a simply supported isotropic cylindrical shell is considered. The material, geometrical properties are given as: $E = 210\,\,{\text{GPa}}$, $\nu = 0.3$, $\rho = 7850\,\,{\text{kg/m}}^{ 3}$, $h = 0.06\,{\text{m}}$, $R = 100h$, $L = 0.5R$. The effects of elastic foundation and temperature are ignored. The natural frequencies are calculated by using Eq. (40) with $a \to \infty$ and listed in Table 1 in comparison with the results reported by Bhimaraddi (1984) using Hamilton’s principle based on higher-order displacement model, and by Shen (2012) utilizing a two-step perturbation technique based on higher-order shear deformation theory, and by Li (2008) using a wave propagation approach and exact solution based on Flugge classical thin shell theory. It is evident that, a good agreement is obtained in this comparison, especially the results in the present study and the results reported by Li (2008) using exact solution are almost the same.

Table 1 Comparison of dimensionless frequencies $\varpi = \omega \left( {h /\pi } \right)\sqrt {2\left( {1 + \nu } \right)\rho /E}$ for an isotropic cylindrical shell ($h = 0.06,R = 100h,\,L = 0.5R,\,E = 210\,\,{\text{GPa}},\,\nu = 0.3,\,\rho = 7850\,\,{\text{kg/m}}^{ 3}$)

In the second numerical example for verification, FGM toroidal shell segments with various $a /R$ ratios are considered. The shells are made by a mixture of ceramic and metal constituents with material properties as: $E_{c} = 380\,{\text{GPa}}$, $E_{m} = 70\,\,{\text{GPa}}$, $\rho_{m} = 2702\,\,{\text{kg/m}}^{ 3}$, $\rho_{c} = 3800\,\,{\text{kg/m}}^{ 3}$, $\nu_{m} = \nu_{c} = 0.3$, $k = 1$. The geometrical properties of toroidal shell segments such as thickness $h$, equator radius $R$ and length $L$ are given as: $h = 0.06\,{\text{m}}$, R=100 h, $L = 0.5R$. The natural frequencies $\omega \left( {\text{rad/s}} \right)$ are calculated by using Eq. (40) in case of without elastic foundation, without temperature effect, without compressive load and compared with results obtained by Bich et al. (2016) as show in Table 2. Again, a good agreement is shown in this comparison for both concave shells i.e. $a < 0$, cylindrical shell i.e. $a \to \infty$ and convex shells i.e. $a > 0$. Furthermore, the values of natural frequency obtained in the present study based on Reddy’s third-order shear deformation theory and analytical approach are always smaller than values that obtained in work (Bich et al. 2016) based on classical shell theory and the similar approach.

Table 2 Comparison of natural frequencies $\omega \left( {\text{rad/s}} \right)$ for FGM toroidal shell segments: $h = 0.06\,{\text{m}}$, $R = 100h$, $L = 0.5R$, $E_{m} = 70\,\,{\text{GPa}}$, $E_{c} = 380\,{\text{GPa}}$, $\rho_{m} = 2702\,\,{\text{kg/m}}^{ 3}$, $\rho_{c} = 3800\,\,{\text{kg/m}}^{ 3}$, $\alpha_{m} = 23 \times 10^{ - 6} \, 1 / {\text{K}}$, $\alpha_{c} = 5.4 \times 10^{ - 6} \, 1 / {\text{K}}$, $k = 1$, $\nu = 0.3$, $\left( {m,n} \right) = \left( {1,1} \right)$

4.2 The natural frequencies

This section will investigate the effects of thermal environment, compressive load, elastic foundation, contribution of material constituents and geometry on natural frequencies of simply supported moderately thick FGM toroidal shell segments under compressive load. The material properties of metal and ceramic constituents are given as (Bich et al. 2016): $E_{m} = 70\,\,{\text{GPa}}$, $E_{c} = 380\,{\text{GPa}}$, $\rho_{m} = 2702\,\,{\text{kg/m}}^{ 3}$, $\rho_{c} = 3800\,\,{\text{kg/m}}^{ 3}$, $\alpha_{m} = 23 \times 10^{ - 6} \, 1 / {\text{K}}$, $\alpha_{c} = 5.4 \times 10^{ - 6} \, 1 / {\text{K}}$, $\nu_{m} = \nu_{c} = 0.3$. Table 3 represents comparison of natural frequencies with various of temperature changes, compressive loads in cases of with and without elastic foundations. It can be observed that, the natural frequency is decreased as compressive load increases and/or environment temperature increases. In contrast, natural frequency is increased due to the presence of elastic foundations. This characteristic of natural frequency also found by analyzing the Eq. (40). The effects of equator radius to thickness ratio $R /h$, length to equator radius $L /R$ and volume fraction index $k$ that defined the contribution of material constituents in FGM on natural frequency of simply supported FGM toroidal shell segments resting on elastic foundations in case of without temperature effect and without compressive load are shown in Table 4. It can be seen, the natural frequency decreases as the volume fraction index and/or the length to equator radius ratio $L /R$ and/or the equator radius to thickness ratio $R /h$ increases. It means that, the richer ceramic shells and/or shorter shells and/or thicker shells have higher natural frequencies. Table 2 shows the effects of the longitudinal curvature radius to equator radius ratio $a /R$ on natural frequency. It can be observed that, convex shells i.e. $a > 0$ have higher natural frequencies in comparison with cylindrical shell $\left( {a \to \infty } \right)$ and concave shells $\left( {a < 0} \right)$. Furthermore, the more convex the shell is, the higher natural frequency it is, in contrast, the more concave the shell is, the lower natural frequency it is.

Table 3 Linear free frequency $\omega = \sqrt {B_{3} /B_{1} }$ of FGM toroidal shell segments ($h = 0.06\,{\text{m,}}\,R = 100h,L = 0.5R,\,a = 5R,\,k = 1,\,m = 1,\,n = 1$)

Table 4 Linear free frequency $\omega = \sqrt {B_{3} /B_{1} }$ of FGM toroidal shell segments $\Delta T = 0\,K,\,P = 0\,{\text{MPa}},\,K_{1} = 2.5 \times 10^{7} {\text{N/m}}^{ 3} ,\,K_{2} = 5 \times 10^{5} {\text{N/m,}}\,h = 0.06\,{\text{m,}}\,a = 5R,\,m = 1,\,n = 1$

4.3 The frequency–amplitude relation

Consider simply supported moderately thick toroidal shell segments made of FGM composed of ceramic and metal constituents with the material properties are given as (Bich et al. 2016): $E_{m} = 70\,\,{\text{GPa}}$, $E_{c} = 380\,{\text{GPa}}$, $\rho_{m} = 2702\,\,{\text{kg/m}}^{ 3}$, $\rho_{c} = 3800\,\,{\text{kg/m}}^{ 3}$, $\alpha_{m} = 23 \times 10^{ - 6} \, 1 / {\text{K}}$, $\alpha_{c} = 5.4 \times 10^{ - 6} \, 1 / {\text{K}}$, $\nu_{m} = \nu_{c} = 0.3$. Using Eq. (42) in case of without temperature and without compressive load, the frequency–amplitude curves are plotted in Figs. 2, 3, 4, 5, 6, and 7 in case of undamped free vibrations and in Figs. 8, 9 and 10 in case of undamped forced vibration. Information in Figs. 2, 3 and 4 shows the effects of elastic foundation on frequency–amplitude curves with modes $\left( {m = 1,n = 3} \right)$, $\left( {m = 1,n = 5} \right)$ and $\left( {m = 1,n = 7} \right)$, respectively. It can see that with the same amplitude, the nonlinear free frequencies of the shells resting on elastic foundation are higher than that of the shells not to be rested on elastic foundation. Figures 5, 6 and 7 analyzes the effects of longitudinal curvature radius to equator radius ratio $a /R$ on frequency–amplitude relation of convex toroidal shell segments. In the region of small amplitude, when $a /R$ ratio decrease, the free frequencies of toroidal shell segment increase. It means that the free frequencies of the more convex shells are greater than that of the less convex ones. Figure 8, 9 and 10 illustrates the effects of exciting force amplitude on frequency–amplitude curves. As expected, the amplitude of nonlinear forced vibration increases as the exciting force amplitude increases. Furthermore, in the region of larger amplitude, frequency–amplitude curves come close together. It means that, in the larger amplitude, exciting force has negligible effect on frequency–amplitude relation.

Fig. 2

Effect of elastic foundation on frequency–amplitude curves of undamped free vibrations $\left( {m = 1,n = 3} \right)$

Fig. 3

Effect of elastic foundation on frequency–amplitude curves of undamped free vibrations $\left( {m = 1,n = 5} \right)$

Fig. 4

Effect of elastic foundation on frequency–amplitude curves of undamped free vibrations $\left( {m = 1,n = 7} \right)$

Fig. 5

Effect of $a /R$ ratio on frequency–amplitude curves of undamped free vibrations $\left( {m = 1,n = 3} \right)$

Fig. 6

Effect of $a /R$ ratio on frequency–amplitude curves of undamped free vibrations $\left( {m = 1,n = 5} \right)$

Fig. 7

Effect of $a /R$ ratio on frequency–amplitude curves of undamped free vibrations $\left( {m = 1,n = 7} \right)$

Fig. 8

Effect of external pressure on frequency–amplitude curves of forced vibration $\left( {m = 1,n = 1} \right)$

Fig. 9

Effect of external pressure on frequency–amplitude curves of forced vibration $\left( {m = 1,n = 3} \right)$

Fig. 10

Effect of external pressure on frequency–amplitude curves of forced vibration $\left( {m = 1,n = 7} \right)$

4.4 Nonlinear vibration of moderately thick toroidal shell segment

In this section, the effects of temperature field, compressive load, external pressure, material and geometrical parameters, and elastic foundation on nonlinear vibration response of simply supported moderately thick FGM toroidal shell segments are presented and discussed. The elastic modulus, mass density, thermal expansion coefficient and Poisson’s ratio of material constituents are given as: $E_{m} = 70\,\,{\text{GPa}}$, $E_{c} = 380\,{\text{GPa}}$, $\rho_{m} = 2702\,\,{\text{kg/m}}^{ 3}$, $\rho_{c} = 3800\,\,{\text{kg/m}}^{ 3}$, $\alpha_{m} = 23 \times 10^{ - 6} \, 1 / {\text{K}}$, $\alpha_{c} = 5.4 \times 10^{ - 6} \, 1 / {\text{K}}$, $\nu_{m} = \nu_{c} = 0.3$.

4.4.1 Effect of environment temperature

The effects of environment temperature on nonlinear vibration response of toroidal shell segments resting on elastic foundations and under external pressure are shown in Figs. 11, 12, and 13 with modes $\left( {m = 1,n = 1} \right)$, $\left( {m = 1,n = 3} \right)$ and $\left( {m = 3,n = 3} \right)$, respectively. It can be observed that the amplitude of nonlinear vibration increases as temperature increases. Environment temperature has deteriorated effects on load bearing capacity shells. Furthermore, it can be seen from Figs. 11, 12 and 13 that temperature have caused negative deflection for shells before it is affected by external pressure. The amplitude of nonlinear vibration of shells corresponding to mode $\left( {m = 1,n = 1} \right)$ in Fig. 11 is greater than that corresponding to modes $\left( {m = 1,n = 3} \right)$ and $\left( {m = 3,n = 3} \right)$ in Figs. 12 and 13.

Fig. 11

Effect of temperature on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 12

Effect of temperature on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

Fig. 13

Effect of temperature on nonlinear vibration response of FGM shell $\left( {m = 3,n = 3} \right)$

4.4.2 Effect of mechanical loads

Figures 14, 15, 16 and 17 indicate the effects of external pressure on nonlinear vibration response of shell with the modes $\left( {m = 1,n = 1} \right)$, $\left( {m = 1,n = 3} \right)$, $\left( {m = 1,n = 5} \right)$ and $\left( {m = 3,n = 3} \right)$, respectively. As expected, the amplitude of vibration increases as exciting force amplitude increases. The effects of compressive loads are analyzed in Figs. 18, 19 and 20. As can be seen, when increasing compressive load, the amplitudes of nonlinear vibration of shell go down. The presence of compressive load reduces the load bearing capacity of shells. Furthermore, the curve corresponding to the case of without compressive load $\left( {P = 0\,{\text{Pa}}} \right)$ is higher than ones in case of presence of compressive load. It means that compressive load makes the shell to be deflected outward.

Fig. 14

Effect of external pressure on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 15

Effect of external pressure on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

Fig. 16

Effect of external pressure on nonlinear vibration response of FGM shell $\left( {m = 1,n = 5} \right)$

Fig. 17

Effect of external pressure on nonlinear vibration response of FGM shell $\left( {m = 3,n = 3} \right)$

Fig. 18

Effect of compressive load on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 19

Effect of compressive load on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

Fig. 20

Effect of compressive load on nonlinear vibration response of FGM shell $\left( {m = 3,n = 3} \right)$

4.4.3 Effect of material constituent contribution

It can be observed from Eq. (1) that when the volume fraction index $k$ decrease, volume fraction of ceramic constituent increases and effective elastic modulus of FGM increases, the material will be stiffer. This material characteristic is also indicated in Figs. 21, 22 and 23, because the amplitude of nonlinear vibration of shell decreases as the volume fraction index decreases.

Fig. 21

Effect of material properties on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 22

Effect of material properties on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

Fig. 23

Effect of material properties on nonlinear vibration response of FGM shell $\left( {m = 3,n = 3} \right)$

4.4.4 Effect of $R /h$ ratio

Effects of equator radius to thickness ratio $R /h$ on nonlinear vibration response of simply supported FGM toroidal shell segments resting on Pasternak type elastic foundation and subjected to harmonic external pressure are illustrated in Figs. 24, 25 and 26 with modes $\left( {m = 1,n = 1} \right)$, $\left( {m = 1,n = 3} \right)$ and $\left( {m = 3,n = 3} \right)$, respectively. As can be observed, the amplitude of nonlinear vibration of shells increases as $R /h$ ratio increases. It is expected, because the thinner the shell is, the softer it is.

Fig. 24

Effect of $R /h$ ratio on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 25

Effect of $R /h$ ratio on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

Fig. 26

Effect of $R /h$ ratio on nonlinear vibration response of FGM shell $\left( {m = 3,n = 3} \right)$

4.4.5 Effect of $L /R$ ratio

Figures 27, 28 and 29 show the effects of length to equator radius ratio $L /R$ on nonlinear vibration responses of shell with modes $\left( {m = 1,n = 1} \right)$, $\left( {m = 1,n = 3} \right)$ and $\left( {m = 3,n = 3} \right)$, respectively. As can be seen, when $L /R$ ratio decreases, the amplitudes of nonlinear vibration of shells also go down. It means that, the shorter the shell is, the stiffer it is.

Fig. 27

Effect of $L /R$ ratio on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 28

Effect of $L /R$ ratio on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

Fig. 29

Effect of $L /R$ ratio on nonlinear vibration response of FGM shell $\left( {m = 3,n = 3} \right)$

4.4.6 Effect of $a /R$ ratio

Effects of longitudinal curvature radius to equator radius ratio $a /R$ on nonlinear vibration responses of FGM toroidal shell segments are analyzed in Figs. 30, 31, 32 and 33. When modifying $a /R$ ratio, the amplitudes of nonlinear vibration of both convex and concave shell slightly change. Moreover, information in Fig. 30 indicates that, the amplitude of nonlinear vibration of convex shell decreases as $a /R$ ratio increases. It means that, the amplitudes of less convex shells are smaller than that of more convex ones.

Fig. 30

Effect of $a /R$ ratio on nonlinear vibration response of convex shell $\left( {m = 1,n = 1} \right)$

Fig. 31

Effect of $a /R$ ratio on nonlinear vibration response of convex shell $\left( {m = 1,n = 3} \right)$

Fig. 32

Effect of $a /R$ ratio on nonlinear vibration response of concave shell $\left( {m = 1,n = 1} \right)$

Fig. 33

Effect of $a /R$ ratio on nonlinear vibration response of concave shell $\left( {m = 1,n = 3} \right)$

4.4.7 Effect of elastic foundations

Figures 34 and 35 illustrates the beneficial influence of elastic foundations on nonlinear forced vibration of shell. The amplitude of shell resting on two-parameters elastic foundation is the smallest, whereas, the amplitude of shell which free of interaction of elastic foundation is the highest.

Fig. 34

Effect of elastic foundation stiffness on nonlinear vibration response of FGM shell $\left( {m = 1,n = 1} \right)$

Fig. 35

Effect of elastic foundation stiffness on nonlinear vibration response of FGM shell $\left( {m = 1,n = 3} \right)$

5 Conclusions

An analytical solution for investigating the nonlinear vibration and dynamic response of simply supported FGM toroidal shell segments in thermal environment resting on Pasternak type elastic foundation subjected to external pressure and compressive load is presented in this study. The governing equations are established within framework of Reddy’s third order shear shell theory taking von Karman nonlinearity into consideration. Galerkin method and Runge–Kutta method are applied to obtain the expressions of natural frequencies, nonlinear relations of frequency–amplitude, and nonlinear dynamic response. The accuracy of formulas is validated by comparisons with works reported in literature. The effects of material and geometrical properties, mechanical and thermal loadings, elastic foundations on natural frequencies, frequency–amplitude curves, and nonlinear forced vibration and dynamic response of moderately thick simply supported are investigated and discussed in detail. This study shows that:

• Environment temperature has deteriorated effects on load bearing capacity and causes the reduction of values of natural frequencies of shells.

• The presence of compressive load makes the convex shell to be deflected outward and causes the reduction of values of natural frequencies of shells.

• Elastic foundation causes the enhancement of both natural frequency and nonlinear free frequency, and reduction of amplitude of nonlinear forced vibration.

• The richer-ceramic and/or thicker and/or shorter the shell is, the higher natural frequency and better dynamic carrying capacity it is.

• With the same equator radius, convex shell has higher natural frequency and better dynamic carrying capacity than those of cylindrical shell and concave shell.