Entropy generation analysis in the electro-osmosis-modulated peristaltic flow of Eyring–Powell fluid

Abstract

In the current paper, numerical study is carried out to investigate the peristaltic propulsion of Eyring–Powell fluid in a vertical symmetric channel with electro-kinetic pumping and transvers Lorentz force. The mass, momentum and energy equations for non-Newtonian fluid are formulated and simplified using suitable transformations and dimensionless variables. The governing equations in dimensionless form are solved numerically by implicit finite difference scheme for stream function and temperature profile in computational software Mathematica 9. The impact of several parameters of interest is analyzed and discussed for both values of Helmholtz–Smoluchowski velocity U_HS and Joule heating parameter through graphs. An entropy generation analysis is also considered and observed for various values of involved parameters. The nonlinear dimensionless equations are also solved by another numerical technique which is built in routine in MATLAB which is commonly known as bvp4c. The results for velocity and temperature are compared by both techniques. The Joule heating parameter also increases the size and number of isothermal bolus. The entropy of the system can be controlled for assisting pumping, i.e., U_HS < 0. The entropy generation decreases with k for U_HS < 0, while increases with k for U_HS > 0.

Introduction

The entropy generation is the loss of energy in thermo-dynamical systems due to resistive forces, diffusion processes, radiation effects and chemical reactions. Mathematicians and physicists observed in detail the analysis and discussion of entropy generation with thermal radiations, which defines the process of irreversibility in various thermal systems. The irreversibility processes are upgraded by the well-known and powerful law called the second law of thermodynamics which is used by many researchers in this field due to these broad applications. Many researchers used the first law of thermodynamics instead of the second law of thermodynamics in the initial stage, but they finalize that latter one gives better results as compared to the former. Entropy generation also tells us about the destruction taking place in the related system. The most useful and tremendous results (factors) which play a vital role in the concept of entropy generation can be reduced by using entropy optimization. The best way to check the effect of energy utilization in during the convective flow is one of the main and ideal problems in the field of engineering. Similarly, the entropy generation has a fundamental and great applications in the process of power collectors, electronic systems, slider bearing and geothermal system. According to the recent research and developing mechanism of the science and engineering field, there is great relation between entropy and fluid mechanics because they are interlinked with each other due to their great behavior and similar relationship.

The role of entropy in universe is either remains same or increases but nevermore subsidence. In the field of physics, the second law of thermodynamics is considered to be the foundation of entropy. Bejan [1] provided a comprehensive material on heat transfer and entropy analysis. After the pioneer work of Bejan, the second law of thermodynamics has been used by Nag and Kumar [2] to investigate the entropy generation in convective heat transfer for the flow of viscous fluid in a duct. The various reasons behind an entropy generation which are applied in thermal energy were studied by Bejan in [3]. He also studied that the entropy generation also destructs the available condition of the system. Entropy generation mechanism for the flow of liquid in a channel has been analytically studied by Mahmud and Fraser [4], and he also obtained the expression for Bejan number and entropy generation. Entropy generation in axisymmetric flow of Williamson fluid was studied by Azam et al. [5]. A numerical study has been conducted by Erbay et al. [6] to analyze the entropy generation during the Couette flow of a viscous fluid between two parallel plates. Makinde and Maserumule [7] realized the production rates of entropy for variable viscous Couette flow through a non-uniform channel having non-uniform wall temperature. Kumar’s function has been used for analytical treatment of the analysis of electrically conducting viscoelastic fluid by Aiboud and souli [8]. Impact of thermal radiations and viscous dissipation on the entropy generation is numerically studied by Butt et al. [9] for the Blasius flow. Effects of viscous dissipation on the entropy generation in laminar fully developed forced convective in a micro-channel have been investigated by Mah et al. [10]. Das and Jana [11] found the exact solutions of entropy generation in that channel using the influence of MHD and constant pressure gradient and familiarized that the large amount of heat transfer and its effects can be detected in the center of that channel, whereas the irreversibility of fluid friction is dominated at the walls of the channel. Adesanya and Makinde [12] performed both the convective heating and suction/injection effects on the entropy generation of a steady fluid through a channel. Adesanya et al. [13] used the perturbation techniques to find the expressions of velocity, temperature and entropy for a couple stress fluid flowing in a channel. The analytical solution of entropy generation in a porous channel with appropriate boundary conditions within the convective heat transfer was treated by Ibanez [14]. A comprehensive review about the entropy generation over rotating frame was presented by Mabood et al. [15]. Numerical solutions for the entropy generation in the flow of Carreau fluid are examined by Raza et al. [16]. More recently, Yusuf and Mabood [17] analyzed the entropy generation for the slip flow of electrically conductivity Williamson fluid with chemical reaction.

In the above-mentioned studies, the flows between fix or moving parallel plates or in the channels with moving walls are considered, but peristalsis is one type of fluid motions in which the fluids are transported due to the contraction and relaxation of the walls of the channels. Furthermore, the flow induced by the combined effects of peristalsis and electro-osmosis was discussed due to their ample applications in biomedical engineering. Entropy generation in the flow of different fluids considering different mediums is reported by several researchers; some latest studies are included here. Soudi et al. [18] discussed the reasons of entropy generation in the peristaltic pumps and circular tubes with contracting walls. A theoretical study has been carried out by Munawar et al. [19] to disclose the entropy production for the peristaltically induced flow of viscous fluid having temperature-dependent viscosity, and they predicted that entropy generation in fluid motion can be minimized for case of low viscous dissipation and variable viscosity. Narla et al. [20] computed the Bejan number and entropy production number for a viscous fluid in curved configuration and concluded that curvature of the channel acts as source of entropy generation. Production of entropy generation in flow of blood in magnetic environment is investigated by Rashidi et al. [21] and concluded that entropy generation enhances with all pertinent parameters. Akbar and Butt [22] investigated the entropy production in the peristaltic flow of copper–water nanoliquid in a circular tube and concluded that near the walls the entropy generation number has high values compared to the center of the tube. Saleem [23] examined the production of entropy in the peristaltically induced flow of viscous fluid having variable viscosity in a channel and established that in the cooled region of channel the variable viscosity enhanced the entropy generation. Nawaz et al. [24] emphasized the effects of radially applied magnetic field and curvature of the channel on entropy generation for the peristaltic motion of Williamson fluid. Bibi et al. [25] consider the variable viscosity and thermal conductivity and discussed their influence on the entropy generation production for peristaltic flow of Sisko fluid in a curved channel and summarized that large values of viscosity and thermal conductivity minimized the irregularity in thermal transport through entropy production. Hayat et al. [26] discussed the entropy generation minimization and non-Darcian resistance on the peristaltic flow of Sutterby fluid with variable properties.

Flows due to the applied of electric field on channel’s walls have extensive range of applications in biomedical engineering. Zhao and Liu [27] discussed entropy generation analysis in electro-osmotic flow in open and closed end micro-channels. Shamshiri et al. [28] analyzed the entropy generation associated with mixed electro-kinetically induced and pressure-driven flow of power law fluid. Goswami et al. [29] studied the entropy generation minimization in a flow of non-Newtonian fluid through electro-osmosis. Bhatti et al. [30] discussed entropy analysis on electro-kinetically regulated peristaltic propulsion of nanofluid flow with magnetic effects over a micro-channel. Xie and Jian [31] performed a study to discuss the entropy generation of double-layer MHD electro-osmotic flow over micro-channel. Ranjit and Shit [32] investigated the entropy generation in the electro-osmosis-modulated peristaltic motion of electrically conducting viscous fluid. In another article, Ranjit et al. [33] analyzed the flow, heat transfer and entropy generation for two-layered flow produced by mutual contribution of peristaltic pumping and electro-osmosis. Narla et al. [34] discussed the phenomena of entropy production for the electro-osmotic flow in curved configuration.

Joule heating is a process by which the thermal energy is produced in an electrical conductor produced by the passage of electric current. Swain and Mahanthesh [35] discussed he phenomena of Joule heating in electrically conducting fluid. Mahanthesh et al. [36] reported significance of Joule heating on the flow of hybrid nanofluid over a wedge. Entropy generation and heat transport analysis were carried out by Gireesha et al. [37] for the flow of Casson fluid flow with viscous and Joule heating in an inclined porous microchannel. Shashikumar et al. [38] investigated the influence of Joule heating and multiple slips on the transport of magneto-nanoliquid in a microchannel. Ahmed et al. [39] discussed the Joule heating in mixed convective peristalsis of Sisko fluid.

During recent years, the impact of magnetic field on the flow has various applications [40,41,42,43,44,45]. Moreover, it is obvious from the above discussion that entropy generation for the flow of Newtonian and non-Newtonian fluids in different geometries has been reported, but the entropy production in the electro-osmosis-modulated peristaltic flow of Eyring–Powell fluid is not reported. In this regard, a numerical study is performed to emphasize the effects of applied magnetic and electric fields on the behavior of flow, thermal transport and entropy generation for the Eyring–Powell fluid. Moreover, how extraordinary physical parameters, all of those, are related to the issue impacts the liquid flow and heat transfer, and those impacts are analyzed through graphs and table so that the present study and outcomes are new. The problem formulation is presented in the “Introduction” section. The relation for entropy generation and Bejan number is given in the “Mathematical formulation” section. Solution methodology is described in the “Mathematical formulation” section. Obtained results along with discussion are documented in the “Numerical method” section, while the obtained results are validated in the “Results and discussion” section and some findings are reported at the end in the “Validation of numerical results” section.

Mathematical formulation

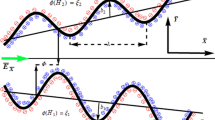
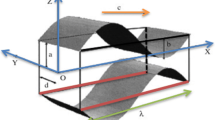
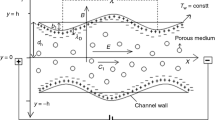
The flow of electrically conducting generalized Newtonian fluid characterized by the constitutive equation of Eyring–Powell fluid in a vertical symmetric channel is taken into consideration. The flow is caused due to propagation of sinusoidal wave with speed $c$ of amplitude $a$ and wavelength $\lambda$ and the application of electric field. The Cartesian coordinate system $\left( {X^{\prime}, Y^{\prime}} \right)$ is used in such a way that $X^{\prime}$-axis is chosen in the direction of the transport of fluid, while $Y^{\prime}$-axis is taken in the direction normal to the flow. The right walls of the channel are represented by $h\left( {X^{\prime},t^{\prime}} \right)$ and mathematically can be expressed as:

$$h\left( {X^{\prime},t^{\prime}} \right) = d - a\cos^{2} \frac{\pi }{\lambda }\left( {X^{\prime} - ct^{\prime}} \right),$$

(1)

where $2d$ is used to represent the width of the channel and $t^{\prime}$ is time (Fig. 1).

Fig. 1

Geometry of the problem

The governing equations for the two-dimensional flow of generalized Newtonian fluid under consideration in Cartesian co-ordinate system are Ranjit and Shit [32]

$$\frac{{\partial U^{\prime}}}{{\partial X^{\prime}}} + \frac{{\partial V^{\prime}}}{{\partial Y^{\prime}}} = 0,$$

(2)

$$\rho \left[ {\frac{{\partial U^{\prime}}}{{\partial t^{\prime}}} + U^{\prime}\frac{{\partial U^{\prime}}}{{\partial X^{\prime}}} + V^{\prime}\frac{{\partial U^{\prime}}}{{\partial Y^{\prime}}}} \right] = - \frac{\partial P}{{\partial X^{\prime}}} + \frac{{\partial \tau_{{{\text{X}}^{\prime}{\text{X}}^{\prime}}} }}{{\partial X^{\prime}}} + \frac{{\partial \tau_{{{\text{X}}^{\prime}{\text{Y}}^{\prime}}} }}{{\partial Y^{\prime}}} + \rho_{\text{e}} E_{0} - \sigma B_{0}^{2} U^{\prime} + \rho g\alpha_{1} \left( {T - T_{0} } \right),$$

(3)

$$\rho \left[ {\frac{{\partial V^{\prime}}}{{\partial t^{\prime}}} + U^{\prime}\frac{{\partial V^{\prime}}}{{\partial X^{\prime}}} + V^{\prime}\frac{{\partial V^{\prime}}}{{\partial Y^{\prime}}}} \right] = - \frac{\partial P}{{\partial Y^{\prime}}} + \frac{{\partial \tau_{{{\text{Y}}^{\prime}{\text{X}}^{\prime}}} }}{{\partial X^{\prime}}} + \frac{{\partial \tau_{{{\text{Y}}^{\prime}{\text{Y}}^{\prime}}} }}{{\partial Y^{\prime}}},$$

(4)

$$\rho C_{\text{p}} \left[ {\frac{{\partial T^{\prime}}}{{\partial t^{\prime}}} + U^{\prime}\frac{{\partial T^{\prime}}}{{\partial X^{\prime}}} + V^{\prime}\frac{{\partial T^{\prime}}}{{\partial Y^{\prime}}}} \right] = k_{1} \left[ {\frac{{\partial^{2} T^{\prime}}}{{\partial X^{{\prime}{2}} }} + \frac{{\partial^{2} T^{\prime}}}{{\partial Y^{{\prime}{2}} }}} \right] + \sigma B_{0}^{2} U^{{\prime}{2}} + \sigma E_{0}^{2} + \frac{{\partial U^{\prime}}}{{\partial X^{\prime}}}\tau_{{{\text{X}}^{\prime}{\text{X}}^{\prime}}} + \left( {\frac{{\partial V^{\prime}}}{{\partial X^{\prime}}} + \frac{{\partial U^{\prime}}}{{\partial Y^{\prime}}}} \right) \tau_{{{\text{X}}^{\prime}{\text{Y}}^{\prime}}} + \frac{{\partial V^{\prime}}}{{\partial Y^{\prime}}}\tau_{{{\text{Y}}^{\prime}{\text{Y}}^{\prime}}} .$$

(5)

The velocity due to no-slip boundary condition at both walls is zero; therefore, appropriate boundary conditions are

$$\begin{aligned} U^{\prime} & = 0,\quad V^{\prime} = \frac{{ - h\left( {X^{\prime},t^{\prime}} \right)}}{{\partial t^{\prime}}},\quad T^{\prime} = T_{0} \;{\text{at}}\;Y^{\prime} = - h \\ U^{\prime} & = 0,\quad V^{\prime} = \frac{{h\left( {X^{\prime},t^{\prime}} \right)}}{{\partial t^{\prime}}},\quad T^{\prime} = T_{1} \;{\text{at}}\;Y^{\prime} = h . \\ \end{aligned}$$

(6)

In the above equations, $\tau_{{\text{{X}}^{\prime}{\text{X}}^{\prime}}}$, $\tau_{{{\text{X}}^{\prime}{\text{Y}}^{\prime}}}$ and $\tau_{{{\text{Y}}^{\prime}{\text{Y}}^{\prime}}}$ are the components of extra stress tensor and for Eyring–Powell fluid is defined as:

$$\tau_{\text{ij}} = \mu \frac{{\partial U_{\text{i}}^{^{\prime}} }}{{\partial X_{\text{j}}^{^{\prime}} }} + \frac{1}{\beta }\sinh^{ - 1} \left[ {\frac{1}{{c_{1} }}\frac{{\partial U_{\text{i}}^{^{\prime}} }}{{\partial X_{\text{j}}^{^{\prime}} }}} \right],$$

(7)

where $U^{\prime}$ and $V^{\prime}$ indicate the velocity components, P is the fluid pressure, $E_{0}$ is the induced electric field and is taken as constant, $B_{0}$ denotes the strength of magnetic field applied in the normal direction of the flow, $\rho$ represents the fluid density, $g$ denotes the gravitational acceleration, $\sigma$ denotes the electrical conductivity, $\beta$ and $c_{1}$ are characteristics of Eyring–Powell fluid, $T^{\prime}$ be the temperature distribution, $k_{1}$ denotes the thermal conductivity of the fluid, whereas $\alpha_{1}$ denotes the coefficient of linear thermal expansion and $\rho_{\text{e}}$ is the ionic charge density, for a symmetric electrolyte the density of ionic energy is defined by Prakash et al. [46]

$$\rho_{\text{e}} = ez\left( {n^{ + } - n^{ - } } \right),$$

(8)

where $n^{ + }$ and $n^{ - }$ are the number of densities of cations and anions, respectively. The charge density $\rho_{\text{e}}$ and the electric potential distribution $E^{\prime}$ are related by the Poisson equation due to the presence of electric double layer in the channel and the well-known Poison equation is given as

$$\frac{{{\text{d}}^{2} E^{\prime}}}{{{\text{d}}X^{{\prime}{2}} }} + \frac{{{\text{d}}^{2} E^{\prime}}}{{{\text{d}}Y^{{\prime}{2}} }} = - \frac{{\rho_{\text{e}} }}{{ \in \in_{0} }},$$

(9)

where $\in$ is the dielectric constant and $\in_{0}$ is the permittivity of the vacuum. To obtain the potential distribution and the charge number density, the Nernst Planck’s equation is given as:

$$\frac{{\partial n_{ \pm }^{^{\prime}} }}{{\partial t^{\prime}}} + U^{\prime}\frac{{\partial n_{ \pm }^{^{\prime}} }}{{\partial X^{\prime}}} + V^{\prime}\frac{{\partial n_{ \pm }^{^{\prime}} }}{{\partial Y^{\prime}}} = D\nabla^{2} n_{ \pm }^{^{\prime}} \pm \frac{Dez}{{K_{\text{B}} T_{\text{av}} }}\left( {\frac{\partial }{{\partial X^{\prime}}}\left( {n_{ \pm }^{^{\prime}} \frac{{\partial E^{\prime}}}{{\partial X^{\prime}}}} \right) + \frac{\partial }{{\partial Y^{\prime}}}\left( {n_{ \pm }^{^{\prime}} \frac{{\partial E^{\prime}}}{{\partial Y^{\prime}}}} \right)} \right),$$

(10)

where $D$ represents the diffusivity, $n$ is the number of ions, $z$ is the charge difference, K_B represents the Boltzmann constant, $e$ represents the electronic charge, $E^{\prime}$ represents the electric potential, and $T_{{{\text{av}}}}$ denotes the average temperature.

As the flow properties of the problem under consideration are time dependent in the laboratory frame, in order to make the flow problem independent of time, we can relate the components of velocity and co-ordinates in the wave frame and in the laboratory frame using the Galilean transformations

$$x^{\prime} = X^{\prime} - ct^{\prime},\,y^{\prime} = Y^{\prime}\, u^{\prime} = U^{\prime} - c,\,v^{\prime} = V^{\prime},P = p^{\prime}\,{\text{and}}\,T = T^{\prime}.$$

(11)

Using the above transformations, Eqs. (2)–(5) and (9) become

$$\frac{{\partial u^{\prime}}}{{\partial x^{\prime}}} + \frac{{\partial v^{\prime}}}{{\partial y^{\prime}}} = 0,$$

(12)

$$\rho \left[ {u^{\prime}\frac{{\partial u^{\prime}}}{{\partial x^{\prime}}} + v^{\prime}\frac{{\partial u^{\prime}}}{{\partial y^{\prime}}}} \right] = - \frac{{\partial p^{\prime}}}{{\partial x^{\prime}}} + \frac{{\partial \tau_{{{\text{x}}^{\prime}{\text{x}}^{\prime}}} }}{{\partial {{x}}^{\prime}}} + \frac{{\partial \tau_{{{\text{x}}^{\prime}y^{\prime}}} }}{{\partial {\text{y}}^{\prime}}} + \rho_{\text{e}} E_{0} - \sigma B_{0}^{2} \left( {u^{\prime} + c} \right) + \rho g\alpha_{1} (T - T_{0} )$$

(13)

$$\rho \left[ {u^{\prime}\frac{{\partial v^{\prime}}}{{\partial x^{\prime}}} + v^{\prime}\frac{\partial v^{\prime}}{{\partial y^{\prime}}}} \right] = - \frac{{\partial p^{\prime}}}{{\partial y^{\prime}}} + \frac{{\partial \tau_{{{\text{y}}^{\prime}{\text{x}}^{\prime}}} }}{{\partial x^{\prime}}} + \frac{{\partial \tau_{{{\text{y}}^{\prime}{\text{y}}^{\prime}}} }}{{\partial y^{\prime}}},$$

(14)

$$\rho C_{\text{p}} \left[ {u^{\prime}\frac{\partial T}{{\partial x^{\prime}}} + v^{\prime}\frac{\partial T}{{\partial y^{\prime}}}} \right] = k_{1} \left[ {\frac{{\partial^{2} T}}{{\partial x^{{\prime}{2}} }} + \frac{{\partial^{2} T}}{{\partial y^{{\prime}{2}} }}} \right] + \sigma B_{0}^{2} (u^{^{\prime}} + c)^{2} + \sigma E_{0}^{2} + \frac{{\partial u^{\prime}}}{{\partial x^{\prime}}}\tau_{\text{xx}} + \left( {\frac{{\partial v^{\prime}}}{{\partial x^{\prime}}} + \frac{{\partial u^{\prime}}}{{\partial y^{\prime}}}} \right) \tau_{\text{xy}} + \frac{{\partial v^{\prime}}}{{\partial y^{\prime}}}\tau_{\text{yy}} ,$$

(15)

$$u^{\prime}\frac{{\partial n_{ \pm }^{^{\prime}} }}{{\partial x^{\prime}}} + v^{\prime}\frac{{\partial n_{ \pm }^{^{\prime}} }}{{\partial y^{\prime}}} = D\left[ {\frac{{\partial^{2} n_{ \pm }^{^{\prime}} }}{{\partial x^{{^{{\prime}{2}} }} }} + \frac{{\partial^{2} n_{ \pm }^{^{\prime}} }}{{\partial y^{{^{{\prime}{2}} }} }}} \right] \pm \frac{Dez}{{K_{{\text{B}}} T_{{{\text{av}}}} }}\left( {\frac{\partial }{{\partial x^{\prime}}}\left( {n_{ \pm }^{^{\prime}} \frac{{\partial E^{\prime}}}{{\partial x^{\prime}}}} \right) + \frac{\partial }{{\partial y^{\prime}}}\left( {n_{ \pm }^{^{\prime}} \frac{{\partial E^{\prime}}}{{\partial y^{\prime}}}} \right)} \right),$$

(16)

The following dimensionless variables are introduced and

$$E = \frac{{E^{\prime}}}{\zeta },u = \frac{{u^{\prime}}}{c},v = \frac{{v^{\prime}}}{c},x = \frac{{x^{\prime}}}{\lambda },y = \frac{{y^{\prime}}}{d}, p = \frac{{p^{\prime}d^{2} }}{\mu c\lambda },n_{ \pm } = \frac{{n_{ \pm }^{^{\prime}} }}{{n_{0} }},\theta = \frac{{T - T_{0} }}{{T_{1} - T_{0} }},\phi = \frac{a}{d},\tau_{{{\text{ij}}}}^{^{\prime}} = \frac{{{\text{d}}\tau_{\text{ij}} }}{c \mu },\delta = \frac{{\text{d}}}{\lambda }.$$

(17)

Using the non-dimensional variables in Eqs (12)–(16) and dropping the primes,

$$\delta \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$

(18)

$${\text{Re}} \left[ {\delta u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right] = - \frac{\partial p}{{\partial x}} + \left[ {\delta \frac{{\partial \tau_{xx}^{^{\prime}} }}{\partial x} + \frac{{\partial \tau_{xy}^{^{\prime}} }}{\partial y}} \right] + k^{2} U_{{{\text{HS}}}} E - Ha^{2} \left( {u + 1} \right) + {\text{Gr}}\theta ,$$

(19)

$${\text{Re}} \delta \left[ {u\delta \frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}}} \right] = - \frac{\partial p}{{\partial y}} + \left[ {\delta^{2} \frac{{\partial \tau_{{{\text{yx}}}}^{^{\prime}} }}{\partial x} + \frac{{\partial \tau_{{{\text{yy}}}}^{^{\prime}.} }}{\partial y}} \right],$$

(20)

$${\text{Re}} \Pr \left[ {u\delta \frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}}} \right] = \left[ {\delta^{2} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right] + \gamma + {\text{BrHa}}^{2} \left( { u + 1} \right)^{2} + {\text{Br}}\left[ {\delta \frac{\partial u}{{\partial x}}\tau_{{{\text{xx}}}}^{^{\prime}} + \left( {\delta \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)\tau_{{{\text{xy}}}}^{^{\prime}} + \frac{\partial v}{{\partial y}}\tau_{{{\text{yy}}}}^{^{\prime}} } \right],$$

(21)

$${\text{Pe}}\left( {\delta u\frac{{\partial n_{ \pm } }}{\partial x} + v\frac{{\partial n_{ \pm } }}{{\partial y^{\prime}}}} \right) = \left( {\delta^{2} \frac{{\partial^{2} n_{ \pm } }}{{\partial x^{{^{{\prime}{2}} }} }} + \frac{{\partial^{2} n_{ \pm } }}{{\partial y^{^{\prime}2} }}} \right) \pm \frac{ezD\zeta }{{K_{\text{B}} T}}\left( {\delta^{2} \frac{\partial }{\partial x}\left( {n_{ \pm } \frac{\partial E}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {n_{ \pm } \frac{\partial E}{{\partial y}}} \right)} \right),$$

(22)

${\tau }_{\mathrm{xx}}^{^{\prime}}$, ${\tau }_{\mathrm{yy}}^{^{\prime}}$ and ${\tau }_{\mathrm{yx}}^{^{\prime}}={\tau }_{\mathrm{xy}}^{^{\prime}}$ are the normal and shear components of extra stress tensor in dimensionless form, $M=\frac{1}{\mu \beta {c}_{1}}$ and $K=\frac{M{c}^{2}}{6{{c}_{1}}^{2}{d}^{2}}$ are the Eyring–Powell fluid parameters, $\mathrm{Pe}=\frac{c\lambda }{D}$ represents the Peclet number, $\mathrm{Ha}={B}_{0}d\sqrt{\frac{\sigma }{\mu }}$ represents the Hartman number, $\mathrm{Pr}=\frac{\mu {c}_{\text{p}}}{{k}_{1}}$ denotes the Prandtl number, $\mathrm{Br}=\frac{\mu {c}^{2}}{({T}_{1}-{T}_{0})d}$ represents the Brinkman number, $\gamma =\frac{\sigma d{{E}_{0}}^{2}}{{T}_{1}-{T}_{0}}$ is the Joule heating parameter, R $\mathrm{e}=\frac{\rho cd}{\mu }$ represents the Reynolds number, $\delta =\frac{d}{\lambda }$, is the wave number, ${U}_{\mathrm{HS}}=-\frac{\in {\in }_{0}{K}_{\mathrm{B}}T{E}_{0}}{\mu ze}$ represents the Helmholtz–Smoluchowski velocity and $\mathrm{Gr}= \frac{\rho g{\alpha }_{1}{d}^{2}\left({T}_{1}-{T}_{0}\right)}{\mu c}$ represent the thermal Grashof number. In order to facilitate the solution of the above equation using low Peclet number and long wavelength approximation in Eq. (22),

$$\frac{{\partial^{2} n_{ \pm } }}{{\partial y^{2} }} \pm \frac{ezD\zeta }{{K_{{\text{B}}} T}}\frac{\partial }{\partial y}\left( {n_{ \pm } \frac{\partial E}{{\partial y}}} \right) = 0,$$

(23)

with the boundary condition

$$\begin{aligned} n_{ \pm } & = 1\,{\text{at}}\,E = 0 \\ \frac{{\partial n_{ \pm } }}{\partial y} & = 0 \,{\text{at}}\,\frac{\partial E}{{\partial y}} = 0, \\ \end{aligned}$$

(24)

where the different types of ions, positive ($n_{ + }$) and negative ($n_{ - }$), are described as:

$$n_{ \pm } = n_{0} \exp \left[ { \mp \frac{{ezE^{\prime}}}{{K_{{\text{B}}} T_{{{\text{av}}}} }}} \right],$$

where $n_{0}$ represents the number of positive and negative ions. The net charge density of the unit volume of fluid Eq. (8) is considered as:

$$\rho_{{\text{e}}} = - 2n_{0} ez\sinh \left( {\frac{ezE}{{k_{{\text{B}}} T_{{{\text{av}}}} }}} \right),$$

After using the dimensionless variables

$$\frac{{{\text{d}}^{2} E}}{{{\text{d}}y^{2} }} = \frac{{{\text{d}}^{2} }}{{\lambda_{{\text{D}}}^{2} }}\sinh \left( {\alpha E} \right),$$

(25)

where $\alpha$ represents the ionic charge density and $\lambda_{{\text{D}}}$ represents the Debye length

$$\alpha = \frac{ez\zeta }{{k_{{\text{B}}} T_{{{\text{av}}}} }},\lambda_{{\text{D}}} = \left( {ez} \right)^{ - 1} \left( {\frac{{ \in \in_{0} k_{{\text{B}}} T_{{{\text{av}}}} }}{{2n_{0} }}} \right)^{\frac{1}{2}}$$

with the conditions

$$\begin{aligned} \frac{{{\text{d}}E}}{{{\text{d}}y}} & = 0 \,{\text{at}}\,y = 0 \\ E & = 1\,{\text{at}}\,y = h. \\ \end{aligned}$$

(26)

Assuming that electrical potential is small compared with the thermal energy of the ions, so for further simplifications, we follow [32, 33] and apply the Debye–Huckel linearization approximation $\left( {\sinh \phi \approx \phi } \right).$ Solving Eq. (25) by applying the conditions described in Eq. (26) to obtain the potential parameter, i.e.,

$$E = \frac{{\cosh \left( {ky} \right)}}{{\cosh \left( {kh} \right)}},$$

(27)

where $k$ is the electro-osmotic parameter defined as $k = d{/}\lambda_{{\text{D}}}$. Using the lubrication (long wave length approximation) approach along with ${\text{Re}} \ll 1$, the stream functions $u = \partial \psi /\partial y$ and $v = - \partial \psi /\partial x$ in term velocity components using and Eq. (27) in (18–21); then, Eq. (18) is satisfied identically, and the remaining equations can be written in the form:

$$\left. {\frac{\partial p }{{\partial x}} = \left( {1 + M} \right)\frac{{\partial^{3} \Psi }}{{ \partial y^{3} }} - 3K\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{2} \frac{{\partial^{3} \Psi }}{{ \partial y^{3} }} - Ha^{2} \left( {\frac{\partial \Psi }{{ \partial y}} + 1} \right) + k^{2} U_{\text{HS}} \frac{{\cosh \left( {ky} \right)}}{{\cosh \left( {kh} \right)}} + {\text{Gr}}\theta } \right\},$$

(28)

$$\frac{\partial p }{{\partial y}} = 0,$$

(29)

$$\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \gamma + {\text{BrHa}}^{2} \left( {\frac{\partial \Psi }{{\partial y}} + 1} \right)^{2} + Br\left[ {\left( {1 + M} \right)\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{2} - K\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{4} } \right] = 0.$$

(30)

In order to eliminate $\frac{\partial p }{{\partial x}}$ from Eq. (28), we differentiate it with respect to ‘y’ and we get

$$\left( {1 + M} \right)\frac{{\partial^{4} \Psi }}{{ \partial y^{4} }} - 3K\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{2} \frac{{\partial^{4} \Psi }}{{ \partial y^{4} }} - 6K\left( {\frac{{\partial^{3} \Psi }}{{ \partial y^{3} }}} \right)^{2} \left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right) - {\text{Ha}}^{2} \frac{{\partial^{2} \Psi }}{{ \partial y^{2} }} + k^{3} U_{{{\text{HS}}}} \frac{{\sinh \left( {ky} \right)}}{{\cosh \left( {kh} \right)}} + {\text{Gr}}\frac{\partial \theta }{{\partial y}} = 0,$$

(31)

with appropriate conditions described by Jayavel et al. (2019)

$$\begin{aligned} \frac{\partial \psi }{{\partial {\text{y}}}} & = - 1,\psi = \frac{F}{2}, \theta = 0 \,{\text{at}}\,y = - h = - 1 + \phi \cos^{2} \left( {\pi \left( x \right)} \right) \\ \frac{\partial \psi }{{\partial {\text{y}}}} & = - 1,\psi = - \frac{F}{2}, \theta = 1\,{\text{at}}\,y = h = 1 - \phi \cos^{2} \left( {\pi \left( x \right)} \right), \\ \end{aligned}$$

(32)

where $F = Q + 1 - \frac{\phi }{2} - h$.

Entropy generation analysis

The irreversibility of heat transfer results in entropy generation. After determining the temperature and velocity fields, we can obtain volumetric entropy generation of the fluid under study by Arikoglu et al. [47]

$$S_{{\text{G}}} = \frac{{k_{1} }}{{T_{{\text{w}}}^{2} }}\left[ {{\Delta }T} \right]^{2} + \frac{\mu }{{T_{{\text{w}}}^{2} }}\phi + \frac{1}{{T_{{\text{w}}}^{2} }}\left( {J - QV} \right)\left( {E \cdot \,V \times B} \right),$$

(33)

$$S_{\text{G}} = \frac{k}{{T_{\text{w}}^{2} }}\left[ {\left( {\frac{\partial T}{{\partial x^{\prime}}}} \right)^{2} + \left( {\frac{\partial T}{{\partial y^{\prime}}}} \right)^{2} } \right] + \frac{\mu }{{T_{\text{w}}^{2} }}\phi + \frac{1}{{T_{\text{w}}^{2} }}\left( {J - QV} \right)\left( {E \cdot \,V \times B} \right),$$

(34)

where ${\Delta }T$ represents the temperature gradient, $k_{1}$ represents the thermal conductivity, $\mu$ represents the viscosity of the fluid, $T^{2}$ represents reference temperature, $J$ represents the electric current, $Q$ represents the charge density, $E$ is represents the electric field, $B$ is represents the magnetic field, $V$ denotes the velocity field, and $\phi$ represents the viscous dissipation. Here, $J = \sigma \left( {E + V \times B} \right)$, as $J \gg QV,$ we can neglect $QV$, where the electric and magnetic fields are defined as $E = \left( {E_{0} ,0,0} \right)$ and $B = \left( {0,0,B_{0} } \right)$. The above expression takes the form

$$\left( {J - QV} \right)\left( {E \cdot \,V \times B} \right) = \sigma E_{0}^{2} - \sigma B_{0}^{2} (U^{^{\prime}2} + V^{^{\prime}2} ).$$

(35)

Using the dimensionless variables and lubrication approach with ${\text{Re}} \ll 1,$ the above equation takes the form

$$\left( {J - QV} \right)\left( {E \cdot \,V \times B} \right) = \gamma - {\text{BrHa}}^{2} \left( {u + 1} \right)^{2} .$$

(36)

Using Eqs. (2.34) and (2.36) in Eq. (1.8) takes the form:

$$S_{{\text{G}}} = \frac{{q^{2} k}}{{T_{{\text{w}}} }}\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \frac{\mu }{{T_{{\text{w}}} }}\left[ {\left( {1 + M} \right)\left( {\frac{\partial u}{{\partial y}}} \right)^{2} - K\left( {\frac{\partial u}{{\partial y}}} \right)^{4} + \gamma + {\text{BrHa}}^{2} \left( {u + 1} \right)^{2} } \right].$$

(37)

The characteristic entropy generation is given by

$$S_{{{\text{G}}_{0} }} = \frac{k}{{{\text{d}}^{2} T_{{\text{W}}}^{2} }}\left( \frac{qd}{k} \right)^{2} .$$

(38)

The relation for dimensionless entropy generation number is

$$N_{{\text{S}}} = \frac{{S_{{\text{G}}} }}{{S_{{{\text{G}}_{0} }} }},$$

(39)

$$N_{{\text{S}}} = \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \frac{1}{ \wedge }\left[ {\left( {1 + M} \right)\left( {\frac{\partial u}{{\partial y}}} \right)^{2} - K\left( {\frac{\partial u}{{\partial y}}} \right)^{4} + \gamma + {\text{BrHa}}^{2} \left( {u + 1} \right)^{2} } \right].$$

(40)

After using the stream function, the above equation becomes

$$N_{{\text{S}}} = \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \frac{1}{ \wedge }\left[ {\left( {1 + M} \right)\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{2} - K\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{4} + \gamma + {\text{BrHa}}^{2} \left( {\frac{\partial \Psi }{{\partial y}} + 1} \right)^{2} } \right],$$

(41)

where the parameter ${\Lambda }$ is defined as $\wedge = \frac{qd}{{kT_{{\text{w}}} }}$.

The Bejan number in the present study is

$${\text{Be}} = \frac{{\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} }}{{\left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} + \frac{1}{ \wedge }\left[ {\left( {1 + M} \right)\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{2} - K\left( {\frac{{\partial^{2} \Psi }}{{ \partial y^{2} }}} \right)^{4} + \gamma + {\text{BrHa}}^{2} \left( {\frac{\partial \Psi }{{\partial y}} + 1} \right)^{2} } \right]}}.$$

(42)

Numerical method

The systems (29) and (30) subject to (31) show a nonlinearity nature, and it seems to be difficult to find the closed form for the considered problem. Hence, the solution is computed numerically by Keller box method. The detail of the method can be found in Abbasi and Farooq [48] and Mustafa et al. [49]. The governing coupled system of nonlinear system of equations is also simulated by built-in sub-routine in computational software MATLAB which is commonly known as bvp4c. For this, first we reduce the corresponding equations into the first-order equations.

Let $\psi = y\left( 1 \right)$

$$\psi^{\prime} = y\left( 2 \right),$$

(43)

$$\psi^{\prime\prime} = y\left( 3 \right),$$

(44)

$$\psi^{\prime\prime\prime} = y\left( 4 \right),$$

(45)

$$\theta = y\left( 5 \right),$$

(46)

$$\theta^{\prime} = y\left( 6 \right),$$

(47)

$$y\left( 4 \right)^{^{\prime}} = \frac{1}{{\left( {1 + M} \right) - 3K\left( {y\left( 3 \right)} \right)^{2} }}\left( {\begin{array}{*{20}c} {6K\left( {y\left( 4 \right)} \right)^{2} y\left( 3 \right) + {\text{Ha}}^{2} y\left( 3 \right)} \\ { - k^{3} U_{{{\text{HS}}}} \frac{{\sinh \left( {ky} \right)}}{{\cosh \left( {kh} \right)}} - {\text{Gr}}y\left( 6 \right)} \\ \end{array} } \right),$$

(48)

$$y\left( 6 \right)^{^{\prime}} = - {\text{BrHa}}^{2} \left( {y\left( 2 \right) + 1} \right)^{2} - {\text{Br}}\left( {\left( {1 + M} \right)y\left( 3 \right)^{2} - K\left( {y\left( 3 \right)} \right)^{4} } \right) - \gamma .$$

(49)

The associated boundary conditions takes the form:

$$ya\left( 1 \right) - \frac{F}{2},{ }yb\left( 1 \right) + \frac{F}{2}{ }1 + ya\left( 2 \right){ }1 + yb\left( 2 \right){ }ya\left( 5 \right) - 0{ }yb\left( 5 \right) - 1.$$

(50)

The graphical results are compared through several graphs for velocity and temperature and also with the published results by Ramesh and Prakash [50]. The essential characteristics of various parameters on velocity profile, temperature distribution entropy and Bejan number are represented graphically.

Results and discussion

In this section, the effects of various parameters like Hartmann number ($\mathrm{Ha}$), Grashof number ($\mathrm{Gr}$), Joule heating parameter ($\gamma )$ and Eyring–Powell fluid parameters $M$ and $K$ on velocity profile, temperature distribution and Entropy generation for some different values of Helmholtz–Smoluchowski velocity ${U}_{\mathrm{HS}}$ are presented graphically and discussed in detail.

Figure 2a is plotted to observe the consequences of variation in the thermal Grashof number $\mathrm{Gr}$ on the axial velocity distribution. The graph is plotted for various values of maximum electro-osmotic velocity also known as Helmholtz–Smoluchowski velocity (${U}_{\mathrm{HS}}$), i.e., for ${U}_{\mathrm{HS}}>0$ and $U_{{{\text{HS}}}} < 0$. It is observed that the Grashof number shows different behavior at vicinity of the walls. Velocity profile after half region of the channel is enhanced by thermal Grashof number. We have noticed a significant increase in the velocity profile for the increasing value of Gr around the right boundary of the plane. The consequence of variation in the Hartmann number Ha on the axial velocity distribution is observed in Fig. 2b for different values of U_HS. The parameter is basically a magnetic parameter, and this behavior is because of the magnetic field that exists in an electrically conducting flow through which a force named Lorentz force is introduced. As we assign greater values to Ha, there is a decrease in the velocity profile at the central region of the channel, but this behavior is different around the boundary for several values of U_HS. Figure 3a shows the behavior of different values of electro-osmotic parameter $k$ on the axial velocity distribution. The effects are discussed for the negative as well as positive values of U_HS. From the graph, it is clear that the electro-osmotic parameter shows maximum velocity for the positive values of U_HS as compared to the negative values of U_HS as the values of electro-osmotic parameter $k$ increases. At the central line, the velocity of the fluid decreases against the increasing values of $k$ when $U_{{{\text{HS}}}} = - 2.0,$ while opposite trend is noticed when the electric field is applied opposite to the flow, i.e., $U_{{{\text{HS}}}} = 2.0.$ The different behavior is due to the presence of electric double layer which act as an agent to provide resistivity. In Fig. 3b, the impacts of Joule heating parameter $\gamma$ on the axial velocity are observed. For greater values of $\gamma,$ the velocity is greater as compared to the smaller values of $\gamma,$ but this behavior gradually changes until the smaller values of $\gamma$ show the maximum velocity. The velocity profile increases for the increasing value of $\gamma$ at central line of the channel, it is also noticed that the parameter $\gamma$ shows opposite behavior near the boundary and the effect of $\gamma$ gradually becomes smaller, and hence, it is negligible at the wall of the channel. Electric field will exert a force which will accelerate a charged particle. If a positive charge is moving in the same direction, it will increase the velocity, and if it is moving in the opposite direction, then it will decrease the velocity. In Fig. 4a, axial velocity u(y) is plotted for increasing values of non-Newtonian fluid parameter (M) for several values of U_HS. It is important to noticed that the axial velocity is increasing function of non-Newtonian fluid parameter when electro-kinetic pumping is in flow direction, i.e., U_HS =  − 2.0. Moreover, when electro-kinetic pumping is opposite to flow, i.e., U_HS = 2.0, the velocity of the fluid at the central line decreases. Actually, this is significant of the electro-kinetic pumping which increases the velocity by changing the rheology of the fluid. Furthermore, the difference in the magnitude exists with the direction of application of electro-osmotic forces. From Fig. 4b, it is clear that the axial velocity decreases by increasing Eyring–Powell fluid parameter (K) for various values of maximum electro-osmotic velocity also known as Helmholtz–Smoluchowski velocity (U_HS), i.e., for U_HS > 0 and U_HS < 0.

Fig. 2

Velocity profile for a thermal Grashof number $(\mathrm{Gr})$ when $Ha=0.5$ and b Hartman number $\left(\mathrm{Ha}\right)$ when $\mathrm{Gr}=0.1.$ Other parameters are $k=1.0,\gamma =2.0,M=1.0,x=0.5,\phi =0.2,Q=1.5$ and $\mathrm{Br}=0.5$

Fig. 3

Velocity profile for a electro-osmotic parameter $(k)$ when $\gamma =2.0$ and b Joule heating parameter $(\gamma )$ when $k=1.0$. Other parameters are $\mathrm{Ha}=0.5=\mathrm{Gr},M=1.0,K=0.1,x=0.5,\phi =0.2,Q=1.5$ and $\mathrm{Br}=0.5$

Fig. 4

Velocity profile for a Eyring–Powell fluid parameter $(M)$ when $K=0.1$ and $Q=2.0$ and b Eyring–Powell fluid parameter $(K)$ when $M=1$ and $Q=1.5.$ Other parameters are $k=1.0,\mathrm{Gr}=\mathrm{Ha}=0.1,\gamma =2.0,x=0.5,\phi =0.2$ and $\mathrm{Br}=0.5.$

The temperature profile increases by enhancing the thermal Grashof number, and increasing trend can be observed in the presence of electro-kinetic pumping. Furthermore, the rise in temperature against the thermal Grashof number is large in case of positive electro-kinetic pumping. The effects of Hartman number Ha on temperature distribution are presented in Fig. 5b; for the increasing value of Ha, the temperature rapidly increases. The behavior is observed for the positive and negative values of U_HS. The temperature is higher for the positive values of Helmholtz–Smoluchowski velocity; it tends to increase as larger values are assigned. Figure 6a is plotted to observe the variation of axial temperature against the raising values of electro-osmotic parameter (k) for both negative and positive electro-kinetic pumping. The temperature is an increasing function of increasing values of electro-osmotic parameter when the electro-kinetic pumping is against the flow direction. As we know that electro-osmotic force is a resistive force to the flow of liquid, it increases the collision between the particles of the fluid. The increase in collision causes the increase in the internal kinetic energy of the rushing particles in the flow direction, and as a result, increase in temperature can be observed for the raising trend of electro-kinetic parameter. Furthermore, the temperature decreases when the electric pumping is in the flow direction for the increasing values of k. From Fig. 6b, it is clear that Joule heating parameter enhances the temperature field for various values of U_HS, i.e., at U_HS > 0 and U_HS < 0. In Fig. 7a and b, the effects of Eyring–Powell fluid parameters are discussed. In these graphs, the behavior of M and K is examined for different values of U_HS, i.e., at U_HS > 0 and U_HS < 0. The fluid parameters M and K show opposite behavior. We have noticed that the parameter K has the opposite effect on the temperature profile; the temperature of the fluid throughout the plane decreases with the increasing values of K, whereas for the increasing values of M, the temperature of the fluid throughout the plane increases. The effect for the positive values of U_HS is greater than the negative values of U_HS.

Fig. 5

Temperature profile for a thermal Grashof number $(\mathrm{Gr})$ when $Ha=2.0$ and b Hartman number $(\mathrm{Ha})$ when $\mathrm{Gr}=1.0.$ Other parameters are $k=1.0,\gamma =2.0,M=1.0,K=0.1,x=0.5,\phi =0.2$ and $\mathrm{Br}=2.0.$

Fig. 6

Temperature profile for a electro-osmotic parameter $(k)$ when $\gamma =2.0$, b Joule heating parameter $(\gamma )$ when $k=1.0.$ Other parameters are $\mathrm{Ha}=1.0,\mathrm{Gr}=1.0,M=1.0,K=0.1,x=0.5,\phi =0.2$ and $\mathrm{Br}=2.0.$

Fig. 7

Temperature profile for a Eyring–Powell fluid parameter $(M)$ when $K=0.1$ and b Eyring–Powell fluid parameter $(K)$ when $M=1.0.$ Other parameters are $\mathrm{Ha}=1.0,\mathrm{Gr}=2.0,k=1.0,\gamma =2,x=0.5,\phi =0.2$ and $\mathrm{Br}=2.$

Figure 8 illustrates the impact of electro-osmotic parameter k on the streamlines for both opposing and assisting electro-kinetic pumping. The rise in the value of electro-osmotic parameter increases the resistance to the flow which rises the size of trapping bolus. For opposing pumping, this increase in size can be seen in the left half of the channel, while for assisting pumping, it can be observed in the right half of the channel. In Fig. 9, the response of isothermal lines against electro-osmotic parameter is reported for both positive electro-kinetic pumping and negative electro-kinetic pumping. For opposing pumping, the lateral expansion and vertical compression are noticed in the micro-channel with increasing k. Furthermore, it is noticed that the size and number of isothermal contour also increase by rising the electro-osmotic parameter. For assisting pumping, the number of bolus decreases by increasing k and therefore, it is significant that heat transfer characteristics are familiar in the micro-channel for positive electro-kinetic pumping. The isothermal lines by varying Joule heating parameter in micro-channel are plotted and discussed for U_HS =  ± 3.0, i.e., opposing electro-kinetic pumping and negative electro-kinetic pumping. The increase in Joule heating parameter also increases the number of isothermal contours, and this means that increase in Joule heating parameter also assists the heat transfer phenomena (Fig. 10).

Fig. 8

Effects of electro-osmotic parameter on stream lines a $k=0.1 \left({U}_{HS}=3.0\right)$, b $k=3.0 \left({U}_{\mathrm{HS}}=3.0\right)$, c $k=0.1 \left({U}_{\mathrm{HS}}=-3.0\right)$ and d $k=3.0 \left({U}_{\mathrm{HS}}=-3.0\right).$ Other parameters are $\mathrm{Ha}=0.1,\mathrm{Gr}=0.2,M=1.0,K=0.1,\gamma =2,\phi =0.8,Q=-0.1$ and $\mathrm{Br}=1.0.$

Fig. 9

Effects of electro-osmotic parameter on isothermal lines a $k=0.1 \left({U}_{HS}=4.0\right),$ b $k=1.0 \left({U}_{\mathrm{HS}}=4.0\right)$, c $k=0.1 \left({U}_{\mathrm{HS}}=-4.0\right)$ and d $k=1.0 \left({U}_{\mathrm{HS}}=-4.0\right).$ Other parameters are $\mathrm{Ha}=0.1,\mathrm{Gr}=1.0,M=1.0,K=0.1,\gamma =1,\phi =0.8,Q=-0.1$ and $\mathrm{Br}=2.0.$

Fig. 10

Effects of Joule heating parameter on isothermal lines a $S=0.0 \left({U}_{\mathrm{HS}}=3.0\right)$, b $S=3.0 \left({U}_{\mathrm{HS}}=3.0\right),$ c $S=0.0 \left({U}_{\mathrm{HS}}=-3.0\right)$ and d $S=3.0 \left({U}_{\mathrm{HS}}=-3.0\right).$ Other parameters are $\mathrm{Ha}=0.1,\mathrm{Gr}=1.0,M=1.0,K=0.1,k=1,\phi =0.8,Q=-0.1$ and $\mathrm{Br}=2.0$

The response of entropy generation number N_s and Bejan number Be against the increasing values of thermal Grashof number Gr, electro-osmotic parameter k, and Hartman number Ha for both positive and negative electro-kinetic pumping, i.e., ± U_HS, is in Figs. 11, 12 and 13. It is observed that entropy generation number N_s rises against Gr, but in the neighborhood of left wall N_s decreases for both types of pumping. It is noted that for the entropy generation in the decreasing region the magnitude is small for U_HS = 3.0; it means that when electric field is in opposite direction, the entropy decreases and these results can be used in the thermal management of many micro-pumps and microchips in bioengineering. The response of Bejan number is totally opposite to the entropy generation number due to irreversibility domination. From Fig. 12, it is clear that both entropy generation number N_s and Bejan number Be increase with rising the electro-kinetic pumping in opposing flow direction, while both quantities decrease with enhancing k for assisting electro-kinetic pumping. From this effective response, we conclude that for the better thermal management of biomedical instruments, the flow and electric field are in the same direction. The effects of Hartman number Ha on entropy generation number N_s and Bejan number Be are illustrated in Fig. 13. The effects of positive values of U_HS are much greater as compared to its negative values. As we assign a positive value to U_HS and then assign different values to Hartman number Ha, we can observe that the entropy increases at a very high rate as compared to U_HS < 0. Furthermore, the response of Bejan number in the vicinity of the channel is decreasing by increasing the magnetic forces for both positive electro-kinetic pumping and negative electro-kinetic pumping.

Fig. 11

a Effects of $\mathrm{Gr}$ on ${N}_{\mathrm{s}}$ and b effects of $\mathrm{Gr}$ on $\mathrm{Be}.$

Fig. 12

a Effects of $k$ on ${N}_{\mathrm{s}}$ and b effects of $k$ on $\mathrm{Be}.$ Other parameters are $\mathrm{Ha}=1.0,M=1,K=0.1,\mathrm{Gr}=1.0,\gamma =2,x=0.5,\phi =0.2,Q=1.5$ and $\mathrm{Br}=2.$

Fig. 13

a Effects of $\mathrm{Ha}$ on ${N}_{\mathrm{s}}$, b effects of $\mathrm{Ha}$ on $\mathrm{Be}.$ Other parameters are $k=1.0,M=1,K=0.1,\mathrm{Gr}=1.0,\gamma =2,x=0.5,\phi =0.2,Q=1.5$ and $\mathrm{Br}=2.$

Validation of numerical results

Figure 14 is plotted to compare the present results obtained by Keller box method and bvp4c. Figure 14 shows that both temperature and axial velocity show good agreement by assigning fixed values of involved parameters. The numerical results in the present study under certain restrictions show a good agreement with Ramesh and Prakash [50] (Fig. 15).

Fig. 14

a Comparison of velocity $u(y)$ and b comparison of temperature $\theta (y)$. Other parameters are $k=M=\mathrm{Gr}=1.0,K=0.1\gamma =2,x=0.5,\phi =0.6,Q=1.5$ and $\mathrm{Br}=2$

Fig.15

Comparison of velocity profile when $\phi =0.0=M=K,k=0.1,{U}_{\mathrm{HS}}=\mathrm{Gr}=\mathrm{Ha}=0$ and $Q=2.$

Conclusions

A numerical study by employing implicit finite difference scheme has been carried out to compute the entropy generation for the electro-osmosis-modulated peristaltic flow of Eyring–Powell fluid in a deformable symmetric channel. Effects of perpendicular magnetic field, Joule heating and thickness of electric double layer are also computed for several features of peristalsis. In order to solve the dimensionless conservation laws, we use implicit finite difference after lubrication approach and low zeta positional approximation. Graphical results are presented and discussed to analyze axial velocity, temperature and heat transfer coefficient. Bejan number distribution and average entropy generation rate are obtained for several values of electro-osmotic velocity and Joule heating parameter. Also the tabular results are presented to validate the numerical results by implicit finite difference scheme and numerical results by bvp4c. The transport and entropy generation characteristics are also presented through tabular data for Newtonian and non-Newtonian fluid for some values of Ohmic heating parameter. The computation can be summarized as follows:

• The Eyring–Powell fluid parameter M assists the velocity at the heart of the channel for negative electro-kinetic pumping while respond if reverse for positive electro-kinetic pumping.

• The velocity of the fluid increases by increasing joule heating parameter (γ), Hartman number (Ha) and Eyring–Powell fluid parameter for all values of electro-kinetic pumping.

• The electro-osmotic parameter assists the axial velocity for the negative electro-kinetic pumping while resisting positive electro-kinetic pumping near the walls of channel.

• The increase in M, K, Ha and Gr increases the effect of heat transfer phenomena.

• The size of streamlines as well as isothermal trapping increases by increasing k.

• The Joule heating parameter also increases the size and number of isothermal bolus.

• The entropy of the system can be controlled for assisting pumping, i.e., U_HS < 0.

• The entropy generation decreases with k for U_HS < 0 while increasing with k for U_HS > 0.

• Hartman number and thermal Grashof number increase entropy at the heart of the channel.