1 Introduction

Electro-osmosis—first introduced by Friedrich Reuss in 1807—is the process of inducing fluid motion inside a microchannel by applying an external electric potential across its walls [1]. In recent years, the electroosmotic flow (or EOF) has incurred a considerable attention of chemical and biomedical engineers due to its utilization in a variety of relevant applications such as soil analysis, chemical processing, capillary electrophoresis, planar chromatography, etc. Among these, capillary electrophoresis is a notable and cost-effective separation approach for the determination of ions in saliva and analysis of biological fluids (and inks) in forensics. Similarly, the polymeric chain reaction process in DNA detection (in forensic analysis) is one of the major applications of the capillary electrophoresis. Another class of applications of electro-osmosis is micropumps (and microchips) exploited by biomedical engineers/researchers for the diagnosis and treatment of different diseases such as; type-1 diabetes, increase of uric acid and cholesterol level in the blood, retina replacement, development of artificial pancreas and artificial stents inserted in the clogged arteries of heart. Different experts relevant to the medical procedures reveal that when the electric potential is applied at the walls of a micropump or medical instruments, then they become more durable as well as their maintenance issues are minimized.

In literature, many researchers have reported several applications of electro-osmosis experimentally, theoretically and numerically. Sadr et al. [2] experimentally discussed the electroosmotic flow (EOF) in a rectangular microchannel. The authors utilized the nanoparticle image velocimeter to measure the components of velocity for a fully-developed electroosmotic flow (steady) of \(B_{4} Na_{2} O_{7}\) buffer solution. For the case of cylindrical capillary, electroosmotic process has been investigated by Herr et al. [3], using the regular perturbation technique to obtain its analytic solution. A computational model was developed by Yao [4] in order to simulate the three-dimensional electroosmotic flow in microfluidic devices. The free surface modeling technique is also incorporated in this study. The interaction between the peristaltic mechanism and electro-osmosis was first introduced theoretically by Chakraboty [5]. In this study, the author highlighted that the features of the peristaltic motion are highly affected under the influence of axial electric field, and the dimensionless mean flow rate increases by enhancing the electroosmotic slip velocity. The influence of electro-osmosis and Helmholtz-Smoluchowski velocity on different features of peristalsis was studied by Tripathi et al. [6], for the blood flow in a finite length tube. This study also concluded that the size of the trapping bolus (for pressure magnitude) reduces by increasing the magnitude of electroosmotic parameter. In another study, Tripathi et al. [7] discussed the effects of peristalsis along with applied electro potential on an unsteady flow in a microchannel. A theoretical analysis on the flow of viscous fluid by means of combined effects of peristalsis and electro-osmosis was presented by Bandopadhyay et al. [8] using the lubrication approach. The applications of both peristalsis and electro-osmosis were indicated in this study, such as in the design of organ chip for an appropriate drug release and for mimicking a physiological system. Further, Yadav et al. [9] investigated the peristaltic motion of viscous fluid in the presence of electrical double layer. Similarly, Narla et al. [10] presented the transient of two-dimensional electro-kinematic transport of viscous fluid. It is concluded that the magnitude of net flow rate reduces with the motility of wall. Jhorar et al. [11] discussed the flow of viscous fluid in asymmetric channel, induced by peristaltic waves in the presence of electrical double layer effects.

It is observed that most of the fluids transported by the combined effects of electro-osmosis and propagation of wave’s conduit are non-Newtonian in nature. The physical importance of the rheology of non-Newtonian fluids flow through a deformable tube in the presence of electric potential using the Power law model has been investigated by Goswami et al. [12]. Their results showed that the magnitude of velocity becomes zero when the flow pressure rises, and it is also affected by the strength of electric potential; and the trapping phenomena vanishes when the high electric field is applied. Afonso et al. [13] approximated the Poisson Nernst Planks (PNP) equations along with viscoelastic fluid using the finite volume method in order to investigate the effects of thin electric double layers on the flow of Maxwell and Phan-Thin-Tanner (PTT) models. Guo and Qi [14] presented an analytical solution for the electroosmotic flow of the classical Jeffery fluid along with fractional derivatives in a cylindrical microchannel. Tripathi et al. [15] discussed the peristaltic flow of coupled stress fluid through a complex wavy channel with electromagnetic kinetic with body force under the usage of lubrication approach and Debye length approximation. In addition, the electroosmotic techniques were also utilized for the improvement of clay soil by Estabragh et al. [16]. The authors indicated that the electro-osmosis could play a significant role in the enhancement of the undrained strength and reimbursement of the soil. Chen et al. [17] utilized the Lattice Poisson-Boltzmann (LPB) method to investigate the electroosmotic flow of the Power law fluid for different microstructures of a porous medium and also showed that the permeability of shear thinning fluids enhances with the increase an external potential. Tripathi et al. [18] utilized the finite difference method to simulate the electrokinetic flow of aqueous solution through a microchannel containing an isotropic homogenous porous medium. Chaube et al. [19] discussed the electro-kinetically-driven peristaltic pumping of micropolar fluid through a microchannel. The constitutive equation of Sutterby fluid is utilized by Akram et al. [20] in order to investigate the effects of graphene oxide on the electroosmotic flow of blood in a capillary. A theoretical study is performed by Remash et al. [21] in order to explore the electroosmotic flow of Jeffrey fluid in a wavy channel. Later, Prakash et al. [22] discussed the effects of Newtonian heating, electrical double layer and slip on the flow of hybrid nanofluid in a microchannel with flexible walls. Tripathi et al. [23] highlighted the simultaneous effects of nanoparticles shape, thermal radiation, electric field and micro-rotation on blood flow in a microchannel. In another study, a mathematical model was developed by Tripathi et al. [24] in order to discuss the aqueous electrolyte motion within a microchannel. Further, Narla et al. [10, 25, 26] discussed the transient blood flow, enhancement in thermophysical properties and the entropy generation in the elector-osmosis modulated peristaltic motion in a curved channel.

In literature, many models exist that are used to formulate the peristaltic flow based on the lubrication theory, but the solution of the flow problem depends upon the time when it is brought together via the symmetric wall motility at both walls. Some researchers used an elliptic tube in order to investigate the peristaltic transport of chyme in the intestine. Eytan et al. [27] used the constitutive relation for viscous fluids in order to model the peristaltic transport in a tapered channel to investigate the transport of sperms in the fallopian tube. Similarly, Kothandapani et al. [28] obtained the perturbation solution to study the impact of transverse magnetic field on the peristaltic flow of fourth-grade fluid in a tapered asymmetric channel. They concluded that the axial velocity profile is a decreasing function of both the Hartman number and non-uniform parameter. Akram et al. [29] simulated the electroosmotic flow of methanol-based aluminum oxide nanofluid in a tapered channel. Prakash et al. [30] studied the flow characteristic for the thermal transport of viscous nanofluid in a tapered channel under the combined effects of peristalsis and electro-osmosis. Abbasi and Farooq [31] discussed the electro-osmosis modulated peristaltic motion of hybrid nanofluid in a trapped channel. Some other researchers like Hayat et al. [32], Prakash and Tripathi [33], and Kothandapani and Prakash [34] utilized the aforementioned models to study the peristaltic flow for different fluid systems under various conditions to describe their diverse rheological aspects.

Based on the above discussion, we can argue that still, there remains some space in research for the electroosmotic flow of the non-Newtonian fluids. It is evident that the nature of non-Newtonian fluids is very complex, and a single constitutive relation is inappropriate to predict the behavior of all non-Newtonian fluids. For the correct and realistic understanding of the physics of non-Newtonian fluids, various constitutive relations have been proposed by many researchers. Among these relations, the rate type models are very popular for characterizing the viscous elastic materials. Ali et al. [35] utilized the implicit finite difference scheme to investigate the peristaltic flow of Oldroyd 4-constant fluid in a planner channel. Oldroyd 4-constant fluid model exhibits the viscoelastic properties of the fluid under the long wavelength approximation. Therefore, in this paper, we have studied the physical mechanism of the electroosmotic flow of Oldroyd 4-constant fluid in a non-uniform channel. Firstly, we used basic laws of conservation of mass and momentum along with Poisson equation for the flow modeling. Subsequently, we simplified the resultant modeled equations for the flow by using the low Reynolds and long wavelength approximation, and solved these equations numerically by employing the shooting technique. In addition, we used the Debye approximation to find the potential function.

The remainder of the paper is presented as follow. Section 2 presents the problem formulation. Section 3 describes the numerical solution of the problem. Section 4 presents our graphical results and provides a detailed discussion on these results. Finally, Sect. 5 lists our main findings and conclusions.

2 Problem formulation

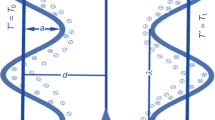
The unsteady flow of an Oldroyd 4-Constant fluid driven by peristalsis and electro-osmosis in a non-uniform channel with half width \({d}_{1}\)(See Fig. 1) is investigated in this study. The Cartesian coordinates \((\overline{X},\overline{Y})\) are considered in such a way that the wave propagates in \(\overline{X}-\) direction, and \(\overline{Y}-\) direction is perpendicular to the wave propagation.

Fig. 1
figure 1

The geometry of the problem

Full size image

The equations of the wall in mathematical form can be expressed as [34]:

$$\bar{H}_{1} (\bar{X},\bar{t}) = - d_{1} - m^{\prime}\bar{X} - b_{1} \left( {\sin \frac{{2\pi }}{\lambda }(\bar{X} - c\bar{t}) + \Phi } \right) ,$$
(1)
$${\overline{H}}_{2}\left(\overline{X},\overline{t}\right)={d}_{1}+{m}^{^{\prime}}\overline{X}+{b}_{2}\left(\mathrm{sin}\frac{2\pi }{\lambda } \left(\overline{X}-c\overline{t}\right) \right).$$
(2)

where \({d}_{1}\) is the half width of the channel, \(\lambda \) is the wavelength,\(m^{\prime} \) is the non-uniform parameter, \({b}_{1}\) and \({b}_{2}\) are the amplitudes of the lower and upper boundaries, respectively, and \(\Phi \) is the phase difference. Furthermore, the condition is followed by \({b}_{1},{b}_{2},{d}_{1}\) and \(\alpha \) is

$${b}_{1}^{2}+{b}_{2}^{2}+2{b}_{1}{b}_{2}\mathrm{cos}\left(\Phi \right)\le {\left(2{d}_{1}\right)}^{2}.$$

The governing equations for mass and momentum are represented mathematically as [18,19,20,21,22]

$$div{V}^{*}=0$$
(3)
$$ \rho \frac{{dV^{*} }}{{dt}} = - \nabla \bar{P} + div~\bar{S} + \rho _{e} \bar{E}$$
(4)

where \( V^{*} = \left[ {\overline{U} (\overline{X} ,\overline{Y} ,\overline{t} ),\overline{V} (\overline{X} ,\overline{Y} ,\overline{t} ),0} \right] \) designate the velocity field, \(\rho \) denotes fluid density, \(\overline{P}\) is pressure, \(I\) is the identity tensor, \({\rho }_{e}\) represents the electric charge density and \(\overline{E}\) is the electric field which is applied in axial direction.

Furthermore, the extra stress tensor \(\overline{S}\) for Oldroyd 4-constant can be expressed as [36]:

$$\overline{S}+{\overline{\lambda }}_{1}\frac{D\overline{S}}{D\overline{t}}+{\overline{\lambda }}_{3}tr\left(\overline{S}\right){\overline{A}}_{1}=\mu \left(1+{\overline{\lambda }}_{2}\frac{D}{D\overline{t}}\right){\overline{A}}_{1},$$
(5)

in which \( \bar{\lambda }_{1}\) and \(\bar{\lambda }_{3}\) relaxation times parameters, \(\bar{\lambda }_{2}\) is the retardation time parameter, \({\stackrel{-}{A}}_{1}\) is the first Revilian Erisken tensor, \(\mu \) is the dynamic viscosity, and \(D\bar{S}/D\bar{t}\) is the upper convected time derivative. The component form of the governing equations in fixed frame is as follows:

$$\frac{\partial \overline{U}}{\partial \overline{X}}+\frac{\partial \overline{V}}{\partial \overline{Y}}=0,$$
(6)
$$\rho \left(\frac{\partial }{\partial \overline{t}}+\overline{U}\frac{\partial }{\partial \overline{X}}+\overline{V}\frac{\partial }{\partial \overline{Y}}\right)\overline{U}=-\frac{\partial \overline{P}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{X} \overline{X}}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{X} \overline{Y}}}{\partial \overline{Y}}+{\rho }_{e}{\overline{E}}_{\overline{X}},$$
(7)
$$\rho \left(\frac{\partial }{\partial \overline{t}}+\overline{U}\frac{\partial }{\partial \overline{X}}+\overline{V}\frac{\partial }{\partial \overline{Y}}\right)\overline{V}=-\frac{\partial \overline{P}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{Y} \overline{X}}}{\partial \overline{X}}+\frac{\partial {\overline{S}}_{\overline{Y} \overline{Y}}}{\partial \overline{Y}}.$$
(8)

where \(\rho ,\overline{U},\overline{V},\overline{P}, {\overline{S}}_{\overline{X} \overline{X}},{\overline{S}}_{\overline{Y} \overline{Y}},{\overline{S}}_{\overline{X} \overline{Y}}\) and \({\overline{E}}_{\overline{X}}\) denotes the density, axial velocity, transverse velocity, normal stress components in \(\overline{X}\) and \(\overline{Y}\) directions, shear stress component and axial electrical field (in the electro kinetic body force term). Due to no-slip at lower and upper wall of the non-uniform channel, the boundary conditions in dimensionless form are:

$$ \left. {\begin{array}{*{20}l} {\bar{U} = 0,\quad \bar{V} = \frac{{\partial \bar{H}_{1} }}{{\partial \bar{t}}}\quad {\text{at}}\quad ~\bar{Y} = \bar{H}_{1} } \hfill \\ {\bar{U} = 0,\quad \bar{V} = \frac{{\partial \bar{H}_{2} }}{{\partial \bar{t}}}~\quad {\text{at}}~\quad \bar{Y} = \bar{H}_{2} } \hfill \\ \end{array} } \right\}, $$
(9)

The electric positional distribution is employed due to the presence of EDL in a non-uniform channel and is defined by Poisson equation [18]:

$${\nabla }^{2}\overline{\phi }=-\frac{{\rho }_{e}}{\varepsilon },$$
(10)

here \({\rho }_{e}\) is the density of the total ionic charge, \(\varepsilon \) is permittivity and \({\rho }_{e}=ez\left({n}^{+}-{n}^{-}\right)\), where \(e\) is the electric charge, \(z\) is charge balance \({n}^{+}\) and \({n}^{-}\) are the number of densities of cautions and anions, respectively. The Nernst-Plank is defined to determine the potential distribution, and it is used to describe the charge density as [18]:

$$\left( {\frac{\partial }{{\partial \bar{t}}} + \bar{U}\frac{\partial }{{\partial \bar{X}}} + \bar{V}\frac{\partial }{{\partial \bar{Y}}}} \right)n^{ \pm } = D\left( {\frac{{\partial ^{2} n^{ \pm } ~}}{{\partial \bar{X}^{2} }} + \frac{{\partial ^{2} n^{ \pm } ~}}{{\partial \bar{Y}^{2} }}} \right) \pm \frac{{ez}}{{K_{B} T}}\left( {\frac{\partial }{{\partial \bar{X}}}\left( {n_{ \pm } \frac{{\partial \bar{\phi }}}{{\partial \bar{X}}}} \right) + \frac{\partial }{{\partial \bar{Y}}}\left( {n_{ \pm } \frac{{\partial \bar{\phi }}}{{\partial \bar{Y}}}} \right)} \right)$$
(11)

in which \({K}_{B}\) is the Boltzmann constant, \(D\) represents the diffusivity of chemical species, and \(T\) is the average temperature.

The governing equations can be reduced to their dimensionless forms by introducing the dimensionless variables:

$$ \begin{gathered} \left. \begin{gathered} x = \frac{{2\pi \bar{X}}}{\lambda }.y = \frac{{\bar{Y}}}{{d_{1} }},u = \frac{{\bar{U}}}{c},v = \frac{{\bar{V}}}{{c\delta }},\delta = \frac{{d_{1} }}{\lambda },h_{1} = \frac{{\bar{H}_{1} }}{{d_{1} }},h_{2} = \frac{{\bar{H}_{2} }}{{d_{1} }},a = \frac{{b_{1} }}{{d_{1} }}, \hfill \\ b = \frac{{b_{2} }}{{d_{1} }},m = \frac{{\lambda m^{\prime}}}{{d_{1} }},t = \frac{{c\bar{t}}}{\lambda },Re = \frac{{\rho cd_{1} }}{\mu },p = \frac{{2\pi d_{1}^{2} }}{{\lambda \mu c}}\bar{P},U_{{hs}} = - \frac{{\bar{E}_{{\bar{X}}} \varepsilon d_{1}^{2} }}{{\mu c}}, \hfill \\ k = ezd_{1} \sqrt {\frac{{2n_{0} }}{{\varepsilon K_{B} T}}} ,\bar{\phi } = \frac{{ez\phi }}{{K_{B} T}},\bar{\xi }_{i} = \frac{{ez\xi _{i} }}{{K_{B} T}},i = 1,2, \hfill \\ \end{gathered} \right\} \hfill \\ \hfill \\ \end{gathered} $$
(12)

where \(\delta \) is the wave number, \(Re\) is the Reynolds number, \(\xi \) is the constant zeta function, \({U}_{hs}\) is the electroosmotic velocity (Helmholtz-Smoluchowski velocity), and \(\lambda \) is the wavelength.

After introducing the dimensionless parameters in Eqs. (6–11), the nonlinear terms are appeared in the form \(O\left(Pe{\delta }^{2}\right),\) where \(Pe\) is ionic Peclet number. Using the limitations \(Re,Pe,\delta \ll 1\) and introducing stream functions \(\psi \) defined as \(u=\partial \psi /\partial y\) and \(v=-\delta \partial \psi /\partial x\), the equation of continuity is identically satisfied, and rest of equations takes the form:

$$-\frac{\partial p}{\partial x}+\frac{\partial {S}_{xy}}{\partial y}+{k}^{2}{U}_{hs}\phi =0,$$
(13)
$$\frac{\partial p}{\partial y}=0,$$
(14)
$$\frac{{\partial }^{2}\phi }{\partial {y}^{2}}={k}^{2}\left(\frac{{n}^{+}-{n}^{-}}{2}\right),$$
(15)
$$\left(\frac{{\partial }^{2}{n}^{\pm } }{\partial {y}^{2}}\right)\pm \left(\frac{\partial }{\partial y}\left({n}_{\pm }\frac{\partial \phi }{\partial y}\right)\right),$$
(16)

The solution of (16) is subject to boundary conditions \({n}^{\pm }=1\) at \(\phi =0\) and \(\partial {n}^{\pm }/\partial y=0\) at \(\partial \phi /\partial y=0\) (bulk condition), we get

$${n}_{\pm }={e}^{\mp \phi }.$$
(17)

After using Eq. (17) in (15), we have

$$\frac{{\partial }^{2}\phi }{\partial {y}^{2}}={k}^{2}\mathrm{sinh}\left(\phi \right).$$
(18)

Assuming that electrical potential is small as compared with the thermal energy of the ions, so for further simplifications, we follow [37,38,39] and apply the Debye–Huckel linearization approximation \((sinh\phi \approx \phi ),\) and using the boundary conditions \(\phi ={\xi }_{1}\) at the lower wall and \(\phi ={\xi }_{2}\) at the upper wall, the potential function can be calculated as:

$$\phi \left(y\right)={\xi }_{1}\frac{\mathrm{sinh}\left[k\left(y-{h}_{2}\right)\right]-{R}_{\xi }\mathrm{sinh}\left[k\left(y-{h}_{1}\right)\right]}{\mathrm{sinh}\left[k\left({h}_{1}-{h}_{2}\right)\right]},$$
(19)

in which \({R}_{\xi }={\xi }_{2}/{\xi }_{1}\) is the ratio of zeta potential of the two walls. Equation (18) holds for \({h}_{1}\le y\le {h}_{2}\) and symmetric potential case discussed in Bandopadhyay et al. [8] is obtained when \({R}_{\xi }=1,\theta =0=\Phi .\)

Eliminating pressure from Eqs. (13) and (14):

$$\frac{{\partial }^{2}{S}_{xy}}{\partial {y}^{2}}+{k}^{2}{U}_{hs}\frac{\partial \phi }{\partial y}=0,$$
(20)

where the expression for \({S}_{xy}\) is obtained from Eq. (5) and is given by:

$${S}_{xy}=\frac{1+2{\alpha }_{1}{\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)}^{2}}{1+2{\alpha }_{2}{\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)}^{2}}\frac{{\partial }^{2}\psi }{\partial {y}^{2}},$$
(21)

in which \({\alpha }_{1}={\overline{\lambda }}_{2} {\overline{\lambda }}_{3}\) and \({\alpha }_{2}={\overline{\lambda }}_{1} {\overline{\lambda }}_{3}.\) here Oldroyd 4-Constant fluid model reduces to viscous fluid, if we take \({\alpha }_{1}={\alpha }_{2}\). The appropriate dimensionless boundary conditions in the fixed frame are [31]:

$$ \left. \begin{gathered} \psi = - \frac{F}{2},\frac{{\partial \psi }}{{\partial y}} = 0~\;{\text{at}}\;~y = h_{1} = - 1 - mx - a~sin\left( {2\pi \left( {x - t} \right) + \Phi } \right) \hfill \\ \psi = \frac{F}{2},\frac{{\partial \psi }}{{\partial y}} = 0~\;{\text{at}}~\;y = h_{2} = 1 + mx + b~sin\left( {2\pi \left( {x - t} \right)} \right) \hfill \\ \end{gathered} \right\} $$
(22)

The instantaneous volume rate of flow \(F(x,t)\) in Eq. (20) can be derived as:

$$F\left(x,t\right)=\Theta +a {sin}\left(2\pi \left(x-t\right)\right)+b {sin}\left(2\pi \left(x-t\right)+\Phi \right)$$
(23)

in the above relation, \(F=\frac{\overline{Q}}{c{d}_{1}},\Theta =\frac{\overline{q}}{c{d}_{1}},F={\int }_{{h}_{1}}^{{h}_{2}}udy=\psi \left({h}_{2}\right)-\psi ({h}_{1})\), where \(\Theta \) is the time average flow of one period of the wave. The expression for shear stress at lower wall can be expressed as:

$${S}_{xy}={\left.\frac{\partial {h}_{1}}{\partial x}\left(\frac{1+2{\alpha }_{1}{\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)}^{2}}{1+2{\alpha }_{2}{\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)}^{2}}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)\right|}_{y={h}_{1}},$$
(24)

Similarly, the shear stress at the upper wall can be expressed by the formula:

$${S}_{xy}={\left.\frac{\partial {h}_{2}}{\partial x}\left(\frac{1+2{\alpha }_{1}{\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)}^{2}}{1+2{\alpha }_{2}{\left(\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)}^{2}}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}\right)\right|}_{y={h}_{2}},$$
(25)

3 Numerical solution

To illustrate the physical importance of various flow patterns of the Oldroyd 4-Constant fluid driven by the combined effects of external electro kinetic and peristalsis in a tapered asymmetric channel. We have solved Eq. (20) subject to the boundary conditions given in Eq. (22) for \(\psi \) by a well-known numerical technique termed as the shooting method, which is frequently used in [40, 41]. After using the value of shear stress, we reduce the Eq. (18) into corresponding system of first-order equations:

Let

$${\psi }^{^{\prime}}=u,$$
(26)
$${u}^{^{\prime}}=v,$$
(27)
$${v}^{^{\prime}}=w,$$
(28)
$$ w^{\prime} = \frac{{\left( {1 + 2v^{2} \alpha _{2} } \right)^{2} A_{1} + 4vw^{2} \left( {\alpha _{1} - \alpha _{2} } \right)\left( { - 3 + 2v^{2} \alpha _{2} } \right)\left( {1 + 2v^{2} \alpha _{2} } \right)^{{ - 3}} }}{{\left( {1 + 2v^{2} \left( { - \alpha _{2} + \alpha _{1} \left( {3 + 2v^{2} \alpha _{2} } \right)} \right)} \right)}}$$
(29)

where \({A}_{1}={k}^{3}{\xi }_{1}\frac{\mathrm{cosh}\left[k\left(y-{h}_{2}\right)\right]-{R}_{\xi }\mathrm{cosh}\left[k\left(y-{h}_{1}\right)\right]}{\mathrm{sinh}\left[k\left({h}_{1}-{h}_{2}\right)\right]}.\)

Subject to the initial conditions

$$ \psi \left( {h_{1} } \right) = - \frac{F}{2},\psi ^{\prime}\left( {h_{1} } \right) = 0~,\psi ^{\prime\prime}\left( {h_{1} } \right) = s_{1} ,\psi ^{\prime\prime\prime}\left( {h_{1} } \right) = s_{2}$$

The above system of first-order equations is now computed with Runge–Kutta-Fehlberg integration scheme, and \({s}_{1}\) and \({s}_{2}\) are missing slopes, which are updated by Newton’s method until the boundary conditions are satisfied. All necessary computation is carried out in the computational software, Mathematica.

4 Graphical results and discussion

The objective of this section is to present the graphical illustrations of the simulation results obtained from the numerical methods mentioned in the previous section. Our main focus is to examine the effects of the rheological parameter of fluid, Helmholtz-Smoluchowski velocity, non-uniform parameter and electroosmotic parameter on axial velocity, pressure rise, axial pressure and shear stress. The trapping phenomenon is also illustrated by plotting streamlines.

4.1 Velocity profile

In this subsection, we examine the effects of fluid parameter \({\alpha }_{1}\) and \({\alpha }_{2}\), electroosmotic parameter \(k\), non-uniform parameter \(m\) and zeta potential function \({R}_{\xi }\) on the axial velocity \(u(y)\) in Figs. 2, 3, 4, 5, 6, for both negative and positive values of Helmholtz-Smoluchowski velocity i.e.\({U}_{hs}=\pm 1.0\). During the analysis, the parameters like \(\Phi =\pi /2,a=0.2,b=0.3,x=0.5,t=0.3\) and \(\Theta =1.7\) are fixed. It is observed that, when we take \({U}_{hs}=1.0\) the velocity increases at the highest velocity point, which is the center of the channel and also in the lower half the velocity decreases, but this decreases is not encountered enlarge at scale near the upper boundary. As we move toward the Newtonian fluid (i.e., \({\alpha }_{1}=0.5\)), the viscous effects reduce and consequently, the velocity increases by increasing \({\alpha }_{1}\). The effects of \({\alpha }_{1}\) for \({U}_{hs}=-1.0\) on the velocity profile are quite opposite in behavior in the upper half of the channel. This behavior is actually due to the positive values of the electroosmotic velocity, which creates its influence in the opposite direction to the flow. The velocity profile decreases at the central line of the channel for both negative and positive values of Helmholtz-Smoluchowski velocity i.e., \({U}_{hs}=\mp 1.0\) when we increase the fluid parameter \({\alpha }_{2}\). Furthermore, when we take the negative values of electroosmotic velocity (i.e., \({U}_{hs}=-1.0\)), the increase in velocity is noticeable in the upper half of the channel. The velocity at the central line decreases because when we increase the non-Newtonian behavior (or the elastico-viscous effects are enhanced), the velocity is reduced consequently. The effects of non-Newtonian fluid parameter \({\alpha }_{2}\) for the positive values of Helmholtz-Smoluchowski velocity i.e., \({U}_{hs}=1.0\) is quite opposite compared to the negative values of electroosmotic velocity. The Fig. 4a and b depict the effects of electroosmotic parameter on the axial velocity profile for both negative and positive values of Helmholtz-Smoluchowski velocity i.e., \({U}_{hs}=\pm 1.0.\) The velocity reduces in the lower half of the channel but increases in the upper half of the channel, for the increasing values of electroosmotic parameter \(k\) when \({U}_{hs}=-1.0\). The velocity increases in the lower half of the channel with increasing the strength of electric field i.e., increasing \(k\) and effects disappear near the upper wall of the channel for the opposing case for flow i.e., \({U}_{hs}=1.0\). The influence of non-uniform parameter \(m\) on the velocity profile for both assisting flow case \(({U}_{hs}=-1.0)\) and opposing flow case \(({U}_{hs}=1.0)\) is presented in Fig. 5a and b. The axial velocity reduces at the highest velocity point, which is the central line of the channel when we move from uniform to non-uniform channel. Furthermore, the increase in the velocity is observed near the boundaries of the channel for both assisting and opposing flows. In addition, the increasing region near the upper wall reduces when \({U}_{hs}=-1.0\); whereas, it increases in case of \({U}_{hs}=1.0\). In Fig. 6, the effects of zeta potential function \({R}_{\xi }\) is examined for both positive and negative values of electro kinetic pumping. This parameter is the ratio of zeta potentials imposed on both boundaries of microchannel. When we increase the zeta potential ratio, the flow is significantly decreased in lower half of the channel, and flow is accelerated in the upper half of the channel when \({U}_{hs}=1.0.\) The converse behavior is observed for \({U}_{hs}=-1.0\) when we increase the zeta potentials ratio in both halves of the channel.

Fig. 2
figure 2

Effects of \({\alpha }_{1}\) on velocity profile \(u(y)\) for (a) \({U}_{hs}=-1.0\)(b) \({U}_{hs}=1.0\). Other parameters are \(k=1.0,{\alpha }_{2}=0.5,\xi =1.0,m=0.1\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 3
figure 3

Effects of \({\alpha }_{1}\) on velocity profile \(u(y)\) for (a) \({U}_{hs}=-1.0\)(b) \({U}_{hs}=1.0\). Other parameters are \(k=1.0,{\alpha }_{1}=0.5,\xi =1.0,m=0.1\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 4
figure 4

Effects of \(k\) on velocity profile \(u(y)\) for (a) \({U}_{hs}=-1.0\)(b) \({U}_{hs}=1.0\). Other parameters are \({\alpha }_{2}=1.0,{\alpha }_{1}=0.5,\xi =1.0,m=0.1\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 5
figure 5

Effects of \(m\) on velocity profile \(u(y)\) for (a) \({U}_{hs}=-1.0\)(b) \({U}_{hs}=1.0\). Other parameters are \({\alpha }_{2}=1.0,{\alpha }_{1}=0.5,\xi =1.0,k=1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 6
figure 6

Effects of \({R}_{\xi }\) on velocity profile \(u(y)\) for (a) \({U}_{hs}=-1.0\)(b) \({U}_{hs}=1.0\). Other parameters are \({\alpha }_{2}=1.0,{\alpha }_{1}=0.5,\xi =1.0,k=1.0\) and \(m=0.1\)

Full size image

4.2 Trapping phenomena

Trapping is an essential transportation phenomenon of physiological fluids driven by the peristaltic pumping. In fluid mechanics, trapping can be observed at a fixed flow rate due to the circulation of streamlines. These streamlines under various conditions split to trap a bolus, that as a whole travels with the speed of the peristaltic wave. The effects of important parameters like \({\alpha }_{2}\), \(k,m\) and \({R}_{\xi }\) are presented in Figures 7, 8, 9, 10, 11, 12, 13 and 14, respectively. The size of streamline bolus decreases, when we transform from Newtonian to non-Newtonian fluid for both negative and positive values of Helmholtz-Smoluchowski velocity (i.e., \({U}_{hs}=\pm 1.0\)), and are depicted in Figs. 7 and 8. The size of trapping bolus reduces in lower half for opposing electro kinetic pumping when we take \({\alpha }_{2}=2.0\) i.e., strong non-Newtonian effects are encountered. On the other hand, the size of trapping bolus reduces by increasing non-Newtonian character when \({U}_{hs}=-1.0.\) Furthermore, the circulation becomes weak, when we move toward non-Newtonian behavior for both assisting and opposing flow cases (i.e., \({U}_{hs}=\mp 1.0\)). Figures 9 and 10 display the effects of electroosmotic parameter on the streamlines for both positive and negative values of Helmholtz-Smoluchowski velocity (i.e., \({U}_{hs}=\mp 1.0\)). For the positive value of Helmholtz-Smoluchowski velocity (i.e., \(U_{hs} = 1\)), the increasing values of electroosmotic parameter \(k\) reduce the size of trapping bolus in the lower half of the channel. It is also observed that, if we take the electric field in the flow direction (i.e., \(U_{hs} = - 1\)) the quite opposite effects are obtained in the pattern of streamlines by increasing the values of \(k\), are taken into account in comparison with the case of positive values of Helmholtz-Smoluchowski velocity (i.e., \(U_{hs} = 1\)). The response of streamlines for the increasing values of non-uniform parameter is presented in Figs. 11 and 12. The size of streamlines increases, when we move from uniform to non-uniform channel for both the assisting and opposing flows. In Fig. 13, the streamlines are plotted for both positive and negative values of zeta potential ratios when \({U}_{hs}=1.0\). It is observed that the size of trapping bolus is large in upper half of the tapered channel for \({R}_{\xi }=-1.0\), whereas the size of bolus is large in lower half for \({R}_{\xi }=1.0\). In addition, the increase in the zeta potential ratios shifts streamlines in the lower half of the channel. From Fig. 14, it is clear that the reverse behavior in both halves of the channel is noticed when \({U}_{hs}=-1.0\) i.e., assisting electrokinetic pumping.

Fig. 7
figure 7

Streamlines (a) \({\alpha }_{2}=0.5\) (b) \({\alpha }_{2}=2.0\) with \({U}_{hs}=1.0\). Other parameter are \(\Phi =\pi /5,a=0.1,b=0.2,m=0.2,k=0.6,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 8
figure 8

Streamlines (a) \({\alpha }_{2}=0.5\) (b) \({\alpha }_{2}=2.0\) with \({U}_{hs}=-1.0\). Other parameter are \(\Phi =\pi /5,a=0.1,b=0.2,m=0.2,k=0.6,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 9
figure 9

Streamlines (a) \(k=0.1\) (b) \(k=0.8\) with \({U}_{hs}=1.0\) Other parameter are \(\Phi =\pi /5,\) \(a=0.1,b=0.2,m=0.1,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,{\alpha }_{2}=2.0,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 10
figure 10

Streamlines (a) \(k=0.1\) (b) \(k=0.8\) with \({U}_{hs}=-1.0\) Other parameter are \(\Phi =\pi /5,a=0.1,b=0.2,k=0.5,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,{\alpha }_{2}=2.0,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 11
figure 11

Streamlines (a) \(m=0.0\) (b) \(m=0.2\) with \({U}_{hs}=1.0\) Other parameter are \(\Phi =\pi /5,a=0.1,b=0.2,k=0.5,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,{\alpha }_{2}=2.0,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 12
figure 12

Streamlines (a) \(m=0.0\) (b) \(m=0.2\) with \({U}_{hs}=1.0\) Other parameter are \(\Phi =\frac{\pi }{5},a=0.1,b=0.2,k=0.5,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,{\alpha }_{2}=2.0,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 13
figure 13

Streamlines (a) \({R}_{\xi }=-1.0\) (b) \({R}_{\xi }=1.0\) with \({U}_{hs}=1.0\) Other parameter are \(\Phi =\pi /5,a=0.1,b=0.2,k=0.5,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,{\alpha }_{2}=1.0,\xi =1.0\) and \(m=0.2\)

Full size image
Fig. 14
figure 14

Streamlines (a) \({R}_{\xi }=-1.0\) (b) \({R}_{\xi }=1.0\) with \({U}_{hs}=-1.0\) Other parameter are \(\Phi =\pi /5,a=0.1,b=0.2,k=0.5,t=0.5,\Theta =1.4,{\alpha }_{1}=0.5,{\alpha }_{2}=1.0,\xi =1.0\) and \(m=0.2\)

Full size image

4.3 Axial Pressure

Figures 15, 16, 17 and 18 are plotted to depict the impact of fluid parameters \({\alpha }_{1}\) and \({\alpha }_{2}\), electroosmotic parameter \(k\) and zeta potentials ratio \({R}_{\xi }\) for both the positive and negative values of \({U}_{hs}\) with fixed parameters \(\Phi =\pi /4,a=0.3,b=0.4\) and \(t=0.2.\) The axial pressure decreases for the increasing values of \({\alpha }_{1}\), and it is depicted in Fig. 15 for both \({U}_{hs}=\pm 2.0\). In addition, the axial pressure is small for the Newtonian case and reduces as we move toward Newtonian fluid from the viscoelastic fluid. Furthermore, the magnitude of axial pressure is large for \({U}_{hs}=2\) i.e., the pressure reduces in the assisting flow case. The effects of non-Newtonian fluid parameter \({\alpha }_{2}\) are represented in Fig. 16 for \({U}_{hs}=\pm 2\). The pressure rise per wavelength increases when the viscoelastic effects are increased in assisting flow case (i.e., \({U}_{hs}=-2.0\)) and opposing flow case (i.e., \({U}_{hs}=2.0\)). The axial pressure decreases for the increasing values of electroosmotic parameter \(k\) when the flow is assisting, whereas it increases for the increasing values of electroosmotic parameter when the flow is opposing (i.e., \({U}_{hs}=2.0.)\). Figure 18 is plotted to examine the effects of zeta potentials ratio on axial pressure for several values of electroosmotic velocity \({U}_{hs}.\) The axial pressure is a decreasing function of \({R}_{\xi }\) for assisting electro kinetic pumping (i.e., \({U}_{hs}=-2.0)\), while on the other hand axial pressure rises with \({R}_{\xi }\) for the opposing electro kinetic pumping.

Fig. 15
figure 15

Axial Pressure \(dp/dx\) for different values of \({\alpha }_{1}\) (a) \({U}_{hs}=-2.0\) (b) \({U}_{hs}=2.0\). Other parameter are \(m=0.1,k=1.0,\Theta =1.2,{\alpha }_{2}=0.5,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 16
figure 16

Axial Pressure \(dp/dx\) for different values of \({\alpha }_{2}\) (a) \({U}_{hs}=-2.0\) (b) \({U}_{hs}=2.0\). Other parameter are \(m=0.1,k=1.0,\Theta =1.2,{\alpha }_{1}=0.5,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 17
figure 17

Axial Pressure \(dp/dx\) for different values of \(k\) (a) \({U}_{hs}=-2.0\) (b) \({U}_{hs}=2.0\). Other parameter are \(\Theta =1.2,{\alpha }_{1}=0.5,{\alpha }_{2}=2.0,\xi =1.0\) and \({R}_{\xi }=0.5\)

Full size image
Fig. 18
figure 18

Axial Pressure \(dp/dx\) for different values of \({R}_{\xi }\) (a) \({U}_{hs}=-2.0\) (b) \({U}_{hs}=2.0\). Other parameter are \(\Theta =1.2,{\alpha }_{1}=0.5,{\alpha }_{2}=2.0,\xi =1.0\) and \(k=2.0.\)

Full size image

4.4 Amplitude of shear stress

In this subsection, we illustrate the effects of electroosmotic parameter \(k\) and non-Newtonian fluid parameter \({\alpha }_{2}\) on the amplitude of shear stress on both walls of the channel in Figs. 19 and 20 when \(\Phi =\pi /2,a=0.3,b=0.4,t=0.2,m=0.2\) and \(\Theta =1.2.\) The results are obtained for both positive and negative values of the electroosmotic velocity (i.e., \({U}_{hs}=\pm 2.0\)). The behavior of shear stress at both the walls of non-uniform asymmetric channel is oscillatory in behavior. For the assisting flow case (i.e., \({U}_{hs}=-2.0\)), the shear stress at the upper wall of the channel increases, while it decreases when the electroosmotic parameter \(k\) increases. Furthermore the response of shear stress at both walls of channel is quite opposite in behavior for the increasing values of electroosmotic parameter \(k\) when the opposing flow case is studied (i.e., \({U}_{hs}=2.0\)). In Fig. 20, the effects of rheological fluid parameter \({\alpha }_{2}\) on the shear stress for both the positive and negative values of electroosmotic velocity (i.e., \({U}_{hs}=\pm 2.0\)) are represented. The shear stress decreases at both walls of the channel, when we move from Newtonian to non-Newtonian for both the assisting and opposing flow cases.

Fig. 19
figure 19

Shear stress \({S}_{xy}\) for different values of \(k\) for (a) \({U}_{hs}=-2.0\) and (b) \({U}_{hs}=2.0.\) Other parameter are \({\alpha }_{1}=0.5,{\alpha }_{2}=1.0=\xi \) and \({R}_{\xi }=0.5\)

Full size image
Fig. 20
figure 20

Shear stress \({S}_{xy}\) for different values of \({\alpha }_{2}\) for (a) \({U}_{hs}=-2.0\) and (b) \({U}_{hs}=2.0.\) Other parameter are \({\alpha }_{1}=0.5,k=1.0=\xi \) and \({R}_{\xi }=0.5\)

Full size image

5 Validation of results

In order to check the accuracy of our numerical results, we solved the equations using finite difference method and presented both the results for comparison in Table 1 for several values of \({U}_{hs}\). Furthermore, comparison is carried out for Newtonian and non-Newtonian fluids. It is observed that the numerical results, by both the techniques, show a good agreement up to 4 decimal places for \({U}_{hs}=\pm 2.0\) and in absence of electric potential. Furthermore, the results of the present study are also compared with the results of Prakash et al. [42] for the viscous fluid in Fig. 21.

Table 1 Comparison of \(u\left(y\right)\) at different cross sections with \(k=1.0,\Phi =\pi /2,a=0.1,\) \(b=0.2,t=0.3,m=0.1,x=0.5,\xi =1.0,{R}_{\xi }=0.5\) and \(\Theta =1.2\)
Full size table
Fig. 21
figure 21

Comparison of axial velocity when \(x=0.4,t=0.2,a=0.6,b=0.4,m=0.1,\) \(\Phi =\pi /8,\Theta =1.2,{\alpha }_{1}={\alpha }_{2}=0.5\) and \({U}_{hs}=0.0\)

Full size image

6 Concluding remarks

In this study, we have rendered a detailed analysis of the physical mechanisms of electro-osmosis fluid flow in a non-uniform channel. Our mathematical model is based on a standard non-Newtonian Oldroyd 4-Constant fluid. We solved the model numerically, and simulated it against a given set of parameters. Our results examined the velocity profile, trapping phenomena, axial pressure and shear stress of the fluid on the basis of these parameters. Our main findings are summarized as follows:

  • Both the rheological parameters have the opposite effects on the velocity profile under the influence of an axial electric field.

  • The velocity increases in the upper half of the channel for the increasing values of electroosmotic parameter \(k\) when \({U}_{hs}=-1.0\), while for the opposing electrokinetic pumping, the velocity manifests an increasing trend.

  • The increase in zeta potentials ratio increases the velocity in the lower half and decreases it in the upper half for \({U}_{hs}=-1.0.\)

  • The size of the circulation bolus increases by increasing the values of the electroosmotic parameter.

  • The increase in the magnitude of non-Newtonian parameter increases the size of trapping bolus.

  • Axial pressure decreases by increasing the values of electroosmotic parameter for assisting the electrokinetic pumping.

  • The axial pressure is an increasing function of the non-Newtonian parameter for both the assisting and opposing cases.

  • The shear stress increases for the negative values of the electroosmotic velocity, whereas it decreases for the positive values of the electroosmotic velocity after an increase in the values of electroosmotic parameter.

  • The shear stress decreases at both walls of the channel by increasing the fluid parameter \({\alpha }_{2}\).