Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina–copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model

Abstract

Sequel to the fact that hybrid nanofluidic systems (e.g. scalable micro-/nanofluidic device) exhibit greater thermal resistance with increasing nanoparticle concentration, little is known on the significance of thermal radiation, surface roughness and linear stability of water conveying alumina and copper oxide nanoparticles. This study presents the effects of thermal radiation and surface roughness on the complex dynamics of water conveying alumina and copper oxide nanoparticles, in the case where the thermophysical properties of the resulting mixture vary meaningfully with the volume fraction of solid nanomaterials, as well as with the Brownian motion and thermophoresis microscopic phenomena. Based on the linear stability theory and normal mode analysis method, the basic partial differential equations governing the transport phenomenon were non-dimensionalized to obtain the simplified stability equations. The optimum values of the critical thermal Rayleigh number depicting the onset of thermo-magneto-hydrodynamic instabilities were obtained using the power series method and the Chock–Schechter numerical integration. The increase in the strength of Lorentz forces, thermal radiation and surface roughness has a stronger stabilizing impact on the appearance of convection cells. On the contrary, the stability diminishes with the increasing values of the volumetric fraction and diameter of nanomaterials. The partial substitution of the alumina nanoparticles by the copper oxide nanomaterials in the mixture stabilizes importantly the hybrid nanofluidic medium.

Introduction

Heat transfer rate in the dynamics of various fluids over a heated interface depends greatly on the surrounding of the contact surface and the intrinsic thermophysical properties of the fluid phases. In such a case, the thermal conductivity of the working fluids plays an important role. In fact, Zhao et al. [1] once remarked the increasing superheats tend to increase significantly the apparent contact angle, speed up the thin film flows and enhance their thermal characteristics. Due to the importance of efficient heating and cooling processes in the manufacturing companies, published facts on nanofluids have been widely embraced by several researchers and chemical experimenters. Compared to the conventional fluids, the nanofluids are chemically produced by dispersing homogeneously nanosized solid materials in a specified base fluid for enhancing their thermal properties. In view of the usefulness of nanofluids, most especially in the nanotechnological sector, the synthesizing of the so-called hybrid nanofluid (HNF) or its modified version (MHNF) for more than two nanoparticles has been embraced recently for further exploration. Likewise to the monotype nanofluids (MNFs), the hybrid nanofluids (HNFs) have also practical exploitations in many applied sciences and biochemical engineering areas, such as cooling of electronic equipment, narrow and tapered microfluidic channels, thermal and mass transportations, medical sciences, solar heating, nuclear reactors, as well as in the homogeneous and heterogeneous chemical catalytic reactions; see Esfe and Afrand [2], Żyła [3], Moldoveanu et al. [4], Animasaun et al. [5], Mahanthesh et al. [6] and Kumar et al. [7].

In a study on the rheological behaviour of monotype and hybrid nanofluids by Khodadadi et al. [8], it was remarked that with an increase in nanoparticles size and volume fraction, higher nanofluid viscosity is ascertained, while the viscosity is a decreasing property of temperature. Experimental and numerical findings concerning the effective thermophysical properties as well as the flow and heat transfer characteristics of HNFs was reviewed by Huminic and Huminic [9]. In this analysis, they concluded that the formation of hybrid nanoparticles is achievable by varying the mixing ratio for the stability of HNFs. Babar and Ali [10] deliberated on the practical uses of HNFs (e.g. manufacturing industry, solar energy, electronic cooling, heat pipes, heat exchangers and automotive industry), physical and chemical synthesis procedures (e.g. single-step method and two-step method) and their extraordinary thermophysical properties (i.e. thermal conductivity, viscosity, density and specific heat capacity). According to Das [11], some of the factors influencing the thermal conductivity of MNFs and HNFs are the acidity of the medium, type of nanoparticles injected into a base fluid, sonication, solid volume fraction, temperature and nanoparticle size. Due to the sensitivity of nanofluids to supplementary amounts of solid nanoparticles, Esfe et al. [12] established a new experimental correlation to accurately predict the heat transfer behaviour of two different hybrid nanofluids (i) ethylene glycol conveying ZnO and MWCNT nanoparticles (ii) pure water conveying the same kinds of solid nanoparticles. For this purpose, the thermal conductivity was estimated empirically over a wide range of temperature and nanoparticles volume fraction. Sajid and Ali [13] provided a critical review on the thermal conductivity of HNFs by examining various probable factors influencing like temperature, volume fraction, size and shape of nanoparticles, stability, sonication time and type of liquid phase. In the same context, Hussien et al. [14] investigated experimentally the flow of MWCNTs/GNPs water-based hybrid nanofluids across a thin circular tube to show the positive impacts of adding the graphene nanoplatelets (GNPs) and multi-walled carbon nanotubes (MWCNTs) in the medium on the resulting thermophysical properties, heat transfer coefficient and pressure drop for that flow. It was remarked that a maximum improvement of about 43.4% and 11% is reachable, respectively, for the heat transfer coefficient and the pressure drop at a Reynolds number of 200 by suspending $0.25\;{\text{mass}}\%$ of MWCNTs with $0.035 \;{\text{mass}}\%$ of GNPs in distilled water. These enhancements were explained by the significant improvement in the thermophysical properties of HNFs due to the important contribution of Brownian motion in the mass transport process. Suresh et al. [15] noticed at the end of an experiment that the convective heat transfer rate can be enhanced up to 13.56% in term of the Nusselt number at a Reynolds number of 1730 by utilizing the hybrid nanofluid (Al₂O₃ + Cu)–H₂O instead of a pure water (H₂O) in a hybrid nanofluid flow driven inside a circular tube under the effect of a constant thermal flux condition. Besides, Syam Sundar et al. [16] correlated experimentally the hydrodynamic and heat transfer characteristics of a new kind of HNFs obtained by scattering successfully the nanodiamond (ND) and nickel nanoparticles (Ni) in distilled water (H₂O). From an analogical experimental comparison between (ND + Ni)–H₂O and (MWCNT + Fe₃O₄)–H₂O, it was evident that the hybrid nanoparticles ND and Ni can enhance considerably the heat transfer rate and reduce the skin friction factor.

In another thorough review, Mashali et al. [17] exploited the existing experimental data of the thermophysical properties offered in the literature to discuss more clearly the potential features of using diamond nanoparticles in HNFs through a critical review on the thermophysical properties of HNFs including diamond nanoparticles and their stability. Minea [18] evaluated numerically the thermophysical properties of HNFs (i.e. density, specific heat, thermal conductivity and viscosity) by adopting a three-dimensional computational fluid dynamics model for three varieties of mixtures Al₂O₃–H₂O, (Al₂O₃ + SiO₂)–H₂O and (Al₂O₃ + TiO₂)–H₂O. From this simulation analysis, it was observed that the thermal characteristics of nanofluids can be improved significantly with hybrid nanomaterials concentration and Reynolds number. In this regard, it was found that the convective heat transfer coefficient of (Al₂O₃ + TiO₂)–H₂O can be enhanced up to 257% by dispersing 2.5% of Al₂O₃ and 1.5% of TiO₂ in pure water. The same experimental conclusions were fully elucidated by Yarmand et al. [19], in which the hybrid nanofluids (GNP + Pt)–H₂O exhibit elevated heat transfer rates compared with their corresponding base fluid (H₂O) depending on the values given to the nanoparticles mass concentration and the Reynolds number. From economic and ecological points of view, Shah and Ali [20] analysed the advantages and challenges of utilizing HNFs in solar energy systems as efficient working fluids. To elucidate the effective role of nanoparticles migration in the heat transfer enhancement of HNFs, Yang et al. [21] suggested a new mathematical formulation for HNFs based on the Buongiorno’s monotype nanofluid model [22] to optimize more precisely the heat transfer and friction factor features of (ZrO₂ + TiO₂)–H₂O and (Al₂O₃ + TiO₂)–H₂O by carrying out a two-dimensional fully developed channel flow. During this study, it was revealed an excellent harmony between the results of the proposed model and those available in the experimental literature on HNFs. Further, they remarked that the hybrid nanofluid (Al₂O₃ + TiO₂)–H₂O presented a higher thermal efficiency and a lower friction factor compared with those of the hybrid nanofluid (ZrO₂ + TiO₂)–H₂O.

Along with the increasing development of new efficient semi-analytical and numerical methods, several computational investigations have been done to HNFs quiet recently for the objective of simulating hybrid nanofluid flows in simple and complex geometrical configurations by adopting appropriate numerical schemes and some accurate approximations. Keeping in mind the extensive applications of computational mathematical methods to handle highly nonlinear problems in fluid mechanics and thermal sciences, Hayat and Nadeem [23] conducted numerically the steady three-dimensional simulation of MHD rotating boundary layer flows over a linearly stretching sheet by considering the hybrid nanofluid (Ag + CuO)–H₂O and utilizing the BVP4C routine with the shooting technique (ST) in MATLAB software. The same solution procedure was followed by Subhani and Nadeem [24] to compare the rheological and thermal behaviours of pure water, copper water-based nanofluid and copper–titanium oxide water-based hybrid nanofluid towards 3D rotating flows over a non-uniformly stretching surface embedded in a Darcy porous medium by considering them as micropolar liquids. Thanks to the straightness accuracy proven by the numerical results of BVP4C and ST procedures. Hayat and Nadeem [25] deliberated the effects of thermal radiation, variable heat generation and first-order chemical reaction on the skin friction coefficients, heat transfer and mass transport of a three-dimensional flow over a linear elongating sheet in a uniformly rotating reference frame for the hybrid nanofluid (Ag + CuO)–H₂O.

Unlike the afore-discussed planar hybrid nanofluid flows, it is difficult to comprehend the flow characteristics with computationally complex configurations by means of a classical numerical method because of their irregular boundaries. For this reason, Ashorynejad and Shahriari [26] applied successfully the lattice Boltzmann method (LBM) to scrutinize the magneto-hydrodynamic natural convective flow occurring in an open wavy cavity for the hybrid nanofluid (Al₂O₃ + Cu)–H₂O in the presence of sinusoidal thermal heating at the left wavy wall of the cavity. Rather than the numerical procedure LBM, other efficiently simulating methods were employed by researchers to tackle nonlinear convective flows in irregular geometries with complex conditions like the control volume-based finite element method (CVFEM) and the Galerkin weighted residual finite element method (GWRFEM). Based on the CVFEM procedure, Izadi et al. [27] addressed numerically the problem of natural convective heat transfer between two hot semi-cylinders for the hybrid nanofluid (MWCNT + Fe₃O₄)–H₂O in a square cavity by adopting the Darcy–Brinkman porous media model and considering the existence of two external variable magnetic field sources as well as the viscous dissipation and Joule heating effects. Additional relevant investigation on the water-based hybrid nanofluid (MWCNT + Fe₃O₄)–H₂O has been carried out numerically with the help of GWRFEM by Mehryan et al. [28] in order to evaluate the MHD natural convection heat transfer within a T-shaped cavity. In this advanced modelling, the studied hybrid nanofluid was simulated in the sense of the local thermal non-equilibrium theory (LNET), in which the lower and upper chambers were filled with a Darcy–Brinkman–Forchheimer porous medium. Other interesting numerical and experimental investigations have recently been accomplished on hybrid nanofluids in [29,30,31,32,33] by pioneering researchers to show their thermal significance as enhanced biphasic mixtures.

Based on a thorough analysis of the aforementioned literature review, it is worth remarking that there is no comprehensive investigation on HNFs induced by free convective instabilities developed in a thin horizontal channel with infinite extensions under the influence of Lorentz forces. Hence, motivated by the wide-ranging applications of HNFs in modern nanotechnology and cooling of sophisticated industrial and electronic equipment, this study not only presents the dynamics of water conveying alumina and copper oxide nanoparticles through an infinite horizontal enclosure due to gravitational buoyancy forces when the effects of thermal radiation and Lorentz forces are highly significant but also explores the impact of other involved parameters on the transport phenomenon. Considering the variation in thermophysical properties with the volume fraction of nanoparticles, this study deliberated on the case where the density, the specific heat, the thermal conductivity, the thermal expansion coefficient, the electrical conductivity and the dynamic viscosity vary linearly or nonlinearly with the volume fraction and supplementary physical factors according to the mixture theory and other known experimental correlations. More so, the upper and lower boundaries limiting the dilute hybrid nanofluid (Al₂O₃ + CuO)–H₂O are taken to be as impermeable rough surfaces, in which there is no-penetration of mass flux through these boundaries.

Mathematical formulation and description of the physical problem

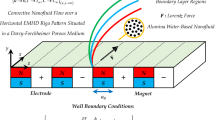
An infinite horizontal enclosure of characteristic thickness $L$ filled with an initially quiescent radiating hybrid nanofluid is schematically portrayed in Fig. 1. In this configuration, the hybrid nanofluid layer (HNL) is exposed to a uniform transverse magnetic field ${\mathbf{H}}_{{\mathbf{0}}} \left( {0,0,H_{0} } \right)$, which is applied perpendicular to the nanofluidic medium by an appropriate magneto-hydrodynamic device. As physical assumptions, it is supposed that the viscous hybrid nanofluidic medium is incompressible, optically thick grey, electrically conducting and presents a Newtonian rheological behaviour, such that the $x^{*}$ and $y^{*}$ components of the radiative heat flux vector ${\mathbf{q}}_{{\mathbf{r}}} \left( {q_{\text{rx}} ,q_{\text{ry}} ,q_{\text{rz}} } \right)$ are insignificant in comparison with that in the $z^{*}$-direction $\left( {{\text{i}}.{\text{e}}.\;q_{\text{rz}} \gg q_{\text{rx}} \;{\text{and}}\;q_{\text{rz}} \gg q_{\text{ry}} } \right)$. In order to explore the combined effects of the Lorentz, Brownian and thermophoretic forces on the onset of buoyancy-driven magneto-convection in single and hybrid water-based nanofluids containing alumina and copper oxide nanoparticles, the nanofluidic system under consideration is disturbed thermally by heating the system from the bottom with an imposed negative temperature gradient $\left( {T_{\text{c}} - T_{\text{h}} } \right)/L$. The upper boundary UIRS is held at a constant temperature $T_{\text{c}}$, while the lower boundary LIRS can take various values $T_{\text{h}} \left( { > T_{\text{c}} } \right)$ until achieving the convective state. To facilitate the formulation of the studied physical phenomenon, the present problem is modelled in Cartesian coordinates $\left( {x^{*} ,y^{*} ,z^{*} } \right)$ by choosing a stationary reference frame $\left( {{\mathbf{e}}_{{\mathbf{x}}} ,{\mathbf{e}}_{{\mathbf{y}}} ,{\mathbf{e}}_{{\mathbf{z}}} } \right)$, in such a way that the $x^{*}$-axis is coincident with the lower surface at $z^{*} = 0.$ Moreover, the hybrid nanofluid (Al₂O₃ + CuO)–H₂O is taken to be infinitely extended in the $x^{*}$ and $y^{*}$ directions and confined between two impermeable rough surfaces LIRS and UIRS. It is worth noting here that the asterisk superscripts are employed in the mathematical description as symbols to distinguish the dimensional variables from the dimensionless variables. Unlike the externally applied magnetic field ${\mathbf{H}}_{{\mathbf{0}}}$, the gravity field ${\mathbf{g}}\left( {0,0, - g} \right)$ is acting uniformly on the medium in the negative vertical $z^{*}$-direction. As a realistic physical constraint, the volume fractions of solid nanoparticles $\phi_{\text{h}}$ and $\phi_{\text{c}}$ are passively controlled at $z^{*} = 0$ and $z^{*} = L$, respectively, by adopting the zero nanoparticle mass flux condition. In view of the fact that the studied hybrid nanofluid having dilute solid suspensions $\left( {{\text{i}}.{\text{e}}.\;\phi_{0} \le 5\% } \right)$, therefore, for given input values of the volume fractions $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }}$ and $\phi_{\text{CuO}}$, all thermophysical properties of the radiative hybrid nanofluid (Al₂O₃ + CuO)–H₂O are considered as constants with negligible influence of temperature, except for density, which can be estimated linearly as a function of the temperature and solid volume fraction based on the Oberbeck–Boussinesq approximation.

Fig. 1

Physical model of the studied hybrid nanofluid flow

Due to the presence of an externally applied magnetic field, thermal radiation and significant slip velocity between water (H₂O), alumina (Al₂O₃) and copper oxide (CuO) inside the metallic oxide hybrid nanofluid (Al₂O₃ + CuO)–H₂O, the generalized transport equations describing the conservation of mass, momentum, energy and solid nanoparticles can be stated formally in this investigation by adopting the Buongiorno’s nanofluid model, invoking the linearized Rosseland approximation in the $z^{*}$-direction and considering the modified Maxwell’s equations.

According to Buongiorno [22], Wakif et al. [34,35,36,37,38] and Rosseland [39], the principal partial differential equations (PDEs) governing the present stability problem are written in the following vectorial forms:

$$ \nabla^{ *} \cdot{\mathbf{V}}^{*} = 0, $$

(1)

$$ \rho_{\text{hnf}} \left[ {\frac{{\partial \varvec{ }}}{{\partial t^{*} }} + \left( {{\mathbf{V}}^{*}\cdot \nabla^{ *} } \right)} \right]{\mathbf{V}}^{*} = - \nabla^{ *} P^{*} + \mu_{\text{hnf}} \nabla^{ *2} {\mathbf{V}}^{*} + {\mathbf{F}}_{{\mathbf{b}}} + {\mathbf{F}}_{{\mathbf{m}}} \varvec{ }, $$

(2)

$$ \left[ {\frac{{\partial \varvec{ }}}{{\partial t^{*} }} + \left( {{\mathbf{V}}^{*}\cdot \nabla^{ *} } \right)} \right]T^{*} = \alpha_{\text{hnf}} \nabla^{ *2} T^{*} + \frac{{16\sigma_{\text{e}} T_{\text{c}}^{3} }}{{3\beta_{\text{R}} \left( {\rho C_{\text{p}} } \right)_{\text{hnf}} }}\frac{{\partial^{2} T^{*} }}{{\partial z^{*2} }} + \tau \left( {D_{\text{B}} \nabla^{ *} \phi^{*} + \frac{{D_{\text{T}} }}{{T_{\text{c}} }}\nabla^{ *} T^{*} } \right).\nabla^{ *} T^{*} , $$

(3)

$$ \left[ {\frac{{\partial \varvec{ }}}{{\partial t^{*} }} + \left( {{\mathbf{V}}^{*}\cdot \nabla^{ *} } \right)} \right]\phi^{*} = D_{\text{B}} \nabla^{ *2} \phi^{*} + \frac{{D_{\text{T}} }}{{T_{\text{c}} }}\nabla^{ *2} T^{*} , $$

(4)

$$ \nabla^{ *}\cdot{\mathbf{H}}^{*} = 0, $$

(5)

$$ \left[ {\frac{{\partial \varvec{ }}}{{\partial t^{*} }} + \left( {{\mathbf{V}}^{*}\cdot \nabla^{ *} } \right)} \right]{\mathbf{H}}^{*} = \left( {{\mathbf{H}}^{*}\cdot \nabla^{ *} } \right){\mathbf{V}}^{*} + \eta_{\text{hnf}} \nabla^{ *2} {\mathbf{H}}^{*} , $$

(6)

For more clarification, the asterisks depicted in Eqs. (1)–(6) as superscripts are used especially to delineate the dimensional variables, like time $t^{ *}$, velocity vector ${\mathbf{V}}^{ *}$, gradient operator $\nabla^{ *}$, pressure $P^{ *}$, hybrid nanofluid temperature $T^{ *}$, nanoparticles volume fraction $\phi^{*}$ and induced magnetic field ${\mathbf{H}}^{ *}$, where ${\mathbf{V}}^{ *} = \left( {u^{*} ,v^{*} ,w^{*} } \right)$, $\nabla^{ *} = \left( {\partial /\partial x^{*} ,\partial /\partial y^{*} ,\partial /\partial z^{*} } \right)$ and ${\mathbf{H}}^{ *} = \left( {H_{\text{x}}^{*} ,H_{\text{y}}^{*} ,H_{\text{z}}^{*} } \right)$. On the other hand, the subscripts $hnf$, $nf$, $f$ and $np$ are used to specify the hybrid nanofluid, the nanofluid, the base fluid and the solid nanoparticles, respectively. From the physical meaning point of view, the terms $\sigma_{\text{e}}$, $\beta_{\text{R}}$, $\alpha_{\text{hnf}} \left( { = k_{\text{hnf}} /\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} } \right)$ and $\tau \left( { = \left( {\rho C_{\text{p}} } \right)_{\text{np}} /\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} } \right)$ are the Stefan–Boltzmann constant, the absorption coefficient of the medium, the thermal diffusivity and the heat capacitance ratio, respectively. Here, $k_{\text{hnf}}$ and $\left( {\rho C_{\text{p}} } \right)_{\text{hnf}}$ refer to the thermal conductivity and heat capacitance of the hybrid nanofluid, whereas $\left( {\rho C_{\text{p}} } \right)_{\text{np}}$ indicates the heat capacitance of the nanoparticles.

Moreover, the external forces ${\mathbf{F}}_{{\mathbf{b}}}$ and ${\mathbf{F}}_{{\mathbf{m}}}$ shown in Eq. (2) represent the gravitational buoyancy force and magnetic Lorentz force, respectively. These forces are acted differently on the nanofluidic system according to the following expressions [37, 40]:

$$ {\mathbf{F}}_{{\mathbf{b}}} = - \rho_{\text{hnf}} \left[ {1 - \beta_{\text{hnf}} \left( {T^{*} - T_{\text{c}} } \right) + \beta_{\upphi } \left( {\phi^{*} - \phi_{0} } \right)} \right] g\, {\mathbf{e}}_{{\mathbf{z}}}, $$

(7)

$$ {\mathbf{F}}_{{\mathbf{m}}} = \frac{{\bar{\mu }_{\text{hnf}} }}{4\pi }\left( {\nabla^{ *} \times {\mathbf{H}}^{*} } \right) \times {\mathbf{H}}^{*} , $$

(8)

where $T_{\text{c}}$ and $T_{\text{h}}$ designate the cold and hot wall temperatures, respectively, $D_{\text{B}}$ refers to the Brownian diffusion coefficient, $D_{\text{T}}$ represents the thermophoretic diffusion coefficient, $\phi_{0}$ denotes the reference value of the volumetric fraction of nanoparticles, $g$ symbolizes the gravity acceleration.

Furthermore, the thermophysical quantities $\rho_{\text{hnf}}$, $\mu_{\text{hnf}}$, $k_{\text{hnf}}$, $\left( {\rho C_{\text{p}} } \right)_{\text{hnf}}$, $\eta_{\text{hnf}}$, $\beta_{\text{hnf}}$ and $\bar{\mu }_{\text{hnf}}$ shown in Eqs. (2)–(8) represent the effective values of the density, dynamic viscosity, thermal conductivity, heat capacitance, magnetic diffusivity, thermal expansion coefficient and the magnetic permeability of the hybrid nanofluid, respectively, whereas $\left( {\rho C_{\text{p}} } \right)_{\text{np}}$ and $\beta_{\upphi}$ denote the heat capacitance and the volumetric expansion coefficient due to the presence of nanoparticles.

For hybrid nanofluids, the coefficients $D_{\text{B}}$ and $D_{\text{T}}$ characterizing the random motion of the nanoparticles are quantified by the following relations:

$$ D_{\text{B}} = \frac{{k_{\text{B}} T_{\text{c}} }}{{3\pi \mu_{\text{f}} d_{\text{np}} }} , $$

(9)

$$ D_{\text{T}} = 0.26\left( {\frac{{k_{\text{f}} }}{{2k_{\text{f}} + k_{\text{np}}^{*} }}} \right)\left( {\frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} }}} \right)\phi_{0} . $$

(10)

Keeping in mind the simultaneous effects of Brownian motion and thermophoresis on the hybrid nanofluid flow and heat transfer characteristics, the mass flux vector can be expressed by:

$$ {\mathbf{J}}^{*} = - \rho_{\text{np}}^{*} \left( {D_{\text{B}} \nabla^{ *} \phi^{*} + \frac{{D_{\text{T}} }}{{T_{\text{c}} }}\nabla^{ *} T^{*} } \right). $$

(11)

Based on the new boundary conditions revised by Nield and Kuznetsov [41, 42] for the nanoparticles mass flux and those developed recently by Celli and Kuznetsov [43] for the roughness of the contact surface, the hydrodynamic and thermal boundary conditions for the problem under consideration are written as follows:

$$ w^{*} = \frac{{\partial u^{*} }}{{\partial z^{*} }} - \frac{{\xi_{1} }}{{\sqrt {K_{1} } }}u^{*} = \frac{{\partial v^{*} }}{{\partial z^{*} }} - \frac{{\xi_{1} }}{{\sqrt {K_{1} } }}v^{*} = 0,\quad T^{*} = T_{\text{h}} ,\quad {\mathbf{J}}^{*}\cdot{\mathbf{e}}_{{\mathbf{z}}} = 0 \quad {\text{at }}\;\; z^{*} = 0, $$

(12)

$$ w^{*} = \frac{{\partial u^{*} }}{{\partial z^{*} }} + \frac{{\xi_{2} }}{{\sqrt {K_{2} } }}u^{*} = \frac{{\partial v^{*} }}{{\partial z^{*} }} + \frac{{\xi_{2} }}{{\sqrt {K_{2} } }}v^{*} = 0, \quad T^{*} = T_{\text{c}} ,\quad {\mathbf{J}}^{*}\cdot{\mathbf{e}}_{{\mathbf{z}}} = 0\quad {\text{at }}\;\; z^{*} = L. $$

(13)

Physically, Eqs. (12) and (13) exhibit more realistic boundary constraints for the present MHD stability problem. Moreover, the significant contributions of Brownian motion and thermophoresis of nanoparticles to the heat and mass transportation inside the hybrid nanofluid are potentially considered in these newly developed boundary conditions. Furthermore, the volumetric fraction of nanoparticles at each rough surface is controlled passively depending on the wall temperature gradient.

According to Celli and Kuznetsov [43], the roughness of each surface is modelled mathematically by assuming that the two horizontal boundaries are shallow porous layers, whose permeabilities are $K_{1}$ and $K_{2}$. Moreover, the terms $\xi_{1}$ and $\xi_{2}$ appeared in Eqs. (12) and (13) designate two dimensionless parameters, which are strongly depend on the pore size distribution in the shallow porous medium.

Based on powerful phenomenological laws, the dimensional physical quantities $\rho_{\text{hnf}}$, $\mu_{\text{hnf}}$, $k_{\text{hnf}}$, $\left( {\rho C_{\text{p}} } \right)_{\text{hnf}}$ and $\left( {\rho \beta } \right)_{\text{hnf}}$ characterizing the hybrid nanofluid (Al₂O₃ + CuO)–H₂O can be expressed as a function of the thermophysical properties of their nanometric constituents including water (H₂O) as fluid phase together with alumina (Al₂O₃) and copper oxide (CuO) nanomaterials as solid phase, whose thermophysical properties are clearly listed in Table 1.

Table 1 Thermophysical properties of water, alumina and copper oxide nanoparticles [36, 45, 46]

More precisely, for predicting the effective dynamic viscosity $\mu_{\text{hnf}}$ and thermal conductivity $k_{\text{hnf}}$, it is more preferable to utilize the Corcione’s nanofluid models [44] as the best empirical correlations to evaluate the quantities $\mu_{\text{hnf}}$ and $k_{\text{hnf}}$ with a higher level of accuracy. By way of a regression analysis, the standard deviation of errors corresponding to these empirical models was estimated to approximately 1.84% for the dynamic viscosity $\mu_{\text{hnf}}$ and 1.86% for the thermal conductivity $k_{\text{hnf}}$. Beside the quantities $\mu_{\text{hnf}}$ and $k_{\text{hnf}}$, the effective values of the density $\rho_{\text{hnf}}$, heat capacitance $\left( {\rho C_{\text{p}} } \right)_{\text{hnf}}$, volumetric mass expansion coefficient $\left( {\rho \beta } \right)_{\text{hnf}}$, electrical conductivity $\sigma_{\text{hnf}}$, magnetic permeability $\bar{\mu }_{\text{hnf}}$ and magnetic diffusivity $\eta_{\text{hnf}}$ can also be estimated in the vicinity of the reference temperature $T_{\text{c}}$ by employing the formulas regrouped in Table 2, which are widely used in the literature.

Table 2 Appropriate thermophysical expressions suggested for hybrid nanofluids

As described tabularly in Table 2 for (Al₂O₃ + CuO)–H₂O, the quantities $\phi_{0}$, $\rho_{\text{np}}^{*}$, $k_{\text{np}}^{*}$, $\left( {\rho C_{\text{p}} } \right)_{\text{np}}^{*}$, $\left( {\rho \beta } \right)_{\text{np}}^{*}$, $\sigma_{\text{np}}^{*}$, ${\text{Re}}$, ${ \Pr }$ and $d_{\text{f}}$ are expressed by the following relationships:

$$ \phi_{0} = \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} , $$

(14)

$$ \rho_{\text{np}}^{*} = \frac{{\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} \rho_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} \rho_{\text{CuO}} }}{{\phi_{0} }}, $$

(15)

$$ k_{\text{np}}^{*} = \frac{{\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} k_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} k_{\text{CuO}} }}{{\phi_{0} }}, $$

(16)

$$ \left( {\rho C_{\text{p}} } \right)_{\text{np}}^{*} = \frac{{\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} \left( {\rho C_{\text{p}} } \right)_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} \left( {\rho C_{\text{p}} } \right)_{\text{CuO}} }}{{\phi_{0} }}, $$

(17)

$$ \left( {\rho \beta } \right)_{\text{np}}^{*} = \frac{{\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} \left( {\rho \beta } \right)_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} \left( {\rho \beta } \right)_{\text{CuO}} }}{{\phi_{0} }}, $$

(18)

$$ \sigma_{\text{np}}^{*} = \frac{{\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} \sigma_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} \sigma_{\text{CuO}} }}{{\phi_{0} }}, $$

(19)

$$ \bar{\mu }_{\text{np}}^{*} = \frac{{\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} \bar{\mu }_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} \bar{\mu }_{\text{CuO}} }}{{\phi_{0} }}, $$

(20)

$$ \bar{\mu }_{\text{np,f}} = \bar{\mu }_{0} \left( {1 + \chi_{\text{np,f}} } \right), $$

(21)

$$ \chi_{\text{np,f}} = \frac{{\rho_{\text{np,f}} \chi_{{{\text{m}}_{\text{np,f}} }} }}{{M_{\text{np,f}} }}, $$

(22)

$$ {\text{Re}} = \frac{{2 \rho_{\text{f}} k_{\text{B}} T_{\text{c}} }}{{\pi \mu_{\text{f}}^{2} d_{\text{np}} }}, $$

(23)

$$ { \Pr } = \frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} \alpha_{\text{f}} }}, $$

(24)

$$ d_{\text{f}} = 0.1\left( {\frac{{6M_{\text{f}} }}{{\pi \rho_{{{\text{f}}_{ 0} }} N_{\text{A}} }}} \right)^{{\frac{1}{3}}} . $$

(25)

Significantly, $\left( {\chi_{\text{np}} ,\chi_{\text{f}} } \right)$ are the magnetic susceptibilities of solid nanoparticles and base fluid, correspondingly, $\bar{\mu }_{0}$ symbolizes the magnetic permeability of vacuum, $\left( {M_{\text{f}} ,M_{\text{np}} } \right)$ corresponds to the molar mass of solid nanoparticles and base fluid, respectively, ${\text{Re}}$ represents the Reynolds number, ${ \Pr }$ designates the Prandtl number, $d_{\text{f}}$ highlights the molecular diameter of water, $T_{\text{fr}}$ corresponds to the freezing point of the base fluid, $k_{\text{B}}$ refers to the Boltzmann constant, $d_{\text{np}}$ denotes the diameter of solid nanoparticles, $\alpha_{\text{f}}$ shows the thermal diffusivity of the base fluid, $M$ signifies the molecular mass weight of water, $\rho_{{{\text{f}}_{ 0} }}$ characterizes the density of water at $293\;{\text{K}}$ and $N_{\text{A}}$ specifies the Avogadro number. Further, it is worth asserting here that the values $\bar{\mu }_{0} = 4\pi \times 10^{ - 7} \;{\text{H}}\;{\text{m}}^{ - 1}$, $M_{\text{f}} = 18\;{\text{g}}\;{\text{mol}}^{ - 1}$, $k_{\text{B}} = 1.38066 \times 10^{ - 23} \;{\text{J}}\;{\text{K}}^{ - 1}$, $\rho_{\text{f0}} = 998\;{\text{kg}}\;{\text{m}}^{ - 3}$ and $N_{\text{A}} = 6.022 \times 10^{23} \;{\text{mol}}^{ - 1}$ are used during the implementation of results as necessary physical constants.

By making use of a feasible non-dimensionalization procedure, the governing PDEs can be simplified accordingly. For this purpose, it is more meaningful methodologically to incorporate the following non-dimensional variables:

$$ \begin{aligned} \left( {x,y,z} \right) & = \frac{{\left( {x^{*} ,y^{*} , z^{*} } \right)}}{L},\quad t = \left( {\frac{{\alpha_{\text{f}} }}{{L^{2} }}} \right)t^{*} , \quad P = \left( {\frac{{L^{2} }}{{\rho_{\text{f}} \alpha_{\text{f}}^{2} }}} \right) P^{*} ,\quad T = \frac{{T^{*} - T_{\text{c}} }}{{T_{\text{h}} - T_{\text{c}} }}, \\ \phi & = \frac{{\phi^{*} - \phi_{0} }}{{\phi_{0} }},\quad {\mathbf{V}} = \left( {\frac{L}{{\alpha_{\text{f}} }}} \right){\mathbf{V}}^{*} ,\quad {\mathbf{H}} = \left( {\frac{1}{{H_{0} }}} \right){\mathbf{H}}^{*} . \\ \end{aligned} $$

(26)

Thus, Eqs. (1)–(6) are altered successfully to the following dimensionless forms:

$$ \nabla \cdot {\mathbf{V}} = 0, $$

(27)

$$ \frac{{\rho_{\text{r}} }}{ \Pr }\left[ {\frac{\partial }{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right)} \right]{\mathbf{V}} = - \frac{1}{ \Pr }\nabla p + \mu_{\text{r}} \nabla^{2} {\mathbf{V}} + \left[ {\left( {\rho \beta } \right)_{\text{r}} R_{\text{a}} T - R_{\text{N}} \phi } \right]{\mathbf{e}}_{{\mathbf{z}}} + \frac{{\bar{\mu }_{\text{r}} { \Pr }Q}}{{{ \Pr }_{\text{m}} }}\left( {\nabla \times {\mathbf{H}}} \right) \times {\mathbf{H}}, $$

(28)

$$ \left( {\rho C_{\text{p}} } \right)_{\text{r}} \left[ {\frac{\partial }{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right)} \right]T = k_{\text{r}} \nabla^{2} T + R_{\text{d}} \frac{{\partial^{2} T }}{{\partial z^{2} }} + N_{\text{b}} \nabla \phi \cdot \nabla T + N_{\text{t}} \nabla T \cdot \nabla T, $$

(29)

$$ N_{\text{b }} {\text{Le}}\left[ {\frac{\partial }{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right)} \right]\phi = N_{\text{b }} \nabla^{2} \phi + N_{\text{t}} \nabla^{2} T, $$

(30)

$$ \nabla\cdot{\mathbf{H}} = 0, $$

(31)

$$ \left[ {\frac{\partial }{\partial t} + \left( {{\mathbf{V}} \cdot \nabla } \right)} \right]{\mathbf{H}} = \left( {{\mathbf{H}} \cdot \nabla } \right){\mathbf{V}} + \frac{ \Pr }{{\bar{\mu }_{\text{r}} \sigma_{\text{r}} { \Pr }_{\text{m}} }}\nabla^{2} {\mathbf{H}}. $$

(32)

Evidently, the modified pressure term $p$ involved in Eq. (28) is given formally by:

$$ p = P + \frac{{\rho_{\text{r}} { \Pr }R_{\text{a}} z }}{{\beta_{\text{f}} \left( {T_{\text{h}} - T_{\text{c}} } \right)}}. $$

(33)

By substituting the non-dimensional variables of Eq. (26) into Eqs. (12) and (13), we get the following dimensionless boundary conditions:

$$ w = \frac{\partial u}{\partial z} - \varLambda_{1} u = \frac{\partial v}{\partial z} - \varLambda_{1} v = N_{\text{b}} \frac{\partial \phi }{\partial z} + N_{\text{t}} \frac{\partial T}{\partial z} = 0 , \quad T = 1\quad {\text{at}}\;\; z = 0, $$

(34)

$$ w = \frac{\partial u}{\partial z} + \varLambda_{2} u = \frac{\partial v}{\partial z} + \varLambda_{2} v = N_{\text{b}} \frac{\partial \phi }{\partial z} + N_{\text{t}} \frac{\partial T}{\partial z} = 0,\quad T = 0\quad {\text{at}}\;\; z = 1. $$

(35)

The reduced quantities $\rho_{\text{r}}$, $\mu_{\text{r}}$, $\left( {\rho \beta } \right)_{\text{r}}$, $\bar{\mu }_{\text{r}}$, $\left( {\rho C_{\text{p}} } \right)_{\text{r}}$, $k_{\text{r}}$ and $\sigma_{\text{r}}$ shown above represent the relative thermophysical properties of the hybrid nanofluid, $\varLambda_{1}$ and $\varLambda_{2}$ are the roughness parameters, $R_{\text{a}}$ is the thermal Rayleigh number, $R_{\text{N}}$ is the nanoparticle Rayleigh number, $Q$ is the magnetic Chandrasekhar number, ${ \Pr }_{\text{m}}$ is the magnetic Prandtl number, $R_{\text{d}}$ is the radiation parameter, ${\text{Le}}$ is the Lewis number, $N_{\text{b}}$ is the Brownian motion parameter and $N_{\text{t}}$ is the thermophoresis parameter. These physical quantities are defined properly as follows:

$$ \left\{ {\begin{array}{*{20}l} {\rho_{\text{r}} = \frac{{\rho_{\text{hnf}} }}{{\rho_{\text{f}} }},\quad \mu_{\text{r}} = \frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }},\quad \left( {\rho \beta } \right)_{\text{r}} = \frac{{\left( {\rho \beta } \right)_{\text{hnf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }},\quad \bar{\mu }_{\text{r}} = \frac{{\bar{\mu }_{\text{hnf}} }}{{\bar{\mu }_{\text{f}} }},\quad \left( {\rho C_{\text{p}} } \right)_{\text{r}} = \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }},} \hfill \\ {k_{\text{r}} = \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }},\quad \sigma_{\text{r}} = \frac{{\sigma_{\text{hnf}} }}{{\sigma_{\text{f}} }},\quad \varLambda_{1} = \frac{{L \xi_{1} }}{{\sqrt {K_{1} } }},\quad \varLambda_{2} = \frac{{L \xi_{2} }}{{\sqrt {K_{2} } }},\quad R_{\text{a}} = \frac{{\left( {\rho \beta } \right)_{\text{f}} \left( {T_{\text{h}} - T_{\text{c}} } \right)g L^{3} }}{{\mu_{\text{f}} \alpha_{\text{f}} }},} \hfill \\ {R_{\text{N}} = \frac{{ \left( {\rho_{\text{np}}^{*} - \rho_{\text{f}} } \right)gL^{3} \phi_{0} }}{{\mu_{\text{f}} \alpha_{\text{f}} }},\quad Q = \frac{{\bar{\mu }_{\text{f}} L^{2} H_{0}^{2} }}{{4\pi \eta_{\text{f}} \mu_{\text{f}} }},\quad { \Pr }_{\text{m}} = \frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} \eta_{\text{f}} }},\quad R_{\text{d}} = \frac{{16\sigma_{\text{e}} T_{\text{c}}^{3} }}{{3\beta_{\text{R}} k_{\text{f}} }}, } \hfill \\ {{\text{Le}} = \frac{{\alpha_{\text{f}} }}{{D_{\text{B}} }},\quad N_{\text{b}} = \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{np}}^{*} D_{{{\text{B}} }} \phi_{0} }}{{\left( {\rho C_{\text{p}} } \right)_{{{\text{f}} }} \alpha_{\text{f}} }},\quad N_{\text{t}} = \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{np}}^{*} D_{{{\text{T}} }} \left( {T_{\text{h}} - T_{\text{c}} } \right)}}{{\left( {\rho C_{\text{p}} } \right)_{{\text{f}}} \alpha_{\text{f}} T_{\text{c}} }}.} \hfill \\ \end{array} } \right. $$

(36)

By virtue of Eq. (27), the resulting boundary conditions [i.e. Eqs. (34) and (35)] are rearranged as follows:

$$ w = \frac{{\partial^{2} w}}{{\partial z^{2} }} - \varLambda_{1} \frac{\partial w}{\partial z} = N_{\text{b}} \frac{\partial \phi }{\partial z} + N_{\text{t}} \frac{\partial T}{\partial z} = 0,\quad T = 1 \;\; \;{\text{at}}\;\; z = 0, $$

(37)

$$ w = \frac{{\partial^{2} w}}{{\partial z^{2} }} + \varLambda_{2} \frac{\partial w}{\partial z} = N_{\text{b}} \frac{\partial \phi }{\partial z} + N_{\text{t}} \frac{\partial T}{\partial z} = 0,\;\;\; T = 0\;\;\;{\text{at}}\;\; z = 1. $$

(38)

Physically, the impermeability and no-slip hydrodynamic boundary conditions (i.e. rigid–rigid case) can be recovered by considering $\varLambda_{1,2} \to \infty$ $\left( {{\text{i}}.{\text{e}}.\;K_{1,2} \to 0 \;\;\;{\text{or}}\;\;L \gg \sqrt {K_{1,2} } /\xi_{1,2} } \right)$. In this limiting case, the roughness effect on the surfaces $z^{ *} = 0$ and $z^{ *} = L$ becomes insignificant, due to the fact that the channel height $L$ is sufficiently larger than the roughness oscillation magnitude $\sqrt {K_{1,2} } /\xi_{1,2}$ of each surface, which emphasizes that the solid surfaces are relatively smooth. By taking $\varLambda_{1,2} \to 0$ $\left( {{\text{i}}.{\text{e}}.\;K_{1,2} \to \infty } \right)$ in Eqs. (34) and (35), the impermeability and stress-free hydrodynamic boundary conditions (i.e. free–free case) can easily be regained. On the other hand, the stress-free/no-slip and no-slip/stress-free hydrodynamic boundary conditions can also be obtained from Eqs. (34) and (35), when the components of the couple $\left( {\varLambda_{1} ,\varLambda_{2} } \right)$ tend asymptotically to $(0,\infty )$ and $(\infty ,0)$, respectively. These mixed boundary conditions are commonly considered in the Rayleigh–Bénard convection (RBC) to characterize the free-rigid and rigid-free cases.

By invoking the proposed hybrid nanofluid models listed in Table 2, the physical quantities $\rho_{\text{r}}$, $\mu_{\text{r}}$, $k_{\text{r}}$, $\sigma_{\text{r}}$, $\left( {\rho \beta } \right)_{\text{r}}$, $\left( {\rho C_{\text{p}} } \right)_{\text{r}}$, $D_{\text{B}}$, $D_{\text{T}}$, $R_{\text{N}}$, $L_{\text{e}}$, $N_{\text{b}}$ and $N_{\text{t}}$ characterized the oxide metallic hybrid nanofluid (Al₂O₃ + CuO)–H₂O are accurately estimated in Tables 3 and 4 for different values of $\phi_{0}$ and $d_{{\text{np}}}$ by setting $L = 4.1 \times 10^{ - 5} \;{\text{m}}$, $T_{\text{c}} = 300\;{\text{K}}$ and $T_{\text{h}} = 301\;{\text{K}}$ as the selected key values.

Table 3 Relative thermophysical properties of (Al₂O₃ + CuO)–H₂O estimated for various values of $\phi_{0}$ and d_np, where $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}}$

Table 4 Numerical ranges of the basic hybrid nanofluid parameters, when $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}}$

As highlighted previously in Table 1, the chemical species Al₂O₃, CuO and H₂O possess very low molar magnetic susceptibilities $\chi_{\text{m}}$. Keeping this fact in mind, it is revealed that the modified magnetic permeability $\bar{\mu }_{\text{np}}^{ *}$ of the hybrid nanoparticles Al₂O₃ and CuO is very close to the magnetic permeability of water $\bar{\mu }_{\text{f}}$. Therefore, the inserted metallic oxide nanoparticles Al₂O₃ and CuO show no sensible influence on the magnetic permeability of the biphasic mixture corresponding to dilute hybrid nanofluids $\left( {{\text{i}}.{\text{e}}.\;\phi_{0} \le 5\% } \right)$. Consequently, the relative quantity $\bar{\mu }_{\text{r}}$ defined in Eqs. (28) and (32) can be straightforwardly replaced by the unit value in all subsequent related scrutinizes.

Based on a thorough statistical analysis, it is revealed from Tables 3 and 4 that with a further consistent increase in the nanoparticles loading, the physical quantities $\rho_{\text{r}}$, $\mu_{\text{r}}$ and $k_{\text{r}}$ exhibit a greater enhancement at the rates of 4.15996400, 20.9436847 and 2.94756320, respectively, when the volumetric fraction $\phi_{0}$ of the hybrid nanoparticles Al₂O₃ and CuO is increased regularly by 1% from 1 to 5%, while a decreasing tendency is depicted for the relative thermophysical properties $\sigma_{\text{r}}$, $\left( {\rho \beta } \right)_{\text{r}}$ and $\left( {\rho C_{\text{p}} } \right)_{\text{r}}$, whose average rates of diminishing are estimated to be of about − 1.45611230, − 0.64777600 and − 0.23227630, correspondingly. As the main consequences of adding nanoparticles in the base fluid, the thermophoretic diffusion coefficient $D_{\text{T}}$, the nanoparticle Rayleigh number $R_{\text{N}}$, the Brownian motion parameter $N_{\text{b}}$ and the thermophoresis parameter $N_{\text{t}}$ are heightened more with the increasing values of the parameter $\phi_{0}$. Moreover, it is divulged that with the progressive escalation in the diameter $d_{\text{np}}$ of the nanoparticles Al₂O₃ and CuO from $20$ to $28\;{\text{nm}}$, the assessed values of the relative dynamic viscosity $\mu_{\text{r}}$ and thermal conductivity $k_{\text{r}}$ decrease slightly at the rates of − 0.00133832 and − 0.00098437, respectively. Furthermore, it is witnessed that the enlargement occurred for the diameter of solid nanoparticles $d_{\text{np}}$ affect decreasingly on the Brownian diffusion coefficient $D_{\text{B}}$, which provokes a higher elevation in the values of Lewis number ${\text{Le}}$, while an opposite behaviour is noticed for the Brownian motion parameter $N_{\text{b}}$. Similarly, Jana et al. [51] remarked that the stability could be influenced by characteristics of nanoparticles. In view of the present statistical scrutiny, it bears noting that the aforementioned rates were estimated accurately through the generated dataset by utilizing the slope linear regression method (SLRM) suggested by Shah et al. [52], Animasaun et al. [53] and Wakif et al. [54].

Linear stability analysis of magneto-convection in hybrid nanofluids

The three-dimensional radiative magneto-convection flow described above for the hybrid nanofluid (Al₂O₃ + CuO)–H₂O is treated physically in this investigation as a modified counterpart of the Rayleigh–Bénard instability problem, in which the hybrid nanofluid layer is confined vertically between two horizontal boundaries with infinite extents. Moreover, the hybrid nanofluid is assumed to be initially in a quiescent stationary state characterized by a purely conductive behaviour. Furthermore, closed-form solutions ${\bar{\mathbf{V}}}$, $\bar{P}$, $\bar{T}$, $\bar{\phi }$ and ${\bar{\mathbf{H}}}$ for the initial conductive state can be obtained formally by resolving the system of Eqs. (27)–(32) along with their associated boundary conditions (34) and (35) and seeking time-independent solutions, whose expressions are functions of the spatial variable $z$ alone. Hence, by introducing the desired solution forms ${\bar{\mathbf{V}}} = \left( {\bar{u}(z),\bar{v}(z),\bar{w}(z)} \right)$, $\bar{P} = \bar{P}(z)$, $\bar{T} = \bar{T}(z)$, $\bar{\phi } = \bar{\phi }(z)$ and ${\bar{\mathbf{H}}} = \left( {\bar{H}_{{\text{x}}} (z),\bar{H}_{{\text{y}}} (z),\bar{H}_{{\text{z}}} (z)} \right)$ into Eqs. (27)–(32) and using the additional Wakif’s condition [55] $\left( { {\text{i}}.{\text{e}}.\;\mathop \smallint \nolimits_{0}^{1} \bar{\phi } {\text{d}}z = 0} \right)$, we get exactly the following solutions:

$$ {\bar{\mathbf{V}}} = (0,0, 0) $$

(39)

$$ \frac{1}{ \Pr }\frac{{{\text{d}}\bar{P}}}{{{\text{d}}z}} = \left( {\rho \beta } \right)_{\text{r}} R_{\text{a}} \bar{T} - R_{\text{N}} \bar{\phi } - \frac{{\rho_{\text{r}} R_{\text{a}} }}{{\beta_{\text{f}} \left( {T_{\text{h}} - T_{\text{c}} } \right)}}, $$

(40)

$$ \bar{T} = 1 - z, $$

(41)

$$ \bar{\phi } = \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\left( {z - \frac{1}{2}} \right), $$

(42)

$$ \left( {\bar{H}_{\text{x}} ,\bar{H}_{\text{y}} ,\bar{H}_{\text{z}} } \right) = (0,0,1). $$

(43)

Based on the linear stability theory (LST), the thermo-magneto-hydrodynamic stability of the hybrid nanofluidic system can be studied thoroughly for various values of the embedded physical parameters $\phi_{0}$, $Q$, $R_{\text{d}}$, $d_{\text{np}}$, $\varLambda_{1}$ and $\varLambda_{2}$. Accordingly, for given input values of these parameters, the criterion for the onset of magneto-convection instability in the hybrid nanofluid (Al₂O₃ + CuO)–H₂O can be developed by superimposing infinitesimal disturbances on the basic solutions as follows:

$$ {\mathbf{V}} = {\bar{\mathbf{V}}} + {\mathbf{V}}^{\prime } \varvec{ },\quad P = \bar{P} + P^{\prime } ,\quad T = \bar{T} + T^{\prime } ,\quad \phi = \bar{\phi } + \phi^{\prime } ,\quad {\mathbf{H}} = {\bar{\mathbf{H}}} + {\mathbf{H}}^{\prime } , $$

(44)

where ${\mathbf{V}}^{\prime }$, $P^{\prime }$, $T^{\prime }$, $\phi^{\prime }$ and ${\mathbf{H}}^{\prime }$ are the perturbed states of velocity, pressure, temperature, nanoparticles volume fraction and magnetic field, respectively.

After substituting Eqs. (39)–(43) into Eqs. (27)–(32) and neglecting the quadratic terms arising from the imposed perturbations, we obtain the following linearized PDEs:

$$ \nabla \cdot {\mathbf{V}}^{\prime } = 0, $$

(45)

$$ \rho_{\text{r}} \frac{{\partial {\mathbf{V}}^{\prime } }}{\partial t} = - \nabla P^{\prime} + \mu_{\text{r}} { \Pr } \nabla^{2 } {\mathbf{V}}^{\prime } + { \Pr }\left[ {\left( {\rho \beta } \right)_{\text{r}} R_{\text{a}} T^{\prime } - R_{\text{N}} \phi^{\prime } } \right]{\mathbf{e}}_{{\mathbf{z}}} + \frac{{\bar{\mu }_{\text{r}} { \Pr }^{2} Q}}{{{ \Pr }_{\text{m}} }}\left( {\nabla \times {\mathbf{H}}^{\prime } } \right) \times {\mathbf{e}}_{{\mathbf{z}}} \varvec{ }, $$

(46)

$$ \left( {\rho C_{\text{p}} } \right)_{\text{r}} \left( {\frac{{\partial T^{\prime } }}{\partial t } - w^{\prime } } \right) = k_{\text{r}} \nabla^{2} T^{\prime } + R_{\text{d}} \frac{{\partial^{2} T^{\prime } }}{{\partial z^{2} }} - N_{\text{b}} \frac{{\partial \phi^{\prime } }}{\partial z } - N_{\text{t}} \frac{{\partial T^{\prime } }}{\partial z }, $$

(47)

$$ N_{\text{b }} \frac{{\partial \phi^{\prime } }}{\partial t } + N_{\text{t}} w^{\prime } = \frac{{N_{\text{b }} }}{\text{Le }}\nabla^{2} \phi^{\prime } + \frac{{N_{\text{t}} }}{\text{Le}}\nabla^{2} T^{\prime } , $$

(48)

$$ \nabla\cdot {\mathbf{H}}^{\prime } = 0, $$

(49)

$$ \frac{{\partial {\mathbf{H}}^{\prime } }}{\partial t } = \frac{{\partial {\mathbf{V}}^{\prime } }}{\partial z} + \frac{ \Pr }{{\bar{\mu }_{\text{r}} \sigma_{\text{r}} { \Pr }_{\text{m}} }}\nabla^{2} {\mathbf{H}}^{\prime } , $$

(50)

where ${\mathbf{V}}^{\prime } = \left( {u^{\prime } ,v^{\prime } ,w^{\prime } } \right)$ and ${\mathbf{H}}^{\prime } = \left( {H_{\text{x}}^{\prime} ,H_{\text{y}}^{\prime} ,H_{\text{z}}^{\prime} } \right)$.

Now, these perturbation equations are subjected to the following boundary conditions:

$$ w^{\prime } = \frac{{\partial^{2} w^{\prime } }}{{\partial z^{2} }} - \varLambda_{1} \frac{{\partial w^{\prime } }}{\partial z } = T^{\prime} = N_{\text{b}} \frac{{\partial \phi^{\prime } }}{\partial z } + N_{\text{t}} \frac{{\partial T^{\prime } }}{\partial z } = 0\;\;\;{\text{at}}\;\;z = 0, $$

(51)

$$ w^{\prime } = \frac{{\partial^{2} w^{\prime } }}{{\partial z^{2} }} + \varLambda_{2} \frac{{\partial w^{\prime } }}{\partial z } = T^{\prime} = N_{\text{b}} \frac{{\partial \phi^{\prime } }}{\partial z } + N_{\text{t}} \frac{{\partial T^{\prime } }}{\partial z } = 0 \;\;\;{\text{at}}\;\; z = 1. $$

(52)

In order to obtain a more compact form for the $z$-component of the perturbed momentum equation as a function of $w^{\prime}$, $T^{\prime}$, $\phi^{\prime}$, $H_{\text{z}}^{\prime}$ only, Eq. (46) can be handled carefully by applying the operator ${\mathbf{e}}_{{\mathbf{z}}}\cdot\left[ {\nabla \times \left( {\nabla \times \blacksquare } \right)} \right]$ on both sides of this equation and using the mathematical identity:

$$ \nabla \times \left( {\nabla \times {\mathbf{X}}} \right) = \nabla \left( {\nabla \cdot {\mathbf{X}}} \right) - \nabla^{2} {\mathbf{X}}, $$

(53)

where ${\mathbf{X}}$ is a specified vector.

Thus, by virtue of Eqs. (45), (49) and (53), the pressure gradient term $\nabla P^{ \prime}$ can justifiably be removed from Eq. (46). Accordingly, the perturbed momentum equation reduces to:

$$ \rho_{\text{r}} \frac{\partial }{\partial t}\left( {\nabla^{2} w^{\prime } } \right) = \mu_{\text{r}} { \Pr } \nabla^{4 } w^{\prime } + \left( {\rho \beta } \right)_{\text{r}} { \Pr }R_{\text{a}} \nabla_{\text{H}}^{2} T^{\prime } - R_{\text{N}} { \Pr } \nabla_{\text{H}}^{2} \phi^{\prime } + \frac{{\bar{\mu }_{\text{r}} { \Pr }^{2} Q}}{{{ \Pr }_{\text{m}} }}\frac{\partial }{\partial z}\left( {\nabla^{2} H_{\text{z}}^{\prime} } \right), $$

(54)

where $\nabla_{\text{H}}^{2} = \partial^{2} /\partial x^{2} + \partial^{2} /\partial y^{2}$.

Similarly, the $z$-component of Eq. (50) is written as follows:

$$ \frac{{\partial H_{\text{z}}^{\prime} }}{\partial t} = \frac{{\partial w^{\prime } }}{\partial z} + \frac{ \Pr }{{\bar{\mu }_{\text{r}} \sigma_{\text{r}} { \Pr }_{\text{m}} }}\nabla^{2} H_{\text{z}}^{\prime} . $$

(55)

Methodically, it is obviously important to mention that the coefficients arising from the set of Eqs. (47), (48), (54) and (55) are neither affected by $x$, $y$ nor $t$. As a result of this mathematical particularity and the translational invariance of their governing equations in the $x$ and $y$ directions, the perturbation quantities $w^{\prime }$, $T^{\prime }$, $\phi^{\prime }$ and $H_{\text{z}}^{\prime}$ can be regarded as two-dimensional waves with periodic time dependence. Consequently, it makes sense physically to express the resulting disturbances in terms of normal modes as follows:

$$ \left[ {\begin{array}{*{20}c} {w^{\prime } (t,x,y,z)} \\ {T^{\prime } (t,x,y,z)} \\ {\begin{array}{*{20}c} {\phi^{\prime } (t,x,y,z)} \\ {H_{\text{z}}^{\prime} (t,x,y,z)} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\fancyscript{w}(z)} \\ {\theta (z)} \\ {\begin{array}{*{20}c} {\varPhi (z)} \\ {{\mathcal{H}}(z)} \\ \end{array} } \\ \end{array} } \right]\,{ \exp }\left[ {i\left( {a_{\text{x}} x + a_{\text{y}} y} \right) + \lambda t} \right], $$

(56)

where the dimensionless couple $\left( {a_{\text{x}} ,a_{\text{y}} } \right)$ represents the $x$ and $y$ components of the wave number vector ${\mathbf{a}}$, whereas $\lambda$ denotes the dimensionless time decay coefficient of the harmonic disturbances.

After substituting the expressions of Eq. (56) into Eqs. (47), (48), (54) and (55), we get the following stability equations:

$$ \mu_{\text{r}} \left( {D^{2} - a^{2} } \right)^{2} \fancyscript{w} - \left( {\rho \beta } \right)_{\text{r}} R_{\text{a}} a^{2} \theta + R_{\text{N}} a^{2} \varPhi + \frac{{\bar{\mu }_{\text{r}} { \Pr }Q}}{{{ \Pr }_{\text{m}} }}D\left( {D^{2} - a^{2} } \right){\mathcal{H}} = \frac{{\rho_{\text{r}} \lambda }}{ \Pr } \left( {D^{2} - a^{2} } \right)\fancyscript{w}, $$

(57)

$$ \left( {\rho C_{\text{p}} } \right)_{\text{r}} \fancyscript{w} + \left[ {\left( {k_{\text{r}} + R_{\text{d}} } \right)D^{2} - N_{\text{t}} D - k_{\text{r}} a^{2} } \right]\theta - N_{\text{b}} D\varPhi = \left( {\rho C_{\text{p}} } \right)_{\text{r}} \lambda \theta , $$

(58)

$$ - N_{\text{t}} \fancyscript{w} + \frac{{N_{\text{t}} }}{\text{Le}} \left( {D^{2} - a^{2} } \right)\theta + \frac{{N_{\text{b}} }}{\text{Le}}\left( {D^{2} - a^{2} } \right)\varPhi = N_{\text{b }} \lambda \varPhi , $$

(59)

$$ D\fancyscript{w} + \frac{ \Pr }{{\bar{\mu }_{\text{r}} \sigma_{\text{r}} { \Pr }_{\text{m}} }}\left( {D^{2} - a^{2} } \right){\mathcal{H}} = \lambda {\mathcal{H}}. $$

(60)

In view of the foregoing procedure, Eqs. (57)–(60) are supported by the following boundary conditions:

$$ \fancyscript{w} = D^{2} \fancyscript{w} - \varLambda_{1} D\fancyscript{w} = \theta = N_{\text{b}} D\varPhi + N_{\text{t}} D\theta = 0 \;\;\; {\text{at}}\;\; z = 0, $$

(61)

$$ \fancyscript{w} = D^{2} \fancyscript{w} + \varLambda_{2} D\fancyscript{w} = \theta = N_{\text{b}} D\varPhi + N_{\text{t}} D\theta = 0 \;\;\;{\text{at}}\;\; z = 1. $$

(62)

Here, the mathematical operator $D^{\text{n}}$ indicates the $n{\text{th}}$-order derivative with respect to $z$ and $a$ represents the dimensionless resultant wave number, where $D^{\text{n}} = d^{\text{n}} /dz^{\text{n}}$ and $a^{2} = a_{\text{x}}^{2} + a_{\text{y}}^{2}$.

As revealed above in Eqs. (57)–(60), the resulting ordinary differential equations (ODEs) together with their related boundary conditions (61) and (62) constitute a generalized eigenvalue problem, which has to be solved semi-analytically and numerically as reported in the next section.

Solution methodologies and validation of results

Inside the hybrid nanofluid layer (Al₂O₃ + CuO)–H₂O, the metallic oxide nanoparticles Al₂O₃ and CuO have very strong tendency to concentrate close to the cold wall to achieve the top-heavy arrangement in the equilibrium state, due to the combined effect of zero nanoparticles mass flux and negative temperature gradient boundary conditions. In this respect, the oscillatory mode of magneto-convection is obviously ruled out for this particular stability problem because of the absence of two opposing buoyancy forces responsible for the appearance of oscillatory convection mode as proved previously by Chand [56]. Consequently, the stationary convective mode $\left( {{\text{i}}.{\text{e}}.,\;\lambda = 0 } \right)$ is the sole possible means of convection heat transfer in the confined medium. This kind of magneto-convection instability can occur in the hybrid nanofluidic medium once the thermal Rayleigh number $R_{\text{a}}$ attains a certain optimum value $R_{\text{ac}}$ called the critical thermal Rayleigh number. It is further worth mentioning here that the control parameter $R_{\text{a}}$ is regarded as the eigenvalue of the present physical problem.

Therefore, the resulting steady ordinary differential equations can be simplified more by combining Eqs. (57) and (60) and adopting the following feasible transformations:

$$ \begin{aligned} U_{1} (z) & = \fancyscript{w}(z),\quad U_{2} (z) = D^{2} \fancyscript{w}(z) - \varLambda_{1} D\fancyscript{w}(z),\quad U_{3} (z) = D^{2} \fancyscript{w}(z) + \varLambda_{2} D\fancyscript{w}(z), \\ U_{4} (z) & = D^{3} \fancyscript{w}(z) - a^{2} D\fancyscript{w}(z),\quad U_{5} (z) = \theta (z),\quad U_{6} (z) = D\theta (z), \\ U_{7} (z) & = N_{\text{b}} D\varPhi (z) + N_{\text{t}} D\theta (z),\quad U_{8} (z) = N_{\text{b}} D^{2} \varPhi (z) + N_{\text{t}} D^{2} \theta (z), \\ \end{aligned} $$

(63)

Accordingly, Eqs. (57)–(60) can be altered to a linear differential system $(S)$, which is written in a reduced form as follows:

$$ (S){:}\,\,\left\{ {{\dot{\mathbf{F}}} = {\boldsymbol{\mathcal{M}}}{\mathbf{F}}/{\dot{\mathbf{F}}} = \frac{{{\text{d}}{\mathbf{F}}}}{{{\text{d}}z}},\quad {\mathbf{F}} = \left( {U_{\text{j}} (z)} \right)_{{1 \le {\text{j}} \le 8}} ,\quad \varvec{ }{\boldsymbol{\mathcal{M}}} = \left( {M_{\text{ij}} } \right)_{{1 \le {\text{i}},{\text{j}} \le 8}} } \right\}. $$

(64)

More explicitly, the nonzero matrix elements $M_{\text{ij}}$ are given by:

$$ \begin{aligned} M_{12} & = - \frac{1}{{\left( {\varLambda_{1} + \varLambda_{2} } \right)}},\quad M_{13} = \frac{1}{{\left( {\varLambda_{1} + \varLambda_{2} } \right)}}, \\ M_{22} &= - \left( {\frac{{a^{2} + \varLambda_{1} \varLambda_{2} }}{{\varLambda_{1} + \varLambda_{2} }}} \right),\quad M_{23} = \left( {\frac{{a^{2} - \varLambda_{1}^{2} }}{{\varLambda_{1} + \varLambda_{2} }}} \right), \\ M_{24} & = 1,\quad M_{32} = - \left( {\frac{{a^{2} - \varLambda_{2}^{2} }}{{\varLambda_{1} + \varLambda_{2} }}} \right),\\ M_{33} &= \left( {\frac{{a^{2} + \varLambda_{1} \varLambda_{2} }}{{\varLambda_{1} + \varLambda_{2} }}} \right), \quad M_{34} = 1, \quad M_{41} = - a^{4} , \\ M_{42} & = \frac{{\varLambda_{2} \left( {\mu_{\text{r}} a^{2} + \bar{\mu }_{\text{r}}^{2} \sigma_{\text{r}} Q} \right)}}{{\mu_{\text{r}} \left( {\varLambda_{1} + \varLambda_{2} } \right)}}, \\ M_{43} &= \frac{{\varLambda_{1} \left( {\mu_{\text{r}} a^{2} + \bar{\mu }_{\text{r}}^{2} \sigma_{\text{r}} Q} \right)}}{{\mu_{\text{r}} \left( {\varLambda_{1} + \varLambda_{2} } \right)}},\quad M_{45} = \left( {\frac{{\left( {\rho \beta } \right)_{\text{r}} R_{\text{a}} }}{{\mu_{\text{r}} }} + \frac{{N_{\text{t}} R_{\text{N}} }}{{\mu_{\text{r}} N_{\text{b}} }} } \right)a^{2} , \\ M_{47} & = - \frac{{R_{\text{N}} a^{2} }}{{\mu_{\text{r}} N_{\text{b}} }},\quad M_{56} = 1,\\ M_{61} &= - \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{r}} }}{{\left( {R_{\text{d}} + k_{\text{r}} } \right)}},\quad M_{65} = \frac{{k_{\text{r}} a^{2} }}{{\left( {R_{\text{d}} + k_{\text{r}} } \right)}}, \\ M_{68} & = \frac{1}{{\left( {R_{\text{d}} + k_{\text{r}} } \right)}},\quad M_{78} = 1,\quad M_{81} = N_{\text{t}} {\text{Le}},\\ M_{87} &= a^{2} . \\ \end{aligned} $$

(65)

As stated above, the resulting autonomous differential system $(S)$ is a set of eight linear first-order ordinary differential equations (ODEs), which are strengthened by the following boundary conditions:

$$ U_{1} (0) = U_{2} (0) = U_{5} (0) = U_{7} (0) = 0, $$

(66)

$$ U_{1} (1) = U_{3} (1) = U_{5} (1) = U_{7} (1) = 0. $$

(67)

From a computational standpoint, the resulting boundary value problem described by Eqs. (64)–(67) can be solved properly by utilizing a robust optimization procedure that guarantees a high degree of precision in terms of the critical stability parameters $a_{\text{c}}$ and $R_{\text{ac}}$. Thus, for given values of the parameters $\phi_{0}$, $Q$, $R_{\text{d}}$, $d_{\text{np}}$, $\varLambda_{1}$ and $\varLambda_{2}$, the thermo-magneto-hydrodynamic stability of the studied hybrid nanofluid can be scrutinized readily in this investigation through the dataset generated for the critical thermal Rayleigh number $R_{\text{ac}}$ characterizing the occurrence of the magneto-convective instability in the hybrid nanofluidic medium.

Based on the power series method (PSM) and the Chock–Schechter numerical integration (CSNI), the desired solutions $\left\{ {U_{\text{i}} (z)/1 \le i \le 8} \right\}$ of the differential system $(S)$ together with its boundary conditions [i.e. Eqs. (66) and (67)] are obtained straightforwardly by converting the boundary value problem (BVP) described above by Eqs. (64)–(67) to a well-defined initial value problem (IVP) and then writing each variable $U_{\text{i}} (z)$ of the problem as a linear combination of eight independent new variable $u_{\text{i}}^{\text{j}} (z)$, where $1 \le i,\,j \le 8$. Explanation details of these computational methods are done more thoroughly in the semi-analytical analysis reported by Wakif et al. [55] as well as in the informative book edited by Platten and Legros [57]. By making use of the boundary conditions (66) and (67) successively during the resolution procedure with PSM or CSNI, the establishing IVP leads to a homogeneous linear algebraic system (HLAS), whose unique variables are the nonzero coefficients of the previously constricted combination. In order to get non-trivial outcomes, the determinant associated with the resulting algebraic system must vanish for specified values of the emerging physical parameters $\phi_{0}$, $Q$, $R_{\text{d}}$, $d_{\text{np}}$, $\varLambda_{1}$ and $\varLambda_{2}$. Finally, the criterion for the onset of magneto-convection in the hybrid nanofluid (Al₂O₃ + CuO)–H₂O can be determined numerically by minimizing the thermal Rayleigh number $R_{\text{a}}$ with respect to the wave number $a$ based on the nonlinear dependence of the control parameters $R_{\text{a}}$ and $a$, which are linked implicitly through a dispersion relation of the form:

$$ f\left( {R_{\text{a}} ,a,\phi_{0} ,Q,R_{\text{d}} ,d_{\text{np}} ,\varLambda_{1} ,\varLambda_{2} } \right) = 0. $$

(68)

Therefore, for fixed values of the input parameters $\phi_{0}$, $Q$, $R_{\text{d}}$, $d_{\text{np}}$, $\varLambda_{1}$ and $\varLambda_{2}$, Eq. (68) reduces to a highly nonlinear equation joining the thermal Rayleigh number $R_{\text{a}}$ and the wave number $a$, which can be solved numerically with the help of a powerful Newton–Raphson iterative solver (NRIS) for each specified value of the wave number $a$. By keeping the lowest positive real value of $R_{\text{a}}$ herein as the unique possible physical solution, the magneto-convective stability threshold $\left( {a_{\text{c}} ,R_{\text{ac}} } \right)$ of the marginal stability curve $R_{\text{a}} = R_{\text{a}} (a)$ can be achieved successfully by employing the golden section search method (GSSM) to find numerically the minimum value $R_{\text{ac}}$ of the thermal Rayleigh number $R_{\text{a}}$ characterizing the commencement of the stationary mode of magneto-convection in the hybrid nanofluidic medium as highlighted graphically in Fig. 2, where $R_{\text{ac}} = R_{\text{a}} \left( {a_{\text{c}} } \right)$.

Fig. 2

Sketch of the marginal stability curve and its corresponding neutral threshold

As emphasized in the solution methodology description, the resulting set of ODEs along with its associated realistic boundary conditions are solved semi-analytically by means of the power series method (PSM) and then numerically with the help of an efficient numerical code generated in MATLAB software based on the Chock–Schechter numerical integration (CSNI), since there is no possibility to establish closed-form solutions for the present hybrid nanofluid stability problem. In order to show the capability and flexibility of PSM as an innovative semi-analytical method towards solving various kinds of stability problems, several feasible comparisons have been done successfully for some limiting cases reported previously by Celli and Kuznetsov [43] for regular fluids, as well as with those provided by Wakif et al. [35, 38] for regular fluids, electrically conducting fluids and nanofluids as shown in Tables 5 and 6, in which the exactness of PSM results are presented quantitatively with four, five and ten orders of magnitude according to the tested case.

Table 5 Validation of PSM outcomes with the previously published results for regular fluids

Table 6 Validation of PSM outcomes with the recently published results for electrically conducting fluids and nanofluids, in the case where $\rho_{\text{r}} = \mu_{\text{r}} = \bar{\mu }_{\text{r}} = k_{\text{r}} = \sigma_{\text{r}} = (\rho \beta )_{\text{r}} = \left( {\rho C_{\text{p}} } \right)_{\text{r}} = 1$, $R_{\text{d}} = 0$, $R_{\text{N}} = 0.1$, $L_{\text{e }} = 5000$ and $N_{\text{b}} = N_{\text{t}} = 10^{ - 6}$

Computationally, it is noticed an excellent harmony between the PSM outcomes and those published recently by eminent researchers in the thermal stability field. Consequently, PSM is a promising semi-analytical tool to efficiently analyse numerous thermal stability problems dealing either with conventional fluids, monotype nanofluids or hybrid nanofluids. The main features of PSM lie in its straightforwardness as a semi-analytical approach of tackling linear stability problems besides its high exactness, whose level can be adjusted accordingly through the truncation order  $N$  of the power series upshots depending on the approximation degree needed to be reached asymptotically during the computational analysis.

To assure the robustness of the semi-analytical computational method utilized in solving the current stability problem, a sufficient convergence criterion for PSM has been established semi-analytically in terms of the critical stability parameters $R_{\text{ac}}$ and $a_{\text{c}}$ for various values of the magnetic Chandrasekhar number $Q$, in the case where $\phi_{0} = 0.01$, $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}}$, $R_{\text{d}} = 0.1$, $d_{\text{np}} = 20\;{\text{nm}}$ and $\varLambda_{1} = \varLambda_{2} = 100$ as portrayed in Figs. 3 and 4. Moreover, the convergence of PSM can be achieved appropriately once the absolute difference value between two successive approximations for $R_{\text{ac}}$ and $a_{\text{c}}$ is equal to or less than a specified small value $\varepsilon$. From these graphical illustrations, it is obviously seen that the convergence of the PSM results can be attained progressively when the truncation order $N$ exceeds a certain value $N_{\text{c}}$, which is in direct relation with the required degree of accurateness. Furthermore, an excellent convergence can be realized by imposing a sufficiently large value for $N$ in the power series expansion. Also, it is intuitively clear that the truncation order $N$ should be selected appropriately in such a way that $N \ge 25$ to ensure a minimum asymptotical convergence offering admissible physical results. Thus, PSM can generate highly reasonable results even if $N_{\text{c}} = 25$ is taken as the necessary convergence order. Based on the numerical outcomes extracted from the dataset of Figs. 3 and 4, further tabular outcomes are summarized in Table 7 in order to evaluate more precisely the values of the convergence order $N_{\text{c}}$ corresponding to the following PSM criterion:

Fig. 3

Convergence of $R_{\text{ac}}$ with respect to $N$ for various values of $Q$

Fig. 4

Convergence of $a_{\text{c}}$ with respect to $N$ for various values of $Q$

Table 7 Effects of $Q$ and $N$ on the PSM results, in the case where $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}} = 0.5{{\% }}$, $R_{\text{d}} = 0.1$, $d_{\text{np}} = 20\;{\text{nm}}$, $\varLambda_{1} = \varLambda_{2} = 100$

$$ \left\{ {\begin{array}{*{20}c} {\left| {R_{\text{ac}} (N + 1) - R_{\text{ac}} (N)} \right| \le 10 ^{ - 5} ,} \\ {\left| {a_{\text{c}} (N + 1) - a_{\text{c}} (N)} \right| \le 10 ^{ - 5} , } \\ \end{array} } \right. $$

(69)

By virtue of the above-proposed convergence criterion, it is observed from Table 7 that the smallest value of the convergence order $N_{\text{c}}$ satisfying the conditions of Eq. (69) is relatively around $N_{\text{c}} = 35$ for increasingly ranged values of the magnetic parameter values  $Q$ from 0 to 60. However, the convergence analysis of the power series method proves that the generated PSM results depend more sensitively on the values given to the emerging parameter $Q$, in which the convergence order $N_{\text{c}}$ is varied increasingly with respect to the magnetic parameter $Q$. Keeping the above-mentioned convergence criterion in mind, additional comparison tests between the power series method (PSM) and the Chock–Schechter numerical integration (CSNI) are carried out successfully in Table 8 with a good concordance. Consequently, the correctness of the results presented in this investigation is authenticated numerically with the help of CSNI.

Table 8 Semi-analytical and numerical estimation of the thermal stability parameters $R_{\text{ac}}$ and $a_{\text{c}}$ with the aid of PSM and CSNI, when $N_{\text{c}} = 35$ and $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}} = 0.5{{\% }}$

Results and discussion

In view of the aforementioned computational advantages of the power series method (PSM), supplementary semi-analytical implementations have been carried out with an absolute accuracy of the order of $10^{ - 5}$ for accomplishing other graphical and tabular results elucidating a thorough physical understanding of the thermo-magneto-hydrodynamic instability phenomenon studied herein for the hybrid nanofluid (Al₂O₃ + CuO)–H₂O under the considerable impacts of thermal radiation and variable thermophysical properties as revealed in Figs. 5–12, Tables 9–11. In these additional illustrations, the significant effects of the pertinent parameters namely, magnetic Chandrasekhar number $Q$, radiation parameter $R_{\text{d}}$, solid nanoparticles diameter $d_{\text{np}}$, roughness parameters $\left( {\varLambda_{1} ,\varLambda_{2} } \right)$ and solid volume fractions $\left( {\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} ,\phi_{\text{CuO}} } \right)$ on the realistic criterion for the growth of magneto-buoyancy convection cells in the medium are depicted and discussed more comprehensively in this section by adopting the default values $Q = 60$, $R_{\text{d}} = 0.1$, $d_{\text{np}} = 20 \;{\text{nm}}$, $\varLambda_{1} = 100$, $\varLambda_{2} = 100$ and $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}} = 0.5{{\% }}$ for the various controlling physical parameters unless otherwise indicated clearly in the tabular and graphical depictions as mentioned in Tables 8–11 and their corresponding Figs. 5–12.

Fig. 5

Marginal stability curves of (Al₂O₃ + CuO)–H₂O for various values of $Q$

Table 9 Comparative PSM results for some special cases, when $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}} = 0.5\% ,\;Q = 60$, $R_{\text{d}} = 0.1$ and $d_{\text{np}} = 20\;{\text{nm}}$

Moreover, the thermo-magneto-hydrodynamic behaviour of the studied metallic oxide hybrid nanofluid against distinct given values of the magnetic Chandrasekhar number $Q \,\left( {{\text{i}}.{\text{e}}.\; 0 \le Q \le 60} \right)$ is illustrated clearly in Table 8 as well as in Fig. 5. In these elucidations, the influence of the externally applied magnetic field ${\mathbf{H}}_{{\mathbf{0}}} \left( {0,0,H_{0} } \right)$ on the thermal stability of the dilute biphasic mixture (Al₂O₃ + CuO)–H₂O is revealed implicitly through the varying values of the magnetic number $Q\left( { = \bar{\mu }_{\text{f}} L^{2} H_{0}^{2} /\left( {4\pi \eta_{\text{f}} \mu_{\text{f}} } \right)} \right)$. From Fig. 5, it is remarked that the marginal stability curves expressed mathematically by the functions $R_{\text{a}} = f_{\text{Q}} (a)$  show a rapid upsurge in both directions of the plan $\left( {a,R_{\text{a}} } \right)$  as long as the magnetic Chandrasekhar number $Q$ is increased discretely from 0 to 60. Consequently, an escalation in the magnetic parameter $Q$ obstructs noticeably the appearance of convection cells and reduces their critical size $L_{\text{c}} \left( { = 2\pi /a_{\text{c}} } \right)$, due to the notable strengthening effect of the parameter $Q$ on the critical stability parameters $R_{\text{ac}}$ and $a_{\text{c}}$ as clarified in Table 8. Hence, the strength of the externally applied magnetic field ${\mathbf{H}}_{{\mathbf{0}}}$ has a stabilizing influence on the deliberated hybrid nanofluidic medium. Indeed, this fact can be explained physically by the effective existence of magnetic Lorentz forces because of the electrically conducting property of the hybrid nanofluid (Al₂O₃ + CuO)–H₂O. These magnetic forces act intensely in the medium as resistive drag forces by retarding noticeably the initiation of MHD convective flows driving by the electrically conducting hybrid nanofluid (Al₂O₃ + CuO)–H₂O.

Even when the magnetic effect $Q$ is included, the same trends are noticed for the thermal stability parameters $R_{\text{ac}}$ and $a_{\text{c}}$ as a result of enhancing the radiative heat flux $q_{\text{rz}}$ in the $z^{ *}$-direction by varying the radiation parameter $R_{\text{d}}$ progressively from 0 to 0.4 $\left( {{\text{i}}.{\text{e}}. \;0 \le R_{\text{d}} \le 0.4} \right)$ as disclosed in Fig. 6 and Table 8. Further, it is important to mention here that the thermal radiation parameter $R_{\text{d}} \left( { = 16\sigma_{\text{e}} T_{\text{c}}^{3} /\left( {3\beta_{\text{R}} k_{\text{f}} } \right)} \right)$ is defined physically as the relative contribution of the thermal radiation transfer to the conduction heat transfer. Basically, the thermal radiation supplies a new mechanism for equilibrating the thermal perturbations by smoothing extensively the temperature fluctuations inside the radiative hybrid nanofluidic medium due to the intensification in its apparent thermal conductivity $k_{{\text{eff}}} \left( { = k_{{\text{hnf}}} + 16\sigma_{{\text{e}}} T_{{\text{c}}}^{3} /\left( {3\beta_{{\text{R}}} } \right)} \right)$. Thus, the radiative effect of the thermal parameter $R_{\text{d}}$ reduces notably the convective heat transfer rate throughout the medium and thereby stabilizes the hybrid nanofluid (Al₂O₃ + CuO)–H₂O. In this case, the medium releases a small amount of thermal energy for the buoyancy-driven forces causing the inception of hybrid nanofluid convection. For this reason, the stability of the hybrid nanofluidic system grows with the enrichment in the radiative heat flux $q_{\text{rz}}$.

Fig. 6

Marginal stability curves of (Al₂O₃ + CuO)–H₂O for various values of $R_{\text{d}}$

Unlike the stabilizing features of the physical parameters $Q$ and $R_{\text{d}}$ towards the radiative hybrid nanofluid (Al₂O₃ + CuO)–H₂O, reverse changes in the critical stability parameters $R_{\text{ac}}$ and $a_{\text{c}}$ are happened as long as the nanometric diameter $d_{\text{np}}$ of the solid nanomaterials Al₂O₃ and CuO is augmented slightly from $20\;{\text{nm}}$ until $28\;{\text{nm}}$ $\left( {{\text{i}}.{\text{e}}. \;20\;{\text{nm}} \le d_{\text{np}} \le 28\;{\text{nm}}} \right)$ as exhibited in Fig. 7 and Table 8. From these tabular and graphical demonstrations, it is worth clarifying here that the solid nanoparticles having a higher diameter $d_{\text{np}}$ speed up thermally the occurrence of magneto-convection instabilities in the medium and hence enlarge meaningfully the size of convection cells $L_{\text{c}}$. These interesting findings can be explicated physically by the enhancement in the thermal energy transfer rate between the solid spherical surface of each nanoparticle and the surrounding fluidic medium when the ideal contact surface area $S \left( { = \left( {\pi N_{\text{np}} d_{\text{np}}^{2} } \right)/4} \right)$ between the solid and fluid phases is widened somewhat through the diameter $d_{\text{np }}$, where $N_{\text{np}}$ is the total number of nanoparticles. This situation indicates that the geometrical dimension $d_{\text{np}}$ of nanoparticles has a destabilizing tendency on the radiative hybrid nanofluid (Al₂O₃ + CuO)–H₂O.

Fig. 7

Marginal stability curves of (Al₂O₃ + CuO)–H₂O for various values of $d_{\text{np}}$

As deliberated theoretically in the last section, the distinct situation of the surfaces LIRS and UIRS featured by the equality in the roughness parameters $\varLambda_{1}$ and $\varLambda_{2}$ implies that both the top and bottom boundaries are identical from the hydrodynamical point of view. Also, this special physical particularity signifies that the horizontal surfaces LIRS and UIRS limiting the hybrid nanofluidic layer are exposed to the same type of dynamical boundary conditions. Besides, these controlling parameters can effectively delay the development of magneto-convections cells in the medium with a reduction in their critical size $L_{\text{c}}$ by reducing significantly the overall heat transport throughout the radiative hybrid nanofluidic medium. This retarding trend can really occur in the radiative hybrid nanofluidic medium when the physical parameters $\varLambda_{1}$ and $\varLambda_{2}$ or at least one of them is elevated separately from 10 to 100 $\left( {{\text{i}}.{\text{e}}. \;10 \le \varLambda_{1} ,\varLambda_{2} \le 100} \right)$ as underlined in Figs. 8, 9 and Table 8, in which the marginal stability curves $R_{\text{a}} = f_{{\Lambda_{1} }} (a)$ and $R_{\text{a}} = f_{{\Lambda_{2} }} (a)$ represented graphically in Figs. 8 and 9 are moved apparently upward with a slight displacement around the right side of the plan $\left( {a,R_{\text{a}} } \right)$ signifying that the roughness parameters $\varLambda_{1}$ and $\varLambda_{2}$ have both a stabilizing impact on the onset of convective heat transfer in the channel. The principal reason behind these consequences is that the height of the channel becomes sufficiently large compared with the roughness oscillation magnitude, in such a way that the surface roughness is turned out to be negligible (i.e. smooth solid walls) to get nearby the case of no-slip velocity boundary conditions, which is commonly known in the literature as the rigid–rigid case $\left[ {{\text{i}}.{\text{e}}.\;\left( {\varLambda_{1} ,\varLambda_{2} } \right) \to (\infty ,\infty )} \right]$. On the contrary, when the surface irregularities are far apart from each other $\left[ {{\text{i}}.{\text{e}}.\;\left( {\varLambda_{1} ,\varLambda_{2} } \right) \to (0,0)} \right],$ the free–free case is recovered as the stress-free boundary conditions. Additionally, other intermediate limiting cases for the roughness parameters $\varLambda_{1}$ and $\varLambda_{2}$ are highlighted in Table 9 in order to compare the thermo-magneto-hydrodynamic stability of the radiative medium under these special boundary conditions. After analysing this tabular illustration, it is concluded that the rigid–rigid case (RR) exhibits higher thermal stability compared successively with the free-rigid case (FR), rigid-free case (RF) and free–free case (FF), such that $R_{\text{ac}} (RR) > R_{\text{ac}} (FR) > R_{\text{ac}} (RF) > R_{\text{ac}} (FF)$ and $L_{\text{c}} (RR) < L_{\text{c}} (FR) < L_{\text{c}} (RF) < L_{\text{c}} (FF)$.

Fig. 8

Marginal stability curves of (Al₂O₃ + CuO)–H₂O for various values of $\varLambda_{1}$

Fig. 9

Marginal stability curves of (Al₂O₃ + CuO)–H₂O for various values of $\varLambda_{2}$

The mutual interaction of the metallic oxide nanoparticles Al₂O₃ and CuO on the thermo-magneto-hydrodynamic stability of water-based hybrid nanofluids is well illustrated in Figs. 10–12, Tables 10 and 11 for various volumetric proportions $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }}$ and $\phi_{\text{CuO}}$. Even though using either the monotype nanofluids Al₂O₃–H₂O and CuO–H₂O $\left( {{\text{i}}.{\text{e}}.\;\phi_{\text{CuO}} = 0 \;{\text{and}}\; \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = 0} \right)$ or the hybrid nanofluid (Al₂O₃ + CuO)–H₂O $\left( {{\text{i}}.{\text{e}}.\text{ }\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} \ne 0\; {\text{and}}\; \phi_{\text{CuO}} \ne 0} \right)$, it is perceived generally from the obtained results shown in Figs. 10, 11 and Table 10 that the augmentation in the total volume fraction $\phi_{0} \left( { = \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} } \right)$ of nanoparticles hastens the establishment of magneto-convective transport phenomena in the confined radiative medium with an elevation in the size $L_{\text{c}}$ of their convection cells. Based on the slope linear regression method (SLRM), it is witnessed in Table 10 that the monotype nanofluid CuO–H₂O presents greater thermo-magneto-hydrodynamic stability compared successively with the hybrid nanofluid (Al₂O₃ + CuO)–H₂O and the monotype nanofluid Al₂O₃–H₂O. Quantitatively, it is evidenced clearly in Table 4 that the Brownian motion and thermophoresis parameters $\left( {N_{\text{b}} ,N_{\text{t}} } \right)$ are monotonically increasing functions of the volume fraction $\phi_{0}$ of hybrid nanoparticles Al₂O₃ and CuO. Consequently, the nanofluid parameters $N_{\text{b}}$ and $N_{\text{t}}$ exert mostly a destabilizing effect in this analysis. Furthermore, it is revealed from Fig. 12 and Table 11 that the substitution of the metallic oxide nanoparticles Al₂O₃ by their nanoparticles counterparts CuO in the monotype nanofluid Al₂O₃–H₂O enhances noticeably the thermo-magneto-hydrodynamic stability of the resulting mixture.

Fig. 10

Marginal stability curves of Al₂O₃–H₂O and CuO–H₂O for various values of $\phi_{0}$

Table 10 PSM results in terms of $R_{\text{ac}}$ and $a_{\text{c}}$ for numerous values of $\phi_{0}$, when $Q = 60$, $R_{\text{d}} = 0.1$, $d_{\text{np}} = 20\;{\text{nm}}$ and $\varLambda_{1} = \varLambda_{2} = 100$

Table 11 PSM estimations of $R_{\text{ac}}$ and $a_{\text{c}}$ for various values of $\phi_{\text{CuO}}$ and $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }}$, when $\phi_{0} = 4{{\% }}$, $Q = 60$, $R_{\text{d}} = 0.1$, $d_{\text{np}} = 20\;{\text{nm}}$ and $\varLambda_{1} = \varLambda_{2} = 100$

Fig. 11

Marginal stability curves of CuO–H₂O and (Al₂O₃ + CuO)–H₂O for various values of $\phi_{0}$

Fig. 12

Marginal stability curves of (Al₂O₃ + CuO)–H₂O for various values of $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }}$ and $\phi_{\text{CuO}}$

Conclusions

A novel physical approach is proposed in this investigation to examine the thermo-magneto-hydrodynamic stability of a confined biphasic medium comprising a dilute hybrid nanofluid whose aqueous phase (i.e. pure water) incorporates the same volumetric proportion of nanoparticles Al₂O₃ and CuO $\left( {{\text{i}}.{\text{e}}.\; \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = \phi_{\text{CuO}} } \right)$ with a volumetric fraction $\phi_{0} \left( { = \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + \phi_{\text{CuO}} } \right)$ of nanoparticles not more than $5\%$. By adopting the Oberbeck–Boussinesq approximation, utilizing the generalized Buongiorno’s nanofluid with variable thermophysical properties, applying the linearized form of Rosseland approximation for the radiative heat flux, exploiting the Corcione’s experimental correlations and invoking necessary conservation equations with the modified Maxwell’s equations, the resulting linear stability equations are then derived analytically for the radiative hybrid nanofluid (Al₂O₃ + CuO)–H₂O based on the linear stability theory and the normal mode technique. These governing equations along with the roughness, isothermal and zero nanoparticles mass flux boundary conditions are successfully tackled semi-analytically and numerically by means of the power series method (PSM) and the Chock–Schechter numerical integration (CSNI), in order to deliberate more physically the effective impacts of various factors affected on the stability of the metallic oxide hybrid nanofluidic medium (Al₂O₃ + CuO)–H₂O like the volume fraction of hybrid solid nanomaterials Al₂O₃ and CuO, the spherical size of solid nanoparticles, the existence of an external magnetic field source, the thermal radiation heat flux as well as the wall’s roughness. The significant outcomes of the current scrutiny can be abridged as follows:

• The present findings are multiply validated and presented with an absolute accuracy of the order of $10 ^{ - 5}$ during this study.

• The Brownian motion and the thermophoresis mechanisms have a destabilizing effect on the radiative metallic oxide hybrid nanofluid (Al₂O₃ + CuO)–H₂O. This perturbating tendency can be reduced either by diminishing the volume fraction of solid nanoparticles Al₂O₃ and CuO or substituting a part of the nanomaterials Al₂O₃ by the same amount of CuO.

• The thermo-magneto-hydrodynamic stability of the hybrid nanofluid (Al₂O₃ + CuO)–H₂O is inversely proportional to the size of convection cells occurring at the onset of convective instability.

• The presence of Lorentz forces, thermal radiation and wall’s roughness delays considerably the appearance of convection cells in the hybrid nanofluidic medium with a notable reduction in their critical size.

• An upsurge in the roughness parameters $\varLambda_{1}$ and $\varLambda_{2}$ from 10 to 100 can improve the stability of the hybrid nanofluid (Al₂O₃ + CuO)–H₂O with an estimated linear regression slope attaining the typical values 3.22715476 and 3.22787803 in term of the critical stability parameter $R_{\text{ac}}$ towards the increasing values of $\varLambda_{1}$ and $\varLambda_{2}$, respectively.

• The thermo-magneto-hydrodynamic stability of the hybrid nanofluid (Al₂O₃ + CuO)–H₂O can be enhanced significantly by reducing the spherical size of nanoparticles.