Significance of Joule heating and viscous heating on heat transport of MoS₂–Ag hybrid nanofluid past an isothermal wedge

Abstract

The problem of flow and heat transport of magneto-composite nanofluid over an isothermal wedge has not been addressed in the literature up to yet. Thus, this article features the laminar transport of Newtonian composite nanomaterial (C₂H₆O₂–H₂O hybrid base liquid + MoS₂–Ag hybrid nanoparticles) in the presence of exponential space- and temperature-dependent heat source past an isothermal wedge. An incompressible and electrically conducting fluid is assumed. The effects of Joule heating and viscous heating are also accounted. Single-phase nanofluid model and boundary layer approximation are utilized to govern the equations of flow and heat transport phenomena. The solution of the simplified coupled system of dimensionless constraints is obtained by using the Runge–Kutta–Fehlberg method based on the shooting technique. Detailed analysis of active quantities of interest has been presented and discussed. The interesting physical quantities (friction factors and Nusselt number) are estimated. Also, the slope of the data point is calculated in order to estimate the amount of decrease/increase in physical quantities.

Introduction

The primary investigation related to the enhancement of thermal characteristics due to the suspension of nanoparticles into ordinary liquids was first performed by Choi [1]. The “Nanofluids,” the colloidal suspensions of the metallic/non-metallic nanomaterial into the conventional fluids, are proven to exhibit the improved thermophysical properties compared to traditional single-phase coolants. The improved thermal efficiency of these novel fluids is attributed to the nanoparticles’ suspension stability, larger effective surface area, Brownian motion, thermophoresis, base fluid micro-convections and the subsequent disruption of the thermoviscous boundary layer. Experimental investigations revealed that heat transfer features and transport characteristics are abundant varieties due to the addition of nanoparticles into ordinary liquids. Nanofluids have numerous applications in nanoscale technology, like solar collectors, air-conditioners, combustors, melt spinning, medicine manufacturing, microelectronics, computer processors and heat exchangers. Further in cancer therapy, wound treatment, hyperthermia and resonance imaging are more supportable for the case of magneto nanofluids (see [2,3,4,5,6]).

The thermophysical abilities of the nanofluids are strongly dependent on the properties of the nanosuspensions and the hosting fluid. Therefore, the desired thermal performance of the nanofluids can be obtained by utilizing the hybrid nanofluids which are prepared by dispersing the dissimilar nanoparticles either in the mixture or in the composite form. Chamkha et al. [7] reported the analysis of transport of hybrid nanofluid flowing between two surfaces. Ghadikolaei et al. [8] utilized the hybrid base fluid and composite nanoparticles to investigate the natural convection in the presence of thermal radiation. Chamkha et al. [9] presented an analysis of transport in a heated horizontal cylinder confined in a square cavity by utilizing single/hybrid nanofluids. Amala and Mahanthesh [10] presented an analytical study to investigate the flow of hybrid nanofluids past a vertical plate in the presence of Hall current and nonlinear Boussinesq approximations. Hayat and Nadeem [11] found that the heat transfer enhancement rate is higher for Ag–Cuo hybrid nanofluid in comparison with mono-nanofluid. Few relevant latest pieces of research on hybrid nanofluids are mentioned in references [12,13,14,15,16]. Another innovative approach to improve the thermal efficiency of the nanofluids is magnetic force-induced convective heat transportation of the magnetic nanofluids. In addition to altering the thermophysical properties of the nanofluids, the implications of external magnetic force offer a driving force for the nanofluid flow [17,18,19].

The magnetohydrodynamic flow past non-isothermal wedge is of practical importance in relevance to its wide range of applications including magnetohydrodynamic power generation systems, cooling of nuclear reactors, installation of the nuclear accelerators, designing the heat exchangers and measurement techniques of the blood flow. In past, multiple scholars explored the hydrothermal characteristics of magnetohydrodynamic (MHD) flow of electrically conducting conventional fluids over isothermal or non-isothermal wedges (see [20,21,22] and the references therein). A limited number of numerical and theoretical investigations presented the heat transportation and friction factor aspects of nanofluid flows over a wedge. Khan et al. [23] analysed the Falkner–Skan wedge flow of multiple nanofluids. Their results displayed a strong dependence of heat transfer and friction factor of nanofluids on the nanoparticle concentration, wedge, viscosity and convection parameters. Kandasamy et al. [24] presented a theoretical study on the Hiemenz flow of Cu nanofluid past a permeable wedge by taking into consideration the impact of incident radiation. This study showed a strong influence of thermal satisfaction, buoyancy force, convective radiation, magnetic strength and wedge sheet permeability. Khan and Pop [25] addressed a numerical investigation on the nanofluid flow across a moving wedge by considering the various parameters including nanoparticle pressure gradient, Brownian motion, Lewis number, thermophoresis and wedge moving parameter. The MHD Falkner–Skan flow of aqueous-based nanofluids was studied by Khan et al. [26]. Rashad [27] probed the impact of radiation on the mixed MHD convection of the ferrofluid over a non-isothermal wedge. This study demonstrated that the local Nusselt number has inverse dependence on the thermal radiation, slip factor and wedge surface temperature. The aspects of nanoparticles and Brownian movement in mixed convected nanofluid are reported by Imran et al. [28]. They addressed that the influence of nanoparticles’ Brownian diffusion and thermophoresis is more significant on the temperature profiles compared to the nanoparticle volume fraction. The impact of the magnetic parameter is relatively less significant for the nanoparticle concentration and temperature.

The literature survey demonstrates that there exist no studies which focus on the fluid flow and thermal characteristics of hybrid nanofluids over an isothermal wedge. Therefore, the prime objective of the current study is to probe laminar transport of Newtonian composite nanomaterial (C₂H₆O₂–H₂O hybrid base liquid + MoS₂–Ag hybrid nanoparticles) in the presence of exponential space and temperature-dependent heat source through the isothermal wedge. Single-phase nanofluid model and boundary layer approximations are implemented to simulate flow and heat transport phenomena of nanofluid. The current work also illustrates the influence of Joule and viscous heating on the thermal and viscous characteristics of the hybrid magnetic nanofluids (Table 1).

Table 1 Thermophysical properties of hybrid nanofluids [8]

Formulation of the problem

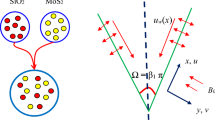
The non-transient dynamics of Newtonian hybrid nanoliquid (C₂H₆O₂–H₂O base liquid + MoS₂–Ag nanoparticles) over an isothermal wedge is considered. The hybrid nanoliquid conducts electricity and incompressible in nature. The motion is due to wedge with an angle π/2 to ease the computations. The rectangular coordinate system is adapted such that the x axis is along with the wedge and y-axis normal to it (Fig. 1). The variable magnetic dipole and porosity are considered in the analysis. Hybrid base fluid C₂H₆O₂–H₂O and hybrid nanoparticles (MoS₂–Ag) are in the thermal equilibrium state, and also there is no slippery between them. The thermophysical values of hybrid base fluid C₂H₆O₂–H₂O and nanoparticles (MoS₂ and Ag) are given in Table 2. Through the boundary layer and Boussinesq approximations along with the above-said assumptions, the governing equations can be written as follows:

Fig. 1

Schematic diagram of the problem

Table 2 Thermophysical properties of C₂H₆O₂–H₂O, MoS₂ and Ag (see [8])

Continuity equation

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0. $$

(1)

Conservation of linear momentum

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = U_{\infty } \frac{{{\text{d}}U_{\infty } }}{{{\text{d}}x}} + \frac{{\mu_{\text{hnl}} }}{{\rho_{\text{hnl}} }} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \left( {\frac{{\sigma_{\text{hnl}} }}{{\rho_{\text{hnl}} }}B^{2} + \frac{{\mu_{\text{hnl}} }}{{\rho_{\text{hnl}} }}\frac{1}{K}} \right)\left( {u - U_{\infty } } \right). $$

(2)

Conservation of energy

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{{k_{\text{hnl}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{hnl}} }} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\sigma_{\text{hnl}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{hnl}} }}B^{2} u^{2} + \frac{{\mu_{\text{hnl}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{hnl}} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} + \frac{{q_{\text{T}}^{*} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{hnl}} }}\left( {T - T_{\infty } } \right) + q_{\text{E}}^{*} \left( {T_{\text{w}} - T_{\infty } } \right)\exp \left( { - n\sqrt {\frac{2c}{{3\nu_{\text{l}} }}} yx^{{ - \frac{1}{3}}} } \right). $$

(3)

The respective boundary conditions are:

$$ \begin{aligned} & u = v = 0,\quad T = T{}_{\rm{w}},\quad y = 0, \\ & u = U_{\infty } (x) = cx^{1/3} ,\quad T \to T_{\infty } ,\quad y \to \infty , \\ \end{aligned} $$

(4)

where $q_{\text{T}}^{*} = q_{\text{T}} x^{m - 1}$, $q_{\text{E}}^{*} = q_{\text{E}} x^{{{\text{m}} - 1}}$ $B = B_{0} x^{{\left( {{\text{m}} - 1} \right)/2}}$ and $K = K_{0} x^{{\left( {1 - {\text{m}}} \right)}}$.

The single-phase nanofluid model assumes that the fluid phase and particles are in thermal equilibrium and move with the same velocity. The effective nanofluid properties are accounted in this model. The effective nanofluid properties are estimated by using convectional mixture theory and phenomenological laws. Specifically, effective thermal conductivity and dynamic viscosity are determined by using modified Brinkman–Garnet and modified Maxwell models correspondingly. The thermophysical properties of hybrid nanofluid are given in Table 1.

Here, $u, v$ are the velocity components in $x$ and $y$ directions, $T, T_{\text{w}} , T_{\infty }$ the temperature of the fluid, wall temperature and ambient temperature, respectively, $B$ the variable magnetic field, $\mu$ the dynamic viscosity, $C_{\text{p}}$ the specific heat, $K$ the variable porosity, $q_{\text{T}}$ the temperature-dependent heat sink/ source, $q_{\text{E}}$ the exponential space-based heat source, $n$ the dimensionless exponential index (positive), $c$ the constant, $\rho$ the density, $k$ the thermal conductivity, $\phi_{{{\text{MoS}}_{2} }}$ and $\phi_{\text{Ag}}$ the volume fractions of ${\text{MoS}}_{2}$ and ${\text{Ag}}$ nanoparticles, respectively, $\phi$ the total volume fraction, $\rho C_{\text{p}}$ the heat capacity, $\nu$ the kinematic viscosity, and the subscripts $hnl$ and $l$ the corresponding properties of hybrid nanoliquid and base liquid, respectively.

The continuity formula can be satisfied by employing the stream function $\psi (x,y)$ s.t.

$$ u = \frac{\partial \psi }{\partial y},\quad v = - \frac{\partial \psi }{\partial x}. $$

(5)

We considered the following variables

$$ \eta = y\sqrt {\frac{2c}{3\gamma }} x^{ - 1/3} ,\quad \psi (x,y) = \sqrt {\frac{3c\gamma }{2}} x^{2/3} f(\eta ),\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}, $$

(6)

The implication of these variables leads to the following expressions:

$$ \frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }} + \frac{{A_{2} }}{{A_{1} }}f\left( \eta \right)\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }} - \frac{{A_{2} }}{{2A_{1} }}\left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right)^{2} + \left( {\frac{{A_{3} }}{{A_{1} }}M + \frac{1}{P}} \right)\left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right) = 0, $$

(7)

$$ \frac{{A_{4} }}{\Pr }\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} + A_{5} f\left( \eta \right)\frac{{{\text{d}}\theta }}{{{\text{d}}\eta }} + A_{1} {\text{Ec}}\left( {\frac{{{\text{d}}^{2} f}}{{{\text{d}}\eta^{2} }}} \right)^{2} + A_{3} {\text{Ec}}M\left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }}} \right)^{2} + Q_{\text{T}} \theta \left( \eta \right) + Q_{\text{E}} \exp \left( { - n\eta } \right) = 0, $$

(8)

with

$$ \begin{aligned} & f\left( 0 \right) = f^{\prime } \left( 0 \right) = 0, \quad \theta \left( 0 \right) = 1 \\ & f^{\prime } \left( \infty \right) = 1,\quad \theta \left( \infty \right) = 0. \\ \end{aligned} $$

where

$$ A_{1} = \frac{1}{{\left( {1 - (\phi_{{{\text{MoS}}_{2} }} + \phi_{\text{Ag}} )} \right)^{2.5} }}, $$

$$ A_{2} = \left( {1 - \phi } \right) + \frac{{\phi_{{{\text{MoS}}_{2} }} \rho_{{{\text{MoS}}_{2} }} + \phi_{\text{Ag}} \rho_{\text{Ag}} }}{{\rho_{\text{l}} }}, $$

$$ A_{3} = 1 + \frac{{3\phi \left( { \phi_{{{\text{MoS}}_{2} }} \sigma_{{{\text{MoS}}_{2} }} + \phi_{\text{Ag}} \sigma_{\text{Ag}} - \sigma_{\text{l}} \phi } \right)}}{{( \phi_{{{\text{MoS}}_{ 2} }} \sigma_{{{\text{MoS}}_{ 2} }} + \phi_{\text{Ag}} \sigma_{\text{Ag}} + 2\sigma_{\text{l}} \phi ) - \phi \left( {( \phi_{{{\text{MoS}}_{2} }} \sigma_{{{\text{MoS}}_{2} }} + \phi_{\text{Ag}} \sigma_{\text{Ag}} } \right) - \sigma_{\text{l}} \phi )}}, $$

$$ A_{4} = \left[ {\frac{{\frac{{ \phi_{{{\text{MoS}}_{ 2} }} k_{{{\text{MoS}}_{ 2} }} + \phi_{\text{Ag}} k_{\text{Ag}} }}{\phi } + 2k_{\text{l}} + 2\left( { \phi_{{{\text{MoS}}_{ 2} }} k_{{{\text{MoS}}_{ 2} }} + \phi_{\text{Ag}} k_{\text{Ag}} } \right) - 2\phi k_{\text{l}} }}{{\frac{{ \phi_{{{\text{MoS}}_{ 2} }} k_{{{\text{MoS}}_{ 2} }} + \phi_{\text{Ag}} k_{Ag} }}{\phi } + 2k_{\text{l}} - \left( { \phi_{{{\text{MoS}}_{ 2} }} k_{{{\text{MoS}}_{ 2} }} + \phi_{\text{Ag}} k_{\text{Ag}} } \right) + \phi k_{\text{l}} }} } \right], $$

$$ A_{5} = \left( {1 - \phi } \right) + \frac{{\left( {\phi_{{{\text{MoS}}_{ 2} }} (\rho C_{\text{p}} )_{{{\text{MoS}}_{ 2} }} + \phi_{\text{Ag}} (\rho C_{\text{p}} )_{\text{Ag}} } \right)}}{{(\rho C_{\text{p}} )_{\text{l}} }}, $$

${\text{Ec}} = \frac{{U_{w}^{2} }}{{C_{{{\text{p}}_{\text{l}} }} \left( {T_{\text{w}} - T_{\infty } } \right) }}$ is the Eckert number, $Q_{\text{T}} = \frac{{q_{\text{T}} }}{{c(\rho C_{\text{p}} )_{\text{l}} }}$ the temperature-based heat source parameter, $Q_{\text{E}} = \frac{{q_{\text{E}} }}{{c(\rho C_{\text{p}} )_{\text{l}} }}$ the exponential space-based heat source parameter, $\Pr = \frac{{\mu_{\text{l}} C_{{{\text{p}}_{\text{l}} }} }}{{k_{\text{l}} }}$ the Prandtl number, and $M = \frac{{\sigma_{\text{l}} B_{0}^{2} }}{{\rho_{\text{l}} c}}$ the magnetic parameter.

Mathematically, expressions of skin friction coefficient and Nusselt numbers in the dimensional form are:

$$ S_{\text{f}} = \frac{{2\tau_{\text{w}} }}{{\rho_{\text{l}} U_{\infty } }},\quad {\text{Nu}}_{\text{x}} = \frac{{xq_{\text{w}} }}{{k_{\text{l}} \left( {T_{\text{w}} - T_{\infty } } \right)}}, $$

where $\tau_{\text{w}} = \mu_{\text{hnl}} \frac{\partial u}{\partial y}$ and $q_{\text{w}} = - k_{\text{hnl}} \frac{\partial T}{\partial y}$.

The dimensionless form of the above expressions is

$$ \sqrt {\text{Re}_{\text{x}} } S_{\text{f}} = \sqrt {\frac{8}{3}} A_{1} f^{\prime \prime } \left( 0 \right), $$

$$ \frac{{{\text{Nu}}_{\text{x}} }}{{\sqrt {\text{Re}_{\text{x}} } }} = - \sqrt {\frac{8}{3}} A_{4} \theta^{\prime } \left( 0 \right), $$

where $\text{Re}_{\text{x}} = \frac{{U_{\infty } x}}{{\nu_{\text{l}} }}$ is the Reynolds number.

Results and discussion

Here, our emphasis is to scrutinize the features of exponential space- and thermal-based heat source for composite nanomaterial’s nanofluid flow over an isothermal wedge by considering the aspects of viscous and Joule heating. In order to solve the governing system of equations, we made the numerical computations by Runge–Kutta–Fehlberg-based shooting scheme. Validation and detailed procedure of the method can be found in [18, 19].

Firstly, the skin friction coefficient is analysed by varying magnetic and porosity parameters. In the numeric computations, the default values of effective parameters are set as ${\text{Ec}} = 1.5,\quad M = 2,\quad \Pr = 25.34,\quad Q_{\text{T}} = Q_{\text{E}} = 0.02,\quad n = 0.5$ and $P = 1.5$ unless otherwise mentioned. The Newtonian hybrid nanoliquid is considered, and the results are presented for three different nanofluids: hybrid nanofluid ($\phi_{{{\text{MoS}}_{ 2} }} = \phi_{\text{Ag}} = 0.02)$, MoS₂ nanofluid and ${\text{Cu}}$ nanofluid. Table 3 demonstrates the impact of magnetic and porosity parameters on the skin friction coefficient. By increasing the magnetic parameter, an increase in skin friction for all three cases of volume fractions (fluids) is observed. The average slopes of $S_{\text{f}}$ and $M$ for three volume fraction cases are also calculated. The impact of increased porosity parameter results in a decrease in $S_{\text{f}}$ for volume fraction cases under consideration. It is also scrutinized from Table 3 that $S_{\text{f}}$ has a reverse trend for increased $M$ and $P$. Moreover, the average slopes of $S_{\text{f}}$ and $M$ are positive, while the slopes of $S_{\text{f}}$ and $P$ are negative. Table 4 shows the Nusselt number trend by varying $M,\,P,\,{\text{Ec}},\,Q_{\text{T}}$ and $Q_{\text{E}}$. Here, also the same three cases of volume fractions are mentioned in Table 3. Heat transfer rate increases due to enhancement in magnetic parameter, Eckert number, temperature-based heat source parameter and exponential space-based heat source parameter. The rate of heat transfer declines for increased porosity parameter. The slopes of ${\text{Nu}}_{\text{x}}$ and $P$ for three volume fraction cases are positive, whereas all other slopes are negative as mentioned in Table 4.

Table 3 Variation in skin friction for different values when ${\text{Ec}} = 1.5,\quad M = 2,\quad \Pr = 25.34,\quad Q_{\text{T}} = Q_{\text{E}} = 0.02,\quad n = 0.5,\quad P = 1.5$

Table 4 Variation in Nusselt number for different values when ${\text{Ec}} = 1.5,\,\,M = 2,\,\,\Pr = 25.34,\,\,Q_{\text{T}} = Q_{\text{E}} = 0.02,\,\,n = 0.5,\,\,P = 1.5$

Now, we discuss the graphical results of physical parameters on velocity and temperature fields. Figure 2a, b shows the behaviour of hybrid nanofluid velocity $f^{\prime } \left( \eta \right)$ and temperature $\theta \left( \eta \right)$ for various values of $M$. As apparent from Fig. 2a, the velocity profiles have increasing nature for the larger magnetic parameter. The temperature distribution exhibits an increasing trend for higher values of the magnetic field parameter. Thermal boundary layer also increased. Physically, when magnetic parameter number increases, then Lorentz force produces more frictional forces between fluid particles due to which temperature and its respective boundary layer thickness elevate. In Fig. 2a, b, the first case $M = 0$ describes the hydrodynamic fluid flow case, whereas the nonzero values of $M$ predict the hydromagnetic flow of hybrid nanofluid. Figure 3a, b illustrates the consequences of the porosity parameter of $f^{\prime } \left( \eta \right)$ and $\theta \left( \eta \right)$. An increase in porosity parameter produces more resistance to the fluid flow due to porosity of the surface; therefore, the velocity curves have a declining trend for $P = 0.1,\,0.25,\,0.4,\,0.55$ (Fig. 3a). From Fig. 3b, it is noticed that the temperature curves enhanced by selecting $P = 1,5,10,15$. It is also noticed that the results are significant for smaller values of porosity parameter as compared to larger values of $P$. The Eckert number expresses the relationship between a flow’s kinetic energy and the boundary layer enthalpy difference and is used to characterize heat transfer dissipation. The Eckert number effect on Newtonian hybrid nanoliquid temperature field is elaborated in Fig. 4a. Similar to the impact of magnetic and porosity parameters, the temperature curves also enhance for increasing Eckert number. Due to frictional heating, heat produced in the fluid which caused an enhancement in temperature field as well as the thickness of the thermal boundary layer. The case ${\text{Ec}} = 0$ depicts that the effect of viscous and Joule heating is neglected. The combined influence of temperature and exponential space-based heat source parameters on temperature field is illustrated in Fig. 4b. Here, four different cases of $Q_{\text{T}}$ and $Q_{\text{E}}$ are considered. It is very clear that the presence of thermal-based heat source and exponential space-based heat source augments the thermal boundary layer thickness. This is due to the fact that a heat source aspect introduces additional heat in the fluid system due to which the temperature of hybrid nanofluid is enhanced. It is also depicts that impact of exponential space-based heat source aspect is more prominent than that of temperature-based heat source aspect.

Fig. 2

Behavior of hybrid nanofluid a velocity and b temperature for various $M$

Fig. 3

Behavior of hybrid nanofluid a velocity and b temperature for various $P$

Fig. 4

Behavior of hybrid nanofluid temperature for various a ${\text{Ec}}$ and b $Q_{\text{T}}$

Figure 5a shows the variations of skin friction coefficient versus porosity parameter and magnetic parameter. Figure 5a depicts that the skin friction increases for larger magnetic parameter values and decreases for larger porosity parameter. Figure 5b describes the outcomes of $S_{\text{f}}$ against $P$ by varying $M$. The two cases of volume fractions $\varphi_{{{\text{MoS}}_{ 2} }} = 0.02,\quad \varphi_{\text{Ag}} = 0$ and $\varphi_{{{\text{MoS}}_{ 2} }} = 0,\,\varphi_{\text{Ag}} = 0.02$ are considered to mention the influence of skin friction coefficient. It is perceived that $S_{\text{f}}$ preserves an increasing tendency. Moreover, the values of $S_{\text{f}}$ are larger for volume fraction $\varphi_{{{\text{MoS}}_{ 2} }} = 0.02,\,\varphi_{\text{Ag}} = 0$ than in the case of $\varphi_{{{\text{MoS}}_{ 2} }} = 0,\,\varphi_{\text{Ag}} = 0.02$. Nusselt number versus Eckert number effect for four different values of the magnetic parameter is shown in Fig. 6. Here, we opt four different cases of volume fractions $\varphi_{{{\text{MoS}}_{ 2} }} = \,\varphi_{\text{Ag}} = 0.02,\,\,\varphi_{{{\text{MoS}}_{ 2} }} = 0.02,\,\,\varphi_{\text{Ag}} = 0\,$ and $\varphi_{{{\text{MoS}}_{ 2} }} = 0,\,\varphi_{\text{Ag}} = 0.02$. Figure 6 describes the variation in Nusselt number against Eckert number showing decreasing behaviour by fixing the magnetic parameter.

Fig. 5

Behavior of hybrid nanofluid skin friction coefficient for various a $P$ and b $M$

Fig. 6

Behavior of hybrid nanofluid Nusselt number for various ${\text{Ec}}$ and $M$

Conclusions

The following key features are extracted from this analysis:

• The temperature profile and its relevant boundary layer thickness have increasing nature for the larger magnetic parameter.

• The exponential heat source aspect is better suited for applications involved high heating processes.

• Both exponential space-based heat source and thermal-based heat source aspects are favourable for hybrid nanofluid temperature profiles.

• The thermal boundary layer thickness is higher for hybrid nanofluid in comparison with the mono-nanofluids.

• An increase in porosity parameter generates much resistance to liquid flow due to which the velocity curves show declining tendency.

• The frictional heating generates more heat in the fluid that results in improving the temperature field. Thus, the Eckert number is useful in determining the relative importance in a heat transfer situation of the kinetic energy of a flow.

• The skin friction increases for a stronger magnetic field.

• The variation in Nusselt number against Eckert number shows decreasing behaviour by fixing the magnetic parameter.