Introduction

Peristaltic transport of viscous and nonlinear viscosity model fluids has been discussed by the number of researchers for their wide range of applications in physiology, biomedical, chemical industries, etc. A vital industrial implementation of this scheme is used in the designing of roller pumps applied in pumping fluids without being mixed due to the contact with the pumping characteristics [1]. In the field of fluid mechanics, the experimental and theoretical investigations regarding peristaltic flow phenomenon have been suggested by a number of researchers due to its considerable applications in medical, physiology, chemical equipment and clinical engineering. Two intriguing mechanisms related to peristaltic flows are liquid trapping and material reflux. The former portrays the advancement and downstream traveling of free vertexes, called liquid boluses. The last alludes to the net upstream convection of liquid particles against the voyaging surface waves. These two phenomena are of extraordinary physiological hugeness, as they might be liable for thrombus arrangement in blood and neurotic transport of microscopic organisms. From the stance of fluid dynamics, these strategies show the multifaceted nature, yet in addition spur the principal investigation of peristaltic streams. Effects of magnetism on the peristaltic flow of a couple stress fluid across a porous space followed by heat and mass transfer have been presented by Eldabe et al. [2] . Tripathi et al. [3] have distributed the peristaltic stream of viscoelastic liquid with fractional Maxwell stress inside a channel. They have discovered the analytical arrangements with the assistance of HPM and Adomian decomposition strategy. Some years back, Nadeem and Maraj [4] have considered the scientific investigation for peristaltic stream of nanofluid in a curved geometry comprising flexible walls. Akbar and Nadeem [5] have published a note on the peristaltic flow with endoscopic effects on biviscosity fluid and produced the results that increasing viscosity factor and values of radius fraction enhance the peristaltic pumping. Bhatti and Zeeshan [6] have concluded the study on heat and mass transfer phenomenon through a peristaltic transport of particle-liquid phase mixture along with boundary slip and declared the point that particles volume fraction affects the flow velocity in inverse manner. More studies on the peristaltic flows of various fluid models have been incorporated by a good number of researchers [7,8,9].

Fig. 1
figure 1

Physical geometry for peristaltic flow in a vertical duct

Full size image
Fig. 2
figure 2

Variation of velocity in present case with Nadeem et al. [27] for fixed \(\phi =0.6,n=0.5,x=0,y=1,We=0.03,\beta =0.64,Q=0.5\)

Full size image
Fig. 3
figure 3

Velocity profile variational curves u for altering magnitudes of \(\beta\) and Q for fixed \(G_{\text{r}}=0.1,B_{\text{r}}=0.9,N_{\text{t}}=0.5,N_{\text{b}}=0.9,We=0.6,n=0.9,\phi =0.1,x=0,y=1,\) a two dimensions, b three dimensions

Full size image
Fig. 4
figure 4

Velocity profile variational curves u for altering magnitudes of \(G_{\text{r}}\) and \(B_{\text{r}}\) for fixed \(\beta =0.6,Q=2,N_{\text{t}}=0.5,N_{\text{b}}=0.9,We=0.1,n=0.9,\phi =0.1,x=0,y=1,\) a two dimensions, b three dimensions

Full size image
Fig. 5
figure 5

Velocity profile variational curves u for altering magnitudes n and We for fixed \(\beta =1.5,Q=2,N_{\text{t}}=0.5,N_{\text{b}}=0.9,G_{\text{r}}=0.1,B_{\text{r}}=0.9,\phi =0.1,x=0,y=1,\) a \(2-\)dimensions, b \(3-\)dimensions

Full size image

Nanotechnology has immense applications in industry since substances of nanometers' dimension execute incomparable structural properties. Cho et al. [10] discuss that to improve the biodistribution of malignant growth drugs, nanoparticles have been assumed for absolute size and surface standards to enlarge their duration time in the circulation system. In addition, they are organized to convey their stacked dynamic medications to malignant growth cells by specifically utilizing the exceptional pathophysiology of tumors, for instance, their upgraded porousness and maintenance influence and the tumor microenvironment. In the recent years, another part of fluid mechanics has raised, specifically nanofluid elements, which finds assorted applications in clinical science, energetics, medical and process frameworks engineering. Beginning advancements were made by Choi [11] in the domain of energy execution improvement. Nanofluids as explained by Xuan et al. [12] are another class of liquids that are built by suspending nanoparticles in base heat transporting liquids. The common examples of base fluid used for nanofluid are water, ethylene glycol and oil. Nanoliquids have their colossal commitment in heat move, similar to microelectronics, energy components, pharmaceutical procedures and hybrid controlled motors, residential fridge, chiller, atomic reactor coolant, pounding and space innovation and a lot more circumstances. More literature on the exploration of nanofluid can be seen in refs. [13,14,15]. Investigation of nanofluid in the field of peristalsis has become the center of consideration by numerous analysts taking a shot at peristalsis, blood streams and numerous clinical issues. Awais et al. [16] have analyzed the hybrid nanofluid phenomenon of peristaltic stream and obtain the endoscopic effects on the flow. They have considered the Ostwald-de-Waele power-law model as a rheological fluid and examined that the effects of buoyancy factors are significant in the neighborhood of wavy tube and also the magnetic effects flourish the peristaltic mechanism along with nanomaterial taken in the flow. Sucharitha et al. [17] achieved the theoretical analysis for pumping flow of magnetized nanofluid in the light of Joule’s heating and found the conclusion that temperature of the system and nanoparticles are resisting the flow velocity. Recently, in [18], Riaz investigated the study of Eyring–Powell fluid model with mixing of nanoparticles in a three-dimensional rectangular channel and shown that thermal and mass transfer rate of Eyring–Powell fluid is lesser than a Newtonian fluid, but it can be increased by high aspect ratio of the rectangular 3D channel.

Although many scientist have put their efforts on exploring the mechanism of viscous fluids, more applicable fluids in industry and biological field are dependent on their rheological properties which can be determined by non-Newtonian models. There are so many nonlinear fluid models which have been presented in the literature, but the one which is incorporated by so many researchers is Carreau fluid due to its viscoelastic nature and the importance of its Weissenberg number in physiological point of view. For instance, Akram [19] investigated analytically the influence of inclined magnetic field on the pumping transport of Carreau fluid saturated with nanoparticles in a two-dimensional channel. Hayat et al. [20] have analyzed the effects of mixed convection on wavy flow of nanofluid using Carreau model producing the result that Weissenberg number and power law index are affecting the shear stress inversely. Vajravelu et al. [21] have published the study on Carreau fluid through peristaltic phenomenon under the features of velocity slip along with magnetic environment by utilizing perturbation theory on small amplitudes of Weissenberg number and established the conclusion that slip of velocity is expanding the bolus volume. Kothandapani et al. [22] produced the investigation on peristaltic flow for electrically conducting Carreau model fluid with the correspondence of porous medium through a tapered channel. They compared the features of Carreau fluid with the Newtonian model and found that Carreau fluid evaluated more pressure rise than a Newtonian fluid in 2D asymmetric channel. More peristaltic studies comprising the Carreau model can be found in [23, 24].

All the above examinations talk about the stream in two-dimensional channels and pipes, yet the most widely recognized stream geometries utilized in modern and clinical gear are three-dimensional channels. Reddy et al. [25] have depicted the impact of aspect ratios on peristaltic stream in a rectangular pipe and assessed that the sagittal cross area of the uterus might be well estimated by a container of rectangular cross segment as compared to a two-dimensional channel. Mekheimer et al. [26] have dissected the impact of parallel walls on peristaltic move through a nonuniform rectangular duct. Peristaltic stream of Carreau liquid in a rectangular channel has been shown by Nadeem et al. [27]. Later on, Mekheimer et al. [28] have determined the scientific model of peristaltic transport through eccentric annuli. Remembering the present implication, authors come to realize that peristaltic motion of nanofluid with non-Newtonian Carreau model has not been talked about in a three-dimensional rectangular channel.

Keeping in mind the applications of nanofluid in three-dimensional biological equipment and the physically exhibition of the features of rheology through Carreau model, the authors are keen to present this examination to visualize the component of peristaltic phenomenon of non-Newtonian Carreau liquid model with nanoparticles fraction in a 3D rectangular channel. The modeled relations are demonstrated with the approximations of long wavelength and laminar assumption of the flow. All the relations for preservation of momentum, energy and nanoparticles fraction are made dimensionless by joining reasonable non-dimensional parameters. The ensuing exceptionally nonlinear and coupled differential equations are assessed analytically with the assistance of (HPM). The physical highlights of appearing parameters are broke down through introducing the diagrams of vertical component of velocity profile, temperature factor, nanoparticles saturation, pressure rise and pressure gradient curves. Three-dimensional graphical introduction is also given for velocity component. Lastly, the streamlines strategy is likewise displayed with the assistance of parallel lines which clarify the liquid bolus pattern.

Mathematical model

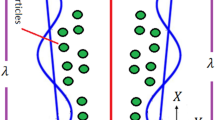
We assume the peristaltic flow of Carreau liquid with nanoparticles mechanism in a cross segment of three-dimensional Cartesian channel (Fig. 1). The stream is created by the proliferation of sinusoidal waves containing length \(\lambda\) going along the vertical axis of the channel having consistent speed c. The equations for the mass, momentum, heat and nanoparticles volume fraction for Carreau model are portrayed as underneath.

$$\begin{aligned}&{\mathrm{div~}}\overline{{\mathbf {V}}}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\rho _{\text{f}}\left( \frac{D\overline{\mathbf {V}}}{Dt}\right) =-{\mathbf {\nabla }}P \nonumber \\&\quad + \mathrm{div~}{\mathbf {S+}}\rho _{\text{f}}\mathbf {g}\beta _{\text{T}}\left( \overline{T} -T_{0}\right) +\rho _{\text{f}}\mathbf {g}\beta _{\text{C}}\left( \overline{C}-C_{0}\right) \mathbf {,} \end{aligned}$$
(2)
$$\begin{aligned}&\rho _{\text{f}}c_{\text{f}}\left( \frac{D\overline{T}}{Dt}\right) =\mathbf {\nabla }\cdot K \mathbf {\nabla }\overline{T}\nonumber \\&\quad +\rho _{\text{p}}c_{\text{p}}\left( D_{\text{B}}\left( \mathbf {\nabla }\overline{C}\cdot \mathbf {\nabla }\overline{T}\right) +\frac{D_{\text{T}}}{T_{0}} \left( \mathbf {\nabla }\overline{T}\cdot \mathbf {\nabla }\overline{T}\right) \right) , \end{aligned}$$
(3)
$$\begin{aligned}&\frac{D\overline{C}}{Dt}=D_{\text{B}}\mathbf {\nabla }^{2}\overline{C}+\frac{D_{\text{T}}}{ T_{0}}\mathbf {\nabla }^{2}\overline{T}, \end{aligned}$$
(4)

where \(\frac{D}{Dt}=\frac{\partial }{\partial t}+\mathbf {V\cdot \nabla }\) represents the material time derivative, \(\mathbf {S}\) denotes the stress strain mathematical model for Carreau fluid which is described as [27]

$$\begin{aligned} \mathbf {S}=\mu \left( 1+\left( \Gamma \overset{\cdot }{\mathbf {\gamma }} \right) ^{2}\right) ^{\frac{\text{n}-1}{2}}\overset{\cdot }{\mathbf {\gamma }}. \end{aligned}$$
(5)

In the above model, \(\mu\) depicts the viscosity of the fluid, \(\overset{\cdot }{ \mathbf {\gamma }}\) implies the symmetric matrix of velocity gradient matrix, n denotes the power law index and \(\Gamma\) is the characteristics time. The peristaltic walls are represented through mathematical form as

$$\begin{aligned} Z=\pm \overline{H}(X,t)=\pm a\pm b\cos \left[ \frac{2\pi }{\lambda }\left( X-ct\right) \right] , \end{aligned}$$
(6)

where a is channel width and b assumes the amplitude of the waves, t is the time characteristic and X means the orientation of propagated wave.

Fig. 6
figure 6

Velocity profile variational curves u for altering magnitudes \(N_{\text{b}}\) and \(N_{\text{t}}\) for fixed \(\beta =0.8,Q=2,n=0.9,We=0.1,G_{\text{r}}=0.6,B_{\text{r}}=0.7,\phi =0.1,x=0,y=1,\) a \(2-\) dimensions, b for \(3-\)dimensions

Full size image
Fig. 7
figure 7

Heat measuring profile \(\theta\) for various values of \(\beta\) for fixed \(N_{\text{t}}=0.5,N_{\text{b}}=0.3,\phi =0.25,x=0,y=1\)

Full size image
Fig. 8
figure 8

Heat measuring profile \(\theta\) for various values of \(N_{\text{b}}\) and \(N_{\text{t}}\) for fixed \(\beta =0.3,\phi =0.25,x=0,y=1\)

Full size image
Fig. 9
figure 9

Nanoparticles volume fraction \(\sigma\) for changing values of \(\beta\) for fixed \(N_{\text{t}}=0.5,N_{\text{b}}=0.3,\phi =0.25,x=0,y=1\)

Full size image
Fig. 10
figure 10

Nanoparticles volume fraction \(\sigma\) for changing values of \(N_{\text{b}}\) and \(N_{\text{t}}\) for fixed \(\beta =0.3,\phi =0.25,x=0,y=1\)

Full size image

Componential derivation

Fig. 11
figure 11

Curves of pressure rise \(\Delta p\) with \(\beta\) and \(N_{\text{t}}\) at \(We=0.9,n=0.4,N_{\text{b}}=0.6,G_{\text{r}}=0.5,\phi =0.6,B_{\text{r}}=0.6\)

Full size image
Fig. 12
figure 12

Curves of pressure rise \(\Delta p\) with n and \(G_{\text{r}}\) at \(We=0.4,N_{\text{t}}=0.4,N_{\text{b}}=0.8,\beta =0.9,\phi =0.1,B_{\text{r}}=0.5\)

Full size image
Fig. 13
figure 13

Curves of pressure rise \(\Delta p\) with \(\phi\) and \(B_{\text{r}}\) at \(We=0.5,n=0.4,N_{\text{b}}=0.3,G_{\text{r}}=0.2,n=0.4,G_{\text{r}}=0.2\)

Full size image
Fig. 14
figure 14

Curves of pressure rise \(\Delta p\) with We and \(N_{\text{b}}\) at \(\beta =0.9,n=0.7,N_{\text{t}}=0.4,G_{\text{r}}=0.5,\phi =0.1,B_{\text{r}}=0.5\)

Full size image
Fig. 15
figure 15

Waves of pressure gradient dp/dx with \(\beta\) and Q at \(N_{\text{t}}=0.5,N_{\text{b}}=0.3,G_{\text{r}}=0.2,n=0.7,We=0.5,\phi =0.25,\) \(B_{\text{r}}=0.2\)

Full size image

The parallel sides to XZ-plane are supposed to be static and do not account for any wavy motion. The lateral velocity is neglected due to no wave in the lateral (y-axis) direction of the frame. The equations representing three-dimensional flow problem in the form of Cartesian coordinates by choosing flow velocity \(\overline{\mathbf {V}}=\left( U,W\right)\) will capture the upcoming arrangement

$$\begin{aligned}&\frac{\partial U}{\partial X}+\frac{\partial W}{\partial Z}=0, \end{aligned}$$
(7)
$$\begin{aligned}&\rho _{\text{f}}\left( \frac{\partial U}{\partial t}+U\frac{\partial U}{\partial X} +W\frac{\partial U}{\partial Z}\right) \nonumber \\&\quad= -\frac{\partial P}{\partial X}+ \frac{\partial }{\partial X}S_{\text{XX}}+\frac{\partial }{\partial Y}S_{\text{XY}}+\frac{ \partial }{\partial Z}S_{\text{XZ}} \nonumber \\&\qquad \mathbf {+}\rho _{\text{f}}g\beta _{\text{T}}\left( \overline{T}-T_{0}\right) +\rho _{\text{f}}g\beta _{\text{C}}\left( \overline{C}-C_{0}\right) , \end{aligned}$$
(8)
$$\begin{aligned}&\left. 0=-\frac{\partial P}{\partial Y}+\frac{\partial }{\partial X}S_{\text{YX}}+ \frac{\partial }{\partial Y}S_{\text{YY}}+\frac{\partial }{\partial Z}S_{\text{YZ}},\right. \end{aligned}$$
(9)
$$\begin{aligned}&\left. \rho_{\text{f}}\left( \frac{\partial W}{\partial t}+U\frac{\partial W}{ \partial X}+W\frac{\partial W}{\partial Z}\right) =-\frac{\partial P}{ \partial Z}+\frac{\partial }{\partial X}S_{\text{ZX}}\right. \nonumber \\&\quad \left. +\frac{\partial }{\partial Y} S_{\text{ZY}}+\frac{\partial }{\partial Z}S_{\text{ZZ}},\right. \end{aligned}$$
(10)
$$\begin{aligned}&\left. \frac{\partial \overline{T}}{\partial t}+U\frac{\partial \overline{T }}{\partial X}+W\frac{\partial \overline{T}}{\partial Z}=\alpha _{\text{f}}\left( \frac{\partial ^{2}\overline{T}}{\partial X^{2}}+\frac{\partial ^{2} \overline{T}}{\partial Y^{2}}+\frac{\partial ^{2}\overline{T}}{\partial Z^{2} }\right) \right. \nonumber \\&\quad \left. +\tau \left( D_{\text{B}}\left( \frac{\partial \overline{C}}{\partial X} \frac{\partial \overline{T}}{\partial X}+\frac{\partial \overline{C}}{ \partial Y}\frac{\partial \overline{T}}{\partial Y}\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +\frac{\partial \overline{C}}{\partial Z}\frac{ \partial \overline{T}}{\partial Z}\right) +\frac{D_{\text{T}}}{T_{0}}\left( \left( \frac{\partial \overline{T}}{\partial X}\right) ^{2}+\left( \frac{\partial \overline{T}}{\partial Y}\right) ^{2}+\left( \frac{\partial \overline{T}}{ \partial Z}\right) ^{2}\right) \right) ,\right. \end{aligned}$$
(11)
$$\begin{aligned}&\left. \frac{\partial \overline{C}}{\partial t}+U\frac{\partial \overline{C} }{\partial X}+W\frac{\partial \overline{C}}{\partial Z}=D_{\text{B}}\left( \frac{ \partial ^{2}\overline{C}}{\partial X^{2}}+\frac{\partial ^{2}\overline{C}}{ \partial Y^{2}}+\frac{\partial ^{2}\overline{C}}{\partial Z^{2}}\right) \right. \nonumber \\&\quad \left. + \frac{D_{\text{T}}}{T_{0}}\left( \frac{\partial ^{2}\overline{T}}{\partial X^{2}}+ \frac{\partial ^{2}\overline{T}}{\partial Y^{2}}+\frac{\partial ^{2} \overline{T}}{\partial Z^{2}}\right) ,\right. \end{aligned}$$
(12)

where \(\tau\) reflects the effective nanoparticles heat capacity and that of the base fluid ratio. Here, we suggest a new frame \(( x,y,z,u,w,p,T,C)\) traveling with a wave velocity c relative to the fixed frame \(\left( X,Y,Z,U,W,P,\overline{T},\overline{C}\right)\) containing the transformations defined in [27]. Moreover, to lessen the number of including parameters, we propose the below-defined transformations

$$\begin{aligned}&\left. \overline{x}=x\lambda ^{-1},\text { }\overline{y}=yd^{-1},\text { } \overline{z}=za^{-1},\text { }\overline{t}=ct\lambda ^{-1},\text { }\overline{u }=c^{-1}u,\text { }\overline{w}=\frac{w}{c\delta },\right. \nonumber \\&\left. \text { }\theta =\frac{ T-T_{0}}{T_{1}-T_{0}},\text { }\sigma =\frac{C-C_{0}}{C_{1}-C_{0}},\right. \nonumber \\&\left. \delta =\frac{a}{\lambda },\text { }\phi =\frac{b}{a},\text { }B_{\text{r}}= \frac{\rho _{\text{f}}g\beta _{\text{C}}a^{2}}{\mu c}\left( C_{1}-C_{0}\right) ,\text { }\right. \nonumber \\&\left. G_{\text{r}}=\frac{\rho _{\text{f}}g\beta _{\text{T}}a^{2}}{\mu c}\left( T_{1}-T_{0}\right) , \text { }\alpha _{\text{f}}=\frac{K}{\left( \rho c\right) _{\text{f}}},\text { }\overline{p}= \frac{a^{2}p}{\mu c\lambda },\right. \nonumber \\&\left. N_{\text{b}}=\frac{\tau D_{\text{B}}}{\alpha _{\text{f}}}\left( C_{1}-C_{0}\right) , \text { }N_{\text{t}}=\frac{D_{\text{T}}}{T_{0}\alpha _{\text{f}}}\left( T_{1}-T_{0}\right) ,\text { } \right. \nonumber \\&\left. S_{\text{c}}=\frac{\mu }{\rho D_{\text{B}}},\text { }P_{\text{r}}=\frac{\mu }{\rho \alpha _{\text{f}}}, \text { }\overline{S}=\frac{a}{\mu c}S,\text { }\mathrm{div~}\text {Re}=\frac{\rho ac}{\mu } ,\right. \nonumber \\&\left. \overline{\psi }=\frac{\psi }{ca},\text { }\overline{\overset{\cdot }{\gamma }}=\frac{\overset{\cdot }{\gamma }d}{c},\text { }We=\frac{\Gamma c}{d} ,\text { }\overline{h}=\frac{\overline{H}}{a},\text { }\beta =\frac{a}{d} .\right. \end{aligned}$$
(13)

Incorporating the constraints of wave length \(a<<\lambda\) and small Reynolds number \(\mathrm{div~}\text {Re}\longrightarrow 0\), we receive the reduced non-dimensional form of Eqs. (7) to  (12) in moving frame of reference

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0, \end{aligned}$$
(14)
$$\begin{aligned}&\left. \beta ^{2}\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u }{\partial z^{2}}+\frac{n-1}{2}We^{2}\beta ^{4}\frac{\partial }{\partial y} \left( \frac{\partial u}{\partial y}\right) ^{3} \right. \nonumber \\&\quad +\left. \frac{n-1}{2}We^{2}\frac{ \partial }{\partial z}\left( \frac{\partial u}{\partial z}\right) ^{3}+\frac{ n-1}{2}We^{2}\beta ^{2}\right. \nonumber \\&\left. \frac{\partial }{\partial y}\left( \frac{\partial u}{\partial y} \left( \frac{\partial u}{\partial z}\right) ^{2}\right) +\frac{n-1}{2} We^{2}\beta ^{2}\frac{\partial }{\partial z} \right. \nonumber \\&\quad \left. \left( \frac{\partial u}{ \partial z}\left( \frac{\partial u}{\partial y}\right) ^{2}\right) +B_{\text{r}}\sigma +G_{\text{r}}\theta =\frac{\text{d}p}{\text{d}x}\right. , \end{aligned}$$
(15)
$$\begin{aligned}&\beta ^{2}\frac{\partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}+N_{\text{b}}\left( \beta ^{2}\frac{\partial \theta }{ \partial y}\frac{\partial \sigma }{\partial y}+\frac{\partial \theta }{ \partial z}\frac{\partial \sigma }{\partial z}\right) \nonumber \\&\quad +N_{\text{t}}\left( \beta ^{2}\left( \frac{\partial \theta }{\partial y}\right) ^{2}+\left( \frac{ \partial \theta }{\partial z}\right) ^{2}\right) =0, \end{aligned}$$
(16)
$$\begin{aligned}&\beta ^{2}\frac{\partial ^{2}\sigma }{\partial y^{2}}+\frac{\partial ^{2}\sigma }{\partial z^{2}}+\frac{N_{\text{t}}}{N_{\text{b}}}\left( \beta ^{2}\frac{ \partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}\right) =0. \end{aligned}$$
(17)

To get the particular solutions of above unknowns, we assume the below-defined boundary relations [29]:

$$\begin{aligned} u&= {} -1\text { when }\left( y,z\right) =\left( \pm 1,\pm h\left( x\right) \right) , \end{aligned}$$
(18)
$$\begin{aligned} \theta&= {} (0,1)\text { when }z=(h,-h), \end{aligned}$$
(19)
$$\begin{aligned} \sigma&= {} (0,1)\text { when }z=(h,-h), \end{aligned}$$
(20)

where \(h=1+\phi \left[ sec\left( 2\pi x\right) \right] ^{-1}.\)

Special cases: It is to be noted that if we take \(B_{r}=0=G_{r},\) we recover the case without considering nanoparticles effect on Carreau fluid in a wavy rectangular duct [27] . Also, if we vanish the effect of lateral walls, i.e., \(\beta =0,\), we approach the case for two-dimensional channel.

Tools for solution

Here, the highly converging analytical technique HPM accounts for the results of unknown physical quantities appearing in the final equations found in above section along with defined conditions at the boundaries. The typical homotopy expressions for the problem are defined as [29,30,31]

$$\begin{aligned}&\left( 1-q^{^{\prime }}\right) \pounds \left[ \widetilde{u}-\widetilde{v}_{0} \right] +q^{^{\prime }}\left( \pounds \left[ \widetilde{u}\right] +\beta ^{2} \frac{\partial ^{2}\widetilde{u}}{\partial y^{2}}\right. \nonumber \\&\quad \left. +\frac{n-1}{2}We^{2}\beta ^{4}\frac{\partial }{\partial y}\left( \frac{\partial \widetilde{u}}{ \partial y}\right) ^{3}+\frac{n-1}{2}We^{2}\frac{\partial }{\partial z} \left( \frac{\partial \widetilde{u}}{\partial z}\right) ^{3}\right. \nonumber \\&\quad +\frac{n-1}{2}We^{2}\beta ^{2}\frac{\partial }{\partial y}\left( \frac{ \partial \widetilde{u}}{\partial y}\left( \frac{\partial \widetilde{u}}{ \partial z}\right) ^{2}\right) \nonumber \\&\quad \left. +\frac{n-1}{2}We^{2}\beta ^{2}\frac{\partial }{\partial z}\left( \frac{\partial \widetilde{u}}{\partial z}\left( \frac{ \partial \widetilde{u}}{\partial y}\right) ^{2}\right) \left. +B_{\text{r}}\Omega +G_{\text{r}}\Theta -\frac{\text{d}p}{\text{d}x}\right) =0, \right. \end{aligned}$$
(21)
$$\begin{aligned}&\left. \left( 1-q^{^{\prime }}\right) \pounds \left[ \Theta -\widetilde{ \theta }_{0}\right] +q^{^{\prime }}\left( \pounds \left[ \Theta \right] +\beta ^{2}\frac{\partial ^{2}\Theta }{\partial y^{2}}+N_{\text{b}}\left( \beta ^{2} \frac{\partial \Omega }{\partial y}\frac{\partial \Theta }{\partial y} +\left. \frac{\partial \Omega }{\partial z}\frac{\partial \Theta }{\partial z }\right) \right. \right. \right. \nonumber \\&\quad \left. +\,N_{\text{t}}\left( \beta ^{2}\left( \frac{\partial \Theta }{\partial y} \right) ^{2}+\left( \frac{\partial \Theta }{\partial z}\right) ^{2}\right) =0,\right. \end{aligned}$$
(22)
$$\begin{aligned}&\left. \left( 1-q^{^{\prime }}\right) \pounds \left[ \Omega -\widetilde{ \sigma }_{0}\right] +q^{^{\prime }}\left( \pounds \left[ \Omega \right] +\beta ^{2}\frac{\partial ^{2}\Omega }{\partial y^{2}}+\frac{N_{\text{t}}}{N_{\text{b}}} \left( \beta ^{2}\frac{\partial ^{2}\Theta }{\partial y^{2}}+\frac{\partial ^{2}\Theta }{\partial z^{2}}\right) \right) =0.\right. \end{aligned}$$
(23)

Here, \(\widetilde{u},\) \(\Theta\) and \(\Omega\) speak to the evaluated answers for speed, temperature and nanoparticles profiles, separately. Additionally, q signifies the implanting parameter which has the range \(0\le q^{\prime }\le 1.\) Here, \(\pounds\) is chosen the linear differential operator which is selected here as \(\pounds =\partial ^{2}/\partial z^{2}\). We consider the subsequent initial approximation for \(\widetilde{u},\) \(\Theta\) and \(\Omega ,\) orderly.

$$\begin{aligned} \widetilde{v}_{0}\left( y,z\right)&= {} -1+\left( z^{2}-h^{2}\right) +\frac{1}{ \beta ^{2}}\left( 1-y^{2}\right) , \end{aligned}$$
(24)
$$\begin{aligned} \widetilde{\theta }_{0}&= {} \beta ^{2}\left( z^{2}-h^{2}\right) +\frac{h-z}{2h}= \widetilde{\sigma }_{0}. \end{aligned}$$
(25)

Let us define the series solution of the form

$$\begin{aligned} \widetilde{u}\left( x,y,z\right)&= {} u_{0}+q^{\prime }*u_{1}+q^{\prime 2}*u_{2}+... \end{aligned}$$
(26)
$$\begin{aligned} \Theta \left( x,y,z\right)&= {} \Theta _{0}+q^{\prime }*\Theta _{1}+q^{\prime 2}*\Theta _{2}+... \end{aligned}$$
(27)
$$\begin{aligned} \Omega \left( x,y,z\right)= &\,{} \Omega _{0}+q^{\prime }*\Omega _{1}+q^{\prime 2}*\Omega _{2}+... \end{aligned}$$
(28)

Putting Eqs. (26)-eq28 into Eqs. (21)-eq23 and collecting the coefficients of the exponents of \(q^{\prime },\), we find the set of equations with the relevant boundary conditions.

$$\begin{aligned}&\left. \begin{array}{l} \pounds \left( u_{0}-\widetilde{v}_{0}\right) =\pounds \left( \Theta _{0}- \widetilde{\theta }_{0}\right) =\pounds \left( \Omega _{0}-\widetilde{\sigma }_{0}\right) =0 \\ u_{0}=-1\text { when }\left( y,z\right) =\left( \pm 1,\pm h\left( x\right) \right) ,\text { }\Theta _{0}=\Omega _{0}=(0,1)\text { when }z=(h,-h) \end{array} \right\} , \end{aligned}$$
(29)
$$\begin{aligned}&\left. \begin{array}{c} \left( \pounds \left[ u_{1}\right] +\beta ^{2}\frac{\partial ^{2}u_{0}}{ \partial y^{2}}+\frac{n-1}{2}We^{2}\beta ^{4}\frac{\partial }{\partial y} \left( \frac{\partial u_{0}}{\partial y}\right) ^{3}+\frac{n-1}{2}We^{2} \frac{\partial }{\partial z}\left( \frac{\partial u_{0}}{\partial z}\right) ^{3}\right. \\ +\frac{n-1}{2}We^{2}\beta ^{2}\frac{\partial }{\partial y}\left( \frac{ \partial u_{0}}{\partial y}\left( \frac{\partial u_{0}}{\partial z}\right) ^{2}\right) +\frac{n-1}{2}We^{2}\beta ^{2}\frac{\partial }{\partial z}\left( \frac{\partial u_{0}}{\partial z}\left( \frac{\partial u_{0}}{\partial y} \right) ^{2}\right) \left. +B_{r}\Omega _{0}+G_{r}\Theta _{0}-\frac{\text{d}p}{\text{d}x} \right) =0, \end{array} \right. \end{aligned}$$
(30)
$$\begin{aligned}&\left. \begin{array}{c} \left( \pounds \left[ \Theta _{1}\right] +\beta ^{2}\frac{\partial ^{2}\Theta _{0}}{\partial y^{2}}+N_{\text{b}}\left( \beta ^{2}\frac{\partial \Omega _{0}}{\partial y}\frac{\partial \Theta _{0}}{\partial y}+\left. \frac{ \partial \Omega _{0}}{\partial z}\frac{\partial \Theta _{0}}{\partial z} \right) \right. \right. \\ +N_{\text{t}}\left( \beta ^{2}\left( \frac{\partial \Theta _{0}}{\partial y}\right) ^{2}+\left( \frac{\partial \Theta _{0}}{\partial z}\right) ^{2}\right) =0, \end{array} \right. \end{aligned}$$
(31)
$$\begin{aligned}&\left. \left( \pounds \left[ \Omega _{1}\right] +\beta ^{2}\frac{\partial ^{2}\Omega _{0}}{\partial y^{2}}+\frac{N_{\text{t}}}{N_{\text{b}}}\left( \beta ^{2}\frac{ \partial ^{2}\Theta _{0}}{\partial y^{2}}+\frac{\partial ^{2}\Theta _{0}}{ \partial z^{2}}\right) \right) =0,\right. \end{aligned}$$
(32)
$$\begin{aligned}&u_{1}=0\text { when }\left( y,z\right) =\left( \pm 1,\pm h\left( x\right) \right) ,\text { }\Theta _{1}=\Omega _{1}=0\text { when }z=\pm h\left( x\right) . \end{aligned}$$
(33)

The achieved final particular solutions up to second orders have been revealed over here

$$\begin{aligned} u&=\frac{1}{1440h^{2}N_{\text{b}}\beta ^{4}}\left( 11520h^{2}c_{33}^{2}N_{\text{b}}We^{4}y^{4}(h^{2}-z^{2})\right. \nonumber \\&\quad -240hN_{\text{b}}\left( 296h^{5}c_{33}^{2}We^{4}y^{2}-c_{22}h^{2}c_{33}\right. \nonumber \\&\quad We^{2}y^{2}z+c_{22}c_{33}We^{2}y^{2}z^{3}+3h^{3}c_{33}We^{2}y^{2}\nonumber \\&\quad \left( -4+c_{22}-2\frac{dp}{dx}-112c_{33}We^{2}z^{2}\right) +h \nonumber \\&\quad \left. \left( -6+y^{2}\left( 6-3c_{33}\left( -4+c_{22}-2\frac{dp}{dx} \right) We^{2}z^{2}+40c_{33}^{2}We^{4}z^{4}\right) \right) \right) \beta ^{2}+5N_{\text{b}} \nonumber \\&\quad \left( -896h^{8}c_{33}^{2}\right. We^{4}+24h^{6}c_{33}We^{2}\nonumber \\&\quad \left( -12-7c_{22}+14\frac{dp}{dx}+10c_{22}y^{2}\right) +40c_{22}h^{5}c_{33}We^{2}z \nonumber \\&\quad +32c_{22}h^{3}c_{33}We^{2}z^{3}+3G_{\text{r}}c_{11}z^{4} \nonumber \\&\quad -72c_{22}hc_{33}We^{2}z^{5}+3h^{4}(-96+5G_{\text{r}}c_{11}-96c_{33}We^{2} \nonumber \\&\quad (-4+c_{22}y^{2})z^{2}+128c_{33}^{2}We^{4}z^{4}) \nonumber \\&\quad +2h^{2}(-144-9(-16+G_{\text{r}}c_{11})z^{2}+12c_{33}We^{2}(-36+ \nonumber \\&\quad 7B_{\text{r}}+7G_{\text{r}}-14\left. \left. \left. \frac{dp}{dx}+2c_{22}y^{2}\right) z^{4}+256c_{33}^{2}We^{4}z^{6}\right) \right) \beta ^{4}\nonumber \\&\quad +8h\left( h^{2}-z^{2}\right) \left( 75B_{\text{r}}h^{3}N_{\text{t}}\right. \nonumber \\&\quad + 158c_{22}h^{5}c_{33}N_{\text{b}}We^{2}-7G_{\text{r}}h^{2}N_{\text{b}}c_{11}z\nonumber \\&\quad +h\left( -15B_{\text{r}}N_{\text{t}}+158c_{22}h^{2}c_{33}N_{\text{b}}We^{2}\right) z^{2}+3G_{\text{r}}N_{\text{b}} \nonumber \\&\quad c_{11}z^{3}-52c_{22}hc_{33}N_{\text{b}}\left. We^{2}z^{4}\right) \beta ^{6} \nonumber \\&\quad +16G_{\text{r}}h^{2}N_{\text{b}}c_{11}\left. \left( 14h^{6}-15h^{4}z^{2}+z^{6}\right) \beta ^{8}\right) , \end{aligned}$$
(34)
$$\begin{aligned} \theta&=\frac{1}{720h^{3}}\left( 15\left( 6h^{3}(4+c_{11})\right. \right. +h^{2}\left( -24+c_{11}(c_{44})\right) z\nonumber \\&\quad -6h\left( c_{11}\right) z^{2}\left. -c_{11}(c_{44})z^{3}\right) - \nonumber \\&60h\left( h^{2}-z^{2}\right) \left( 12h^{2}+2h(2N_{\text{b}}+N_{\text{t}})z\right. +c_{11}\left. (c_{44})z^{2}\right) \beta ^{2}+16h^{2}\left( h^{2}-z^{2}\right) \nonumber \\&\left. \left( 15h^{3}N_{\text{b}}\right. +h^{2}c_{11}(c_{44})z \right. \nonumber \\&\quad \left. +15hN_{\text{b}}z^{2}+6\left. c_{11}(c_{44})z^{3}\right) \beta ^{4}-64h^{3}c_{11}(c_{44})\right. \nonumber \\&\left. \left( h^{6}-z^{6}\right) \beta ^{6}\right) , \end{aligned}$$
(35)
$$\begin{aligned} \sigma&=\frac{1}{24h^{2}N_{\text{b}}}\left( 3N_{\text{t}}c_{11}\right. z^{2}-24h^{4}(N_{\text{b}}-N_{\text{t}})\beta ^{2}\nonumber \\&\quad +8h^{3}N_{\text{t}}c_{11}z\beta ^{2}-8h^{6}N_{\text{t}}c_{11}\beta ^{4}-4h \nonumber \\&\left( 2N_{\text{t}}^{2}z^{3}\beta ^{2}\right. +N_{\text{b}}z\left. \left( 3+2N_{\text{t}}z^{2}\beta ^{2}\right) \right) \nonumber \\&\quad +h^{2}\left( N_{\text{t}}\left( -3N_{\text{t}}-24z^{2}\beta ^{2}+\right. \right. \left. 8N_{\text{t}}z^{4}\beta ^{4}\right) +N_{\text{b}} \nonumber \\&\left. \left. \left( 12-3N_{\text{t}}+24z^{2}\beta ^{2}+8N_{\text{t}}z^{4}\beta ^{4}\right) \right) \right) . \end{aligned}$$
(36)

The volumetric flow rate \(\overline{q}\) is described as

$$\begin{aligned} \left. \overline{q}=\int \limits _{0}^{h\left( x\right) }\int \limits _{0}^{1}u*\text{d}y\text{d}z.\right. \end{aligned}$$
(37)

The average value of the above-defined flow rate per unit period is represented as

$$\begin{aligned} Q=\int \limits _{0}^{h\left( x\right) }\int \limits _{0}^{1}\left( u+1\right) \text{d}y\text{d}z=\overline{ q}+h\left( x\right) . \end{aligned}$$
(38)

The pressure gradient factor dp/dx can be evaluated by utilizing Eqs. (37) and \(\left( 38\right)\) and is displayed as

$$\begin{aligned} \frac{dp}{dx}&=\frac{1}{112h^{3}c_{33}N_{\text{b}}We^{2}\beta ^{2}\left( 5+21h^{2}\beta ^{2}\right) }\nonumber \\&\quad \left( -2688h^{3}c_{33}^{2}\right. N_{\text{b}}We^{4}+35hN_{\text{b}}\left( -48+h^{2}c_{33}We^{2}\right. \nonumber \\&\left( -32+7c_{22}+768h^{2}c_{33}We^{2}\right) )\beta ^{2}\nonumber \\&\quad +12N_{\text{b}}(-7h^{3}(-20+Grc_{11})+210Q+7\left( 8+7c_{22}\right) \nonumber \\&h^{5}c_{33}We^{2}+544h^{7}\left. c_{33}{}^{2}We^{4}\right) \beta ^{4}\nonumber \\&\quad -3h^{5}(224BrN_{\text{t}}-7GrN_{\text{b}}c_{11}\left. +576c_{22}h^{2}c_{33}N_{\text{b}}We^{2}\right) \nonumber \\&\beta ^{6}-\left. 256Grh^{7}N_{\text{b}}c_{11}\beta ^{8}\right) . \end{aligned}$$
(39)

The numerical integration of the above-defined dp/dx over unit wavelength provides the pressure rise \(\Delta p\) which is described as

$$\begin{aligned} \Delta p=\int \limits _{0}^{1}\left( \frac{\text{d}p}{\text{d}x}\right) \text{d}x, \end{aligned}$$
(40)

whose numerical data have been computed on symbolic software Mathematica by built in tool (NIntegrate) over a constant range of all included parameters. The variation in pressure rise data is available in Table 2. The substitutive parameters used in above expressions are summarized as

$$\begin{aligned} c_{11}=N_{\text{b}}+N_{\text{t}},\text { }c_{22}=G_{\text{r}}+B_{\text{r}},\text { }c_{33}=n-1,\text { } c_{44}=N_{\text{b}}+2N_{\text{t}}. \end{aligned}$$
(41)
Fig. 16
figure 16

Waves of pressure gradient dp/dx with \(G_{\text{r}}\) and \(B_{\text{r}}\) at \(N_{\text{t}}=0.5,N_{\text{b}}=0.3,\beta =0.6,n=0.4,We=0.5,\phi =0.2,\) \(Q=0.5\)

Full size image
Fig. 17
figure 17

Waves of pressure gradient dp/dx with n and We at \(N_{\text{t}}=0.5,N_{\text{b}}=0.3,G_{\text{r}}=0.2,\beta =0.6,Q=0.4,\phi =0.5,\) \(B_{\text{r}}=0.2\)

Full size image
Fig. 18
figure 18

Waves of pressure gradient dp/dx with \(N_{\text{b}}\) and \(N_{\text{t}}\) at \(\beta =0.8,Q=0.5,G_{\text{r}}=0.5,n=0.7,We=0.11,\phi =0.2,\) \(B_{\text{r}}=0.6\)

Full size image
Fig. 19
figure 19

Trapping boluses for values of \(\beta ,\) (a) for \(\beta =0.7,\) (b) for \(\beta =0.8,\) (c) for \(\beta =0.9.\) The other parameters are \(B_{\text{r}}=0.9,\) \(G_{\text{r}}=0.1,\) \(N_{\text{t}}=0.5,\) \(We=0.6,\) \(n=0.9,N_{\text{b}}=0.9,\) \(\phi =0.1,\) \(Q=0.5,\) \(y=0.1\)

Full size image
Fig. 20
figure 20

Trapping boluses for values of \(G_{\text{r}},\) (a) for \(G_{\text{r}}=0.5,\) (b) for \(G_{\text{r}}=0.7,\) (c) for \(G_{\text{r}}=0.9.\) The other parameters are \(B_{\text{r}}=0.9,\) \(\beta =0.9,\) \(N_{\text{t}}=0.5,\) \(We=0.6,\) \(n=0.9,N_{\text{b}}=0.6,\) \(\phi =0.1,\) \(Q=0.5,\) \(y=0.1\)

Full size image

Numerical results and graphical discussions

The investigative arrangements are assessed for the expressions of linear momentum, temperature and nanoparticles volume fraction for Carreau liquid with the assistance of notable HPM up to second-order systems. In the current segment, all obtained articulations are introduced and talked about graphically to watch the varieties of different relevant parameters. The impacts of parallel walls executing waves (aspect ratio \(\beta\)), Weissenberg number We, power law parameter n, average volume flow rate Q, amplitude proportion \(\phi\), the Brownian motion parameter \(N_{\text{b}}\), the thermophoresis parameter \(N_{\text{t}}\), local temperature Grashof number \(G_{\text{r}}\) and local nanoparticle Grashof number \(B_{\text{r}}\) on the profiles of velocity u, temperature \(\theta\), nanoparticles volume fraction \(\sigma\), pressure gradient dp/dx and pressure rise \(\Delta p\) are given the showcase of graphs for dual and triple dimensions. The consequences of present examination are likewise contrasted and that of introduced in past writing with tables and graphs. The catching bolus statue is also joined through drawing figures of streamlines for different developing parameters.

Fig. 21
figure 21

Trapping boluses for values of We,  (a) for \(We=0.7,\) (b) for \(We=0.8,\) (c) for \(We=0.9.\) The other parameters are \(B_{\text{r}}=0.9,\) \(G_{\text{r}}=0.1,\) \(N_{\text{t}}=0.5,\) \(\beta =0.9,\) \(n=0.9,N_{\text{b}}=0.9,\) \(\phi =0.1,\) \(Q=0.5,\) \(y=0.1\)

Full size image
Fig. 22
figure 22

Trapping boluses for values of \(N_{\text{b}},\) a for \(N_{\text{b}}=0.5,\) b for \(N_{\text{b}}=0.7,\) c for \(N_{\text{b}}=0.9.\) The other parameters are \(B_{\text{r}}=0.9,\) \(G_{\text{r}}=0.1,\) \(N_{\text{t}}=0.5,\) \(We=0.6,\) \(n=0.9,\beta =0.9,\) \(\phi =0.1,\) \(Q=0.5,\) \(y=0.1\)

Full size image
Fig. 23
figure 23

Trapping boluses for values of \(\phi ,\) a for \(\phi =0.1,\) b for \(\phi =0.2,\) c for \(\phi =0.3.\) The other parameters are \(B_{\text{r}}=0.9,\) \(G_{\text{r}}=0.1,\) \(N_{\text{t}}=0.5,\) \(We=0.6,\) \(n=0.9,N_{\text{b}}=0.9,\) \(\beta =0.9,\) \(Q=0.5,\) \(y=0.1\)

Full size image
Fig. 24
figure 24

Trapping boluses for values of Q,  a for \(Q=0.5,\) b for \(Q=0.6,\) c for \(Q=0.7.\) The other parameters are \(B_{\text{r}}=0.9,\) \(G_{\text{r}}=0.6,\) \(N_{\text{t}}=0.5,\) \(We=0.6,\) \(n=0.9,N_{\text{b}}=0.6,\) \(\phi =0.1,\) \(\beta =0.9,\) \(y=0.1\)

Full size image

Table 1 and Fig. 2 indicate the variation of velocity u to see the comparison of the present work with the study of Nadeem et al. [27], and it is very obvious from this table and figure that if we neglect the effects of nanofluid, we recover the results of Nadeem et al. [27] . It is also observed here that in the presence of nanoparticles phenomenon, velocity profile is dropping. Table 2 contains the variation in pressure rise \(\Delta p\) by considering the special cases for Newtonian fluid and Carreau fluid in rectangular duct \(\beta =0.5\) and square duct \(\beta =1.\) It is appeared from this table that pressure rise increases for Carreau (non-Newtonian) fluid as compared with Newtonian fluid and also the pressure rise falls down in a square duct.

Figures 3a, b account for the two- and three-dimensional analysis of velocity profile u for the variation in aspect ratio \(\beta\) and mean volume flow rate Q. It is noted here that velocity is an increasing function of both \(\beta\) and Q,  and also it is observed from three-dimensional graph that velocity is decreasing with increasing aspect ratio. The three-dimensional graph emphasizes that an increasing aspect ratio gives rise to the length of the channel and on the other hand, width will be reduced and due to this reason fluid will travel faster in the axial direction but will face a reduction in velocity along the lateral walls. However, from the same graph, it is also considerable that there is no change in velocity of fluid along lateral direction (\(y-\)axis). It is observed from Fig. 4a, b that velocity has opposite behavior with the parametric change in \(G_{\text{r}}\) and \(B_{\text{r}}.\) One can analyze from Figs. 5a, b to 6a, b that increase in n and \(N_{\text{b}}\) shows increase in velocity profile height, while increase in We and \(N_{\text{t}}\) gives decrease in velocity distribution. It follows some physical aspects that when we increase the concentration of nanoparticles through Brownian diffusion, the fluid speed flourishes due to increase in its temperature, but oppositely an increase in thermal transfer through thermophoresis factor reduces the velocity accordingly.

Figure 7 implies the influence of aspect ratio \(\beta\) (showing the variation in lateral walls) on temperature distribution \(\theta .\) It is seen that temperature profile is decreasing with \(\beta\) and also the variation of \(\theta\) is nonlinear, i.e., for \(z<0.5,\) curves are launching down but as we go further those are elevating up to \(z=1.2.\) It is due to the reason that large aspect ratio decreases the volume of the duct which produces the high speed flow reducing its temperature. It is concluded from Fig. 8 that temperature curves are varying directly with \(N_{\text{b}}\) and \(N_{\text{t}}.\) It is also seen that variation in curves is linear for \(N_{\text{b}}=1\) and \(N_{\text{t}}=0.2\) but nonlinear for the other values of \(N_{\text{b}}\) and \(N_{\text{t}}.\) It can be described through physical aspect that an increase in Brownian parameter \(N_{\text{b}}\) gives rise to the Brownian motion which enhances the temperature of the nanofluid and same is the reason for enlargement of temperature against the thermophoresis parameter which lifts the thermal variance with its increasing effects. Figure 9 comprises the effects of lateral walls for nanoparticles concentration \(\sigma\) in the section \(z\in \left[ -h,h\right]\), and it is illustrated here that velocity is directly proportional to \(\beta .\) It is also observed that the curves are bending down with \(\beta =0.1\) and \(\beta =0.2\) while lifted up with \(\beta =0.3\) and \(\beta =0.4.\) To observe the variation of \(\sigma\) with \(N_{\text{b}}\) and \(N_{\text{t}},\) Fig. 10 is sketched. It is measured here that \(\sigma\) profile is diminishing with \(N_{\text{b}}\) while lifting up with \(N_{\text{t}}.\)

The variation in pressure rise \(\Delta p\) with the corresponding change in \(\beta\) and \(N_{\text{t}}\) is shown by drawing the graph of \(\Delta p\) versus flow rate Q in Fig. 11. It is important to note that we discuss the \(\left( \Delta p-Q\right)\) plane into four regions, namely peristaltic pumping \(\left( \Delta p>0,Q>0\right) ,\) retrograde pumping \(\left( \Delta p>0,Q<0\right) ,\) free pumping \(\left( \Delta p=0\right)\) and augmented pumping \(\left( \Delta p<0,Q>0\right) .\) It is executed from Fig. 11 that in retrograde pumping region, \(\Delta p\) rises up with the increase in \(\beta\) while for augmented pumping, it slides down with \(\beta ,\) and also the free pumping region occurs at \(Q=0.\) It can also be predicted here that peristaltic pumping rate increases for \(N_{\text{t}}.\) We can also extract from Fig. 12 that same behavior is reported with n and \(G_{\text{r}},\) only the difference is that pressure rise is increasing in the peristaltic pumping region and the height of \(\Delta p\) profile reaches about 30 which was 23 in the previous graph. Figure 13 depicts the very similar attitude of \(\Delta p\) with \(\phi\) and \(B_{\text{r}}\) except the fact that pressure rise curves are fallen down for \(\phi\) and \(B_{\text{r}}.\) However, the behavior of pressure rise distribution is quite opposite with \(N_{\text{b}}\) and We (see Fig. 14). It can be discussed that peristaltic pumping decreases with both the parameters. Also in the augmented pumping part, the curves are reversed. It is to be noted that free pimping region occurs at \(Q=0.2\) and peristaltic pumping region is \(0<Q<0.2.\) It is also very obvious to see that in Fig. 14, that height of the pressure rise curves approaches 80, i.e., pressure rise is approaching its maximum altitude. It is also observed that variation in pressure curves is linear with all parameters.

Pressure gradient profile dp/dx under the variation of \(\beta\) and Q is disclosed in Fig. 15. It is found here that pressure gradient is an inverse function of \(\beta\) and Q. It can also be described that pressure gradient has maximum height at \(x=0.5\) and much pressure gradient is observed in the middle part to maintain the flow as compared with the corner regions. Figure 16 denotes that dp/dx is varying directly with \(B_{\text{r}}\) and \(G_{\text{r}}.\) It is observed that pressure gradient curves are rising up with power law index n but fetching down with Weissenberg number We (see Fig. 17). It can be mentioned from Fig. 18 that pressure gradient is inverse function of \(N_{\text{b}}\) while direct variation with \(N_{\text{t}}\) is observed. Also, the variation is smooth and continuous with \(N_{\text{b}}\) and \(N_{\text{t}}.\)

Trapping scheme

The phenomenon of trapping bolus (a circulating hole followed by continuous streamlines moving forward as the flow progresses) is discussed through Figs. 19–24. Figure 19 contains variation in trapping bolus with aspect ratio \(\beta .\) It is derived here that for \(\beta =0.7,\) we have only one central bolus which is converted into two separate boluses for \(\beta \ge 0.8.\) It is also noted that more streamlines are appeared with increasing aspect ratio \(\beta ,\) which reflects the physics of flow pattern that when we reduce the channel width by increasing the length presses the fluid which results in increasing the number of boluses but reduces their dimensions due to narrow enclosure, while Fig. 20 shows the opposite behavior of trapping bolus with the increasing effects of \(G_{\text{r}}.\) Figure 21 shows that for \(We=0.7,\) we have a very tiny bolus in the lower part which also gets larger as we increase the value of Weissenberg number but enclosed by less streamlines. It can been observed from Fig. 22 that for \(N_{\text{b}}=0.5,\) we have two boluses one at above the center line and the second one is below and it is depicted that the lower bolus reduces its size for \(N_{\text{b}}=0.7\) and then increases again for \(N_{\text{b}}=0.9\) and the same attitude is seen for upper bolus. In Fig. 23, it is seen that the both upper and lower boluses are reduced in size with increasing values of amplitude ratio \(\phi .\) With the increase in flow rate Q,  upper bolus is getting larger while lower is shrinking in size (see Fig. 24).

Table 1 Validity of the present results through comparison with the existing literature when \(\phi =0.6,x=0,y=1,n=0.5,We=0.03,\beta =0.64,Q=0.5\)
Full size table
Table 2 Variation in pressure rise when \(\phi =0.08,G_{\text{r}}=0.5,B_{\text{r}}=0.5,N_{\text{b}}=0.5,N_{\text{t}}=0.5,We=0.03\)
Full size table

Conclusions

In the current investigation, peristaltic stream of a non-Newtonian (Carreau) nanofluid has been considered in a cross area of rectangular conduit to depict the scientific outcomes under convective heat transfer features and nanoparticles saturation. The main interest to discuss this study is to explore the viscoelastic features of Carreau fluid along with the enhancing thermal conductivity through nanoparticles and keeping in mind the three-dimensional nature of industrial and medical equipment. All the administering equations are planned under the approximations of long wavelength and low Reynolds number. The stream is estimated in a wave casing of reference moving with a steady speed c normal axis of the channel. Explanatory outcomes are acquired by utilizing HPM, and the impacts of every physical parameter showing up in the current examination are talked about with detail. A velocity of Newtonian fluid and generalized (Carreau) fluid are compared in the study too. Special cases have also been reported for two-dimensional channel and square duct. The finishing up focuses got from the above perception are expressed as

  1. 1.

    It is calculated that velocity profile goes linearly with aspect ratio, power law index, Brownian motion factor and average flow rate. On the other hand, it is reciprocal function of local nanoparticles Grashof number, local temperature Grashof number, thermophoresis parameter and Weissenberg number.

  2. 2.

    Temperature curves are showing inverse relation with aspect ratio, but direct link is depicted in case of Brownian motion factor and thermophoresis representative.

  3. 3.

    It is emphasized that nanoparticles volume fraction varies upward with larger variation in aspect ratio and thermophoresis parameter, but opposite scene is reported against Brownian motion parameter.

  4. 4.

    One can find from above measurements that peristaltic pumping curves are showing direct proportionality with the aspect ratio, power law index, amplitude ratio, thermophoresis parameter, local nanoparticles and local temperature Grashof numbers; however, they are suppressing against Weissenberg number and Brownian motion parameter.

  5. 5.

    It is measured that pressure gradient trajectories are exhibiting inverse relation with aspect ratio, flow rate, Weissenberg number and Brownian motion parameter while giving higher with power law parameter, thermophoresis parameter, local nanoparticles and local temperature Grashof numbers.

  6. 6.

    The results are declaring that the trapping circular boluses are becoming larger with local nanoparticles Grashof number, Weissenberg number and flow rate while shrinking with amplitude ratio, Brownian motion parameter and aspect ratio of the channel.

  7. 7.

    It is computed that the present results are in well agreement with the previous literature [27] and pressure rise increases in rectangular duct as compared with square duct. Also, the velocity is decreasing in the presence of nanoparticles phenomenon.

  8. 8.

    It is also presented that Newtonian fluid moves faster than the Carreau fluid if we incorporate the effects of nanoparticles concentration along with their temperature distribution. The important feature of this study is that a 3D rectangular duct produce higher pumping order than a square shaped duct.