Introduction

Entropy production is a material phenomenon which corresponds to the degree of disorder in the system. According to thermodynamics second law, in real-world examples entropy of the system rises with time and this procedure is irreversible. As entropy production occurs, the standard/status of energy reduces. To preserve the energy standard/status during flow of fluid or to minimize the entropy production, it is essential to investigate the entropy production distribution in the fluid. Proficient energy consumption is the foremost objective while designing the thermal devices. This target can be accomplished by minimizing entropy generation in thermodynamic processes. With the development of industry and enhanced engineering capabilities, entropy production is perceived as a suitable solution, in order to get better performance in industrial procedures. It is not possible to regain the energy which was lost, but actions can be taken to minimize the irreversibilities. Bejan [1] was the pioneer researcher to initiate this idea by means of entropy production minimization. Sciacovelli et al. [2] presented entropy production analysis as a design tool. Zhao and Liu [3] studied entropy production for electro-kinetically flowing fluid in open- and close-ended micro-conduit. Rashidi et al. [4] investigated the entropy production of steady flow in a rotating disk having porous medium. Afridi et al. [5] analyzed the entropy generation of MHD (boundary layer) stagnation point flow in the existence of joule and friction heating. Gull et al. [6] investigated the entropy production of mixed convection Poiseuille flow of MDJN (molybdenum disulfide Jeffrey nanofluid) and found that the reason behind the mixed convection is external pressure gradient and buoyancy force. Saqib et al. [7] studied the entropy production of electrically conducting, various types of fractionalized nanofluids moving on a vertical plate of infinite length embedded in porous medium. Natural convection process within the conduits has been a focus of extensive research in the last few decades because of its tremendous applications in engineering in electronic cooling systems, heat exchangers and nuclear reactors. The proficient utilization of energy and best possible utilization of resources have provoked the investigations for improving the competence of industrial procedures. Some recent studies exploring the outcomes of entropy analysis are given in Refs. [8,9,10,11,12,13,14].

Micro-fluids got a significant attention in recent few decades due to its tremendous applications in engineering and industry. The scientists have used micro-fluids based on electrokinetics, as it is very efficient mechanism to manipulate and control flow of liquid in micro-devices. Micro-fluidics is also applicable in biological transports such as DNA concentration, species separation and amalgamation of fluids. It can be applied in analysis of different biochemical reactions. Coulomb force causes the electroosmotic flow, influenced by the electric potential through the micro-channel. Electroosmosis refers to the movement of counter ions in the diffused part of electric double layer. The technique of electro-osmotically flowing fluid via peristaltic pumping in a non-Darcy porous medium is a physically very significant study as it can be used in hemodialysis.

Cameselle and Reddy [15] worked on the progress and improvement in electroosmotic flow for the exclusion of contaminations from soils. Zhou et al. [16] studied how electroosmotic process is affected by the material of electrode. Tripathi et al. [17] investigated the peristaltic movement of electrically conducted fluids under the influence of transverse magnetic field. Bouriat et al. [18] experimentally found the zeta potential of grains by using the electroosmotic technique. Li et al. [19] studied the flow rate of fluid in microporous medium under the effect of gravitational and electroosmotic forces.

Most of the liquids in the physiology are transported by the natural system of pumping known as peristalsis. Such phenomenon is caused by the continuous wave of area contraction and extension of a flexible tube holding liquid. Among the most recent explorations, peristaltic mechanism is exclusively significant due to its wide-ranging applications in biosciences, engineering, physiological and industrial world. Peristaltic pumping is an intrinsic property of numerous physiological muscles. Such muscles are present in gastrointestinal channel, blood vessels, lymphatic vessels and ducts of many glands. In industry, peristaltic transport mechanism is used in finger and roller pumps, sanitary and in transport of many corroding materials. In biosciences, it is used in many appliances, for example in heart–lung machine, catheter and endoscope and in many others. Currently, due to the extensive applications of peristaltic transport in several fields, a lot of work has been done on this topic. First initiative was taken by Latham [20] who investigated the transport of fluid via a peristaltic pump. Later on, researchers and scientists contributed a wealth of the literature in the biofluid mechanics. They studied the peristaltic transport under different conditions with different approaches like analytical, experimental and numerical. Some recent studies are mentioned in references [21,22,23,24,25,26,27,28,29].

Peristaltic pumps are used in hemodialysis machines in order to transfer the fluids. Dialysis machine and special filter, i.e., artificial kidney (dialyzer) are used to purify the blood in hemodialysis. The dialyzer (filter or walls with semipermeable membrane) has two parts: one for blood and the other for cleaning fluid called dialyzate. A thin membrane acts as a boundary between these two parts. Protein, blood cells and other essential components remain in blood since they are too big in size to pass across the membrane. Smaller waste particles in the blood, such as urea, potassium, creatinine and access of fluid, pass through the membrane (porous) and are washed away. Hence peristaltic pumps can be utilized for fluid flow and electroosmosis technique helps in separating essential components from waste materials with the help of porous medium.

Transportation of fluids across a porous medium plays a vital role in many applications, such as geophysics, chemical reactors, petroleum industries, nuclear reactors, hydrogeology and environmental sciences. DNA is composed of four building blocks, which are adenine, guanine, cytosine and thymine. Adenine and thymine are always attached as a pair, and cytosine and guanine are attached as a pair. DNA is the sequence of these pairs that acts as a set of instructions that makes all living things. DNA analysis is the name given to the interpretation of genetic sequences and can be used for a wide variety of purposes. It can be used to identify a species, but can also differentiate individuals within a species. Capillary electrophoresis plays a significant role in the advancement of DNA analysis technologies. Hence electro-osmotically flowing fluid influenced by peristaltic pumping can also be used in DNA analysis, which is further used in DNA sequencing, finding length of DNA and in identification of genetic diseases. An admirable study on flow across the porous media is by Starov and Zhdanov [30] who investigated dependence of permeability on porous medium. Reddy [31] studied the impact of mass and heat transfer on peristaltic flow along porous medium. Elshehawey et al. [32] investigated the peristaltic movement of incompressible fluid through a porous medium. Noreen [33] worked on magneto-thermo-hydrodynamic peristaltic flow of Eyring–Powell nanofluid in asymmetric channel. Khalid et al. [34] studied the MHD free convection of blood flow with nanotubes, the blood is flowing on vertical plate (oscillating) immersed in a porous medium. Khan et al. [35] examined the heat transfer of nanofluid for the Stokes’ second problem. They found that fluid motion is opposed by the Hartman number and porosity. Kouloulias et al. [36] analyzed the flow characteristics of nanofluids during turbulent natural convection.

Studies cited above were established on Darcy law to include the porous medium. But in numerous conditions, flow rates become high or have irregular porosity due to which Darcy law becomes irrelevant. In the case of non-Darcy flow, the kinetic energy and the inertial forces vary considerably due to the expansion and contraction of fluid in the porous media. Due to these consequences, flow will show signs of non-linearity regarding velocity. To explain this turbulent and nonlinear behavior, Forchheimer [37] added a non-Darcy expression to the Darcy equation. Many researchers have focused on an important behavior of non-Darcy flow, i.e., good deliverability and performance inside a tank. Non-Darcy approach is also applicable across the fractured and porous rocks which may happen during high flux and insertion of waste fluids into underground configurations. Begum et al. [38] investigated the mixed convective flow of nanofluids in non-Darcy porous medium. Wu [39] studied the immiscible fluids by both analytical and numerical approaches in non-Darcy porous medium. Veyskarami et al. [40] investigated the impact of throat curvature on fundamental properties of non-Darcy porous medium.

Technique of electroosmosis in porous medium is used in many applications of geoenvironmental and geotechnical engineering, oil and gas organizations and bio-environmental sciences. The accumulated toxic heavy metal ions which lead to serious health and environmental issues are also removed from soil by this method. It is also used in dewatering and consolidation of soft clay which is a reason for land sliding. Gupta et al. [41] investigated the universal formulae for electroosmosis in porous medium. Tripathi [42] studied the electroosmosis peristaltic heat flow through a finite porous channel.

Being encouraged from the above discussion, we have analyzed the entropy generation minimization in electroosmotic flow provoked by peristaltic pumping across a non-Darcy porous medium. Such analysis has not been done before and we encourage researches to pay attention in this direction. Objectively system performance is investigated by the combine effects of magnetohydrodynamics and electroosmotic phenomena in a non-Darcy porous medium via peristalsis. The deviations in Nusselt number and Bejan number under the manipulation of relatable parameters are also generated.

Mathematical model and analysis

Let us examine the heat transfer of peristaltic flow induced by electroosmosis through a non-Darcy porous medium. Consider that the biofluid (fulfilling the Newtonian viscous model) is flowing in non-Darcy porous medium under the impact of electric field and magnetic field. The temperature of conduit wall is constant and it is denoted as \(T_{\text{w}}\), while temperature of bulk fluid is denoted as T.

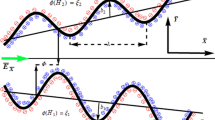
Consider two-dimensional flow (\(\tilde{x},\tilde{y}\)) of a viscous fluid in a micro-channel, in which wave propagation is along \(\tilde{x}\) direction. Furthermore, the flow is symmetric about the middle line of the conduit, i.e., \(\tilde{y} = 0.\) Let \(\tilde{y} = \tilde{h}\left( {\tilde{x},\tilde{t}} \right)\) and \(\tilde{y} = - \tilde{h}\left( {\tilde{x},\tilde{t}} \right)\) are the upper and lower boundaries of the conduit, respectively, as shown in Fig. 1. Moreover, assume that the electric field with strength E0 and magnetic field with strength B0 are acting together on biofluid flow. The electric field is exerted in the direction parallel to length of micro-channel which provides the required compelling force for electrokinetic flow.

Fig. 1
figure 1

A geometrical portrayal of flow regime in the presence of electric field E (applied in the axial direction) and magnetic field B (applied in the transverse direction). A peristaltic wave is traveling with the wave velocity (c1), amplitude (\(b_{1}\)) and wave length (\(\lambda\)) in a micro-channel through a non-Darcy porous medium

Full size image

Due to symmetric channel, it is enough to study the characteristics of fluid flow in the domain \(0 \le \tilde{y} \le \tilde{h}\). The geometry of wall [42] is:

$$\tilde{h}\left( {\tilde{x},\tilde{y}} \right) = d_{h} - \tilde{b}_{1} \cos^{2} \frac{\pi }{\lambda }\left( {\tilde{x} - c_{1} \tilde{t}} \right).$$
(1)

Here \(d_{h}\) is representing the semichannel width, while b1, λ and c1 depict the amplitude, wavelength and velocity of the wave, respectively.

Electrical potential distribution

The Poisson–Boltzmann equation [43, 44] is used to describe the electric potential in the micro-channel.

$$\nabla^{2} \tilde{\phi } = - \frac{{\rho_{\text{e}} }}{{\varepsilon \varepsilon_{0} }},$$
(2)

where \(\tilde{\phi }, \rho_{\text{e}} , \varepsilon , \varepsilon_{0}\) are electroosmotic potential, net ionic charge density, dielectric constant and permittivity of free space, respectively. Permittivity of free space is a constant and its value is \(8.854 \times 10^{ - 12} \;{\text{F}}\,{\text{m}}^{ - 1} .\) The possibility of detecting an ion at a specific point within electric double layer (EDL) is proportional to Boltzmann factor \({\text{e}}^{{\left( {\frac{{ - ze\tilde{\phi }}}{{K_{\text{B}} T_{\text{av}} }}} \right)}}\) where \(z, e, K_{\text{B}} , T_{\text{av}}\) depict the valence of ions, electron charge, Boltzmann constant and the average temperature, respectively. The number densities of positive \((n^{ + } )\) and negative ions \((n^{ - } )\) can be explained by the Boltzmann equation as:

$$n^{ \pm } = n_{0} {\text{e}}^{{\left( { \mp \tfrac{{ze\tilde{\varphi }}}{{K_{\text{B}} T_{\text{av}} }}} \right)}} ,$$
(3)

where in the buffer solution the average number of negative and positive ions are denoted by \(n_{0}\). When in the micro-channel there is no gradient of ionic concentration in the axial direction, the distribution of ionic concentration is believed to be valid. In a unit fluid volume, the total charge is taken as [45].

$$\rho_{\text{e}} = ez\left( {n^{ + } - n^{ - } } \right) = - 2n_{0} ez\sinh \left( {\frac{{ez\tilde{\varphi }}}{{K_{\text{B}} T_{\text{av}} }}} \right).$$
(4)

Now, with the help of Eqs. (3) and (4) we approximate the Poisson–Boltzmann Eq. (2) as:

$$\frac{{{\text{d}}^{2} \tilde{\phi }}}{{{\text{d}}\tilde{y}^{2} }} = \frac{{ - 2n_{0} ez}}{{\varepsilon \varepsilon_{0} }}\sinh \left( {\frac{{ - ze\tilde{\phi }}}{{K_{\text{B}} T_{\text{av}} }}} \right).$$
(5)

In order to proceed with dimensionless variables, we introduce:

$$\begin{aligned} &\delta = \frac{{d_{\text{h}} }}{\lambda }, Re = \frac{{\rho c_{1} d_{\text{h}} }}{\mu }, \beta = \frac{{U_{\text{HS}} }}{{c_{1} }}, U_{\text{HS}} = \frac{{E_{0} \varepsilon \varepsilon_{0} \zeta }}{\mu }, \nu = \frac{\mu }{\rho }, H_{\text{m}} = B_{0} d_{\text{h}} \sqrt {\frac{\sigma }{\mu }} , \Omega^{2} = \frac{{d_{\text{h}}^{2} }}{{k^{*} }}, \hfill \\ &\phi = \frac{{\tilde{\phi }}}{\zeta }, y = \frac{{\tilde{y}}}{{d_{\text{h}} }}, x = \frac{{\tilde{x}}}{\lambda }, t = \frac{{c_{1} \tilde{t}}}{\lambda }, h = \frac{{\tilde{h}}}{{d_{\text{h}} }}, b_{1} = \frac{{\tilde{b}_{1} }}{{d_{\text{h}} }}, \theta = \frac{{T - T_{\text{w}} }}{{\frac{{qd_{\text{h}} }}{k}}}, p = \frac{{\tilde{p}d_{\text{h}}^{2} }}{{c_{1} \lambda \mu }}, u = \frac{{\tilde{u}}}{{c_{1} }}, \hfill \\& v = \frac{{\tilde{v}}}{{c_{1} \delta }},c_{\text{F}} = c_{{k^{*} }} \frac{{d_{h}^{2} c_{1} }}{{\nu \sqrt {k^{*} } }},Pr = \frac{{\mu c_{\text{p}} }}{K}, Br = \frac{{\mu c_{1}^{2} }}{{qd_{\text{h}} }}, \gamma = \frac{{\sigma d_{\text{h}} E_{0}^{2} }}{q}, \hfill \\ \end{aligned}$$
(6)

in which \(\phi\) and \(\zeta\) are the electroosmotic potential and zeta potential of the medium, \(\delta\) denotes the wave number, \(q\) is the heat flux, \(Re\) is the Reynolds number, \(\beta\) is the mobility of the medium, \(U_{\text{HS}} , H_{\text{m}} , \Omega^{2}\) are the Helmholtz–Smoluchowski velocity, Hartmann number and the Darcy number. Further \(c_{\text{F}}\) is Forchheimer number where \(\frac{{c_{{k^{*} }} }}{{\sqrt {k^{*} } }}\) represents the non-Darcy coefficient and \(Pr, Br, \gamma , \nu\) are the Prandtl number, Brinkman number, joule heating parameter and the kinematic viscosity, respectively.

By using the non-dimensional variables defined in Eq. (6), Eq. (5) becomes

$$\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}y^{2} }} = \frac{{d_{\text{h}}^{2} }}{{\lambda_{\text{D}}^{2} \alpha }}\sinh \left( {\alpha \phi } \right),$$
(7)

where \(\alpha\) a is parameter for ionic energy and is equal to \(\frac{ze\zeta }{{K_{\text{B}} T_{\text{av}} }}\) and \(\lambda_{\text{D}}\) is the Debye length which is defined as \(\left( {ez} \right)^{ - 1} \left( {\frac{{\varepsilon \varepsilon_{0} K_{\text{B}} T_{\text{av}} }}{{2n_{0} }}} \right)^{{\frac{1}{2}}}\). Because of symmetry of potential function across the middle line of the channel, we use the following boundary conditions:

$$\begin{aligned} \frac{{{\text{d}}\phi }}{{{\text{d}}y}} = 0\quad {\text{at}}\quad y = 0, \hfill \\ \phi = 1 \quad {\text{at}}\quad y = h. \hfill \\ \end{aligned}$$
(8)

Moreover, we suppose that wall zeta potential is sufficiently small such that Debye–Hückel linearization approximation is applicable. The linear Poisson–Boltzmann equation is solved, by using the boundary conditions given in Eq. (8) to obtain the potential distribution function as:

$$\phi = \frac{\cosh (my)}{\cosh (mh)},$$
(9)

where m is known as electroosmotic parameter and is defined as \(\frac{{d_{\text{h}} }}{{\lambda_{\text{D}} }}\). Suppose that electric and magnetic field are simultaneously acting upon flowing biofluid. Due to low electric conductivity, we suppose that magnetic Reynolds number is also very low, and hence, we can neglect the induced magnetic field from the current study.

Flow analysis

Nield [46] modeled the heat transfer and flow of the fluid through the porous medium. Following Eqs. (3) and (8) of [46], the governing equations for electro-osmotically flowing fluid influenced by the peristaltic pumping in a non-Darcy porous medium become nonlinear in nature and are stated here as:

$$\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} + \frac{{\partial \tilde{v}}}{{\partial \tilde{y}}} = 0$$
(10)
$$\rho \left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{t}}} + \tilde{u}\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right) = - \frac{{\partial \tilde{p}}}{{\partial \tilde{x}}} + \mu \left( {\frac{{\partial^{2} \tilde{u}}}{{\partial \tilde{x}^{2} }} + \frac{{\partial^{2} \tilde{u}}}{{\partial \tilde{y}^{2} }}} \right) - \sigma \tilde{B}_{0}^{2} \tilde{u} + \rho E_{0} - \frac{\mu }{{k^{*} }}\tilde{u} - \frac{{\rho c_{{k^{*} }} }}{{\sqrt {k^{*} } }}\tilde{u}\sqrt {\tilde{u}^{2} + \tilde{v}^{2} ,}$$
(11)
$$\rho \left( {\frac{{\partial \tilde{v}}}{{\partial \tilde{t}}} + \tilde{u}\frac{{\partial \tilde{v}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{v}}}{{\partial \tilde{y}}}} \right) = - \frac{{\partial \tilde{p}}}{{\partial \tilde{y}}} + \mu \left( {\frac{{\partial^{2} \tilde{v}}}{{\partial \tilde{x}^{2} }} + \frac{{\partial^{2} \tilde{v}}}{{\partial \tilde{y}^{2} }}} \right) - \frac{\mu }{{k^{*} }}\tilde{v} - \frac{{\rho c_{{k^{*} }} }}{{\sqrt {k^{*} } }}\tilde{v}\sqrt {\tilde{u}^{2} + \tilde{v}^{2} ,}$$
(12)
$$\rho c_{\text{p}} \left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{t}}} + \tilde{u}\frac{{\partial \tilde{T}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{T}}}{{\partial \tilde{y}}}} \right) = K\left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{x}^{2} }} + \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }}} \right) + \Phi + \sigma \tilde{B}_{0}^{2} \tilde{u}^{2} + \sigma \tilde{E}_{0}^{2} + \frac{\mu }{{k^{*} }}\left( {\tilde{u}^{2} + \tilde{v}^{2} } \right) + \frac{{\rho c_{{k^{*} }} }}{{\sqrt {k^{*} } }}\left[ {\left( {\tilde{u}^{2} + \tilde{v}^{2} } \right)\sqrt {\tilde{u}^{2} + \tilde{v}^{2} } } \right],$$
(13)

where \(\Phi\) represents the viscous dissipation and mathematically expressed as:

$$\Phi = \mu \left[ {2\left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}}} \right)^{2} + 2\left( {\frac{{\partial \tilde{v}}}{{\partial \tilde{y}}}} \right)^{2} + \left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}} + \frac{{\partial \tilde{v}}}{{\partial \tilde{x}}}} \right)^{2} } \right].$$

Here \(\left( {\tilde{u},\tilde{v}} \right)\) are components of velocity along \(\tilde{x}\) and \(\tilde{y}\) direction, respectively. \(\rho , \tilde{p}\;{\text{and}}\; \mu\) depict the density, pressure and viscosity of fluid, respectively, and it is supposed that the electric field \(E_{0}\) is constant and is imposed in the axial direction. Magnetic field \(B_{0}\) is applied in the transverse direction of fluid flow. Moreover, \(k^{*}\) and \(c_{{k^{*} }} /\sqrt {k^{*} }\) are the permeability of porous medium and the non-Darcy coefficient. Further we supposed that it is a fully developed flow and axial velocity is dependent on \(\tilde{y}\) and \(\tilde{t}\) only.

In peristaltic flows when the fluid is forced to flow due to the sinusoidal displacements of the tract boundaries, the fluid gains some velocity as well as kinetic energy. The viscosity of the fluid takes that kinetic energy and converts it into internal or thermal energy of the fluid. Consequently, the fluid is heated up and heat transfer occurs. This phenomenon is modeled by the energy equation with dissipation effects. Dissipative heat transfer is the most important and essential feature of peristaltic flows and cannot be neglected.

Using the non-dimensional variables in Eq. (6), into Eqs. (10–13), our Eq. (10) is satisfied and Eqs. (11–13) capitulate:

$$Re\delta \left( {\frac{\partial }{\partial t} + u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)u = - \frac{\partial p}{\partial x} + \left( {\delta^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)u + \beta m^{2} \phi - c_{\text{F}} u\sqrt {u^{2} + \delta^{2} v^{2} ,}$$
(14)
$$Re\delta^{3} \left( {\frac{\partial }{\partial t} + u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)v = - \frac{\partial p}{\partial y} + \delta^{2} \left( {\delta^{2} \frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \delta^{2} \Omega^{2} v - \delta^{3} c_{\text{F}} v\sqrt {u^{2} + \delta^{2} v^{2} ,}$$
(15)
$$RePr\delta \left( {\frac{\partial \theta }{\partial t} + u\frac{\partial \theta }{\partial x} + v\frac{\partial \theta }{\partial y}} \right) = \left( {\delta^{2} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) + \gamma + Br\left[ {2\delta^{2} \left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\delta^{2} \left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial y} + \delta^{2} \frac{\partial v}{\partial x}} \right)^{2} } \right] + Br\Omega^{2} \left( {u^{2} + \delta^{2} v^{2} } \right) + c_{\text{F}} Br\left( {\left( {u^{2} + \delta^{2} v^{2} } \right)\sqrt {u^{2} + \delta^{2} v^{2} } } \right) + H_{m}^{2} Bru^{2} .$$
(16)

Implementing the approximation of long wavelength and low Reynolds number on Eqs. (14–16) as proposed by Jaffrin and Shapiro [47] and Shapiro et al. [48] (i.e., neglect the terms containing \(\delta\) and higher powers of \(\delta\)), we get the reduced equations as:

$$\frac{\partial p}{\partial x} = \frac{{\partial^{2} u}}{{\partial y^{2} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)u + \beta m^{2} \phi - c_{\text{F}} u^{2} ,$$
(17)
$$\frac{\partial p}{\partial y} = 0,$$
(18)
$$\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \gamma + Br\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Bru^{2} + c_{\text{F}} Bru^{3} = 0.$$
(19)

By using cross-differentiation, we will now eliminate pressure term from the dimensionless Eqs. (17) and (18) and can write it as a single nonlinear differential equation.

$$\frac{{\partial^{3} u}}{{\partial y^{3} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{\partial u}{\partial y} + \beta m^{2} \frac{\partial \phi }{\partial y} - c_{\text{F}} \frac{\partial }{\partial y}\left( {u^{2} } \right) = 0.$$
(20)

Now let us define \(\psi\), the stream function as \(u = \frac{\partial \psi }{\partial y}, v = - \frac{\partial \psi }{\partial x},\) satisfying the continuity Eq. (10). Equations (17), (19) and (20) can be written in terms of stream function as:

$$\frac{\partial p}{\partial x} = \frac{{\partial^{3} \psi }}{{\partial y^{3} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{\partial \psi }{\partial y} + \beta m^{2} \phi - c_{\text{F}} \left( {\frac{\partial \psi }{\partial y}} \right)^{2} ,$$
(21)
$$\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \gamma + Br\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Br\left( {\frac{\partial \psi }{\partial y}} \right)^{2} + c_{\text{F}} Br\left( {\frac{\partial \psi }{\partial y}} \right)^{3} = 0,$$
(22)
$$\frac{{\partial^{4} \psi }}{{\partial y^{4} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \beta m^{2} \frac{\partial \phi }{\partial y} - c_{\text{F}} \frac{\partial }{\partial y}\left( {\frac{\partial \psi }{\partial y}} \right)^{2} = 0,$$
(23)

where the boundary conditions in terms of \(\psi\), the stream function, are:

$$\begin{aligned} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0, \;\psi = 0,\;\frac{\partial \theta }{\partial y} = 0 \quad {\text{at}}\quad y = 0 \hfill \\ \frac{\partial \psi }{\partial y} = 0, \;\psi = F, \;\theta = 0 \quad {\text{at}}\quad y = h, \hfill \\ \end{aligned}$$
(24)

where h is the dimensionless form of wave traveling along channel. Here we have introduced two extra stream function boundary conditions in order to find the solution of differential equation of order four. The flow rate F in its non-dimensional form is defined as \(F = Q_{0} {\text{e}}^{ - At}\), while A and \(Q_{0}\) are constants. The negative or the positive flow rates are dependent on the value of constant \(Q_{0}\). If \(Q_{0} < 0\), then \(F < 0\); similarly, \(F > 0\) if \(Q_{0} > 0\). The positive flow rate indicates that the flow is in the direction of peristaltic pumping. Negative flow rate refers to the situation when flow is in the opposite direction of peristaltic motion, also known as reverse pumping. Kikuchi [49] investigated experimentally that with time there is an exponential decrease in the blood flow rate. Further it is suggested that the changes in the flow rate are independent of structural details of micro-channel.

Solution method

In order to obtain an analytical solution, we aim to solve the higher-order differential Eqs. (21–23) by using perturbation technique about \(c_{\text{F}}\) parameter.

$$\psi = \psi_{0} + c_{\text{F}} \psi_{1} + O(c_{\text{F}} )^{2}$$
(25)
$$p = p_{0} + c_{\text{F}} p_{1} + O(c_{\text{F}} )^{2}$$
(26)
$$F = F_{0} + c_{\text{F}} F_{1} + O(c_{\text{F}} )^{2}$$
(27)
$$\theta = \theta_{0} + c_{\text{F}} \theta_{1} + O(c_{\text{F}} )^{2} .$$
(28)

Zeroth-order system

$$\frac{{\partial^{4} \psi_{0} }}{{\partial y^{4} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} + \beta m^{2} \frac{\partial \phi }{\partial y} = 0,$$
(29)
$$\frac{{\partial p_{0} }}{\partial x} = \frac{{\partial^{3} \psi_{0} }}{{\partial y^{3} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{{\partial \psi_{0} }}{\partial y} + \beta m^{2} \phi = 0,$$
(30)
$$\frac{{\partial p_{0} }}{\partial y} = 0$$
(31)
$$\frac{{\partial^{2} \theta_{0} }}{{\partial y^{2} }} + \gamma + Br\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{2} + \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Br\left( {\frac{{\partial \psi_{0} }}{\partial y}} \right)^{2} = 0,$$
(32)
$$\begin{aligned} \frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} = 0, \;\psi_{0} = 0,\;\frac{{\partial \theta_{0} }}{\partial y} = 0 \quad {\text{at}} \quad y = 0 \hfill \\ \frac{{\partial \psi_{0} }}{\partial y} = 0, \;\psi_{0} = F, \;\theta_{0} = 0\quad {\text{at}} \quad y = h. \hfill \\ \end{aligned}$$
(33)

First-order system

$$\frac{{\partial^{4} \psi_{1} }}{{\partial y^{4} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} - \frac{\partial }{\partial y}\left( {\frac{{\partial \psi_{0} }}{\partial y}} \right)^{2} = 0,$$
(34)
$$\frac{{\partial p_{1} }}{\partial x} = \frac{{\partial^{3} \psi_{1} }}{{\partial y^{3} }} - \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)\frac{{\partial \psi_{1} }}{\partial y} - \left( {\frac{\partial \psi_{0} }{\partial y}} \right)^{2} = 0,$$
(35)
$$\frac{{\partial p_{1} }}{\partial y} = 0$$
(36)
$$\frac{{\partial^{2} \theta_{1} }}{{\partial y^{2} }} + 2Br\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)\left( {\frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }}} \right) + 2\left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Br\left( {\frac{{\partial \psi_{1} }}{\partial y}} \right)\left( {\frac{{\partial \psi_{0} }}{\partial y}} \right) + Br\left( {\frac{{\partial \psi_{0} }}{\partial y}} \right)^{3} = 0,$$
(37)
$$\begin{aligned} \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} = 0, \;\psi_{1} = 0,\;\frac{{\partial \theta_{1} }}{\partial y} = 0\quad {\text{at}} \quad y = 0 \hfill \\ \frac{{\partial \psi_{1} }}{\partial y} = 0, \;\psi_{1} = 0, \;\theta_{1} = 0\quad {\text{at}} \quad y = h. \hfill \\ \end{aligned}$$
(38)

Zeroth-order solution

$$\psi_{0} = {\text{e}}^{ - Ly} (m^{2} (L^{2} + m^{2} )({\text{e}}^{2Ly} C_{1} + C_{2} ) + {\text{e}}^{Ly} L^{2} L_{2} \sinh (my)) + C_{3} + yC_{4} b_{1} ,$$
(39)
$$\frac{{{\text{d}}p_{0} }}{{{\text{d}}x}} = d_{1} - C_{4} L^{2} + b_{1} L^{2} L_{2} m( - L^{2} + m^{2} ),$$
(40)
$$\frac{{{\text{d}}p_{0} }}{{{\text{d}}y}} = 0,$$
(41)
$$\begin{aligned} \theta_{0} & = E_{1} + yE_{2} + a_{4} {\text{e}}^{ - 2Ly} ( - 16Br{\text{e}}^{Ly} L^{2} (a_{5} ({\text{e}}^{2Ly} C_{1} + C_{2} ) + a_{2} C_{4} {\text{e}}^{Ly} (a_{3} )^{2} + a_{7} (a_{1} ({\text{e}}^{2Ly} C_{1} - C_{2} ) + a_{3} b_{1} ({\text{e}}^{2Ly} C_{1} + C_{2} )m^{2} ))) + \cosh (my) - a_{8} {\text{e}}^{2Ly} \cosh (2my) \\ & \quad - 2m^{2} (8Br{\text{e}}^{Ly} L^{2} (a_{9} {\text{e}}^{Ly} - m(a_{6} ( - {\text{e}}^{2Ly} C_{1} + C_{2} ) + a_{1} (2a_{2} ({\text{e}}^{2Ly} C_{1} + C_{2} )L + a_{10} ( - {\text{e}}^{2Ly} C_{1} + C_{2} ))))\sinh (my) + (a_{3} )^{2} ( - 2a_{1} Br( - {\text{e}}^{2Ly} C_{1} + C_{2} ) \\ & \quad \times (4C_{4} {\text{e}}^{Ly} + a_{3} b_{1} ({\text{e}}^{2Ly} C_{1} + C_{2} )m^{2} ) + a_{1}^{2} Br({\text{e}}^{4Ly} C_{1}^{2} + C_{2}^{2} - 4C_{1} C_{2} {\text{e}}^{2Ly} L^{2} y^{2} ) + {\text{e}}^{Ly} (a_{11} + {\text{e}}^{Ly} (a_{12} {\text{e}}^{Ly} + y^{2} a_{14} )) + a_{13} {\text{e}}^{2Ly} \sinh (2my)))). \\ \end{aligned}$$
(42)

First-order solution

$$\begin{aligned} \psi_{1} & = C_{7} + yC_{8} + b_{3} ({\text{e}}^{ - 2Ly} ({\text{e}}^{Ly} ({\text{e}}^{2Ly} C_{1} + C_{2} )b_{4} \cosh (my) - b_{5} {\text{e}}^{Ly} ( - C_{4} {\text{e}}^{Ly} (4L^{4} - 5L^{2} m^{2} + m^{4} ) + ( - {\text{e}}^{2Ly} C_{1} + C_{2} )m^{2} b_{6} )\sinh (my) + b_{7} ((L^{2} \\ & \quad - 4m^{2} )(b_{8} - b_{9} e^{4Ly} - b_{10} C_{1} {\text{e}}^{3Ly} ( - 5 + 2Ly) + C_{2} b_{10} {\text{e}}^{Ly} (5 + 2Ly) - 6{\text{e}}^{Ly} ({\text{e}}^{2Ly} C_{5} + C_{2} )) + b_{11} {\text{e}}^{2Ly} , \\ \end{aligned}$$
(43)
$$\begin{aligned} \frac{{{\text{d}}p_{1} }}{{{\text{d}}x}} & = - C_{4}^{2} - C_{8} L^{2} + 4C_{1} b_{10} b_{3} b_{7} L^{5} - 4C_{2} b_{10} b_{3} b_{7} L^{5} + 6b_{3} b_{7} L^{5} (b_{8} + b_{9} ) + 2C_{4} b_{1} L^{3} m^{2} (C_{2} - C_{1} ) + 16b_{10} b_{3} b_{7} L^{3} m^{2} (C_{2} - C_{1} ) - 24b_{3} b_{7} L^{3} m^{2} (b_{8} + b_{9} ) - b_{1}^{2} L^{4} L_{2}^{2} m^{2} + 2C_{4} b_{1} Lm^{4} (C_{1} - C_{2} ) \\ & \quad - C_{1}^{2} b_{1}^{2} L^{6} m^{4} + 2C_{1} C_{2} b_{1}^{2} L^{6} m^{4} - C_{2}^{2} b_{1}^{2} L^{6} m^{4} + 2b_{11} b_{3} b_{7} m(L^{2} - m^{2} ) + m(C_{4} ( - 2b_{1} L^{2} L_{2} + b_{3} b_{5} (L^{2} - m^{2} )^{2} (4L^{2} - m^{2} )) + (C_{2} - C_{1} )m\left( {2b_{1}^{2} L^{3} L_{2} m(L^{2} - m^{2} ) + b_{3} (3b_{4} L + b_{5} b_{6} m(2L^{2} + m^{2} ))} \right), \\ \end{aligned}$$
(44)
$$\frac{{{\text{d}}p_{1} }}{dy} = 0,$$
(45)
$$\begin{aligned} \theta_{1} & = E_{3} + E_{4} y + a_{46} ( - C_{1} {\text{e}}^{3Ly} a_{32} - 36(aA_{4}^{3} + 16C_{1} a_{2} C_{2} b_{1} b_{10} b_{3} b_{7} L^{4} m^{2} (L^{2} - m^{2} ) + C_{4} L^{2} (4C_{8} + b_{1} m^{2} a_{34} ))y^{2} \\ & \quad + 36{\text{e}}^{2Ly} ( - 3C_{1}^{2} C_{4} b_{1}^{2} m^{4} (L^{2} - m^{2} )^{2} - 4a_{17} b_{3} b_{7} L(C_{4} b_{9} + 2C_{1} b_{1} Lm^{2} (L^{2} - m^{2} )(3C_{5} + C_{1} b_{10} ( - 2 + Ly)))) \\ & \quad - 36{\text{e}}^{2Ly} ( - 3C_{2}^{2} C_{4} b_{1}^{2} m^{4} (L^{2} - m^{2} )^{2} + 4a_{17} b_{3} b_{7} L(C_{4} b_{9} - 2C_{1} b_{1} Lm^{2} (L^{2} - m^{2} )( - 3C_{5} + C_{1} b_{10} (2 + Ly)))) \\ & \quad - a_{47} {\text{e}}^{Ly} (C_{1} b_{1} ma_{26} + 4a_{2} b_{3} b_{7} L^{2} (2C_{2} b_{1} b_{9} Lm^{2} (L^{2} - m^{2} ) + C_{4} (6C_{5} + C_{1} b_{10} ( - 7 + 2Ly)))) \\ & \quad + a_{47} {\text{e}}^{ - Ly} (C_{2} b_{1} ma_{26} + 4a_{2} b_{3} b_{7} L^{2} (2C_{2} b_{1} b_{9} Lm^{2} (L^{2} - m^{2} ) + C_{4} (6C_{5} + C_{1} b_{10} ( - 7 + 2Ly)))) \\ & \quad - a_{35} \cosh (3my) + a_{38} (a_{44} - {\text{e}}^{ - 2Ly} a_{18} - {\text{e}}^{2Ly} a_{19} - a_{36} {\text{e}}^{Ly} (6a_{2} C_{5} b_{1} b_{3} b_{7} L^{2} L_{2} m(L + m) - C_{1} (C_{4} (L + m)a_{43} \\ & \quad + a_{2} b_{1} b_{10} b_{3} b_{7} L^{2} L_{2} m(m - 2L^{2} y + L(7 - 2my)))) - a_{37} {\text{e}}^{ - Ly} (6a_{2} C_{6} b_{1} b_{3} b_{7} L^{2} L_{2} m( - L + m) - C_{2} (C_{4} (L - m)a_{42} \\ & \quad + a_{2} b_{1} b_{10} b_{3} b_{7} L^{2} L_{2} m(m - 2L^{2} y + L(7 - 2my))))(\cosh (my) + \sinh (my)) + a_{38} (a_{44} - {\text{e}}^{2Ly} a_{20} - {\text{e}}^{ - 2Ly} a_{21} \\ & \quad - a_{37} {\text{e}}^{Ly} (6a_{2} C_{5} b_{1} b_{3} b_{7} L^{2} L_{2} m( - L + m) - C_{1} (C_{4} (L - m)a_{42} + a_{2} b_{1} b_{10} b_{3} b_{7} L^{2} L_{2} m(m + 2L^{2} y - L(7 + 2my)))) \\ & \quad - a_{36} {\text{e}}^{ - Ly} ( - 6a_{2} C_{6} b_{1} b_{3} b_{7} L^{2} L_{2} m(L + m) + C_{2} (C_{4} (L + m)a_{40} + a_{2} b_{1} b_{10} b_{3} b_{7} L^{2} L_{2} m(m + 2L^{2} y + L(7 + 2my)))) \\ & \quad \times ((\cosh (my) + \sinh (my))^{2} (\cosh (my) + \sinh (my)) + 9a_{22} {\text{e}}^{ - Ly} L^{2} (C_{4} e^{Ly} a_{29} + 4b_{1} m^{2} (C_{2} (L - 2m)^{2} (L + m)a_{27} \\ & \quad + C_{1} {\text{e}}^{2Ly} (L - m)(L + 2m)^{2} a_{28} ))( - \cosh (2my) + \sinh (2my)) - 9a_{22} {\text{e}}^{ - Ly} L^{2} ( - C_{4} {\text{e}}^{Ly} a_{29} - 4b_{1} m^{2} (C_{1} (L - 2m)^{2} \\ & \quad \times (L + m)a_{27} C_{2} a_{28} (L - m)(L + 2m)^{2} a_{28} ))(\cosh (2my) + \sinh (2my)))), \\ \end{aligned}$$
(46)

where \(C_{1} - C_{8} , E_{1} - E_{4} , b_{1} - b_{11}\) and \(a_{1} - a_{47}\) are constants and obtained by Mathematica software. By putting the zeroth- and first-order solution of stream function ψ, pressure gradient \({\text{d}}p/{\text{d}}x\) and temperature \(\theta\) in Eq. (27–30), we get the final first-order solution for \(\psi , {\text{d}}p/{\text{d}}x\) and \(\theta\). By using velocity distribution and temperature profile, the dimensionless temperature of bulk mean flow can be attained as:

$$\theta_{\text{bulk}} = \frac{{T_{\text{wall}} - T_{\text{bulk}} }}{{{\raise0.7ex\hbox{${qd_{\text{h}} }$} \!\mathord{\left/ {\vphantom {{qd_{\text{h}} } k}}\right.\kern-0pt} \!\lower0.7ex\hbox{$k$}}}} = \frac{{\mathop \smallint \nolimits_{0}^{h} u\theta {\text{d}}y}}{{\mathop \smallint \nolimits_{0}^{h} u{\text{d}}y}}.$$
(47)

The chief attribute that has noteworthy relevance in the current study is the dimensionless Nusselt number \(N_{\text{us}}\), which is the ratio between the heat transfers due to convection and conduction. It illustrates that how frequently the heat transfer is intensified due to motion of fluid. Observe that heat transfer always increases due to the motion of fluid therefore for convection \(N_{\text{us}} > 1\). If Nusselt number is equal to one then the fluid is sedentary and heat is transfer through conduction. Mathematically Nusselt number is expressed as:

$$N_{\text{us}} = \frac{{2qd_{\text{h}} }}{{k\left( {T_{\text{wall}} - T_{\text{bulk}} } \right)}} = \frac{2}{{\theta_{\text{bulk}} }}.$$
(48)

Entropy generation investigation

Entropy production determines the intensity of irreversibilities that take place in any thermal procedure. According to [50,51,52,53,54,55,56], the rate of local entropy production can be mathematically expressed as:

$$S_{{{\tilde{\text{G}}}}} = \frac{k}{{\tilde{T}_{\text{w}}^{2} }}\left[ {\left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{x}}}} \right)^{2} + \left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{y}}}} \right)^{2} } \right] + \frac{1}{{\tilde{T}_{\text{w}} }}\Phi + \frac{{\sigma E_{0}^{2} }}{{\tilde{T}_{\text{w}} }} + \frac{{\sigma B_{0}^{2} }}{{\tilde{T}_{\text{w}} }}\left[ {\tilde{u}^{2} + \tilde{v}^{2} } \right] + \frac{\mu }{{k^{*} \tilde{T}_{\text{w}} }}\left[ {\tilde{u}^{2} + \tilde{v}^{2} } \right] + \frac{{\rho c_{{k^{*} }} }}{{\sqrt {k^{*} } \tilde{T}_{\text{w}} }}\left[ {\left( {\tilde{u}^{2} + \tilde{v}^{2} } \right)\sqrt {\tilde{u}^{2} + \tilde{v}^{2} } } \right].$$
(49)

Here Eq. (49) depicts the dimensional form of entropy production due to thermal irreversibility, irreversibilities due to friction, joule dissipation and porous matrix. The characteristic entropy production is defined as:

$$S_{{C{\tilde{\text{G}}}}} = \frac{{k\left( {\frac{{qd_{\text{h}} }}{k}} \right)^{2} }}{{\tilde{T}_{\text{w}}^{2} d_{\text{h}}^{2} }}.$$
(50)

The non-dimensional form of entropy production can be obtained by utilizing Eqs. (49) and (50) and can be stated as:

$$N_{\text{ts}} = \frac{{S_{{{\tilde{\text{G}}}}} }}{{S_{{C{\tilde{\text{G}}}}} }} = \frac{{\tilde{T}_{\text{w}}^{2} d_{\text{h}}^{2} }}{{k\left( {\frac{{qd_{\text{h}} }}{k}} \right)^{2} }}S_{{{\tilde{\text{G}}}}} ,$$
(51)
$$N_{\text{ts}} = \left( {\frac{\partial \theta }{\partial y}} \right)^{2} + \frac{1}{\eta }\left[ {Br\left( {\frac{\partial u}{\partial y}} \right)^{2} + \gamma + \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Bru^{2} + c_{\text{F}} Bru^{3} } \right].$$
(52)

Total entropy generation in terms of stream function is expressed as:

$$N_{\text{ts}} = \left( {\frac{\partial \theta }{\partial y}} \right)^{2} + \frac{1}{\eta }\left[ {Br\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} + \gamma + \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Br\left( {\frac{\partial \psi }{\partial y}} \right)^{2} + c_{\text{F}} Br\left( {\frac{\partial \psi }{\partial y}} \right)^{3} } \right],$$
(53)

where variable \(\eta\) is described as \(\eta = \left[ {\frac{{\frac{{qd_{\text{h}} }}{k}}}{{\tilde{T}_{\text{w}} }}} \right]\). The first term in Eq. (52) denoted as:

$$N_{\text{tt}} = \left( {\frac{\partial \theta }{\partial y}} \right)^{2} ,$$
(54)

depicts the entropy production because of heat transfer. The dominance of the irreversibility system is actually significant as the entropy production number is incapable to overcome this difficulty. Bejan number (is defined as the ratio of \(N_{\text{tt}}\) (thermal irreversibility) to the \(N_{\text{ts}}\) (total entropy generation)) is used to comprehend the entropy production mechanisms. The Bejan number \(B_{\text{e}}\) for the current study can be demonstrated as:

$$B_{\text{e}} = \frac{{N_{\text{tt}} }}{{N_{\text{ts}} }} = \left[ {\frac{{\left( {\frac{\partial \theta }{\partial y}} \right)^{2} }}{{\left( {\frac{\partial \theta }{\partial y}} \right)^{2} + \frac{1}{\eta }\left[ {Br\left( {\frac{\partial u}{\partial y}} \right)^{2} + \gamma + \left( {H_{\text{m}}^{2} + \Omega^{2} } \right)Bru^{2} + c_{\text{F}} Bru^{3} } \right]}}} \right].$$
(55)

Bejan number varies between 0 and 1. From the above relation, it is clear that \(B_{\text{e}} = 0\) implies that entropy production due to the impacts of fluid friction, electric field, magnetic field and porous matrix are significant. \(B_{\text{e}} = 0.5\) signifies that thermal irreversibility is equal to the irreversibilities due to fluid friction, electric field, magnetic field and porous matrix. \(B_{\text{e}} = 1\) is the instance when thermal irreversibility is dominant.

In this paper, we have modeled all the equations by considering the viscous dissipation. However, in the absence of viscous dissipation, we cannot study the contribution of viscous irreversibility in the entropy generation. Secondly, without taking the effects of viscous dissipation, i.e., Br = 0, Bejan number is identically one.

Discussion of graphs

The results of different parameters such as \(H_{\text{m}} , m, c_{\text{F}}\) and \(\Omega\) on the flow quantities \(u, \frac{{{\text{d}}p}}{{{\text{d}}x}}, \Delta p, \theta\) and entropy production are presented in Figs. 2, 3, 4, 5, 6, 7, 8 and 9.

Fig. 2
figure 2

Axial velocity u versus y for am = 5, Ω = 1, cF = 1.0, for bHm = 1, Ω = 1, cF = 1.0, for cHm = 1, m = 5, cF = 1.0 and for dm = 5, Ω = 1, Hm = 1 and the other parameters are x = 0.5, a1, b1, dh, β = 1 and Q0 = 1

Full size image
Fig. 3
figure 3

Pressure gradient dp/dx versus x for am = 5, Ω = 1.0, cF = 0.5, for bHm = 1, Ω = 1.0, m = 5, for cHm = 1.0, m = 5, cF = 0.5 and for dcF = 1.0, Ω = 1, Hm = 1.0 and the other parameters are x = 0.5, a1 = 0.5, b1 = 0.5, dh = 1.0, β = 1.0 and Q0 = 1.0

Full size image
Fig. 4
figure 4

Pressure rise \(\Delta p\) versus \(y\) for a\(m = 5, \;\Omega = 1,\; c_{\text{F}} = 0.5\), for b\(H_{\text{m}} = 1,\;\Omega = 1, c_{\text{F}} = 0.5,\) for cHm = 1, m = 5, cF = 0.1 and for d m = 5, Ω = 1, Hm = 1 and the other parameters are x = 0.5, a1 = 0.5, b1 = 0.5, dh = 1.0, β = 1 and Q0 = 1

Full size image
Fig. 5
figure 5

Temperature distribution θ versus y for a\(m = 5, \;\Omega = 1, \;Br = 0.05, \;H_{\text{m}} = 1.0 ,\;c_{\text{F}} = 0.5\), for b\(H_{\text{m}} = 1,\;\gamma = 0.9,\; \Omega = 1, \;c_{\text{F}} = 1.0, \;Br = 0.05\) for c\(H_{\text{m}} = 1,\; m = 5, \;c_{\text{F}} = 0.5, \;\Omega = 1, \;\gamma = 1,\) for d\(m = 5, \;\Omega = 1, \;\gamma = 1, \;c_{\text{F}} = 0.5, \;Br = 0.05\) for e\(m = 5,\; H_{\text{m}} = 1, \;\gamma = 0.9, \;c_{\text{F}} = 0.5,\; Br = 0.05\) and for f\(m = 5,\; H_{\text{m}} = 1, \;\gamma = 0.9, \;\Omega = 1,\; Br = 0.05\) and the other parameters are x = 0.5, a1 = 0.5, b1 = 0.5, dh = 1.0, β = 1 and Q0 = 1

Full size image
Fig. 6
figure 6

Nusselt number \(N_{\text{us}}\) versus \(Br\) for different values of \(\gamma\) for a\(m = 5, \;H_{\text{m}} = 1, \;\Omega = 1, \;c_{\text{F}} = 0.5\), The Nusselt number \(N_{\text{us}}\) versus γ for different values of \(Br\)b\(m = 5,\; H_{\text{m}} = 1,\; \Omega = 0.1,\; c_{\text{F}} = 0.1\) and the other parameters are x = 0.5, a1 = 0.5, b1 = 0.5, dh = 1.0, β = 1, η = 0.5 and Q0 = 1

Full size image
Fig. 7
figure 7

Entropy \(N_{\text{ts}}\) against the axial distance y for a\(H_{\text{m}} = 1\) and for b\(\gamma = 1.0\) and the other parameters are \(x = 0.5, \;Br = 0.5, \;a_{1} = 0.5,\; \Omega = 0.1,\; c_{\text{F}} = 0.1,\; m = 5, \;b_{1} = 0.5, \;d_{\text{h}} = 1, \;\beta = 1,\;\eta = 0.5 \;{\text{and}}\; Q_{0} = 1\)

Full size image
Fig. 8
figure 8

Entropy \(N_{\text{tt}}\) against the axial distance y for different values of Joule heating parameter \(\gamma\) with \(H_{\text{m}} = 1.0, \;x = 0.5, \;a_{1} = 0.5,\; \Omega = 1,\; c_{\text{F}} = 0.5, \;m = 5,\; b_{1} = 0.5, \;d_{\text{h}} = 1, \;\beta = 1,\;\eta = 0.5, \;Br = 0.05 \;{\text{and}}\; Q_{0} = 1\)

Full size image
Fig. 9
figure 9

Variability of Bejan number \(B_{\text{e}}\) against the axial distance y for a\(Br = 0.05,\; \gamma = 1, \;c_{\text{F}} = 0.8,\; \Omega = 1, \;m = 5\), for b\(H_{\text{m}} = 1.0, \;Br = 0.05, \;\gamma = 1, \;c_{\text{F}} = 0.5,\; \Omega = 1\), c\(H_{\text{m}} = 1.0, \;Br = 0.05,\; m = 5,\; c_{\text{F}} = 0.5,\; \Omega = 1\), for d\(H_{\text{m}} = 1.0, \;m = 05,\; \gamma = 1,\; c_{\text{F}} = 0.5,\; \Omega = 1\), for e\(H_{\text{m}} = 1.0,\; Br = 0.05, \;\gamma = 1, \;c_{\text{F}} = 0.5, \;m = 5\) and for f\(H_{\text{m}} = 1.0,\; Br = 0.05,\; \gamma = 1, \;m = 5,\; \Omega = 1\) and the other parameters are x = 0.5, a1 = 0.5, b1 = 0.5, dh = 1, β = 1, η = 0.5 and Q0 = 1

Full size image

Flow characteristics

Velocity distribution is described in this subsection. Figure 2a–d shows the plots to explain the variations in velocity profile for various values of Hartmann number \(H_{\text{m}}\), electroosmotic parameter m, Darcy number \(\Omega^{2}\) and Forchheimer number \(c_{F}\). Figure 2a shows that as we increase the Hartmann number \(H_{\text{m}}\), the axial velocity decreases in the central area of the conduit because the magnetic field provides resistance to the fluid flow in this region. As the magnetic field and axial velocity are perpendicular to each other, there arises a Lorentz force which has tendency to slow down fluid motion. And an opposite trend is observed near the walls of the conduit. In Fig. 2b, we observe the variations in velocity distribution for various values of electroosmotic parameter m. Velocity has decelerating behavior in the central area of conduit while accelerating effects near the conduit walls. Since m is defined as ratio of height of the conduit to Debye length \(\lambda_{D}\), it implies that as the height of the conduit increases the velocity also increases. Figure 2c, d indicates the effect of Darcy number \(\Omega^{2}\) and Forchheimer number \(c_{\text{F}}\) on velocity field. By increasing Darcy number and Forchheimer number, velocity of fluid decreases in the center of the channel, while opposite trend is observed in the vicinity of the conduit walls. The Darcy number and Forchheimer number are inversely proportional to permeability of porous medium, so the greater the Darcy number and Forchheimer number, the lesser will be the permeability which provides more hindrance to the flow. In Fig. 2d, one can observe that velocity was 1.27 (approximately) when the Forchheimer number was zero, but as we increase the Forchheimer number, it starts decreasing and reduces to 1.24 (approximately), when the Forchheimer number is 0.9. Hence it makes it clear that the introduction of non-Darcy porous medium reduces the velocity of the fluid.

Pumping characteristics

It is eminent fact that the peristaltic transport is connected with the perception of mechanical pumping. Therefore, it is justifiable to investigate the performance of pumping in the view of current study. Figure 3a highlights that by increasing the values of Hartmann number \(H_{\text{m}}\), magnitude of pressure gradient also increases. It is noticed that the rise in pressure gradient is less at the wider portion of conduit, while it is highest at narrowing portion. That is, much pressure is required to go by the similar volume of fluid through the wider region of conduit, for greater values of Hartmann number \(H_{\text{m}}\). As Hartmann number \(H_{\text{m}}\) is the ratio of Lorentz force (electromagnetic force) to viscous force, higher values of the Hartmann number indicate the stronger Lorentz force; hence, more pressure is required to overcome the resistance provided by the Lorentz force. Furthermore, same trend is observed in Fig. 3b, c, due to variation in Forchheimer \(c_{\text{F}}\) and Darcy number \(\Omega^{2}\) at the wider and narrowing region of the conduit, respectively. As the Darcy number and Forchheimer number are inversely proportional to permeability of porous medium, for the higher values of Darcy number and Forchheimer number (i.e., for lesser permeability) more pressure is needed to pass through the porous medium. Figure 3b shows that magnitude of pressure is low in the absence of non-Darcy porous medium, i.e., the case when \(c_{\text{F}} = 0\), as we increase the values of Forchheimer number the magnitude of pressure gradient also increases. Figure 3d shows that magnitude of pressure gradient decreases by increasing the electroosmotic parameter m. Electroosmotic parameter m is defined as ratio of height of the conduit to Debye length \(\lambda_{\text{D}}\); it implies that the lesser the thickness of EDL, the lesser will be the pressure gradient. Hence the overall flow can be managed by regarding the appropriate electric and magnetic field.

Variations in pressure rise \(\Delta p\) w.r.t flow rate F are plotted in Fig. 4a–d for various physical parameters. These figures illustrate that pressure rise and flow rate are linearly proportional to each other. We categorize the pumping phenomena into three categories according to variation in pressure rise \(\Delta p\). The area where \(\Delta p\) is greater than zero (pressure gradient is adverse in that case) is called pumping region, which is further categorized as negative and positive pumping corresponding to \(F < 0\) and \(F > 0\). The area where \(\Delta p < 0\) is called co-pumping region. The area where \(\Delta p\) is equal to zero is called free pumping region. Figure 4a illustrates that by increasing Hartmann number \(H_{\text{m}}\), pressure rise also increases in negative pumping region. Same behavior is followed in co-pumping region. The variations in \(\Delta p\) for various values of electroosmotic parameter m are shown in Fig. 4b. It shows that by increasing values of electroosmotic parameter \(m\), pressure rise also increases in negative pumping region, while it decreases in co-pumping region. Figure 4c illustrates the effect of different values of Darcy number \(\Omega^{2}\). Figure 4c shows that same trend is observed for Darcy number \(\Omega^{2}\) as in the case of Hartmann number \(H_{\text{m}}\). Figure 4d shows that by increasing Forchheimer number \(c_{\text{F}}\), \(\Delta p\) decreases in the negative pumping region, while reverse trend is observed in co-pumping area.

Heat characteristics

The generation of joule heating effect during electroosmotic flow is the built-in property. It is caused due to resistance produced by electrolyte. Figure 5a–f shows the temperature characteristics for of various values of Joule heating parameter \(\gamma\), electroosmotic parameter m, Brinkman number \(Br\) and Hartmann number \(H_{\text{m}}\). In Fig. 5a, we can observed that temperature increases very quickly in the central area of conduit by increasing values of Joule heating parameter \(\gamma\), while near the conduit walls this effect becomes insignificant. Joule heating parameter \(\gamma\) is directly proportional to square of electric field; hence, stronger electric field results in rise in temperature. The temperature profile for various values of electroosmotic parameter m is presented in Fig. 5b, while keeping the values of other parameters constant. Temperature decreases by increasing m at the central area of conduit, while the opposite trend is observed near the walls of the conduit. The reason behind this lies in the thickness of EDL; a decrease in EDL causes a rise in temperature. Figure 5c explains that the Brinkman number has an increasing effect on temperature distribution near the central area of the conduit. The cause behind this behavior is that of Brinkman number being ratio of viscous dissipation to molecular conductivity. As Brinkman number increases, the friction between the adjacent layers of fluid increases and consequently the kinetic energy of fluid converted into thermal energy which in turn rises the fluid temperature in the middle of the channel (see Fig. 5c). This increase in energy is according to the first law of thermodynamics, i.e., one form of energy (kinetic) is converted to another form (thermal energy). According to the second law of thermodynamics, all real processes are irreversible, i.e., entropy increases during a real process. It is a well-known fact that heat is the most disorganized form of energy, and therefore, the conversion of kinetic energy into heat energy is according to the second law of thermodynamics. Variation in temperature distribution against different values of Hartmann number \(H_{\text{m}}\) is shown in Fig. 5d. It signifies that the temperature increases by increasing the Hartmann number. This rise in temperature is more significant in the central area of the micro-channel, because the Lorentz force effects are stronger in the central region of the conduit, for higher values of Hartmann number \(H_{\text{m}}\) which provides hindrance to fluid flow. The fall in kinetic energy is accompanied with the rise in thermal energy. Figure 5e, f represents the impact of Darcy number \(\Omega^{2}\) and Forchheimer number \(c_{\text{F}}\) on temperature profile. It is noticed that the existence of porous medium boost the temperature throughout the channel. The higher values of Darcy \(\Omega^{2}\) and Forchheimer number \(c_{\text{F}}\) are responsible for lesser permeability of the medium. Hence the lesser the permeability, the greater will be the temperature rise.

Figure 6a, b shows the changes in Nusselt number for various values of Joule heating parameter \(\gamma\) and Brinkman number \(Br\). It can be observed from these two figures that the Nusselt number decreases very quickly for the impact of these two parameters up to specific values, after which it decreases very slowly. Higher values of Nusselt number refer to valuable convection, whereas low Nusselt number signifies the low motion more efficient than the conduction of fluid. The outcomes reveal that Brinkman number and Joule heating parameter are considerably accountable for managing the rate of heat transfer near the walls. One of the paramount issues in experimental estimation of Nusselt number is to find out the temperature of mean fluid in the micro-fluidic apparatus. Hence it is significant while computing Nusselt number theoretically, in micro-fluidic apparatus that gradient of temperature should be very high in the micro-channel. The impact of EDL thickness and viscous dissipation should be considered while designing micro-fluidic apparatus.

Entropy production

Figures 7–9 show the plots to illustrate the impact of various physical characteristics on the entropy production. Figure 7a represents the changes in \(N_{\text{ts}}\) (total entropy production) for different values of \(\gamma\) (Joule heating parameter). Figure shows that for increasing values of \(\gamma , N_{\text{ts}}\) also increases with the conduit height, while it becomes steady in the middle region of the conduit. From the definition of \(\gamma\), it is clear that the greater the height of conduit, the greater will be the \(\gamma\) and hence the greater will be the \(N_{\text{ts}}\) near the walls of the conduit. Similarly electric field strength also has enhancing effects on \(N_{\text{ts}}\) (total entropy production), so we can control entropy production by managing the intensity of electric field. Figure 7b illustrates the impact of \(H_{\text{m}}\) Hartmann number on total entropy production \(N_{\text{ts}}\). It has accelerating impact on entropy production in the locality of conduit walls as compared to the middle region of the conduit. The Hartmann number is ratio of Lorentz force to viscous force. As in the central region of the conduit, the viscous effects are less and the flow is fully developed. Hence the magnetic field impacts are not very strong. Figure 8 demonstrates the changes in \(N_{\text{tt}}\) (thermal irreversibility) for various values of \(\gamma\) (Joule heating parameter). It is noticed that for higher values of \(\gamma\), thermal irreversibility also increases very quickly near the conduit walls. However, it shows constant behavior in the middle region of conduit. Hence from the figure, one can conclude that the impact of \(\gamma\) is strong near the conduit walls. The reason behind this is the strength of electric field, i.e., the stronger the electric field, the greater will be the thermal irreversibility. Figure 9a–f represents the impact of joule heating parameter \(\gamma\), Hartmann number \(H_{\text{m}}\), Darcy number \(\Omega^{2}\), Forchheimer number \(c_{\text{F}}\) and electroosmotic parameter m on Bejan number \(B_{\text{e}}\). From the figures, it is observed that at the middle region \((y = 0)\) of the conduit Bejan number is zero in all the cases. Here it depicts that at this region irreversibilities due to friction, joule dissipation and porous matrix are dominant. Figure 9a represents that increasing the value of Hartmann number \(H_{\text{m}}\) has enhancing impact on Bejan number \(B_{\text{e}}\) which shows that thermal irreversibility is prominent near the channel walls. Figure 9b represents the strong disturbance in the thermal irreversibility in the EDL for greater values of electroosmotic parameter m. The reason is that the lesser the thickness of EDL (electric double layer), the lesser will be the Bejan number \(B_{\text{e}}\). Figure 9c shows that for increasing values of \(\gamma\), there is a very clear increase in the Bejan number. It reflects that an increase in conduit height and stronger electric field strength are the reasons behind the rise in the Bejan number. Figure 9d depicts the variation in Bejan number w.r.t increasing values of Brinkman Br. We noticed that the changes in the Bejan number are high near the conduit walls. As Brinkman number is relation between viscous dissipation to molecular conduction, the greater the values of Br, the lesser will be the heat conduction generated by viscous dissipation and thus the greater will be the Bejan number. Figure 9e, f shows that for increasing values of Darcy number \(\Omega^{2}\) and Forchheimer number \(c_{\text{F}}\) the Bejan number increases near the walls of the conduit. The higher values of Darcy number \(\Omega^{2}\) and Forchheimer number \(c_{\text{F}}\) indicate the less permeability of porous medium which provide more hindrance to fluid flow and results in rise in Bejan number. In all cases, Bejan number \(B_{\text{e}}\) increases near wall which shows that irreversibility due to heat transfer is prominent as compared to irreversibilities due to fluid friction, Joule heating and porous medium.

Concluding remarks

The current study is concerned with analysis of entropy generation in electroosmotic flow aggravated by peristaltic pumping through non-Darcy porous medium. Assumption of long wavelength approximation and Debye–Hückel linearization are used to solve the resultant governing equations. Series solutions have been calculated with the help of regular perturbation technique. Moreover, the impact of some parameters like Hartmann number, electroosmotic parameter, Darcy number and Forchheimer number on the different profiles such as velocity, pressure gradient and pressure rise will be analyzed graphically. Following are the main results of the current study:

  • The axial velocity decreases due to the presence of non-Darcy porous medium.

  • The axial pressure gradient is increased due to the existence of non-Darcy porous medium. Hence permeability of the medium has greater effect on fluid motion.

  • Th existence of porous medium boosts the temperature throughout the channel.

  • Entropy production increases for increasing values of Darcy number \(\Omega^{2}\) and Forchheimer number \(c_{\text{F}}\), i.e., the lesser the permeability of the medium, the greater will be the entropy generation. Hence entropy generation is enhanced due to the presence of non-Darcy porous medium (see Fig. 9e, f).