Optimizing fluid dynamics: An in-depth study for nano-biomedical applications with a heat source

Abstract

A review of the existing literature on the theoretical study of peristalsis reveals that the results of a lot of investigations on peristaltic motion in a variety of complex geometries such as symmetry/asymmetric channel, tube, annulus, non-uniform channel, and curved channel are significantly improved referring to a wide range of biological, biomedical and engineering circumstances. However, as of now, the combined impacts of curvature and asymmetric displacement of walls on wall-induced fluid motion are still kept open even though the structure of the channel may also exist in the form of a curved asymmetric channel in nature. In the current investigation, a theoretical analysis of the peristaltic motion of hybrid nanofluids within a curved asymmetric channel having systematically contracting and expanding sinusoidal heated walls is examined with reference to applications of physiological conduits. Moreover, According to theory, nanofluids are mono-phase liquids in which the base fluid and the floating nanoparticles are at local temperature equilibrium, preventing slippage. The severely nonlinear governing equations of hybrid nanofluid motion powered by peristalsis are restricted to approximations based on a long wavelength and minuscule Reynolds numbers. After that, exact analytical solutions of the hybrid nanofluid were found. Finally, diagrams for the impact of relevant parameters are efficiently used to discuss and conclude the results. The outcomes demonstrate that, in comparison to the base fluid, the hybrid nanofluid has a lower temperature. The difference in heat conductivity between copper (Cu) and silver (Ag) nanoparticles has a small influence, which may be the reason for the extremely small difference in importance between nanofluid and hybrid nanofluid. These findings have several practical implications, some of which, improved drug delivery systems where the lower temperature and efficient heat transfer properties of hybrid nanofluids can be leveraged to design more effective and reliable micro-pumps for drug delivery.

Introduction

Due to its large range of usages in biological systems, biomedical engineering, and industry, the fluid flow generated and regulated by continuous wave propagation on the pliable walls of the channel referred to as peristalsis has sparked the interest of numerous scientists, researchers, and physiologists. In the physiology system, the working rule of peristaltic pumping can be notified in many biological organs, such as the motion of a nutrient bolus through the gastrointestinal tract, blood movement within the arteries and veins, urine movement from the kidneys to the urinary bladder by the urethra, the passage of ovum in woman's Fallopian tubes, transportation of embryos in the uterus, and swallowing food through the esophagus. Extracorporeal membrane oxygenation (ECMO) is a kind of artificial lung and/or heart that works based on peristaltic pumping. More recently, physicians have found during the ongoing pandemic situation due to the outbreak of Covid 19 that ECMO, according to the Extracorporeal life support organization, ECMO could save the lives of severely sick COVID-19 patients to whom ventilation is not supported. Hemodialysis machines, roller pumps, and finger pumps are also operated depending on the phenomenon of peristalsis. The day-to-day applications of the peristaltic pump are often seen in the infusion of vitamins A & D, the circulation of cell suspension in fermentation, the supply of nutrients for cultures, the aspiration of tissue culture media, the dispensing of cosmetics, handling of chemicals and transportation of fuels and lubricants, among other uses. Latham [1] Peristaltic motion had significantly improved Fung and Yih [2]. Several practical applications in biomedical engineering, physiology, medical physics, industry, modern engineering, and technology led researchers and scientists to develop so many innovative concepts and theories in the field of peristaltic motion with reference to various plain and complex geometries of flow and references therein [3,4,5].

The magnetohydrodynamics (MHD) phenomenon has garnered wide attention due to its realistic uses in frequent industrial and engineering areas, including in MRI, detection of tumors, fusion reactors, Hydrogen combustion, plasma physics, geophysics, high electric conductivity fluid pumping, optical filter manufacturing process, stops bleeding in surgeries, cell separation, MHD pumps and usage of magnetic nanoparticles as a drug-delivering agent for targeting tumor, to name a few. A study on the characteristics of the velocity of electrically conductive fluid acting upon the electromagnetic field is generally referred to as Magnetohydrodynamic (MHD) in the branch of fluid dynamics. The peristaltic movement with varying magnetic fields, particle–fluid suspension, and endoscope, has been investigated by Bhatti and Zeeshan [6]. Kumar et al.[7] reported MHD non-Newtonian fluid motion within an annulus of rotating cylinders.

In recent years, studying the momentum and mixed convection energy transfer in a channel/tube has been paid wide attention due to its fundamental and variety of uses in engineering, such as cooling and heating systems. A combination of forced and free convection to transfer heat is known as mixed (combined) convection. Energy transfer involves a critical role in industry, and biomedical engineering applications such as distillation, crystallization, food processing, dynamics of lakes, and vasodilation. Thermotherapy, which involves using heat to destroy cancerous cells, is one of the efficient therapeutic options for cancer treatment. Thermal ablation and hyperthermia are the two main types of heating being applied in thermotherapy. Hyperthermia is a form of thermotherapy in which heat is used to raise the temperature of the entire or a part of the human body from a standard temperature of 37 °C to 41–45 °C. The heating created by hyperthermia can destroy cancer cells selectively without causing damage to healthy tissue in the surrounding area. Since the heating caused by thermal ablation with an application to a high temperature (more than 45 °C) can kill cells in both the tumor and the underlying tissues, it must be used with care [8]. The consequence of heat transfer, variable, and endoscope wall-induced third-order fluid motion has been described by Nadeem et al. [9]. The influence of Dufour and Soret on rotating fluid flow within porous sheets has been discussed by Hayat et al. [10].

Researchers using heat and cooling fluids have been testing new strategies for increasing the thermal conductivity of working fluids. After several attempts, a novel technique is applied to boost the thermal efficiency of the working fluid by dispersing nano-sized solid particles in the base fluid. Nanofluids are produced by mixing one or more nanoparticles with a base fluid. As a result of exceptional physicochemical properties not found in single nanofluids and base liquids, hybrid nanofluids' thermal conductivity is higher compared to them. Nanoparticles possess various uses, including pharmaceutical, clinical diagnostic, therapeutic applications, cosmetics, energy, nutritional, environmental, and removing toxins from water. After introducing nanofluid by Choi et al. [16]. Its effect was successfully set into motion generated by peristalsis [17,18,19,20,21,22].

Even though the shape of the channel of flow geometry in reality, whether in industry or physiology, is not straight in nature and fluid induced by its rhythmically oscillatory movement of the walls having different amplitudes, phase differences, and asymmetric width, all the studies of peristaltic motion about a verity of biological and mechanical situations, as of now, have been addressed only in a flatted channel [4] and/or asymmetric channel [11,12,13,14], micro channel [15] or curved channel [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37], or tube [16, 17] and/or annulus [6, 7] or circular rotating disk [40]. The fluid motion driven due to the coupled effects of electroosmosis and peristalsis phenomenon has been analyzed numerically at length by Narla and Tripathi [34]. In a recent examination, Afridi et al. [35] have successfully studied aluminum oxide and copper nanoparticle-based nanofluid motion over an elastic curved surface under viscous dissipation, heat transfer, and entropy generation. The movement of hybrid $\left( {Cu/{\text{blood}}} \right)$ and $\left( {Cu - Ag/{\text{blood}}} \right)$ nanofluid caused by peristaltic motion inside an annulus tube having ciliated walls was presented by Saleem et al.[36]. Nadeem et al.[37] have focused on transporting $\left( {Cu - Al_{2} O_{3} /{\text{water}}} \right)$ over exponentially stretching channels and surprisingly observed that the hybrid nano liquid attains maximum heat transfer than nanofluid. The creeping flow of silica-titania/ ethylene glycol hybrid nanoliquid in a curved channel because of the metachronal waves through lubrication theory approximations has been examined by employing an explicit finite difference method for solving coupled equations by Javid et al.[38].

Based on the preceding description and a thorough literature review, it is easy to infer that no investigation has been made thus far to discuss the peristaltic movement of hybrid nanofluids in a curved asymmetric conduit. As a result, momentum and thermal transfer characteristics of a hybrid nanofluid driven by peristalsis in the appearance of the radial magnetic field in an asymmetric curved channel are explored in this investigation. By solving the equations of motion and energy, the exact analytical solutions of temperature and stream function have been obtained after adopting lubrication approaches. The proposed mathematical research aims to determine the efficacy of magneto-nanoparticle-carrying drugs in a curved asymmetric channel during peristaltic motion. Eventually, the graphs for the impact of the relevant parameters are used to explain the key findings in more depth.

Mathematical structure

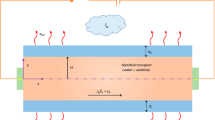
Consider an electrically conducting fluid motion of nanoparticle liquid in a curved asymmetric channel in two dimensions with a non-uniform width $d_{1} + d_{2} .$ Describe $\left( {\overline{R};\overline{S};\overline{Z}} \right)$ the coordinates in the cross, downstream, and vertical directions. The motion in a curved asymmetric channel is caused by rhythmic waves of modest amplitudes moving along the extensible walls see Fig. 1. The peristaltic waveform is depicted by

$$\begin{gathered} \overline{H}_{1}^{\prime } = - d_{2} - b_{1} \cos \left[ {\frac{2\pi }{\lambda }\left( {\overline{S} - c\overline{t}} \right) + \varphi } \right] \hfill \\ \overline{H}_{2}^{\prime } = d_{1} + a_{1} \cos \left[ {\frac{2\pi }{\lambda }\left( {\overline{S} - c\overline{t}} \right)} \right] \hfill \\ \end{gathered}$$

(1)

where $\lambda ,\;d_{1} + d_{2}$ are wavelength, channel width, $a_{1} ,b_{1}$ are wave amplitudes, the phase difference $\varphi$ varies $0 \le \varphi \le \pi ,\;\varphi = \pi$ the waves are in phase, $\varphi = 0$, the channel changes to a symmetric channel with waves out of phase, $a_{1} ,d_{1} ,b_{1} ,d_{2}$ and $\varphi$ obeys the following relation

$$b_{1}^{2} + a_{1}^{2} + 2a_{1} b_{1} \cos \varphi \le (d_{1} + d_{2} )^{2}$$

(2)

Fig. 1

Flow geometry

When a magnetic field is applied in the transverse direction, an electrically conducting liquid flow can be obtained in the form of $B = \left( {\frac{{B_{0} }}{{\tilde{\Re }}},0,0} \right).$ Here $B_{0}$ is the magnetic field strength, Ohm's law leads as follows, $J \times B = \left( {0, - \frac{{\sigma B_{0}^{\prime 2} \overline{U}}}{{\tilde{\Re }^{2} }},0} \right).$

where $\sigma$ is the electrical conductivity,$J$ is the current density.

The governing equations of the problems are

$$\frac{{R^{*} }}{{\tilde{\Re }}}\frac{\partial }{{\partial \overline{R}}}\left( {\frac{{\tilde{\Re }\overline{V}}}{{R^{*} }}} \right) + \frac{{R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{U}}}{{\partial \overline{S}}} = 0,$$

(3)

$$\begin{aligned} \rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{V}}}{{\partial \overline{t}}} + \overline{V}\frac{{\partial \overline{V}}}{{\partial \overline{R}}} + \frac{{\overline{U}R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{V}}}{{\partial \overline{S}}} - \frac{{\overline{U}^{2} }}{{\tilde{\Re }}}} \right) = - \frac{{\partial \overline{P}}}{{\partial \overline{R}}} + 2\mu_{{{\text{nf}}}} \frac{\partial }{{\partial \overline{R}}}\left( {\frac{{\partial \overline{V}}}{{\partial \overline{R}}}} \right) \\ & \quad + \frac{{R^{*} \mu_{{{\text{nf}}}} }}{{\tilde{\Re }}}\frac{\partial }{{\partial \overline{S}}}\left( {\frac{{\partial \overline{U}}}{{\partial \overline{R}}} - \frac{{\overline{U}}}{{\tilde{\Re }}} + \frac{{R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{V}}}{{\partial \overline{S}}}} \right) - \frac{{2\mu_{nf} }}{{\tilde{\Re }}}\left( {\frac{{R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{U}}}{{\partial \overline{S}}} + \frac{{\overline{V}}}{{\tilde{\Re }}}} \right) \\ \end{aligned}$$

(4)

$$\begin{aligned} \rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{U}}}{{\partial \overline{t}}} + \overline{V}\frac{{\partial \overline{U}}}{{\partial \overline{R}}} + \frac{{R^{*} \overline{U}}}{{\tilde{\Re }}}\frac{{\partial \overline{U}}}{{\partial \overline{S}}} + \frac{{\overline{V}\overline{U}}}{{\tilde{\Re }}}} \right) & \quad = - \frac{{R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{P}}}{{\partial \overline{S}}} + \mu_{{{\text{nf}}}} \frac{\partial }{{\partial \overline{R}}}\left( {\frac{{R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{V}}}{{\partial \overline{S}}} - \frac{{\overline{U}}}{{\tilde{\Re }}} + \frac{{\partial \overline{U}}}{{\partial \overline{R}}}} \right) \\ & \quad + 2\frac{{\mu_{{{\text{nf}}}} R^{*} }}{{\tilde{\Re }}}\frac{\partial }{{\partial \overline{S}}}\left( {\frac{{R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{V}}}{{\partial \overline{S}}} + \frac{{\overline{V}}}{{\tilde{\Re }}}} \right) + (\rho \alpha )_{{{\text{nf}}}} g\left( {\overline{T} - \overline{T}_{0} } \right) - \frac{{\sigma_{{{\text{nf}}}} B_{0}^{\prime 2} \overline{U}}}{{\tilde{\Re }^{2} }} \\ \end{aligned}$$

(5)

$$\left( {\rho c_{p} } \right)_{{{\text{nf}}}} \left( {\frac{{\partial \overline{T}}}{{\partial \overline{t}}} + \overline{V}\frac{{\partial \overline{T}}}{{\partial \overline{R}}} + \frac{{\overline{U}R^{*} }}{{\tilde{\Re }}}\frac{{\partial \overline{T}}}{{\partial \overline{S}}}} \right) = k_{{{\text{nf}}}} \left( {\frac{{\partial^{2} \overline{T}}}{{\partial \overline{R}^{2} }} + \left( {\frac{{R^{*} }}{{\tilde{\Re }}}} \right)^{2} \frac{{\partial^{2} \overline{T}}}{{\partial \overline{S}^{2} }}} \right) + Q_{0} ,$$

(6)

In the above equations, $\tilde{\Re } = \overline{R} + R^{*} .$

In which are the coordinates of the downstream velocity $\overline{U}$ and the cross-stream velocity $\overline{V},\;\alpha_{{{\text{nf}}}} ,\;\mu_{{{\text{nf}}}} ,\;\overline{P},\;\rho_{{{\text{nf}}}} ,\overline{T},\;(\rho c_{{\text{p}}} )_{{{\text{nf}}}} ,\;k_{{{\text{nf}}}} ,\;\sigma_{{{\text{nf}}}}$ represents the effective thermal diffusivity of the hybrid nanofluids, effective dynamic viscosity, pressure, effective density, temperature, effective heat capacitance, effective thermal conductivity, electrical conductivity, respectively which are defined as follows (Table 1).

Table 1 Water,$Cu$ and $A{g}{\prime}$ s thermo-physical properties

In Table 2, $k_{{\text{f}}} ,\;\phi ,\;\sigma_{{\text{f}}}$ are the effective thermal conductivity, the solid fractional volume, base fluid's effective electrical conductivity of the hybrid nanofluid.

Table 2 Thermophysical properties of hybrid nanofluid

In the above laboratory frame, $\left( {\overline{R},\overline{S}} \right)$ the flow in the channel is unsteady. For steady analysis, we change from fixed to wave frame $\left( {\overline{r},\overline{s}} \right)$ by

$$\tilde{v} = \overline{V},\;\overline{s} = \overline{S} - c\overline{t},\tilde{u} = \overline{U} - c,\;\overline{r} = \overline{R},$$

(7)

Equations. (3)–(6) becomes

$$\frac{{R^{*} }}{\Re }\frac{\partial }{{\partial \overline{r}}}\left( {\frac{\Re }{{R^{*} }}\tilde{v}} \right) + \frac{{R^{*} }}{\Re }\frac{{\partial \tilde{u}}}{{\partial \overline{s}}} = 0,$$

(8)

$$\begin{aligned} \rho_{{{\text{nf}}}} \left( {\frac{{R^{*} \tilde{u}}}{\Re }\frac{{\partial \tilde{v}}}{{\partial \overline{s}}} + \tilde{v}\frac{{\partial \tilde{v}}}{{\partial \overline{r}}} + \frac{{(\tilde{u} + c)^{2} }}{\Re }} \right) & \quad = - \frac{{\partial \overline{P}}}{{\partial \overline{r}}} + 2\mu_{{{\text{nf}}}} \frac{\partial }{{\partial \overline{r}}}\left( {\frac{{\partial \tilde{v}}}{{\partial \overline{r}}}} \right) \\ & \quad + \mu_{{{\text{nf}}}} \frac{{R^{*} }}{\Re }\frac{\partial }{{\partial \overline{s}}}\left( {\frac{{R^{*} }}{\Re }\frac{{\partial \tilde{v}}}{{\partial \overline{s}}} - \frac{{\tilde{u} + c}}{\Re } + \frac{{\partial \tilde{u}}}{{\partial \overline{r}}}} \right) - 2\frac{{\mu_{{{\text{nf}}}} R^{*} }}{\Re }\left( {\frac{{R^{*} }}{\Re }\frac{{\partial \tilde{u}}}{{\partial \overline{s}}} + \frac{{\tilde{v}}}{\Re }} \right), \\ \end{aligned}$$

(9)

$$\begin{aligned} \rho_{nf} \left( {\tilde{v}\frac{{\partial \tilde{u}}}{{\partial \overline{r}}} + \frac{{\tilde{u}R^{*} }}{\Re }\frac{{\partial \tilde{u}}}{{\partial \overline{s}}} + \frac{{\left( {\tilde{u} + c} \right)\tilde{v}}}{\Re }} \right) & \quad = - \frac{{R^{*} }}{\Re }\frac{{\partial \overline{P}}}{{\partial \overline{s}}} + \mu_{{{\text{nf}}}} \frac{\partial }{{\partial \overline{r}}}\left( {\frac{{R^{*} }}{\Re }\frac{{\partial \tilde{v}}}{{\partial \overline{s}}} - \frac{{\tilde{u} + c}}{\Re } + \frac{{\partial \tilde{u}}}{{\partial \overline{r}}}} \right) \\ & \quad + 2\frac{{\mu_{{{\text{nf}}}} R^{*} }}{\Re }\frac{\partial }{{\partial \overline{s}}}\left( {\frac{{R^{*} }}{\Re }\frac{{\partial \tilde{v}}}{{\partial \overline{s}}} + \frac{{\tilde{v}}}{\Re }} \right) + (\rho \alpha )_{{{\text{nf}}}} g\left( {\overline{T} - \overline{T}_{0} } \right) - \frac{{\sigma_{{{\text{nf}}}} B_{0}^{\prime 2} \left( {\tilde{u} + c} \right)}}{{\Re^{2} }}, \\ \end{aligned}$$

(10)

$$\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} \left( {\tilde{v}\frac{{\partial \overline{T}}}{{\partial \overline{r}}} + \frac{{\tilde{u}R^{*} }}{\Re }\frac{{\partial \overline{T}}}{\partial s}} \right) = k_{{{\text{nf}}}} \left( {\frac{{\partial^{2} \overline{T}}}{{\partial \overline{r}^{2} }} + \left( {\frac{{R^{*} }}{\Re }} \right)^{2} \frac{{\partial^{2} \overline{T}}}{{\partial \overline{s}^{2} }}} \right) + Q_{0} ,$$

(11)

Here $\Re = \overline{r} + R^{*} .$

The non-dimensional quantities are

$$\begin{gathered} v = \frac{{\tilde{v}}}{\delta c},\;s = \frac{{\overline{s}}}{\lambda },P = \frac{{d_{1}^{2} }}{{\mu_{{\text{f}}} \lambda c}}\overline{p},\;\delta = \frac{{d_{1} }}{\lambda },\;k = \frac{{R^{*} }}{{d_{1} }},\;\theta = \frac{{\overline{T} - \overline{T}_{0} }}{{\overline{T}_{1} - \overline{T}_{0} }},\;\beta = \frac{{Q_{0} d_{1}^{2} }}{{k_{{\text{f}}} \left( {\overline{T}_{1} - \overline{T}_{0} } \right)}},\;r = \frac{{\overline{r}}}{{d_{1} }}, \hfill \\ {\text{Gr}} = \frac{{\rho_{f} g\alpha_{f} d_{1}^{2} \left( {\overline{T}_{1} - \overline{T}_{0} } \right)}}{{c\mu_{f} }},\;a = \frac{{a_{1} }}{{d_{1} }},h_{1} = \frac{{\overline{H}_{1}^{\prime } }}{{d_{1} }},h_{2} = \frac{{\overline{H}_{2}^{\prime } }}{{d_{1} }},\;H^{2} = \frac{{\sigma_{{\text{f}}} B_{0}^{\prime 2} }}{{\mu_{{\text{f}}} }},d = \frac{{d_{2} }}{{d_{1} }}, \hfill \\ {\text{Re}} = \frac{{\rho_{{\text{f}}} cd_{1} }}{{\mu_{{\text{f}}} }},\;b = \frac{{b_{1} }}{{d_{1} }},u = \frac{{\tilde{u}}}{c}, \hfill \\ \end{gathered}$$

(12)

where ${\text{Gr}},\;\beta ,\;{\text{Re}} ,\,H$ are the Grashof number, heat source parameter, Reynolds number, and Hartmann number. $T_{0} ,\;T_{1}$ with conditions of $T_{1} > T_{0}$ is the temperature of the lower and upper walls,

The values $A_{1} \;{\text{to}}\;A_{5}$ for the conventional hybrid nanofluid as

$$A_{1} = \left[ {\left( {1 - \phi_{{_{{{\text{Ag}}}} }} - \phi_{{_{{{\text{cu}}}} }} } \right) + \frac{{\phi_{{{\text{Ag}}}} \rho_{{{\text{Ag}}}} }}{{\rho_{{\text{f}}} }} + \frac{{\phi_{{_{{{\text{cu}}}} }} \rho_{{{\text{cu}}}} }}{{\rho_{{\text{f}}} }}} \right],\;A_{2} = \frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{{\text{f}}} }},\;A_{3} = \left[ {\left( {1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{cu}}}} } \right) + \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{Ag}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }} + \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{cu}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}} \right],\;A_{4} = \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }},\;A_{5} = \frac{{\left( {\rho \alpha } \right)_{{{\text{nf}}}} }}{{\left( {\rho \alpha } \right)_{{\text{f}}} }}.$$

(13)

Using the aforementioned dimensionless quantities in Eqs. (8)–(11) and applying lengthy wavelength and very small Reynolds number approximation, Eq. (8) vanishes and Eqs. (9)–(11) we have the following equations,

$$\frac{\partial p}{{\partial r}} = 0,$$

(14)

$$- \frac{k}{k + r}\frac{\partial p}{{\partial s}} + \frac{1}{{(1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{Cu}}}} )^{2.5} }}\frac{\partial }{\partial r}\left( {\frac{\partial u}{{\partial r}} - \frac{u + 1}{{r + k}}} \right) + A_{5} G_{{\text{r}}} \theta - A_{2} H^{2} \frac{{\left( {u + 1} \right)}}{{(r + k)^{2} }} = 0,$$

(15)

$$A_{4} \frac{{\partial^{2} \theta }}{{\partial r^{2} }} + \beta = 0,$$

(16)

Equation (15) transforms to

$$\frac{\partial p}{{\partial s}} = \frac{r + k}{{k(1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{Cu}}}} )^{2.5} }}\frac{\partial }{\partial r}\left( {\frac{\partial u}{{\partial r}} - \frac{1 + u}{{k + r}}} \right) + \left( {\frac{k + r}{k}} \right)A_{5} G_{{\text{r}}} \theta - A_{2} \frac{{H^{2} }}{k}\left( {\frac{u + 1}{{k + r}}} \right)$$

(17)

To remove pressure, differentiate Eq. (17) with respect to $r$ and with the help of Eq. (14) we get

$$\frac{\partial }{\partial r}\left( {\frac{k + r}{{k(1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{Cu}}}} )^{2.5} }}\frac{\partial }{\partial r}\left( {\frac{\partial u}{{\partial r}} - \frac{u + 1}{{k + r}}} \right)} \right) + \frac{{A_{5} }}{k}G_{{\text{r}}} \theta + \left( {\frac{k + r}{k}} \right)A_{5} G_{{\text{r}}} \frac{\partial \theta }{{\partial r}} - A_{2} \frac{{H^{2} }}{k}\frac{\partial }{\partial r}\left( {\frac{u + 1}{{k + r}}} \right) = 0,$$

(18)

Now, introducing the following stream functions are

$$v = \frac{{k\psi_{{\text{s}}} }}{k + r},u = - \psi_{{\text{r}}}$$

(19)

Equation (18) in terms of Eq. (19) as follows

$$\frac{\partial }{\partial r}\left( {\frac{k + r}{{k(1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{Cu}}}} )^{2.5} }}\frac{\partial }{\partial r}\left( { - \psi_{{{\text{rr}}}} - \frac{{1 - \psi_{{\text{r}}} }}{k + r}} \right)} \right) + \frac{{A_{5} }}{k}G_{{\text{r}}} \theta + \left( {\frac{k + r}{k}} \right)A_{5} G_{{\text{r}}} \frac{\partial \theta }{{\partial r}} - A_{2} \frac{{H^{2} }}{k}\frac{\partial }{\partial r}\left( {\frac{{1 - \psi_{{\text{r}}} }}{k + r}} \right) = 0,$$

(20)

$$\frac{{\partial^{2} \theta }}{{\partial r^{2} }} + N_{1} \beta = 0,$$

(21)

Mean volume flow rate

In the fixed frame, the volume flow rate $\overline{Q}\left( {S,t} \right)$ is determined by

$$\overline{Q} = \left( {S,t} \right) = \mathop \int \limits_{{H_{1}{\prime} \left( {X,t} \right)}}^{{H_{2}^{\prime } \left( {X,t} \right)}} U\left( {S,\overline{R},t} \right)\text{d}\overline{R}$$

(22)

In the waveform, the volume flow rate is equivalently represented as

$$\overline{q}\left( {x,t} \right) = \mathop \int \limits_{{H_{1}^{\prime } }}^{{H_{2}^{\prime } }} \tilde{u}\left( {\overline{s},\overline{r}} \right)\text{d}\overline{r}$$

(23)

Applying Eq. (7) to Eq. (22) and use of Eq. (23) to get a relation between unsteady and steady volume flow rates Eq. (23), one can obtain,

$$\overline{Q}\left( {S,t} \right) = \overline{q} + cH_{2}^{\prime } - cH_{1}^{\prime }$$

(24)

Over a period, $T,$ the time-average flow $X$ is

$$\overline{Q} = \frac{1}{T}\mathop \int \limits_{0}^{T} Q\text{d}t.$$

(25)

Applying Eq. (25) into Eq. (23) and integrating,

$$\overline{Q} = cd_{1} + cd_{2} + q.$$

(26)

The dimensionless mean volume flow rate $\Theta$ and $F$ are defined as

$$\Theta = \frac{{\overline{Q}}}{{cd_{1} }},\;F = \frac{q}{{cd_{1} }},$$

(27)

Equation (26) implies that

$$\Theta = d + F +$$

(28)

in which

$$F = \mathop \int \limits_{{h_{1} }}^{{h_{2} }} \frac{\partial \psi }{{\partial r}}dr = \psi \left( {h_{2} } \right) - \psi \left( {h_{1} } \right)$$

(29)

By choosing $\psi \left( {h_{1} } \right) = - \frac{F}{2}$_, one can obtain $\psi \left( {h_{2} } \right) = \frac{F}{2}.$

The boundary conditions are

$$\psi = - \frac{F}{2},\;\frac{\partial \psi }{{\partial r}} = - 1,\;\theta = 0,\,\sigma = 0,\;{\text{at}}\;r = h_{1} = - d - b\sin (2\pi s + \varphi )$$

(30)

$$\psi = \frac{F}{2},\;\frac{\partial \psi }{{\partial r}} = - 1,\;\theta = 1,\;\sigma = 1\;{\text{at}}\; = h_{2} = 1 + a\sin 2\pi s$$

(31)

The criterion for preventing a collision between two walls of an asymmetric curved channel is given as $b^{2} + a^{2} + 2ab\cos \varphi \le (1 + d)^{2}$.

Result of the problem

The result of Eqs. (19) and (20) with the help of Eqs. (30) and (31), we get

$$\psi \left( {r,s} \right) = \frac{{c_{1} \left( {r + k} \right)}}{{2 - \sqrt { - k_{1} } }}^{{2 - \sqrt { - k_{1} } }} + \frac{{c_{2} \left( {k + r} \right)}}{{2 + \sqrt { - k_{1} } }}^{{2 + \sqrt { - k_{12} } }} + c_{3} \left( {kr + \frac{r}{2}^{2} } \right) + c_{4} + j_{1} r + j_{2} r^{2} + j_{3} r^{3} + j_{4} r^{4} + j_{5} r^{5} ,$$

(32)

$$\theta \left( {r,s} \right) = \frac{{h_{1} }}{{h_{1} - h_{2} }} - \frac{{N_{1} \beta }}{2}h_{1} h_{2} + \left[ {\frac{1}{{h_{2} - h_{1} }} + \frac{{N_{1} \beta }}{2}\left( {h_{1} + h_{2} } \right)} \right]r - \frac{{N_{1} \beta r^{2} }}{2}$$

(33)

The appendix gives all the constants appearing in Eqs. (31) and (32).

The pressure gradient is given by

$$\frac{\partial p}{{\partial s}} = \frac{1}{k}\left[ {\begin{array}{*{20}l} {k^{{\sqrt { - k_{1} } }} - j_{1} k^{{\sqrt { - k_{1} } }} + 2j_{2} k^{{1 + \sqrt { - k_{1} } }} - 6j_{3} k^{{2 + \sqrt { - k_{1} } }} + c_{1} kk_{1} + \frac{{c_{2} k_{1} k^{{1 + 2\sqrt { - k_{1} } }} }}{{(1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{cu}}}} )^{2.5} k^{{2 + \sqrt { - k_{1} } }} }}} \\ { + \frac{{A_{2} H^{2} \left( {j_{1} + c_{2} k^{{1 + \sqrt { - k_{1} } }} + c_{3} k + c_{1} k^{{1 - \sqrt { - k_{1} } }} } \right)}}{k} + \frac{{A_{5} Gr\left( {\beta N_{1} h_{2}^{2} - \beta N_{1} h_{1} h_{2} + 2} \right)}}{{3\left( {h_{1} - h_{2} } \right)}}} \\ \end{array} } \right]$$

(34)

In non-dimensional form, the pressure rise over a single wavelength is as follows.

$$\Delta p_{\lambda } = \mathop \int \limits_{0}^{2\pi } \frac{\partial p}{{\partial s}}\text{d}s$$

(35)

The physical interpretation of numerical results

The results of axial velocity distribution, pumping characteristics, temperature profiles, and the trapping phenomenon of MHD peristaltic movement of hybrid nano liquids in a curved asymmetric conduit under the influence of curvature parameter $\left( k \right)$, magnetic parameter $\left( H \right)$, Grashof number $\left( {{\text{Gr}}} \right)$, heat sink/source parameter $\left( \beta \right)$, the phase difference ($\varphi$) and upper wall amplitude ($a$) are presented in this section.

Figure 2a–d are prepared to note down the influences of $k,H,Gr$ and $\beta$ with constant values of $d = 1.1,a = 0.4,\varphi = \pi /6,\;b = 0.3,x = 0.1,$ on the axial velocity across the radial direction of the curved asymmetric channel $h_{1} \le r \le h_{2} .$ The salient feature of $k$ on the hybrid nanofluid velocity is presented in Fig. 2a. Significantly huge $\left( {k \to \infty } \right)$ and small $\left( {{\text{Near to}}\;k = 2} \right)$ values of $k$ represent straight and curved channels, respectively. From the figure, one can note that the amplitude of the velocity profile of hybrid nanofluids is moved downward when the centerline of a straight channel $k$ is boosted. Figure 2b depicts to discuss the behaviour of $H$ on the velocity field. It is concluded that owing to a magnetic field strengthening, the velocity profile becomes flatter in the channel's center as anticipated. A magnetic field introduced transversely to the flow direction of an electrically conducting fluid generates a resistive force known as the Lorentz force, which yields flow resistance of the fluid particle. The impact of ${\text{Gr}}$ (Proposition of buoyancy force to the viscous force) on the axial velocity is computed in Fig. 2c. It demonstrates that when ${\text{Gr}}$ grows the hybrid nanofluid, velocity improves in the upper part of the channel. This is because the fluid's internal resistance automatically decreases when viscosity lessens. On the other hand, the opposite behavior can be seen in the remaining part of the channel. The captured result of Fig. 2d indicates that the $\beta$ acts similarly to the Grashof number on the hybrid nanofluids velocity profile.

Fig. 2

Velocity profile for a Curvature parameter b Hartmann number c Grashof number d heat source parameter

To visualize the impact of sequential coordinated expansion or contraction wave of the channel walls that propels fluid forward from lower pressure towards high pressure along wave velocity, the diagram of the pressure rise $\left( {\Delta P_{\lambda } } \right)$ against the mean volume flow rate $\left( {\Theta :{\text{positive}}\;{\text{pumping}}} \right)$ are depicted in Fig. 3a–d. This phenomenon naturally arises in various physiological conduits. These graphs demonstrate that the pressure rise/drop and volume flow rate are inversely connected. We have plotted Fig. 3a to see the upshot of the curvature parameter on $\Delta P_{\lambda }$ against $\Theta$, wherein all other parameters are kept fixed. The figure shows that the $\Delta P_{\lambda }$ is increases in $- 0.2 \le \Theta \le - 0.054$ and diminishes $\Theta \in \left( { - 0.054,1} \right).$ Also, peristaltic pumping $(\triangle P_{\lambda } > 0,\Theta > 0)$, co-pumping $\left( {\triangle P_{\lambda } < 0,\Theta } > 0 \right)$ and free pumping $\left( {\triangle P_{\lambda } = 0} \right)$. are slowed down as the curvature of the asymmetric channel rises. Furthermore, to maintain no pumping $\left( {\Theta = 0} \right)$_, the straight channel provides resistance to adverse pressure gradients $(\triangle P_{\lambda } > 0).$ The effect of ${\text{Gr}},\;\beta \;{\text{and}}\;\varphi \;{\text{on}}\;\Delta P_{\lambda }$ is demonstrated in Fig. 3b–d. It was evident from these figures that the regions of peristaltic, co-pumping, backward, and free pumps are hindered by increasing ${\text{Gr}},\;\beta \;{\text{and}}\;\varphi .$

Fig. 3

Pressure rise against $\Theta$ for a $k$ b ${\text{Gr}}$ c $\beta$ d $\varphi$

Hybrid nanofluid/ nanofluid are mainly used to enhance heat transfer. Therefore, the heat transfer analysis of nanofluids for the proposed geometric configuration is examined through Fig. 4a–d with various pertinent parameters. The temperature curves are nearly parabolic in form, and a rise in the temperature with increasing phase difference values is seen in Fig. 4a. In heat transfer management, heat generation or absorption effects are critical in a wide range of demands and uses in the industry. The consequence of $\beta$on the temperature of the hybrid nanofluid is captured in Fig. 4b . It is evident from this plot that the hybrid nano liquids temperature is improved when $\beta$ boosted. The effect of the amplitude of $a$ on the temperature is portrayed in Fig. 4c. From this figure, the temperature of the hybrid nanofluid is enhanced as $a$ improved. Figure 4d is drawn for the temperature profile to visualize nanoparticles' role in enhancing the base fluid's thermal conductivity. It is apparent from the plotted graph that the temperature of the hybrid nanofluid is lower when comparing the nanofluid to the base fluid. However, the significance between nanofluid and hybrid nanofluid is very minimal, which may be because the variation in thermal conductivity between copper $\left( {Cu} \right)$ and silver $\left( {Ag} \right)$. nanoparticles have a negligible effect comparatively.

Fig. 4

Temperature profile for a $\beta$ b $\varphi$ c $a$ d comparison of base fluid, nanofluid and hybrid nanofluid

The term "trapping" refers to the flow condition in which the boluses formed by the closed streamlines on either side of the center of the channel entirely block the fluid flow in the channel middle part, and a trapped bolus travels alongside the peristaltic wave velocity as a whole. Magnetic nanoparticles are employed as drug carriers for targeted therapeutic delivery and have prompted research into peristaltic flow in a magnetic field. Trapping is perhaps more essential since the flow creates an internally circulating bolus that pushes forward along with peristaltic wave speed for the safe transportation of medical substances to a particular location [39]. In Fig. 5a–d, we have captured the impact of k on the trapping for $\beta = 0.5,\;H = 2,\;{\text{Gr}} = 1.0\;a = 0.5,\;b = 0.4,\;d = 1.1,\;\varphi = \pi /18$. Indeed, the small value of k corresponds to a curved channel, and when $\left( {k \to \infty } \right)$. The curvature of the channel vanishes, and it becomes a flattened channel. It is fascinating from the figure that the almost elliptical shape of the trapped boluses is formed in both halves of a curved asymmetric channel.

Fig. 5

Streamlines for $k = 2,3,4,\infty \;{\text{with}}\;\beta = 0.5,\;H = 2,\;{\text{Gr}} = 1a = 0.5,\,b = 0.4,\;d = 1.1,\;\varphi = \frac{\pi }{18}$

Further, the size and volume of boluses diminish in the lower part of the channel when the channel takes on a more curved shape. Meanwhile, the situation is fully reversed at the top of the wall. The magnetic parameter $\left( H \right)$ effect on the streamlines for the fixed values and other appearing parameters is $\beta = 0.1,\;k = 3,\;a = 0.4,\;b = 0.3,\;{\text{Gr}} = 0.5,\;d = 1.1,\,\varphi = \pi /18$ is illustrated in Fig. 6a–d. It is clear that by increasing the Hartmann number $\left( H \right)$ from (a) to (d), the size and number of trapping bolus gradually decline at the lower part of the curved asymmetric channel.

Fig. 6

Streamlines for $H \to 0,\;H = 2,\;H = 4,\;H = 6\;{\text{with}}\;\beta = 0.1,\;k = 3,\;{\text{Gr}} = 0.5,\;a = 0.4,\;b = 0.3,\;d = 1.1,\;\varphi = \frac{\pi }{18}$

In contrast, trapping behavior is completely reversed in the opposite portion of the channel. The effect of the phase difference parameter $\left( \varphi \right)$ on the streamlines is examined with the help of Fig. 7a–d by fixing $\beta = 0.1,\;k = 3,\;{\text{Gr}} = 0.5,\;H = 2,\;a = 0.4,\;b = 0.3,\;d = 1.1$. It is inferred that with an increasing phase difference between two channel walls, the bolus passes towards the left and shrinks in the sizes, and there is no trapping when the phase difference attains its maximum $\varphi = \pi .$

Fig. 7

Streamlines for $\varphi = 0,\frac{\pi }{6},\frac{\pi }{3},\pi \;{\text{with}}\;\beta = 0.1,\;k = 3,\,{\text{Gr}} = 0.5,\;H = 2a = 0.4,\;b = 0.3,\;d = 1.1$

Concluding remarks

In this investigation, the sinusoidal oscillatory movement with varying amplitudes and phase differences of the walls of a curved channel has been used to develop a hybrid nano liquids novel mathematical model for the pressure-driven flow. The governing equations are embedded with a radial magnetic field and heat sink/sour effects. Exact analytical solutions for velocity and temperature have been found by employing the long wavelength assumption. For validation, the results of this analysis have also been related to the analytical results of Mishra and Rao [11] at $k \to \infty ,H \to 0,\;Gr = 0$ and found to be in fair agreement see Fig. 8. The following are a few of the most important findings from this study:

• The amplitude of the walls, phase difference, and channel width all play important roles in determining the flow characteristics in the curved channel.

• Increasing the Grashof number (Gr) generally accelerates the axial velocity in the upper region of the curved asymmetric channel, where things are entirely different in the rest of the channel.

• The amplitude of the velocity of the hybrid nanofluids is moved downward when the middle of a straight channel goes downward when the curvature of the channel is boosted.

• The regions of peristaltic, co-pumping, backward and free pumps are hindered by increasing Gr and $\beta$.

• The temperature curves are nearly parabolic in form, and an enhancement in the temperature is found with an enhancement of the phase difference.

• The number and shape of trapped bolus gradually decline at the lower part of the curved asymmetric channel with the growth of Hartmann number, whereas trapping behaviour is completely reversed in the opposite portion of the channel.

Fig. 8

Validation result

Appendix

$\begin{gathered} N_{1} = \frac{1}{{A_{4} }},\;k_{1} = - A_{2} H^{2} (1 - \phi_{{{\text{Ag}}}} - \phi_{{{\text{Cu}}}} )^{2.5} ,k_{2} = - A_{5} Gr(1 - \phi_{{{\text{Ag}}}} - \phi \, )^{2.5} ,l_{1} = 2 - k_{1} ,\;l_{2} = 2 + k_{1} , \hfill \\ l_{3} = \frac{{h_{1} }}{{h_{1} - h_{2} }} - \frac{{N_{1} \beta }}{2}h_{1} h_{2} ,\;l_{4} = \frac{1}{{h_{2} - h_{1} }} + \frac{{N_{1} \beta }}{2}\left( {h_{1} + h_{2} } \right)j_{5} = \frac{{N_{1} \beta k_{2} }}{{10\left( {9 + k_{1} } \right)}},\;j_{4} = \frac{{\left( { - N_{1} \beta k\left( { - 1 + k_{1} } \right) + c_{2} \left( {9 + k_{1} } \right)} \right)k_{2} }}{{4\left( {4 + k_{1} } \right)\left( {9 + k_{1} } \right)}}, \hfill \\ j_{3} = \frac{{\left( {2l_{3} \left( {36 + 13k_{1} + k_{1}^{2} } \right) - k\left( {18l_{4} \left( {9 + k_{1} } \right) + A_{1} \beta k\left( {6 - 17k_{1} + k_{1}^{2} } \right)} \right)} \right)k_{2} }}{{6\left( {9 + k_{1} } \right)\left( {4 + 5k_{1} + k_{1}^{2} } \right)}}, \hfill \\ j_{2} = \frac{{k\left( {l_{3} \left( { - 36 + 23k_{1} + l_{2} k_{1}^{2} + k_{1}^{3} } \right) + k\left( {A_{1} \beta kk_{1} \left( { - 17 + 7k_{1} } \right) - l_{4} \left( { - 72 + 91k_{1} + 20k_{1}^{2} + k_{1}^{3} } \right)} \right)} \right)}}{{2k_{1} \left( {9 + k_{1} } \right)\left( {4 + 5k_{1} + k_{1}^{2} } \right)}} \hfill \\ j_{1} = \frac{{14k_{1}^{3} + k_{1}^{4} + 36k^{2} \left( { - l_{3} + 2l_{4} k} \right)k_{2} + k_{1}^{2} \left( {49 - l_{3} k^{2} k_{2} - A_{1} \beta k^{2} k_{2} } \right) - k_{1} \left( { - 36 + 13l_{3} k^{2} k_{2} + l_{4} k^{3} k_{2} + l_{1} A_{1} \beta k} \right)}}{{k_{1} \left( {9 + k_{1} } \right)\left( {4 + 5k_{1} + k_{1}^{2} } \right)}} \hfill \\ e_{1} = \left( {h_{1} + k} \right)^{{l_{2} - 1}} - \left( {h_{2} + k} \right)^{{l_{2} - 1}} ,\;e_{2} = \left( {h_{1} + k} \right)^{{l_{1} - 1}} - \left( {h_{2} + k} \right)^{{l_{1} - 1}} ,\;e_{3} = h_{1} - h_{2} , \hfill \\ e_{7} = F - \left( {h_{2} - h_{1} } \right)j_{1} ,e_{8} = \left( {h_{1} + k} \right)e_{4} - e_{6} \left( {h_{1} + k} \right)^{{l_{2} - 1}} ,e_{9} = \left( {h_{1} + k} \right)e_{5} - e_{6} \left( {h_{1} + k} \right)^{{l_{1} - 1}} , \hfill \\ e_{10} = \left( {h_{1} + k} \right)e_{7} + e_{6} \left( {1 + j_{1} } \right),e_{11} = e_{1} e_{6} - e_{3} e_{4} ,e_{12} = e_{2} e_{6} - e_{3} e_{5} ,e_{13} = - e_{3} e_{7} , \hfill \\ c_{1} = \frac{{e_{9} e_{13} - e_{10} e_{12} }}{{\left( {e_{9} e_{11} - e_{8} e_{12} } \right)l_{2} }},c_{2} = \frac{{e_{10} - c_{1} e_{8} }}{{l_{1} e_{9} }},c_{3} = - \frac{{c_{1} e_{1} + c_{2} e_{2} }}{{2e_{3} }}, \hfill \\ c_{4} = \frac{F}{2} - \left[ {j_{1} h_{2} + c_{1} \frac{{\left( {h_{2} + k} \right)^{{l_{2} }} }}{{l_{2} }} + c_{2} \frac{{\left( {h_{2} + k} \right)^{{l_{1} }} }}{{l_{1} }} + c_{3} \left( {k + h_{2} + \frac{{h_{2}^{2} }}{2}} \right)} \right] \hfill \\ \end{gathered}$