1 Introduction

The thermally coupled incompressible magnetohydrodynamic (MHD) model, which describes the hydrodynamical behaviors of a conductive fluid in an electromagnetic field when buoyancy effects cannot be neglected in the momentum equation, has many vital applications in the metal hardening, casting, melting, magnetic propulsion devices, design of electromagnetic pumps, nuclear reactor technology, semi-conductor manufacture, etc. The governing equations of this model are formed by coupling the incompressible Navier-Stokes equation in fluid mechanics, the Maxwell equation in electromagnetism and the heat equation through the Boussinesq approximation.

Let \(\Omega \subset {\mathbb {R}}^d(d=2,3)\) be a bounded region and final time \(T>0\), find fluid velocity field \({\textbf{u}}:(0,T]\times \Omega \rightarrow {\mathbb {R}}^d,\) the pressure \( p:(0,T]\times \Omega \rightarrow {\mathbb {R}}\), the magnetic field \({\textbf{H}}:(0,T]\times \Omega \rightarrow {\mathbb {R}}^d\) and temperature \(\theta :(0,T]\times \Omega \rightarrow {\mathbb {R}}\) satisfying [27]

$$\begin{aligned} \begin{aligned} {\textbf{u}}_{t}-R_e^{-1}\Delta {\textbf{u}}+\nabla {p}-\beta \theta {\textbf{j}}&={\textbf{f}} -({\textbf{u}}\cdot \nabla ){\textbf{u}}+s~\text {curl}{\textbf{H}}\times {\textbf{H}},&\textrm{in}~ \Omega \times (0,T],\\ \textrm{div}{\textbf{u}}&=0,&\textrm{in}~ \Omega \times (0,T],\\ {\textbf{H}}_{t}+R_m^{-1}s~\text {curl} \text {curl}{\textbf{H}}&=\textrm{curl}{\textbf{g}}+s~\text {curl}({\textbf{u}}\times {\textbf{H}}),&\textrm{in}~ \Omega \times (0,T],\\ \textrm{div}{\textbf{H}}&=0,&\textrm{in}~ \Omega \times (0,T],\\ \theta _{t}-\kappa \Delta \theta&=\omega -({\textbf{u}}\cdot \nabla )\theta ,&\textrm{in}~ \Omega \times (0,T],\\ \end{aligned} \end{aligned}$$
(1)

where \(R_e\) denotes the fluid Reynolds number, \(R_m\) the magnetic Reynolds number, s the coupling number, \(\kappa \) the thermal conductivity, and \(\beta \) is the thermal expansion coefficient. Besides, the given function \({\textbf{f}}\) is the external force, \({\textbf{g}}\) is the known applied current with \(\textrm{div}{\textbf{g}}=0\), \(\omega \) is the heat source and \({\textbf{j}}\) denotes a unit vector in the direction opposite to the gravitational for \({\textbf{u}}\). The system is equipped with the following initial values and boundary conditions [23]

$$\begin{aligned}&{\textbf{u}}({\textbf{x}},0)={\textbf{u}}_{0}({\textbf{x}}),\ \; {\textbf{H}}({\textbf{x}},0)={\textbf{H}}_{0}({\textbf{x}}),\ \; \theta ({\textbf{x}},0)=\theta _{0}({\textbf{x}})\ \ \quad \text {in}\;\Omega , \end{aligned}$$
(2)
$$\begin{aligned}&{\textbf{u}}|_{S_{T}}=0,\ \;({\textbf{H}}\cdot {\textbf{n}})|_{S_{T}}=0,\;({\textbf{n}}\times \text {curl} {\textbf{H}})|_{S_{T}}=0,\ \ \theta |_{S_{T}}=0, \end{aligned}$$
(3)

with \(\textrm{div}{\textbf{u}}_0=0\) and \( \textrm{div}{\textbf{H}}_0=0\). Here \(S_{T}:=\partial \Omega \times [0,T]\), and \({\textbf{n}}\) represents the unit outer normal to the boundary \(\partial \Omega \).

For the steady-state thermally coupled incompressible MHD equations, Meir has proven the existence and uniqueness of solutions in [27, 28], in which the dissipative heating and Joule heating are disregarded. Bermúdez et al. [10] have studied the existence and uniqueness of weak solutions. Yang and Zhang [38] have proposed three iterative finite element methods on 2D/3D bounded domain and established the analyses of convergence and stability. Based on the Arrow-Hurwicz iterative method, the finite element method has been proposed to avoid solving saddle-point system coming from the considered problem [22]. For the time-dependent thermally coupled incompressible MHD equations, Ravindran [29] has presented a decoupled Crank-Nicolson time-stepping scheme, in which mixed finite element method is used for spatial discretization, and has derived optimal order error estimates in suitable norms. It is noteworthy that this scheme only decouples the MHD equations from the heat equation. Ding et al. [17] have studied the Crank-Nicolson extrapolation scheme, where the generalized Taylor-Hood element, Nédélec edge element, Lagrange element are employed to approximate the Navier-Stokes, Maxwell’s and thermal equations, respectively. Meanwhile, the authors have proven that the proposed scheme is unconditionally energy stable, and have established optimal error estimates for the velocity, magnetic induction and temperature under a weak regularity hypothesis of the exact solution. In [31], a modified characteristics finite element method, which approximates the hyperbolic part with the modified characteristics tracking scheme, has been presented by Si et al. When dissipative heating and Joule heating are taken into account, a stabilized finite element method, which splits the unknowns into a finite element component and a subscale, has been designed by Codina and Hernández in [14]. Finally, for solving the thermally coupled inductionless MHD equations, Badia et al. [9] have designed a new family of recursive block LU preconditioners. Although the works mentioned above have made essential contributions to the construction of the numerical method for the thermally coupled incompressible MHD model, there is less research on explicit treatment for the nonlinear terms in the model, and efficient scheme for the divergence-free constraint concerning velocity and magnetic fields.

On the one hand, inspired by the scalar auxiliary variable method [25, 30], the “zero-energy-contribution” idea has been proposed by Yang in [32,33,34,35,36], where an ordinary differential equation is constructed to decouple the nonlinear system. With the help of “zero-energy-contribution” idea, a fully decoupled finite element scheme, which involves a pressure-correction method, explicit treatment for the nonlinear terms, second-order backward differential scheme, has been proposed by Zhang et al. [39] for the MHD equations. Note that the stability analysis for fully discrete scheme is carried out, but the error analysis is not established. A fully decoupled algorithm for the MHD equations without “magnetic pressure” can be found in [37].

On the other hand, for the time-dependent thermally coupled incompressible MHD flows, it is essential to construct a numerical scheme that generates the numerical solution satisfying the conservation of mass and Gauss’s law. As is known, by using Mini element or Taylor-Hood element for spatial discretization, the velocity solutions are not divergence-free [13]. Recently, the vector penalty-projection (VPP) method, which approximately satisfies the divergence-free conditions, has aroused the researchers’ attention. Based on the augmented Lagrangian and splitting methods under vector form, Angot et al. firstly presented the two-step artificial compressibility (VPP\(_\varepsilon \)) method and the two-parameter vector penalty-projection (VPP\(_{r,\varepsilon }\)) method in [1]. For the VPP\(_\varepsilon \) method, the authors have developed it into incompressible non-homogeneous or multiphase Navier-Stokes problems [2] and the fast numerical computation of incompressible flows with variable viscosity and density [5]. Furthermore, Bruneau et al. [11] have applied the combinatorial method of the VPP\(_\varepsilon \) method and corrected pressure gradient scheme to the displacement of a moving body for the incompressible viscous flows. Based on the stability result, the authors have proven the weak convergence of the scheme towards the continuous incompressible Navier-Stokes problem with a penalization term when time step and penalty parameter go to zero. In a following work of Angot et al. [1], the VPP\(_{r,\varepsilon }\) method has been applied to compute the solution of unsteady incompressible Navier-Stokes equations [3, 8], the incompressible MHD equations [26], the time-dependent incompressible Stokes equations with Dirichlet boundary conditions [6] and open boundary conditions [7]. To be specific, the authors have proven that the numerical solution converges to the weak solution of the Navier-Stokes equations when the penalty parameters tend to zero [8]. Moreover, the stability of the proposed method and second convergence rate with respect to time step of velocity and pressure are analyzed in [6]. As a matter of fact, based on Helmholtz-Hodge decomposition [4], the divergence of the velocity is controlled by the parameter \(\varepsilon \) and r in [1].

The aim of this paper is to construct a fully discrete decoupled finite element scheme for the thermally coupled incompressible MHD problem. First, we introduce an ordinary differential equation containing the nonlinear terms in the thermally coupled MHD equations, which leads to an equivalent system of (1)–(3). Further, the VPP\(_{r,\varepsilon }\) method is used to penalize lack of the mass conservation and Gauss’s law in the fully discrete scheme. Finally, we develop a fully decoupled unconditionally stable finite element scheme by employing first-order backward Euler scheme for the time derivative terms and explicit treatment for the nonlinear terms. Theoretically, the unconditional stability of the proposed scheme will be derived, and error estimates will be established. Numerically, several examples are given to test the stability and accuracy of the presented scheme. By comparing with the implicit-explicit scheme, namely Algorithm 5.1 in this paper, we illustrate the effectiveness of the proposed scheme.

The arrangement of this paper is organized in the following way. We start in Sect. 2 by writing down some notations, functional spaces and the basic facts. In Sect. 3, a fully decoupled finite element scheme is proposed, and its stability is given. Then, some error estimates of the velocity, magnetic and temperature are showed in Sect. 4. In the next section, we present various numerical experiments to test the stability, accuracy and performance of the presented scheme. In Sect. 6, the conclusion is given. The stability and error estimates of the presented method are proved in the Appendix.

2 Preliminaries

Let us give some mathematical preliminaries and notations which will be frequently applied throughout the paper. For \(m\in {\mathbb {N}}^+\) and \(1\le p\le \infty \), let \(W^{m,p}(\Omega )\) be the usually Sobolev space, which is equipped with the norm \(\Vert \cdot \Vert _{W^{m,p}(\Omega )}\), with abbreviations \(L^{p}(\Omega )=W^{0,p}(\Omega )\) and \(H^{m}(\Omega )=W^{m,2}(\Omega )\). \(\Vert \cdot \Vert _{L^{p}(\Omega )}\) and \(\Vert \cdot \Vert _{m}\) denote \(L^{p}(\Omega )\), \(H^{m}(\Omega )\) norm, respectively. Particularly, \((\cdot ,\cdot )\) and \(\Vert \cdot \Vert _0\) denote \(L^{2}\) inner product and norm on the domain \(\Omega \). For a function space X on \(\Omega \), \(L^{p}(0,t;X)\) and \(L^{\infty }(0,t;X)\) are the function spaces defined on \((0,T]\times \Omega \) for which the norm

$$\begin{aligned}{} & {} \Vert \cdot \Vert _{L^{p}(0,t;X)}=\left( \int _{0}^{t}\Vert \cdot \Vert _{X}^{p} \textrm{dt}\right) ^{\frac{1}{p}},~ \text {if} ~p\in [1,\infty ), \\{} & {} \Vert \cdot \Vert _{L^{\infty }(0,t;X)}=\text {ess~sup}_{t\in [0,t]}\Vert \cdot \Vert _{X}, ~\text {if}~ p=\infty . \end{aligned}$$

To setup the mathematical formulation of the problem (1)–(3), we introduce the following Sobolev spaces:

$$\begin{aligned} {\textbf{X}}&=\{{\textbf{v}}\in {H}^{1}(\Omega )^d:{\textbf{v}}|_{\partial \Omega }=0\},\quad \quad {\textbf{W}}=\{{\textbf{B}}\in {H}^{1}(\Omega )^d:{\textbf{B}}\cdot {\textbf{n}}|_{\partial \Omega }=0\},\\ M&=\{q\in L^{2}(\Omega ):(1,q)=0\},\quad \quad \quad Y=\{\varphi \in {H}^{1}(\Omega ):\varphi |_{\partial \Omega }=0\}. \end{aligned}$$

Besides, for \({\textbf{f}}\) an element in the dual space of \({\textbf{X}}\), denoted by \({\textbf{X}}'\), its norm is defined by \(\Vert {\textbf{f}}\Vert _{-1}=\sup _{{\textbf{v}}\in {\textbf{X}}}\frac{|({\textbf{f}},{\textbf{v}})|}{\Vert \nabla {\textbf{v}}\Vert _{0}}.\)

Next, we define the trilinear forms

$$\begin{aligned}&b_{1}({\textbf{u}},{\textbf{v}},{\textbf{w}})=0.5(({\textbf{u}}\cdot \nabla ){\textbf{v}},{\textbf{w}}) -0.5(({\textbf{u}}\cdot \nabla ){\textbf{w}},{\textbf{v}}) ,~~\forall {\textbf{u}},{\textbf{v}},{\textbf{w}}\in {\textbf{X}},\\&b_2({\textbf{H}},{\textbf{B}},{\textbf{v}})=( {\textbf{H}}\times \textrm{curl}{\textbf{B}},{\textbf{v}}),~~\forall {\textbf{B}},{\textbf{H}}\in {\textbf{W}},~{\textbf{v}}\in {\textbf{X}},\\&b_{3}({\textbf{u}},\theta ,\varphi )=0.5({\textbf{u}}\cdot \nabla \theta ,\varphi ) -0.5({\textbf{u}}\cdot \nabla \varphi ,\theta ) ,~~\forall {\textbf{u}}\in {\textbf{X}},~\theta ,\varphi \in Y. \end{aligned}$$

The following properties of the trilinear terms will be used in the next analysis and given in the following lemma.

Lemma 2.1

[16, 19, 20, 24] The above trilinear forms satisfy following properties

$$\begin{aligned} |b_{1}({\textbf{u}},{\textbf{v}},{\textbf{w}})|&\le c\Vert \nabla {\textbf{u}}\Vert _0\Vert \nabla {\textbf{v}}\Vert _0\Vert \nabla {\textbf{w}}\Vert _0,\quad |b_{1}({\textbf{u}},{\textbf{v}},{\textbf{w}})|\le c\Vert {\textbf{u}}\Vert _{0}^{\frac{1}{2}}\Vert \nabla {\textbf{u}}\Vert _{0}^{\frac{1}{2}}\Vert \Vert {\textbf{v}}\Vert _0^{\frac{1}{2}}\Vert \nabla {\textbf{v}}\Vert _0^{\frac{1}{2}}\Vert \nabla {\textbf{w}}\Vert _0,\\ |b_2({\textbf{H}},{\textbf{B}},{\textbf{v}})|&\le c\Vert \textrm{curl}{\textbf{H}}\Vert _0\Vert \textrm{curl}{\textbf{B}}\Vert _0\Vert \nabla {\textbf{v}}\Vert _0,\\ |b_{3}({\textbf{u}},\theta ,\varphi )|&\le c\Vert \nabla {\textbf{u}}\Vert _0\Vert \nabla \theta \Vert _0\Vert \nabla \varphi \Vert _0,\quad |b_{3}({\textbf{u}},\theta ,\varphi )|\le c\Vert {\textbf{u}}\Vert _{0}^{\frac{1}{2}}\Vert \nabla {\textbf{u}}\Vert _{0}^{\frac{1}{2}}\Vert \Vert \theta \Vert _0^{\frac{1}{2}}\Vert \nabla \theta \Vert _0^{\frac{1}{2}}\Vert \nabla \varphi \Vert _0, \end{aligned}$$

for all \({\textbf{u}},{\textbf{v}},{\textbf{w}}\in {\textbf{X}}\), \({\textbf{H}},{\textbf{B}}\in {\textbf{W}}\) and \(\theta , \varphi \in Y\). Moreover, if \({\textbf{v}},{\textbf{B}}\in H^2(\Omega )^2, \theta \in H^2(\Omega )\)

$$\begin{aligned} |b_{1}({\textbf{u}},{\textbf{v}},{\textbf{w}})|&\le c\Vert {\textbf{u}}\Vert _0\Vert {\textbf{v}}\Vert _2\Vert \nabla {\textbf{w}}\Vert _0,\\ |b_2({\textbf{H}},{\textbf{B}},{\textbf{v}})|&\le c\Vert {\textbf{H}}\Vert _0\Vert \textrm{curl}{\textbf{B}}\Vert _0\Vert {\textbf{v}}\Vert _{2}, \quad |b_2({\textbf{H}},{\textbf{B}},{\textbf{v}})|\le c\Vert {\textbf{H}}\Vert _0\Vert {\textbf{B}}\Vert _{2}\Vert \nabla {\textbf{v}}\Vert _0,\\ |b_{3}({\textbf{u}},\theta ,\varphi )|&\le c\Vert {\textbf{u}}\Vert _0\Vert \theta \Vert _2\Vert \nabla \varphi \Vert _0. \end{aligned}$$

Here and after, we denote c and C (with or without a subscript) are general positive constants depending on \(R_e,\) \(R_m,\) s,  \(\kappa ,\) \(\beta ,\) \(\Omega ,\) T,  \({\textbf{u}}_0,\) \({\textbf{H}}_0,\) \(\theta _0,\) \({\textbf{f}}\), \(\omega \) and \({\textbf{g}}\), which may represent for different values at their different occurrences. Additionally, we recall the following essential formulas that are useful in the numerical analysis [15, 18]: for all \({\textbf{u}},{\textbf{v}},{\textbf{w}}\in H^1(\Omega )^d\) and \({\textbf{H}}\in {\textbf{W}},\)

$$\begin{aligned}&\textrm{curl}{\textbf{u}} \times {\textbf{u}} = ({\textbf{u}} \cdot \nabla ){\textbf{u}}- \frac{1}{2} \nabla |{\textbf{u}}| ^2, \end{aligned}$$
(4)
$$\begin{aligned}&\quad \textrm{curl}({\textbf{v}} \times {\textbf{w}}) = ({\textbf{w}} \cdot \nabla ){\textbf{v}} -({\textbf{v}} \cdot \nabla ){\textbf{w}} + (\nabla \cdot {\textbf{w}}){\textbf{v}} -(\nabla \cdot {\textbf{v}}){\textbf{w}},\end{aligned}$$
(5)
$$\begin{aligned}&\quad \Vert \nabla {\textbf{H}}\Vert _0^2\le \Vert \textrm{curl}{\textbf{H}}\Vert _0^2+\Vert \textrm{div}{\textbf{H}}\Vert _0^2. \end{aligned}$$
(6)

By using the above notations and function spaces, the desired weak formulation of the problem (1)–(3) reads: find \({\textbf{u}}\in L^2(0,T;{\textbf{X}}),{\textbf{H}}\in L^2(0,T;{\textbf{W}}),\theta \in L^2(0,T;Y)\) and \(p \in L^2(0,T;M)\) such that for any \(({\textbf{v}},q,{\textbf{B}},\theta ) \in {\textbf{X}} \times M \times {\textbf{W}}\times Y \) and \(t\in (0,T]\),

$$\begin{aligned}&({\textbf{u}}_{t},{\textbf{v}})+a_1({\textbf{u}},{\textbf{v}})+b_{1}({\textbf{u}},{\textbf{u}},{\textbf{v}}) +sb_{2}({\textbf{H}},{\textbf{H}},{\textbf{v}})-d({\textbf{v}},p)-(\beta \theta {\textbf{j}}, {\textbf{v}})=({\textbf{f}},{\textbf{v}}), \end{aligned}$$
(7)
$$\begin{aligned}&\quad ({\textbf{H}}_{t},{\textbf{B}})+a_2({\textbf{H}},{\textbf{B}})-sb_{2}( {\textbf{H}}, {\textbf{B}},{\textbf{u}})=({\textbf{g}},\textrm{curl}{\textbf{B}}), \end{aligned}$$
(8)
$$\begin{aligned}&\quad (\theta _{t},\varphi )+a_3(\theta ,\varphi )+b_{3}( {\textbf{u}},\theta ,\varphi )=(\omega ,\varphi ), \end{aligned}$$
(9)
$$\begin{aligned}&\quad d({\textbf{u}},q)=0, \end{aligned}$$
(10)
$$\begin{aligned}&\quad {\textbf{u}}({\textbf{x}},0)={\textbf{u}}_{0}({\textbf{x}}),\; {\textbf{H}}({\textbf{x}},0)={\textbf{H}}_{0}({\textbf{x}}),\; \theta ({\textbf{x}},0)=\theta _{0}({\textbf{x}}), \end{aligned}$$
(11)

where \(a_1({\textbf{u}},{\textbf{v}})=R_e^{-1}(\nabla {\textbf{u}},\nabla {\textbf{v}}),\) \(a_2({\textbf{H}},{\textbf{B}})=R_m^{-1}s(\textrm{curl}{\textbf{H}},\textrm{curl}{\textbf{B}}),\) \(a_3(\theta ,\varphi )=\kappa (\nabla \theta ,\nabla \varphi )\) and \(d({\textbf{v}},q)=(\textrm{div}{\textbf{v}},q).\)

Through this paper, we make the following assumption in advance for (7)–(11), which will be used in the subsequent analysis.

Assumption 2.1

Assume that the initial data \({\textbf{u}}_{0}\), \({\textbf{H}}_{0}\), \(\theta _0,\) the force \({\textbf{f}}\), heat source \(\omega \) and the current \({\textbf{g}}\) satisfy

$$\begin{aligned} \sup _{0\le t\le T}\Big (\Vert {\textbf{f}}(t)\Vert _0+\Vert \omega (t)\Vert _0+\Vert {\textbf{g}}(t)\Vert _{0}\Big )+\Vert {\textbf{u}}_{0}({\textbf{x}})\Vert _{2} +\Vert {\textbf{H}}_{0}({\textbf{x}})\Vert _{2}+\Vert \theta _{0}({\textbf{x}})\Vert _{2}\le c. \end{aligned}$$

From now on, let \(\pi _{h}\) be a uniform partition of the domain \(\Omega \) into element K with diameters bounded by a real positive parameter \(h=\max _{K\in \pi _h}\{\text{ diam }(K)\}.\) Next, we introduce \({\textbf{X}}_{h}\subset {\textbf{X}},\) \(M_{h}\subset M,\) \({\textbf{W}}_{h}\subset {\textbf{W}}\) and \(Y_{h}\subset Y\) as the conforming finite element spaces under the partition \(\pi _{h}\)

$$\begin{aligned} {\textbf{X}}_h&=\{{\textbf{v}}_h\in C^0(\Omega )^d\cap {\textbf{X}}: {\textbf{v}}_h|_K\in P_2(K)^d,~~\forall K\in \pi _h\},\\ M_{h}&=\{q_{h}\in C^{0}(\Omega )\cap M:q_{h}|_{K}\in P_{1}(K),\forall K\in \pi _{h}\},\\ {\textbf{W}}_{h}&=\{{\textbf{B}}_{h}\in C^{0}(\Omega )^d\cap {\textbf{W}}:{\textbf{B}}_{h}|_{K}\in P_{2}(K)^d,\forall K\in \pi _{h}\},\\ Y_{h}&=\{\varphi _{h}\in C^{0}(\Omega )\cap Y:\varphi _{h}|_{K}\in P_{2}(K),\forall K\in \pi _{h}\}. \end{aligned}$$

Furthermore, the finite element space pair \({\textbf{X}}_{h}\times M_{h}\) is assumed to satisfy the usual discrete inf-sup condition or \(LBB_{h}\) condition for the stability of the discrete pressure: there is a constant \(\alpha \) independent of the mesh size h such that

$$\begin{aligned} \inf _{q_{h}\in M_{h}}\sup _{{\textbf{v}}_{h}\in {\textbf{X}}_h}\frac{(q_{h},\textrm{div}{\textbf{v}}_{h})}{\Vert \nabla {\textbf{v}}_{h}\Vert _0\Vert q_{h}\Vert _0}\ge \alpha >0. \end{aligned}$$

We also recall the Poincaré inequality: there exists a positive constant c such that

$$\begin{aligned} \Vert {\textbf{v}}_h\Vert _0\le c\Vert \nabla {\textbf{v}}_h\Vert _0,\ \ \forall {\textbf{v}}_h\in X_h. \end{aligned}$$

The standard inverse inequality [12] will be used:

$$\begin{aligned} \Vert \nabla {\textbf{v}}_{h}\Vert _0\le c_{in}h^{-1}\Vert {\textbf{v}}_{h}\Vert _0,\quad \forall {\textbf{v}}_{h}\in {\textbf{X}}_h, \end{aligned}$$

where the constant \(c_{in}>0\) depends on the domain.

As is known, the discrete Grönwall’s inequality will play an important role in analysis of convergence, so we list it in the following lemma.

Lemma 2.2

[21] Let k and \(a_{n},b_{n},d_{n},\) for integers \(n_{1}\le n\) be nonnegative numbers such that:

$$\begin{aligned} a_{m}+k\sum \limits _{n=n_{1}}^{m}b_{n}\le k\sum \limits _{n=n_{1}}^{m-1}a_{n}d_{n}+C, \quad \forall m\ge n_{1}. \end{aligned}$$

Then, one has

$$\begin{aligned} a_{m}+k\sum \limits _{n=n_{1}}^{m}b_{n}\le \exp \left( k\sum \limits _{n=n_{1}}^{m-1}d_{n}\right) C, \quad \forall m\ge n_{1}. \end{aligned}$$

3 A Fully Decoupled Linearized Scheme for the Thermally Coupled MHD Equations

In this section, we construct a fully decoupled unconditional stable finite element scheme, which approximately satisfies the conversation of mass and Gauss’s law, to solve the thermally coupled incompressible MHD system (1)–(3).

Introduce an auxiliary scalar variable Q and an ordinary differential equation, which is being shown as follows:

$$\begin{aligned} \begin{aligned}&\frac{\textrm{d}Q}{\textrm{dt}}=b_1({\textbf{u}},{\textbf{u}},{\textbf{u}})+sb_2 ({\textbf{H}},{\textbf{H}},{\textbf{u}}) -sb_2({\textbf{H}},{\textbf{H}},{\textbf{u}})+b_3({\textbf{u}},\theta ,\theta ),\qquad Q|_{t=0}=1. \end{aligned} \end{aligned}$$

Note that \(b_1({\textbf{u}},{\textbf{u}},{\textbf{u}})+sb_2 ({\textbf{H}},{\textbf{H}},{\textbf{u}}) -sb_2({\textbf{H}},{\textbf{H}},{\textbf{u}})+b_3({\textbf{u}},\theta ,\theta )=0.\) So we have the exact solution \(Q(t)\equiv 1\). Then, the thermally coupled MHD system (1)–(3) can be rewritten in the following equivalent system:

figure a

Let \(\{t_n\}_{n=0}^{N}~(N>0)\) be a uniform partition of [0, T] with time step \(\Delta t =\frac{T}{N}\). Next, \(({\textbf{u}}_h^n,p_h^n,{\textbf{H}}_h^n,\theta _h^n)\) denotes the fully discrete approximation to the solution \(({\textbf{u}}(t_n),p(t_n),{\textbf{H}}(t_n),\theta (t_n))\) of the problem (12)–(17) at \(t=t_{n}.\) Besides, we set \({\textbf{f}}^n={\textbf{f}}(t_n),\) \({\textbf{g}}^n={\textbf{g}}(t_n)\) and \(\omega ^n=\omega (t_n).\)

Then, we propose a fully discrete decoupled finite element scheme, which combines the first order backward Euler scheme for temporal discretization and explicit treatment for nonlinear terms. Moreover, a modified VPP\( _{r,\varepsilon }\) method is introduced to decouple the pressure and penalize the lack of mass conservation and Gauss’s law.

Algorithm 3.1

Step 1: Given \({\textbf{u}}_h^{n}\in {\textbf{X}}_h,{\textbf{H}}^{n}_h\in {\textbf{W}}_h,{\tilde{p}}_h^n\in M_h,\theta _h^{n}\in Y_h\), find \((\tilde{{\textbf{u}}}^{n+1}_{1,h},\tilde{{\textbf{u}}}^{n+1}_{2,h}, \tilde{{\textbf{H}}}^{n+1}_{1,h},\tilde{{\textbf{H}}}^{n+1}_{2,h})\in {\textbf{X}}_h \times {\textbf{X}}_h \times {\textbf{W}}_h \times {\textbf{W}}_h\) satisfying: for all \(({\textbf{v}}_h,{\textbf{B}}_h)\in {\textbf{X}}_h\times {\textbf{W}}_h\),

$$\begin{aligned}&\left( \frac{\tilde{{\textbf{u}}}^{n+1}_{1,h}-{\textbf{u}}_h^{n}}{\Delta t},{\textbf{v}}_h\right) +a_1\left( \tilde{{\textbf{u}}}_{1,h}^{n+1},{\textbf{v}}_h\right) -d\left( {\textbf{v}}_h,{\tilde{p}}_h^{n}\right) -(\beta \theta ^{n}_h{\textbf{j}},{\textbf{v}}_h)\nonumber \\&\quad +r\left( \textrm{div}\tilde{{\textbf{u}}}^{n+1}_{1,h},\textrm{div}{\textbf{v}}_h\right) =\left( {\textbf{f}}^{n+1},{\textbf{v}}_h\right) , \end{aligned}$$
(18)
$$\begin{aligned}&\quad \left( \frac{\tilde{{\textbf{H}}}_{1,h}^{n+1}-{\textbf{H}}_h^{n}}{\Delta t},{\textbf{B}}_h\right) +a_2\left( \tilde{{\textbf{H}}}_{1,h}^{n+1},{\textbf{B}}_h\right) =\left( \textrm{curl}{\textbf{g}}^{n+1},{\textbf{B}}_h\right) ,\end{aligned}$$
(19)
$$\begin{aligned}&\quad \left( \frac{\tilde{{\textbf{u}}}^{n+1}_{2,h}}{\Delta t},{\textbf{v}}_h\right) +a_1\left( \tilde{{\textbf{u}}}_{2,h}^{n+1},{\textbf{v}}_h\right) +b_1({\textbf{u}}_h^{n},{\textbf{u}}_h^{n},{\textbf{v}}_h)+s b_2 ({\textbf{H}}^{n}_h,{\textbf{H}}_h^{n},{\textbf{v}}_h)\nonumber \\&\quad +r\left( \textrm{div}\tilde{{\textbf{u}}}^{n+1}_{2,h}, \textrm{div}{\textbf{v}}_h\right) =0,\end{aligned}$$
(20)
$$\begin{aligned}&\quad \left( \frac{\tilde{{\textbf{H}}}_{2,h}^{n+1}}{\Delta t},{\textbf{B}}_h\right) +a_2\left( \tilde{{\textbf{H}}}_{2,h}^{n+1},{\textbf{B}}_h\right) - sb_2({\textbf{H}}_h^{n},{\textbf{B}}_h,{\textbf{u}}^{n}_h)=0, \end{aligned}$$
(21)

where \(r>0\) is the augmentation parameter.

Step 2 : Given \({\textbf{u}}_h^{n}\in {\textbf{X}}_h,\theta _h^n\in Y_h\), find \((\theta ^{n+1}_{1,h},\theta ^{n+1}_{2,h})\in Y_h\times Y_h\) satisfying: for all \(\varphi _h\in Y_h\),

$$\begin{aligned}&\left( \frac{\theta ^{n+1}_{1,h}-\theta _h^{n}}{\Delta t},\varphi _h\right) +a_3\left( \theta _{1,h}^{n+1},\varphi _h\right) =\left( \omega ^{n+1},\varphi _h\right) , \end{aligned}$$
(22)
$$\begin{aligned}&\left( \frac{\theta ^{n+1}_{2,h}}{\Delta t},\varphi _h\right) +a_3\left( \theta _{2,h}^{n+1},\varphi _h\right) +b_3({\textbf{u}}_h^{n},\theta _h^{n},\varphi _h)=0. \end{aligned}$$
(23)

Step 3: Compute \(Q^{n+1}\in {\mathbb {R}}\) satisfying

$$\begin{aligned} \begin{aligned}&\quad \left( 1-{\mathbb {A}}_1^{n+1}\right) Q^{n+1}=Q^n+ {\mathbb {A}}_2^{n+1}, \end{aligned} \end{aligned}$$
(24)

where \({\mathbb {A}}_1^{n+1}=\Delta t\left( b_1({\textbf{u}}_{h}^{n},{\textbf{u}}_{h}^{n},\tilde{{\textbf{u}}}_{2,h}^{n+1})+sb_2 ({\textbf{H}}^{n}_h,{\textbf{H}}_h^{n},\tilde{{\textbf{u}}}_{2,h}^{n+1}) -sb_2({\textbf{H}}_h^{n},\tilde{{\textbf{H}}}_{2,h}^{n+1},{\textbf{u}}^{n}_h) +b_3({\textbf{u}}_{h}^{n},\theta _{h}^{n},\theta _{2,h}^{n+1})\right) ,\) and \({\mathbb {A}}_2^{n+1}=\Delta t\left( b_1({\textbf{u}}_{h}^{n},{\textbf{u}}_{h}^{n},\tilde{{\textbf{u}}}_{1,h}^{n+1})+sb_2 ({\textbf{H}}^{n}_h,{\textbf{H}}_h^{n},\tilde{{\textbf{u}}}_{1,h}^{n+1}) -sb_2({\textbf{H}}_h^{n},\tilde{{\textbf{H}}}_{1,h}^{n+1},{\textbf{u}}^{n}_h)+b_3({\textbf{u}}_{h}^{n},\theta _{h}^{n},\theta _{1,h}^{n+1})\right) .\)

Step 4: Find \(\tilde{{\textbf{u}}}^{n+1}_h\in {\textbf{X}}_h\), \(\tilde{{\textbf{H}}}^{n+1}_h\in {\textbf{W}}_h\), \(\theta ^{n+1}_h\in Y_h\) such that

$$\begin{aligned} \begin{aligned}&\tilde{{\textbf{u}}}^{n+1}_h = \tilde{{\textbf{u}}}^{n+1}_{1,h} + Q^{n+1}\tilde{{\textbf{u}}}^{n+1}_{2,h},\quad \tilde{{\textbf{H}}}^{n+1}_h = \tilde{{\textbf{H}}}^{n+1}_{1,h} + Q^{n+1}\tilde{{\textbf{H}}}^{n+1}_{2,h},\\&\theta ^{n+1}_h = \theta ^{n+1}_{1,h} + Q^{n+1}\theta ^{n+1}_{2,h}. \end{aligned} \end{aligned}$$
(25)

Step 5: Update \({\tilde{p}}^{n+1}_h\in M_{h}\) satisfying: for all \(q_h \in M_h\),

$$\begin{aligned} ({\tilde{p}}^{n+1}_h-{\tilde{p}}^{n}_h,q_h)+rd(\tilde{{\textbf{u}}}_h^{n+1},q_h)=0. \end{aligned}$$
(26)

Step 6: Based on \(\tilde{{\textbf{u}}}^{n+1}_h\) and \(\tilde{{\textbf{H}}}^{n+1}_h\) from (25), find \((\hat{{\textbf{u}}}^{n+1}_h,\hat{{\textbf{H}}}^{n+1}_h)\in {\textbf{X}}_h\times {\textbf{W}}_h\) satisfying: for all \(({\textbf{v}}_h,{\textbf{B}}_h)\in {\textbf{X}}_h\times {\textbf{W}}_h\),

$$\begin{aligned}&\left( \frac{\hat{{\textbf{u}}}^{n+1}_h}{\Delta t},{\textbf{v}}_h\right) +a_1(\hat{{\textbf{u}}}_h^{n+1},{\textbf{v}}_h)+\frac{1 }{\varepsilon _1}\left( \textrm{div}\hat{{\textbf{u}}}^{n+1},\textrm{div}{\textbf{v}}_h\right) =-\frac{1 }{\varepsilon _1}\left( \textrm{div}\tilde{{\textbf{u}}}^{n+1}_h,\textrm{div}{\textbf{v}}_h\right) , \end{aligned}$$
(27)
$$\begin{aligned}&\left( \dfrac{\hat{{\textbf{H}}}_h^{n+1}}{\Delta t},{\textbf{B}}_h\right) +a_2(\hat{{\textbf{H}}}_h^{n+1},{\textbf{B}}_h)+\frac{1}{\varepsilon _2}\left( \textrm{div}\hat{{\textbf{H}}}_h^{n+1},\textrm{div}{\textbf{B}}_h\right) =-\frac{1}{\varepsilon _2}\left( \textrm{div}\tilde{{\textbf{H}}}_h^{n+1},\textrm{div}{\textbf{B}}_h\right) \end{aligned}$$
(28)

with some penalty parameters \(0 < \varepsilon _{1},\varepsilon _{2} \le 1\).

Step 7: Combine the Step 4 and Step 6, then get \(({\textbf{u}}^{n+1}_h,{\textbf{H}}^{n+1}_h)\in {\textbf{X}}_h\times {\textbf{W}}_h\) by

$$\begin{aligned} \begin{aligned} {\textbf{u}}_h^{n+1}=\tilde{{\textbf{u}}}_h^{n+1}+\hat{{\textbf{u}}}_h^{n+1},\quad {\textbf{H}}^{n+1}_h=\tilde{{\textbf{H}}}_h^{n+1}+\hat{{\textbf{H}}}_h^{n+1}. \end{aligned} \end{aligned}$$
(29)

Step 8: Update \(p^{n+1}_h\in M_{h}\) satisfying: for all \(q_h \in M_h\),

$$\begin{aligned} (p^{n+1}_h-{\tilde{p}}^{n+1}_h,q_h)+\frac{1}{\varepsilon _1}d({\textbf{u}}_h^{n+1},q_h)=0. \end{aligned}$$
(30)

Remark 3.1

Note that some initial values are required for the unknowns in Step 1, 2 and 5. Setting \({\textbf{u}}_h^{0}=R_h{\textbf{u}}_0({\textbf{x}}),\) \({\textbf{H}}_h^{0}=T_h{\textbf{H}}_0({\textbf{x}}),\) \({{\tilde{p}}}_h^{0}=L_hp_0(x)\) and \(\theta _h^{0}=G_h\theta _0(x)\), the definitions of the projections \(R_h,T_h,L_h,G_h\) are displayed in next section. Under the Assumption 2.1, we have \(\Vert {\textbf{u}}_h^{0}\Vert _0\le c,\) \(\Vert {\textbf{H}}_h^{0}\Vert _0\le c,\) \(\Vert {{\tilde{p}}}_h^{0}\Vert _0\le c,\) and \(\Vert \theta _h^{0}\Vert _0\le c.\)

Remark 3.2

In (18), (20) and (26), the added penalty terms can be seen as artificial compressibility method but the augmentation parameter r is totally independent of the time step \(\Delta t\). Further, in order to ensure the fully discrete numerical method is unconditionally stable, we choose \({\tilde{p}}^n_{i,h}\) instead of \(p^n_{i,h}\) in (18) and (26), which is different from the common VPP\(_{r,\varepsilon }\) method in [7].

Remark 3.3

In Step 1 and 2, the explicit treatment for convection terms and Lorentz force terms results in constant coefficient system at each time layer, which makes the computation easy. Moreover, the addition of penalty term further decouples the pressure from the momentum equation and achieves full decoupling of the physical variables in (1).

Remark 3.4

From Helmholtz-Hodge decomposition in [4], Step 6-8, called the vector penalty-projection step, perform the penalty for lack of mass conservation and Gauss’s law. When the penalty parameters are small enough, Step 6 and 7 are used to approximate well divergence-free solution for velocity and magnetic fields.

We next establish stability of the partitioned scheme in Algorithm 3.1.

First of all, one needs to check the solvability of (24). In fact, if \(1-{\mathbb {A}}_1^{n+1}=0,\) then one can not solve (24). Moreover, if one can prove \(-{\mathbb {A}}_1^{n+1}\ge 0\), then \(1-{\mathbb {A}}_1^{n+1}\ge 1\ne 0\). So (24) can be solved.

In fact, by taking \({\textbf{v}}_h=\Delta t\tilde{{\textbf{u}}}^{n+1}_{2,h}\), \({\textbf{B}}_h=\Delta t\tilde{{\textbf{H}}}^{n+1}_{2,h}\), \(\varphi _h=\Delta t\theta ^{n+1}_{2,h}\) in (20), (21) and (23), respectively, and combining the ensuing equations, one has

$$\begin{aligned}&-{\mathbb {A}}_1^{n+1} =-\Delta t \left( b_1({\textbf{u}}_h^{n},{\textbf{u}}_h^{n},\tilde{{\textbf{u}}}^{n+1}_{2,h})+s b_2 ({\textbf{H}}^{n}_h,{\textbf{H}}_h^{n},\tilde{{\textbf{u}}}^{n+1}_{2,h})-s b_2({\textbf{H}}_h^{n},\tilde{{\textbf{H}}}_{2,h}^{n+1},{\textbf{u}}^{n}_h)\right. \\&\quad \left. +b_3({\textbf{u}}_h^{n},\theta _h^{n},\theta _{2,h}^{n+1})\right) \\&\quad =\Vert \tilde{{\textbf{u}}}^{n+1}_{2,h}\Vert _0^2+R_e^{-1}\Delta t\Vert \nabla \tilde{{\textbf{u}}}_{2,h}^{n+1}\Vert _0^2+r\Delta t\Vert \textrm{div}\tilde{{\textbf{u}}}^{n+1}_{2,h}\Vert _0^2\\&\quad +\Vert \tilde{{\textbf{H}}}_{2,h}^{n+1}\Vert _0^2+R_m^{-1}\Delta t\Vert \textrm{curl}\tilde{{\textbf{H}}}_{2,h}^{n+1}\Vert _0^2\\&\quad +\Vert \theta ^{n+1}_{2,h}\Vert _0^2 +\kappa \Delta t\Vert \nabla \theta _{2,h}^{n+1}\Vert _0^2 \ge 0, \end{aligned}$$

which implies the solvability of (24).

Now, we mainly list and prove the stability of Algorithm 3.1.

Theorem 3.1

Under Assumption 2.1, there holds

$$\begin{aligned}&\Vert {\textbf{u}}_h^{N} \Vert _0^2+ \Vert {\textbf{H}}_h^{N} \Vert _0^2+\frac{\Delta t}{r}\Vert {\tilde{p}}_h^{N} \Vert _0^2+\Vert \theta ^{N}_{h}\Vert _0^2+| Q^{N} |^2+\sum _{n=0}^{N-1}\Vert \tilde{{\textbf{u}}}_h^{n+1} -{\textbf{u}}_h^{n} \Vert _0^2\\&\quad +\sum _{n=0}^{N-1}\Vert {\textbf{u}}_h^{n+1} -\tilde{{\textbf{u}}}_h^{n+1} \Vert _0^2\\&\quad +\sum _{n=0}^{N-1}\Vert \tilde{{\textbf{H}}}_h^{n+1} -{\textbf{H}}_h^{n} \Vert _0^2+\sum _{n=0}^{N-1}\Vert {\textbf{H}}_h^{n+1} -\tilde{{\textbf{H}}}_h^{n+1} \Vert _0^2\\&\quad +\sum _{n=0}^{N-1}\Vert \theta ^{n+1}_{h}-\theta ^{n}_{h}\Vert _0^2+\sum _{n=0}^{N-1}|Q^{n+1}_{h}-Q^{n}_{h}|^2\\&\quad +R_e^{-1}\Delta t \sum _{n=0}^{N-1}( \Vert \nabla {\textbf{u}}_h^{n+1} \Vert _0^2+\Vert \nabla {\textbf{u}}_h^{n+1} -\nabla \tilde{{\textbf{u}}}_h^{n+1} \Vert _0^2)\\&\quad +\frac{\Delta t}{\varepsilon _1}\sum _{n=0}^{N-1}\Vert \textrm{div}{{\textbf{u}}}_{h}^{n+1}\Vert _0^2\\&\quad +R_m^{-1}\Delta t\sum _{n=0}^{N-1}( \Vert \textrm{curl}{\textbf{H}}_h^{n+1} \Vert _0^2 +\Vert \textrm{curl}{{\textbf{H}}}_h^{n+1}-\textrm{curl}\tilde{{\textbf{H}}}_h^{n+1} \Vert _0^2)\\&\quad +\frac{2\Delta t}{\varepsilon _2}\sum _{n=0}^{N-1}\Vert \textrm{div}{\textbf{H}}_h^{n+1} \Vert _0^2\\&\quad +\Delta t\sum \limits _{n=0}^{N-1}r\Vert \textrm{div}\tilde{{\textbf{u}}}^{n+1}_{h}\Vert _0^2+\kappa \Delta t\sum _{n=0}^{N-1}\Vert \nabla \theta ^{n+1}_{h}\Vert _0^2\\&\quad +\varepsilon _1\Delta t\sum _{n=0}^{N-1}\Vert p_h^{n+1} -{\tilde{p}}_h^{n+1} \Vert _0^2\le C, \end{aligned}$$

where \(C=C(R_e,R_m,\kappa ,\beta ,T,\Omega ,{\textbf{u}}_0,{\textbf{H}}_0,\theta _0,{\textbf{f}},\omega ,{\textbf{g}})\) is a positive constant.

Proof

See Appendix A.1. \(\square \)

4 Error Estimates

In this section, we establish error estimate results of Algorithm 3.1 for the thermally coupled incompressible MHD equations. First, we make the following regularity assumption for the weak solution to system (7)–(11).

Assumption 4.1

The exact solution of (7)–(11) satisfies

$$\begin{aligned} \begin{array}{lll} {\textbf{u}}\in L^{\infty }(0,T;H^{3}(\Omega )^d),&{}\quad {\textbf{u}}_t\in L^{2}(0,T;H^{3}(\Omega )^d),&{}\quad {\textbf{u}}_{tt}\in L^{2}(0,T;H^{-1}(\Omega )^d),\\ {\textbf{H}}\in L^{\infty }(0,T;H^{3}(\Omega )^d),&{}\quad {\textbf{H}}_t\in L^{2}(0,T;H^3(\Omega )^d),&{}\quad {\textbf{H}}_{tt}\in L^{2}(0,T;H^{-1}(\Omega )^d),\\ {\theta }\in L^{\infty }(0,T;H^{3}(\Omega )),&{}\quad {\theta }_t\in L^{2}(0,T;H^{3}(\Omega )),&{}\quad \theta _{tt}\in L^{2}(0,T;H^{-1}(\Omega )),\\ p\in L^{\infty }(0,T;H^{2}(\Omega )),&{}\quad p_t\in L^{2}(0,T;H^{2}(\Omega ))\cap L^{\infty }(0,T;L^{2}(\Omega )).&{} \end{array} \end{aligned}$$

Next, we introduce the Stokes projection for the velocity field and pressure, \(L^2\)-orthogonal projection for the magnetic field and Ritz projection for temperature as follows [17,18,19]: given \({\textbf{u}}\in {\textbf{X}}\cap H^3(\Omega )^d\), \({\textbf{H}}\in {\textbf{W}}\cap H^3(\Omega )^d\), \(p\in M\cap H^2(\Omega )\), \(\theta \in Y\cap H^3(\Omega ),\) find \((R_h{\textbf{u}}, T_h{\textbf{H}}, L_hp, G_h\theta ) \in {\textbf{X}}_h\times {\textbf{W}}_h \times M_h \times Y_h\) such that

$$\begin{aligned}&a_1({\textbf{u}}-R_h{\textbf{u}}, {\textbf{v}}_h)- d({\textbf{v}}_h, p-L_hp)= 0,\quad d({\textbf{u}}-R_h{\textbf{u}}, q_h) =0, \ \quad \forall {\textbf{v}}_h\in {\textbf{X}}_h, q_h\in M_h,\\&({\textbf{H}}-T_h{\textbf{H}}, {\textbf{B}}_h) = 0,\quad \forall {\textbf{B}}_h\in {\textbf{W}}_h,\qquad \ \ a_3(\theta -G_h\theta , \varphi _h)= 0,\quad \forall \varphi _h\in Y_h, \end{aligned}$$

which satisfy the following approximation properties

$$\begin{aligned}&\nu \Vert {\textbf{u}}- R_h{\textbf{u}}\Vert _0+ h(\nu \Vert {\textbf{u}}-R_h{\textbf{u}}\Vert _1+\Vert p-L_hp\Vert _0)\le ch^{3}(\nu \Vert {\textbf{u}}\Vert _{3}+\Vert p\Vert _2), \end{aligned}$$
(31)
$$\begin{aligned}&\quad \Vert {\textbf{H}}-T_h{\textbf{H}}\Vert _0+ h\Vert {\textbf{H}}-T_h{\textbf{H}}\Vert _1\le ch^{3}\Vert {\textbf{H}}\Vert _{3},\quad \Vert \theta -G_h\theta \Vert _0+h\Vert \theta -G_h\theta \Vert _1\le ch^{3}\Vert \theta \Vert _{3}. \end{aligned}$$
(32)

In order to facilitate the error estimates, we set \({\textbf{v}}={\textbf{v}}_{h}\) in (7), \({\textbf{B}}={\textbf{B}}_{h}\) in (8), \(\varphi =\varphi _{h}\) in (9) and \(q=q_h\) in (10) with \(t=t_{n+1}\) to get

$$\begin{aligned}&\left( \frac{{\textbf{u}}(t_{n+1})-{\textbf{u}}(t_n)}{\Delta t},{\textbf{v}}_{h}\right) +a_1({\textbf{u}}(t_{n+1}),{\textbf{v}}_{h})\nonumber \\&\qquad -d({\textbf{v}}_h,p(t_{n+1})) +Q(t_{n+1})b_1({\textbf{u}}(t_{n+1}),{\textbf{u}}(t_{n+1}),{\textbf{v}}_{h})\nonumber \\&\qquad +s Q(t_{n+1})b_2({\textbf{H}}(t_{n+1}),{\textbf{H}}(t_{n+1}),{\textbf{v}}_{h}) -(\beta \theta (t_{n+1}){\textbf{j}},{\textbf{v}}_h)\nonumber \\&\quad =({\textbf{f}}^{n+1},{\textbf{v}}_{h})-\frac{1}{\Delta t}\int _{t_n}^{t_{n+1}}(t-t_n)({\textbf{u}}_{tt},{\textbf{v}}_h)\textrm{dt}, \end{aligned}$$
(33)
$$\begin{aligned}&\left( \frac{{\textbf{H}}(t_{n+1})-{\textbf{H}}(t_n)}{\Delta t},{\textbf{B}}_{h}\right) +a_2({\textbf{H}}(t_{n+1}),{\textbf{B}}_{h})-s Q(t_{n+1})b_2({\textbf{H}}(t_{n+1}),{\textbf{B}}_{h},{\textbf{u}}(t_{n+1}))\nonumber \\&\quad =({\textbf{g}}^{n+1},\textrm{curl}{\textbf{B}}_{h})-\frac{1}{\Delta t}\int _{t_n}^{t_{n+1}}(t-t_n)({\textbf{H}}_{tt},{\textbf{B}}_h)\textrm{dt}, \end{aligned}$$
(34)
$$\begin{aligned}&\left( \frac{\theta (t_{n+1})-\theta (t_n)}{\Delta t},\varphi _h\right) +a_3(\theta (t_{n+1}),\varphi _{h})+ Q(t_{n+1})b_3({\textbf{u}}(t_{n+1}),\theta (t_{n+1}),\varphi _{h})\nonumber \\&\quad =(\omega ^{n+1},\varphi _{h})-\frac{1}{\Delta t}\int _{t_n}^{t_{n+1}}(t-t_n)(\theta _{tt},\varphi _{h})\textrm{dt}, \end{aligned}$$
(35)
$$\begin{aligned}&\quad \left( p(t_{n+1})-p(t_n),q_h\right) +rd\left( {\textbf{u}}(t_{n+1}),q_h\right) =\left( p(t_{n+1})-p(t_n),q_h\right) . \end{aligned}$$
(36)

Then, we show the following notations here and hereafter

$$\begin{aligned} \tilde{{\textbf{e}}}_{u}^{n}&= {\textbf{u}}(t_{n}) -\tilde{{\textbf{u}}}_{h}^{n},\quad \tilde{{\textbf{e}}}_{H}^{n}={\textbf{H}}(t_{n})- \tilde{{\textbf{H}}}_{h}^{n},\quad {\tilde{e}}_p^{n}=p(t_{n})- {\tilde{p}}_{h}^{n},\quad e_Q^{n}=Q(t_{n})- {Q}_{h}^{n},\\ {{\textbf{e}}}_{u}^{n}&= {\textbf{u}}(t_{n}) -{{\textbf{u}}}_{h}^{n},\quad {{\textbf{e}}}_{H}^{n}={\textbf{H}}(t_{n})- {{\textbf{H}}}_{h}^{n},\quad e_p^{n}=p(t_{n})- {p}_{h}^{n},\quad e_\theta ^{n}=\theta (t_{n})- {\theta }_{h}^{n}. \end{aligned}$$

Next, we get the following error equations by subtracting (A.1)–(A.3) from (33)–(35), respectively.

$$\begin{aligned}&\quad \left( \frac{\tilde{{\textbf{e}}}_{u}^{n+1}-{\textbf{e}}_u^n}{\Delta t},{\textbf{v}}_{h}\right) \nonumber \\&\quad +a_1(\tilde{{\textbf{e}}}_{u}^{n+1},{\textbf{v}}_{h})+Q(t_{n+1})b_1({\textbf{u}}(t_{n+1}), {\textbf{u}}(t_{n+1}),{\textbf{v}}_{h})\nonumber \\&\quad -Q^{n+1}b_1({\textbf{u}}_{h}^{n},{\textbf{u}}_{h}^{n},{\textbf{v}}_{h})\nonumber \\&\quad +s Q(t_{n+1})b_{2}({\textbf{H}}(t_{n+1}),{\textbf{H}}(t_{n+1}),{\textbf{v}}_{h})-sQ^{n+1} b_2({\textbf{H}}_{h}^{n},{\textbf{H}}_{h}^{n},{\textbf{v}}_{h})\nonumber \\&\quad -d({\textbf{v}}_h,{\tilde{e}}_p^{n})+r(\textrm{div}\tilde{{\textbf{e}}}^{n+1}_{u},\textrm{div}{\textbf{v}}_{h})\nonumber \\&\quad -(\beta \theta (t_{n+1}){\textbf{j}},{\textbf{v}}_h)+(\beta \theta _h^{n}{\textbf{j}},{\textbf{v}}_h)\nonumber \\&\quad =-\frac{1}{\Delta t}\int _{t_{n}}^{t_{n+1}}(t-t_{n})({\textbf{u}}_{tt},{\textbf{v}}_{h})\textrm{dt}-d({\textbf{v}}_{h},p(t_n)-p(t_{n+1})), \end{aligned}$$
(37)
$$\begin{aligned}&\quad \left( \frac{\tilde{{\textbf{e}}}_{H}^{n+1}-{\textbf{e}}^n_H}{\Delta t},{\textbf{B}}_{h}\right) +a_2(\tilde{{\textbf{e}}}_{H}^{n+1}, {\textbf{B}}_{h})\nonumber \\&\quad -sQ(t_{n+1}) b_{2}({\textbf{H}}(t_{n+1}),{\textbf{B}}_{h},{\textbf{u}}(t_{n+1}))+s Q^{n+1}b_2({\textbf{H}}_h^{n},{\textbf{B}}_{h},{\textbf{u}}_h^{n})\nonumber \\&\quad =-\frac{1}{\Delta t}\int _{t_{n}}^{t_{n+1}}(t-t_{n})({\textbf{H}}_{tt},{\textbf{B}}_{h})\textrm{dt}, \end{aligned}$$
(38)
$$\begin{aligned}&\quad \left( \frac{e_\theta ^{n+1}-e^n_\theta }{\Delta t},\varphi _{h}\right) \nonumber \\&\quad +a_3(e_\theta ^{n+1},\varphi _{h})+Q(t_{n+1}) b_{3}({\textbf{u}}(t_{n+1}),\theta (t_{n+1}),\varphi _{h})- Q^{n+1}b_3({\textbf{u}}_h^{n},\theta _h^{n},\varphi _{h})\nonumber \\&\quad =-\frac{1}{\Delta t}\int _{t_{n}}^{t_{n+1}}(t-t_{n})(\theta _{tt},\varphi _{h})\textrm{dt}. \end{aligned}$$
(39)

Besides, subtracting (26) from (36), we arrive at

$$\begin{aligned} \begin{aligned} ({\tilde{e}}_p^{n+1}-{\tilde{e}}_p^{n},q_h)+rd(\tilde{{\textbf{e}}}_u^{n+1},q_h)=(p(t_{n+1})-p(t_n),q_h). \end{aligned} \end{aligned}$$
(40)

Further, in order to derive estimate for error, we need to split the errors. For future convenience, we define here and hereafter,

$$\begin{aligned} \begin{array}{llll} \tilde{{\textbf{e}}}_{u}^{n}= \varvec{\eta }_u^n-\tilde{\varvec{\phi }}_h^n,&{}\tilde{{\textbf{e}}}_{H}^{n}= \varvec{\eta }_H^n-\tilde{\varvec{\psi }}_h^n,&{} {\tilde{e}}_p^{n}= \eta _p^n-{\tilde{\chi }}_h^n,&{}\quad {\textbf{e}}_{u}^{n}= \varvec{\eta }_u^n-{\varvec{\phi }}_h^n,\\ {{\textbf{e}}}_{H}^{n}= \varvec{\eta }_H^n-{\varvec{\psi }}_h^n,&{}{e}_p^{n}= \eta _p^n-{\chi }_h^n ,&{} {e}_\theta ^{n}= \eta _\theta ^n-{\vartheta }_h^n, \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{llll} \varvec{\eta }_u^n= {\textbf{u}}(t_{n})-R_h{\textbf{u}}(t_{n}),&{} \tilde{\varvec{\phi }}_h^n=\tilde{{\textbf{u}}}_{h}^{n}-R_h{\textbf{u}}(t_{n}), &{}\varvec{\eta }_H^n={\textbf{H}}(t_{n})-T_h{\textbf{H}}(t_{n}),&{} \tilde{\varvec{\psi }}_h^n=\tilde{{\textbf{H}}}_{h}^{n}-T_h{\textbf{H}}(t_{n}),\\ \eta _p^n=p(t_{n})-L_hp(t_{n}),&{}{\tilde{\chi }}_h^n ={\tilde{p}}_{h}^{n}-L_hp(t_{n}),&{}{\varvec{\phi }}_h^n={{\textbf{u}}}_{h}^{n}-R_h{\textbf{u}}(t_{n}), &{} {\varvec{\psi }}_h^n={{\textbf{H}}}_{h}^{n}-T_h{\textbf{H}}(t_{n}), \\ {\chi }_h^n= {p}_{h}^{n}-L_hp(t_{n}),&{} \eta _\theta ^n=\theta (t_{n})-G_h\theta (t_{n}),&{}{\vartheta }_h^n={\theta }_{h}^{n}- G_h\theta (t_{n}). \end{array} \end{aligned}$$

Lemma 4.1

Consider Step 6 in Algorithm 3.1. The following estimate holds

$$\begin{aligned} \begin{aligned}&\Vert \tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}+\Vert \tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0 ^{2}\\&\quad \ge \Vert {\varvec{\phi }}_{h}^{n+1}\Vert _0^{2} +\Vert \varvec{\phi }_{h}^{n+1}-\tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}+R_e^{-1}\Delta t\left( \Vert \nabla {\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}-\Vert \nabla \tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}\right) +\Vert \varvec{\psi }_{h}^{n+1}\Vert _0^{2}\\&\quad +R_m^{-1} \Delta t \left( \Vert \textrm{curl}\varvec{\psi }_{h}^{n+1}\Vert _0^{2}- \Vert \textrm{curl}\tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0 ^{2}\right) +R_m^{-1} \Delta t \Vert \textrm{curl}( \varvec{\psi }_{h}^{n+1}-\tilde{\varvec{\psi }}_{h}^{n+1})\Vert _0 ^{2}\\&\qquad +R_e^{-1}\Delta t\Vert \nabla ({\varvec{\phi }}_{h}^{n+1}-\tilde{\varvec{\phi }}_{h}^{n+1})\Vert _0^2 +\Vert \varvec{\psi }_{h}^{n+1}-\tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0 ^{2}+\frac{\Delta t}{\varepsilon _1}\Vert \textrm{div}{\varvec{\phi }}_{h}^{n+1}\Vert _0^2\\&\qquad +\frac{\Delta t}{\varepsilon _2}\Vert \textrm{div}{\varvec{\psi }}_{h}^{n+1}\Vert _0^2-\frac{\Delta t}{\varepsilon _1}\Vert \textrm{div}{\varvec{\eta }}_{u}^{n+1}\Vert _0^2-\frac{\Delta t}{\varepsilon _2}\Vert \textrm{div}{\varvec{\eta }}_{H}^{n+1}\Vert _0^2. \end{aligned} \end{aligned}$$
(41)

Proof

From (13) and (15), it is found that the following equations hold

$$\begin{aligned}&\left( \frac{{\textbf{u}}(t_{n+1})-{\textbf{u}}(t_{n+1})}{\Delta t},{\textbf{v}}_{h}\right) +a_1({\textbf{u}}(t_{n+1})-{\textbf{u}}(t_{n+1}),{\textbf{v}}_{h})+\frac{1}{\varepsilon _{1}}(\textrm{div}{\textbf{u}}(t_{n+1}),\textrm{div}{\textbf{v}}_h)=0, \end{aligned}$$
(42)
$$\begin{aligned}&\left( \frac{{\textbf{H}}(t_{n+1})-{\textbf{H}}(t_{n+1})}{\Delta t},{\textbf{B}}_{h}\right) +a_2({\textbf{H}}(t_{n+1})-{\textbf{H}}(t_{n+1}),{\textbf{B}}_{h}) +\frac{1}{\varepsilon _{2}}(\textrm{div}{\textbf{H}}(t_{n+1}),\textrm{div}{\textbf{B}}_h)=0. \end{aligned}$$
(43)

Applying (29) to (27)–(28) and subtracting ensuing equations from (42) and (43), respectively, we get

$$\begin{aligned}&\left( \frac{{{\textbf{e}}}_{u}^{n+1}-\tilde{{\textbf{e}}}_u^{n+1}}{\Delta t},{\textbf{v}}_{h}\right) +a_1({\textbf{e}}_{u}^{n+1}-\tilde{{\textbf{e}}}_{u}^{n+1},{\textbf{v}}_{h})+\frac{1}{\varepsilon _1}(\textrm{div}{{\textbf{e}}}_{u}^{n+1},\textrm{div}{\textbf{v}}_{h})=0,\end{aligned}$$
(44)
$$\begin{aligned}&\left( \frac{{{\textbf{e}}}_{H}^{n+1}-\tilde{{\textbf{e}}}_H^{n+1}}{\Delta t},{\textbf{B}}_{h}\right) +a_2({\textbf{e}}_{H}^{n+1}-\tilde{{\textbf{e}}}_{H}^{n+1},{\textbf{B}}_{h})+\frac{1}{\varepsilon _2}(\textrm{div}{{\textbf{e}}}_{H}^{n+1},\textrm{div}{\textbf{B}}_{h})=0. \end{aligned}$$
(45)

Then, set \({\textbf{v}}_{h}=2\Delta t\varvec{\phi }_h^{n+1},{\textbf{B}}_{h}=2\Delta t\varvec{\psi }_h^{n+1}\) in (44) and (45), respectively, and decompose the errors.

$$\begin{aligned} \begin{aligned}&\Vert {\varvec{\phi }}_{h}^{n+1}\Vert _0^{2} -\Vert \tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}+\Vert \varvec{\phi }_{h}^{n+1}-\tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2} \\&\quad +R_e^{-1}\Delta t\left( \Vert \nabla {\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}-\Vert \nabla \tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0 ^{2}+\Vert \nabla ({\varvec{\phi }}_{h}^{n+1}-\tilde{\varvec{\phi }}_{h}^{n+1})\Vert _0^2\right) \\&\quad +\Vert \varvec{\psi }_{h}^{n+1}\Vert _0 ^{2}-\Vert \tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0 ^{2} +\Vert \varvec{\psi }_{h}^{n+1}-\tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0 ^{2}+R_m^{-1} \Delta t \left( \Vert \textrm{curl}\varvec{\psi }_{h}^{n+1}\Vert _0^{2}- \Vert \textrm{curl}\tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0 ^{2}\right) \\&\quad +R_m^{-1} \Delta t \Vert \textrm{curl}(\varvec{\psi }_{h}^{n+1}-\tilde{\varvec{\psi }}_{h}^{n+1})\Vert _0^{2}+\frac{2\Delta t}{\varepsilon _1}\Vert \textrm{div}{\varvec{\phi }}_{h}^{n+1}\Vert _0^2+\frac{2\Delta t}{\varepsilon _2}\Vert \textrm{div}{\varvec{\psi }}_{h}^{n+1}\Vert _0^2\\&\quad \le \frac{\Delta t}{\varepsilon _1}\Vert \textrm{div}{\varvec{\eta }}_{u}^{n+1}\Vert _0^2+\frac{\Delta t}{\varepsilon _1}\Vert \textrm{div}\varvec{\phi }_{h}^{n+1}\Vert _0^2+\frac{\Delta t}{\varepsilon _2}\Vert \textrm{div}{\varvec{\eta }}_{H}^{n+1}\Vert _0^2+\frac{\Delta t}{\varepsilon _2}\Vert \textrm{div}\varvec{\psi }_{h}^{n+1}\Vert _0^2, \end{aligned} \end{aligned}$$

where we have used the Cauchy-Schwarz and Young inequalities. Then, the desired result is obtained. \(\square \)

Now, we are ready to state the main result of this section.

Theorem 4.1

For the 2D thermally coupled incompressible MHD equations, under Assumption 4.1 and the assumption of Theorem 3.1, we have the following estimate

$$\begin{aligned}&\Vert {\textbf{u}}(t_N)-{\textbf{u}}_h^N\Vert _0 ^{2} +\Vert {\textbf{H}}(t_N)-{\textbf{H}}_h^N\Vert _0 ^{2} +\Vert \theta (t_N)-\theta _h^N\Vert _0 ^{2}\\&\quad +\frac{\Delta t}{r}\Vert p(t_N)-{\tilde{p}}_h^{N}\Vert _0^2+|Q(t_N)-Q^{N}|^2\\&\quad +\frac{R_e^{-1}}{2} \Delta t \sum \limits _{n=0}^{N-1}\Vert \nabla ({\textbf{u}}(t_n)-{\textbf{u}}_h^n)\Vert _0 ^{2}+\frac{R_m^{-1}}{2} \Delta t\sum \limits _{n=0}^{N-1} \Vert \textrm{curl}({\textbf{H}}(t_n)-{\textbf{H}}_h^n)\Vert _0 ^{2}\\&\quad +\kappa \sum \limits _{n=0}^{N-1}\Delta t \Vert \nabla (\theta (t_n)-\theta _h^n)\Vert _0 ^{2} \\&\quad +\frac{\Delta t}{\varepsilon _1}\sum \limits _{n=0}^{N-1}\Vert \textrm{div}({\textbf{u}}(t_n)-{\textbf{u}}_h^n)\Vert _0^2+\frac{\Delta t}{2\varepsilon _2}\sum \limits _{n=0}^{N-1}\Vert \textrm{div}({\textbf{H}}(t_n)-{\textbf{H}}_h^n)\Vert _0^2\le c_1(\Delta t^2+h^4), \end{aligned}$$

where \(c_1=c_1(R_e,R_m,s,\kappa ,\varepsilon _1,\varepsilon _2,r,\beta )\) is a positive constant.

Proof

The proof is similar to the 3D case (see Theorem 4.2) except some bounds as follows. For the 2D case, the terms \(A_2,D_2,E_2,F_2\) can be bounded by

$$\begin{aligned} \begin{aligned} A_2&\le \delta _4R_e^{-1}\Delta t\Vert \nabla \tilde{{\varvec{\phi }}}_h^{n+1}\Vert _{0}^{2}+\delta _5R_e^{-1}\Delta t\Vert \nabla {\varvec{\phi }}_h^{n}\Vert _{0}^{2}\\&\quad +cR_e\Delta t^2\Vert \nabla {\textbf{u}}_{t}\Vert ^{2}_{L^{2}(t_{n},t_{n+1};L^{2}(\Omega )^2)}\Vert \nabla R_h{\textbf{u}}(t_n)\Vert _{0}^{2}\\&\quad +cR_e^{3}\Delta t^3\Vert \nabla {\textbf{u}}_{t}\Vert ^{4 }_{L^{2}(t_{n},t_{n+1};L^{2}(\Omega )^2)}\Vert {\varvec{\phi }}_h^n\Vert _{0}^{2}+cR_e\Delta t\Vert \nabla {\varvec{\eta }}_u^{n}\Vert _{0}^{2}\Vert \nabla {\textbf{u}}_{h}^{n}\Vert _{0}^{2}\\&\quad +cR_e^3\Delta t\Vert {\textbf{u}}_{h}^{n}\Vert _{0}^{2}\Vert \nabla {\textbf{u}}_{h}^{n}\Vert _{0}^{2}\Vert {\varvec{\phi }}_h^{n}\Vert _{0}^{2},\\ D_2&\le \delta _{6}R_e^{-1}\Delta t\Vert \nabla \tilde{\varvec{\phi }}_{h}^{n+1}\Vert _0^2 +cR_es^2\Delta t^2\Vert {\textbf{H}}_{t}\Vert ^2_{L^2(t_n,t_{n+1};H^2(\Omega )^2)}\Vert {\textbf{H}}_h^n\Vert _0^2\\&\quad +cR_es^2\Delta t\Vert \textrm{curl}\varvec{\eta }_H^{n}\Vert _0^2\Vert \textrm{curl}{\textbf{H}}_{h}^{n}\Vert _0^2\\&\quad +cR_es^2\Delta t\Vert \varvec{\psi }_h^n\Vert _0^2(\Vert {\textbf{H}}(t_n)\Vert _2^2+\Vert \textrm{curl}{\varvec{\psi }}_h^n\Vert _0^2 +\Vert \textrm{div}{\varvec{\psi }}_h^n\Vert _0^2+h^{-2}\Vert \textrm{curl}\varvec{\eta }_H^{n}\Vert _0^2),\\ E_2&\le \delta _{7}R_m^{-1}\Delta t\Vert \textrm{curl}\tilde{\varvec{\psi }}_{h}^{n+1}\Vert _0^2+\delta _{8}R_e^{-1}\Delta t\Vert \nabla {\varvec{\phi }}_h^{n}\Vert _{0}^{2}\\&\quad + cR_ms^2\Delta t^2\Vert {\textbf{u}}_{t}\Vert ^2_{L^2(t_n,t_{n+1};H^2(\Omega )^2)}\Vert {\textbf{H}}_h^n\Vert _0^2\\&\quad +cR_ms^2\Delta t\Vert \nabla \varvec{\eta }_u^{n}\Vert _0^2\Vert \textrm{curl}{\textbf{H}}_{h}^{n}\Vert _0^2+cR_m^2s^2R_e\Delta t\Vert {\textbf{H}}_h^n\Vert _0^2(\Vert \textrm{curl}{\textbf{H}}_h^n\Vert _0^2+\Vert \textrm{div}{\textbf{H}}_h^n\Vert _0^2)\Vert {\varvec{\phi }}_h^n\Vert _0^2,\\ F_2&\le \delta _{9}\kappa \Delta t\Vert \nabla \vartheta _{h}^{n+1}\Vert _0^2+\delta _{10}\kappa \Delta t\Vert \nabla \vartheta _{h}^{n}\Vert _0^2+c\kappa ^{-1}\Delta t^2\Vert \theta _{t}\Vert ^2_{L^2(t_n,t_{n+1};H^2(\Omega ))}\Vert {\textbf{u}}_h^n\Vert _0^2\\&\quad +c\kappa ^{-1}\Delta t\Vert \nabla \varvec{\eta }_\theta ^{n}\Vert _0^2\Vert \nabla {\textbf{u}}_{h}^{n}\Vert _0^2+c\kappa ^{-3}\Delta t\Vert {\textbf{u}}_h^n\Vert _0^2\Vert \nabla {\textbf{u}}_h^n\Vert _0^2\Vert \vartheta _{h}^{n}\Vert _0^2. \end{aligned} \end{aligned}$$

Then, according to the proof in Appendix A.2, it is easy to get the desired result.

\(\square \)

For the 2D thermally coupled incompressible MHD equations, we find that there is no constraint on the time step. Further, we consider the error estimate for the 3D case.

Theorem 4.2

For the 3D thermally coupled incompressible MHD equations, under Assumption 4.1 and the assumption of Theorem 3.1, if

$$\begin{aligned} \begin{aligned}&c_2(R_e+\kappa ^{-1})\exp \left( T{\mathbb {W}}_0\right) (\Delta t+h^2)(\Delta t^{\frac{1}{2}} R_e^{\frac{1}{2}}+c_{in}h)\\&\quad \le \frac{\min \{R_e^{-1},\kappa \}}{4},\\&c_2s^2\exp \left( T{\mathbb {W}}_0\right) (\Delta t+h^2)\left( R_m\Delta t^{\frac{1}{2}} R_e^{\frac{1}{2}}+R_e\Delta t^{\frac{1}{2}}(R_m^{\frac{1}{2}}\right. \\&\quad \left. +\varepsilon _2^{\frac{1}{2}})+(R_e+R_m)c_{in}h)\right) \le \frac{\min \{R_m^{-1},\varepsilon _2^{-1}\}}{4}, \end{aligned} \end{aligned}$$
(46)

where \(c_2=c_2(R_e,R_m,s,\kappa ,\varepsilon _1,\varepsilon _2,r,\beta )\) is a positive constant, \({\mathbb {W}}_0=W_1+W_2+W_3+\frac{9}{2}\) and \(W_1,W_2,W_3\) are defined in (A.32), then we have

$$\begin{aligned}&\Vert {\textbf{u}}(t_N)-{\textbf{u}}_h^N\Vert _0 ^{2} +\Vert {\textbf{H}}(t_N)-{\textbf{H}}_h^N\Vert _0 ^{2} +\Vert \theta (t_N)-\theta _h^N\Vert _0 ^{2}\\&\quad +\frac{\Delta t}{r}\Vert p(t_N)-{\tilde{p}}_h^{N}\Vert _0^2+|Q(t_N)-Q^{N}|^2\\&\quad +\frac{R_e^{-1}}{2} \Delta t \sum \limits _{n=0}^{N-1}\Vert \nabla ({\textbf{u}}(t_n)-{\textbf{u}}_h^n)\Vert _0 ^{2}+\frac{R_m^{-1}}{2} \Delta t\sum \limits _{n=0}^{N-1} \Vert \textrm{curl}({\textbf{H}}(t_n)-{\textbf{H}}_h^n)\Vert _0 ^{2}\\&\quad +\kappa \sum \limits _{n=0}^{N-1}\Delta t \Vert \nabla (\theta (t_n)-\theta _h^n)\Vert _0 ^{2} \\&\quad +\frac{\Delta t}{\varepsilon _1}\sum \limits _{n=0}^{N-1}\Vert \textrm{div}({\textbf{u}}(t_n)-{\textbf{u}}_h^n)\Vert _0^2\\&\quad +\frac{\Delta t}{2\varepsilon _2}\sum \limits _{n=0}^{N-1}\Vert \textrm{div}({\textbf{H}}(t_n)-{\textbf{H}}_h^n)\Vert _0^2\le c_2(\Delta t^2+h^4). \end{aligned}$$

Proof

See Appendix A.2. \(\square \)

5 Numerical Experiment

In this section, we present some numerical examples to verify the established theoretical findings, and show the performances of Algorithm 3.1 for the thermally coupled incompressible MHD problem. In order to gauge the effectiveness of the proposed algorithm, we compare it with the classical implicit/explicit scheme, which reads as

Algorithm 5.1

Given \({\textbf{u}}_h^{n}\in {\textbf{X}}_h,{\textbf{H}}^{n}_h\in {\textbf{W}}_h\) and \(\theta ^n_h\in Y_h\), find \(({\textbf{u}}^{n+1}_{h},p^{n+1}_{h},{\textbf{H}}^{n+1}_{h},\theta ^{n+1}_{h})\in {\textbf{X}}_h\times M_h\times {\textbf{W}}_h\times Y_h\) satisfying: for all \(({\textbf{v}}_h,q_h,{\textbf{B}}_{h},\varphi _h) \in {\textbf{X}}_h\times M_h\times {\textbf{W}}_h\times Y_h\),

$$\begin{aligned} \begin{aligned}&\left( \frac{{\textbf{u}}^{n+1}_{h}-{\textbf{u}}^{n}_{h}}{\Delta t},{\textbf{v}}_{h}\right) +a_1\left( {\textbf{u}}^{n+1}_{h}, {\textbf{v}}_{h}\right) +b_{1}\left( {\textbf{u}}^{n}_{h},{\textbf{u}}^{n}_{h},{\textbf{v}}_{h}\right) +s b_{2}\left( {\textbf{H}}^{n}_{h}, {\textbf{H}}^{n}_{h},{\textbf{v}}_{h}\right) -d( {\textbf{v}}_{h},p_h^{n+1})+d({\textbf{u}}_h^{n+1}, q_h)\\&\quad -({\textbf{j}}\beta \theta ^{n}_h,{\textbf{v}}_h)=\left( {\textbf{f}}^{n+1},{\textbf{v}}_{h}\right) ,\\&\quad \left( \dfrac{{\textbf{H}}^{n+1}_{h}-{\textbf{H}}^{n}_{h}}{\Delta t},{\textbf{B}}_{h}\right) +a_2\left( {\textbf{H}}^{n+1}_{h},\textrm{curl}{\textbf{B}}_{h}\right) -s b_{2}\left( {\textbf{H}}^{n}_{h},{\textbf{B}}_{h},{\textbf{u}}^{n}_{h} \right) +R_m^{-1}s\left( \textrm{div}{\textbf{H}}^{n+1}_{h},\textrm{div}{\textbf{B}}_h\right) =\left( {\textbf{g}}^{n+1},\textrm{curl}{\textbf{B}}_{h}\right) ,\\&\quad \left( \frac{\theta ^{n+1}_{h}-\theta ^{n}_{h}}{\Delta t},\varphi _{h}\right) +a_3\left( \theta ^{n+1}_{h},\varphi _{h}\right) + b_{3}\left( {\textbf{u}}^{n}_{h},\theta ^{n}_{h},\varphi _{h} \right) =\left( \omega ^{n+1},\varphi _{h}\right) . \end{aligned} \end{aligned}$$

5.1 Stability Test

In order to verify the stability of the presented algorithm, the thermally coupled incompressible MHD problem (1)–(3) in the unit square domain \( [0,1]^2\) is considered. Set physical parameters \(R_e=R_m=50,\) \(s=\kappa =\beta =1\) and the final time \(T = 10\). We choose \(r=\varepsilon _1=\varepsilon _2=1\) and impose the source functions \({\textbf{f}}={\textbf{g}}={\textbf{0}},\) \(\omega =0.\) The initial values are taken as follows:

$$\begin{aligned} {\textbf{u}}_0(x,y)&=(10x^2 (x-1)^2 y (y-1) (2y-1), -10y^2 (y-1)^2 x (x-1) (2x-1)),\\ {\textbf{B}}_0(x,y)&=(\sin (\pi x) \cos (\pi y),-\sin (\pi y) \cos (\pi x)),\quad p_0(x,y)=0,\\ \theta _0(x,y)&=10x^2 (x-1)^2 y (y-1) (2y-1)-10y^2 (y-1)^2 x (x-1) (2x-1). \end{aligned}$$

Due to the zero source functions and the homogeneous boundary conditions in the considered domain, the numerical solutions are expected to remain bounded over time.

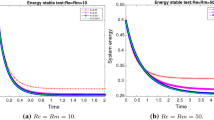
We denote \(E_h^n= \Vert {\textbf{u}}^n_h\Vert ^2_0 +\Vert {\textbf{H}}^n_h\Vert _0^2 +\Vert \theta _h^n\Vert _0^2+\frac{\Delta t}{r}\Vert {\tilde{p}}_h^n\Vert _0^2+|Q^n|^2\), which will be computed with the fixed mesh size \(h=\frac{1}{32}\). Figure 1 shows the values of \(E_h^n\) and \(Q^n\) versus time evolution for different time steps \(\Delta t= 0.1,~0.05,~0.01,~0.005\). We observe that it shows monotonic decay for all time step sizes, which numerically confirms that the proposed algorithm is unconditionally stable. The scalar auxiliary variable \(Q^n\) of the numerical algorithm converges to 1 when the time step \(\Delta t\) decreases.

Fig. 1
figure 1

The values of \(E_h^n\) (a) and \(Q^n\) (b) with different time steps

Full size image

Further, resetting the physical parameters \(R_e=R_m=100,~s=10,\) and taking the time-step \(\Delta t=0.1,~0.05,~0.01\), we compare the value of \(\Vert {\textbf{u}}_h^n\Vert _0^2+\Vert {\textbf{H}}_h^n\Vert _0^2+\Vert \theta _h^n\Vert _0^2\) by Algorithm 3.1 with that of Algorithm 5.1 showed in Fig. 2. It is clear that both algorithms are stable with the time step \(\Delta t=0.01\). However, Algorithm 5.1 blows up when \(\Delta t =0.1,~0.05\), which shows that the classical implicit/explicit algorithm does not work well when some large time steps are adopted. On the contrary, Algorithm 3.1 still works well.

Fig. 2
figure 2

The values obtained by Algorithm 3.1 (a) and Algorithm 5.1 (b) with different time steps

Full size image

5.2 Convergence Test

5.2.1 2D Convergence Test

Based on the same bounded domain as it in the unconditional stability test, we consider two-dimensional time-dependent thermally coupled incompressible MHD equations with the exact solution as follows:

$$\begin{aligned} u_{1}&=\alpha \pi \sin ^2(\pi x)\sin (\pi y)\cos (\pi y)\cos (t),\quad u_{2}=-\alpha \pi \sin (\pi x)\sin ^2(\pi y)\cos (\pi x)\cos (t),\\ H_{1}&=\alpha \sin (\pi x)\cos (\pi y)\cos (t),\quad H_{2}=-\alpha \cos (\pi x)\sin (\pi y)\cos (t),\\ \theta&=\alpha \pi \sin ^2(\pi x)\sin (\pi y)\cos (\pi y)\cos (t)-\alpha \pi \sin (\pi x)\sin ^2(\pi y)\cos (\pi x)\cos (t),\\ p&=\alpha \cos (\pi x)\cos (\pi y)\cos (t), \end{aligned}$$

where we choose \(\alpha =0.01.\) The boundary conditions and the body forces are given by the exact solution. Set \(Err({e}_i)=\Big (\Delta t\sum \limits _{n=0}^{N-1}\Vert {e}_i^{n+1}\Vert _{0}^2 \Big )^{\frac{1}{2}}\) with \(i={\textbf{u}},\) \({\textbf{H}},\) p and \(\theta .\) The errors for corresponding norms and convergence rates are tested with parameters \(R_e=R_m=s=\kappa =\beta =1\), \(r=\varepsilon _1=\varepsilon _2=1\) and the terminal time \(T=1\). Results with various time-space steps such that \(\Delta t=h^2\) are listed in Table 1. This table shows that the proposed algorithm works well and keeps the convergence rates just like the theoretical analysis.

Table 1 Errors and convergence rates of the current algorithm with \(\Delta t=h^2\) for the 2D problem
Full size table

5.2.2 3D Convergence Test

This example is to test the convergence rate for the 3D thermally coupled incompressible magnetohydrodynamic system in the domain \(\Omega =[0,1]\times [0,1]\times [0,1]\). The right-hand sides \({\textbf{f}}, {\textbf{g}},\omega \) and boundary conditions are chosen such that the exact solution is given as

$$\begin{aligned}&u_{1}=y^2z^2\sin (t),\quad u_{2}=x^2z^2\sin (t),\quad u_{3}=x^2y^2\sin (t),\\&H_{1}=y(1-y)^2z(1-z)^2\sin (t),\quad H_{2}=x(1-x)^2z(1-z)^2\sin (t),\\&\quad H_{3}=x(1-x)^2y(1-y)^2\sin (t), \\&\theta = \sin (\pi x)\sin (\pi y)\sin (\pi z)\sin (t),\quad p=(1-x)(1-y)(1-z)\sin (t). \end{aligned}$$

The selection of parameters \(R_e,~R_m,~s,~\kappa ,~\beta ,~r\) and the terminal time T is the same as those in the 2D convergence test. The other parameters are set as \(\varepsilon _1=\varepsilon _2=0.001\). The errors for corresponding norms and convergence rates are displayed in Table 2, from which we can see that numerical results are in good agreement with the theoretical analysis.

Table 2 Errors and convergence rates of the current algorithm with \(\Delta t=h^2\) for the 3D problem
Full size table

5.3 Assessment 2D Driven Cavity Flow

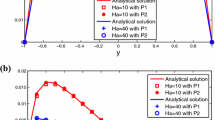
The following numerical simulations are carried out with the 2D lid-driven flow as the experimental model. The external body force is vanished for this problem. Besides, we choose the same bounded domain as it in the unconditional stability test. The initial values are given by \({\textbf{H}}_0=(0,0)\), \(\theta _0=x\) and \({\textbf{u}}_0=(0,0)\). Then, the boundary conditions are \({\textbf{u}}|_{S_T}=(w,0),~ ({\textbf{H}}\times {\textbf{n}})|_{S_T}={\textbf{H}}_1\times {\textbf{n}}\) and \(\theta |_{S_T}=\theta _0,\) where w satisfies \(w(x,1)=1\) and \(w(x,y)=0,~\forall y\in [0,1),\) and \({\textbf{H}}_1=(1,0).\) Next, we set \(R_e=10,~R_m=10,~s=\kappa =r=1,\) and \(\varepsilon _1=\varepsilon _2=0.1.\) The time step and mesh size are \(\Delta t=0.01\) and \(h=\frac{1}{32}.\) The final time T is chosen such that \(\Vert {\textbf{u}}_h^N-{\textbf{u}}_h^{N-1}\Vert _0+\Vert {\textbf{H}}^N_h-{\textbf{H}}^{N-1}_h\Vert _0\le 1.0\)E\(-05,\) which implies that the fluid fields are almost steady state. Figures 3 and 4 show numerical velocity streamlines, magnetic and isotherms obtained by Algorithms 3.1 and 5.1 with different thermal expansion coefficient. By comparison, it is easy to find that the numerical results of both algorithms are almost consistent with \(\beta =1\) and 100.

Fig. 3
figure 3

The numerical velocity field (a), magnetic field (b) and temperature (c) by Algorithm 3.1 for \(\beta =1\), \(\beta =100\) from up to down

Full size image
Fig. 4
figure 4

The numerical velocity field (a), magnetic field (b) and temperature (c) by Algorithm 5.1 for \(\beta =1\), \(\beta =100\) from up to down

Full size image

Further, we compare the computed divergence values which are listed in Tables 3 and 4. From these tables, we see that the current algorithm computes approximations with significantly better mass conservation and Gauss’s law than those of the implicit/explicit algorithm.

5.4 Assessment 3D Driven Cavity Flow

In this example, let us consider thermally coupled incompressible MHD problem in a 3D case. The domain is defined in \(\Omega = [0, 1]\times [0, 1]\times [0, 1]\). Impose boundary conditions: \({\textbf{u}}|_{S_T}=(w,0,0),~ ({\textbf{H}}\times {\textbf{n}})|_{S_T}={\textbf{H}}_1\times {\textbf{n}}\) and \(\theta |_{S_T}=\theta _0,\) where w satisfies \(w(x,y,1)=1\) and \(w(x,y,z)=0\) for \(z\ne 1 ,\) and \({\textbf{H}}_1=(1,0,0).\) We choose initial values \({\textbf{H}}_0=(0,0,0)\), \(\theta _0=x\) and \({\textbf{u}}_0=(0,0,0)\), and set time-mesh step sizes as \(\Delta t=0.01,\) \(h=\frac{1}{8}\). The final time T is chosen such that \(\Vert {\textbf{u}}_h^N-{\textbf{u}}_h^{N-1}\Vert _0+\Vert {\textbf{H}}^N_h-{\textbf{H}}^{N-1}_h\Vert _0\le 1.0E-05.\) Next, we plot the velocity streamline, isodynamic and isotherm obtained by Algorithms 3.1 and 5.1 with \(R_e=R_m=\beta =s=\kappa =r=\varepsilon _1=\varepsilon _2=1\) in Fig. 5. It is easy to find that the numerical results of both algorithms are almost consistent. Finally, we list divergence values for different algorithms in Tables 5 and 6, from which we can get that the current scheme is superior to the classical implicit/explicit scheme.

Fig. 5
figure 5

The velocity field, magnetic field and temperature from top to down by Algorithm 3.1 (left) and Algorithm 5.1 (right)

Full size image
Table 3 The divergence of velocity and magnetic fields with \(\beta =1,~r=1\) for the 2D problem
Full size table
Table 4 The divergence of velocity and magnetic fields with \(\beta =1,~\varepsilon =0.1\) for the 2D problem
Full size table

6 Conclusion

In this paper, we propose a fully decoupled finite element for solving the thermally coupled incompressible MHD problem (1)–(3), which allows solving single variable at each time layer. Theoretically, we use energy estimate to prove unconditional stability of the proposed algorithm. Further information of the convergence properties is obtained using numerical analysis under certain assumptions. Numerically, a series of numerical simulations, including the stability test, convergence rate test and assessment driven cavity flow are presented to validate the stability and accuracy of the proposed algorithm. All computational results support the theoretical analysis and demonstrate the effectiveness of the presented algorithm.

Table 5 The divergence of velocity and magnetic fields with \(~r=1\) for the 3D problem
Full size table
Table 6 The divergence of velocity and magnetic fields with \(\varepsilon =0.1\) for the 3D problem
Full size table