Abstract
In this paper, we consider the penalty based finite element methods for the 2D/3D stationary incompressible magnetohydrodynamics (MHD) equations with different Reynolds numbers. Penalty method is applied to address the incompressible constraint “\(div \,\mathbf{u }=0\)” based on two different finite element pairs \(P_{1}{-}P_{0}{-}P_{1}\) and \(P_{1}b{-}P_{1}{-}P_{1}b\). Furthermore, the proposed methods are the interesting combination of three different iterations and two-level finite element algorithm such that the uniqueness condition holds. Besides, the rigorous analysis of stability and optimal error estimate with respect to the penalty parameter \(\epsilon \) for the proposed methods are given. Extensive 2D/3D numerical tests demonstrated the competitive performance of penalty methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
MHD mainly studies the behavior of the dynamics of electrically conducting fluids (such as liquid metals, plasmas, salt water, etc.) [1,2,3]. The corresponding incompressible MHD model is a system of PDEs, which are governed by the Navier–Stokes equations and coupled with the pre-Maxwell equations. Incompressible MHD has a number of technological and industrial applications such as metallurgical engineering, electromagnetic pumping, stirring of liquid metals, and measuring flow quantities based on induction [2]. More detail physical background knowledge refer to resources [4, 5].
A considerable amount of finite element method research activity has been devoted to the analysis of the simulation of MHD flows in recent years. As far as we know that the basic research for the MHD equations can be traced back to Sermange et al. [6]. And Gunzburger et al. proposed the existence and uniqueness of the solution of a weak formulation of the MHD equations [4]. Then, Gerbeau et al. studied a stabilized method for the steady MHD equations in [7]. Recently, Wu et al. [8] given an efficient two-step algorithm for the stationary incompressible MHD equations. Zhang et al. [9] presented a streamline diffusion method for stationary incompressible MHD. Zhao et al. [10] proposed an anisotropic adaptive finite element method for MHD equations at high Hartmann numbers. And Hu et al. [11] given a stable finite element method preserving \(\nabla \cdot \mathbf{B }=0\) exactly for MHD models. More extensive investigations of the steady MHD equations can be referred to [12,13,14,15] and their references.
In this paper, we consider the following 2D/3D stationary incompressible MHD model:
under the boundary conditions:
where \({\varOmega }\) represents a convex polygonal/polyhedral domain in \(\mathbb {R}^d\), \(d=\)2 or 3, with boundary \(\partial {\varOmega }\), \(\mathbf{u }\) the velocity field, \(\mathbf{B }\) the magnetic field, \(\mathbf{f }\) and \(\mathbf{g }\) the external force terms, p the pressure, \(R_e\) the hydrodynamic Reynolds number, \(R_m\) the magnetic Reynolds number, \(S_c\) the coupling number, and \(\mathbf{n }\) is the outer unit normal of \(\partial {\varOmega }\).
It is observed that Eqs. (1) and (2) contain three nonlinear terms \((\mathbf{u }\cdot \nabla )\mathbf{u }\), \(\mathrm{curl}\mathbf{B }\times \mathbf{B }\), \(\mathrm{curl}(\mathbf{u }\times \mathbf{B })\) and velocity \(\mathbf{u }\) and pressure p are coupled together by the incompressible constraint “\(\hbox {div}\mathbf{u }=0\)”, which makes the coupled nonlinear system typically requires a very large number of degrees of freedom to resolve numerically. Hence, great attentions have been paid on iterative method to deal with the nonlinearity in recent years. The Stokes, Newton and Oseen iterative methods are considered for the stationary Navier–Stokes equations by He et al. [16] and it’s references. Then, the iterative methods in finite element approximation for the incompressible MHD equations are investigated and analyzed in [17,18,19,20].
In order to handle the incompressible constrain, the general practice is to relax the incompressibility constraint in an approximate way, resulting in a class of pseudo-compressibility methods, among which are the penalty method, the pressure stabilization method, the artificial compressibility method and the projection method [21,22,23,24,25], etc. Besides, we also proposed some decoupling method with Uzawa-type idea for the incompressible MHD equations in [26, 27]. In this study, we consider the penalty method to decouple the strong coupled stationary incompressible MHD equations.
The penalty method applied to (1) is to approximate the solution \((\mathbf{u },p,\mathbf{B })\) by \((\mathbf{u }_{\epsilon },p_{\epsilon },\mathbf{B }_{\epsilon })\) satisfying the following stationary MHD equations:
with the homogeneous boundary conditions:
where \(0<\epsilon <1\) is a penalty parameter and \(\nu _{e}=1/R_{e}\).
Although, the iterative method and penalty method decoupled and lineralized the system, the final resulting system is still a large problem to solve. Two-level scheme is an efficient key to save a large amount of CPU time with reasonable results. This idea is put forward by Xu for the nonlinear elliptic boundary value problem in [28, 29]. Recently, Layton et al. given a two-level method for the reduced MHD problem in [30, 31] and Zhang al et. studied a two-level coupled correction and decoupled parallel correction finite element methods for solving the stationary MHD equations in [32].
To complete our previous work [19, 20], we consider the two-level penalty finite element methods related to different Reynolds numbers for 2D/3D steady incompressible MHD equations in this article. In brief, we mainly consider the finite element space pair \(\mathbf{X }_{h}\times \text{ M }_{h}\times \mathbf{W }_{h}\) which does not satisfy the discrete inf-sup condition (\(P_{1}{-}P_{0}{-}P_{1}\)) or satisfies the discrete inf-sup condition (\(P_{1}b{-}P_{1}{-}P_{1}b\)). For a small \(\sigma :=\frac{\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}\Vert {\mathbf{F}}\Vert _{-1}}{(\min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\})^2}\) satisfying the uniqueness condition \(0<\sigma \le 1-(\frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}})^{\frac{1}{2}}\), we propose three two-level penalty iterative finite element method by solving the iteration solution \(((\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}^{m}),p_{\epsilon H}^{m})\) on a coarse mesh and finding a correction solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) on a fine mesh. Specifically, in the case of \(0<\sigma \le \frac{2}{5}\), \(((\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}^{m}),p_{\epsilon H}^{m})\) is obtained by the Stokes, Newton or Oseen iteration; in the case of \(\frac{2}{5}<\sigma \le \frac{5}{11}\), \(((\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}^{m}),p_{\epsilon H}^{m})\) is obtained by the Newton or Oseen iteration; in the case of \(\frac{5}{11}<\sigma \le 1-(\frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}})^{\frac{1}{2}}\), \(((\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}^{m}),p_{\epsilon H}^{m})\) is obtained by the Oseen iteration. Furthermore, the rigorous analysis of the stability and optimal error estimate under the penalty parameter \(\epsilon \) are given for the proposed schemes. Numerical tests verify the theoretical results.
The paper is organized as follows. In Sect. 2, some basic results are given. Penalty mixed finite element method is given in Sect. 3. Section 4 is devoted to uniform stability and convergence of the two-level penalty iterative methods. Numerical tests are given in Sect. 5. Finally we end with a short conclusion.
2 Functional Setting of the Stationary MHD Equations
In order to derive the appropriate variational form of problems (1) and (3), we introduce the following spaces
Denote product space \(\mathbf{W }_{0n}=H^1_0({\varOmega })^d\times H^1_n({\varOmega })^d\) equipped with the graph norm \(\Vert (\mathbf{v },\mathbf{B })\Vert _1\), where \(\Vert (\mathbf{v },\mathbf{B })\Vert _i=(\Vert \mathbf{v }\Vert _i^2+\Vert \mathbf{B }\Vert _i^2)^{\frac{1}{2}}\) for all \(\mathbf{v }\in H^i({\varOmega })^d\cap \mathbf{X }, \mathbf{B }\in H^i({\varOmega })^d\cap \mathbf{W }\)\((i=0,1,2)\). And \(H^{-1}({\varOmega })^d\) denotes the dual of \(H^1_0({\varOmega })^d\) with norm \(\Vert \mathbf{f }\Vert _{-1}=\sup \limits _{0\ne \mathbf{w }\in H^1_0({\varOmega })^d}\frac{\langle \mathbf{f },\mathbf{w }\rangle }{\Vert \mathbf{w }\Vert _1},\) where \(\langle \cdot ,\cdot \rangle \) denotes duality product between the function space \(H^1_0({\varOmega })^d\) and its dual.
Besides, we set
and we know that \(\Vert \mathbf F \Vert _{-1}\le \Vert \mathbf F \Vert _{*}\).
Then we define the following forms by
The variational formulation for (1) consists in finding \(((\mathbf{u },\mathbf{B }),p)\in \mathbf{W }_{0n}\times \text{ M }\) such that
for all \(((\mathbf{v },\varvec{{\varPsi }}),q)\in \mathbf{W }_{0n}\times \text{ M }\) and the variational formulation of (3) reads: find \(((\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\in \mathbf{W }_{0n}\times \text{ M }\) such that for all \(((\mathbf{v },\varvec{{\varPsi }}),q)\in \mathbf{W }_{0n}\times \text{ M }\),
Besides, \(A_0(\cdot ,\cdot )\) and \(A_1(\cdot ,\cdot ,\cdot )\) possess the following properties in [4]: \(\forall \)\((\mathbf{u },\mathbf{B })\), \((\mathbf{v },\varvec{{\varPsi }})\), \((\mathbf{w },\varvec{{\varPhi }})\in \mathbf{W }_{0n}\), there holds
where \(\underline{\nu }\!:=\!\min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\},\, \overline{\nu }\!:=\!\max \{R_{e}^{-1},(2+d)S_{c}R_{m}^{-1}\},\,\!\)\(N\!:=\!\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}\).
And we introduce two properties of trilinear form in [17]:
For the sake of convenience, C or c (with or without a subscript) will denotes a generic positive constant throughout the paper and we set
The following existence and uniqueness for (6) and (7) are classical results (see [19]).
Theorem 2.1
If \(R_e\), \(R_{m}\) and \(S_{c}\) satisfy the uniqueness condition
the problem (6) has a unique solution \(((\mathbf{u },\mathbf{B }),p)\in \mathbf{W }_{0n}\times \mathrm{M}\) which satisfies
Moreover, suppose that \(\mathbf{f },\ \mathbf{g }\in {L}^{2}({\varOmega })^d\), then solution \(((\mathbf{u },\mathbf{B }),p)\) of the problem (6) satisfies the following regularity
Theorem 2.2
If \(R_e\), \(R_{m}\) and \(S_{c}\) satisfy the uniqueness condition
and \(\epsilon c_{0}\le 1\), then the problem (7) has a unique solution \(((\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\in \mathbf{W }_{0n}\times \mathrm{M}\) which satisfies
Moreover, suppose that \(\mathbf{f },\ \mathbf{g }\in L^{2}({\varOmega })^d\), then solution \(((\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\) of the problem (7) satisfies the following regularity
The bounds of the error \((\mathbf u -\mathbf u _{\epsilon },\mathbf B -\mathbf B _{\epsilon })\) and \(p-p_{\epsilon }\) are stated in the following theorem (see [19] for detatil).
Theorem 2.3
Under the assumptions of Theorem 2.2, we have
3 Penalty Finite Element Galerkin Discretization
For the finite element discretization, let \(\{\tau _\mu \}\) be a family of triangulations or tetrahedrons of \({\varOmega }\) into affine-equivalent finite elements K with \(\bar{{\varOmega }}=\bigcup \limits _{K\in \tau _{\mu }}K\). Choose conforming finite element space \(\mathbf X _{H}\subset \mathbf X \), \(\text{ M }_{H}\subset \text{ M }\), \(\mathbf W _{H}\subset \mathbf W \) and \((\mathbf X _{H},\text{ M }_{H},\mathbf W _{H})\subset (\mathbf X _{h},\text{ M }_{h},\mathbf W _{h})\). Then we denote the set of all polynomials on K by \(P_{l}(K)\), \(l\ge 0\) and \(\mathbf W _{0n}^{\mu }=\text{ X }_{\mu }\times \text{ M }_{\mu }\), \(\mu =h ~or ~ H\).
We consider the following finite element pairs to investigate the relation of penalty parameter. In detail, \(\mathbf X _{\mu }\times \text{ M }_{\mu }\times \mathbf W _{\mu }\) satisfies the following properties [13, 16, 17, 24, 33]:
Let \(\rho _{\mu }\) denote the \(L^2\)-orthogonal projection which defined by
(\(\mathcal {P}_{1}\)). Firstly, we consider the unstable finite element pair
And the pair \(\mathbf X _{\mu }\times \text{ M }_{\mu }\) does not satisfy the inf-sup condition,
Then, there exists mappings \(\pi _{\mu }: H^2({\varOmega })^d\cap \mathbf V \rightarrow \mathbf X _{\mu }\) and \(\rho _{\mu }: \text{ M }\rightarrow \text{ M }_{\mu }\) satisfy
for all \(\mathbf v \in H^{2}({\varOmega })^{d}\cap \mathbf V \), \(q\in H^{1}({\varOmega })\cap \text{ M }\), and a mapping \(R_{\mu }:H^{2}({\varOmega })^d\cap \mathbf V _{n}\rightarrow \mathbf W _{\mu }\) satisfy
It is important that this pair satisfy the relation
(\(\mathcal {P}_{2}\)). Next, we employ the following stable finite element pair
where \(P_{1,\mu }^{b}=\{v_{\mu }\in C^{0}(\bar{{\varOmega }}): v_{\mu }|_{K}\in P_{1}(K)\oplus span\{\hat{b}\},~\forall K\in \tau _{\mu }\}\).
Here, \(\mathbf X _{\mu }\times \text{ M }_{\mu }\) satisfies the discrete inf-sup condition (24). In addition, (27) does not hold. Besides, there exists mappings \(\pi _{\mu }:H^{2}({\varOmega })^d\cap \mathbf X \rightarrow \mathbf X _{\mu }\), \(\rho _{\mu }:\text{ M }\rightarrow \, \text{ M }_{\mu }\) satisfy (25) and
Besides, mapping \(R_{\mu }: H^{2}({\varOmega })^d\cap \mathbf V _{n}\rightarrow \mathbf W _{\mu }\) satisfies (26).
Then, the penalty finite element discretization of (7) is: find \(((\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),p_{\epsilon \mu })\in \mathbf W _{0n}^{\mu }\times \text{ M }_{\mu }\) such that
Next, we introduce the discrete analogue of space \(\mathbf V \) as
Here, we define discrete Stokes operator \(\mathcal {A}_{1\mu }=-P_{\mu }{\varDelta }_{\mu }\), and \({\varDelta }_{\mu }\) (see [34])
where \(P_{\mu }: L^2({\varOmega })^d\rightarrow \mathbf V _{\mu }\) and define discrete operator \(\mathcal {A}_{2\mu }\mathbf B _{\mu }=R_{0\mu } (\nabla _{\mu }\times \nabla \times \mathbf{B }_{\mu }+\nabla _{\mu }\nabla \cdot \mathbf{B }_{\mu })\in \mathbf W _{\mu }\) as follows (see [33])
where \(R_{0\mu }: L^2({\varOmega })^d\rightarrow \mathbf W _{\mu }\).
Recalling the following stability and optimal error estimate (see [19]).
Theorem 3.1
Under the assumptions of Theorem 2.2 and if \(\text{ X }_{\mu }\times \text{ M }_{\mu }\) satisfies property \(\mathcal {P}_{k}\), \(k=1,2\), then (29) admits a unique solution \(((\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),p_{\epsilon \mu })\in \mathbf W _{0n}^{\mu }\times \text{ M }_{\mu } \) such that
Theorem 3.2
Under the assumptions of Theorem 2.2 and if \(\mathbf{X }_{\mu }\times \text{ M }_{\mu }\) satisfies property \(\mathcal {P}_{k}\), \(k=1,2\) and assume that \(\mu \le \left( \frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}}\right) ^{\frac{1}{2}}(1-\sigma )\), then we have the following error estimate
for \(\mathcal {P}_{1}\) and \(\mathcal {P}_{2}\), respectively.
4 Penalty Iterative Methods for the 2D/3D Stationary MHD Equations
Three iterative methods in penalty method based on finite element pair \(\mathcal {P}_{1}\) and \(\mathcal {P}_{2}\) and several two-level schemes with different stability conditions are introduced as follows.
Method 1 (Stokes iterative method). Find \(((\mathbf{u }_{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),p_{\epsilon \mu }^{n})\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\) such that for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\)
Method 2 (Newton iterative method). Find \(((\mathbf{u }_{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),p_{\epsilon \mu }^{n})\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\) such that for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\)
Method 3 (Oseen iterative method). Find \(((\mathbf{u }_{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),p_{\epsilon \mu }^{n})\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\) such that for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\)
Here, \(((\mathbf{u }_{\epsilon \mu }^{0},\mathbf{B }_{\epsilon \mu }^{0}),p_{\epsilon \mu }^{0})\) is defined by the discrete penalty equation:
for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W ^{\mu }_{0n}\times \text{ M }_{\mu }\).
On the basis of our previous work [19, 20], we have the following stability of the iterative method for \((\mathbf e ^{n},\mathbf b ^{n})=(\mathbf{u }_{\epsilon \mu }-\mathbf{u }_{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }-\mathbf{B }_{\epsilon \mu }^{n})\) and \(\eta ^{n}=p_{\epsilon \mu }-p_{\epsilon \mu }^{n}\) for \(n\ge 0\).
Theorem 4.1
Under the assumptions of Theorem 3.2 and suppose that \(\mathcal {P}_{1}\) and \(\mathcal {P}_{2}\) are valid, if \(0<\sigma \le \frac{2}{5},\) then \((\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})\) and \(p_{\epsilon \mu }^{m}\) defined by the Method 1 satisfy
and \((\mathbf e ^m,\mathbf b ^m)\), \(\eta ^m\) satisfy the following bounds:
for all \(m\ge 0\); if \(0<\sigma \le \frac{5}{11}\), then \((\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})\) and \(p_{\epsilon \mu }^{m}\) defined by the Method 2 satisfy
and \((\mathbf e ^m,\mathbf b ^m)\), \(\eta ^m\) satisfy the following bounds:
for all \(m\ge 0\); if \(0<\sigma <1\), then \((\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})\) and \(p_{\epsilon \mu }^{m}\) defined by the Method 3 satisfy
and \((\mathbf e ^m,\mathbf b ^m)\) and \(\eta ^m\) satisfy the following bounds:
for all \(m\ge 0\).
Remark 4.1
From the formulation, Method 1 is the simplest and Method 2 is the most complicated one. Then, Methods 1, 2 and 3 are stable and convergent in terms of \(0<\sigma \le 2/5\); Methods 2 and 3 are stable and convergent in terms of \(2/5<\sigma \le 5/11\); Methods 3 is stable and convergent in terms of \(5/11<\sigma <1\). Besides, Method 2 has the second order convergence rate and the best precision among them. The stability and error estimation of pressure p for finite element pair \(P_{1}{-}P_{0}{-}P_{1}\) is related to the reciprocals of penalty parameter \(\frac{1}{\epsilon }\). But, these estimations for finite element pair \(P_{1}b{-}P_{1}{-}P_{1}b\) are independent of \(\epsilon \).
4.1 Two-Level Penalty Iterative Methods with \(0<\sigma \le \frac{2}{5}\)
In this section, we consider the two-level penalty finite element methods with \(0<\sigma \le \frac{2}{5}\). The methods includes two algorithms: m iteration steps by Stokes, Newton, Oseen technique on the coarse mesh H and once correction by the three corresponding iteration on the fine mesh h.
Step I. Find a coarse grid penalty iterative solution \(((\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf W _{0n}^{H}\times \text{ M }_{H}\) defined by Method 1, 2 and 3, respectively.
Step II. Find a fine grid solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\) defined by the following Stokes, Newton and Oseen corrections, respectively.
Correction 1 Find a fine grid solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\) defined by the Stokes correction problem
for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\).
Correction 2 Find a fine grid solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\) defined by the Newton correction problem
for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\).
Correction 3 Find a fine grid solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\) defined by the Oseen correction problem
for all \(((\mathbf v ,\varvec{{\varPsi }}),q)\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\).
For the simplicity, we take \((\mathbf e _{h},\mathbf b _{h})=(\mathbf u _{\epsilon h}-\mathbf u _{\epsilon mh},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon mh})\), \(\eta _{h}=p_{\epsilon h}-p_{\epsilon mh}\). Then, we have the following theorem.
Lemma 4.1
Under the assumptions of Theorem 4.1 and \(0\!<\!\sigma \!\le \frac{2}{5}\), then \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 1–3 with Corrections 1 and 3 satisfies the following stability and error estimates:
and \((\mathbf e _{h},\mathbf b _{h})\), \(\eta _{h}\) satisfy the following bounds:
Proof
The stability estimate (43) and the error estimate obtained by Methods 1–3 with Correction 1 can be obtained by the similar technique used in [20].
Then, we give the error estimate for \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) obtained by Methods 1–3 with Correction 3.
And we have the error equation with (29) and (41)
Taking \((\mathbf v ,\varvec{{\varPsi }})=(\mathbf e _{h},\mathbf b _{h})\), \(q=\eta _{h}\) in (45), together with (9), (11), Lemma 4.1 and Theorem 3.2, we have
For \(\mathcal {P}_{1}\), from Theorem 3.2 we have
and
which implies that
For \(\mathcal {P}_{2}\), it follows from (45)–(46) and (24), we observe that
Then, we complete the proof. \(\square \)
Lemma 4.2
Under the assumptions of Theorem 4.1 and \(0\!<\!\sigma \!\le \frac{2}{5}\), then \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 1–3 with Correction 2 satisfies the following stability and error estimates:
and \((\mathbf e _{h},\mathbf b _{h})\), \(\eta _{h}\) satisfy the following bounds:
in the 2D case, and
in the 3D case.
Proof
Let \((\mathbf v ,\varvec{{\varPsi }})=(\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\) and \(q=p_{\epsilon mh}\) in (41), we derive from (9) and (10) that
which implies that
For \(\mathcal {P}_{1}\), from (53), we have
which is that
Apply the similar technique used in Lemma 4.1, we have the following estimate for \(\mathcal {P}_{2}\)
Next, we will give the error estimate.
Subtracting (41) from (29) with \(\mu =h\), we have
Taking \((\mathbf v ,\varvec{{\varPsi }})=(\mathbf e _{h},\mathbf b _{h})\), \(q=\eta _{h}\) in (58), with (9), (10), (15) and Theorem 3.1, we have
which is that
For \(\mathcal {P}_{1}\), from (60), Theorems 3.2 and 4.1, we have
and with (59) and (61), we have
with some simple calculations, we complete the proof of the estimate for \(\mathcal {P}_{1}\).
And for \(\mathcal {P}_{2}\), from (60), Theorems 3.2 and 4.1, we have
and with (24), (8), Theorems 3.2 and 4.1, we deduce that
On the other hand, in the 2D case, applying the inverse inequality
in the estimate of the trilinear term, from (64), Theorems 3.2 and 4.1, we derive that
For \(\mathcal {P}_{1}\), with (67), Theorems 3.2 and 4.1, we have
and with (68), we have
which is that
And for \(\mathcal {P}_{2}\), from Theorems 3.2, 4.1 and (67), we have
and with (24), (8), (70), Theorems 3.2 and 4.1, we deduce that
Then, we complete the proof. \(\square \)
Theorem 4.2
Under the assumptions of Theorem 4.1, \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 1–3 with Corrections 1 and 3 satisfies the following error estimates for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^2=O(\epsilon ^{\frac{1}{2}}h)\) and the convergence rate is \(O(h^{\frac{1}{2}})\); for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^2=O(h)\) and the convergence rate is O(h).
And \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 1–3 with Correction 2 satisfies the following error estimates, for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^3=O(\epsilon h|\ln h|^{-1})\) and the convergence rate is \(O(h^{\frac{1}{2}})\) in the 2D case; for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^3=O( h|\ln h|^{-1})\) and the convergence rate is O(h) in the 2D case; and for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^\frac{5}{2}=O(\epsilon ^{\frac{3}{4}} h)\) and the convergence rate is \(O(h^{\frac{1}{2}})\) in the 3D case; for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^\frac{5}{2}=O( h)\) and the convergence rate is O(h) in the 3D case.
Proof
We can finish the proof by Theorems 2.3, 3.2, Lemmas 4.1, 4.2, triangle inequality and some simple calculations. \(\square \)
Furthermore, we can conclude the comparison for the presented methods from Theorem 4.2 as follows:
Remark 4.2
From the Theorem 4.2, we know that Methods 1, 2 and 3 are stable and convergent with \(0<\sigma \le 2/5\). Accordingly, nine combinations are proposed with Methods i and Corrections j (\(i,j=1,2,3\)). And Method 2 with Correction 2 is the better choice for it’s high precision and convergence rate in terms of \(0<\sigma \le 2/5\).
4.2 Two-Level Iterative Penalty Methods with \(\frac{2}{5}<\sigma \le \frac{5}{11}\)
Here, we consider the two-level methods based on Newton and Oseen iterative solution \(((\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m),p_{\epsilon H}^{m})\) on a coarse grid \(\tau _{H}\) and the Stokes, Newton and Oseen correction solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) on a fine grid \(\tau _{h}\).
Step I. Find a coarse grid iterative solution \(((\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf W _{0n}^{H}\times \text{ M }_{H}\) defined by Method 2 and 3, respectively.
Step II. Find a fine grid solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\) defined by Correction 1–3, respectively.
Lemma 4.3
Under the assumptions of Theorem 4.1 and \(\frac{2}{5}<\sigma \le \frac{5}{11}\), then \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 2–3 with Corrections 1 and 3 satisfies the following stability:
and \((\mathbf e _{h},\mathbf b _{h})\), \(\eta _{h}\) satisfy the following bounds:
Proof
The proof is completed by a similar procedure to that of Lemma 4.1. \(\square \)
Lemma 4.4
Under the assumptions of Theorem 4.1 and \(\frac{2}{5}<\sigma \le \frac{5}{11}\), then \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 2–3 with Correction 2 satisfies the following stability and error estimates:
and \((\mathbf e _{h},\mathbf b _{h})\), \(\eta _{h}\) satisfy the following bounds:
in the 2D case, and
in the 3D case.
Proof
Refer to the proof of Lemma 4.2, we can finish the proof. \(\square \)
Theorem 4.3
Under the assumptions of Theorem 4.3, \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 2–3 with Corrections 1 and 3 satisfies the following error estimates, for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^2=O(\epsilon ^{\frac{1}{2}}h)\) and the convergence rate is \(O(h^{\frac{1}{2}})\); for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^2=O(h)\) and the convergence rate is O(h);
And \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Methods 2–3 with Correction 2 satisfies the following error estimates, for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^3=O(\epsilon h|\ln h|^{-1})\) and the convergence rate is \(O(h^{\frac{1}{2}})\) in the 2D case; for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^3=O( h|\ln h|^{-1})\) and the convergence rate is O(h) in the 2D case; and
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^\frac{5}{2}=O(\epsilon ^{\frac{3}{4}} h)\) and the convergence rate is \(O(h^{\frac{1}{2}})\) in the 3D case; for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^\frac{5}{2}=O( h)\) and the convergence rate is O(h) in the 3D case.
Proof
We can finish the proof by Theorems 2.3, 3.2, Lemmas 4.3, 4.4, triangle inequality and some simple calculations. \(\square \)
Remark 4.3
From the Theorem 4.3, we know that Methods 2 and 3 are stable and convergent with \(2/5<\sigma \le 5/11\). Accordingly, six combinations are proposed with Methods i and Corrections j (\(i=2,3; j=1,2,3\)). And Method 2 with Correction 2 is the better choice for it’s high precision and convergence rate.
4.3 Two-Level Iterative Penalty Methods with \(\frac{5}{11}<\sigma \le 1-\left( \frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}}\right) ^{\frac{1}{2}}\)
Here, we consider the two-level methods based on the iterative solution \(((\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m),p_{\epsilon H}^{m})\) on a coarse grid \(\tau _{H}\) and the Stokes, Newton and Oseen correction solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) on a fine grid \(\tau _{h}\).
Step I. Find a coarse grid iterative solution \(((\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf W _{0n}^{H}\times \text{ M }_{H}\) defined by Method 3.
Step II. Find a fine grid solution \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \text{ M }_{h}\) defined by the Correction 1–3, respectively.
Lemma 4.5
Under the assumptions of Theorem 4.1 and \(\frac{5}{11}<\sigma \le 1-\left( \frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}}\right) ^{\frac{1}{2}}\), then \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Method 3 with Corrections 1 and 3 satisfies the following stability and error estimates:
and \((\mathbf e _{h},\mathbf b _{h})\), \(\eta _{h}\), satisfy the following bounds:
Proof
The stability can be derive by the same technique used in Lemma 4.1.
Next, we give the error estimate for \((\mathbf e _{h},\mathbf b _{h}), \eta _{h}\) provided by Methods 3 with Correction 1. Refer to [20], we have
which we can get
that is
which combines Theorem 3.2 and (24), we can finish the proof of the error estimates. \(\square \)
Lemma 4.6
Under the assumptions of Theorem 4.1 and \(\frac{5}{11}<\sigma \le 1-\left( \frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}}\right) ^{\frac{1}{2}}\), then \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Method 3 with Correction 2 satisfies the following stability and error estimates:
and \((\mathbf e _{h},\mathbf b _{h})\), \(\eta _{h}\) satisfy the following bounds:
in the 2D case, and
in the 3D case.
Proof
We can complete the proof by the same fashion of the proof of lemmas 4.2 and 4.6. \(\square \)
Theorem 4.4
Under the assumptions of Theorem 4.3, \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Method 2–3 with Correction 3 satisfies the following error estimates, for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^2=O(\epsilon ^{\frac{1}{2}}h)\) and the convergence rate is \(O(h^{\frac{1}{2}})\); for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^2=O(h)\) and the convergence rate is O(h);
And \(((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\) provided by Method 3 with Correction 2 satisfies the following error estimates, for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^3=O(\epsilon h|\ln h|^{-1})\) and the convergence rate is \(O(h^{\frac{1}{2}})\) in the 2D case; for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^3=O( h|\ln h|^{-1})\) and the convergence rate is O(h) in the 2D case; and for \(\mathcal {P}_{1}\)
\(\epsilon \) and H can be taken as \(\epsilon =O(h^{\frac{1}{2}})\), \(H^\frac{5}{2}=O(\epsilon ^{\frac{3}{4}} h)\) and the convergence rate is \(O(h^{\frac{1}{2}})\) in the 3D case; for \(\mathcal {P}_{2}\), the optimal error estimates are
\(\epsilon \) and H can be taken as \(\epsilon =O(h)\), \(H^\frac{5}{2}=O( h)\) and the convergence rate is O(h) in the 3D case.
Proof
We can finish the proof by Theorems 2.3, 3.2, Lemmas 4.5, 4.6, triangle inequality and some simple calculations. \(\square \)
Remark 4.4
From the Theorem 4.4, we know that Method 3 is stable and convergent with \(\frac{5}{11}<\sigma \le 1-\left( \frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}}\right) ^{\frac{1}{2}}\). Hence, three combinations are proposed with Methods i and Corrections j (\(i=3; j=1,2,3\)). And Method 3 with Correction 2 is the better choice to solve the considered problem.
5 Numerical Results
In this section, we investigate the numerical performance of the proposed methods via a flow problem with a smooth solution and a driven cavity flow problem for the 2D/3D MHD problem. Penalty parameter \(\epsilon \) is selected as \(\epsilon =O(h^{\frac{1}{2}})\) for \(\mathcal {P}_{1}\) and \(\epsilon =O(h)\) for \(\mathcal {P}_{2}\) based on Theorems 4.2, 4.3 and 4.4 in all the following numerical tests. Then, by defining \(M_{i}+C_{j}\) denote the combination of the Method i and Correction j (\(i,\ j=1,2,3\)). The stopping criterion is based on a relative reduction in the energy norm with a tolerance of \(10^{-10}\).
5.1 Problems with Smooth Solutions
We test the accuracy performance of our proposed methods with 2D/3D smooth solution in this case. On the square domain \({\varOmega }=[0,1]^d\), \(d=2, 3\) and the exact solutions be given by
for \(d=2\) and
\(d=3\). Here, \(\alpha \) is chosen such that \(0<\sigma \le \frac{2}{5}, \frac{5}{11}\) and \( 1-\varepsilon \), where \(\varepsilon =\left( \frac{\Vert \mathbf F \Vert _{-1}}{\Vert \mathbf F \Vert _{0}}\right) ^{\frac{1}{2}}\). And the body forces \(\mathbf f \), \(\mathbf g \) are determined accordingly for any \(R_{e}\), \(R_{m}\) and \(S_{c}\).
Tables 1 and 2 present several groups of the parameter (Refer to the Remark 6.1 in our previous work [20] for the detail computational formulas). Numerical results of the presented methods with the first group parameters of Tables 1 and 2 are shown in Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14. It is observed that the results are in very good agreement with the convergence rates that are predicted by the analysis in Theorems 4.2, 4.3 and 4.4. Specifically, the magnetic field \(\mathbf B \) and the velocity field \(\mathbf u \) for \(\mathcal {P}_{1}\) has an improved convergence rate, it is even higher than the theoretical result \(O(h^{1/2})\) on count of the chosen smooth solutions for the 3D case. Since, the degrees of freedom for \(P_{1}b{-}P_{1}{-}P_{1}b\) is greater, the relative errors of \(P_{1}b{-}P_{1}{-}P_{1}b\) is smaller and the operating speed is slower than the \(P_{1}{-}P_{0}{-}P_{1}\) one.
Then, the comparison results indicate that the relative errors are almost the same for the same finite element pairs with three different iterative methods. Moreover, \(M_{1}+C_{j}\) is the quickest and \(M_{2}+C_{j}\) is the slowest one for both \(\mathcal {P}_{1}\) and \(\mathcal {P}_{2}\). The complexity of the discretization of the nonlinear terms and the order of the finite element pair are the main reasons for it. For fixed iterative methods \(M_{i} (i=1,2,3)\), \(M_{i}+C_{2}\) is more accurate than \(M_{i}+C_{1}\) and \(M_{i}+C_{3}\); \(M_{i}+C_{1}\) is the fastest one and \(M_{i}+C_{2}\) is the slowest one.
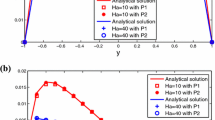
To study the effective combinative methods, the two-level combinations with respect to \(M_{2}\) and \(M_{3}\) are only considered in this paper. The relative error of \(M_{i}+C_{2}\) and \(M_{i}+C_{3}\) for \(\mathcal {P}_{1}\) and \(\mathcal {P}_{2}\) with fixed \(\alpha \) given in Tables 1 and 2 are shown in Figs. 1, 2, 3 and 4. The relative error is defined by \(\frac{\Vert |((\mathbf u -\mathbf u _{\epsilon mh},\mathbf B -\mathbf B _{\epsilon mh}),p-p_{\epsilon mh})\Vert |}{\Vert |((\mathbf u ,\mathbf B ),p)\Vert |},\) where \(\Vert |((\mathbf u ,\mathbf B ),p)\Vert |=\Vert |(\mathbf u ,\mathbf B )\Vert |_{1}+\Vert p\Vert _{0}\). The numerical results indicate that the Correction \(C_{j}, (j=2,3)\) is fixed, the nearly same convergence rates and relative errors can be obtained for current parameter configurations. Figures 5 and 6 present the comparison results of \(M_{i}+C_{2}\) and \(M_{i}+C_{3}, (i=2,3)\) for larger \(\alpha \) to investigate which combination is more effective. But it is difficult to separate the major difference between them for the estimation of \(C_{0}\) is not exactly sharp (refer to our previous work [20]). Then as a consequence, we can only conclude that \(M_{i}+C_{2}\) is more effective than \(M_{i}+C_{3}\) in accuracy comparing and we can not figure out \(M_{2}+C_{2}\) and \(M_{3}+C_{2}\) which one is the superior one from this experiment.
But in our previous work [19, 20], we closely compared \(M_{2}\) and \(M_{3}\) in numerical computation aspects. Based on these experiences, we can conclude that \(M_{2}+C_{2}\) has higher convergence speed than \(M_{3}+C_{2}\). And \(M_{3}+C_{2}\) has the most adaptability for \(\sigma \). Therefore, we only consider the scheme \(M_{2}+C_{2}\) in the next driven cavity flow problem.
5.2 Driven Cavity Flow
Let us consider a 2D/3D driven cavity flow which used in fluid dynamics. In this example, we consider the implementation domain \({\varOmega }=(-1,1)^{d}, d=2\) and \({\varOmega }=(0,1)^{3}, d=3\) with \({\varGamma }_{D}=\partial {\varOmega }\), and set the source terms to be zero. The boundary conditions are prescribed as follows:
where \(\mathbf{B }_{D}=(1,0)\) for \(d=2\);
where \(\mathbf{B }_{D}=(1,0,0)\) for \(d=3\).
According to the numerical analysis above, we only relate to the scheme \(M_{2}+C_{2}\) with \(P_{1}b{-}P_{1}{-}P_{1}b\) finite element pair for the 2D/3D driven cavity flow problem in this example. Here, we develop the further research for the hydrodynamic number \(R_{e}\). Numerical results of \(M_{2}+C_{2}\) are compared with the standard two-level iterative method to show the performance of the proposed scheme.
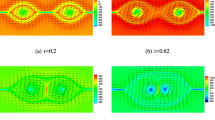
The horizontal velocity and magnetic field distribution at the mid-width with different \(R_{e}\) for 2D/3D case are presented in Figs. 7 and 8. It is observed that our results show an excellent agreement with the standard two-level iterative method. Figures 9, 10, 11, 12, 13 and 14 illustrate the numerical results of \(M_{2}+C_{2}\) for \(R_{e}=1,5\times 10^2,5\times 10^3\) and \(R_{e}=10^{-1},10, 10^2\) with \(R_{m}=1\), \(S_{c}=1\) in 2D case and 3D case, respectively. As can be seen that the velocity main vortex grows into several small ones and become more complex with the increase of \(R_{e}\). It can be inferred that more resolved vortexes may captured with the increase of \(R_{e}\).
6 Conclusions
In this article, we have presented some two-level penalty finite element methods for solving the 2D/3D steady incompressible MHD equations. And we give the rigorous proof of the stability and optimal error estimate for different finite element pair \(\mathcal {P}_{1}\) and \(\mathcal {P}_{2}\) under the penalty parameter \(\epsilon \). Based on the theoretical analysis, we know that \(M_{i}+C_{2}\, (i=1,2,3)\) is the best choice with the convergence speed and accurancy perspective than \(M_{i}+C_{1}\, (i=1,2,3)\) and \(M_{i}+C_{3}\, (i=1,2,3)\). Moreover, \(M_{3}+C_{j}\, (j=1,2,3)\) has the most adaptability for \(\sigma \). Numerical simulation results verified the theoretical results. Furthermore, \(M_{3}+C_{2}\) is the best choice to deal with large Reynolds number flows from the numerical simulations.
References
Davidson, P.: An Introduction to Magnetohydrodynamics. Cambridge University Press, Cambridge (2001)
Gerbeau, J., Bris, C., Lelièvre, T.: Mathematical Methods for the Magnetohydrodynamics of Liquid Metals, Numerical Mathematics and Scientific Computation. Oxford University Press, New York (2006)
Müller, U., Bühler, L.: Magnetofluiddynamics in Channels and Containers. Springer, Berlin (2001)
Gunzburger, M., Meir, A., Peterson, J.: On the existence, uniquess and finite element approximation of solutions of the equations of sationary, incompressible magnetohydrodynamic. Math. Comput. 56, 523–563 (1991)
Moreau, R.: Magneto-hydrodynamics. Kluwer Academic Publishers, Dordrecht (1990)
Sermange, M., Temam, R.: Some mathematical questions related to the MHD equations. Commun. Pure Appl. Math. 36, 635–664 (1983)
Gerbeau, J.: A stabilized finite element method for the incompressible magnetohydrodynamic equations. Numer. Math. 87, 83–111 (2000)
Wu, J., Liu, D., Feng, X., Huang, P.: An efficient two-step algorithm for the stationary incompressible magnetohydrodynamic equations. Appl. Math. Comput. 302, 21–33 (2017)
Zhang, G., He, Y., Zhang, Y.: Streamline diffusion finite element method for stationary incompressible magnetohydrodynamics. Numer. Methods Partial Differ. Equ. 30, 1877–1901 (2014)
Zhao, J., Mao, S., Zheng, W.: Anisotropic adaptive finite element method for magnetohydrodynamic flow at high Hartmann numbers. Appl. Math. Mech. 37, 1479–1500 (2016)
Hu, K., Ma, Y., Xu, J.: Stable finite element methods preserving \(\nabla \cdot { B}=0\) exactly for MHD models. Numer. Math. 135, 371–396 (2017)
Li, L., Zheng, W.: A robust solver for the finite element approximation of stationary incompressible MHD equations in 3D. J. Comput. Phys. 351, 254–270 (2017)
Ravindran, S.: Linear feedback control and approximation for a system governed by unsteady MHD equations. Comput. Methods Appl. Mech. Eng. 198, 524–541 (2008)
Salah, N., Soulaimani, A., Habashi, W.: A finite element method for magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 190, 5867–5892 (2001)
Meir, A., Schmidt, P.: Analysis and numerical approximation of a stationary MHD flow problem with nonideal boundary. SIAM J. Numer. Anal. 36, 1304–1332 (1999)
He, Y., Li, J.: Convergence of three iterative methods based on the finite element discretization for the stationary Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 198, 1351–1359 (2009)
Dong, X., He, Y., Zhang, Y.: Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 276, 287–311 (2014)
Dong, X., He, Y.: Two-level Newton iterative method for the 2D/3D stationary incompressible magnetohydrodynamics. J. Sci. Comput. 63, 426–451 (2015)
Su, H., Feng, X., Huang, P.: Iterative methods in penalty finite element discretization for the steady MHD equations. Comput. Methods Appl. Mech. Eng. 304, 521–545 (2016)
Su, H., Feng, X., Zhao, J.: Two-level penalty Newton iterative method for the 2D/3D stationary incompressible magnetohydrodynamics equations. J. Sci. Comput. 70(3), 1144–1179 (2017)
Shen, J.: On error estimates of some higher order projection and penalty-projection methods for Navier–Stokes equations. Numer. Math. 62, 49–73 (1992)
Shen, J.: On error estimates of the penalty method for unsteady Navier–Stokes equations. SIAM J. Numer. Anal. 32, 386–403 (1995)
He, Y.: Optimal error estimate of the penalty finite element method for the time-dependent Navier–Stokes equations. Math. Comput. 74, 1201–1216 (2005)
He, Y., Li, J., Yang, X.: Two-level penalized finite element methods for the stationary Navier–Stoke equations. Int. J. Inf. Syst. Sci. 2, 131–143 (2006)
An, R., Li, Y.: Error analysis of first-order projection method for time-dependent magnetohydrodynamics equations. Appl. Numer. Math. 112, 167–181 (2017)
Zhu, T., Su, H., Feng, X.: Some Uzawa-type finite element iterative methods for the steady incompressible magnetohydrodynamic equations. Appl. Math. Comput. 302, 34–47 (2017)
Zhang, Q., Su, H., Feng, X.: A partitioned finite element scheme based on Gauge–Uzawa method for time-dependent MHD equations. Numer. Algorithms 78(1), 277–295 (2018)
Xu, J.: A novel two two-grid method for semilinear elliptic equations. SIAM J. Sci. Comput. 15, 231–237 (1994)
Xu, J.: Two-grid discretization techniques for linear and nonlinear PDEs. SIAM J. Numer. Anal. 33, 1759–1777 (1996)
Layton, W., Lenferink, H., Peterson, J.: A two-level Newton finite element algorithm for approximating electrically conducting incompressible fluid flows. Comput. Math. Appl. 28, 21–31 (1994)
Layton, W., Meir, A., Schmidtz, P.: A two-level discretization method for the stationary MHD equations. Electron. Trans. Numer. Anal. 6, 198–210 (1997)
Zhang, G., Zhang, Y., He, Y.: Two-level coupled and decoupled parallel correction methods for stationary incompressible magnetohydrodynamics. J. Sci. Comput. 65, 920–939 (2015)
He, Y.: Unconditional convergence of the Euler semi-implicit scheme for the 3D incompressible MHD equations. IMA J. Numer. Anal. 35, 767–801 (2014)
He, Y.: Two-level method based on fnite element and Crank–Nicolson extrapolation for the time-dependent Navier–Stokes equations. SIAM J. Numer. Anal. 41, 1263–1285 (2003)
Acknowledgements
The authors would like to thank the editor and referees for their valuable comments and suggestions which helped us to improve the results of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is in part supported by The National Key Research and Development Program of China (2016YFB0201304), National Magnetic Confinement Fusion Science Program of China (No. 2015GB110003), the NSF of China (Nos. 11271313, 11471329, 11401511, 11701493, 11871467 and 11461068) and the Natural Science Foundation of Xinjiang Province (No. 2016D01C073).
Rights and permissions
About this article
Cite this article
Su, H., Mao, S. & Feng, X. Optimal Error Estimates of Penalty Based Iterative Methods for Steady Incompressible Magnetohydrodynamics Equations with Different Viscosities. J Sci Comput 79, 1078–1110 (2019). https://doi.org/10.1007/s10915-018-0883-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0883-7