Two-Level Penalty Newton Iterative Method for the 2D/3D Stationary Incompressible Magnetohydrodynamics Equations

Abstract

This work is concerned with the study of two-level penalty finite element method for the 2D/3D stationary incompressible magnetohydrodynamics equations. The new method is an interesting combination of the Newton iteration and two-level penalty finite element algorithm with two different finite element pairs $P_{1}b$-$P_{1}$-$P_{1}b$ and $P_{1}$-$P_{0}$-$P_{1}$. Moreover, the rigorous analysis of stability and error estimate for the proposed method are given. Numerical results verify the theoretical results and show the applicability and effectiveness of the presented scheme.

1 Introduction

MHD mainly studies the dynamics of electrically conducting fluids and these MHD flows are governed by the Navier–Stokes equations and coupled with the pre-Maxwell equations. In addition, MHD is of great importance in many problems of engineering. The design of cooling systems with liquid metals for a nuclear reactor, MHD generators, accelerators, pumps and flowmeters are all such applications. Therefore, it is necessary to devise efficient numerical strategy for solving the MHD problem. Resources [1, 2] provide more physical background knowledge.

In this paper, we consider the stationary incompressible MHD model as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} -R_e^{-1}\Delta \mathbf u +(\mathbf u \cdot \nabla )\mathbf u +\nabla p-S_c\mathrm{curl}{} \mathbf B \times \mathbf B =\mathbf f , &{}\hbox {in}~{\Omega },\\ \mathrm{div} \mathbf u =0,&{} \hbox {in}~\Omega ,\\ S_c R_m^{-1}\hbox {curl}(\hbox {curl}{} \mathbf B )-S_c \hbox {curl}( \mathbf u \times \mathbf B ) =\mathbf g , &{} \hbox {in}~\Omega ,\\ \mathrm{div} \mathbf B =0, &{}\hbox {in}~\Omega ,\\ \end{array} \right. \end{aligned}$$

(1)

along with the boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{llll} \mathbf u |_{\partial \Omega }=0, ~(\hbox {no-slip condition}),\\ \mathbf B \cdot \mathbf n |_{\partial \Omega }=0,\ \ \mathbf n \times \mathrm{curl}{} \mathbf B |_{\partial \Omega }=0, ~(\hbox {perfectly wall}),\\ \end{array} \right. \end{aligned}$$

(2)

where $\Omega$ represents a polyhedral domain in $\mathbb {R}^d$, $d=$2 or 3, with boundary $\partial \Omega$, $\mathbf u$ the velocity field, $\mathbf B$ the magnetic field, $\mathbf f$ and $\mathbf g$ the external force terms, p the pressure, $R_e$ the hydrodynamic Reynolds number, $R_m$ the magnetic Reynolds number, $S_c$ the coupling number, and $\mathbf n$ is the outer unit normal of $\partial \Omega$. Correspondingly, the functions $\mathbf u$, $\mathbf B$, $\mathbf f$ and $\mathbf g$ can be described by:

$$\begin{aligned} \mathbf u&=(u_1(x),u_2(x)), \quad \mathbf B =(B_1(x),B_2(x)),\\ \mathbf f&=(f_1(x),f_2(x)), \quad \mathbf g =(g_1(x),g_2(x)), \end{aligned}$$

for $d=2$, and

$$\begin{aligned} \mathbf u&=(u_1(x),u_2(x),u_3(x)),\quad \mathbf B =(B_1(x),B_2(x),B_3(x)),\\ \mathbf f&=(f_1(x),f_2(x),f_3(x)),\quad \mathbf g =(g_1(x),g_2(x),g_3(x)), \end{aligned}$$

for $d=3$.

Investigations for the MHD equations from the perspective of various mathematical expectations thrives in the recent years. For instance, references [3–6] gave some study of well posedness, regularity and long-time behaviors of solutions and [3, 7, 8] devoted to the MHD problems from the numerical aspects. To our knowledge, the basic research for the MHD equations can be traced back to Sermange et al. [9]. And Gunzburger et al. [1] proposed the standard Galerkin finite element discretization for the stationary MHD equations. Then, Gerbeau et al. studied a stabilized finite element method for the steady MHD equations in [10]. For more extensive investigation of the steady MHD equations, please see [11–13] and their references.

It is well known that the stationary MHD equations is a strong coupled nonlinear system and it is still very difficulty to process to this system. It is because that equations (1)–(2) contain three nonlinear terms $(\mathbf u \cdot \nabla )\mathbf u$, $\mathrm{curl}{} \mathbf B \times \mathbf B$, $\mathrm{curl}(\mathbf u \times \mathbf B )$ and velocity $\mathbf{u }$, pressure p and $\mathbf{B }$ are coupled together. Hence, great attentions have been paid on iterative method in recent years. Besides, Newton iterative method for its high precision and fast resolving speed has attracted a lot of attention. For example, Newton iterative method is considered for the stationary Navier–Stokes equations by He [14], Xu and He [15]. Then, the Newton iterative method in finite element approximation for the incompressible MHD equations are investigated and analyzed in [16–18].

In addition, velocity $\mathbf u$ and pressure p are coupled together by the incompressible constraint “$\hbox {div}\mathbf u$=0”, which makes the system difficult to solve numerically. To overcome this difficulty, the usual practice is to relax the incompressibility constraint in an approximate way, resulting in a class of pseudo-compressibility methods, among which are the penalty method, the pressure stabilization method, the artificial compressibility method and the projection method [19–22], etc. In this study, we consider the penalty method to decouple the strong coupled stationary incompressible MHD equations.

The penalty method applied to (1) is to approximate the solution $(\mathbf u ,p,\mathbf{B })$ by $(\mathbf u _{\epsilon },p_{\epsilon },\mathbf{B }_{\epsilon })$ satisfying the following stationary MHD equations:

$$\begin{aligned} \left\{ \begin{array}{lll} -R_e^{-1}\Delta \mathbf u _{\epsilon }+(\mathbf u _{\epsilon }\cdot \nabla )\mathbf u _{\epsilon } -S_c\hbox {curl}{} \mathbf B _{\epsilon }\times \mathbf B _{\epsilon } +\nabla p_{\epsilon }=\mathbf f ,&{}\mathrm{in}~\Omega ,\\ \hbox {div} \mathbf u _{\epsilon } +\frac{\epsilon }{\nu _{e}} p_{\epsilon }=0,&{}\mathrm{in}~\Omega ,\\ S_c R_m^{-1}\hbox {curl}(\hbox {curl}{} \mathbf B _{\epsilon })-S_c \hbox {curl}( \mathbf u _{\epsilon }\times \mathbf B _{\epsilon }) =\mathbf g , &{} \hbox {in}~\Omega ,\\ \mathrm{div} \mathbf B _{\epsilon }=0,&{} \hbox {in}~\Omega ,\\ \end{array} \right. \end{aligned}$$

(3)

and with the homogeneous boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{llll} &{}\mathbf u _{\epsilon }|_{\partial \Omega }=0, ~(\hbox {no-slip condition}),\\ &{}\mathbf B _{\epsilon }\cdot \mathbf n |_{\partial \Omega }=0,\ \ \mathbf n \times \mathrm{curl}{} \mathbf B _{\epsilon }|_{\partial \Omega }=0, ~(\hbox {perfectly wall}),\\ \end{array} \right. \end{aligned}$$

(4)

where $0<\epsilon <1$ is a penalty parameter and $\nu _{e}=1/R_{e}$.

Although, the penalty method is to decouple $(\mathbf u ,\mathbf B )$ and p, the resulting system is still a large problem to solve. Two-level scheme is very efficient to save a large amount of computing time and give reasonable results. The main idea is to solve a small problem on a coarse mesh and correct the solution with a large linear problem on a fine mesh. This idea is put forward by Xu for the nonlinear elliptic boundary value problem in [23, 24]. Currently, some two-level strategy has been studied for the MHD equations, such as Layton et al. studied a two-level method for the reduced MHD problem in [25, 26] and Zhang studied a two-level coupled correction and decoupled parallel correction finite element methods for solving the stationary MHD equations in [27].

The present paper uses penalty finite element with two-level strategy based on two finite element discretizations for the 2D/3D stationary incompressible MHD equaions. The two-level penalty Newton iterative method involves solving m linearized variable coefficient MHD problems on the coarse mesh and a linear MHD problem with positive definite symmetric matrix. In brief, we mainly consider the finite element space pair $\mathbf X _{h}\times \hbox {M}_{h}\times \mathbf W _{h}$ which satisfies the discrete inf-sup condition ($P_{1}b$-$P_{1}$-$P_{1}b$) or does not satisfy the discrete inf-sup condition ($P_{1}$-$P_{0}$-$P_{1}$). Furthermore, the rigorous analysis of the stability and error estimate are given for the proposed scheme. Numerical tests verify the theoretical results.

The paper is organized as follows. In Sect. 2, some basic results are given. Penalty mixed finite element method is given in Sect. 3. Section 4 is devoted to the Newton penalty iterative finite element scheme. Section 5 devotes to uniform stability and convergence of the two-level Newton penalty iterative method. Section 6 is reported to show numerical performance and accuracy of our algorithm. Finally, the article is concluded in the last section.

2 Functional Setting of the Stationary MHD Equations

To obtain the weak forms of system (1) and (3), we introduce the following notations

$$\begin{aligned} \mathbf{X }&:=H^{1}_{0}(\Omega )^{d}=\{\mathbf{u }\in {H^{1}(\Omega )^{d}}: \mathbf{u }|_{\partial \Omega }=0\},\\ \mathbf{W }&:=H^{1}_{n}(\Omega )^{d}=\{\mathbf{v }\in H^{1}(\Omega )^d : \mathbf{v }\cdot \mathbf{n }|_{\partial \Omega }=0\},\\ \mathbf{V }&:=\{\mathbf{u }\in \mathbf{X }: \hbox {div}\mathbf{u }=0~\hbox {in}~\Omega \},\\ {\mathbf{V }_{n}}&:=\{\mathbf{v }\in \mathbf{W }: \hbox {div}\mathbf{v }=0~\hbox {in}~\Omega \},\\ {\hbox {M}}&:=L^{2}_{0}(\Omega )=\left\{ q\in L^{2}(\Omega ) : \int _{\Omega }qd\mathbf{x }=0\right\} . \end{aligned}$$

For simplicity, we employ the product space $\mathbf W _{0n}=H^1_0(\Omega )^d\times H^1_n(\Omega )^d$ with the usual graph norm $\Vert (\mathbf v ,\mathbf B )\Vert _1$, where $\Vert (\mathbf v ,\mathbf B )\Vert _i=(\Vert \mathbf v \Vert _i^2+\Vert \mathbf B \Vert _i^2)^{\frac{1}{2}}$ for all $\mathbf v \in H^i(\Omega )^d\cap \mathbf X , \mathbf B \in H^i(\Omega )^d\cap \mathbf W$ $(i=0,1,2)$. $\mathbf X '$, $\mathbf W '$ are the dual space of $\mathbf X$ and $\mathbf W$, respectively. And $H^{-1}(\Omega )^d$ denotes the dual of $H^1_0(\Omega )^d$ with the norm:

$$\begin{aligned} \Vert \mathbf f \Vert _{-1}=\sup _{0\ne \mathbf w \in H^1_0(\Omega )^d}\frac{\langle \mathbf f ,\mathbf w \rangle }{\Vert \mathbf w \Vert _1}, \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes duality product between the function space $H^1_0(\Omega )^d$ and its dual.

Now, it is convenient to introduce the following forms:

$$\begin{aligned} A_0((\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi }))= & {} a_0(\mathbf v ,\mathbf w )+ b_0(\varvec{\Psi },\varvec{\Phi }),\\ a_0(\mathbf v ,\mathbf w )= & {} R_e^{-1}(\nabla \mathbf v ,\nabla \mathbf w ),\\ b_0(\varvec{\Psi },\varvec{\Phi })= & {} S_c R_m^{-1}(\hbox {curl}\varvec{\Psi },\hbox {curl} \varvec{\Phi })+S_c R_m^{-1}(\hbox {div} \varvec{\Psi },\hbox {div}\varvec{\Phi }),\\ d((\mathbf v ,\varvec{\Phi }),q)= & {} (\hbox {div} \mathbf v ,q),\\ \langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle= & {} \langle \mathbf f , \mathbf v \rangle +(\mathbf g ,\varvec{\Psi }),\\ A_1((\mathbf u ,\mathbf B ),(\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi }))= & {} a_1(\mathbf u ,\mathbf v ,\mathbf w ) +c(\varvec{\Phi },\mathbf B ,\mathbf v )-c(\varvec{\Psi },\mathbf{B },\mathbf w ),\\ a_1(\mathbf u ,\mathbf v ,\mathbf w )= & {} \frac{1}{2}((\mathbf u \cdot \nabla )\mathbf v ,\mathbf w ) -\frac{1}{2}((\mathbf u \cdot \nabla )\mathbf w , \mathbf v ), \\ c(\varvec{\Phi },\mathbf B ,\mathbf v )= & {} S_c(\hbox {curl}\varvec{\Phi }\times \mathbf B ,\mathbf v ). \end{aligned}$$

Then, the standard weak form of (1) reads: find $((\mathbf u ,\mathbf B ),p)\in \mathbf W _{0n}\times \hbox {M}$ such that

$$\begin{aligned}&A_0((\mathbf u ,\mathbf B ),(\mathbf v ,\varvec{\Psi }))-d((\mathbf v ,\varvec{\Psi }),p)+ d((\mathbf u ,\mathbf B ),q) +A_1((\mathbf u ,\mathbf B ),(\mathbf u ,\mathbf B ), (\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad =\langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle , \end{aligned}$$

(5)

for all $((\mathbf{v },\varvec{\Psi }),q)\in \mathbf W _{0n}\times \hbox {M}$ and the variational formulation of (3) is: find $((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\in \mathbf W _{0n}\times \hbox {M}$ such that for all $((\mathbf{v },\varvec{\Psi }),q)\in \mathbf W _{0n}\times \hbox {M}$,

$$\begin{aligned}&A_0((\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf v ,\varvec{\Psi }))-d((\mathbf v ,\varvec{\Psi }),p_{\epsilon })+ d((\mathbf u _{\epsilon },\mathbf B _{\epsilon }),q) +A_1((\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf u _{\epsilon },\mathbf B _{\epsilon }), (\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad +\,\frac{\epsilon }{\nu _{e}}(p_{\epsilon },q)=\langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle . \end{aligned}$$

(6)

The following properties of $A_0(\cdot ,\cdot )$ and $A_1(\cdot ,\cdot ,\cdot )$ are important to give the theoretical analysis [1]: $\forall$ $(\mathbf u ,\mathbf B )$, $(\mathbf v ,\varvec{\Psi })$, $(\mathbf w ,\varvec{\Phi })\in \mathbf W _{0n}$, there holds

$$\begin{aligned} A_0((\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi }))\le & {} \max \{R_e^{-1},(2+d)S_{c}R_m^{-1}\}\Vert (\mathbf v ,\varvec{\Psi })\Vert _1\Vert (\mathbf w ,\varvec{\Phi })\Vert _1, \end{aligned}$$

(7)

$$\begin{aligned} A_0((\mathbf v ,\varvec{\Psi }),(\mathbf v ,\varvec{\Psi }))\ge & {} \min \{R_e^{-1},S_{c}C_1 R_m^{-1}\}\Vert (\mathbf v ,\varvec{\Psi })\Vert _1^2, \end{aligned}$$

(8)

$$\begin{aligned} A_1((\mathbf u ,\mathbf B ),(\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi }))\le & {} \sqrt{2}C_0^2\max \{1,\sqrt{2}S_{c}\}\Vert (\mathbf u ,\mathbf B )\Vert _1 \Vert (\mathbf v ,\varvec{\Psi })\Vert _1\Vert (\mathbf w ,\varvec{\Phi })\Vert _1, \end{aligned}$$

(9)

$$\begin{aligned} A_1((\mathbf u ,\mathbf B ),(\mathbf v ,\varvec{\Psi }),(\mathbf v ,\varvec{\Psi }))= & {} 0, \end{aligned}$$

(10)

where $C_1$ (only dependent on $\Omega$) an embedding constant of $H^1_n(\Omega )^d\hookrightarrow H^1(\Omega )^d$ ($\hookrightarrow$ denotes the continuous embedding), i.e.,

$$\begin{aligned} {\Vert \mathrm{curl} \mathbf B \Vert _0^2+\Vert \mathrm{div} \mathbf B \Vert _0^2}\ge C_1\Vert \mathbf B \Vert _1^2,\quad \forall \mathbf B \in \mathbf W , \end{aligned}$$

(11)

where $\sqrt{2}$ and d comes from the following two inequalities

$$\begin{aligned} \Vert \hbox {curl}\mathbf v \Vert _{0}\le \sqrt{2}\Vert \nabla \mathbf v \Vert _{0}, \qquad \Vert \hbox {div}\mathbf v \Vert _{0}\le \sqrt{d}\Vert \nabla \mathbf v \Vert _{0}. \end{aligned}$$

(12)

and $C_{0}$ (only dependent on $\Omega$) an embedding constant of $H^{1}(\Omega )^d\hookrightarrow L^{4}(\Omega )^d$, i.e.

$$\begin{aligned} \Vert \mathbf w \Vert _{L^{4}}\le C_{0}\Vert \nabla \mathbf w \Vert _{0},\quad \forall \mathbf w \in \mathbf X . \end{aligned}$$

Next, we define the Stokes operator $\mathcal {A}_{1}=-P\Delta$, and $\Delta$ (see [28] for details) as

$$\begin{aligned} -(\Delta \mathbf u ,\mathbf v )=(\nabla \mathbf u ,\nabla \mathbf v ), \quad \forall \mathbf u ,\mathbf v \in \mathbf X , \end{aligned}$$

where $P: L^2(\Omega )^d\rightarrow \{\mathbf{v }\in L^2(\Omega )^d,\hbox {div}\mathbf{v }=0, \mathbf{v }\cdot \mathbf n |_{\partial \Omega }=0\}$ is a $L^{2}$-orthogonal projector and define $\mathcal {A}_{1\epsilon }:=\nabla \mathbf u -\frac{1}{\epsilon }\nabla \hbox {div}\mathbf u$.

Similarly, define operator $\mathcal {A}_{2}\mathbf B =R_{0} (\nabla \times \nabla \times \mathbf{B }+\nabla \nabla \cdot \mathbf{B })\in \mathbf W$ as follows

$$\begin{aligned} (\mathcal {A}_{2}\mathbf{B },\varvec{\Psi })= (\nabla \times \mathbf{B },\nabla \times \varvec{\Psi })+(\nabla \cdot \mathbf{B },\nabla \cdot \varvec{\Psi }),\quad \forall \mathbf{B },\varvec{\Psi }\in \mathbf W , \end{aligned}$$

where $R_{0}: L^2(\Omega )^d\rightarrow \mathbf W$ is a $L^{2}$-orthogonal projector and define $\mathcal {A}_{2\epsilon }:=\mathcal {A}_{2}$.

Then, we shall make use of the following assumption for the regularity estimate of $(\mathbf u ,p,\mathbf B )$ (see [29]). Assume that the boundary of $\Omega$ is smooth and if $\partial \Omega$ is of $C^{2}$, or if $\Omega$ is a convex polygon/polyhedron, we have the following results:

Assumption A

The unique solution $(\mathbf v ,q)$ of the steady Stokes problem

$$\begin{aligned}&\Delta \mathbf v +\nabla q=\mathbf f ,\quad \hbox {div}\mathbf v =0,\quad \hbox {in}~ \Omega ,\quad \\&\mathbf v |_{\partial \Omega }=0, \end{aligned}$$

for the prescribed $\mathbf f \in L^{2}(\Omega )^d$ satisfies

$$\begin{aligned} \Vert \mathbf v \Vert _{2}+\Vert q\Vert _{1}\le C\Vert \mathbf f \Vert _{0}, \end{aligned}$$

and the Maxwell’s equations

$$\begin{aligned} \begin{array}{ll} \hbox {curl}\hbox {curl}\mathbf B =\mathbf g ,\quad \hbox {div}\mathbf B =0, &{}\hbox {in}~ \Omega ,\\ \hbox {curl}\mathbf B \times \mathbf n =0,\quad \mathbf B \cdot \mathbf n =0,&{}\hbox {on}~\partial \Omega , \end{array} \end{aligned}$$

for the prescribed $\mathbf g \in L^{2}(\Omega )^{d}$ admits a unique solution $\mathbf B \in \mathbf V _{n}$ which satisfies

$$\begin{aligned} \Vert \mathbf B \Vert _{2}\le C\Vert \mathbf g \Vert _{0}. \end{aligned}$$

Besides, we set

$$\begin{aligned} \Vert \mathbf F \Vert _{-1}=\sup _{ (0,0)\ne (\mathbf v ,\varvec{\Psi })\in \mathbf W _{0n}}\frac{\langle \mathbf F ,(\mathbf v ,\varvec{\Psi }) \rangle }{\Vert (\mathbf v ,\varvec{\Psi })\Vert _1}, \qquad \Vert \mathbf F \Vert ^2_{*}=\Vert \mathbf f \Vert ^2_{-1}+\Vert \mathbf g \Vert ^2_{0}, \end{aligned}$$

(13)

and we know that $\Vert \mathbf F \Vert _{-1}\le \Vert \mathbf F \Vert _{*}$.

And we introduce two properties of trilinear form in [16]:

$$\begin{aligned}&|A_{1}((\mathbf u ,\mathbf B ),(\mathbf w ,\varvec{\Phi }),(\mathbf v ,\varvec{\Psi }))| \le C\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\} \Vert (\mathbf u ,\mathbf B )\Vert _{0}\Vert (\mathbf w ,\varvec{\Phi })\Vert _{2} \Vert (\mathbf v ,\varvec{\Psi })\Vert _{1},\nonumber \\&\quad \forall (\mathbf u ,\mathbf B )\in L^{2}(\Omega )^d\times L^{2}(\Omega )^d, (\mathbf w ,\varvec{\Phi })\in H^{2}(\Omega )^{d}\times H^{2}(\Omega )^{d}, (\mathbf v ,\varvec{\Psi })\in \mathbf W _{0n}(\Omega ),\nonumber \\&|A_{1}((\mathbf u ,\mathbf B ),(\mathbf w ,\varvec{\Phi }),(\mathbf v ,\varvec{\Psi }))| \le C\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\} \Vert (\mathbf u ,\mathbf B )\Vert _{2}\Vert (\mathbf w ,\varvec{\Phi })\Vert _{1} \Vert (\mathbf v ,\varvec{\Psi })\Vert _{0},\nonumber \\&\quad \forall (\mathbf u ,\mathbf B )\in H^{2}(\Omega )^{d}\times H^{2}(\Omega )^{d}, (\mathbf w ,\varvec{\Phi })\in \mathbf W _{0n}(\Omega ), (\mathbf v ,\varvec{\Psi })\in L^{2}(\Omega )^d\times L^{2}(\Omega )^d. \end{aligned}$$

(14)

For the sake of convenience in writing, we set

$$\begin{aligned}&\Vert |(\mathbf w ,\varvec{\Phi })\Vert |_{i}=\hbox {min}\{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\} (\Vert \mathbf w \Vert _{i}^{2}+\Vert \varvec{\Phi }\Vert _{i}^{2})^{\frac{1}{2}},\\&\forall \mathbf w \in H^{i}(\Omega )^d\cap \mathbf X ,~\varvec{\Phi }\in H^{i}(\Omega )^d\cap \mathbf W ,~i=0,1,2, \end{aligned}$$

and

$$\begin{aligned} \hat{\nu }:=\min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\},\quad \underline{\nu }:=\max \{R_{e}^{-1},(2+d)S_{c}R_{m}^{-1}\},\quad N:=\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}. \end{aligned}$$

Here and after, C or c (with or without a subscript) will denotes a generic positive constant.

Furthermore, we recall the following lemma given in [20].

Lemma 2.1

There exists a constant $c_{0}>0$, depending only on $\Omega$ and such that if $\epsilon c_{0}\le 1$

$$\begin{aligned} \Vert \mathcal {A}_{1}\mathbf v \Vert _{0} \le c_{0}\Vert \mathcal {A}_{1\epsilon }\mathbf v \Vert _{0}. \end{aligned}$$

(15)

The following existence and uniqueness of the solution of (5) are classical results [16].

Theorem 2.1

If $R_e$, $R_{m}$ and $S_{c}$ satisfy the uniqueness condition

$$\begin{aligned} 0< \sigma :=\frac{N\Vert \mathbf F \Vert _{-1}}{\hat{\nu }^2}<1, \end{aligned}$$

(16)

the problem (5) has a unique solution $((\mathbf u ,\mathbf{B }),p)\in \mathbf W _{0n}\times \mathrm{M}$ which satisfies

$$\begin{aligned} \Vert |(\mathbf u ,\mathbf{B })\Vert |_{1}\le \Vert \mathbf{F }\Vert _{-1}. \end{aligned}$$

(17)

Moreover, suppose that $\mathbf f ,\ \mathbf g \in {L}^{2}(\Omega )^d$, then solution $((\mathbf u ,\mathbf{B }),p)$ of the problem (5) satisfies the following regularity

$$\begin{aligned} \Vert |(\mathbf u ,\mathbf{B })\Vert |_{2}+\Vert p\Vert _{1}\le C\Vert \mathbf F \Vert _{0}. \end{aligned}$$

(18)

Theorem 2.2

If $R_e$, $R_{m}$ and $S_{c}$ satisfy the uniqueness condition

$$\begin{aligned} 0< \sigma <1 \end{aligned}$$

(19)

and $\epsilon c_{0}\le 1$, then the problem (6) has a unique solution $((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\in \mathbf W _{0n}\times \mathrm{M}$ which satisfies

$$\begin{aligned} \Vert |(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon })\Vert |_{1}\le \Vert \mathbf{F }\Vert _{-1}. \end{aligned}$$

(20)

Moreover, suppose that $\mathbf f ,\ \mathbf g \in L^{2}(\Omega )^d$, then solution $((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })$ of the problem (5) satisfies the following regularity

$$\begin{aligned} \Vert |(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon })\Vert |_{2}+\Vert p_{\epsilon }\Vert _{1}\le C\Vert \mathbf F \Vert _{0}. \end{aligned}$$

(21)

Proof

We can finish the proof by the same technique used in the proof of Theorem 2.1 or refer to [18]. $\square$

The optimal bounds of the error $(\mathbf u -\mathbf u _{\epsilon },\mathbf B -\mathbf B _{\epsilon })$ and $p-p_{\epsilon }$ are stated in the following theorem (see [18] for detail).

Theorem 2.3

Under the assumptions of Theorem 2.2, we have

$$\begin{aligned} \Vert |(\mathbf u -\mathbf u _{\epsilon },\mathbf{B }-\mathbf{B }_{\epsilon })\Vert |_{1}+\Vert p-p_{\epsilon }\Vert _{0}\le C\epsilon . \end{aligned}$$

(22)

3 Penalty Finite Element Discretizations

We consider the mixed finite element method for (5) and (6). Let $\{K_H\}$ be a family of triangulations or tetrahedrons of $\Omega$ into affine-equivalent finite elements K with $\bar{\Omega }=\bigcup \limits _{K\in K_{\mu }}K$, which is assumed to be a regular and quasi-uniform partition of the domain $\Omega$ in usual sense as $\mu \rightarrow 0$. Let $\mathbf X _{H}\subset \mathbf X$, $\hbox {M}_{H}\subset \hbox {M}$ and $\mathbf W _{H}\subset \mathbf W$ and $(\mathbf X _{H},\hbox {M}_{H},\mathbf W _{H})\subset (\mathbf X _{h},\hbox {M}_{h},\mathbf W _{h})$. For simplicity sake, we denote the set of all polynomials on K by $P_{l}(K)$, $l\ge 0$ and $\mathbf W _{0n}^{\mu }=\mathbf X _{\mu }\times \hbox {M}_{\mu }$, $\mu =h ~or ~ H$.

In order to investigate the relation of penalty parameter with the finite element pair, we consider the following finite element pairs to approximate the velocity, pressure and magnetic fields. Note that $\mathbf X _{\mu }\times \hbox {M}_{\mu }\times \mathbf W _{\mu }$ satisfies the following properties [11, 14, 16, 22, 30]:

Let $\rho _{\mu }$ denote the $L^2$-orthogonal projection which defined by

$$\begin{aligned} (\rho _{\mu }q,q_{\mu })=(q,q_{\mu }),\quad \forall q\in \hbox {M},~ q_{\mu }\in \hbox {M}_{\mu }. \end{aligned}$$

(23)

($\mathcal {P}_{1}$). Firstly, we consider the unstable finite element pair

$$\begin{aligned} {\mathbf{X }_{\mu }}= & {} \{\mathbf{u }\in C^{0}({\bar{\Omega }})^d\cap \mathbf{X }: \mathbf u |_{K}\in P_{1}(K)^d,~ \forall K \in K_{\mu }\},\\ \hbox {M}_{\mu }= & {} \{q\in C^{0}({\bar{\Omega }})\cap \hbox {M}: q|_{K}\in P_{0}(K),~\forall K \in K_{\mu }\},\\ {\mathbf{W }_{\mu }}= & {} \{\mathbf{B }\in C^{0}({\bar{\Omega }})^d\cap \mathbf{W }: \mathbf{B }|_{K}\in P_{1}(K)^d,~ \forall K \in K_{\mu }\}. \end{aligned}$$

It is known that $\mathbf X _{\mu }\times \hbox {M}_{\mu }$ does not satisfy the discrete inf-sup condition,

$$\begin{aligned} \sup _{(0,0)\ne (\mathbf v _{\mu },\mathbf B _{\mu })\in \mathbf W _{0n}^{\mu } }\frac{ d((\mathbf v _{\mu },\mathbf B _{\mu }),q)}{\Vert (\mathbf v _{\mu },\mathbf B _{\mu })\Vert _1}\ge \beta _{0} \Vert q_{\mu }\Vert _0, \quad \forall q_{\mu }\in \hbox {M}_{\mu }. \end{aligned}$$

(24)

However, there exists a mapping $\pi _{\mu }: H^2(\Omega )^d\cap \mathbf V \rightarrow \mathbf X _{\mu }$ and $\rho _{\mu }: \hbox {M}\rightarrow \hbox {M}_{\mu }$ satisfy

$$\begin{aligned} \Vert \nabla (\mathbf v -\pi _{\mu }\mathbf v )\Vert _{0}\le C \mu \Vert \mathbf v \Vert _{2}, \quad \Vert q-\rho _{\mu }q\Vert _{0}\le C \mu \Vert q\Vert _{1}, \end{aligned}$$

(25)

for all $\mathbf v \in H^{2}(\Omega )^{d}\cap \mathbf V$, $q\in H^{1}(\Omega )\cap \hbox {M}$, and a mapping $R_{\mu }:H^{2}(\Omega )^d\cap \mathbf V _{n}\rightarrow \mathbf W _{\mu }$ satisfying

(26)

Meanwhile, there holds the following relation:

$$\begin{aligned} \hbox {div}\mathbf X _{\mu }=\hbox {M}_{\mu }. \end{aligned}$$

(27)

($\mathcal {P}_{2}$). Then, we may employ a stable finite element pair to approximate the velocity, pressure and magnetic field:

$$\begin{aligned} \mathbf X _{\mu }= & {} (P_{1,\mu }^{b})^d\cap \mathbf X ,\\ \hbox {M}_{\mu }= & {} \{q\in C^{0}(\bar{\Omega })\cap \hbox {M}: q|_{K}\in P_{1}(K), ~\forall K \in K_{\mu }\},\\ \mathbf W _{\mu }= & {} (P_{1,\mu }^{b})^d\cap \mathbf W , \end{aligned}$$

where

$$\begin{aligned} (P_{1,\mu }^{b})=\{v_{\mu }\in C^{0}(\bar{\Omega }): v_{\mu }|_{K}\in P_{1}(K)\oplus span\{\hat{b}\},~\forall K\in K_{\mu }\}. \end{aligned}$$

In this case, $\mathbf X _{\mu }\times \hbox {M}_{\mu }$ satisfies the discrete inf-sup condition (24). However, (27) does not hold. Besides, there exists a mapping $\pi _{\mu }:H^{2}(\Omega )^d\cap \mathbf X \rightarrow \mathbf X _{\mu }$, and $\rho _{\mu }:\hbox {M}\rightarrow$ $\hbox {M}_{\mu }$ satisfy (25) and

$$\begin{aligned} (\nabla \cdot (\mathbf v -\pi _{\mu }\mathbf v ),q)=0,~~ \forall \mathbf v \in H^{2}(\Omega )^d\cap \mathbf V , ~q\in \hbox {M}_{\mu }. \end{aligned}$$

(28)

Besides, mapping $R_{\mu }: H^{2}(\Omega )^d\cap \mathbf V _{n}\rightarrow \mathbf W _{\mu }$ satisfies (26).

Now, the corresponding discrete weak form of (6) is recast: find $((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),p_{\epsilon \mu })\in \mathbf W _{0n}^{\mu }\times \hbox {M}_{\mu }$ such that

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),(\mathbf v ,\varvec{\Psi })) +A_{1}((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon \mu })\nonumber \\&\quad +\,d((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon \mu },q) =<\mathbf F ,(\mathbf v ,\varvec{\Psi })>. \end{aligned}$$

(29)

Next, we introduce the discrete analogue of space $\mathbf V$ as

$$\begin{aligned} \mathbf{V }_{\mu }=\{\mathbf{v }\in \mathbf{X }_{\mu }:d((\mathbf{v },\varvec{\Psi }),q)=0,\forall q\in \hbox {M}_{\mu },~\varvec{\Psi }\in \mathbf W _{\mu }\}. \end{aligned}$$

Denote $P_{\mu }: L^2(\Omega )^d\rightarrow \mathbf V _{\mu }$ and $R_{0\mu }: L^2(\Omega )^d\rightarrow \mathbf W _{\mu }$ by $L^{2}$-orthogonal projectors.

Here, we define discrete Stokes operator $\mathcal {A}_{1\mu }=-P_{\mu }\Delta _{\mu }$, and $\Delta _{\mu }$ (see [28])

$$\begin{aligned} -(\Delta _{\mu }\mathbf u _{\mu },\mathbf v _{\mu })=(\nabla \mathbf u _{\mu },\nabla \mathbf v _{\mu }), \quad \forall \mathbf u _{\mu },\mathbf v _{\mu }\in \mathbf X _{\mu }, \end{aligned}$$

and define discrete operator $\mathcal {A}_{2\mu }\mathbf B _{\mu }=R_{0\mu } (\nabla _{\mu }\times \nabla \times \mathbf{B }_{\mu }+\nabla _{\mu }\nabla \cdot \mathbf{B }_{\mu })\in \mathbf W _{\mu }$ as follows (see [30])

$$\begin{aligned} (\mathcal {A}_{2\mu }\mathbf{B }_{\mu },\varvec{\Psi })= (\nabla \times \mathbf{B }_{\mu },\nabla \times \varvec{\Psi })+(\nabla \cdot \mathbf{B }_{\mu },\nabla \cdot \varvec{\Psi }),\quad \forall \mathbf{B }_{\mu },\varvec{\Psi }\in \mathbf W _{\mu }. \end{aligned}$$

Theorem 3.1

Under the assumptions of Theorem 2.2 and if $\mathbf{X }_{\mu }\times \hbox {M}_{\mu }$ satisfies property $\mathcal {P}_{k}$, $k=1,2$, then (29) admits a unique solution $((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),p_{\epsilon \mu })\in \mathbf W _{0n}^{\mu }\times \hbox {M}_{\mu }$ such that

$$\begin{aligned} \Vert |(\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu })\Vert |_{1}\le \Vert \mathbf F \Vert _{-1}, \end{aligned}$$

and

$$\begin{aligned} \Vert p_{\epsilon \mu }\Vert _{0}\le & {} \left( \frac{\nu _{e}}{\epsilon \hat{\nu }}\right) ^{\frac{1}{2}}\Vert \mathbf F \Vert _{-1}, \quad for \quad \mathcal {P}_{1},\\ \Vert p_{\epsilon \mu }\Vert _{0}\le & {} C\Vert \mathbf F \Vert _{-1}, \quad for\quad \mathcal {P}_{2}. \end{aligned}$$

Proof

Refer to the proof of Theorem 3.3 in [18] for details. $\square$

3.1 $H^1$-Error Estimate for Penalty Finite Element Galerkin Method

Theorem 3.2

Under the assumptions of Theorem 2.2 and if $\mathbf{X }_{\mu }\times \hbox {M}_{\mu }$ satisfies property $\mathcal {P}_{k}$, $k=1,2$, then we have the following error estimate

$$\begin{aligned}&\Vert |(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert |_{1} +\epsilon ^{\frac{1}{2}}\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0} \le C\epsilon ^{-\frac{1}{2}}\mu ,\quad for\quad \mathcal {P}_{1},\\&\Vert |(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert |_{1} +\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0} \le C \mu ,\quad for\quad \mathcal {P}_{2}.\\ \end{aligned}$$

Proof

Subtracting (29) from (6), we have the error equation

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf v ,\varvec{\Psi })) +A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad +\,A_{1}((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon }-p_{\epsilon \mu })\nonumber \\&\quad +\,d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },q)=0. \end{aligned}$$

(30)

Taking $(\mathbf v ,\varvec{\Psi })=(\mathbf e ,\mathbf b )$ and $q=\eta$ in (30) with $(\mathbf e ,\mathbf b )=(\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })$ and $\eta =\rho _{\mu }p_{\epsilon }-p_{\epsilon \mu }$. According to (10) and (23), we can get

$$\begin{aligned}&A_{0}((\mathbf e ,\mathbf b ),(\mathbf e ,\mathbf b )) +A_{1}((\mathbf e ,\mathbf b ),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b )) +\frac{\epsilon }{\nu _{e}}(\eta ,\eta )\nonumber \\&\quad =A_{0}((\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b ))\nonumber \\&\qquad +\,A_{1}((\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b ))\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b ))\nonumber \\&\qquad +\,d((\mathbf e ,\mathbf b ),p_{\epsilon }-\rho _{\mu }p_{\epsilon })-d((\mathbf u _{\epsilon }-\pi _{\mu }\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }-R_{\mu }\mathbf{B }_{\epsilon }),\eta ). \end{aligned}$$

(31)

Combining (8)–(9) with (16), gives

$$\begin{aligned}&A_{0}((\mathbf e ,\mathbf b ),(\mathbf e ,\mathbf b )) +A_{1}((\mathbf e ,\mathbf b ),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b )) +\frac{\epsilon }{\nu _{e}}(\eta ,\eta )\nonumber \\&\quad \ge \hat{\nu }(1-\sigma )\Vert (\mathbf e ,\mathbf b )\Vert _{1}^{2} +\frac{\epsilon }{\nu _{e}}\Vert \eta \Vert _{0}^{2}. \end{aligned}$$

(32)

Together with (7), (9) and (16), we can derive

$$\begin{aligned}&A_{0}((\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b )) +A_{1}((\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b ))\nonumber \\&\qquad +A_{1}((\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon }),(\mathbf e ,\mathbf b ))\nonumber \\&\qquad \quad \le C\Vert (\mathbf e ,\mathbf b )\Vert _{1}\Vert (\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon })\Vert _{1}. \end{aligned}$$

(33)

For $\mathcal {P}_{1}$, we use (27) to get

$$\begin{aligned}&|d((\mathbf e ,\mathbf b ),p_{\epsilon }-\rho _{\mu }p_{\epsilon })|+|d((\mathbf u _{\epsilon }-\pi _{\mu }\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }-R_{\mu }\mathbf{B }_{\epsilon }),\eta )|\nonumber \\&\quad =|d((\mathbf u _{\epsilon }-\pi _{\mu }\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }-R_{\mu }\mathbf{B }_{\epsilon }),\eta )|\nonumber \\&\quad \le \frac{\epsilon }{2\nu _{e}}\Vert \eta \Vert _{0}^2+\frac{\nu _{e}}{2\epsilon }\Vert (\mathbf u _{\epsilon }-\pi _{\mu }\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }-R_{\mu }\mathbf{B }_{\epsilon })\Vert _{1}^2, \end{aligned}$$

(34)

applying (32)–(34) and assumption $\mathcal {P}_{1}$ gives

$$\begin{aligned} \hat{\nu } (1-\sigma )\Vert (\mathbf e ,\mathbf b )\Vert _{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert \eta \Vert _{0}^2\le & {} \frac{C^2}{\hat{\nu }(1-\sigma )} \Vert (\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon })\Vert _{1}^2\nonumber \\&+\,\frac{\nu _{e}}{\epsilon }\Vert (\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon })\Vert _{1}^2\nonumber \\\le & {} C\epsilon ^{-1}\Vert (\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu }\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon })\Vert _{1}^2, \end{aligned}$$

(35)

which imply that

$$\begin{aligned} \Vert |(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert |_{1} +\epsilon ^{\frac{1}{2}}\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0} \le C\epsilon ^{-\frac{1}{2}}\mu . \end{aligned}$$

(36)

For $\mathcal {P}_{2}$, we use (28) to get

$$\begin{aligned}&|d((\mathbf e ,\mathbf b ),p_{\epsilon }-\rho _{\mu }p_{\epsilon })|+|d((\mathbf u _{\epsilon }-\pi _{\mu }\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }-R_{\mu }\mathbf{B }_{\epsilon }),\eta )|\nonumber \\&\quad =|d((\mathbf e ,\mathbf b ),p_{\epsilon }-\rho _{\mu }p_{\epsilon })|\nonumber \\&\quad \le \frac{\hat{\nu }(1-\sigma )}{4}\Vert (\mathbf e ,\mathbf b )\Vert _{1}^{2} +\frac{2}{\hat{\nu }(1-\sigma )}\Vert p_{\epsilon }-\rho _{\mu }p_{\epsilon }\Vert _{0}^{2}, \end{aligned}$$

(37)

which and (32)–(33), $\mathcal {P}_{2}$ give

$$\begin{aligned} \begin{array}{lll} \hat{\nu }\Vert (\mathbf e ,\mathbf b )\Vert _{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert \eta \Vert _{0}^2 \le \frac{4C^2}{\hat{\nu }}\Vert (\pi _{\mu }\mathbf u _{\epsilon }-\mathbf u _{\epsilon },R_{\mu } \mathbf{B }_{\epsilon }-B_{\epsilon })\Vert _{1}^{2} +\frac{4}{\hat{\nu }(1-\sigma )}\Vert p_{\epsilon }-\rho _{\mu }p_{\epsilon }\Vert _{0}^2, \end{array} \end{aligned}$$

(38)

and using (25), (26) imply that

$$\begin{aligned} \begin{array}{lll} \Vert |(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert |_{1} \le C \mu . \end{array} \end{aligned}$$

(39)

Finally, combining the discrete inf-sup condition (24) with (7), (9), (30), (39), Theorems 2.2 and 3.1, gives

$$\begin{aligned} \beta _{0}\Vert \eta \Vert _{0}\le & {} \underline{\nu }\Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1} +N\left( \Vert (\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon \mu })\Vert _{1}+\Vert (\mathbf u _{\epsilon },\mathbf{B }_{\epsilon })\Vert _{1}\right) \nonumber \\&\times \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1} +\Vert p_{\epsilon }-\rho _{\mu } p_{\epsilon }\Vert _{0}\nonumber \\\le & {} C(\Vert |(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert |_{1}+\Vert p_{\epsilon }-\rho _{\mu } p_{\epsilon }\Vert _{0}), \end{aligned}$$

(40)

which imply that

$$\begin{aligned} \begin{array}{lll} \Vert \eta \Vert _{0} \le C \mu . \end{array} \end{aligned}$$

(41)

This completes the proof. $\square$

3.2 $L^2$-Error Estimate for Penalty Finite Element Galerkin Methods

In order to analyze the error $(\mathbf u -\mathbf u _{\epsilon \mu },\mathbf B -\mathbf B _{\epsilon \mu })$ with $L^{2}$-norm, we now use the standard duality argument. Before that, we will give the duality form of (3).

Lemma 3.1

For some given $\mathbf G :=(G_{1},G_{2})\in L^{2}(\Omega )^{d}\times L^{2}(\Omega )^{d}$ and the solution of $((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })$ of (3), the duality form of (3) is find $(\mathbf w ,s,\varvec{\Phi })\in \mathbf X \times \hbox {M}\times \mathbf W$ by

$$\begin{aligned}&A_{0}((\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf v ,\varvec{\Psi }),(\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi }))\nonumber \\&\quad -\,d((\mathbf w ,\varvec{\Phi }),q)+d((\mathbf v ,\varvec{\Psi }),s) +\frac{\epsilon }{\nu _{e}}(q,s)=((\mathbf v ,\varvec{\Psi }),\mathbf G ). \end{aligned}$$

(42)

Proof

The duality form of (3) can be derived by the following technique.

Subtract (29) from (6) to get the error equation

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu }))\\&\quad +\,A_{1}(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu }))\\&\quad +\,A_{1}((\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu })) -d((\mathbf v _{\mu },\varvec{\Psi }_{\mu }),p_{\epsilon }-p_{\epsilon \mu })\\&\quad +\,d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),q_{\mu }) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },q_{\mu })=0, \end{aligned}$$

which is

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu })) +A_{1}(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu }))\\&\qquad +\,A_{1}((\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu })) -d((\mathbf v _{\mu },\varvec{\Psi }_{\mu }),p_{\epsilon }-p_{\epsilon \mu })\\&\qquad +\,d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),q_{\mu }) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },q_{\mu })\\&\quad =A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu })). \end{aligned}$$

Let $(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf B _{\epsilon }-\mathbf B _{\epsilon \mu })=(\mathbf v ,\varvec{\Psi })$, $p_{\epsilon }-p_{\epsilon \mu }=q$ and $(\mathbf v _{\mu },\varvec{\Psi }_{\mu })=(\mathbf w ,\varvec{\Phi })$, $q_{\mu }=s$ in the above equation, we have

$$\begin{aligned}&A_{0}((\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf v ,\varvec{\Psi }),(\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf w ,\varvec{\Phi }))\nonumber \\&\qquad -\,d((\mathbf w ,\varvec{\Phi }),q)+d((\mathbf v ,\varvec{\Psi }),s) +\frac{\epsilon }{\nu _{e}}(q,s)\\&\quad =A_{1}((\mathbf v ,\varvec{\Psi }),(\mathbf v ,\varvec{\Psi }) ,(\mathbf w ,\varvec{\Phi })), \end{aligned}$$

and let $A_{1}((\mathbf v ,\varvec{\Psi }),(\mathbf v ,\varvec{\Psi }) ,(\mathbf w ,\varvec{\Phi }))=(((\mathbf v ,\varvec{\Psi }),\mathbf G )$, then we can derive the duality form of (3). $\square$

As for (42), we can prove the following existence, uniqueness and regularity results.

Theorem 3.3

Under the assumptions of Theorem 3.2, (42) admits a unique solution $(\mathbf w ,s,\varvec{\Phi })\in \mathbf X \times \hbox {M}\times \mathbf W$, and $(\mathbf w ,\varvec{\Phi })$ satisfies the following estimate:

$$\begin{aligned} \begin{array}{lll} \Vert |(\mathbf w ,\varvec{\Phi })\Vert |_{1} \le C\Vert \mathbf G \Vert _{-1}. \end{array} \end{aligned}$$

(43)

Moreover, the solution $(\mathbf w ,\varvec{\Phi })$ of (42) satisfies the following regularity:

$$\begin{aligned} \begin{array}{lll} \Vert (\mathcal {A}_{1}\mathbf w ,\mathcal {A}_{2}\varvec{\Phi })\Vert _{0} +\Vert s\Vert _{1} \le C\Vert \mathbf G \Vert _{0}. \end{array} \end{aligned}$$

(44)

Proof

If $\mathbf f \in \mathbf X '$ and $\mathbf g \in \mathbf W '$, then $(\mathbf u _{\epsilon },\mathbf B _{\epsilon })$ satisfies Theorem 2.2. Then, taking $(\mathbf v ,\varvec{\Psi })=(\mathbf w ,\varvec{\Phi })$ and $q=s$ in

$$\begin{aligned}&A_{0}((\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf v ,\varvec{\Psi }),(\mathbf u _{\epsilon h},\mathbf B _{\epsilon h}),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf u _{\epsilon h},\mathbf B _{\epsilon h}),(\mathbf v ,\varvec{\Psi }),(\mathbf w ,\varvec{\Phi }))\nonumber \\&\quad -\,d((\mathbf w ,\varvec{\Phi }),q)+d((\mathbf v ,\varvec{\Psi }),s) +\frac{\epsilon }{\nu _{e}}(q,s), \end{aligned}$$

(45)

we can have

$$\begin{aligned}&A_{0}((\mathbf w ,\varvec{\Phi }),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf w ,\varvec{\Phi }),(\mathbf u _{\epsilon h},\mathbf B _{\epsilon h}),(\mathbf w ,\varvec{\Phi })) +\frac{\epsilon }{\nu _{e}}(s,s)\nonumber \\&\quad \ge \hat{\nu }\Vert (\mathbf w ,\varvec{\Phi })\Vert _{1}^2 -N \Vert (\mathbf u _{\epsilon },\mathbf B _{\epsilon })\Vert _{1}\Vert (\mathbf w ,\varvec{\Phi })\Vert _{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert s\Vert _{0}^2\nonumber \\&\quad \ge \frac{1-\sigma }{\hat{\nu }} \Vert |(\mathbf w ,\varvec{\Phi })\Vert |_{1}^2+\frac{\epsilon }{\nu _{e}}\Vert s\Vert _{0}^2, \end{aligned}$$

(46)

then we can prove that (45) is $(\mathbf W _{0n},\hbox {M})$-coercive. By the Lax-Milgram’s Lemma, (42) admits a unique solution. Using (42) and (46), we can have (43).

Moreover, we derive from (42) that

$$\begin{aligned} \left\{ \begin{array}{lll} R_{e}^{-1}\mathcal {A}_{1\epsilon }\mathbf w +\bar{a}_{1}'(\mathbf u _{\epsilon },\mathbf w )-\bar{a}_{1}(\mathbf u _{\epsilon },\mathbf w ) +S_{c}\hbox {curl}\varvec{\Phi }\times \mathbf B _{\epsilon }=G_{1},\\ S_{c}R_{m}^{-1}\mathcal {A}_{2\epsilon }{\varvec{\Phi }} +{S_{c}\hbox {curl}(\mathbf w \times \mathbf B _{\epsilon }})-c'(\mathbf B _{\epsilon },\mathbf w ) +c'(\varvec{\Phi },\mathbf u _{\epsilon })=G_2, \end{array} \right. \end{aligned}$$

(47)

where $\bar{a}_{1}'(\mathbf v ,\mathbf w )$ and $c'(B,w)$ are defined as

$$\begin{aligned} \begin{array}{lll} \langle \mathbf u ,B'(\mathbf v ,\mathbf w )\rangle _\mathbf{X ,\mathbf X '} =a_{1}(\mathbf u ,\mathbf v ,\mathbf w ), \quad \langle \varvec{\Psi },c'(\mathbf B _{\epsilon },\mathbf w )\rangle _\mathbf{W ,\mathbf W '} =c(\mathbf B _{\epsilon },\varvec{\Psi },\mathbf w ). \end{array} \end{aligned}$$

Taking the scalar product of (47) with $(\mathcal {A}_{1\epsilon }\mathbf w ,\mathcal {A}_{2\epsilon }\varvec{\Phi })$ in $L^{2}(\Omega )^{d}$ yields

$$\begin{aligned}&R_{e}^{-1}(\mathcal {A}_{1\epsilon }\mathbf w ,\mathcal {A}_{1\epsilon }\mathbf w ) +S_{c}R_{m}^{-1} ({\mathcal {A}_{1\epsilon }}\varvec{\Phi },\mathcal {A}_{2\epsilon }\varvec{\Phi }) +A_{1}(({\mathcal {A}_{1\epsilon }}\mathbf w ,\mathcal {A}_{2\epsilon }\varvec{\Phi }) ,(\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf w ,\varvec{\Phi }))\nonumber \\&\quad -A_{1}((\mathbf u _{\epsilon },\mathbf B _{\epsilon }),(\mathbf w ,\varvec{\Phi }), ({\mathcal {A}_{1\epsilon }}\mathbf w ,\mathcal {A}_{2\epsilon }\varvec{\Phi })) =(\mathbf G ,{\mathcal {A}_{1\epsilon }}\mathbf w ,\mathcal {A}_{2\epsilon }\varvec{\Phi }). \end{aligned}$$

(48)

It follows from (14), Theorem 2.1 and (43) that

$$\begin{aligned} \begin{array}{lll} \frac{1}{4\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}} \Vert (\mathcal {A}_{1\epsilon }\mathbf w ,\mathcal {A}_{2\epsilon }\varvec{\Phi })\Vert _{0}^{2} \le C(\Vert (\mathbf w ,\varvec{\Phi })\Vert _{1}^2+\Vert \mathbf G \Vert _{0}^2) \le C\Vert \mathbf G \Vert _{0}^2. \end{array} \end{aligned}$$

Taking $q=0$ in (42) with Assumption A, (14) yields

$$\begin{aligned} \Vert \nabla s\Vert _{0}\le & {} \max \{R_{e}^{-1},S_{c}R_{m}^{-1}\} \Vert (\mathcal {A}_{1\epsilon }\mathbf w ,\mathcal {A}_{2\epsilon }\varvec{\Phi })\Vert _{0}\\&+\,CN\Vert (\mathbf u _{\epsilon },\mathbf B _{\epsilon })\Vert _{1} \Vert (\mathbf w ,\varvec{\Phi })\Vert _{1}\\&+\,C\Vert (\mathcal {A}_{1}\mathbf u _{\epsilon },\mathcal {A}_{2}\mathbf B _{\epsilon })\Vert _{0}\Vert (\mathbf w ,\varvec{\Phi })\Vert _{1}\\\le & {} C\Vert \mathbf G \Vert _{0}, \end{aligned}$$

Then, we can finish the proof with the above estimations and Lemma 2.1. $\square$

From (44) and the property $\mathcal {P}_{1}$ or $\mathcal {P}_{2}$, we deduce that $((\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }),\rho _{\mu }s)$ satisfies the following error estimate results:

$$\begin{aligned} \begin{array}{lll} \Vert (\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi })\Vert _{1} +\Vert s-\rho _{\mu }s\Vert _{0}\le C \mu \Vert \mathbf G \Vert _{0}. \end{array} \end{aligned}$$

(49)

Theorem 3.4

Under the assumptions of Theorem 3.2, there holds the following error bound:

$$\begin{aligned} \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}\le & {} C\epsilon ^{-1}\mu ^2, \quad for ~\mathcal {P}_{1},\\ \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}\le & {} C\mu ^2, \quad for ~\mathcal {P}_{2}.\\ \end{aligned}$$

Proof

Taking $\mathbf G =(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })$ and $(\mathbf v ,\varvec{\Psi })=(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })$, $q=p_{\epsilon }-p_{\epsilon \mu }$ in (42), we can get

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf w ,\varvec{\Phi })) +A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf w ,\varvec{\Phi }))\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf w ,\varvec{\Phi })) -d((\mathbf w ,\varvec{\Phi }),p_{\epsilon }-p_{\epsilon \mu })\nonumber \\&\qquad +\,d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),s) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },s)\nonumber \\&\quad =((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })). \end{aligned}$$

(50)

Next, we derive from (6) and (29) with $(\mathbf v ,\varvec{\Psi })=(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi })$, $q=\rho _{\mu } s$ that

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }))\nonumber \\&\quad +\,A_{1}((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }))\nonumber \\&\quad +\,A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }))\nonumber \\&\quad -\,A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }))\nonumber \\&\quad +\,d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),\rho _{\mu }s) -d((\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }),p_{\epsilon }-p_{\epsilon \mu }) {+\frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },\rho _{\mu }s)=0.}\nonumber \\ \end{aligned}$$

(51)

Subtracting (51) from (50), yields

$$\begin{aligned}&\Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}^2 \equiv \sum \limits _{i=1}^{6}(I)_{i}\nonumber \\&\quad =A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }))\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }))\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }))\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }))\nonumber \\&\qquad +\,d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),s-\rho _{\mu }s) -d((\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }),p_{\epsilon }-p_{\epsilon \mu })\nonumber \\&\qquad +\frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },s-\rho _{\mu }s). \end{aligned}$$

(52)

From (7), (9) and (49), we can get

$$\begin{aligned} (I)_{1}= & {} A_{0}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }))\nonumber \\\le & {} \max \{R_{e}^{-1},5S_{c}R_{m}^{-1}\} \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1} \Vert (\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi })\Vert _{1}\nonumber \\\le & {} C\mu \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1} \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}. \end{aligned}$$

(53)

Applying (9), (49) and Theorem 2.2, yields

$$\begin{aligned} (I)_{2}+(I)_{3}= & {} A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }))\nonumber \\&+A_{1}((\mathbf u _{\epsilon },\mathbf{B }_{\epsilon }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }))\nonumber \\\le & {} 2N \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1} \Vert (\mathbf u _{\epsilon },\mathbf{B }_{\epsilon })\Vert _{1} \Vert (\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi })\Vert _{1}\nonumber \\\le & {} C\mu \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1} \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}, \end{aligned}$$

(54)

$$\begin{aligned} (I)_{4}= & {} A_{1}((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),(\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi }))\nonumber \\\le & {} \sqrt{2}\max \{1,\sqrt{2}\hbox {S}_{c}\}\Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1}^2 \Vert (\pi _{\mu }\mathbf w ,R_{\mu }\varvec{\Phi })\Vert _{0}\nonumber \\\le & {} C\Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1}^2 \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}, \end{aligned}$$

(55)

$$\begin{aligned} (I)_{5}= & {} |d((\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }),s-\rho _{\mu }s)| +|d((\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi }),p_{\epsilon }-p_{\epsilon \mu })|\nonumber \\\le & {} C\left( \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1}+\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0}\right) \nonumber \\&\times \left( \Vert (\mathbf w -\pi _{\mu }\mathbf w ,\varvec{\Phi }-R_{\mu }\varvec{\Phi })\Vert _{1}+{\Vert s-\rho _{h}\varvec{\Psi }\Vert _{0}}\right) \nonumber \\\le & {} C\mu \left( \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{1}+\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0} \right) \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0},\nonumber \\ \end{aligned}$$

(56)

$$\begin{aligned} (I)_{6}= & {} \frac{\epsilon }{\nu _{e}}(p_{\epsilon }-p_{\epsilon \mu },s-\rho _{\mu }s) \le C\mu \Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0} \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}. \end{aligned}$$

(57)

Finally, from $\mathcal {P}_{1}$ and $\mathcal {P}_{2}$, we can derive that

$$\begin{aligned} \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}\le & {} C\epsilon ^{-1}\mu ^2, \quad for~~\mathcal {P}_{1},\\ \Vert (\mathbf u _{\epsilon }-\mathbf u _{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu })\Vert _{0}\le & {} C\mu ^2, \quad for~~\mathcal {P}_{2}. \end{aligned}$$

Then, the proof ends. $\square$

4 Newton Iterative Method

Newton iterative method in penalty finite element method based on finite element pair $\mathcal {P}_{1}$ and $\mathcal {P}_{2}$ is introduced as follows.

Algorithm 4.1

Find $((\mathbf u _{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),p_{\epsilon \mu }^{n})\in \mathbf W ^{\mu }_{0n}\times \hbox {M}_{\mu }$ such that for all $((\mathbf v ,\varvec{\Psi }),q)\in \mathbf W ^{\mu }_{0n}\times \hbox {M}_{\mu }$

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon \mu }^n,\mathbf{B }_{\epsilon \mu }^n),(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon \mu }^{n})+d((\mathbf u _{\epsilon \mu }^n,\mathbf{B }_{\epsilon \mu }^n),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon \mu }^{n},q)\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon \mu }^{n-1},\mathbf{B }_{\epsilon \mu }^{n-1}),(\mathbf u _{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),(\mathbf v ,\varvec{\Psi })) +A_{1}((\mathbf u _{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),(\mathbf u _{\epsilon \mu }^{n-1},\mathbf{B }_{\epsilon \mu }^{n-1}),(\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad =\langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle +A_{1}((\mathbf u _{\epsilon \mu }^{n-1},\mathbf{B }_{\epsilon \mu }^{n-1}),(\mathbf u _{\epsilon \mu }^{n-1},\mathbf{B }_{\epsilon \mu }^{n-1}),(\mathbf v ,\varvec{\Psi })). \end{aligned}$$

(58)

Here, $((\mathbf u _{\epsilon \mu }^{0},\mathbf B _{\epsilon \mu }^{0}),p_{\epsilon \mu }^{0})$ is defined by the discrete penalty equations:

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon \mu }^{0},\mathbf B _{\epsilon \mu }^{0})(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon \mu }^{0})+d((\mathbf u _{\epsilon \mu }^{0},\mathbf B _{\epsilon \mu }^{0}),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon \mu }^{0},q)\nonumber \\&\quad =\langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle , \end{aligned}$$

(59)

for all $((\mathbf v ,\varvec{\Psi }),q)\in \mathbf W _{0 n}^{\mu }\times \hbox {M}_{\mu }$.

Next, we establish the stability of the iterative method for $(\mathbf e ^{n},\mathbf b ^{n})=(\mathbf u _{\epsilon \mu }-\mathbf u _{\epsilon \mu }^{n},\mathbf B _{\epsilon \mu }-\mathbf B _{\epsilon \mu }^{n})$ and $\eta ^{n}=p_{\epsilon \mu }-p_{\epsilon \mu }^{n}$. Firstly, we give a key lemma from [16].

Lemma 4.1

The trilinear term $A_{1}(\cdot ,\cdot ,\cdot )$ satisfies the following estimate

$$\begin{aligned}&|A_{1}((\mathbf u _{\mu },\mathbf B _{\mu }),(\mathbf w _{\mu },\varvec{\Phi }_{\mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu }))| +|A_{1}((\mathbf w _{\mu },\varvec{\Phi }_{\mu }),(\mathbf u _{\mu },\mathbf B _{\mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu }))|\nonumber \\&\quad \le C\Vert (\mathbf u _{\mu },\mathbf B _{\mu })\Vert _{1}^{\frac{1}{2}}\Vert (\mathcal {A}_{1\mu }\mathbf u _{\mu },\mathcal {A}_{2\mu }\mathbf B _{\mu }) \Vert _{0}^{\frac{1}{2}}\Vert (\mathbf w _{\mu },\varvec{\Phi }_{\mu })\Vert _{1}\Vert (\mathbf v _{\mu },\varvec{\Psi }_{\mu })\Vert _{0}, \end{aligned}$$

(60)

for all $(\mathbf u _{\mu },\mathbf B _{\mu }),(\mathbf w _{\mu },\varvec{\Phi }_{\mu }),(\mathbf v _{\mu },\varvec{\Psi }_{\mu })\in \mathbf W _{0n}^{\mu }$.

Theorem 4.1

Under the assumptions of Theorem 2.2 and suppose that $\mathcal {P}_{1}$ and $\mathcal {P}_{2}$ are valid, if

$$\begin{aligned} 0<\sigma <\frac{5}{11}, \end{aligned}$$

(61)

then $(\mathbf u _{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})$ and $p_{\epsilon \mu }^{m}$ defined by the Newton iterative method satisfy

$$\begin{aligned} \Vert |(\mathbf u _{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})\Vert |_{1}\le & {} \frac{4}{3}\Vert \mathbf F \Vert _{-1}, \quad \Vert |(\mathcal {A}_{1\mu }\mathbf u _{\epsilon \mu }^{m},\mathcal {A}_{2\mu }\mathbf{B }_{\epsilon \mu }^{m})\Vert |_{1} \le C\Vert \mathbf F \Vert _{0}, \end{aligned}$$

(62)

$$\begin{aligned} \Vert p_{\epsilon \mu }^{m}\Vert _{0}\le & {} \left( \frac{9\nu _{e}}{5\epsilon \hat{\nu }}\right) ^{\frac{1}{2}}\Vert \mathbf F \Vert _{-1}, \quad for~~\mathcal {P}_{1}, \end{aligned}$$

(63)

$$\begin{aligned} \Vert p_{\epsilon \mu }^{m}\Vert _{0}\le & {} \left( \frac{4\underline{\nu }}{3\hat{\nu }} +\frac{17}{10} \right) \Vert \mathbf F \Vert _{-1},\quad for~~\mathcal {P}_{2} \end{aligned}$$

(64)

and $(\mathbf e ^m,\mathbf b ^m)$, $\eta ^m$ satisfy the following bounds:

$$\begin{aligned} \Vert |(\mathbf e ^m,\mathbf b ^m)\Vert |_{1}\le & {} (\frac{33}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}, \end{aligned}$$

(65)

$$\begin{aligned} \Vert \eta ^{m}\Vert _{0}\le & {} \left( \frac{\nu _{e}}{\epsilon \hat{\nu }}\right) ^{\frac{1}{2}}\sigma ^2 (\frac{33}{13}\sigma )^{2^{m}-\frac{3}{2}}(\frac{5}{11})^{\frac{3}{2}}\Vert \mathbf F \Vert _{-1}, \quad for~~\mathcal {P}_{1}, \end{aligned}$$

(66)

$$\begin{aligned} \Vert \eta ^{m}\Vert _{0}\le & {} \beta _{0}^{-1}\left( \frac{5\underline{\nu }}{11\hat{\nu }}+3\sigma ^2\right) \left( \frac{33}{13}\sigma \right) ^{2^{m}-1} \Vert \mathbf F \Vert _{-1}, \quad for~~\mathcal {P}_{2}, \end{aligned}$$

(67)

for all $m\ge 0$.

Proof

We can derive the estimate (62)–(66) with the similar technique used in [18]. $\square$

5 Two-Level Newton Iterative Penalty Finite Element Method

In this part, we consider the two-level penalty finite element method. The method includes two algorithms: m steps by Newton iteration on the coarse mesh H and once correction by Stokes iteration on the fine mesh h.

Algorithm 5.1

Step I. Find a coarse grid iterative solution $((\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf W _{0n}^{H}\times \hbox {M}_{H}$ defined by

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon H}^{n},\mathbf B _{\epsilon H}^{n}),(\mathbf v ,\varvec{\Psi })) +A_{1}((\mathbf u _{\epsilon H}^{n-1},\mathbf B _{\epsilon H}^{n-1}), (\mathbf u _{\epsilon H}^{n},\mathbf B _{\epsilon H}^{n}),(\mathbf v ,\varvec{\Psi }))\nonumber \\&\qquad +\,A_{1}((\mathbf u _{\epsilon H}^{n},\mathbf B _{\epsilon H}^{n}), (\mathbf u _{\epsilon H}^{n-1},\mathbf B _{\epsilon H}^{n-1}),(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon H}^{n})\nonumber \\&\qquad +\,d((\mathbf u _{\epsilon H}^{n},\mathbf B _{\epsilon H}^{n}),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon H}^{n},q)\nonumber \\&\quad =A_{1}((\mathbf u _{\epsilon H}^{n-1},\mathbf B _{\epsilon H}^{n-1}), (\mathbf u _{\epsilon H}^{n-1},\mathbf B _{\epsilon H}^{n-1}),(\mathbf v ,\varvec{\Psi })) +\langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle , \end{aligned}$$

(68)

for $n=1,2,\ldots ,m$, where $((\mathbf u _{\epsilon H}^0,\mathbf B _{\epsilon H}^0),p_{\epsilon H}^{0})$ is determined by

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon H}^{0},\mathbf B _{\epsilon H}^{0}),(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon H}^{0}) +d((\mathbf u _{\epsilon H}^{0},\mathbf B _{\epsilon H}^{0}),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon H}^{0},q)\nonumber \\&\quad =\langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle , \end{aligned}$$

(69)

for all $((\mathbf v ,\varvec{\Psi }),q)\in \mathbf W _{0n}^{H}\times \hbox {M}_{H}$.

Step II. Find a fine grid solution $((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})\in \mathbf W _{0n}^{h}\times \hbox {M}_{h}$ defined by

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),(\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon mh}) +d((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),q) +\frac{\epsilon }{\nu _{e}}(p_{\epsilon mh},q)\nonumber \\&\quad =A_{1}((\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}^{m}), (\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}^{m}),(\mathbf v ,\varvec{\Psi })) + \langle \mathbf F ,(\mathbf v ,\varvec{\Psi })\rangle , \end{aligned}$$

(70)

for all $((\mathbf v ,\varvec{\Psi }),q)\in \mathbf W _{0n}^{H}\times \hbox {M}_{H}$.

For the simplicity, we take $(\mathbf e _{h},\mathbf b _{h})=(\mathbf u _{\epsilon h}-\mathbf u _{\epsilon mh},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon mh})$, $\eta _{h}=p_{\epsilon h}-p_{\epsilon mh}$. Then, we have the following theorem.

Theorem 5.1

Under the assumptions of Theorem 4.1, then $((\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh}),p_{\epsilon mh})$ of (69)–(70) satisfy

$$\begin{aligned} \Vert |(\mathbf u _{\epsilon mh},\mathbf{B }_{\epsilon mh})\Vert |_{1}\le & {} 2\Vert \mathbf F \Vert _{-1}, \end{aligned}$$

(71)

$$\begin{aligned} \Vert p_{\epsilon m h}\Vert _{0}\le & {} \left( \frac{10\nu _{e}}{\epsilon }\right) ^{\frac{1}{2}}\Vert \mathbf F \Vert _{-1},\quad for~~\mathcal {P}_{1}, \end{aligned}$$

(72)

$$\begin{aligned} \Vert p_{\epsilon m h}\Vert _{0}\le & {} 2\beta _{0}\left( \frac{\max \{R_{e}^{-1},5S_{c}R_{m}^{-1}\}}{\hat{\nu }}+1\right) \Vert \mathbf F \Vert _{-1}, \quad for~~\mathcal {P}_{2}, \end{aligned}$$

(73)

and $(\mathbf e _{h},\mathbf b _{h})$, $\eta _{h}$ satisfy the following bounds:

$$\begin{aligned}&\Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1}\le C\left( \sigma \frac{\hat{\nu }^2\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}\Vert \mathbf F \Vert _{-1}}\epsilon ^{-1}H^2 +(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) , \end{aligned}$$

(74)

$$\begin{aligned}&\quad \Vert \eta _{h}\Vert _{0}\le C\left( \epsilon ^{\frac{-3}{2}}H^2+(\frac{15}{13}\sigma )^ {2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) \quad for~~\mathcal {P}_{1}, \end{aligned}$$

(75)

$$\begin{aligned}&\Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1}\le C\left( \sigma \frac{\hat{\nu }^2\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}\Vert \mathbf F \Vert _{-1}}H^2 +(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) , \end{aligned}$$

(76)

$$\begin{aligned}&\quad \Vert \eta _{h}\Vert _{0}\le C\beta _{0}\left( H^2+(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) , \quad for~~\mathcal {P}_{2}. \end{aligned}$$

(77)

Proof

Taking $(\mathbf v ,\varvec{\Psi })=(\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})$ and $q=p_{\epsilon mh}$ in (70) with (8), (9), (61) and (62), we arrive at

$$\begin{aligned} \hat{\nu }\Vert (\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert _{1}^2+\frac{\epsilon }{\nu _{e}}\Vert p_{\epsilon mh}\Vert _{0}^2\le & {} N \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}^2\Vert (\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert _{1}\nonumber \\&+\,\Vert \mathbf F \Vert _{-1}\Vert (\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert _{1}, \end{aligned}$$

(78)

then, we can have

$$\begin{aligned} \begin{array}{lll} \Vert |(\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert |_{1} \le (\frac{16}{9}\sigma +1)\Vert \mathbf F \Vert _{-1} \le 2\Vert \mathbf F \Vert _{-1}. \end{array} \end{aligned}$$

(79)

And for $\mathcal {P}_{1}$, from (78), we can have

$$\begin{aligned} \frac{\epsilon }{\nu _{e}}\Vert p_{\epsilon mh}\Vert _{0}^2\le & {} N \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}^2\Vert (\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert _{1} +\Vert \mathbf F \Vert _{-1}\Vert (\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert _{1}\\\le & {} \left( 2\times (\frac{3}{4})^{4}\sigma +2\right) \Vert \mathbf F \Vert _{-1}^{2} \le 10\Vert \mathbf F \Vert _{-1}^2, \end{aligned}$$

which is that

$$\begin{aligned} \begin{array}{lll} \Vert p_{\epsilon mh}\Vert _{0} \le (\frac{10\nu _{e}}{\epsilon })^{\frac{1}{2}}\Vert \mathbf F \Vert _{-1}. \end{array} \end{aligned}$$

For $\mathcal {P}_{2}$, taking $q=0$ in (70) with (7), (9), (24), (79), (61) and (62), we can have

$$\begin{aligned} \beta _{0}\Vert p_{\epsilon mh}\Vert _{0}\le & {} \frac{d((\mathbf v ,\varvec{\Psi }),p_{\epsilon mh})}{\Vert (\mathbf v ,\varvec{\Psi })\Vert _{1}}\\\le & {} \max \{R_{e}^{-1},5S_{c}R_{m}^{-1}\} \Vert (\mathbf u _{\epsilon mh},\mathbf B _{\epsilon mh})\Vert _{1} +N \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}^2+\Vert \mathbf F \Vert _{-1}\\\le & {} 2\left( \frac{\max \{R_{e}^{-1},5S_{c}R_{m}^{-1}\}}{\hat{\nu }}+1\right) \Vert \mathbf F \Vert _{-1}. \end{aligned}$$

Next, we will give the error estimate.

Subtracting (70) from (29) with $\mu =h$, we can have the following error equation

$$\begin{aligned}&A_{0}((\mathbf u _{\epsilon h}-\mathbf u _{\epsilon mh},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon mh}), (\mathbf v ,\varvec{\Psi })) -d((\mathbf v ,\varvec{\Psi }),p_{\epsilon h}-p_{\epsilon mh})\nonumber \\&\quad +\,d((\mathbf u _{\epsilon h}-\mathbf u _{\epsilon mh},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon mh}),q)\nonumber \\&\quad +\,\frac{\epsilon }{\nu _{e}}(p_{\epsilon h}-p_{\epsilon mh},q) +A_{1}((\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H}),(\mathbf u _{\epsilon h},\mathbf B _{\epsilon h}),(\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad +\,A_{1}((\mathbf u _{\epsilon H},\mathbf B _{\epsilon H}),(\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H}), (\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad +\,A_{1}((\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^{m},\mathbf B _{\epsilon H}-\mathbf u _{\epsilon H}^{m}),(\mathbf u _{\epsilon H},\mathbf B _{\epsilon H}),(\mathbf v ,\varvec{\Psi }))\nonumber \\&\quad +\,A_{1}((\mathbf u _{\epsilon H}^m,\mathbf{B }_{\epsilon H}^m),(\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf{B }_{\epsilon H}-\mathbf{B }_{\epsilon H}^m),(\mathbf v ,\varvec{\Psi }))=0. \end{aligned}$$

(80)

Take $(\mathbf v ,\varvec{\Psi })=(\mathbf e _{h},\mathbf b _{h})$, $q=\eta _{h}$ in (80) with (8), (9), (14) and Theorem 3.1, we have

$$\begin{aligned}&\hat{\nu } \Vert (\mathbf e _{h},\mathbf b _{h})\Vert _{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^{2}\\&\quad \le N \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0} \Big \{\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0}\nonumber \\&\qquad +\,\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0}\Big \} \Vert (\mathbf e _{h},\mathbf b _{h})\Vert _{1}\\&\qquad +\,N \Vert (\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}-\mathbf B _{\epsilon H}^m)\Vert _{1} \Big \{\Vert (\mathbf u _{\epsilon H},\mathbf B _{\epsilon H})\Vert _{1}\\&\qquad +\, \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}\Big \} \Vert (\mathbf e _{h},\mathbf b _{h})\Vert _{1}, \end{aligned}$$

which guarantees that

$$\begin{aligned}&\Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1}\nonumber \\\le & {} CN \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0} \Big \{\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0} +\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0}\Big \}\nonumber \\&\quad +\,N \Vert (\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}-\mathbf B _{\epsilon H}^m)\Vert _{1} \Big \{\Vert (\mathbf u _{\epsilon H},\mathbf B _{\epsilon H})\Vert _{1}+ \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}\Big \}\nonumber \\\le & {} C\frac{N\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}} \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0}\nonumber \\&\quad +\,\frac{N\Vert \mathbf F \Vert _{-1}}{\hat{\nu }^2} \Vert (\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}-\mathbf B _{\epsilon H}^m)\Vert _{1}\nonumber \\\le & {} C\sigma \frac{\hat{\nu }^2\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}\Vert \mathbf F \Vert _{-1}} \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0}\nonumber \\&\quad +\,\sigma \Vert |(\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}-\mathbf B _{\epsilon H}^m)\Vert |_{1}. \end{aligned}$$

(81)

For $\mathcal {P}_{1}$, from Theorems 3.4, 4.1 and (81), we derive that

$$\begin{aligned} \begin{array}{lll} \Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1} \le C\left( \sigma \frac{(\hat{\nu })^2\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}\Vert \mathbf F \Vert _{-1}}\epsilon ^{-1}H^2 +(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) , \end{array} \end{aligned}$$

(82)

and with (82), we have

$$\begin{aligned} \frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^{2}\le & {} CN \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0} \times \Big \{\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0}\\&\qquad +\,\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0}\Big \} \Vert (\mathbf e _{h},\mathbf b _{h})\Vert _{1} +N \Vert (\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}-\mathbf B _{\epsilon H}^m)\Vert _{1}\\&\qquad \times \,\Big \{\Vert (\mathbf u _{\epsilon H},\mathbf B _{\epsilon H})\Vert _{1}+ \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}\Big \} \Vert (\mathbf e _{h},\mathbf b _{h})\Vert _{1}\\\le & {} C\epsilon ^{-2}H^{4}+C\Big \{(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\Big \}^2, \end{aligned}$$

which is that

$$\begin{aligned} \begin{array}{lll} \Vert \eta _{h}\Vert _{0}\le C\left( \epsilon ^{\frac{-3}{2}}H^2+(\frac{15}{13}\sigma )^ {2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) . \end{array} \end{aligned}$$

(83)

And for $\mathcal {P}_{2}$, with the aids of $\mathcal {P}_{1}$, from Theorem 3.4, Theorem 4.1 and (81),

$$\begin{aligned} \begin{array}{lll} \Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1} \le C\left( \sigma \frac{\hat{\nu }^2\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}\Vert \mathbf F \Vert _{-1}}H^2 +(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) , \end{array} \end{aligned}$$

(84)

and with (24), (81), (7), (84), Theorem 3.4 and Theorem 4.1, we deduce that

$$\begin{aligned} \beta _{0}\Vert \eta _{h}\Vert _{0}\le & {} \frac{\max \{R_{e}^{-1},5S_{c}R_{m}^{-1}\}}{\hat{\nu }} \Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1} +CN \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0}\nonumber \\&\quad \times \, \Big \{\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0} +\Vert (\mathcal {A}_{1h}\mathbf u _{\epsilon h},\mathcal {A}_{2h}\mathbf B _{\epsilon h})\Vert _{0}\Big \}\nonumber \\&\quad +\,N \Vert (\mathbf u _{\epsilon H}\!-\!\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}\!-\!\mathbf B _{\epsilon H}^m)\Vert _{1} \Big \{\Vert (\mathbf u _{\epsilon H},\mathbf B _{\epsilon H})\Vert _{1}\!+\! \Vert (\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}^m)\Vert _{1}\Big \}\!+\!\Vert \mathbf F \Vert _{-1}\nonumber \\\le & {} \frac{\max \{R_{e}^{-1},5S_{c}R_{m}^{-1}\}}{\hat{\nu }} \Vert |(\mathbf e _{h},\mathbf b _{h})\Vert |_{1}\nonumber \\&\quad +\,C\sigma \frac{\hat{\nu }^2\Vert \mathbf F \Vert _{0}}{\min \{R_{e}^{-1},S_{c}R_{m}^{-1}\}\Vert \mathbf F \Vert _{-1}} \Vert (\mathbf u _{\epsilon h}-\mathbf u _{\epsilon H},\mathbf B _{\epsilon h}-\mathbf B _{\epsilon H})\Vert _{0}\nonumber \\&\quad +\,\sigma \Vert |(\mathbf u _{\epsilon H}-\mathbf u _{\epsilon H}^m,\mathbf B _{\epsilon H}-\mathbf B _{\epsilon H}^m)\Vert |_{1}+\Vert \mathbf F \Vert _{-1}\nonumber \\\le & {} C\left( H^2+(\frac{15}{13}\sigma )^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) . \end{aligned}$$

(85)

Then, we complete the proof. $\square$

Theorem 5.2

Under the assumptions of Theorem 3.2, for the two-level Newton iterative penalty finite element method with $\mathcal {P}_{1}$, the optimal error estimate is

$$\begin{aligned}&\Vert |(\mathbf u -\mathbf u _{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh})\Vert |_{1} \le C\epsilon + C\epsilon ^{-\frac{1}{2}}\left( h+\epsilon ^{\frac{1}{2}}H^2\right) +\left( \frac{15}{13}\sigma \right) ^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1},\nonumber \\&\Vert p-p_{\epsilon m h}\Vert _{0} \le C\epsilon + C\epsilon ^{-1}\left( h+\epsilon ^{\frac{1}{2}}H^2\right) +\left( \frac{15}{13}\sigma \right) ^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}, \end{aligned}$$

(86)

$\epsilon$ and H can be taken as $\epsilon =O(h^{\frac{1}{2}})$, $H^2=O(\epsilon ^{\frac{1}{2}}h)$ and the convergence rate is $O(h^{\frac{1}{2}})$; for the two-level Newton iterative penalty finite element method with $\mathcal {P}_{2}$, the optimal error estimates are

$$\begin{aligned} \Vert |(\mathbf u -\mathbf u _{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh})\Vert |_{1} \!+\! \Vert p-p_{\epsilon mh}\Vert _{0} \le C\left( \epsilon \!+\!h\!+\!H^2 \!+\!\left( \frac{33}{13}\sigma \right) ^{2^{m}-1}\frac{5}{11}\Vert \mathbf F \Vert _{-1}\right) ,\quad \end{aligned}$$

(87)

$\epsilon$ and H can be taken as $\epsilon =O(h)$, $H^2=O(h)$ and the convergence rate is O(h).

Proof

We can finish the proof by Theorems 2.3, 3.2 and 5.1, triangle inequality and some simple calculations. $\square$

6 Numerical Results

In this section we report on the numerical performance of the method established in this paper with two finite element pairs $\mathcal {P}_{k}$ ($k=$ 1, 2) for the 2D/3D MHD cases. The first one is a flow problem with a smooth solution. The second one is a Hartmann flow problem. And the last one is a driven cavity flow problem. The iterative tolerance is set as $10^{-10}$ for numerical implementations.

Remark 6.1

(1) The penalty parameter $\epsilon$ is selected as $\epsilon =O(h^{\frac{1}{2}})$ for $\mathcal {P}_{1}$ and $\epsilon =O(h)$ for $\mathcal {P}_{2}$ based on Theorem 5.2 in all the following numerical tests.

(2) $R_{e}$, $R_{m}$ and $S_{c}$ are optional constants in uniqueness condition $\sigma$ which defined in (16).

(3) The constant $C_{0}$ can be obtained by the Ladyzhenskaya inequalities and the Poincar$\acute{e}$ inequality (see [18])

$$\begin{aligned} C_{0}=\left\{ \begin{array}{lll} \left( 2\kappa \right) ^{\frac{1}{4}},&{} d=2,\\ \left( 2\kappa ^{\frac{1}{4}}\right) ^{\frac{1}{2}},&{} d=3, \end{array} \right. \end{aligned}$$

(88)

for the bounded domain, the $\kappa$ is given by

$$\begin{aligned} \kappa =\frac{1}{\lambda _{min}}, \end{aligned}$$

where $\lambda _{min}$ is the smallest eigenvalue of Laplace operator. And, for the unit domain $[0,1]^d$

$$\begin{aligned} \lambda _{\min }=\left\{ \begin{array}{lll} 2\pi ^2,\quad d=2,\\ 3\pi ^2,\quad d=3. \end{array} \right. \end{aligned}$$

(4) The constant $C_{1}$ can be estimated by (11) and (12),

$$\begin{aligned} C_{1} \le \frac{\Vert \hbox {curl} \mathbf B \Vert _{0}^2+\Vert \hbox {div}\mathbf B \Vert _{0}^2}{\Vert \mathbf B \Vert _{1}^2} \le 3. \end{aligned}$$

(89)

(5) The negative norm $\Vert \mathbf F \Vert _{-1}$ by $\left( \Vert \mathbf f \Vert ^2_{-1}+\Vert \mathbf g \Vert ^2_{*}\right) ^{\frac{1}{2}},$ where $\Vert \mathbf f \Vert _{-1}$ and $\Vert \mathbf g \Vert _{*}$ are evaluated by the following two problems (refer to [16] for details):

• Solving the following Poisson’s equation

  $$\begin{aligned} -\Delta \varvec{\Upsilon }=\mathbf f ,~\hbox {in}~ \Omega , \end{aligned}$$

  (90)

  with the homogeneous Drichlet boundary condition. So that we have

  $$\begin{aligned} \Vert \mathbf f \Vert _{-1}=\Vert \nabla \varvec{\Upsilon }\Vert _{0}. \end{aligned}$$

  (91)

• Solving the problem

  $$\begin{aligned} \left\{ \begin{array}{lll} \hbox {curl}\hbox {curl}\varpi =\mathbf g ,&{} \hbox {in}~\Omega ,\\ \hbox {div}\varpi =0, &{} \hbox {in}~\Omega ,\\ \varpi \cdot \mathbf n =0,&{} \hbox {on}~\partial \Omega ,\\ \hbox {curl}\varpi \times \mathbf n =0,&{} \hbox {on}~\partial \Omega , \end{array} \right. \end{aligned}$$

  (92)

  results in

  $$\begin{aligned} \Vert \mathbf g \Vert _{*}=\Vert \hbox {curl}\varpi \Vert _{0}. \end{aligned}$$

Table 1 Algorithm 5.1 with $\epsilon =O(h^{\frac{1}{2}})$ for $P_{1}$-$P_{0}$-$P_{1}$ element (2D)

Table 2 Algorithm 4.1 with $\epsilon =O(h^{\frac{1}{2}})$ for $P_{1}$-$P_{0}$-$P_{1}$ element (2D)

Table 3 Algorithm 5.1 with $\epsilon =O(h)$ for $P_{1}b$-$P_{1}$-$P_{1}b$ element (2D)

Table 4 Algorithm 4.1 with $\epsilon =O(h)$ for $P_{1}b$-$P_{1}$-$P_{1}b$ element (2D)

Table 5 Algorithm 5.1 with $\epsilon =O(h^{\frac{1}{2}})$ for $P_{1}$-$P_{0}$-$P_{1}$ element (3D)

Table 6 Algorithm 4.1 with $\epsilon =O(h^{\frac{1}{2}})$ for $P_{1}$-$P_{0}$-$P_{1}$ element (3D)

Table 7 Algorithm 5.1 with $\epsilon =O(h)$ for $P_{1}b$-$P_{1}$-$P_{1}b$ element (3D)

Table 8 Algorithm 4.1 with $\epsilon =O(h)$ for $P_{1}b$-$P_{1}$-$P_{1}b$ element (3D)

Fig. 1

(2D) Slices along $x=5,-1<y<1$: computed (points) and theoretical (lines)

Fig. 2

(3D) Slices along $x=5,-2<y<2,z=0$: computed (points) and theoretical (lines)

Fig. 3

Errors $\Vert |(\mathbf e ^{m},\mathbf b ^{m})\Vert |_{1}$ versus iterative number m by a log–log plot: 2D (a); 3D (b)

Fig. 4

Comparison results versus $R_{e}$ by a log–log plot

Fig. 5

Comparison results versus $R_{m}$ by a log–log plot

Fig. 6

Comparison results versus $S_{c}$ by a log–log plot

Fig. 7

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $R_{e}=1$

Fig. 8

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $R_{e}=5\cdot 10^2$

Fig. 9

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $R_{e}=5\cdot 10^3$

Fig. 10

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $R_{m}=5\cdot 10^2$

Fig. 11

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $R_{m}=5\cdot 10^3$

Fig. 12

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $S_{c}=10^3$

Fig. 13

Numerical streamlines (a); the isobars (b); and isodynamic (c) with $S_{c}=10^5$

6.1 Problems with Smooth Solutions

In this case, we test the accuracy performance of our proposed methods with a smooth solution. On the square domain $\Omega =[0,1]^d$, $d=2,3$ and the exact solutions be given by

$$\begin{aligned} \left\{ \begin{array}{llll} u_1=\alpha x^2(x-1)^2y(y-1)(2y-1), ~~~ u_2=\alpha y^2(y-1)^2x(x-1)(2x-1),\\ B_1=\alpha \sin (\pi x)\cos (\pi y), ~~~ B_2=-\alpha \sin (\pi y)\cos (\pi x), \\ p=\alpha (2x-1)(2y-1), \end{array} \right. \end{aligned}$$

for $d=2$ and

$$\begin{aligned} \left\{ \begin{array}{llll} u_1=\alpha (y^4+z), ~~~ u_2=\alpha (x+z^3), ~~~ u_3=\alpha (x^2+y^2)\\ B_1=\alpha \sin (yz), ~~~ B_2=-\alpha \sin (x+z), ~~~ B_3=-\alpha y\sin (x^2) \\ p=\alpha (2x-1)(2y-1)(2z-1), \end{array} \right. \end{aligned}$$

for $d=3$. $\alpha$ is chosen such that $0<\sigma <\frac{5}{11}$ and the body forces $\mathbf f$, $\mathbf g$ are determined accordingly for any $R_{e}$, $R_{m}$ and $S_{c}$.

Firstly, we consider the convergence performance of Algorithm 5.1 with $R_{e}=1$, $R_{m}=1$ and $S_{c}=1$. According to Theorem 5.2, the settings of coarse, fine mesh and penalty parameter scales are based on $\epsilon =O(h^{\frac{1}{2}})$, $H^2=O(\epsilon ^{\frac{1}{2}}h)$ for $\mathcal {P}_{1}$ and $\epsilon =O(h)$, $H^2=O(h)$ for $\mathcal {P}_{2}$. To illustrate the property of Algorithm 5.1, we compare the numerical results with Algorithm 4.1.

Tables 1, 2, 3, 4, 5, 6, 7 and 8 present the convergence performances of Algorithm 5.1 and Algorithm 4.1 with $\mathcal {P}_{1}$ and $\mathcal {P}_{2}$ for 2D/3D cases, in which $K_{div\mathbf u }=\max \limits _{K_{h}(\Omega )}|\int _{K}\hbox {div}\mathbf u _{h}dx|$ and $K_{div\mathbf{B }}=\max \limits _{K_{h}(\Omega )}|\int _{K}\hbox {div}\mathbf{B }_{h}dx|$. From the comparison results, we can conclude that the relative errors are almost the same for the same finite element pair for Algorithm 5.1 and Algorithm 4.1, respectively. And the relative errors of $\mathcal {P}_{1}$ is smaller than $\mathcal {P}_{2}$ with decrease of mesh size h. Moreover, the proposed scheme remain much the same property (i.e. $\hbox {div}\mathbf u =0$, $\hbox {div}\mathbf{B }=0$) as the original equations. However, the computing CPU time of Algorithm 5.1 takes a lot less time than Algorithm 5.1 and the method with $\mathcal {P}_{1}$ save much computational time than the one with $\mathcal {P}_{2}$.

And we can see that all kinds of methods work well and keep the convergence rates just like the theoretical analysis in Theorem 5.2. In details, the method with $\mathcal {P}_{1}$ converge with a rate of 1 / 2 and the method with $\mathcal {P}_{2}$ converge with 1. Specifically, the magnetic field $\mathbf B$ and the velocity field $\mathbf u$ has an improved convergence rate, it is even higher than the theoretical result $O(h^{1/2})$.

6.2 Hartman Flow

In this example, we consider both 2D and 3D Hartmann flow with $Ha=\sqrt{R_{e}R_{m}S_{c}}$. For 2D, we treat a steady undirectional flow in the channel $\Omega =[0,10]\times [-1,1]$ under the influence of the transverse magnetic field $B_{0}=(0,1)$. The analytical solutions are:

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf u (x,y)=(u(y),~0),\qquad \mathbf{B }(x,y)=(B(y),~1),\\ p(x,y)=-Gx-S_{c}B^2(y)/2+p_{0}, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \begin{array}{lll} u(y)=\frac{R_{e}G}{Ha\cdot \tanh (Ha)} \left( 1-\frac{\cosh (yHa)}{\cosh (Ha)}\right) ,\quad B(y)=\frac{G}{S_{c}}\left( \frac{\sinh (yHa)}{\sinh (Ha)}-y\right) . \end{array} \end{aligned}$$

We impose the following boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf u =0,&{}\hbox {on} ~~y=\pm 1,\\ \left( p\mathbf I -R_{e}^{-1}\nabla \mathbf u \right) \mathbf n =p_{d}{} \mathbf n , &{} \hbox {on}~~ x=0 ~ \hbox {and} ~ x=10,\\ \mathbf n \times \mathbf{B }=\mathbf n \times \mathbf{B }_{d},&{}\hbox {on} ~~\partial \Omega , \end{array} \right. \end{aligned}$$

where $p_{d}(x,y)=p(x,y)$, $p_{0}$ is a constant and I is identity matrix. Whilst, 3D Hartmann flow in a rectangular duct $\Omega =[0,L]\times [-y_{0},y_{0}]\times [-z_{0},z_{0}]$ with $L=10, y_{0}=2, z_{0}=1$ under the influence od a magnetic field $\mathbf B _{d}=(0,1,0)$ has the following form

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf u (x,y,z)=(u(y,z),~0,~0),\quad \mathbf{B }(x,y,z)=(B(y,z),~1,0),\\ p(x,y,z)=-Gx-S_{c}B^2(y,z)/2+p_{0}, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \begin{array}{lll} u(y,z)=-\frac{1}{2}GR_{e}(z^2-z_{0}^2)+\sum \limits _{i=0}^{+\infty }u_{i}(y)\cos (\lambda _{i}z),\quad B(y,z)=\sum \limits _{i=0}^{+\infty }b_{i}(y)\cos (\lambda _{i}z), \end{array} \end{aligned}$$

where

$$\begin{aligned} u_{i}(y)= & {} A_{i}\cosh (p_{1}y)+B_{i}\cosh (p_{2} y),\\ b_{i}(y)= & {} \frac{1}{R_{e}S_{c}}\left( A_{i}\frac{\lambda _{i}^{2}-p_{1}^2}{p_{1}}\sinh (p_{1}y)+B_{i}\frac{\lambda _{i}^{2}-p_{2}^2}{p_{1}}\sinh (p_{2}y)\right) ,\\ \lambda _{i}= & {} \frac{(2i+1)\pi }{2z_{0}},\quad u_{i}(y_{0})=\frac{-2GR_{e}}{\lambda _{i}^{3}z_{0}}\sin (\lambda _{i}z_{0}),\\ p_{1,2}^{2}= & {} \lambda _{i}^2+Ha^2/2\pm Ha\sqrt{\lambda _{i}^2+Ha^2/4},\\ \gamma _{i}= & {} p_{2}(\lambda _{i}^2-p_{1}^2)\sinh (p_{1}y_{0})\cosh (p_{2}y_{0})-p_{1}(\lambda _{i}^2-p_{2}^2)\sinh (p_{2}y_{0})\cosh (p_{1}y_{0}),\\ A_{i}= & {} \frac{-p_{1}(\lambda _{i}^2-p_{2}^2)}{\gamma _{i}}u_{i}(y_{0})\sinh (p_{2}y_{0}), \quad B_{i}=\frac{-p_{2}(\lambda _{i}^2-p_{1}^2)}{\gamma _{i}}u_{i}(y_{0})\sinh (p_{1}y_{0}), \end{aligned}$$

the boundary conditions are imposed by

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf u =0,&{}\hbox {on} ~~y=\pm y_{0}~~ \hbox {and} ~~z=\pm z_{0}\\ \left( p\mathbf I -R_{e}^{-1}\nabla \mathbf u \right) \mathbf n =p_{d}{} \mathbf n , &{}\hbox {on}~~ x=0 ~~ \hbox {and}~~ x=L,\\ \mathbf n \times \mathbf{B }=\mathbf n \times \mathbf{B }_{d},&{} \hbox {on} ~~\partial \Omega . \end{array} \right. \end{aligned}$$

Take $G=0.1$ and choose the following two cases to simulate 2D problem:

$$\begin{aligned} \begin{array}{lll} (a)~~ Ha=10:R_e=5,~~R_m=5,~~S_{c}=4;\\ (b)~~ Ha=40:R_e=10,~~R_m=10,~~S_{c}=16. \end{array} \end{aligned}$$

and choose the following two cases to simulate 3D problem:

$$\begin{aligned} \begin{array}{lll} (c)~~ Ha=1:R_e=1,~~R_m=0.1,~~S_{c}=10;\\ (d)~~ Ha=10:R_e=10,~~R_m=1,~~S_{c}=10. \end{array} \end{aligned}$$

For the 2D problem, the analytical solutions of u(y) and B(y) along with numerical ones $u(y_{k})$ and $B(y_{k})$ ($y_{k}=-1+0.1k,~k=0,\ldots ,20$) obtained by Algorithm 5.1 for $\mathcal {P}_{i}(i=1,2)$ with parameters (a)–(b) are presented in Fig. 1. And the analytical solutions u(y, z) and B(y, z) along with numerical ones $u(y_{k},0)$ and $B(y_{k},0)$($y_{k}=-2+0.1k,~k=0,\ldots ,40$) with parameters (c)–(d) for the 3D problem are shown in Fig. 2. It can be inferred that Algorithm 5.1 can achieve the desired results with $\mathcal {P}_{i}(i=1,2)$ for different Hartmann numbers.

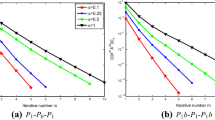
The following work is to investigate the convergence exponent m in (76). It is known that $(\frac{15}{13}\sigma )^{2^m-1}$ will converge gradually under $\frac{15}{13}\sigma <1$ with the increase of m. But it is difficult to give the direct verification of m. Figure 3 presents the relation between the error $\Vert |(\mathbf e _{m},\mathbf b _{m})\Vert |_{1}$ and the iterative number m by a log–log plot compared with a reference curve defined by $f(m)=c(\sigma )^{2^m-1}$, where c is constant. Thereout, we can see that the curve by $\Vert |(\mathbf e _{m},\mathbf b _{m})\Vert |_{1}$ have almost the same shape as the curve f(m). Then, we finished the verification of the relation in (76) indirectly.

6.3 Driven Cavity Flow

Let us consider a classic 2D test problem used in fluid dynamics, known as driven cavity flow. It is a model of the flow in a cavity with the lid moving in one direction: In this example, we consider the two-dimensional domain $\Omega =(-1,1)\times (-1,1)$ with $\Gamma _{D}=\partial \Omega$, and set the source terms to be zero. The boundary conditions are prescribed as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf u =0,&{}\hbox {on}~ x\pm 1~~\hbox {and} ~~y=-1,\\ \mathbf u =(1,0),&{}\hbox {on}~~y=1,\\ \mathbf n \times \mathbf{B }=\mathbf n \times \mathbf{B }_{D},&{}\hbox {on}~~\partial \Omega , \end{array} \right. \end{aligned}$$

where $\mathbf{B }_{D}=(1,0)$.

In this case, we consider the deep research on the relation between $R_{e}$, $R_{m}$ and $S_{c}$. According to the experiment 6.1, we know that finite element pair $\mathcal {P}_{1}$ is of low measurement accuracy. Here we only test the method with $\mathcal {P}_{2}$ for different equation parameters. Numerical results of Algorithm 5.1 are compared with the standard two-level Newton iterative method to show the merits of the proposed scheme.

Figures 4, 5 and 6 present the horizontal velocity, pressure and magnetic field distribution at the mid-width for various $R_{e}$, $R_{m}$ and $S_{c}$. It can be concluded that our results show an excellent agreement with the standard two-level Newton iterative method. And the numerical streamline, isobar and isodynamic of the cavity flow for different hydrodynamic Reynolds numbers, magnetic Reynolds numbers and coupling coefficients are presented in Figs. 7, 8, 9, 10, 11, 12 and 13.

Figures 7, 8 and 9 illustrate the numerical results of Algorithm 5.1 for $R_{e}=1,5\cdot 10^2,5\cdot 10^3$ with $R_{m}=1$ and $S_{c}=1$. As can be seen that the velocity main vortex grows into several small ones and become more complex with the increase of $R_{e}$. The experiment results of the proposed method for $R_{m}=5\cdot 10^2,\ 5\cdot 10^3$ with $R_{m}=1$ and $S_{c}=1$ are reported in Figs. 10 and 11. We can see that the velocity vortex and isobar remain almost unchanged, but the isodynamic has changed a lot. And the numerical results for $S_{c}=10^3,10^5$ with $R_{e}=1$ and $R_{m}=1$ are presented in Figs. 12 and 13. It can be inferred that more resolved vortexes may captured with the increase of $S_{c}$.

7 Conclusions

Combining the best algorithmic features of two-level scheme and Newton iterative technique based on penalty method, we presented a two-level Newton penalty finite element method for the 2D/3D stationary incompressible MHD equations. The main idea includes three part: firstly, to decouple the strong coupled system with a penalty term in the incompressible constraint; secondly, to save large amount of CPU time with two-level strategy; last, to deal with the nonlinear term with Newton iteration. Stability and error estimates of the method was analysed. Numerical results illustrated the theoretical results and demonstrated the efficiency of the proposed method. Besides, this method can be extended to time-dependent problems and more decoupling method will be discussed in the future.