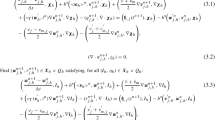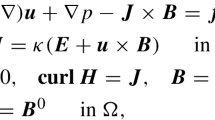A Decoupled, Linear and Unconditionally Energy Stable Scheme with Finite Element Discretizations for Magneto-Hydrodynamic Equations

Abstract

In this paper, we consider numerical approximations for solving the nonlinear magnetohydrodynamical system, that couples the Navier–Stokes equations and Maxwell equations together. By combining the projection method and some subtle implicit–explicit treatments for nonlinear coupling terms, we develop a fully decoupled, linear and unconditionally energy stable scheme for solving this system, where a new auxiliary velocity field is specifically introduced in order to decouple the computations of the magnetic field from the velocity field. We further prove that the fully discrete scheme with finite element approximations is unconditional energy stable. By deriving the $L^{\infty }$ bound of the numerical solution and the relation between the new auxiliary velocity field and the velocity field, and using negative norm technique, we obtain the optimal error estimates rigorously. Various numerical experiments are implemented to demonstrate the stability and the accuracy in simulating some benchmark problems, including the Kelvin–Helmholtz shear instability and the magnetic-frozen phenomenon in the lid-driven cavity.

1 Introduction

The hydrodynamical behaviors of conducting fluids (plasmas, liquid metals, and electrolytes, etc.) under external electromagnetic field are usually modeled by the so-called magnetohydrodynamical (MHD) system, see [12, 23, 25]. The fundamental image behind the MHD system is that magnetic fields can induce currents in a moving conductive fluid, which in turn polarizes the fluid and reciprocally changes the magnetic field itself. Thus the governing equations, which describe the MHD system, couple the Navier–Stokes equations for hydrodynamics and Maxwell’s equations for electromagnetism. Concerning the corresponding extensive theoretical modeling/numerical analysis of the MHD system, we refer to [2,3,4, 10, 15, 16, 18,19,20,21,22, 24, 28, 29] and the references therein.

For solving the nonlinear coupled MHD system numerically, one challenging issue is to design linear and decoupled schemes while preserving the energy stability, i,e., the energy dissipation laws hold in the discrete level. The main associated difficulty is to decouple nonlinear couplings between the magnetic field and the velocity field appearing in the convection and Lorentz forces. Simple discretizations, like fully explicit or implicit type schemes to handle these terms can lead to considerable instabilities or suffer from costly time expense. We recall there are many attempts that have been made in this direction recently. For examples, in [18], the authors developed two implicit–explicit type methods where the first order method is shown to be unconditionally stable and the second order method is shown to be conditionally stable. However, the model considered in [18] is the reduced version, namely, the magnetic field is assumed to be a fixed function. In [32, 33], the authors developed a decoupled type scheme for the full MHD system, but it is conditionally energy stable with a time step constraint. In [7], the authors developed some unconditionally energy stable schemes based on the projection type methods for the Navier–Stokes equations. However, the velocity field and the magnetic field are coupled together. In [31], the authors presented optimal error estimates for the first order energy stable projection scheme where the velocity field and the magnetic field are still coupled together (partially decoupled scheme). In [21], the authors developed a totally decoupled scheme where the computations of Navier–Stokes equations are based on the commutator of Laplacian and Leray projection, and all nonlinear and coupling terms are treated explicitly. However, the scheme is still conditionally stable. In [26], the author had developed a fully decoupled scheme by treating the coupled terms explicitly, however the scheme does not allow the discrete energy stability. Furthermore, the error estimate for pressure is suboptimal.

In this paper, we develop a fully decoupled, linear, and unconditionally energy stable scheme for solving the MHD system, and carry out the corresponding rigorous stability and error analysis for the fully discrete scheme in the context of finite element approximations. We adopt the first order projection method to solve the Navier–Stokes equation and introduce an auxiliary intermediate velocity variable to decouple the computation of the magnetic field from velocity. Meanwhile, we make some subtle implicit–explicit treatments for nonlinear coupling terms to linearize the system and ensure the energy stability, that is proved rigorously. Our decoupled idea is somewhat similar to matrix splitting algorithms in [4]. The key ingredient are all the introduction of an auxiliary velocity variable to decouple the computations of velocity from the magnetic field. Furthermore, the error estimates and numerical studies of unconditional stabilities are not presented in [4].

It is remarkable that the error analysis for the fully discrete finite element scheme we propose is rather challenging while its energy stability is quite straightforward once the scheme is appropriately designed. In [31], the error bound is derived directly by using the standard energy approach since the scheme is skew-symmetric hence many challenging terms are cancelled. However, there are some essential difficulties to derive the error bound in the developed scheme in this paper. More precisely, the introduction of the auxiliary velocity variable actually leads to some essential hurdles in establishing the $L^{\infty }$ bound of the numerical solutions that is the key ingredient to derive error estimates, and obtaining optimal error estimates for the pressure. To this end, the quantitative relations between the auxiliary velocity and velocity field is needed to be verified. By using the mathematical induction method combined with the convergence analysis, we further prove the $L^{\infty }$ stabilities of the numerical solution, and obtain the optimal error estimate for the pressure by means of the negative norm estimate method. It is shown that the velocity and magnetic field are of optimal error orders when $\delta t |\log h| \le 1$, and the pressure can attain the optimal convergence order when $\delta t |\log h|^{\frac{1}{2}} \lesssim h$. Finally, several benchmark numerical experiments, including the Kelvin–Helmholtz shear instability and the magnetic-frozen phenomenon in the lid-driven cavity, are implemented to confirm the stability and the accuracy of the scheme.

The rest of paper is organized as follows. In Sect. 2, we present the model and derive the associated energy dissipation law. In Sect. 3, we develop the fully discrete finite element scheme. We prove the associated energy dissipation law in the fully discrete level. In Sect. 4, we derive the error estimates of the fully discrete scheme. In Sect. 5, various numerical experiments are presented to demonstrate the stability and effectiveness of the scheme. Finally, some concluding remarks are given in Sect. 6.

2 The MHD Model and Energy Law

The incompressible MHD equations reads as follows,

$$\begin{aligned}&\varvec{u}_t-\nu \Delta \varvec{u} +(\varvec{u}\cdot \nabla )\varvec{u} + \nabla p + s \varvec{B} \times \nabla \times \varvec{B} = 0, \end{aligned}$$

(2.1)

$$\begin{aligned}&\varvec{B}_t+\eta \nabla \times \nabla \times \varvec{B} - \nabla \times (\varvec{u} \times \varvec{B}) = 0, \end{aligned}$$

(2.2)

$$\begin{aligned}&\nabla \cdot \varvec{u}=0, \end{aligned}$$

(2.3)

$$\begin{aligned}&\nabla \cdot \varvec{B} =0, \end{aligned}$$

(2.4)

for $(\varvec{x},t)\in \Omega \times [0,T)$ with $\Omega \subset \mathbb {R}^d, d=2, 3$, where $\varvec{u}$ denotes the velocity field, p is the pressure, and $\varvec{B}$ is the magnetic field. For the physical parameters, $\nu ^{-1} = R_e$ (fluid Reynolds number), $\eta ^{-1}= R_m$ (magnetic Reynolds number), and s is the coupling coefficient, which are given by

$$\begin{aligned} R_e = \frac{UL}{\mu _f},~~ R_m = \mu _m \sigma UL,~~ s =\frac{B^2}{\rho \mu _m U^2}, \end{aligned}$$

where U is the characteristic velocity, L is the characteristic length, $\mu _f$ is the kinematic viscosity, $\mu _m$ is the magnetic permeability, $\sigma$ is the electric conductivity, B is the characteristic magnetic field, and $\rho$ is the fluid density. The system is equipped with the following boundary conditions

$$\begin{aligned} \varvec{u}|_{\partial \Omega }=0,\quad \varvec{B}\times {\varvec{n}}|_{\partial \Omega }=0, \end{aligned}$$

(2.5)

and initial conditions

$$\begin{aligned} \varvec{u}|_{( t= 0)}=\varvec{u}_0(\varvec{x}), ~~\varvec{B}|_{( t= 0)}=\varvec{B}_0(\varvec{x}), \end{aligned}$$

(2.6)

with $\nabla \cdot \varvec{u}_0 =0$, $\nabla \cdot \varvec{B}_0 =0$, where ${\varvec{n}}$ denotes the outward unit normal of $\partial \Omega$.

We fix some notations here. In this paper, we focus on the numerical analysis of the MHD system in two dimensional case ($d=2$). The corresponding results in three dimensional case ($d = 3$) are listed in subsequent remarks. Here and after, for two vector functions $\varvec{x}, \varvec{y}$, we denote the $L^2$ inner product as $(\varvec{x}, \varvec{y} ) = \int _{\Omega } \varvec{x} \cdot \varvec{y} dx$ and $L^2$ norm $\Vert \varvec{x}\Vert ^2 = (\varvec{x}, \varvec{x})$. Let $W^{k,r}(\Omega )$ stands for the standard Sobolev spaces equipped with the standard Sobolev norms $\Vert \cdot \Vert _{k,r}$. For $r = 2$, we write $H^k(\Omega )$ for $W^{k,2}(\Omega )$ and its corresponding norm is $\Vert \cdot \Vert _k$. We let $L^r(\Omega )$ denote the usual Lebesgue space on $\Omega$ with the norm $\Vert \cdot \Vert _{L^r}$.

For appropriate function setting of the MHD equations, we define

$$\begin{aligned} \begin{aligned}&H^1_0(\Omega ) =\left\{ \phi \in H^1(\Omega ): \phi |_{\partial \Omega } =0\right\} ,&\varvec{V}=\{\varvec{u} \in H_0^1(\Omega )^2: \nabla \cdot \varvec{u} =0\}\\&L_0^2(\Omega )=\left\{ \phi \in L^2(\Omega ): \int _{\Omega } \phi dx =0\right\} ,&\varvec{H}_{\tau }^1(\Omega )=\left\{ \varvec{w} \in H^1(\Omega )^2: \varvec{w} \times \varvec{n}|_{\partial \Omega } =0\right\} . \end{aligned} \end{aligned}$$

The following Poincaré type inequalities are well-known, see [11], which will be frequently used in our proof,

$$\begin{aligned} \Vert \varvec{w}\Vert _1\le & {} C_{\Omega }\Vert \nabla \varvec{w}\Vert , ~~~\varvec{w} \in H^1_0(\Omega )^d, \end{aligned}$$

(2.7)

$$\begin{aligned} \Vert \varvec{w}\Vert _1\le & {} C_{\Omega } (\Vert \nabla \times \varvec{w}\Vert + \Vert \nabla \cdot \varvec{w}\Vert ), ~~~\varvec{w} \in \varvec{H}_{\tau }^1 (\Omega ), \end{aligned}$$

(2.8)

$$\begin{aligned} \Vert \phi \Vert _1\le & {} C_{\Omega } \Vert \nabla \phi \Vert , ~~~ \phi \in H^1(\Omega )\cap L_0^2(\Omega ). \end{aligned}$$

(2.9)

The model (2.1)–(2.6) follows the energy dissipation law. By taking the $L^2$ inner product of (2.1) with ${\varvec{u}}$, and of (2.2) with $s \varvec{B}$, using (2.3)–(2.4) and $((\varvec{u} \cdot \nabla ) \varvec{u}, \varvec{u}) =0$ and integration by parts, we have

$$\begin{aligned}&({\varvec{u}}_t, {\varvec{u}})+\nu \Vert \nabla {\varvec{u}}\Vert ^2+s(\varvec{B}\times \nabla \times \varvec{B}, {\varvec{u}})=0, \end{aligned}$$

(2.10)

$$\begin{aligned}&s({\varvec{B}}_t,\varvec{B})+s\eta \Vert \nabla \times \varvec{B}\Vert ^2 +s\eta \Vert \nabla \cdot \varvec{B}\Vert ^2-s({\varvec{u}}\times \varvec{B},\nabla \times \varvec{B})=0. \end{aligned}$$

(2.11)

By taking the summation of the two equalities, we obtain

$$\begin{aligned} \frac{d}{dt} E({\varvec{u}},\varvec{B})=-\nu \Vert \nabla {\varvec{u}}\Vert ^2-s\eta \Vert \nabla \times \varvec{B}\Vert ^2-s\eta \Vert \nabla \cdot \varvec{B}\Vert ^2, \end{aligned}$$

(2.12)

where $E({\varvec{u}},\varvec{B})=\frac{1}{2} \Vert {\varvec{u}}\Vert ^2+\frac{s}{2}\Vert \varvec{B}\Vert ^2$ is the total energy of the MHD system (2.1)–(2.6).

3 Numerical Scheme and Energy Stability

In this section, we develop a fully decoupled, linearized, and unconditionally energy stable scheme in the fully discrete forms for solving the system (2.1)–(2.6), and show the unconditional energy stability in the fully discrete form with finite element discretizations for the spatial direction.

For $l \ge 1$, $r \ge 1$, we define the conforming finite element spaces $\varvec{V}_h \subset H_0^1(\Omega )^2, \varvec{U}_h \subset H^1(\Omega )^2$ with $\varvec{V}_h \subset \varvec{U}_h$, which consist of continuous piecewise polynomials of degree l, and $\varvec{C}_h \subset \varvec{H}^1_{\tau }(\Omega ), M_h \subset H^1(\Omega )\cap L_0^2(\Omega )$, which consist of continuous piecewise polynomials of degree r, and $l-1$, respectively. Moreover, the $\varvec{V}_h$ and $M_h$ satisfy the inf–sup condition:

$$\begin{aligned} \beta \Vert q_h\Vert \le \sup _{\varvec{v}_h \in \varvec{V}_h} \frac{(\nabla \cdot \varvec{v}_h, q_h)}{\Vert \nabla \varvec{v}_h\Vert }, \quad \forall q_h \in M_h. \end{aligned}$$

(3.1)

A well known mixed finite element pair for $\varvec{V}_h$ and $M_h$ satisfying (3.1) is the Taylor-Hood element [11]. For $\varvec{w}_h \in \varvec{U}_h$ or $\varvec{C}_h$, the following inverse inequalities hold

$$\begin{aligned} \begin{aligned}&\Vert \varvec{w}_h\Vert _{L^q} \le c h^{(\frac{1}{q} -\frac{1}{p})2}\Vert \varvec{w}_h\Vert _{L^p}, ~~{ p \le q,} \\&\Vert \varvec{w}_h\Vert _{L^{\infty }} \le c |\log h|^{\frac{1}{2}} \Vert \varvec{w}_h\Vert _1, \\&\Vert \varvec{w}_h\Vert _1 \le c h^{-1}\Vert \varvec{w}_h\Vert . \end{aligned} \end{aligned}$$

(3.2)

In order to derive the error estimates in spatial discretization, we recall the well-known Stokes projection and Maxwell projection, see [11, 32], i.e., given $\varvec{u} \in \varvec{V}, p \in L^2_0(\Omega )$, find $R_{(\varvec{u}, p)} \in \varvec{V}_h$ and $Q_{(\varvec{u}, p) }\in M_h$, such that

$$\begin{aligned} \left\{ \begin{aligned}&\nu (\nabla R_{(\varvec{u}, p)}, \nabla \varvec{v}_h ) - (Q_{(\varvec{u}, p)}, \nabla \cdot \varvec{v}_h) = \nu (\nabla \varvec{u}, \nabla \varvec{v}_h ) - (p, \nabla \cdot \varvec{v}_h), \quad \forall \varvec{v}_h \in \varvec{V}_h,\\&(\nabla \cdot R_{(\varvec{u}, p)}, q_h ) = (\nabla \cdot \varvec{u}, q_h), \quad \forall q_h \in M_h; \end{aligned} \right. \end{aligned}$$

and given $\varvec{B} \in \varvec{H}^1_{\tau }(\Omega )$, find $J_{\varvec{B}} \in \varvec{C}_h$, such that

$$\begin{aligned} (\nabla \times {J_{\varvec{B}}}, \nabla \times \varvec{C}_h) + (\nabla \cdot {J_{\varvec{B}}}, \nabla \cdot \varvec{C}_h) = (\nabla \times \varvec{B}, \nabla \times \varvec{C}_h) + (\nabla \cdot \varvec{B}, \nabla \cdot \varvec{C}_h). \end{aligned}$$

It is obvious that $R_{(\varvec{u}, p)}, Q_{(\varvec{u}, p)}, J_{\varvec{B}}$ are stable in the sense that

$$\begin{aligned} \Vert \nabla R_{(\varvec{u}, p)}\Vert + \Vert Q_{(\varvec{u}, p)}\Vert \le c (\Vert \nabla \varvec{u}\Vert + \Vert p\Vert ),\quad \Vert J_{\varvec{B}}\Vert _1 \le c \Vert \varvec{B}\Vert _1. \end{aligned}$$

(3.3)

Besides, if assuming $({\varvec{u}}, p, \varvec{B}) \in H^{l+1}(\Omega )^2 \times H^l(\Omega ) \times H^{r+1}(\Omega )^2$, then the following approximations hold

$$\begin{aligned}&\Vert \varvec{u} - R_{(\varvec{u}, p)}\Vert + h (\Vert \nabla (\varvec{u} - R_{(\varvec{u}, p)} )\Vert + \Vert p - Q_{(\varvec{u}, p)}\Vert ) \le C_{\Omega } h^{l+1} (\Vert \varvec{u}\Vert _{l+1} + \Vert p\Vert _l), \nonumber \\&\Vert \varvec{B} - {J_{\varvec{B}}}\Vert + h \Vert \varvec{B} - {J_{\varvec{B}}}\Vert _1 \le C_{\Omega } h^{r+1} \Vert \varvec{B}\Vert _{r+1}. \end{aligned}$$

(3.4)

Since $Q_{(\varvec{u}, p)}$ is in $H^1(\Omega )$, we can derive its $H^1$ stability as follows, which will be used in our analysis.

Theorem 3.1

The Stokes projection $Q_{(\varvec{u}, p)}$ is $H^1$ stable in the sense that

$$\begin{aligned} \Vert Q_{(\varvec{u}, p)}\Vert _1 \le c (\Vert \varvec{u}\Vert _2 + \Vert p\Vert _1). \end{aligned}$$

Proof

We define $H^1$ projection $P_1: H^1(\Omega )\cap L^2_0(\Omega )\rightarrow M_h$ by

$$\begin{aligned} (\nabla p - \nabla P_1 p, \nabla q_h)=0, ~~\forall q_h \in M_h, \end{aligned}$$

and it is easy to find

$$\begin{aligned} \Vert p- P_1 p\Vert + h \Vert p -P_1 p\Vert _1 \le c h \Vert p\Vert _1. \end{aligned}$$

Using the above property, (3.4) and inverse inequality $\Vert q_h\Vert _1 \le c h^{-1}\Vert q_h\Vert$, we derive

$$\begin{aligned} \begin{aligned} \Vert Q_{(\varvec{u}, p)}\Vert _1&\le \Vert p-Q_{(\varvec{u}, p)}\Vert _1 + \Vert p\Vert _1 \le \Vert p-P_1p\Vert _1 + \Vert P_1 p - Q_{(\varvec{u}, p)}\Vert _1 +\Vert p\Vert _1\\&\le c \Vert p\Vert _1 +c h^{-1} \Vert P_1 p - Q_{(\varvec{u}, p)}\Vert \\&\le c\Vert p\Vert _1 + ch^{-1} \Vert P_1 p - p\Vert +c h^{-1} \Vert p -Q_{(\varvec{u}, p)}\Vert \\&\le c\Vert p\Vert _1 + c h^{-1} h (\Vert \varvec{u}\Vert _2 + \Vert p\Vert _1) \le c(\Vert \varvec{u}\Vert _2 + \Vert p\Vert _1). \end{aligned} \end{aligned}$$

The proof is finished. $\square$

We assume the solution to (2.1)–(2.6) has the following regularity conditions

$$\begin{aligned} (\mathbf{A0}):&\varvec{u} \in L^{\infty }(0, T; H^{l+1}(\Omega )^2),~~ p \in L^{\infty }(0, T; H^l(\Omega )),~~ \varvec{B} \in L^{\infty }(0, T; H^{r+1}(\Omega )^2),\nonumber \\ \end{aligned}$$

(3.5)

such that the following approximate properties hold

$$\begin{aligned}&\Vert \varvec{u}(t_n) - R_{(\varvec{u}(t_n), p(t_n))}\Vert + h (\Vert \nabla (\varvec{u}(t_n) - R_{(\varvec{u}(t_n), p(t_n))} )\Vert \nonumber \\&\quad +\, \Vert p(t_n) - Q_{(\varvec{u}(t_n), p(t_n))}\Vert ) \le c h^{l+1}, \end{aligned}$$

(3.6)

$$\begin{aligned}&\Vert \varvec{B}(t_n) - J_{\varvec{B}(t_n)}\Vert + h \Vert \varvec{B}(t_n) - J_{\varvec{B}(t_n)}\Vert _1 \le c h^{r+1}. \end{aligned}$$

(3.7)

Now, we develop the fully discrete scheme based on the finite element discretization. It reads as follows.

Given the initial data $\varvec{B}_h^0 = {J_{\varvec{B}}}_0, (\varvec{u}_h^0, p_h^0) = (R_{(\varvec{u}_0, p_0)}, Q_{(\varvec{u}_0, p_0)})$, where $p_0$ is obtained by $\varvec{u}_0, \varvec{B}_0$ and (2.1) following the method in [14], we compute $\varvec{B}_h^{n+1}$, $\tilde{\varvec{u}}_h^{n+1}$, $p_h^{n+1}$, ${\varvec{u}}_h^{n+1}$ by the following steps.

Step 1 Find $\varvec{B}_h^{n+1} \in \varvec{C}_h, \varvec{u}^n_{h*} \in \varvec{U}_h$ such that

$$\begin{aligned}&\frac{1}{\delta t}(\varvec{B}_h^{n+1} - \varvec{B}_h^{n}, \varvec{c}_h ) + \eta (\nabla \times \varvec{B}_h^{n+1},\nabla \times \varvec{c}_h) + \eta (\nabla \cdot \varvec{B}_h^{n+1}, \nabla \cdot \varvec{c}_h) \nonumber \\&\quad -\, (\varvec{u}^n_{h*} \times \varvec{B}_h^{n}, \nabla \times \varvec{c}_h) = 0, \quad \varvec{c}_h \in \varvec{C}_h, \end{aligned}$$

(3.8)

$$\begin{aligned}&\frac{1}{\delta t}( \varvec{u}_{h*}^{n} - \varvec{u}_h^{n}, \varvec{w}_h ) + s (\varvec{B}_h^n \times \nabla \times \varvec{B}^{n+1}_h, \varvec{w}_h) =0, \quad \varvec{w}_h \in \varvec{U}_h. \end{aligned}$$

(3.9)

Step 2 Find $\tilde{\varvec{u}}_h^{n+1} \in \varvec{V}_h$ such that

$$\begin{aligned}&\frac{1}{\delta t}(\tilde{\varvec{u}}_h^{n+1} - \varvec{u}_{h*}^n,\varvec{v}_h ) + \nu (\nabla \tilde{\varvec{u}}_h^{n+1}, \nabla \varvec{v}_h) +b({\varvec{u}}_h^{n}, \tilde{\varvec{u}}_h^{n+1}, \varvec{v}_h) \nonumber \\&\quad -\,(p^{n}_h, \nabla \cdot \varvec{v}_h) = 0, \quad \varvec{v}_h \in \varvec{V}_h. \end{aligned}$$

(3.10)

Step 3 Find $p_h^{n+1} \in M_h$ such that

$$\begin{aligned}&(\nabla p_h^{n+1}, \nabla q_h) = -\frac{1}{\delta t} (\nabla \cdot \tilde{\varvec{u}}_h^{n+1}, q_h) + (\nabla p_h^{n}, \nabla q_h), \quad q_h \in M_h. \end{aligned}$$

(3.11)

Step 4 Update $\varvec{u}_h^{n+1} \in \varvec{V}_h + \nabla M_h$ from

$$\begin{aligned} \varvec{u}_h^{n+1} = \tilde{\varvec{u}}_h^{n+1} - \delta t \nabla (p_h^{n+1} - p_h^{n}). \end{aligned}$$

(3.12)

Remark 3.2

To avoid some technical difficulties in the error estimates at the initial time, here we set the initial data $\varvec{u}_h^0$, $p_h^0$ by the Stokes projection of $\varvec{u}(0)$ and p(0). The difficulties at the initial time can be also overcome by making some approximation assumptions as (5.18) in [13]. In the numerical implementations, we can obtain the initial data through solving two equations at $t=0$ like (3.7) and (3.8) in [1].

Remark 3.3

For the convective term in (3.10), we use the trilinear form as follows (cf. [30]),

$$\begin{aligned} b(\varvec{u}, \varvec{v}, \varvec{w}): = \frac{1}{2}((\varvec{u} \cdot \nabla ) \varvec{v}, \varvec{w})-\frac{1}{2}((\varvec{u} \cdot \nabla ) \varvec{w}, \varvec{v}). \end{aligned}$$

(3.13)

Note when $\varvec{u} \in H^1(\Omega )^2, \varvec{v}, \varvec{w} \in H_0^1(\Omega )^2$, by using the integration by parts, we derive

$$\begin{aligned} b(\varvec{u}, \varvec{v}, \varvec{w}) = ((\varvec{u}\cdot \nabla ) \varvec{v}, \varvec{w}) +\frac{1}{2} ((\nabla \cdot \varvec{u}) \varvec{v}, \varvec{w}). \end{aligned}$$

(3.14)

Therefore, when $\nabla \cdot \varvec{u} =0$, we have $b(\varvec{u}, \varvec{v}, \varvec{w}) = ((\varvec{u} \cdot \nabla ) \varvec{v}, \varvec{w})$.

Remark 3.4

For the fully discrete scheme (3.8), the exact divergence free for the magnetic field $\varvec{B}_h^{n+1}$ is not valid any more. Therefore a common practice is to add a penalty term $(\nabla \cdot \varvec{B}_h^{n+1}, \nabla \cdot \varvec{c}_h)$ in the momentum equation in order to verify the coercivity of the magnetic equation, and approximate the divergence free condition of the magnetic field for the spatial discrete case, cf. [15].

Remark 3.5

The final velocity field $\varvec{u}_h^{n+1}$ satisfies the discrete divergence free condition. This can be deduced by taking the $L^2$ inner product of (3.12) with $\nabla q_h$, we obtain

$$\begin{aligned} (\varvec{u}_h^{n+1}, \nabla q_h) =- (\nabla \cdot \tilde{\varvec{u}}_h^{n+1}, q_h) - \delta t (\nabla (p_h^{n+1} - p_h^{n}) ,\nabla q_h). \end{aligned}$$

After combining with (3.11), we arrive at

$$\begin{aligned} (\varvec{u}_h^{n+1}, \nabla q_h)=0, \quad \forall q_h \in M_h. \end{aligned}$$

(3.15)

There are two advantages in the scheme (3.8)–(3.12): linear and decoupled, where the magnetic field $\varvec{B}$, pressure p and velocity $\varvec{u}$ can be solved linearly and independently at each time step. In addition, the unconditional energy stability holds, which is shown as follows.

Theorem 3.6

The scheme (3.8)–(3.12) is unconditionally energy stable in the sense that

$$\begin{aligned} \begin{aligned}&s \Vert \varvec{B}_h^{n+1}\Vert ^2 + \Vert \varvec{u}_h^{n+1}\Vert ^2+ \delta t^2\Vert \nabla p_h^{n+1}\Vert ^2\\&\quad + 2 \delta t \left( s \eta \Vert \nabla \times \varvec{B}_h^{n+1}\Vert ^2 +s \eta \Vert \nabla \cdot \varvec{B}_h^{n+1}\Vert ^2+ \nu \Vert \nabla \tilde{\varvec{u}}_h^{n+1}\Vert ^2\right) \\&\quad \le s \Vert \varvec{B}_h^n\Vert ^2 + \Vert \varvec{u}_h^n\Vert ^2 +\delta t^2 \Vert \nabla p_h^n\Vert ^2. \end{aligned} \end{aligned}$$

(3.16)

Proof

By taking $\varvec{c}_h =s \varvec{B}_h^{n+1}$ in (3.8) and $\varvec{w}_h = \varvec{u}^n_{h*}$ in (3.9), and using the following identity

$$\begin{aligned} 2a(a-b)=a^2-b^2+(a-b)^2, \end{aligned}$$

(3.17)

we obtain

$$\begin{aligned} \begin{aligned}&\frac{s}{2 \delta t}\left( \Vert \varvec{B}_h^{n+1} - \varvec{B}_h^n\Vert ^2 + \Vert \varvec{B}_h^{n+1}\Vert ^2 - \Vert \varvec{B}_h^n\Vert ^2\right)&+ s \eta \Vert \nabla \times \varvec{B}_h^{n+1}\Vert ^2 + s \eta \Vert \nabla \cdot \varvec{B}_h^{n+1}\Vert ^2 \\&\quad + s (\varvec{B}_h^n \times \varvec{u}^n_{h *}, \nabla \times \varvec{B}_h^{n+1}) =0, \end{aligned} \end{aligned}$$

(3.18)

and

$$\begin{aligned} \frac{1}{2 \delta t}\left( \Vert \varvec{u}^{n}_{h*} - \varvec{u}_h^n \Vert ^2 + \Vert \varvec{u}^{n}_{h*}\Vert ^2 - \Vert \varvec{u}_h^n\Vert ^2\right) - s(\nabla \times \varvec{B}_h^{n+1} \times \varvec{B}_h^n, \varvec{u}^n_{h *})=0. \end{aligned}$$

(3.19)

By taking $\varvec{v}_h = \tilde{\varvec{u}}_h^{n+1}$ in (3.10) and using the skew-symmetric property:

$$\begin{aligned} {b({\varvec{u}}, \varvec{v}, \varvec{v})=0, \varvec{u} \in L^2(\Omega )^2, \varvec{v} \in H^1(\Omega )^2,} \end{aligned}$$

(3.20)

we derive

$$\begin{aligned} \frac{1}{2 \delta t}\left( \Vert \tilde{\varvec{u}}_h^{n+1} - \varvec{u}_{h *}^n \Vert ^2 + \Vert \tilde{\varvec{u}}_h^{n+1}\Vert ^2- \Vert \varvec{u}_{h*}^n\Vert ^2\right) + \nu \Vert \nabla \tilde{\varvec{u}}_h^{n+1}\Vert ^2 +(\nabla p_h^n, \tilde{\varvec{u}}_h^{n+1}) =0.\nonumber \\ \end{aligned}$$

(3.21)

We rewrite (3.12) as

$$\begin{aligned} \frac{1 }{\delta t} \varvec{u}_h^{n+1}+ \nabla p_h^{n+1} = \frac{1}{\delta t}\tilde{\varvec{u}}_h^{n+1} +\nabla p_h^n. \end{aligned}$$

By taking the $L^2$ inner product of the above with itself on both sides, and using (3.15), we obtain

$$\begin{aligned} \frac{1}{2 \delta t}\Vert \varvec{u}_h^{n+1}\Vert ^2 - \frac{1}{2 \delta t}\Vert \tilde{\varvec{u}}_h^{n+1}\Vert ^2 + \frac{\delta t}{2}\Vert \nabla p_h^{n+1}\Vert ^2 - \frac{\delta t}{2} \Vert \nabla p_h^n\Vert ^2 = (\tilde{\varvec{u}}_h^{n+1}, \nabla p_h^n). \end{aligned}$$

(3.22)

Finally, by taking the summations (3.18), (3.19), (3.21) and (3.22), we obtain

$$\begin{aligned} \begin{aligned}&\frac{s}{2 \delta t}(\Vert \varvec{B}_h^{n+1}\Vert ^2 - \Vert \varvec{B}_h^n\Vert ^2+\Vert \varvec{B}_h^{n+1} - \varvec{B}_h^n\Vert ^2 ) + s \eta \Vert \nabla \times \varvec{B}_h^{n+1}\Vert ^2 + s \eta \Vert \nabla \cdot \varvec{B}_h^{n+1}\Vert ^2\\&\quad +\frac{1}{2 \delta t}\left( \Vert \varvec{u}_h^{n+1}\Vert ^2 - \Vert \varvec{u}_h^n\Vert ^2+\Vert \varvec{u}^{n}_{h*} - \varvec{u}_h^n \Vert ^2 \right) +\frac{1}{2 \delta t} \Vert \tilde{\varvec{u}}_h^{n+1} - \varvec{u}_{h*}^n \Vert ^2 \\&\quad + \nu \Vert \nabla \tilde{\varvec{u}}_h^{n+1}\Vert ^2 + \frac{\delta t}{2}\Vert \nabla p_h^{n+1}\Vert ^2 - \frac{\delta t}{2} \Vert \nabla p_h^n\Vert ^2 = 0. \end{aligned} \end{aligned}$$

(3.23)

After multiplying with $2\delta t$ and dropping some positive terms, we obtain (3.16). $\square$

4 Error Estimates

In this section, we provide the convergence analysis for the fully discrete scheme (3.8)–(3.12). We first develop the error estimates for velocity and magnetic field in Sect. 4.1, then improve the error estimate for pressure in Sect. 4.2. Without loss of generality, we denote by C a generic constant that is independent of $\delta t$ and h but possibly depends on the data and the solution, and use $f \lesssim g$ to denote that there is a generic constant C such that $f\le Cg$.

4.1 Error Estimates for the Velocity and Magnetic Field

For convenience, we denote $d_t \phi ^n = \frac{\phi ^n - \phi ^{n-1}}{\delta t}$, $d_t \phi (t_n) = \frac{\phi (t_n) - \phi (t_{n-1})}{\delta t}$ for any variable $\phi , \phi (t)$. The model system (2.1)–(2.2) at $t_{n+1}$ can be written as the truncation forms:

$$\begin{aligned}&\left( d_t \varvec{B}(t_{n+1}), \varvec{c} \right) + \eta ( \nabla \times \varvec{B}(t_{n+1}), \nabla \times \varvec{c}) + \eta ( \nabla \cdot \varvec{B}(t_{n+1}), \nabla \cdot \varvec{c}) \nonumber \\&\quad - ( \varvec{u}(t_n) \times \varvec{B}(t_n), \nabla \times \varvec{c}) = (R^{n+1}_b, \varvec{c}), \quad \forall \varvec{c}\in \varvec{H}_{\tau }^1(\Omega ), \end{aligned}$$

(4.1)

$$\begin{aligned}&\left( d_t \varvec{u}(t_{n+1}) , \varvec{v}\right) +\nu (\nabla \varvec{u} (t_{n+1}), \nabla \varvec{v}) + b({\varvec{u}}(t_n), \varvec{u}(t_{n+1}), \varvec{v}) - ( p(t_n), \nabla \cdot \varvec{v}) \nonumber \\&\quad + s (\varvec{B}(t_n) \times \nabla \times \varvec{B}(t_{n+1}), \varvec{v}) = (R^{n+1}_u, \varvec{v}), \quad \forall \varvec{v} \in H^1_0(\Omega )^2, \end{aligned}$$

(4.2)

$$\begin{aligned}&\frac{\varvec{u}(t_{n+1}) - \varvec{u}(t_{n+1})}{\delta t} + \nabla (p(t_{n+1}) - p(t_n)) =R^{n+1}_p, \end{aligned}$$

(4.3)

where $R_b^{n+1}, R_u^{n+1}, R_p^{n+1}$ are the truncation terms.

We denote the error functions as

$$\begin{aligned} \left\{ \begin{aligned}&\theta _b^n = J_{\varvec{B}(t_n)} - \varvec{B}_h^n, \rho _b^n = \varvec{B}(t_n) - J_{ \varvec{B}(t_n)},\\&{\tilde{\theta }}_u^n = R_{(\varvec{u}(t_n), p(t_n))} - \tilde{\varvec{u}}_h^n, \rho _u^n = \varvec{u}(t_n) - R_{(\varvec{u}(t_n), p(t_n))}, \theta _u^n = R_{(\varvec{u}(t_n), p(t_n))} - \varvec{u}_h^n,\\&\theta _p^n = Q_{(\varvec{u}(t_n), p(t_n))} - p_h^n, \rho _p^n= p(t_n) -Q_{(\varvec{u}(t_n), p(t_n))},\\&e_b^n = \varvec{B}(t_n) - \varvec{B}_h^n = \theta ^n_b + \rho _b^n, {\tilde{e}}_u^n = \varvec{u}(t_n) -\tilde{\varvec{u}}_h^n = {\tilde{\theta }}^n_u + \rho _u^n, \\&e_u^n = \varvec{u}(t_n) -\varvec{u}_h^n= \theta ^n_u + \rho _u^n, e_p^n = p(t_n) -p_h^n= \theta ^n_p + \rho _p^n. \end{aligned} \right. \end{aligned}$$

(4.4)

By subtracting (3.8) from (4.1), (3.10) from (4.2) and applying (3.9), and (3.12) from (4.3), we obtain the following error equations,

$$\begin{aligned}&(d_te^{n+1}_b, \varvec{c}_h) + \eta ( \nabla \times e^{n+1}_b, \nabla \times \varvec{c}_h) + \eta ( \nabla \cdot e^{n+1}_b, \nabla \cdot \varvec{c}_h) \nonumber \\&\quad +\, (\varvec{B}(t_n) \times \varvec{u}(t_n) , \nabla \times \varvec{c}_h) - (\varvec{B}_h^n \times \varvec{u}^n_{h*}, \nabla \times \varvec{c}_h) = (R^{n+1}_b, \varvec{c}_h), ~~\varvec{c}_h \in \varvec{C}_h, \end{aligned}$$

(4.5)

$$\begin{aligned}&\frac{1}{\delta t}({\tilde{e}}_u^{n+1} - e_u^n, \varvec{v}_h ) + \nu (\nabla {\tilde{e}}_u^{n+1}, \nabla \varvec{v}_h) + b({\varvec{u}}(t_n), \varvec{u}(t_{n+1}), \varvec{v}_h)\nonumber \\&\quad - b(\varvec{u}_h^n, \tilde{\varvec{u}}_h^{n+1}, \varvec{v}_h)- ( e_p^n, \nabla \cdot \varvec{v}_h) \nonumber \\&\quad +\, s (\varvec{B}(t_n) \times \nabla \times \varvec{B}(t_{n+1}), \varvec{v}_h) - s (\varvec{B}_h^n \times \nabla \times \varvec{B}_h^{n+1}, \varvec{v}_h) = (R^{n+1}_u, \varvec{v}_h), ~~\varvec{v}_h \in \varvec{V}_h, \nonumber \\\end{aligned}$$

(4.6)

$$\begin{aligned}&\frac{e_u^{n+1} }{\delta t}+ \nabla e_p^{n+1} = \frac{{\tilde{e}}_u^{n+1}}{\delta t}+ \nabla e_p^n + R^{n+1}_p. \end{aligned}$$

(4.7)

We assume the exact solution $({\varvec{u}},\varvec{B},p)$ to the system (2.1)–(2.6) possesses the following regularity conditions,

$$\begin{aligned} \text{(A1): } \qquad&\varvec{u}_t, \varvec{B}_t \in L^{\infty }(0,T; H^1(\Omega )^2), ~~p_t \in L^{\infty }(0,T; H^1(\Omega )),~~\\&{\varvec{u}}_{tt}, \varvec{B}_{tt} \in L^{\infty }(0,T; L^2(\Omega )^2). \end{aligned}$$

One can easily establish the following estimates for the truncation errors, provided that the exact solutions are sufficiently smooth or satisfy the assumptions (A0), (A1).

Lemma 4.1

Under the assumptions (A0) and (A1), the truncation errors satisfy

$$\begin{aligned} \Vert R^n_u\Vert + \Vert R^n_b\Vert + \Vert R^n_p\Vert \lesssim \delta t , \quad 0\le n\le [\frac{T}{\delta t}]. \end{aligned}$$

Proof

Due to the page limit, we omit the proof since it is rather standard. $\square$

There are two essential challenges in deriving the error analysis for velocity and magnetic field. One is from the auxiliary intermediate function $\varvec{u}_{h*}^n$ since there is no error equation corresponding to it. The other is how to obtain the $L^{\infty }$ bound of the numerical solution $\varvec{B}_h^n$ directly from the Eq. (3.8). To this end, we first build the relation between $\varvec{u}_{h*}^n$ and $\varvec{u}_h^n$ in Lemma 4.2. Then, by using the mathematical induction method, we establish the $L^{\infty }$ bound for $\varvec{B}_h^n$ in Lemma 4.3. The final error estimates are derived in Theorem 4.4.

Lemma 4.2

Under the assumption $(\mathbf A0)$, the following estimate holds

$$\begin{aligned} \Vert \varvec{u}_{h*}^{n} - \varvec{u}_h^{n}\Vert ^2 \lesssim \Vert \theta _u^n\Vert ^2 + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 \Vert \nabla \times \theta ^{n+1}_b \Vert ^2. \end{aligned}$$

Proof

By taking $\varvec{w}_h = \varvec{u}_{h *}^n - R_{(\varvec{u}(t_n), \varvec{p}(t_n))}$ in (3.9) and using (3.17), we get

$$\begin{aligned} \begin{aligned}&\frac{1}{2\delta t} ( \Vert \varvec{u}_{h*}^{n} - \varvec{u}_h^{n}\Vert ^2 + \Vert \varvec{u}_{h *}^n - R_{(\varvec{u}(t_n), \varvec{p}(t_n))}\Vert ^2 - \Vert \theta _u^n\Vert ^2 )\\&\quad =- s \left( \varvec{B}_h^n \times \nabla \times \varvec{B}^{n+1}_h, \varvec{u}_{h *}^n - R_{(\varvec{u}(t_n), \varvec{p}(t_n))} \right) \\&\quad \le s \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \nabla \times \varvec{B}^{n+1}_h\Vert \Vert \varvec{u}_{h *}^n - R_{(\varvec{u}(t_n), \varvec{p}(t_n))} \Vert \\&\quad \lesssim \frac{1}{2\delta t} \Vert \varvec{u}_{h *}^n - R_{(\varvec{u}(t_n), \varvec{p}(t_n)) }\Vert ^2 + \delta t\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 \Vert \nabla \times \varvec{B}^{n+1}_h\Vert ^2, \end{aligned} \end{aligned}$$

(4.8)

which implies

$$\begin{aligned} \Vert \varvec{u}_{h*}^{n} - \varvec{u}_h^{n}\Vert ^2&\lesssim \Vert \theta _u^n\Vert ^2 + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 \Vert \nabla \times \varvec{B}^{n+1}_h\Vert ^2 \nonumber \\&\lesssim \Vert \theta _u^n\Vert ^2 + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 (\Vert \nabla \times \varvec{B}(t_{n+1})\Vert ^2+ \Vert \nabla \times \rho ^{n+1}_b \Vert ^2 + \Vert \nabla \times \theta ^{n+1}_b \Vert ^2) \nonumber \\\\&\lesssim \Vert \theta _u^n\Vert ^2 + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 \Vert \nabla \times \theta ^{n+1}_b \Vert ^2,\nonumber \end{aligned}$$

(4.9)

where we use (3.7). $\square$

In order to demonstrate the $L^{\infty }$ stability of $\varvec{B}_h^n$, we first show the $L^{\infty }$ bound of $J_{\varvec{B}(t_n)}$. We denote $\Pi : H^{r+1}(\Omega )^2 \cap \varvec{H}_{\tau }^1(\Omega ) \rightarrow C_h$ the interpolation operator, then we have the approximation properties (cf. [11])

$$\begin{aligned} \begin{aligned} {\Vert \varvec{B} - \Pi \varvec{B}\Vert _{L^{\infty }} \lesssim h^{r}\Vert \varvec{B}\Vert _{r+1},\quad \Vert \varvec{B} - \Pi \varvec{B}\Vert \lesssim h^{r+1}\Vert \varvec{B}\Vert _{r+1}}. \end{aligned} \end{aligned}$$

(4.10)

Suppose the assumption $(\mathbf A0)$ holds, from (4.10), (3.7) and the inverse inequality (3.2), we derive

$$\begin{aligned} \begin{aligned} \Vert J_{\varvec{B}(t_n)}\Vert _{L^{\infty }}&\le \Vert \varvec{B}(t_n) - J_{\varvec{B}(t_n)}\Vert _{L^{\infty }} + \Vert \varvec{B}(t_n)\Vert _{L^{\infty }}\\&\le \Vert \varvec{B}(t_n) - \Pi \varvec{B}(t_n) \Vert _{L^{\infty }}+ \Vert \Pi \varvec{B}(t_n) - J_{\varvec{B}(t_n)}\Vert _{L^{\infty }} + \Vert \varvec{B}(t_n)\Vert _{L^{\infty }} \\&\le C_{\Omega } h^r \Vert \varvec{B}(t_n) \Vert _{r+1} + C_{\Omega }h^{-1} \Vert \Pi \varvec{B}(t_n) - J_{\varvec{B}(t_n)}\Vert + \Vert \varvec{B}(t_n)\Vert _{L^{\infty }} \\&\le C_{\Omega } h^r \Vert \varvec{B}(t_n) \Vert _{r+1} +C_{\Omega }h^{-1}( \Vert \Pi \varvec{B}(t_n) - \varvec{B}(t_n)\Vert \\&\quad + \Vert \varvec{B}(t_n)- J_{\varvec{B}(t_n)}\Vert ) + \Vert \varvec{B}(t_n)\Vert _{L^{\infty }} \\&\le C_{\Omega } h^r \Vert \varvec{B}(t_n) \Vert _{r+1} + \Vert \varvec{B}(t_n)\Vert _{L^{\infty }} \le C_0, \quad 0 \le n \le \left[ \frac{T}{\delta t}\right] . \end{aligned} \end{aligned}$$

(4.11)

Furthermore, (4.11) also implies that the $l^2(L^{\infty })$ bound of $J_{ \varvec{B}(t_n)}$ satisfies

$$\begin{aligned} \delta t \sum _{n=0}^{[\frac{T}{\delta t}]} \Vert J_{ \varvec{B}(t_n)}\Vert ^2_{L^{\infty }} \le T C^2_0. \end{aligned}$$

(4.12)

Let $\kappa _0 = 2 T C^2_0 +1$, and assume the following regularity conditions hold

$$\begin{aligned} {(\mathbf A2)}: \varvec{u}_t \in L^2(0, T; H^{l+1}(\Omega )^2), p_t \in L^2(0, T; H^l(\Omega )), \varvec{B}_t \in L^2(0, T; H^{r+1}(\Omega )^2). \end{aligned}$$

For the error estimates of velocity and magnetic field, we need the $l^2(L^{\infty })$ bound of $\varvec{B}_h^n$. Meanwhile for the error estimate of pressure, we further need the $l^{\infty }(L^{\infty })$ bound of $\varvec{B}_h^n$. Now, we state the $l^2(L^{\infty })$ stability of $\varvec{B}_h^n$ in the following lemma.

Lemma 4.3

Assuming that the solution to (2.1)–(2.6) satisfies the regularity assumptions (A0)-(A2), then there exist two positive constants $\delta t_0$ and $h_0$ such that, when $\delta t \le \delta t_0, h \le h_0$ and $\delta t |\log h| \le 1$, the solution $\varvec{B}_h^n$ of scheme (3.8)–(3.12) satisfies

$$\begin{aligned} \delta t \sum _{n=0}^{[\frac{T}{\delta t}]}\Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _0,\quad \max _{0\le n \le [\frac{T}{\delta t}]} \delta t \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\} +1}, \end{aligned}$$

(4.13)

where $\kappa _1 = 2C_0^2 + C_{\Omega } C(\kappa _0), \kappa _2 = C_{\Omega } C(\kappa _0)$, and the constants $\delta t_0, h_0$, $C(\kappa _0)$ will be verified in the proof.

Proof

We use the mathematical induction method here.

When $n=0$, we have $\delta t \Vert \varvec{B}_h^0\Vert ^2_{L^{\infty }} = \delta t \Vert J_{\varvec{B}_0}\Vert ^2_{L^{\infty }} \le C_0^2 \delta t \le \kappa _0$, and $\delta t\Vert \varvec{B}_h^0\Vert ^2_{L^{\infty }}\le C_0^2 \delta t \le \kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\}+1}$ ( $\kappa _1\ge C_0^2$).

Assuming that

$$\begin{aligned} \delta t \sum _{n=0}^{N}\Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _0,\quad \max _{0\le n \le N} \delta t \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\}+1} \end{aligned}$$

(4.14)

are valid, we will show

$$\begin{aligned} \delta t \sum _{n=0}^{N+1}\Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _0,\quad \max _{0\le n \le N+1} \delta t \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\} +1} \end{aligned}$$

(4.15)

are also valid via the following two steps. In Step i, we use the induction assumptions to derive the convergence analysis. In Step ii, using the convergence results obtained in Step i and inverse inequalities, we get the $l^2(L^{\infty })$ bounds of $\varvec{B}_h^{N+1}$.

(Step i). By taking $\varvec{c}_h =\theta _b^{n+1}$ in (4.5), we obtain

$$\begin{aligned}&\frac{1}{2 \delta t} (\Vert \theta _b^{n+1}\Vert ^2 -\Vert \theta _b^{n}\Vert ^2 +\Vert \theta _b^{n+1} - \theta _b^{n}\Vert ^2 ) + \eta (\Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2) \nonumber \\&\quad +\, (d_t \rho _b^{n+1}, \theta _b^{n+1}) + ( \varvec{B}(t_n) \times \varvec{u}(t_n) - \varvec{B}_h^n \times \varvec{u}^n_{h*}, \nabla \times \theta _b^{n+1}) = (R^{n+1}_b, \theta _b^{n+1}).\nonumber \\ \end{aligned}$$

(4.16)

By taking $\varvec{v}_h={\tilde{\theta }}_u^{n+1}$ in (4.6), we derive

$$\begin{aligned} \begin{aligned}&\frac{1}{2 \delta t} ( \Vert {\tilde{\theta }}_u^{n+1}\Vert ^2 - \Vert \theta _u^{n}\Vert ^2 + \Vert {\tilde{\theta }}_u^{n+1} - {\theta }_u^{n}\Vert ^2) + \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2\\&\quad + \nu (\nabla \rho _u^{n+1}, \nabla {\tilde{\theta }}_u^{n+1}) +(d_t \rho _u^{n+1}, {\tilde{\theta }}_u^{n+1}) \\&\quad + b( {\varvec{u}}(t_n), \varvec{u}(t_{n+1}), {\tilde{\theta }}_u^{n+1}) - b ({\varvec{u}}_h^n, \tilde{\varvec{u}}_h^{n+1}, {\tilde{\theta }}_u^{n+1}) + (\nabla \rho _p^n, {\tilde{\theta }}_u^{n+1}) + (\nabla \theta _p^n, {\tilde{\theta }}_u^{n+1})\\&\quad + s (\varvec{B}(t_n) \times \nabla \times \varvec{B}(t_{n+1}), {\tilde{\theta }}_u^{n+1} ) - s(\varvec{B}_h^n \times \nabla \times \varvec{B}_h^{n+1},{\tilde{\theta }}_u^{n+1}) = (R^{n+1}_u, {\tilde{\theta }}_u^{n+1}). \end{aligned} \end{aligned}$$

(4.17)

We rewrite (4.7) to obtain

$$\begin{aligned} \frac{1}{\delta t} \theta _u^{n+1} + \nabla \theta _p^{n+1} = \frac{1}{\delta t}{\tilde{\theta }}_u^{n+1} + \nabla \theta _p^n + \rho ^{n+1}, \end{aligned}$$

(4.18)

where $\rho ^{n+1} = R_p^{n+1}- \delta t \nabla d_t \rho ^{n+1}_p$. By taking the $L^2$ inner product of (4.18) with itself on both sides, we obtain

$$\begin{aligned} \begin{aligned} ({\tilde{\theta }}_u^{n+1}, \nabla \theta _p^n)&= \frac{1}{2 \delta t}(\Vert \theta _u^{n+1}\Vert ^2 - \Vert {\tilde{\theta }}_u^{n+1}\Vert ^2) + \frac{\delta t}{2} (\Vert \nabla \theta _p^{n+1}\Vert ^2 - \Vert \nabla \theta _p^{n}\Vert ^2) \\&\quad -({\tilde{\theta }}_u^{n+1}, \rho ^{n+1})- \delta t (\nabla \theta ^n_p, \rho ^{n+1}) - \frac{\delta t}{2} \Vert \rho ^{n+1}\Vert ^2. \end{aligned} \end{aligned}$$

(4.19)

We combine (4.16), (4.17) and (4.19) to obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{2 \delta t} (\Vert \theta _b^{n+1} - \theta _b^{n}\Vert ^2 + \Vert \theta _b^{n+1}\Vert ^2 - \Vert \theta _b^{n}\Vert ^2) \\&\qquad + \eta ( \Vert \nabla \times \theta _b^{n+1}\Vert ^2 + \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2)+ \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2\\&\qquad +\frac{\delta t}{2} (\Vert \nabla \theta _p^{n+1}\Vert ^2 - \Vert \nabla \theta _p^{n}\Vert ^2) +\frac{1}{2 \delta t} (\Vert {\tilde{\theta }}_u^{n+1} - \theta _u^{n}\Vert ^2 + \Vert \theta _u^{n+1}\Vert ^2 - \Vert \theta _u^{n}\Vert ^2)\\&\quad = ( \varvec{u}(t_n) \times \varvec{B}(t_n) - \varvec{u}^n_{h*}\times \varvec{B}_h^n , \nabla \times \theta _b^{n+1})&(:\text{ term } \text{ A })\\&\qquad - b({\varvec{u}}(t_n), \varvec{u}(t_{n+1}), {\tilde{\theta }}_u^{n+1}) + b ({\varvec{u}}_h^n, \tilde{\varvec{u}}_h^{n+1}, {\tilde{\theta }}_u^{n+1})&(: \text{ term } \text{ B }) \\&\qquad - s (\varvec{B}(t_n) \times \nabla \times \varvec{B}(t_{n+1})- \varvec{B}_h^n \times \nabla \times \varvec{B}_h^{n+1},{\tilde{\theta }}_u^{n+1})&(: \text{ term } \text{ C })\\&\qquad + ({\tilde{\theta }}_u^{n+1}, \rho ^{n+1})+ \delta t (\nabla \theta ^n_p, \rho ^{n+1})&(: \text{ term } \text{ D })\\&\qquad + ( \rho _p^n- \rho ^{n+1}_p, \nabla \cdot {\tilde{\theta }}_u^{n+1})- (d_t \rho ^{n+1}_b, \theta _b^{n+1}) - (d_t \rho ^{n+1}_u, {\tilde{\theta }}_u^{n+1} )&(: \text{ term } \text{ E })\\&\qquad +(R^{n+1}_b, \theta _b^{n+1})+ (R^{n+1}_u, {\tilde{\theta }}_u^{n+1})&(: \text{ term } \text{ F })\\&\qquad +\frac{\delta t}{2} \Vert \rho ^{n+1}\Vert ^2. \end{aligned}\quad \quad \end{aligned}$$

(4.20)

We estimate the terms (A–F) one by one as follows.

For term A, using the Lemma 4.2, (3.6), (3.7) and regularity assumptions, we derive

$$\begin{aligned} \begin{aligned} \text{(term } \text{ A) }&\le |( \varvec{u}(t_n) \times \varvec{B}(t_n) - \varvec{u}^n_{h*} \times \varvec{B}_h^n, \nabla \times \theta _b^{n+1})|\\&= |(\varvec{u}(t_n) \times e_b^n + ( \varvec{u}(t_n) - \varvec{u}^n_{h*} ) \times \varvec{B}_h^n, \nabla \times \theta _b^{n+1})| \\&\le \left( \Vert e_b^n\Vert \Vert \varvec{u}(t_n)\Vert _{L^{\infty }} + \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \varvec{u}(t_n) - \varvec{u}^n_{h*} \Vert \right) \Vert \nabla \times \theta _b^{n+1}\Vert \\&\lesssim \frac{\eta }{8} \Vert \nabla \times \theta _b^{n+1}\Vert ^2 + \Vert \theta _b^n\Vert ^2 + \Vert \rho _b^n\Vert ^2 \\&\quad + \Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 (\Vert \varvec{u}(t_n) - \varvec{u}^n_{h}\Vert ^2+\Vert \varvec{u}^n_{h} - \varvec{u}^n_{h*}\Vert ^2)\\&\lesssim \frac{\eta }{8} \Vert \nabla \times \theta _b^{n+1}\Vert ^2 + \Vert \theta _b^n\Vert ^2 + h^{2r+2} + \Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 (h^{2l+2}+ \Vert \theta _u^n\Vert ^2) + \delta t^2 \Vert \varvec{B}_h^n\Vert _{L^{\infty }}^4\\&\quad + \delta t^2\Vert \varvec{B}_h^n\Vert _{L^{\infty }}^4 \Vert \nabla \times \theta ^{n+1}_b \Vert ^2. \end{aligned} \end{aligned}$$

For term B, by using (3.20), regularity assumptions, the inverse inequalities (3.2) and (3.6), we derive

$$\begin{aligned} \begin{aligned} \text{(term } \text{ B) }&\le |b({\varvec{u}}(t_n), \varvec{u}(t_{n+1}),{\tilde{\theta }}_u^{n+1}) - b({\varvec{u}}_h^n, \tilde{\varvec{u}}_h^{n+1}, {\tilde{\theta }}_u^{n+1})|\\&=|b (e_u^n, \varvec{u}(t_{n+1}), {\tilde{\theta }}_u^{n+1}) - b(\varvec{u}_h^n, {\tilde{\theta }}_u^{n+1}, \rho _u^{n+1})|\\&=|b (e_u^n, \varvec{u}(t_{n+1}), {\tilde{\theta }}_u^{n+1}) + b(e_u^n, {\tilde{\theta }}_u^{n+1}, \rho _u^{n+1}) - b(\varvec{u}(t_n), {\tilde{\theta }}_u^{n+1}, \rho _u^{n+1})|\\&\lesssim \Vert e_u^n\Vert ~ \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert \Vert \varvec{u}(t_{n+1})\Vert _{2} + \Vert e_u^n\Vert ~ \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert _{L^3} \Vert \nabla \rho _u^{n+1}\Vert + { \Vert e_u^n\Vert ~ \Vert {\tilde{\theta }}_u^{n+1}\Vert _{L^{\infty }} \Vert \nabla \rho _u^{n+1}\Vert }\\&\quad + \Vert \varvec{u}(t_n)\Vert _{L^{\infty }} \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert \Vert \rho _u^{n+1}\Vert \\&\lesssim \Vert e_u^n\Vert ~ \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert + \Vert e_u^n\Vert ~ \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert h^{-\frac{1}{3}} h^{l} + \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert \Vert \rho _u^{n+1}\Vert \\&\lesssim \frac{\nu }{10} \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \Vert \theta _u^n\Vert ^2 + \Vert \rho _u^n\Vert ^2 +\Vert \rho _u^{n+1}\Vert ^2 \lesssim \frac{\nu }{10} \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \Vert \theta _u^n\Vert ^2 + h^{2l+2}. \end{aligned} \end{aligned}$$

For term C, from the equality of $\nabla \times (a \times b) = b\nabla a- a \nabla b + a\nabla \cdot b - b \nabla \cdot a$, the inverse inequality (3.2), regularity conditions and (3.7), we derive

$$\begin{aligned} \text{(term } \text{ C) }&\le s |( \varvec{B}(t_n) \times \nabla \times \varvec{B}(t_{n+1}) -\varvec{B}_h^n \times \nabla \times \varvec{B}_h^{n+1},{\tilde{\theta }}_u^{n+1})|\\&= s |( e_b^n \times \nabla \times \varvec{B}(t_{n+1}), {\tilde{\theta }}_u^{n+1}) + ( \varvec{B}_h^n \times \nabla \times e_b^{n+1}, {\tilde{\theta }}_u^{n+1} )|\\&\le s |( e_b^n \times \nabla \times \varvec{B}(t_{n+1}), {\tilde{\theta }}_u^{n+1})| + s|( \varvec{B}_h^n \times \nabla \times \theta _b^{n+1}, {\tilde{\theta }}_u^{n+1} )|\\&\quad +\, s |( \varvec{B}_h^n \times \nabla \times \rho _b^{n+1}, {\tilde{\theta }}_u^{n+1} )|\\&\le s |( e_b^n \times \nabla \times \varvec{B}(t_{n+1}), {\tilde{\theta }}_u^{n+1})| + s|( \varvec{B}_h^n \times \nabla \times \theta _b^{n+1}, {\tilde{\theta }}_u^{n+1} - \theta _u^n )|\\&\quad +\, s |( \varvec{B}_h^n \times \nabla \times \theta _b^{n+1}, \theta _u^{n} )|\\&\quad +\, s |( e_b^n \times \nabla \times \rho _b^{n+1}, {\tilde{\theta }}_u^{n+1} )| +s |( \varvec{B}(t_n) \times \nabla \times \rho _b^{n+1}, {\tilde{\theta }}_u^{n+1} )|\\&\le s |( e_b^n \times \nabla \times \varvec{B}(t_{n+1}), {\tilde{\theta }}_u^{n+1})| + s|( \varvec{B}_h^n \times \nabla \times \theta _b^{n+1}, {\tilde{\theta }}_u^{n+1} - \theta _u^n )|\\&\quad +\, s |( \varvec{B}_h^n \times \nabla \times \theta _b^{n+1}, \theta _u^{n} )| + s |( e_b^n \times \nabla \times \rho _b^{n+1}, {\tilde{\theta }}_u^{n+1} )|\\&\quad +\,s |( \varvec{B}(t_n) \nabla {\tilde{\theta }}_u^{n+1} - {\tilde{\theta }}_u^{n+1} \nabla \varvec{B}(t_n) - \varvec{B}(t_n) \nabla \cdot {\tilde{\theta }}_u^{n+1} , \rho _b^{n+1} )|\\&\lesssim \Vert e_b^n\Vert \Vert \nabla \times \varvec{B}(t_{n+1})\Vert _{L^3} \Vert {\tilde{\theta }}_u^{n+1}\Vert _{L^6} + \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \nabla \times \theta _b^{n+1}\Vert \Vert {\tilde{\theta }}_u^{n+1} - \theta _u^n\Vert \\&\quad +\, \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \nabla \times \theta _b^{n+1}\Vert \Vert \theta _u^{n}\Vert + \Vert e_b^n\Vert \Vert \nabla \times \rho _b^{n+1}\Vert \Vert {\tilde{\theta }}_u^{n+1} \Vert _{L^{\infty }}\\&\quad +\, \Vert \varvec{B}(t_n)\Vert _{L^{\infty }}\Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert \Vert \rho _b^{n+1}\Vert +\Vert {\tilde{\theta }}_u^{n+1}\Vert _{L^6} \Vert \nabla \varvec{B}(t_n)\Vert _{L^3} \Vert \rho _b^{n+1} \Vert \\&\lesssim \Vert e_b^n\Vert \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert + \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \nabla \times \theta _b^{n+1}\Vert \Vert {\tilde{\theta }}_u^{n+1} - \theta _u^n\Vert \\&\quad +\, \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \nabla \times \theta _b^{n+1}\Vert \Vert \theta _u^{n}\Vert + \Vert e_b^n\Vert h^r h^{-\frac{1}{3}}\Vert \nabla {\tilde{\theta }}_u^{n+1} \Vert + \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert h^{r+1} \\&\lesssim \frac{\nu }{10}\Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \frac{\eta }{8} \Vert \nabla \times \theta _b^{n+1}\Vert ^2 +\Vert \theta _b^n\Vert ^2 + \Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 \Vert {\tilde{\theta }}_u^{n+1} - \theta _u^n\Vert ^2\\&\quad +\, \Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 \Vert \theta _u^{n}\Vert ^2 + h^{2r+2}. \end{aligned}$$

For term D, term E and term F, using (2.7), (2.8), and Lemma 4.1, we derive

$$\begin{aligned} \begin{aligned} \text{(term } \text{ D) }&\le \Vert {\tilde{\theta }}_u^{n+1}\Vert \Vert \rho ^{n+1}\Vert + \delta t \Vert \nabla \theta ^n_p\Vert \Vert \rho ^{n+1}\Vert \lesssim \frac{\nu }{10} \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 +\Vert \rho ^{n+1}\Vert ^2 + \delta t^2 \Vert \nabla \theta ^n_p\Vert ^2\\&\lesssim \frac{\nu }{10} \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \delta t^2 + \delta t^2\Vert \nabla d_t \rho _p^{n+1}\Vert ^2+ \delta t^2 \Vert \nabla \theta ^n_p\Vert ^2, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \text{(term } \text{ E) }&\lesssim \delta t \Vert d_t\rho ^{n+1}_p\Vert \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert +\Vert d_t \rho ^{n+1}_b\Vert (\Vert \nabla \times \theta _b^{n+1}\Vert \\&\quad +\Vert \nabla \cdot \theta _b^{n+1}\Vert ) + \Vert d_t \rho ^{n+1}_u\Vert \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert \\&\lesssim \frac{\nu }{10} \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \frac{\eta }{8} ( \Vert \nabla \times \theta _b^{n+1}\Vert ^2+\Vert \nabla \cdot \theta _b^{n+1}\Vert ^2)\\&\quad + \delta t^2 \Vert d_t\rho ^{n+1}_p\Vert ^2+ \Vert d_t \rho ^{n+1}_b\Vert ^2 +\Vert d_t \rho ^{n+1}_u\Vert ^2, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} ( \text{ term } \text{ F })&\le \Vert R^{n+1}_b\Vert \Vert \theta _b^{n+1}\Vert + \Vert R^{n+1}_u\Vert \Vert {\tilde{\theta }}_u^{n+1}\Vert \\&\lesssim \frac{\nu }{10}\Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \frac{\eta }{8}(\Vert \nabla \times \theta _b^{n+1}\Vert ^2 +\Vert \nabla \cdot \theta _b^{n+1}\Vert ^2 ) +\Vert R^{n+1}_b\Vert ^2 + \Vert R^{n+1}_u\Vert ^2\\&\lesssim \frac{\nu }{10}\Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 + \frac{\eta }{8}(\Vert \nabla \times \theta _b^{n+1}\Vert ^2 +\Vert \nabla \cdot \theta _b^{n+1}\Vert ^2 ) +\delta t^2. \end{aligned} \end{aligned}$$

Combining the above estimates with (4.20), we obtain

$$\begin{aligned} \begin{aligned}&\Vert \theta _b^{n+1}\Vert ^2 - \Vert \theta _b^{n}\Vert ^2 + \Vert \theta _u^{n+1}\Vert ^2 - \Vert \theta _u^{n}\Vert ^2 +\Vert {\tilde{\theta }}_u^{n+1} - \theta _u^n\Vert ^2 + \delta t^2 (\Vert \nabla \theta _p^{n+1}\Vert ^2 - \Vert \nabla \theta _p^{n}\Vert ^2)\\&\qquad + \delta t \eta (\Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2)+ \delta t \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 \\&\quad \lesssim \delta t \Vert \theta _b^n\Vert ^2 + \delta t \Vert \theta _u^n\Vert ^2 + \delta t \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^2 \Vert \theta _u^n\Vert ^2 +\delta t^3 \Vert \nabla \theta _p^n\Vert ^2\\&\qquad + \delta t \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^2 \Vert {\tilde{\theta }}_u^{n+1}-\theta _u^n\Vert ^2 + \delta t^3 \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^4\\&\qquad + \delta t^3 \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^4\Vert \nabla \times \theta _b^{n+1}\Vert ^2 +\delta t^3 \Vert d_t \rho _p^{n+1}\Vert _1^2 +\delta t (\Vert d_t \rho _b^{n+1}\Vert ^2 + \Vert d_t \rho _u^{n+1}\Vert ^2)\\&\qquad + \delta t^3 +\delta t (h^{2l+2} + h^{2r+2} + \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} h^{2l+2}). \end{aligned} \end{aligned}$$

(4.21)

We choose any two positive constants $\delta t_1$ and $h_1$ that satisfy $\kappa _1 \delta t_1 + \kappa _2 h_1^{2\min \{l, r\}+1}\le min (1, \sqrt{\frac{\eta }{2}}, \frac{\eta }{4})$. Then when $\delta t \le \delta t_1$ and $h\le h_1$, from the induction assumptions (4.14) for $n \le N$, we have

$$\begin{aligned} \begin{aligned}&\delta t \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^2 \Vert {\tilde{\theta }}_u^{n+1}-\theta _u^n\Vert ^2\le (\kappa _1 \delta t_1 + \kappa _2 h_1^{2\min \{l, r\}+1})\Vert {\tilde{\theta }}_u^{n+1}-\theta _u^n\Vert ^2\le \Vert {\tilde{\theta }}_u^{n+1}-\theta _u^n\Vert ^2,\\&\delta t^3 \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^4\Vert \nabla \times \theta _b^{n+1}\Vert ^2\le (\kappa _1 \delta t_1 + \kappa _2 h_1^{2\min \{l, r\}+1})^2 \delta t \Vert \nabla \times \theta _b^{n+1}\Vert ^2 \le \frac{\eta }{2} \delta t\Vert \nabla \times \theta _b^{n+1}\Vert ^2. \end{aligned} \end{aligned}$$

Besides, from the inverse inequality (3.2), (4.14), and the assumption $\delta t |\log h| \le 1$, $\delta t\le \delta t_1$ and $h\le h_1$, we get

$$\begin{aligned} \delta t^3 \Vert \varvec{B}^n_h\Vert _{L^{\infty }}^4= & {} \delta t^3 \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }} \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }} \lesssim \delta t^3 \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }} ( \Vert \theta _b^n\Vert ^2_{L^{\infty }} + \Vert J_{ \varvec{B}(t_n)}\Vert ^2_{L^{\infty }})\\\lesssim & {} \delta t^3 \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }}|\log h| (\Vert \nabla \times \theta _b^n\Vert ^2+ \Vert \nabla \cdot \theta _b^n\Vert ^2)+ \delta t^3 \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }}\\\lesssim & {} (\kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\}+1})\delta t (\Vert \nabla \times \theta _b^n\Vert ^2+ \Vert \nabla \cdot \theta _b^n\Vert ^2)+ \delta t^3 \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }}\\\lesssim & {} \frac{\eta }{4}\delta t (\Vert \nabla \times \theta _b^n\Vert ^2+ \Vert \nabla \cdot \theta _b^n\Vert ^2)+ \delta t^3 \Vert \varvec{B}^n_h\Vert ^2_{L^{\infty }}. \end{aligned}$$

Therefore, (4.21) becomes

$$\begin{aligned} \begin{aligned}&\Vert \theta _b^{n+1}\Vert ^2 - \Vert \theta _b^{n}\Vert ^2 + \Vert \theta _u^{n+1}\Vert ^2 - \Vert \theta _u^{n}\Vert ^2 + \delta t^2 (\Vert \nabla \theta _p^{n+1}\Vert ^2 - \Vert \nabla \theta _p^{n}\Vert ^2)\\&\qquad + \delta t\frac{\eta }{2}(\Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2) -\frac{\eta }{4}\delta t (\Vert \nabla \times \theta _b^n\Vert ^2+ \Vert \nabla \cdot \theta _b^n\Vert ^2)+ \delta t \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2 \\&\quad \lesssim \delta t \Vert \theta _b^n\Vert ^2 + \delta t \Vert \theta _u^n\Vert ^2 + \delta t \Vert \varvec{B}_h^{n}\Vert _{L^{\infty }}^2 \Vert \theta _u^n\Vert ^2 +\delta t^3 \Vert \nabla \theta _p^n\Vert ^2+ \delta t^3 \Vert \varvec{B}_h^n\Vert _{L^{\infty }}^2 +\delta t^3 \Vert d_t \rho _p^{n+1}\Vert _1^2\\&\qquad +\delta t (\Vert d_t \rho _b^{n+1}\Vert ^2 + \Vert d_t \rho _u^{n+1}\Vert ^2) + \delta t^3 +\delta t (h^{2l+2} + h^{2r+2} + \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} h^{2l+2}). \end{aligned} \end{aligned}$$

Summing up the above inequality from $n=0$ to N, and using the induction assumptions (4.14) and $\theta _b^0 = \theta _u^0 =\theta _p^0 =0$, we obtain

$$\begin{aligned} \begin{aligned}&\Vert \theta _b^{N+1}\Vert ^2 + \Vert \theta _u^{N+1}\Vert ^2+ \delta t^2 \Vert \nabla \theta _p^{N+1}\Vert ^2 \\&\qquad +\delta t\sum _{n=0}^N \left( \frac{ \eta }{4} \Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \frac{ \eta }{4} \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2 + \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2\right) \\&\quad \lesssim \delta t \sum _{n=0}^N \left( \Vert \theta _b^{n}\Vert ^2 + \Vert \theta _u^{n}\Vert ^2 + \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }}\Vert \theta _u^{n}\Vert ^2 + \delta t^2\Vert \nabla \theta _p^{n}\Vert ^2\right) +\delta t^3 \sum _{n=0}^N \Vert d_t \rho _p^{n+1}\Vert _1^2 \\&\qquad + \delta t \sum _{n=0}^N(\Vert d_t \rho _b^{n+1}\Vert ^2 + \Vert d_t \rho _u^{n+1}\Vert ^2) +\delta t^2 + h^{2l+2} + h^{2r+2} + \kappa _0 (\delta t^2+h^{2l+2}). \end{aligned} \end{aligned}$$

(4.22)

In addition, using (3.6), (3.7), Theorem 3.1 and regularity condition $(\mathbf {A2})$, we obtain

$$\begin{aligned} \begin{aligned} \delta t\sum _{n=0}^N\Vert d_t \rho _b^{n+1}\Vert ^2 + \Vert d_t \rho _u^{n+1}\Vert ^2&\lesssim h^{2r+2} \delta t \sum _{n=0}^N\Vert d_t \varvec{B}(t_{n+1})\Vert ^2_{r+1}\\&\quad +h^{2l+2} \delta t\sum _{n=0}^N(\Vert d_t \varvec{u}(t_{n+1})\Vert ^2_{l+1} + \Vert d_t p(t_n)\Vert ^2_l)\\&\lesssim h^{2r+2}+h^{2l+2}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \delta t^3 \sum _{n=0}^N \Vert d_t \rho _p^{n+1}\Vert _1^2&\lesssim \delta t^3 \sum _{n=0}^N \Vert d_t p(t_{n+1})\Vert _1^2+ \delta t^3 \sum _{n=0}^N \Vert Q_{(d_t \varvec{u}(t_{n+1}), d_t p(t_{n+1}))}\Vert _1^2\\&\lesssim \delta t^3 \sum _{n=0}^N \Vert d_t p(t_{n+1})\Vert _1^2+ \delta t^3 \sum _{n=0}^N (\Vert d_t \varvec{u}(t_{n+1})\Vert _2^2+ \Vert d_t p(t_{n+1})\Vert _1^2) \lesssim \delta t^2. \end{aligned} \end{aligned}$$

Then, (4.22) becomes

$$\begin{aligned} \begin{aligned}&\Vert \theta _b^{N+1}\Vert ^2 + \Vert \theta _u^{N+1}\Vert ^2+ \delta t^2 \Vert \nabla \theta _p^{N+1}\Vert ^2\\&\qquad +\delta t\sum _{n=0}^N \left( \eta \Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \eta \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2 + \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2\right) \\&\quad \lesssim \delta t \sum _{n=0}^N \left( \Vert \theta _b^{n}\Vert ^2 + \Vert \theta _u^{n}\Vert ^2 + \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }}\Vert \theta _u^{n}\Vert ^2 + \delta t^2\Vert \nabla \theta _p^{n}\Vert ^2\right) \\&\qquad + (\kappa _0+1) \delta t^2+ (\kappa _0+1) h^{2l+2} + h^{2r+2}. \end{aligned} \end{aligned}$$

(4.23)

By applying the Gronwall’s inequality to (4.23), we obtain

$$\begin{aligned}&\Vert \theta _b^{N+1}\Vert ^2 +\Vert \theta _u^{N+1}\Vert ^2+ \delta t^2 \Vert \nabla \theta _p^{N+1}\Vert ^2 \nonumber \\&\quad +\,\delta t\sum _{n=0}^N \left( \eta \Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \eta \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2+ \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2\right) \nonumber \\&\quad \le C(\kappa _0)(\delta t^2 + h^{2l+2} + h^{2r+2}), \end{aligned}$$

(4.24)

where $C(\kappa _0)$ is a constant depending on $\kappa _0$.

(Step ii). We assume that the condition $\delta t|\log h| \le 1$ holds. By using the inverse inequality (3.2), (2.8), (4.11), (4.12) and (4.24), we derive

$$\begin{aligned} \delta t \sum _{n=0}^{N+1} \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }}\le & {} 2 \delta t \sum _{n=0}^{N+1} \Vert J_{\varvec{B}(t_n)}\Vert ^2_{L^{\infty }} +2 \delta t \sum _{n=0}^{N+1} \Vert \theta _b^n\Vert ^2_{L^{\infty }}\\\le & {} 2 T C^2_0 + C_{\Omega }|\log h| \delta t \sum _{n=0}^{N+1} (\Vert \nabla \times \theta _b^n\Vert ^2 + \Vert \nabla \cdot \theta _b^n\Vert ^2)\\\le & {} 2 T C^2_0 + C_{\Omega } C(\kappa _0) |\log h| (\delta t^2 + h^{2l+2} + h^{2r+2})\\\le & {} 2 T C^2_0 + C_{\Omega } C(\kappa _0) (\delta t + |\log h| h^{2\min \{l, r\}+2})\\\le & {} 2 T C^2_0 +1 = \kappa _0, \end{aligned}$$

where we assume $\delta t \le \delta t_2, h\le h_2$ and $\delta t_2$ and $h_2$ satisfy $C_{\Omega } C(\kappa _0) ({\delta t_2} + |\log h_2| h_2^{2\min \{l, r\}+2})<1$.

By setting $\kappa _1 = 2C_0^2 + C_{\Omega } C(\kappa _0), \kappa _2 = C_{\Omega } C(\kappa _0)$, we derive

$$\begin{aligned} \delta t \Vert \varvec{B}_h^{N+1}\Vert ^2_{L^{\infty }}\le & {} 2 \delta t \Vert J_{\varvec{B}(t_{N+1})} \Vert ^2_{L^{\infty }} + 2 \delta t \Vert \theta _b^{N+1} \Vert ^2_{L^{\infty }} \\\le & {} 2C_0^2 \delta t + C_{\Omega }|\log h| \delta t (\Vert \nabla \times \theta _b^{N+1} \Vert ^2+ \Vert \nabla \cdot \theta _b^{N+1} \Vert ^2)\\\le & {} 2C_0^2 \delta t + C_{\Omega } C(\kappa _0)|\log h|(\delta t^2 + h^{2l+2} + h^{2r+2})\\\le & {} 2C_0^2 \delta t + C_{\Omega } C(\kappa _0)(\delta t + h^{2\min \{l, r\}+1})\\= & {} \kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\}+1}. \end{aligned}$$

The proof is completed if we simply let $\delta t\le \delta t_0(:= min (\delta t_1, \delta t_2))$ and $h\le h_0(:= min ( h_1, h_2))$. $\square$

Based on the above Lemma, now it is ready to obtain the error estimates for the velocity field and magnetic field, as follows.

Theorem 4.4

Under the conditions of Lemma 4.3, the following estimates hold

$$\begin{aligned} \begin{aligned}&\max _{0\le m \le [\frac{T}{\delta t}]} \left( \Vert e_b^{m}\Vert + \Vert e_u^{m}\Vert + \delta t \Vert \nabla e_p^{m}\Vert \right) \lesssim \delta t + {h^{\min \{l , r\}+1},} \\&\quad \delta t\sum _{n=0}^{[\frac{T}{\delta t}]} \left( \eta \Vert \nabla \times e_b^{n+1}\Vert ^2+ \eta \Vert \nabla \cdot e_b^{n+1}\Vert ^2+ \nu \Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2\right) \lesssim \delta t^2 +{ h^{2\min \{l, r\}}.} \end{aligned} \end{aligned}$$

(4.25)

Proof

By Lemma 4.3, we already obtained

$$\begin{aligned} \delta t \sum _{n=0}^{[\frac{T}{\delta t}]}\Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _0,\quad \max _{0\le n \le [\frac{T}{\delta t}]} \delta t \Vert \varvec{B}_h^n\Vert ^2_{L^{\infty }} \le \kappa _1 \delta t + \kappa _2 h^{2\min \{l, r\} +1}. \end{aligned}$$

(4.26)

By following the same procedures of Step i of the proof in Lemma 4.3, for $m\le [\frac{T}{\delta t}]$, we obtain

$$\begin{aligned}&\Vert \theta _b^{m+1}\Vert ^2 + \Vert \theta _u^{m+1}\Vert ^2+ \delta t^2 \Vert \nabla \theta _p^{m+1}\Vert ^2\nonumber \\&\quad +\,\delta t\sum _{n=0}^m \left( \eta \Vert \nabla \times \theta _b^{n+1}\Vert ^2+ \eta \Vert \nabla \cdot \theta _b^{n+1}\Vert ^2+ \nu \Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert ^2\right) \lesssim \delta t^2 + h^{2l+2} + h^{2r+2}.\nonumber \\ \end{aligned}$$

(4.27)

By using the triangle inequality, (3.6) and (3.7), the desired results (4.25) are concluded. $\square$

Remark 4.5

The convergence results in Theorem 4.4 are still valid for the three dimensional case ($d=3$), but the condition between the time step and grid size becomes more restrictive. More precisely, the condition is $\delta t \lesssim h$ for $d=3$ instead of $\delta t|\mathrm{log}h|<1$ for $d=2$. This is because a different inverse inequality will be used for $d=3$ [11], namely

$$\begin{aligned} \Vert \varvec{B}_h\Vert _{L^{\infty }} \lesssim h^{-\frac{1}{2}}\Vert \varvec{B}_h\Vert _{L^6} \lesssim h^{-\frac{1}{2}} \Vert \varvec{B}_h\Vert _1. \end{aligned}$$

(4.28)

We omit the details due to the page limit and leave this to the interested readers.

4.2 Optimal Error Estimate for Pressure

Note the convergence order for the pressure term in Theorem 4.4 is not optimal. In this subsection, we aim at proving the optimal error estimate for the pressure. Due to the introduction of the auxiliary velocity field $\varvec{u}^n_{h*}$, there exist two specific difficulties to improve the order for the pressure, including (i) how to derive the error between $d_t \varvec{u}(t_n)$ and $d_t \varvec{u}^n_{h*}$ since there does not exist an error equation for $d_t \varvec{u}^n_{h*}$; and (ii) how to derive the optimal error estimate for $\Vert d_t \theta _b^n\Vert$ which is needed for the estimate of the pressure.

For (i), we solve it by developing a relation between $\Vert d_t \varvec{u}_h^n -d_t \varvec{u}^n_{h*}\Vert$ and other error functions in Lemma 4.7. For (ii), we build the error estimate for $\Vert d_t \theta _b^{m+1}\Vert _{-1}^2 + \delta t \sum _{n=1}^m\Vert d_t \theta _b^{n+1}\Vert ^2$ by means of negative norm estimate technique in Lemmas 4.9 and 4.10. Based on these estimates, by using the inf–sup condition, the optimal convergence order of the pressure is finally obtained in Theorem 4.11.

For the error estimate of the pressure, we need the $l^{\infty }(L^{\infty })$ stability of $\varvec{B}_h^n$ that is derived in the following Lemma.

Lemma 4.6

Assuming that the solution to (2.1)–(2.6) satisfies assumptions $(\mathbf A0)$–$(\mathbf A2)$, then when $\delta t \le h$, the following estimates hold

$$\begin{aligned} \max _{0 \le n \le [\frac{T}{\delta t}]}\Vert \varvec{B}_h^n\Vert _{L^{\infty }} \le \kappa _3, \quad \max _{0 \le n \le [\frac{T}{\delta t}]}\Vert \varvec{B}_h^n\Vert _1 \le \kappa _4, \end{aligned}$$

where $\kappa _3, \kappa _4$ will be verified in the proof.

Proof

From (4.27), if $\delta t|\mathrm{log}h|\le 1$, we have

$$\begin{aligned} \max _{0\le n\le [\frac{T}{\delta t}]} \Vert \theta _b^{n}\Vert \lesssim \delta t + h^{l+1} + h^{r+1}. \end{aligned}$$

We further assume a more restrictive condition for the time step: $\delta t\le h$, then by the inverse inequality (3.2), we derive

$$\begin{aligned} \Vert \varvec{B}_h^n \Vert _{L^{\infty }}\le & {} \Vert J_{\varvec{B}(t_n)}\Vert _{L^{\infty }} + \Vert \theta _b^n\Vert _{L^{\infty }} \le \Vert J_{\varvec{B}(t_n)}\Vert _{L^{\infty }} + C_{\Omega }h^{-1}\Vert \theta _b^n\Vert \\\le & {} C_0 + C h^{-1}(\delta t + h^{l+1} + h^{r+1} )= \kappa _3; \end{aligned}$$

and

$$\begin{aligned} \Vert \varvec{B}_h^n\Vert _1\le & {} \Vert e_b^n\Vert _1 + \Vert \varvec{B}(t_n)\Vert _1 \le \Vert \theta _b^n\Vert _1 +\Vert \rho _b^n\Vert _1 + \Vert \varvec{B}(t_n)\Vert _1\\\le & {} C_{\Omega } h^{-1} \Vert \theta _b^n\Vert +\Vert \rho _b^n\Vert _1 + \Vert \varvec{B}(t_n)\Vert _1\\\le & {} C h^{-1}(\delta t + h^{l+1} + h^{r+1}) +C= \kappa _4. \end{aligned}$$

The proof is finished. $\square$

We assume the solution $\varvec{B}(t)$ to (2.1)–(2.6) satisfies:

$$\begin{aligned} (\mathbf{A3}): \varvec{B}_t \in L^{\infty }(0, T; H^1(\Omega )^2 ) \cap L^{\infty } (0, T; L^{\infty }(\Omega )^2 ). \end{aligned}$$

In the next Lemma, we find the $L^2$ relation between $d_t \varvec{u}^n_h$ and $d_t\varvec{u}^n_{h*}$ with other error functions which will be used in the error estimate for pressure.

Lemma 4.7

Assuming that the solution to (2.1)–(2.6) satisfies assumptions $(\mathbf A0)$–$(\mathbf A3)$, when $\delta t \lesssim h$, the following estimate holds

$$\begin{aligned} \Vert d_t \varvec{u}^n_h - d_t\varvec{u}^n_{h*}\Vert ^2 \lesssim \delta t^2 + \Vert d_t \theta _u^n\Vert ^2 + \Vert \nabla \times (e^{n+1}_b- e_b^n)\Vert ^2 + \frac{\eta }{8}\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \rho _b^n\Vert ^2. \end{aligned}$$

Proof

By applying $d_t$ to (3.9), we obtain

$$\begin{aligned} \left( \frac{d_t\varvec{u}_{h*}^{n} - d_t \varvec{u}_h^{n}}{\delta t}, \varvec{w}_h \right) + s (\varvec{B}_h^n \times \nabla \times d_t \varvec{B}^{n+1}_h, \varvec{w}_h) + s (d_t \varvec{B}_h^n \times \nabla \times \varvec{B}^{n}_h, \varvec{w}_h) =0. \end{aligned}$$

By taking $\varvec{w}_h = 2\delta t d_t \varvec{u}^n_{h*} - 2\delta t d_t R_{(\varvec{u}(t_n), p(t_n))}$ and using Lemma 4.6, regularity condition ($\mathbf {A3}$) and inverse inequality (3.2), we derive

$$\begin{aligned} \begin{aligned}&\Vert \varvec{w}_h\Vert ^2 +\Vert d_t\varvec{u}_{h*}^{n} - d_t \varvec{u}_h^{n}\Vert ^2 = \Vert d_t \theta _u^n\Vert ^2\\&\qquad - 2\delta t s (\varvec{B}_h^n \times \nabla \times d_t \varvec{B}^{n+1}_h, \varvec{w}_h) - 2 \delta t s (d_t \varvec{B}_h^n \times \nabla \times \varvec{B}^{n}_h, \varvec{w}_h)\\&\quad \lesssim \Vert d_t \theta _u^n\Vert ^2+ \delta t \Vert \varvec{B}_h^n\Vert _{L^{\infty }} \Vert \nabla \times d_t \varvec{B}^{n+1}_h\Vert \Vert \varvec{w}_h\Vert + \delta t \Vert d_t \varvec{B}_h^n \times \nabla \times \varvec{B}^{n}_h\Vert \Vert \varvec{w}_h\Vert \\&\quad \lesssim \Vert d_t \theta _u^n\Vert ^2+ \Vert \varvec{w}_h\Vert ^2 + \delta t^2\Vert \nabla \times d_t \varvec{B}^{n+1}_h\Vert ^2 + \delta t^2 \Vert d_t \varvec{B}_h^n \times \nabla \times \varvec{B}^{n}_h\Vert ^2 \\&\quad \lesssim \Vert d_t \theta _u^n\Vert ^2+ \Vert \varvec{w}_h\Vert ^2 + \delta t^2\Vert \nabla \times d_t \varvec{B}(t_{n+1})\Vert ^2 + \delta t^2\Vert \nabla \times d_t e^{n+1}_b\Vert ^2\\&\qquad + \delta t^2 \Vert d_t \varvec{B}(t_n) \times \nabla \times \varvec{B}^{n}_h\Vert ^2 + \delta t^2 \Vert d_t e_b^n \times \nabla \times \varvec{B}^{n}_h\Vert ^2 \\&\quad \lesssim \Vert d_t \theta _u^n\Vert ^2+ \Vert \varvec{w}_h\Vert ^2 + \delta t^2 + \Vert \nabla \times (e^{n+1}_b- e_b^n)\Vert ^2\\&\qquad + \delta t^2 \Vert d_t \varvec{B}(t_n)\Vert _{L^{\infty }}^2 \Vert \nabla \times \varvec{B}^{n}_h\Vert ^2 + \delta t^2 \Vert d_t e_b^n\Vert ^2 \Vert \nabla \times \varvec{B}^{n}_h\Vert _{L^{\infty }}^2 \\&\quad \lesssim \Vert d_t \theta _u^n\Vert ^2+ \Vert \varvec{w}_h\Vert ^2 + \delta t^2 + \Vert \nabla \times (e^{n+1}_b- e_b^n)\Vert ^2 + \delta t^2 \Vert d_t e_b^n\Vert ^2 h^{-2} \Vert \nabla \times \varvec{B}^{n}_h\Vert ^2 \\&\quad \lesssim \Vert d_t \theta _u^n\Vert ^2+ \Vert \varvec{w}_h\Vert ^2 + \delta t^2 + \Vert \nabla \times (e^{n+1}_b- e_b^n)\Vert ^2 + \frac{\eta }{8}\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \rho _b^n\Vert ^2, \end{aligned} \end{aligned}$$

where we assume $\delta t^2 \lesssim \frac{\eta }{8} h^2$. After eliminating $\Vert \varvec{w}_h\Vert ^2$, we arrive at the conclusion. $\square$

We apply $d_t$ to (4.5)–(4.7) to obtain the following error equations:

$$\begin{aligned}&\left( \frac{d_t {\tilde{e}}_u^{n+1} - d_t e_u^n}{ \delta t}, \varvec{v}_h \right) + \nu (\nabla d_t {\tilde{e}}^{n+1}_u, \nabla \varvec{v}_h) + b(\varvec{u}(t_n), d_t \varvec{u}(t_{n+1}), \varvec{v}_h) + b(d_t \varvec{u}(t_n), \varvec{u}(t_n), \varvec{v}_h) \nonumber \\&\qquad - b(\varvec{u}_h^n, d_t \tilde{\varvec{u}}_h^{n+1}, \varvec{v}_h) - b(d_t \varvec{u}_h^n, \tilde{\varvec{u}}_h^n, \varvec{v}_h) + (\nabla d_t e_p^n, \varvec{v}_h) \nonumber \\&\qquad + s (\varvec{B}(t_n) \times \nabla \times d_t \varvec{B}(t_{n+1}), \varvec{v}_h) + s (d_t \varvec{B}(t_n) \times \nabla \times \varvec{B}(t_n), \varvec{v}_h) \nonumber \\&\qquad - s (\varvec{B}_h^n \times \nabla \times d_t \varvec{B}_h^{n+1}, \varvec{v}_h) - s (d_t \varvec{B}_h^n \times \nabla \times \varvec{B}_h^n, \varvec{v}_h) \nonumber \\&\quad = (d_t R^{n+1}_u, \varvec{v}_h). \end{aligned}$$

(4.29)

$$\begin{aligned}&\frac{d_t e_u^{n+1} }{\delta t} + \nabla d_t e_p^{n+1} = \frac{d_t {\tilde{e}}_u^{n+1}}{\delta t} + \nabla d_t e_p^n + d_tR^{n+1}_p. \end{aligned}$$

(4.30)

$$\begin{aligned}&\left( \frac{d_t e^{n+1}_b - d_t e^n_b}{\delta t}, \varvec{c}_h \right) + \eta (\nabla \times d_t e^{n+1}_b, \nabla \times \varvec{c}_h) + \eta (\nabla \cdot d_t e^{n+1}_b, \nabla \cdot \varvec{c}_h) \nonumber \\&\qquad + (d_t \varvec{B}(t_n) \times \varvec{u}(t_n) , \nabla \times \varvec{c}_h) + ( \varvec{B}(t_{n-1}) \times d_t \varvec{u}(t_n), \nabla \times \varvec{c}_h) \nonumber \\&\qquad - ( d_t \varvec{B}_h^n \times \varvec{u}^n_{h*}, \nabla \times \varvec{c}_h) - (\varvec{B}_h^{n-1} \times d_t \varvec{u}^n_{h*}, \nabla \times \varvec{c}_h) \nonumber \\&\quad = (d_t R^{n+1}_b, \varvec{c}_h). \end{aligned}$$

(4.31)

We assume the solution $\varvec{u}, p, \varvec{B}$ to (2.1)–(2.6) also satisfy the following regularities:

$$\begin{aligned}&(\mathbf{A4}): \varvec{u}_{tt}, \varvec{B}_{tt} \in L^2(0, T; H^1(\Omega )^2),\\&p_{tt} \in L^2(0, T; H^1(\Omega )), ~~ \varvec{u}_{ttt}, \varvec{B}_{ttt} \in L^2(0, T; L^2(\Omega )^2),\\&(\mathbf{A5}): \varvec{u}_t \in L^{\infty }(0, T; H^{l}(\Omega )^2 \cap H^2(\Omega )^2), \\&p_t \in L^{\infty }(0, T; H^1 \cap H^{l-1}),~~ \varvec{B}_t \in L^{\infty }(0, T; H^r(\Omega )^2). \end{aligned}$$

For the truncation errors in (4.29)–(4.31), we have the following Lemma.

Lemma 4.8

Under the assumptions $(\mathbf A0)$, $(\mathbf A1)$ and $(\mathbf A4)$, the truncation errors satisfy

$$\begin{aligned} \delta t \sum _{n=0}^{[\frac{T}{\delta t}]} (\Vert d_tR^n_u\Vert ^2 + \Vert d_tR^n_b\Vert ^2 + \Vert d_tR^n_p\Vert ^2) \lesssim \delta t^2. \end{aligned}$$

(4.32)

Proof

Due to the page limit, we omit the proof since it is rather standard. $\square$

We define a symmetric positive definite operator $A_h : \varvec{C}_h \rightarrow \varvec{C}_h$ through

$$\begin{aligned} (A_h \varvec{B}_h, \varvec{c}_h) = (\nabla \times \varvec{B}_h, \nabla \times \varvec{c}_h) + (\nabla \cdot \varvec{B}_h, \nabla \cdot \varvec{c}_h). \end{aligned}$$

Moreover, we denote

$$\begin{aligned} \Vert \varvec{B}_h\Vert _{-1}^2 = (A_h^{-1} \varvec{B}_h, \varvec{B}_h), \end{aligned}$$

and it is easy to find $\Vert A_h^{-1} \varvec{B}_h\Vert \lesssim \Vert \varvec{B}_h\Vert _{-1} \lesssim \Vert \varvec{B}_h\Vert$.

We will estimate the errors of $\Vert d_t \theta _b^1\Vert _{-1}$ and $\Vert d_t \theta _u^1\Vert$ at the initial time step in the following Lemma, that are needed to estimate $\Vert d_t \theta _b^n \Vert _{-1}$ and $\Vert d_t \theta _u^n\Vert$, both of which are crucial to derive the optimal error estimate for pressure.

Lemma 4.9

Under the conditions of Lemma 4.3 and $(\mathbf A 5)$, the following three estimates hold

$$\begin{aligned} \begin{aligned}&\mathrm {(i)}\; \Vert d_t \theta _b^1 \Vert _{-1}^2 + \delta t\Vert d_t \theta _b^1\Vert ^2 \lesssim h^{2l} + h^{2r}+\delta t^2,\\&\mathrm {(ii)}\; \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \frac{1}{\delta t} \Vert \nabla {\tilde{\theta }}_u^1 \Vert ^2 \lesssim h^{2l} +h^{2r} + \delta t^2,\\&\mathrm {(iii)}\; \left\| d_t \theta _u^1\right\| ^2 + \delta t^2 \Vert \nabla d_t \theta _p^1 \Vert ^2 \lesssim h^{2l} +h^{2r} + \delta t^2. \end{aligned} \end{aligned}$$

Proof

(i). By taking $n=0$ in (4.5) and setting $\varvec{c}_h = A_h^{-1} \frac{\theta _b^1}{\delta t}$, from $\theta _b^0 =0$, we obtain

$$\begin{aligned} \begin{aligned}&\left\| \frac{\theta _b^1}{\delta t} \right\| _{-1}^2 +\frac{\eta }{\delta t} \Vert \theta ^{1}_b\Vert ^2 +\left( d_t \rho _b^1, A_h^{-1} \frac{\theta _b^1}{\delta t}\right) \\&\quad + \left( \varvec{B}_0 \times \varvec{u}_0 , \nabla \times A_h^{-1} \frac{\theta _b^1}{\delta t} \right) - \left( \varvec{B}_h^0 \times \varvec{u}^0_{h*}, \nabla \times A_h^{-1} \frac{\theta _b^1}{\delta t} \right) = \left( R^{1}_b, A_h^{-1} \frac{\theta _b^1}{\delta t} \right) . \end{aligned} \end{aligned}$$

(4.33)

We estimate the inner product terms in (4.33) as follows.

$$\begin{aligned}&\left| \left( d_t \rho _b^1, A_h^{-1} \frac{\theta _b^1}{\delta t}\right) \right| \le \Vert d_t \rho _b^1\Vert \left\| A_h^{-1} \frac{\theta _b^1}{\delta t}\right\| \lesssim \Vert d_t \rho _b^1\Vert \left\| \frac{\theta _b^1}{\delta t} \right\| _{-1} \lesssim \frac{1}{6} \left\| \frac{\theta _b^1}{\delta t} \right\| _{-1}^2 + \Vert d_t \rho _b^1\Vert ^2. \\&\left| \left( R^{1}_b, A_h^{-1} \frac{\theta _b^1}{\delta t} \right) \right| \le \Vert R^{1}_b\Vert \left\| A_h^{-1} \frac{\theta _b^1}{\delta t}\right\| \lesssim \Vert R^{1}_b\Vert \left\| \frac{\theta _b^1}{\delta t} \right\| _{-1} \lesssim \frac{1}{6} \left\| \frac{\theta _b^1}{\delta t} \right\| _{-1}^2 + \Vert R^{1}_b\Vert ^2. \end{aligned}$$

From the Lemma 4.2 and (4.27), we have $\Vert \varvec{u}_0-\varvec{u}^0_{h*}\Vert ^2 \le \delta t^2 + h^{2l+2} + h^{2r+2}$. Thus, we obtain

$$\begin{aligned} \begin{aligned}&\left| \left( \varvec{B}_0 \times \varvec{u}_0 , \nabla \times A_h^{-1} \frac{\theta _b^1}{\delta t} \right) - \left( \varvec{B}_h^0 \times \varvec{u}^0_{h*}, \nabla \times A_h^{-1} \frac{\theta _b^1}{\delta t}\right) \right| \\&\quad \le \left| \left( e_b^0 \times \varvec{u}_0 , \nabla \times A_h^{-1} \frac{\theta _b^1}{\delta t} \right) \right| + \left| \left( \varvec{B}_h^0 \times (\varvec{u}_0-\varvec{u}^0_{h*}), \nabla \times A_h^{-1} \frac{\theta _b^1}{\delta t}\right) \right| \\&\quad \le \Vert e_b^0\Vert \Vert \varvec{u}_0\Vert _{L^{\infty }} \left\| \frac{\theta _b^1}{\delta t} \right\| _{-1} + \Vert \varvec{B}_h^0\Vert _{L^{\infty }} \Vert \varvec{u}_0-\varvec{u}^0_{h*}\Vert \left\| \frac{\theta _b^1}{\delta t}\right\| _{-1}\\&\quad \lesssim \Vert e_b^0\Vert \left\| \frac{\theta _b^1}{\delta t} \right\| _{-1} + \Vert \varvec{u}_0-\varvec{u}^0_{h*}\Vert \left\| \frac{\theta _b^1}{\delta t}\right\| _{-1} \lesssim \frac{1}{6}\left\| \frac{\theta _b^1}{\delta t} \right\| _{-1} +\delta t^2 + h^{2l+2} + h^{2r+2}. \end{aligned} \end{aligned}$$

Combining the above estimates with (4.33) and using Lemma 4.1 and (3.7), we deduce

$$\begin{aligned} \frac{1}{2}\left\| \frac{\theta _b^1}{\delta t} \right\| _{-1}^2 + \frac{\eta }{\delta t} \Vert \theta ^{1}_b\Vert ^2 \lesssim \Vert d_t \rho _b^1\Vert ^2 +\delta t^2 + h^{2l+2} + h^{2r+2}+ \Vert R^{1}_b\Vert ^2 \lesssim \delta t^2 + h^{2l} + h^{2r},\nonumber \\ \end{aligned}$$

(4.34)

which leads to the conclusion (i).

(ii). By setting $n=0$ in (4.6) and taking $\varvec{v}_h = \frac{1}{\delta t}{\tilde{\theta }}_u^1$, since $\theta _u^0 =\theta _p^0=0$, we obtain

$$\begin{aligned} \begin{aligned}&\left( d_t \rho _u^1, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) + \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \frac{\nu }{\delta t} \Vert \nabla {\tilde{\theta }}_u^1 \Vert ^2 + b\left( {\varvec{u}}_0, \varvec{u}(t_1), \frac{{\tilde{\theta }}_u^1}{\delta t}\right) - b\left( \varvec{u}_h^0, \tilde{\varvec{u}}_h^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t}\right) \\&\quad + s \left( \varvec{B}_0 \times \nabla \times \varvec{B}(t_{1}), \frac{{\tilde{\theta }}_u^1}{\delta t}\right) - s \left( \varvec{B}_h^0 \times \nabla \times \varvec{B}_h^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \\&\quad - \left( \nabla (\rho ^1_p-\rho _p^0), \frac{{\tilde{\theta }}_u^1}{\delta t} \right) =\left( R^{1}_u, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) . \end{aligned} \end{aligned}$$

(4.35)

The inner product terms in (4.35) can be estimated as follows. By using (3.6) and regularity conditions, we get

$$\begin{aligned} \left| \left( d_t \rho _u^1, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \right| \le \Vert d_t \rho _u^1\Vert \left\| \frac{{\tilde{\theta }}_u^1}{\delta t} \right\| \lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t} \right\| ^2 + \Vert d_t \rho _u^1\Vert ^2 \lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t} \right\| ^2 + h^{2l}. \end{aligned}$$

By using (3.20) and (3.6), we get

$$\begin{aligned} \begin{aligned}&\left| b\left( {\varvec{u}}_0, \varvec{u}(t_1), \frac{{\tilde{\theta }}_u^1}{\delta t}\right) - b\left( \varvec{u}_h^0, \tilde{\varvec{u}}_h^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t}\right) \right| \le \left| b\left( e_u^0, \varvec{u}(t_1), \frac{{\tilde{\theta }}_u^1}{\delta t}\right) \right| + \left| b\left( \varvec{u}_h^0, \rho _u^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t}\right) \right| \\&\quad \lesssim \Vert \nabla e_u^0\Vert \Vert \varvec{u}(t_1)\Vert _2 \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| + (\Vert \varvec{u}_h^0\Vert _{L^{\infty }} + \Vert \nabla \cdot \varvec{u}_h^0\Vert _{L^3})\Vert \nabla \rho _u^{1}\Vert \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| \\&\quad \lesssim \frac{1}{10} \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \Vert \nabla e_u^0\Vert ^2 + \Vert \nabla \rho _u^{1}\Vert ^2 \lesssim \frac{1}{10} \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + h^{2l}. \end{aligned} \end{aligned}$$

By using the integration by parts and (3.7), we obtain

$$\begin{aligned} \begin{aligned}&s \left| \left( \varvec{B}_0 \times \nabla \times \varvec{B}(t_{1}), \frac{{\tilde{\theta }}_u^1}{\delta t} \right) - \left( \varvec{B}_h^0 \times \nabla \times \varvec{B}_h^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \right| \\&\quad = s \left| \left( e_b^0 \times \nabla \times \varvec{B}(t_{1}), \frac{{\tilde{\theta }}_u^1}{\delta t} \right) + \left( \varvec{B}_h^0 \times \nabla \times e_b^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \right| \\&\quad = s \left| \left( e_b^0 \times \nabla \times \varvec{B}(t_{1}), \frac{{\tilde{\theta }}_u^1}{\delta t} \right) + \left( \varvec{B}_h^0 \times \nabla \times \theta _b^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t}\right) + \left( \varvec{B}_h^0 \times \nabla \times \rho _b^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \right| \\&\quad = s \left| \left( e_b^0 \times \nabla \times \varvec{B}(t_{1}), \frac{{\tilde{\theta }}_u^1}{\delta t} \right) + \left( \varvec{B}_h^0 \nabla \frac{{\tilde{\theta }}_u^1}{\delta t}- \frac{{\tilde{\theta }}_u^1}{\delta t} \nabla \varvec{B}_h^0, \theta _b^{1}\right) + \left( \varvec{B}_h^0 \times \nabla \times \rho _b^{1}, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \right| \\&\quad \lesssim \Vert \nabla e_b^0\Vert \Vert \varvec{B}(t_1)\Vert _2 \left\| \frac{{\tilde{\theta }}_u^1}{\delta t} \right\| + \frac{1}{\delta t}(\Vert \varvec{B}_h^0\Vert _{L^{\infty }} +\Vert \nabla \varvec{B}_h^0\Vert _{L^3}) \Vert \nabla {\tilde{\theta }}_u^1\Vert \Vert \theta _b^{1}\Vert \\&\qquad + \Vert \varvec{B}_h^0\Vert _{L^{\infty }}\Vert \nabla \times \rho _b^{1}\Vert \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| \\&\quad \lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t} \right\| ^2 + \Vert \nabla e_b^0\Vert ^2 + \frac{\nu }{2\delta t} \Vert \nabla {\tilde{\theta }}_u^1\Vert ^2 + \frac{1}{\delta t} \Vert \theta _b^{1}\Vert ^2 + \Vert \nabla \times \rho _b^{1}\Vert ^2,\\&\quad \lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t} \right\| ^2 + \frac{\nu }{2\delta t} \Vert \nabla {\tilde{\theta }}_u^1\Vert ^2 + \frac{1}{\delta t} \Vert \theta _b^{1}\Vert ^2+ h^{2r}. \end{aligned} \end{aligned}$$

From the Theorem 3.1 and ($\mathbf {A5}$), we get

$$\begin{aligned} \begin{aligned} \delta t \left| \left( \nabla d_t \rho ^1_p, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \right|&\le \delta t \Vert \nabla d_t \rho ^1_p\Vert \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| \lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \delta t^2 \Vert \nabla d_t \rho ^1_p\Vert ^2\\&\lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \delta t^2 (\Vert d_t p(t_1)\Vert _1^2+ \Vert d_t \varvec{u}(t_1)\Vert _2^2) \lesssim \frac{1}{10}\left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \delta t^2. \end{aligned} \end{aligned}$$

From the Lemma 4.1, we have

$$\begin{aligned} \begin{aligned} \left( R^{1}_u, \frac{{\tilde{\theta }}_u^1}{\delta t} \right) \le \Vert R^{1}_u\Vert \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| \lesssim \Vert R^{1}_u\Vert ^2 +\frac{1}{10} \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 \lesssim \frac{1}{10} \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 +\delta t^2. \end{aligned} \end{aligned}$$

Combining these estimates with (4.35) and using (4.34), we derive

$$\begin{aligned} \begin{aligned} \left\| \frac{{\tilde{\theta }}_u^1}{\delta t}\right\| ^2 + \frac{\nu }{\delta t} \Vert \nabla {\tilde{\theta }}_u^1 \Vert ^2 \lesssim h^{2l} + h^{2r} + \frac{1}{\delta t} \Vert \theta _b^{1}\Vert ^2 + \delta t^2 \lesssim h^{2l} +h^{2r} + \delta t^2, \end{aligned} \end{aligned}$$

(4.36)

which is the conclusion (ii).

(iii) By setting $n=0$ in (4.7), taking the $L^2$ inner product of the obtained equation with itself on both sides, and using (4.36), we obtain

$$\begin{aligned} \left\| \frac{\theta _u^{1}}{\delta t}\right\| ^2 + \Vert \nabla \theta _p^{1}\Vert ^2 = \left\| \frac{{\tilde{\theta }}_u^{1}}{\delta t}\right\| ^2 + \!\Vert \rho ^{1}\Vert ^2 + 2 \left( \frac{{\tilde{\theta }}_u^{1}}{\delta t}, \rho ^{1} \right) \lesssim \left\| \frac{{\tilde{\theta }}_u^{1}}{\delta t}\right\| ^2 +\! \Vert \rho ^{1}\Vert ^2\lesssim h^{2l} +h^{2r} + \delta t^2,\nonumber \\ \end{aligned}$$

(4.37)

where $\rho ^1 = R^1_p-\delta t \nabla d_t \rho ^1_p$, and $\Vert \rho ^1\Vert \lesssim \delta t \Vert d_t \rho _p^1\Vert _1 + \Vert R_p^1\Vert \lesssim \delta t+ \delta t (\Vert d_t p(t_1)\Vert _1 + \Vert d_t \varvec{u}(t_1)\Vert _2) \lesssim \delta t$ by using Theorem 3.1 and Lemma 4.1. Since $\theta _u^0 = 0, \theta _p^0 =0$, we obtain the conclusion (iii). $\square$

We assume the solution to (2.1)–(2.6) has the following regularity:

$$\begin{aligned}&(\mathbf{A6}): \varvec{B}_{tt} \in L^2(0, T; H^r(\Omega )^2), \quad \varvec{u}_{tt} \in L^2(0, T; H^2(\Omega )^2 \cap H^l(\Omega )^2), \quad \\&\quad p_{tt} \in L^2(0, T; H^{l-1}(\Omega )). \end{aligned}$$

In the following Lemma, we will obtain the error estimate for $\Vert d_t \theta _u^n\Vert$.

Lemma 4.10

Under assumptions $(\mathbf A0)$–$(\mathbf A6)$, when $\delta t |\log h|^{\frac{1}{2}}\lesssim h$, $\delta t \le \delta t_0$ and $h \le h_0$, the following estimate holds for $1\le m \le [\frac{T}{\delta t}]-1$,

$$\begin{aligned} \begin{aligned} \Vert d_t \theta _u^{m+1}\Vert ^2 + \delta t^2 \Vert \nabla d_t \theta _p^{m+1}\Vert ^2+ \delta t \sum _{n=1}^m \nu \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 \lesssim \delta t^2 + h^{2l} + h^{2r}. \end{aligned} \end{aligned}$$

Proof

In Step i, we first prove the error estimate of $\Vert d_t \theta _b^{m}\Vert _{-1}^2$$+\delta t \sum _{n=1}^m \Vert d_t \theta _b^{n}\Vert ^2$ using the negative norm technique; and in Step ii, we establish the error estimate for $\Vert d_t \theta _u^n\Vert$ using the result from Step i.

(Step i). By taking $\varvec{c}_h =A_h^{-1} d_t \theta ^{n+1}_b$ in (4.31), we have

$$\begin{aligned} \begin{aligned}&\frac{1}{2 \delta t} (\Vert d_t \theta _b^{n+1}\Vert _{-1}^2 - \Vert d_t \theta _b^{n}\Vert _{-1}^2 + \Vert d_t \theta _b^{n+1} - d_t \theta _b^{n}\Vert _{-1}^2 ) + \eta \Vert d_t \theta _b^{n+1}\Vert ^2 \\&\quad = -( d_t \varvec{B}(t_n) \times \varvec{u}(t_n), \nabla \times A_h^{-1} d_t \theta ^{n+1}_b )+ (d_t \varvec{B}_h^n \times \varvec{u}^n_{h*}, \nabla \times A_h^{-1} d_t \theta _b^{n+1}) \\&\qquad - ( \varvec{B}(t_{n-1}) \times d_t \varvec{u}(t_n), \nabla \times A_h^{-1} d_t \theta ^{n+1}_b ) + (\varvec{B}_h^{n-1} \times d_t \varvec{u}^n_{h*}, \nabla \times A_h^{-1} d_t \theta _b^{n+1}) \\&\qquad - (d_{tt} \rho ^{n+1}_b, A_h^{-1} d_t \theta _b^{n+1})+ (d_t R^{n+1}_b, A_h^{-1} d_t \theta _b^{n+1}). \end{aligned} \end{aligned}$$

(4.38)

We estimate the terms on the right hand side as follows.

By using Lemmas 4.2 and 4.6 and Theorem 4.4, we obtain $\Vert \varvec{u}(t_n)-\varvec{u}^n_{h*}\Vert ^2\lesssim \delta t^2+ h^{2l+2} + h^{2r+2}$. Hence from the inverse inequality (3.2) and (3.7), we derive

$$\begin{aligned} \begin{aligned}&|( d_t \varvec{B}(t_n) \times \varvec{u}(t_n),\nabla \times A_h^{-1} d_t \theta ^{n+1}_b ) - (d_t \varvec{B}_h^n \times \varvec{u}^n_{h*}, \nabla \times A_h^{-1}d_t \theta _b^{n+1})|\\&\quad =|( d_t e_b^n \times \varvec{u}(t_n), \nabla \times A_h^{-1} d_t \theta ^{n+1}_b ) + (d_t \varvec{B}_h^n \times (\varvec{u}(t_n)-\varvec{u}^n_{h*}), \nabla \times A_h^{-1}d_t \theta _b^{n+1})| \\&\quad =|( d_t e_b^n \times \varvec{u}(t_n), \nabla \times A_h^{-1} d_t \theta ^{n+1}_b ) + ((d_t \varvec{B}(t_n)-d_t e_b^n) \times (\varvec{u}(t_n)-\varvec{u}^n_{h*}), \nabla \times A_h^{-1} d_t \theta ^{n+1}_b )|\\&\quad \lesssim \Vert d_t e_b^n\Vert \Vert \varvec{u}(t_n)\Vert _{L^{\infty }} \Vert d_t \theta ^{n+1}_b\Vert _{-1} +\Vert d_t \varvec{B}(t_n)\Vert _{L^{\infty }} \Vert \varvec{u}(t_n)-\varvec{u}^n_{h*}\Vert \Vert d_t \theta _b^{n+1}\Vert _{-1}\\&\qquad + \Vert d_t e_b^n\Vert \Vert \varvec{u}(t_n)-\varvec{u}^n_{h*}\Vert \Vert \nabla \times A_h^{-1} d_t \theta ^{n+1}_b\Vert _{L^{\infty }} \\&\quad \lesssim \frac{\eta }{8}\Vert d_t e_b^n\Vert ^2 + \Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 + \Vert \varvec{u}(t_n)-\varvec{u}^n_{h*}\Vert ^2+ \Vert \varvec{u}(t_n)-\varvec{u}^n_{h*}\Vert ^2\Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 h^{-2} \\&\quad \lesssim \frac{\eta }{8}\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \rho _b^n\Vert ^2 + \Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 + \delta t^2 + h^{2l +2}+ h^{2r +2}\\&\quad \lesssim \frac{\eta }{8}\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 + \delta t^2 + h^{2l +2}+ h^{2r}. \end{aligned} \end{aligned}$$

By using Lemmas 4.7, 4.6, Theorem 4.4, (3.6), and (3.7), we derive the following three inequalities:

$$\begin{aligned}&|( \varvec{B}(t_{n-1}) \times d_t \varvec{u}(t_n), \nabla \times A_h^{-1}d_t \theta ^{n+1}_b ) - (\varvec{B}_h^{n-1} \times d_t \varvec{u}^n_{h*}, \nabla \times A_h^{-1} d_t \theta _b^{n+1})|\\&\quad =|( e_b^{n-1} \times d_t \varvec{u}(t_n), \nabla \times A_h^{-1} d_t \theta ^{n+1}_b ) + (\varvec{B}_h^{n-1} \times d_t (\varvec{u}(t_n)-\varvec{u}^n_{h*}), \nabla \times A_h^{-1}d_t \theta _b^{n+1})| \\&\quad \le \Vert e_b^{n-1}\Vert \Vert d_t \varvec{u}(t_n)\Vert _{L^{\infty }} \Vert d_t \theta ^{n+1}_b\Vert _{-1} + \Vert \varvec{B}_h^{n-1}\Vert _{L^{\infty }} \Vert d_t (\varvec{u}(t_n)-\varvec{u}^n_{h*})\Vert \Vert d_t \theta _b^{n+1}\Vert _{-1} \\&\quad \lesssim \Vert e_b^{n-1}\Vert ^2 + \Vert d_t \theta ^{n+1}_b\Vert ^2_{-1} + (\Vert d_t e_u^n\Vert + \Vert d_t (\varvec{u}_h^n-\varvec{u}^n_{h*})\Vert ) \Vert d_t \theta _b^{n+1}\Vert _{-1} \\&\quad \lesssim \Vert e_b^{n-1}\Vert ^2 + \Vert d_t \theta ^{n+1}_b\Vert ^2_{-1} + \Vert d_t \theta _u^n\Vert ^2 + \Vert d_t \rho _u^n\Vert ^2 + \delta t^2 + \Vert \nabla \\&\quad \times (e^{n+1}_b- e_b^n)\Vert ^2 + \frac{\eta }{8}\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \rho _b^n\Vert ^2\\&\quad \lesssim \Vert d_t \theta ^{n+1}_b\Vert ^2_{-1} + \Vert d_t \theta _u^n\Vert ^2 + \Vert \nabla \\&\qquad \times (e^{n+1}_b- e_b^n)\Vert ^2 + \frac{\eta }{8}\Vert d_t \theta _b^n\Vert ^2 +\delta t^2 +h^{2r} +h^{2l},\\&\quad (d_t R^{n+1}_b, A_h^{-1} d_t \theta _b^{n+1})\le \Vert d_t R^{n+1}_b\Vert \Vert A_h^{-1} d_t \theta _b^{n+1}\Vert \\&\quad \lesssim \Vert d_t R^{n+1}_b\Vert \Vert d_t \theta _b^{n+1}\Vert \lesssim \frac{\eta }{8} \Vert d_t \theta _b^{n+1}\Vert ^2 + \Vert d_t R^{n+1}_b\Vert ^2, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} | (d_{tt} \rho ^{n+1}_b, A_h^{-1}d_t \theta _b^{n+1})| \le \Vert d_{tt} \rho ^{n+1}_b\Vert \Vert A_h^{-1} d_t \theta _b^{n+1}\Vert \lesssim \Vert d_{tt} \rho ^{n+1}_b\Vert ^2+ \frac{\eta }{8}\Vert d_t \theta _b^{n+1}\Vert ^2. \end{aligned} \end{aligned}$$

Combining the above estimates with (4.38), we obtain

$$\begin{aligned} \begin{aligned}&\Vert d_t \theta _b^{n+1}\Vert _{-1}^2 - \Vert d_t \theta _b^{n}\Vert _{-1}^2 + \eta \delta t \Vert d_t \theta _b^{n+1}\Vert ^2 + \frac{\eta }{2} \delta t( \Vert d_t \theta _b^{n+1}\Vert ^2 - \Vert d_t \theta _b^{n}\Vert ^2) \\&\quad \lesssim \delta t( \delta t^2 + h^{2l}+ h^{2r} + \Vert d_{tt} \rho ^{n+1}_b\Vert ^2)\\&\qquad +\delta t ( \Vert \nabla \times e^{n+1}_b\Vert ^2 + \Vert \nabla \times e_b^n\Vert ^2) \\&\qquad +\delta t \Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 + \delta t \Vert d_t \theta _u^n\Vert ^2 + \delta t \Vert d_t R^{n+1}_b\Vert ^2. \end{aligned} \end{aligned}$$

Summing above inequality from $n =1$ to m, using Theorem 4.4, Lemma 4.8, and (i) of Lemma 4.9, we derive

$$\begin{aligned} \begin{aligned}&\Vert d_t \theta _b^{m+1}\Vert _{-1}^2 + \eta \delta t \sum _{n=1}^m\Vert d_t \theta _b^{n+1}\Vert ^2 \lesssim \delta t \sum _{n=1}^m \Vert d_{tt} \rho ^{n+1}_b\Vert ^2\\&\qquad +\delta t \sum _{n=1}^m \Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 + \delta t \sum _{n=1}^m \Vert d_t \theta _u^n\Vert ^2\\&\qquad + \Vert d_t \theta _b^{1}\Vert _{-1}^2+ \delta t \Vert d_t \theta _b^{1}\Vert ^2+ \delta t^2 + h^{2l}+ h^{2r}\\&\quad \lesssim \delta t \sum _{n=1}^m \Vert d_t \theta ^{n+1}_b\Vert _{-1}^2 + \delta t \sum _{n=1}^m \Vert d_t \theta _u^n\Vert ^2+ \delta t^2 + h^{2l}+ h^{2r}. \end{aligned} \end{aligned}$$

Therefore, by Gronwall’s inequality, we obtain if $\delta t \le \delta t_0$,

$$\begin{aligned} \begin{aligned} \Vert d_t \theta _b^{m+1}\Vert _{-1}^2&+ \eta \delta t \sum _{n=1}^m\Vert d_t \theta _b^{n+1}\Vert ^2 \lesssim \delta t \sum _{n=1}^m \Vert d_t \theta _u^n\Vert ^2+ \delta t^2 + h^{2l}+ h^{2r}. \end{aligned} \end{aligned}$$

(4.39)

(Step ii). By taking $\varvec{v}_h = d_t {\tilde{\theta }}_u^{n+1}$ in (4.29), we have

$$\begin{aligned} \begin{aligned}&\frac{1}{ 2 \delta t}(\Vert d_t {\tilde{\theta }}_u^{n+1}\Vert ^2 - \Vert d_t {\theta }_u^{n}\Vert ^2 +\Vert d_t {\tilde{\theta }}_u^{n+1} - d_t \theta _u^n\Vert ^2 ) + \nu \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + b(\varvec{u}(t_n), d_t \varvec{u}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u)\\&\quad - b(\varvec{u}_h^n, d_t \tilde{\varvec{u}}_h^{n+1}, d_t {\tilde{\theta }}^{n+1}_u) + b(d_t \varvec{u}(t_n), \varvec{u}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - b(d_t \varvec{u}_h^n, \tilde{\varvec{u}}_h^n, d_t {\tilde{\theta }}^{n+1}_u)\\&\quad + s (\varvec{B}(t_n) \times \nabla \times d_t \varvec{B}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) - s (\varvec{B}_h^n \times \nabla \times d_t \varvec{B}_h^{n+1}, d_t {\tilde{\theta }}^{n+1}_u) \\&\quad + s (d_t \varvec{B}(t_n) \times \nabla \times \varvec{B}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - s (d_t \varvec{B}_h^n \times \nabla \times \varvec{B}_h^n, d_t {\tilde{\theta }}^{n+1}_u) + (d_{tt}\rho _u^{n+1}, d_t {\tilde{\theta }}_u^{n+1})\\&\quad + (\nabla d_t \theta _p^n, d_t {\tilde{\theta }}_u^{n+1}) + (\nabla d_t \rho _p^n- \nabla d_t \rho _p^{n+1}, d_t {\tilde{\theta }}_u^{n+1}) =(d_t R^{n+1}_u, d_t {\tilde{\theta }}^{n+1}_u). \end{aligned} \end{aligned}$$

(4.40)

From (4.30), we derive

$$\begin{aligned} \frac{d_t \theta _u^{n+1} }{\delta t} + \nabla d_t \theta _p^{n+1} = \frac{ d_t {\tilde{\theta }}_u^{n+1}}{\delta t} +\nabla d_t \theta _p^n + d_t \rho ^{n+1}, \end{aligned}$$

(4.41)

where $d_t \rho ^{n+1}= \nabla d_t \rho _p^n -\nabla d_t \rho _p^{n+1} + d_t R_p^{n+1}$.

By taking the $L^2$ inner product of (4.41) with itself on both sides, we obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{2 \delta t}(\Vert d_t \theta _u^{n+1}\Vert ^2 - \Vert d_t {\tilde{\theta }}_u^{n+1}\Vert ^2) + \frac{\delta t}{2} (\Vert \nabla d_t \theta _p^{n+1}\Vert ^2 - \Vert \nabla d_t \theta _p^{n}\Vert ^2) -(d_t {\tilde{\theta }}_u^{n+1}, d_t \rho ^{n+1})\\&\quad - \delta t (\nabla d_t \theta ^n_p, d_t \rho ^{n+1}) - \frac{\delta t}{2} \Vert d_t \rho ^{n+1}\Vert ^2=(d_t {\tilde{\theta }}_u^{n+1}, \nabla d_t \theta _p^n). \end{aligned} \end{aligned}$$

(4.42)

Combining (4.40) and (4.42), we get

$$\begin{aligned} \begin{aligned}&\frac{1}{ 2 \delta t}(\Vert d_t \theta _u^{n+1}\Vert ^2 - \Vert d_t {\theta }_u^{n}\Vert ^2 +\Vert d_t {\tilde{\theta }}_u^{n+1} - d_t \theta _u^n\Vert ^2 ) + \nu \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2\\&\qquad + \frac{\delta t}{2} (\Vert \nabla d_t \theta _p^{n+1}\Vert ^2 - \Vert \nabla d_t \theta _p^{n}\Vert ^2)\\&\qquad + b(\varvec{u}(t_n), d_t \varvec{u}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) - b(\varvec{u}_h^n, d_t \tilde{\varvec{u}}_h^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)&(\text{ I })\\&\qquad + b(d_t \varvec{u}(t_n), \varvec{u}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - b(d_t \varvec{u}_h^n, \tilde{\varvec{u}}_h^n, d_t {\tilde{\theta }}^{n+1}_u)&(\text{ II })\\&\qquad + s (\varvec{B}(t_n) \times \nabla \times d_t \varvec{B}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) - s (\varvec{B}_h^n \times \nabla \times d_t \varvec{B}_h^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)&(\text{ III })\\&\qquad + s (d_t \varvec{B}(t_n) \times \nabla \times \varvec{B}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - s (d_t \varvec{B}_h^n \times \nabla \times \varvec{B}_h^n, d_t {\tilde{\theta }}^{n+1}_u)&(\text{ IV })\\&\qquad + (d_{tt}\rho _u^{n+1}, d_t {\tilde{\theta }}_u^{n+1}) + (\nabla d_t \rho _p^n- \nabla d_t \rho _p^{n+1}, d_t {\tilde{\theta }}_u^{n+1})&(\text{ V })\\&\quad =(d_t R^{n+1}_u, d_t {\tilde{\theta }}^{n+1}_u)+ \delta t (\nabla d_t \theta ^n_p, d_t \rho ^{n+1})\\ {}&\qquad + \frac{\delta t}{2} \Vert d_t \rho ^{n+1}\Vert ^2+(d_t {\tilde{\theta }}_u^{n+1}, d_t \rho ^{n+1}) .&(\text{ VI }) \end{aligned} \end{aligned}$$

(4.43)

We estimate the terms I–VI as follows.

For term I, by using (3.20), Theorem 4.4, and the inverse inequality (3.2), we derive

$$\begin{aligned} \begin{aligned} |(\text{ I })|&= |b(\varvec{u}(t_n), d_t \varvec{u}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) - b(\varvec{u}_h^n, d_t \tilde{\varvec{u}}_h^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&= |b(e_u^n, d_t \varvec{u}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) + b(\varvec{u}_h^n, d_t \rho _u^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&=|b(e_u^n, d_t \varvec{u}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u)- b(e_u^n, d_t \rho _u^{n+1}, d_t {\tilde{\theta }}^{n+1}_u) + b(\varvec{u}(t_n), d_t \rho _u^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&\lesssim \Vert e_u^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert (\Vert d_t \varvec{u}(t_{n+1})\Vert _{L^{\infty }}+\Vert \nabla d_t \varvec{u}(t_{n+1})\Vert _{L^3} )\\&\quad + \Vert e_u^n\Vert \Vert \nabla d_t \rho ^{n+1}_u\Vert (\Vert d_t {\tilde{\theta }}_u^{n+1}\Vert _{L^{\infty }} \\&\quad + \Vert \nabla d_t {\tilde{\theta }}_u^{n+1}\Vert _{L^{3}} ) + \Vert \varvec{u}(t_n)\Vert _{L^{\infty }} \Vert d_t \rho _u^{n+1}\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\lesssim \frac{\nu }{12}\Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert e_u^n\Vert ^2 \Vert d_t \varvec{u}(t_{n+1})\Vert ^2_2 + h^{-\frac{2}{3}}\Vert e_u^n\Vert ^2 \Vert d_t \rho ^{n+1}_u\Vert _1^2 + \Vert d_t \rho _u^{n+1}\Vert ^2\\&\lesssim \frac{\nu }{12}\Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \delta t^2 +h^{2r}+h^{2l} + \Vert d_t \rho ^{n+1}_u\Vert _1^2. \end{aligned} \end{aligned}$$

(4.44)

For term II, by applying the inverse inequality (3.2) and (3.6), we get

$$\begin{aligned} \begin{aligned} |(\text{ II })|&=| b(d_t \varvec{u}(t_n), \varvec{u}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - b(d_t \varvec{u}_h^n, \tilde{\varvec{u}}_h^n, d_t {\tilde{\theta }}^{n+1}_u)|\\&=| b(d_t e_u^n, \varvec{u}(t_n), d_t {\tilde{\theta }}^{n+1}_u) + b(d_t \varvec{u}_h^n, {\tilde{e}}_u^n, d_t {\tilde{\theta }}^{n+1}_u)|\\&=| b(d_t e_u^n, \varvec{u}(t_n), d_t {\tilde{\theta }}^{n+1}_u)- b(d_t e_u^n, {\tilde{e}}_u^n, d_t {\tilde{\theta }}^{n+1}_u) + b(d_t \varvec{u}(t_n), {\tilde{e}}_u^n, d_t {\tilde{\theta }}^{n+1}_u)|\\&=| b(d_t e_u^n, \varvec{u}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - b(d_t e_u^n, {\tilde{\theta }}_u^n +\rho _u^n, d_t {\tilde{\theta }}^{n+1}_u) + b(d_t \varvec{u}(t_n), {\tilde{e}}_u^n, d_t {\tilde{\theta }}^{n+1}_u)|\\&\lesssim \Vert d_t e_u^n\Vert \Vert \varvec{u}(t_n)\Vert _2 \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + \Vert d_t e_u^n\Vert (\Vert \nabla {\tilde{\theta }}_u^n\Vert \Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^{\infty }} + \Vert {\tilde{\theta }}_u^n\Vert _{L^{\infty }} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert )\\&\quad + \Vert d_t e_u^n\Vert (\Vert \nabla \rho _u^n\Vert \Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^{\infty }}+ \Vert \rho _u^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^{\infty }})\\&\quad +\Vert d_t \varvec{u}(t_n)\Vert _1 \Vert \nabla {\tilde{e}}_u^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\lesssim \Vert d_t e_u^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + |\log h|^{\frac{1}{2}}\Vert d_t e_u^n\Vert \Vert \nabla {\tilde{\theta }}_u^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\quad + \Vert d_t e_u^n\Vert (h^l h^{-\frac{1}{3}}\Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^6}+ h^{l+1} h^{-1} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ) + \Vert \nabla {\tilde{e}}_u^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\lesssim \frac{\nu }{12}\Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert d_t e_u^n\Vert ^2 + |\log h| \Vert \nabla {\tilde{\theta }}_u^n\Vert ^2 \Vert d_t e_u^n\Vert ^2 + \Vert \nabla {\tilde{e}}_u^n\Vert ^2\\&\lesssim \frac{\nu }{12}\Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert d_t \theta _u^n\Vert ^2 + h^{2l} + \Vert \nabla {\tilde{\theta }}_u^n\Vert ^2 + |\log h| \Vert \nabla {\tilde{\theta }}_u^n\Vert ^2 \Vert d_t \theta _u^n\Vert ^2 + \Vert \nabla {\tilde{e}}_u^n\Vert ^2. \end{aligned} \end{aligned}$$

(4.45)

For term III, by using the integration by parts, the inverse inequality (3.2), Theorem 4.4 and (3.7), we derive

$$\begin{aligned} \begin{aligned} |(\text{ III })|&=s| (\varvec{B}(t_n) \times \nabla \times d_t \varvec{B}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) - (\varvec{B}_h^n \times \nabla \times d_t \varvec{B}_h^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&=s| (e_b^n \times \nabla \times d_t \varvec{B}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) + (\varvec{B}_h^n \times \nabla \times d_t e_b^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&=s| (e_b^n \times \nabla \times d_t \varvec{B}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u) + ((\varvec{B}(t_n) - e_b^n) \times \nabla \times d_t e_b^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&\lesssim | (e_b^n \times \nabla \times d_t \varvec{B}(t_{n+1}), d_t {\tilde{\theta }}^{n+1}_u)| + |( \varvec{B}(t_n)\nabla d_t {\tilde{\theta }}^{n+1}_u - d_t {\tilde{\theta }}^{n+1}_u \nabla \varvec{B}(t_n), d_t e_b^{n+1})| \\&\quad + |(e_b^n \times \nabla \times d_t \theta _b^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)| + |(e_b^n \times \nabla \times d_t \rho _b^{n+1}, d_t {\tilde{\theta }}^{n+1}_u)|\\&\lesssim \Vert e_b^n\Vert _1 \Vert d_t \varvec{B}(t_{n+1})\Vert _1 \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + (\Vert \varvec{B}(t_n)\Vert _{L^{\infty }} + \Vert \nabla \varvec{B}(t_n)\Vert _{L^3}) \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \Vert d_t e_b^{n+1}\Vert \\&\quad + \Vert e_b^n\Vert \Vert \nabla \times d_t \theta _b^{n+1}\Vert \Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^{\infty }} + \Vert e_b^n\Vert _1 \Vert d_t \rho _b^{n+1}\Vert _1 \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\lesssim \Vert e_b^n\Vert _1 \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \Vert d_t e_b^{n+1}\Vert + \Vert e_b^n\Vert h^{-1} |\log h|^{\frac{1}{2}}\Vert d_t \theta _b^{n+1}\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\quad + \Vert e_b^n\Vert _1 \Vert d_t \rho _b^{n+1}\Vert _1 \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert e_b^n\Vert _1^2 + \Vert d_t e_b^{n+1}\Vert ^2 + |\log h|h^{-2} \Vert e_b^n\Vert ^2 \Vert d_t \theta _b^{n+1}\Vert ^2 \\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert e_b^n\Vert _1^2 + \Vert d_t \theta _b^{n+1}\Vert ^2+\Vert d_t \rho _b^{n+1}\Vert ^2 \\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert e_b^n\Vert _1^2 + \Vert d_t \theta _b^{n+1}\Vert ^2+h^{2r}, \end{aligned} \end{aligned}$$

(4.46)

where we also use $\Vert d_t \rho _b^{n+1}\Vert _1 \lesssim \Vert d_t \varvec{B}(t_{n+1})\Vert _1$ and $\delta t |\log h|^{\frac{1}{2}} \lesssim h$.

For term IV, by using the integration by parts, the inverse inequality (3.2), Theorem 4.4 and (3.7), we derive

$$\begin{aligned} \begin{aligned} |(\text{ IV })|&=s|(d_t \varvec{B}(t_n) \times \nabla \times \varvec{B}(t_n), d_t {\tilde{\theta }}^{n+1}_u) - (d_t \varvec{B}_h^n \times \nabla \times \varvec{B}_h^n, d_t {\tilde{\theta }}^{n+1}_u)| \\&=s|(d_t e_b^n \times \nabla \times \varvec{B}(t_n), d_t {\tilde{\theta }}^{n+1}_u) + (d_t \varvec{B}_h^n \times \nabla \times e_b^n, d_t {\tilde{\theta }}^{n+1}_u)| \\&\lesssim |(d_t e_b^n \times \nabla \times \varvec{B}(t_n), d_t {\tilde{\theta }}^{n+1}_u)| + |(d_t \varvec{B}(t_n) \times \nabla \times e_b^n, d_t {\tilde{\theta }}^{n+1}_u)| \\&\quad + |(d_t \rho _b^n \times \nabla \times e_b^n, d_t {\tilde{\theta }}^{n+1}_u)| + |(d_t \theta _b^n \times \nabla \times e_b^n, d_t {\tilde{\theta }}^{n+1}_u)| \\&\lesssim |(d_t e_b^n \times \nabla \times \varvec{B}(t_n), d_t {\tilde{\theta }}^{n+1}_u)| + |(d_t \varvec{B}(t_n) \times \nabla \times e_b^n, d_t {\tilde{\theta }}^{n+1}_u)| \\&\quad + |(d_t \rho _b^n \times \nabla \times e_b^n, d_t {\tilde{\theta }}^{n+1}_u)| + |(d_t \theta _b^n \nabla d_t {\tilde{\theta }}^{n+1}_u- d_t {\tilde{\theta }}^{n+1}_u \nabla d_t \theta _b^n, e_b^n )|\\&\lesssim \Vert d_t e_b^n\Vert \Vert \nabla \times \varvec{B}(t_n)\Vert _{L^3}\Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^6} +\Vert d_t \varvec{B}(t_n)\Vert _{L^3} \Vert \nabla \times e_b^n\Vert \Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^6}\\&\quad + \Vert d_t \rho _b^n\Vert _{L^3} \Vert \nabla \times e_b^n\Vert \Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^6} +(\Vert d_t \theta _b^n\Vert _{L^{\infty }} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\quad +\Vert d_t {\tilde{\theta }}^{n+1}_u\Vert _{L^{\infty }} \Vert \nabla d_t \theta _b^n\Vert ) \Vert e_b^n\Vert \\&\lesssim \Vert d_t e_b^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + \Vert \nabla \times e_b^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + \Vert d_t \rho _b^n\Vert _1 \Vert \nabla \times e_b^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \\&\quad +(h^{-1}\Vert d_t \theta _b^n\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + |\log h|^{\frac{1}{2}}h^{-1}\Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert \Vert d_t \theta _b^n\Vert ) \Vert e_b^n\Vert \\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert d_t e_b^n\Vert ^2 +\Vert \nabla \times e_b^n\Vert ^2 + |\log h| h^{-2} \Vert e_b^n\Vert ^2\Vert d_t \theta _b^n\Vert ^2\\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \Vert d_t \rho _b^n\Vert ^2 +\Vert \nabla \times e_b^n\Vert ^2 +\Vert d_t \theta _b^n\Vert ^2\\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 +\Vert \nabla \times e_b^n\Vert ^2 +\Vert d_t \theta _b^n\Vert ^2 +h^{2r}. \end{aligned} \end{aligned}$$

(4.47)

For terms V and VI, by (2.7), we derive

$$\begin{aligned} \begin{aligned} |\text{(term } \text{ V) }|&\lesssim |(d_{tt}\rho _u^{n+1}, d_t {\tilde{\theta }}_u^{n+1})| + \delta t |( d_{tt} \rho _p^{n+1}, \nabla \cdot d_t {\tilde{\theta }}_u^{n+1})|\\&\lesssim \Vert d_{tt}\rho _u^{n+1}\Vert \Vert d_t {\tilde{\theta }}_u^{n+1}\Vert + \delta t \Vert d_{tt} \rho _p^{n+1}\Vert \Vert \nabla \cdot d_t {\tilde{\theta }}_u^{n+1}\Vert \\&\lesssim \frac{\nu }{12} \Vert \nabla d_t {\tilde{\theta }}_u^{n+1}\Vert ^2 + \Vert d_{tt}\rho _u^{n+1}\Vert ^2 + \delta t^2 \Vert d_{tt} \rho _p^{n+1}\Vert ^2, \end{aligned} \end{aligned}$$

(4.48)

and

$$\begin{aligned} \begin{aligned} \text{(VI) }&\le |(d_t R^{n+1}_u, d_t {\tilde{\theta }}^{n+1}_u)|+ \delta t |(\nabla d_t \theta ^n_p, d_t \rho ^{n+1})| + \frac{\delta t}{2} \Vert d_t \rho ^{n+1}\Vert ^2+ |(d_t {\tilde{\theta }}_u^{n+1}, d_t \rho ^{n+1})|\\&\lesssim \Vert d_t R^{n+1}_u\Vert \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert + \delta t \Vert \nabla d_t \theta ^n_p\Vert \Vert d_t \rho ^{n+1}\Vert \\&\qquad + \frac{\delta t}{2} \Vert d_t \rho ^{n+1}\Vert ^2+ \Vert \nabla d_t {\tilde{\theta }}_u^{n+1}\Vert \Vert d_t \rho ^{n+1}\Vert \\&\lesssim \frac{\nu }{12}\Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2+ \Vert d_t R^{n+1}_u\Vert ^2 +\delta t^2 \Vert \nabla d_t \theta ^n_p\Vert ^2+ \Vert d_t \rho ^{n+1}\Vert ^2. \end{aligned} \end{aligned}$$

(4.49)

Combining (4.44)–(4.49) with (4.43), we obtain

$$\begin{aligned} \begin{aligned} \Vert d_t \theta _u^{n+1}\Vert ^2&- \Vert d_t {\theta }_u^{n}\Vert ^2 + \delta t \nu \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \delta t^2 (\Vert \nabla d_t \theta _p^{n+1}\Vert ^2 - \Vert \nabla d_t \theta _p^{n}\Vert ^2)\\&\lesssim \delta t (1+|\log h|\Vert \nabla {\tilde{\theta }}_u^n\Vert ^2) \Vert d_t \theta _u^n\Vert ^2 + \delta t^3 \Vert \nabla d_t \theta _p^{n}\Vert ^2\\&\quad + \delta t (\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \theta _b^{n+1}\Vert ^2)\\&\quad +\delta t(\Vert d_t \rho _u^{n+1}\Vert _1^2 + \delta t^2 +h^{2l} +h^{2r} + \Vert d_{tt} \rho _u^{n+1}\Vert ^2 + \Vert d_t \rho ^{n+1}\Vert ^2)\\&\quad + \delta t^3 \Vert d_{tt}\rho _p^{n+1}\Vert ^2 +\delta t \Vert d_t R_u^{n+1}\Vert ^2 + \delta t (\Vert \nabla {\tilde{\theta }}_u^n\Vert ^2 + \Vert \nabla {\tilde{e}}_u^n\Vert ^2 + \Vert e_b^n\Vert _1^2). \end{aligned} \end{aligned}$$

(4.50)

By taking the summation of (4.50) from $n=1$ to m, and using Lemma 4.8, Theorem 4.4, Lemma 4.9, (4.39), and (3.6), (3.3), we obtain

$$\begin{aligned} \begin{aligned}&\Vert d_t \theta _u^{m+1}\Vert ^2 + \delta t \sum _{n=1}^m\nu \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2 + \delta t^2 \Vert \nabla d_t \theta _p^{m+1}\Vert ^2 \\&\quad \lesssim \delta t \sum _{n=1}^m (1+|\log h|\Vert \nabla {\tilde{\theta }}_u^n\Vert ^2) \Vert d_t \theta _u^n\Vert ^2 + \delta t^3\sum _{n=1}^m \Vert \nabla d_t \theta _p^{n}\Vert ^2\\&\qquad + \delta t \sum _{n=1}^m(\Vert d_t \theta _b^n\Vert ^2 + \Vert d_t \theta _b^{n+1}\Vert ^2)\\&\qquad +\delta t\sum _{n=1}^m(\Vert d_t \rho _u^{n+1}\Vert _1^2 + \Vert d_{tt} \rho _u^{n+1}\Vert ^2 + \Vert d_t \rho ^{n+1}\Vert ^2) \\&\qquad + \delta t^3 \sum _{n=1}^m\Vert d_{tt}\rho _p^{n+1}\Vert ^2 +\delta t^2+h^{2l} +h^{2r}\\&\quad \lesssim \delta t \sum _{n=1}^m (1+|\log h|\Vert \nabla {\tilde{\theta }}_u^n\Vert ^2) \Vert d_t \theta _u^n\Vert ^2 + \delta t^3\sum _{n=1}^m \Vert \nabla d_t \theta _p^{n}\Vert ^2 \\&\qquad +\delta t\sum _{n=1}^m \Vert d_t \rho ^{n+1}\Vert ^2 +\delta t^2+h^{2l} +h^{2r}. \end{aligned} \end{aligned}$$

In addition, by applying the Theorem 3.1 and Lemma 4.8,

$$\begin{aligned} \begin{aligned} \delta t\sum _{n=1}^m \Vert d_t \rho ^{n+1}\Vert ^2&\le \delta t^3\sum _{n=1}^m \Vert d_{tt} \rho _p^{n+1}\Vert _1^2 + \delta t\sum _{n=1}^m \Vert d_t R_p^{n+1}\Vert ^2\\&\lesssim \delta t^3\sum _{n=1}^m (\Vert d_{tt}p(t_{n+1})\Vert _1^2+\Vert d_{tt} \varvec{u}(t_{n+1})\Vert _2^2) + \delta t^2 \\&\lesssim \delta t^2. \end{aligned} \end{aligned}$$

Therefore, by using (4.27) and the Gronwall’s inequality, we obtain

$$\begin{aligned} \begin{aligned} \Vert d_t \theta _u^{m+1}\Vert ^2&+ \delta t^2 \Vert \nabla d_t \theta _p^{m+1}\Vert ^2+ \delta t \sum _{n=1}^m \nu \Vert \nabla d_t {\tilde{\theta }}^{n+1}_u\Vert ^2\\&\lesssim \delta t \sum _{n=1}^m (1+|\log h|\Vert \nabla {\tilde{\theta }}_u^n\Vert ^2) \Vert d_t \theta _u^n\Vert ^2 \\&\qquad + \delta t^3 \sum _{n=1}^m \Vert \nabla d_t \theta _p^{n}\Vert ^2 + \delta t^2 + h^{2l} + h^{2r}\\&\lesssim (\delta t^2 + h^{2l} + h^{2r})\exp \left( \delta t \sum _{n=1}^m(1+|\log h|\Vert \nabla {\tilde{\theta }}_u^n\Vert ^2) \right) \lesssim \delta t^2 + h^{2l} + h^{2r}, \end{aligned} \end{aligned}$$

(4.51)

that is the desired result. $\square$

Finally, we are ready to obtain the optimal error estimate for pressure in the next Theorem.

Theorem 4.11

Under the assumptions of Lemma 4.10, the following estimate holds

$$\begin{aligned} \Vert \nabla {\tilde{e}}_u^n\Vert + \Vert e_p^n\Vert \lesssim \delta t +{ h^{\min \{l, r\}},} \; 1\le n \le \left[ \frac{T}{\delta t}\right] . \end{aligned}$$

(4.52)

Proof

From the inequality $\Vert \nabla {\tilde{\theta }}_u^{n+1}\Vert -\Vert \nabla {\tilde{\theta }}_u^{n}\Vert \le \Vert \nabla {\tilde{\theta }}_u^{n+1} -\nabla {\tilde{\theta }}_u^{n}\Vert$ and Lemma 4.10, we derive

$$\begin{aligned} \Vert \nabla {\tilde{\theta }}_u^{m+1}\Vert -\Vert \nabla {\tilde{\theta }}_u^{1}\Vert&\le \sum _{n=1}^m\Vert \nabla {\tilde{\theta }}_u^{n+1} -\nabla {\tilde{\theta }}_u^{n}\Vert \\&\le \left( \sum _{n=1}^m\Vert \nabla {\tilde{\theta }}_u^{n+1} -\nabla {\tilde{\theta }}_u^{n}\Vert ^2\right) ^{\frac{1}{2}}\left( \sum _{n=1}^m 1\right) ^{\frac{1}{2}} \lesssim \delta t + h^l + h^r. \end{aligned}$$

By applying (ii) of Lemma 4.9, we derive

$$\begin{aligned} \Vert \nabla {\tilde{\theta }}_u^{m}\Vert \lesssim \delta t + h^l + h^r, ~\text{ for } \text{ all } 1\le m \le \left[ \frac{T}{\delta t}\right] . \end{aligned}$$

From the triangle inequality, we have

$$\begin{aligned} \Vert \nabla {\tilde{e}}_u^m \Vert \le \Vert \nabla {\tilde{\theta }}_u^{m}\Vert + \Vert \nabla \rho _u^m\Vert \lesssim \delta t + h^l + h^r, ~\text{ for } \text{ all } 1\le m \le \left[ \frac{T}{\delta t}\right] . \end{aligned}$$

(4.53)

By taking the summation of (4.6) and (4.7), we obtain the error equation with respective to pressure p

$$\begin{aligned} \begin{aligned} ( \theta _p^{n+1}, \nabla \cdot \varvec{v}_h)&= (d_t e_u^{n+1}, \varvec{v}_h ) + \nu (\nabla {\tilde{e}}_u^{n+1}, \nabla \varvec{v}_h) + b(e_u^n, \varvec{u}(t_{n+1}), \varvec{v}_h) + b({\varvec{u}}_h^n, {\tilde{e}}_u^{n+1}, \varvec{v}_h)\\&\quad + s \left( e_b^n \times \nabla \times \varvec{B}(t_{n+1}), \varvec{v}_h \right) + s \left( \varvec{B}_h^n \times \nabla \times e_b^{n+1}, \varvec{v}_h\right) \\&\quad - (R^{n+1}_u+R^{n+1}_p, \varvec{v}_h)-(\rho _p^{n+1}, \nabla \cdot \varvec{v}_h). \end{aligned} \end{aligned}$$

(4.54)

For the four trilinear terms in (4.54), we estimate them one by one as follows.

$$\begin{aligned} \begin{aligned} b(e_u^n, \varvec{u}(t_{n+1}), \varvec{v}_h) \lesssim \Vert e_u^n\Vert \Vert \varvec{u}(t_{n+1})\Vert _2 \Vert \nabla \varvec{v}_h\Vert \lesssim \Vert e_u^n\Vert \Vert \nabla \varvec{v}_h\Vert . \end{aligned} \end{aligned}$$

(4.55)

By applying the inverse inequality (3.2) and Theorem 4.4, we obtain

$$\begin{aligned} \begin{aligned} b({\varvec{u}}_h^n, {\tilde{e}}_u^{n+1}, \varvec{v}_h)&= b({\varvec{u}}(t_n), {\tilde{e}}_u^{n+1}, \varvec{v}_h) - b( e_u^n, {\tilde{e}}_u^{n+1}, \varvec{v}_h)\lesssim \Vert \nabla {\varvec{u}}(t_n)\Vert \Vert \nabla {\tilde{e}}_u^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert \\&\quad + \Vert e_u^n\Vert \Vert \nabla {\tilde{e}}_u^{n+1}\Vert ( \Vert \nabla \varvec{v}_h\Vert _{L^3} + \Vert \varvec{v}_h\Vert _{L^{\infty }})\\&\lesssim \Vert \nabla {\tilde{e}}_u^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert + h^{-\frac{1}{3}}\Vert e_u^n\Vert \Vert \nabla {\tilde{e}}_u^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert \lesssim \Vert \nabla {\tilde{e}}_u^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert , \end{aligned} \end{aligned}$$

(4.56)

and

$$\begin{aligned} \begin{aligned} s \left( e_b^n \times \nabla \times \varvec{B}(t_{n+1}), \varvec{v}_h \right) \le s \Vert e_b^n\Vert \Vert \nabla \times \varvec{B}(t_{n+1})\Vert _{L^3} \Vert \varvec{v}_h\Vert _{L^6} \lesssim \Vert e_b^n\Vert \Vert \nabla \varvec{v}_h\Vert . \end{aligned} \end{aligned}$$

(4.57)

By using the integration by parts and the inverse inequality (3.2), (3.7) and Theorem 4.4, we get

$$\begin{aligned} \begin{aligned}&s\left( \varvec{B}_h^n \times \nabla \times e_b^{n+1}, \varvec{v}_h\right) = s\left( \varvec{B}(t_n) \times \nabla \times e_b^{n+1}, \varvec{v}_h\right) - s\left( e_b^n \times \nabla \times e_b^{n+1}, \varvec{v}_h\right) \\&\quad =s\left( \varvec{B}(t_n) \nabla \varvec{v}_h -\varvec{v}_h \nabla \varvec{B}(t_n), e_b^{n+1}\right) - s\left( e_b^n \times \nabla \times \rho _b^{n+1}, \varvec{v}_h\right) - s\left( e_b^n \times \nabla \times \theta _b^{n+1}, \varvec{v}_h\right) \\&\quad \lesssim (\Vert \varvec{B}(t_n)\Vert _{L^{\infty }} + \Vert \nabla \varvec{B}(t_n)\Vert _{L^3}) \Vert \nabla \varvec{v}_h\Vert \Vert e_b^{n+1}\Vert + \Vert e_b^n\Vert \Vert \nabla \times \rho _b^{n+1}\Vert \Vert \varvec{v}_h\Vert _{L^{\infty }}\\&\qquad +\Vert e_b^n\Vert \Vert \nabla \times \theta _b^{n+1}\Vert \Vert \varvec{v}_h\Vert _{L^{\infty }}\\&\quad \lesssim \Vert \nabla \varvec{v}_h\Vert \Vert e_b^{n+1}\Vert + \Vert e_b^n\Vert \Vert \nabla \times \rho _b^{n+1}\Vert |\log h|^{\frac{1}{2}}\Vert \nabla \varvec{v}_h\Vert +\Vert e_b^n\Vert \Vert \theta _b^{n+1}\Vert h^{-1}|\log h|^{\frac{1}{2}}\Vert \nabla \varvec{v}_h\Vert \\&\quad \lesssim \Vert \nabla \varvec{v}_h\Vert \Vert e_b^{n+1}\Vert + \Vert e_b^n\Vert \Vert \nabla \varvec{v}_h\Vert . \end{aligned} \end{aligned}$$

(4.58)

Combining (4.55)–(4.58) with (4.54), we obtain

$$\begin{aligned} \begin{aligned} ( \theta _p^{n+1}, \nabla \cdot \varvec{v}_h)&\lesssim \Vert d_te_u^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert + \Vert \nabla {\tilde{e}}_u^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert \\&\quad +\Vert e_u^n\Vert \Vert \nabla \varvec{v}_h\Vert + \Vert e_b^n\Vert \Vert \nabla \varvec{v}_h\Vert + \Vert \nabla \varvec{v}_h\Vert \Vert e_b^{n+1}\Vert \\&\quad + \Vert R^{n+1}_u\Vert \Vert \nabla \varvec{v}_h\Vert + \Vert R^{n+1}_p\Vert \Vert \nabla \varvec{v}_h\Vert + \Vert \rho _p^{n+1}\Vert \Vert \nabla \varvec{v}_h\Vert . \end{aligned} \end{aligned}$$

By applying the inf–sup condition (3.1), Lemma 4.10, (4.53), Theorem 4.4, Lemma 4.1 and (3.6), we obtain

$$\begin{aligned} \begin{aligned} \beta \Vert \theta _p^{n+1}\Vert&\lesssim \Vert d_t e_u^{n+1}\Vert + \Vert \nabla {\tilde{e}}_u^{n+1}\Vert + \Vert e_u^n\Vert + \Vert e_b^n\Vert + \Vert e_b^{n+1}\Vert \\&\quad + \Vert R^{n+1}_u\Vert + \Vert R^{n+1}_p\Vert + \Vert \rho _p^{n+1}\Vert \lesssim \delta t + h^{l} + h^{r}. \end{aligned} \end{aligned}$$

The proof is completed by triangle inequality and (3.6). $\square$

Remark 4.12

For the three dimensional case ($d=3$), since the inverse inequalities are more restrictive: $\Vert \varvec{w}_h\Vert _{L^{\infty }} \lesssim h^{-\frac{3}{2}}\Vert \varvec{w}_h\Vert , \Vert \varvec{w}_h\Vert _{L^{\infty }} \lesssim h^{-\frac{1}{2}}\Vert \varvec{w}_h\Vert _{L^6} \lesssim h^{-\frac{1}{2}}\Vert \varvec{w}_h\Vert _1$, Theorem 4.11 is still valid but provided that $\delta t \lesssim h^{\frac{3}{2}}$.

5 Numerical Examples

We now implement various 2D numerical experiments to validate the stability and accuracy of the scheme. We use the inf–sup stable P2/P1 element [6] for the velocity and pressure, and linear element for the magnetic field.

5.1 Accuracy Test

We first perform numerical simulations to test the convergence rates of the proposed scheme. The computational domain is $\Omega = [0, 1]\times [0,1].$ We assume the following functions

$$\begin{aligned} \varvec{u}=(y^5+t^2, x^5+t^2),~ p=10(2x-1)(2y-1)(1+t^2),~ \varvec{B} =(\sin (y) + t^2, \sin (x) + t^2) \end{aligned}$$

to be the exact solution, and impose some suitable force fields such that the given solution can satisfy the system. Choose $\nu = \eta =s=1$. In Table 1, we list the numerical errors between the numerical solution and the exact solution at $T =1$ with different time step sizes. Since the relation between the spatial grid size h and temporal step size $\delta t$ to be $\delta t = h^2$, we observe the second order accuracy asymptotically for $\Vert e_u\Vert _{L^2}, \Vert e_u\Vert _{H^1}, \Vert e_p\Vert _{L^2}, \Vert e_b\Vert _{L^2}$ and the first order accuracy for $\Vert e_b\Vert _{H^1}$, as predicted theoretically.

Table 1 The numerical errors and convergence order for $\Vert e_u\Vert _{L^2}$, $\Vert e_u\Vert _{H^1}$, $\Vert e_p\Vert _{L^2}$, $\Vert e_b\Vert _{L^2}$, and $\Vert e_b\Vert _{H^1}$ at $t=1$. Here we set $\nu =\eta =s=1$ and $\delta t=h^2$

5.2 Stability Test

We show the evolution of the total free energy in this example. We set the computed domain to be $\Omega =[0,1]^2$, and the initial conditions for ${\varvec{u}}, p, \varvec{B}$ are

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{u}^0= ( x^2(x-1)^2y(y-1)(2y-1), \;-y^2(y-1)^2x(x-1)(2x-1)), p^0=0,\\&\varvec{B}^0= ( \sin (\pi x)\cos (\pi y), \; -\sin (\pi y)\cos (\pi x)). \end{aligned} \right. \end{aligned}$$

(5.1)

We test the energy stability over matching time of the proposed scheme under varing physical parameters of $R_e=R_m=10, 50$. The coupling parameter is fixed as $s=1$, and mesh size is $h=1/64$. In Fig. 1, we present the time evolution of the total free energy for four different time steps of $\delta t=0.05, 0.01, 0.001, 0.0001$ until $T=5$. We observe that all four energy curves decay monotonically for all time step sizes, which numerically confirms that our algorithm is unconditionally energy stable.

Fig. 1

Time evolution of the free energy functional till $T = 5$ for four different time steps and two sets of order parameters a$R_e=R_m=10$ and b$R_e=R_m=50$. The energy curves show the decays for all time steps $\delta t=0.05, 0.01, 0.001, 0.0001$

5.3 Hydromagnetic Kelvin–Helmholtz instability

The Kelvin–Helmholtz (K–H) instability in sheared flow configurations is an efficient mechanism to initiate mixing of fluids, transport of momentum and energy, and the development of turbulence. This phenomenon is of interest in investigating a variety of space, astrophysical, and geophysical situations involving sheared plasma flows. Configurations where it is relevant include the interface between the solar wind and the magnetosphere, coronal streamers moving through the solar wind, etc. Since most astrophysical environments are electrically conducting and relevant fluids are likely to be magnetized, it is thus of prime importance to understand the role of magnetic fields in the K–H instability. About the theoretical and numerical study of Hydromagnetic K–H instability, we refer to [5, 8, 9, 12, 17, 24, 27] and the references therein.

Fig. 2

The dynamical behaviors of the magnetic field together with the velocity field that shows the hydromagnetic K–H instability. Snapshots of the numerical approximation are taken at $t=0.1, 1, 2, 2.2, 2.5, 3, 3.5, 4$

We study the occurring of the K–H instability in a single shear flow configuration that is embedded in a uniform flow-aligned magnetic field. The simulation is performed in the computed domain of $[0, 2] \times [0, 1]$. The initial velocity field is $\varvec{u}_0=(1.5, 0)$ in the top half domain, and $\varvec{u}_0= (-1.5, 0)$ in the bottom half domain. The sheared initial magnetic field is $\varvec{B}_0 = (\tanh (y / \epsilon ), 0)$ where $\epsilon =0.07957747154595$ (cf. [9]). The velocity $\varvec{u}$, magnetic field $\varvec{B}$ and pressure p are periodic boundary conditions on left and right boundaries. On the top and bottom boundary, the second component v of the velocity field ${\varvec{u}}=(u,v)$ is imposed. The boundary conditions for $\varvec{B}$ are $\varvec{B} \times \varvec{n} = \varvec{B}_0\times \varvec{n}$ for the top boundary and $- \varvec{B}_0 \times \varvec{n}$ for the bottom. We let $R_e=R_m=1000$, $s=0.09$, and use the time step $\delta t = 0.01$, grid size $h=\frac{1}{40}$ to compute it.

In Fig. 2, we show snapshots of the magnitude of $\varvec{B}_1$ that is the first component of $\varvec{B}=(\varvec{B}_1,\varvec{B}_2)$ together with the velocity field $\varvec{u}$ at $t=0.1, 1, 2, 2.2, 2.5, 3, 3.5, 4$. When time evolves, we can observe the vortexes start to form around $t=2$. After $t=2.5$, the profiles of vortexes and the magnetic field show the typical structure of K-H instability, and soon it deforms and rotates along with the flow. The obtained numerical results coincide well with the numerical/experimental results discussed in [5, 8, 17, 27], qualitatively.

5.4 Lid Driven Cavity

Finally we perform the lid driven cavity flow simulation of a conducting fluid. The computed domain is $(x,y)\in \Omega =[0,1]\times [0,1]$. The boundary condition of the magnetic field is either horizontal case $\varvec{B}|_{\partial \Omega }=(1, 0)$ (denoted by H-magnetic) or vertical case $\varvec{B}|_{\partial \Omega }=(0, 1)$ (denoted by V-magnetic). The no-slip boundary conditions are imposed on the bottom, left, and right sides of the cavity and the lid moves from left to right with the constant speed ${\varvec{u}}|_{y=1}=(1,0)$.

Fig. 3

The steady state of the streamlines for the velocity field for three cases, where a No magnetic field, b H-magnetic, and c V-magnetic

Fig. 4

The steady state of the velocity field ${\varvec{u}}$ and the magnetic field $\varvec{B}$ for five set of order parameters, shown in the caption of each subfigure, in which, the left one is the velocity field and the right one is the magnetic field

First, we set $R_e=400, R_m=40$ and Hartmann number $H_a(:=\sqrt{sR_eR_m})=100$. In Fig. 3, we show the steady state for three cases: no magnetic field, H-magnetic and V-magnetic, respectively. For the case of no magnetic field, this situation is actually a pure hydrodynamic problem, in which we observe the cavity is dominated by one large primary eddy in the center, together with a smaller secondary eddy in the right corner. For the H-magnetic case, two large eddies appear in the upper and lower part. For the V-magnetic case, two large eddies are located in the upper left and upper right. Similar features had been observed in [3] as well.

Second, we perform the so-called “magnetic frozen” simulations by varying the magnetic Reynolds number $R_m$. We set the fluid Reynolds number and Hartmann number to be $R_e=1000,H_a = 10$, and five different values of $R_m=10, 100, 200, 400, 1000$ in Fig. 4. We observe that the magnetic field bends gradually as $R_m$ grows, which means the convection of magnetic field yields more and more notable influences. When the magnetic field is strong enough, for instance when $R_m=100, 200, 400, 1000$, the magnetic field form a big eddy at the center of the cavity which is quite similar to the corresponding fluid flow. This feature is called as the magnetic field is frozen inside the velocity field. Similar phenomenon had been reported in [28] as well.

6 Concluding Remarks

In this paper, we develop a fully decoupled, linear and unconditionally energy stable scheme for solving the incompressible MHD system, and prove the unconditional energy stability for the fully discrete scheme with the finite element approximations. We further rigorously establish the optimal error estimates for this scheme, and implement ample benchmark numerical experiments to demonstrate the stability and the accuracy in simulating some benchmark problems, including the Kelvin–Helmholtz shear instability and the magnetic-frozen phenomenon in the lid-driven cavity.