1 Introduction

Earthquakes, as one of the most recognized tragic natural disasters, are potentially highly destructive and unpredictable. The statistics of human losses and enormous financial casualties induced by earthquakes signify the importance of risk assessment and evaluation of the effect of seismic forces on foundations failure and its corresponding severe damage to superstructures. Hence, the attention of many researchers has been garnered to the problem of seismic bearing capacity of shallow foundations. To this end, proposing novel solutions to mitigate risks and casualties, implementation of more accurate analytical and numerical analysis methods to evaluate the key parameters contributing to the seismic bearing capacity assessment have been targeted accordingly. Furthermore, consideration of more realistic problem conditions involving seismic excitations, soil strength profiles, third dimension effect of the problem, and evaluation of the effects of body and surface waves excitations on foundation failure have been covered.

The simplicity and capability of the pseudo-static scheme of analysis associated with different methods of analysis such as limit equilibrium method (LEM), bound theorems of limit analysis, stress characteristics as well as numerical analysis to take into account seismic forces make it more favorable than the pseudo-dynamic loading consideration to investigate the seismic bearing capacity of shallow foundations. The study of Meyerhof (1963) is among the first documented uses of the pseudo-static approach to capture the effect of seismic forces on the ultimate limit load of shallow foundations. In these studies, the effects of seismic forces on the soil mass, i.e. inertia forces of the soil media, were neglected and the seismic forces were only applied by an additional inclination angle to the gravity forces of superstructures. However, innumerable numerical and experimental studies showed that seismic forces admittedly have great impacts on the soil properties and inertia of soil mass. Consequently, the ultimate load of the shallow foundations is strongly dependent on the assumption of seismic excitation effects on the soil media.

Over the several recent decades, many researchers studied the problem of seismic bearing capacity of shallow foundations by taking into account pseudo-static earthquake coefficients of acceleration for both superstructures and soil mass by the implementation of different numerical and analytical methods including limit equilibrium, bound theorem of limit analysis, and stress characteristics method. Budhu and Al-Karni (1993), Paolucci and Pecker (1997), Soubra (1999), Kumar and Rao (2002), Askari and Farzaneh (2003), Kumar and Kumar (2003), Choudhury and Rao (2005), Yamamoto (2010), Kumar and Chakraborty (2013), Chakraborty and Kumar (2015), Ghosh and Debnath (2017), Foroutan Kalourazi et al. (2019), Haghsheno et al. (2020), Nouzari et al. (2021), and Izadi et al. (2021) are among many on this problem.

Despite its robustness, the pseudo-static approach is not able to capture the effect of excitation time duration, excitation frequency, and phase differences. By subjecting the entire soil mass to the same value of accelerations, the pseudo-static method essentially assumes the magnitude and phase of the accelerations to be invariant through the soil body. By taking into account the influences of both shear and primary waves, the amplification of seismic excitations, and the period of lateral shaking, the pseudo-dynamic approach was firstly proposed by Steedman and Zeng (1990) and extended by Choudhury and Nimbalkar (2005). Over recent years, the problems of bearing capacity of shallow foundations (Ghosh 2008; Ghosh and Choudhury 2011; Saha and Ghosh 2015; Zhou et al. 2016; Saha and Ghosh 2017; Kurup and Kolathayar 2018; Izadi et al. 2019b; Pakdel et al. 2021) and stability of retaining walls (Ghosh and Kolathayar 2011; Bellezza 2014, 2015; Pain et al. 2015; Fathipour et al. 2021) in conjunction with different methods of analysis and application of the pseudo-dynamic approach have received considerable attention.

Although numerous studies were reported on the problem of seismic bearing capacity of shallow foundation via different methods of analysis and different assumptions for capturing the effects of the earthquake excitation, there seem to be little if any published evidence on the influence of the Love wave propagation on foundation failure. Moreover, an additional difficulty arises from the fact that the Love wave velocity is frequency-dependent in nature.

In this study, the limit equilibrium method (LEM) associated with the 3D Coulomb failure mechanism is used to investigate the influence of the Love wave propagation on the seismic bearing capacity of shallow footings. Despite all the other studies on the effects of wave propagation on bearing capacity, the problem under consideration is assumed to be 3D. In fact, the body and surface waves propagate in any arbitrary direction and the bearing capacity of shallow footings strongly depends on the ratio of the wavelength to the dimensions of the foundation. Furthermore, the Love wave cycles along the footing length/ width and exerts excitations transversely. To overcome these concerns, the 3D Coulomb failure mechanism was adopted and the most critical case, the direction of the Love wave along the footing length and particle’s oscillation perpendicular to the train of Love wave, was considered.

2 Love Wave Propagation

Body waves including primary and shear waves as well as Rayleigh waves propagate through homogeneous elastic half-space. For a soil profile consisting of at least a semi-infinite medium and a soil layer, primary and shear waves may be reflected and partly transmitted through the shared interfaces between the layers. In this case, the successive reflections of SH waves from the interface of the thin soft layer and the semi-infinite stiffer soil as shown in Fig. 1a may lead to generate Love wave (Kramer 1996; Verruijt 2010). In other words, the necessary condition to observe Love waves is that a low-velocity layer is underlain by a high-velocity half-space. The Love waves are indeed resultant of interference of shear waves in the surficial layer and are often described as SH-waves trapped in the surface layer.

Fig. 1
figure 1

a Generation of the Love wave by successive reflections of SH-wave in a surficial layer, b Love wave propagation and generated transverse particle motion

Full size image

The particle motion of a Love wave, representing a transverse wave, is a side-to-side (back and forth) motion perpendicular to the main direction of the wave propagation without either vertical or longitudinal components as shown in Fig. 1b (Love 1927). In geotechnical earthquake engineering and seismology, the Love waves are known as surface seismic waves that cause horizontal shifting of the surface ground during the action of an earthquake dispersing as a long train of waves to the substantial distances from the source. As the amplitude of Love waves decays more slowly than body waves, these waves lead to strong ground motion and consequently to strong seismic motions even for earthquakes originated from distant sources (Shearer 2009).

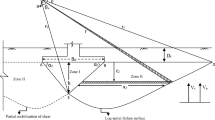
For a surficial layer of thickness H, shear modules of G1 and density of ρ1 overlying a homogenous half-space with shear modulus and density of G2 and ρ2, respectively, as shown in Fig. 2, the love wave travels in the + x direction with the particles oscillating in the \(\pm \,y\) directions, perpendicular to the plane of wave propagation (x–z). The particle displacement can then be described as the basic form of Eq. (1).

$$v(x,z,t) = V(z)e^{{i(k_{l} x - \omega t)}}$$
(1)

where v is the particle displacement in the y-direction, V(z) is the amplitude describing the variation of the particle displacement with depth, kl is the Love wave number, ω is the angular frequency and t is the time of vibration (Kramer 1996).

Fig. 2
figure 2

Schematic illustration of the soil profile, shallow foundation with corresponding failure mechanism, and Love-wave propagation in the soil layer

Full size image

Note that the third dimension of the failure surface is formed in the out-of-plane direction and the footing length, as illustrated schematically in Fig. 2, is assumed sufficiently long to assure plane strain condition in the out-of-plane direction. Therefore, the foundation width is assumed to lie in the particles’ transverse displacement direction.

According to Aki and Richards (1980) and Kramer (1996), while satisfying the traction-free surface assumption atop, the particle displacement can be found by:

$$\begin{gathered} v(x,z,t) = 2A_{1} \cos \left[ {\omega \left( {\frac{1}{{v_{s1}^{2} }} - \frac{1}{{v_{l}^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} z} \right]e^{{^{{i(k_{{_{l} }} x - \omega t)}} }} {\text{ for 0}} \le {\text{z}} \le {\text{H}} \hfill \\ \hfill \\ \end{gathered}$$
(2)
$$v(x,z,t) = 2A_{1} \cos \left[ {\omega \left( {\frac{1}{{v_{s1}^{2} }} - \frac{1}{{v_{l}^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} H} \right]\exp \left[ { - \omega \left( {\frac{1}{{v_{l}^{2} }} - \frac{1}{{v_{s2}^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} (z - H)} \right]e^{{^{{i(k_{l} x - \omega t)}} }} {\text{ for z}} \ge {\text{H}}$$
(3)

where vsi and vl are the shear wave velocity in each layer (i = 1, 2) and Love wave velocity, respectively. As seen from Eqs. (2) and (3), the variation of the particle displacement amplitude of the Love wave with depth is harmonic and exponential for the surface layer and the half-space, respectively, decaying readily by getting away from the surface as shown schematically in Fig. 3. Surface waves such as the Love wave, decay more slowly with distance than body waves do. Therefore, the effect of the surface waves is more eminent in comparison to the body waves in structures and superstructures afar. Hence, Love waves could be arguably the most destructive waves in areas that are far away from the focus of an earthquake. The Love wave velocity is admitted to be dependent on the excitation frequency, the surface layer thickness, and the shear moduli of both layers as well as the shear wave velocities of each layer as shown in Eq. (4a). It is observed that the Love waves propagate at higher velocities with low frequencies which is limited to shear wave velocity of the stiffer underlying half-space. By increasing the excitation frequency, the Love waves are more inclined to propagate with the shear wave velocity of the softer surface layer, i.e. vs1  < vl  < vs2.

$$\begin{gathered} \tan \left[ {\omega H\left( {\frac{1}{{v_{s1}^{2} }} - \frac{1}{{v_{l}^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} } \right] = \frac{{G_{2} }}{{G_{1} }}\frac{{\sqrt {\frac{1}{{v_{l}^{2} }} - \frac{1}{{v_{s2}^{2} }}} }}{{\sqrt {\frac{1}{{v_{s1}^{2} }} - \frac{1}{{v_{l}^{2} }}} }} \hfill \\ \hfill \\ \end{gathered}$$
(4a)
Fig. 3
figure 3

Variation of the particle displacement amplitude with depth

Full size image

In principle, the Love wave velocity can be found both graphically and numerically for given values of frequency, surficial layer thickness, shear modules ratio, and shear wave velocities of the surficial layer and semi-infinite half-space. In the graphical scheme of analysis, a new variable (X) was defined, and the Love wave velocity equation was re-written in the following form of Eq. (4b).

$$\begin{gathered} \tan \left[ {\omega X} \right] = \frac{{G_{2} \sqrt {\frac{{H^{2} }}{{v_{l}^{2} }} - \frac{{H^{2} }}{{v_{s2}^{2} }}} }}{{G_{1} X}} \hfill \\ \hfill \\ \end{gathered}$$
(4b)

where

$$X = H\sqrt {\frac{1}{{v_{s1}^{2} }} - \frac{1}{{v_{l}^{2} }}}$$

It is worth noting that, as the Love wave velocity is always more than the shear wave velocity of the surficial layer, the X variable is always positive. In order to find the Love wave velocity, the left- and right-hand sides of Eq. (4b) were sketched simultaneously. For a particular value of ω and a different value of X, the left-hand side (LHS) of Eq. (4b) could vary from − ∞ to + ∞, while the right-hand side (RHS) of Eq. (4b) is always positive within the interval of interest. Each intersection between the left-hand side and the right-hand side with respect to the constraint of vs1  <  vl  <  vs2 corresponds to a real value of vl. For real values of vl boundary conditions are satisfied for the given value of ω. Another worth mentioning point is that there are several possible solutions (called modes) for a given value of X which are dependent on the ω values. The lowest Love wave velocity corresponds to the fundamental mode while the other solutions are called overtones. Figure 4 shows schematically the Love wave solution by the graphical approach (Verruijt 2010).

Fig. 4
figure 4

Variation of the Love wave velocity with frequency

Full size image

Another approach which is followed in this study is the numerical scheme of analysis. For this purpose, by factorizing the Love wave velocity from the right and left-hand sides of Eq. (4a), substituting Eqs. (5)–(7) in Eq. (4a), and after simplification, the Love wave velocity equation can be expressed as Eq. (8).

$$k_{l} = \frac{\omega }{{v_{l} }} = \frac{2\pi }{\lambda }$$
(5)
$$\overline{c} = \frac{{v_{s2} }}{{v_{s1} }}$$
(6)
$$G_{i} = \rho v_{si}^{2}$$
(7)
$$\begin{gathered} \tan \left( {\frac{2\pi H}{\lambda }\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right) = \tan \left( {k_{l} H\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right) = \frac{{\rho_{2} }}{{\rho_{1} }}\overline{c}^{2} \frac{{\sqrt {1 - \frac{1}{{\overline{c}^{2} }}\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} } }}{{\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} }} \hfill \\ \hfill \\ \end{gathered}$$
(8)

where λ is the Love wavelength. Now for any arbitrary value of the dimensionless frequency of the Love wave (klH), shear waves velocity ratio (\(\overline{c }\)), and density ratio (ρ2/ρ1), the ratio of Love wave velocity to the shear wave velocity of the surficial layer (vl/vs1) can be yielded numerically. By applying this formulation, a specific value can be found for the ratio of the Love wave velocity to the shear wave velocity of the surficial layer (vl/vs1) for fixed and particular values of the Love wave non-dimensional frequency (klH), the shear waves velocity ratio (\(\overline{c }\)), and the density ratio (ρ2/ρ1).

3 Problem Definition and Assumptions

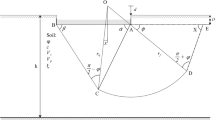
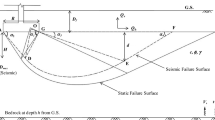
This study aims to evaluate the effect of the Love wave propagation on the seismic bearing capacity of a shallow foundation which is shown in Fig. 5. A shallow strip footing of width B is placed at a depth of Df, over soil with the unit weight of γ and shear strength parameters friction angle, φ and cohesion, c, with an underlying bedrock stretching horizontally to infinity and located at a depth of H to the footing. An idealized uniform pressure is assumed to simulate the effect of the surcharge. Moreover, the resistive effect of the soil overlying the foundation top is neglected. Following the study of Richards et al. (1993, 1994), the efficiency of the Coulomb failure mechanism as a viable alternative to the general shear failure mechanism was proven by Ghosh (2008), Ghosh and Debnath (2017), Saha and Ghosh (2017), and Izadi et al. (2019a) in the case of calculation of seismic bearing capacity. The simplified Coulomb failure mechanism consists of an active wedge (ΔABC) directly beneath the foundation, a passive wedge (ΔBCD) adjacent to the active wedge, and an interface wall between the active and passive zones (line BC) as shown in Fig. 5. In the simplified Coulomb failure mechanism, the transitional shear fan zone is not eliminated; instead, it is merged with the passive wedge due to asymmetric seismic loading condition as pointed out by Izadi et al. (2019a). This can be easily deduced by comparing different parts of Fig. 6. It is noteworthy that the implementation of the Prandtl failure mechanism and consequently the simplified Coulomb failure mechanism was widely proven to be more accurate when the soil-foundation interface was perfectly rough. In the case of smooth soil-foundation interface, the Hill mechanism will be used to calculate bearing capacity of foundations (Fang 2013).

Fig. 5
figure 5

Seismic Coulomb failure mechanism adopted in the current study

Full size image
Fig. 6
figure 6

Schematic representations of the slip lines; a static condition; and b seismic condition (Richards et al. 1994; Izadi et al. 2019a)

Full size image

The borders of active and passive zones make the inclination angles of α and β with horizontal surface, respectively. PA is the active thrust pushing the adjacent passive zone and PP is the passive thrust, resisting the active wedge as shown in Fig. 7. The active and passive lateral earth pressures are equated to satisfy equilibrium conditions and should be found in a way that led to the more conservative ultimate load P. The soil shear strength parameters were adopted to be independent of the occurrence of an earthquake. No water table was considered and the critical failure mechanism is solely placed in the surficial layer which is schematically shown in Fig. 5.

Fig. 7
figure 7

Forces acting on the failure wedges

Full size image

In this study, the joint bearing capacity factors (Nγeq) considering the simultaneous actions of all the contributors including soil cohesion, soil unit weight, and surcharge are calculated by limit equilibrium method. Despite the fact that individual consideration of the different contributors and their superposition may lead to a more conservative solution in comparison to the simultaneous action of all the contributors as discussed by Jamshidi Chenari et al. (2018), a single failure mechanism will be invoked in the course of calculations. The formulation of modified pseudo-dynamic bearing capacity as introduced by Ghosh and Kolathayar (2011), and Bellezza (2014, 2015) was extended for the case of the Love wave propagation. A parametric analysis was also conducted to evaluate the influence of the most effective parameters such as the soil internal friction angle (φ), the interface wall friction angle (δ), the earthquake coefficient of acceleration (kh), and the Love wave non-dimensional frequency (klH).

4 Method of Analysis

The seismic bearing capacity formulation to capture the effect of the Love wave propagation was derived using the limit equilibrium method (LEM) associated with the two-wedge Coulomb failure mechanism. As stated earlier, the propagation of the Love wave solely induces horizontal particle motion in the direction perpendicular to the wave traveling course. In order to calculate the inertia forces induced by the seismic excitation, the seismic acceleration due to the Love wave-induced particle motion should be calculated. According to Eq. (2), the horizontal acceleration field for the Love wave can be written as Eq. (9).

$$a(x,z,t) = \frac{{\partial^{2} v}}{{\partial t^{2} }} = - 2A_{1} \omega^{2} \cos \left[ {\omega \left( {\frac{1}{{v_{s1}^{2} }} - \frac{1}{{v_{l}^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} z} \right]e^{{^{{i(k_{{_{l} }} x - \omega t)}} }} \,$$
(9)

Assuming a thin element with the thickness of dz at depth z in the active wedge as shown in Fig. 7, the horizontal inertia force acting on the active wedge can be obtained through integration within the failure mechanism depth.

$$Q_{hA} (t) = \frac{{k_{h} \gamma \left[ {\cos \left( {k_{l} H\frac{B\tan \alpha }{H}\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right) - 1} \right]\left[ {\sin (\omega t - k_{l} L) - \sin (\omega t)} \right]}}{{k_{l}^{3} \tan \alpha \cos \left[ {k_{l} H\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right]\left( {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} \right)}} \,$$
(10)

The total horizontal inertia force acting on the passive wedge can be written in the form of Eq. (11).

$$Q_{hP} (t) = \frac{{k_{h} \gamma \left[ {\cos \left( {k_{l} H\frac{B\tan \alpha }{H}\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right) - 1} \right]\left( {1 + \frac{{2D_{f} }}{B\tan \alpha }} \right)\left[ {\sin (\omega t - k_{l} L) - \sin (\omega t)} \right]}}{{k_{l}^{3} \tan \beta \cos \left[ {k_{l} H\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right]\left( {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} \right)}} \,$$
(11)

Equilibrium conditions enforce the following equations on the forces applied to the active wedge:

$$\mathop {\sum H }\limits^{{\mathop{\longrightarrow}\limits^{{}}}} = 0$$
(12)
$$P_{A} L\cos \delta = R_{A} L\sin \left( {\alpha - \varphi } \right) + Q_{hA} - c BL$$
(12a)
$$\uparrow \sum V = 0$$
(13)
$$P_{A} L \sin \delta = - R_{A} L\cos \left( {\alpha - \varphi } \right) + W_{A} - 2cBL \tan \alpha + p_{L} BL$$
(13a)

where c is soil cohesion, RA and PA are the resultant force acting on the slip surfaces and the total seismic active resistance force, respectively, and WA is the weight of the active wedge as follows:

$$W_{A} = \frac{1}{2}\gamma B^{2} L \tan \alpha$$
(14)

After simplification and manipulation of Eqs. (12) and (13), the active force (PA) can be found as Eq. (15):

$$\begin{aligned} P_{A} = & \frac{{Q_{hA} \cos \left( {\alpha - \varphi } \right)}}{{L\cos \left( {\alpha - \varphi - \delta } \right)}} + \frac{{W_{A} \sin \left( {\alpha - \varphi } \right)}}{{L\cos \left( {\alpha - \varphi - \delta } \right)}} + p_{L} B\frac{{ \sin \left( {\alpha - \varphi } \right)}}{{\cos \left( {\alpha - \varphi - \delta } \right)}} \\ & - c B\left\{ {\frac{{\cos \left( {\alpha - \varphi } \right)}}{{\cos \left( {\alpha - \varphi - \delta } \right)}} + \frac{{2 \tan \alpha \sin \left( {\alpha - \varphi } \right)}}{{\cos \left( {\alpha - \varphi - \delta } \right)}}} \right\} \\ \end{aligned}$$
(15)

Similarly, equilibrium conditions enforce the following equations on the forces applied to the passive wedge:

$$\mathop {\sum H }\limits^{{\mathop{\longrightarrow}\limits^{{}}}} = 0$$
(16)
$$P_{p} L\cos \delta = R_{p} L\sin \left( {\beta + \varphi } \right) - Q_{hP} + c BL\frac{\tan \alpha }{{\tan \beta }}$$
(16a)
$$\uparrow \sum V = 0$$
(17)
$$P_{p} L\sin \delta = R_{p} L\cos \left( {\beta + \varphi } \right) - W_{p} - 2cBL \tan \alpha$$
(17a)

where WP is the weight of the passive wedge defined as

$$W_{P} = \frac{{\gamma_{e} }}{2} \frac{{B^{2} L\tan^{2} \alpha }}{\tan \beta }$$
(18)

After simplification and manipulation of Eqs. (16) and (17), the total passive force (Pp) is obtained as:

$$\begin{aligned} P_{p} = & - \frac{{Q_{hP} \cos \left( {\beta + \varphi } \right)}}{{L\cos \left( {\delta + \beta + \varphi } \right)}} + \frac{{W_{p} \sin \left( {\beta + \varphi } \right)}}{{L\cos \left( {\delta + \beta + \varphi } \right)}} \\ & + c B\left\{ {\frac{{\tan \alpha \cos \left( {\beta + \varphi } \right)}}{{\tan \beta \cos \left( {\delta + \beta + \varphi } \right)}} + \frac{{2 \tan \alpha \sin \left( {\beta + \varphi } \right)}}{{\cos \left( {\delta + \beta + \varphi } \right)}}} \right\} \\ \end{aligned}$$
(19)

As previously mentioned, PP and PA are equated to satisfy the equilibrium condition. Therefore, the ultimate limit load of PL can be found:

$$\begin{aligned} p_{L} B\frac{{ \sin \left( {\alpha - \varphi } \right)}}{{\cos \left( {\alpha - \varphi - \delta } \right)}} = & - \frac{{Q_{hA} \cos \left( {\alpha - \varphi } \right)}}{{L\cos \left( {\alpha - \varphi - \delta } \right)}} - \frac{{Q_{hP} \cos \left( {\beta + \varphi } \right)}}{{L\cos \left( {\delta + \beta + \varphi } \right)}} \\ & + \frac{{W_{p} \sin \left( {\beta + \varphi } \right)}}{{L\cos \left( {\delta + \beta + \varphi } \right)}} - \frac{{W_{A} \sin \left( {\alpha - \varphi } \right)}}{{L\cos \left( {\alpha - \varphi - \delta } \right)}} \\ & + c B\left\{ {\frac{{\tan \alpha \cos \left( {\beta + \varphi } \right)}}{{\tan \beta \cos \left( {\delta + \beta + \varphi } \right)}} + \frac{{2 \tan \alpha \sin \left( {\beta + \varphi } \right)}}{{\cos \left( {\delta + \beta + \varphi } \right)}} + \frac{{\cos \left( {\alpha - \varphi } \right) + 2 \tan \alpha \sin \left( {\alpha - \varphi } \right)}}{{\cos \left( {\alpha - \varphi - \delta } \right)}}} \right\} \\ \end{aligned}$$
(20)

After simplifying and manipulation the Eq. (20), the equivalent seismic bearing capacity factor (Nγeq = 2pL/γB) capturing the effect of the Love wave propagation can be found as Eq. (21).

$$\begin{aligned} N_{{\gamma_{eq} }} = & \left[ {\frac{{\sin \left( {\beta + \varphi } \right)\cos \left( {\alpha - \varphi - \delta } \right)\tan^{2} \alpha }}{{\sin (\alpha - \varphi )\cos \left( {\delta + \beta + \varphi } \right)\tan \beta }}\left( {1 + \frac{{2D_{f} }}{B\tan \alpha }} \right) - \tan \alpha } \right] \\ & - \left[ {\frac{{2k_{h} \left[ {\cos \left( {k_{l} H\frac{B\tan \alpha }{H}\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right) - 1} \right]\left[ {\sin \left( {2\pi (\frac{t}{T} - \frac{L}{\lambda })} \right) - \sin (\frac{2\pi t}{T})} \right]}}{{\left( {\frac{2\pi B}{\lambda }} \right)^{2} \left( {\frac{2\pi L}{\lambda }} \right)\tan \alpha \cos \left[ {k_{l} H\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right]\left( {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} \right)\tan (\alpha - \varphi )}}} \right] \\ & - \left[ {\frac{{2k_{h} \left[ {\cos \left( {k_{l} H\frac{B\tan \alpha }{H}\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right) - 1} \right]\left( {1 + \frac{{2D_{f} }}{B\tan \alpha }} \right)\left[ {\sin \left( {2\pi (\frac{t}{T} - \frac{L}{\lambda })} \right) - \sin (\frac{2\pi t}{T})} \right]}}{{\left( {\frac{2\pi B}{\lambda }} \right)^{2} \left( {\frac{2\pi L}{\lambda }} \right)\tan \beta \cos \left[ {k_{l} H\sqrt {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} } \right]\left( {\left( {\frac{{v_{l} }}{{v_{s1} }}} \right)^{2} - 1} \right)}}} \right]\left( {\frac{{ \cos \left( {\beta + \varphi } \right)\cos \left( {\alpha - \varphi - \delta } \right)}}{{\sin (\alpha - \varphi )\cos \left( {\delta + \beta + \varphi } \right)}}} \right) \\ & + \frac{{2c \cos \left( {\alpha - \varphi - \delta } \right)}}{\gamma B\sin (\alpha - \varphi )}\left\{ \begin{gathered} \frac{{\tan \alpha \cos \left( {\beta + \varphi } \right)}}{{\tan \beta \cos \left( {\delta + \beta + \varphi } \right)}} + \frac{{2 \tan \alpha \sin \left( {\beta + \varphi } \right)}}{{\cos \left( {\delta + \beta + \varphi } \right)}} \hfill \\ + \frac{{\cos \left( {\alpha - \varphi } \right) + 2 \tan \alpha \sin \left( {\alpha - \varphi } \right)}}{{\cos \left( {\alpha - \varphi - \delta } \right)}} \hfill \\ \end{gathered} \right\} \\ \end{aligned}$$
(21)

The pseudo-dynamic bearing capacity factor depends on the soil properties (c, φ, γ), interface wall friction angle (δ), geometric parameters of the foundation (B, L, Df), the corresponding failure mechanism (α, β) and the surficial soil layer (H), the seismic coefficient of acceleration (kh), the dimensionless frequency of the Love wave (klH), the ratio of the Love wave velocity to the shear wave velocity of the surficial layer (vl/vs1), the dimensionless wavelength ratios (B/λ, L/λ) and the dimensionless time (t/T). Note that the ratio of the Love wave velocity to the shear wave velocity of the surficial layer (vl/vs1) is also a function of the dimensionless frequency of the Love wave (klH), the shear wave velocity ratio (\(\overline{c }\)), and the density ratio (ρ2/ρ1) as stated before. Steedman and Zeng (1990) stated that for most of the earthquakes, the dominant earthquake periods vary between 0.2 and 0.5 s and the value of H/TVs has the range of 0.2–0.5 while Ghosh (2008) and Saha and Ghosh (2015) proposed a wider range of 0.3–0.6 for H/TVs. As the Love wave velocity is higher than the shear wave velocity of the surficial layer, the proposed range of Steedman and Zeng (1990) is deemed more appropriate.

5 Result and discussion

The results are reported for practical ranges of parameters as φ = 20–40°, δ/φ = 0–1, 2c/γB = 0–0.5, Df/B = 0.25–1, kh = 0–0.3, and different ratios of the Love wave velocity to the shear wave velocity of the surficial layer (vl/vs1). The solutions were found through an optimization process with the best combinations of geometry variables and time parameter which led to the least limit load. The objective function of this study (joint bearing capacity factor), input parameters of the Love wave velocity and the constraints of the objective function are as follow:

Input parameter of the Love wave velocity, i.e. Equation (8);

$$\frac{H}{\lambda },\overline{c},\frac{{\rho_{2} }}{{\rho_{1} }}$$

The output of Eq. (8):

$$\frac{{v_{l} }}{{v_{s1} }}$$

Input parameters of the bearing capacity factor, i.e. Equation (21):

$$\frac{c}{\gamma B},\varphi ,\delta ,k_{l} H,\frac{H}{\lambda },\frac{{D_{f} }}{B},\frac{B}{L,H},k_{h} ,\frac{{v_{l} }}{{v_{s1} }}$$

where

$$N_{{\gamma_{eq} }} = f\left( {\frac{c}{\gamma B},\varphi ,\alpha ,\beta ,\delta ,k_{l} H,\frac{H}{\lambda },\frac{{D_{f} }}{B},\frac{B}{L,H},k_{h} ,\frac{t}{T},\frac{{v_{l} }}{{v_{s} }},\overline{c},\frac{{\rho_{2} }}{{\rho_{1} }}} \right)$$
(22)
$$\begin{gathered} {\text{Minimize }}N_{{\gamma_{eq} }} \hfill \\ {\text{Variable parameters: }}\alpha {,}\beta {,}\frac{t}{T} \hfill \\ {\text{Subjected to: 0}}^{o} \le \alpha \le {90}^{o} \hfill \\ { 0}^{o} \le \beta \le {90}^{o} \hfill \\ \, N_{{\gamma_{eq} }} \ge 0 \hfill \\ \end{gathered}$$

The results of equivalent static bearing capacity factors were reported in Table 1. For the sake of validation of the computation procedure, a comparison was made between the results of the current study and Saha and Ghosh (2017). It should be noted that in the scarcity of any solution for pseudo-dynamic bearing capacity of shallow foundations with consideration of the effect of the Love wave on seismic bearing capacity, only the static bearing capacity factors were comparable to validate the results of the current findings. It is worth mentioning that the dimensionless H/B and L/B ratios were maintained at 10, shear waves velocity ratio was assumed \(\overline{c}\)=5 and density ratio of ρ2/ρ1 = 1.5 was selected to find the ratio of the Love wave velocity to the shear wave velocity of the surficial layer (Fig. 8).

Table 1 Static bearing capacity factor (Nγeq)
Full size table
Fig. 8
figure 8

Validation of the equivalent bearing capacity factor with Saha and Ghosh (2017); a δ = 0, 2c/γB = 0; and b δ = φ/2, 2c/γB = 0.5

Full size image

The simultaneous actions of all contributors including, φ, δ/φ, 2c/γB, Df/B, and klH on the equivalent bearing capacity factors of shallow foundations are presented for different earthquake coefficients of accelerations in Tables 2, 3 and 4. In the following sections, the impact of each effective parameter is elaborated and discussed.

Table 2 Equivalent seismic bearing capacity factor (Nγeq) for kh = 0.1
Full size table
Table 3 Equivalent seismic bearing capacity factor (Nγeq) for kh = 0.2
Full size table
Table 4 Equivalent seismic bearing capacity factor (Nγeq) for kh = 0.3
Full size table

5.1 Soil Friction Angle Impact

Superimposed on Fig. 9 are the results of equivalent seismic bearing capacity factors for different Love wave acceleration coefficients and φ = 20–40°. In general, it is observed that the excitation induced by the Love wave propagation gives rise to a reduction in the seismic bearing capacity of shallow foundations. As expected, the soil with a higher internal friction angle has a higher range of the pseudo-dynamic bearing capacity factor. This is obvious as the bearing capacity coefficient Nγ varies exponentially with the internal friction angle. It is further observed that almost for all frequency levels the seismic bearing capacity decreases with the Love wave amplitude; however, when the frequency rises due to the reduced wavelength, out-of-plane inertia forces along the footing length counteract in integral form. This means that the seismic bearing capacity does not undergo changes with the Love wave propagation substantiated in form of the horizontal bearing capacity lines in Fig. 9 and also almost similar numbers corresponding to klH = 10 among Tables 2, 3 and 4.

Fig. 9
figure 9

Effect of the soil friction angle and Love wave acceleration coefficient on the equivalent seismic bearing capacity factor (δ = φ/2, 2c/γB = 0.25, and Df/B = 0.5)

Full size image

5.2 Interface Wall Friction Angle Impact

It can be seen from Fig. 10 that the equivalent seismic bearing capacity factor of a shallow foundation increases significantly with an increase of the wall interface friction angle. The values of the seismic bearing capacity factor of δ = φ/2 and δ = φ are relatively 2 and 4 times the seismic bearing capacity factor of the case when δ = 0, respectively. Similar to the impact of the soil internal friction angle, the effect of the Love wave excitation is more eminent for a lower frequency.

Fig. 10
figure 10

Effect of the interface wall friction angle and Love wave acceleration coefficient on the equivalent seismic bearing capacity factor (φ = 30°, 2c/γB = 0.25, and Df/B = 0.5)

Full size image

5.3 Embedment Depth Impact

As illustrated in Fig. 11, the footings with higher embedment depth ratio have a higher range of surcharge and passive resistance. Consequently, these increases raise the limit load sustained by the footings.

Fig. 11
figure 11

Effect of the embedment depth ratio and Love wave acceleration coefficient on the equivalent seismic bearing capacity factor (φ = 30°, δ = φ/2, and 2c/γB = 0.25)

Full size image

5.4 Soil Cohesion Impact

Figure 12 demonstrates the variation of the equivalent seismic bearing capacity factor for different values of the dimensionless cohesion factor. As the resisting forces acting on the slip surfaces of the assumed failure mechanism increase, the ultimate limit pressure and the equivalent bearing capacity factor increase, accordingly.

Fig. 12
figure 12

Effect of the dimensionless cohesion ratio and Love wave acceleration coefficient on the equivalent seismic bearing capacity factor (φ = 30°, δ = φ/2, and Df/B = 0.5)

Full size image

5.5 The Influence of the Love wavelength

The bearing capacity of shallow footings subjected to the Love wave propagations becomes more complicated if the wavelength is comparable with the foundation length. This means that the Love wave cycles along the footing length/width and exerts excitation transversely. Depending on the footing dimension along the propagation direction and the Love wavelength compared to it, the bearing capacity of the footing may be reduced or unaltered in some circumstances when the integral influence of the inertia forces becomes immaterial.

Incorporating this effect properly entails due adoption of a failure mechanism, which is relevant in three-dimension geometry. If plane strain condition is concerned, the most critical case is admittedly when the Love wave travels along the longer dimension. Even in such cases, the wavelength must be compared to the footing length. If the footing is infinitely long, the Love wave-induced inertia forces in the out-of-plane direction harmonically fluctuate across the footing length and this presumably yields counteracted destabilizing force, hence the bearing capacity may remain unchanged.

Figure 13 demonstrates the results of the pseudo-dynamic bearing capacity factor by capturing the effect of the Love wavelength. As seen in this figure, the seismic bearing capacity factor reaches the static bearing capacity factor by increasing the value of the non-dimensional frequency klH. In fact, by increasing the Love wave frequency, its wavelength diminishes and therefore due to the periodic nature of the assumed wave front, many harmonic cycles of the back and forth particle displacement along the direction of the wave propagation would have a neutralized influence. Hence, the net effect of the seismic excitation was negligible.

Fig. 13
figure 13

Variation of the seismic bearing capacity factor with the Love wave frequency for different seismic coefficients of acceleration and φ = 30°, δ = φ/2, and Df/B = 0.5, and 2c/γB = 0.25

Full size image

6 Summary and Conclusion

The equivalent seismic bearing capacity factor of shallow strip foundations in the presence of pseudo-dynamic earthquake accelerations induced by Love wave propagation has been evaluated by the limit equilibrium method (LEM). The equation of the particle displacement induced by the propagation of the Love wave was manipulated and the pseudo-dynamic bearing capacity formulation for shallow footings was extended to the three-dimensional Coulomb failure mechanism. The bearing capacity factor has been evaluated for the impacts of the most effective factors including geo-material properties, geometrical characteristics, and earthquake excitation frequency. The results of the equivalent bearing capacity of shallow foundations with three-dimensional Coulomb failure mechanism are in good agreement with those reported in the literature. Based on the results of this study, the equivalent seismic bearing capacity factor showed a direct relationship with soil strength parameters and non-dimensional frequency factor. The main conclusion of this study are:

  1. 1.

    An increase in shear strength parameters raises the resisting forces acting on the failure surface and consequently increases the ultimate limit load acting on the footing.

  2. 2.

    Love wave acceleration coefficient was found to have a decreasing impact on the bearing capacity of overlying shallow footing. The reduction of the limit load is more pronounced for higher values of the Love wave acceleration coefficient.

  3. 3.

    The influence of the Love wave propagation on the seismic bearing capacity of overlying shallow footings was found to be frequency-dependent. In other words, for lower non-dimensional frequency values, the bearing capacity of overlying shallow footings is expected to undergo reduction. Therefore, increasing the frequency of the Love wave, reflected in form of diminished wavelength, will in effect have less impact on bearing capacity reduction. This observation can be ascribed to the very fact that in the direction of wave propagation, depending on the Love wavelength relative to the footing length, phase shift will give rise to the out-of-plane displacement direction to shift in short distances; hence, yielding counteracted unbalancing forces.

  4. 4.

    The results showed that the seismic bearing capacity factor increased gradually with the frequency of the Love wave up to the value of the static bearing capacity factor.

  5. 5.

    It was observed that augmentation of the soil cohesion and foundation embedment depth would hamper the destructing effects of Love wave interaction with the overlying shallow footings.

  6. 6.

    The practical significance of the findings of the current study lies in the importance of the surface wave propagation on performance of shallow foundations. Indeed, in areas located close to earthquake sources, or even sometime the locations far away from the earthquake source, it might happen the surface waves to adversely influence our infrastructures. Thus, provision of charts, similar to those presented in the current study, would pave the way towards better understanding of the seismic soil-structure interactions.