Modified Pseudo-dynamic Bearing Capacity of Shallow Strip Footing Considering Fully Log-Spiral Passive Zone with Global Center

Abstract

The subject seismic bearing capacity is one of the most important aspects of geotechnical earthquake engineering. As the existing pseudo-dynamic method has certain drawbacks, this paper presents a modified pseudo-dynamic approach to evaluate the seismic bearing capacity of shallow strip footing resting on c–Φ soil considering the log-spiral failure mechanism. Since damping is present in all materials, more realistic results can be obtained by modeling the soil as a visco-elastic material. Here, the passive failure region is considered a fully log-spiral zone with an arbitrary location of the center of log-spiral. A single seismic bearing capacity coefficient (N_γe) is evaluated for the simultaneous resistance of unit weight, surcharge and cohesion, which is more practical to simulate the field failure mechanism. The effects of soil and seismic parameters are taken into account to evaluate the seismic bearing capacity of the foundation. The results obtained from the present analysis are presented in both tabular and graphical non-dimensional form. Results are thoroughly compared with the existing values in the literature, and a reasonably good agreement is found with the existing studies.

1 Introduction

Structural foundations are the substructure elements which transmit the structural load to the earth in such a way that the supporting soil is not overstressed and does not undergo deformations that would cause excessive settlement of the structure. The evaluation of bearing capacity of shallow strip footing under seismic loading condition is an important phenomenon in the earthquake-prone region. The pioneering works in determining the bearing capacity in static condition were done by Prandtl (1921), Terzaghi (1943), Meyerhoff (1957), (1963), Vesic (1973), Saran and Agarwal (1991) and many others. Geotechnical Earthquake researchers have investigated the problem of seismic bearing capacity of foundation using different mechanisms. The design of foundation in seismic areas needs special consideration compared to the static case. A number of researchers had analyzed the seismic bearing capacity of shallow strip footings using the pseudo-static approach with the help of different solution techniques such as the method of slices, limit equilibrium, method of stress characteristics an upper bound limit analysis. Budhu and Al-karni (1993), Dormieux and Pecker (1995), Soubra (1993), (1997), (1999), Richards et al. 1993, Choudhury and Subha Rao (2005), Kumar and Ghosh (2006) and many more had considered the effect of earthquake on the bearing capacity of a surface to a shallow strip footing under pseudo-static method using different approaches. IS 64031981 also gives a formulation of ultimate bearing capacity for different types of shallow foundations in different types of soils considering pseudo-static method. In the pseudo-static method, the dynamic nature of earthquake loading is considered in a very approximate way without taking any effect of time, frequency and soil amplification. To overcome this drawback, Ghosh (2008), Ghosh and Choudhury (2011), Saha and Ghosh (2014) give solutions of pseudo-dynamic bearing capacity of shallow strip footing considering the Coulomb failure mechanism using limit analysis method and limit equilibrium method, respectively. Later on, Saha and Ghosh (2015) analyzed pseudo-dynamic bearing capacity using composite failure mechanism.

But the current form of the pseudo-dynamic method does not satisfy the zero stress boundary condition at the ground surface, and it requires assuming an amplification factor as the acceleration value amplifies linearly toward the ground surface and does not consider energy dissipation as all materials have some damping properties. Considering visco-elastic behavior of soil material, Bellezza (2014) and Bellezza (2015) proposed a modified pseudo-dynamic method to analyze soil-retaining wall which overcomes all those mentioned limitations. Later on, Pain et al. (2015a, b) and Pain et al. (2016) carried out this modified pseudo-dynamic method to analyze the seismic stability of retaining wall, the uplift capacity of horizontal strip anchors and bearing capacity of strip footings, respectively. In this paper, an attempt is made to solve this problem of bearing capacity of shallow strip footing considering log-spiral failure mechanism using modified pseudo-dynamic approach. Here in this analysis, the active region is considered linear with the logarithmic passive region. Unlike the earlier assumption, the passive failure region is considered as fully log-spiral zone despite composite failure surface. In this passive region, the center of the log-spiral curve is arbitrarily chosen and the bearing capacity coefficient optimized for not only different radii angle subtended by those radii at the center but also for different locations of the center of the log-spiral curve. To evaluate the bearing capacity under seismic loading condition, the simultaneous resistance of unit weight, surcharge and cohesion are taken into account, and a single seismic bearing capacity coefficient (N_γe) is presented here. Results are presented in both tabular and graphical non-dimensional form including comparison with other available methods. Effects of wide range of variation of parameters such as soil friction angle (Φ), cohesion factor (2c/γB₀), depth factor (D_f/B₀), mobilization factors (m) and horizontal and vertical seismic accelerations (k_h, k_v) along with primary wave and shear wave velocity on the pseudo-dynamic bearing capacity coefficient (N_γe) have been studied.

2 Method of Analysis

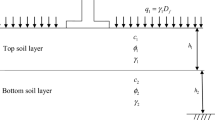
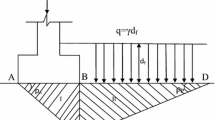
In this paper, an attempt has been made to give a formulation of modified pseudo-dynamic bearing capacity of a shallow strip footing resting on c–Φ soil using limit equilibrium method. The homogeneous soil of effective unit weight γ has Mohr–Coulomb characteristic c–Φ soil and can be considered as a rigid plastic body. Let us consider a shallow strip footing of width (B₀) resting below the ground surface at a depth of (D_f) over which a column load (P) acts vertically with the overburden pressure over the level BD acting as a surcharge (q = γD_f). The extension of the failure surface is shown in Fig. 1. ΔABE is the active zone just below the foundation. BDE is the log-spiral passive zone with the arbitrarily chosen center of the log-spiral curve at one side of the center line of the foundation. The soil on the other side of the center line gets partially mobilized, and this is characterized by a mobilization factor m. The shear strength of the soil is expressed as $\tau = mc + \sigma \tan \phi_{m}$, where $\phi_{m} = \tan^{ - 1} \left( {m\tan \phi } \right)$. It is a log-spiral failure mechanism that is defined by the angular parameters α₁, α₂, θ and β.

Fig. 1

Log-spiral failure mechanism

The radial log-spiral shearing zone BED is bounded by a log-spiral curve ED, where the equation for the curve in polar coordinates (r, θ_x) is $r = r_{0} e^{{\theta _{x} \tan \phi }}$. The center of this log-spiral ED is at an arbitrary point O, and the initial radius r₀ is the length of the line OE.

where $\overline{OE} = r_{0} = \frac{{B_{0} \sin \alpha_{1} \sin \alpha_{2} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)\left\{ {\sin \left( {\theta + \beta } \right) - e^{\theta \tan \phi } \sin \beta } \right\}}}$

$\alpha_{2} = \tan^{ - 1} \left( {m\tan \alpha_{1} } \right)$ and the final radius r_f (OD) is given by $r_{\text{f}} = r_{0} e^{{\theta \tan {\kern 1pt} \phi }}$.

Figure 2a and b shows the detailed free-body diagram of elastic zone ABE and log-spiral shear zone BED, respectively.

Fig. 2

a Elastic wedge. b Log-spiral zone

2.1 Wave Propagation Through Visco-Elastic Soil Media

In real materials, the elastic energy of a traveling wave is always converted to heat for which the amplitude of the wave decreases. In visco-elastic wave propagation, soils are usually modeled as Kelvin–Voigt solids. A purely elastic spring and a purely viscous dashpot are connected in parallel in this type of model. The resistance to shearing deformation is the sum of an elastic component and a viscous component in 2D Kelvin–Voigt model (Kramer 1996).

$$\tau = 2\gamma_{\text{s}} G + 2\eta \frac{{\partial \gamma_{\text{s}} }}{\partial t}$$

(1)

where τ is the shear stress, γ_s is shear strain, η is the soil viscosity, G is the shear modulus and t is the time.

The equation of motion of Kelvin–Voigt visco-elastic medium in vectorial form (Yuan et al. 2006) is given by

$$\rho \frac{{\partial^{2} U}}{{\partial t^{2} }} = \left\{ {\left( {\lambda + G} \right) + \left( {\eta_{ 1} + \eta_{\text{s}} } \right)\frac{\partial }{\partial t}} \right\}{\text{grad}}\left( \theta \right) + \left( {G + \eta_{\text{s}} \frac{\partial }{\partial t}} \right)\nabla^{2} U$$

(2)

where ρ is the soil density, U is the displacement vector of components u_x,u_y and u_z and $\theta = {\text{div}}\left( U \right)$.

Considering wave propagating along the z-axis in a Kelvin–Voigt homogeneous medium, a solution of Eq. (2) yields

$$\rho \frac{{\partial^{2} u_{\text{h}} }}{{\partial t^{2} }} = G\frac{{\partial^{2} u_{\text{h}} }}{{\partial z^{2} }} + \eta_{\text{s}} \frac{{\partial^{3} u_{\text{h}} }}{{\partial t\partial z^{2} }}$$

(3)

$$\rho \frac{{\partial^{2} u_{\text{v}} }}{{\partial t^{2} }} = \left( {\lambda + 2G} \right)\frac{{\partial^{2} u_{\text{v}} }}{{\partial z^{2} }} + \left( {\eta_{1} + 2\eta_{\text{s}} } \right)\frac{{\partial^{3} u_{\text{v}} }}{{\partial t\partial z^{2} }}$$

(4)

where $u_{\text{h}} = u_{x}$ and $u_{\text{v}} = u_{z}$.

For harmonic waves, solution of the equation of motion may be written as

$$u\left( {z,t} \right) = Ae^{{i\left( {\omega t - k^{*} z} \right)}} + Be^{{i\left( {\omega t + k^{*} z} \right)}}$$

(5)

where A and B are the constants that depend on boundary condition and k* is the complex wave number, i.e., $k^{*} = \omega \sqrt {\frac{\rho }{{G^{*} }}}$

G* = the complex shear modulus $= G\left( {1 + 2i\xi } \right)$

According to Kolsky (1963), k* is given by $k^{*} = k_{1} + ik_{2}$.

2.1.1 Expression of Horizontal Acceleration

For harmonic shaking,$\eta_{\text{s}} = \frac{{2G\xi_{\text{s}} }}{{\omega {}_{\text{s}}}}$, where ξ_s = damping ratio. Applying the boundary condition, i.e., shear stress at the free surface z = 0 and at a depth z = H the displacement coincides with the rigid base, $u_{\text{b}} = u_{\text{h0}} e^{i\omega t}$ solution of Eq. (5) yields

$$A = B = \frac{{u_{\text{h0}} }}{{2\cos \left( {k^{*} H} \right)}}$$

So,

$$u\left( {z,t} \right) = u_{\text{ho}} e^{i\omega t} \frac{{\cos \left( {k^{*} z} \right)}}{{\cos \left( {k^{*} H} \right)}}$$

(6)

Differentiating Eq. (5) twice w.r.t. time and defining $k_{\text{h}} g = - \omega_{\text{s}}^{2} u_{\text{h0}}$, the real part of horizontal acceleration is expressed as (Bellezza 2014)

$$a_{\text{h}} (z,t) = \frac{{k_{\text{h}} g}}{{c_{\text{s}}^{2} + s_{\text{s}}^{2} }}\left[ {\left( {c_{\text{s}} c_{\text{sz}} + s_{\text{s}} s_{\text{sz}} } \right)\cos (\omega_{\text{s}} t) + (s_{\text{s}} c_{\text{sz}} - c_{\text{s}} s_{\text{sz}} )\sin (\omega_{\text{s}} t)} \right]$$

(7)

2.1.2 Expression of Vertical Acceleration

For vertical harmonic motion, Eq. (4) can be written in a form similar to Eq. (3) provided that u_h, G and η_s are replaced by u_v, $E{}_{c} = \left( {\lambda + 2G} \right)$ and $\eta_{p} = \left( {\eta_{1} + 2\eta_{s} } \right)$, respectively. Similarly, applying the boundary condition, i.e., shear stress at the free surface z = 0 and at a depth, $z = h$ the displacement coincides with the rigid base, $u_{b} = u_{\text{v0}} e^{i\omega t}$ Then, the real part of vertical acceleration defining $k_{\text{v}} g = - \omega_{\text{p}}^{2} u_{\text{v0}}$ can be obtained as (Bellezza 2015)

$$a_{\text{v}} (z,t) = \frac{{k_{\text{v}} g}}{{c_{\text{p}}^{2} + s_{\text{p}}^{2} }}\left[ {\left( {c_{\text{p}} c_{\text{pz}} + s_{\text{p}} s_{\text{pz}} } \right)\cos (\omega_{\text{p}} t) + (s_{\text{p}} c_{\text{pz}} - c_{\text{p}} s_{\text{pz}} )\sin (\omega_{\text{p}} t)} \right]$$

(8)

2.2 Bearing Capacity Expression

2.2.1 Elastic Wedge

The forces acting on the wedge include uniformly distributed total column load P on AB; horizontal and vertical inertia forces (Q_h1 and Q_v1) are acting at the center of ΔABE. Active earth pressure P_A and cohesion c are acting on the side BE, whereas mobilized cohesion c_m$\left( {c_{m} = mc} \right)$ and mobilized active earth pressure P_m are acting on the face of AE, respectively.

The mass of a thin element of the elastic wedge at depth z₁ (Fig. 2a) is

$$m\left( {z_{1} } \right) = \frac{\gamma }{g}\left( {\cot \alpha_{1} + \cot \alpha_{2} } \right)\left( {h - z_{1} } \right){\text{d}}z_{1}$$

(9)

where$h = \frac{{B_{0} \sin \alpha_{1} \sin \alpha_{2} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}}$and weight of the wedge ABE,

$$W_{1} = \int\limits_{0}^{h} {m\left( {z_{1} } \right) \cdot g = } \frac{\gamma }{2}B_{0}^{2} \frac{{\sin \alpha_{1} \sin \alpha_{2} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}}$$

(10)

If the base of the foundation is subjected to a harmonic horizontal seismic acceleration of amplitude k_hg at any depth z₁ and time t, below the base of the foundation, the total horizontal inertia force acting within the elastic zone (Fig. 2a) can be expressed as follows:

$$\begin{aligned} Q_{\text{h1}} = & \int\limits_{0}^{h} {m\left( {z_{1} } \right)} a_{\text{h}} \left( {z_{1} ,t} \right){\text{d}}z_{1} \\ = & \frac{{\gamma k_{\text{h}} h^{2} \left( {\cot \alpha_{1} + \cot \alpha_{2} } \right)}}{{\left( {c_{\text{s}}^{2} + s_{\text{s}}^{2} } \right)\left( {y_{\text{s1}}^{2} + y_{\text{s2}}^{2} } \right)^{2} }} \\ & \left[ \begin{aligned} \left( {c_{\text{s}} \cos \omega t + s_{\text{s}} \sin \omega t} \right)\left\{ {2y_{\text{s1}} y_{\text{s2}} \sin y_{\text{s1}} \sinh y_{\text{s2}} - \left( {y_{\text{s1}}^{2} - y_{\text{s2}}^{2} } \right)\left( {\cos y_{\text{s1}} \cosh y_{\text{s2}} - 1} \right)} \right\} \hfill \\ + \left( {s_{\text{s}} \cos \omega t - c_{\text{s}} \sin \omega t} \right)\left\{ {2y_{\text{s1}} y_{\text{s2}} \left( {\cos y_{\text{s1}} \cosh y_{\text{s2}} - 1} \right) + \left( {y_{\text{s1}}^{2} - y_{\text{s2}}^{2} } \right)\sin y_{\text{s1}} \sinh y_{\text{s2}} } \right\} \hfill \\ \end{aligned} \right] \\ \end{aligned}$$

(11)

Similarly, as horizontal inertia force, the vertical inertia force acting within the elastic zone (Fig. 2a) can be expressed as follows:

$$\begin{aligned} Q_{\text{v1}} = & \int\limits_{0}^{h} {m\left( {z_{1} } \right)} a_{v} \left( {z_{1} ,t} \right){\text{d}}z_{1} \\ = & \frac{{\gamma k_{\text{v}} h^{2} \left( {\cot \alpha_{1} + \cot \alpha_{2} } \right)}}{{\left( {c_{\text{p}}^{2} + s_{\text{p}}^{2} } \right)\left( {y_{\text{s1}}^{2} + y_{\text{s2}}^{2} } \right)^{2} }} \\ & \left[ \begin{aligned} \left( {c_{\text{p}} \cos \omega t + s_{\text{p}} \sin \omega t} \right)\left\{ {2y_{\text{p1}} y_{\text{p2}} \sin y_{\text{p1}} \sinh y_{\text{p2}} - \left( {y_{\text{p1}}^{2} - y_{\text{p2}}^{2} } \right)\left( {\cos y_{\text{p1}} \cosh y_{\text{p2}} - 1} \right)} \right\} \hfill \\ + \left( {s_{\text{p}} \cos \omega t - c_{\text{p}} \sin \omega t} \right)\left\{ {2y_{\text{p1}} y_{\text{p2}} \left( {\cos y_{\text{p1}} \cosh y_{\text{p2}} - 1} \right) + \left( {y_{\text{p1}}^{2} - y_{\text{p2}}^{2} } \right)\sin y_{\text{p1}} \sinh y_{\text{p2}} } \right\} \hfill \\ \end{aligned} \right] \\ \end{aligned}$$

(12)

where

$c_{\text{s}} = \cos \left( {y_{\text{s1}} } \right)\cosh \left( {y_{\text{s2}} } \right)$; $s_{\text{s}} = - \sin \left( {y_{\text{s1}} } \right)\sinh \left( {y_{\text{s2}} } \right)$

$c_{\text{p}} = \cos \left( {y_{\text{p1}} } \right)\cosh \left( {y_{\text{p2}} } \right)$;$s_{\text{p}} = - \sin \left( {y_{\text{p1}} } \right)\sinh \left( {y_{\text{p2}} } \right)$$y_{\text{s1}} = k_{1} h = \frac{{\omega_{\text{s}} h}}{{V_{\text{s}} }}\left( {\frac{{\left( {1 + 4\xi_{\text{s}}^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} + 1}}{{2\left( {1 + 4\xi_{\text{s}}^{2} } \right)}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$;$y_{\text{s2}} = k_{2} h = - \frac{{\omega_{\text{s}} h}}{{V_{\text{s}} }}\left( {\frac{{\left( {1 + 4\xi_{\text{s}}^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} - 1}}{{2\left( {1 + 4\xi_{\text{s}}^{2} } \right)}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$

and $y_{\text{p1}} = \frac{{\omega_{\text{p}} h}}{{V_{\text{p}} }}\left( {\frac{{\left( {1 + 4\xi_{\text{p}}^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} + 1}}{{2\left( {1 + 4\xi_{\text{p}}^{2} } \right)}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$; $y_{\text{p2}} = - \frac{{\omega_{\text{p}} h}}{{V_{\text{p}} }}\left( {\frac{{\left( {1 + 4\xi_{\text{p}}^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} - 1}}{{2\left( {1 + 4\xi_{\text{p}}^{2} } \right)}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$Considering the force equilibrium conditions (∑V = ∑H = 0) on the elastic wedge ABE

$$\begin{aligned} P_{\text{L}} B_{0} \left( {1 \pm \mu_{\text{v}} } \right) = & \, P_{\text{A}} \cos \left( {\alpha_{1} - \phi } \right) + P_{m} \cos \left( {\alpha_{2} - \phi_{m} } \right) - W_{1} \pm Q_{\text{v1}} + \frac{{cB_{0} \sin \alpha_{1} \sin \alpha_{2} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}} \\ & + \frac{{c_{m} B_{0} \sin \alpha_{2} \sin \alpha_{1} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}} \\ \end{aligned}$$

(13)

$$P_{\text{L}} B_{0} \mu_{\text{h}} = P_{\text{A}} \sin \left( {\alpha_{1} - \phi } \right) - P_{m} \sin \left( {\alpha_{2} - \phi_{m} } \right) - Q_{\text{h1}} - \frac{{cB_{0} \cos \alpha_{1} \sin \alpha_{2} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}} + \frac{{c_{m} B_{0} \cos \alpha_{2} \sin \alpha_{1} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}}$$

(14)

So,

$$P_{\text{L}} = \frac{{\left[ \begin{aligned} P_{\text{A}} \left\{ {\sin \left( {\alpha_{1} - \phi } \right) + \cos \left( {\alpha_{1} - \phi } \right)} \right\} - P_{m} \left\{ {\sin \left( {\alpha_{2} - \phi_{m} } \right) - \cos \left( {\alpha_{2} - \phi_{m} } \right)} \right\} - W_{1} \pm Q_{\text{v1}} \hfill \\ - Q_{\text{h1}} + \frac{{cB_{0} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}}\left\{ {\sin \alpha_{2} \left( {\sin \alpha_{1} - \cos \alpha_{1} } \right) + m\sin \alpha_{1} \left( {\sin \alpha_{2} + \cos \alpha_{2} } \right)} \right\} \hfill \\ \end{aligned} \right]}}{{B_{0} \left\{ {1 + \mu_{\text{h}} \pm \mu_{\text{v}} } \right\}}}$$

(15)

where $\mu_{\text{h}} = k_{\text{h}} \sin 2\pi \left( {\frac{t}{T} - 0.3} \right)$ and $\mu_{\text{V}} = k_{\text{V}} \sin 2\pi \left( {\frac{t}{T} - 0.16} \right)$

Equilibrium P_A as obtained from active zone must be equal to passive earth pressure P_p of the passive zone. So,

$$P_{\text{A}} = P_{\text{P}}$$

(16)

where $P_{P} = P_{P\gamma } + P_{Pq} + P_{Pc}$ and $P_{m} = P_{m\gamma } + P_{mq} + P_{mc}$

Passive earth resistances P_pγ, P_pq and P_pc are determined by considering the moment equilibrium of the forces which are acting on the soil mass BED (log-spiral passive zone) as shown in Fig. 2b.

2.2.2 Log-Spiral Shear Zone

Let us consider a thin elemental horizontal strip of thickness dz₂ at any depth z₂ from the footing surface. At an angle θ_x, the radius (r) of the logarithmic spiral may be expressed as $r = r_{0} e^{{\theta_{x} \tan {\kern 1pt} \phi }}$; the length of this strip from the same depth z₂ is assumed as x₂. So, the mass of strip of the log-spiral zone BDE (Fig. 2b):

$$m(z_{2} ) = \frac{\gamma }{g}x_{2} {\text{d}}z_{2}$$

(17)

where $x_{2} = r_{0} \left[ {e^{{\theta_{x} \tan \phi }} \left\{ {\cos \left( {\beta + \theta - \theta_{x} } \right) - \cot \alpha_{1} \sin \left( {\beta + \theta - \theta_{\text{x}} } \right)} \right\} - \cos \left( {\beta + \theta } \right) + e^{\theta \tan \phi } \sin \left( {\theta + \beta } \right)\cot \alpha_{1} } \right]$

$${\text{d}}z_{2} = r_{0} e^{{\theta_{x} \tan \phi }} \left[ {\tan \phi \sin \left( {\beta + \theta - \theta_{x} } \right) - \cos \left( {\beta + \theta - \theta_{x} } \right)} \right]{\text{d}}\theta_{x}$$

So, weight of the log-spiral shear zone BDE,

$$\begin{aligned} W_{2} =\, & g\int\limits_{0}^{\theta } {m\left( {z_{2} } \right) \cdot {\text{d}}z_{2} } \\ =\, & I_{1} \\ \end{aligned}$$

(18)

The horizontal and vertical inertia forces acting on the log-spiral shear zone can be expressed as follows:

$$\begin{aligned} Q_{\text{h2}} = & \int\limits_{0}^{\theta } {m\left( {z_{2} } \right)} a_{\text{h}} \left( {z,t} \right){\text{d}}z_{2} \\ = & \, I_{2} \\ \end{aligned}$$

(19)

$$\begin{aligned} Q_{\text{v2}} = & \int\limits_{0}^{\theta } {m\left( {z_{2} } \right)} a_{\text{v}} \left( {z,t} \right){\text{d}}z_{2} \\ = & \, I_{3} \\ \end{aligned}$$

(20)

The intensity of surcharge $q = \gamma D_{\text{f}}$, where γ is the unit weight of soil and D_f is the depth of footing, acts as uniformly distributed over BH. So, the force due to surcharge load q

$$Q = \gamma D_{\text{f}} \cdot \overline{\text{BD}} \left( {1 - \mu_{\text{h}} \pm \mu_{\text{v}} } \right)$$

(21)

where $\overline{\text{BD}} = r_{0} e^{\theta \tan \phi } \cos \beta - r_{0} \cos \left( {\theta + \beta } \right) - \frac{{B_{0} \sin \alpha_{2} \cos \alpha_{1} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}}$.

Taking moment equilibrium of the forces acting on the log-spiral failure zone BED about the center of the log-spiral (O), we get

$$P_{{{\text{P}}\gamma }} \left[ {\overline{OY} } \right] = \left( {W_{2} \pm Q_{{{\text{v}}2}} } \right)\left[ {X + r_{0} \cos \left( {\beta + \theta } \right)} \right] - Q_{{{\text{h}}2}} \left[ {Y + r_{\text{f}} \sin \beta } \right]$$

(22)

$$\begin{aligned} \left( {P_{{{\text{P}}q}} - P_{{{\text{P}}c}} } \right)\left[ {\overline{OX} } \right] = & Q\left[ {0.5\overline{\text{BD}} + \frac{{B_{0} \cos \alpha_{1} \sin \alpha_{2} }}{{\sin \left( {\alpha_{1} + \alpha_{2} } \right)}} + r_{0} \cos \left( {\beta + \theta } \right)} \right] \\ & + cr_{0}^{2} \left[ {\frac{{\left( {e^{2\theta \tan \phi } - 1} \right)}}{2\tan \phi } + \frac{{\sin \left( {\theta + \beta + \alpha_{1} } \right)\left( {\sin \left( {\theta + \beta } \right) - e^{\theta \tan \phi } \sin \beta } \right)}}{{\sin \alpha_{1} }}} \right] \\ \end{aligned}$$

(23)

where OX and OY are the lever arm of the passive resistances P_Pq,P_Pc and P_Pγ, respectively.

$$\overline{OX} = r_{0} \left[ {\frac{{\left( {e^{\theta \tan \phi } \sin \beta - \sin \left( {\theta + \beta } \right)} \right)\cos \phi }}{{2\sin \alpha_{1} }} - \cos \left( {\alpha_{1} + \theta + \beta - \phi } \right)} \right]$$

$$\overline{OY} = r_{0} \left[ {\frac{{\left( {e^{\theta \tan \phi } \sin \beta - \sin \left( {\theta + \beta } \right)} \right)\cos \phi }}{{3\sin \alpha_{1} }} - \cos \left( {\alpha_{1} + \theta + \beta - \phi } \right)} \right]$$

And X and Y are horizontal and vertical distances between the center of gravity of log-spiral zone BDE and the arbitrary center of the log-spiral (O)

where $X = \frac{{\int\limits_{0}^{\theta } {\frac{{x_{1}^{2} }}{2}{\text{d}}z_{2} } }}{{\int\limits_{0}^{\theta } {x_{1} \cdot {\text{d}}z_{2} } }} = \frac{{I_{4} }}{{I_{6} }}$ and $Y = \frac{{\int\limits_{0}^{\theta } {x_{1} \cdot z_{2} \cdot dz_{2} } }}{{\int\limits_{0}^{\theta } {x_{1} \cdot dz_{2} } }} = \frac{{I_{5} }}{{I_{6} }}$

$$x_{1} = r_{0} \left[ {e^{{\theta_{x} \tan \phi }} \cos \left( {\beta + \theta - \theta_{x} } \right) - \cos \left( {\beta + \theta } \right)} \right]$$

The values of I₁, I₂, I₃, I₄, I₅ and I₆ are evaluated by numerical integration method (Simpson 1/3 rule) using MATLAB (2013).

Now, from Eqs. (22) and (23) we can get the values of P_Pγ and (P_Pq,P_Pc), respectively. So,

$$P_{\text{P}} = P_{{{\text{P}}\gamma }} + P_{{{\text{P}}q}} + P_{{{\text{P}}c}}$$

(24)

The values of passive resistances P_mγ, P_mq and P_mc at a mobilization factor m can be obtained by substituting the angle Φ by Φ_m and changing the wedge angle α₁ to α₂ and α₂ to α₁ in the Equations of P_Pγ, P_Pq and P_Pc. So,

$$P_{m} = P_{m\gamma } + P_{mq} + P_{mc}$$

(25)

Now, putting these values of P_p and P_m in Eq. (15), we can get the value of P_L. So, the ultimate single seismic bearing capacity coefficient of shallow strip footing can be given by

$$N_{\gamma } = {\raise0.7ex\hbox{${2P_{L} }$} \!\mathord{\left/ {\vphantom {{2P_{L} } {\gamma B_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\gamma B_{0} }$}}$$

(26)

3 Result and Discussion

After optimization of bearing capacity coefficient (Nγ) w.r.t. α, β, θ and t/T for different locations of the center of the log-spiral curve by iterative technique, the optimum resistance is found out using MATLAB (2013). From the global concave curve, the minimum value is taken. This process is repeated for different values of mobilization factor m. The optimized bearing capacity coefficients are obtained for the maximum value of m as it satisfies the three equilibrium conditions. These optimized bearing capacity coefficients (N_γe) are presented in Tables 1, 2, 3 and 4 for static and seismic conditions (k_h = 0.1, 0.15 and 0.2), respectively. Here, the values of bearing capacity coefficients are given for ξ = 10% and ω_p/ω_s ratio as 1.87. The corresponding value of α₁, β and θ for optimized bearing capacity coefficients (N_γe) gives the critical focus of the log-spiral failure surface for a certain condition. Steps to calculate the ultimate bearing capacity using the suggested methodology are as follows:

Table 1 Static bearing capacity coefficient (N_γe) for k_h = 0, k_v = 0

Table 2 Pseudo-dynamic bearing capacity coefficient (N_γe) for k_h = 0.1

Table 3 Pseudo-dynamic bearing capacity coefficient (N_γe) for k_h = 0.15

Table 4 Pseudo-dynamic bearing capacity coefficient (N_γe) for k_h = 0.2

• 1. Choose the depth of the foundation (D_f) and the width of the foundation (B₀).

• 2. Collect soil parameters such as soil friction angle (Φ), cohesion (c), unit weight of soil (γ) and seismic parameters such as horizontal and vertical seismic accelerations (k_h and k_v).

• 3. Calculate depth factor (D_f/B₀) and cohesion factor (2c/γB₀).

• 4. Now, using the values provided in Tables 1, 2, 3 and 4 calculate seismic bearing capacity coefficient. For intermediate portion, linear interpolation is suggested.

• 5. Taking the value of N_γe (as calculated above), we can evaluate the ultimate bearing capacity of shallow foundation resting on c–Φ soil.

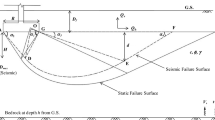
Figure 3 shows the variations of bearing capacity coefficients (N_γe) with respect to horizontal seismic acceleration (k_h) at different soil friction angles (Φ = 20°, 25°, 30°) for 2c/γB₀ = 0.25, D_f = 0.5, k_v = k_h/2 and m = 1. It is seen that (N_γe) increases with increase in soil friction angle (Φ). Due to the increase in Φ, the internal resistance of the soil particles will be increased which resembles the increase in seismic bearing capacity factors. Figure 4 shows the variations of bearing capacity coefficients (N_γe) with respect to seismic acceleration (k_h) at different cohesion factors (2c/γB₀ = 0, 0.25, 0.5) for Φ = 25°, D_f = 0.5, k_v = k_h/2 and m = 1. It shows that (N_γe) increases with an increase in cohesion factor (2c/γB₀). Due to an increase in cohesion, seismic bearing capacity factor will be increased as an increase in cohesion causes an increase in intermolecular attraction among the soil particles which offers more bearing capacity. Figure 5 shows the variations of bearing capacity coefficients (N_γe) with respect to seismic acceleration (k_h) for different depth factors (D_f/B₀ = 0.25, 0.5, 1) for Φ = 25°, 2c/γB₀ = 0.25, k_v = k_h/2 and m = 1. It is seen that bearing capacity coefficients (N_γe) increase with an increase in depth factor (D_f/B₀). Due to increase in depth factor (D_f/B₀), surcharge weight increases which increase in the passive resistance and hence increase in seismic bearing capacity factor. From Figs. 3, 4, 5 and 6, it is seen that the bearing capacity coefficients (N_γe) decrease along with an increase in horizontal seismic acceleration (k_h). And Fig. 6 shows the variations of bearing capacity coefficients (N_γe) with respect to seismic acceleration (k_h) at different vertical seismic accelerations (k_v = 0, k_h/2, k_h) for Φ = 25°, D_f = 0.5, m = 1 and 2c/γB₀ = 0.25. It is seen that bearing capacity coefficients (N_γe) decrease with the increase in vertical seismic acceleration (k_v) also. Due to an increase in seismic acceleration, the disturbances in the soil particles increase and hence decrease its resistance against bearing capacity. Figure 7 shows the variations of slip surfaces with respect to seismic acceleration (k_h = 0.1, 0.15, 0.2) on failure mechanism. It shows that as the seismic acceleration increases, the effect on soil media under the foundation increases. In the figure, the slip surfaces show the depth of elastic wedge increases from 1.2 to 1.7 m as k_h value increases from 0.1 to 0.2 for B₀ = 2 m, Φ = 20°, 2c/γB₀ = 0.5, D_f = 0.25 and k_v = k_h/2.

Fig. 3

Variations of bearing capacity coefficient with respect to seismic acceleration (k_h) at different soil friction angles (Φ = 20°, 25°, 30°) for 2c/γB₀ = 0.25, D_f/B₀ = 0.5, k_v = k_h/2 and m = 1

Fig. 4

Variations of bearing capacity coefficient with respect to seismic acceleration (k_h) at different cohesion factors (2c/γB₀ = 0, 0.25, 0.5) for Φ = 25°, D_f/B₀ = 0.5, k_v = k_h/2 and m = 1

Fig. 5

Variations of bearing capacity coefficient with respect to seismic acceleration (k_h) at different depth factors (D_f/B₀ = 0.25, 0.5, 0.75) for Φ = 25°, 2c/γB₀ = 0.25, k_v = k_h/2 and m = 1

Fig. 6

Variations of bearing capacity coefficient with respect to seismic acceleration (k_h) at different vertical seismic accelerations (k_v = 0, k_h/2, k_h) for Φ = 25°, 2c/γB₀ = 0.25, D_f/B₀ = 0.5 and m = 1

Fig. 7

Effect of slip surfaces for various values of k_h on failure mechanism

4 Comparison of Result

On the basis of different assumptions considering different mathematical models, the bearing capacity factors are evaluated. So, each method will give its own optimized value. Table 5 shows the comparison of the pseudo-dynamic bearing capacity coefficient (N_γe) obtained from the present analysis with the values obtained from previous seismic analyses for different horizontal seismic accelerations (k_h) at Ф = 30°. To broaden the perspectives of different authors on their same or similar type of works considering different approaches have been compared here to the present analysis. Budhu and Al-karni (1993), Soubra (1997), and Choudhury and Subha Rao (2005) determine the seismic bearing capacity coefficient considering composite failure mechanism using pseudo-static approach, whereas Ghosh (2008) and Saha and Ghosh (2014) consider linear failure surface using pseudo-dynamic approach. On the other hand, the present analysis is performed considering the log-spiral failure mechanism in which passive zone is fully log-spiral and instead of a fixed center of log-spiral it will create its own center at optimization. The pseudo-dynamic method is used to solve this problem. It has been seen that the values of seismic bearing capacity obtained from this present approach are less than all seismic analyses which are taken here for comparison. For example, the values obtained from the present analysis are less than those of Budhu and Al-karni (1993) and Soubra (1997) because they had analyzed pseudo-static bearing capacity considering composite failure mechanism with fixed log-spiral focus. Again, the values obtained from the present analysis are much closer to those of Choudhury and Subha Rao (2005) analysis because they had also considered arbitrary log-spiral focus but pseudo-static analysis with composite failure mechanism. On the other hand, Ghosh (2008), Saha and Ghosh (2014) and Saha and Ghosh (2015) considered pseudo-dynamic analysis assuming Coulomb failure mechanism and composite failure mechanism, so the present seismic bearing capacity coefficient (N_γe) is much less than from these analyses, respectively.

Table 5 Comparison of seismic bearing capacity coefficient (N_γe) for different values of k_h and k_v with Φ = 30°

5 Conclusion

A mathematical model is suggested to evaluate modified pseudo-dynamic bearing capacity of shallow strip footing resting on c–Φ soil.

A fully log-spiral shear failure zone with arbitrary focus is assumed to analyze this problem using limit equilibrium method.

A single bearing capacity coefficient is proposed for the simultaneous resistance of unit weight, surcharge and cohesion.

Optimization of the seismic bearing capacity coefficient is done, and results are presented in tabular non-dimensional form.

The effects of various parameters are studied here. It is seen that the pseudo-dynamic bearing capacity coefficient (N_γe) increases with increase in Φ, 2c/γB₀, D_f/B₀ and m, but it decreases with the increase in horizontal and vertical seismic acceleration (k_h, k_v).

The values obtained from the present analysis are thoroughly compared with available pseudo-static analysis as well as pseudo-dynamic analysis, and it is seen that the values obtained from the present study are in the lower side in comparison with the available analyses.

The values as provided in the present analysis can be used for the determination of bearing capacity; and for the intermediate portion, linear interpolation is suggested.