1 Introduction

Estimating the seismic bearing capacity of shallow foundations is a critical issue in earthquake-prone regions. Observations from significant earthquakes such as the one that occurred on February 6, 2023, in Turkey indicated that structures constructed by the same contractor displayed varying levels of resilience, with some remaining intact while others suffered damage (Franke et al. 2019; Maleki et al. 2019, 2023). One of the primary factors contributing to this discrepancy is the variability in the reduction of the seismic bearing capacity of shallow foundations. In large earthquakes where soil behavior becomes nonlinear, the seismic bearing capacity of shallow foundations presents a complex challenge influenced by various factors. Therefore, further research is essential to investigate different aspects of this issue.

Seismic accelerations are well-known for exerting inertial forces on both the structure and the underlying soil mass, thereby diminishing the seismic bearing capacity of foundations. Despite the detailed recording of seismic acceleration time histories using accelerometers, these records have not been applied in analytical methods for evaluating the seismic bearing capacity of foundations. In most previous studies, a constant acceleration or a harmonic acceleration with a fixed frequency was used instead of recorded earthquake acceleration time histories. Therefore, the interaction of frequencies was neglected.

Traditionally, analytical methods have primarily relied on the pseudo-static approach, characterized by constant accelerations. Several techniques have been employed within the pseudo-static approach framework to evaluate the seismic bearing capacity of foundations. These techniques include limit analysis (Conti 2018; Zhang et al. 2020; Mortara 2021), the stress characteristics method (Cascone et al. 2016; Ganesh et al. 2022; Casablancaet al. 2023), the limit equilibrium method (Nouzari et al. 2021), the finite element method (Nguyen et al. 2022; Jitchaijaroen et al. 2024; Garzón-Roca et al. 2024), and the finite difference method (Hamrouni et al. 2021). The pseudo-static approach is also commonly used for other aspects of geotechnical earthquake engineering, e.g., (Maleki et al. 2021, 2022; Rahmani et al. 2022). Additionally, Ghosh et al. (2017) and Debnath et al. (2018) evaluated the seismic bearing capacity of cohesive-frictional soil using this approach, considering concurrent resistance factors of unit weight, surcharge, and cohesion. Despite the widespread use of the pseudo-static approach due to its simplicity, it assumes seismic accelerations to be time-independent and constant with depth. As a result, it neglects dynamic factors such as wave propagation, amplification, phase difference, and ground motion frequency content.

The limitations of the pseudo-static approach led to the development of the pseudo-dynamic approach for the estimation of seismic earth pressure on retaining walls (Steedman et al. 1990; Choudhury et al. 2005; Debnath et al. 2018). The application of this approach has also been extended to seismic bearing capacity analysis (Choudhury et al. 2006; Ghosh et al. 2008; Saha et al. 2015; Izadi et al. 2021, 2022; Zhong et al. 2022; Chen et al. 2022). The pseudo-dynamic approach, despite its advantages, does not incorporate the zero-stress condition at the ground surface in its equations and requires an assumption regarding the amplification factor of the underlying soil deposit. Moreover, the pseudo-dynamic approach assumes a linear variation of the soil deposit amplification factor with depth.

Furthermore, Belleza (2014, 2015) introduced a modified pseudo-dynamic approach to address the limitations of the pseudo-dynamic approach and inherently consider the amplification factor. In a subsequent study, Zhou et al. (2023), (Krishnan and Chakraborty 2021), and Akhavan Tavakoli et al. (2023) incorporated this approach into finite element limit analysis procedures. Moreover, Saha et al. (2020), Debnath et al. (2021) and Nadgouda et al. (2023) applied this approach to determine the seismic bearing capacity of strip foundations using the limit equilibrium method. Kang et al. (2024) evaluated the seismic bearing capacity based on this approach, adopting the nonlinear Mohr–Coulomb criterion. The modified pseudo-dynamic approach, like the pseudo-dynamic approach, is designed to respond to harmonic excitation, while disregarding the recorded ground motion and its characteristics. Additionally, its further development is impeded by the elimination of the imaginary part of the equations and the emergence of hyperbolic functions. Notably, the existing literature lacks examination of the effects of ground motion frequency content and the predominant natural period of the soil deposit on seismic bearing capacity. Analytical techniques have also been developed without considering the effects of significant earthquakes on seismic bearing capacity.

The aim of this study, is to develop an extended pseudo-dynamic approach to estimate the seismic bearing capacity of strip foundations by considering the time-history seismic accelerations recorded during large earthquakes. This approach inherently accounts for the frequency content of the ground motion and its interactions with the natural periods of the soil deposit. Progressing incrementally in time enables the incorporation of nonlinear values based on stress–strain conditions, allowing for the consideration of shear strength reduction from peak to residual values and the decrease in shear wave velocity within the soil deposit (Seed et al. 1986). Therefore, the primary innovations of this study are: i) Considering the recorded earthquake acceleration as an input excitation in the time domain, none of the analytical methods previously presented have this capability. ii) The inclusion of non-linear behavior, which has been overlooked in previous analytical methods, leading to more realistic results.

In this study, the subgrade soil is assumed to be a frictional cohesive material with viscoelastic behavior. Since soil behavior exhibits nonlinearity during medium and large earthquakes, this study represents the seismic bearing capacity with a single coefficient denoted as Nγe for the three resistance components: unit weight, surcharge, and cohesion. The failure mechanism involves a composite planar and logarithmic spiral surface. The transient accelerations are computed for the active and passive triangular zones, along with the radial shear zone based on the wave propagation theory. This method considers the imaginary part of the response while implicitly considering the amplification of the soil deposit layer. The results of the proposed approach are consistent with some experimental and analytical results available in the literature. Considering a large earthquake a parametric study is conducted to evaluate the impacts of the ratio of soil deposit thickness to soil shear wave velocity, frequency content, soil damping ratio, and other influencing factors on the seismic bearing capacity of strip footings. The results of the parametric study indicate a more rapid decline in bearing capacity compared to previous findings, highlighting the significant challenge faced by shallow foundations in large earthquakes.

2 Method of Analysis

2.1 Problem Definition and Assumptions

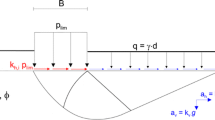
To estimate the seismic bearing capacity of shallow foundations, a rupture mechanism is first considered. Once the failure mechanism is determined, the static forces can be easily calculated. In order to determine the inertial forces, it is necessary to use wave propagation equations to determine the average seismic acceleration in each zone. After determining the static and dynamic forces, the seismic bearing capacity can be calculated using equilibrium equations.

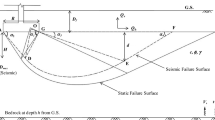
Figure 1 illustrates a strip foundation with a width of B, placed at a depth of D on dry viscoelastic frictional cohesive (φ–c) soil, where φ represents the soil friction angle and c is the soil cohesion. The failure mechanism for strip foundations is divided into three distinct zones: an active triangular zone beneath the footing labeled ABC, a transitional logarithmic spiral zone marked OCD, and a passive triangular zone denoted as ADE. During seismic events, the failure mechanism displays asymmetry, with one side (left side) being smaller than the other side (right side). The vertical distance from the center O to the ground surface, represented by d, can be easily determined as

$$d=\frac{{r}_{0}sin\psi cos\left(\beta -\varphi +\alpha \right)}{cos\left(\theta -x-\alpha \right)}-D$$
(1)

where r0 represents the initial radius of the log spiral zone, and θ is the angle between r0 and OD, creating the log-spiral part. x indicates the angle of r0 relative to the vertical. Angles α and β are the basic angles of the active triangular zone; while ψ and X represent the basic angles of the passive triangular zone as illustrated in Fig. 2

Fig. 1
figure 1

General failure mechanism

Full size image
Fig. 2
figure 2

General failure mechanism where the centre of the log spiral is located at A

Full size image

The highest stress gradient is observed at the edge of the foundation (point A). Therefore, as shown in Fig. 2, the assumption is made that the center of the logarithmic spiral (point O) aligns with the corner of the foundation (point A) (Budhu et al. 1993). Geometrically, this implies that with increased seismic acceleration, the angle β decreases proportionally to the increment in the angle α. The chosen composite failure surface is asymmetric as the angles α and β (or ψ and X) are not equal. Utilizing a search method with small increments in active angles (α or β) and passive angles (ψ or X) yields the most critical failure surface to obtain the minimum seismic bearing capacity. Note that in Fig. 1, when point O is located at point A, as shown in Fig. 2, the distance d must equal − D and (β-φ + α) must equal π/2.

In order to obtain the inertia forces and seismic acceleration of each zone, it is necessary to solve the wave propagation equations. The velocities of soil shear and primary waves, as well as the damping ratio, are denoted by Vs, Vp, and ξ, respectively. In accordance with the Kelvin-Voigt model for soil as a viscoelastic material, the equation of motion governing the vertical propagation of shear and primary waves through a homogeneous soil can be expressed as follows (Bellezza 2015):

$$\rho \frac{{\partial }^{2}{u}_{h}}{{\partial }^{2}t}=G\frac{{\partial }^{2}{u}_{h}}{{\partial }^{2}z}+{\eta }_{s}\frac{{\partial }^{3}{u}_{h}}{{\partial }^{2}z\partial t}$$
(2)
$$\rho \frac{{\partial }^{2}{u}_{v}}{{\partial }^{2}t}=(\lambda +2G)\frac{{\partial }^{2}{u}_{v}}{{\partial }^{2}z}+({\eta }_{1}+2{\eta }_{s})\frac{{\partial }^{3}{u}_{v}}{{\partial }^{2}z\partial t}$$
(3)

where uh and uv are the horizontal and vertical components of the displacement, ηs and G represent the viscous damping and shear modulus of the soil, respectively; ρ, λ, and ηl indicate the density, the first Lame constant, and the viscosity component, respectively; t and z represent time and depth from the ground surface, respectively. γ and τ represent the shear strain and the shear stress, respectively, while ω denotes the angular frequency.

Solving Eqs. (2) and (3) yields the following transfer functions at a depth z beneath the ground surface for the soil layer above the solid bedrock (Jiryaei 2022):

$$f_{ha} \left( {z, \omega } \right) = \frac{{\cos k_{s}^{ * } z}}{{\cos k_{s}^{ * } h}}$$
(4)
$$f_{va} \left( {z,\omega } \right) = \frac{{\cos k_{p}^{ * } z}}{{\cos k_{p}^{ * } h}}$$
(5)

where fha and fva are the horizontal and vertical components of the transfer functions, h represents the thickness of the soil deposit, and kp* and ks* denote the complex wave numbers corresponding to the P-wave and the S-wave, respectively.

By considering the horizontal and vertical components of seismic acceleration Ah and Av in the Fourier domain, the acceleration components ah and av at depth z can be calculated as (Jiryaei 2022)

$$a_{h} \left( {z, \omega } \right) = A_{h} \frac{{\cos k_{s}^{ * } z}}{{\cos k_{s}^{ * } h}}$$
(6)
$$a_{v} \left( {z, \omega } \right) = A_{v} \frac{{\cos k_{p}^{ * } z}}{{\cos k_{p}^{ * } h}}$$
(7)

Any random motion, such as seismic ground motion, can be defined as input to Av and Ah. It is important to note that the modified pseudo-dynamic approach solely accounts for harmonic motion. Eqations. (6) and (7) are used to calculate the inertial forces acting on the soil mass below the footing.

2.2 Computations for Seismic and Static Forces

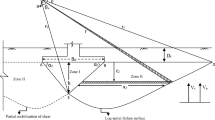
Once the failure mechanism is identified, the calculation of inertial forces exerted on the soil mass within a particular zone can be accomplished by utilizing the seismic accelerations outlined in Eqs. (6) and (7). In Figure 2, calculations can commence from the triangular passive zone ADE. To ascertain the passive resistance (Pp1) acting on GD between GDE and GDCA (as shown in Fig. 3), a hypothetical wall (GD) with a friction angle δ is assumed. Pp1 is resolved into two components: Pp1cq represents the cohesion and surcharge component, while Pp1γ denotes the unit weight component. These components are delineated separately because of variations in their application points. The friction angle δ in Fig. 3 is calculated as δ = Cd × φ, where Cd is a coefficient that ranges from − 1 to + 1 and depends on B, D, φ, and c; thus, Cd can be determined under static conditions. In Fig. 3, the sole unknown factor is Pp1, which is calculated by considering the equilibrium of horizontal and vertical forces acting on the GED:

$${P}_{p1}={P}_{p1cq}+{P}_{p1\gamma }$$
(8)

where

$${P}_{p1cq}=\frac{1}{sin\left(\delta \right)tan\left(\varphi +X\right)-cos\left(\delta \right)}\left[-2c{h}_{2}tan\left(\varphi +X\right)-q{h}_{2}cot\left(X\right)\left(1-\frac{{a}_{vd}}{g}\right)tan\left(\varphi +X\right)-c{h}_{2}cot\left(X\right)+q{h}_{2}cot\left(X\right)\left(\frac{{a}_{hd}}{g}\right)\right]$$
(9)
$${P}_{p1\gamma }=\frac{1}{sin\left(\delta \right)tan\left(\varphi +X\right)-cos\left(\delta \right)}\left[{Q}_{v1}tan\left(\varphi +X\right)-{W}_{1}tan\left(\varphi +X\right)+{Q}_{h1}\right]$$
(10)

q represents the surcharge, while h2 indicates the depth of DGE:

Fig. 3
figure 3

The hypothetical wall GD with the frictional angle of δ

Full size image
$${h}_{2}=B\frac{sin\left(\psi \right){e}^{\theta tan\varphi }}{cos\left(x\right)\left(cot\left(\alpha \right)+cot\left(\beta \right)\right)}$$
(11)

W1 is the weight of the GED:

$${W}_{1}=\gamma \frac{{{h}_{2}}^{2}}{2}cot\left(X\right)$$
(12)

Additionally, ahd and avd in Eq. (9) represent seismic acceleration components at a depth of D:

$${a}_{hd}\left(t\right)=ift\left({A}_{h}\frac{\text{cos}{k}_{s}^{*}D}{\text{cos}{k}_{s}^{*}h}\right)$$
(13)
$${a}_{vd}\left(t\right)=ift\left({A}_{v}\frac{\text{cos}{k}_{p}^{*}D}{\text{cos}{k}_{p}^{*}h}\right)$$
(14)

where ift stands for the inverse Fourier transform.

Qh1 and Qv1 in Eq. (10) represent inertial forces acting on the GED due to the seismic accelerations. These inertial forces are calculated by integrating the product of a mass element and the seismic acceleration corresponding to the depth of the mass element. Therefore, amplification resulting from wave propagation is inherently taken into account. The calculation of dQh1 for a small mass element dm is given by dQh1 = ah × dm. thus,

$$Q_{h1} \left( t \right) = ift\left( {\smallint a_{h} \left( {z, \omega } \right)dm} \right) = ift\left\{ {\mathop \smallint \limits_{D}^{h2 + D} \left[ {\frac{{A_{h} \cos \left( {k_{s} z} \right)}}{{\cos \left( {k_{s} h} \right)}}} \right]\left[ {\frac{\gamma }{g}\frac{{\left( {h_{2} + D - z} \right)}}{\tan \left( X \right)}} \right]dz} \right\} = a_{ha1} \left( t \right)\frac{{W_{1} }}{g}$$
(15)

Similarly, in the vertical direction:

$$Q_{v1} \left( t \right) = ift\left( {\smallint a_{v} \left( {z, \omega } \right)dm} \right) = ift\left\{ {\mathop \smallint \limits_{D}^{h2 + D} \left[ {\frac{{A_{v} \cos \left( {k_{p} z} \right)}}{{\cos \left( {k_{p} h} \right)}}} \right]\left[ {\frac{\gamma }{g}\frac{{\left( {h_{2} + D - z} \right)}}{\tan \left( X \right)}} \right]dz} \right\} = a_{va1} \left( t \right)\frac{{W_{1} }}{g}$$
(16)

where

$$a_{ha1} \left( t \right) = ift\left\{ {\frac{{2A_{h} }}{{k_{s}^{2} h_{2}^{2} \cos \left( {k_{s} h} \right)}}\left[ { - \cos \left( {k_{s} h_{2} + k_{s} D} \right) - k_{s} h_{2} \sin \left( {k_{s} D} \right) + \cos \left( {k_{s} D} \right)} \right]} \right\}$$
(17)
$$a_{va1} \left( t \right) = ift\left\{ {\frac{{2A_{v} }}{{k_{p}^{2} h_{2}^{2} \cos \left( {k_{p} h} \right)}}\left[ { - \cos \left( {k_{p} h_{2} + k_{p} D} \right) - k_{p} h_{2} \sin \left( {k_{p} D} \right) + \cos \left( {k_{p} D} \right)} \right]} \right\}$$
(18)

aha1 and ava1 represent the horizontal and vertical components of the weighted average acceleration for GED in the time domain. Multiplying these average accelerations by the mass of GED yields Qh1 and Qv1 in the time domain. Calculating the force Pp1 according to Eq. (8) helps determine the passive force of Pp on the GDCA. In Fig. 4, the force Pp can be determined by considering the equilibrium of moments around point A. It is important to note that the reaction force R2 passes through the center of the logarithmic spiral and can be excluded from the moment equilibrium equation around point A.

$${P}_{p}=\frac{{M}_{P1cqh}-{M}_{P1cqv}+{M}_{q}+{M}_{C2}}{\frac{1}{2}{r}_{0}cos\left(\varphi \right)}+\frac{{M}_{P1\gamma h}-{M}_{P1\gamma v}+{M}_{W2}-{M}_{Qh2}-{M}_{Qv2}+{M}_{W3}-{M}_{Q3}}{\frac{2}{3}{r}_{0}cos\left(\varphi \right)}$$
(19)

where MW2, Mq, and Mc represent the moments of the weight of AGD (W2) the surcharge (q), and the cohesive resistance along the logarithmic spiral (C2), respectively. MP1cqh and MP1cqv denote the moments of components of P1cq while MP1γh and MP1γv represent the moments of the components of P1γ.

$${M}_{W2}={\int }_{D}^{h2+D}\gamma \left({h}_{2}+D-z\right)cot\psi \left[{h}_{2}cot\psi -\frac{\left({h}_{2}+D-z\right)cot\psi }{2}\right]dz=\frac{1}{3}\gamma {cot}^{2}\left(\psi \right){h}_{2}^{3}$$
(20)
$${M}_{q}=q\left(1-\frac{{a}_{vd}}{g}\right){h}_{2}cot\left(\psi \right)\left[\frac{{h}_{2}cot\left(\psi \right)}{2}\right]$$
(21)
$${M}_{P1cqh}={P}_{p1cq}cos\left(\delta \right)\left[\frac{1}{2}{h}_{2}\right]$$
(22)
$${M}_{P1\gamma h}={P}_{p1\gamma }cos\left(\delta \right)\left[\frac{2}{3}{h}_{2}\right]$$
(23)
$${M}_{P1cqv}={P}_{p1cq}sin\left(\delta \right)\left[{h}_{2}cot\left(\psi \right)\right]$$
(24)
$${M}_{P1\gamma v}={P}_{p1\gamma }sin\left(\delta \right)\left[{h}_{2}cot\left(\psi \right)\right]$$
(25)
$${M}_{C2}={\int }_{0}^{\theta }c\frac{r}{\text{cos}\left(\varphi \right)}\left[r\text{cos}\left(\varphi \right)\right]d{\theta }_{x}=\frac{c{{r}_{0}}^{2}}{2tan\left(\varphi \right)}\left({e}^{2\theta tan\left(\varphi \right)}-1\right)$$
(26)

where θx represents the angle between the passing radius of any differential element and the initial radius as illustrated in Fig. 4.

Fig. 4
figure 4

Seismic and static forces acting on GDCA

Full size image

By considering a differential element with infinitesimal thickness dz as shown in Fig. 4, the moment of the horizontal and vertical components of the inertial forces MQh2 and MQv2 about point A can be determined. It should be mentioned that the arm of each moment is simply determined using geometry, which is included within the brackets in the Eqs. (20)–(28), (31) and (33).

$${M}_{Qh2}=ift\left\{{\int }_{D}^{{h}_{2}+D}\frac{{A}_{h}cos\left({k}_{s}z\right)}{cos\left({k}_{s}h\right)}\frac{\gamma }{g}\left({h}_{2}+D-z\right)cot\psi \left[z-D\right]dz\right\}={a}_{ha2}\left(t\right)\frac{{M}_{W2}}{g}$$
(27)
$${M}_{Qv2}=ift\left\{{\int }_{D}^{D+h2}{A}_{v}\frac{cos\left({k}_{p}z\right)}{cos\left({k}_{p}h\right)}\frac{\gamma }{g}\left({h}_{2}+D-z\right)cot\psi \left[{h}_{2}cot\psi - \frac{\left({h}_{2}+D-z\right)cot\psi }{2}\right]dz\right\}={a}_{va2}\left(t\right)\frac{{M}_{W2}}{g}$$
(28)

where,

$${a}_{ha2}\left(t\right)=ift\left\{\frac{3}{cot\psi {k}_{s}^{3}{h}_{2}^{3}}\frac{{A}_{h}}{cos\left({k}_{s}h\right)}\left[2sin\left({k}_{s}{h}_{2}+{k}_{s}D\right)-2sin\left({k}_{s}D\right)-{k}_{s}{h}_{2}cos\left({k}_{s}{h}_{2}+{k}_{s}D\right)-{k}_{s}{h}_{2}cos\left({k}_{s}D\right)\right]\right\}$$
(29)
$${a}_{va2}\left(t\right)=ift\left\{\frac{3}{2{h}_{2}^{3}{k}_{p}^{3}}\frac{{A}_{v}}{cos\left({k}_{p}h\right)}\left[2sin\left({k}_{p}{h}_{2}+{k}_{p}D\right)-2sin\left({k}_{p}D\right)-{2k}_{p}{h}_{2}cos\left({k}_{p}{h}_{2}+{k}_{p}D\right)-{h}_{2}^{2}{k}_{p}^{2}sin\left({k}_{p}D\right)\right]\right\}$$
(30)

aha2 and ava2 represent the horizontal and vertical components of the weighted average acceleration for GAD in the time domain. The ADC weight moment MW3 and the inertial force moment MQ3 about point A can be computed by considering an element with dimensions dρ × ρdθx as illustrated in Fig. 4, where ρ denotes the distance of this element from point A. It is noteworthy that MQr is zero and is hence eliminated from the moment equilibrium equation.

$$\begin{aligned} M_{{W3}} & = \gamma \int\limits_{0}^{\theta } {\int\limits_{0}^{r} {\rho \left[ {\rho {\text{sin}}\left( {\theta _{x} - x} \right)} \right]d\rho d\theta _{x} = \gamma \int\limits_{0}^{\theta } {\frac{{r^{3} }}{3}\sin \left( {\theta _{x} - x} \right)d\theta _{x} } } } \\ & = \frac{{\gamma r_{0}^{3} }}{{3\left( {9tan^{2} \left( \varphi \right) + 1} \right)}}\left[ {cos\left( x \right) + 3tan\left( \varphi \right)sin\left( x \right) - e^{{3\theta tan\left( \varphi \right)}} \left( {cos\left( {\theta - x} \right) - 3tan\left( \varphi \right)sin\left( {\theta - x} \right)} \right)} \right] \\ \end{aligned}$$
(31)

In polar coordinates with point A as the center, the seismic acceleration in the θx-direction aθ can be calculated accordingly.

$$\begin{aligned} a_{\theta } = & a_{h} cos\left( {\theta_{x} - x} \right) + a_{v} sin\left( {\theta_{x} - x} \right) = A_{h} \frac{{cos\left( {k_{s} z} \right)}}{{cos\left( {k_{s} h} \right)}}cos\left( {\theta_{x} - x} \right) + A_{v} \frac{{cos\left( {k_{s} z} \right)}}{{cos\left( {k_{p} h} \right)}}sin\left( {\theta_{x} - x} \right) \\ & = A_{h} \frac{{cos\left[ {k_{s} \rho cos\left( {\theta_{x} - x} \right) + k_{s} D} \right]}}{{cos\left( {k_{s} h} \right)}}cos\left( {\theta_{x} - x} \right) + A_{v} \frac{{cos\left[ {k_{p} \rho cos\left( {\theta_{x} - x} \right) + k_{p} D} \right]}}{{cos\left( {k_{p} h} \right)}}sin\left( {\theta_{x} - x} \right) \\ \end{aligned}$$
(32)

therefore,

$${M}_{Q3}=ift\left\{{\int }_{0}^{\theta }{\int }_{0}^{{r}_{0}\times exp\left({\theta }_{x}tan\left(\varphi \right)\right)}{A}_{h}\frac{cos\left({k}_{s}\rho cos\left({\theta }_{x}-x\right)+{k}_{s}D\right)}{cos\left({k}_{s}h\right)}\left[\rho cos\left({\theta }_{x}-x\right)\right]\frac{\gamma }{g}\rho d\rho d{\theta }_{x}+{\int }_{0}^{\theta }{\int }_{0}^{{r}_{0}\times exp\left({\theta }_{x}tan\left(\varphi \right)\right)}{A}_{v}\frac{cos\left({k}_{p}\rho cos\left({\theta }_{x}-x\right)+{k}_{p}D\right)}{cos\left({k}_{p}h\right)}\left[\rho sin\left({\theta }_{x}-x\right)\right]\frac{\gamma }{g}\rho d\rho d{\theta }_{x}\right\}=\frac{\gamma }{g}{\int }_{0}^{\theta }cos\left({\theta }_{x}-x\right)\times ift\left\{{\int }_{0}^{{r}_{0}\times exp\left({\theta }_{x}tan\left(\varphi \right)\right)}{A}_{h}\frac{cos\left({k}_{s}\rho cos\left({\theta }_{x}-x\right)+{k}_{s}D\right)}{cos\left({k}_{s}h\right)}{\rho }^{2}d\rho \right\}d{\theta }_{x}+\frac{\gamma }{g}{\int }_{0}^{\theta }sin\left({\theta }_{x}-x\right)\times ift\left\{{\int }_{0}^{{r}_{0}\times exp\left({\theta }_{x}tan\left(\varphi \right)\right)}{A}_{v}\frac{cos\left({k}_{p}\rho cos\left({\theta }_{x}-x\right)+{k}_{p}D\right)}{cos\left({k}_{p}h\right)}{\rho }^{2}d\rho \right\}d{\theta }_{x}=\frac{\gamma }{g}{\int }_{0}^{\theta }cos\left({\theta }_{x}-x\right){a}_{ha3}{\int }_{0}^{{r}_{0}\times exp\left({\theta }_{x}tan\left(\varphi \right)\right)}{\rho }^{2}d\rho d{\theta }_{x}+\frac{\gamma }{g}{\int }_{0}^{\theta }sin\left({\theta }_{x}-x\right){a}_{va3}{\int }_{0}^{{r}_{0}\times exp\left({\theta }_{x}tan\left(\varphi \right)\right)}{\rho }^{2}d\rho d{\theta }_{x}=\frac{\gamma {r}_{0}^{3}}{3g}{\int }_{0}^{\theta }cos\left({\theta }_{x}-x\right){a}_{ha3}\text{exp}\left((3{\theta }_{x}\text{tan}(\left(\varphi \right)\right)))d{\theta }_{x}+\frac{\gamma {r}_{0}^{3}}{3g}{\int }_{0}^{\theta }sin\left({\theta }_{x}-x\right){a}_{va3}\text{exp}(\left(3{\theta }_{x}\text{tan})\left(\varphi \right)\right)d{\theta }_{x}$$
(33)

where,

$${a}_{ha3}\left(t\right)=ift\left\{\frac{{3A}_{h}}{{k}_{s}^{3}{r}_{2}^{3}{cos\left({k}_{s}h\right)cos}^{3}\left({\theta }_{x}-x\right)}\left[2sin\left({k}_{s}D\right)-2sin\left({k}_{s}{r}_{2}cos\left({\theta }_{x}-x\right)+{k}_{s}D\right)+2{k}_{s}{r}_{2}cos\left({\theta }_{x}-x\right)cos\left({k}_{s}{r}_{2}cos\left({\theta }_{x}-x\right)+{k}_{s}D\right)+{k}_{s}^{2}{r}_{2}^{2}{cos}^{2}\left({\theta }_{x}-x\right)sin\left({k}_{s}{r}_{2}cos\left({\theta }_{x}-x\right)+{k}_{s}D\right)\right]\right\}$$
(34)
$${a}_{va3}\left(t\right)=ift\left\{\frac{{3A}_{v}}{{k}_{p}^{3}{r}_{2}^{3}{cos\left({k}_{p}h\right)cos}^{3}\left({\theta }_{x}-x\right)}\left[2sin\left({k}_{p}D\right)-2sin\left({k}_{p}{r}_{2}cos\left({\theta }_{x}-x\right)+{k}_{p}D\right)+2{k}_{p}{r}_{2}cos\left({\theta }_{x}-x\right)cos\left({k}_{p}{r}_{2}cos\left({\theta }_{x}-x\right)+{k}_{p}D\right)+{k}_{p}^{2}{r}_{2}^{2}{cos}^{2}\left({\theta }_{x}-x\right)sin\left({k}_{p}{r}_{2}cos\left({\theta }_{x}-x\right)+{k}_{p}D\right)\right]\right\}$$
(35)
$${{r}_{2}=r}_{0}exp\left({\theta }_{x}tan\varphi \right)$$
(36)

aha3 and ava3 represent the horizontal and vertical components of the weighted average seismic acceleration for a sector of radius r2 and angle dθx in the time domain where r2 denotes the radius of the log-spiral at any θx. Consequently, MQ3 can be calculated through integration with respect to the single variable θx. The introduction of these average accelerations and the method for determining MW3 and MQ3 as described in Eqs. (31)–(36) for the radial shear zone of ADC can be viewed as additional innovations in this research.

2.3 Computations for Seismic Bearing Capacity

Figure 5 illustrates the forces acting on wedge ABC beneath the footing. Ppm and C4 represent the cohesive and frictional resistance forces on the left side of the failure mechanism. It is assumed that full mobilization is achieved for cohesion, while partial mobilization is considered for the friction components. The calculation for C4 is as follows:

$${C}_{4}=c\frac{h1}{sin\beta }$$
(37)

where h1 represents the heigh of ABC triangle passing through point C. The only remaining unknowns are the seismic bearing capacity que and Ppm. By applying the horizontal and vertical equilibrium equations to the forces acting on wedge ABC, these two variables can be determined. Therefore, que and the seismic bearing capacity factor Nγe can be obtained as:

$${q}_{ue}=\frac{1}{B\left(1-\frac{{a}_{vd}}{g}\right)sin\left(\beta -\varphi \right)+B\left(\frac{{a}_{hd}}{g}\right)cos\left(\beta -\varphi \right)}\left[2c{h}_{1}sin\left(\beta -\varphi \right)+{P}_{p}cos\left(\alpha -\varphi \right)sin\left(\beta -\varphi \right)+{Q}_{v4}sin\left(\beta -\varphi \right)-{W}_{4}sin\left(\beta -\varphi \right){-ch}_{1}cot\left(\alpha \right)cos\left(\beta -\varphi \right)+{P}_{p}sin\left(\alpha -\varphi \right)cos\left(\beta -\varphi \right)+c{h}_{1}cot\left(\beta \right)cos\left(\beta -\varphi \right)-{Q}_{h4}cos\left(\beta -\varphi \right)\right]$$
(38)
$${N}_{\gamma e}=\frac{{q}_{ue}}{\frac{1}{2}\gamma B}$$
(39)

where W4 denotes the weight of wedge ABC:

Fig. 5
figure 5

Seismic and static forces acting on ABC

Full size image
$${W}_{4}=\frac{\gamma B{h}_{1}}{2}$$
(40)

The inertial forces of wedge ABC, Qh4 and Qv4, are calculated in a similar manner to the seismic forces Qh1 and Qv1.

$${Q}_{h4}\left(t\right)={a}_{ha4}\left(t\right)\frac{{W}_{4}}{g}$$
(41)
$${Q}_{v4}\left(t\right)={a}_{va4}\left(t\right)\frac{{W}_{4}}{g}$$
(42)

where

$${a}_{ha4}\left(t\right)=ift\left\{\frac{{2A}_{h}}{{k}_{s}^{2}{h}_{1}^{2}cos\left({k}_{s}h\right)}\left[-cos\left({k}_{s}{h}_{1}+{k}_{s}D\right)-{h}_{1}{k}_{s}sin\left({k}_{s}D\right)+cos\left({k}_{s}D\right)\right]\right\}$$
(43)
$${a}_{va4}\left(t\right)=ift\left\{\frac{2{A}_{v}}{{k}_{p}^{2}{h}_{1}^{2}cos\left({k}_{p}h\right)}\left[-cos\left({k}_{p}{h}_{1}+{k}_{p}D\right)-{h}_{1}{k}_{p}sin\left({k}_{p}D\right)+cos\left({k}_{p}D\right)\right]\right\}$$
(44)

aha4 and ava4 represent the horizontal and vertical components of the weighted average acceleration for wedge ABC in the time domain. Eq. (39) defines Nγe as an integrated seismic bearing capacity factor encompassing cohesion, surcharge, and unit weight resistance components. It is important to highlight that the non-linear behavior of the soil precludes the use of the principle of superposition. As a result, a seismic bearing capacity coefficient is applied to all components.

3 Results and Discussion

The development of the extended pseudo-dynamic approach is the main achievement and innovation of this study. It can be used for estimating the seismic bearing capacity of shallow foundations. A computer program within the Matlab package has been developed to calculate the seismic bearing capacity of foundations according to the method proposed in this study. The program evaluates various values of the angles α, ψ, as well as the time step n treating them as independent geometric and temporal variables to estimate the minimum value of Nγe. The input excitation is the random ground motion data recorded during an earthquake. Depending on the seismic activity in the specific area of interest, a seismic acceleration time history can be chosen from the earthquake database. Baseline correction and frequency filtering are typically conducted utilizing signal processing software like Seismsignal. Subsequently, the data is adjusted to achieve the desired peak ground acceleration denoted by PGA. Following building codes, this procedure is commonly carried out using an average of three or more previously recorded acceleration time histories from the specific target region. In order to derive Ah(w) and Av(w), the scaled seismic acceleration is converted from the time domain to the Fourier domain. Additional parameters required for the program include D, B, c, φ, Vs, Vp, and ζ.

Figure 6 illustrates a flow chart detailing the program’s operation. Within the flow chart: J and K serve as counters for seismic variations in α and ψ; n is the time step; quem represents the minimum of que; Jm, Km, and nm correspond to the minimum of quem; m is an index assigned to aham(t) where m = 1, 2, 3, 4; fft represents the Fast Fourier Transform algorithm. The computations progress step by step in the time domain, enabling the consideration of alterations in soil shear and primary velocities, along with changes in cohesion and friction angle due to nonlinear behavior.

Fig. 6
figure 6

Flow chart of the program

Full size image

3.1 Verification of the Proposed Method

To validate the proposed method, the results of two shaking table experiments and previous analytical methods are compared with the proposed method. The first comparison is based on data from a shaking table test conducted by Knappett et al. (2006). Their study involved tests on a strip foundation placed on dry sand with specific parameters such as φ = 36°, Gs = 2.65, emax = 0.82, emin = 0.495, and a relative density of 67% (e = 0.6). Note that Gs, e, emax, and emin represent the specific gravity, void ratio, maximum void ratio, and minimum void ratio, respectively. The footing had a width of 5 cm and was placed on a 30 cm thick soil layer. The vertical stress exerted by the foundation on the supporting soil was approximately 8.42 kPa, slightly below the static bearing capacity of 10 kPa leading to failure triggered by the applied motion. The foundation experienced sinusoidal input motion at a frequency of 3.6 Hz for 3 s. The experimental observations were compared with analytical results proposed by Paolucci et al. (1997). Failure initiation occurred at an acceleration amplitude of 0.16 g, with the failure mechanism becoming evident at accelerations of 0.21 g, 0.26 g, and 0.3 g. It was noted that the failure mechanism changed during each cycle of the seismic acceleration. When the seismic acceleration increased from zero, the center of rotation of the failure surface was at the corner of the foundation. However, when the acceleration decreased from its peak, the center of rotation of the failure surface shifted from the corner of the foundation towards the center due to the moment of the inertial forces.

To apply the proposed method, the shear wave velocity, primary wave velocity, and damping ratio of the soil are approximated at 105 m/s, 196 m/s, and 10%, respectively, as proposed by Seed et al. (1986) considering the level of shear strain effective vertical stress. The results obtained from the proposed method, as presented in Table 1, closely align with the experimental observations across various acceleration amplitudes.

Table 1 Comparison of the proposed method results and the values measured in the shaking table test
Full size table

Another experimental study that can be used to validate the proposed method, was conducted by Al-Karni (2001). The experiment involved testing a foundation positioned on dry sand with properties such as Gs = 2.64, emax = 0.95, emin = 0.58, Dr = 67%, and φ = 40°. The foundation had an embedment depth of D = 0 and a width of B = 1 m. Two models were tested individually. In the first model, a load of 615 kN was exerted on the soil. In the second model, a load of 205 kN was applied from the foundation to the supporting soil. The input motion was a horizontal acceleration with a frequency of 3 Hz and a linearly increasing magnitude until reaching the critical accelerations that led to failure. The critical accelerations were determined to be 0.08 g for the first model and 0.25 g for the second model. The results are summarized in Table 2. It is worth noting that a shape factor of 0.6 can be utilized when using the equations associated with strip footings to determine the seismic bearing capacity of square footings. A close match is evident between the results obtained using the proposed method (607 and 192 kN) and the values measured in the experiments (615 and 205 kN).

Table 2 Comparison of the proposed method results and the values measured in the shaking table test
Full size table

Figure 7 shows a comparison of the seismic bearing capacity factors obtained by the proposed method with those obtained by available analytical methods, including the characteristic stress method by Kumar et al. (2002), the pseudo-static approach by Choudhury et al. (2005), the upper-bound limit analysis by Soubra (1997 and 1999), the modified pseudo-dynamic method by Pain (2016) and Nadgouda et al. (2021), and the node-based smoothed finite element method by Nguyen et al. (2022). The results were computed for φ = 30°, δ = 0.7φ, ahmax = 0, 0.1 g, 0.2 g, and 0.3 g, av = 0, ξ = 0.10, Vp/Vs = 1.87, Vs = 200 m/s, B = 2 m, h = 5 m, w = 6π rad/s, and D = 0. The proposed method’s results were obtained for both harmonic excitation and the 1990 Manjil earthquake, adjusted to the desired maximum acceleration. The proposed method’s results align well with other results when the acceleration is low.

Fig. 7
figure 7

Comparison of the results of the proposed method and the analytical results

Full size image

As the acceleration increases, the proposed method’s results for harmonic input exhibit slower degradation compared to other analytical solutions. The slight increase in the seismic bearing capacity factor could be attributed to the phase difference of seismic accelerations throughout the depth. In contrast, the proposed method’s results for the earthquake input motion depreciate rapidly due to the substantial amplitudes of seismic accelerations across a broad frequency range, triggering significant responses corresponding to the system’s natural frequencies. For a 5 m-thick soil layer, at an acceleration magnitude of 0.3 g, the bearing capacity diminishes to zero. However, with a soil layer thickness of 20 m, the seismic bearing capacity coefficient increases to 5.2 due to the alteration in the soil layer’s fundamental frequency.

3.2 A Parametric Study on a Large Earthquake

A parametric study was conducted using the 1990 Manjil earthquake with a magnitude of 7.6 as the input motion. Figure 8 shows the seismic accelerations recorded during the earthquake, as reported by the Iran Strong Motion Network database, scaled with peak horizontal and vertical ground accelerations of 0.6 g and 0.4 g, respectively. Soil properties were assumed to be φp = 35°, φr = 30°, cp = 20 kPa, cr = 10 kPa, Vs = 250 m/s, Vp = 1.87 Vs, damping ratio of 10%, and unit weight of γ = 17 kN/m3. The foundation width and embedment depth were 2.5 m and 1.5 m, respectively. The time history of Nγe obtained through the proposed method is shown in Fig. 9, highlighting the minimum value marked by a red circle. The Figure demonstrates that the proposed method can calculate the seismic bearing capacity at any given moment.

Fig. 8
figure 8

Manjil earthquake acceleration a horizontal component and b vertical component

Full size image
Fig. 9
figure 9

The time history of Nγe, obtained by proposed method

Full size image

The impact of shear wave velocity on Nγe was studied by assuming different shear wave velocities while keeping other parameters constant. Nγe values were calculated for shear wave velocities of 150, 250, and 350 m/s. Figure 10 illustrates the effect of soil shear wave velocity on Nγe for various h/Vs ratios, where T1 is defined as 4 h/Vs, representing the fundamental natural period of the soil deposit. The curves for different shear wave velocities show a consistent trend, influenced by ground motion characteristics such as frequency content and T1 or h/Vs. Changes in shear wave velocity or soil deposit thickness affect h/Vs or T1, leading to fluctuations in Nγe. Higher T1 values correspond to either decreases or increases in Nγe. During intense earthquakes, a reduction in Vs causes Nγe to shift towards higher h/Vs values. Critical h/Vs values ranged from 0.02 to 0.05, where seismic bearing capacity reached a minimum due to significant inertial forces effects, indicating a resonance condition. In these conditions, the seismic bearing capacity factor drops substantially to 15% of the static value, emphasizing the necessity of reinforcement techniques such as micropiles beneath the footing. In weaker soil seismic bearing capacity may diminish to zero during a major earthquake.

Fig. 10
figure 10

Effects of Vs on Nγe for different h/Vs

Full size image

Shear strength parameters have a significant impact on Nγe: Fig. 11a shows how the soil friction angle affects Nγe for different h/Vs ratios. Nγe exhibits a more pronounced fluctuating trend for φ = 40° compared to φ = 32° and φ = 35°. The variation of Nγe for a soil friction angle of φ = 32° follows a similar trend with h/Vs compared to φ = 35°, but with a smaller amplitude. During a large earthquake, the soil friction angle decreases due to large strains and plastic zones in the soil, leading to a shift in the Nγe path to lower levels.

Fig. 11
figure 11

Effects of the soil shear strength parameters on Nγe for different h/Vs a effects of the soil frictional angles, b effects of the soil cohesion

Full size image

Figure 11b illustrates the impact of soil cohesion on Nγe for various h/Vs ratios. Nγe increases with higher soil cohesion, with a consistent trend across different cohesion values of 12, 20, and 30 kPa. The minimum of Nγe occurs at h/Vs = 0.05 and 0.02 for all soil cohesion values. Similarly, during significant earthquakes, a decrease in soil cohesion can cause Nγe to decrease following a lower trend.

The impact of embedment depth on Nγe for different h/Vs ratios is shown in Fig. 12. Minimum Nγe values occur at h/Vs = 0.05 and 0.02 for all depths considered. Increasing the embedment depth leads to higher Nγe values, therefore, selecting the deepest possible embedment can enhance Nγe in seismic regions. For D = 2.5 m, the seismic bearing capacity has significantly increased for all h/Vs ratios compared to smaller D values. Furthermore, this figure clearly demonstrates that the depth of embedment is a key factor in seismic stability, and even deep foundations like piles and micropiles exhibit favorable seismic performance.

Fig. 12
figure 12

Effects of the depth embedment on Nγe for different h/Vs

Full size image

Figure 13 illustrates the relationship between the foundation width and Nγe. With an increase in the foundation width (B), Nγe decreases, but the overall seismic bearing capacity rises. This increase is due to the seismic bearing capacity formula (Que = 0.5γBNγe × B), which is derived by multiplying the Nγe factor by B2. At h/Vs = 0.05 the minimum of Nγe values and (Que) values are 32.9 (1118.6 kN/m), 24 (1275 kN/m), and 13.1 (1364 kN/m) for B = 2, 2.5, and 3.5 m, respectively. The rocking moment resulting from structural inertial forces reduces the effective foundation width, leading to a higher trend in Nγe. However, Que decreases due to this reduction in effective width.

Fig. 13
figure 13

Effects of foundation width on Nγe for different h/Vs

Full size image

The impact of the damping ratio on Nγe is depicted in Fig. 14 across various h/Vs ratios. As expected, an increase in the damping ratio leads to a higher Nγe value. Additionally, the.

Fig. 14
figure 14

Effects of damping ratio on Nγe for different h/Vs

Full size image

damping ratio mitigates the fluctuation of Nγe, resulting in a more gradual trend. The curve exhibits a smoother variation with ξ = 20% compared to ξ = 10%, and ξ = 5%. During a large earthquake, nonlinear soil behavior may elevate soil damping (Seed et al. 1986), causing a slight increase in Nγe. However, overall Nγe values decrease due to a decline in soil shear strength.

Figure 15 illustrates Nγe for different fundamental periods of the soil deposit (T = T1) as well as Ah and Av for Fourier periods (T). The values were normalized with the corresponding maximum value. The average of 15 sequential values was used to smooth the normalized Ah and Av. The minimum value of Nγe occurs at a period of T = 0.2 (h/Vs = 0.05) when the normalized Ah peaks at 1.0 and the normalized value of Av is equal to 0.32. Nγe has a high value at T = 0.057 when Ah and Av have small values. Nγe is significantly affected from T = 0.06 to T = 0.5 s due to the high magnitudes of Ah and Av for this T range.

Fig. 15
figure 15

Nγe and smoothed Ah and Av for different periods

Full size image

Figure 16 illustrates the Nγe values for different major earthquakes (reported by the Iran Strong Motion Network database) with the same PGA in Iran. The figure clearly shows a significant reduction in bearing capacity for most earthquakes across all T1 values. The earthquakes in Tabas (1978, Mw = 7.8), Bam (2003, Mw = 6.6), and Buin Zahra (2002, Mw = 6.5) particularly exhibit this pronounced reduction in seismic bearing capacity for almost all T1 values. On the other hand, the Manjil (1990, Mw = 7.6) earthquake demonstrates a similar drastic reduction but with a range of T1 = 0.06–0.3 s. For T1 values greater than 0.3, a higher seismic bearing capacity is observed. In Fig. 16, the minimum of Nγe for all earthquakes is depicted by a red line, showing a range of 78–88% reduction in seismic bearing capacity depending on the fundamental period of the soil deposit. Therefore, due to the substantial decrease in the foundation’s bearing capacity during major earthquakes, it becomes necessary to consider the use of deep foundations, such as piles or micropiles, to ensure greater stability, just as the root is necessary to protect the tree from wind.

Fig. 16
figure 16

Nγe for different large earthquakes scaled to PGA = 0.6g

Full size image

4 Conclusions

An extended pseudo-dynamic approach was proposed to calculate the seismic bearing capacity for strip foundations on φ-c soils. This approach allows for analysis in the time domain and can directly consider earthquake acceleration records as input excitation. Furthermore, by solving the problem step by step in time, it can account for nonlinear behavior and the reduction of soil resistance and stiffness during large earthquakes. This approach can be combined with numerical methods, limit analysis, and many techniques, in future research to create a more efficient tool for seismic analysis. Additionally, this method can be applied to other seismic geotechnical issues. A limitation of the presented method is that the soil subgrade was considered as a dry viscoelastic medium. Future research could investigate the effects of water saturation. The results of the parametric study for a major earthquake show that the variation of the seismic bearing capacity factor for different ratios of deposit thickness to shear wave velocity follows a distinct trend based on the ground motion’s frequency content and the fundamental period of the soil deposit. The study also discusses the effects of foundation width, foundation embedment, and soil damping ratio. Increasing the foundation width leads to a decrease in seismic bearing capacity, but the overall seismic bearing capacity increases. The damping ratio helps mitigate the fluctuation of seismic bearing capacity resulting in a more gradual trend. Increasing the embedment depth leads to higher seismic bearing capacity values. Therefore, selecting the deepest possible embedment can enhance seismic bearing capacity in seismic regions. The significant decrease in the foundation's bearing capacity during major earthquakes highlights the importance of considering the use of deep foundations like piles or micropiles for enhanced stability and safety.