1 Introduction

The effect of natural calamity like earthquakes on the bearing capacity of a surface to a very shallow strip footing was studied here: as this knowledge is very important in designing the footing under seismic conditions. The damages associated with foundation failure under seismic conditions are very much common and may cause tremendous loss of life and wealth. Hence, the importance of research in the area of seismic bearing capacity cannot be ignored at all. A number of investigations were performed by several researchers [1, 4, 6–9, 13, 14, 16–18] to predict the seismic bearing capacity of shallow footings using pseudo-static approach with the help of different solution techniques such as method of slices, limit equilibrium, method of stress characteristics and upper bound limit analysis. However, in the pseudo-static analysis, the dynamic loading induced by earthquake is considered as time independent, which ultimately assumes that the magnitude and phase of acceleration are uniform throughout the soil layer. To overcome this constraint, Choudhury and Nimbalkar [3] and Steedman and Zeng [19] came out with pseudo-dynamic solutions where the effects of both shear and primary waves as well as the amplification of excitation were considered during the earthquake along with the duration of earthquake and period of lateral shaking to predict the seismic earth pressure behind a vertical retaining wall. It is worth mentioning here that the amplification of vibration generally takes place towards the ground surface which depends on various soil properties such as stiffness, damping, elastic and shear modulus [15, 19]. However, the importance of determining the bearing capacity of shallow footing under the seismic condition and influence of amplification of vibration using pseudo-dynamic approach have not drawn much attention from the researchers though the results obtained by this approach predict the seismic effect on the footing more realistically.

The present study explores the effects of soil friction angle (ϕ), horizontal earthquake acceleration coefficient (α h), vertical earthquake acceleration coefficient (α v), shear wave velocity (V s), primary wave velocity (V p) and amplification factor (f a) on the seismic bearing capacity factor N γE using the pseudo-dynamic approach. Upper bound limit analysis was used in association with the failure mechanism similar to Soubra [16] to determine the seismic bearing capacity factor N γE of surface to very shallow strip footing. The advantage of using the upper bound technique to the limit equilibrium method, proposed by Richards et al. [13] is that the kinematic admissibility of the failure mechanism can be assured and the solution is a rigorous upper bound solution for an associated flow rule material. Also the present analysis does not require an assumption regarding the interwedge frictional force as proposed by Richards et al. [13].

It is quite expected that the soil properties such as damping, elastic and shear modulus do not remain constant through out the depth of the soil layer rather they go on changing from the footing surface to the greater depth [15, 19]. However, the influence of the distribution of those soil properties was not explored in this paper as it requires different solution techniques, which can be a further extension of this work.

2 Definition of the problem

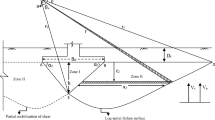
A rough strip footing (AB) of width b rests horizontally on a dry, cohesionless soil layer as shown in Fig. 1. The objective is to determine the seismic bearing capacity factor N γE in the presence of horizontal and vertical earthquake accelerations with a linear variation of accelerations from the bottom extreme point (z = H) to the footing surface (z = 0) (Fig. 1a). The parameters shown in Fig. 1 are considered as positive and the unit weight of the soil is taken as γ.

Fig. 1
figure 1

Collapse mechanism and velocity hodograph

Full size image

3 Assumptions

  1. (a)

    The footing is placed on the ground surface or at a very shallow depth. The shear resistance offered by the soil medium above the footing level was not considered.

  2. (b)

    The shear modulus (G) of the soil medium was constant with depth.

  3. (c)

    The nature of the amplification depends on many factors such as stiffness and damping of the soil mass, depth of the soil layer, geometry and rigidity of adjacent structures. However, a simplified linear variation of amplification of vibration was considered.

  4. (d)

    The soil mass follows Mohr–Coulomb’s failure criterion and an associated flow rule.

4 Theories and collapse mechanism

4.1 Pseudo-dynamic analysis

The formulation of pseudo-dynamic analysis, which considers a finite shear wave velocity, can be developed with constant shear modulus G. The present analysis considers both shear wave velocity \( V_{{\text{s}}} \, = \,{\sqrt {\frac{{\text{\it G}}} {\rho }} } \) and primary wave velocity\( V_{{\text{p}}} \, = \,{\sqrt {\frac{{{\text{\it G}}{\left( {2\, - \,2\nu } \right)}}} {{\rho {\left( {1\, - \,2\nu } \right)}}}} }, \) where ρ and ν are the density and Poisson’s ratio of soil medium, acting within the soil layer during earthquake in the direction as shown in Fig. 1a. The analysis includes a period of lateral shaking T, which can be expressed as \( T\, = \,\frac{{2\pi }} {\omega }. \)

Steedman and Zeng [19] proposed that for a sinusoidal base shaking subjected to linearly varied horizontal and vertical earthquake accelerations with amplitude of \( \,{\left[ {1\, + \,\frac{{{\left( {H\, - \,z} \right)}}} {H}{\left( {f_{{\text{a}}} \, - \,1} \right)}} \right]}\alpha _{{\text{h}}} g \) and \( \,{\left[ {1\, + \,\frac{{{\left( {H\, - \,z} \right)}}} {H}{\left( {f_{{\text{a}}} \, - \,1} \right)}} \right]}\alpha _{{\text{v}}} g, \), respectively, the acceleration at any depth z below the ground surface and time t can be expressed as

$$ a_{{\text{h}}} {\left( {z,\,t} \right)}\, = \,{\left[ {1\, + \,\frac{{{\left( {H\, - \,z} \right)}}} {H}{\left( {f_{{\text{a}}} \, - \,1} \right)}} \right]}\alpha _{{\text{h}}} g\sin \omega {\left( {t\, - \,\frac{{H\, - \,z}} {{V_{{\text{s}}} }}} \right)} $$
(1)
$$ a_{{\text{v}}} {\left( {z,\,t} \right)}\, = \,{\left[ {1\, + \,\frac{{{\left( {H\, - \,z} \right)}}} {H}{\left( {f_{{\text{a}}} \, - \,1} \right)}} \right]}\alpha _{{\text{v}}} g\sin \omega {\left( {t\, - \,\frac{{H\, - \,z}} {{V_{{\text{p}}} }}} \right)} $$
(2)

The mass of the small shaded part of thickness dz (Fig. 1a) in the triangular failure wedge ABC is given by

$$ m{\left( z \right)}\, = \,\frac{{\gamma {\left( {H_{{\text{a}}} \, - \,z} \right)}}} {{g\tan \alpha }}dz $$
(3)

The total weight of the failure wedge W 1 can be derived from Eq. 3 and is given by

$$ W_{1} \, = \,\frac{{\gamma H^{2}_{{\text{a}}} }} {{2\tan \alpha }} $$
(4)

The horizontal inertia force exerted on the small element due to horizontal earthquake acceleration can be expressed as m(z)a h(z, t). Therefore, the total horizontal inertia force Q h1(t) acting in the failure wedge ABC is given by

$$ Q_{{{\text{h1}}}} {\left( t \right)}\, = \,{\int\limits_0^{H_{{\text{a}}} } {\,{\left[ {1\, + \,\frac{{{\left( {H\, - \,z} \right)}}} {H}{\left( {f_{{\text{a}}} \, - \,1} \right)}} \right]}\alpha _{{\text{h}}} g\sin \omega {\left( {t\, - \,\frac{{H\, - \,z}} {{V_{{\text{s}}} }}} \right)}\,\frac{{\gamma {\left( {H_{{\text{a}}} \, - \,z} \right)}}} {{g\tan \alpha }}{\rm d}z} } $$
(5)

After integration, Eq. 5 may be expressed as

$$ Q_{{{\text{h1}}}} {\left( t \right)}\, = \,\frac{{\alpha _{{\text{h}}} \gamma }} {{\tan \alpha }}{\left[ {{\left( {H_{{\text{a}}} \, - \,H} \right)}I_{1} \, - \,I_{2} } \right]} $$
(6a)

where,

$$ \begin{aligned}{} I_{1} \, = & \,\frac{\lambda } {{2\pi }}{\left[ {\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}\, - \,\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}} \right]} \\ \,\,\,\,\;\; & + \,\frac{\lambda } {{4\pi ^{2} H}}{\left( {f_{{\text{a}}} \, - \,1} \right)}{\left[ \begin{aligned}{} & 2\pi {\left\{ {H\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}\, - \,{\left( {H\, - \,H_{{\text{a}}} } \right)}\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}} \right\}} \\ & \, + \,\lambda {\left\{ {\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}\, - \,\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}\,\,} \right\}} \\ \end{aligned} \right]} \\ \end{aligned} $$
(6b)
$$ \begin{aligned}{} I_{2} \, = \, & \frac{\lambda } {{4\pi ^{2} }}{\left[ \begin{aligned}{} & 2\pi {\left\{ {{\left( {H\, - \,H_{{\text{a}}} } \right)}\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}\, - \,H\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}} \right\}} \\ & + \,\lambda {\left\{ {\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}\, - \,\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}\,} \right\}} \\ \end{aligned} \right]} \\ \,\,\,\,\;\; & + \,\frac{\lambda } {{4\pi ^{3} H}}{\left( {f_{{\text{a}}} \, - \,1} \right)}{\left[ \begin{aligned}{} & 2\pi {\left( {H\, - \,H_{{\text{a}}} } \right)}{\left\{ {\pi {\left( {H\, - \,H_{{\text{a}}} } \right)}\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}\, + \,\lambda \sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}} \right\}} \\ & - \,2\pi H{\left\{ {\pi H\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}\, + \,\lambda \sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}} \right\}} \\ & \, + \,\lambda ^{2} {\left\{ {\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)}\, - \,\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\lambda }} \right)}\,\,} \right\}} \\ \end{aligned} \right]} \\ \end{aligned} $$
(6c)

where λ = TV s is the wavelength of the shear wave. Similarly, the total vertical inertia force Q v1(t) acting in the failure wedge ABC is given by

$$ Q_{{{\text{v1}}}} {\left( t \right)}\, = \,{\int\limits_0^{H_{{\text{a}}} } {{\left[ {1\, + \,\frac{{{\left( {H\, - \,z} \right)}}} {H}{\left( {f_{{\text{a}}} \, - \,1} \right)}} \right]}\alpha _{{\text{v}}} g\sin \omega {\left( {t\, - \,\frac{{H\, - \,z}} {{V_{{\text{p}}} }}} \right)}\,\frac{{\gamma {\left( {H_{{\text{a}}} \, - \,z} \right)}}} {{g\tan \alpha }}{\rm d}z} } $$
(7)

After integration, Eq. 7 may be expressed as

$$ Q_{{{\text{v1}}}} {\left( t \right)}\, = \,\frac{{\alpha _{{\text{v}}} \gamma }} {{\tan \alpha }}{\left[ {{\left( {H_{{\text{a}}} \, - \,H} \right)}{I}\ifmmode{'}\else$'$\fi_{1} \, - \,{I}\ifmmode{'}\else$'$\fi_{2} } \right]} $$
(8a)

where

$$ \begin{aligned}{} {I}\ifmmode{'}\else$'$\fi_{1} \, = \, & \frac{\eta } {{2\pi }}{\left[ {\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}\, - \,\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}} \right]} \\ \,\,\,\,\;\; & + \,\frac{\eta } {{4\pi ^{2} H}}{\left( {f_{{\text{a}}} \, - \,1} \right)}{\left[ \begin{aligned}{} & 2\pi {\left\{ {H\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}\, - \,{\left( {H\, - \,H_{{\text{a}}} } \right)}\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}} \right\}} \\ & \, + \,\eta {\left\{ {\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}\, - \,\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}\,\,} \right\}} \\ \end{aligned} \right]} \\ \end{aligned} $$
(8b)
$$ \begin{aligned}{} {I}\ifmmode{'}\else$'$\fi_{2} \, = \, & \frac{\eta } {{4\pi ^{2} }}{\left[ \begin{aligned}{} & 2\pi {\left\{ {{\left( {H\, - \,H_{{\text{a}}} } \right)}\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}\, - \,H\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}} \right\}} \\ & + \,\eta {\left\{ {\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}\, - \,\sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}\,} \right\}} \\ \end{aligned} \right]} \\ \,\,\,\,\;\; & + \,\frac{\eta } {{4\pi ^{3} H}}{\left( {f_{{\text{a}}} \, - \,1} \right)}{\left[ \begin{aligned}{} & 2\pi {\left( {H\, - \,H_{{\text{a}}} } \right)}{\left\{ {\pi {\left( {H\, - \,H_{{\text{a}}} } \right)}\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}\, + \,\eta \sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}} \right\}} \\ & - \,2\pi H{\left\{ {\pi H\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}\, + \,\eta \sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}} \right\}} \\ & \, + \,\eta ^{2} {\left\{ {\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)}\, - \,\cos 2\pi {\left( {\frac{t} {T}\, - \,\frac{{H\, - \,H_{{\text{a}}} }} {\eta }} \right)}\,\,} \right\}} \\ \end{aligned} \right]} \\ \end{aligned} $$
(8c)

where, η = TV p is the wavelength of the primary wave.

In a very similar fashion, if the triangular failure wedge BCD is considered, the total weight of the failure wedge W 2 can be expressed as

$$ W_{2} \, = \,\frac{{\gamma H^{2}_{{\text{a}}} }} {{2\tan \beta }} $$
(9)

and, the total horizontal Q h2(t) and vertical Q v2(t) inertia force acting in the failure wedge BCD can be obtained from Eqs. 6 and 8, respectively, by simply replacing α with β.

4.2 Upper bound theorem of limit analysis

The theorem says, if a compatible mechanism of plastic deformation \( \ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{p*}}_{{ij}} ,\ifmmode\expandafter\dot\else\expandafter\.\fi{v}^{{p*}}_{i} , \) is assumed, which satisfies the condition \( \ifmmode\expandafter\dot\else\expandafter\.\fi{v}^{{p*\,}}_{i} = \,0 \) on the displacement boundary S v; then the loads T i , F i determined by equating the rate at which the external forces do work at the rate of internal dissipation of energy will be either higher or equal to the actual limit load [2], and this can be written as

$$ {\int\limits_V {\sigma ^{{p*}}_{{ij}} \ifmmode\expandafter\dot\else\expandafter\.\fi{\varepsilon }^{{p*}}_{{ij}} {\text{d}}V\, \ge \,} }{\int\limits_{\text{S}} {T_{{{i}}} \ifmmode\expandafter\dot\else\expandafter\.\fi{v}^{{p*}}_{i} {\text{d\it S}}\, + \,{\int\limits_V {F_{{{i}}} \ifmmode\expandafter\dot\else\expandafter\.\fi{v}^{{p*}}_{i} {\text{d}}V} }} } $$
(10)

4.3 Collapse mechanism

The collapse mechanism was chosen to comprise two triangular rigid blocks ABC and BCD as shown in Fig. 1a. At collapse, the footing and the underlying rigid block ABC were assumed to move in phase with each other with the same absolute velocity U 1, whereas U 2 is the absolute velocity of the triangular block BCD. U 21 is the relative velocity of the block BCD with respect to the block ABC and the velocity hodograph is shown in Fig. 1b. The interface (BC) of both the blocks as well as the lines AC and CD were treated as velocity discontinuity lines. The directions of U 1, U 2, and U 21 make an angle ϕ with the corresponding velocity discontinuity lines. The collapse mechanism can be completely defined by means of α and β where α and β are the values of ∠BAC and ∠BDC (Fig. 1a).

By using the upper bound theorem of limit analysis, the failure load (P u) was computed by using the following expression:

$$ P_{{\text{u}}} = \,\frac{{{\left[ \begin{aligned}{} & U_{1} {\left\{ {Q_{{{\text{v1}}}} \sin {\left( {\alpha \, - \,\phi } \right)}\, - Q_{{{\text{h1}}}} \cos {\left( {\alpha \, - \,\phi } \right)} - W_{1} \sin {\left( {\alpha \, - \,\phi } \right)}} \right\}}\, \\ & \,\;\quad \quad \quad \quad + \,U_{2} {\left\{ {\,W_{2} \sin {\left( {\beta \, + \,\phi } \right)}\, - Q_{{{\text{v2}}}} \sin {\left( {\beta \, + \,\phi } \right)} - Q_{{{\text{h2}}}} \cos {\left( {\beta \, + \,\phi } \right)}} \right\}} \\ \end{aligned} \right]}}} {{U_{1} {\left[ {\sin {\left( {\alpha \, - \,\phi } \right)}\, + \,\xi _{{\text{h}}} \cos {\left( {\alpha \, - \,\phi } \right)}\, - \,\xi _{{\text{v}}} \sin {\left( {\alpha \, - \,\phi } \right)}} \right]}}} $$
(11)

where ξ h and ξ v are the coefficients of horizontal and vertical contribution of ultimate vertical failure load P u caused due to seismic condition (Fig. 1a) and can be expressed as \( \xi _{{\text{h}}} \, = \,f_{{\text{a}}} \alpha _{{\text{h}}} \sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\lambda }} \right)} \) and \( \xi _{{\text{v}}} \, = \,f_{{\text{a}}} \alpha _{{\text{v}}} \sin 2\pi {\left( {\frac{t} {T}\, - \,\frac{H} {\eta }} \right)} \) , respectively. In Eq. 11, the vertical components of the velocities were taken as positive in the downward direction, and the horizontal components of the velocities were considered positive from left to right of Fig. 1. It can be observed from Eq. 11 that P u is a function of α, β, t/T, H/λ and H/η. H/λ is simply the ratio of time taken by the shear wave to travel the depth of failure wedge to the period of lateral shaking T, whereas H/η is the ratio of time taken by the primary wave to travel the depth of failure wedge to T. It is known that for most of the geological materials, V p/V s can be taken as 1.87 and the same ratio was maintained throughout the analysis [5]. By varying independently the three variables, namely α, β, and t/T, the magnitude of P u was then minimized. It was ensured that the magnitudes of all the velocity terms, in terms of U 1, must remain always positive. While doing the computations, the values of angles α and β were varied with minimum interval of 0.1°. On the other hand, the minimum interval for t/T was chosen equal to 0.01. In terms of failure load, the bearing capacity factor N γ can be expressed as

$$ N_{{\gamma E}} \, = \,\frac{{2P_{{\text{u}}} }} {{\gamma b^{2} }} $$
(12)

5 Results

The computations were carried out for ϕ = 10°–40°, α h = 0.0–0.5, α v = 0.0–α h, f a = 1.0–2.0, H/λ = 0.3–0.6, H/η = 0.16–0.32. In the case of cohesionless soils, the equation proposed by Richards et al. [12] to avoid the shear fluidization, (i.e. the plastic flow of the material at a finite effective stress) for certain combinations of α h and α v can be modified for amplification as follows:

$$ \phi \ge \tan ^{{ - 1}} {\left[ {\frac{{f_{{\text{a}}} \alpha _{{\text{h}}} }} {{1 - f_{{\text{a}}} \alpha _{{\text{v}}} }}} \right]} $$
(13)

In the present study, the combinations of α h and α v were considered to satisfy the relationship given in Eq. 13.

The variations of the bearing capacity factor N γ with α h and α v for different values of ϕ and soil amplification factor (f a) with H/λ = 0.3 and H/η = 0.16 are presented in Fig. 2. From these results it can be observed that the presence of seismic forces causes significant reduction in the seismic bearing capacity factor which in turn reduces the seismic bearing capacity for a shallow strip footing. The present study shows a significant influence of the vertical seismic acceleration on the seismic bearing capacity particularly for α h > 0.1. As expected, with increase in ϕ, the seismic bearing capacity factor was found to increase for all cases of amplification factor. However, a significant increase in the magnitude of N γE can be observed for ϕ = 40°.

Fig. 2
figure 2

Variation of N γE with α h and α v for different values of ϕ with H/λ = 0.3, H/η = 0.16, a f a = 1.0, b f a = 1.2, c f a = 1.4, d f a = 1.6, e f a = 1.8, f f a = 2.0

Full size image

Figure 3 shows the effect of soil amplification on the seismic bearing capacity factor N γE for different values of α h with ϕ = 30°, α v = 0.5α h, H/λ = 0.3 and H/η = 0.16. It can be seen that the seismic bearing capacity factor continuously decreases with increase in the soil amplification and α h. Proper attention must be given to determine the effect of soil amplification on N γE for designing a shallow strip footing as a significant reduction in the magnitude of seismic bearing capacity due to soil amplification which may lead to the catastrophic failure.

Fig. 3
figure 3

Effect of soil amplification on N γE for different values of α h with ϕ = 30°, α v = 0.5α h, H/λ = 0.3 and H/η = 0.16

Full size image

The effect of variation in the dimensionless parameters H/λ and H/η on the seismic bearing capacity factor for different values of α h with ϕ = 30°, f a = 1.4 and α v = 0.5α h is given in Table 1. It can be observed from the results that the magnitude of N γE decreases significantly with decrease in H/λ and H/η, i.e. with increase in both the shear and primary wave velocities travelling through the soil layer and this important observation cannot be made by using the conventional pseudo-static analysis. Table 2 shows the effect of soil amplification factor (f a) on seismic bearing capacity factor for different values of H/λ and H/η with ϕ = 30°, α h = 0.2 and α v = 0.5α h. The results also show that a substantial decrease in the seismic bearing capacity with increase in the soil amplification.

Table 1 Effect of variation in H/λ and H/η on N γE for different values of α h with ϕ = 30°, f a = 1.4 and α v = 0.5αh
Full size table
Table 2 Effect of f a on N γE for different values of H/λ and H/η with ϕ = 30°, α h = 0.2 and α v = 0.5α h
Full size table

For the critical collapse mechanisms, the values of α and β associated with the computation of N γE are given in Table 3, with α v = 0.5α h, H/λ = 0.3 and H/η = 0.16. The values of α and β were found to decrease with the increase in f a and α h. On the other hand, for greater values of ϕ, the magnitudes of α become higher and simultaneously the values of β become lower.

Table 3 Values of α and β for the critical collapse mechanism with α v = 0.5α h, H/λ = 0.3 and H/η = 0.16
Full size table

6 Comparison

The application of pseudo-dynamic analysis in bearing capacity problem has not drawn much attention from the researchers, which makes the results for the seismic bearing capacity by the pseudo-dynamic method still scarce in the literature. In Table 4, the present values of seismic bearing capacity factor N γE for f a = 1.0, H/λ = 0.3 and H/η = 0.16 were compared with the pseudo-static results reported by Budhu and Al-Karni [1] and Choudhury and Subba Rao [4] for different values of α h and α v with ϕ = 30°. The present values were found to be on the higher side, which may be due to the fact that the present analysis considers time-dependent dynamic loading induced by earthquake instead of a single peak value of seismic accelerations used in the pseudo-static method and also the failure mechanism employed in the present analysis was different from that generally used in the conventional approach. In Fig. 4, the present values of N γE were compared with pseudo-static results reported in the literature [1, 2, 4, 7–11, 13, 14, 18, 20] for f a = 1.0, α v = 0.0, H/λ = 0.3 and H/η = 0.16 with ϕ = 30°. As expected, being an upper bound solution the present values of N γE obtained by pseudo-dynamic analysis are greater than the existing values. It is worthwhile to mention here that the similar trend was also observed by Soubra [16]. Using the upper bound technique, for higher value of ϕ, it was noticed that the present collapse mechanism predicts higher values of N γE than those obtained from the conventional failure mechanism adopted for determining the seismic bearing capacity. However, the present study considers the dynamic properties of soil more realistically compared to the pseudo-static approach and assures the kinematic admissibility of the solutions.

Table 4 Comparison of seismic bearing capacity factor N γE for different values of α h and α v with ϕ = 30°
Full size table
Fig. 4
figure 4

Comparison of N γE with f a = 1.0, α v = 0.0, H/λ = 0.3 and H/η = 0.16 for ϕ = 30°

Full size image

7 Conclusion

By considering the pseudo-dynamic approach, the effect of soil friction angle, horizontal and vertical seismic accelerations, soil amplification, shear and primary wave velocities travelling through the soil layer during earthquake on the seismic bearing capacity factor N γE for a surface to very shallow strip footing was examined. The analysis was carried out by using the upper bound limit analysis. The values of N γE were found to decrease extensively with increase in both α h and α v. It was also observed that the magnitude of N γE decreases with increase in soil amplification, shear and primary wave velocities, which cannot be predicted by the existing pseudo-static approach. For higher values of ϕ, a significant increase in the seismic bearing capacity factor N γE was observed at lower value of α h. The values obtained from the present analysis were compared with the available results reported by pseudo-static method of analysis.