1 Introduction

It has long been known that dense molecular clouds (DMCs) in interstellar medium (ISM) are the birth sites of stars and like bounded structures formed via the process of self-gravitational instabilities and fluctuations. Being highly dense, the DMCs become gravitationally unstable, with a propensity to gradual collapse leading to formation of stars. The fragmentation, clumping and filamentation processes of the global cloud into cloudlets occur due to the fact that the gravitational energy (organizing) supersedes the thermal energy (randomizing) of the cloud. In this direction, many authors have studied the gravitational collapse mechanism of isothermal DMCs in the framework of a hydrostatic homogeneous equilibrium macrostate (Shu et al. 1987; Binney and Tremaine 1987; Pandey et al. 1994; Bliokh et al. 1995; Nakano 1998; Spitzer 2004; Shukla and Stenflo 2006). It has been shown that the DMCs exhibit a new type of dynamic mode, called the pulsational mode (Dwivedi et al. 1999; Pandey et al. 2002), the excitation of which requires the presence of both massive neutral dust grains (sourcing to inward self-gravity) and massive charged grains (sourcing to both inward gravity and outward electric field) relative to the center of cloud fluid matter distribution. In other words, the onset threshold for such overlapped hybrid instabilities requires an exact gravito-electrostatic force-balanced condition for the biggish dusty species (Gisler et al. 1992; Pandey et al. 1994). It has also been reported later that the conjugational mode gets damped due to dust-charge variation (Pandey et al. 2002). Besides, the pulsational mode in idealized cloud configurations has also been shown to saturate in the form of solitary spectral patterns in the nonlinear regime of perturbation (Karmakar and Borah 2013; Borah and Karmakar 2015). It is seen that the eigen-spectrum coevolves as electrostatic rarefactive damped oscillatory shock-like structures and self-gravitational compressive damped oscillatory shock-like patterns. In the presence of massive bi-polar multi-dust grains with partial ionization, the weakly nonlinear eigen-spectrum has been found to coevolve as electrostatic rarefactive damped oscillatory shock-like structures and self-gravitational compressive damped oscillatory shock-like patterns (Haloi and Karmakar 2017). In the fully nonlinear regime, the excitation of compressive dispersive transitional shock-like eigen-mode structures in similar astro-situations has also been reported (Karmakar and Haloi 2017a). It can thus be seen, to the best of our knowledge, that the existing reports on the pulsational mode dynamics are indeed analytically quite simplified in nature due to various important excluded factors yet to be inclusively studied, such as kinematic viscosity, nonthermal distribution laws, turbulence, and so forth (Frenkel 1946; Vasyliunas 1968; Vazquez-Semadeni and Gazol 1995; Myers and Gammie 1999; Pierrad and Lazar 2010). As a consequence, a full description of the conjunctional mode behaviors with micro-illustrations has been lying as a long-sought goal for years yet to achieve.

The focal aim of this so-motivated paper is to study the pulsational mode dynamics excitable in an unbounded nonthermal complex partially ionized DMC in the turbulent multi-fluidic framework. The main motivation behind the proposed work is that the interstellar media are highly nonthermal because of diversified nonlocal effects (Vasyliunas 1968; Leubner 2004; Pierrad and Lazar 2010; Livadiotis and McComas 2013) and turbulent because of multiple irregular flow scales (Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996; Vazquez-Semadeni and Passot 1999) in nature, which as a consequence, affects the non-homological cloud collapse drastically. The lighter electrons and ions are governed by the \(\kappa\)-distribution laws originated from the anti-equilibrium thermostatistics sourced in diversified nonlocal effects (Vasyliunas 1968; Leubner 2004; Pierrad and Lazar 2010; Livadiotis and McComas 2013). In contrast, the constituent heavier neutral and charged grains are dealt with the turbulent viscous multi-fluidic formalism based on an asymptotically small value of the characteristic mean-free paths. Application of normal mode analysis around the defined homogeneous static equilibrium is carried out to arrive at a generalized dispersion relation with diversified multi-parametric coefficients. A numerical illustrative scheme is provided to see the basic characteristic features of the pulsational (gravito-electrostatic) mode dynamics pictorially in a judicious astrophysical multi-parametric space. The theoretical analysis reveals mainly that both the kinematic viscosities of the dust fluids and nonthermality parameters (power-law tail spectral exponents) of the usual thermal species play stabilizing (damping) roles to the fluctuations; and so forth. The paper expansively ends up with the main implications and applications essentially significant for hierarchical bounded structure formation mechanics in diversified space, astrophysical and cosmic naturalistic environments.

2 Model and formalism

We consider a self-gravitating four-component unmagnetized unbounded dusty plasma system of infinite spatial extension in homogeneous hydrostatic equilibrium under spatially-flat (sheet-like) geometric approximation. It is comprised of the kappa-distributed electrons and ions; and inertial neutral and charged dust grains in a globally quasi-neutral condition in planar framework. It is hereby presumed that the radius of the geometric cloud curvature is much larger than all the characteristic scale lengths associated with the complex multi-fluidic dynamics. The linear frictional couplings of electronic and ionic species with the dust components are ignored for simplicity. The neutral and charged massive dust grains are treated as turbulent viscous fluids of distinct sporadic characteristics. The dust grains are arrogated to be micron-sized microspheres of identical geometric shape so that they acquire homo-polar indistinguishable electric charges due to dynamic interactions of the sporadic electron-ion thermal currents over the grain surfaces (Draine and Salpeter 1979; Bliokh et al. 1995; Krugel 2003; Spitzer 2004). Their kinematic viscosities are assumed to be constant on the observation scales of space and time. The net pressures associated with the dust fluids are modelled with the help of the Larson logatropic equation of state comprising of an isothermal component for the fluid thermal pressure (linear) and a logatropic component for the fluid turbulence pressure (nonlinear) contributions (Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996). The key sources responsible for generation of turbulence, particularly in the form of aperiodic irregular motions here, may be fluid convection, collision, or even shearing effects. The linear processes behind collisional effects of neutral and charged dust grains are considered. The model is idealized to avoid analytic complications, such as ion-drag force, dust-size distribution, Coriolis effects, etc. The mechanisms responsible for dust self-fragmentation, nucleation and growth processes (Bliokh et al. 1995) are also ignored. Such adoption of electro-dynamical response of the plasma constituents is quite justifiable for the Jeansian low-frequency pulsational fluctuations with the differential mass- and temperature-scaling laws, with all the usual notations given as, \(m_{e} / m_{d} < m_{i} / m_{d}\sim 10^{ - 20} \to 0\) and \(T_{e}, T_{i} \gg T_{d}\) (Gisler et al. 1992; Pandey et al. 1994). Here, \(m_{e}\), \(m_{i}\) and \(m_{d}\) are the inertial masses of the electrons, ions and identical dust grains (in kg); respectively. Further, \(T_{e}\), \(T_{i}\) and \(T_{d}\) are the temperatures of electrons, ions and identical dust grains (in eV); respectively. The macroscopic state of the electronic and ionic thermostatistical dynamics in such a nonthermal complex plasma medium is described by the nonlocality-induced \(\kappa\)-distribution (non-Maxwellian) laws in the customary symbolic scheme (Shukla and Stenflo 2006; Baluku and Hellberg 2008; Pierrad and Lazar 2010; Livadiotis and McComas 2013; Dutta et al. 2016) given respectively in an astrophysically relevant dimensional form as

$$\begin{aligned} &{n_{e} = n_{e0} \biggl[ 1 - \frac{e\phi}{T_{e} ( \kappa_{e} - \frac{3}{2} )} \biggr]^{ - ( \kappa_{e} - \frac{1}{2} )},} \end{aligned}$$
(1)
$$\begin{aligned} &{n_{i} = n_{i0} \biggl[ 1 + \frac{e\phi}{T_{i} ( \kappa_{i} - \frac{3}{2} )} \biggr]^{ - ( \kappa_{i} - \frac{1}{2} )},} \end{aligned}$$
(2)

where, \(n_{e0} ( n_{i0} )\) is the equilibrium number density of electrons (ions). \(T_{e} ( T_{i} )\) is the electron (ion) temperatures (in eV). Further, \(\phi\) denotes the electrostatic potential created by the charged density fields of the astrophysical constituent fluids conjointly. Lastly, \(\kappa_{e} ( \kappa_{i} )\) is the nonextensivity parameter (power-law tail index) for electron (ion) arising because of the Tsallis thermostatistics (Vasyliunas 1968; Leubner 2004; Pierrad and Lazar 2010; Livadiotis and McComas 2013). The inertial electrodynamic response of the neutral dust fluid under the usual scheme of physical notations is represented with the help of continuity equation (for flux conservation) and momentum equation (for force conservation) in spatially-flat coordination space (\(x, t\)) relative to the center of the entire cloud mass distribution respectively cast as

$$\begin{aligned} &{\frac{\partial n_{dn}}{\partial t} + \frac{\partial}{\partial x} ( n_{dn}v_{dn} ) = 0,} \end{aligned}$$
(3)
$$\begin{aligned} &{m_{dn}n_{dn}\biggl[ \frac{\partial v_{dn}}{\partial t} + v_{dn}\frac{\partial v_{dn}}{\partial x} \biggr] + \frac{\partial P_{dn}}{\partial x} + m_{dn}n_{dn}\frac{\partial \psi}{\partial x} } \\ &{\quad{}+ m_{dn}v_{dn}\upsilon_{nc} ( v_{dn} - v_{dc} ) = \eta_{dn}\frac{\partial^{2}v_{dn}}{\partial x^{2}}.} \end{aligned}$$
(4)

The evolutionary hydrodynamics of the charged dust fluid is analogously described as

$$\begin{aligned} &{\frac{\partial n_{dc}}{\partial t} + \frac{\partial}{\partial x} ( n_{dc}v_{dc} ) = 0,} \end{aligned}$$
(5)
$$\begin{aligned} &{m_{dc}n_{dc} \biggl[ \frac{\partial v_{dc}}{\partial t} + v_{dc}\frac{\partial v_{dc}}{\partial x} \biggr] + \frac{\partial P_{dc}}{\partial x} + q_{d}n_{dc}\frac{\partial \phi}{\partial x} } \\ &{\quad{}+ m_{dc}n_{dc}\frac{\partial \psi}{\partial x} + m_{dc}v_{dc}\upsilon_{cn} ( v_{dc} - v_{dn} ) = \eta_{dc}\frac{\partial^{2}v_{dc}}{\partial x^{2}},} \end{aligned}$$
(6)

where, \(x\) is the spatial coordinate specifying the instantaneous extension of the considered unbounded sheet-like cloud relative to the center of the entire cloud plasma mass distribution at any instant of time \(t\). The physical variables \(m_{dn} ( m_{dc} )\), \(n_{dn} ( n_{dc} )\), \(v_{dn} ( v_{dc} )\) are the mass, number density, velocity of neutral (charged) dust; respectively. Moreover, \(q_{d}\) is the electric charge of the identical dust grains having identical geometrical shapes. Then, \(\psi\) is the self-gravitational potential developed by the material density fields associated with the astrophysical constituent fluids conjointly. The term \(\eta_{dn} ( \eta_{dc} )\) denotes the uniform coefficient of kinematic viscosity (Frenkel 1946; Landau and Lifshitz 1987; Brevik 2016) associated with the neutral (charged) dust fluid. In this model, the turbulence effects associated with the component dust fluids in the molecular cloud are also taken into account. So, the equations of states for neutral and charged dust grains in the Larson logatropic-framework (Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996) are given respectively as, \(P_{dn} = c_{ss}^{2}\rho_{dn} + P_{0}\log ( \rho_{dn} / \rho_{dn0} )\) and \(P_{dc} = c_{ss}^{2}\rho_{dc} + P_{0}\log ( \rho_{dc} / \rho_{dc0} )\). The spectro-strategic derivation of the semi-empirical baroscopic laws, stemming from the non-thermal spectral line-widths in turbulent DMCs, is available in Karmakar and Haloi (2017b). Here, \(c_{ss} = \sqrt{T_{i} / m_{d}}\) is the usual phase speed of the normal longitudinal plasma acoustic mode (dust acoustic). Further, \(\rho_{dn0} = m_{dn}n_{dn0}\) and \(\rho_{dc0} = m_{dc}n_{dc0}\) are the equilibrium (fixed) material densities of neutral dust and charged dust, respectively. Similarly, \(\rho_{dn} = m_{dn}n_{dn}\) and \(\rho_{dc} = m_{dc}n_{dc}\) are the non-equilibrium (variable) material densities of neutral dust and charged dust, respectively. The mean equilibrium thermal pressure of the cloud at temperature \(T~\mbox{eV}\) is presumptively designated by an isothermal law as \(P_{0} = n_{d0}T\).

Finally, the closing electrostatic and self-gravitational Poisson equations for the electrostatic and self-gravitational potentials (produced by charge density and material density fields) with all the earlier conventional notations read respectively as

$$\begin{aligned} &{\frac{\partial^{2}\phi}{\partial x^{2}} = - 4\pi \bigl[ e ( n_{i} - n_{e} ) + q_{d}n_{dc} \bigr],} \end{aligned}$$
(7)
$$\begin{aligned} &{\frac{\partial^{2}\psi}{\partial x^{2}} = 4\pi G [ m_{dn}n_{dn} + m_{dc}n_{dc} ].} \end{aligned}$$
(8)

Before executing the pulsational stability analysis, we obtain the standard scale-free invariant (normalized) form of Eqs. (1)–(8) by applying a conventional astrophysical normalization scheme in the light of the Jeansian equilibrium multi-parametric values (Dutta et al. 2016; Dutta and Karmakar 2017; Haloi and Karmakar 2017; Karmakar and Haloi 2017a, 2017b). We, accordingly, introduce \(\xi = x / \lambda_{J}\) as the normalized position; \(\tau = t / \omega_{J}\) as the normalized time; \(\varOmega = \omega / \omega_{J}\) as the normalized fluctuation frequency; \(F_{nc ( cn )} = \upsilon_{nc ( cn )} / \omega_{J}\) as the normalized collision frequency for neutral-charged (charged-neutral) dust; \(K = k / k_{J}\) as the normalized angular wavenumber; \(N_{j} = n_{j} / n_{j0}\) as the normalized number density (\(j=e\) for electrons, \(i\) for ions, \(dn\) for neutral dust, \(dc\) for charged dust); \(Q_{d} = q_{d} / q_{d0}\) as the normalized dust-charge; \(M_{j} = v_{j} / c_{ss}\) as the normalized velocity, also termed as the Mach number (\(j=e\) for electrons, \(i\) for ions, \(dn\) for neutral dust, \(dc\) for charged dust); \(\varPhi = \phi / ( T_{i} / e )\) as the normalized electrostatic potential, and \(\varPsi = \psi / c_{ss}^{2}\) as the normalized self-gravitational potential. Thus, the normalized standard form of Eqs. (1)–(8) can respectively be presented as

$$\begin{aligned} &{N_{e} = 1 + \frac{T_{i}}{T_{e}} \biggl( \frac{\kappa_{e} - \frac{1}{2}}{\kappa_{e} - \frac{3}{2}} \biggr)\varPhi,} \end{aligned}$$
(9)
$$\begin{aligned} &{N_{i} = 1 - \biggl( \frac{\kappa_{i} - \frac{1}{2}}{\kappa_{i} - \frac{3}{2}} \biggr)\varPhi,} \end{aligned}$$
(10)
$$\begin{aligned} &{\frac{\partial N_{dn}}{\partial \tau} + \frac{\partial}{\partial \xi} ( N_{dn}M_{dn} ) = 0,} \end{aligned}$$
(11)
$$\begin{aligned} &{N_{dn} \biggl[ \frac{\partial M_{dn}}{\partial \tau} + M_{dn}\frac{\partial M_{dn}}{\partial \xi} \biggr] + \frac{\partial}{ \partial \xi} \biggl[ N_{dn} + \frac{P_{0}}{c_{ss}^{2}\rho_{dn}}\log ( N_{dn} ) \biggr] } \\ &{\qquad{}+ N_{dn}\frac{\partial \varPsi}{\partial \xi} + N_{dn}F_{nc} ( M_{dn} - M_{dc} )} \\ &{\quad{}= \eta_{dn}^{*}\frac{\partial^{2}M_{dn}}{\partial \xi^{2}},} \end{aligned}$$
(12)
$$\begin{aligned} &{\frac{\partial N_{dc}}{\partial \tau} + \frac{\partial}{\partial \xi} ( N_{dc}M_{dc} ) = 0,} \end{aligned}$$
(13)
$$\begin{aligned} &{N_{dc} \biggl[ \frac{\partial M_{dc}}{\partial \tau} + M_{dc}\frac{\partial M_{dc}}{\partial \xi} \biggr] + \frac{\partial}{ \partial \xi} \biggl[ N_{dc} + \frac{P_{0}}{c_{ss}^{2}\rho_{dc}}\log ( N_{dc} ) \biggr] } \\ &{\qquad{}+ z_{d0}Q_{d}N_{dc}\frac{\partial \varPhi}{\partial \xi} + N_{dc}\frac{\partial \varPsi}{\partial \xi}+ N_{dc}F_{cn} ( M_{dc} - M_{dn} ) } \\ &{\quad= \eta_{dc}^{*}\frac{\partial^{2}M_{dn}}{\partial \xi^{2}},} \end{aligned}$$
(14)
$$\begin{aligned} &{\frac{\partial^{2}\varPhi}{\partial \xi^{2}} = \frac{4\pi e^{2}}{m_{d}\omega_{J}^{2}} \biggl[ ( n_{e0}N_{e} - n_{i0}N_{i} ) - n_{dc0}Q_{d}N_{dc}\frac{q_{d0}}{e} \biggr],} \end{aligned}$$
(15)
$$\begin{aligned} &{\frac{\partial^{2}\varPsi}{\partial \xi^{2}} = \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr)N_{dn} + \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr)N_{dc},} \end{aligned}$$
(16)

where, \(\eta_{dn}^{*} = \eta_{dn} / ( m_{dn}n_{dn0}\omega_{J}^{ - 1}c_{ss}^{2} )\) and \(\eta_{dc}^{*} = \eta_{dc} / ( m_{dc}n_{dc0}\omega_{J}^{ - 1}c_{ss}^{2} )\) are the effective rescaled viscosities of the neutral and charged dust fluids, respectively. As the cloud consists of identical dust micro-spheres, it is assumed that \(m_{dn} \approx m_{dc} = m_{d}\). The symbol, \(\omega_{J} = \sqrt{\omega_{Jn}^{2} + \omega_{Jc}^{2}}\), stands for effective Jeans frequency (Jeans 1902; Mo et al. 2010), sourced by both the neutral (via \(\omega_{Jn} = \sqrt{4\pi Gm_{d}n_{dn0}}\)) and charged dust fluids (via \(\omega_{Jc} = \sqrt{4\pi Gm_{d}n_{dc0}}\)). Here, \(G = 6.67 \times 10^{ - 11}~\mbox{N}\,\mbox{m}^{2}\,\mbox{kg}^{-2}\) is the Newtonian gravitational coupling constant via which the philosophy of the long-range gravitational interaction is realized (Draine and Salpeter 1979; Bliokh et al. 1995; Krugel 2003; Spitzer 2004). It may be noted here that, the pulsational mode in a partially ionized astrocloud, which is an overlapped hybrid instability stemming in coupled gravito-electrostatic interplay in a bimodal pattern leading to bounded equilibrium structure formation in astro-cosmic environs, would be operative on common astrophysical scales of space and time, provided the dust mass-to-charge ratio fulfills the limiting value as, \(m_{d} / q_{d}\sim \sqrt{0.5 G} \approx 10^{ - 5}\) (Gisler et al. 1992). It is repeated that all other symbolic notations used above are quite generic and customary in nature (Karmakar and Borah 2013; Borah and Karmakar 2015; Dutta et al. 2016; Dutta and Karmakar 2017; Karmakar and Haloi 2017b).

The pivotal objective of the paper lies in investigating the pulsational mode dynamics in the complex astrocloud around its defined homogeneous static equilibrium in the framework of a standard Fourier analysis. Thus, all the relevant physical parameters characterizing the cloud are slightly perturbed around the respective defined static equilibrium values as

$$ \left .\textstyle\begin{array}{l} N_{e} = 1 + N_{e1},\qquad N_{i} = 1 + N_{i1},\\ N_{dn} = 1 + N_{dn1},\qquad N_{dc} = 1 + N_{dc1},\\ M_{dn} = 0 + M_{dn1},\qquad M_{dc} = 0 + M_{dc1},\\ \varPhi = 0 + \varPhi_{1},\qquad \varPsi = 0 + \varPsi_{1}. \end{array}\displaystyle \right \} $$
(17)

We now apply the above perturbation technique (Eq. (17)) on Eqs. (9)–(16) to find their respective linearized forms. It is pertinent to add that the complex unbounded cloud under the action of continuous periodic gravito-electrostatic interplay having no influence from the geometrical boundary effects. The linear fluctuations in such circumstances can be assumed to dynamically evolve as plane waves in the form \(\sim\exp [ - i ( \varOmega \tau - K\xi ) ]\), where \(\varOmega\) is the Jeans-normalized angular frequency and \(K\) is the Jeans-normalized angular wavenumber of the perturbations. As a result of this tricky exercise, the algebraic linearized (Fourier-transformed) form of Eqs. (9)–(16) in the defined wave space \(( K, \varOmega )\) can respectively be written as

$$\begin{aligned} &{N_{e1} = \biggl( \frac{T_{i}}{T_{e}} \biggr) \biggl( \frac{\kappa_{e} - \frac{1}{2}}{\kappa_{e} - \frac{3}{2}} \biggr)\varPhi_{1},} \end{aligned}$$
(18)
$$\begin{aligned} &{N_{i1} = - \biggl( \frac{\kappa_{i} - \frac{1}{2}}{\kappa_{i} - \frac{3}{2}} \biggr)\varPhi_{1},} \end{aligned}$$
(19)
$$\begin{aligned} &{N_{dn1} = \frac{ ( i\varOmega F_{nc} - \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} )N_{dc1}}{\varOmega^{2} + i\varOmega ( F_{nc} + K^{2}\eta_{dn}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dn}} ) + \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}}},} \\ \end{aligned}$$
(20)
$$\begin{aligned} &{N_{dc1}} \\ &{\quad = \frac{K^{2}z_{d0}Q_{d}\varPhi_{1}}{ [ \varOmega^{2} + i\varOmega ( F_{cn} + K^{2}\eta_{dc}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dc}} ) + \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ]}} \\ &{\qquad{} - \frac{ ( i\varOmega F_{cn} - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) ( i\varOmega F_{nc} - \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} )}{ [ \varOmega^{2} + i\varOmega ( F_{nc} + K^{2}\eta_{dn}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dn}} ) + \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} ]},} \\ \end{aligned}$$
(21)
$$\begin{aligned} &{K^{2}\varPhi_{1} = - \biggl( \frac{\omega_{ed}^{2}}{\omega_{J}^{2}} \biggr)N_{e1} - \biggl( \frac{\omega_{id}^{2}}{\omega_{J}^{2}} \biggr)N_{i1} {+} \biggl( \frac{\omega_{pd}^{2}}{\omega_{J}^{2}} \biggr)\frac{Q_{d}}{z_{d0}}K^{2}N_{dc1},} \end{aligned}$$
(22)

where, \(\omega_{ed} = \sqrt{4 \pi e^{2}n_{e0} / m_{d}}\), \(\omega_{id} = \sqrt{4 \pi e^{2}n_{i0} / m_{d}}\), \(\omega_{pd} = \sqrt{4 \pi q_{d0}^{2}n_{dc0} / m_{d}}\), \(\omega_{ed}^{2} / \omega_{J}^{2} = \varOmega_{ed}^{2}\), \(\omega_{id}^{2} / \omega_{J}^{2} = \varOmega_{id}^{2}\), \(\omega_{pd}^{2} / \omega_{J}^{2} = \varOmega_{pd}^{2}\) and \(T_{i} / T_{e} = \sigma_{e}\). Substituting the expressions for \(N_{e1}\), \(N_{i1}\), \(N_{dc1}\) from Eqs. (19)–(21) in Eq. (22) followed by a systematic decomposition and simplification, we obtain the general linearized dispersion relation under the appropriate condition of non-vanishing fluctuating potentials of gravito-electrostatic origin as

$$\begin{aligned} &{1 + \sigma_{e}\frac{\varOmega_{ed}^{2}}{K^{2}} \biggl( \frac{\kappa_{e} - \frac{1}{2}}{\kappa_{e} - \frac{3}{2}} \biggr) + \frac{\varOmega_{id}^{2}}{K^{2}} \biggl( \frac{\kappa_{i} - \frac{1}{2}}{\kappa_{i} - \frac{3}{2}} \biggr) = \varOmega_{pd}^{2}Q_{d}^{2}\left [ \textstyle\begin{array}{l} \{ \varOmega^{2} + i\varOmega ( F_{cn} + K^{2}\eta_{dc}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dc}} ) + \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \} \\ \quad{}-\frac{ ( i\varOmega F_{cn} - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) ( i\varOmega F_{nc} - \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} )}{ \{ \varOmega^{2} + i\varOmega ( F_{nc} + K^{2}\eta_{dn}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dn}} ) + \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \}} \end{array}\displaystyle \right ]^{ - 1}.} \end{aligned}$$
(23)

It is evident from Eq. (23) that the dispersive effects arising from the deviation from global quasi-neutrality (via ‘1’), nonthermal effects sourced by deviation from the local thermodynamical equilibrium (via the second term on LHS) and turbulence effects arising due to the dominancy of the inertial forces over the viscous ones (via RHS) are mutualistically balanced in the considered initially static quasi-neutral astrocloud. An algebraic exercise for analytic simplification of Eq. (23) results in a regular quartic form of the generalized linear dispersion relation depicting the mode characteristics as

$$ \varOmega^{4} + a_{3}\varOmega^{3} + a_{2}\varOmega^{2} + a_{1}\varOmega + a_{0} = 0, $$
(24)

which contains all the relevant evolutionary information about the nonthermal pulsational cloud dynamics in a multi-parametric space. The various involved coefficients here are presented as

$$\begin{aligned} &{a_{3} = i \bigl( F_{nc} + F_{cn} + K^{2}\eta_{dn}^{*} + K^{2}\eta_{dc}^{*} \bigr),} \\ &{a_{2} = 1 - K^{2} ( x + y ) - F_{nc}K^{2}\eta_{dc}^{*} - F_{cn}K^{2}\eta_{dn}^{*} - \eta_{dn}^{*}\eta_{dc}^{*}K^{4} - \biggl( \frac{\varOmega_{pd}^{2}Q_{d}^{2}K^{2}}{K^{2} + \sigma_{e} l\varOmega_{ed}^{2} + m\varOmega_{id}^{2}} \biggr),} \\ &{a_{1} = i \biggl\{ F_{nc} \bigl( 1 - K^{2}y \bigr) - F_{cn} \bigl( 1 - K^{2}x \bigr) - K^{4} \bigl( \eta_{dn}^{*}y + \eta_{dc}^{*}x \bigr) + K^{2}\eta_{dn}^{*}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} + K^{2}\eta_{dc}^{*}\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr\} } \\ &{\phantom{a_{1}=}{}- \biggl\{ \frac{i ( F_{nc} + K^{2}\eta_{dn}^{*} ) \varOmega_{pd}^{2}Q_{d}^{2}K^{2}}{K^{2} + \sigma_{e} l\varOmega_{ed}^{2} + m\varOmega_{id}^{2}} \biggr\} ,} \\ &{a_{0} = K^{4}xy - K^{2}y\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2}x\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} - \biggl[ \frac{\varOmega_{pd}^{2}Q_{d}^{2} ( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2}y )K^{2}}{K^{2} + \sigma_{e} l\varOmega_{ed}^{2} + m\varOmega_{id}^{2}} \biggr].} \end{aligned}$$

where, \(x = 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dn}}\), \(y = 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dc}}\), \(l = \frac{\kappa_{e} - 1 / 2}{\kappa_{e} - 3 / 2}\), \(m = \frac{\kappa_{i} - 1 / 2}{\kappa_{i} - 3 / 2}\).

As Eq. (23) describes the nonthermal cloud fluctuation dynamics having the gravito-electrostatic origin, it may be of interest to readers to know its reverse fate upon consideration of the usual Boltzmann distribution law for the thermal species. In principle, Eq. (23) recovers the Boltzmann picture if \(\kappa_{e}, \kappa_{i} \to \infty\). Applying this condition in Eq. (23), one gets

$$\begin{aligned} &{1 + \sigma_{e}\frac{\varOmega_{ed}^{2}}{K^{2}} + \frac{\varOmega_{id}^{2}}{K^{2}} = \varOmega_{pd}^{2}Q_{d}^{2}\left [ \textstyle\begin{array}{l} \{ \varOmega^{2} + i\varOmega ( F_{cn} + K^{2}\eta_{dc}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dc}} ) + \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \}\\ \quad{} - \frac{ ( i\varOmega F_{cn} - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) ( i\varOmega F_{nc} - \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} )}{ \{ \varOmega^{2} + i\varOmega ( F_{nc} + K^{2}\eta_{dn}^{*} ) - K^{2} ( 1 + \frac{P_{0}}{c_{ss}^{2}\rho_{dn}} ) + \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \}} \end{array}\displaystyle \right ]^{ - 1}.} \end{aligned}$$
(25)

In the extremely low-frequency fluctuation regime, the above equation gets transformed into an equation with vanishing propagatory part (\(\varOmega_{r}\sim 0\), wave condensation) and with non-vanishing decay/growth part (\(\varOmega_{i} \ne 0\), wave collapse) given as

$$ \varOmega_{i} = \frac{xK^{2}\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} + yK^{2}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} - xyK^{4} - \varOmega_{pd}^{2}Q_{d}^{2}K^{2} ( K^{2}x - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) ( K^{2} + \sigma_{e}\varOmega_{ed}^{2} + \varOmega_{id}^{2} )^{ - 1}}{\left [ \textstyle\begin{array}{l} ( F_{nc} + F_{cn} ) ( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} + \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} ) + K^{2}\eta_{dn}^{*}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} + K^{2}\eta_{dc}^{*}\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - x ( F_{cn} +K^{2}\eta_{dc}^{*} )K^{2}\\ \quad{} - y ( F_{nc} + K^{2}\eta_{dn}^{*} ) K^{2} - \varOmega_{pd}^{2}Q_{d}^{2} ( F_{nc} + K^{2}\eta_{dn}^{*} ) ( K^{2} + \sigma_{e}\varOmega_{ed}^{2} + \varOmega_{id}^{2} )^{ - 1} \end{array}\displaystyle \right ]} $$
(26)

It is clear from Eq. (26) that the pulsational mode dynamics in the thermalized cloud plasma would undergo decay or growth depending on the thresholds dictated by the diversified equilibrium poly-parametric values of the cloud plasma system. This clearly confirms the previously reported predictions on the same instability (Dwivedi et al. 1999; Pandey et al. 2002).

3 Results and discussions

A linear perturbation (slight relative to the static equilibrium) analysis of a complex viscous nonthermal astrocloud of an infinite spatial extension is methodologically carried out in the astrophysical multi-fluidic model framework to see the excitation scenarios of the pulsational mode dynamics. It is demonstrated that the mode dynamics in such astrophysical clouds is governed by a unique form of generalized linear quartic dispersion relation (Eq. (24)) having various involved coefficients dependent on the diversified equilibrium cloud parameters. We numerically analyze the slightly perturbed cloud (via solving Eq. (24)) to understand the microphysical detailed insights associated with the mode dynamics in the graphical form of Figs. 1–2. The numerical illustrative results, thus obtained by the root-finder method of decomposition (Lindfield and Penny 2012), are displayed and interpreted in the following.

Fig. 1
figure 1

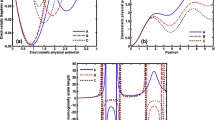
Profiles of the normalized (a) real frequency part \(( \varOmega_{r} )\) and (b) growth rate \(( \varOmega_{i} )\) for different values of the effective rescaled viscosity coefficients \(( \eta_{dn}^{*}, \eta_{dc}^{*} )\) of the neutral dust fluid and charged dust fluid with variation in the normalized angular wavenumber (\(K\)) as shown in the legends, respectively. The input and initial values are presented in the text

Full size image
Fig. 2
figure 2

Profiles of the normalized (a) real frequency part \(( \varOmega_{r} )\) and (b) growth rate \(( \varOmega_{i} )\) for different values of the nonextensive indices \(( \kappa_{e}, \kappa_{i} )\) associated with the cloud electrons and ions with variation in the normalized angular wavenumber (\(K\)) as shown in the legends, respectively. The fine details of various inputs are described in the text

Full size image

In Fig. 1, we depict the profiles of the normalized (a) real frequency part and (b) growth rate of the pulsational mode with variation in the normalized angular wavenumber (\(K\)) for different values of the effective rescaled viscosity coefficients for the neutral and charged dust grains \(( \eta_{dn}^{*}, \eta_{dc}^{*} )\). The various inputs employed in the analysis are borrowed from different reliable sources of realistic astrophysical significance available in Gehman et al. (1996), Spitzer (2004), Shukla and Stenflo (2006), Dutta et al. (2016). We take \(n_{e0} = 10 \mbox{--} 50~\mbox{cm}^{-3}\), \(n_{i0} = 5 \mbox{--} 30~\mbox{cm}^{-3}\), \(n_{d0} = 10^{ - 2} \mbox{--} 10~\mbox{cm}^{-3}\), \(T_{e} = 1 \mbox{--} 10~\mbox{eV}\), \(T_{i} = 0.08 \mbox{--} 0.5~\mbox{eV}\), \(T_{d} = 10^{ - 3} \mbox{--} 10^{ - 2}~\mbox{eV}\), \(r_{d} = 1.28~\upmu \mbox{m}\), \(q_{d} = 1.6 \times 10^{ - 16}~\mbox{C}\), \(P_{0} \approx 10^{ - 12}~\mbox{N}\,\mbox{m}^{-2}\), \(\kappa_{e} = 6\) and \(\kappa_{i} = 6\). We see that the real frequency part decreases gradually with increase in the charged dust fluid viscosity (\(\eta_{dc}^{*}\)); whereas, it decreases sharply with increase in the neutral dust fluid viscosity (Fig. 1(a)). It implicates that the neutral dust fluid viscosity (\(\eta_{dn}^{*}\)) plays a decelerating role to the propagatory dynamics of the pulsational mode. It is further seen that the charged dust fluid viscosity offers a gradual damping effect. In contrast, the neutral dust viscosity introduces a sharp damping agency to the pulsational mode evolutionary dynamics (Fig. 1(b)). Thus, we can infer that the neutral dust viscosity (\(\eta_{dn}^{*}\)) acts as a sharp stabilizing agency and the charged dust viscosity (\(\eta_{dc}^{*}\)) as a gradual stabilizing agency to the pulsating cloud. This happens because of weak turbulence due to the viscous forces winning over the inertial forces (Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996).

In Fig. 2, we portray the normalized (a) real frequency part and \(( \varOmega_{r} )\) (b) growth rate \(( \varOmega_{i} )\) with variation in the normalized angular wavenumber (\(K\)) for different values of non-extensive nonthermality spectral indices for electrons and ions \(( \kappa_{e}, \kappa_{i} )\). The fine quantitative details are the same as Fig. 1. We find that the real frequency part of the fluctuations decreases gradually with increasing \(\kappa_{e}\). However, it decreases sharply with enhancement in \(\kappa_{i}\). It indicates that \(\kappa_{i}\) acts a sharper decelerating agency to the fluctuations in comparison with that by \(\kappa_{e}\) (Fig. 2(a)). Moreover, we see that the mode growth decreases more sharply with augmentation in \(\kappa_{i}\) than in \(\kappa_{e}\). It implicates that \(\kappa_{i}\) acts as a stronger stabilizer to the fluctuations than \(\kappa_{e}\). It may, therefore, be summarized from the presented numerical graphics that, the pulsational mode dynamics in the considered cloud is significantly affected by both the component fluid viscosities associated with the inertial species and nonthermality indices associated with the inertialess species on the astrophysical non-homologous cloud scales of space and time.

4 Conclusions

The pulsational mode stability dynamics of gravito-electrostatic source in a thermostatistically anti-equilibrium self-gravitating complex dusty plasma cloud with partial ionization in the presence of multi-fluidic kinematic viscosities and logatropic turbulence pressures is theoretically investigated. It is done by exploring how an equilibrium-neighboring solution of the slightly perturbed astrocloud evolves in a flat space-time configuration. We use the Larson logatropic equation of state, nonlinearly relating the net fluid pressure with other thermodynamical variables of relevance to incorporate the realistic neutral and charged dust turbulence pressure effects in a coupled form. In the considered homogeneous, quasineutral and hydrostatic equilibrium configuration, the complex plasma system contains a spatially uniform distribution of the nonthermal (\(\kappa\)-distributed, thermostatistically anti-equilibrium, lighter) electrons and ions; and inertial gravitating neutral and charged dust (fluid, hydrostatic equilibrium, heavier). Such situations are quite significant in multifarious gaseous fluids encountered in astro-cosmic environments because of the prevailing differential scaling of inertial masses and kinetic temperatures of the constituent plasma species.

Application of linear normal mode analysis (Fourier-formulaic) transforms the slightly perturbed complex astrocloud model into a generalized quartic linear dispersion relation with variable complex multi-parametric coefficients. A numerical illustrative standpoint is constructed to unveil the microphysical insights of the pulsational mode fluctuation dynamics in the framework of realistic astrophysical parametric windows on a common graphical platform. It is seen from the numerical and graphical analyses that both the viscosity coefficients (\(\eta_{dn}^{*},\eta_{dc}^{*}\)) as well as the nonextensive nonthermality indices (\(\kappa_{e},\kappa_{i}\)) induce damping effects to the perturbed plasma system. But, the neutral dust fluid viscosity (\(\eta_{dn}^{*}\)) and the ion nonthermality index (\(\kappa_{i}\)) initiate more stabilizing influences (in comparison with \(\eta_{dc}^{*}\) and \(\kappa_{e}\)) to the perturbed cloud.

It is admitted that the complex fluid turbulence pressure, which is a nonlinear function of fluid density, is found to have no significant distinct influence in a linear order of normal mode analysis. This is because of the fact that various astronomical spectroscopic observations (Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996) have already predicted that the turbulence pressure acting against dynamic collapse is indeed very small (\(P_{0}\sim 10^{ - 12}~\mbox{N}\,\mbox{m}^{-2}\)). As a consequence, in order to see the effects of turbulence, one needs to execute the next higher-order (weakly nonlinear) perturbation analysis. Thus, we recognize that the analysis presented here relies on a bit simplistic approach to understand the astrocloud collective pulsational fluctuation dynamics under the counter-action of inward self-gravity and outward non-gravitational factors, such as the thermal, electrostatic and turbulence forces. Besides, the equipartition of energy between the solid phase of dust grains and the fluid phase of background plasma causes the grains to execute both the translatory Brownian motion (speed \(\sim0.30~\mbox{m}\,\mbox{s}^{-1}\)) and rotational Brownian motion (speed \(\sim10^{5}~\mbox{rad}\,\mbox{s}^{-1}\)) rooted in chaotic gaseous bombardment phenomena (Draine and Salpeter 1979; Krugel 2003). Such effects need to be considered in the basic model setup. Despite the idealizations to pure picturization, the semi-analytic Jeansian exploration may be useful as applicable elements to understand self-gravitational non-homologous cloud collapse mechanisms leading to the galactic heretical building-block structure formation extensible from the Jeansian scales up to the cosmological scales of space and time.