1 Introduction

The interstellar space, which is the region between stars, is well known from astronomical observations to be both magnetized and turbulent in nature (Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996; Mo et al. 2010). The pressures developed due to magnetic and turbulent effects play a significant role in the active mechanism of bounded structure formation in the dense sites of such interstellar media known as dust molecular clouds (DMCs). The modified waves and instabilities due to such key kinetic factors play an important role in triggering new distribution of interstellar fluid materials in the form of structure formation via various kinetic transport processes sourced by re-distribution of mass, energy and angular momentum in the media.

As clearly seen in the past, a number of researchers have investigated various waves and instabilities of such complex astrophysical fluids (Pudritz 1990; Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Gehman et al. 1996; Balsara 1996; Elmegreen and Scalo 2004; Karmakar 2011; Karmakar and Borah 2013; Murray et al. 2017; Orkisz et al. 2017). For example, Gehman and his group investigated the instability behaviors in magnetized turbulent complex astroclouds, thereby revealing mainly that the magneto-active fluid turbulence introduces a stability influence against the self-gravitational cloud-collapse dynamics (Gehman et al. 1996). Even in the nonlinear regime, a number of investigators have found diversified nonlinear eigenmodes and eigenpatterns triggering the fragmentation, filamentation and clumping of the global cloud leading to cloud collapsing as bounded sub-structures (Adams et al. 1994; Karmakar and Borah 2013). In contrast, the pure characteristic eigen-features (field-free), named as nonlinear pulsational mode, in the presence of grain-charge fluctuations have also been specifically reported in the literature (Karmakar and Borah 2013). The pulsational instability arises due to the dynamic coupling between the bipolar Coulombic interaction (among constituent charged species) and unipolar Newtonical interaction (among constituent heavier species) in a periodic fashion. Moreover, people have studied also the nonlinear formation processes of stars in self-gravitating turbulent fluids with the help of high-resolution simulation techniques (Murray et al. 2017). Recently, the nonlinear fluctuation dynamics in related magnetized degenerate plasma environments with the quantum diffraction effects (Bohm potential) taken into account has been addressed (Hussain and Mahmood 2017). It has been demonstrated therein the excitation insights of soliton hump structures (high-Mach) and soliton dip structures (low-Mach) in such high-beta (\(\beta \sim 10^{6}\)) plasmas. It can, however, be noted that the instability analyses of complex magneto-active turbulent astroclouds, alongside various heterogeneous collisional and grain-charge dynamics triggering star-formation processes, still constitute an open long-standing long-spurred challenge yet to be well addressed.

The present paper, after being well motivated by the above astrophysical stability scenarios, is constructed to deal with the linear pulsational instability analysis of such a complex molecular cloud with all the key kinetic factors included afresh. In other words, it includes the effects of magnetic field, turbulence and collisional dynamics concurrently. A standard technique of the Fourier-formulaic-based normal mode analysis (Tignol 2001) over the slightly perturbed cloud yields a generalized linear dispersion relation (octic in degree) of unique form for the pulsational mode fluctuations under consideration. A numerical tapestry analysis (on the basis of a standard root-finder) portrays the unique characteristic features of the cloud instability dynamics, focusing mainly on the role of dust mass sourcing to dispersive stability. Lastly, we indicate an elaborate interpretation of the pulsational propagatory dynamics together with non-trivial implications and futuristic applications in the astro-cosmic context.

2 Physical and mathematical models

We consider an astrophysical situation of self-gravitating magnetized collisional dust molecular clouds (DMCs) in fluid model framework. It compositionally consists of lighter electrons and ions; and massive negatively charged dust grains together with partial ionization. The dust grains are electrically charged, and hence, are coupled to the plasma through the long-range electromagnetic interactions. It may be worth mentioning that the grains are composed mainly of graphites, silicates and metallic compounds (Pandey et al. 1999). The dust grains are assumed to be micro-sphere of identical shape with variable electric charge due to random surface-interactions with the thermal electron-ion currents (Pandey et al. 1999). For the low-frequency analysis, we consider the dust species to behave as isothermal (inertial) fluids, whereas the electrons and ions as inertialess ones. A global quasi-neutrally is assumed to pre-exist in the adopted spatially flat-geometry (sheet-like) configuration under hydrostatic homogeneous equilibrium of the unbounded DMC. The justification of the flat geometry is that the radius of the cloud curvature is much greater than all the characteristic scale lengths in the cloud. The complex grainy plasma fluid is turbulent in nature due to irregular aperiodic distribution of flow energy and vorticity. In other words, the model supports energy cascading processes, whereby large-scale flow energy gets transformed into short-scale ones. The complex admixture of the diversified constituent species is embedded in a uniform background magnetic field, \(\vec{B} = B \hat{z}\), acting along the \(z\)-direction. The vindication for considering the magnetic field in our model is that the estimated value of the plasma-beta, \(\beta = 4.03 \times 10^{ - 25} ( n_{d} T_{p} / B^{2} )\ll 1\) with all the usual notations in SI units (Bellan 2006) described in the following, which is also known as the bulk plasma relative thermo-magnetic pressure ratio, is estimated as small as \(\beta \approx 10^{ - 2} \mbox{--} 10^{ - 3}\). This is for the realistic magnetic field, \(B \approx 10^{ - 9} \mbox{--} 3 \times 10^{ - 9}\) Tesla, present in the interstellar molecular clouds (Adams et al. 1994). As a consequence of the low plasma-beta, \(\beta\ll 1\) (Bellan 2006), the net pressure, comprising of an isothermal component of the thermal, a logatropic component of the turbulent pressure and a quadratic component of the magnetic pressure, is modelled with the Larson logatropic equation of state (Larson 1981; Lizano and Shu 1989; Adams et al. 1994; Vazquez-Semadeni and Gazol 1995; Lada and Kylafis 1999). It may be added that, in the case of alike magnetized degenerate plasma environments with the quantum diffraction effects (Bohm potential) taken into account (Hussain and Mahmood 2017), there is a rapid augmentation in the plasma-beta (\(\beta \sim 10^{6}\)).

The macroscopic state of the astrofluid dynamics is described by the continuity, momentum and closed electro-gravitational Poisson potential distribution equations given respectively in dimensional form with all the customary symbols as

$$\begin{aligned} &\frac{\partial n_{e}}{\partial t} + \vec{\nabla}. ( n_{e}\vec{u}_{e} ) = - \nu_{edc} ( n_{e} - n_{e0} ), \end{aligned}$$
(1)
$$\begin{aligned} & 0 = - \vec{\nabla} p_{e} - en_{e} \vec{\nabla} \phi - m_{e} n_{e}\nu_{edc}\vec{u}_{e}, \end{aligned}$$
(2)
$$\begin{aligned} & \frac{\partial n_{i}}{\partial t} + \vec{\nabla}. ( n_{i}\vec{u}_{i} ) = - \nu_{idc} ( n_{i} - n_{i0} ), \end{aligned}$$
(3)
$$\begin{aligned} & 0 = - \vec{\nabla} p_{i} + en_{i} \vec{\nabla} \phi - m_{i} n_{i}\nu_{idc}\vec{u}_{i}, \end{aligned}$$
(4)
$$\begin{aligned} & \frac{\partial n_{dc}}{\partial t} + \vec{\nabla}. ( n_{dc}\vec{u}_{dc} ) = 0, \end{aligned}$$
(5)
$$\begin{aligned} & m_{dc}n_{dc} \biggl( \frac{\partial}{\partial t} + \vec{u}_{dc}.\vec{\nabla} \biggr) \vec{u}_{dc} \\ &\quad= - \vec{\nabla} p_{dc} - q_{d}n_{dc}\vec{\nabla} \phi - m_{dc}n_{dc}\vec{\nabla} \psi \\ &\qquad{}- m_{dc}n_{dc} \nu_{cn} ( \vec{u}_{dc} - \vec{u}_{dn} ), \end{aligned}$$
(6)
$$\begin{aligned} & \frac{\partial n_{dn}}{\partial t} + \vec{\nabla}. ( n_{dn}\vec{u}_{dn} ) = 0, \end{aligned}$$
(7)
$$\begin{aligned} & m_{dn}n_{dn} \biggl( \frac{\partial}{\partial t} + \vec{u}_{dn}.\vec{\nabla} \biggr)\vec{u}_{dn} \\ &\quad= - \vec{\nabla} p_{dn} - m_{dn}n_{dn}\vec{\nabla} \psi - m_{dn}n_{dn}\nu_{nc} ( \vec{u}_{dn} - \vec{u}_{dc} ), \end{aligned}$$
(8)
$$\begin{aligned} & \nabla^{2}\phi = - 4\pi \bigl\{ e ( n_{i} - n_{e} ) - q_{d}n_{dc} \bigr\} , \end{aligned}$$
(9)
$$\begin{aligned} & \nabla^{2}\psi = 4\pi G ( m_{dc}n_{dc} + m_{dn}n_{dn} ). \end{aligned}$$
(10)

The dust grain charge-fluctuation dynamics at the cost of the colliding plasma thermal currents in the presence of interstellar ultra-weak magnetic field (Spitzer 2004) is governed by

$$ \biggl( \frac{\partial}{\partial t} + \vec{u}_{dc}.\vec{\nabla} \biggr)q_{d} = e \biggl[ \nu_{ed} \biggl( \frac{n_{e} - n_{e0}}{n_{d0}} \biggr) - \nu_{id} \biggl( \frac{n_{i} - n_{i0}}{n_{d0}} \biggr) \biggr]. $$
(11)

It is, as mentioned before too, clearly seen from (11) that the grain-charge (LHS) is contributed purely by the random collisional interaction of the thermal electron-ion currents (RHS) at the grain surfaces. In other words, if the thermal species cease to collide (\(\nu_{ed}, \nu_{id}\sim 0\)) onto the grains, the grain-charge becomes static (\(dq_{d} / dt\sim 0\)).

The dynamics of the embedded magnetic field lines is governed by the magnetic induction equation (field lines frozen-in condition) in the absence of any kind of advective-convective contribution in the mean fluid (highly conducting) framework with all the usual notations (Goedbloed and Poedts 2004) as

$$ \biggl( \frac{\partial}{\partial t} + \vec{v}_{a}.\vec{\nabla} \biggr)\vec{B} = \vec{\nabla} \times ( \vec{v}_{a} \times \vec{B} ). $$
(12)

The parameters \(n_{j}\), \(m_{j}\), \(u_{j}\) and \(T_{j}\) are the population density, mass, flow velocity and temperature of the \(j\)th-species, respectively. Here, subscript \(j = e\) for electrons, \(i\) for ions, \(dc\) for charged dust and \(dn\) for neutral dust. The notations, \(n_{e0}\), \(n_{i0}\) and \(n_{d0}\) denote the equilibrium population densities of electrons, ions and charged dust grains. Moreover, \(p_{j}\) is the total pressure composed of three parts: thermal pressure \(p_{j(iso)}= T_{j}n_{j}\), turbulent pressure \(p_{j(turbo)}= T_{j}n_{j0}\log ( \rho_{j} / \rho_{0} )\) and magnetic pressure \(p_{j(mag)}= B^{2} / 8\pi\). It may be worth mentioning here that, the logatropic equation of state originally stems in a semi-emperical intervention consistent with observational mensuration of non-thermal spectral line-widths in the turbulent DMCs (Larson 1981; Lizano and Shu 1989; Adams et al. 1994; Lada and Kylafis 1999). In a broader sense, the line-width in the accustomed generic notations is \(( \Delta \upsilon )\sim \rho^{ - 1 / 2}\), which implicates to \(( \Delta \upsilon )^{2} = u_{turb}^{2} = \partial p / \partial \rho \approx p_{0} / \rho\), and, finally, \(p = p_{0} \log ( \rho / \rho_{0} )\), upon introverted integration. Further, we consider \(T_{e} \approx T_{i} =T_{p}\gg T_{dc} \approx T_{dn} = T_{d}\) and \(m_{dc} = m_{dn} = m_{d}\). The terms, \(\phi\) and \(\psi\) present respectively the electric and self-gravitational potentials. Moreover, \(\vec{v}_{a} = ( \vec{u}_{i} - \vec{u}_{e} + \vec{u}_{d} ) \approx \vec{u}_{e} - \vec{u}_{i}\) denotes the mean fluid velocity contributed by the ionic flow (\(\vec{u}_{i}\)) and electronic flow (\(\vec{u}_{e}\)) for the considered cold dust configuration (\(\vec{u}_{e}, \vec{u}_{i} \gg \vec{u}_{d}\)). Besides, \(q_{d}\) is the grain charge and \(G\) (\(=6.67 \times 10^{ - 11}~\mbox{m}^{3}\,\mbox{kg}^{-1}\,\mbox{s}^{-2}\)) is the universal gravitational constant representing gravitational coupling. Finally, the symbols \(\nu_{edc}\), \(\nu_{idc}\), \(\nu_{cn}\), \(\nu_{nc}\), \(\nu_{ed}\) and \(\nu_{id}\) denote the collisional momentum transfer frequencies between the different constituent species as indicated by the corresponding subscripts (Pandey et al. 2002); respectively.

We are interested in a scale-invariant formalism of the fluctuations for which a standard scheme of astrophysical normalization (Karmakar and Borah 2013) is invoked. The details of the normalizing parameters alongside the typical values are discussed in Appendix A. Accordingly, the normalized set of (1)–(12) is respectively presented as

$$\begin{aligned} &\frac{\partial N_{e}}{\partial T} + \frac{\partial}{\partial X} ( N_{e}M_{e} ) = - F_{edc} ( N_{e} - 1 ), \end{aligned}$$
(13)
$$\begin{aligned} & \frac{\partial N_{e}}{\partial X} + \frac{1}{N_{e}}\frac{\partial N_{e}}{\partial X} + \alpha_{1}B_{N} \frac{\partial B_{N}}{\partial X} + N_{e}\frac{\partial \varPhi}{\partial X} \\ &\quad{} + \beta_{1}F_{edc}N_{e}M_{e} = 0, \end{aligned}$$
(14)
$$\begin{aligned} & \frac{\partial N_{i}}{\partial T} + \frac{\partial}{\partial X} ( N_{i} M{}_{i} ) = - F_{idc} ( N_{i} - 1 ), \end{aligned}$$
(15)
$$\begin{aligned} & \frac{\partial N_{i}}{\partial X} + \frac{1}{N_{i}}\frac{\partial N_{i}}{\partial X} + \alpha_{2}B_{N}\frac{\partial B_{N}}{\partial X} - N_{i} \frac{\partial \varPhi}{\partial X} \\ &\quad{} + \beta_{2} F_{idc} N_{i}M_{i} = 0, \end{aligned}$$
(16)
$$\begin{aligned} & \frac{\partial N_{dc}}{\partial T} + \frac{\partial}{\partial X} ( N_{dc}M_{dc} ) = 0, \end{aligned}$$
(17)
$$\begin{aligned} & \biggl[ \frac{\partial M_{dc}}{\partial T} + M_{dc}\frac{\partial M_{dc}}{\partial X} \biggr] \\ &\quad{} = - \biggl( \frac{T_{d}}{T_{p}} \biggr)\frac{1}{N_{dc}}\frac{\partial N_{dc}}{\partial X} - \biggl( \frac{T_{d}}{T_{p}} \biggr)\frac{1}{N_{dc}^{2}}\frac{\partial N_{dc}}{\partial X} \\ &\qquad{} - \alpha_{3}\frac{1}{N_{dc}}B_{N}\frac{\partial B_{N}}{\partial X} - \biggl( \frac{q_{d0}}{e} \biggr)Q_{d}\frac{\partial \varPhi}{\partial X} - \frac{\partial \varPsi}{\partial X} \\ &\qquad{} - F_{cn} ( M_{dc} - M_{dn} ), \end{aligned}$$
(18)
$$\begin{aligned} & \frac{\partial N_{dn}}{\partial T} + \frac{\partial}{\partial X} ( N_{dn}M_{dn} ) = 0, \end{aligned}$$
(19)
$$\begin{aligned} & \biggl[ \frac{\partial M_{dn}}{\partial T} + M_{dn}\frac{\partial M_{dn}}{\partial X} \biggr] \\ &\quad{}= - \biggl( \frac{T_{d}}{T_{p}} \biggr)\frac{1}{N_{dn}}\frac{\partial N_{dn}}{\partial X} - \biggl( \frac{T_{d}}{T_{p}} \biggr)\frac{1}{N_{dn}^{2}}\frac{\partial N_{dn}}{\partial X} - \frac{\partial \varPsi}{\partial X} \\ &\qquad{}- F_{nc} ( M_{dn} - M_{dc} ), \end{aligned}$$
(20)
$$\begin{aligned} & \frac{\partial^{2}\varPhi}{\partial X^{2}} = - \mu \bigl[ e ( n_{io}N_{i} - n_{eo}N_{e} ) - n_{dco}q_{do}Q_{d}N_{dc} \bigr], \end{aligned}$$
(21)
$$\begin{aligned} & \frac{\partial^{2}\varPsi}{\partial X^{2}} = \frac{1}{\rho_{0}}m_{d} ( n_{dno}N_{dn} + n_{dco}N_{dc} ), \end{aligned}$$
(22)
$$\begin{aligned} & \biggl( \frac{\partial}{\partial T} + M_{dc}\frac{\partial}{\partial X} \biggr)Q_{d} \\ &\quad{}= \frac{e}{q_{do}} \biggl[ \biggl( \frac{n_{eo}}{n_{dco}} \biggr)F_{ed} ( N_{e} - 1 ) - \biggl( \frac{n_{io}}{n_{dco}} \biggr)F_{id} ( N_{i} - 1 ) \biggr], \end{aligned}$$
(23)
$$\begin{aligned} & \frac{\partial B_{N}}{\partial T} = - \frac{\partial}{\partial X} ( M_{a} B_{N} ). \end{aligned}$$
(24)

The normalized position (\(X\)) and time (\(T\)) here are normalized by the Jeans length (\(\lambda_{J}\)) and jeans time (\(\omega_{J}^{ - 1}\)), respectively. Then, \(N_{j}\) and \(M_{j}\) are the normalized population density and fluid velocity of the \(j\)th-species, normalized by their respective equilibrium value (\(n_{j0}\)) and dust acoustic phase speed (\(c_{ss} = \sqrt{T_{p} / m_{d}}\)). Moreover, \(\beta_{1} = m_{e} / m_{d}\) and \(\beta_{2} = m_{i} / m_{d}\) represent the masses of electrons and ions divided by the grain mass, respectively. Besides, \(\mu = e / ( \rho_{0}m_{d}G )\) denotes a new electro-gravitational coupling parameter, where \(\rho_{0}\) is the material density of the cloud. Further, the grain charge \(Q_{d}\) is the normalized by the equilibrium grain charge \(q_{d0} = Z_{d0}e\), where \(Z_{d0}\) is the equilibrium dust surface charge number with \(e\) as the electronic charge unit. Furthermore, \(\varPhi\) and \(\varPsi\) denote the normalized electrostatic and self-gravitational potentials, normalized by the plasma thermal potential (\(T_{p} / e\)) and square of dust acoustic phase speed (\(c_{ss}^{2} = T_{p} / m_{d}\)); respectively. Moreover, \(F_{edc}\), \(F_{idc}\), \(F_{cn}\), \(F_{nc}\), \(F_{ed}\) and \(F_{id}\) are the normalized inter-species collision (indicated by the subscripts as before), each normalized by the Jeans frequency, \(\omega_{J} = ( 4\pi \rho_{0}G )^{1 / 2}\). Additionally, the symbols \(B_{N}\) and \(M_{a}\) represent the normalized magnetic field and mean flow velocity, normalized by equilibrium magnetic field (\(B_{0}\)) and \(c_{ss} = \sqrt{T_{p} / m_{d}}\), respectively. Finally, \(\alpha_{1} = B_{0}^{2} / 4\pi n_{e0}T_{p}\), \(\alpha_{2} = B_{0}^{2} / 4\pi n_{i0}T_{p}\) and \(\alpha_{3} = B_{0}^{2} / 4\pi n_{dc0}T_{p}\) respectively typify the relative strength of the inter-species magneto-thermal interactions.

3 Linear analyses

The focal goal of the present investigation lies in the linear stability analysis of the gravito-electrostatic waves and fluctuations supported in the unbounded dusty cloud of infinite spatial extension. It, therefore, indicates that any effect of geometric curvature in the model configuration is irretrievably ignorable. As a first step, we linearly perturb all the physical dependent variables, appearing in (13)–(24), in the form of plane waves with the normalized angular frequency \(\varOmega\) and normalized angular wave number \(K\) in accordance with the standard Fourier techniques (Tignol 2001) as

$$ f\left( X, T \right) = f_{0} + f_{1}(X,T) = f_{0} + f_{10} e^{ - i\left( \varOmega T - KX \right)}, $$
(25)

where, the dynamical variables undergoing linear perturbation with amplitude \(f_{10}\) as \(f = f_{0} + f_{1}\) are \(f =N_{e}, N_{i}, N_{dc}, N_{dn}, M_{e}, M_{i}, M_{dc}, M_{dn}, \varPhi, \varPsi, B_{N}, Q_{d}\); and their homogeneous equilibrium values are \(f_{0}= 1, 1, 1, 1, 0, 0, 0, 0, 0,0, 1, 1\); respectively.

Now, using (25) in (13)–(24), one gets the following respective linearized set of algebraic equations in the Fourier space defined by (\(\varOmega, K\)) as

$$\begin{aligned} &M_{e1} = ( \varOmega + iF_{edc} )K^{ - 1} N_{e1}, \end{aligned}$$
(26)
$$\begin{aligned} & \bigl\{ 2iK + \beta_{1}F_{edc} ( i \varOmega - F_{edc} ) ( iK )^{ - 1} \bigr\} N_{e1} \\ &\quad{}+ i \alpha_{1}K B_{N1} + i K \varPhi_{1} = 0, \end{aligned}$$
(27)
$$\begin{aligned} & M_{i1} = ( \varOmega + iF_{idc} )K^{ - 1} N_{i1}, \end{aligned}$$
(28)
$$\begin{aligned} & \bigl\{ 2iK + \beta_{2}F_{idc} ( i \varOmega - F_{idc} ) ( iK )^{ - 1} \bigr\} N_{i1} \\ &\quad{}+ i \alpha_{2}K B_{N1} - i K \varPhi_{1} = 0, \end{aligned}$$
(29)
$$\begin{aligned} & M_{dc1} = \varOmega K^{ - 1} N_{dc1}, \end{aligned}$$
(30)
$$\begin{aligned} & \biggl\{ 2i \biggl( \frac{T_{d}}{T_{p}} \biggr)K - i\varOmega^{2}K^{ - 1} + F_{cn} \varOmega K^{ - 1} \biggr\} N_{dc1} \\ &\quad{}= - i \alpha_{3}KB_{N1} - i \biggl( \frac{q_{d0}}{e} \biggr)K \varPhi_{1} - iK\varPsi_{1} \\ &\qquad{}+ F_{cn}M_{dn1}, \end{aligned}$$
(31)
$$\begin{aligned} & M_{dn1} = \varOmega K^{ - 1} N_{dn1}, \end{aligned}$$
(32)
$$\begin{aligned} & \biggl\{ 2i \biggl( \frac{T_{d}}{T_{p}} \biggr)\beta_{3}K - i \varOmega^{2}K^{ - 1} + F_{nc} \varOmega K^{ - 1} \biggr\} N_{dn1} \\ &\quad{}= - iK \varPsi_{1} + F_{nc}\varOmega K^{ - 1}N_{dc1}, \end{aligned}$$
(33)
$$\begin{aligned} & K^{2} \varPhi_{1} = \mu \bigl[ e(n_{i0}N_{i1} - n_{e0}N_{e1}) - q_{d0}n_{dc0} ( Q_{d1} + N_{dc1} ) \bigr], \end{aligned}$$
(34)
$$\begin{aligned} & K^{2} \varPsi_{1} = - \frac{1}{\rho_{0}}m_{d} [ n_{dn0}N_{dn1} + n_{dc0}N_{dc1} ], \end{aligned}$$
(35)
$$\begin{aligned} & i \varOmega Q_{d1} = - \biggl( \frac{e}{q_{d0}} \biggr) \biggl[ \biggl( \frac{n_{e0}}{n_{dc0}} \biggr)F_{ed}N_{e1} - \biggl( \frac{n_{i0}}{n_{dc0}} \biggr)F_{id}N_{i1} \biggr], \end{aligned}$$
(36)
$$\begin{aligned} & B_{N1} = \bigl( \varOmega^{ - 1}K \bigr) M_{a1} = \bigl( \varOmega^{ - 1}K \bigr) ( M_{i1} - M_{e1} ). \end{aligned}$$
(37)

We now carry out a systematic algebraic exercise to transform (26)–(37) into the following generalized dispersion relation as

$$\begin{aligned} &\varOmega^{8} + A_{7}\varOmega^{7} + A_{6}\varOmega^{6} + A_{5} \varOmega^{5} + A_{4}\varOmega^{4} + A_{3}\varOmega^{3} \\ &\quad{}+ A_{2} \varOmega^{2} + A_{1}\varOmega + A_{0} = 0, \end{aligned}$$
(38)

where, the different coefficients, \(A_{7}\)–\(A_{0}\), are presented explicitly in Appendix B.

It is seen that the obtained dispersion relation (see (38)) is octic in structure; so, it has eight roots. By using the methods of decomposition (Lindfield and Penny 2012) and of Ferrari (Tignol 2001), we analytically obtain all the eight roots. To see the sensible real stability behavior of the considered model as per the present motivation, the root with positive real part (\(\varOmega_{r} > 0\)) and negative imaginary part (\(\varOmega_{i} < 0\)) are solely physically acceptable for realistic fluctuations to evolve. This choice of the roots enables us to investigate the stability mechanism as per our present goal too. We, therefore, choose only the seventh root, out of the eight roots of (38) containing the spurious ones as well, given as

$$ \varOmega = \varOmega_{7} = - \frac{A_{7}}{8} + S_{2} + \frac{1}{2} \biggl[ - 4S_{2}^{2} - 2p_{2} - \frac{q_{2}}{S_{2}} \biggr]^{1 / 2}, $$
(39)

where,

$$\begin{aligned} &p_{2} = \frac{1}{8} \biggl[ 8 \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} + A_{9} \biggr) - 3 \biggl( \frac{A_{7}}{2} \biggr)^{2} \biggr], \\ &\!\begin{aligned} q_{2}& = \frac{1}{8} \biggl[ \biggl( \frac{A_{7}}{2} \biggr)^{3} - 4 \biggl( \frac{A_{5}}{2} - \frac{A_{6}A_{7}}{4} + \frac{A_{7}^{3}}{16} + \frac{A_{10}}{A_{9}} \biggr)\\ &\quad{}\times \biggl( \frac{A_{7}}{2} - 2 \biggr) \biggr], \end{aligned} \\ & S_{2} = \frac{1}{2} \biggl[ - \frac{2}{3}p_{2} + \frac{1}{3} \biggl( c_{1} + \frac{c_{0}}{c_{1}} \biggr) \biggr]^{1 / 2}, \\ & c_{1} = \biggl[ \frac{1}{2} \bigl\{ b_{1} + \bigl( b_{1}^{2} - 4c_{0}^{3} \bigr)^{1 / 2} \bigr\} \biggr]^{3 / 2}, \\ & \!\begin{aligned} b_{1} &= \biggl[ 2 \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} + A_{9} \biggr)^{3} \\ &\quad{}- 9 \biggl( \frac{A_{7}}{2} \biggr) \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} + A_{9} \biggr) \\ &\quad{}\times\biggl( \frac{A_{5}}{2} - \frac{A_{6}A_{7}}{4} + \frac{A_{7}^{3}}{16} + \frac{A_{10}}{A_{9}} \biggr) \\ &\quad{}+ 27A_{0}^{1 / 2} \biggl( \frac{A_{7}}{2} \biggr)^{2} + 27 \biggl( \frac{A_{5}}{2} - \frac{A_{6}A_{7}}{4} + \frac{A_{7}^{3}}{16} + \frac{A_{10}}{A_{9}} \biggr)^{2} \\ &\quad{}- 72A_{0}^{1 / 2} \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} + A_{9} \biggr) \biggr], \end{aligned} \\ &\!\begin{aligned} c_{0} & = \biggl[ \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} + A_{9} \biggr)^{2} \\ &\quad{}- 3 \biggl( \frac{A_{7}}{2} \biggr) \biggl( \frac{A_{5}}{2} - \frac{A_{6}A_{7}}{4} + \frac{A_{7}^{3}}{16} + \frac{A_{10}}{A_{9}} \biggr) + 12A_{0}^{1 / 2} \biggr], \end{aligned} \\ &\!\begin{aligned} A_{9} &= \biggl[ \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} \biggr)^{2} + 2A_{0}^{1 / 2} \\ &\quad{}+ A_{7} \biggl( \frac{A_{5}}{2} - \frac{A_{6}A_{7}}{4} + \frac{A_{7}^{3}}{16} \biggr) \biggr], \end{aligned} \\ &\!\begin{aligned} A_{10} &= \biggl[ - \biggl( \frac{A_{3}}{2} \biggr) + A_{0}^{1 / 2} \biggl( \frac{A_{7}}{2} \biggr) \\ &\quad{}+ \biggl( \frac{A_{6}}{2} - \frac{A_{7}^{2}}{8} \biggr) \biggl( \frac{A_{5}}{2} - \frac{A_{6}A_{7}}{4} + \frac{A_{7}^{3}}{16} \biggr) \biggr]. \end{aligned} \end{aligned}$$

4 Results and discussion

The work presented here aims to explore the linear stability of gravito-electrostatic (pulsational) waves in the partially ionized DMC. For this purpose, the hydrostatic homogeneous equilibrium model is methodologically reduced to derive a generalized polynomial octic dispersion relation (see (38)). We numerically analyze the system in the judicious plasma parameter windows (Adams et al. 1994; Verheest 2002; Pandey et al. 2002; Karmakar and Borah 2013; Dutta et al. 2016). The numerical outcomes are shown graphically in Figs. 1, 2 and 3.

Fig. 1
figure 1

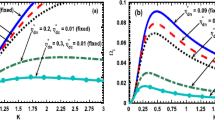
Profile of the normalized (a) real frequency (\(\varOmega_{r}\)), and (b) damping rate (\(\varOmega_{i}\)) of the gravito-electrostatic fluctutations with variation in the normalized wave number (\(K\)). Various lines correspond to (a): \(m_{d} =2 \times 10^{ - 11}\) kg (blue line), (b): \(m_{d} =3 \times 10^{ - 11}\) kg (red line), and (c): \(m_{d} =4 \times 10^{ - 11}\) kg (black line); respectively. The other parameters kept fixed are \(n_{e0} = 1.20 \times 10^{12}~\mbox{m}^{-3}\), \(n_{i0} = 4.95 \times 10^{12}~\mbox{m}^{-3}\), \(n_{dc0} = 2.35 \times 10^{6}~\mbox{m}^{-3}\), \(n_{dn0} = 4 \times 10^{6}~\mbox{m}^{-3}\), \(q_{d0} = 100 e\), \(T_{p} = 1.00\) eV, \(T_{d} = 2.00 \times 10^{ - 2}\) eV, \(B_{0} = 1 \times 10^{ - 3}~\upmu \mbox{T}\), \(\nu_{edc} / \omega_{J} = 0.1\), \(\nu_{idc} / \omega_{J} = 0.1\), \(\nu_{dcn} / \omega_{J} = 0.1\), and \(\nu_{ndc} / \omega_{J} = 0.1\)

Full size image
Fig. 2
figure 2

Profile of the normalized (a) group velocity (\(V_{G}\)), and (b) group dispersion (\(D_{G}\)) of the gravito-electrostatic fluctutations with variation in the normalized wave number (\(K\)). The fine details are the same as Fig. 1

Full size image
Fig. 3
figure 3

Profile of the normalized (a) real frequency (\(\varOmega_{r}\)), and (b) damping rate (\(\varOmega_{i}\)) of the gravito-electrostatic fluctutations with variation in the normalized wave number (\(K\)) and unnormalized dust mass (\(m_{d}\) in kg). The ‘zero’ on the \(m_{d}\)-scale signifies \(m_{d} \approx 10^{ - 21}\) kg. The fine details are the same as disscused in Fig. 1 in the text

Full size image

As in Fig. 1, we show the profile of the normalized (a) real frequency (\(\varOmega_{r}\)), and (b) damping rate (\(\varOmega_{i}\)) of the gravito-electrostatic fluctutations with variation in the normalized wave number (\(K\)). Various lines correspond to (a): \(m_{d} =2 \times 10^{ - 11}\) kg (blue line), (b): \(m_{d} =3 \times 10^{ - 11}\) kg (red line), and (c): \(m_{d} =4 \times 10^{ - 11}\) kg (black line); respectively. The other parameters kept fixed are \(n_{e0} = 1.20 \times 10^{12}~\mbox{m}^{-3}\), \(n_{i0} = 4.95 \times 10^{12}~\mbox{m}^{-3}\), \(n_{dc0} = 2.35 \times 10^{6}~\mbox{m}^{-3}\), \(n_{dn0} = 4 \times 10^{6}~\mbox{m}^{-3}\), \(q_{d0} = 100 e\), \(T_{p} = 1.00\) eV, \(T_{d} = 2.00 \times 10^{ - 2}\) eV, \(B_{0} = 1 \times 10^{ - 3}~\upmu \mbox{T}\), \(\nu_{edc} / \omega_{J} = 0.1\), \(\nu_{idc} / \omega_{J} = 0.1\), \(\nu_{dcn} / \omega_{J} = 0.1\) and \(\nu_{ndc} / \omega_{J} = 0.1\). It is seen that the real frequency (Fig. 1(a)) and damping (Fig. 1(b)) rate increase with increase in the dust mass, \(m_{d}\). It is noticeable that, there exists a critical value in the angular wave number space, \(K_{c} \approx 0.18\), above which the pulsational fluctuations propagate as a dispersive mode, but with damping in amplitude. This happens physically due to the fact that enhanced grain mass increases the strength of gravitational interaction leading to a reorganized stabilized equilibrium amid the periodic gravito-electrostatic counter-play. Thus, it enables us to conclude that the dust mass (\(m_{d}\)) plays a stabilizing influential role to the wave fluctuation dynamics under consideration dispersively.

Figure 2 depicts the profile of the normalized (a) group velocity (\(V_{G}\)), and (b) group dispersion (\(D_{G}\)) of the fluctutations with variation in the normalized angular wave number (\(K\)) under the same conditions as Fig. 1. Here, we see the magnitude of both \(V_{G}\) (Fig. 2(a)) and \(D_{G}\) (Fig. 2(b)) increase with increase in \(K\). It indicates that the fluctuations in the astro-fluid medium are dispersive in nature. In other words, the medium through which fluctuations propagate is relatively dispersive in character. It is seen that, in the ultra low-frequency domain (\(K \to 0\)), the long-wavelength fluctuations (gravitational) undergo group dipersion of singular (Fig. 2(b)). It means that the ultra low-frequency perturbations are spectrally degenerate in the defined Fourier space. Moreover, it is interesting to note that \(D_{G} > 0\), which indicates that in a wave packet model, the waves of shorter wavelength propagate faster in a time duration than the longer wavelength ones. It exhibits that the plasma medium spectrally behaves as an anamolous dispersive medium (\(D_{G} > 0\)); but, not as a normal dispersive one (\(D_{G} < 0\)).

Finally, Fig. 3 shows the spectral profile of (a) real frequency (\(\varOmega_{r}\)), and (b) damping rate (\(\varOmega_{i}\)) of the gravito-electrostatic fluctutations with conjoint variation in the normalized wave number (\(K\)) and unnormalized dust mass (\(m_{d}\) in kg) concurently. The fine details are the same as Fig. 1, but the grain mass lies in the range of \(m_{d}\sim10^{ - 9}\)–\(10^{ - 21}\) kg in the realistic cloud parametric window (Verheest 2002). It may be noted here that the ‘zero’ on the \(m_{d}\)-scale (Fig. 3) signifies \(m_{d} \approx 10^{ - 21}\) kg. We see that \(\varOmega_{r}\) (\(\varOmega_{i}\)) increases (decreases) with increase in both \(K\) and \(m_{d}\), but the wave amplitude decreases. Thus, the graphical findings now comprehensively confirm the stability characteristic features of the pulsational mode fluctuations as depicted before as well (Figs. 1 and 2).

In addition to the above, it is seen that the mean phase velocity of the fluctuations is \(\langle v_{p} \rangle \approx 1.6 \times 10^{ - 1}c_{ss}\) (as in Fig. 1(a)). It means that the linear pulsational modes propagate through the cloud plasma fluid with velocities roughly comparable with the usual fluid acoustic phase velocity. It can further be seen that the real value of the mode frequency comes out as \(\omega_{r} = \varOmega_{r}\omega_{J} = 2.7 \times 10^{ - 1}~\upmu \mbox{Hz}\). This indeed validates our low-frequency pulsational mode stability analysis in complex charge-varying magnetized turbulent astrofluids amid homogeneous quasi-neutral hydrostatic equilibrium. Here, we want to present a quantitative glance on the pulsational fluctuations under the auspice of normal cloud multi-parametric window (Bliokh et al. 1995; Verheest 2002). The physical strength of the electrostatic fluctuations can be \(\sim2\) V for \(T_{p}\sim10^{4}\) K; while, the gravitational fluctuations can go as \(\sim10^{-10}~\mbox{J}\,\mbox{kg}^{-1}\) for \(m_{d}= 10^{-8}\) kg and \(T_{p}\sim10^{4}\) K. The smallness in the gravito-electrostatic potential strengths is subject to the chosen multi-parametric set of diverse plasma properties considered in different astro-plasma circumstances.

5 Conclusions

The pulsational instability phenomena in complex charge-varying magnetized turbulent astrofluids are theoretically investigated in the framework of multi-fluidic approach. The instability behaviors, depending mainly on the dust mass, are illustrated numerically in detail. It is shown that the grain mass acts as a dispersive stabilizing source to the instability. In addition, the main conclusive remarks are presented as follows

  1. 1.

    A theoretical model study of the pulsational mode instability in complex charge-fluctuating, magnetized, turbulent and collisional astroclouds is procedurally constructed.

  2. 2.

    The gravito-electrostatic (pulsational) instability is characterized to have both propagatory and dispersive features.

  3. 3.

    The dust grain introduces both dispersive and stabilizing sources to the instability.

  4. 4.

    The instability propagates through the plasma fluid with velocities approximately comparable with the usual dust acoustic phase velocity.

  5. 5.

    The group dispersion of the pulsational instability interestingly exhibits a singular type of behaviors in the ultra low-frequency domain; whereas, the dispersion turns into an intermittent (sporadic) pattern in the relatively high-frequency domain.

  6. 6.

    The propagatory features of the pulsational wave dynamics are further illustratively confirmed also in the framework of mass-energy-spectral integration scheme.

It is an important point to be admitted here that the simplistic choice of the normalizing velocity as the dust acoustic phase speed, instead of the effective fluid acoustic speed contributed by both the normal acoustic speed and turbulence-induced speed (Mo et al. 2010), may not be physically so justifiable in highly turbulent cloud complexes. The presented analysis, amid some facts and faults however, may be commodiously useful in understanding the formation insights of dusty structures, associated wave instability processes, and early phases of large-scale bounded structures via global gravitating cloud collapse in astro-cosmic environments.