Viscoelastic pulsational mode

Abstract

We present a theoretical model analysis to study the linear pulsational mode dynamics in viscoelastic complex self-gravitating infinitely extended clouds in the presence of active frictional coupling and dust-charge fluctuations. The complex cloud consists of uniformly distributed lighter hot mutually thermalized electrons and ions, and heavier cold dust grains amid partial ionization in a homogeneous, quasi-neutral, hydrostatic equilibrium configuration. A normal mode analysis over the closed set of slightly perturbed cloud governing equations is employed to obtain a generalized dispersion relation (septic) of unique analytic construct on the plasma parameters. Two extreme cases of physical interest depending on the perturbation scaling, hydrodynamic limits and kinetic limits are considered. It is shown that the grain mass and viscoelastic relaxation time associated with the charged dust fluid play stabilizing roles to the fluctuations in the hydrodynamic regime. In contrast, however in the kinetic regime, the stabilizing effects are introduced by the dust mass, dust equilibrium density and equilibrium ionic population distribution. Besides, the oscillatory and propagatory features are illustrated numerically and interpreted in detail. The results are in good agreement with the previously reported findings as special corollaries in like situations. Finally, a focalized indication to new implications and applications of the outcomes in the astronomical context is foregrounded.

1 Introduction

It is a well-established fact that the dense locations of the interstellar molecular clouds, which are self-gravitating partially ionized plasmas in the regions between stars, are active sites for the formation of stars, planets and other bounded structures in galaxies (Draine and Salpeter 1979; Pudritz 1990; Spitzer 2004; Murray et al. 2017). The formation processes, which are indeed highly complex in nature, are triggered by a plethora of collective waves, instabilities and oscillations (Pandey et al. 1994; Jeans 1902; Yaroshenko et al. 2007; Haloi and Karmakar 2017; Karmakar and Haloi 2017). It indicates that understanding such complex wave kinetic processes prevalent in cosmogenic fluids is essential to see the seed mechanism responsible for the galactic structure formation and evolution via collective transport processes (Bliokh et al. 1995; Spitzer 2004).

It can be seen that several authors in the past have explored various instability phenomena leading to bounded structure formation by using different techniques (Shu et al. 1987). Later, Nakano has boldly studied the star formation in magnetized cloud cores, revealing, mainly that, the gravitational collapse dynamics is significantly halted due to gyro-magnetic action of the cloud constituents (Nakano 1998). More interestingly, it has also been predicted that partially charged clouds exhibit a new type of collective mode, termed as the pulsational mode (Dwivedi et al. 1999; Pandey et al. 2002; Karmakar and Borah 2013; Borah and Karmakar 2015). This pulsational mode arises because of dynamic frictional coupling of the gravitational attraction (inwards) and electrostatic repulsion (outwards) of the massive like-charged grains constituting the cloud. As far as known to the best of our knowledge, the pulsational mode dynamics in interstellar viscoelastic clouds still remains an open problem yet to address.

Motivated by the current stage of understanding of the molecular cloud dynamics, we herein develop an evolutionary model analysis to study the linear pulsational mode dynamics in viscoelastic complex self-gravitating infinitely extended clouds. It implements the roles of active frictional coupling and dust-charge fluctuations in the multi-fluidic cloud. A normal mode analysis based on the Fourier formalism over the closed set of cloud governing equations is employed to obtain a generalized dispersion relation. Two extreme cases depending on the perturbation scaling, hydrodynamic limit and kinetic limit, are considered. It is seen that the grain mass, viscoelastic relaxation time associated with the charged dust fluid play stabilizing roles to the fluctuations in hydrodynamic regime. In the kinetic regime, we see that the stabilizing effects are introduced by the dust mass and equilibrium density, and equilibrium ionic population. In addition to above, new implications and future directions are concisely indicated.

2 Physical model and formalism

In the present work, we consider a four-component isothermal strongly coupled dusty plasma comprised of thermal electrons, ions; and inertial neutral and charged spherical dust particles of identical shape. The cloud is unbounded, infinitely extended and globally quasi-neutral in nature. The dynamical response frequency of the electrons and ions with the conventional asymptotic mass scaling, $m_{e} / m_{d} < m_{i} / m_{d}\sim 10^{ - 20} \to0$ in the interstellar diffuse matter (Spitzer 2004), is very high in comparison with that of the gravitating grains. As usual, here, the masses of electrons, ions and grains are denoted respectively by $m_{e}$, $m_{i}$ and $m_{d}$; respectively. The thermal species with zero-inertia and mutual thermalization are therefore treated under the Boltzmann distribution formalism for the low-frequency fluctuations on the gravitational scales of space and time; whereas the heavier dust species with strong inertia are modelled as fluids. Besides, the dust grains have low thermal velocities and hence, possess highly correlative effects on any macroscopic scale. The grains are treated therefore as viscoelastic fluids, for which in principle, the mean-free path of the gravitationally interacting grains is almost zero. It is seen that the only massive grains in the cloud, which interact gravitationally under the long-range Newtonian coupling processes, contribute to the net mass of the cloud. The charge fluctuation dynamics of the dust grains, which arises due to interaction of electron and ion thermal currents on the grain surface randomly (Pandey et al. 2002), is accounted. The effects of collisional momentum transfer among all the constituent species are included. The collective correlation effects are considered through a generalized hydrodynamic model (Frenkel 1946; Brevik 2016). Influences from external gravitating objects or stars, electromagnetic fields, dust-size distribution and dust growth dynamics are ignored for simplicity. The dynamics of such a self-gravitating grainy plasma system is governed by all the basic set of fluid equations in the framework of generalized hydrodynamic model tailored by viscoelasticity (Frenkel 1946; Brevik 2016).

The classical dynamics of the thermal electrons and ions constituting the dust cloud are governed by the equation of continuity for flux density conservation and momentum for force density conservation respectively given in the customary notations (Dwivedi et al. 1999; Pandey et al. 2002; Haloi and Karmakar 2017; Karmakar and Haloi 2017) in flat space-time $(x, t)$ in the non-relativistic regime as

$$\begin{aligned}& \frac{\partial n_{j}}{\partial t} + \frac{\partial}{\partial x} ( n_{j}v_{j} ) = - \upsilon_{jdc} ( n_{j} - n_{j0} ), \end{aligned}$$

(1)

$$\begin{aligned}& - T_{j}\frac{\partial n_{j}}{\partial x} + en_{j} \frac{\partial\phi}{ \partial x} - m_{j}n_{j}\upsilon_{jdc}v_{j} = 0, \end{aligned}$$

(2)

where, $n_{j0}$, $n_{j}$, $m_{j}$, $v_{j}$ and $T_{j}$ stand for the equilibrium number density, non-equilibrium number density, mass, velocity and temperature (in eV) of the $j$th species ($j=e$ for electrons and $i$ for ions). Moreover, $\upsilon_{jdc}$ denotes the collision frequencies of the $j$th species with the charged dust, $e$ represents the electronic charge and $\phi$ is the electrostatic plasma potential.

The dynamics of the viscoelastic fluid composed of the neutral dust grains is described by the equation of continuity and viscoelastic momentum equation given respectively as

$$\begin{aligned}& \frac{\partial n_{dn}}{\partial t} + \frac{\partial}{\partial x} ( n_{dn}v_{dn} ) = 0, \end{aligned}$$

(3)

$$\begin{aligned}& \biggl[ 1 + \tau_{mdn} \biggl( \frac{\partial}{\partial t} + v_{dn}\frac{\partial}{\partial x} \biggr) \biggr] \\& \quad\quad{}\times\biggl[ m_{dn}n_{dn} \biggl( \frac{\partial v_{dn}}{\partial t} + v_{dn}\frac{\partial v_{dn}}{\partial x} \biggr) + T_{dn} \frac{\partial n_{dn}}{\partial x} \\& \qquad{}+ m_{dn}n_{dn}\frac{\partial\psi}{\partial x} + m_{dn}n_{dn}\upsilon_{nc} ( v_{dn} - v_{dc} ) \biggr] \\& \quad= \biggl( \zeta_{dn} + \frac{4\eta_{dn}}{3} \biggr) \frac{\partial^{2}v_{dn}}{\partial x^{2}}. \end{aligned}$$

(4)

The evolutionary dynamics of the viscoelastic fluid composed of the charged grains is dictated by the equation of continuity and viscoelastic momentum equations given respectively as

$$\begin{aligned}& \frac{\partial n_{dc}}{\partial t} + \frac{\partial}{\partial x} ( n_{dc}v_{dc} ) = 0, \end{aligned}$$

(5)

$$\begin{aligned}& \biggl[ 1 + \tau_{mdc} \biggl( \frac{\partial}{\partial t} + v_{dc}\frac{\partial}{\partial x} \biggr) \biggr] \\& \qquad{}\times \biggl[ m_{dc}n_{dc} \biggl( \frac{\partial v_{dc}}{\partial t} + v_{dc}\frac{\partial v_{dc}}{\partial x} \biggr) + q_{d}n_{dc} \frac{\partial\phi}{\partial x} + T_{dc}\frac{\partial n_{dc}}{\partial x} \\& \qquad{}+ m_{dc}n_{dc}\frac{\partial\psi}{\partial x} + m_{dc}n_{dc}\upsilon_{cn} ( v_{dc} - v_{dn} ) \biggr] \\& \quad= \biggl( \zeta_{dc} + \frac{4\eta_{dc}}{3} \biggr) \frac{\partial^{2}v_{dc}}{\partial x^{2}}. \end{aligned}$$

(6)

The symbols $n_{dn ( dc )}$, $m_{dn ( dc )}$, $v_{dn ( dc )}$ and $T_{dn ( dc )}$ denote the population density, mass, flow velocity and temperature of neutral (charged) dust, respectively. $q_{d}$ is the charge of dust grain treated as a dynamical variable. Also, $\tau_{mdn ( dc )}$, $\eta_{dn ( dc )}$, $\zeta_{dn ( dc )}$ stand for viscoelastic relaxation time, shear viscosity coefficient (resistance to flow) and bulk viscosity coefficient (resistance to expansion) of neutral (charged) dust particles, respectively. The symbols $\upsilon_{nc}$ and $\upsilon_{cn}$ represent the electron-dust, ion-dust, neutral-charged and charged-neutral collision frequencies, respectively. $\phi$ and $\psi$ are electrostatic potential and self-gravitational potential developed by fluid density fields, respectively. The Poisson equation for these potential distributions in unnormalized form can respectively be written as

$$\begin{aligned}& \frac{\partial^{2}\phi}{\partial x^{2}} = 4\pi e \biggl[ ( n_{e} - n_{i} ) - q_{d}\frac{n_{dc}}{e} \biggr], \end{aligned}$$

(7)

$$\begin{aligned}& \frac{\partial^{2}\psi}{\partial x^{2}} = 4\pi G ( m_{dn}n_{dn} + m_{dc}n_{dc} ), \end{aligned}$$

(8)

where, $G = 6.673 \times10^{ - 11}\mbox{ N m}^{2}\mbox{ kg}^{-2}$ is the universal gravitational (Newtonian) coupling constant via which gravitational interaction is perceptible.

Assuming, $m_{dn} \approx m_{dc} = m_{d}$, Eq. (8) can be written as

$$ \frac{\partial^{2}\psi}{\partial x^{2}} = 4\pi G m_{d} ( n_{dn} + n_{dc} ). $$

(9)

Lastly, the dynamics of the fluctuating electric charge of the dust grains is governed by the charge fluctuation equation given as

$$ \begin{aligned}[b] & \biggl( \frac{\partial}{\partial t} + v_{d}\frac{\partial}{\partial x} \biggr)q_{d} \\ &\quad= e \biggl[ \upsilon_{ed}\frac{ ( n_{e} - n_{e0} )}{n_{d0}} - \upsilon_{id}\frac{ ( n_{i} - n_{i0} )}{n_{d0}} \biggr]. \end{aligned} $$

(10)

It can be seen from Eqs. (1)–(10) that the plasma thermal species (hot, mutually thermalized) constitute here inertialess fluids (Eqs. (1)–(2)); whereas, the cold dusty species form the inertial fluids (Eqs. (3)–(6)). In the extreme limits of $m_{d} \to0$, $\upsilon_{nc} \to0$ and $\upsilon_{cn} \to0$, all the species can collectively be treated in a common footing of the Boltzmann (thermal) equilibrium and associated distribution laws. Now, for simplicity of our analysis, we adopt a standard astrophysical normalization procedure to be applied in Eqs. (1)–(10) to study the scale-free scenarios. The details of the normalization scheme together with typical values are presented in Table 1. The normalization scheme together with normalized notations, for instant reference, is mathematically highlighted as

$$\begin{aligned} &\xi= \frac{x}{\lambda_{J}},\qquad\tau= \frac{t}{\omega_{J}^{ - 1}},\qquad N_{j} = \frac{n_{j}}{n_{j0}},\qquad N_{\beta} = \frac {n_{\beta}}{ n_{\beta0}}, \\ & M_{\beta} = \frac{v_{\beta}}{c_{ss}},\qquad\varPhi= \frac{\phi e}{T},\qquad \varPsi= \frac{\psi}{c_{ss}^{2}},\qquad Q_{d} = \frac{q_{d}}{q_{d0}} \end{aligned} $$

and

$$\tau_{mdn(mdc)}^{*} = \tau_{mdn(mdc)}\omega_{J}. $$

Here, $j= \text{`$e$'}$ for electrons, ‘$i$’ for ions; and $\beta=\text{`$dn$'}$ for neutral dust and ‘$dc$’ for charged dust. The normalized form of Eqs. (1)–(10), thus constructed, is respectively written as

$$\begin{aligned}& \frac{\partial N_{j}}{\partial\tau} + \frac{\partial}{\partial\xi} ( N_{j}M_{j} ) = - F_{jdc} ( N{}_{j} - 1 ), \end{aligned}$$

(11)

$$\begin{aligned}& \frac{\partial N_{j}}{\partial\xi} + N_{j}\frac{\partial\varPhi}{ \partial \xi} + F_{jdc} \biggl( \frac{m_{j}}{m_{d}} \biggr)N_{j}M_{j} = 0, \end{aligned}$$

(12)

$$\begin{aligned}& \frac{\partial N_{dn}}{\partial\tau} + \frac{\partial}{\partial\xi} ( N_{dn}M_{dn} ) = 0, \end{aligned}$$

(13)

$$\begin{aligned}& \biggl[ 1 + \tau_{mdn}^{*} \biggl( \frac{\partial}{\partial \tau} + M_{dn}\frac{\partial}{\partial\xi} \biggr) \biggr] \\& \qquad{}\times\biggl[ N_{dn} \biggl( \frac{\partial M_{dn}}{\partial\tau} + M_{dn}\frac{\partial M_{dn}}{\partial\xi} \biggr) + \biggl( \frac{T_{dn}}{T} \biggr) \frac{\partial N_{dn}}{\partial\xi} \\& \qquad{}+ N_{dn}\frac{\partial\varPsi}{\partial\xi}+ F_{nc} \bigl\{ N_{dn} ( M_{dn} - M_{dc} ) \bigr\} \biggr] \\& \quad= \chi_{rxn}^{2}\tau_{mdn}^{*} \frac{\partial^{2}M_{dn}}{\partial \xi^{2}}, \end{aligned}$$

(14)

$$\begin{aligned}& \frac{\partial N_{dc}}{\partial\tau} + \frac{\partial}{\partial\xi} ( N_{dc}M_{dc} ) = 0, \end{aligned}$$

(15)

$$\begin{aligned}& \biggl[ 1 + \tau_{mdc}^{*} \biggl( \frac{\partial}{\partial \tau} + M_{dc}\frac{\partial}{\partial\xi} \biggr) \biggr] \\& \qquad{}\times\biggl[ N_{dc} \biggl( \frac{\partial M_{dc}}{\partial\tau} + M_{dc}\frac{\partial M_{dc}}{\partial\xi} \biggr) + \biggl( \frac{T_{dc}}{T} \biggr) \frac{\partial N_{dc}}{\partial\xi} \\& \qquad{}+ Q_{d}N_{dc}\frac{\partial\varPhi}{\partial\xi}+ N_{dc} \frac{\partial\varPsi}{\partial\xi} + F_{cn} \bigl\{ N_{dc} ( M_{dc} - M_{dn} ) \bigr\} \biggr] \\& \quad= \chi_{rxc}^{2}\tau_{mdc}^{*} \frac{\partial^{2}M_{dc}}{\partial \xi^{2}}, \end{aligned}$$

(16)

$$\begin{aligned}& \frac{\partial^{2}\varPhi}{\partial\xi^{2}} = \frac{4\pi e^{2}}{m_{d}\omega_{J}^{2}} \biggl[ ( n_{e0}N_{e} - n_{i0}N_{i} ) - n_{dc0}Q_{d}N_{dc}\frac{q_{d0}}{e} \biggr], \end{aligned}$$

(17)

$$\begin{aligned}& \frac{\partial^{2}\varPsi}{\partial\xi^{2}} = \biggl[ \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr)N_{dc} + \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr)N_{dn} \biggr], \end{aligned}$$

(18)

$$\begin{aligned}& \frac{\partial Q_{d}}{\partial\tau} + M_{dc}\frac{\partial Q_{d}}{\partial \xi} = \frac{e}{q_{d0}}\biggl[ F_{ed} \biggl( \frac{n_{e0}}{n_{d0}} \biggr) ( N_{e} - 1 ) \\& \phantom{\frac{\partial Q_{d}}{\partial\tau} + M_{dc}\frac{\partial Q_{d}}{\partial \xi} =} - F_{id} \biggl( \frac{n_{i0}}{n_{d0}} \biggr) ( N_{i} - 1 ) \biggr]. \end{aligned}$$

(19)

The scale-invariant dynamic properties of the cloud in an unperturbed arrangement are governed by the closed set of Eqs. (11)–(19) devised in normalized form. This coupled set is used to disclose the properties of the dynamic stability of the complex astrocloud against slight perturbations under consideration.

Table 1 Adopted normalization scheme

3 Normal mode analysis

We apply a standard normal mode analysis locally to the unbounded self-gravitating grainy plasma to study the local stability behavior of the viscoelastic pulsational mode. To do that, the relevant dependent normalized variables describing the cloud are allowed to undergo slight perturbation around the respective hydrostatic equilibrium values as

$$ \left ( \textstyle\begin{array}{l} N_{e} \\ N_{i} \\ N_{dn} \\ N_{dc} \\ M_{e} \\ M_{i} \\ M_{dn} \\ M_{dc} \\ \varPhi\\ \varPsi\\ Q_{d} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{l} 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{array}\displaystyle \right ) + \left ( \textstyle\begin{array}{l} N_{e1} \\ N_{i1} \\ N_{dn1} \\ N_{dc1} \\ M_{e1} \\ M_{i1} \\ M_{dn1} \\ M_{dc1} \\ \varPhi_{1} \\ \varPsi_{1} \\ Q_{d1} \end{array}\displaystyle \right ). $$

(20)

Applying the above Fourier perturbation scheme, as given by Eq. (20), the linearized set of Eqs. (11)–(19) respectively reads as

$$\begin{aligned}& \frac{\partial N_{e1}}{\partial\tau} + \frac{\partial M_{e1}}{\partial \xi} = - F_{edc}N{}_{e1}, \end{aligned}$$

(21)

$$\begin{aligned}& \frac{\partial N_{e1}}{\partial\xi} - \frac{\partial\varPhi _{1}}{\partial \xi} + F_{edc} \biggl( \frac{m_{e}}{m_{d}} \biggr)M_{e1} = 0, \end{aligned}$$

(22)

$$\begin{aligned}& \frac{\partial N_{i1}}{\partial\tau} + \frac{\partial M_{i1}}{\partial \xi} = - F_{idc}N{}_{i1}, \end{aligned}$$

(23)

$$\begin{aligned}& \frac{\partial N_{i1}}{\partial\xi} + \frac{\partial\varPhi _{1}}{\partial \xi} + F_{idc} \biggl( \frac{m_{i}}{m_{d}} \biggr)M_{i1} = 0, \end{aligned}$$

(24)

$$\begin{aligned}& \frac{\partial N_{dn1}}{\partial\tau} + \frac{\partial M_{dn1}}{\partial \xi} = 0, \end{aligned}$$

(25)

$$\begin{aligned}& \biggl( 1 + \tau_{mdn}^{*}\frac{\partial}{\partial\tau} \biggr) \biggl[ \frac{\partial M_{dn1}}{\partial\tau} + \biggl( \frac{T_{dn}}{T} \biggr) \frac{\partial N_{dn1}}{\partial\xi} + \frac{\partial\varPsi_{1}}{\partial\xi} \\& \quad\quad{}+ F_{nc} ( M_{dn1} - M_{dc1} ) \biggr] \\& \quad= \chi^{2}\tau_{mdn}^{*}\frac{\partial^{2}M_{dn1}}{\partial\xi^{2}}, \end{aligned}$$

(26)

$$\begin{aligned}& \frac{\partial N_{dc1}}{\partial\tau} + \frac{\partial M_{dc1}}{\partial \xi} = 0, \end{aligned}$$

(27)

$$\begin{aligned}& \biggl( 1 + \tau_{mdc}^{*}\frac{\partial}{\partial\tau} \biggr) \biggl[ \frac{\partial M_{dc1}}{\partial\tau} + \biggl( \frac{T_{dc}}{T} \biggr) \frac{\partial N_{dc1}}{\partial\xi} + \frac{\partial\varPhi_{1}}{\partial\xi} + \frac{\partial\varPsi _{1}}{\partial \xi} \\& \quad\quad{}+ F_{cn} ( M_{dc1} - M_{dn1} ) \biggr] \\& \quad= \chi^{2}\tau_{mdc}^{*}\frac{\partial^{2}M_{dc1}}{\partial\xi^{2}}, \end{aligned}$$

(28)

$$\begin{aligned}& \frac{\partial^{2}\varPhi_{1}}{\partial\xi^{2}} = \frac{4\pi e^{2}}{m_{d}\omega_{J}^{2}}\biggl[ ( n_{e0}N_{e1} - n_{i0}N_{i1} ) \\& \phantom{\frac{\partial^{2}\varPhi_{1}}{\partial\xi^{2}} =} - n_{dc0}\frac{q_{d0}}{e} ( N_{dc1} + Q_{d1} ) \biggr], \end{aligned}$$

(29)

$$\begin{aligned}& \frac{\partial^{2}\varPsi_{1}}{\partial\xi^{2}} = \biggl[ \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr) N_{dc1} + \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) N_{dn1} \biggr], \end{aligned}$$

(30)

$$\begin{aligned}& \frac{\partial Q_{d1}}{\partial\tau} = \frac{e}{q_{d0}} [ F_{ed}N_{e1} - F_{id}N_{i1} ]. \end{aligned}$$

(31)

The unbounded infinitely extended geometry of the interstellar molecular cloud allows the fluctuations in the relevant cloud parameters to grow periodically in the Fourier form of plane waves as ${\sim}\exp \{ - i ( \varOmega\tau- K\xi ) \}$. Here, $\varOmega= \omega/ \omega_{J}$ is the Jeans-normalized fluctuation frequency and $K = k / k_{J}$ is the Jeans-normalized angular wavenumber. The Fourier analysis of Eqs. (21)–(31) mapped in the coordination space $( \xi, \tau )$, on mutual parametric decoupling, yields respectively the following set of algebraic equations in the Fourier space $( K, \varOmega )$ as

$$\begin{aligned}& N_{e1} = \frac{K^{2}\varPhi_{1}}{ ( \frac{m_{e}}{m_{d}} ) F_{edc} ( i\varOmega- F_{edc} ) - K^{2}}, \end{aligned}$$

(32)

$$\begin{aligned}& N_{i1} = \frac{ - K^{2}\varPhi_{1}}{ ( \frac{m_{i}}{m_{d}} ) F_{idc} ( i\varOmega- F_{idc} ) - K^{2}}, \end{aligned}$$

(33)

$$\begin{aligned}& N_{dc1} = K^{2}Z_{d0} \varPhi_{1} \\& \phantom{N_{dc1} =} \Big/\biggl[ \varOmega ( \varOmega+ iF_{cn} ) - K^{2} \biggl( \frac{T_{dc}}{T} \biggr) \\& \phantom{N_{dc1} =} + i \varOmega K^{2} \biggl( \frac{\chi_{rxc}^{2}\tau_{mdc}^{*}}{1 - i\varOmega\tau_{mdc}^{*}} \biggr) + \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr) \biggr] \\& \phantom{N_{dc1} =}- \biggl[ \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) - i \varOmega F_{cn} \biggr] \biggl[ \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr) - i \varOmega F_{nc} \biggr] \\& \phantom{N_{dc1} =} \Big/\biggl[ \varOmega ( \varOmega+ iF_{nc} ) - K^{2} \biggl( \frac{T_{dn}}{T} \biggr) \\& \phantom{N_{dc1} =} + i \varOmega K^{2} \biggl( \frac{\chi_{rxn}^{2}\tau_{mdn}^{*}}{1 - i\varOmega\tau_{mdn}^{*}} \biggr) + \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) \biggr], \end{aligned}$$

(34)

$$\begin{aligned}& \varPhi_{1} = \frac{4\pi e^{2}}{m_{d}K^{2}\omega_{J}^{2}}\biggl[ ( n_{i0}N_{i1} - n_{e0}N_{e1} ) \\& \phantom{\varPhi_{1} =} + n_{dc0}\frac{q_{d0}}{e} ( N_{dc1} + Q_{d1} ) \biggr], \end{aligned}$$

(35)

$$\begin{aligned}& Q_{d1} = \frac{ie}{\varOmega q_{d0}}(F_{edc} N_{e1} - F_{idc} N_{i1}). \end{aligned}$$

(36)

Therefore, applying the method of decomposition and elimination, Eqs. (32)–(36) can be transformed into the following linear generalized dispersion relation under the condition of non-vanishing gravito-electrostatic potentials in the linear order as

$$ \begin{aligned}[b] & 1 + \frac{\varOmega_{pe}^{2}}{ ( 1 - \frac{i}{\varOmega} F_{ed} )^{ - 1} [ i\varOmega F_{edc} - \{ F_{edc}^{2} + ( \frac{m_{d}}{m_{e}} ) K^{2} \} ]} \\ &\qquad{}+ \frac{\varOmega_{pi}^{2}}{ ( 1 - \frac{i}{\varOmega} F_{id} )^{ - 1} [ i\varOmega F_{idc} - \{ F_{idc}^{2} + ( \frac{m_{d}}{m_{i}} ) K^{2} \} ]} \\ &\quad= {\varOmega_{pd}^{2}} \\ &\qquad \Big/\biggl[ \varOmega ( \varOmega+ iF_{cn} ) - K^{2} \biggl( \frac{T_{dc}}{T} \biggr) \\ &\qquad{}+ i \varOmega K^{2} \biggl( \frac{\alpha_{dc}}{1 - i \varOmega\tau_{mdc}^{*}} \biggr) + \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr) \biggr] \\ &\qquad{}- { \biggl[ \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) - i \varOmega F_{cn} \biggr] \biggl[ \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr) - i \varOmega F_{nc} \biggr]} \\ &\qquad \Big/\biggl[ \varOmega ( \varOmega+ iF_{nc} ) - K^{2} \biggl( \frac{T_{dn}}{T} \biggr) \\ &\qquad{}+ i \varOmega K^{2} \biggl( \frac{\alpha_{dn}}{1 - i \varOmega\tau_{mdn}^{*}} \biggr) + \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) \biggr], \end{aligned} $$

(37)

where, $\varOmega_{pe}$, $\varOmega_{pi}$ and $\varOmega_{pd}$ are electron-plasma frequency, ion-plasma frequency and dust-plasma oscillation frequency, respectively. The role of each of the terms in Eq. (37) is self-explanatory and centered around the customary scheme of notations. If the contributions from the viscoelastic sources, via $\tau_{mdn}^{*}$, $\tau_{mdc}^{*}$, $\alpha_{dn}$ and $\alpha_{dc}$, are altogether ignored; then Eq. (37) agreeably reduces to the well-known form of the linear pulsational mode dispersion relation in a charge-fluctuating cloud (Pandey et al. 2002). Moreover, if the grain charge dynamics, alongside viscoelasticity, too is neglected in Eq. (37), the pulsational mode dispersion relation for static clouds (Dwivedi et al. 1999) gets reproduced. These functional matching of the three distinct classes of dispersion relation put forward a quick reliability check-up of our entire analytical calculation scheme. We now use Eq. (37) to investigate the oscillatory and propagatory dynamics of the linear gravito-electrostatic (pulsational) mode in the viscoelastic complex cloud. To do that, two extreme cases of physical interest depending on the perturbations, such as hydrodynamic and kinetic limits, in the wave propagation dynamics are considered and elaborately discussed the next sub-sections.

3.1 Hydrodynamic limit

In the hydrodynamic limits ($\varOmega\tau_{mdn}^{*}, \varOmega \tau_{mdc}^{*} \ll 1$), which typify the low-frequency fluctuations in the cloud, the generalized dispersion relation (Eq. (37)) reduces to

$$ \begin{aligned}[b] &1 + \frac{\varOmega_{pe}^{2}}{ ( 1 - \frac {i}{\varOmega} F_{ed} )^{ - 1} [ i\varOmega F_{edc} - \{ F_{edc}^{2} + ( \frac{m_{d}}{m_{e}} ) K^{2} \} ]} \\ &\qquad{}+ \frac{\varOmega_{pi}^{2}}{ ( 1 - \frac{i}{\varOmega} F_{id} )^{ - 1} [ i\varOmega F_{idc} - \{ F_{idc}^{2} + ( \frac{m_{d}}{m_{i}} ) K^{2} \} ]} \\ &\quad= \frac{\varOmega_{pd}^{2}}{ [ \varOmega^{2} + i \varOmega ( F_{cn} + K^{2}\alpha_{dc} ) - K^{2} ( \frac{T_{dc}}{T} ) + ( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} ) ]} \\ &\qquad{}- \frac{ [ ( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) - i \varOmega F_{cn} ] [ ( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} ) - i \varOmega F_{nc} ]}{ [ \varOmega^{2} + i \varOmega ( F_{nc} + K^{2}\alpha_{dn} ) - K^{2} ( \frac{T_{dn}}{T} ) + ( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) ]}. \\\end{aligned} $$

(38)

An execution of algebraic operation for mathematical simplification reduces Eq. (38) into the following simplified septic form in the hydrodynamic regime as

$$ \begin{aligned}[b] &\varOmega^{7} + a_{6} \varOmega^{6} + a_{5}\varOmega^{5} + a_{4}\varOmega^{4} \\ &\quad{}+ a_{3}\varOmega^{3} + a_{2} \varOmega^{2} + a_{1}\varOmega+ a_{0} = 0; \end{aligned} $$

(39)

where, the different involved coefficients are described in Appendix A. The different coefficients control the dynamics of the instability under the considered limit. The root of the instability lies in dynamic relaxation processes by virtue of sources of free energy stemming in the long-range gravito-electrostatic interplay. Applying now the condition for extremely low-frequency fluctuations in Eq. (39), we obtain the expression for the growth rate as

$$ \varOmega_{i} = f ( K, \alpha_{dn}, \alpha_{dc} ) = \frac{\sqrt{4a_{0}a_{2} - a_{1}^{2}}}{2a_{2}}. $$

(40)

It is evident from Eq. (40) that the source responsible behind the extremely low-frequency instability growth is attributable to the conjoint action of the viscosity (sourcing to energy dissipation) and elasticity (sourcing to wave energy restoration).

3.2 Kinetic limit

In the kinetic limits ($\varOmega\tau_{mdn}^{*}, \varOmega\tau_{mdc}^{*} \gg 1$), which account for the high-frequency fluctuations in the adopted cloud, Eq. (37) gets transformed into

$$ \begin{aligned}[b]& 1 + \frac{\varOmega_{pe}^{2}}{ ( 1 - \frac {i}{\varOmega} F_{ed} )^{ - 1} [ i\varOmega F_{edc} - \{ F_{edc}^{2} + ( \frac{m_{d}}{m_{e}} ) K^{2} \} ]} \\ &\qquad{}+ \frac{\varOmega_{pi}^{2}}{ ( 1 - \frac{i}{\varOmega} F_{id} )^{ - 1} [ i\varOmega F_{idc} - \{ F_{idc}^{2} + ( \frac{m_{d}}{m_{i}} ) K^{2} \} ]} \\ &\quad= \frac{\varOmega_{pd}^{2}}{ [ \varOmega^{2} + i \varOmega F_{cn} - K^{2} ( \frac{T_{dc}}{T} + \chi_{rxc}^{2} ) + ( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} ) ]} \\ &\qquad{}- \frac{ [ ( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) - i \varOmega F_{cn} ] [ ( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} ) - i \varOmega F_{nc} ]}{ [ \varOmega^{2} + i \varOmega F_{nc} - K^{2} ( \frac{T_{dn}}{T} + \chi_{rxn}^{2} ) + ( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} ) ]}. \end{aligned} $$

(41)

An algebraic exercise reduces Eq. (40) in the kinetic regime into the following simplified septic form as

$$ \begin{aligned}[b] &\varOmega^{7} + a_{6} \varOmega^{6} + a_{5}\varOmega^{5} + a_{4}\varOmega^{4} \\ &\quad{}+ a_{3}\varOmega^{3} + a_{2} \varOmega^{2} + a_{1}\varOmega+ a_{0} = 0; \end{aligned} $$

(42)

where, the different involved coefficients are presented explicitly in Appendix B. More particularly, the origin of the free energy sources can also be derived and interpreted specifically by reducing Eq. (42) for the kinetic regimes as follows.

$$ \varOmega_{i} = f ( K, \chi_{rxn}, \chi_{rxc} ) = \frac{\sqrt{4a_{5} - a_{6}^{2}}}{2}. $$

(43)

We see from Eq. (43) that the source of the onset for the high-frequency instability is ascribable to the diversified joint interaction of the collective correlative interaction processes (dissipation-restoration of wave energy) introduced through viscoelasticity.

4 Results and discussions

The focal goal of the present contribution is to investigate the gravito-electrostatic (pulsational) stability properties of a complex astrophysical viscoelastic cloud. The closed set of basic governing equations is accordingly reduced into two extreme forms of dispersion relations in the hydrodynamic limit (Eq. (38)) and kinetic limit (Eq. (41)). We carry out a numerical analysis to extract the dispersion properties by using a suitable root-finding method of polynomial decomposition (Lindfield and Penny 2012). The numerical analysis is based in the framework of parametric domains of realistic astrophysical fluids (McKelvey 1984). The results, thus obtained by numerical analysis, are illustrated and interpreted in Figs. 1–8 as follows

Fig. 1

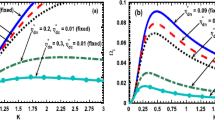
Profile of the normalized (a) real frequency ($\varOmega_{r}$) and (b) growth rate ($\varOmega_{i}$) of the gravito-electrostatic fluctuations in the hydrodynamic limits ($\varOmega\tau_{mdn}^{*}, \varOmega\tau_{mdc}^{*} \ll 1$) for different values of the dust mass ($m_{d}$) as shown in the legends. The fine numerical details are given in the text

In Fig. 1, we present the dynamic profile patterns of the normalized (a) real frequency ($\varOmega_{r}$) and (b) growth rate ($\varOmega_{i}$) of the gravito-electrostatic fluctuations in the hydrodynamic limits ($\varOmega\tau_{mdn}^{*}, \varOmega\tau _{mdc}^{*} \ll 1$) for different values of the dust mass ($m_{d}$). The other inputs are $n_{e0} = 10\text{--}50\mbox{ cm}^{-3}$, $n_{i0} = 5\text{--} 30\mbox{ cm}^{-3}$, $n_{d0} = 10^{ - 2} \text{--} 10\mbox{ cm}^{-3}$, $m_{e} = 9.1 \times10^{ - 28}\mbox{ g}$, $m_{i} = 1.67 \times10^{ - 24}\mbox{ g}$, $T_{e} \approx T_{i} = 1 \text{--} 10\mbox{ eV}$, $T_{dn} \approx T_{dc} \approx T_{d} = 0.01\mbox{ eV}$, $\tau_{mdn}^{*} = 0.01$, $\tau_{mdc}^{*} = 0.01$, $q_{d0} = 1.6 \times10^{ - 16}\mbox{ C}$ and $r = 1.28\mbox{ }\mu \mbox{m}$ (Spitzer 2004; Shukla and Stenflo 2006; Dutta et al. 2016; Karmakar and Haloi 2017). It is seen from Fig. 1a that the fluctuations of the astrocloud in the hydrodynamic regime are comprised of bi-scale dynamic behaviors. In this perturbation domain, the Jeans mode is speculated to exist for the large-wavelength zone ($K \to0$). The mode here is found to be highly dispersive in nature. Moreover, as the spectral domain beyond $K = 1$ is reached, a quasi-linear mode transformation into non-dispersive acoustic wave is found to occur. It can be seen that, in the considered cloud model, the origin of the dispersive properties is sourced collectively by deviation from the exact gravito-acoustic neutrality triggered by the Poisson potential curvatures (via Eqs. (17)–(18)). It is further noteworthy that the increasing magnitude of the dust mass reduces the velocity (both phase as well as group velocity), and vice-versa (Fig. 1a). It may therefore be concluded that the dust mass plays a decelerating role to the collective wave fluctuations. It is further seen that the critical limit in the $K$-space, as indicated by $K = 1$, allows the perturbations to undergo explosive growth (Fig. 1b). The growth is persistent in the relatively high-$K$ spectral domain. It is pertinent to note further that the grain mass develops a stabilizing propensity thereby allowing the wave fluctuations to damp out with the increment in dust inertia. The basic physics underlying the above fluctuation properties (Figs. 1, 2, 3, 4) is ascribable to the long-range gravito-electrostatic coupling of the long-wavelength Jeans mode and its transformed form of relatively short-wavelength pure acoustic (electrostatic) mode amid the stabilizing agency incorporated afresh via the charge-varying dust dynamics on the astrophysical scales of space and time.

Fig. 2

Same as Fig. 1, but for different values of the equilibrium dust charge ($q_{d0}$) as in the legends

Fig. 3

Same as Fig. 1, but for different values of viscoelastic relaxation time for neutral dust ($\tau_{mdn}^{*}$) as in the legends

Fig. 4

Same as Fig. 1, but for different values of normalized viscoelastic relaxation time for charged dust ($\tau_{mdc}^{*}$) as in the legends

We also obtain the spectral pattern profiles of the wave parameters $( \varOmega_{r}, \varOmega_{i} )$ having functional dependence on $K$ for enhancing values of $q_{d0}$ (Fig. 2), $\tau_{mdn}^{*}$ (Fig. 3) and $\tau_{mdc}^{*}$ (Fig. 4). They show analogous characteristic wave features, but with minor quantitative modifications in the propagation dynamical properties. It is thereby revealed that an enhancement in $q_{d0}$ results in a two-step behavior for the excitation of the collective gravito-electrostatic waves and oscillations (Fig. 2). The wave mode gets first highly decelerated due to the $q_{d0}$-increment in the domain $K<1$ (Fig. 2a). However, in the $K$-space defined by $K \ge1$, the $q_{d0}$-increment acts as a destabilizing agency to the collective wave fluctuations (Fig. 2b). An enhancement in $\tau_{mdn}^{*}$ (Fig. 3) results in similar wave patterns as in Fig. 2; however, reverse propensities in the dynamics are speculated for the $\tau_{mdc}^{*}$ enhancement and vice-versa (Fig. 4). It can therefore, be added that the propagatory features of the wave patterns supported in the cloud in the hydrodynamic regime are numerically revealed.

As in Fig. 5, we display the profile structures of the normalized (a) real frequency ($\varOmega_{r}$) and (b) growth rate ($\varOmega_{i}$) of the gravito-electrostatic fluctuations in the kinetic limits ($\varOmega\tau_{mdn}^{*}, \varOmega\tau _{mdc}^{*} \gg 1$) for different values of the dust mass ($m_{d}$). The input and initial values used here are the same as Fig. 1, but now with $\tau_{mdn}^{*} = 0.1$ and $\tau_{mdc}^{*} = 0.1$, against the hydrodynamic limits. It is found in the kinetic limits that the $m_{d}$-enhancement results in acceleration process of the wave fluctuation mode (Fig. 5a). Also, it imparts a stabilizing effect on the fluctuations (Fig. 5b), because the magnitude of the fluctuation growth decreases with the augmentation in the grain mass. The gravito-electrostatic perturbations in this case are found to be highly dispersive in nature because of linear dispersive functional dependence of $\varOmega$ on $K$. As a consequence, the group velocity and the phase velocity in this case are equal, unlike those found in the earlier hydrodynamic limits. Moreover, a reverse effect on the fluctuation propagation dynamics is speculated to be induced by the $n_{e0}$-enhancement. The profile patterns with the $n_{i0}$-enhancement (Fig. 7) are almost similar to Fig. 5, but with an opposite evolutionary trend. In other words, the equilibrium electron number density plays a destabilizing role to the fluctuations. Thus, it is seen that the characteristic features revealed in Fig. 5 and Fig. 7 are fairly equivalent on the same comparative footing, but with a pronounced dynamic reversibility. It is pertinent to mention here that $m_{d}$, $n_{i0}$ and $n_{d0}$ introduce stabilizing effects to the cloud fluctuations (Fig. 5 and Figs. 7, 8) at the cost of gravito-acoustic interplay in the presence of charge-fluctuating grain dynamics.

Fig. 5

Profile of the normalized (a) real frequency ($\varOmega_{r}$) and (b) growth rate ($\varOmega_{i}$) of the gravito-electrostatic fluctuations in the kinetic limits ($\varOmega \tau_{mdn}^{*}, \varOmega\tau_{mdc}^{*} \gg 1$) for different values of the dust mass ($m_{d}$) as shown in the legends. The fine details are given in the text

Fig. 6

Same as Fig. 5, but for different values of the equilibrium electron density ($n_{e0}$) as in the legends

Fig. 7

Same as Fig. 5, but for different values of the equilibrium ion density ($n_{i0}$) as in the legends

Fig. 8

Same as Fig. 5, but for different values of the equilibrium dust density ($n_{d0}$) as in the legends

As a consequence of our numerical calculation scheme, we can say that the relevant wave features in both the hydrodynamic and kinetic limits, under the conjoint action of gravito-electrostatic interplay in the presence grain-charge fluctuation dynamics in the viscoelastic astrocloud fluid, are explored along with the stabilizing sources identified and characterized. We invoke isothermal dust-fluid formulation for analytic simplification. It is, however, expected that the variable dust-temperature if considered, would introduce additional stability effects (sourced not only by density fluctuations, but also by temperature fluctuations) against the global dynamic cloud collapse leading to stars, planets, etc. In order to obtain a naturalistic illustrative pattern of the fluctuations responsible for fluid material redistribution processes on the verge of structure formation, it is admitted that a suitably constructed set of initial and input values of sensible astro-space parameters from different sources in the literature (Spitzer 2004; Shukla and Stenflo 2006; Dutta et al. 2016; Karmakar and Haloi 2017) is adopted. It may, however, be noted that, for a realistic bounded astrophysical equilibrium structure to form in the gravitating dust molecular clouds, the dust charge-to-mass ratio, $m_{d} / Q_{d} \sim \sqrt{G}$ (Gisler et al. 1992) leading to a perfect gravito-electrostatic equilibrium, needs to be asymptotically fulfilled against the collective plasma wave excitations and oscillations.

5 Conclusions

The stability dynamics of the viscoelastic pulsational mode, which is an outcome of complex gravito-electrostatic interplay in the presence of viscoelasticity in a charge-fluctuating cloud, is theoretically analyzed. The closed set of the cloud structure equations in normalized form accordingly undergoes a slight perturbation around the defined hydrostatic homogeneous equilibrium implicating uniform distribution of the cloud plasma constituents. The perturbed model, on being decoupled in the Fourier space, reduces to a generalized septic dispersion relation with diversified plasma-dependent coefficients of explicit nature. It is shown from the dispersion arguments that the fluctuation dynamics under consideration is an outcome of the plasma dynamic relaxation processes at the cost of free energy sources stemming in the long-range gravito-electrostatic interplay and associated fluid currents. Two extreme cases of practical relevants sourced by perturbation dimensions in the fluctuation dynamics, termed as the hydrodynamic and kinetic regimes, are considered. The graphical shape-analysis of the fluctuation features shows that the dust mass ($m_{d}$) and viscoelastic relaxation time for the charged dust fluid ($\tau_{mdc}^{*}$) give rise to stabilizing influences in the hydrodynamic limits. Furthermore, the equilibrium dust charge ($q_{d0}$) and viscoelastic relaxation time for the neutral dust fluid ($\tau_{mdn}^{*}$) introduce destabilizing effects to the fluctuations in the same regime. It is concurrently demonstrated that the dust mass ($m_{d}$), equilibrium ion number density ($n_{i0}$) and equilibrium dust number density ($n_{d0}$) play the stabilizing roles. On the other hand, the equilibrium electron number density ($n_{e0}$) plays the destabilizing role to the collective excited fluctuations in the kinetic limits.

The analysis presented here is based on isothermal dusty plasma fluid-framework as an idealization against analytic complications. In reality, the thermodynamic variables in space and astrophysical environments keep on changing from point to point due to the presence of large-scale inhomogeneities and gradient forces. Thus, it opens a new scope for future refinements of the analysis in the framework of non-local stability theory. The mathematical ansatz used herein, despite the pros and pons, might have commodious applications in the theoretical study of instability phenomenology in different types of astrophysical fluids, provided that the equilibrium remains a local (uniform, homogeneous and static) one. The results may in parallel also be extensively useful in apprehending the triggering mechanisms responsible for the excitation of active gravito-electrostatic collapse dynamics in interstellar clouds giving birth to astrophysical large-scale structures in galaxies.

Appendices

Appendix A: Dispersion coefficients in the hydrodynamic regime

$$\begin{aligned} &{a_{6} = i \biggl\{ F_{nc} + F_{cn} + K^{2} ( \alpha_{dn} + \alpha_{dc} )}\\ &{\phantom{a_{6} =} + \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr\} , }\\ &{a_{5} = \bigl\{ 1 - 2K^{2} - ( F_{nc} \alpha_{dc} + F_{cn}\alpha_{dn} )K^{2} - \alpha_{dn}\alpha_{dc}K^{4} \bigr\} }\\ &{\phantom{a_{5} =} + \biggl( \frac{m\varOmega_{pe}^{2} + n\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{5} =} - \varOmega_{pd}^{2} - \bigl\{ F_{nc} + F_{cn} + K^{2} ( \alpha_{dn} + \alpha_{dc} ) \bigr\} }\\ &{\phantom{a_{5} =}\times \biggl\{ \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr) \biggr\} , }\\ &{a_{4} = i \biggl\{ ( F_{nc} + F_{cn} ) \bigl( 1 - K^{2} \bigr)}\\ &{\phantom{a_{4} =} + \alpha_{dn}K^{2} \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) + \alpha_{dc}K^{2} \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) \biggr\} } \\ &{\phantom{a_{4} =} + i \bigl\{ 1 - 2K^{2} - ( F_{cn}\alpha_{dn} + F_{nc} \alpha_{dc} )K^{2} - \alpha_{dn} \alpha_{dc}K^{4} \bigr\} }\\ &{\phantom{a_{4} =}\cdot \biggl\{ \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr\} }\\ &{\phantom{a_{4} =}\times i \biggl\{ \frac{m\varOmega_{pe}^{2} + n\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr\} }\\ &{\phantom{a_{4} =}\cdot \bigl\{ F_{nc} + F_{cn} + K^{2} ( \alpha_{dn} + \alpha_{dc} ) \bigr\} }\\ &{\phantom{a_{4} =} - i \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{idc}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)}\\ &{\phantom{a_{4} =} - i \biggl\{ \bigl( F_{nc} + K^{2}\alpha_{dn} \bigr) + \biggl( \frac{n}{F_{idc}} + \frac{m}{F_{edc}} \biggr) \biggr\} \varOmega_{pd}^{2}, }\\ &{a_{3} = K^{4} - \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{3} =}\cdot \biggl\{ ( F_{nc} + F_{cn} ) \bigl( 1 - K^{2} \bigr)}\\ &{\phantom{a_{3} =} + \alpha_{dn}K^{2} \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) + \alpha_{dc}K^{2} \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) \biggr\} }\\ &{\phantom{a_{3} =} + \biggl\{ \frac{m\varOmega_{pe}^{2} + n\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr\} }\\ &{\phantom{a_{3} =}\times \bigl\{ 1 - 2K^{2} - ( F_{cn}\alpha_{dn} + F_{nc} \alpha_{dc} )K^{2} - \alpha_{dn} \alpha_{dc}K^{4} \bigr\} }\\ &{\phantom{a_{3} =} + \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)}\\ &{\phantom{a_{3} =}\times\bigl\{ F_{nc} + F_{cn} + K^{2} ( \alpha_{dn} + \alpha_{dc} ) \bigr\} }\\ &{\phantom{a_{3} =} + \biggl\{ \biggl( K^{2} - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) + \bigl( F_{nc} + K^{2}\alpha_{dn} \bigr) \biggl( \frac{n}{F_{idc}} + \frac{m}{F_{edc}} \biggr)}\\ &{\phantom{a_{3} =} + \frac{mn}{F_{edc}F_{idc}} \biggr\} \varOmega_{pd}^{2}, }\\ &{a_{2} = i \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{2} =}\times K^{4} i \biggl( \frac{m\varOmega_{pe}^{2} + n\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{2} =}\cdot \biggl\{ ( F_{nc} + F_{cn} ) \bigl( 1 - K^{2} \bigr)}\\ &{\phantom{a_{2} =} + \alpha_{dn}K^{2} \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) + \alpha_{dc}K^{2} \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) \biggr\} }\\ &{\phantom{a_{2} =} - i \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)}\\ &{\phantom{a_{2} =}\times\bigl\{ 1 - 2K^{2} - ( F_{cn} \alpha_{dn} + F_{nc}\alpha_{dc} )K^{2} - \alpha_{dn}\alpha_{dc}K^{4} \bigr\} }\\ &{\phantom{a_{2} =} + i \biggl\{ \biggl( \frac{m}{F_{edc}} + \frac{n}{F_{idc}} \biggr) \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2} \biggr)}\\ &{\phantom{a_{2} =} + \frac{mn ( F_{nc} + K^{2}\alpha_{dn} )}{F_{edc}F_{idc}} \biggr\} \varOmega_{pd}^{2}, }\\ &{a_{1} = \biggl( \frac{m\varOmega_{pe}^{2} + n\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)K^{4}}\\ &{\phantom{a_{1} =} + \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)}\\ &{\phantom{a_{1} =}\times \biggl\{ ( F_{nc} + F_{cn} ) \bigl( 1 - K^{2} \bigr) + \alpha_{dn}K^{2} \biggl( \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} - K^{2} \biggr)}\\ &{\phantom{a_{1} =} + \alpha_{dc}K^{2} \biggl( \frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} - K^{2} \biggr) \biggr\} }\\ &{\phantom{a_{1} =} - \frac{mn ( K^{2} - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} )\varOmega_{pd}^{2}}{F_{edc}F_{idc}}, }\\ &{a_{0} = - i \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)\cdot K^{4}.} \end{aligned}$$

Appendix B: Dispersion coefficients in the kinetic regime

$$\begin{aligned} &{a_{6} = i \biggl( F_{nc} + F_{cn} + \frac{m - \varOmega _{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr), }\\ &{a_{5} = 1 - K^{2} \bigl( \chi_{rxn}^{2} + \chi_{rxc}^{2} + 2 \bigr)}\\ &{\phantom{a_{5} =} - ( F_{nc} + F_{cn} ) \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{5} =} + \biggl( \frac{n\varOmega_{pe}^{2} + m\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{5} =} - \varOmega_{pd}^{2}, }\\ &{a_{4} = i ( F_{nc} + F_{cn} )}\\ &{\phantom{a_{4} =}\times \biggl( \frac{n\varOmega_{pe}^{2} + m\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{4} =} + i \biggl\{ 1 - K^{2} \bigl( \chi_{rxn}^{2} + \chi_{rxc}^{2} + 2 \bigr)}\\ &{\phantom{a_{4} =}\times \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr) \biggr\} }\\ &{\phantom{a_{4} =} + i \biggl\{ \biggl( F_{nc} \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} + F_{cn}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} \biggr)}\\ &{\phantom{a_{4} =} - K^{2} \bigl( F_{nc}\chi_{rxc}^{2} + F_{cn} \chi_{rxn}^{2} \bigr) \biggr\} }\\ &{\phantom{a_{4} =} - i \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)}\\ &{\phantom{a_{4} =} - i \biggl( \frac{n}{F_{idc}} + \frac{m}{F_{edc}} + F_{nc} \biggr)\varOmega_{pd}^{2}, }\\ &{a_{3} = K^{2} \bigl( 1 + \chi_{rxc}^{2} \bigr) \biggl\{ K^{2} \bigl( 1 + \chi_{rxn}^{2} \bigr) - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr\} }\\ &{\phantom{a_{3} =} + \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr) }\\ &{\phantom{a_{3} =}\times\biggl\{ \biggl( F_{nc}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} + F_{cn}\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr)}\\ &{\phantom{a_{3} =} + K^{2} \bigl( F_{nc}\chi_{rxc}^{2} + F_{cn} \chi_{rxn}^{2} \bigr) \biggr\} }\\ &{\phantom{a_{3} =} + \bigl\{ 1 - K^{2} \bigl( \chi_{rxn}^{2} + \chi_{rxc}^{2} + 2 \bigr) \bigr\} }\\ &{\phantom{a_{3} =}\times \biggl( \frac{n\varOmega_{pe}^{2} + m\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{3} =} + \biggl\{ \frac{mn}{F_{edc}F_{idc}} + F_{nc} \biggl( \frac{m}{F_{edc}} + \frac{n}{F_{idc}} \biggr) + K^{2} \bigl( 1 + \chi_{rxn}^{2} \bigr) \biggr\} }\\ &{\phantom{a_{3} =}\times\varOmega_{pd}^{2}}\\ &{\phantom{a_{3} =} - ( F_{nc} + F_{cn} ) \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr), }\\ &{a_{2} = iK^{2} \bigl( 1 + \chi_{rxc}^{2} \bigr) \biggl\{ K^{2} \bigl( 1 + \chi_{rxn}^{2} \bigr) - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr\} }\\ &{\phantom{a_{2} =}\times \biggl( \frac{m - \varOmega_{pe}^{2}}{F_{edc}} + \frac{n - \varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{2} =} - i \bigl\{ 1 - K^{2} \bigl( \chi_{rxn}^{2} + \chi_{rxc}^{2} + 2 \bigr) \bigr\} }\\ &{\phantom{a_{2} =}\times\biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr)}\\ &{\phantom{a_{2} =} + i \biggl\{ \biggl( K^{2} + K^{2}\chi_{rxn}^{2} - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) \biggl( \frac{m}{F_{edc}} + \frac{n}{F_{idc}} \biggr)}\\ &{\phantom{a_{2} =} + \frac{mnF_{nc}}{F_{edc}F_{idc}} \biggr\} \varOmega_{pd}^{2}}\\ &{\phantom{a_{2} =} + i \biggl( \frac{n\varOmega_{pe}^{2} + m\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{2} =}\times \biggl\{ \biggl( F_{nc}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} + F_{cn}\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr)}\\ &{\phantom{a_{2} =} - K^{2} \bigl( F_{nc}\chi_{rxc}^{2} + F_{cn}\chi_{rxn}^{2} \bigr) \biggr\} , }\\ &{a_{1} = K^{2} \bigl( 1 + \chi_{rxc}^{2} \bigr) \biggl\{ K^{2} \bigl( 1 + \chi_{rxn}^{2} \bigr) - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr\} }\\ &{\phantom{a_{1} =}\times \biggl( \frac{n\varOmega_{pe}^{2} + m\varOmega_{pi}^{2} - mn}{F_{edc}F_{idc}} - \frac{F_{ed}\varOmega_{pe}^{2}}{F_{edc}} - \frac{F_{id}\varOmega_{pi}^{2}}{F_{idc}} \biggr)}\\ &{\phantom{a_{1} =} - \frac{mn \{ K^{2} ( 1 + \chi_{rxn}^{2} ) - \frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \}\varOmega_{pd}^{2}}{F_{edc}F_{idc}}}\\ &{\phantom{a_{1} =} + \biggl\{ \biggl( F_{nc}\frac{\omega_{Jc}^{2}}{\omega_{J}^{2}} + F_{cn}\frac{\omega_{Jn}^{2}}{\omega_{J}^{2}} \biggr) - \bigl( F_{nc}\chi_{rxc}^{2} + F_{cn}\chi_{rxn}^{2} \bigr)K^{2} \biggr\} }\\ &{\phantom{a_{1} =}\times \biggl( \frac{nF_{ed}\varOmega_{pe}^{2} + mF_{id}\varOmega_{pi}^{2}}{F_{edc}F_{idc}} \biggr).} \end{aligned}$$