1 Introduction

The dynamics of nonlinear waves has long been a widely interesting area of research due to their diversified roles played in interstellar space and cosmic plasma environments (Bliokh et al. 1995; Verheest 2000; Fortov et al. 2005). A rich modified variety of these waves develops normally due to the presence of the atypical massive hetero-polar charged dust grains in the contact plasma background (Verheest 2000; Fortov et al. 2005). In other words, the presence of charged grains interestingly adapts the copious waves and instabilities, and also, introduces new saturation patterns of the normal dust-modified waves in the form of diversified instability eigen-structures, such as solitary waves, shocks, double layers, etc. (Shukla and Mamun 2003; Popel and Gisko 2006; Borah et al. 2016). Such eigen-patterns in self-gravity play an important role via a unique source mechanism responsible for various cosmic, space and astrophysical phenomena. To name a few, it includes particle acceleration to high-energy regime, material transportation and energy-momentum transfer processes in interstellar space, thereby leading to the formation of different bounded astro-structures (Blandford and Ostriker 1978; Bergin et al. 2004; Fortov et al. 2005; Borah et al. 2016).

The evolutionary dynamics of astro-space eigen-modes has previously been investigated theoretically (Gisler et al. 1992; Shukla and Mamun 2003; Borah et al. 2016) as well as experimentally (Samsonov et al. 2003) in diverse plasma systems. Their signatures and dynamical features have also been confirmed by various multi-space satellite-based observations (Gosling et al. 1968; Dovner et al. 1994; Berthomier et al. 2003; Lee et al. 2009). In this context, worth mentioning instances are Freja, Polar, FAST, Vela 3, etc. It can be seen that most of the earlier studies have assumed simplified models constituted of electrons, ions, negatively charged massive dust grains exclusively. Moreover, the positively charged grains are known to play crucial roles in reorganizing the wave-kinetic processes in cometary tails (Horanyi 1996), Jupiter’s magnetosphere (Horanyi et al. 1993; Horanyi 1996), Earth’s mesosphere (Havnes et al. 1996), molecular clouds (Shukla et al. 2007), etc. Many researchers have reported extensive studies on the wave dynamics in bi-polar grainy plasmas both with (Mamun and Schlickeiser 2015) and without (Mamun and Shukla 2002; Rahman et al. 2008; Ahmad et al. 2013) self-gravity. Rahman et al. have theoretically investigated the dust acoustic shock waves by using reductive perturbation method in unmagnetized viscous dusty plasma with no gravity (Rahman et al. 2008). Likewise, researchers have also studied the strongly nonlinear characteristics of the dust acoustic solitary waves with opposite-polarity adiabatic dust grains, non-thermal electrons and ions in the Sagdeev-framework (Ahmad et al. 2013). Later, Mamun and Schlickeiser have reported the excitation of finite-amplitude dust acoustic solitary waves in self-gravitating bi-polar dusty plasma system in the small-wavelength limit (Mamun and Schlickeiser 2015). In this direction, although important, the dynamics of neutrals and positively charged grains have never been included simultaneously to the best of our knowledge. It indicates that the evolution of strongly nonlinear waves (gravito-electrostatic in origin) in self-gravitating viscous bi-polar dust clouds in active neutral gaseous background with all the possible driving factors taken into account still remains to be explored.

In this work, after being motivated by the above lacunae, we propose a simplistic theoretical model to investigate the evolutionary dynamics of the strongly nonlinear realistic gravito-electrostatic fluctuations on the Jeans scales of space and time. A modified fluid formalism is constructed to derive a new pair of gravito-electrostatically coupled energy integral equations on the basis of the Sagdeev pseudo-potential approach (Sagdeev 1966). The Jeans-normalized coupled governing equations are further reduced to a unique pair of intermixed forced Korteweg-de Vries-Burgers (\(f\)-KdVB) equations. It is numerically shown that the electrostatic fluctuations evolve as compressive dispersive shock-like structures with a unique transition from quasi-monotonic profile to non-monotonic oscillatory compressive shock-like patterns. In contrast, the self-gravitational and effective gravito-electrostatic waves propagate as non-monotonic compressive dispersive oscillatory shock-like structures. The main implications and applications of the new results in the complex astrophysical context are briefly indicated.

The structure of the paper has a usual layout as follows. In Sect. 1, the introduction is already described. Section 2 contains the physical model and mathematical formalisms. Section 3 describes the methodological derivation of the canonical energy integral and intermixed \(f\)-KdVB equations. Further, Sect. 4 depicts the numerical results and discussions. Lastly, Sect. 5 presents the main conclusions together with non-trivial implications and applications.

2 Physical and mathematical formalisms

We consider an astrophysical cloud model composed of viscous bi-polar multi-component fluid dust species amid active neutral background in a global quasi-neutral hydrodynamic equilibrium. The dust grains in the interstellar clouds (Spitzer 1978) compositionally may be Silicates, Graphites, Amorphous Carbons, Polycyclic Aromatic Hydrocarbon molecules, Silicon Carbides and Magnesium Sulfides (with material density \({\sim}10^{7}\mbox{--}10^{11}~\mbox{kg}\,\mbox{m}^{-3}\)). The electrons and ions are assumed to be inertialess on the Jeans scales of space and time. The cold multi-component fluid dust grains are fully inertial adiabatic fluids, with equal polytropic indices, \(\gamma_{ +} = \gamma_{ -} = \gamma_{n} = 3\) (Ahmad et al. 2013; Maharaj et al. 2015). Furthermore, complications, like turbulence, non-thermal chemical kinetics, plasma-neutral collisions, etc. are neglected. Finally, the Jeans swindle (Jeans 1902), which is preponderantly useful in assuming homogeneous equilibrium, is also relaxed. This is because plasma fluids in the presence of gravity-induced (mass-dependent) stratification are indeed inhomogeneous in nature.

We begin our study by using the continuity equations, momentum equations, pressure equations and coupling electro-gravitational Poisson equations in a planar geometry (1-D). The basic justification behind the plane-geometry approximation is that the considered model extension (∼Jeans length) is much greater than all the characteristic plasma scale lengths. The inertialess electronic and ionic dynamics (in dimensional form) with all the conventional notations (Pandey et al. 1994) are respectively presented as

$$\begin{aligned} &n_{e} = n_{e0}\exp \biggl( \frac{e\phi}{T_{e}} \biggr),\quad \end{aligned}$$
(1)

and

$$\begin{aligned} &n_{i} = n_{i0}\exp \biggl( - \frac{e\phi}{T_{i}} \biggr). \end{aligned}$$
(2)

The inertial dust dynamics in the similar customary symbols is described by

$$\begin{aligned} &\frac{\partial n_{j}}{\partial t} + \frac{\partial}{\partial x} ( n_{j}u_{j} ) = 0, \end{aligned}$$
(3)
$$\begin{aligned} &\frac{\partial u_{j}}{\partial t} + u_{j} \frac{\partial u_{j}}{\partial x} = - \frac{q_{j}}{m_{j}} \frac{\partial \phi}{\partial x} - \frac{1}{m_{j}n_{j}}\frac{\partial p_{j}}{\partial x} - \frac{\partial \psi}{\partial x} + \upsilon_{j}\frac{\partial^{2}u_{j}}{\partial x^{2}}, \end{aligned}$$
(4)

and

$$ \frac{\partial p_{j}}{\partial t} + u_{j}\frac{\partial p_{j}}{\partial x} + \gamma_{j} p_{j}\frac{\partial u_{j}}{\partial x} = 0. $$
(5)

The closing electro-gravitational Poisson equations are respectively presented as

$$ \frac{\partial^{2}\phi}{\partial x^{2}} = 4\pi e [ n_{e} - n_{i} + Z_{ -} n_{ -} - Z_{ +} n_{ +} ], $$
(6)

and

$$ \frac{\partial^{2}\psi}{\partial x^{2}} = 4\pi G [ m_{ -} n_{ -} + m_{ +} n_{ +} + m_{n}n_{n} ]. $$
(7)

To see the effective nature of the electric and self-gravitational fields (Pandey et al. 1994), we re-formulate the effective gravito-electrostatic Poisson equation as

$$\begin{aligned} &\frac{\partial^{2}}{\partial x^{2}} \biggl[ \psi - \biggl( \frac{q_{ +}}{m_{ +}} + \frac{q_{ -}}{m_{ -}} \biggr) \phi \biggr] \\ &\quad = 4\pi \biggl[ G \{ m_{ -} n_{ -} + m_{ +} n_{ +} + m_{n}n_{n} \} \\ &\qquad{} - \biggl( \frac{q_{ +}}{m_{ +}} + \frac{q_{ -}}{m_{ -}} \biggr)e \{ n_{e} - n_{i} + Z_{ -} n_{ -} - Z_{ +} n_{ +} \} \biggr]. \end{aligned}$$
(8)

Here, \(n_{e0}\) and \(n_{i0}\) are the equilibrium population densities of electrons and ions; respectively. The terms \(n_{j}\), \(u_{j}\), \(p_{j}\), \(\gamma_{j}\), \(m_{j}\) and \(\upsilon_{j}\) are the population density, flow velocity, adiabatic pressure, adiabatic index, mass and coefficient of viscosity of the \(j\)th species; respectively. Here, \(j = +\) (positive grains), − (negative grains) and \(n\) (neutral grains). The notation, \(q_{j}= Z_{j}| e |\), is the grain charge with \(e\) as the electronic charge and \(Z_{j}\) as the charge number. Besides, \(\phi\) and \(\psi\) are respectively the electrostatic and self-gravitational potentials.

The normalized set of Eqs. (1)–(8) is respectively set out as

$$\begin{aligned} &N_{e} = N_{e0}\exp ( \varPhi ), \end{aligned}$$
(9)
$$\begin{aligned} &N_{i} = N_{i0}\exp ( - \varPhi ), \end{aligned}$$
(10)
$$\begin{aligned} &\frac{\partial N_{j}}{\partial T} + \frac{\partial}{\partial X} ( N_{j} M_{j} ) = 0, \end{aligned}$$
(11)
$$\begin{aligned} &\frac{\partial M_{j}}{\partial T} + M_{j} \frac{\partial M_{j}}{\partial X} \\ &\quad = - \delta_{ -,j} \biggl( \frac{q_{j}}{e} \biggr) \frac{\partial \varPhi}{ \partial X} - 3\delta_{ -,j} \biggl( \frac{T_{j}}{T_{p}} \biggr) N_{j}\frac{\partial N_{j}}{\partial X} \\ &\qquad{}- \frac{\partial \varPsi}{\partial X} + \kappa_{j} \frac{\partial^{2}M_{j}}{\partial X^{2}}, \end{aligned}$$
(12)
$$\begin{aligned} &\frac{\partial P_{j}}{\partial T} + M_{j}\frac{\partial P_{j}}{\partial X} + \gamma P_{j} \frac{\partial M_{j}}{\partial X} = 0, \end{aligned}$$
(13)
$$\begin{aligned} &\!\begin{aligned}[b] \frac{\partial^{2}\varPhi}{\partial X^{2}} &= \biggl[ \frac{e^{2}}{ ( \rho_{0}m_{ -} G )} \biggr] [ n_{e0}N_{e} - n_{i0}N_{i} \\ &\quad{}+ Z_{ -} n_{ - 0}N_{ -} - Z_{ +} n_{ + 0}N_{ +} ], \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned} &\frac{\partial^{2}\varPsi}{\partial X^{2}} = \frac{1}{\rho_{0}} [ m_{ -} n_{ - 0}N_{ -} + m_{ +} n_{ + 0}N_{ +} + m_{n}n_{n0}N_{n} ], \end{aligned}$$
(15)

and

$$\begin{aligned} \frac{\partial^{2}\theta}{\partial X^{2}}& = \frac{4\pi}{\omega_{J}^{2}} \bigl[ G \{ m_{ -} n_{ - 0}N_{ -} + m_{ +} n_{ + 0} N_{ +} + m_{n}n_{n0}N_{n} \} \\ &\quad{}- 2 \{ n_{e0}N_{e} - n_{i0}N_{i} + Z_{ -} n_{ - 0}N_{ -} - Z_{ +} n_{ + 0}N_{ +} \} \bigr]. \end{aligned}$$
(16)

The usual parameters \(N_{e}\), \(N_{i}\) and \(N_{j}\) are the normalized population densities of electrons, ions and dust species; normalized by their respective equilibrium values \(n_{e0}\), \(n_{i0}\) and \(n_{j0}\), respectively. The independent variables \(X\) and \(T\) are normalized by the Jeans wavelength \(\lambda_{J}\) and Jeans time \(\omega_{J}^{ - 1} = ( c_{ss} / \lambda_{J} )^{ - 1}\), respectively. The parameter \(M_{j}\) is the normalized fluid velocity, normalized by the dust acoustic phase speed \(c_{ss} = ( T_{p} / m_{ -} )^{1 / 2}\), where \(T_{e} \sim T_{i}=T_{p}\) is the plasma temperature (in eV). Further, \(T_{p}\gg T_{j}\), where \(T_{j}\) is the temperature (in eV) for the \(j\)th species. Moreover, \(P_{j} = p_{j} / p_{j0} = N_{j}^{\gamma}\) denotes the normalized adiabatic pressure, where, \(p_{j0} = n_{j} T_{j}\) is the equilibrium isothermal pressure. The electrostatic potential \(\varPhi\) and self-gravitational potential \(\varPsi\) are normalized by the cloud thermal potential \(T_{p} / e\) and \(c_{ss}^{2}\), respectively. Moreover, \(\theta = ( \varPsi - 2\varPhi )\) denotes the normalized effective gravito-electrostatic potential, which gives a measure of competitive strength between \(\varPhi\) and \(\varPsi\). In other words, it describes the effective gravito-electrostatic force field experienced by dust particles with unit mass and unit charge in the considered cloud model. Besides, the viscosity coefficient, \(\kappa_{j}\), is normalized by the Jeans viscosity \(\upsilon_{j} = \omega_{J} \lambda_{J}^{2}\) (Rahman et al. 2008). In addition, the term \(\delta_{ -,j} = m_{ -} / m_{j}\) represents the mass ratio of the negative to the \(j\)th dust species.

3 Sagdeev pseudo-potential method

To analyze the strongly nonlinear fluctuations, we, as already mentioned above, apply the Sagdeev pseudo-potential method (Sagdeev 1966). Then, we transform all the equations into a time-stationary form by using the Galilean coordinate transformation, \(\xi = X - \mu T\), with \(\mu\) as the reference frame velocity. We introduce two integral functions for mathematical simplicity as, \(f_{j} ( \varPhi ) = \int_{0}^{\varPhi} N_{j} d\varPhi\), approximating pure electrostatic case with \(\varPsi\) as constant; and \(g_{j} ( \varPsi ) = \int_{0}^{\varPsi} N_{j} d \varPsi\), assuming pure self-gravitational case with \(\varPhi\) as constant.

In the electrostatic analysis, a simplifying situation with small but non-zero \(\kappa_{j}\) is considered. We used the boundary conditions as, \(N_{e} \to 1\), \(N_{i} \to 1\), \(N_{j} \to 1\), \(M_{j} \to 0\), \(\varPhi \to 0\), \(\varPsi \to 0\) and \(\partial \varPhi / \partial \xi \to 0\) at \(\xi \to \pm \infty\) in Eqs. (11)–(13) with the \(O(\kappa_{j})\)-retention to get

$$\begin{aligned} N_{ +} &= \mu ( 3\alpha_{1}\delta_{ -, +} )^{ - 1 / 2} \\ &\quad{}\times \biggl\{ 1 - \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1}\delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 - \frac{3}{2} \alpha_{1}\delta_{ -, +} \mu^{ - 4} \\ &\quad{}\times \biggl\{ 1 + 4 \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2} \alpha_{1}\delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ \mu^{2} - ( 3\alpha_{1}\delta_{ -, +} )^{ - 1 / 2} \kappa_{ +} \frac{\partial \varPhi}{\partial \xi} \\ &\quad{}\times \biggl\{ 1 + \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2} \alpha_{1}\delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 + \frac{3}{2}\alpha_{1}\delta_{ -, +} \mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 + 4 \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1}\delta_{ -, +} \biggr) \mu^{ - 2} \biggr\} \biggr] \\ &\quad{}\times\biggl[ - 2Z_{ +} - 6Z_{ +} \alpha_{1}\delta_{ -, +}^{2} \mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 + 4 \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1}\delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \biggr] \biggr] \biggr], \end{aligned}$$
(17)

and

$$\begin{aligned} N_{ -} &=\mu ( 3\alpha_{2} )^{ - 1 / 2} \biggl\{ 1 + \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 - \frac{3}{2} \alpha_{2}\mu^{ - 4} \biggl\{ 1 - 4 \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ \mu^{2} - ( 3\alpha_{2} )^{ - 1 / 2} \kappa_{ -} \frac{\partial \varPhi}{\partial \xi} \\ &\quad{}\times \biggl\{ 1 - \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 + \frac{3}{2}\alpha_{2}\mu^{ - 2} \biggl\{ 1 - 4 \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2} \alpha_{2} \biggr)\mu^{ - 2} \biggr\} \biggr] \\ &\quad{}\times \biggl[ 2Z_{ -} + 6Z_{ -} \alpha_{2}\mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 - 4 \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2} \alpha_{2} \biggr)\mu^{ - 2} \biggr\} \biggr] \biggr] \biggr], \end{aligned}$$
(18)

where \(\alpha_{1} = T_{ +} / T_{p}\) and \(\alpha_{2} = T_{ -} / T_{p}\) represent the temperature ratios of the positive and negative grains to the plasma temperature.

Now, we substitute the derived expressions for \(N_{e}\), \(N_{i}\) and \(N_{j}\) from Eqs. (9)–(10), (17) and (18) in Eq. (14), and then, multiply both sides of Eq. (14) by \(\partial \varPhi / \partial \xi\). Thereafter, we integrate it under the boundary conditions as \(N_{e} \to 1\), \(N_{i} \to 1\), \(N_{j} \to 1\), \(M_{j} \to 0\), \(\varPhi \to 0\), \(\varPsi \to 0\) and \(\partial \varPhi / \partial \xi \to 0\) at \(\xi \to \pm \infty\) for local disturbance. The outcome is the electrostatic energy integral equation given as follows

$$ \frac{1}{2} \biggl( \frac{\partial \varPhi}{\partial \xi} \biggr)^{2} + V_{E} ( \varPhi,\varPsi ) = 0, $$
(19)

where the electrostatic Sagdeev potential \(V_{E} ( \varPhi,\varPsi )\) is derived as

$$\begin{aligned} &V_{E} ( \varPhi,\varPsi ) \\ &\quad= - \biggl( \frac{e^{2}}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} e^{ ( \varPhi )} + n_{i0}e^{ ( - \varPhi )} \\ &\qquad{}+ Z_{ -} n_{ - 0}f_{ -} ( \varPhi ) - Z_{ +} n_{ + 0}f_{ +} ( \varPhi ) \bigr] \\ &\qquad{} + \biggl( \frac{e^{2}}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} + n_{i0} + Z_{ -} n_{ - 0} f_{ -} ( \varPhi ) \vert _{\varPhi = 0, \varPhi_{\xi} = 0} \\ &\qquad{} - Z_{ +} n_{ + 0} f_{ +} ( \varPhi ) \vert_{\varPhi = 0, \varPhi_{\xi} = 0} \bigr]. \end{aligned}$$
(20)

The analytical solution of Eq. (19) can be obtained by the analytic integration as

$$\begin{aligned} &\int - \biggl[ \biggl( - \frac{2e^{2}}{\rho_{0} G m_{ -}} \biggr) \bigl\{ n_{e0} e^{ ( \varPhi )} + n_{i0}e^{ ( - \varPhi )} \\ &\quad{} + Z_{ -} n_{ - 0}f_{ -} ( \varPhi ) - Z_{ +} n_{ + 0}f_{ +} ( \varPhi ) \bigr\} \\ &\quad{} + \biggl( \frac{2e^{2}}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} + n_{i0} + Z_{ -} n_{ - 0} f_{ -} ( \varPhi ) \vert _{\varPhi = 0, \varPhi_{\xi} = 0} \\ &\quad{} - Z_{ +} n_{ + 0} f_{ +} ( \varPhi ) \vert_{\varPhi = 0, \varPhi_{\xi} = 0} \bigr] \biggr]^{-1 / 2}d \varPhi=\xi+C_{E}, \end{aligned}$$
(21)

where \(C_{E}\) is the constant of integration.

It is seen that the mathematical shape of Eq. (21) is highly complicated and nonlinear in nature. So, it is non-integrable analytically, except with numerical techniques. Now, to see the structural evolutions, we execute analytical tests to check the existential conditions for the possible nonlinear coherent structures. It is seen that Eq. (20) satisfies the following conditions intended for the electrostatic compressive shock-like structures (Haloi and Karmakar 2015) as

$$\begin{aligned} &V_{E} ( \varPhi,\varPsi ) = 0,\qquad \frac{\partial V_{E} ( \varPhi,\varPsi )}{\partial \varPhi} \ne 0,\quad \mbox{at}\ \varPhi = 0,\ \varPsi = 0, \end{aligned}$$
(22a)
$$\begin{aligned} &\frac{\partial^{2}V_{E} ( \varPhi,\varPsi )}{\partial \varPhi^{2}} < 0, \quad \mbox{at}\ \varPhi = 0,\ \varPsi = 0, \end{aligned}$$
(22b)
$$\begin{aligned} &V_{E} ( \varPhi,\varPsi ) \ne 0,\quad \mbox{at}\ \varPhi = \varPhi_{\max}, \end{aligned}$$
(22c)
$$\begin{aligned} &V_{E} ( \varPhi,\varPsi ) < 0,\quad \mbox{at}\ 0 < \vert \varPhi \vert < \vert \varPhi_{\max} \vert . \end{aligned}$$
(22d)

Moreover, differentiating Eq. (14) with respect to \(\xi\) and applying normal simplistic approximations as, \(\alpha_{1}\ll 1\), \(\alpha_{2}\ll1\), \(Z_{ \pm} \gg1\), \(\mu>1\) and \(\varPhi^{3},\varPsi^{3} \approx 0\); we get the following \(f\)-KdVB equation for the electrostatic disturbance as follows

$$ \frac{\partial \varPhi}{\partial \xi} + A_{1}\varPhi \frac{\partial \varPhi}{ \partial \xi} + A_{2} \frac{\partial^{2}\varPhi}{\partial \xi^{2}} + A_{3}\frac{\partial^{3}\varPhi}{\partial \xi^{3}} = F_{E} ( \varPhi, \varPsi ), $$
(23)

where, the associated coefficients, namely, nonlinear convective coefficient (\(A_{1}\)), dissipative coefficient (\(A_{2}\)), dispersive coefficient (\(A_{3}\)) and self-consistent nonlinear driving force (\(F_{E}(\varPhi,\varPsi)\)) term are sensitively dependent on the diverse plasma parameters and are shown in Appendix A. Clearly, the self-consistent nonlinear driving force arising because of coupled gravito-electrostatic fluctuations in an intermixed form (sourced by gravito-electrostatic polarization effects resulting in deviation from quasi-neutrality) depends on the diverse plasma parameters.

Similarly, for the self-gravitational counterparts, we apply the boundary conditions as \(N_{e} \to 1\), \(N_{i} \to 1\), \(N_{j} \to 1\), \(M_{j} \to 0\), \(\varPhi \to 0\), \(\varPsi \to 0\) and \(\partial \varPsi / \partial \xi \to 0\) at \(\xi \to \pm \infty\) and considering the similar \(\kappa_{j}\)-behaviors as before. The excise reduces Eqs. (11)–(13) to

$$\begin{aligned} N_{ +} &= \mu ( 3\alpha_{1}\delta_{ -, +} )^{ - 1 / 2} \\ &\quad{}\times\biggl\{ 1 - \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1}\delta_{ -, +} \biggr) \mu^{ - 2} \biggr\} \\ &\quad{}\times\biggl[ 1 - \frac{3}{2}\alpha_{1} \delta_{ -, +} \mu^{ - 4} \\ &\quad{}\times\biggl\{ 1 - 4 \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1} \delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ \mu^{2} - ( 3\alpha_{1}\delta_{ -, +} )^{ - 1 / 2} \kappa_{ +} \frac{\partial \varPsi}{\partial \xi} \\ &\quad{}\times \biggl\{ 1 + \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1}\delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 + \frac{3}{2} \alpha_{1}\delta_{ -, +} \mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 + 4 \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2} \alpha_{1}\delta_{ -, +} \biggr) \mu^{ - 2} \biggr\} \biggr] \\ &\quad{}\times \biggl[ - 2 - 6\alpha_{1}\delta_{ -, +} \mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 + 4 \biggl( Z_{ +} \delta_{ -, +} \varPhi + \varPsi - \frac{3}{2}\alpha_{1}\delta_{ -, +} \biggr)\mu^{ - 2} \biggr\} \biggr] \biggr] \biggr], \end{aligned}$$
(24)
$$\begin{aligned} N_{ -} &=\mu ( 3\alpha_{2} )^{ - 1 / 2} \biggl\{ 1 + \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times\biggl[ 1 - \frac{3}{2} \alpha_{2}\mu^{ - 4} \biggl\{ 1 - 4 \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times\biggl[ \mu^{2} - ( 3\alpha_{2} )^{ - 1 / 2} \kappa_{ -} \frac{\partial \varPsi}{\partial \xi} \\ &\quad{}\times \biggl\{ 1 - \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 + \frac{3}{2}\alpha_{2}\mu^{ - 2} \biggl\{ 1 - 4 \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2} \alpha_{2} \biggr) \mu^{ - 2} \biggr\} \biggr] \\ &\quad{}\times \biggl[ - 2 - 6 \alpha_{2}\mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 - 4 \biggl( Z_{ -} \varPhi - \varPsi + \frac{3}{2}\alpha_{2} \biggr)\mu^{ - 2} \biggr\} \biggr] \biggr] \biggr], \end{aligned}$$
(25)

and

$$\begin{aligned} N_{n} &= \mu ( 3\alpha_{3}\delta_{ -,n} )^{ - 1 / 2} \biggl\{ 1 - \biggl( \varPsi - \frac{3}{2} \alpha_{3}\delta_{ -,n} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 - \frac{3}{2}\alpha_{3}\delta_{ -,n} \mu^{ - 4} \biggl\{ 1 + 4 \biggl( \varPsi - \frac{3}{2} \alpha_{3}\delta_{ -,n} \biggr)\mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ \mu^{2} - ( 3\alpha_{3}\delta_{ -,n} )^{ - 1 / 2} \kappa_{n}\frac{\partial \varPsi}{\partial \xi} \\ &\quad{}\times \biggl\{ 1 + \biggl( \varPsi - \frac{3}{2}\alpha_{3}\delta_{ -,n} \biggr) \mu^{ - 2} \biggr\} \\ &\quad{}\times \biggl[ 1 + \frac{3}{2}\alpha_{3} \delta_{ -,n}\mu^{ - 2} \biggl\{ 1 + 4 \biggl( \varPsi - \frac{3}{2}\alpha_{3}\delta_{ -,n} \biggr) \mu^{ - 2} \biggr\} \biggr] \\ &\quad{}\times \biggl[ - 2 - 6\alpha_{3} \delta_{ -,n}\mu^{ - 2} \\ &\quad{}\times \biggl\{ 1 + 4 \biggl( \varPsi - \frac{3}{2}\alpha_{3}\delta_{ -, +} \biggr) \mu^{ - 2} \biggr\} \biggr] \biggr] \biggr], \end{aligned}$$
(26)

where \(\alpha_{3} = T_{n} / T_{p}\) is the temperature ratio between neutral grains and that of plasma.

Now, we replace the derived expression \(N_{j}\) from Eqs. (24)–(26) in Eq. (15) and multiply both sides of Eq. (15) by \(\partial \varPsi / \partial \xi\). Then, we integrate Eq. (15) with the appropriate boundary conditions, i.e., \(N_{e} \to 1\), \(N_{i} \to 1\), \(N_{j} \to 1\), \(M_{j} \to 0\), \(\varPhi \to 0\), \(\varPsi \to 0\) and \(\partial \varPsi / \partial \xi \to 0\) at \(\xi \to \pm \infty\) for local disturbance. It gives the self-gravitational energy integral equation as

$$ \frac{1}{2} \biggl( \frac{\partial \varPsi}{\partial \rho} \biggr)^{2} + V_{G} ( \varPhi,\varPsi ) = 0, $$
(27)

where, the self-gravitational Sagdeev potential, \(V_{G}\left( \varPsi \right)\) is described as

$$\begin{aligned} V_{G} ( \varPhi,\varPsi ) & = - \frac{1}{\rho_{0}} \bigl[ m_{ +} n_{ + 0}g_{ +} ( \varPsi ) + m_{ -} n_{ - 0}g_{ -} ( \varPsi ) \\ &\quad{} + m_{n}n_{n0}g_{n} ( \varPsi ) \bigr] \\ &\quad{} + \frac{1}{\rho_{0}} \bigl[ m_{ +} n_{ + 0} g_{ +} ( \varPsi ) \vert _{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\quad{} + m_{ -} n_{ - 0}g_{ -} ( \varPsi ) \vert _{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\quad{} + m_{n}n_{n0}g_{n} ( \varPsi ) \vert _{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \bigr]. \end{aligned}$$
(28)

The analytical solution of Eq. (27) can also be found from direct integration as

$$\begin{aligned} &\int - \bigl[ - 2\rho_{0}^{ - 1} \bigl[ m_{ +} n_{ + 0}g_{ +} ( \varPsi ) + m_{ -} n_{ - 0}g_{ -} ( \varPsi ) \\ &\quad{}+ m_{n}n_{n0}g_{n} ( \varPsi ) \bigr] + 2\rho_{0}^{ - 1} \bigl[ m_{ +} n_{ + 0} g_{ +} ( \varPsi ) |_{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\quad{} + m_{ -} n_{ - 0} g_{ -} ( \varPsi ) |_{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\quad{}+ m_{n}n_{n0} g_{n} ( \varPsi ) |_{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \bigr] \bigr]^{-1 / 2} d \varPsi=\xi+C_{G}, \end{aligned}$$
(29)

where \(C_{G}\) is the integration constant.

It is clear that the mathematical structure of Eq. (29) is also highly complicated and nonlinear in nature, like non-integrable Eq. (21), as discussed earlier. Now, Eq. (28) fulfills the following conditions for existence of self-gravitational compressive shock-like structures (Sagdeev 1966; Haloi and Karmakar 2015) as

$$\begin{aligned} &V_{G} ( \varPhi,\varPsi ) = 0,\qquad \frac{\partial V_{G} ( \varPhi,\varPsi )}{\partial \varPsi} \ne 0,\quad \mathrm{at}\ \varPhi = 0,\ \varPsi = 0, \end{aligned}$$
(30a)
$$\begin{aligned} &\frac{\partial^{2}V_{G} ( \varPhi, \varPsi )}{\partial \varPsi^{2}} < 0,\quad \mathrm{at}\ \varPhi = 0,\ \varPsi = 0, \end{aligned}$$
(30b)
$$\begin{aligned} &V_{G} ( \varPhi, \varPsi ) = 0,\quad \mathrm{at}\ \varPsi = \varPsi_{\max}, \end{aligned}$$
(30c)
$$\begin{aligned} &V_{G} ( \varPhi, \varPsi ) < 0,\quad \mathrm{at}\ 0 < \vert \varPsi \vert < \vert \varPsi_{\max} \vert . \end{aligned}$$
(30d)

Moreover, differentiating Eq. (15) with respect to \(\xi\) and using the same analytical approximations already mentioned above with \(\alpha_{3}\ll 1\), we get

$$ \frac{\partial \varPsi}{\partial \xi} + B_{1}\varPsi \frac{\partial \varPsi}{ \partial \xi} + B_{2} \frac{\partial^{2}\varPsi}{\partial \xi^{2}} + B_{3}\frac{\partial^{3}\varPsi}{\partial \xi^{3}} = F_{G} ( \varPhi, \varPsi ). $$
(31)

This is the self-gravitational \(f\)-KdVB equation governing the considered fluctuations. The various involved coefficients are nonlinear convective coefficient (\(B_{1}\)), dissipative coefficient (\(B_{2}\)), dispersive coefficient (\(B_{3}\)) and self-consistent nonlinear driving force (\(F_{G} (\varPhi,\varPsi)\)), as shown in Appendix B. The self-consistent nonlinear self-gravitational driving force arising because of nonlinear gravito-electrostatic coupling processes in an intermixed form (sourced by deviation from exact inertial mass neutrality) as an explicit function of the diverse plasma parameters is well described therein in the Appendix.

Analogously, we multiply both sides of Eq. (16) by \(\partial \theta / \partial \xi\) and integrate under the previously projected conditions. Finally, we obtain the effective gravito-electrostatic energy integral equation as follows

$$ \frac{1}{2} \biggl( \frac{\partial \theta}{\partial \xi} \biggr)^{2} + V_{G - E} ( \theta ) = 0, $$
(32)

and its associated gravito-electrostatic Sagdeev potential, \(V_{G - E} ( \theta )\), presented as

$$\begin{aligned} &V_{G - E} ( \theta ) \\ &\quad= - \frac{1}{\rho_{0}} \bigl[ m_{ +} n_{ + 0}g_{ +} ( \varPsi ) + m_{ -} n_{ - 0}g_{ -} ( \varPsi ) + m_{n}n_{n0}g_{n} ( \varPsi ) \bigr] \\ &\qquad{} + \frac{1}{\rho_{0}} \bigl[ m_{ +} n_{ + 0} g_{ +} ( \varPsi ) \vert _{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\qquad{} + m_{ -} n_{ - 0} g_{ -} ( \varPsi ) \vert _{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\qquad{} + m_{n}n_{n0} g_{n} ( \varPsi ) \vert _{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \bigr] \\ &\qquad{} + \biggl( \frac{1}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} e^{ ( \varPhi )} + n_{i0}e^{ ( - \varPhi )} + Z_{ -} n_{ - 0}f_{ -} ( \varPhi ) \\ &\qquad{} - Z_{ +} n_{ + 0}f_{ +} ( \varPhi ) \bigr] \\ &\qquad{} - \biggl( \frac{1}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} + n_{i0} + Z_{ -} n_{ - 0} f_{ -} ( \varPhi ) \vert _{\varPhi = 0, \varPhi_{\xi} = 0} \\ &\qquad{} - Z_{ +} n_{ + 0}f_{ +} ( \varPhi ) \vert_{\varPhi = 0, \varPhi_{\xi} = 0} \bigr]. \end{aligned}$$
(33)

Moreover, the analytical solution of Eq. (32) can also be obtained from direct integration as

$$\begin{aligned} & \int - \biggl[ - 2\rho_{0}^{ - 1} \bigl[ m_{ +} n_{ + 0}g_{ +} ( \varPsi ) + m_{ -} n_{ - 0}g_{ -} ( \varPsi ) \\ &\quad{} + m_{n}n_{n0}g_{n} ( \varPsi ) \bigr] + 2\rho_{0}^{ - 1} \bigl[ m_{ +} n_{ + 0} g_{ +} ( \varPsi ) |_{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \\ &\quad{} + m_{ -} n_{ - 0} g_{ -} ( \varPsi ) |_{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} + m_{n}n_{n0} g_{ +} ( \varPsi ) |_{\varPsi = 0, \frac{\partial \varPsi}{\partial \xi} = 0} \bigr] \\ &\quad{} + \biggl( \frac{1}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} e^{ ( \varPhi )} + n_{i0}e^{ ( - \varPhi )} + Z_{ -} n_{ - 0}f_{ -} ( \varPhi ) \\ &\quad{} - Z_{ +} n_{ + 0}f_{ +} ( \varPhi ) \bigr] \\ &\quad{} - \biggl( \frac{1}{\rho_{0} G m_{ -}} \biggr) \bigl[ n_{e0} + n_{i0} + Z_{ -} n_{ - 0} f_{ -} ( \varPhi ) |_{\varPhi = 0, \varPhi_{\xi} = 0} \\ &\quad{} - Z_{ +} n_{ + 0} f_{ +} ( \varPhi ) \vert_{\varPhi = 0, \varPhi_{\xi} = 0} \bigr] \biggr]^{-1 / 2} d\theta=\xi+C_{G-E}, \end{aligned}$$
(34)

where \(C_{G-E}\) is the integration constant.

For the compressive shock-like structures (Haloi and Karmakar 2015) to exist, Eq. (33) must satisfy the following extreme conditions

$$\begin{aligned} &V_{G - E} ( \theta ) = 0,\qquad \frac{\partial V_{G - E} ( \theta )}{\partial \theta} \ne 0,\quad \text{at} \ \theta = 0, \end{aligned}$$
(35a)
$$\begin{aligned} &\frac{\partial^{2}V_{G - E} ( \theta )}{\partial \theta^{2}} < 0,\quad \text{at}\ \theta = 0, \end{aligned}$$
(35b)
$$\begin{aligned} &V_{G - E} ( \theta ) = 0,\quad \text{at}\ \theta = \theta_{\max}, \end{aligned}$$
(35c)
$$\begin{aligned} &V_{G - E} ( \theta ) < 0,\quad \text{at}\ 0 < | \theta | < | \theta_{\max} |. \end{aligned}$$
(35d)

It is evident that the fluctuations satisfy all the analytical conditions (Eqs. (22a)–(22d), (30a)–(30d) and (35a)–(35d)) needed for the compressive shock-like patterns to evolve. It may be noted from Eqs. (23) and (31) that, if the nonlinear convective effects are balanced under the combined action of dispersion and dissipation, then the fluctuations evolve as dispersive shock-like patterns (Asgari et al. 2011). In contrast, otherwise, the fluctuations propagate as non-dispersive shock-like eigen-modes. The analytical tests show explicit possibilities for the fluctuations to propagate either as compressive dispersive shock-like or compressive non-dispersive shock-like patterns.

4 Results and discussion

The proposed theoretical work is mainly focused to study the evolutionary dynamics of strongly nonlinear gravito-electrostatic waves reinforced in multi-component fluid viscous dust clouds by using the modified Sagdeev pseudo-potential technique. To see the exact eigen-patterns, we numerically analyze the developed model dynamics (Eqs. (14)–(15), (18), (27) and (32)) by using the fourth-order Runge-Kutta method (Kiusalaas 2005) in the astrophysical domain of judicious parametric conditions (Spitzer 1978; Bliokh et al. 1995; Verheest 2000; Fortov et al. 2005). The results, thus numerically obtained in the sensible parametric domains (without deviating from order of magnitudes), are graphically displayed in Figs. 1, 2, 3 and 4.

Fig. 1
figure 1

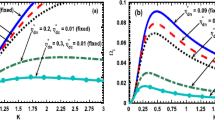
Profile of the normalized electrostatic (a) Sagdeev potential [\(V_{E} ( \varPhi, \varPsi )\)], (b) physical potential (\(\varPhi\)), and (c) potential inhomogeneity scale length [\(L_{\varPhi} =\varPhi ( \partial \varPhi / \partial \xi )^{ - 1}\)] for the different \(\mu\)-values. Various lines correspond to (A): \(\mu = 2.90\) (blue solid line), (B): \(\mu = 2.94\) (red dashed line), and (C): \(\mu = 2.98\) (black dotted line), respectively. Different input and initial values used in our numerical analysis are discussed in the text

Full size image
Fig. 2
figure 2

Same as Fig. 1, but for the self-gravitational wave dynamics

Full size image
Fig. 3
figure 3

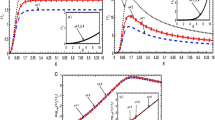
Same as Fig. 1, but for the effective gravito-electrostatic wave dynamics

Full size image
Fig. 4
figure 4

Phase diagram of the effective gravito-electrostatic potential (\(\theta\)) evolving as a function of electrostatic real potential (\(\varPhi\)) and self-gravitational real potential (\(\varPsi\)). Different input and initial values here are the same as Fig. 1, but with \(\mu = 2.90\) only

Full size image

In the numerical platform of analysis, this may be note worthy here that, it is only the supersonic domain of the referral frame (\(\mu>1\)) that allows our numerical illustrative platform to run. Since, we are interested to analyze the fluctuation dynamics on the astrophysical spatial scale, the evolutionary profiles are restricted to \(\xi=10\) on the Jeans scale length only. We take the diverse input parametric values of the dust grain properties relevant in the cold (\(T_{\mathrm{d}} = 10^{ - 3}\mbox{--}10^{ - 2}~\mbox{eV}\)) interstellar medium (Spitzer 1978; Bliokh et al. 1995; Verheest 2000). It is pertinent to add further that the hydrodynamical approximation (here, on the Jeans scale) is based on vanishingly small mean free path, and hence, small viscosity (Fridman and Polyachenko 1984). Therefore, the numerical analysis here deals only with small viscosity scenarios of the H II clouds (infrared clouds) including heterogeneous cloud complexes (Spitzer 1978).

Figure 1 shows the profiles of normalized electrostatic (a) Sagdeev potential [\(V_{E} ( \varPhi, \varPsi )\)], (b) physical (real) potential (\(\varPhi\)), and (c) potential inhomogeneity scale length [\(L_{\varPhi} =\varPhi ( \partial \varPhi / \partial \xi )^{ - 1}\)] on the \(\xi\)-space for the different \(\mu\)-values. Various lines correspond to (A): \(\mu = 2.90\) (blue solid line), (B): \(\mu = 2.94\) (red dashed line), and (C): \(\mu = 2.98\) (black dotted line), respectively. Different input values used are \(( \xi )_{i} = 1.00 \times 10^{ - 2}\) with \(\Delta \xi = 1.00 \times 10^{ - 2}\), \(( \varPhi )_{i} = 2.00 \times 10^{ - 9}\), \(( \varPhi_{\xi} )_{i} = 1.00 \times 10^{ - 11}\), \(( \varPsi )_{i} = 1.00 \times 10^{ - 4}\), and \(( \varPsi_{\xi} )_{i} = 1.00 \times 10^{ - 3}\). The other parameters kept fixed are \(n_{e0} = 5.00 \times 10^{3}~\mbox{m}^{-3}\), \(n_{i0} = 5.00 \times 10^{3}~\mbox{m}^{-3}\), \(n_{ - 0} = 7.00 \times 10^{ - 1}~\mbox{m}^{-3}\), \(n_{ + 0} = 1.00 \times 10^{ - 1}~\mbox{m}^{-3}\), \(n_{n0} = 9.00 \times 10^{ - 1}~\mbox{m}^{-3}\), \(Z_{ -} = 1.50 \times 10^{2}\), \(Z_{ +} = 1.00 \times 10^{2}\), \(m_{ -} = 2.80 \times 10^{ - 8}\) kg, \(m_{ +} = 1.00 \times 10^{ - 8}\) kg, \(m_{n} = 1.00 \times 10^{ - 11}\) kg, \(\alpha_{1} = 1.10 \times 10^{ - 2}\), \(\alpha_{2} = 1.20 \times 10^{ - 2}\), \(\alpha_{3} = 1.00 \times 10^{ - 2}\), \(\kappa_{ -} = 2.00 \times 10^{ - 2}\), \(\kappa_{ +} = 2.00 \times 10^{ - 2}\), and \(\kappa_{n} = 1.00 \times 10^{ - 2}\) (Spitzer 1978; Fridman and Polyachenko 1984; Bliokh et al. 1995). It is seen that \(V_{E} ( \varPhi, \varPsi )\) satisfies all the approximate analytic conditions, Eqs. (22a)–(22d), mentioned before, with minor deviations, in the context of Eq. (27) for the evolution of compressive shock-like fluctuation structures. The corresponding \(\varPhi\) (Fig. 1b) evolves as quasi-monotonic compressive dispersive shock-like structure for \(\mu = 2.90\). The \(\varPhi\)-amplitude decreases with increase in \(\mu\), and vice versa. It is interestingly noted that, when \(\mu \ge 2.94\), there exists a unique transition from the quasi-monotonic type to non-monotonic oscillatory compressive shock-like patterns at \(\xi = 2.50\). The physics behind such transition is attributable to the Doppler-shifting mechanism enhancing the resonant mode-mode coupling and anti-resonant mode-mode decoupling mechanisms, producing thereby consonances (crests) and dissonances (troughs) via adiabatic energy exchange processes among the background spectral wave components, respectively. Likewise, Fig. 1c depicts the corresponding locative poles for \(L_{\varPhi}\) specifying the consonances and dissonances thus formed. It is interesting to see that the different \(\mu\)-values pertain to the different \(L_{\varPhi}\)-singular behaviors reflecting the said potential resonances and anti-resonances rhythmically.

Figure 2 depicts the normalized self-gravitational (a) Sagdeev (pseudo) potential [\(V_{G} ( \varPhi, \varPsi )\)], (b) physical (real) potential (\(\varPsi\)), and (c) potential inhomogeneity scale length [\(L_{\varPsi} =\varPsi ( \partial \varPsi / \partial \xi )^{ - 1}\)] under the same conditions as Fig. 1. Here, \(V_{G} ( \varPhi, \varPsi )\) satisfies all the analytic conditions, Eqs. (30a)–(30d), thereby fulfilling the germination of compressive shock-like structures. Analogously, the corresponding \(\varPsi\)-fluctuations evolve as non-monotonic compressive oscillatory shock-like structures (Fig. 2b). Here, we see that the \(\varPsi\)-amplitude increases with increase in \(\mu\), and vice versa. Figure 2c shows the same physics of pole-characterization as Fig. 1c.

Figure 3 portrays the normalized effective gravito-electrostatic (a) Sagdeev potential [\(V_{G - E} ( \theta ) = V_{E} ( \varPhi, \varPsi ) - V_{G} ( \varPhi, \varPsi )\)], (b) physical (real) potential [\(\theta = ( \varPsi - 2\varPhi )\)], and (c) potential inhomogeneity scale length [\(L_{\theta} = \theta ( \partial \theta / \partial \xi )^{ - 1}\)] under the same conditions as Fig. 1. It self-consistently shows the profile features of potential structural evolution analogous to Fig. 2.

Finally, Fig. 4 shows the phase diagram (in 3-D) of the effective gravito-electrostatic potential (\(\theta\)) mapped as an explicit function of electrostatic real potential (\(\varPhi\)) and self-gravitational real potential (\(\varPsi\)). It simply depicts the reproduced \(\theta\)-evolution in the defined potential phase plane constructed from the above results (Figs. 1b–3b). Different input and initial values here are the same as Fig. 1, but with \(\mu = 2.90\) only. Here, we see that \(\theta\) decreases with increase in \(\varPhi\), but increases with increase in \(\varPsi\). This further confirms that the formation of bounded structures is possible if and only if the gravitational attraction is at least comparable with the effective strength of electrostatic repulsion among the diverse dust grains in the astroclouds prevailing in the galaxies.

While comparing with the existing like works, the stability analysis presented here deals strategically with the modeled massive viscous bi-polar dust clouds in dynamic neutral dusty background in the modified Sagdeev framework evolving as diverse shock-like patterns. In the formation mechanism of such eigen-structures, the nonlinear steepening effects are attributable to fluid convection; whereas, dissipative effects, to fluid viscosity, as widely seen in the literature (Shukla and Mamun 2003; Haloi and Karmakar 2015). A quantitative glimpse on the basis of existing normal cloud parameters (Bliokh et al. 1995; Verheest 2000) may be drawn as the following. In our analysis, the physical strength of the \(\varPhi\)-fluctuations is comes out as \({\sim}2~\mbox{V}\) for \(T_{p} \sim10^{4}~\mbox{K}\); while, that of the \(\varPsi\)-fluctuations is \({\sim}10^{-10}~\mbox{J}\,\mbox{kg}^{-1}\) for \(m_{ -} = 10^{-8}~\mbox{kg}\) and \(T_{p} \sim10^{4}~\mbox{K}\). The smallness in the strength is a subject to the chosen set of diverse plasma properties considered herein. Our investigation, however, differs from the other reports depicting weakly nonlinear fluctuations with self-gravity (Mamun and Schlickeiser 2015) and strongly nonlinear analyses without self-gravity (Mamun and Shukla 2002; Ahmad et al. 2013). Nevertheless, the obtained findings are quite similar with the Vela 3 observations (Gosling et al. 1968) and in-situ measurements (Lee et al. 2009).

5 Conclusions

In summary, a theoretical model analysis is presented to explore the strongly nonlinear waves supported in inhomogeneous complex viscous astroclouds in the Sagdeev pseudo-potential framework. It reveals the excitation of electrostatic compressive dispersive shock-like structures undergoing a unique transitory behavior from quasi-monotonic to non-monotonic oscillatory compressive shock-like patterns. The self-gravitational and effective gravito-electrostatic fluctuations evolve as non-monotonic compressive oscillatory shock-like patterns. The gradient scale behavior, aboard intensive numerical illustrations, confirms that the perturbation extrema are indeed irregular in nature due to the gravito-electrostatic aperiodic counter-action. A few more concluding remarks drawn from the study are highlighted as follows.

  1. 1.

    A theoretical strategic model to study the excitation physics of strongly nonlinear waves in complex viscous astroclouds with active neutral gas dynamics taken into account is methodologically constructed in the amended Sagdeev-framework.

  2. 2.

    The fluctuations are sourced by the atypical redistribution of massive (Newtonian) positively-negatively charged (Columbic) dust grains amid active neutrals (Newtonian) on the relevant astrophysical fluid scales of space and time.

  3. 3.

    It supports electrostatic compressive dispersive shock-like structures undergoing a unique transitory feature from quasi-monotonic to non-monotonic oscillatory compressive shock-like patterns; and self-gravitational and effective gravito-electrostatic non-monotonic compressive shock-like structures.

  4. 4.

    Different frame velocities (\(\mu\)-values) pertain to the different scale length (\(L_{\varPhi}\)) singular behaviors showing the resonant (on-phase) and non-resonant (off-phase) extrema of the fluctuations in a correlative coordination with the noisy spectral background.

  5. 5.

    The fluctuations investigated here are quite similar with the multi-space satellite-based observations reported before (Gosling et al. 1968; Lee et al. 2009).

  6. 6.

    Finally, the results, despite the simplicity, can be useful to see diverse wave-instabilities and eigen-modes leading to large-scale bounded structures via the transfer of energy, momentum and mass in a re-distributed form in space and cosmic plasma environments.

It is finally admitted that the proposed investigation highlights a fully nonlinear wave spectrum excitable merely in a pure (external field-free) gravito-electrostatic fluid form. The nonlocal effects, stemming in the secular instabilities due to diversified dissipative mechanisms, are also ignored. The eigen-spectral purity would likely be bewildered resulting in additional spectral plethora (Bliokh et al. 1995; Verheest 2000), if we consider other intrinsically influential factors, like grain magnetizations, grain distributions, rotational (Coriolis) effects, temperature distribution, collective correlative dynamics, and so forth. Despite the analytic model simplification, a base for experimental reliability checking in the domain of practical validity of the proposed shock theory via scale-invariant shock physics in laboratory plasma devices, apart from triggering astronomical bounded structure formation via self-gravitational collapse dynamics, in sensible microgravity conditions (Samsonov et al. 2003) may also be established.