Elite fuzzy clustering ensemble based on clustering diversity and quality measures

Abstract

In spite of some attempts at improving the quality of the clustering ensemble methods, it seems that little research has been devoted to the selection procedure within the fuzzy clustering ensemble. In addition, quality and local diversity of base-clusterings are two important factors in the selection of base-clusterings. Very few of the studies have considered these two factors together for selecting the best fuzzy base-clusterings in the ensemble. We propose a novel fuzzy clustering ensemble framework based on a new fuzzy diversity measure and a fuzzy quality measure to find the base-clusterings with the best performance. Diversity and quality are defined based on the fuzzy normalized mutual information between fuzzy base-clusterings. In our framework, the final clustering of selected base-clusterings is obtained by two types of consensus functions: (1) a fuzzy co-association matrix is constructed from the selected base-clusterings and then, a single traditional clustering such as hierarchical agglomerative clustering is applied as consensus function over the matrix to construct the final clustering. (2) a new graph based fuzzy consensus function. The time complexity of the proposed consensus function is linear in terms of the number of data-objects. Experimental results reveal the effectiveness of the proposed approach compared to the state-of-the-art methods in terms of evaluation criteria on various standard datasets.

1 Introduction

Clustering has been used for exploration, analysis and pattern discovery in an unsupervised manner in machine learning, image segmentation (e.g. dental x-ray image segmentation [1] and weather nowcasting from satellite image sequences by hybrid forecast methods based on picture fuzzy clustering [2]) and data mining.

The objective of clustering is to place similar data-objects based on a similarity criterion in groups called clusters, which have the minimum intra-grouping distances and the maximum inter-grouping distances.

Based on the relationship of each data-object to the clusters, the clustering algorithms can also be categorized into crisp and fuzzy clustering algorithms. In crisp-clustering, a data-object definitely belongs to one cluster. But some data are inherently fuzzy (i.e. the ones that will not be definitively assigned to a cluster), and are doubtful. For example, in gene-expression data clustering, genes may belong to different biological processes and thus they are part of different collections. In fuzzy clustering, data-objects are assigned to every cluster with a membership degree. Crisp-clustering is a special case of fuzzy clustering, in which the membership degree of a data-object to a cluster is equal to one and zero to other clusters. The basic FCM clustering algorithm proposed by Don and completed by Bezdek [3] is the foundation of the fuzzy clustering analysis. In due time, the famous fuzzy clustering algorithms have been developed based on the FCM in order to increase its performance and adapt it to different datasets. Gustafson-Kessel algorithm (GK) [4], Gath-Geva algorithm (GG), [5], Kernel-based fuzzy clustering (KFCM) [6], MKFC [7], modified fuzzy ant clustering (MFAC) [8] and FCM–IDPSO [9] algorithms can be mentioned as some examples. It is worth mentioning that some extensions of FCM such as FC-PFS [10], DPFCM [11], AFC-PFS [12] and HPC [13] are developed for picture fuzzy clustering to resolve the limitations of FCM in terms of membership representation, the determination of hesitancy and the vagueness of prototype parameters.

In the clustering context, various clustering algorithms have emerged, each using a different similarity criterion and consequently, having different objective functions. By applying different algorithms or a fixed algorithm with different parameters, one can obtain a set of varying clustering results. In specific conditions, some of these algorithms might outperform others. For example, some algorithms have high computational complexity, some others have good accuracy rate, and the others suit the datasets with special characteristics (e.g. k-means fits the datasets with circular-shape clusters). In other words, a single clustering algorithm cannot be found to learn from every dataset [14]. Hence, an alternative solution is to combine some of these algorithms for managing all the objectives regarding the clustering, some of which might be contradictory. This idea is named combining clusterings and is called cluster ensemble in many scientific contexts [15], and has recently become popular in the scientific community [16,17,18,19,20,21,22,23]. Clustering ensembles generally outperform the single clustering in several respects, such as robustness, novelty, quality enhancement, knowledge reusability, multi-view clustering, stability, parallel/distributed data processing [24], and data privacy protection [25]. In addition, it provides heterogeneous data clustering (e.g. clustering popular music [26]).

Cluster ensemble involves following two phases [15]:

• 1) Base-clustering generation phase: Produce base-clusterings through single clustering algorithms (in this study single clustering is used versus ensemble clustering). Given a dataset, the ensemble of diverse base clusterings can be produced via initialization by running a clustering algorithm with different parameters [27], running different “clustering” algorithms [23, 28], clustering via different subsets of the features [19, 29], clustering via different subsets of data-objects [30, 31], and clustering via a projection of the data-object subsets [16, 21]. In this study this phase is not addressed. However, in the experiments section (Section 4.1), we generate base-clusterings using different algorithms with different cluster-numbers.

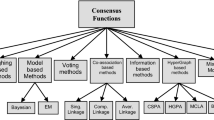
• 2) Base clustering combination phase: Our study focuses on this phase. In this phase the base-clusterings produced in phase 1 must be combined in order to generate the final clustering, which is the objective of this phase. The job is done through a consensus function. Generally, consensus ensemble methods can be categorized into: (1) intermediate space clustering ensemble methods [19, 32], (2) co-association matrix based clustering ensemble methods [29, 33, 34], (3) hyper-graph based clustering ensemble methods [15, 17, 34], (4) expectation maximization clustering ensemble methods [23], (5) mathematical modeling clustering ensemble methods (median partition) [35], (6) voting-based approach [36,37,38], and (7) quadratic mutual information approach [30].

Considerable work has been performed in the field of crisp-cluster ensemble. The researches of Fred and Jain [33] and also Strehl and Ghosh [15] can be assumed as the starting points in the cluster ensemble. These researchers proposed a consensus method which does not require accessing the features and algorithms comprising the base-clusterings. They formulated the cluster ensemble problem in the form of a combinatorial optimization problem based on the mutual information. Here we can consider the studies related to ensemble selection, especially when the ensemble consists of fuzzy clusterings, among which the following are briefed:

• Alizadeh et al. transformed the fuzzy ensemble clustering problem to a 0–1 bit string problem [39]. Their proposed model consists of a constrained nonlinear objective function, named fuzzy string data-objective function (FSOF). FSOF simultaneously maximizes the agreement and minimizes the disagreement between the ensemble members. They solved this nonlinear model using genetic algorithm by applying two modified crossover operators and one modified mutation operator. Based on these operators, two consensus functions named FSCEOGA1 and FSCEOGA2 were proposed. It is worth noting that in this method the base-clusters must be crisp.

• Bedalli et al. proposed a heterogeneous cluster ensemble to increase the stability of fuzzy cluster analysis [40]. First, they applied single fuzzy clustering algorithms like FCM, GG, GK and KFCM and then applied the FCM algorithm to the co-association matrix and in the end, they obtained the final clustering. In this method, all of the clusterings participate in forming the co-association matrix in an equal manner.

• Berikov presented the probabilistic model for the fuzzy Clustering ensemble based on the weighted co-association matrix [41]. In this model, each of the base-clusterings is created by different single clustering algorithms. Each single algorithm performs a certain number of times on each data set (i.e. r times). The Hellinger distance [42] between the membership value of every data-object pair to all clusters in each clustering is calculated r times and then, the variance of these distances is obtained. The calculated variance of the distances is considered as the weight of each base-clustering in the calculation of the reverse co-association matrix (the matrix is based on the distance of the data-object pair rather than the similarity of the data-object pair). In this algorithm, the variance of the distance between the data-object pairs is considered as a consistency criterion. Then, the final clustering is obtained by applying a hierarchical agglomerative clustering such as “cl” (complete linkage) on the resulting matrix.

• sCSPA is proposed by Punera and Ghosh [43] which is similar to CSAPA [15], it creates a graph of all data-objects where edges are weighted by pair-wise similarities. It first transforms the data-objects into a label-space. Then each data-object is visualized as a vector in a c dimensional space (c: number of all clusters in the ensemble), and then the Euclidean distance in the label-space is used to calculate the similarity between each data-object pair. Punera and Ghosh also developed sMCLA and sHBGF approaches [43] which are the fuzzy extension versions of MCLA [15] and HBGF [17], respectively. In these methods, all base-clusterings participate in generation of the final clustering; there is not a selection process though.

• An Information Theory K-means algorithm named ITK proposed by Dhiloon for clustering the words of a text is applied in order to reduce the number of features [44]. In ITK, for each data-object, the concatenation of its membership degree to all clusters in each fuzzy base-clustering is considered as its feature values in a new space (each base-clustering is a feature). Therefore, the distance between data-object pairs is obtained using the KL-divergence [45]. In the end, the final clustering is obtained by applying an algorithm similar to the K-means algorithm on the distances resulted from the KL-divergence.

• A Particle Swarm optimization based method for fuzzy clustering ensemble was proposed by Oliveira [46]. Diverse base-clusterings are generated using Particle Swarm Clustering (PSC) algorithm and through parameter change. Then β^′ among β base-clusterings (β^′ < β) are selected through the pruning process: first the fitness of each base-clustering is measured using one of the internal cluster validity indices like Ball-Hall [47], Calinski-Harabasz [48], Dunn index [49], Silhouette index [50] or Xie-Beni [51], and then the elite clusterings are chosen using one of the genetic selection mechanisms like tournament or roulette wheel. Lastly, again the PSC algorithm is applied as a consensus function in order to produce the final clustering. Unlike some other PSO-based methods where each clustering is represented as a particle, in this study, each cluster is represented as a particle.

• Parvin et al. proposed a weighted locally adaptive clustering algorithm (FWLAC) for handling the imbalanced clusterings. FWLAC assigns weights to features and clusters during the clustering process. Computing these weights is dependent on two regularization terms. Because the performance of FWLAC algorithm is dependent on the tuning of these terms, they propose an elite clustering ensemble to tune these parameters and obtain an optimized clustering. Their proposed elitism procedure first converts fuzzy clusters into crisp-clusters and considers each cluster as a clustering. Finally, the NMI measure was used to assess each cluster [52].

• Sevillano et al. [37] proposed a method based on voting mechanism in order to obtain consensus clustering from fuzzy clustering ensemble. This method includes two procedures, 1. Disambiguation and 2. Voting. In disambiguation phase of clusters, the re-labeling problem is performed using the Hungarian algorithm [53] with O(K³) time complexity, K representing the number of clusters in each clustering (we summarize the notation introduced in this paper in Table 7). The final consensus clustering is obtained through the voting procedure. Two confidence-based voting methods named Sum Voting Rule and Product Voting Rule [54] and also two positional-based voting methods named Borda Voting Rule [55] and Copeland Voting Rule [56] are presented and the time complexity of these four algorithms is O(MKβ), where K represents the number of clusters in each clustering, M shows the number of data-objects and β indicates the number of base-clusterings. Based on the combination of re-labeling and voting being direct or repetitive, there exists eight different consensus functions, named DSC (direct sum consensus), DPC (direct product consensus), DBC (direct Borda consensus), DCC (direct Copeland consensus), ISC (iterative sum consensus), IPC (iterative product consensus), IBC (iterative Borda consensus) and ICC (iterative Copeland consensus).

• Seera et al. combined Fuzzy Min–Max clustering neural network and ensemble clustering trees to propose a learning model with the ability of performing online clustering [57]. This method extended the Fuzzy Min-Max neural network [58] by adding a centroid hyper-box and a confidence-factor. They computed centroid data of each hyper-box using one of the four mean measures: harmonic, geometric, arithmetic, and root mean square. This extended Fuzzy Min-Max neural network recalculates hyper-boxes confidence-factor after placing each arriving data-object in one of the hyper-boxes. After all data-objects are partitioned by this process, these centroids and their confidence-factors are considered a goodness-of-split measure for building a tree in the next step. Finally, an ensemble of multiple trees is built by a bagging method with random feature selection.

• In [59] Son et al. generate base-clusterings by FCM [3], KFCM [6] and GK [4] algorithms. Then, they calculate the weight of each base-clustering in the ensemble according to Dunn and PC [60] internal clustering validation measure and after that, they compute the weighted co-association matrix. Finally, they obtain the final clustering by the minimization of sum of square error between the weighted co-association matrix and final clustering through the gradient descent method.

  It is noteworthy to mention a crisp ensemble clustering which contains a selection method:

• Alizadeh et al. [61] developed a method for selecting stable clusters (crisp-cluster) based on stability of clusters. To compute the stability of each cluster, first they generated an ensemble of base-clusterings using the resampling technique, and then they transformed the ensemble into a cluster representation. After that, the stability value of each cluster in relation to other clusters was computed. Finally, they selected the clusters with the most stability value. It is notable that, a new measure for computing the NMI of each cluster was introduced. Their proposed selection method operates at crisp- cluster level and ignores the diversity of the base-clusterings.

  It is also worth noting that considerable work has been performed in the field of multi-view learning and ensemble clustering via co-training. Among them, the following lists are briefed:

• Kumar and Daume [62] apply the idea of co-training [63] to the problem of multi-view spectral clustering [64]. The using of co-training in clustering is that if two points are assigned to one cluster in one view, they should be assigned to the same cluster in all views. Spectral clustering was extended for multi view data clustering in the following manner. For each two views of the data, K eigenvectors (discriminative eigenvectors) of the normalized Laplacian matrix of every similarity matrix of every view are calculated. Based on the discriminative eigenvectors of each view, the similarity matrix of the other one is modified. This process is repeated for a certain number of iterations. Then similar to traditional spectral clustering, the discriminative eigenvectors are concatenated as a matrix, normalized, and clustered by k-means algorithm, and finally, the data-objects are assigned to the clusters. The algorithm does not have any hyper-parameters to set, but its time complexity is O(M³), where M is the number of data-objects. This approach is not appropriate for clustering high-dimensional datasets. Later, Hong et al. [65] extended this approach via the use of spectral embedded clustering instead of spectral clustering. Spectral embedded clustering has better performance than spectral clustering on high-dimensional data.

• Appice and Malerba [66] used trace clustering (an ordered list of activities invoked by a process execution in an event log) as a pre-processing step for minimizing the spaghetti-like (complex or hard to understand) problem of process models discovered by other process mining algorithms. They proposed a multiple-view method for multiple-perspective (profile) clustering by applying the co-training strategy [63]. A general co-training strategy was formulated for application to any distance-based clustering algorithm. Also, Silhouette width was used as a measure for stopping the iterative procedure in multi-view spectral clustering algorithm. Because the traces being grouped in a cluster are related, the model discovered by each cluster is more comprehensive and accurate (compared to a state where no clustering is applied).

In Table 1, only the mentioned researches in the field of fuzzy clustering ensemble are summarized. The idea of this summarization is to determine the limitations of related works that can be dealt with in this paper.

Table 1 Summarized fuzzy clustering ensemble related works

In the clustering ensemble, not all base-clusterings have a positive influence on the final clustering [15, 19]. Therefore, selecting appropriate base-clusterings is a critical process. Some researchers such as Parvin et al. [52], Alizadeh et al. [61, 67], selected a subset of base-clusters instead of all clusters to construct the final clustering based on cluster stability criterion. Nadli et al. proposed a method for selecting the finest base-clusterings according to validity indices [68]. Despite fuzzy clustering being more generalized compared to crisp-clustering, researches in elite fuzzy clustering ensemble are still in their initial stages and there exist relatively few approaches for this field. Converting fuzzy clustering into crisp-clustering and selecting the clusters results in the loss of some information. In addition to the quality of base-clustering in the ensemble, the diversity of the base-clustering highly influences the quality of final clustering obtained by consensus process in ensemble clustering and leads to better ensemble quality [16]. The consensus results may be severely affected by low-quality and even not diverse base-clusterings. To deal with low-quality base-clusterings, some researchers investigated the quality-evaluation of the base-clusterings or base-clusters to improve the quality of the consensus functions’ results [34, 52, 61, 69,70,71,72] . Also, some researchers investigated the diversity evaluation of the crisp base-clusterings [73,74,75]. However, these approaches and all researches previously mentioned in this paper, do not consider the diversity and quality evaluation for selecting a subset of fuzzy base-clusterings in the ensemble simultaneously (main limitation).

In order to address the above-mentioned main limitation and some limitations in Table 1, this study was devoted towards the development of a new elite fuzzy clustering ensemble framework based on diversity-quality of fuzzy base-clustering. Specifically, the main ideas of the new approach are:

• Select a subset of initial fuzzy base-clustering set whereby the selected fuzzy base-clusterings satisfy diversity and high-quality simultaneously by a fuzzy clustering criterion.

• Construct an extended fuzzy co-association matrix from the selected fuzzy base-clusterings

• Calculate final clustering from the selected base-clusterings through a new consensus function or single traditional clustering algorithms.

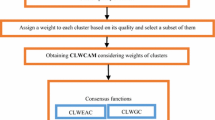
The overall process of this framework is illustrated in Fig. 1. By considering the advantage of the ensemble diversity and the fuzzy clustering-level quality, a selection scheme is proposed to select a subset of fuzzy base-clusterings. Briefly, the diversity among the base-clusterings and the clustering-level quality are integrated to enhance the quality of the final clustering result. Here, first, a new fuzzy normalized mutual information (FNMI) is calculated (step 1), then the diversity of each fuzzy base-clustering in relation to other fuzzy base-clusterings is calculated (step 2), next, all base-clusterings are clustered based on the calculated diversity (step 3); the output of this step is clusters of base-clusterings that we name base-clusterings-clusters. Then a subset of fuzzy base-clusterings (a base-clusterings-cluster) that satisfies the quality measure is selected in step 4 (addresses main limitation). Finally, in order to achieve the final clustering:

• (1) a new consensus method based on graph portioning algorithm (we named FCBGP method) is applied as consensus algorithm (path 3 in Fig. 1) or

• (2) the extended fuzzy co-association matrix (EFCo) is formed. At the end the EFCo is considered as similarity matrix and one of the single clustering algorithms such as hierarchical clustering or K-means or FCM is applied on it; we named it DQEAFC method (path 2 in Fig. 1). It is worth mentioning that the proposed approach is followed in paths 2 and 3; path 1 is done when the proposed selection strategy is not used and all base-clusterings directly participate in fuzzy co-association matrix; we name this matrix FCO and this algorithm EAFC.

Fig. 1

The proposed approach framework

The contributions of this paper are as follows:

• A method is proposed to compute diversity of each fuzzy clustering in relation to other clusterings.

• A method is proposed to compute the quality of each fuzzy clustering in terms of fuzzy mutual information.

• A method is proposed to select a subset of diverse and high-quality base-clusterings among all fuzzy base-clusterings.

• A graph based consensus function is proposed whose time complexity is linear in terms of data-object numbers

• Extensive experiments carried out on a variety of datasets indicate that this proposed fuzzy clustering ensemble approach outperforms the state-of-the-art approaches in terms of clustering quality.

The rest of the paper is organized as follows: The formal background knowledge about ensemble clustering is introduced in Section (2). The proposed selection fuzzy clustering ensemble framework is described in Section (3). The experimental results are reported in Section (4) and the conclusion is presented in Section (5).

2 Preliminary concepts

Before explaining this proposed approach, the general formulation of the data and fuzzy clustering ensemble should be introduced as follows:

• Definition 1. A data-object is a multi-tuple $\left({x}_d^1,{x}_d^2,\dots {x}_d^N\right)$ presented as $\overrightarrow{x_d}$, where ${x}_d^a$ is the a-th feature from d-th data, ${x}_{:}^a$ is the a-th feature from whole data x. N is the number of features, $N=\left|{x}_1^{:}\right|$ and M is the number of the data-objects‘$M=\left|{x}_{:}^i\right|$.

• Definition 2. Fuzzy clustering of data set x is a two dimensional matrix with M ∗ K size, where $M=\left|{x}_{:}^1\right|$ and K is the number of clusters, presented as π(x) so that:

$$ \forall \mathrm{j}\in \left\{1,\dots, K\right\},i:\pi {\left(\overrightarrow{x_d}\right)}^i\in \left[0,1\right] $$

(1)

where

$$ \forall d:{\sum}_{i=1}^K\pi {\left({\overrightarrow{x}}_d\right)}^i=1 $$

(2)

where $\pi {\left({\overrightarrow{x}}_d\right)}^i$ is the membership degree of d-th data-object belonging to i-th cluster.

• Definition 3. A clustering ensemble which consists of β base-clusterings is defined as:

$$ \varPi =\left\{{\pi}^1,\dots, {\pi}^{\upbeta}\right\} $$

(3)

where

$$ {\pi}^j=\left\{{C}_1^j,\dots, {C}_{n^j}^j\right\} $$

(4)

where π^j is the j-th base-clustering in Π, ${C}_i^j$ is the i-th cluster in base-clustering π^j, ${\pi}^j{\left(\overrightarrow{x_d}\right)}^i$ is the membership degree of d-th data-object belonging to i-th cluster in base-clustering π^j and n^j is the number of clusters in π^j.

To sum up, the set of all clusters in the ensemble is presented as

$$ C=\left\{{C}_1^1,\dots, {C}_{n^{\beta}}^{\beta}\right\} $$

(5)

where ${C}_i^j$ is the i-th cluster of clustering π^j, thus the number of all clusters in the clustering ensemble Π is represented as c and computed as:

$$ c={n}^1+\dots +{n}^{\beta } $$

(6)

• Example 1. Assume we have a dataset x with 10 data-objects (M = 10) and assume we have produced an ensemble with eight base-clusterings on π¹ to π⁸ (β = 8) on dataset x as shown in Table 2. Each base-clustering contains two clusters except base-clustering π² and π⁵ each of which contains 3 clusters.

Table 2 An example of Fuzzy clustering ensemble

3 Proposed approach

In the following sub sections, answers to four major questions regarding the presented approach are presented:

• 1. How can the diversity between each pair of fuzzy base-clusterings be measured?

• 2. How can the quality of fuzzy base-clusterings be measured?

• 3. How can diverse base-clusterings be selected with an acceptable level of quality (diversity and quality simultaneously)?

• 4. How is the final clustering derived from the selected base-clusterings?

Section 3.2 answers question 1, but it needs pre-calculation in Section 3.1. Section 3.1 answers question 2. Question 3 is answered in Sections 3.3 and 3.4. Section 3.5 is the overall answer to questions 1, 2 and 3. Question 4 is answered by Sections 3.6 and 3.7.1 or Section 3.7.2.

Here, first the proposed approach is briefly outlined, and then its steps are described in detail. The main idea of our proposed elite clustering ensemble framework is utilizing a subset of the best diverse and high-quality fuzzy base-clusterings in the ensemble instead of using all base-clusterings. Only the base-clusterings that satisfy the diversity and quality measures can participate in the final clustering construction. The clustering diversity and the clustering quality are defined according to Fuzzy Normalized Mutual Information (FNMI). The proposed elite clustering ensemble framework is depicted in phase 2 of Fig. 1. Generally, Fig. 1 consists of two phases: 1) base-clustering generation phase: initially base-clusterings were generated before (usually by single clustering algorithms) and are feed forwarded as input to the phase 2. 2) combination phase: combines base-clusterings and derives final clustering (this phase contains the proposed approach). This research focuses on phase 2 and decomposes it into 6 steps. The manner of computing the diversity between two base-clusterings based on their FNMI is described in the Sections 4.1 and 4.2 in detail (step 1 and step 2). To select a diverse and high-quality base-clustering subset of base-clusterings for combination, we cluster all base-clusterings based on diversity measure by a single traditional clustering algorithm such as FCM, as will be illustrated in Section 4.3 (step 3). We name the output of FCM as base-clustering-clusters. Each base-clustering-cluster contains diverse base-clusterings. Then the base-clustering-cluster with the highest FNMI-average (FNMI mean of base-clusterings in each base-clustering-cluster) is selected as elite clustering for participating in forming the final clustering as will be illustrated in Section 4.4 (step 4). After selection phase, the selected base-clusterings are used to: (1) construct weighted graph for the fuzzy clusters, and by partitioning this graph, the final clustering is obtained (FCGP of step 6). Or (2) construct the extended fuzzy co-association matrix from selected base-clusterings (step 5). Finally, a hierarchical clustering algorithm, such as Complete-Linkage (‘CL’) is used to extract the final clustering out of this matrix (DQEAFC of step 6).

In other words, the proposed framework in Fig. 1 tries to overcome some limitations of the related work in Table 1 as: before step 1 is started base-clusterings were generated depending on whether generation phase limitation occurs here (in spite of [52],). Lack of diversity selection, also quality selection problems are solved by step 2 through 5 (selection process). Steps 2 and 3 components (quality and diversity criteria) are computed based on membership values of each data-object to clusters and their computations do not require dataset records; they are not dependent on the original data objects (in spite of [52, 57]), in addition, these components operate on fuzzy clusters and do not need to convert fuzzy clusters into crisp (in spite of [39]). The FCGP consensus function is proposed to solve high computational cost to obtain final clustering. Looking at the used equation in the framework steps, it appears that the number of clusters in base-clusterings can be different and clustering relabeling is unnecessary (in spite of [37]).

3.1 Fuzzy normalized mutual information (FNMI) calculation

The first step in Fig. 1 is calculation of fuzzy normalized mutual information (FNMI). Normalized Mutual Information (NMI) indicates how much information is shared between two clusterings, in other words how similar these clusterings are. We use NMI as a measure to compute the similarity between two clusterings, because it has some properties such as (1) it takes into account the number of data-objects in and not in a clusters. (2) it takes in to account the entire distribution of each clustering. (3) no bias from small clusters. (4) symmetric (5) nonlinear relations between clusterings detection. The traditional NMI between two crisp-clusterings πⁱ and π^j is calculated using Eq. (7) [15].

$$ NMI\left({\pi}^i,{\pi}^j\right)=\raisebox{1ex}{$ MI\left({\pi}^i,{\pi}^j\right)$}\!\left/ \!\raisebox{-1ex}{$\mathit{\max}\left(H\left({\pi}^i\right),H\left({\pi}^j\right)\right)$}\right. $$

(7)

where, MI(πⁱ, π^j) denotes the mutual information between two clusterings and is computed by Eq. (8),

$$ MI\left({\pi}^i,{\pi}^j\right)=H\left({\pi}^i\right)+H\left({\pi}^j\right)- JH\left({\pi}^i,{\pi}^j\right) $$

(8)

where JH(πⁱ, π^j) denotes the join entropy between two clusterings πⁱ and π^j, which is computed by Eq. (9),

$$ JH\left({\pi}^i,{\pi}^j\right)=-{\sum}_{t=1}^{n^i}{\sum}_{l=1}^{n^j}\frac{M_{tr}^{ij}}{M}\log \frac{M_{tl}^{ij}}{M} $$

(9)

and H(πⁱ) denotes the entropy of πⁱ which is computed by Eq. (10).

$$ H\left({\pi}^i\right)=-{\sum}_{t=1}^{n^i}\frac{M_t^i}{M}\log \frac{M_t^i}{M} $$

(10)

where ${M}_{tl}^{ij}$ is the number of shared data-objects between clusters c_t ∈ πⁱ and c_l ∈ π^j, ${M}_t^i$ is the number of data-objects in c_t and M is the number of data-objects.

The traditional NMI is used for crisp-clustering and cannot be used directly for fuzzy clustering. Hence in this study, we extended it for computing the amount of shared information between two fuzzy clusterings as a clustering-pair similarity measure. We named this extended NMI as fuzzy NMI (FNMI) measure. In this extension: we define ${M}_{tl}^{ij}$ as the similarity between two fuzzy clusters ${C}_t^i$ and ${C}_l^j$ and denoted it by $sim\left({C}_t^i,{C}_l^j\right)$ (computed according to Definition 5). Also, in fuzzy clustering ${M}_t^i$ means the sum of similarities between cluster ${C}_t^i$ and all clusters in the clustering π^j (${C}_t^i$ in the view of clustering π^j) and denoted it by $Ssim\ \left({C_t^i}_{\kern0.75em {\pi}^j}\right)$ (computed according to Eq. (15)). M means the sum of similarities between each cluster ${C}_t^i$ and all clusters in the clustering π^j and vice versa (similarities between each cluster ${C}_t^j$ and all clusters in the clustering πⁱ). M here is expressed by SSsim(πⁱ, π^j) (computed according to Eq. (16)). The term H(πⁱ) of crisp-clustering in fuzzy clustering is denoted as $H\left({\pi^i}_{\pi^j}\right)$ and means the entropy of fuzzy clustering πⁱwith respect to clustering π^j (computed according to Eq. (14)) and the term JH(πⁱ, π^j) of crisp-clustering denotes the join entropy between two fuzzy clusterings πⁱ and π^j (computed according to Eq. (13)).

As a summary, the FNMI between two base-clusterings πⁱ, π^j is computed according to Definition 4.

• Definition 4. Fuzzy Normalized Mutual Information between two fuzzy clusterings πⁱ, π^j is expressed by FNMI (πⁱ, π^j) and is computed as:

$$ FNMI\left({\pi}^i,{\pi}^j\right)=\raisebox{1ex}{$ FMI\left({\pi}^i,{\pi}^j\right)$}\!\left/ \!\raisebox{-1ex}{$\mathit{\max}\left(H\left({\pi^i}_{\pi^j}\right),\left({\pi^j}_{\pi^i}\right)\right)$}\right. $$

(11)

where FMI(πⁱ, π^j) is the fuzzy mutual information between two clusterings πⁱ and π^j, and is computed by Eq. (12),

$$ FMI\left({\pi}^i,{\pi}^j\right)=H\left({\pi^i}_{\pi^j}\right)+H\left({\pi^j}_{\pi^i}\right)- JH\left({\pi}^i,{\pi}^j\right) $$

(12)

where JH(πⁱ, π^j) is the joint entropy between two fuzzy clusterings πⁱ and π^j, and is computed by Eq. (13),

$$ JH\left({\pi}^i,{\pi}^j\right)=-{\sum}_{t=1}^{n^i}{\sum}_{l=1}^{nj}\left(\frac{sim\left({C}_t^i,{C}_l^j\right)}{SSsim\left({\uppi}^{\mathrm{i}},{\uppi}^{\mathrm{j}}\right)}\ \log \left(\frac{sim\left({C}_t^i,{C}_l^j\right)}{SSsim\left({\uppi}^{\mathrm{i}},{\uppi}^{\mathrm{j}}\right)}\right)\right)\kern0.5em $$

(13)

and $H\left({\pi^i}_{\pi^j}\right)$ is the entropy of fuzzy clustering πⁱwith respect to clustering π^j, that is computed by Eq. (14) and $H\left({\pi^j}_{\pi^i}\right)$ is the entropy of fuzzy clustering π^jwith respect to clustering πⁱ

$$ H\left({\pi^i}_{\pi^j}\right)=-{\sum}_{t=1}^{n^i}\frac{Ssim\ \left({C_t^i}_{\kern0.75em {\pi}^j}\right)}{SSsim\left({\uppi}^{\mathrm{i}},{\uppi}^{\mathrm{j}}\right)}\log \frac{Ssim\ \left({C_t^i}_{\kern0.75em {\pi}^j}\right)}{SSsim\left({\uppi}^{\mathrm{i}},{\uppi}^{\mathrm{j}}\right)} $$

(14)

where $sim\left({C}_t^i,{C}_r^j\right)$ is the similarity between two fuzzy clusters c_t ∈ πⁱ, c_r ∈ π^j and is computed according to Definition 5, $Ssim\ \left({C_t^i}_{\kern0.75em {\pi}^j}\right)$ is the sum of similarity between the fuzzy clusters c_t ∈ πⁱ and all clusters ${C}_l^j\in {\uppi}^{\mathrm{j}}$ and is computed according to Eq. (15) and SSsim(πⁱ, π^j) is the sum of similarity between each cluster of clustering πⁱ in relation to each cluster of clustering π^j and is computed according to Eq. (16).

$$ Ssim\ \left({C_t^i}_{\kern0.75em {\pi}^j}\right)={\sum}_{l=1}^{n^j} sim\left({C}_t^i,{C}_l^j\right) $$

(15)

$$ SSsim\left({\uppi}^{\mathrm{i}},{\uppi}^{\mathrm{j}}\right)={\sum}_{t=1}^{n^i}{\sum}_{l=1}^{n^j} sim\left({C}_t^i,{C}_l^j\right) $$

(16)

As can be seen, to compute Fuzzy Normalized Mutual Information (FNMI) we need to compute fuzzy cluster pairwise similarity:

• Definition 5. The similarity of cluster ${C}_t^i$ (cluster C_t ∈ πⁱ) from cluster ${C}_l^j$ (cluster C_l ∈ π^j), is computed using Eq. (17):

$$ sim\left(\ {C}_t^i,{C}_l^j\ \right)={\sum}_{d=1}^M\left({\pi}^i{\left(\overrightarrow{x_d}\right)}^t\ast {\pi}^j{\left(\overrightarrow{x_d}\right)}^l\right) $$

(17)

where ${\pi}^i{\left(\overrightarrow{x_d}\right)}^t$ is the membership degree of d-th data-object belonging to t-th cluster in clustering πⁱ.

In fact, the similarity of C_t ∈ πⁱ indicates how the membership degree of data-objects belonging to cluster C_t in base- clustering πⁱ is similar to the membership degree of them belonging to cluster C_l in the base-clustering π^j.

• Example 2 (Continuation of example 1). The similarity between fuzzy clusters ${C}_1^1$ and ${C}_1^2$ of fuzzy clustering ensemble in Table 2 based on the Eq. 17 has been computed as $sim\left({C}_1^1,{C}_1^2\ \right)=0.7\ast 0.8+0.0\ast 1.0+$ 0.1 ∗ 0.4+ 0.1 ∗ 0.2+ 0.4 ∗ 0.1+ 0.3 ∗ 0.2+ 0.6 ∗ 0.6+ 0.0 ∗ 0.9 + 0.6 ∗ 0.1+ 0.8 ∗ 0.2 = 1.30. Other values have been calculated in the same way and matrix sim is shown in Table 3.

• Example 3 (Continuation of example 2). The $Ssim\ \left({C_1^1}_{\kern0.75em {\pi}^2}\right)$ based on the Eq. (15) has been calculated as $Ssim\ \left({C_1^1}_{\kern0.75em {\pi}^2}\right)= sim\left({C}_1^1,{C}_1^2\right)+ sim\left({C}_1^1,{C}_2^2\right)+ sism\left({C}_1^1,{C}_3^2\right)=$1.3 + 1.43 + 0.87 = 3.6. Other Ssim values have been calculated in the same way, e.g. $Ssim\ \left({C_1^1}_{\kern0.75em {\pi}^2}\right)=6.4$, $Ssim\ \left({C_1^2}_{\kern0.75em {\pi}^1}\right)=4.5$, $Ssim\ \left({C_2^2}_{\kern0.75em {\pi}^1}\right)=2.8$, $Ssim\ \left({C_3^2}_{\kern0.75em {\pi}^1}\right)=2.7$. Considering the Computed Ssim and based on the Eq. (16) SSsim(π¹, π²) has been calculated as $SSsim\left({\uppi}^1,{\uppi}^2\right)= sim\left({C}_1^1,{C}_1^2\right)+ sim\left({C}_1^1,{C}_2^2\right)+ sism\left({C}_1^1,{C}_3^2\right)+ sim\left({C}_2^1,{C}_1^2\right)+ sim\left({C}_2^1,{C}_2^2\right)+ sim\left({C}_2^1,{C}_3^2\right)=1.3+1.47+1.08+3.20+1.37+1.83=10$. Other SSsim values have been calculated in the same way. Based on the Eq. (14) $H\left({\pi^1}_{\pi^2}\right)=-\left(\frac{Ssim\ \left({C_1^1}_{\pi^2}\right)}{SSsim\left({\pi}^1,{\pi}^2\right)}\log \frac{Ssim\ \left({C_1^1}_{\pi^2}\right)}{SSsim\left({\pi}^1,{\pi}^2\right)}+\frac{Ssim\ \left({C_2^1}_{\pi^2}\right)}{SSsim\left({\pi}^1,{\pi}^2\right)}\log \frac{Ssim\ \left({C_2^1}_{\pi^2}\right)}{SSsim\left({\pi}^1,{\pi}^2\right)}\right)=-\left(\frac{3.6}{10}\log \frac{3.6}{10}+\frac{6.4}{10}\log \frac{6.4}{10}\right)=0.6534$. Entropy of other fuzzy clusterings has been calculated in the same way, e.g. $H\left({\pi^2}_{\pi^1}\right)=1.0693$. Based on the Eq. (13) $JH\left({\pi}^1,{\pi}^2\right)=-\left(\frac{sim\left({C}_1^1,{C}_1^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\ast \log \left(\frac{sim\left({C}_1^1,{C}_1^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\right)+\frac{sim\left({C}_1^1,{C}_2^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\ast \log \left(\frac{sim\left({C}_1^1,{C}_2^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\right)+\frac{sim\left({C}_1^1,{C}_3^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\ast \log \left(\frac{sim\left({C}_1^1,{C}_3^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\right)+\frac{sim\left({C}_2^1,{C}_1^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\ast \log \left(\frac{sim\left({C}_2^1,{C}_1^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\right)+\frac{sim\left({C}_2^1,{C}_2^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\ast \log \left(\frac{sim\left({C}_2^1,{C}_2^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\right)+\frac{sim\left({C}_2^1,{C}_3^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\ast \log \left(\frac{sim\left({C}_2^1,{C}_3^2\right)}{SSsim\left({\uppi}^1,{\uppi}^2\right)}\right)\right)=-\left(\frac{1.3}{10}\log \frac{1.3}{10}+\frac{1.43}{10}\log \frac{1.43}{10}+\frac{0.87}{10}\log \frac{0.87}{10}+\frac{3.2}{10}\log \frac{3.2}{10}+\frac{1.37}{10}\log \frac{1.37}{10}+\frac{1.83}{10}\log \frac{1.83}{10}\right)=1.7035$ . Finally, the FNMI between two fuzzy clusterings π¹ and π² based on the Eq. (11) has been calculated as $FNMI\left({\pi}^1,{\pi}^2\right)=\raisebox{1ex}{$ FMI\left({\pi}^1,{\pi}^2\right)$}\!\left/ \!\raisebox{-1ex}{$\mathit{\max}\left(H\left({\pi^1}_{\pi^2}\right),\left({\pi^2}_{\pi^1}\right)\right)$}\right.=\frac{H\left({\pi^1}_{\pi^2}\right)+H\left({\pi^2}_{\pi^1}\right)- JH\left({\pi}^1,{\pi}^2\right)}{\max \left(H\left({\pi^1}_{\pi^2}\right),H\left({\pi^2}_{\pi^1}\right)\right)}=\frac{0.6534+1.0693-1.7035}{\max \left(\mathrm{0.6534,1.0693}\right)}=0.0179$ . The FNMI of other fuzzy clustering pairs has been calculated in same way and the result is shown in Table 4.

Table 3 Values of sim corresponding to fuzzy clustering ensemble presented in Table 2

Table 4 The values of FNMI corresponding to Table 1

3.2 Computing the clustering diversity

As can be seen in Fig. 1, step 2 is devoted to compute the diversity of the base-clusterings. A few diversity measures have been developed for determining the diversity among base-clusterings [18, 19, 76]. These measures can be divided in two categories: (1) 1- pass measures: when ensemble process is forwarded the diversity between each pair of base-clustering is measured, e.g. [16, 68, 72, 77, 78]. b) 2- pass measures: first, in one pass the consensus clustering is obtained by consensus function(s) then the ensemble process is restarted and the diversity of each base-clustering is computed in relation to the obtained consensus clustering (obtained in pass one) e.g. [18, 76].

In this study we define diversity as dissimilarity between two clusterings. Since we define fuzzy normalized mutual information (FNMI) as a measure to compute the similarity between two clusterings, the two clusterings are diverse if shared information between them is low.

• Definition 6. The diversity of clustering πⁱ in relation to clustering π^j, πⁱ ≠ π^jis computed according to:

$$ FDiv\left({\pi}^i,{\pi}^j\right)=1- FNMI\ \left({\pi}^i,{\pi}^j\right) $$

(18)

where FNMI is computed according to Eq. (11).

• Example 3 (Continuation of example 2). The matrix FDiv of the fuzzy clustering ensemble in Table 2 with regard to the matrix FNMI in Table 4, which was computed according to Eq. (18) is shown in Table 5.

Table 5 The values of FDiv corresponding to Table 1

3.3 Base-clustering clustering

As can be seen in Fig. 1, in the third step the base-clusterings are clustered by a single traditional clustering algorithm such as FCM. The objective of this step is to put diverse base-clusterings in a group based on FDiv criterion. As can be seen in Fig. 1, at first, the diversity of the base-clusterings is computed and is considered as clustering pairwise similarity (step 2 of Fig. 1), in other words the base-clusterings are mapped in a new space. In the new space, each base-clustering is considered as a point and the diversity between them is considered as their feature values. Then these base-clusterings are clustered by FCM algorithm (or other single traditional clustering algorithm). Here, output of FCM algorithm is clusters of base-clustering; We name these base-clustering-clusters. We denote the number of base-clustering-clusters as k_BC,, the base-clustering-cluster i − th is represented as BCC_i (k_BC≥i ≥ 1). Let |BCC_i| denote the number of base-clusterings in the BCC_i.

3.4 Elitism

The fourth step in Fig. 1 is eliciting a subset of base-clusterings based on diversity and quality measures. Because the elements in a cluster are more similar rather than the other cluster elements (with regard to the general definition of clustering), each of the base-clustering-clusters generated in the previous step, contains diverse base-clusterings. So far, diversity factor is satisfied by clustering the base-clusterings, now we must select one of the base-clustering-clusters based on the quality measure. The quality measure which is used as selection criterion is the average FNMI between base-clustering within each base-clustering-clusters, and is defined as Defamation 8.

• Definition 7. The quality of a base-clustering-cluster BCC_i which contains |BCC_i| base-clusterings is calculated as: π^j, πⁱ ≠ π^jis computed according to:

$$ Q\left({BCC}_i\right)=\frac{\sum_{i=1}^{\left|{BCC}_i\right|-1}{\sum}_{j=i+1}^{\left|{BCC}_i\right|} FNMI\kern0.5em \left({\uppi}^{\mathrm{i}},{\uppi}^{\mathrm{j}}\right)}{\left|{BCC}_i\right|-1} $$

(19)

• Example 4(Continuation of example 3). We use FCM algorithm as clustering algorithm with k_BC = 2 for partitioning base-clusterings π¹, π², π³, π⁴, π⁵, π⁶, π⁷ and π⁸ (example 1), based on their pair-wise diversity computed in Table 5, BCC₁ = {π¹, π², π³, π⁴, π⁵} and BCC₂ = {π⁶, π⁷, π⁸} are obtained. Average FNMI of base-clustering-cluster BCC₂ according to Eq. (19) and with regard to Table 4 is computed as $Q\left({BCC}_2\right)=\frac{FNMI\left({\pi}^6,{\pi}^7\right)+ FNMI\left({\pi}^6,{\pi}^8\right)+ FNMI\left({\pi}^7,{\pi}^8\right)}{\ \left|{BCC}_i\right|-1}=\frac{0.3958+0.3958+1.0}{\ 3-1}=0.8958$, in the same way Q(BCC₁) = 0.2860. As can be seen, BCC₂ has the highest Q values and is selected. Hence, only base-clusterings π⁶, π⁷and π⁸ participate in final clustering construction.

3.5 Selection process

As can be seen in Fig. 1, the selection strategy consists of steps 1 through 4. The goal of this process in the framework is selecting the elite base-clusterings. If the base-clusterings are diverse and they also have an acceptable quality, a better final clustering can be obtained [79]. In this study diverse base-clusterings with acceptable quality in terms of FNMI are considered elite clusterings. The overall selection process is shown in Algorithm 1. As can be seen, at first, the diversity of the base clustering is computed and is considered as clustering pairwise similarity. Then, these base-clusterings are clustered by FCM algorithm. Because the elements in a cluster are more similar rather than the other cluster elements, each of these base-clustering-clusters contains diverse (similar) base-clustering. So far, diversity factor is satisfied. Following this process, the quality factor is satisfied; the average FNMI of the base-clustering-clusters are measured according to Definition 7 and is considered as the base-clustering-cluster quality (Q). Finally the base-clustering-cluster with the highest Q (average FNMI) is selected (we denote it as π_sel).

3.6 Computing fuzzy co-association matrix

As can be seen in Fig. 1, the fifth step is computing weighted fuzzy co-association matrix of the selected base-clusterings π_sel. Evidence accumulation clustering (EAC), which was first proposed by Fred and Jain [33] is the most common method used to consolidate the base-clusterings. The EAC maps the clustering ensemble into a pairwise co-association matrix of data-objects. The EAC which is used for crisp-clustering ensemble, cannot derive the co-association matrix from fuzzy clusters efficiently, so the EAC method was developed as:

The accumulation method proposed by Fred and Jain was formed on this idea: “The results of multiple clusterings are consolidated in a single clustering supposing that the result of each clustering is independent of dataset organization”. This method is proposed for crisp clustering ensemble. In crisp clustering data member belongs to one of the clusters but does not belong to other clusters. Then in crisp clustering, the answer to the question “are two data-objects x_i and x_j Co-clustered?” is certain and the counts of Co-cluster in the ensemble are considered as their corresponding entry in the co-association matrix. But in fuzzy clustering the answer is uncertain, and we must compute the probability of co-clustering x_i and x_j by considering their membership-degrees to all clusters. As the sum of the probability that two data-objects are Co -cluster and are not Co-cluster by considering a base-clustering is 1 (we present as (Co-cluster($\overrightarrow{x_i}$, $\overrightarrow{x_j}$) and $\overline{\mathrm{Co}-\mathrm{cluster}\Big(\overrightarrow{x_i},\overrightarrow{x_j\Big)}}$ respectively)

$$ \mathrm{Prob}\left(\mathrm{Co}-\mathrm{cluster}\left(\overrightarrow{x_i},\overrightarrow{x_j}\right)\right)=1-\mathrm{prob}\left(\overline{\mathrm{Co}-\mathrm{cluster}\left(\overrightarrow{x_i},\overrightarrow{x_j}\right)}\right) $$

(20)

then it is easier to first compute prob.($\overline{\mathrm{Co}-\mathrm{cluster}\left(\overrightarrow{x_i},\overrightarrow{x_j}\right)}$ . prob.($\overline{\mathrm{Co}-\mathrm{cluster}\left(\overrightarrow{x_i},\overrightarrow{x_j}\right)}$ means that x_i and x_j are not Co-clusters in any of the clusters (not occurred in the same cluster). The probability that x_i and x_j are not placed in the same cluster is represented as $\overline{p}$($\overrightarrow{x_i}$, $\overrightarrow{x_j}$) and computed as.

$\overline{p}$($\overrightarrow{x_i}$, $\overrightarrow{x_j}$) = 1- p($\overrightarrow{x_i}$, $\overrightarrow{x_j}$), where ($\overrightarrow{x_i}$, $\overrightarrow{x_j}$) is the probability that x_i and x_j are placed in same cluster. Because in the clustering π^k, x_i belonging to cluster ${C}_t^k$ is independent of x_j belonging to ${C}_t^k$ then p($\overrightarrow{x_i}$, $\overrightarrow{x_j}$)=${\pi}^k{\left(\overrightarrow{x_i}\right)}^t\ast {\pi}^k{\left(\overrightarrow{x_j}\right)}^t$, so

$$ \overline{p}\left(\overrightarrow{x_i},\overrightarrow{x_j}\right)=1-{\pi}^k{\left(\overrightarrow{x_i}\right)}^t\ast {\pi}^k{\left(\overrightarrow{x_j}\right)}^t $$

(21)

and

$$ \mathrm{prob}\left(\overline{\mathrm{Co}-\mathrm{cluster}\Big(\overrightarrow{x_i},\overrightarrow{x_j\Big)}}\ \right)={\prod}_{t=1}^{n^k}\left(1-{\pi}^k{\left(\overrightarrow{x_i}\right)}^t\ast {\pi}^k{\left(\overrightarrow{x_j}\right)}^t\right) $$

(22)

By substituting Eq.(22) in Eq.(20) we obtain the probability of co-clustering x_i and x_j in clustering π^k as

$$ \mathrm{Prob}\left(\mathrm{Co}-\mathrm{cluster}\left(\overrightarrow{x_i},\overrightarrow{x_j}\right)\right)=1-{\prod}_{t=1}^{n^k}\left(1-{\pi}^k{\left(\overrightarrow{x_i}\right)}^t\ast {\pi}^k{\left(\overrightarrow{x_j}\right)}^t\right) $$

(23)

Finally, co-association matrix 1) of all fuzzy base-clustering of ensemble Π (β base-clusterings) with using Eq. (23) is constructed as Eq. (24) and 2) of the β^′ selected fuzzy base-clusterings of ensemble Π (not all β base-clusterings), which is named extended fuzzy co-association matrix (EFCo) is formed as Eq. (25).

$$ {FCo}_{i,j}^{\varPi\ (x)}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.{\sum}_{k=1}^{\beta}\left[1-{\prod}_{t=1}^{n^k}\left(1-{\pi}^k{\left(\overrightarrow{x_i}\right)}^t\ast {\pi}^k{\left(\overrightarrow{x_j}\right)}^t\right)\right] $$

(24)

$$ {EFCo}_{i,j}^{\pi_{\boldsymbol{sel}}(x)}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\beta}^{\prime }$}\right.{\sum}_{k=1}^{\beta^{\prime }}\left[1-{\prod}_{t=1}^{n^k}\left(1-{\pi}^k{\left(\overrightarrow{x_i}\right)}^t\ast {\pi}^k{\left(\overrightarrow{x_j}\right)}^t\right)\right] $$

(25)

where $\overrightarrow{x_i}$ and $\overrightarrow{x_j}$ are the data-objects.

• Example 5 (Continuation of example 4). The EFCo corresponds to selected base-clustering π⁶, π⁷and π⁸ from fuzzy clustering ensemble in Table 2 was computed according to Eq. (25) and its value is shown in Table 6, e.g.

Table 6 The EFCo matrix corresponds to selected base-clustering π⁶, π⁷ and π⁸ from fuzzy clustering ensemble in Table 2

$\raisebox{1ex}{$ EFCo\ \left(\overrightarrow{x_i},\overrightarrow{x_2}\right)=1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\ast \left(\left[1-\left(1-{\pi}^6{\left(\overrightarrow{x_i}\right)}^1\ast {\pi}^6{\left(\overrightarrow{x_2}\right)}^1\right)\ast \left(1-{\pi}^6{\left(\overrightarrow{x_i}\right)}^2\ast {\pi}^6{\left(\overrightarrow{x_2}\right)}^2\right)\right]+\left[1-\left(1-{\pi}^7{\left(\overrightarrow{x_i}\right)}^1\ast {\pi}^7{\left(\overrightarrow{x_2}\right)}^1\right)\ast \left(1-{\pi}^7{\left(\overrightarrow{x_i}\right)}^2\ast {\pi}^7{\left(\overrightarrow{x_2}\right)}^2\right)\right]\left[1-\left(1-{\pi}^8{\left(\overrightarrow{x_i}\right)}^1\ast {\pi}^8{\left(\overrightarrow{x_2}\right)}^1\right)\ast \left(1-{\pi}^8{\left(\overrightarrow{x_i}\right)}^2\ast {\pi}^8{\left(\overrightarrow{x_2}\right)}^2\right)\right]\right)=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\ast \left(\left[1-\left(1-1\ast 1\right)\ast \left(1-0\ast 0\right)\right]+\left[1-\left(1-1\ast 1\right)\ast \left(1-0\ast 0\right)\right]\left[1-\left(1-1\ast 1\right)\ast \left(1-0\ast 0\right)\right]\right)$=1.

3.7 The consensus functions

As can be seen in Fig. 1, in the last step, we must derive final clustering. To obtain final clustering from base-clusterings Π according to the diversity-quality selection method in the ensemble, at first selection process must be executed to select the diverse base-clusterings with acceptable quality (Q), then two ways are used to construct final clustering: 1- by EAFC methods (Section 3.7.1) and 2- by a new consensus function (graph based partitioning algorithm). We propose it in Section 3.7.2. All used notations in this paper are depicted in Table 7.

Table 7 Summary of notation

3.7.1 EAFC methods

First we select diverse and high-quality base-clusterings based on selection process, secondly the selected base-clusterings are transformed into an extended fuzzy co-association matrix. Each entry in the co-association matrix EFCo corresponds to summarized similarities between two data-objects in the ensemble. Hence, the co-association matrix is considered as similarity matrix and by applying a single traditional clustering algorithm such as hierarchical clustering it can be clustered. Because in the experiment section we need to compare the selection strategy versus consolidating without selection, we divide EAFC method into some types as follows:

• (1) Derive finale clustering based on selection: The extended fuzzy co-association clustering ensemble matrix (EFCo) is obtained according Eq. (25). Then, matrix EFCo is treated as the similarity matrix of data. Finally, one of the single traditional algorithms such as K-Means, FCM or hierarchical clustering algorithm is applied as consensus function over the EFCo matrix to obtain the final clustering. Here, hierarchical clustering CL (Complete Linkage) is applied as the consensus function for comparison in experimental process. The flow of this algorithm is path 2 in Fig. 1. This algorithm is named DQEAFC (Diversity-Quality based EAFC) and is presented in Algorithm 2 in detail. In this algorithm Π is the base-clustering ensemble and K is the number of clusters in the final clustering.

• (2) Derive finale clustering based on all base-clustering: This algorithm is similar to DQEAFC (Algorithm 2), in that the selection process is omitted; all base-clusterings participate in the fuzzy co-association matrix construction. Then co-association matrix is calculated by using Eq. (24). The flow of this algorithm is path 1 in Fig. 1. This algorithm is named EAFC and is shown in Algorithm 3.

3.7.2 Fuzzy cluster-based graph partitioning clustering algorithm

In this section, we propose a consensus function, which is named FCBGP (fuzzy cluster-based graph partitioning), with the ability of producing fuzzy clusters. After selection of diverse and high-quality base-clusterings (by selection process), first we construct weighted graph for the fuzzy clusters of selected base-clusterings, then this graph is partitioned by a graph portioning algorithm. We present this graph as G_clusters(π_sel) = (V(π_sel), E(π_sel)), where π_sel is the selected base-clusterings by selection process, all clusters in π_sel are considered as the graph nodes V(π_sel) and E(π_sel) is the weight of the edges. For the given two clusters v_t ϵ πⁱ and v_lϵ π^j, where πⁱϵπ_sel and π^jϵ π_sel, the weighted edge between v_t and v_l is E(v_t, v_l). (E(v_t, v_l) is an edge which connects two clusters v_t and v_l).

$$ E\left({v}_t,{v}_l\right)= sim\left({C}_{t,}^i{C}_l^j\right) $$

(26)

where $sim\left({C}_{t,}^i{C}_l^j\right)$ is the similarity between two fuzzy clusters v_t and v_l, which is computed according to Eq. (17).

After constructing the weighted graph, it is partitioned by using graph partitioning techniques like METIS [80] into K partitions, where K is the number of clusters in the final clustering (we denote these partitions as π^p∗). π^p∗ is a partition that contains K clusters (we denote the q-th partition of partitioning π^p∗ as part_q) . Indeed each partition part_q contains |part_q| fuzzy-base-clusters. We consider ${C}_q^{p\ast }$ as a cluster corresponding to part_q in which (${C}_q^{p\ast }$) contains the data-objects belonging to base-fuzzy-clusters in part_q, and represent this cluster as ${C}_q^{p\ast }$. At the end the membership-degree of each data-object to each cluster ${C}_q^{p\ast }$ is computed based on a min, max or sum belonging to membership-scheme. Algorithm FCGP is detailed in Algorithm 4. The flow of this algorithm is path 3 in Fig. 1.

• Example 6 (Continuation of example 4). With regard to Example 4, the selected base-clusterings are π⁶, π⁷and π⁸ (π_sel = {π⁶, π⁷, π⁸ }) and all clusters in π_sel are $\left\{{C}_1^6,{C}_2^6,{C}_1^7,{C}_2^7,{C}_1^8,{C}_2^8\right\}$. The weighted graph for these fuzzy clusters (G_clusters(π_sel)) was computed according to Eq. (26) and is shown in Fig. 2. The partitioning obtained by π^p∗ = METIS (G_clusters(π_sel), 2)  (the number of final clusters is 2) is: π^p∗ = {part₁, part₂} where ${part}_1=\left\{{C}_2^6,{C}_2^7,{C}_2^8\right\} and\ {part}_2=\left\{{C}_1^6,{C}_1^7,{C}_1^8\right\}$and the final clustering by using FCGP with max membership scheme after normalization is shown in Table 8; e.g. ${\pi}^{\ast }{\left(\overrightarrow{x_1}\right)}^1=\max \left({\pi}^6{\left(\overrightarrow{x_5}\right)}^2,{\pi}^7{\left(\overrightarrow{x_5}\right)}^2,{\pi}^8{\left(\overrightarrow{x_5}\right)}^2\right)\Big)=\max \left(0.0,0.1,0.0\right)=1.0$ and ${\pi}^{\ast }{\left(\overrightarrow{x_5}\right)}^1=\max \left({\pi}^6{\left(\overrightarrow{x_5}\right)}^2,{\pi}^7{\left(\overrightarrow{x_5}\right)}^2,{\pi}^8{\left(\overrightarrow{x_5}\right)}^2\right)\Big)=\max \left(1.0,0.0,0.0\right)=1.0$. after normalization: ${\pi}^{\ast }{\left(\overrightarrow{x_5}\right)}^1=\frac{1.0}{1.0+1.0}=0.50$${\pi}^{\ast }{\left(\overrightarrow{x_5}\right)}^2=\frac{1.0}{1.0+1.0}=0.5$.

Fig. 2

G_clusters of selected clusters $\left\{{C}_1^6,{C}_2^6,{C}_1^7,{C}_2^7,{C}_1^8,{C}_2^8\right\}$

Table 8 Final fuzzy clustering (π^∗) of fuzzy base-clusterings in Table 2 obtained by FCBGP

3.7.3 Time complexity analysis

We denoted c is the number of all clusters in the base-clusterings, K is the number of final clusters, t is the number of K-means iterations, M is the number of data-objects and the K_BC is the number of base-clustering clusters. We supposed the number of selected base-clustering by elitism process is (β^′ (β^′ < β ) and the number of clusters in β^′ base-clustering is c^′ (c^′ < c).

According to algorithm 1, the time complexity of selection process is $O(selection)=\mathrm{O}\left(M{c}^2+\raisebox{1ex}{${c}^2$}\!\left/ \!\raisebox{-1ex}{$4$}\right.+\beta t{K}_{BC}+\raisebox{1ex}{${\left({\beta}^{\prime}\right)}^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+{K}_{BC}+{\beta}^{\prime}\right)$ refers to line 5 (quality (Q) calculation; because the FNMI values were computed in line 2, they are not computed in line 5) and K_BC refers to line 6 .

According to algorithm 2, the time complexity of DQEAFC algorithm is O(selection) + O(c^′M²) + O(MKt or MlogM), the term O(selection) corresponds to line 1(the time complexity of selection process), O(c^′M²) corresponds to line 2 for computing EFCo matrix. Term O(MKt or MlogM corresponds to line 3; if K-means is used as consensus function term O(MKt) is added else the term O(M² ) is added as hierarchical clustering algorithm.

According to algorithm 3, the time complexity of FCBGP is O(selection) + O(c^′2 + c^′2 + MK|part_q| + MK), where the term O(selection) corresponds to line 1(the time complexity of selection process), term c^′2 corresponds to forming graph (line 2); because the similarity computation between clustering graph is done in selection process, we ignore it here. The second term c^′2 corresponds to METIS algorithm in worst case (line 3), MK|part_q| corresponds to computing data-objects membership to final clusters (lines 4 and 5) and term MK corresponds to membership matrix normalization (line 6) where |part_q| is the number of base-clusters in the partition part_q.

In reality, since the size of datasets grows rapidly, the majority term in algorithm 2 is O(c^′M²) and in algorithm 3 is O(Mc²) provided that M ≫ c and M ≫ k, it can be deduced that FCBGP is efficient compared to other algorithms and is appropriate for large datasets.

4 Experiments

The fuzzy ensemble clustering approach presented in this study is written in Matlab. It is evaluated on several datasets. The goal of the evaluation study is to answer the following questions: (1) Is final clustering discovered through the selected base-clusterings with the proposed selection strategy better (in terms of quality criteria such as NMI and RI) if compared to the final clustering derived through all base-clusterings (no selection strategy)? Furthermore, (2) Is the proposed approach competitive to several state-of-art fuzzy ensemble clustering algorithms (with respect to RI and AC criteria of derived final clustering)? (3) How does changing the input parameters of the proposed approach influence the performance of the final clustering? (sensitivity analysis).

All experiments are run in Matlab R2014a 64-bit environment on a Windows Server 2008 64-bit, Intel Xeon CPU E5–2609(2.5 GHz 2.5 GHz) 2 processors and 16 GB of RAM workstation.

4.1 Base-clusterings

To evaluate the performance of the proposed fuzzy cluster ensemble approach, 9 data sets are selected from UCI Machine Learning Data repository [81] and dataset Glass from KEEL-dataset repository [82]. The description of these datasets is shown in Table 9.

Table 9 Overview of used datasets

To evaluate the performance of the proposed approaches and the compared algorithms on the same base-clusterings of each dataset, we construct a pool of base-clusterings by using the FCM and FCM–IDPSO [9] clustering algorithms at first (phase 1 in Fig. 1). In order to construct diverse base-clusterings, the FCM and FCM–IDPSO are run with different numbers of cluster. The number of clusters for FCM and FCM–IDPSO methods are randomly chosen from the interval $\left[2,\sqrt{M}\right]$, where M is the number of data-objects in the dataset under experiment.

The ensemble size for performance evaluation was considered as β = 200, k_BC valued 1 through 10. To rule out the occasional luck factor and provide a fair comparison, in this proposed approach, the state-of-the-art fuzzy cluster ensemble methods were assessed by their performance criteria over numerous runs (50 runs).

4.2 Experimental set-up

Our study aims at evaluating the performance of the proposed approach when it is applied to derive final clustering of the base-clusterings on several datasets.

4.2.1 Evaluation metrics

Three evaluation criteria AC, NMI and RI are applied here to assess the performance of clustering. We measure the AC, NMI and RI between the final clustering and the ground truth cluster labels (real data clustering; column four from Table 9) of each dataset. The accuracy (AC) provides a sound indication between final clustering and ground truths (the prior labeling information) of the examined dataset. The AC of final clustering π^∗ compared with ground truths labels π^′ is computed as: Each cluster is relabeled with the most similar cluster label in π^′. Then the AC of the new labels is measured by counting the number of correctly labeled data-objects (in comparison to their corresponding labels in the π^′), divided by the total number of data-objects (M) [83]. If m_iis the number of intersected data-objects in the cluster c_i ∈ π^∗ and the most similar cluster to it in π^′, the AC is calculated as

$$ AC\left({\pi}^{\ast },{\pi}^{\prime}\right)=\frac{\sum_{i=1}^{\pi^{\ast }}{m}_i}{M} $$

(27)

AC is in the range [0,1], if the AC value 1 of a clustering result denotes that all data-objects are clustered correctly. Larger values of AC indicate a better clustering result.

Other criterion used here is NMI [15], which is computed according to Eq. (7). For computing NMI(πⁱ, π^j) by Eq. (7), πⁱ is final clustering and π^j is ground truth of each dataset. NMI is in the range [0,1]; a larger value of NMI indicates a better clustering result.

RI criteria is a validity measure that considers the number of data-object pairs that are placed in the same and different clusters [84]. The RI of final clustering π^∗ compared with ground truths labels π^′ is computed as:

$$ RI\left({\pi}^{\ast },{\pi}^{\prime}\right)=\frac{m_{11}+{m}_{00}}{\left(\begin{array}{c}M\\ {}2\end{array}\right)} $$

(28)

where m₁₁ is the number of data-objects that are in the same cluster in π^∗ and in same cluster in π^′. Where m₀₀ is the number of data-objects that are in different clusters in π^∗ and in different clusters in π^′ (ground truth labels). Larger values of RI indicate a better clustering result.

4.2.2 Compared algorithms

In order to evaluate the influence of selection strategy on the final clustering performance four algorithm types need to be compared:

• (1) The FCo matrix of all base-clusterings according to Eq. (24) is constructed and the hierarchical CL (complete linkage) clustering algorithm is applied as consensus function (Algorithm 3), we call this algorithm EAFC (path 1 in Fig. 1).

• (2) We apply the selection strategy, then EFCo matrix is constructed by using Eq. (25), the final clustering is derived by applying the CL algorithm on it as consensus function. We named this algorithm DQEAFC (Algorithm 2; path 2 in Fig. 1).

• (3) We apply the selection strategy, then the final clustering is derived by using FCGP method with min, max and sum membership scheme; we call these algorithms as FCGP-min, FCGP-max and FCGP-sum (Algorithm 4; path 3 in Fig. 1).

• (4) Other fuzzy clustering ensemble methods, i.e. Berikov [41], DPC [37], FSCEOGA1 [39], ITK [44], sCSPA [43], IPC [37], FWLAC [52] and the crisp-clustering ensemble methods WEAC [69] and GPMGLA [69].

We design two comparison scenarios and a sensitivity analysis scenario in order to evaluate the performance of the final clustering derived by using the proposed selection strategy: (1) compare the DQEAFC algorithm (type 2) with EAFC algorithm (type 1); selection strategy versus no-selection (section 4.3.1). (2) compare the mentioned algorithms types 2 and 3 with other algorithms (type 4) (section 4.3.2). In both mentioned scenarios the algorithms were run 50 times. We calculate the mean of NMI and RI of the final clustering obtained by each algorithm, and consider them as comparison criteria. The number of final clusters in each dataset is the same as the number of pre-defined classes (ground truth) in each dataset. (3) at the end a scenario is done in order to evaluate the sensitivity of the proposed approach along the set-up of the input parameters (section 5.3.3).

In scenario 1, in order to statistically determine whether there is significant difference between the performance (in terms of NMI and RI) of the EAFC algorithm and DQEAFC algorithm, the Wilcoxon sign rank-test with a significance level of 5% will be used. But the Friedman test [85] is applied in scenario 2 with the goal of determining the significant difference among mean ranks of the proposed algorithms and state-of-the-art algorithms. All tests will be performed with a 5% significance level and the null hypothesis that the compared algorithms are the same. The Wilcoxon and Friedman tests are selected due to the fact that they are non-parametric tests; they do not consider any assumptions about data distribution.

4.3 Results and discussion

The analysis of the result with regard to the mentioned scenarios in section 4.2.2 is illustrated in the following.

4.3.1 Selection strategy analysis

Tables 10 and 11 report the measures of performance for the final clustering derived by the EAFC and DQRBEAFC algorithms in terms of NMI and RI respectively (the result of scenario 1 which is explained in section 4.2.2). The last row shows the average performance-term for each algorithm over all the datasets. The resulting P value of running the paired Wilcoxon test of NMI and RI between the EAFC and DQEAFC algorithms is 0.0020 and 0.0020, respectively; if the P value is less than 0.5 then there is a significant difference between the two compared algorithms. The results confirm that the final clustering derived by algorithms that use the proposed selection mechanism (type 2 algorithms) has better performance than the algorithm without selection process. Moreover, it was also better for the NMI and RI in all datasets.

Table 10 The NMI (%) resulted with and without using selection process

Table 11 The RI (%) result with and without using selection process

4.3.2 Comparison with state of the art algorithms

The result of the previous section confirmed that the selection strategy can achieve good performances. To confirm the usefulness of the selection strategy, we compare the NMI and RI of the final clustering derived by DQEAFC, FCGP-min, FCGP-max and FCGP-sum algorithms with a number of state-of-the-art ensemble clustering algorithms (scenario 2).

Tables 12 and 13 report the measures of performance for the final clustering derived by the DQRBEAFC, FCGP-min, FCGP-max, FCGP-sum and the type 4 algorithms in terms of NMI and RI respectively (the result of scenario 1 which was explained in section 4.2.2). The value in bold in the rows represents the best performance-term of each dataset yield by all the examined algorithms. The Friedman test is applied here to the results of Tables 12 and 13, and the test results in the Fig. 3 and Fig. 4 respectively.

Table 12 The NMI (%) resulted from different algorithms

Table 13 The RI (%) resulted from different algorithms

Fig. 3

The Friedman test result of Table 12

Fig. 4

The Friedman test result of Table 13

As can be seen in Fig. 3 and the null hypothesis, the mean rank of the NMI being equal in all algorithms is rejected, because p value is 4.00E-9, indicating that there exist significant differences among them. From Table 12 and Fig. 3, we can see that the proposed DQEAFC algorithm has the best performance on 4 datasets DS1, DS3 and DS9 out of a total of 10 datasets, additionally DQEAFC and FCGP-Max obtain the maximum value NMI on dataset DS7. This algorithm achieves the second best results on datasets DS2, DS4, DS5, DS8 and DS10 and on DS6 obtains the fourth best result. On mean ranks DQEAFC ranks first with a value of 12.05. For DS4, DS5, DS8 and DS10 the proposed FCGP_sum algorithm achieves the best performance. FCGP_sum ranks third with a mean rank value of 10.08. Also, the proposed algorithm FCGP-max outperforms other algorithms on datasets DS2 and DS6 in addition to DS7, and ranks second with a value of 10.95. Among the proposed algorithm FCGP_min ranks fourth. Among the state-of-the-art clustering ensemble methods FSCEOGA1 has the best mean rank with the value of 6.70. It is worth noting that neither of these algorithms can achieve good NMI on Bupa and Pima dataset. One reason may lie in the role of single-clustering algorithm in the underlying structure of the datasets.

Figure 4 shows that the null hypothesis is rejected. In other words, there is a significant difference among the performances of all algorithms in the term RI, because p value is 8.250e-09. Concerning Table 13 the proposed FCGP-sum algorithm achieves the best RI results on DS3, DS4, DS8 and DS10 datasets. The proposed DQEAFC algorithm has the best performance on three datasets DS1, DS6 and DS7. Also, the proposed algorithm FCGP-max outperforms other algorithms on datasets DS2, DS5 and DS9. It is clear in Fig. 4 that: on mean rank, the DQEAFC ranks the first with a value of 10.65, FCGP_MAX ranks the second with a value of 10.50, FCGP_sum ranks the third with a value of 10.30 and FWLAC with the value of 9.50 proceeds them, the proposed algorithm FCGP_min ranks the fifth with 8.50. It is clear that among state-of-the-art clustering ensemble methods, FWLAC ranks the first, IPC ranks second with a value of 7.20, FSCEOGA1 ranks third with 6.60, WEAC ranks fourth, sCSPA ranks fifth, ITK ranks the sixth, DPC ranks the seventh, DPC ranks the eighth and the Berikov algorithm is ranked last.

By focusing the analysis on the fuzzy clustering ensemble algorithms, we can see that final clustering derived by the proposed algorithms has the desired quality (compared to other methods). Results on RI and NMI show that the selection strategy almost improves the quality of the final clustering. In addition to the selection strategy, consensus function has a great influence on the final clustering.

4.3.3 Sensitivity analysis

The input parameters of the proposed approach are shown in Table 14. Due to comparison of the final clustering with ground truths labels of each dataset we fix the K as the predefined number of the classes and evaluate the sensitivity of the proposed algorithms on 4 datasets Wine, Glass, Vehicle and IS, with consider 2 scenarios as follows:

Table 14 The input parameters of proposed approach

• 1) We let ensemble size β = 200 and measure the AC of the final clustering derived by proposed algorithms by varying the number of base-clustering-cluster k_Bc between 2 and 9 on the 4 datasets and depicted them in Fig. 5a-d. The horizontal axis represents the k_Bc, and the vertical axis is the performance in terms of Accuracy (AC) values between the final clustering and the ground truth cluster labels. With regard to these Figs:

  There is gradual change in the performance (AC criterion) of DQEAFC and FCGP_sum on dataset Wine when k_Bc varies from 2 to 8, after k_Bc = 8 their performances decrease dramatically. The performance of FCGP-min and FCGP_max increases rapidly by varying k_Bc between 2, 3 and 4, their performance approximately reaches the performance of DQEAFC and FCGP_sum when k_Bc is in the range [5, 6], after k_Bc = 6 a rapid decrease in their performances can be seen. On dataset Glass the variation of performance of FCGP-sum and FCGP_min is more tangible in contrast to other algorithms and these algorithms have better performance than others. On dataset Vehicle: performance of DQEAFC deceases suddenly then increases to achieve a high value of performance. Although FCGP_sum changes smoothly, DQEAFC has a higher performance than others on this dataset. There are tangible changes in the performance of FCGP-sum and FCGP_max on dataset IS, the performances of these are greater than other algorithms’ performances. Performance of DQEAFC changes smoothly when k_Bc changes, although there is a jump in the performance of FCGP-min at k_Bc = 4 and after that it changes gradually, but it is very low in contrast to other algorithms. Overall, DQEAFC achieves maximum performance when k_Bc is in the interval [3, 6] and maximum performance of other algorithms is achieved when k_Bc is in the interval [4, 6]; the performance of DQEAFC changes smoothly, FCGP_max and FCGP_um change sharply by varying k_Bc but have higher performance than others. It is obvious that performance of the algorithms changes with k_Bc variations, indeed by tuning the k_Bc the diversity and quality of selected base-clusterings is adjusted with respect to consensus function.

• 2) We compute AC of proposed methods on the 4 datasets by varying ensemble size β between 40, 100, 200 and 300, and report them in Fig. 6a-d. The horizontal axis represents the ensemble size, and the vertical axis is the AC values between the final clustering and the ground truth cluster labels. According to Fig. 6a-d:

Fig. 5

Effect of the numbers of base-clustering-cluster (k_Bc) on the performance of the proposed algorithms

Fig. 6

Effect of ensemble size (β) on the performance of the proposed algorithms

Although on Wine dataset DQEAFC and FCGP_sum improved smoothly by increasing ensemble size, they are approximately robust to β variation. A great improvement can be seen in the performance of FCGP_max and FCGP_MIN then after this FCGP_max has a steady state but the performance of FCGP_min decreases; the sensitivity of FCGP_min by varying β is more than other algorithms. The performance of all algorithms improved by increasing β although the improvement of FCGP_sum is more significant, and the performance of DQEAFC increases gradually. All proposed algorithms are robust to β increasing on dataset Vehicle. On dataset IS: the performance of FCGP_MIN is less than other algorithms and its minimum performance is at β = 200, minimum performance of other algorithms occurred at β = 100. After β = 100 the performance of all algorithms except FCGP_min is increased, although the performance of FCGP_sum increased slightly.

To sum up, DQEAFC is the most robust to β variation and the improvements of FCGP_sum are more significant than other algorithms. The performance variation of all algorithms except FCGP_min by varying β between 100, 200 and 300 is little; except the FCGP_min the other algorithms are robust for variation in ensemble size.

4.4 Real-world application

Process mining application in [66] can be done by our proposed method, especially for traces with high perspective (profiles). In this application each profile can be clustered (by single traditional clustering algorithms) without considering other views and finally combining this generated clustering will be done by the ensemble clustering technique. For detecting analysis of gene expression profiles, where gene-expression data can contain many thousands of variables (features), the proposed method can be used. Resampling and subspace methods can be used to generate multiple sets (views) of gene data then an ensemble of base-clusterings is generated by single traditional clustering algorithms, and applying the proposed method the final robust clustering will be obtained. Satellite image segmentation can be used in some domains such as forest monitoring, remote sensing [86], monitoring marine environment (a pixel corresponds to an area of the land space, which may not necessarily belong to a single type of land cover), is another application of the proposed approach. The captured image is clustered by multiple single traditional clustering algorithms to form a pool of clustering, finally a segmentation of image (final clustering) is obtained. For most engineering design optimization problems (especially mechanical simulation), finding the global optimum due to the unaffordable computational cost is difficult (or even impossible) [87]. Then clustering technique can reduce the space of the problem. But to ensure accuracy of the generated model of reduced space is improved, an ensemble of reduced space (via clustering) is formed to obtain meta-model. Distributed clustering where data sets are stored in different sites is one of the applications of ensemble clustering [10]. In this case database records (rows) or database features (columns) can be distributed across multiple sites (or peers in the peer-to-peer networks). Then the data of each site can be clustered at each solely; an ensemble of clustering is formed. Finally, the proposed method will be applied to generate final clustering. Text detection in video can be considered one of the applications. Firstly, β (ensemble size) frame of the video is extracted. Each frame is divided into M blocks. Then each frame of blocks is clustered solely (β base-clusterings is generated). Finally, the proposed methods will be used to obtain final clustering.

5 Conclusion and future work

In this paper, a novel elite fuzzy clustering ensemble framework based on new fuzzy diversity measure and a fuzzy-clustering quality measure has been proposed. Diversity of fuzzy clustering is computed based on fuzzy NMI criterion (FNMI). The base-clusterings in the ensemble are clustered based on the diversity criterion and the quality of each base-clustering-cluster is computed. Then a selective strategy has been taken to choose the diverse and high-quality fuzzy base-clusterings (based on FDiv and Q). The final clustering is obtained: 1) by new efficient consensus function (FCBGP) or 2) after extraction of the extended co-association matrix from the ensemble, a single clustering algorithm is applied on the matrix (DQEAFC consensus function). The experimental results on ten datasets confirm the quality improvement in comparison to other fuzzy clustering ensemble methods. Dealing with the influence of reliability on the fuzzy clustering ensemble can be considered as an issue in future works. Also, for future works, we can investigate the effect of different clustering algorithm used for partitioning base-clusterings on the performance of final clustering. Examination of different sampling mechanisms on the performance of the proposed method could be considered as yet another issue. We shall also investigate the influence of different fuzzy cluster similarity measures on the proposed framework. The influence of applying different consensus functions on the selected base-clustering can be investigated in the future works, too.