Abstract
Dental X-ray image segmentation has an important role in practical dentistry and is widely used in the discovery of odontological diseases, tooth archeology and in automated dental identification systems. Enhancing the accuracy of dental segmentation is the main focus of researchers, involving various machine learning methods to be applied in order to gain the best performance. However, most of the currently used methods are facing problems of threshold, curve functions, choosing suitable parameters and detecting common boundaries among clusters. In this paper, we will present a new semi-supervised fuzzy clustering algorithm named as SSFC-FS based on Interactive Fuzzy Satisficing for the dental X-ray image segmentation problem. Firstly, features of a dental X-Ray image are modeled into a spatial objective function, which are then to be integrated into a new semi-supervised fuzzy clustering model. Secondly, the Interactive Fuzzy Satisficing method, which is considered as a useful tool to solve linear and nonlinear multi-objective problems in mixed fuzzy-stochastic environment, is applied to get the cluster centers and the membership matrix of the model. Thirdly, theoretically validation of the solutions including the convergence rate, bounds of parameters, and the comparison with solutions of other relevant methods is performed. Lastly, a new semi-supervised fuzzy clustering algorithm that uses an iterative strategy from the formulae of solutions is designed. This new algorithm was experimentally validated and compared with the relevant ones in terms of clustering quality on a real dataset including 56 dental X-ray images in the period 2014–2015 of Hanoi Medial University, Vietnam. The results revealed that the new algorithm has better clustering quality than other methods such as Fuzzy C-Means, Otsu, eSFCM, SSCMOO, FMMBIS and another version of SSFC-FS with the local Lagrange method named SSFC-SC. We also suggest the most appropriate values of parameters for the new algorithm.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
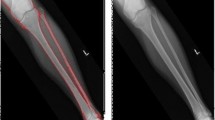
One of the most interesting topics in medical science, especially practical dentistry, is the segmentation problem from a dental X-Ray image. This kind of segmentation was used to assist the discovery of odontological diseases such as dental caries, diseases of pulp and periapical tissues, gingivitis and periodontal diseases, dentofacial anomalies, and dental age prediction. It was also applied to tooth archeology and automated dental identification systems [31] for examining surgery corpses from complicated criminal cases. Because of the special structure and composition, tooth cannot be easily destroyed even in severe conditions such as bombing, blasts, water falling, etc. Thus, it brings valuable information to those analyses, and is of great interests to researchers and practicians of how such the information can be discovered from an image without much experience of experts [27]. This demand relates to the so-called accuracy of dental segmentation, which requires various machine learning methods to be applied in order to gain the best performance [8–13, 15]. Figure 1 shows the result of dental segmentation where the blue cluster in the segmented image may correspond to a dental disease that needs special treatments from clinicians. The more accurate the segmentation the more efficiently patients could receive medical treatment.
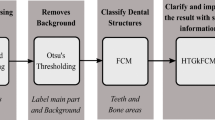
There are many different techniques used in dental X-ray image segmentation, which can be divided into some strategies [5, 20, 30]: i) applying image processing techniques such as thresholding methods, the boundary-based and the region-based methods; ii) applying clustering methods such as Fuzzy C-Means (FCM). The first strategy either transforms a dental image to the binary representation through a threshold or uses a pre-defined complex curve to approximate regions. A typical algorithm belonging to this strategy is Otsu [26]. However, a drawback of this group is how to define the threshold and the curve, which are quite important to determine main part pixels especially in noise images [38]. On the other hand, the second strategy utilizes clustering, e.g. Fuzzy C-Means (FCM) [3] to specify clusters without prior information of the threshold and the curve. But again, it meets challenges in choosing parameters and detecting common boundaries among clusters [4, 21, 22, 33]. This raises the motivation of improving these methods, especially the clustering approach, in order to achieve better performance of segmentation.
An observation in [2, 39] revealed that if additional information is attached to clustering process then the clustering quality is enhanced. This is called the semi-supervised fuzzy clustering where additional information represented in one of the three types: must-link and cannot link constraints, class labels, and pre-defined membership matrix is used to orient the clustering. For example, if we know that a region represented by several pixels definitely corresponds to gingivitis then those pixels are marked by the class label. Other pixels in the dental image are classified with the support of known pixels; thus making the segmentation more accurate. In fuzzy clustering, the pre-defined membership matrix is often opted to be the additional information. For this kind of information, the most efficient semi-supervised fuzzy clustering algorithm is Semi-supervised Entropy regularized Fuzzy Clustering algorithm (eSFCM) [40], which integrates prior membership matrix \(\overline {u_{kj}} \) into objective function of the semi-supervised clustering algorithm.
Our idea in this research is to design a new semi-supervised fuzzy clustering model for the dental X-ray image segmentation problem. This model takes into account the prior membership matrix of eSFCM and provides a new part regarding dental structures in the objective function. The new objective function consists of three parts: the standard part of FCM, the spatial information part, and the additional information represented by the prior membership matrix. It, equipped with constraints, forms a multi-objective optimization problem. In order to solve the problem, we will utilized the ideas of Interactive Fuzzy Satisficing method [19, 23, 32] which is considered a useful tool to solve linear and nonlinear multi-objective problems in mixed fuzzy-stochastic environment wherein various kinds of uncertainties related to fuzziness and/or randomness are presented [6]. The outputs of this process are cluster centers and a membership matrix. A novel semi-supervised fuzzy clustering algorithm, which is in essence an iterative method to optimize the cluster centers and the membership matrix, is presented and evaluated on the real dental X-ray image set with respect to the clustering quality. The new clustering algorithm can be regarded as a new and efficient tool for dental X-Ray image segmentation.
From this perspective, our contributions in this paper are summarized as follows.
-
a)
Modeling dental structures or features of a dental X-Ray image into a spatial objective function;
-
b)
Design a new semi-supervised fuzzy clustering model including the objective function and constraints for the dental X-ray image segmentation;
-
c)
Solve the model by Interactive Fuzzy Satisficing method to get the cluster centers and the membership matrix;
-
d)
Theoretically examine the convergence rate, bounds of parameters, and the comparison with solutions of other relevant methods;
-
e)
Propose a new semi-supervised fuzzy clustering algorithm that segments a dental X-Ray image by the formulae of cluster centers and membership matrix above;
-
f)
Evaluate and compare the new algorithm with the relevant ones in terms of clustering quality on a real dataset including 56 dental X-ray images in the period 2014–2015 of Hanoi Medial University, Vietnam. Suggest the most appropriate values of parameters for the new algorithm.
The rests of this paper are organized as follow: Section 2 gives the background knowledge regarding literature review and the Interactive Fuzzy Satisficing method. Section 3 presents the main contributions of the paper. Section 4 shows the validation of the new algorithm by experimental simulation. Finally, Section 5 gives conclusions and highlight further works.
2 Preliminary
In this section, we firstly present details of two typical relevant methods namely Otsu and Fuzzy C-Means (FCM) as well as the most efficient semi-supervised fuzzy clustering algorithm – eSFCM in Section 2.1. A summary of the Interactive Fuzzy Satisficing method is given in Section 2.2.
2.1 Literature review
In the previous section, we have mentioned two approaches for the dental X-Ray image segmentation. Regarding the first one, the most typical method namely Otsu [26] recursively divides an image into two separate regions according to a threshold value. Descriptions of Otsu are shown in Table 1. Similarly, Table 2 shows the descriptions of FCM [3] which in essence is an iterative algorithm to calculate cluster centers and a membership matrix until stopping conditions are met.
However, those algorithms have drawbacks regarding the selection of the threshold value, choosing parameters and detecting common boundaries among clusters [12, 13, 15–17, 20, 22, 24, 25, 29, 34–36, 38, 41, 42]. Thus, semi-supervised fuzzy clustering especially the eSFCM algorithm [40] can be regarded as an alternative method to handle these limitations. Table 3 shows the steps of this algorithm. However, this algorithm does not contain any information about spatial structures of an X-ray image and thus must be improved if applying to the dental X-Ray image segmentation problem.
2.2 The interactive fuzzy satisficing method
The Interactive Fuzzy Satisficing method was applied to many programming problems such as: linear programming [19], stochastic linear programming [28] and mixed fuzzy-stochastic programming [19]. In those problems, multi-objective objective functions are considered. The basic idea of Interactive Fuzzy Satisficing method is: Firstly, separate each part of the multi-objective function and solve these isolated prolems via a suitable method. After that, based on the solutions of the subproblems, build fuzzy satisficing functions for each subproblem. Lastly, fomulate these isolated functions into a combination fuzzy satisficing function and solve the original problem by using an iterative scheme. In the case of linear programming problems, consider a multi-objective function formed as follows.
With x∈R n satisfying
To understand the interactive fuzzy satisficing schema, we have some definitions.
Definition 1 ([19]: (Fuzzy satisficing function))
In a feasible region X, for each objective function z i , i = 1,...p, the fuzzy satisficing function is defined as:
Where \(\underline {z}_{i} ,\bar {{z}}_{i} ,i=1,...p\) are maximum and minimum values of z i in X.
Definition 2 ([19]: (Pareto optimal solution))
In a feasible region X, a point x* ∈X is said to be a M-Pareto optimal solution if and only if there does not exist another solution x ∈X such that μ i (x) ≤ μ i (x∗) for all i = 1,..., p and μ j (x)≠μ j (x∗) for at least one \(j\in \left \{ {1,...,p} \right \}\).
The interactive fuzzy satisficing method consists of two parts: initialization and iteration as below:
-
Initialization
-
Solve subproblems below:
$$ \min z_{i} (x),i=1,...,p, $$(4)satisfying constraints in (2). Suppose that we get optimal solutions x 1,..., x p corresponding.
-
Compute values of objective functions z i , i = 1,...p at p solutions and create a pay-off table. After that, determine lower and upper bounds of z i . Denote that:
$$\begin{array}{@{}rcl@{}} \bar{{z}}_{i} &=&\max \left\{ {z_{i} \left({x^{j}} \right),j=1,...,p} \right\};\underline{z}_{i} \\ &=&\min \left\{ {z_{i} \left({x^{j}} \right),j=1,...,p} \right\},i=1,...,p. \end{array} $$(5) -
Define fuzzy satisficing functions for each objective z i , i = 1,...p by fomula:
$$ \mu_{i} (z_{i} )=\frac{z_{i} -\underline{z}_{i}} {\bar{{z}}_{i} -\underline{z}_{i}} ,i=1,...,p. $$(6) -
Set \(S_{p} =\left \{ {x^{1},...,x^{p}} \right \}\), \(r=1,a_{i}^{\left (r \right )} =\underline {z}_{i} \).
-
-
Iteration:
-
Step 1:
-
Build a combination fuzzy satisficing function:
$$ u=b_{1} \mu_{1} (z_{1} )+b_{2} \mu_{2} (z_{2} )+...+b_{p} \mu_{p} (z_{p} ). $$(7)Randomly selected b 1,..., b p satisfying:
$$ b_{1} +b_{2} +b_{3} =1, 0\le b_{1} ,b_{2} ,b_{3} \le 1. $$(8) -
Solve the problem (7)–(8) with m constraints in (2) and p constraints in (9), we get optimal solutions x (r).
$$ z_{i} (x)\ge \underline{z}_{i} ,i=1,...,p. $$(9)
-
-
Step 2 :
-
If \(\mu _{\min } =\min \left \{ {\mu _{i} (z_{i} ),i=1,...,p} \right \}>\theta \), with θ as a threshold then x (r) is not acceptable. Otherwise, if x (r)∉S p then put x (r)on S p .
-
In the case of needing to expand S p then set r = r + 1 and check these conditions:
If r > L 1 or after L 2 consecutive iterations that S p is not expanded (L 1, L 2 has optional values) then set \(a_{i}^{\left (r \right )} =\underline {z}_{i} ,i=1, 2, 3\) and get a randomly index h in {1, 2,..., p} to put \(a_{h}^{\left (r \right )} \in \left [ {\underline {z}_{h} ,\bar {{z}}_{h}} \right )\). Then return to Step 1.
-
In the case of not needing to expand S p then go to Step 3.
-
-
Step 3: End of process.
-
3 The proposed method
In this section, we present the main contributions of this paper including: i) Modeling dental structures of a dental X-Ray image into a spatial objective function; ii) Designing a new semi-supervised fuzzy clustering model for the dental X-ray image segmentation; iii) Proposing a semi-supervised fuzzy clustering algorithm based on the interactive fuzzy satisficing method; iv) Examining the convergence rate, bounds of parameters, and the comparison with solutions of other relevant methods; v) Elaborating advantages of the new method. Those parts are presented in sub-sections accordingly.
3.1 Modeling dental structures
Dental images are valuable for the analysis of broken lines and tumors. There are four main regions in a panoramic image such as teeth and alveolar blood area, upper jaw, lower jaw and Temporomandibular Joint syndrome (TMJ) that should be detected for further diagnoses. In what follows, we present 4 existing image features and equivalent extraction functions that are applied to dental X-Ray images. Lastly, the formulation of a spatial objective function for these features is given.
3.1.1 Entropy, edge-value and intensity feature
-
a)
Entropy: is used to measure the randomness level of achieved information within a certain extent and can be calculated by the formula below [14].
$$ r\left({x,y} \right)=-\sum\limits_{i=1}^{L} {p\left({z_{i}} \right)\log_{2} p\left({z_{i}} \right)} , $$(10)In which we have a random variable z, probability of i th pixel p(z i ), for all i = 1,2, ..., L and the number of pixels L).
$$ R\left({x,y} \right)=\frac{r\left({x,y} \right)}{\max \left\{ {r\left({x,y} \right)} \right\}}. $$(11) -
b)
Edge-value and intensity: these features measure the numbers of changes of pixel values in a region [14].
$$\begin{array}{@{}rcl@{}} e\left({x,y} \right)&=&\sum\limits_{p=-\left\lfloor {w/2} \right\rfloor}^{\left\lfloor {w/2} \right\rfloor} {\sum\limits_{q=-\left\lfloor {w/2} \right\rfloor}^{\left\lfloor {w/2} \right\rfloor} {b\left({x,y} \right)}} , \end{array} $$(12)$$\begin{array}{@{}rcl@{}} b\left({x,y} \right)&=&\left\{ {\begin{array}{ll} 1, & \quad \nabla f\left({x,y} \right)\ge T_{1} \\ 0, & \quad \nabla f\left({x,y} \right)<T_{1} \end{array}} \right., \end{array} $$(13)$$\begin{array}{@{}rcl@{}} \nabla f\left({x,y} \right)&=&\sqrt {\left({\frac{\partial g\left({x,y} \right)}{\partial x}} \right)^{2}+\left({\frac{\partial g\left({x,y} \right)}{\partial y}} \right)^{2}} , \end{array} $$(14)Where \(\nabla f\left ({x,y} \right )\) is the length of gradient vector \(f\left ({x,y} \right )\), \(b\left ({x,y} \right )\) is a binary image and \(e\left ({x,y} \right )\) is intensity of the X-ray image respectively. T 1 is a threshold. These features are normalized as:
$$\begin{array}{@{}rcl@{}} E\left({x,y} \right)&=&\frac{e\left({x,y} \right)}{\max \left\{ {e\left({x,y} \right)} \right\}}, \end{array} $$(15)$$\begin{array}{@{}rcl@{}} G\left({x,y} \right)&=&\frac{g\left({x,y} \right)}{\max \left\{ {g\left({x,y} \right)} \right\}}. \end{array} $$(16)
3.1.2 Local binary patterns - LBP
This feature is invariant to any light intensity transformation and ensures the order of pixel density in a given area. LBP [1] is determined under following steps:
-
1.
Select a 3 × 3 window template from a given central pixel.
-
2.
Compare its value with those of pixels in the window. If greater then mark as 1; otherwise mark as 0.
-
3.
Put all binary values from the top-left pixel to the end pixel by clock-wise direction into a 8-bit string. Convert it to decimal system.
$$ LBP\left({x_{c} ,y_{c}} \right)=\sum\limits_{n=0}^{7} {s\left({g_{n} -g_{c}} \right)2^{n}} , $$(17)$$ s(x)=\left\{ {\begin{array}{ll} 1 & \quad{x\ge 0} \\ 0 & \quad{\textit{otherwise}} \\ \end{array}} \right.. $$(18)Where g c is value of the central pixel (x c , y c ) and g n is value of n th pixel in the window.
3.1.3 Red-green-blue - RGB
This characterize for the color of an X-ray image according to Red-Green-Blue values. For a 24 bit image, the RGB feature [43] is computed as follows (N is the number of pixels).
There is another way to calculate the RGB feature that is isolating three matrices h R [], h G [] and h B [] with values being specified from the equivalent color band in the image.
3.1.4 Gradient feature
This feature is used to differentiate various teeth’s parts such as enamel, cementum, gum, root canal, etc [7]. The following steps calculate the Gradient value: Firstly, apply Gaussian filter to the X-ray image to reduce the background noises. Secondly, Difference of Gaussian (DoG) filter is applied to calculate gradient of the image according to x and y axes. Each pixel is characterized by a gradient vector. Lastly, get the normalization form of the gradient vector and receive a 2D vector for each pixel as follows.
where α is direction of the gradient vector. For instance, length and direction of a pixel are calculated as follows.
Where I(x,y) is a pixel vector, G(x,y,k) is a Gaussian function of the pixel vector, * is the convolution operation between x and y, θ 1 is a threshold.
3.1.5 Formulation of dental structure
The spatial objective function is formulated as in equations below.
Where
The aim of J 2a is to minimize the fuzzy distances of pixels in a cluster so that those pixels will have high similarity. Fuzzy distance R i k is defined as,
Where \(\tilde {{\alpha } }\in [0,1]\) is the controlling parameter. When \(\tilde {{\alpha } }=0\), the function (28) returns to the traditional Euclidean distance. x k is k th pixel, and v i is i th cluster center. The spatial information function SI i k is shown in (29).
Where u j i is the membership degree of data point X i to cluster j th. The distance d j k is the square Euclidean function between (x k , y k ) and (x j , y j ). The meaning of this function is to specify spatial information relationship of k th pixel to i th cluster since this value will be high if its color is similar to those of neighborhood and vice versa. The inverse function \(d_{jk}^{-1} \) is used to measure the similarity between two data points.
The aim of J 2b is to minimize the features stated in Sections 3.1.1– 3.1.4 for better separation of spatial clusters. l is the number of features and belongs to [1, 4]. In the case that we use all features, l = 4. w i is the normalized value of features,
Where p w i (i = 1,..,4) is the value of dental features stated in Sections 3.1.1 – 3.1.4.
It is obvious that the new spatial objective function in (25) combines the dental features and neighborhood information of a pixel.
3.2 A new semi-supervised fuzzy clustering model
In this section, we present a new semi-supervised fuzzy clustering model for dental X-Ray image segmentation problem. The model is given in equations below.
With the constraint:
It is obvious that in (31), the first part is the objective function of FCM [3]. It contains standard information of object function in fuzzy clustering.
The second and third parts are contained in the spatial objective function in (25). The last part relates to the semi-supervised fuzzy clustering model wherein additional information represented in prior membership matrix \(\overline u_{jk} \) is taken into the objective function.
According to [40], \(\overline u_{jk} \) satisfies the following constraint:
In the paper [40], the authors did not show any method to determine this kind of additional information. Thus, in order for better implementation, we propose a method to specify the prior membership matrix for dental X-Ray image segmentation as follows.
Where \(\alpha \in \left [ {0,1} \right ]\) is the expert’s knowledge with α = 0 implying that the additional value \(\overline u_{kj} \) is not necessary for the entire clustering process. u 1 is the final membership matrix taken from FCM on the same image. u 2 is calculated as follows.
w i is the normalized value of features given in (30).
It is clear that the problem in (31)–(32) is a multi-objective optimization problem. Therefore, it is better if we apply the Interactive Fuzzy Satisficing method for this problem.
3.3 The SSFC-FS algorithm
In this section, we propose a novel clustering algorithm namely Semi-Supervised Fuzzy Clustering algorithm with Spatial Constraints using Fuzzy Satisficing (SSFC-FS) to find optimal solutions including cluster centers and the membership matrix for the problem stated in (31)–(32). The new algorithm which is based on the Interactive Fuzzy Satisficing method is presented as follows.
Analysis the problem
In the previous section, we have defined the multi-objective function below.
Three single objectives are:
Applying the Weierstrass theorem for this problem, the existence of optimal solutions is described as in Lemma 1.
Lemma 1
The multi-objective optimization problem in (39)–(41) with the constraint in (32) has objective functions being continuous on a compact and not empty domain. Thus this problem has global optimal solutions that are continuous and bounded.
Based on Lemma 1 and the Interactive Fuzzy Satisficing method, we build a schema to find out the optimal solution of this problem as follow.
Finding optimal solutions:
Initialization:
Solve the following subproblems by Lagrange method:
- - Problem 1::
-
Min{ J 1(u)}, u∈R C×Nsatisfies (32)}. From this problem, we get the formulas of cluster centers and membership degree:
$$\begin{array}{@{}rcl@{}} V_{j} &=&\frac{\sum\limits_{k=1}^{N} {u_{jk}^{m} X_{k}} } {\sum\limits_{k=1}^{N} {u_{jk}^{m}} } , \end{array} $$(42)$$\begin{array}{@{}rcl@{}} u_{jk}^{1} &=&\left({\frac{-\lambda_{k}} {m\ast d_{jk}} } \right)^{\frac{1}{m-1}},\\ \lambda_{k}&=&\frac{1}{\left({\sum\limits_{j=1}^{C} {\left({\frac{1}{m\ast d_{jk}} } \right)^{\frac{1}{m-1}}}} \right)^{m-1}}, \end{array} $$(43)Where \(d_{kj} =\left \| {X_{k} -V_{j}} \right \|^{2}\), k = 1,…, N; j = 1,…, C. Rewrite objective function J 1 as:
$$ J_{1} =\sum\limits_{k=1}^{N} {\sum\limits_{j=1}^{C} {u_{jk}^{m}} d_{jk}}. $$(44) - - Problem 2::
-
Min {J 2 (u)}, u∈R C×Nsatisfies (32)}. Let \(\alpha _{jk} =R_{jk}^{2} +\frac {1}{l}\sum \limits _{i=1}^{l} {w_{ki}} \), k = 1,…, N; j = 1,…, C, we have:
$$ J_{2} =\sum\limits_{k=1}^{N} {\sum\limits_{j=1}^{C} {u_{jk}^{m}} \alpha_{jk}}. $$(45)The optimal solutions are shown as follows.
$$ u_{jk}^{2} =\left({\frac{-\beta_{k}} {m\ast \alpha_{jk}} } \right)^{\frac{1}{m-1}}, \quad\beta_{k} =\frac{1}{\left({\sum\limits_{j=1}^{C} {\left({\frac{1}{m\ast \alpha_{jk}} } \right)^{\frac{1}{m-1}}}} \right)^{m-1}}. $$(46) - - Problem 3::
-
Min {J 3 (u)}, u∈R C×Nsatisfies (32)}.It is easy to find out cluster centers.
$$ V_{j} =\frac{\sum\limits_{k=1}^{N} {\left| {u_{jk} -\bar{{u}}_{jk}} \right|^{m}X_{k}}} {\sum\limits_{k=1}^{N} {\left| {u_{jk} -\bar{{u}}_{jk}} \right|^{m}}} . $$(47)Objective function J 3 can be rewritten as,
$$ J_{3} =\sum\limits_{k=1}^{N} {\sum\limits_{j=1}^{C} {\left| {u_{jk} -\overline u_{jk}} \right|^{m}} d_{jk}}. $$(48)The optimal solution of this problem is \(u_{jk}^{3} \) which is computed by:
$$ u_{jk}^{3} \,=\,\left({\frac{-\gamma_{k}} {m\ast d_{jk}} } \right)^{\frac{1}{m-1}}+\bar{{u}}_{jk} ,\,\,\, \gamma_{k} \,=\,\left({\frac{1-\bar{{u}}_{jk}} {\sum\limits_{j=1}^{C} {\frac{1}{\left({m\ast d_{jk}} \right)^{\frac{1}{m-1}}}}} } \right)^{m-1}\!. $$(49)From obtained optimal solutions of isolated problems, values of objective functions at these solutions are given in pay-off table (Table 4).
Denote that:
Iterative steps:
- Step 1::
-
Fuzzy satisficing functions for each of subproblems are defined by,
$$ \mu_{1} (J_{1} )=\frac{J_{1} -\underline{z}_{1}} {\overline z_{1} -\underline{z}_{1}} ; \mu_{2} (J_{2} )=\frac{J_{2} -\underline{z}_{2}} {\overline z_{2} -\underline{z}_{2}} ; \mu_{3} (J_{3} )=\frac{J_{3} -\underline{z}_{3}} {\overline z_{3} -\underline{z}_{3}} . $$(54)Based on these functions, we have the combination satisficing function:
$$ Y=b_{1} \mu_{1} (J_{1} )+b_{2} \mu_{2} (J_{2} )+b_{3} \mu_{3} (J_{3} )\to \min , $$(55)Where,
$$ b_{1} +b_{2} +b_{3} =1 \text{ and } 0\le b_{1} ,b_{2} ,b_{3} \le 1. $$(56)Then we solve the optimal problem with the objective function as in (55) and the constraints including original constraints (32) and additional constraints below.
$$ J_{i} (x)\ge a_{i}^{(r)} ,i=1, 2, 3.. $$(57)The objective function of this problem can be clearly written as,
$$\begin{array}{@{}rcl@{}} Y&=&\frac{b_{1}} {\overline z_{1} -\underline{z}_{1}} J_{1} +\frac{b_{2}} {\overline z_{2} -\underline{z}_{2}} J_{2} +\frac{b_{3}} {\overline z_{3} -\underline{z}_{3}} J_{3}\\ &&-\left({\frac{b_{1} \underline{z}_{1}} {\overline z_{1} -\underline{z}_{1}} +\frac{b_{2} \underline{z}_{2}} {\overline z_{2} -\underline{z}_{2}} +\frac{b_{3} \underline{z}_{3}} {\overline z_{3} -\underline{z}_{3}} } \right). \end{array} $$(58)Taking the derivative of (58), we obtain
$$\begin{array}{@{}rcl@{}} \frac{\partial Y}{\partial u_{jk}} &=&\frac{b_{1}} {\overline z_{1} -\underline{z}_{1}} \frac{\partial J_{1}} {\partial u_{jk}} +\frac{b_{2}} {\overline z_{2} -\underline{z}_{2}} \frac{\partial J_{2}} {\partial u_{jk}} +\frac{b_{3}} {\overline z_{3} -\underline{z}_{3}} \frac{\partial J_{3}} {\partial u_{jk}}\\ &&+\eta_{k} ,j=\overline {1,C} ,k=\overline {1,N} . \end{array} $$(59)For each of sets (b 1, b 2, b 3) satisfying (56), we have an optimal solution \(u^{\left (r \right )}=\left ({u_{jk}^{(r)}} \right )_{C\times N} \)of this problem.
- Step 2::
-
-
If \(\mu _{\min } =\min \left \{ {\mu _{i} (J_{i} ),i=1,...,3} \right \}>\theta \), with θ is an optional threshold then u (r) is not acceptable. Otherwise, if u (r)∉S p then u (r)is put on S p .
-
In the case of needing to expand S p , set r = r + 1 and check the conditions:
If r >L 1 or after L 2 consecutive iterations that S p is not expanded (L 1, L 2 has optional values) then set \(a_{i}^{\left (r \right )} =\underline {z}_{i} ,i=1, 2, 3\) and get a random index h in {1, 2, 3} to put \(a_{h}^{\left (r \right )} \in \left [ {\underline {z}_{h} ,\bar {{z}}_{h}} \right )\). Then return to step 1.
-
In the case of not needing to expand S p then go to step 3.
-
- Step 3::
-
-
Rejecting dominant solutions from S p .
-
End of process.
-
Lemma 2
With the given parameter set \(\left ({b_{1} ,b_{2} ,b_{3}} \right )\) , the solution u (r) to minimize objective function Y in ( 58 ) are:
3.4 Theoretical analyses of the SSFC-FS algorithm
In Section 3.3, we used the Interactive Fuzzy Satisficing method to get the optimal solutions u (r). This section provides the theoretical analyses of the solutions including the convergence rate, bounds of parameters, and the comparison with solutions of other relevant methods.
Firstly, from the formula of cluster centers \(V_{j}^{\left (r \right )} \) in (62), it is obvious that the following properties and propositions hold.
Property 1
When b 2 = 1, b 1 = b 3 = 0, the cluster centers are not defined.
Property 2
Solution u (r) is continuous and bounded by \(\left ({b_{1} ,b_{2} ,b_{3}} \right )\).
Proposition 1
For all values of \(\left ({b_{1} ,b_{2} ,b_{3}} \right )\) , from formulas of u (r) in ( 61 ) we have:
Proof
This characteristic can easily be achieved based on constraints of u j k :
Secondly, we compare the solutions with those achieved by local Lagrange method. Consider the optimization problem in (31)–(32), one can regard the function as a single objective and uses the Lagrange method to get the optimal solutions. To differentiate with our approach in this paper, we name this method the local Lagrange. It is easy to derive the following proposition. □
Proposition 2
The optimal solutions of the problem ( 31 )–( 32 ) are,
Now, we measure the quanlities of optimal solutions using the local Lagrange and Interactive Fuzzy Satisficing methods in terms of clustering quality represented by the IFV criterion. The maximal value of IFV indicates the better quality.
Let IFV (LA) be the value of IFV index at the optimal solutions obtained by using Lagrange method and IFV (FS) stands for this value at the one by using fuzzy satisfacing method. It follows that,
To evaluate the difference of IFV values in these methods, we need an assumption presented in Lemma 3 below.
Lemma 3
In the local Lagrange method, the parameter λ k is computed by formula ( 66 ). Thus, in order to compare the local Lagrange with Interactive Fuzzy Satisficing, we can choose parameters \(\left ({b_{1} ,b_{2} ,b_{3}} \right )\) in which the below condition is satisfied ( \(j=\overline {1,C} ,k=\overline {1,N} )\) :
Theorem 1
Given the set of parameters \(\left ({b_{1} ,b_{2} ,b_{3}} \right )\) satisfied the condition as in Lemma 3, we have:
Proof
Thus, \(IFV^{\left ({LA} \right )}-IFV^{\left ({FS} \right )}=\frac {1}{C}\times \frac {1}{N}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \sum \limits _{j=1}^{C} {\sum \limits _{k=1}^{N} {\left ({A_{jk} +B_{jk}} \right )\left ({A_{jk} -B_{jk}} \right )}} \). Where,
It is clear that,
Then
□
Property 3
The optimal solutions obtained by using Interactive Fuzzy Satisficing are better than those using local Lagrange.
From Theorem 1, we have
It means that the optimal solutions obtained by Interactive Fuzzy Satisficing are better than by local Lagrange.Thirdly, we would like to investigate the range of IFV values of the solutions at an iteration step u (r) obtained by Interactive Fuzzy Satisficing method. This question is handled by the following theorem.
Theorem 2
The lower bound of IFV index on optimal solution u=u (r) obtained by Interactive Fuzzy Satisficing is evaluated by:
Proof
We have
where
It follows that
Apply Cauchy–Schwarz inequality, we obtain
From that, we get:
In Theorem 2, we consider the lower bound of IFV index, the upper bound of this index will be evaluated in Theorem 3 below. For this purpose, limitation L is defined.
□
Lemma 4
For every set of \(\left ({b_{1} ,b_{2} ,b_{3}} \right )\) , we always have:
It is easy to get this from property of logarithm.
Theorem 3
The upper bound of IFV index of the optimal solution obtained by the Interactive Fuzzy Satisficing is evaluated by:
Proof
Again, from formula of IFV, we have:
Using the inequality in Lemma 3, this is equivalent to:
It follows that,
□
Consequence 1
From the Cauchy–Schwarz inequality, used in above transformation, the equality happens when:
With the constraint (32), it can be deduced as follow.
The result in Consequence 1 has revealed some typically cases:
- Suppose that b 2 is a constant that differs from 1, we can represent b 1 and b 3 by this expression:
In this case, according to (79), we can express parameter b 3 by b 2 as below:
Where
In which:
Where
Replacing \(\frac {\eta _{k}} {2}\) in (81) by formula (82) and denotations in (83), we have:
Together with assumptions in (83), we get the value of b 3 belonging to [0,0.2]. Again with the changing role of b 2, b 3 as constants, we also get values of b 1 belonging to [0.1, 0.4] and b 2 belonging to [0.3, 0.7]. These remarks help us choosing appropriate values for the parameters of the algorithm.
Fourthly, we would like to investigate the difference between two consecutive iterations of the algorithm using Interactive Fuzzy Satisficing, let us denote:
The following theorem helps us answer this question.
Theorem 4
When the parameters of r th iteration \(\left ({b_{1}^{\left (r \right )} ,b_{2}^{\left (r \right )} ,b_{3}^{\left (r \right )}} \right )\) and (r+1) th iteration \(\left ({b_{1}^{\left ({r+1} \right )} ,b_{2}^{\left ({r+1} \right )} ,b_{3}^{\left ({r+1} \right )}} \right )\) are determined as in Lemma 4, the difference between solutions of two consecutive iterations can be evaluated by
Proof
Based on the (61), we have
where
Apply the inequality in Proposition 1:
and denotations in (85), we have:
Again, apply the inequality in Proposition 1:
Use denotation ε 3 in (85), we get:
Combine (87) and (89), we obtain the result in (86). □
Consequence 2
The termination of the method using Interactive Fuzzy Satisficing is:
In this situation, the relation between the number of iterations and the stopping condition is presented by following formula:
3.5 Theoretical analyses of the new method
From the above presentation, we reach the advantages and differences of the new algorithm in comparison with the relevant methods.
-
a)
This research presents the first attempt to model the dental X-Ray image segmentation in the form of semi-supervised fuzzy clustering. By the introduction of a new spatial objective function in (25) of Section 3.1.5 that combines the dental features and neighborhood information of a pixel, results of the semi-supervised fuzzy clustering model including cluster centers and the membership matrix are oriented by dental structures of a dental X-ray image. This brings much meaning to practical dentistry for getting segmented images that are close to accurate results.
-
b)
Additional information, represented in a prior membership matrix in (36) of Section 3.2, that combines expert’s knowledge, spatial information of a dental X-Ray image, and the optimal results of FCM is proposed. Comparing with the semi-supervised fuzzy clustering – eSFCM in [40], the new algorithm provides deterministic ways to specify the additional information as well as integrate the spatial objective function into the model. The new components are significant to the dental X-Ray image segmentation, and promise to enhance the accuracy of results.
-
c)
This research firstly considers the solutions of the optimization problem under the Interactive Fuzzy Satisficing view. Unlike traditional methods using local Lagrange, the proposed algorithm differentiates isolated problems and solves them in a same context. The efficiency of the new method has been theoretically validated on Section 3.4 where the clustering quality of the algorithm using Interactive Fuzzy Satisficing is better than that using local Lagrange (See Theorem 1 and Property 3). Thus, this proves reasons of developing the algorithm based on Interactive Fuzzy Satisficing but not by other approaches.
-
d)
The new algorithm has been equipped with theoretical analyses. Many theorems and propositions have been presented, but some main paints can be demonstrated as below. These remarks help us better understanding of the new algorithm and are significant to implementation.
-
The clustering quality of the new method SSFC-FS is better than the algorithm using local Lagrange denoted as SSFC-SC as proven in Theorem 1 and Property 3.
-
The upper and lower bounds of IFV index of the optimal solution at an iteration step obtained by the Interactive Fuzzy Satisficing are shown in (75), (78) of Theorem 2 & 3. This shows us the interval that the quality value of the new algorithm can fall into.
-
Consequence 1 suggests appropriate values for the parameters of the algorithm, namely b 3 belonging to [0,0.2], b 1 belonging to [0.1, 0.4] and b 2 belonging to [0.3, 0.7].
-
The difference between two consecutive iterations of the SSFC-FS algorithm is expressed in (86) of Theorem 4. This helps us control the variation of results between iterations, which is a basis to predict the termination point.
-
A generalized termination of the SSFC-FS method is given in (91) of Consequence 2, which is likely to avoid redundant iterations and reduce the processing time of the algorithm.
-
4 Experimental Evaluation
The proposed algorithm called SSFC–FS has been implemented in addition to the relevant methods - FCM [3], Otsu [26], SSCMOO [2] and FMMBIS [5] as well as a semi-supervised fuzzy clustering - eSFCM [40] and a variant of the proposed method using local Lagrange – SSFC-SC in Matlab 2014 and executed on a PC VAIO laptop with Core i5 processor. The experimental results are taken as the average values after 20 runs. Experimental datasets are taken from Hanoi Medical University, Vietnam including 56 dental images in the period 2014 – 2015 (Fig. 2). The datasets were uploaded to Matlab Central for sharing [18].
The aims of the experimental validation are: i) Evaluating accuracy of segmentation of the algorithms through 8 validity functions [37] whose descriptions are shown below; ii) Investigating the most appropriate values of parameters of the SSFC-FS algorithm; iii) Verifying the theoretical analyses summed up in Section 3.5 on real datasets.
The following shows the validity functions and their criteria:
-
Davies-Bouldin (DB): relates to the variance ratio criterion, which is based on the ratio between the distance inner group and outer group. Especially, quality of partition is determined by the following formula:
Where \(\bar {{d}}_{l} ,\bar {{d}}_{m} \) are the average distances of clusters l and m, respectively. d l, m is the distance between these clusters.
The lower value of DB criterion is better.
-
Simplified Silhouete Width Criterion (SSWC):
Where a p, j is defined as the difference of object j to its cluster p. Similarly, d q, j is the difference of objects to cluster j to q, q≠ p and b p, j . The minimum value of d q, j , j = 1, 2, …k and q≠p becomes different levels of objects to cluster j nearest neighbor. The idea is to replace the average distance by the distance to the expected point. Using SSWC, the greater value shows more efficient algorithm.
-
PBM : based on the distance of the clusters and the distance between the clusters and is calculated by the formula:
It is clear that in PBM criteria, higher value means higher algorithm performance. Hence the best partition indicates when PBM get the highest value, D K maximizes and E K reaches minimization.
-
IFV :
The maximal value of IFV indicates the better performance.
-
Ball and Hall index (BH): to measure the sum of within-group distances. The larger value of BH criterion is better.
$$ BH=\frac{1}{N}\sum\limits_{l=1}^{k} {\sum\limits_{x_{i} \in C_{l}}{\left\| {x_{i} -\bar{{x}}_{l}} \right\|}} . $$(104) -
Calinski-Harabasz index (VCR): is used to evaluate the quality of a data partition by variance ratio of between and within group matrices. The larger value of VCR is better.
$$ VCR=\frac{trace(B)}{trace(W)}\times \frac{N-k}{k-1}, $$(105)$$ UW=\sum\limits_{l=1}^{k} {U_{l} ,UW_{l} =\sum\limits_{x_{i} \in C_{l}} {\left({x_{i} -\bar{{x}}_{l}} \right)\left({x_{i} -\bar{{x}}_{l}} \right)}^{T}} , $$(106)$$\begin{array}{@{}rcl@{}} trace(W)&=&\sum\limits_{l=1}^{k} {trace(W_{l} )} ;\\ trace(W_{l} )&=&\sum\limits_{p=1}^{r} {\sum\limits_{x_{i} \in C_{l}} {\left({x_{ip} -\bar{{x}}_{lp}} \right)}} , \end{array} $$(107)$$\begin{array}{@{}rcl@{}} B=\sum\limits_{l=1}^{k} {N_{l} \left({\bar{{x}}_{l} -\bar{{x}}} \right)\left({\bar{{x}}_{l} -\bar{{x}}} \right)^{T}}, \end{array} $$(108)$$\begin{array}{@{}rcl@{}} trace(B)&=&trace(T)-trace(W),\\trace(T)&=&\sum\limits_{p=1}^{r} {\sum\limits_{i=1}^{N} {\left({x_{ip} -\bar{{x}}_{p}} \right)}}^{2}. \end{array} $$(109) -
Banfeld-Raftery index (BR): is an index using variance-covariance matrix of each cluster. This index is calculated as below.
Where n k is number of data points in k th cluster. We note that if n k = 1, this trace is equal to 0 and then the logarithm is undefined.
-
Difference-like index (TRA): is shown below where trace(W) is calculated in (51). The larger value of TRA is better.
Firstly, in the following Table 5, the experimental results of the algorithms on 56 dental images with parameters C =3, m =2, weights b 1 = 0.3, b 2 = 0.6, b 3 = 0.1 are given. According to the results in Table 5, SSFC-FS obtains the best values in most of criteria (4 per 8 criteria) and in all datasets. Among 4 worse criteria to SSFC-FS, the IFV values of SSFC-FS are always higher than those of SSFC-SC. This clearly affirms that the clustering quality of SSFC-FS is better than that of SSFC-SC as proven in Theorem 1 and Property 3. Furthermore, it is clear that SSFC-FS is also better than SSCMOO and FMMBIS in most of criteria.
In order to understand the values of criteria by all datasets, we have synthesized mean and variance of each criterion from Table 5 and presented them in Table 6. From this table, we record the best result in a row as 1 and calculate the number of times that the best algorithm is better than another in the same row. The statistics are given in Table 7.
Now, we illustrate the segmentation results on a dataset in Fig. 3.
Secondly, we verify the values of parameters calculated in Consequence 1 by evaluating SSFC-FS in six different cases of parameter set (b 1, b 2, b 3) as follows.
-
Case 1:
(b 1 > b 2 > b 3): (b 1 = 0.6, b 2 = 0.3, b 3 = 0.1).
-
Case 2:
(b 1 > b 3 > b 2): (b 1 = 0.6, b 2 = 0.1, b 3 = 0.3).
-
Case 3:
(b 2 > b 1 > b 3): (b 1 = 0.3, b 2 = 0.6, b 3 = 0.1).
-
Case 4:
(b 2 > b 3 > b 1): (b 1 = 0.1, b 2 = 0.6, b 3 = 0.3).
-
Case 5:
(b 3 > b 1 > b 2): (b 1 = 0.3, b 2 = 0.1, b 3 = 0.6).
-
Case 6:
(b 3 > b 2 > b 1): (b 1 = 0.1, b 2 = 0.3, b 3 = 0.6).
In Table 8, we measure the results of SSFC-FS on 6 cases by the number of clusters. It is clear that except C =3, other results showed that Case 3 obtains more number of best results in term of validity indices. Again, similar to Table 6 & 7, we also calculate means of the criteria for SSFC-FS on six cases in a real dataset (Table 9) and the performance comparison (Table 10). The results pointed out the most appropriate values of parameters namely Case 3 (b 1 = 0.3, b 2 = 0.6, b 3 = 0.1). Those values are identical with the observation in Consequence 1.
Thirdly, we validate the lower bounds of IFV index of the optimal solution stated in (75) of Theorem 2 on six cases in Tables 8-10. The results are shown below.
-
Case 1:
IFV = 88.78 >\(\frac {1}{C^{2}}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \times \left [ {\log _{2} C} \right ]^{2} \quad =\) 4.89.
-
Case 2:
IFV = 96.65 > \(\frac {1}{C^{2}}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \times \left [ {\log _{2} C} \right ]^{2} \quad =\) 5.43.
-
Case 3:
IFV = 110.62 >\(\frac {1}{C^{2}}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \times \left [ {\log _{2} C} \right ]^{2} \quad =\) 6.15.
-
Case 4:
IFV = 102.63 >\(\frac {1}{C^{2}}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \times \left [ {\log _{2} C} \right ]^{2} \quad =\) 5.72.
-
Case 5:
IFV = 123.53 >\(\frac {1}{C^{2}}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \times \left [ {\log _{2} C} \right ]^{2} \quad =\) 6.88.
-
Case 6:
IFV = 134.76>\(\frac {1}{C^{2}}\times \frac {SD_{\max } } {\overline {\sigma _{D}} } \times \left [ {\log _{2} C} \right ]^{2} \quad =\) 7.56.
It is obvious that the experimental results satisfy Theorem 2. The upper bound validation in Theorem 3 is checked analogously.
Lastly, we check the difference between two consecutive iterations of the SSFC-FS algorithm expressed in (86) of Theorem 4. The validation is made on six cases above and expressed in Table 11. We can clearly recognize that the theoretical values are nearly approximate to the experimental ones.
5 Conclusions
In this paper, we concentrated on the dental X-ray image segmentation problem and proposed a new semi-supervised fuzzy clustering algorithm based on Interactive Fuzzy Satisficing named as SSFC-FS. The new contributions include: i) Modeling dental structures of a dental X-Ray image into a spatial objective function; ii) Designing a new semi-supervised fuzzy clustering model for the dental X-ray image segmentation; iii) Proposing a semi-supervised fuzzy clustering algorithm – SSFC-FS based on the Interactive Fuzzy Satisficing method; iv) Examining theoretical aspects of SSFC-FS comprising of the convergence rate, bounds of parameters, and the comparison with solutions of other relevant methods. SSFC-FS has been experimentally validated and compared with the relevant ones in terms of clustering quality on a real dataset including 56 dental X-ray images in the period 2014-2015 of Hanoi Medial University, Vietnam.
As discussed in Section 3.5 and later verified in the experiments, we summarize the main findings of this research as follows. Firstly, SSFC-FS has better clustering quality than the relevant methods – FCM, Otsu, SSCMOO [2] and FMMBIS [5] as well as the well-known semi-supervised fuzzy clustering - eSFCM and a variant of the proposed method using local Lagrange – SSFC-SC. Besides, the clustering quality of SSFC-FS is better than SSFC-SC theoretically proven in Theorem 1 and Property 3. Secondly, the most appropriate values for the parameters of the algorithm are: b 3 belongs to [0, 0.2], b 1 belongs to [0.1, 0.4] and b 2 belongs to [0.3, 0.7] (Consequence 1). Thirdly, the upper and lower bounds of IFV index of the optimal solution at an iteration step obtained by the Interactive Fuzzy Satisficing, which shows us the interval that the quality value of the new algorithm can fall into, were shown in equations (75, 78) of Theorem 2 & 3. Fourthly, the difference between two consecutive iterations of the SSFC-FS algorithm, which helps us control the variation of results between iterations, was expressed in equation (86) of Theorem 4. Lastly, a generalized termination of the SSFC-FS method, which is used to avoid redundant iterations and reduce the processing time of the algorithm, was given in (91) of Consequence 2. Those findings are significant to both theoretical and practical implication, especially to the dental X-ray image segmentation problem and semi-supervised fuzzy clustering approaches.
Further works of this research can be done in the following ways: (1) Speeding up the algorithm by approximation methods; (2) Finding the most appropriate additional values for semi-supervised fuzzy clustering; and (3) Investigating fast matching strategy in the medical diagnosis context.
Abbreviations
- Spatial constraints:
-
Refer to the conditions regarding dental structure of a dental X-ray image. Some similar terms are: “spatial features”, “dental feature”
- FCM:
-
Fuzzy C-Means
- SSFC-SC:
-
Semi-Supervised Fuzzy Clustering algorithm with Spatial Constraints
- FS:
-
Fuzzy Satisficing method
- LA:
-
Lagrange method
- SSFC-FS:
-
Semi-Supervised Fuzzy Clustering algorithm with Spatial Constraints using Fuzzy Satisficing method
- Membership matrix/degrees:
-
Refer to the level that a data point belongs to a given cluster
- eSFCM:
-
Semi-supervised Entropy regularized Fuzzy Clustering
- LBP:
-
Local Binary Patterns
- RGB:
-
Red-Green-Blue
- DB:
-
Davies-Bouldin validity index
- SSWC:
-
Simplified Silhouete Width Criterion validity index
- PBM:
-
A validity index
- IFV:
-
A spatial validity index
- BH:
-
Ball and Hall index
- VCR:
-
Calinski - Harabasz index
- BR:
-
The Banfeld - Raftery index
- TRA:
-
Difference-like index
- SSCMOO:
-
Semi-Supervised Clustering technique using Multi- Objective Optimization
- FMMBIS:
-
Fuzzy Mathematical Morphology for Biological Image Segmentation
References
Ahonen T, Hadid A, Pietikainen M (2006) Face description with local binary patterns: Application to face recognition. IEEE Trans Pattern Anal Mach Intell 28(12):2037–2041
Alok AK, Saha S, Ekbal A (2015) A new semi-supervised clustering technique using multi-objective optimization. Appl Intell 43(3):633–661
Bezdek JC, Ehrlich R (1984) FCM: The fuzzy c-means clustering algorithm. Comput Geosci 10(2):191–203
Bouchachia A, Pedrycz W (2006) Data clustering with partial supervision. Data Min Knowl Disc 12 (1):47–78
Caponetti L, Castellano G, Basile MT, Corsini V (2014) Fuzzy mathematical morphology for biological image segmentation. Appl Intell 41(1):117–127
Caramia M, Dell’Olmo P (2008) Multi-objective management in freight logistics: Increasing capacity, service level and safety with optimization algorithms. Springer Science & Business Media
Ghazali KH, Mustafa MM, Hussain A, Bandar MEC, Kuantan G (2007) Feature Extraction technique using SIFT keypoints descriptors. In: The international conference on electrical and engineering and informatics institut technology , pp 17–19
Jiayin K, Zhicheng J (2010) Dental plaque segmentation and quantification using histogram-aided fuzzy c-means algorithm. In: Control conference (CCC), 2010 29th chinese (pp. 3068-3071). IEEE
Kang JY, Min LQ, Luan QX, Li X, Liu JZ (2007) Dental plaque quantification using FCM-based classification in HSI color space. In: Wavelet analysis and pattern recognition, 2007. ICWAPR’07. International conference on (vol. 1, pp. 78-81). IEEE
Kang J, Li X, Luan Q, Liu J, Min L (2006) Dental plaque quantification using cellular neural network-based image segmentation. In: Intelligent computing in signal processing and pattern recognition (pp. 797-802). Springer berlin heidelberg
Kang J, Min L, Luan Q, Li X, Liu J (2009) Novel modified fuzzy c-means algorithm with applications. Digital Signal Process 19(2):309–319
Kondo T, Ong SH, Foong KW (2004) Tooth segmentation of dental study models using range images. IEEE Trans Med Imaging 23(3):350–362
Kumar Y, Janardan R, Larson B, Moon J (2011) Improved segmentation of teeth in dental models. Comput-Aided Des Applic 8(2):211–224
Lai YH, Lin PL (2008) Effective segmentation for dental X-ray images using texture-based fuzzy inference system. In: Advanced concepts for intelligent vision systems (pp. 936-947). Springer berlin heidelberg
Li S, Fevens T, KrzyŻak A, Li S (2006) An automatic variational level set segmentation framework for computer aided dental X-rays analysis in clinical environments. Comput Med Imaging Graph 30(2):65–74
Li S, Fevens T, KrzyŻak A (2006) Automatic clinical image segmentation using pathological modeling, PCA and SVM. Eng Appl Artif Intell 19(4):403–410
Mahoor MH, Abdel-Mottaleb M (2005) Classification and numbering of teeth in dental bitewing images. Pattern Recogn 38(4):577–586
Mathworks (2015) Dental Image Segmentation. Available at: https://www.mathworks.com/matlabcentral/fileexchange/52762-semi-supervised-fuzzy-clustering-with-fuzzy-satisficing (Accessed on: Aug 31, 2015)
Mohan C, Nguyen HT (2001) An interactive satisficing method for solving multiobjective mixed fuzzy-stochastic programming problems. Fuzzy Sets Syst 117(1):61–79
Narkhede HP (2013) Review of image segmentation techniques. Int J Sci Mod Eng 1(5461):28
Nayak J, Naik B, Behera HS (2015) Fuzzy C-Means (FCM) Clustering Algorithm A Decade Review from 2000 to 2014. In: Computational intelligence in data mining-volume 2 (pp. 133-149). Springer India
Ngo LT, Mai DS, Pedrycz W (2015) Semi-supervising Interval Type-2 Fuzzy C-Means clustering with spatial information for multi-spectral satellite image classification and change detection. Comput Geosci 83:1–16
Thanh NH (2002) PRELIM–An interactive computer package for solving realistic optimization problems in fuzzy environment. Proceedings of VJFUZZY’98: Vietnam −Japan bilateral symposium on fuzzy systems and applications 652–659
Nomir O, Abdel-Mottaleb M (2005) A system for human identification from X-ray dental radiographs. Pattern Recogn 38(8):1295–1305
Nomir O, Abdel-Mottaleb M (2007) Human identification from dental X-ray images based on the shape and appearance of the teeth. IEEE Trans Inf Forensics Secur 2(2):188–197
Otsu N (1975) A threshold selection method from gray-level histograms. Automatica 11(285-296):23–27
Pham TD, Eisenblätter U, Golledge J, Baune BT, Berger K (2009) Segmentation of medical images using geo-theoretic distance matrix in fuzzy clustering. In: Image processing (ICIP), 2009 16th IEEE international conference on (pp. 3369-3372). IEEE
Perkgoz C, Sakawa M, Kato K, Katagiri H (2005) An interactive fuzzy satisficing method for multiobjective stochastic integer programming problems through a probability maximization model. Asia Pacific Manag Rev 10 (1):29
Rad AE, Rahim MS M, Norouzi A Level Set and Morphological Operation Techniques in Application of Dental Image Segmentation
Rad AE, Mohd Rahim MS, Rehman A, Altameem A, Saba T (2013) Evaluation of current dental radiographs segmentation approaches in computer-aided applications. IETE Tech Rev 30(3):210–222
Said EH, Nassar DEM, Fahmy G, Ammar HH (2006) Teeth segmentation in digitized dental X-ray films using mathematical morphology. IEEE Trans Inf Forensics Secur 1(2):178–189
Sakawa M, Matsui T (2012) An Interactive Fuzzy Satisficing Method for Multiobjective Stochastic Integer Programming with Simple Recourse
Sato-Ilic M, Jain LC (2006) Introduction to fuzzy clustering. In: Innovations in fuzzy clustering (pp. 1-8). Springer berlin heidelberg
Setarehdan SK, Singh S (eds.) (2012) Advanced algorithmic approaches to medical image segmentation: state-of-the-art applications in cardiology, neurology, mammography and pathology Springer Science & Business Media
Shah S, Abaza A, Ross A, Ammar H (2006) Automatic tooth segmentation using active contour without edges. In: Biometric consortium conference, 2006 biometrics symposium: Special session on research at the (pp. 1-6). IEEE
Stolojescu-CriŞan C, Holban Ş (2013) A comparison of X-Ray image segmentation techniques. Advances Electr Comput Eng Eng 13(3)
Vendramin L, Campello RJ, Hruschka ER (2010) Relative clustering validity criteria: A comparative overview. Stat Anal Data Min: The ASA Data Sci J 3(4):209–235
Xu X, Xu S, Jin L, Song E (2011) Characteristic analysis of Otsu threshold and its applications. Pattern Recogn Lett 32(7):956–961
Yasunori E, Yukihiro H, Makito Y, Sadaaki M (2009) On semi-supervised fuzzy c-means clustering. In: Fuzzy systems, 2009. FUZZ-IEEE 2009. IEEE international conference on (pp. 1119-1124). IEEE
Yin X, Shu T, Huang Q (2012) Semi-supervised fuzzy clustering with metric learning and entropy regularization. Knowl-Based Syst 35:304–311
Zhao M, Ma L, Tan W, Nie D (2006) Interactive tooth segmentation of dental models. In: Engineering in medicine and biology society, 2005. IEEE-EMBS 2005. 27th annual international conference of the (pp. 654-657). IEEE
Zhou J, Abdel-Mottaleb M (2005) A content-based system for human identification based on bitewing dental X-ray images. Pattern Recogn 38(11):2132–2142
Tee CS (2008) Feature selection for content-based image retrieval using statistical discriminant analysis Doctoral dissertation, Universiti Teknologi Malaysia, Faculty of Computer Science and Information System
Acknowledgments
The authors are greatly indebted to the editor-in-chief, Prof. Moonis Ali and anonymous reviewers for their comments and their valuable suggestions that improved the quality and clarity of paper. This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.05-2014.01.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Matlab source codes of all algorithms and experimental data can be found at the URL:
Rights and permissions
About this article
Cite this article
Tuan, T.M., Ngan, T.T. & Son, L.H. A novel semi-supervised fuzzy clustering method based on interactive fuzzy satisficing for dental x-ray image segmentation. Appl Intell 45, 402–428 (2016). https://doi.org/10.1007/s10489-016-0763-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-016-0763-5