Picture fuzzy clustering: a new computational intelligence method

Abstract

Fuzzy clustering especially fuzzy $C$-means (FCM) is considered as a useful tool in the processes of pattern recognition and knowledge discovery from a database; thus being applied to various crucial, socioeconomic applications. Nevertheless, the clustering quality of FCM is not high since this algorithm is deployed on the basis of the traditional fuzzy sets, which have some limitations in the membership representation, the determination of hesitancy and the vagueness of prototype parameters. Various improvement versions of FCM on some extensions of the traditional fuzzy sets have been proposed to tackle with those limitations. In this paper, we consider another improvement of FCM on the picture fuzzy sets, which is a generalization of the traditional fuzzy sets and the intuitionistic fuzzy sets, and present a novel picture fuzzy clustering algorithm, the so-called FC-PFS. A numerical example on the IRIS dataset is conducted to illustrate the activities of the proposed algorithm. The experimental results on various benchmark datasets of UCI Machine Learning Repository under different scenarios of parameters of the algorithm reveal that FC-PFS has better clustering quality than some relevant clustering algorithms such as FCM, IFCM, KFCM and KIFCM.

1 Introduction

Fuzzy clustering is considered as a useful tool in the processes of pattern recognition and knowledge discovery from a database; thus being applied to various crucial, socioeconomic applications. Fuzzy C-means (FCM) algorithm (Bezdek et al. 1984) is a well-known method for fuzzy clustering. It is also considered as a strong aid of rule extraction and data mining from a set of data, in which fuzzy factors are really common and rise up various trends to work on (De Oliveira and Pedrycz 2007; Zimmermann 2001). The growing demands for the exploitation of intelligent and highly autonomous systems put FCM in a great challenge to be applied to various applications such as data analysis, pattern recognition, image segmentation, group-positioning analysis, satellite images and financial analysis like what can be seen nowadays. Nonetheless, the clustering quality of FCM is not high since this algorithm is deployed on the basis of the traditional fuzzy sets, which have some limitations in the membership representation, the determination of hesitancy and the vagueness of prototype parameters. The motivation of this paper is to design a novel fuzzy clustering method that could obtain better clustering quality than FCM.

Scanning the literature, we recognize that one of the most popular methods to handle with those limitations is designing improvement versions of FCM on some extensions of the traditional fuzzy sets. Numerous fuzzy clustering algorithms based on the type-2 fuzzy sets (T2FS) (Mendel and John 2002) were proposed such as in Hwang and Rhee (2007), Linda and Manic (2012), Zarandi et al. (2012) and Ji et al. (2013). Those methods focused on the uncertainty associated with fuzzifier that controls the amount of fuzziness of FCM. Even though their clustering qualities are better than that of FCM, the computational time is quite large so that researchers prefer extending FCM on the intuitionistic fuzzy sets (IFS) (Atanassov 1986). Some early researches developing FCM on IFS were conducted by Hung et al. (2004), Iakovidis et al. (2008) and Xu and Wu (2010). Chaira (2011) and Chaira and Panwar (2013) presented another intuitionistic FCM (Chaira’s IFCM) method considering a new objective function for clustering the CT scan brain images to detect abnormalities. Some works proposed by Butkiewicz (2012) and Zhao et al. (2013) developed fuzzy features and distance measures to assess the clustering quality. Son et al. (2012a, (2012b, (2013, (2014) and Son (2014a, (2014b, (2014c, (2015) proposed intuitionistic fuzzy clustering algorithms for geodemographic analysis based on recent results regarding IFS and the possibilistic FCM. Kernel-based fuzzy clustering (KFCM) was applied to enhance the clustering quality of FCM such as in Graves and Pedrycz (2010), Kaur et al. (2012) and Lin (2014). Summaries of the recent intuitionistic fuzzy clustering are referenced in (Xu 2012).

Recently, Cuong (2014) have presented picture fuzzy sets (PFS), which is a generalization of the traditional fuzzy sets and the intuitionistic fuzzy sets. PFS-based models can be applied to situations that require human opinions involving more answers of types: yes, abstain, no and refusal so that they could give more accurate results for clustering algorithms deployed on PFS. The contribution in this paper is a novel picture fuzzy clustering algorithm on PFS, the so-called FC-PFS. Experimental results conducted on the benchmark datasets of UCI Machine Learning Repository are performed to validate the clustering quality of the proposed algorithm in comparison with those of relevant clustering algorithms. The proposed FC-PFS both ameliorates the clustering quality of FCM and enriches the knowledge of developing clustering algorithms on the PFS sets for practical applications. In other words, the findings are significant in both theoretical and practical sides. The detailed contributions and the rest of the paper are organized as follows. Section 2 presents the constitution of FC-PFS including,

• Taxonomies of fuzzy clustering algorithms available in the literature that help us understand the developing flow and the reasons why PFS should be used for the clustering introduced in Sect. 2.1. Some basic picture fuzzy operations, picture distance metrics and picture fuzzy relations are also mentioned in this subsection;

• the proposed picture fuzzy model for clustering and its solutions are presented in Sect. 2.2;

• in Sect. 2.3, the proposed algorithm FC-PFS is described.

Section 3 validates the proposed approach through a set of experiments involving benchmark UCI Machine Learning Repository data. Finally, Sect. 4 draws the conclusions and delineates the future research directions.

2 Methodology

2.1 Taxonomies of fuzzy clustering

Bezdek et al. (1984) proposed the fuzzy clustering problem where the membership degree of a data point $X_k$ to cluster $j$th denoted by the term $u_{kj}$ was appended to the objective function in Eq. (1). This clearly differentiates with hard clustering and shows that a data point could belong to other clusters depending on the membership degree. Notice that in Eq. (1), $N$, $C$, $m$ and $V_j$ are the number of data points, the number of clusters, the fuzzifier and the center of cluster $j$th ($j=1,\ldots ,C)$, respectively.

$$\begin{aligned} J=\sum \limits _{k=1}^N {\sum \limits _{j=1}^C {u_{kj} ^m\left\| {X_k -V_j } \right\| ^2} } \rightarrow \min . \end{aligned}$$

(1)

The constraints for (1) are,

$$\begin{aligned} \left\{ {\begin{array}{ll} u_{kj} \in \left[ {0,1} \right] \\ \sum \limits _{j=1}^C {u_{kj} } =1 \\ \end{array}} \right. . \end{aligned}$$

(2)

Using the Lagrangian method, Bezdek et al. showed an iteration scheme to calculate the membership degrees and centers of the problem (1, 2) as follows.

$$\begin{aligned} V_j= & {} \frac{\sum \limits _{k=1}^N {u_{kj} ^m} X_k }{\sum \limits _{k=1}^N {u_{kj} ^m} };\quad j=1,\ldots ,C, \end{aligned}$$

(3)

$$\begin{aligned} u_{kj}= & {} \frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } ^{\frac{2}{m-1}}};\quad k=\!1,\ldots ,N, \quad j=1,\ldots ,C.\nonumber \\ \end{aligned}$$

(4)

FCM was proven to converge to (local) minimal or the saddle points of the objective function in Eq. (1). Nonetheless, even though FCM is a good clustering algorithm, how to opt suitable number of clusters, fuzzifier, good distance measure and initialization is worth considering since bad selection can yield undesirable clustering results for pattern sets that include noise. For example, in case of pattern sets that contain clusters of different volume or density, it is possible that patterns staying on the left side of a cluster may contribute more for the other than this one. Misleading selection of parameters and measures would make FCM fall into local optima and sensitive to noises and outliers.

Graves and Pedrycz (2010) presented a kernel version of the FCM algorithm namely KFCM in which the membership degrees and centers in Eqs. (3, 4) are replaced with those in Eqs. (5, 6) taking into account the kernel distance measure instead of the traditional Euclidean metric. By doing so, the new algorithm is able to discover the clusters having arbitrary shapes such as ring and ‘$X$’ form. The kernel function used in (5, 6) is the Gaussian expressed in Eq. (7).

$$\begin{aligned}&V_j =\frac{\sum \limits _{k=1}^N {u_{kj} ^m} K( {X_k ,V_j })X_k }{\sum \limits _{k=1}^N {u_{kj} ^mK( {X_k ,V_j })} };\quad j=1,\ldots ,C,\end{aligned}$$

(5)

$$\begin{aligned}&u_{kj} =\frac{1}{\sum \limits _{i=1}^C {\left( {\frac{1-K( {X_k ,V_j })}{1-K( {X_k ,V_i })}}\right) }^{\frac{1}{m-1}}};\quad k\!=\!1,\ldots ,N,\nonumber \\&\quad j\!=\!1,\ldots ,C\end{aligned}$$

(6)

$$\begin{aligned}&K( {x,y})=\exp ( {-\left\| {x-y} \right\| ^2/\sigma ^2}),\quad \sigma >0. \end{aligned}$$

(7)

However, modifying FCM itself with new metric measures or new objective functions with penalized terms or new fuzzifier is somehow not sufficient and deploying fuzzy clustering on some extensions of FS such as T2FS and IFS would be a good choice. Hwang and Rhee (2007) suggested deploying FCM on (interval) T2FS sets to handle the limitations of uncertainties and proposed an IT2FCM focusing on fuzzifier controlling the amount of fuzziness in FCM. A T2FS set was defined as follows.

Definition 1

A type-2 fuzzy set (T2FS) (Mendel and John 2002) in a non-empty set $X$ is,

$$\begin{aligned} \tilde{A}=\left\{ {( {x,u,\mu _{\tilde{A}} ( {x,u})})\vert \, \forall x\in A,\forall u\subseteq J_X \in \left[ {0,1} \right] } \right\} . \end{aligned}$$

(8)

where $J_X$ is the subset of $X$, $\mu _{\tilde{A}} ( {x,u})$ is the fuzziness of the membership degree $u(x)$, $\forall x\in X$. When $\mu _{\tilde{A}} ( {x,u})=1$, $\tilde{A}$ is called the interval T2FS. Similarly, when $\mu _{\tilde{A}} ( {x,u})=0$, $\tilde{A}$ returns to the FS set. The interval type-2 FCM method aimed to minimize both functions below with $\left[ {m_1 ,m_2 } \right]$ is the interval fuzzifier instead of the crisp fuzzifier $m$ in Eqs. (1, 2).

$$\begin{aligned} J_1= & {} \sum \limits _{k=1}^N {\sum \limits _{j=1}^C {u_{kj} ^{m_1 }\left\| {X_k -V_j } \right\| ^2} } \rightarrow \min ,\end{aligned}$$

(9)

$$\begin{aligned} J_2= & {} \sum \limits _{k=1}^N {\sum \limits _{j=1}^C {u_{kj} ^{m_2 }\left\| {X_k -V_j } \right\| ^2} } \rightarrow \min . \end{aligned}$$

(10)

The constraints in (2) are kept intact. By similar techniques to solve the new optimization problem, the interval membership $U=\left[ {\underline{U},\overline{U} } \right]$ and the crisp centers are calculated in Eqs. (11–13) accordingly. Within these values, after iterations, the objective functions $J_1$ and $J_2$ will achieve the minimum.

$$\begin{aligned} \overline{u_{kj} } =\left\{ {\begin{array}{l} \frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } ^{\frac{2}{m_1 -1}}}\quad \text {if }\, {\frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } }<\frac{1}{C}} \\ \frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } ^{\frac{2}{m_2 -1}}} \quad \mathrm{otherwise} \\ \end{array}} \right. , \end{aligned}$$

(11)

$$\begin{aligned} \underline{u_{kj} }=\left\{ {\begin{array}{l} \frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } ^{\frac{2}{m_1 -1}}}\quad \text {if }\, {\frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } }\ge \frac{1}{C}} \\ \frac{1}{\sum \limits _{i=1}^C {\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) } ^{\frac{2}{m_2 -1}}}\quad \mathrm{otherwise} \\ \end{array}} \right. , \end{aligned}$$

(12)

$$\begin{aligned} V_j =\frac{\sum \limits _{k=1}^N {u_{kj} ^m} X_k }{\sum \limits _{k=1}^N {u_{kj} ^m} };\quad j=1,\ldots ,C, \end{aligned}$$

(13)

Where $m$ is a ubiquitous value between $m_1$ and $m_2$. Nonetheless, the limitation of the class of algorithms that deploy FCM on T2FS is heavy computation so that developing FCM on IFS is preferred than FCM on T2FS. IFS (Atanassov 1986), which comprised elements characterized by both membership and non-membership values, is useful mean to describe and deal with vague and uncertain data.

Definition 2

An intuitionistic fuzzy set (IFS) (Atanassov 1986) in a non-empty set $X$ is,

$$\begin{aligned} \hat{A}=\left\{ {\left\langle {x,\mu _{\tilde{A}} ( x),\gamma _{\tilde{A}} ( x)} \right\rangle \vert x\in X} \right\} , \end{aligned}$$

(14)

where $\mu _{\hat{A}} ( x)$ is the membership degree of each element $x\in X$ and $\gamma _{\hat{A}} ( x)$ is the non-membership degree satisfying the constraints,

$$\begin{aligned}&\mu _{\hat{A}} ( x),\gamma _{\hat{A}} ( x)\in \left[ {0,1} \right] ,\quad \forall x\in X,\end{aligned}$$

(15)

$$\begin{aligned}&0\le \mu _{\hat{A}} ( x)+\gamma _{\hat{A}} ( x)\le 1,\quad \forall x\in X. \end{aligned}$$

(16)

The intuitionistic fuzzy index of an element (also known as the hesitation degree) showing the non-determinacy is denoted as,

$$\begin{aligned} \pi _{\hat{A}} ( x)=1-\mu _{\hat{A}} ( x)-\gamma _{\hat{A}} ( x),\quad \forall x\in X. \end{aligned}$$

(17)

When $\pi _{\hat{A}} ( x)=0$, IFS returns to the FS set. The hesitation degree can be evaluated through the membership function by Yager generating operator (Burillo and Bustince 1996), that is,

$$\begin{aligned} \pi _{\hat{A}} ( x)=1-\mu _{\hat{A}} ( x)-( {1-\mu _{\hat{A}} ( x)^\alpha })^{1/\alpha }, \end{aligned}$$

(18)

where $\alpha >0$ is an exponent coefficient. This operator is used to adapt with the entropy element in the objective function for intuitionistic fuzzy clustering in Eq. (19) according to Chaira (2011). Most intuitionistic FCM methods, for instance, the IFCM algorithms in Chaira (2011) and Chaira and Panwar (2013) integrated the intuitionistic fuzzy entropy with the objective function of FCM to form the new objective function as in Eq. (19).

$$\begin{aligned} J=\sum \limits _{k=1}^N {\sum \limits _{j=1}^C {u_{kj} ^m\left\| {X_k -V_j } \right\| ^2} } +\sum \limits _{j=1}^C {\pi _j ^*\mathrm{e}^{1-\pi _j ^*}} \rightarrow \min , \end{aligned}$$

(19)

where,

$$\begin{aligned} \pi _j ^*=\frac{1}{N}\sum \limits _{k=1}^N {\pi _{kj} } . \end{aligned}$$

(20)

Notice that when $\pi _{\hat{A}} ( x)=0$, the function (19) returns to that of FCM in (1). The constraints for (19–20) are similar to those of FCM so that the authors, for simplicity, separated the objective function in (19) into two parts and used the Lagrangian method to solve the first one and got the solutions as in (3–4). Then, the hesitation degree is calculated through Eq. (18) and used to update the membership degree as follows.

$$\begin{aligned} u_{kj} =u_{kj} +\pi _{kj} . \end{aligned}$$

(21)

The new membership degree is used to calculate the centers as in Eq. (3). The algorithm stops when the difference between two consecutive membership degrees is not larger than a pre-defined threshold.

A kernel-based version of IFCM, the so-called KIFCM, has been introduced by Lin (2014). The KIFCM algorithm used Eqs. (5–7) to calculate the membership degrees and the centers under the Gaussian kernel measure. Updating with the hesitation degree is similar to that in IFCM through equation (21). The main activities of KIFCM are analogous to those of IFCM except the kernel function was used instead of the Euclidean distance.

Recently, Cuong (2014) have presented PFS, which is a generalization of FS and IFS. The definition of PFS is stated below.

Definition 3

A picture fuzzy set (PFS) (Cuong 2014) in a non-empty set $X$ is,

$$\begin{aligned} \dot{A}=\left\{ {\left\langle {x,\mu _{\dot{A}} ( x),\eta _{\dot{A}} ( x),\gamma _{\dot{A}} ( x)} \right\rangle \vert x\in X} \right\} , \end{aligned}$$

(22)

where $\mu _{\dot{A}} ( x)$ is the positive degree of each element $x\in X$, $\eta _{\dot{A}} ( x)$ is the neutral degree and $\gamma _{\dot{A}} ( x)$ is the negative degree satisfying the constraints,

$$\begin{aligned}&\mu _{\dot{A}} ( x),\eta _{\dot{A}} ( x),\gamma _{\dot{A}} ( x)\in \left[ {0,1} \right] ,\quad \forall x\in X,\end{aligned}$$

(23)

$$\begin{aligned}&0\le \mu _{\dot{A}} ( x)+\eta _{\dot{A}} ( x)+\gamma _{\dot{A}} ( x)\le 1,\quad \forall x\in X. \end{aligned}$$

(24)

The refusal degree of an element is calculated as $\xi _{\dot{A}} ( x)=1-( {\mu _{\dot{A}} ( x)+\eta _{\dot{A}} ( x)+\gamma _{\dot{A}} ( x)})$, $\forall x\in X$. In cases $\xi _{\dot{A}} ( x)=0$ PFS returns to the traditional IFS set. Obviously, it is recognized that PFS is an extension of IFS where the refusal degree is appended to the definition. Yet why we should use PFS and does this set have significant meaning in real-world applications? Let us consider some examples below.

Example 1

In a democratic election station, the council issues 500 voting papers for a candidate. The voting results are divided into four groups accompanied with the number of papers that are “vote for” (300), “abstain” (64), “vote against” (115) and “refusal of voting” (21). Group “abstain” means that the voting paper is a white paper rejecting both “agree” and “disagree” for the candidate but still takes the vote. Group “refusal of voting” is either invalid voting papers or did not take the vote. This example was happened in reality and IFS could not handle it since the refusal degree (group “refusal of voting”) does not exist.

Example 2

A patient was given the first emergency aid and diagnosed by four states after examining possible symptoms that are “heart attack”, “uncertain”, “not heart attack”, “appendicitis”. In this case, we also have a PFS set.

From Figs. 1, 2 and 3, we illustrate the PFS, IFS and FS for 5 election stations in Example 1, respectively. We clearly see that PFS is the generalization of IFS and FS so that clustering algorithms deployed on PFS may have better clustering quality than those on IFS and FS. Some properties of PFS operations, the convex combination of PFS, etc., accompanied with proofs are referenced in the article (Cuong 2014).

Fig. 1

Picture fuzzy sets

Fig. 2

Intuitionistic fuzzy sets

Fig. 3

Fuzzy sets

2.2 The proposed model and solutions

In this section, a picture fuzzy model for clustering problem is given. Supposing that there is a dataset $X$ consisting of $N$ data points in $d$ dimensions. Let us divide the dataset into $C$ groups satisfying the objective function below.

$$\begin{aligned} J= & {} \sum \limits _{k=1}^N \sum \limits _{j=1}^C {( {u_{kj} ( {2-\xi _{kj} })})^m\left\| {X_k -V_j } \right\| ^2}\nonumber \\&+\sum \limits _{k=1}^N{\sum \limits _{j=1}^C {\eta _{kj} ( {\log \eta _{kj} +\xi _{kj} })} } \rightarrow \min , \end{aligned}$$

(25)

Some constraints are defined as follows:

$$\begin{aligned}&u_{kj} +\eta _{kj} +\xi _{kj} \le 1,\end{aligned}$$

(26)

$$\begin{aligned}&\sum \limits _{j=1}^C {( {u_{kj} ( {2-\xi _{kj} })})} =1,\end{aligned}$$

(27)

$$\begin{aligned}&\sum \limits _{j=1}^C {\left( {\eta _{kj} +\frac{\xi _{kj} }{C}}\right) } =1, \end{aligned}$$

(28)

$$\begin{aligned} k=1,\ldots ,N,\quad j=1,\ldots ,C. \end{aligned}$$

The proposed model in Eqs. (25–28) relies on the principles of the PFS set. Now, let us summarize the major points of this model as follows.

• The proposed model is the generalization of the intuitionistic fuzzy clustering model in Eqs. (2, 19, 20) since when $\xi _{kj} =0$ and the condition (28) does not exist, the proposed model returns to the intuitionistic fuzzy clustering model;

• When $\eta _{kj} =0$ and the conditions above are met, the proposed model returns to the fuzzy clustering model in Eqs. (1, 2);

• Equation (27) implies that the “true” membership of a data point $X_k$ to the center $V_j$, denoted by $u_{kj} ( {2-\xi _{kj} })$ still satisfies the sum-row constraint of memberships in the traditional fuzzy clustering model.

• Equation (28) guarantees the working on the PFS sets since at least one of two uncertain factors namely the neutral and refusal degrees always exist in the model.

• Another constraint (26) reflects the definition of the PFS sets (Definition 3).

Now, Lagrangian method is used to determine the optimal solutions of model (25–28).

Theorem 1

The optimal solutions of the systems (25–28) are:

$$\begin{aligned}&\xi _{kj} =1-( {u_{kj} +\eta _{kj} })-( {1-( {u_{kj} +\eta _{kj} })^\alpha })^{\frac{1}{\alpha }},\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C),\end{aligned}$$

(29)

$$\begin{aligned}&u_{kj} =\frac{1}{\sum \limits _{i=1}^C {( {2-\xi _{ki} })\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) ^{\frac{2}{m-1}}} },\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C),\end{aligned}$$

(30)

$$\begin{aligned}&\eta _{kj} =\frac{\mathrm{e}^{-\xi _{kj} }}{\sum \limits _{i=1}^C {\mathrm{e}^{-\xi _{ki} }} }\left( {1-\frac{1}{C}\sum \limits _{i=1}^C {\xi _{ki} } }\right) ,\quad (k=1,\ldots ,N,\,\nonumber \\&\qquad \qquad j=1,\ldots ,C),\end{aligned}$$

(31)

$$\begin{aligned}&V_j =\frac{\sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^m} X_k }{\sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^m} },\quad (j=1,\ldots ,C). \end{aligned}$$

(32)

Proof

Taking the derivative of $J$ by $v_j$, we have:

$$\begin{aligned} \frac{\partial J}{\partial V_j }= & {} \sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^m( {-2X_k +2V_j })} ,\nonumber \\&(k=1,\ldots ,N,\,j=1,\ldots ,C) \end{aligned}$$

(33)

Since $\frac{\partial J}{\partial V_j }=0$, we have:

$$\begin{aligned}&\sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^m( {-2X_k +2V_j })} =0,\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(34)

$$\begin{aligned}&\Leftrightarrow \sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^mX_k } =\sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^mV_j},\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(35)

$$\begin{aligned}&\Leftrightarrow V_j =\frac{\sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^mX_k }}{\sum \limits _{k=1}^N {( {u_{kj} ( {2-\xi _{kj} })})^m}},\quad (j=1,\ldots ,C). \end{aligned}$$

(36)

The Lagrangian function with respect to $U$ is,

$$\begin{aligned} L( u)= & {} \sum \limits _{k=1}^N \sum \limits _{j=1}^C {( {u_{kj} ( {2-\xi _{kj} })})^m\left\| {X_k -V_j } \right\| ^2}\nonumber \\&+\sum \limits _{k=1}^N{\sum \limits _{j=1}^C {\eta _{kj} ( {\log \eta _{kj} +\xi _{kj} })} }\nonumber \\&-\lambda _k \left( {\sum \limits _{j=1}^C {( {u_{kj} ( {2-\xi _{kj} })})} -1}\right) \end{aligned}$$

(37)

Since $\frac{\partial L(u)}{\partial u_{kj} }=0$, we have:

$$\begin{aligned} \frac{\partial L(u)}{\partial u_{kj} }= & {} mu_{kj}^{m-1} ( {2-\xi _{kj} })^m\left\| {X_k -V_j } \right\| ^2\nonumber \\&-\lambda _k ( {2-\xi _{kj} })=0,\quad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(38)

$$\begin{aligned} \Leftrightarrow u_{kj}= & {} \frac{1}{2-\xi _{kj} }\left( {\frac{\lambda _k }{m\left\| {X_k -V_j } \right\| ^2}}\right) ^{\frac{1}{m-1}},\nonumber \\&(k=1,\ldots ,N,\,j=1,\ldots ,C) \end{aligned}$$

(39)

From Eqs. (37, 49), the solutions of $U$are set as follows:

$$\begin{aligned}&\sum \limits _{j=1}^C {\left( {\frac{\lambda _k }{m\left\| {X_k -V_j } \right\| ^2}}\right) ^{\frac{1}{m-1}}} =1,\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(40)

$$\begin{aligned}&\Leftrightarrow \lambda _k =\left( {\frac{1}{\sum \limits _{j=1}^C {\left( {m\left\| {X_k -V_j } \right\| ^2}\right) ^{\frac{1}{1-m}}} }}\right) ^{m-1},\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C) \end{aligned}$$

(41)

Plugging (41) into (39), we have:

$$\begin{aligned} u_{kj}= & {} \frac{1}{\sum \limits _{i=1}^C {( {2-\xi _{kj} })\left( {\frac{\left\| {X_k -V_j } \right\| }{\left\| {X_k -V_i } \right\| }}\right) ^{^{\frac{2}{m-1}}}} },\nonumber \\&(k=1,\ldots ,N,\,j=1,\ldots ,C) \end{aligned}$$

(42)

Similarly, the Lagrangian function with respect to $\eta$ is,

$$\begin{aligned} L( \eta )= & {} \sum \limits _{k=1}^N {\sum \limits _{j=1}^C {( {u_{kj} ( {2-\xi _{kj} })})^m\left\| {X_k -V_j } \right\| ^2}}\nonumber \\&{+\sum \limits _{k=1}^N {\sum \limits _{j=1}^C {\eta _{kj} ( {\log \eta _{kj} +\xi _{kj} })} } }\nonumber \\&-\lambda _k \left( {\sum \limits _{j=1}^C {\left( {\eta _{kj} +\frac{\xi _{kj} }{C}}\right) } -1}\right) .\end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial L(\eta )}{\partial \eta _{kj} }= & {} \log \eta _{kj} +1-\lambda _k +\xi _{kj} =0,\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(44)

$$\begin{aligned} \Leftrightarrow \,\eta _{kj}= & {} \exp \left\{ {\lambda _k -1-\xi _{kj} } \right\} ,\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C) \end{aligned}$$

(45)

From Eqs. (38, 55), we have:

$$\begin{aligned}&\sum \limits _{j=1}^C {\mathrm{e}^{\lambda _k -1-\xi _{kj} }} +\frac{1}{C}\sum \limits _{j=1}^C {\xi _{kj} } =1,\nonumber \\&\qquad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(46)

$$\begin{aligned}&\Leftrightarrow \mathrm{e}^{\lambda _k -1}\sum \limits _{j=1}^C {\mathrm{e}^{-\xi _{kj} }} =1-\frac{1}{C}\sum \limits _{j=1}^C {\xi _{kj} },\nonumber \\&\qquad (k=1,\ldots ,N,\,j=1,\ldots ,C)\end{aligned}$$

(47)

$$\begin{aligned}&\Leftrightarrow \mathrm{e}^{\lambda _k -1}\!=\!\frac{1-\frac{1}{C}\sum \limits _{j=1}^C {\xi _{kj} } }{\sum \limits _{j=1}^C {\mathrm{e}^{-\xi _{kj} }} },\quad (k\!=1,\ldots ,N,\,j\!=\!1,\ldots ,C)\nonumber \\ \end{aligned}$$

(48)

Combining (48) with (45), we have:

$$\begin{aligned} \eta _{kj}= & {} \left( {1-\frac{1}{C}\sum \limits _{i=1}^C {\xi _{ki} } }\right) \frac{\mathrm{e}^{-\xi _{kj} }}{\sum \limits _{i=1}^C {\mathrm{e}^{-\xi _{ki} }} },\nonumber \\&\quad (k=1,\ldots ,N,\,j=1,\ldots ,C) \end{aligned}$$

(49)

Finally, using similar techniques of Yager generating operator (Burillo and Bustince 1996), we modify the Eq. (18) by replacing $\mu _{\hat{A}} ( x)$ by $( {u_{kj} +\eta _{kj} })$ to get the value of the refusal degree of an element as follows:

$$\begin{aligned} \xi _{kj} =1-( {u_{kj} +\eta _{kj} })-( {1-( {u_{kj} +\eta _{kj} })^\alpha })^{\frac{1}{\alpha }}, \end{aligned}$$

(50)

where $\alpha \in \left( {0,1} \right]$ is an exponent coefficient used to control the refusal degree in PFS sets. The proof is complete. $\square$

2.3 The FC-PFS algorithm

In this section, the FC-PFS algorithm is presented in details.

3 Findings and discussions

3.1 Experimental design

In this part, the experimental environments will be described such as,

• Experimental tools the proposed algorithm—FC-PFS has been implemented in addition to FCM (Bezdek et al. 1984), IFCM (Chaira 2011), KFCM (Graves and Pedrycz 2010) and KIFCM (Lin 2014) in C programming language and executed them on a Linux Cluster 1350 with eight computing nodes of 51.2GFlops. Each node contains two Intel Xeon dual core 3.2 GHz, 2 GB Ram. The experimental results are taken as the average values after 50 runs.

• Experimental dataset the benchmark datasets of UCI Machine Learning Repository such as IRIS, WINE, WDBC (Wisconsin Diagnostic Breast Cancer), GLASS, IONOSPHERE, HABERMAN, HEART and CMC (Contraceptive Method Choice) (University of California 2007). Table 1 gives an overview of those datasets.

• Cluster validity measurement Mean accuracy (MA), the Davies–Bouldin (DB) index (1979) and the Rand index (Vendramin et al. 2010) are used to evaluate the qualities of solutions for clustering algorithms. The DB index is shown as below.

$$\begin{aligned}&\mathrm{DB}=\frac{1}{C}\sum \limits _{i=1}^C {\left( {\mathop {\max }\limits _{j:j\ne i} \left\{ {\frac{S_i +S_j }{M_{ij} }} \right\} }\right) } ,\end{aligned}$$

(51)

$$\begin{aligned}&S_i =\sqrt{\frac{1}{T_i }\sum \limits _{j=1}^{T_i } {\left| {X_j -V_i } \right| ^2} } ,\quad (i=1,\ldots ,C),\end{aligned}$$

(52)

$$\begin{aligned}&M_{ij} =\left\| {V_i -V_j } \right\| ,\quad (i,j=1,\ldots ,C,\,i\ne j), \end{aligned}$$

(53)

where $T_i$ is the size of cluster $i$th. $S_i$ is a measure of scatter within the cluster, and $M_{ij}$ is a measure of separation between cluster $i$th and $j$th. The minimum value indicates the better performance for DB index. The Rand index is defined as,

$$\begin{aligned} \mathrm{RI}=\frac{a+d}{a+b+c+d}, \end{aligned}$$

(54)

where $a(b)$ is the number of pairs of data points belonging to the same class in $R$ and to the same (different) cluster in $Q$ with $R$ and $Q$ being two ubiquitous clusters. $c(d)$ is the number of pairs of data points belonging to the different class in $R$ and to the same (different) cluster. The larger the Rand index is, the better the algorithm is.

• Parameters setting Some values of parameters such as fuzzifier $m=2$, $\varepsilon =10^{-3}$, $\alpha \in ( {0,1})$, $\sigma$ and $\max Steps=1000$ are set up for all algorithms as in Bezdek et al. (1984), Chaira (2011), Graves and Pedrycz (2010) and Lin (2014).

• Objectives

  • to illustrate the activities of FC-PFS on a given dataset;

  • to evaluate the clustering qualities of algorithms through validity indices. Some experiments on the computational time of algorithms are also considered;

  • to validate the performance of algorithms by various cases of parameters.

Table 1 The descriptions of experimental datasets

3.2 An illustration of FC-PFS

First, the activities of the proposed algorithm FC-PFS will be illustrated to classify the IRIS dataset. In this case, $N=150$, $r=4$, $C=3$. The initial positive, the neutral and the refusal matrices, whose sizes are $150 \times 3$, are initialized as follows:

$$\begin{aligned} \mu ^{(0)}=\left( {\begin{array}{lll} 0.174279&{}\quad 0.164418&{}\quad 0.198673 \\ 0.140933&{}\quad 0.169170&{}\quad 0.198045 \\ &{}\quad \ldots \ldots &{}\\ 0.225422&{}\quad 0.161006&{}\quad 0.125153 \\ \end{array}}\right) , \end{aligned}$$

(55)

$$\begin{aligned} \eta ^{(0)}=\left( {\begin{array}{lll} 0.215510&{}\quad 0.321242&{}\quad 0.320637 \\ 0.324118&{}\quad 0.312415&{}\quad 0.330315 \\ &{}\quad \ldots \ldots &{} \\ 0.306056&{}\quad 0.329532&{}\quad 0.326154 \\ \end{array}}\right) , \end{aligned}$$

(56)

$$\begin{aligned} \xi ^{(0)}=\left( {\begin{array}{lll} 0.469084&{}\quad 0.422466&{}\quad 0.402644 \\ 0.433791&{}\quad 0.424756 &{}\quad 0.397048 \\ &{}\quad \ldots \ldots &{}\\ 0.395095&{}\quad 0.419692&{}\quad 0.440974 \\ \end{array}}\right) . \end{aligned}$$

(57)

The distribution of data points according to these initializations is illustrated in Fig. 4. From Step 5 of FC-PFS, the cluster centroids are expressed in Eq. (58).

$$\begin{aligned} V=\left( {\begin{array}{llll} 5.833701&{}\quad 3.027605&{}\quad 3.845183&{}\quad 1.248464 \\ 5.784128&{}\quad 3.041955&{}\quad 3.650875&{}\quad 1.148453 \\ 5.677982&{}\quad 3.079381&{}\quad 3.456761&{}\quad 1.073087 \\ \end{array}}\right) . \end{aligned}$$

(58)

The new positive, neutral and refusal matrices are calculated in the equations below.

$$\begin{aligned} \mu ^{(1)}=\left( {\begin{array}{lll} 0.118427&{}\quad 0.169661&{}\quad 0.344978 \\ 0.117641&{}\quad 0.171776&{}\quad 0.340098 \\ &{}\quad \ldots \ldots &{}\\ 0.400281&{}\quad 0.159727&{}\quad 0.067458 \\ \end{array}}\right) , \end{aligned}$$

(59)

$$\begin{aligned} \eta ^{(1)}=\left( {\begin{array}{lll} 0.182454&{}\quad 0.191161&{}\quad 0.194988 \\ 0.190864&{}\quad 0.192596&{}\quad 0.198008 \\ &{}\quad \ldots \ldots &{} \\ 0.198376&{}\quad 0.193556&{}\quad 0.189481 \\ \end{array}}\right) , \end{aligned}$$

(60)

$$\begin{aligned} \xi ^{(1)}=\left( {\begin{array}{lll} 0.495291&{}\quad 0.479725&{}\quad 0.389716 \\ 0.493854&{}\quad 0.478521&{}\quad 0.390903 \\ &{}\quad \ldots \ldots &{} \\ 0.350145&{}\quad 0.482186&{}\quad 0.499905 \\ \end{array}}\right) . \end{aligned}$$

(61)

From these matrices, the value of $\left\| {u^{(t)}-u^{(t-1)}} \right\| +\big \Vert {\eta ^{(t)}} {-\eta ^{(t-1)}} \big \Vert +\left\| {\xi ^{(t)}-\xi ^{(t-1)}} \right\|$ is calculated as 0.102, which is larger than $\varepsilon$ so other iteration steps will be made. The distribution of data points after the first iteration step is illustrated in Fig. 5.

Fig. 4

Clusters in the initialization step

Fig. 5

Clusters after the first iteration step

By the similar process, the centers and the positive, neutral and refusal matrices will be continued to be calculated until the stopping conditions hold. The final positive, neutral and refusal matrices are shown below.

$$\begin{aligned} \mu ^{*} =\left( {\begin{array}{lll} 0.000769&{}\quad 0.001656&{}\quad 0.551091 \\ 0.004785&{}\quad 0.010665&{}\quad 0.543119 \\ &{}\ldots \ldots &{} \\ 0.261915&{}\quad 0.350356&{}\quad 0.017994\\ \end{array}}\right) , \end{aligned}$$

(62)

$$\begin{aligned} \eta ^{*} =\left( {\begin{array}{lll} 0.182155&{}\quad 0.182103&{}\quad 0.245264 \\ 0.181528&{}\quad 0.181223&{}\quad 0.242352 \\ &{}\ldots \ldots &{} \\ 0.186777&{}\quad 0.195800&{}\quad 0.176763 \\ \end{array}}\right) , \end{aligned}$$

(63)

$$\begin{aligned} \xi *=\left( {\begin{array}{lll} 0.489544&{}\quad 0.489825&{}\quad 0.192064 \\ 0.490654&{}\quad 0.492324&{}\quad 0.201595 \\ &{}\ldots \ldots &{} \\ 0.442305&{}\quad 0.385736&{}\quad 0.493112 \\ \end{array}}\right) . \end{aligned}$$

(64)

The final cluster centroids are expressed in Eq. (65). Final clusters and centers are illustrated in Fig. 6. The total number of iteration steps is 11.

$$\begin{aligned} V^{*} =\left( {\begin{array}{llll} 6.762615&{}\quad 3.048669&{}\quad 5.631044&{}\quad 2.047229 \\ 5.879107&{}\quad 2.757631&{}\quad 4.349495&{}\quad 1.389834 \\ 5.003538&{}\quad 3.403553&{}\quad 1.484141&{}\quad 0.251154 \\ \end{array}}\right) . \end{aligned}$$

(65)

Fig. 6

Final clusters

3.3 The comparison of clustering quality

Second, the clustering qualities and the computational time of all algorithms are validated. The experimental results with the exponent $\alpha =0.6$ are shown in Table 2.

Table 2 The comparison of algorithms ($\alpha =0.6)$

It is obvious that FC-PFS obtains better clustering quality than other algorithms in many cases. For example, the Mean Accuracy of FC-PFS for the WINE dataset is 87.1 % which is larger than those of FCM, IFCM, KFCM and KIFCM with the numbers being 85.9, 82.6, 86.2 and 86.6 %, respectively. Similarly, the mean accuracies of FC-PFS, FCM, IFCM, KFCM and KIFCM for the GLASS dataset are 74.5, 71.2, 73.4, 73.5 and 64 %, respectively. When the Rand index of FC-PFS is taken into account, it will be easily recognized that the Rand index of FC-PFS for the CMC dataset is 55.6 % while the values of FCM, IFCM, KFCM and KIFCM are 55.4, 55.1, 50.8 and 48.3 %, respectively. Analogously, the DB value of FC-PFS is better than those of other algorithms. The experimental results on the HEART dataset point out that the DB value of FC-PFS is 2.03, which is smaller and better than those of FCM, IFCM, KFCM and KIFCM with the numbers being 2.05, 2.29, 4.67 and 4.82, respectively. The DB value of FC-PFS on the CMC dataset is equal to that of FCM and is smaller than those of IFCM, KFCM and KIFCM with the numbers being 2.59, 2.59, 2.85, 4.01 and 3.81, respectively. Taking the average MA value of FC-PFS would give the result 79.85 %, which is the average classification performance of the algorithm. This number is higher than those of FCM (77.3 %), IFCM (77.9 %), KFCM (75.84 %) and KIFCM (70.32 %). Figure 7 clearly depicts this fact.

Fig. 7

The average accuracies of algorithms

Nonetheless, the experimental results within a validity index are quite different. For example, the MA values of all algorithms for the IRIS dataset are quite high with the range being (73.3–96.7 %). However, in case of noisy data such as the WDBC dataset, the MA values of all algorithms are small with the range being (56.5–76.2 %). Similar results are conducted for the Rand index where the standard dataset such as IRIS would result in high Rand index range, i.e., (76–95.7 %) and complex, noisy data such as WDBC, IONOSPHERE and HABERMAN would reduce the Rand index ranges, i.e., (51.7–62.5 %), (49.9–52.17 %) and (49.84–49.9 %), respectively. In cases of DB index, the complex data such as GLASS would make high DB values of algorithm than other kinds of datasets. Even though the ranges of validity indices of algorithms are diversified, all algorithms especially FC-PFS would result in high clustering quality with the classification ranges of algorithms being recorded in Table 3.

Table 3 The classification ranges of algorithms

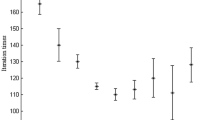
In Fig. 8, the computational time of all algorithms is depicted. It is clear that the proposed algorithm—FC-PFS is little slower than FCM and IFCM and is faster than KFCM and KIFCM. For example, the computational time of FC-PFS to classify the IRIS dataset is 0.033 seconds (s) in 11 iteration steps. The computational time of FCM, IFCM, KFCM and KIFCM on this dataset is 0.011, 0.01, 0.282 and 0.481 s, respectively. The maximal difference in term of computational time between FC-PFS and other algorithms is occurred on the CMC dataset with the standard deviation being approximately 7.6 s. In some cases of datasets, FC-PFS runs faster than other algorithms, e.g., in the WINE dataset the computational time of FC-PFS, FCM, IFCM, KFCM and KIFCM is 0.112, 0.242, 0.15, 2.56 and 1.28 s, respectively.

Fig. 8

The computational time of algorithms

Some remarks are the following:

• FC-PFS obtains better clustering quality than other algorithms in many cases;

• The average MA, Rand index and DB values of FC-PFS in this experiment are 79.85, 62.7 and 3.19 %, respectively;

• FC-PFS takes small computational time (approx. 0.22 s) to classify a dataset.

3.4 The validation of algorithms by various parameters

Third, we validate whether or not the change of exponent $\alpha$ has great impact to the performance of algorithms. To understand the influence of this matter, statistics of the numbers of times that all algorithms obtain best results have been made in Table 4.

Table 4 The statistics of best results

This table states that when the value of the exponent is small, the number of times that FC-PFS obtains best Mean Accuracy (MA) values among all algorithms is small, e.g., 2 times with $\alpha =0.2$. In this case, FC-PFS is not as effective as FCM since this algorithm achieves 3 times “Best results”. However, when the value of the exponent increases, the clustering quality of FC-PFS is also getting better. The numbers of times that FC-PFS obtains best MA values among all when $\alpha =0.4$, $\alpha =0.6$ and $\alpha =0.8$ are 2, 3 and 3, respectively. Thus, large value of exponent should be chosen to achieve high clustering quality of FC-PFS.

In Fig. 9, the average mean accuracies of algorithms will be computed for a given exponent and list those average MA values in the chart. It has been revealed that FC-PFS is quite stable with the clustering quality expressed through the MA value being approximately 80.6 %, while those of FCM, IFCM, KFCM and KIFCM being 77.3, 72.5, 75.8 and 67.4 %, respectively. The clustering quality of FC-PFS was proven to be better than those of other algorithms through various cases of exponents. In Fig. 10, the average computational time of algorithms will be depicted by exponents. It has been shown that the computational time of FC-PFS is larger than those of FCM and IFCM but smaller than those of KFCM and KIFCM. The average computational time of FC-PFS to cluster a given dataset is around 0.22 s.

Fig. 9

The mean accuracies of algorithms by exponents

Fig. 10

The computational time of algorithms by exponents (s)

Some remarks are the following:

• The value of exponent should be large to obtain the best clustering quality in FC-PFS;

• the clustering quality of FC-PFS is stable through various cases of exponents (approx. MA $\sim$ 80.6 %). Furthermore, it is better than those of FCM, IFCM, KFCM and KIFCM.

4 Conclusions

In this paper, we aimed to enhance the clustering quality of fuzzy $C$-means (FCM) and proposed a novel picture fuzzy clustering algorithm on picture fuzzy sets, which are generalized from the traditional fuzzy sets and intuitionistic fuzzy sets. A detailed description of the previous works regarding the fuzzy clustering on the fuzzy sets and intuitionistic fuzzy sets was presented to facilitate the motivation and the mechanism of the new algorithm. By incorporating components of the PFS set into the clustering model, the proposed algorithm produced better clustering quality than other relevant algorithms such as fuzzy $C$-means (FCM), intuitionistic FCM (IFCM), kernel FCM (KFCM) and kernel IFCM (KIFCM). Experimental results conducted on the benchmark datasets of UCI Machine Learning Repository have re-confirmed this fact even in the case of the values of exponents changed and showed the effectiveness of the proposed algorithm. Further works of this theme aim to modify this algorithm in distributed environments and apply it to some forecast applications such as stock prediction and weather nowcasting.