1 Introduction

Main idea of data clustering is the separation of data samples from each other and placing them into the similar groups; it means that data samples similar to each other should be placed into a same group and should have maximum dissimilarity with the samples of other group(s) [16, 29, 35]. Each group in the above definition is usually referred to as a cluster. All clusters together are named a clustering. It is a very traditional task in any field for us to intend to group a host of data points. It can be due to lack of any insight into dataset. So, a first grouping in data that there is no primary insight can provide us with a good initial understanding and insight. Because of its utility, clustering has emerged as one of the leading methods of multivariate analysis. It has been shown that cluster analysis (CA) is among the most versatile concepts for analyzing datasets with many (more than three) features [68].

Indeed, data clustering is a necessary tool for finding groups (or clusters) in unlabeled datasets [45, 48, 50, 52, 53, 58]. One of the most important objective functions in data clustering is maximization of intra-cluster similarity simultaneous with minimization of inter-cluster similarity. In other words, data clustering objective functions usually intend to maximize inter-cluster variance and minimize intra-cluster variance. It is worthy to be mentioned that there is not any supervision during data clustering to guide the clusterer. It is considered as a subfield in statistical pattern recognition (SPR), machine learning (ML), and data mining (DM) fields. Two main tasks in learning [46, 49, 72] are considered as data classification [6, 64] and data clustering [2, 17, 19, 56]. Data clustering is an interesting topic, and it has diverse applications [47, 50, 54, 55, 59]. There are many reasons why data clustering has many applications. Generally data clustering is used for two aims: (a) receiving a primary understanding of a huge amount of raw data and (b) reducing the size of a huge amount of raw data.

Based on Kleinberg’s theorem, there is no base clustering method that is able to learn any dataset [37]. It means that each basic clustering algorithm is suitable for some datasets having a shared special feature. So we need a new approach that combines basic clustering algorithms in such a way that surpasses the basic clustering algorithms. Due to the lack of supervision in data clustering, choosing a special basic clustering algorithm for an unknown dataset is an impossible and incorrect topic. The lack of a unique clustering assessment metric is also an additive reason to make us be unable to select an absolutely superior clustering algorithm even out of a set of two basic clustering algorithms. Because choosing any objective function for data clustering, it is sometimes desired to find a data clustering algorithm that produces a robust output or even a stable output [7, 10, 27, 30, 61]. Reaching a robust clustering algorithm or a stable clustering algorithm is very hard with simple data clustering algorithms and is easier by ensemble-based data clustering algorithms.

Lack of a guideline for selecting the best data clustering algorithm for a given dataset can be considered as one of the most important delicacies in this field. Indeed, there is no automatic organized method for selection of the most suitable data clustering algorithm for an unknown given dataset.

One of the most important steps in pattern recognition is feature selection. In a more general manner, feature selection can be viewed as feature weighting. Both of them are frequently are considered during data classification, but they are usually hard to be considered during data clustering. It can be very challenging to consider any weighting mechanism in data clustering algorithms. In this paper, a weighting mechanism has been used in data clustering framework, but with the help of ensemble concept.

Data clustering with the help of an ensemble of clusterers is named clustering ensemble. The main aim of clustering ensemble is to search a better and more stable result with the aggregation of the information extracted from a set of base data clusterings. The better and more stable result that is extracted from the set of base data clusterings (also called clusterings pool) is named consensus partition or consensus clustering [22, 62, 63]. There are many researches that have been accomplished in classifier ensemble [1, 36, 57, 54, 55]. Inspired by classifier ensemble success during past researches, clustering ensemble have emerged as a new concept in pattern recognition communities recently. It has been shown that clustering ensemble can be better in terms of both clustering quality and clustering stability. It is worthy to be mentioned that their parallelization ability is suitable for distributed data mining. Clustering ensemble can produce consensus partitions that are more robust, more novel, more stable, and more flexible than the clusterings produced by the base data clustering algorithms [8, 22, 25, 65].

In summary, clustering ensemble composes of the following two steps [22, 62]:

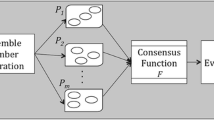
Ensemble generation step: in this step a set of base data clusterings should be produced. These base data clusterings should have two fundamental features to be considered as a suitable ensemble: quality and diversity. It is widely known as an effective approach to produce a large set of base data clusterings and then select a diverse subset of those base data clusterings with the highest qualities [3, 4, 58].

Aggregation of base data clusterings step: in this step all base data clusterings produced in the previous step should be aggregated. The aggregation mechanism is named ensemble consensus function (ECF).

Assigning weights to voter based on their qualities can be an effective mechanism to improve an ensemble. The process of weighting to basic learners in an ensemble of learners can be optimally set if accuracy of each base learner is known [38]. But if the learners are of type clusterers, the accuracy for learner is meaningless [29]. So, quality of each quality clusterer can be used as its approximation for its accuracy. Fred and Lourenco [25] have proposed a clustering ensemble based on selection of a subset of the base data clusterings with the highest qualities. They first assessed base clusterings then selected those with the most qualities. They finally employed an ECF named evidence accumulation clustering (EAC). They ignored the diversity of the base data clusterings (indeed they consider it implicitly).

Alizadeh et al. [4] have proposed a similar work in the cluster level. They have first produced an ensemble, and then they have transformed the ensemble into a cluster representation. After that, they have attached a quality value to each cluster based on its stability in a reference set. Finally, they have selected the clusters with the most qualities. They have improved their previous work by introducing a new metric [3]. Like the previous work of Fred and Lourenco [25], their proposed frameworks also ignored the diversity of the base data clusterings.

In general, applying weighting in clustering has been discussed recently and rarely. As the first and the most complete methods that used weighting mechanism, we can refer to a paper by Gullo et al. [29], and another paper by Domeniconi and Al-Razgan [14]. These methods are Weighted Similarity Partitioning Algorithm (WSPA) [29] and Weighted Bipartite Partitioning Algorithm (WBPA) [14] where the WBPA is the better one.

In all previous researches, both diversity and clustering weighting have not considered simultaneously. They have dealt with either weighting primary data clusterings based on their qualities or selecting of a subset of the primary data clusterings based on their diversity. But diversity and quality have been rarely considered simultaneously. They are considered simultaneously in some works by Parvin and Minaei-Bidgoli [52] and Parvin and Minaei-Bidgoli [53], but they are considered only implicitly. Also in some works, Alizadeh et al. [3] and Alizadeh et al. [4] have considered both of them explicitly and simultaneously, but they have done it in the level of clustering. Also they only used binary weighting. It means that they first have selected a subset of clusterings with the best quality values and have named it the high quality clusterings. Then they have selected a subset of diverse clusterings among the high quality clusterings. Seeking to tackle the abovementioned issue, in this paper, an original data clustering ensemble method has been proposed. So, in the present paper we assign a weight to each cluster based on their quality value. Then, the most diverse subset of clusters is selected into the final ensemble. To reach the final consensus results, a new function termed cluster-level weighting evidence accumulation clustering (\({\text{CLWEAC}}\)). Using the model of \({\text{CLWEAC}}\), consensus clustering is finally produced by an agglomerative hierarchical clustering algorithm. Figure 1 illustrates the diagram of the proposed method. We make use of the diversity concept at the cluster level and incorporate the cluster quality into a weighting structure for boosting the consensus clustering.

Fig. 1
figure 1

Flow diagram of the proposed approach

Full size image

To emphasize the main contributions of the paper, they are briefly listed here:

  • A new metric has been proposed to assess quality of a cluster based on coherence in its data points. It is worthy to be mentioned that the metric don not need the original features of the given dataset.

  • A weighting framework has been introduced to weight up the better clusters (clusters with higher qualities).

  • A new novel consensus function that considers the cluster quality and diversity has been introduced.

  • A large number of experimentations have been performed on many real standard benchmarks showing the proposed clustering ensemble performs better than the state-of-the-art clustering ensembles.

This manuscript is arranged as follows. Section 2 contains the related work. Section 3 explains the proposed clustering ensemble approach. Section 4 presents the experimental study. Finally, conclusion will be presented in Sect. 5.

2 Related work

Clustering is the problem of putting a set of data samples into similar categories (widely named as clusters) where similarity can be calculated based on Euclidean distance. In clustering, the algorithm aims at two objectives: (a) Groups have maximal intra-cluster similarities (or data samples in a same group have minimal Euclidean distances with each other or with cluster center) and (b) different groups have minimal inter-cluster similarities (it can be interpreted either as “each pair of data samples belonging to two different clusters has maximal Euclidean distances” or as “cluster centers of different clusters have maximal Euclidean distances with each other”) [38]. So, clustering means the separating data into a number of groups in such a way that all pairs of the samples in a same group have the least possible dissimilarities from (or the most possible similarities with) each other, and all pairs of the samples assigned to different groups have the least possible similarities with each other.

In some application, we need a robust clustering (RC); for example if the clustering mechanism is employed in a preliminary stage of a classification algorithm (to find and omit outliers). Another reason to desire a RC is hidden in the strong relationship between the CA and Robust Statistics (RS) [60]. RC methods are discussed in detail by García-Escudero et al. [27]. Coretto and Hennig [10] have shown experimentally that the RIMLE method, their previously proposed method, can be recommended as optimal in some situations and acceptable in all situations.

Finding the best clustering for a given dataset is almost impossible [37]; the lack of a totally acceptable criterion to assess the quality of a clustering is the main reason. It means that the measurement is subjective and so the best is also sensitive to that measurement. One of the most challenging tasks in CA is discovery of a mechanism how the stability of a clustering is obtained. Hennig [30] acclaimed that this problem is mainly due to the fact that robustness and stability in CA are not only data dependent, but even cluster dependent. Therefore, some researchers consider stability as the measurement to find which clustering algorithm is the best. It means that if clustering algorithm A is producing more stable results than clustering algorithm B, then we can assume that clustering algorithm B is better than clustering algorithm A. To find stable clustering algorithms, the clustering ensemble methods have emerged. They attempt to find a better and more stable clustering solution by fusing information from several primary data clusterings [3, 4].

The transfer distance (TD) between clusterings [9, 12] is defined as the minimum number of data points that should be moved from one cluster to another (possibly empty) to turn one clustering into another. This distance has been studied under the name of “partition-distance”. Based on the concept of the TD between clusterings, a consensus clustering has been proposed by Guénoche [28]. Given a host of primary clusterings over a dataset, Guénoche [28] has proposed a consensus clustering containing a maximum number of joined or separated pairs in the given dataset that are also joined or separated in the primary clusterings. To do so, he has defined a utility function mapping a clustering to score value. He first transforms the problem to a graph clustering. Then, using some mathematical tricks converts it to an integer linear programming optimization. Finally, he seeks for a partition that maximizes the score. The score can be maximized by an integer linear programming only in certain cases. He has shown that in those certain cases that the method converges to a solution the method produces a consensus partition that is very close to the optimum. Although the method is a very simple and clear one, it fails in many real-world cases as the author mentions it.

Although some researchers have tried to find the best consensus clustering out of an ensemble of base data clusterings, it is widely believed that all ensembles do not perform well. It has been shown that an ensemble needs two elements to be considered as good ensemble. Diversity among the members of an ensemble is one of the most fundamental factors in the ensemble. It means that an ensemble will fail if the diversity among its members is not high. While the diversity is important, the qualities of primary clusterings are also important, so both of them are recently considered by the researchers. But rarely both of them are dealt with in an integrated approach. A new algorithm for choosing a subset of many primary clusters is proposed in this paper where it simultaneously considers both of them. A good selection is very decisive. The selection of some base clusterings (or some base clusters) can be done by a heuristic algorithm. To do this, a criterion to evaluate a cluster is necessary. To evaluate a cluster, normalized mutual information (NMI), a metric based on information theory, can be employed [21]. Alternatively to evaluate a cluster, edited normalized mutual information, ENMI, can be employed [3].

To preserve the diversity, some researchers [23] have suggested a clustering ensemble approach which selects a subset of base data clusterings. They form a smaller but better-performing clustering ensemble than using all primary clusterings. The ensemble selection method is designed based on quality and diversity, the two factors that have been shown to influence cluster ensemble performance. Their method attempts to select a subset of primary clusterings which simultaneously has both the highest quality and diversity. The Sum of Normalized Mutual Information, SNMI [22, 24, 70], is used to measure the quality of an individual partition with respect to other partitions. Also, the NMI is employed to measure the diversity among clusterings. Although the ensemble size in this method is relatively small, this method achieves significant performance improvement over full ensembles.

Inspiring by bagging and boosting algorithms in classification, Parvin et al. [58] have proposed boosting clustering ensemble. They have proposed a subsampling with and without replacement bagging and boosting methods. They have examined the effect of ensemble size, sampling size, and cluster number over quality of consensus clustering. Then, they have proposed a weighted locally adaptive clustering ensemble [53].

Law et al. [40] have proposed a multi-objective data clustering method based on the selection of individual clusters produced by several clustering algorithms through an optimization procedure. This technique chooses the best set of objective functions for different parts of the feature space from the results of base clustering algorithms.

Fred and Jain [24] have offered a new clustering ensemble technique which learns the pair-wise similarity between points in order to facilitate a proper clustering of the data without the a priori information of the number of clusters and of the nature of the clusters. This method which is based on cluster stability assesses the principal clustering results instead of final clustering.

The current article proposes a new clustering ensemble attitude in that it is tried to choose a subset of clusters instead of a subset of clusterings. Also here NMI is utilized to assess a cluster. A scheme introduced by Alizadeh et al. [3] is employed to match two clusters based on which two clusterings are created that they are used in cluster-based NMI calculation.

To make the consensus clustering, a technique based on co-association matrix (\({\text{CAM}}\)) is employed. The results are reported on a variety of experimentations. Extensive experiments on a variety of real-world datasets have shown that our approach exhibits significant advantages in clustering accuracy and efficiency over the state-of-the-art approaches. Experimental results are reported on some real standard dataset from UCI repository [51], and they prove the efficacy of the proposed technique.

The pair-wise co-occurrence-based approaches typically construct a \({\text{CAM}}\) by considering how many times two objects occur in the same cluster among the multiple base clusterings [22]. By exploiting the \({\text{CAM}}\) as the similarity matrix, the conventional clustering techniques, such as the agglomerative clustering methods [44], can be exploited to build the final clustering result. Fred and Jain [22] for the first time presented the concept of \({\text{CAM}}\) and proposed the evidence accumulation clustering (EAC) method. Wang et al. [68] extended the EAC method by taking the sizes of clusters into consideration and proposed the probability accumulation method. Iam-On et al. [34] refined the \({\text{CAM}}\) by considering the shared neighbors between clusters to improve the consensus results. Wang [67] introduced a dendrogram-like hierarchical data structure termed CA-tree to facilitate the co-association-based ensemble clustering process.

The graph partitioning-based approaches [18, 63] address the ensemble clustering problem by constructing a graph model to reflect the ensemble information. The consensus clustering is then obtained by partitioning the graph into a certain number of segments. Strehl and Ghosh [63] proposed three graph partitioning-based ensemble clustering algorithms, i.e., cluster-based similarity partitioning algorithm (CSPA), hypergraph partitioning algorithm (HGPA), and meta-clustering algorithm (MCLA). Fern and Brodley [18] constructed a bipartite graph for the clustering ensemble by treating both clusters and objects as graph nodes and obtain the consensus clustering by partitioning the bipartite graph.

The median partition-based approaches [11, 20] formulate the ensemble clustering problem into an optimization problem, which aims to find a median partition (or clustering) by maximizing the similarity between this clustering and the multiple base clusterings. The median partition problem is NP hard [66]. Finding the globally optimal solution in the huge space of all possible clusterings is computationally infeasible for large datasets. Cristofor and Simovici [11] proposed to obtain an approximate solution using the genetic algorithm, where clusterings are treated as chromosomes. Topchy et al. [66] cast the median partition problem into a maximum likelihood problem and approximately solve it by the EM algorithm. Franek and Jiang [20] cast the median partition problem into an Euclidean median problem by clustering embedding in vector spaces. The median vector is found by the Weiszfeld algorithm [69] and then transformed into a clustering again, which is treated as the consensus clustering.

Although all approaches have tried to find the solution of the ensemble clustering problem in different perspectives [13, 31, 39], they have a shared limitation that they generally look at all local clusters in the ensemble equally and possibly encounter low-quality clusters. In some of previous published works, this challenge has been discussed [26, 32, 42, 66, 68, 71]. In these papers, a weight is assigned to each base data clustering, but weighting is considered at the clustering level not in cluster level.

3 Proposed clustering ensemble

3.1 Notations

Consider a dataset with \(N\) data instances. Let us assume we have an ensemble of the basic data clusterings denoted by \(\varphi\). The ensemble size is denoted by \(\beta\), i.e., \(\varphi = \left\{ {\varphi^{1} , \ldots ,\varphi^{\beta } } \right\}\). The \(\beta\) is set to 30 in this paper throughout all experimentations. Each base data clustering is defined as \(\varphi^{i} = \left\{ {\varphi_{1}^{i} , \ldots ,\varphi_{{n_{i} }}^{i} } \right\}\) where \(\mathop {\bigcup }\limits_{j = 1}^{{n_{i} }} \varphi_{j}^{i} = \left\{ {1,2, \ldots ,N} \right\}\) and \(n_{i}\) is the number of clusters in the \(i\)th base data clustering and is greater than or equal to \(2\) and less than or equal to \(4k\) where \(k\) is the real number of clusters in the given dataset. The \(j\)th cluster the \(i\)th base data clustering is denoted by \(\varphi_{j}^{i}\) where \(\varphi_{j}^{i} \subset \left\{ {1,2, \ldots ,N} \right\}\), \(\varphi_{j}^{i} \ne \emptyset\), and for all \(p \ne q\) the term \(\varphi_{p}^{i} \cap \varphi_{q}^{i} = \emptyset\) is hold. So \(N = \sum\nolimits_{j = 1}^{{n_{i} }} {\left| {\varphi_{j}^{i} } \right|}\) where \(\left| Q \right|\) is the cardinality of a set \(Q\). We denote the number of all base clusters, i.e., \(\mathop \sum \nolimits_{i = 1}^{\beta } n_{i}\), by \(B\). While it may be assumed that the consensus function needs the original data features of dataset as inputs along with the base clusterings [73], the proposed consensus function does not need the original features of dataset as it is widely an ordinary approach [3, 4, 7, 10, 14, 27, 29, 30, 58, 61, 63].

3.2 Backgrounds

In this study, it is illustrated that the diverse clusters in the ensemble can play a role as an indicator for evaluating the reliability of each individual cluster. Next, the conventional \({\text{CAM}}\) is revised into a weighted co-association matrix (\({\text{WCAM}}\)). First, we introduce \({\text{CAM}}\) as a function where its input is an ensemble of data clusterings \(\varphi\) and its output is a matrix of size \(N \times N\). The \(\left( {i,j} \right)\)th element of \({\text{CAM}}\) is denoted by \({\text{CAM}}\left( \varphi \right)_{ij}\) and defined by Eq. (1).

$${\text{CAM}}\left( \varphi \right)_{ij} = \frac{1}{\beta }\mathop \sum \limits_{q = 1}^{\beta } \mathop \sum \limits_{p = 1}^{{n_{q} }} \pi \left( {\left\{ {i,j} \right\} \subseteq \varphi_{p}^{q} } \right)$$
(1)

where \(\pi \left( a \right)\) is defined by Eq. (2).

$$\pi \left( a \right) = \left\{ {\begin{array}{*{20}c} 1 & {\text{if}} & {a = = {\text{true}}} \\ 0 & {\text{if}} & {a = = {\text{false}}} \\ \end{array} } \right.$$
(2)

Let us assume \(Q\) is a subset of data points (or a cluster), i.e., \(Q \subseteq \left\{ {1,2, \ldots ,N} \right\}\). Now, we define \({}_{Q}^{ } \varphi\) as projection of a clustering ensemble on the given cluster \(Q\). The projection of the clustering \(\varphi^{i}\) on cluster \(Q\) is defined according to Eq. (3).

$${}_{Q}^{ } \varphi^{i} = \varphi^{i} \cap Q$$
(3)

So it means \({}_{Q}^{ } \varphi_{j}^{i} = \varphi_{j}^{i} \cap Q\). It can be inferred that the term \(\mathop {\bigcup }\limits_{j = 1}^{{n_{i} }} {}_{Q}^{ } \varphi_{j}^{i} = Q\) holds for any \(i \in \left\{ {1,2, \ldots ,\beta } \right\}\). The average \({\text{CAM}}\) of a clustering ensemble is denoted by \({\text{ACAM}}\left( \varphi \right)\), and it is defined according to Eq. (4).

$${\text{ACAM}}\left( \varphi \right) = \frac{1}{{N^{2} }}\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{j = 1}^{N} {\text{CAM}}\left( \varphi \right)_{ij}$$
(4)

The average \({\text{CAM}}\) of the projection of a clustering ensemble on the given cluster \(Q\), i.e., \({}_{Q}^{ } \varphi\), is denoted by \({\text{ACAM}}\left( {{}_{Q}^{ } \varphi } \right)\), and it is defined as an extension of \({\text{ACAM}}\left( \varphi \right)\). It is defined based on Eq. (5).

$${\text{ACAM}}\left( {{}_{Q}^{ } \varphi } \right) = \frac{1}{{\left| Q \right|^{2} }}\mathop \sum \limits_{i \in Q} \mathop \sum \limits_{j \in Q} {\text{CAM}}\left( {{}_{Q}^{ } \varphi } \right)_{ij}$$
(5)

If \({\text{ACAM}}\left( {{}_{Q}^{ } \varphi } \right)\) hits its maximum at one, the cluster \(Q\) can be considered as the most reliable cluster for the given ensemble \(\varphi\). If \({\text{ACAM}}\left( {{}_{Q}^{ } \varphi } \right)\) hits its minimum at \(\frac{1}{\left| Q \right|}\), the cluster \(Q\) can be considered as the least reliable cluster for the given ensemble \(\varphi\). So the reliability of a cluster in an ensemble \(\varphi\) is defined as follows in Eq. (6).

$${\text{Reliability}}\left( {Q,\varphi } \right) = \frac{{\left| Q \right| \times {\text{ACAM}}\left( {{}_{Q}^{ } \varphi } \right) - 1}}{\left| Q \right| - 1}$$
(6)

The traditional \({\text{CAM}}\) proposed first by Fred and Jain [22] is a \(N \times N\) matrix whose \(\left( {i,j} \right)\)th element reflects how many times the \(i\)th data object is put into the same cluster with the \(j\)th data object in the base data clusterings of the ensemble.

3.3 Proposed CLWCAM

Although it is a widely versatile approach to use the \({\text{CAM}}\) in solving the ensemble clustering problem [3, 4, 23, 22, 58], it considers the entire clusters and also the entire primary clusterings in the ensemble in the same way. So it is unable to weight the ensemble members based on their dependability. Huang et al. [32] have utilized the NCAI index to weigh the base clusterings and thereby build a weighted co-association matrix (\({\text{WCAM}}\)). On the other hand, it only considers the dependability of primary clusterings and still pays no attention to the cluster-level quality. Now we introduce a revised version of \({\text{CAM}}\), called \({\text{CLWEAC}}\) and denoted by cluster-level weighted co-association matrix (\({\text{CLWCAM}}\)). The \(\left( {i,j} \right)\)th element of the mentioned matrix denoted by \({\text{CLWCAM}}\left( \varphi \right)_{\text{ij}}\) is defined by Eq. (7).

$${\text{CLWCAM}}\left( \varphi \right)_{ij} = \frac{{\mathop \sum \nolimits_{p = 1}^{\beta } \mathop \sum \nolimits_{q = 1}^{{n_{p} }} \pi \left( {{\text{Reliability}}\left( {\varphi_{q}^{p} ,\varphi } \right) > {\text{MR}}} \right) \times {\text{Reliability}}\left( {\varphi_{q}^{p} ,\varphi } \right) \times {\text{CAM}}\left( {\varphi_{q}^{p} } \right)_{ij} }}{{\mathop \sum \nolimits_{p = 1}^{\beta } \mathop \sum \nolimits_{q = 1}^{{n_{p} }} \pi \left( {{\text{Reliability}}\left( {\varphi_{q}^{p} ,\varphi } \right) > {\text{MR}}} \right) \times {\text{CAM}}\left( {\varphi_{q}^{p} } \right)_{ij} }}$$
(7)

where \({\text{MR}}\) is the median of the base clusters’ reliabilities (or even a less value as later will be explained) and \({\text{CAM}}\left( {\varphi_{q}^{p} } \right)\) is co-association matrix of the base cluster \(\varphi_{q}^{p}\). The \(\left( {i,j} \right)\)th element of \({\text{CAM}}\left( {\varphi_{q}^{p} } \right)\) is denoted by \({\text{CAM}}\left( {\varphi_{q}^{p} } \right)_{ij}\) and defined by Eq. (8).

$${\text{CAM}}\left( {\varphi_{q}^{p} } \right)_{ij} = \pi \left( {\left\{ {i,j} \right\} \subseteq \varphi_{p}^{q} } \right)$$
(8)

Using the following example, the proposed method has been illustrated. Assume we have a dataset with 14 samples. Also assume we have produced an ensemble \(\varphi\) with eight base data clusterings on those data. Each clustering contains three clusters except base data clustering \(\varphi^{5}\), \(\varphi^{7}\) and \(\varphi^{8}\) each of which contains 2 clusters.

$$\varphi = \left\{ \begin{aligned} &\left\{ {\varphi_{1}^{1} = \left\{ {1,2,3,8,9,10,12} \right\},\varphi_{2}^{1} = \left\{ {4,5,6,7} \right\},\varphi_{3}^{1} = \left\{ {11,13,14} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{2} = \left\{ {1,2,3,4,7} \right\},\varphi_{2}^{2} = \left\{ {5,6,8,9,10} \right\},\varphi_{3}^{2} = \left\{ {11,12,13,14} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{3} = \left\{ {1,2,3,4,5,6,7} \right\},\varphi_{2}^{3} = \left\{ {8,9,10,11,12} \right\},\varphi_{3}^{3} = \left\{ {13,14} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{4} = \left\{ {1,2,3,5,6,8,9} \right\},\varphi_{2}^{4} = \left\{ {4,7,10,12} \right\},\varphi_{3}^{4} = \left\{ {11,13,14} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{5} = \left\{ {1,8,9,10,11,12,13,14} \right\},\varphi_{2}^{5} = \left\{ {2,3,4,5,6,7} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{6} = \left\{ {10,11,12,13} \right\},\varphi_{2}^{6} = \left\{ {1,2,3,4,5,14} \right\},\varphi_{3}^{6} = \left\{ {6,7,8,9} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{7} = \left\{ {1,4,5,8,9,12,13} \right\},\varphi_{2}^{7} = \left\{ {2,3,6,7,10,11,14} \right\}} \right\}, \hfill \\& \left\{ {\varphi_{1}^{8} = \left\{ {3,4,7,8,11,12} \right\},\varphi_{2}^{8} = \left\{ {1,2,5,6,9,10,13,14} \right\}} \right\} \hfill \\ \end{aligned} \right\}$$
(9)

The reliabilities of clusters have been computed based on the proposed method, and then, they are shown in Table 1.

Table 1 Computed reliabilities of clusters of Eq. (9) and selected clusters for the final ensemble
Full size table

After computing the reliabilities of clusters, the proposed method has selected the half most reliable base clusters as shown in Table 1. Indeed, \({\text{MR}}\) is first set to median of the sorted vector of the base clusters’ reliabilities, i.e., 0.51, so the selected base clusters are as mentioned in Table 1. Then, \({\text{CLWCAM}}\left( \varphi \right)\) of our example is computed in Table 2. About this matrix, any value in the main diagonal should at least be a positive value indicating that any data point should be appeared in at least one base selected cluster. If there exists at least one data point whose corresponding value in the main diagonal is zero, we will select the subsequent most reliable base cluster; i.e., \({\text{MR}}\) will be equal to the subsequent smaller value in the sorted vector of the base clusters’ reliabilities. After that \({\text{CLWCAM}}\left( \varphi \right)\) is computed, and again if there exists at least one data point whose corresponding value in the main diagonal is zero, we will select the subsequent most reliable base cluster i.e., \({\text{MR}}\) will be equal to the subsequent smaller value in the sorted vector of the base clusters’ reliabilities. This procedure is continued until there is no zero in the main diagonal.

Table 2 Computed \({\text{CLWCAM}}\left( \varphi \right)\) of the ensemble presented in Eq. (9)
Full size table

After determining \({\text{MR}}\), we compute \({\text{CLWCAM}}\left( \varphi \right)\). As you can expect the most value of \(i\)th row (or \(i\)th column) must be in \(i\)th column (in \(i\)th row) in \({\text{CLWCAM}}\left( \varphi \right)\). But it does not hold in Table 2 (it is simple to show why it happens). So the value of major diagonal in each row is first replaced with the most value possible, i.e., 1. Next, we transform the matrix into a distance matrix (\({\text{DisM}}\)). To do so, we compute the distance matrix based on Eq. (10).

$${\text{DisM}}\left( \varphi \right) = 1 - {\text{CLWCAM}}\left( \varphi \right)$$
(10)

It is worthy to be mentioned that the major diagonal of \({\text{DisM}}\) is zero.

3.4 Consensus functions

The cluster reliability has been first introduced in this study. Then, based on cluster reliability, we select a subset of the most reliable clusters. Finally by employing a cluster-level weighting approach, 2 novel consensus functions have been introduced: (a) cluster-level weighting evidence accumulation clustering (CLWEAC) and (b) cluster-level weighting graph clustering (CLWGC).

Cluster-level weighting evidence accumulation clustering We first transform an ensemble into a \({\text{CLWCAM}}\left( \varphi \right)\). Then \({\text{DisM}}\left( \varphi \right)\) is computed and using a hierarchical agglomerative clustering, the final consensus clustering is produced. The metric of cluster similarity is “average linkage” method. This method is abbreviated as CLWEAC.

Cluster-level weighting graph clustering We first transform an ensemble into a bipartite graph. Each base cluster and each data point are considered as a node. The links are defined as follows. (1) There is no link between any pair of data points. (2) There is no link between any pair of base clusters. (3) There is a link between any pair of nodes when one node is a data point and the other is a base cluster; the weight of the link is the reliability of that cluster. So the graph \(G\left( \varphi \right) = \left( {V\left( \varphi \right),E\left( \varphi \right)} \right)\) is defined as follows. \(V\left( \varphi \right)\) is defined as a vector whose first \(N\) members are dedicated to the \(N\) data points of dataset and the last members are the selected base clusters. \(E\left( \varphi \right)\) is defined based on Eq. (11).

$$E\left( \varphi \right)_{ij} = \left\{ {\begin{array}{*{20}l} {{\text{Reliability}}\left( {V_{i} ,\varphi } \right)} \hfill & {V_{i} \in \left\{ {\varphi_{p}^{q} \left| {{\text{Reliability}}\left( {\varphi_{p}^{q} } \right)} \right\rangle {\text{MR}}} \right\} \wedge V_{j} = \left\{ {1, \ldots ,N} \right\} \wedge V_{j} \in V_{i} } \hfill \\ {{\text{Reliability}}\left( {V_{j} ,\varphi } \right)} \hfill & {V_{j} \in \left\{ {\varphi_{p}^{q} \left| {{\text{Reliability}}\left( {\varphi_{p}^{q} } \right)} \right\rangle {\text{MR}}} \right\} \wedge V_{i} = \left\{ {1, \ldots ,N} \right\} \wedge V_{i} \in V_{j} } \hfill \\ 0 \hfill & {\text{else}} \hfill \\ \end{array} } \right.$$
(11)

This method is abbreviated as CLWGC. After building the CLWGC based on Eq. (11), the graph is partitioned through the TCUT method where it is a fast method for bipartite graphs [43]. The data points located in each partition are considered as a consensus cluster.

In our example, the consensus partition or clustering obtained by CLWEAC and CLWGC is \(\left\{ {\left\{ {11,12,13,14} \right\},\left\{ {8,9,10} \right\},\left\{ {1,2,3,4,5,6,7} \right\}} \right\}\). But the consensus clustering obtained by EAC is \(\left\{ {\left\{ {11,13,14} \right\},\left\{ {8,9,10,12} \right\},\left\{ {1,2,3,4,5,6,7} \right\}} \right\}\). It is clear that the consensus partition obtained by CLWEAC and CLWGC is better than the one obtained by EAC.

4 Experimentations

The proposed CLWEAC and CLWGC have been assessed in the current section. Also the state-of-the-art ensemble clustering methods have been evaluated comparatively. The experimentations have been done a number of standard datasets.

4.1 Datasets and evaluation metric

In our experiments, 10 real benchmark datasets have been utilized: Semeion (with 1593 data points, 256 features, and 10 classes), multiple features (MF) (with 2000 data points, 649 features, and 10 classes), image segmentation (IS) (with 2310 data points, 19 features, and 7 classes), Forest-Cover-Type (FCT) (with 3780 data points, 54 features, and 7 classes), MNIST(with 5000 data points, 784 features, and 10 classes), optical digit recognition (ODR) (with 5620 data points, 64 features, and 10 classes), Landsat Satellite (LS) (with 6435 data points, 36 features, and 6 classes), ISOLET (with 7797 data points, 617 features, and 26 classes), USPS (with 11,000 data points, 256 features, and 10 classes), and letter recognition (LR) (with 20,000 data points, 16 features, and 26 classes). Except the MNIST benchmark dataset [41] and the USPS benchmark dataset [15], the other eight dataset benchmarks have been from the UCI machine learning repository [51].

We apply the normalized mutual information (NMI) [22, 62, 63] to assess the quality of any clustering. The NMI measure indicates the information shared between a pair of clusterings. It has been one of the most widespread evaluation metrics to analyze a data clustering. The bigger the NMI, the higher the clustering quality.

The base clusterings are produced by k-means and fuzzy c-means clustering algorithms. It is worthy to be mentioned that clusters produced by the fuzzy c-means clustering algorithm are first transformed into crisp clusters. Then in following, the all process for both base clustering algorithms is the same.

The number of clusters in each base clustering is randomly chosen from range \(\left[ {2,4k} \right]\). Each result is average of 30 independent runs. For each run of the algorithm, an ensemble of size 30 is produced. After computing the consensus clustering over the ensemble of size 30 with a clustering method, the NMI between the consensus clustering and the ground-truth labels is stored. After repeating the process for 30 independent runs, 30 NMI values are stored. The average of these 30 NMI values is reported as the performance of the clustering method over that dataset.

4.2 Simple clustering algorithms

It is widely acceptable in SPR communities that the clustering ensembles outperform the simple base clusterings in terms of quality and robustness. The performance of the proposed CLWGC with the k-means and fuzzy c-means clustering algorithms as its simple basic clusterer is compared with the ones of the k-means and fuzzy c-means clustering algorithms in terms of NMI in Table 3. Each result is an averaged NMI over 30 independent runs. The proposed CLWGC clearly outperforms the simple k-means and fuzzy c-means clustering algorithms on all benchmark datasets.

Table 3 Performance comparison of the base clustering algorithms with CLWGC when k-means and fuzzy c-means are used as its base clustering algorithm
Full size table

4.3 State-of-the-art clustering algorithms

The proposed CLWEAC and CLWGC methods with the k-means and fuzzy c-means clustering algorithms as its simple basic clusterer are evaluated, and their results have been compared to 12 state-of-the-art ensemble clustering methods, that is, CSPA [63], HGPA [63], MCLA [63], hybrid bipartite graph formulation (HBGF) [18], SimRank similarity-based method (SRS) [33], weighted connected triple-based method (WCT) [34], cluster selection evidence accumulation clustering (CSEAC) [4], weighted evidence accumulation clustering (WEAC) [32], Wisdom of Crowds Ensemble (WCE) [5], graph partitioning with multi-granularity link analysis (GPMGLA) [32], and two-level co-association matrix ensemble (TME) [73], elite cluster selection evidence accumulation clustering (ECSEAC) [53].

Each method is executed 30 independent trials for a dataset. So, each of the reported results are the averaged value on 30 independent trials. Table 4 reports the results of the proposed CLWEAC and CLWGC methods with the k-means and fuzzy c-means clustering algorithms as its simple basic clusterer along with those of the state-of-the-art ensemble clustering methods.

Table 4 Performances of the proposed CLWEAC and CLWGC methods with the k-means and fuzzy c-means clustering algorithms as its simple basic clusterer compared with 12 state-of-the-art ensemble clustering methods
Full size table

According to Table 4, the proposed CLWEAC and CLWGC methods outperform all the state-of-the-art ensemble clustering methods irrespective to the simple basic clusterer (it should be either the k-means clustering algorithm or the fuzzy c-means clustering algorithm). Table 5 summarizes Table 4. According to Table 5, both of the proposed CLWEAC and CLWGC methods are always the best two methods among all of the state-of-the-art ensemble clustering methods.

Table 5 Summary of the results presented in Table 4
Full size table

4.4 Robustness analysis

The performances of the proposed CLWEAC and CLWGC methods and the state-of-the-art ensemble clustering methods have been evaluated on all dataset with different ensemble sizes, i.e., \(\beta\). For each dataset, for each method, and for each ensemble size, the experiment has been done 30 times and the averaged performance has been considered to make our results reliable. Then the average NMIs over all datasets are depicted in Fig. 2 when the k-means clustering algorithm is considered as its simple basic clusterer. The same results are repeated in Fig. 3 when the fuzzy c-means clustering algorithm is employed as its simple basic clusterer.

Fig. 2
figure 2

Effect of different ensemble sizes on different clustering methods when the k-means clustering algorithm is considered as their simple basic clusterer. NMI values of the different clustering methods with varying ensemble sizes

Full size image
Fig. 3
figure 3

Effect of different ensemble sizes on different clustering methods when the fuzzy c-means clustering algorithm is considered as their simple basic clusterer. NMI values of the different clustering methods with varying ensemble sizes

Full size image

According to Figs. 2 and 3, in terms of the average NMI scores over all 10 benchmark datasets with different \(\beta\), the proposed CLWEAC and CLWGC methods have the best consensus performances. They are also robust to ensemble size.

4.5 Complexity analysis

In this section, the run time of multiple ensemble clustering methods varying data sizes is compared. The experiments are yielded on various subsets of the LR dataset made up of totally 20,000 data objects. Different methods are executed on randomly selected subsets of N′ objects from the LR dataset to evaluate their run time. As depicted in Fig. 4, the MCLA method and the proposed CLWGC method are, respectively, the fastest methods to process the entire LR dataset. So, CLWGC method is superior to CLWEAC method, both in terms of output clustering quality and time complexity.

Fig. 4
figure 4

Run time of different methods with varying data sizes

Full size image

5 Conclusion and future works

This study has proposed a new clustering ensemble framework based on cluster-level weighting. The paper has considered the certainty amount the given ensemble has about a cluster as the reliability of that cluster. The certainty amount the given ensemble has about a cluster has been computed by the accretion amount of that cluster by the ensemble. Then by selecting the best clusters and assigning a weight to each selected cluster based on its reliability, the final ensemble has been created. At the next step, the paper has proposed CLWCAM instead of traditional CAM. Then, two consensus functions have been introduced and used for production of the consensus partition. The proposed framework completely overshadows the state-of-the-art clustering ensemble methods experimentally.

For the future work, one can explore more diversity-oriented reliability metrics. Using optimization methods to select an optimized subset of clusters can be also explored. For example, the most diverse subset can be sought while considering cluster-level weighting.