Long-wave interfacial instabilities in a thin electrolyte film undergoing coupled electrokinetic flows: a nonlinear analysis

Abstract

Spatiotemporal deformations of the free charged surface of a thin electrolyte film undergoing a coupled electrokinetic flow composed of an electroosmotic flow (EOF) on a charged solid substrate and an electrophoretic flow (EPF) at its free surface are explored through linear stability analysis and the long-wave nonlinear simulations. The nonlinear evolution equation for the deforming surface is derived by considering both the Maxwell’s stresses and the hydrodynamic stresses. The electric potential across the film is obtained from the Poisson–Boltzmann equation under the Debye–Hückel approximation. The simulations show that at the charged electrolyte–air interface, the applied electric field generates an EPF similar to that of a large charged particle. The EOF near the solid–electrolyte interface and the EPF at the electrolyte–air interface are in the same (or opposite) directions when the zeta potentials at the two interfaces are of the opposite (or same) signs. The linear and nonlinear analyses of the evolution equation predict the presence of travelling waves, which is strongly modulated by the applied electric field and the magnitude/sign of the interface zeta potentials. The time and length scales of the unstable modes reduce as the sign of zeta potential at the two interfaces is varied from being opposite to same and also with the increasing applied electric field. The increased destabilization is caused by a reverse EPF near the free surface when the interfaces bear the same sign of zeta potentials. Flow reversal by EPF at the free surface occurs at smaller zeta potential of the free surface when the film is thicker because of less influence of the EOF arising at the solid–electrolyte boundary. The amplitude of the surface waves is found to be smaller when the unstable waves travel at a faster speed. The films can undergo pseudo-dewetting when the free surface is almost stationary under the combined influences of EPF and EOF. The free surface instability of the coupled EOF and EPF has some interesting implications in the development of micro/nano fluidic devices involving a free surface.

1 Introduction

Fluid transport is crucial for heat and mass transfer, separation or mixing operations in diverse miniaturized technologies such as power generators in microfuel cells, MEMS applications, sensors, lab-on-a-chip devices, and drug delivery modules, among many others (Lyklema 1995; Hunter 1996; Li 2004; Masliyah and Bhattacharjee 2006; Gravesen et al. 1993). In this regard, the conventional pressure-driven flows are not so attractive because of their limitations to overcome the large frictional losses associated with the micro/nano channels (Fu et al. 2003). The electroosmotic flows (EOF) driven by external electric field can be a suitable alternative where the electrolytes are transported on a charged surface with the help of an external electric field (Anderson 1989; Yang et al. 2004; Suresh and Homsy 2004; Hadermann et al. 1974). Figure 1 schematically describes an EOF situation where a thin electrolyte film flows on a stationary charged solid surface under the influence of an externally applied electric field. In the EOF, the electrical double layer (EDL) with excess counter-ions near the charged surface migrate under the action of the external electric field, which in turn induces flow to the bulk of the film outside the EDL. High precision flow control and flow reversibility are some distinct advantages of EOF in the micro/nano fluidic devices. Thus, the different characteristics of EOF have been intensively studied as summarized in review articles by Lyklema (1995), Hunter (1996), Li (2004), Masliyah and Bhattacharjee (2006) and Stone et al. (2004).

Fig. 1

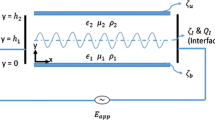
Schematic diagram of an electroosmotic flow of an electrolyte film with free interface. The Debye length is indicated by λ _d and the base-state film thickness by d. The symbols ζ_s and ζ_a are the zeta potentials at the solid–electrolyte and the electrolyte–air interfaces. The negatively charged interface in the diagram moves toward the anode under the applied field, as shown by the arrow

The literature suggests that the studies related to the open channel EOF with a deformable free surface have received far less attention as compared to those related to EOF inside confined channels. Even in the situations where the confined multi-layer EOFs (Gao et al. 2005a, b, c, 2007; Brask et al. 2003, 2005; Ngoma and Erchiqui 2006; Choi et al. 2010, 2011) are considered, the interfacial deformation is ignored for the sake of simplicity. A few recent studies (Joo 2008a, b; Qian et al. 2009; Rizwan Sadiq and Joo 2009) examined the possibility of surface instability for an EOF with free-boundary. However, these studies considered only the hydrodynamic stress components and ignored the stress contributions from the electrostatic field. Interestingly, some recent experimental studies (Lee and Li 2006; Lee et al. 2006) have shown that the free surface instability in EOF shows ‘shearing’ wall-like behavior due to the accumulation of surface charges at the electrolyte–air interface. These studies point that the free electrolyte–air interface can also have a zeta potential because of the preferential adsorption, accumulation, depletion, or dissociation of ions near the surface compared to the bulk electrolyte (McShea and Callaghan 1983). Choi et al. (2010, 2011) considered the full description of the Maxwell’s stresses (Melcher and Taylor 1969; Saville 1997; Burcham and Saville 2002) along with the hydrodynamic stresses in their formulation without considering the free surface deformation. The most interesting result is the existence of an electrophoretic flow (EPF) driven by the charged electrolyte–air interface, in addition to the EOF at the solid–electrolyte interface. The EOF and the EPF are in the same or opposite directions depending on whether the two interfacial potentials have the opposite or same signs, respectively. This is because the EOF is derived from the motion of counter-ions near an immobile surface, whereas the EPF is the motion of the charged, mobile surface itself. Choi et al. (2010, 2011) thus showed that when an electrolyte with a free surface undergoes EOF, the similar or dissimilar zeta potentials at the electrolyte–air and electrolyte–solid interfaces can cause a variety of interesting flow patterns including the Poiseuille, Couette or free surface flows. Recently, Ray et al. (2011, 2012) performed a comprehensive Orr–Sommerfeld (O–S) analysis to reveal the coexistence of a long-wave interfacial mode and a finite wave number shear flow mode of instability in the coupled EOF and EPF. The analyses further showed that the interfacial mode is the dominant mode of instability when the surface waves are under the strong influence of the viscous force and experience a retarding influence from the EPF at the electrolyte–air free surface. In contrast, the shear mode was found to dominate when the contribution from the inertial stresses is larger at larger flow rates and when the EPF causes a significant synergistic or retarding influence on the electrolyte–air interface. These studies highlight that it is the interfacial mode of instability that behaves like a ‘shearing wall’ in the same or opposite direction of the electric field when the zeta potentials at the interfaces are either opposite or similar. In such situations, the shear mode always travels in the direction of the applied electric field. Further, the linear stability analysis (LSA) showed the interfacial mode to be a long-wave instability thus motivating the present study on its nonlinear evolution.

The objective of this study is to examine the nonlinear evolution of the interfacial mode of the free surface instability in the coupled EOF and EPF in a thin electrolyte film with charged interfaces. The nonlinear evolution equation in the long-wave limit is derived by employing the Maxwell and hydrodynamic stresses in the governing equations with appropriate boundary conditions. The basic equations employed are same as in the LSA of Ray et al. (2011, 2012). The electric potential across the film is modeled by the Poisson–Boltzmann equation under the Debye–Hückel approximation. The LSA uncovers the influence of the operating conditions such as the zeta potentials at the interfaces and external electric field on the length and time scales of the instability. The nonlinear simulations show that the applied electric field in the direction of the EOF can indeed generate an interfacial mode of instability, as predicted by the linear stability (Ray et al. 2011, 2012). Further, the simulations show the travelling nature of the interfacial modes of instability and support the fact that the EPF can retard (accelerate) the EOF when both interfaces have the same (opposite) sign of the zeta potential and can also cause reverse flow near the electrolyte–air interface of the film. Interestingly, the films can also undergo larger amplitude deformations leading to pseudo-dewetting when the electrolyte–air interface is almost stationary. The modeling methodology and results discussed here can thus contribute in the studies related to the EOF with a free surface.

2 Problem formulation

The computational domain is schematically shown in Fig. 1. A two-dimensional (2-D) Cartesian coordinate system (x, y) is employed with the origin set at the shear line, y = 0. The EOF is driven by electric field (E _el) applied across an incompressible, Newtonian, binary electrolyte of density ρ, kinematic viscosity v, dynamic viscosity μ, dielectric permittivity ε, and mean thickness d. The solid–electrolyte and the electrolyte–air interfaces have fixed zeta potentials ζ_s and ζ_a, respectively.

The dimensional equations governing the electrokinetic flow (EKF) are the mass and the momentum conservation with the hydrodynamic and electrostatic (Maxwell’s) stress contributions,

$$ \nabla \cdot {\mathbf{U}} = 0 $$

(2.1)

$$ \rho \frac{{\text{D}{\mathbf{U}}}}{\text{D}T} = - \nabla P + \mu \nabla^{2} {\mathbf{U}} + \varepsilon \nabla^{2} \Upphi \nabla \Upphi . $$

(2.2)

where P is the pressure, U (U, V) is the velocity vector, T is time, and Φ is the electric potential. Here D indicates the substantial derivative. The governing equations are converted to the following dimensionless forms by choosing the length and time scales to be, d and d ²/v,

$$ \nabla \cdot {\mathbf{u}} = 0 $$

(2.3)

$$ \frac{{{\text{D}}\mathbf{u}}}{{{\text{D}}t}} = - \nabla p + \nabla^{2} {\mathbf{u}} + \frac{{E_{O} }}{{E_{R} }}\nabla^{2} \phi \nabla \phi $$

(2.4)

The dimensionless numbers $E_{O} = \varepsilon E_{\text{el}} {d}\zeta_{\text{s}} /(\rho \nu^{2} )$ and $E_{R} = \zeta_{\text{s}} /(E_{\text{el}} d)$ are the measures of the applied electroosmotic force and the zeta potential at the solid surface, respectively. The dimensionless time t, pressure p, velocity u (u, v) and electric potential ϕ are in the units of d ²/v, ρv ²/d ², v/d and E _el d, respectively.

No-slip and no-penetration boundary conditions (u = 0) are enforced along the shear line, y = 0. At the electrolyte–air interface, y = h(x, t), the normal $({\mathbf{n}} \cdot {\bar{\mathbf{T}}} \cdot {\mathbf{n}} = - \Upgamma \kappa )$ and tangential $({\mathbf{t}} \cdot {\bar{\mathbf{T}}} \cdot {\mathbf{n}} = 0)$ stress balances are enforced. The total stress, ${\bar{\mathbf{T}}}$ is the combination of Maxwell’s and hydrodynamic stresses $\left[ {\mu \left( {\nabla {\mathbf{u}} + \nabla {\mathbf{u}}^{T} } \right) + \varepsilon \left( {{\mathbf{EE}} - 0.5\left( {{\mathbf{E}} \cdot {\mathbf{E}}} \right){\mathbf{I}}} \right)} \right]$, where E is the electric field. Here ${\mathbf{n}} = {{( - h_{x} ,1)} \mathord{\left/ {\vphantom {{( - h_{x} ,1)} {\left( {\sqrt {1 + h_{x}^{2} } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sqrt {1 + h_{x}^{2} } } \right)}}$, ${\mathbf{t}} = {{(1,h_{x} )} \mathord{\left/ {\vphantom {{(1,h_{x} )} {\left( {\sqrt {1 + h_{x}^{2} } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sqrt {1 + h_{x}^{2} } } \right)}}$ and $\kappa = - \nabla \cdot {\mathbf{n}}$ are the normal vector pointing outward, tangent vector, and the curvature of the electrolyte–air interface, respectively. The dimensionless parameter $\Upgamma = \gamma d/\left( {\rho \nu^{2} } \right)$ is a measure of surface tension where γ is the surface tension coefficient. The location of the electrolyte–air free surface, y = h(x, t) is defined by the kinematic condition, ${\text{D}}h/{\text{D}}t = {\mathbf{u}} \cdot {\mathbf{n}}$.

In the current study, we assume that the external electric field is much weaker than the electric field arising from the charged interfaces and the EDLs of the two interfaces are not overlapped. Therefore, the EDLs are under equilibrium and are not distorted by the external field. In addition, we assume that the zeta potentials of the interfaces are much lower than the thermal potential. The dimensionless electric potential can be expressed as $\phi = \phi_{e} + \phi_{z}$, where the two potentials are: (1) potential of the externally applied electric field, $\phi_{e} = - x$, and (2) potential arising from the charged interfaces, $\phi_{z} = E_{R} [\cosh (y/De) + A\sinh (y/De)]$. The latter is obtained from the Poisson–Boltzmann equation under Debye–Hückel approximation, $d^{2} \phi_{z} /{\text{d}}y^{2} = \phi_{z} /De^{2}$, with the boundary conditions at $y = 0, \, \phi_{z} = E_{R}$ and at $y = h, \, \phi_{z} = E_{R} Z_{R}$. The total electric potential ϕ can thus be expressed as,

$$ \phi = - x + E_{R} [\cosh (y/De) + A\sinh (y/De)]. $$

(2.5)

where De = λ _d /d is the Debye number, which relates Debye length (λ _d ) and the mean liquid height (d), $Z_{R} = \zeta_{\text{a}} /\zeta_{\text{s}}$ is the ratio of the zeta potentials at the electrolyte–air and electrolyte–solid interfaces, and $A = \left( {Z_{R} - \cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right)/\left( {\sinh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right)$.

3 Base-state analysis

Steady x-directional EKF with undisturbed electrolyte–air interface (h = 1 and v = 0) leads to the base-state velocity profile (Choi et al. 2010, 2011; Ray et al. 2011, 2012) $\bar{u}(y) = E_{O} \left[ {\cosh \left( {{y \mathord{\left/ {\vphantom {y {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) + \bar{A}\sinh \left( {{y \mathord{\left/ {\vphantom {y {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right]$, where the no slip $\bar{u} = 0$ at y = 0, and the tangential stress balance $\bar{u}_{y} = - \left( {{{E_{O} } \mathord{\left/ {\vphantom {{E_{O} } {E_{R} }}} \right. \kern-\nulldelimiterspace} {E_{R} }}} \right)\bar{\phi }_{\zeta y} (\bar{\phi }_{\zeta x} - 1)$ at y = 1 boundary conditions are enforced. Here $\bar{A} = \left[ {Z_{R} - \cosh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right]/\sinh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)$ is a constant. The expression for the base-state velocity profile provides the velocity of the undeformed electrolyte–air interface, $u(1) = - E_{O} (1 - Z_{R} )$. Based on this result, the electrolyte–air interface behaves like: (1) a stationary wall at Z _R  = 1, (2) a shearing wall moving in the direction of the EOF when Z _R  < 1, and (3) a wall shearing in the direction opposite to the EOF when Z _R  > 1 (Choi et al. 2010, 2011; Ray et al. 2011). The velocity profile confirms that the net EKF is composed of: (1) EOF near the charged immobile substrate due to the presence of the counter-ions within its EDL and the movement of the counter-ions within the EDL along the direction of the applied electric field; (2) EPF of the charged mobile electrolyte–air interface which undergoes motion by the externally applied electric field. The flow of the electrolyte–air interface is analogous to the electrophoretic motion (EPF) of a large charged particle (RDe ⁻¹ ≫ 1) where De is the Debye length and R is the radius of the particle (Hiemenz and Rajagopalan 1997).

Figure 2 shows the base-state velocity profiles across the film at different values of Z _R and E _O . Comparing the velocity profiles in the curves 1–4 and 1a–4a, it is clear that although the strength of the applied field governs the flow rate of the EKF, the qualitative nature of the velocity profiles remains similar. Further, the figure clearly depicts two different types of EKF near the electrolyte–solid and electrolyte–air interfaces, which influence the overall characteristics of the base-state velocity profile. Under the conditions depicted in Fig. 1 for illustration, the fluid within the EDL of the positively charged solid surface always moves from left to right under the influence of the applied electric field. In contrast, the charged electrolyte–air interface can move in either direction depending on the sign of its zeta potential and the influence of the EOF extending to the free surface. The figure shows a Couette-type flow (curve 1 and 1a) when the interfaces have opposite zeta potentials, Z _R  < 0. In this situation, the charged electrolyte–air interface also moves in the direction of the EOF, but at even higher speed because of the EPF. The curves 2 and 2a show that when the electrolyte–air interface is free of charge, the base-state velocity profile appears as a fully developed boundary layer profile. The EPF in this case does not influence the flow profile and under this condition only the surface of an electrolyte film undergoing EOF can be considered to be truly ‘free’! Further, the curves 3 and 3a show that when the interfaces have same sign zeta potentials (Z _R  = 1), the EPF counterbalances the EOF to develop a Poiseuille-type flow with a parabolic velocity profile. The EPF is now in a direction opposite to that of the EOF. Under this condition the characteristics of the electrolyte–air interface are similar to a soft deformable wall. In the situation where the electrolyte–air interface has the same sign, but a higher zeta potential than the solid–electrolyte interface (Z _R  > 1), a highly shearing EPF acting in the opposite direction of the EOF is observed (curves 4 and 4a). A reverse flow near the electrolyte–air interface against the EOF near the solid surface is induced under this condition. Briefly, Fig. 2 summarizes all the possible flow regimes of a thin film with a free surface undergoing the EPF coupled with the EOF near the charged solid wall.

Fig. 2

Base-state velocity profiles where curves 1(1a)–4(4a) correspond to Z _R  = −1, 0, 1 and 2, respectively, when E _O  = 0.05 (solid lines) and 0.1 (broken lines), respectively, for film thickness De = 0.1, E _R  = 1 and Γ = 100

4 Nonlinear formulation

The analysis has been performed for small Debye number (De ≪ 1), which ensures that the film is much thicker than the distance over which significant charge separation can occur. This ensures that the electrical double layers (EDLs) of the bottom substrate and the free surface are non-overlapping and in equilibrium. The evolution equation for the electrolyte film is derived under the lubrication approximation, in which the characteristic length ξ in the x-direction is assumed to be much larger than the thickness of the film (Benney 1966; Ray et al. 2011). For this purpose, the governing equations and boundary conditions are rescaled with the parameters, ξ = αx, η = y and τ = αt. The velocities and pressure in the governing equations and boundary conditions are expanded in power series of α ≪ 1, $u = u_{0} (y) + \alpha u_{1} (x,y,t) + O(\alpha^{2} ),$ $v = \alpha v_{1} (x,y,t) + O(\alpha^{2} )$ and $p = p_{0} (y) + \alpha p_{1} (x,y,t) + O(\alpha^{2} )$. The resulting leading order and first order governing equations and boundary conditions (Benney 1966; Ray et al. 2011) lead to the following evolution equation for the electrolyte–air interface after considerable labor and rearrangements,

$$ \begin{aligned} h_{t} & = E_{O} F_{1} (h)h_{x} \\ &\quad - \alpha \left[ {E_{O}^{2} De^{2} F_{2} (h)h_{x} + \left( { - \frac{{E_{O} E_{R} }}{{De^{3} }} + \frac{{E_{O}^{2} }}{De}} \right)F_{3} (h)h_{x} + E_{O}^{2} DeF_{4} (h)h_{x} + \frac{{E_{O} }}{{E_{R} }}\Upgamma^{*} F_{5} (h)h_{x} + F_{6} (h)h_{xxx} } \right]_{x} , \\ \end{aligned} $$

(4.1)

where $A = {{\left[ {Z_{R} - \cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {Z_{R} - \cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right]} {\sinh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}} \right. \kern-\nulldelimiterspace} {\sinh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}$, $B = {{\left[ {Z_{R} \cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right]} \mathord{\left/ {\vphantom {{\left[ {Z_{R} \cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right]} {\sinh^{2} \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}} \right. \kern-\nulldelimiterspace} {\sinh^{2} \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}$, $F_{1} (h) = [1 - Z_{R} ] - B\left[ {1 - \cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right]$, $\begin{aligned} F_{2} (h) & = B\left[ {\left( {1 - \left( {{{h^{2} } \mathord{\left/ {\vphantom {{h^{2} } {2De^{2} }}} \right. \kern-\nulldelimiterspace} {2De^{2} }}} \right)} \right)\cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right]\left( {\cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - B\left( {\cosh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right) + A\sinh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right) \\ \quad - BA\left[ {\left( {1 - \left( {{{h^{2} } \mathord{\left/ {\vphantom {{h^{2} } {2De^{2} }}} \right. \kern-\nulldelimiterspace} {2De^{2} }}} \right)} \right)\sinh \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right] \\ \end{aligned}$, $F_{3} (h) = AB{{h^{3} } \mathord{\left/ {\vphantom {{h^{3} } 3}} \right. \kern-\nulldelimiterspace} 3}$, $F_{4} (h) = ABh$, $F_{5} (h) = {{h^{2} } \mathord{\left/ {\vphantom {{h^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}$, and $F_{6} (h) = {{h^{3} } \mathord{\left/ {\vphantom {{h^{3} } 3}} \right. \kern-\nulldelimiterspace} 3}$.

Equation (4.1) describes the spatiotemporal evolution of the electrolyte–air interface undergoing EKF. Essential steps for the derivation are outlined in the “Appendix” (Ray et al. 2011).

The evolution equation is perturbed by employing the customary normal linear modes, $h(x,t) = 1 + \delta (e^{ikx + \Upomega t} + c.c.)$, and the following long-wave dispersion relation is thus obtained (Ray et al. 2011),

$$ \begin{aligned} \Upomega &= E_{O} [1 - Z_{R} ]ik - DeE_{O} \frac{{Z_{R} \cosh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1}}{{\sinh^{2} \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}\left[ {1 - \cosh \left( {1/De} \right)} \right]ik \\ &\quad + \alpha \left[ \begin{gathered} E_{O}^{2} De^{2} \bar{B}k^{2} \left\{ {\cosh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - \bar{B}\left( {\cosh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right) + \bar{A}\sinh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right\}\left\{ {\left( {1 - \frac{1}{{2De^{2} }}} \right)\cosh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right) - 1} \right\} \hfill \\ - E_{O}^{2} De^{2} \bar{A}\bar{B}\left\{ {\left( {1 - \frac{1}{{2De^{2} }}} \right)\sinh \left( {{1 \mathord{\left/ {\vphantom {1 {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)} \right\}k^{2} - \frac{1}{3}\left( {\frac{{E_{O} E_{R} }}{{De^{3} }} - \frac{{E_{O}^{2} }}{De}} \right)ABk^{2} + \frac{{E_{O} }}{{2E_{R} }}k^{2} + E_{O}^{2} De\bar{B}\bar{A}k^{2} - \frac{1}{3}\Upgamma k^{4} \hfill \\ \end{gathered} \right] \\ \end{aligned} $$

(4.2)

Here (Ω = −ikc) is the linear growth coefficient where (c) is the phase-speed of the travelling wave, and (k) is the wavenumber of instability. The terms c.c. and δ in the normal linear mode denote complex conjugate and perturbations of infinitesimal amplitude. The dispersion relation clearly shows that the growth coefficient possesses a real and an imaginary part. Thus, the instability has travelling wave characteristics with temporally growing amplitudes. The first term in the dispersion relation shows the changeover of the direction of travel of the interfacial waves with the change in Z _R , as observed previously in the base-state and O–S analyses (Choi et al. 2010; Ray et al. 2011, 2012). This effect is more pronounced when the contribution from the second term is negligible (De ≪ 1) in the first two imaginary terms of Eq. (4.2). In the real part, the term with k ⁴ accounts for the stabilizing influence of the surface tension, Γ. For De ≪ 1 and Z _R  = 0, the first two terms combine to give a constant value of (E _O ik), which indicates the presence of traveling waves with a constant velocity for a thicker film and under a constant applied field. Further, for De ≪ 1 the destabilizing term with k ² remains constant for a given E _O regardless of the value of Z _R . Thus, for very thick films, the growth rate does not change at given E _O and Γ. For thinner films (De ≥ 0.2), the system can be stable beyond a critical value of E _O when Z _R  ≪ 0.

The temporal deformations at the electrolyte–air interface and the subsequent interfacial morphologies are explored by the numerical integration of Eq (4.1). The nonlinear evolution equation was discretized in space by employing the finite difference scheme and the resulting ordinary differential equation was time marched by employing Gear’s algorithm. A periodic boundary condition was employed at the spatial boundaries and a volume preserving, small amplitude random perturbation was enforced to initiate the numerical simulations (initial maximum amplitude was 0.01). The typical domain size of the simulations was chosen in the multiples of the dimensionless dominant wavelength and the grid independence of the solutions was confirmed by varying the number of grid points.

5 Results and discussion

In this section, we discuss the results with the variation of three key parameters: $Z_{R} = \zeta_{\text{a}} /\zeta_{\text{s}}$, $E_{O} = \varepsilon E_{\text{el}} {d}\zeta_{\text{s}} /(\rho \nu^{2} )$, $E_{R} = \zeta_{s} /(E_{\text{el}} d)$, and De = λ _d /d. The non-dimensional number Z _R signifies the ratio of the zeta potentials at the electrolyte–air and electrolyte–solid interfaces. The electrolyte–air interface potential is independent of the potential at the solid–electrolyte interface and is regulated by the adsorption, accumulation, depletion, or dissociation of ions near the free surface as compared to the bulk electrolyte (McShea and Callaghan 1983). The key features of the coupled EKF can be understood under the following scenarios: the interfaces have opposite (or similar) sign potentials, Z _R  < 0 (Z _R  > 0) or when the electrolyte–air interface is free of charge, Z _R  = 0. For a given charged surface, the electroosmotic number E _O is the ratio of the applied electric field to the viscous forces. Increase in E _O signifies a stronger EOF under a weaker viscous influence. The dimensionless number E _R signifies the influence of the substrate–electrolyte surface charge (causing EOF) when the applied electric field strength (E _el) is kept constant. The dimensionless number De correlates with the film thickness when the thickness of the EDL is constant. A thicker film has a smaller value of De whereas a thinner film possesses a larger value of De. It may be noted that the results from the long-wave LSA and nonlinear simulations capture the salient features of the interfacial modes of instabilities for a range of Z _R , E _O , and E _R . In what follows, the dimensionless parameters in the results are evaluated within the physically realistic ranges of the dimensional parameters: ρ ~ 1,000 kg/m³, μ ~ 0.001 Pa s, ε ~ 80, ε ₀ = 8.85 × 10⁻¹² F/m, d ~ 1–100 μm, ζ_s = ζ_a ~ ±10–25 mV, ϕ ₀ ~ 10–100 V, and γ ~ 0.03–0.07 N/m. Previous studies show that the typical ζ_s for the deionized (DI) water and 1 mM brine solution on oxidized PDMS (polydimethylsiloxane) are −98 and −85 mV, respectively (Lee and Li 2006). The studies also show that ζ_a for the deionized water and 1 mM brine water at a liquid–air interface are ~65 mV and −40 mV, respectively (Lee and Li 2006). At the base state, a liquid film with ζ_a = 25 mV undergoing EOF on a surface with ζ_s = −10 to +25 mV leads to the dimensionless Z _R  = −2.5 to 1. Further, when a 100 μm water film (μ ~ 0.001 Pa s and ε ~ 80) undergoes EOF on a charged surface having ζ_s = 50 mV and between a pair of electrodes having distance 0.001 m, the dimensionless variables E _O and E _R range from 0.0354 to 0.354 and 0.05 to 0.5, respectively, as the applied voltage in the flow direction is varied from 10 to 100 V. Variations in the dimensionless parameters for a wider range demonstrate the importance of the ratio of the zeta potentials at the interfaces, the strength of the applied field and resulting flow rate, and the film thickness on the long-wave interfacial mode of instability.

5.1 Linear stability analysis

Previous studies by Ray et al. (2011, 2012) predicted that instabilities for the system under consideration can posses both a long-wave interfacial mode and a finite-wavenumber shear mode. In the present study, we focus on the nonlinear aspects of the long-wave interfacial mode of instability of an electrolyte film undergoing coupled EOF (originating at the solid–electrolyte interface) and EPF (at the free surface). A comparative study between the results for the O–S and the long-wave LSA by Ray et al. (2012) shows similar length and time scales for the interfacial mode at higher values of De (0.1–0.2) and for |Z _R | < 1.0. They also showed that when Z _R  = 1.5 and De = 0.1–0.2, the O–S and LW results are comparable in the range E _O  = 0–4 and E _R  = 0–10. Thus, we confine the present analysis around these parameters where the instability essentially has a long-wave characteristic.

In Figs. 3, 4 and 5, we present the results obtained from the LSA in the long-wave regime for different values of Z _R , E _O , and E _R , respectively, keeping the other parameters fixed. The plots 3a–d show the variations in the dominant growth rate (kc _i ) _m , the corresponding wavenumber (k _m ), the neutral stability plots (k _c ), and the dominant wave speed (c _rm ) with the change in Z _R . The broken and the solid lines depict the results for relatively thicker and thinner films at larger and smaller De. Plots a–c in Fig. 3 show that when the EPF is in the same direction as EOF (Z _R  < 0), the thinner films (De is higher) are more stable as (kc _i ) _m is smaller or the wave length is larger. In such a situation, larger wall friction from the solid surface reduces the growth of instability in a thinner film (higher De). In contrast, when the EPF moves in the opposite direction of the EOF and at low velocities (Z _R  ~ 1), the thinner films are more unstable than the thicker ones because now the vertical zeta potential gradient enforces a larger destabilization at the electrolyte–air interface. Plot d shows that the dominant wave speed (c _rm ) changes its direction (sign) near Z _R  = 1 where the electrolyte–air interface becomes stationary. Importantly, the reversal in the direction of travel of the unstable waves happens at higher Z _R when the films are thinner (higher De). Further, the plot confirms that the wave speed at the interface increases for both the situations when the electrolyte–air interface moves at a higher speed in the same (Z _R  < 1) or in the opposite (Z _R  > 1) direction of the EOF. The nonlinear simulations also confirm this observation in the next section.

Fig. 3

Plots a–d show the variation of (kc _i ) _m , k _m , k _c , and c _rm , respectively, with Z _R when E _O  = 0.5, E _R  = 1 and Γ = 100

Fig. 4

Plots a, c show variations of (kc _i ) _m with E _O and E _R and the plots b, d show the variation of k _m with E _O and E _R when Z _R  = 1.5 and Γ = 100

Fig. 5

The spatiotemporal evolution of the electrolyte–air interface over a domain size of Λ. Plots a–f show the evolution of free interface for Z _R  = −0.5, 0.5, 1, 1.2, 1.5 and 2, respectively, when E _O  = 1, E _R  = 1 and De = 0.05. The profiles 1–2 correspond to: a t = 1,350.6 and 1,364.4; b t = 1,666.9 and 1,718.6; c t = 670.7 and 833.6; d t = 905.6 and 928.1; e t = 312.2 and 321.3; and f t = 124.8 and 127.5. The waves travel in the direction of the arrow

Figure 4a, b shows that the length and time scales of instability progressively reduce. i.e., both (kc _i ) _m and (k _m ) increase with E _O . For fixed, Z _R  = 1.5, E _R  = 1, and Γ = 100, increase in E _O corresponds to the increase in the applied electroosmotic potential in the flow direction because E _O  ~ E _el. Thus, a higher electroosmotic force imparts larger destabilization to the system. Figure 4c, d shows (kc _i ) _m and (k _m ) initially decrease, reach a minimum value, and then slowly increase with E _R . In this situation, for the fixed values of Z _R  = 1.5, E _O  = 0.5 and Γ = 100, (kc _i ) _m initially decreases because at Z _R  = 1.5, increase in E _R enhances the reverse flow due to the EPF at the interface, thus decreasing the overall EKF (EOF + EPF). However, beyond a threshold value of E _R , the reverse flow is now strong enough to contribute to the growth of instability and (kc _i ) _m again increases slowly with E _R .

5.2 Nonlinear simulations

5.2.1 Effect of zeta potential ratio

Figures 5, 6, and 7 show the spatiotemporal morphologies at the free surfaces with the change in Z _R at different film thickness (De = 0.05, 0.1, and 0.2) when E _O  = E _R  = 1 and Γ = 100. The plots a–f in all the figures correspond to Z _R  = −0.5, 0.5, 1.0, 1.2, 1.5, and 2, respectively.

Fig. 6

The spatiotemporal evolution of the electrolyte–air interface over a domain size of Λ. Plots a–f show the evolution of free interface for Z _R  = −0.5, 0.5,1, 1.2, 1.5 and 2, respectively, when E _O  = 1, E _R  = 1 and De = 0.1. The profiles 1–2 correspond to: a t = 1,853.3 and 1,860.6; b t = 2,124.2 and 2,154.7; c t = 2,873.1 and 2,975.4; d t = 3,064.4 and 3,171; e t = 2,426.7 and 2,469.1 and f t = 2,317.3 and 2,337.6. The waves travel in the direction of the arrow

Fig. 7

The spatiotemporal evolution of the electrolyte–air interface over a domain size of Λ. Plots a–f show the evolution of free interface for Z _R  = −0.5, 0.5, 1, 1.2, 1.5 and 2, respectively, when E _O  = 1, E _R  = 1 and De = 0.2. The profiles 1–2 corresponds to: a t = 4829.7 and 4841.4; b t = 1083 and 1101.3; c t = 838.4 and 864.6; d t = 710.9 and 790.2; e t = 548.5 and 572.9; and f t = 347.4 and 359.3. The waves travel in the direction of the arrow

Figure 5 (De = 0.05) shows that after a short time, a small amplitude initially random perturbation at the free surface evolves on the dominant length scale as predicted by the linear analysis. The amplitude of the resulting traveling wave grows in time. The arrowheads show the direction of the travel of the interface with time. The details on the amplitude and speed of the waves at different Z _R from the linear and the nonlinear analyses are discussed later after the discussion of the simulations, with the help of Figs. 8, 9, and 10. Figure 5a shows that when the zeta potentials have opposite signs (Z _R  = −0.5), the EPF at the electrolyte–air interface moves in the direction of the EOF from right to left, as predicted by both the LSA and the base-state analysis. In this situation, the EPF at the interfaces acts as an synergistic influence to the EOF because the electrolyte–air interface shears in the direction of the EOF, thus mimicking a Couette-type flow as shown by the plots 1 and 1a in Fig. 2. However, the wave amplitude remains small and saturates to a constant value after in the long time limit. Figure 5b shows another interesting scenario where the EPF at the electrolyte–air interface moves with a small velocity but in the opposite direction of the EOF at Z _R  = 0.5. The retardation introduced by the EPF at the deforming interface slows down the speed of the travelling waves, which leads to a larger amplitude of deformation as compared to the case Z _R  = −0.5 in Fig. 5a. However, in the nonlinear regime the strong EOF drags the interface in its direction. Figure 5c shows that when the base-state EKF is similar to a plane Poiseuille flow because of the retardation effect of the EPF at the electrolyte–air interface, the interfacial mode of instability shows similar features as found in Fig. 5b. In such a situation, although the deformable interface behaves like a non-slipping wall in the base state, the strong drag force arising from the EOF moves it in the direction depicted by the arrowhead (from right to left). In comparison, Fig. 5d displays that for Z _R  = 1.2, the EPF now becomes strong enough to pull the electrolyte–air interface in the opposite direction of the EOF. Under this condition, the direction of the travelling waves governed by the EPF also reverses and the unstable waves corresponding to the interfacial mode now travel from left to right. The nonlinear simulations show that although the wave speed at the deformable electrolyte–air interface is considerably small under such situations, the wave amplitude is the largest. Figure 5e, f shows that when the shearing EPF acting against the EOF gains further strength with increasing Z _R , the interfacial travelling waves can again impart larger inertial influence to the EKF by means of a strong reverse flow near the interface. Thus, an interfacial mode of instability with faster traveling waves and smaller amplitudes of deformations is observed.

Fig. 8

Evolution of maximum (h _max ) and minimum (h _min ) thicknesses of the electrolyte films for a–f representing Z _R  = −0.5, 0.5,1, 1.2, 1.5 and 2, respectively, when E _O  = 1, E _R  = 1 and (i) De = 0.05 and (ii) De = 0.2. The broken and the solid lines indicate h _max and h _min , respectively

Fig. 9

a The maximum and minimum thicknesses at the equilibrium (h ^eq) at different Z _R at De = 0.05 and 0.2. b Linear (solid line, square symbols) and nonlinear (broken line, circular symbols) growth of instabilities for Z _R  = −0.5 and 1.2 when E _O  = 1, E _R  = 1, and De = 0.2

Fig. 10

a Speed of the travelling waves (c _rm/NL ) nonlinear simulations, b ratio of the speeds of the travelling waves (c _rm,NL /c _rm,LSA ) from nonlinear simulations and LSA, at different Z _R and De when E _O  = 1, E _R  = 1. The triangle, square, and circular symbols represent De = 0.05, 0.1, and 0.2, respectively

Figure 6 (De = 0.1) shows that increase in the thickness of the film can lead to a similar type of EKF including the EPF at the deforming interface and EOF near the EDL as Z _R is varied. The simulations in Fig. 6a, f show that when the interfaces have opposite or same sign potentials and the EPF near the interface moves at a faster speed, the waves travel at a faster speed with smaller amplitude. In comparison, when the retarding influence of the EPF near the electrolyte–air interface is strong, the waves travel at a much lower speed and the interfacial deformations are much larger as can be seen in the Fig. 6b, e. Figure 6 also predicts a reversal of flow in the nonlinear regime near Z _R  = 1.2 as predicted in the case for a thicker film in Fig. 5.

When the films thickness is reduced further (De = 0.2), one can observe another interesting occurrence as shown in Fig. 7. For thinner films, the wave speed is always found to be smaller because of the large viscous resistance arising from the wall friction. Further, the movement of the EDL layer is expected to influence the EPF more because they are now separated by a smaller distance. Figure 7a, f for the thinner films shows a reversal of the wave movement at a larger Z _R  = 1.5. Owing to its closer proximity, the EOF undercurrent influences the EPF at the interface until a larger value Z _R . The thinner films require a stronger EPF to overcome the effect of the movement of nearby EDL and to cause a reverse flow at the electrolyte–air interface. Previously, the LSA in Fig. 3d also predicted that the reverse flow for a thicker film (for De = 0.1) occurs at a lower Z _R as compared to the thinner films (De = 0.2). Figure 7d shows that the thinner films can also develop a situation where the film can pseudo-dewet the solid surface especially when the EPF near the interface of the film moves at small speeds and the film is under the vertical gradient of the zeta potential gradient. The precursor layer thickness is found to be of the order of a few hundred nanometers under these conditions, which could further break up by means of the van der Waals intermolecular interaction on a non-wettable substrate.

Figure 8 considers the same cases discussed in Figs. 5, 6, and 7 and shows the temporal histories of the highest (h _max ) to lowest (h _min ) film thickness from the nonlinear simulations. The columns (i) and (ii) in this figure depict the results for De = 0.05 and 0.2 and the plots a–f display the results for Z _R  = −0.5, 0.5, 1.0, 1.2, 1.5, and 2, respectively. The plots clearly show that the deformation amplitude (h _max  − h _min ) at the free electrolyte–air interface initially increases in the linear growth regime and then saturates to a constant value in the long-time evolution. The extent of deformation is rather small when the free surface travels at a higher speed either in the same (row A) or in the opposite direction (row F) of the EOF for very high (row A) or very low Z _R (row F). However, the interfacial deformation can lead to a pseudo-dewetting of the film when the wave speed is low (rows C and D), where the flow-induced stabilization is minimal because surface is almost stationary, and under strong influence of the vertical zeta potential gradient. Further the deformations at the electrolyte–air interface are found to be larger for a thinner film as compared to the thicker film as shown by the columns (i) and (ii).

Figure 9a more clearly shows that when the electrolyte–air interface is nearly stationary (Z _R  ~ 1) the long-time near-equilibrium deformation, h ^eq, is found to be the largest for both the thinner and the thicker films. The thinner films (higher De) are found to deform more under the influence of a larger vertical zeta potential gradient as compared to the similar thicker films. Figure 9b shows the linear and nonlinear regimes of the growth of the interfacial instabilities for Z _R  = −0.5 and 1.2. The linear (1 − h _min ) theory points are obtained from the thickness perturbation equation ($h = 1 + \delta e^{\Upomega t}$) where Ω is the dimensionless dominant growth coefficient and the small amplitude perturbation δ is taken as 0.01. In the former case when the interface travels at a higher speed with smaller amplitude of deformation the linear (solid line) and nonlinear (broken line) growth rates are almost similar before the nonlinear growth saturates to a constant value. In contrast, when the interface is almost stationary (Z _R  = 1.2), the nonlinear growth is rather catastrophic after an initial exponential growth predicted by the linear theory.

Figure 10a shows that the wave speed of the travelling waves from the nonlinear simulations (c _rm,NL ) also behave in the similar manner as predicted by the LSA. The figure shows that for thinner films, the unstable waves travel at a lower speed because of the larger influence from the wall friction. The figure also confirms that the changeover of the direction of the movement of electrolyte–air interface takes place near Z _R  = 1. At either side of this point, the wave speed increases, both in the EOF- and EPF-dominated regimes, where the surface flow is in the same or opposite direction of the applied electric field, respectively. Figure 10b shows that even the magnitude of the wave speed obtained from the nonlinear simulations is quite comparable to LSA (c _rm,LSA ) as the ratio c _rm,NL /c _rm,LSA varies between 0.9 and 1.05 at different Z _R .

5.2.2 Effect of electro osmotic force

Figures 11, 12, and 13 show the influence of the E _O on the spatiotemporal morphologies at the electrolyte–air interface. Plots a–c in Fig. 11 show the morphologies for Z _R  = 0.5 when E _O is 0.05, 0.5 and 2, respectively. The plots a–c in Fig. 12 show the profiles of highest (h _max ) to lowest (h _min ) film thickness when E _O is 0.05, 0.5 and 2, respectively. Plots d–f in the Figs. 11 and 12 show the same as a–c when Z _R  = 1.2. The plots a and b in Fig. 13 show the changes in c _rm,NL and c _rm,NL /c _rm,LSA with E _O .

Fig. 11

The spatiotemporal evolution of the electrolyte–air interface over a domain size Λ. Plots a–c show the evolution of free interface for Z _R  =  0.5 and d–f for Z _R  =  1.2 for E _O  = 0.05, 0.5 and 2, respectively, when E _R  = 1 and De = 0.1. The profiles 1–2 correspond to: a t = 539229 and 541431.7; b t = 8201.7 and 8266.1; c t = 569.6 and 580.1; d t = 945148.9 and 959845.2; e t = 11562.9 and 12001.6 and f t = 824.1 and 851.3. The waves travel in the direction shown by the arrow

Fig. 12

The broken and solid lines indicate the evolution of h _max and h _min for 0.05, 0.5, and 2, when Z _R  = 0.5 (a–c) and 1.2 (d–f)

Fig. 13

a Speed of the travelling waves (c _rm/NL ) nonlinear simulations, b ratio of the speeds of the travelling waves (c _rm,NL /c _rm,LSA ) from nonlinear simulations and LSA, at different E _O and Z _R when De = 0.1 and E _R  = 1. The square and the circular symbols represent Z _R  = 0.5 and 1.2

The simulations in Fig. 11 indicate that the free surface quickly starts to reflect a dominant, fastest growing length scale which is in accord with the linear analysis. Thereafter, the amplitude of the traveling wave grows without further changes in its length scale. Eventually, the growth slows down and at near equilibrium, the amplitude saturates to a constant value. Plots a–c in the Figs. 11 and 12 corroborate that when the EPF is in the direction of the EOF, the amplitude (h _max  − h _min ) initially increases exponentially in the linear growth regime and then saturates to a constant value after a long time. With increase in E _O as the unstable interfacial wave travels faster in the same direction, but its amplitude remains similar. In comparison, plots d–f in the Figs. 11 and 12 highlight that the amplitude is higher in the case of Z _R  = 1.2, because of the lower wave speed at the electrolyte–air interface and larger zeta potential gradient across the film. Further, with increase in E _O , the EPF at the electrolyte–air interface also gains strength against the EOF, which in turn significantly reduces the flow at the electrolyte–air interface. Thus, a larger deformation can be observed at the electrolyte–air interface when E _O is higher.

The plots in Fig. 13 show that the EPF at the electrolyte–air interface gains strength with E _O irrespective of whether the EPF is in the same (Z _R  = 0.5) or in the opposite (Z _R  = 1.2) direction of the EOF. As the electric field potential is increased, the speed of the EPF increases more significantly for Z _R  = 0.5, when both EOF and EPF act in the same direction (Fig. 13a). In contrast, the increase in the wave speed is much slower when they act in the opposite directions at Z _R  = 1.2. Figure 13b shows that the travelling wave speed obtained from LSA and nonlinear simulations is of similar order of magnitude as the ratio c _rm,NL /c _rm,LSA varies between a narrow range of 0.96–1.0 at different E _O .

5.2.3 Effect of substrate zeta potential

Figures 14, 15, and 16 show the influence of the E _R on the spatiotemporal evolution of the free surface. Plots a–c in Fig. 14 show the morphologies for Z _R  = 0.5 when E _R is 0.05, 0.5 and 2, respectively, whereas plots a–c in Fig. 15 show the highest (h _max ) and lowest (h _min ) film thickness when E _R is 0.05, 0.5 and 2, respectively. Plots d–f in Figs. 14 and 15 show the same when Z _R  = 1.2. The plots a and b in Fig. 16 show the change in c _rm,NL and c _rm,NL /c _rm,LSA with E _R .

Fig. 14

The spatiotemporal evolution of the electrolyte–air interface over a domain size of Λ. Plots a–c show the evolution of free interface for Z _R  = 0.5 and d–f for Z _R  = 1.2 for E _R  = 0.05, 0.5 and 2, respectively, when E _O  = 1 and De = 0.1. The profiles 1–2 correspond to: a t = 10 and 12; b t = 672.1 and 696.9; c t = 5889.2 and 5930; d t = 10 and 11; e t = 937 and 991; and f t = 7271 and 7456.9

Fig. 15

Evolution of maximum and minimum amplitude for E _R  = 0.05, 0.5 and 2, when Z _R  = 0.5 (a–c) and Z _R  = 1.2 (d–f), and dashed and solid lines indicate h _max and h _min , respectively

Fig. 16

a Speed of the travelling waves (c _rm/NL ) nonlinear simulations, b ratio of the speeds of the travelling waves (c _rm,NL /c _rm,LSA ) from nonlinear simulations and LSA, at different E _R and Z _R when De = 0.1, E _O  = 1. The square and circular symbols represent Z _R  = 0.5 and 1.2

Figure 14a, d shows that a low E _R can reduce the strength of the EOF significantly and reduce the overall flow rate of the EKF. In such a scenario, the EPF near the deforming interface travels at a lower speed and can undergo a pseudo-dewetting on the solid surface irrespective of whether it is moving in the same or opposite direction of the EOF. However, when the substrate potential is increased by increasing E _R , the EOF gains strength, which leads to a much smaller deformation at the unstable interface as observed in the plots b, d–f. Figure 15 further supports the observation that the amplitude (h _max  − h _min ) is indeed higher at the lower values of E _R and decreases with an increase in E _R . Figure 16 shows that under such conditions, the wave speed of EPF does not vary much and the nonlinear wave speed is similar to that obtained by the linear analysis.

6 Conclusions

We explore the interfacial evolution of a thin electrolyte film undergoing an EKF composed of an EOF near the substrate–film interface coupled with an EPF at the free surface of the film. The nonlinear simulations confirm that the interfacial waves could travel in either the same or the opposite direction of the applied electric field, as previously predicted by the linear analysis (Choi et al. 2010, 2011; Ray et al. 2011, 2012). The speed of the unstable waves is found to increase as the zeta potentials at the interfaces are more dissimilar and with increasing applied field strength. The EPF proximal to the free surface resembles the motion of a liquid near a charged particle with large radius and can greatly influence the growth of the interfacial mode of instability. For example, when the substrate–film and the electrolyte–air interfaces are of opposing zeta potentials, the EPF adds to the EOF thus generating a Couette-type flow with fast moving interfacial waves. The wave speed is lower for the thinner films because of the larger frictional influence of the substrate. Interestingly, the lower wave speeds correspond to larger amplitudes. When the interfaces have similar zeta potentials, the EPF at the free surface can generate a Poiseuille-type flow where the interface moves in the opposite direction of the EOF. In such a scenario, when the potential at the free surface is small, although at the base-state EPF predicts movement of the interface in the direction opposite to that of the EOF. However, the nonlinear simulations show that a stronger EOF can still drag the EPF in its direction. In contrast, when the zeta potentials at the interfaces are of the same sign and the potential at the free surface is high, the EPF can be strong enough to drag the overall flow in its own direction, i.e., in the opposite direction of EOF. The threshold potential for such an EPF-dominated reverse flow is larger for the thinner film because EPF has to overcome the additional viscous resistance arising from the substrate. Thus, depending upon the zeta potentials, applied electric field, film thickness, either an EOF- or EPF-dominated EKF can be observed in the free film. Interestingly, the transition from the EPF to EOF-dominated flow takes place near the condition when the interfaces have similar zeta potentials with same sign. In such a situation, the waves are found to travel at a much lower speed and the wave amplitude is found to be the largest. Thinner electrolyte films with low speeds of travel can also pseudo-dewet the solid surface, which can cause a disruption in the overall EKF. By means of a parametric analysis the nonlinear simulations also show that when the potentials at the interfaces are kept constant, the amplitudes of deformations are found to increase with an increase in the applied electric field (increasing E _O ) and reduction in the surface zeta potential (decreasing E _R ). A comparison between the linear and nonlinear wave speed shows that both the predictions are almost similar. However, the nonlinear simulations show that the growth of the unstable modes is often dissimilar deep into the nonlinear regime as the amplitude of the unstable travelling waves saturates to a constant value when they travel faster. Even when the unstable waves travel slower, an explosive growth of the amplitude is observed in the nonlinear regime leading to pseudo-dewetting.

In summary, the present analysis uncovers the key features of the interfacial instabilities of thin electrolyte films undergoing coupled EKF. This will motivate the design and interpretation of free surface electrokinetics in future micro/nano fluidic applications.

Appendix

The governing equations and boundary conditions of order O(1) are,

$$ \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} = \frac{{E_{O} }}{{De^{2} }}[\cosh (y/De) + A\sinh (y/De)], $$

(5)

$$ \frac{{\partial u_{0} }}{\partial x} + \frac{{\partial v_{0} }}{\partial y} = 0, $$

(6)

$$ \frac{{\partial p_{0} }}{\partial y} = \frac{{E_{O} }}{{De^{2} }}[\cosh (y/De) + A\sinh (y/De)]\left[ {\frac{{E_{R} }}{De}[\sinh (y/De) + A\cosh (y/De)]} \right], $$

(7)

At y = 0,

$$ u_{0} = v_{0} = 0 , $$

(8)

At y = h,

$$ u_{0y} - \frac{{E_{O} }}{De}[\sinh (h/De) + A\cosh (h/De)] = 0, $$

(9)

$$ - p_{0} - \left[ {\frac{1}{2}\frac{{E_{O} }}{{E_{R} }}\left( {1 - \frac{{E_{R}^{2} }}{{De^{2} }}\left[ \begin{gathered} \sinh^{2} (h/De) + 2A\sinh (h/De)\cosh (h/De) \hfill \\ + A^{2} \cosh^{2} (h/De) \hfill \\ \end{gathered} \right]} \right)} \right] = \Upgamma h_{xx} , $$

(10)

$$ h_{\tau 0} = - u_{0} h_{x} + v_{0} . $$

(11)

The expressions for the O(1)velocities and pressure are,

$$ u_{0} = E_{O} [\cosh (y/De) + A\sinh (y/De) - 1] , $$

(12)

$$ v_{0} = DeE_{O} A_{x} [1 - \cosh (y/De)], $$

(13)

$$ p_{0} = \frac{{E_{O} E_{R} }}{{4De^{2} }}[(1 + A^{2} )\cosh (2y/De) + A\sinh (2y/De)] - \frac{1}{2}\frac{{E_{O} }}{{E_{R} }} - \frac{{E_{O} E_{R} }}{{4De^{2} }}(1 - A^{2} ) - \Upgamma h_{xx} , $$

(14)

The O(α) order governing equations and boundary conditions are,

$$ \frac{{\partial u_{1} }}{\partial x} + \frac{{\partial v_{1} }}{\partial y} = 0, $$

(15)

$$ \frac{{\partial u_{0} }}{\partial t} + u_{0} \frac{{\partial u_{0} }}{\partial x} + v_{1} \frac{{\partial u_{0} }}{\partial y} = - \frac{{\partial p_{0} }}{\partial x} + \frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} - \frac{{E_{O} E_{R} }}{{De^{3} }}\frac{\partial h}{\partial x}\left( {\frac{B}{2}\sinh (2y/De) + AB\sinh^{2} (y/De)} \right), $$

(16)

$$ \frac{{\partial p_{1} }}{\partial y} = - \frac{{\partial^{2} v_{1} }}{{\partial y^{2} }} + \frac{{E_{O} }}{{De^{2} }}[\cosh (y/De) + A\sinh (y/De)]\left[ {\frac{{E_{R} }}{De}[\sinh (y/De) + A\cosh (y/De)} \right], $$

(17)

$$ {\text{At}}\;y = 0,u_{1} = v_{1} = 0 $$

(18)

At y = h,

$$ p_{1} + 2\frac{{\partial u_{0} }}{\partial x} + \frac{{E_{O} }}{De}\left( {B\frac{\partial h}{\partial x}\sinh (h/De)} \right) = 0, $$

(19)

$$ \begin{aligned} &\frac{{\partial u_{1} }}{\partial y} + \frac{{E_{O} E_{R} }}{{2De^{2} }}B\frac{\partial h}{\partial x}( - \cosh (2h/De) - A\sinh (2h/De) + 1) \\&\quad-\frac{\partial h}{\partial x}\left[ {\frac{{E_{O} }}{{E_{R} }} - \frac{{E_{O} E_{R} }}{{De^{2} }}(\sinh^{2} (h/De) + A^{2} \cosh^{2} (h/De) + A\sinh (2h/De))} \right] = 0, \\ \end{aligned} $$

(20)

$$ h_{\tau 1} = - \frac{\partial }{\partial x}\int\limits_{0}^{h} {u_{1} } {\text{d}}y. $$

(21)

The expressions for the O(α) x-directional velocity is,

$$ \begin{aligned} u_{1} &= E_{O}^{2} De\frac{{\left( {1 - Z_{R} \cosh {h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}{{\sinh^{2} {h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}}}\left[ {\frac{\partial }{\partial x}(h + De[A - \sinh (h/De) - A\cosh (h/De)])} \right]\sinh (y/De) \\ &\quad + E_{O}^{2} A_{x} A\left[ {De^{2} \cosh (y/De) - \frac{{y^{2} }}{2}} \right] + (E_{O} E_{R} A_{x} A - \Upgamma^{*} h_{xxx} )\frac{{y^{2} }}{2} \\ &\quad + \left( \begin{gathered} \frac{{E_{O} }}{{E_{R} }}h_{x} - E_{O}^{2} \frac{{\left( {1 - Z_{R} \cosh {h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}{{\sinh^{2} \left( {{h \mathord{\left/ {\vphantom {h {De}}} \right. \kern-\nulldelimiterspace} {De}}} \right)}}\left[ {\frac{\partial }{\partial x}(h + De[A - \sinh (h/De) - A\cosh (h/De)])} \right]\cosh (h/De) \hfill \\ - E_{O}^{2} A_{x} A[De\sinh (h/De) - h] - \left( {\frac{{E_{O} E_{R} }}{{De^{2} }}A_{x} A - \Upgamma^{*} h_{xxx} } \right)h \hfill \\ \end{gathered} \right)y \\ &\quad - E_{O}^{2} De^{2} A_{x} A \\ \end{aligned} $$

(22)

Substituting the O(1) and O(α) order equation in $h_{t} = h_{\tau 0} + \alpha h_{\tau 1} + O(\alpha^{2} )$ results in the evolution equation.