1 Introduction

Flows induced by the electro-osmosis are studied mostly for internal flows of micro-scale, such as a channel flow with the channel width very small but much larger than the Debye length λD of the electrolytes of the medium, as explained by Heeren et al. (2007), Hunter (1996), Khan and Reppert (2005), Nguyen and Wereley (2002), and Reppert and Morgan (2002) among others. If the channel wall is negatively charged, as for glass or polymer-based microfluidic devices, a thin layer, called Stern layer, with positive charges and no fluid motion is formed adjacent to the wall. Next to this layer is the diffuse layer, which reacts to an electrical field due to its charges. Beyond this electrical double layer (EDL) is electrically neutral core with fluid motions due to viscous diffusion. Under a direct current (DC) this electro-osmotic flow exhibits a plug flow except up to a small distance (∼3λD) from the channel wall, where the fluid velocity approaches zero on the channel wall, or on the Stern layer. A comprehensive review on the fundamentals of the electro-osmosis and other related electrokinetic effects can be found in a monograph by Li (2004).

In microfluidic devices situations may arise where a liquid with free surface must be transported and the electro-osmosis is a viable option for a driving force. Free-surface electro-osmotic flows, however, can become unstable, and corrugations may develop on the free surface. For a precise control of the liquid, the free-surface deformations must be accurately predicted. Severe deformations may lead to local rupture, which can imply breakup of the liquid film into isolated pieces. The electric current then will be severed, resulting in the loss of the electro-osmotic driving force. For electro-osmotic flows with free surfaces information on the surface deformation thus can be extremely useful.

Electro-osmotic flows with free surface, or interface, are studied previously, in the context of two-fluid electro-osmotic flow in microchannels, by Gao et al. (2005a, b), and Ngoma and Erchiqui (2006) to name a few. In some practical applications, direct electro-osmosis for a target fluid may be unsuitable due to low mobility or various undesirable side effects (Gao et al. 2005a), and two-fluid configuration can be used. In the aforementioned studies, however, the deformation of the interface between the fluid fluids is not systematically taken into account. An experimental study by Lee and Li (2006) for an electro-osmotic flow with liquid-air interface reports on the reduced velocity at the interface possibly due to its surface charge, but does not focus on the interfacial deformation, either.

An electro-osmotic flow with free-surface deformations is studied by Joo (2007), who identified a flow instability of the interfacial mode based on the Debye–Hückel approximation. The linear stability analysis performed shows that the flow is unstable to long-wave disturbances and the instability is accompanied by free-surface deformations. The linear electro-osmotic instability thus appears to have an analogy to the surface-wave instability of a vertical viscous layer (see Chang 1994 for a review). The growth rate of the instability increases with the strength of the electrical field applied and with the decrease of the layer thickness relative to the Debye length.

The objectives of the present study are rather straightforward. The linearly unstable free-surface electro-osmotic flow needs to be tested in the nonlinear regime, and the fate of the unstable flow then must be inspected through a nonlinear study. As an efficient method of calculating the surface deformations and understanding associated fluid dynamics beyond the linear instability, we apply a long-wave approximation to derive an evolution for the local liquid thickness, as performed for various other thin-film instabilities by many researchers, including Burelbach et al. (1988). The evolution equation is then integrated numerically to show some interesting flow behaviors, including the incipient rupture of the liquid layer.

2 Evolution equation

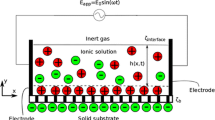
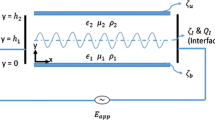
As shown in Fig. 1, a thin incompressible viscous layer, bounded below by a rigid substrate and above by its free surface, is driven by an electro-osmotic force present due to an electrical field applied along the horizontal x-axis. The governing system based on continuum hypothesis would be identical to that for a typical viscous film flow driven by gravity, as reviewed by Chang (1994), except that the horizontal component of the momentum equation here has two new driving-force terms, the van der Waals and the electro-osmotic body force, in place of the gravitational acceleration. In a nondimensional form, it is expressed as

$$u_t+uu_x+vu_y=-\left(p+\frac{A} {h^3} \right)_x+\, u_{xx}+u_{yy}+\frac{\rm Eo}{\rm De^2} e^{-y/{\rm De}}, $$
(1)

where (u,v) and p are, respectively, velocity components and pressure, scaled by ν/d and ρv 2/d 2, respectively, where d, ρ,v are mean thickness, density, and kinematic viscosity of the liquid. The subscripts denote partial differentiations in time and space in units of d 2/ν and d, respectively. Here the Hamaker constant a, made dimensionless as

$$A=\frac{a}{d\rho\nu^2}, $$
(2)

measures the unretarded London–van der Waals forces modeled, as discussed by Slattery (1990). The local layer thickness h(x,t), scaled by the mean film thickness, is unknown a priori, and must be obtained as a solution to the present moving-boundary problem. The last term in Eq. 1 represents the electro-osmotic force, obtained by applying the Debye–Hückel approximation to the Poisson–Boltzmann equation for the electrical potential. This approximation is basically a Taylor-series-expansion linearization of a hyperbolic sine term, and is valid for small surface charge. The Debye length λD of the electrolyte is defined by

$$\lambda_{\rm D} =\left(\frac{\varepsilon KT}{2z^2F^2c_\infty}\right)^{1/2}, $$
(3)

where ε, K, T, z, F, and c ∞ are, respectively, the dielectric constant, the Boltzmann constant, absolute temperature, charge number (valence) of each ion, Faraday’s constant, and bulk concentration of ions. We define electro-osmosis number

$${\rm Eo}=\frac{\varepsilon E_{\rm el}\zeta d}{\rho\nu^2} $$
(4)

as a measure of the electrical field strength E el, where the zeta potential ζ is the potential at the shear line S. The nondimensional parameter

$${\rm De}=\frac{\lambda_{\rm D}}{d} $$
(5)

is defined as Debye number, which measures the Debye length relative to the mean thickness of the liquid layer.

Fig. 1
figure 1

Configuration of electro-osmotic flow with free surface. Vertical scale is exaggerated. S shear line (divides the stern and the diffuse layer) and EDL diffusion line (divides EDL and viscous diffusion region)

Full size image

A complete set of the governing equations are listed in the work of Joo (2007), and only the free-surface boundary conditions are repeated here. The normal component of surface traction across the liquid–gas interface has a jump due to surface tension, which is expressed by ignoring the dynamics of the ambient gas phase with much smaller viscosity as

$$-p+\frac{2}{N}\left[ u_x(h_x^2-1)-h_x(u_y+v_x)\right]=\frac{S}{N^3} h_{xx} \quad \hbox{on}\, y=h, $$
(6)

where \(N=\sqrt{1+h_x^2},\) and the surface-tension coefficient γ is nondimensionalized as

$$S=\frac{\gamma d} {3\rho\nu^2}. $$
(7)

The interface is assumed clean and free of electrocapillary complications, and so the tangential component of the surface traction vanishes:

$$(u_y+v_x)(1-h_x^2)-4u_xh_x=0\quad \hbox{on}\ y=h. $$
(8)

The location of the interface is defined by the kinematic condition

$$v=h_t+uh_x\quad \hbox{on}\ y=h, $$
(9)

which states that the interface is a material surface.

The derivation procedure for an evolution equation for the local liquid thickness h(x,t) is quite straightforward and identical to that used for falling viscous films, detailed by Joo et al. (1991) among others. By noting ∂/∂t and \(\partial/\partial x \ll \partial/\partial y\) and using asymptotic expansions of all dependent variables except h, solutions are obtained sequentially at each order. Substitution of these solutions to the free-surface kinematic condition (9), or equivalently

$$h_t+\left(\int\limits_0^h u(x,y,t) \hbox{\rm d}y\right)_x=0, $$
(10)

yields

$$ \begin{aligned} h_t &+ {\rm Eo}\left[1+\left(\frac{h^2}{2{\rm De}^2}-\frac{h} {\rm De}-1\right)e^{-h/{\rm De}}\right]h_x \\ &\quad +\left\{A \frac{h_x}{h} +\frac{{\rm Eo}^2}{{\rm De}^2} \left[ \left(\frac{5h^6}{48{\rm De}^2}-\frac{2h^5}{15{\rm De}}\right.\right.\right.\\ &\quad \left. + \frac{h^4}{24}-\frac{1} {2} {\rm De}^2h^2-2{\rm De}^3h-3{\rm De}^4\right)e^{-h/{\rm De}}\\ &\quad \left.\left. +{\rm De}^3h+3{\rm De}^4 \right] e^{-h/{\rm De}}h_x +Sh^3h_{xxx}\right\}_x=0. \\ \end{aligned} $$
(11)

For a given surface configuration the evolution equation 11 predicts the subsequent dynamics of the film surface for small-Reynold number flows (A = O(1) and Eoe −1/De/De2 = O(1)) with finite surface slopes without the need to solve a fully coupled nonlinear system. For larger Reynold-number flows, evolution equation of this type is known to overestimate nonlinear flow developments but generate qualitatively useful information, as discussed by Ramaswamy et al. (1996) with comparisons with fully-coupled ALE finite-element computations. The left-hand-side of the equation following the term h t is composed of two parts. The first part, multiplied by h x , makes surface waves propagate downstream, and so is related to the nonlinear phase of the wave. The second part, or the rest of the left-hand-side, determines their growth or decay, and is related to the stability. Unlike the constant gravitational terms in the falling-film instability the electro-osmotic instability terms vary with the local thickness h, giving rise to the need for further nonlinear study as the present work. The first part reveals that the linear phase speed is Eo[1 + (1/(2De2)−1/De−1)e −1/De], which is Eo for De → 0, reaches a maximum for De ≈ 1/4, and approaches zero for De → ∞. The linear growth rate σ of a disturbance with wavenumber k is obtained by substituting

$$h(x,t)=1+\delta\left( e^{{\rm i}kx+\sigma t}+{\rm c.c.}\right), $$
(12)

where c.c. denotes the complex conjugate, and linearizing for small disturbance amplitude δ:

$$ \begin{aligned} \sigma &=k^2\left\{A+\frac{\rm Eo^2}{\rm De^2} \left[ \left(\frac{5} {48{\rm De}^2} -\frac{2}{15{\rm De}} +\frac{1}{24}-\frac{1}{2} {\rm De}^2 \right.\right.\right.\\ & \quad \left.\left.\left. -2{\rm De}^3-3{\rm De}^4\right)e^{-1/{\rm De}}+{\rm De}^3+3{\rm De}^4\right] e^{-1/{\rm De}}-k^2S\right\} \\ \end{aligned} $$
(13)

It is seen that the van der Waals attraction, whose strength is modeled by A, and the electro-osmosis, proportional to Eo2/De2, are destabilizing, while the surface tension can stabilize the flow for small enough wavenumber k. For films much thicker than their Debye length (De → 0) the electro-osmotic instability tends to disappear.

3 Nonlinear development of the free surface

Flow developments beyond the linear instability are studied by posing an initial-value problem on Eq. 11 with

$$h(x,0)=1+0.1\cos (k_{\rm m} x) \quad \left( -\frac{2\pi}{k_{\rm m}}\leq x\leq \frac{2\pi}{k_{\rm m}}\right) $$
(14)

and integrating Eq. 11 in time in a periodic domain, where k = k m is the wavenumber corresponding to the maximum linear growth rate according to Eq. 13 for a given set of parameters

$${{\mathbf{P}}}=(A, {\rm Eo}, {\rm De}, S). $$
(15)

Setting the disturbance wavenumber to k m and the computational domain to a period would restrict the numerical experiment to a certain narrow scope. For the present problem with multiple parameters, however, the focus is put on answering the following important questions:

  1. 1.

    It is well known, as discussed by Burelbach et al. (1988) among others, that the van der Waals attraction, which can be a dominant factor for extremely thin liquid layers, generates incipient rupture. Can electro-osmotic flows, under appropriate conditions, survive this rupture mechanism and maintain a continuous film?

  2. 2.

    In the absence of the van der Waals attraction, can the electro-osmotic instability by itself cause rupture, making it necessary to replace the Debye–Hückel approximation with a fully coupled model for fluid flow, ionic concentration, and electric field?

We will simply try to answer these questions here, leaving the precise determination of parametric ranges for each different evolution for future studies.

The integration of Eq. 11 is performed with a fourth-order central finite difference in space and a fully implicit second-order Euler time-marching scheme with an absolute error bound of 10−9. Rather extensive parametric study has been performed, but only a few cases necessary in drawing conclusions are presented. Considering that the Debye length of most common aqueous solutions is no greater than 102 nm order, we acknowledge that the Debye number chosen in some of the cases represents extremely thin layers, beyond the scope of the present study. They are nevertheless invaluable in logical reasoning for physical insights into the phenomena studied here.

We first present an evolution where a linear instability leads to a nonlinear traveling wave on the free surface. In the absence of the van der Waals attraction, it occurs for a wide range of layer thickness until it becomes inappropriately small. Figure 2 shows the changes in free-surface configuration in time for an extreme case of small thickness, P = (0, 1, 0.5, 1). The van der Waals attraction is set to zero, while a strong electrical field is applied. Initial sinusoidal wave with amplitude 0.1 travels downstream due to the action of the electro-osmotic force with an increase in the amplitude. As the disturbance wave grows, higher harmonics are excited and the wave changes its form from a simple sinusoidal shape. The growth rate of the wave diminishes as the re-shaping is completed, and a saturated wave with a permanent form develops and flows down stream with a constant speed. The figure for the maximum and minimum thickness clearly shows the saturation process to a permanent wave. This case shows the possibility of an open electro-osmotic flow of nano-scale layers in the absence of other destabilizing effects, such as the van der Waals attraction. For films with smaller De (thicker films, not shown), similar evolutions are observed but with reduced wave amplitude.

Fig. 2
figure 2

Free surface configurations for A = 0, Eo = 1, De = 0.5, and S = 1 with k m = 0.26. Evolution of the maximum and the minimum shown additionally indicates saturation in time

Full size image

In Fig. 3 an evolution beyond the limit of the nonlinear saturation is provided as a reference for future study. The layer thickness is taken to be half of that for Fig. 2 by setting P = (0, 1, 1, 1). The evolution shows that the trough thins substantially while it travels downstream. In a short period of time (t = 12.1) it reaches below the absolute error bound, at which time step the computation is terminated assuming that the layer has ruptured. Beyond the rupture the electro-osmotic force will no longer be effective due to the breakup of the layer. A capillary-force-driven rewetting of the dry patches can be a possibility, but we will not attempt to simulate this complex phenomenon in the present study. It suffices to state here that the electro-osmotic flow with a free surface can be sustained with a traveling surface wave and there exists a critical layer thickness below which breakup of the layer occurs even in the absence of the van der Waals attraction. In the absence of other destabilizing dynamics, the incipient rupture appears for nano-scale films. Micro-scale films seems to be free from the rupture unless a severe local depletion occurs due to other driving forces. If one wishes to analyze the rupture process in further detail or to determine the boundary between the permanent travel wave and the rupture, a more appropriate model than the Debye–Hückel approximation or the Poisson–Boltzmann equation must be applied.

Fig. 3
figure 3

Free surface configurations for A = 0, Eo = 1, De = 1, and S = 1 with k m = 0.6037

Full size image

For very thin layers considered above the van der Waals attraction can be important. In Fig. 4, the case of Fig. 2 is examined with a significantly large van der Waals force by choosing P = (0.1, 1, 0.5, 1). As the disturbance wave travels downstream its growth in amplitude has increased substantially from the case without the van der Waals attraction. The slope following the trough steepens continuously while the region near the trough sharpens, and the computation is terminated at t = 86 in view of the long-wave approximation made in Eq. 11. It can be speculated that the layer tends to rupture since the van der Waals force strengthens itself as the local minimum thickness decreases. The van der Waals attraction indeed can hinder or destroy an electro-osmotic flow which otherwise can be sustained. An experiment for a thinner layer with P = (0.1, 1, 1, 1), not presented here, shows similar evolution to that for Fig. 3, but with conspicuously increased growth rate and subsequently reduced rupture time (t = 8.1).

Fig. 4
figure 4

Free surface configurations for A = 0.1, Eo = 1, De = 0.5, and S = 1 with k m = 0.348

Full size image

If we weaken the electrical field for the case of Fig. 3 by setting P = (0, 0.5, 1, 1), the incipient rupture appears to disappear (figures not shown), which obviously indicates that the critical layer thickness for rupture increases with the electrical field applied. Again, parametric ranges for the rupture is not pursued with the present Debye–Hückel approximation. Figure 5 shows evolutions at some final moments for P = (0.1, 0.5, 0.5, 1), a case with a reduced electrical field from that of Fig. 4. The rupture process in Fig. 4 is not of the electro-osmotic but of the van der Waals origin. Reduction in electro-osmotic effects thus does not seem to prevent the rupture but can substantially delay it. The electro-osmotic flow tends to reinforce the van der Waals rupture mechanism rather than sweeping it off. Computations performed so far for layers with thickness in the order of the Debye length indicate that the van der Waals attraction, if present, tends to destroy a continuous electro-osmotic flow.

Fig. 5
figure 5

Free surface configurations for A = 0.1, Eo = 0.5, De = 0.5, and S = 1 with k m = 0.2603

Full size image

Now it is logical to question the fate of the rupture-free micro-scale films in the presence of the van der Waals attraction. One might expect that the van der Waals rupture would disappear for a sufficiently thick layer. However, Eq. 11 indicates that as De → 0 electro-osmotic effects disappear exponentially regardless of the electrical-field strength except for a linear phase speed Eo. The van der Waals attraction, albeit inversely proportional to layer thickness, persists, and can drive the layer to rupture. Figure 6 shows a case in which an apparent saturation to a permanent wave is seen during early time steps. As shown in the figure for a much later time, the trough eventually sharpens, and the rupture due to the van der Waals attraction seems imminent. It is thus speculated that open electro-osmotic flows are always susceptible to the van der Waals rupture and so a continuous or steady flow of the layer is not to be expected.

Fig. 6
figure 6

Free surface configurations for A = 0.1, Eo = 1, De = 0.1, and S = 1 with k m = 0.224

Full size image

4 Concluding remarks

The flow of thin viscous layer driven by the electro-osmotic force is examined. A previous linear stability analysis suggests that the flow is unstable and corrugations would develop on the free surface of the layer. In this study, the predictions of the linear analysis is confirmed and nonlinear evolutions of the resulting corrugations are studied by deriving an evolution equation for the local layer thickness and numerically integrating it with a specific interest in the potential effect of interface dynamics on the transport capability of the electro-osmosis with interfaces.

It is seen that the electro-osmotic force by itself does not cause rupture for layers with micro-scale thickness. The dormant rupture mechanism with reduction in thickness has yet to be confirmed by a more appropriate analysis in nano-scale. In the presence of the van der Waals attraction, however, rupture seems unavoidable, although it can be postponed with the increase in the layer thickness. If one wishes to transport a fluid layer via electro-osmosis, one must carefully calculate the van der Waals force applicable and compare the rupture time and the time required for the transport distance.

The present study is limited in scope. More realistic investigations would require other physical effects than those considered here and more rigorous nonlinear modeling than the long-wave approximation used here. The Debye–Hückel approximation must be replaced by a fully coupled electro-hydrodynamic system, including the Nernst–Plank equation for the ionic concentration and the Poisson equation for the electric potential. The present work nevertheless appears to be the first attempt to predict free-surface evolutions based on the first principle in electro-osmotic flows, and can be a useful base for further studies.