1 Introduction

The ever-growing attention toward understanding the dynamics of thin liquid films can be attributed to their ubiquitous presence all around us. From biological entities like tear film (Braun 2012) in the eyes or mucous lining in the organs, they are also found in manmade objects like bearings, paints, adhesives. As widespread is the availability of thin films in the nature, equally divergent are the properties of the constituent fluids and their physicochemical interactions with their environments. One of the major challenges in the film dynamics is to understand and model their interfacial evolution and stability thresholds under the influence of a wide range of liquid properties like surface tension, viscosity, van der Waals forces and imposed static and time-dependent phenomena such as gravity, temperature gradients, or electric fields. Owing to the complex interaction of the mentioned phenomena, a detailed and all-inclusive analysis is required, which is not easy and still unheard of. However, reviews by Oron and Bankoff (1997), Craster and Matar (2009) and Chang et al. (2012) provide comprehensive details on the contribution of various physical phenomena toward film dynamics with the help of a single evolution equation of the film thickness. Further, one of the mechanisms to create smooth pulsatile motion of fluid in thin geometries is time-periodic electro-osmotic flow (EOF), which is ascribed to the interactions between a wall or interface adhering charged layer [also known as the electrical double layer (EDL) (Kirby 2010)] and an externally applied pulsating electrical field in electrolytic solutions. Although the use of electric fields to actuate liquid flows or modification of liquid–substrate interactions have been widely studied, the ever-growing literature in the field highlights its complexity of contributions from wide range of small-scale physical phenomena. Moreover, as soon as a physical discontinuity such as a solid–liquid or liquid–gas interface is introduced in such systems, the major concerns are limited to sustaining either such interfaces or their controlled deformation. The previous studies of the fluid interface instability under electric fields have been discussed in a review by Lin et al. (2004). Many of the previously mentioned studies have focused on EOF where the EDL is very thin and consequently contributes to the bulk dynamics through an electro-osmotic slip velocity. However, when the characteristic length scale of the liquid flow becomes comparable to the EDL thickness, a more detailed analysis of the influence of the space charge distribution on the bulk liquid dynamics is required (Kirby 2010). Such a system in the presence of a deformable interface as in a thin liquid film can lead to a complex interaction of various effects like surface tension, disjoining pressure and Coulombic forces. This can lead to an overlap of their individual contributions toward film stability thresholds, generating interesting stability trends, which are tunable over a wide range of external field strengths and fluid properties. Ray et al. (2011) have presented interesting insights into the combined effect of surface tension and Coulombic forces on the long wave instability of thin electrolytic films. They have also studied the nonlinear evolution of the film surface under such instabilities (Ray et al. 2013). Conroy et al. (2010) demonstrated the stability and evolution of thin annular electrolytic films with the help of full numerical solutions of the interfacial evolution and estimation of film breakdown time. Ketelaar and Ajaev (2014) studied the stability of thin electrolytic films under charge regulation that defines the electrostatic behavior of the film surface. They identified constant potential and constant charge density at the interface as special cases of charge regulation and presented the corresponding stability bounds of thin electrolytic films. Savettaseranee et al. (2003) investigated the effect of Maxwell stress and van der Waals forces on the instability of leaking dielectric films, where the effect of Maxwell stress on film stability is restricted to the interfacial stress balance conditions. However, all the mentioned studies have limited their scope to steady electric fields, overlooking the possible contribution of van der Waals and capillary forces in thin film instability under a pulsating actuation. In this paper, the interfacial instability of an electrically conducting aqueous film is explored under the combined influence of oscillating electric field, capillary, and intermolecular forces. An asymptotic long wave stability analysis is performed to obtain the stability boundaries of the system as a function of relevant dimensionless groups, each representing the relative strengths of the above-mentioned forces.

2 The physical system

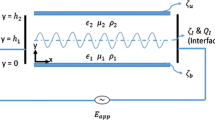
The system under study consists of a thin electrolyte film spread over a rigid solid substrate exposed to an inert gaseous atmosphere (see Fig. 1). The film thickness is denoted by h(x, t). The dynamics of such a film is studied under the effect of a longitudinal oscillating electric field, \( E_{\text{app}} = E_{0} \sin \left( {\omega t} \right) \), where E 0 is the amplitude and ω is the frequency. The electrolyte concentration is considered to be small in magnitude (~0.1–10 mM) in order to neglect the liquid property changes due to Joules heating (Lin et al. 2004), even so in the case of an applied electric field of large amplitude. This low electrolyte concentration also avoids complexities in flow modeling by reducing the nonlinear dependence of electrophoretic mobility of ions on the sparse space–charge distribution (Wei and Patey 1991; Borukhov et al. 1998; Yossifon et al. 2009; Fedorov and Kornyshev 2008; Dufreche et al. 2005; Song and Kim 2011). When such aqueous electrolyte comes into contact with a substrate like silica, glass, polymers, and some other chemically active substrates, there is a possibility of a series of ionic exchanges such as protonation, de-protonation, adsorption, and some chemical reactions at the solid–liquid interface. The ionic exchanges, after attaining equilibrium, leave the surface charged (Israelachvili 2011). Such a charged surface can be associated with a zeta potential. In this study, the solid substrate zeta potential is considered to be \( \zeta_{b} \), which is a function of the substrate–liquid interaction, ionic concentration, and pH of the solution (Kirby and Hasselbrink 2004a). A liquid surface exposed to a gaseous environment (liquid–gas interface) develops a charge which is a function of various parameters like ionic concentration, pH of the solution and valence of the ions involved (Gray-Weale and Beattie 2009; Manciu and Ruckenstein 2012a; Li and Somasundaran 1991). The origin of interfacial potential (\( \zeta_{\text{Interface}} \)) at the air–water interface is one of the least understood phenomenon in the world of surface science (Chaplin 2009). The plausible mechanisms for the origin of air–water interfacial charge include preferential presence of hydroxyl, hydrogen, or various other dissolved ions and/or restructuring of water molecules near the air–water interface. Although the source of charges at the liquid–gas interface has been highly debated in the existing literature (Garrett 2004; Manciu and Ruckenstein 2012b), one of the concluding evidences of a charged air–water interface is the presence of an interfacial zeta potential at such interfaces, which is independent of the interfacial extent and has been found to demonstrate both positive and negative values (Manciu and Ruckenstein 2012a, b; Ciunel et al. 2005). The associated zeta potential (\( \zeta_{\text{Interface}} \)) has been measured experimentally and is found to vary over a wide range of magnitudes (Yang et al. 2001; Graciaa et al. 1995; Choi et al. 2011).

Fig. 1
figure 1

Schematics of the thin film time-periodic EOF system

Full size image

3 Electric potential field

3.1 Electric potential field due to ionic charge distribution

The electrostatic potential distribution in liquid due to the space charge distribution (ϕ sc), can be expressed by Gauss law as,

$$ - \nabla \cdot \left( {\varepsilon \nabla \phi_{\rm sc} } \right) = \rho_{e} = \mathop \sum \limits_{i} ez_{i} C_{i} $$
(1)

where, ρ e is the net charge density, e is the electronic charge, z i is the valence of the ions, C i is the ionic concentration of the ith ionic species and ε is the permittivity of liquid. The charge transport equation in the liquid solution can be modeled using the Poisson–Nernst–Planck equation (Israelachvili 2011) as,

$$ \frac{{\partial C_{i} }}{\partial t} + \nabla \cdot \left( {\varvec{u}C_{i} } \right) = \nabla \cdot \left( {D_{i} \nabla C_{i} } \right) + \frac{{z_{i} e}}{{k_{B} T}}\nabla \cdot \left( {D_{i} C_{i} \nabla \phi_{\rm sc} } \right) $$
(2)

where, u and D i are, respectively, the convective velocity field and the diffusivity in the liquid solution of the ith ionic species, k B is the Boltzmann constant and T is the liquid temperature.

The dimensionless form of Eq. (2) leads to,

$$ {Wo}^{2} {\text{Sc}}_{i} \frac{{\partial \bar{C}_{i} }}{\partial \varTheta } + {\text{Pe}}_{i} \nabla \cdot \left( {\bar{\varvec{u}}\bar{C}_{i} } \right) = \nabla \cdot \left( {\nabla \bar{C}_{i} } \right) + \chi_{i} \nabla \cdot \left( {\bar{C}_{i} \varPhi_{\text{sc}} } \right) $$
(3)

where \( \overline{C}_{i} = \frac{{C_{i} }}{{{\text{C}}_{\text{ref}} }} \), \( \overline{\varvec{u}} = \frac{\varvec{u}}{{{\text{u}}_{\text{ref}} }} \), \( \varTheta = \omega t \), and \( \varPhi_{\text{sc}} = \phi_{\text{sc}} /\zeta_{\text{b}} \) (ω is the imposed frequency). The three non-dimensional parameters appearing in Eq. (3) are the Péclet number, \( Pe_{i} = \frac{{u_{\text{ref}} h_{0} }}{{D_{i} }} \) (\( h_{0} \) is the height of the initial flat interface), the Womersley number expressing the relative strength of temporal inertial force over the viscous force, \( Wo = \sqrt {\omega h_{0}^{2} /\nu } \), the Schmidt number, \( Sc_{i} = \nu /D_{i} \), and the ionic energy parameter which measures the relative strength of the electrostatic energy of ions with respect to the thermal energy of ions, \( \chi_{i} = z_{i} e\zeta_{b} /\left( {k_{\text{B}} T} \right) \). In this study, we will be focusing on films of thickness, \( h_{0} \sim\,O(10^{ - 7} )\;{\text{m}} \). In such a limit, the reference velocity can be considered as the electro-osmotic slip velocity, \( u_{\text{ref}} = u_{\text{HS}} = - \varepsilon \zeta_{b} E_{\text{app}} /\mu \) (Ghosal 2006), where \( E_{\text{app}} \) is the applied electric field. With the help of representative values considered in Sect. 7.1, and \( D_{i} \sim\,O(10^{ - 9} )\;{\text{m}}^{2} /{\text{s}} \) (Cussler 2009), one can estimate \( Pe_{i} \sim\,O(0.1) \). Thus, in such cases, the advective terms of ionic species can be neglected as compared to the diffusive transport. The resulting quasi-equilibrium system (steady assumption) gives a Boltzmann distribution of ionic species from Eq. (2),

$$ C_{i} = C_{0,i} \exp \left( { - \frac{{z_{i} e\phi_{\text{sc}} }}{{k_{\text{B}} T}}} \right) $$
(4)

where C 0,i is the bulk concentration of ith ionic species. Considering the electrolyte to be symmetric \( {\text{i}} . {\text{e}} . \;\left| {z_{ + } } \right| = \left| {z_{ - } } \right| = z \), with isotropic permittivity, one can obtain the classical Poisson–Boltzmann equation (PBE) from Eqs. (1) and (4) as,

$$ \varepsilon \nabla^{2} \phi_{\text{sc}} = 2zeC_{0} \sinh \left( {\frac{{ze\phi_{\text{sc}} }}{{k_{\text{B}} T}}} \right) $$
(5)

where C 0 is the neutral bulk ionic concentration of the solution. In order to isolate the electric effects as the dominating forcing mechanism, the system under study is considered to have large lateral extents, which results into negligible x-gradients as compared to y-gradients. Upon non-dimensionalizing the PBE (Israelachvili 2011) using \( \varPhi_{\text{sc}} = \phi_{\text{sc}} /\zeta_{b} \), and \( Y = y/h_{0} \), Eq. (5) leads to,

$$ \frac{{{\text{d}}^{2} \varPhi_{\text{sc}} }}{{{\text{d}}Y^{2} }} = \beta \sinh \left( {\chi \varPhi_{\text{sc}} } \right) $$
(6)

where, \( \beta = h_{0}^{2} /\left( {\lambda_{D}^{2} \chi } \right) \) and \( \lambda_{\text{D}} = \sqrt {\varepsilon k_{\text{B}} T/\left( {2z^{2} e^{2} C_{0} } \right)} \) is the Debye length. The associated boundary conditions are,

$$ \varPhi_{\text{sc}} \left( 0 \right) = 1,\quad \varPhi_{\text{sc}} \left( 1 \right) = Z_{R} $$
(7)

where \( Z_{R} = \zeta_{\rm Interface} /\zeta_{b} \). However, for low-concentration aqueous electrolytes, the interfacial zeta potentials show low magnitudes that can lead to a low χ (Kirby and Hasselbrink 2004b). For a monovalent symmetric electrolyte χ < 1 corresponds to \( \zeta_{\text{b}} < 25\,{\text{mV}} \) at 25 °C. In that case Eq. (6) can be linearized as (also known as the Debye–Hückel linearization),

$$ \frac{{{\text{d}}^{2} \varPhi_{\text{sc}} }}{{{\text{d}}Y^{2} }} = \frac{{\varPhi_{\text{sc}} }}{{De^{2} }} $$
(8)

where \( De = \lambda_{\text{D}} /h_{0} \) is the Debye number which represents the relative extent of the electric double layer with respect to the liquid film thickness. Under this formalism, which includes a diffusion dominant transport of ionic charges (\( Pe < 1 \)) and a low-concentration aqueous electrolyte (χ < 1) assumption, Eq. (3) can be reduced to a simplified boundary value problem for \( \varPhi_{\text{sc}} \) which includes Eqs. (7) and (8). They can be solved analytically to obtain the following closed-form solution,

$$ \varPhi_{\text{sc}} \left( Y \right) = \frac{1}{{\sinh \left( {\frac{1}{De}} \right)}}\left\{ {Z_{R} \sinh \left( {\frac{Y}{De}} \right) + \sinh \left( {\frac{1 - Y}{De}} \right)} \right\} . $$
(9)

3.2 Electric potential field due to the applied electric field

The applied electric field is assumed to be a time-periodic field which can be represented as,

$$ E_{\text{app}} = - \frac{{{\text{d}}\phi_{\text{app}} }}{{{\text{d}}x}} = \text{Im} \left( {E_{0} e^{i\omega t} } \right) $$
(10)

The electric potential due to the externally oscillating applied electric field (\( \varPhi_{\text{app}} \)) can be written in the dimensionless form as,

$$ \varPhi_{\text{app}} = - \int \frac{{E_{\text{app}} h_{0} }}{{\zeta_{b} }}{\text{d}}X = - \frac{X}{{E_{R} }}\text{Im} \left( {e^{i\varTheta } } \right) $$
(11)

where \( \varPhi_{\text{app}} = \phi_{\text{app}} /\zeta_{b} \), \( X = x/h_{0} \), \( \varTheta = \omega t \) are the dimensionless variables and \( E_{R} = \zeta_{b} /E_{0} h_{0} \) is the relative strength of electric field due to space charge distribution and the amplitude of the external field. The net electric potential in the system can be written as a sum of the potential field due to the space charge distribution (\( \varPhi_{\rm sc} \)) and the externally applied electric field (\( \varPhi_{\text{app}} \)). While, the space charge potential distribution (\( \varPhi_{\text{sc}} \)) for large wall zeta potential systems (\( \chi \ge 1 \)) has to be obtained numerically, for low wall zeta potential systems (\( \chi < 1 \)), the net potential field is obtained analytically and can be written as,

$$ \begin{aligned} \varPhi \left( {X,Y,\varTheta } \right) & = \varPhi_{\text{app}} \left( {X,\varTheta } \right) + \varPhi_{\text{sc}} \left( Y \right) = - \frac{X}{{E_{R} }}\text{Im} \left( {e^{i\varTheta } } \right) \\ & \quad + \frac{1}{{\sinh \left( {\frac{1}{De}} \right)}}\left\{ {Z_{R} \sinh \left( {\frac{Y}{De}} \right) + \sinh \left( {\frac{1 - Y}{De}} \right)} \right\} \\ \end{aligned} $$
(12)

where \( \varPhi = \phi /\zeta_{b} \) is the dimensionless total electric potential of the system.

4 Hydrodynamic modeling

4.1 Governing equations

The oscillating electric field along with the space charge distribution induces a time-dependent Maxwell stress (\( \varvec{\varSigma}^{\varvec{M}} \)) in the liquid, which in the absence of magnetic fields can be represented as,

$$ \varvec{\varSigma}^{\varvec{M}} = - \frac{{\varepsilon \left| \varvec{E} \right|^{2} }}{2}\varvec{I} + \varepsilon \varvec{E} \otimes \varvec{E} $$
(13)

where \( \varvec{E} = - \nabla \phi \) is the electric field vector in the system. The total stress tensor (\( \varvec{\varSigma}^{\varvec{T}} \)) (along with the hydrodynamic stress tensor (\( \varvec{\varSigma}^{\varvec{H}} \)) for a Newtonian fluid) can then be expressed as,

$$ \varvec{\varSigma}^{\varvec{T}} =\varvec{\varSigma}^{\varvec{H}} +\varvec{\varSigma}^{\varvec{M}} = - \left( {p + \frac{{\varepsilon \left| \varvec{E} \right|^{2} }}{2}} \right)\varvec{I} + \mu \left( {\varvec{\nabla u} + \varvec{\nabla u}^{T} } \right) + \varepsilon \varvec{E} \otimes \varvec{E} $$
(14)

where \( \varvec{u} = u\varvec{i} + v\varvec{j} \) is the liquid velocity vector,\( p \) is the hydrostatic pressure in the liquid, \( \mu \) is the dynamic viscosity of the solvent, \( \varvec{I} \) is the unit tensor.

In situations involving thin films where the Debye length is of the order of the film thickness, the effect of intermolecular interactions cannot be ignored. This intermolecular interaction for a plane-parallel film manifests itself in the momentum equations as an excess pressure term, also known as the disjoining pressure (Derjaguin and Churaev 1978) given by,

$$ p_{d} = - \frac{a}{{6\pi h^{3} }} $$
(15)

where a is the Hamaker constant and h is the film thickness. Considering an incompressible flow, the conservation of mass and momentum result into the following equations, respectively,

$$ \varvec{\nabla } \cdot \varvec{u} = 0 $$
(16)
$$ \rho \left( {\frac{{\partial \varvec{u}}}{\partial t} + \left( {\varvec{u} \cdot \varvec{\nabla }} \right)\varvec{u}} \right) = \varvec{\nabla }p_{d} + \varvec{\nabla } \cdot\varvec{\varSigma}^{\varvec{T}} = \varvec{\nabla }p_{d} - \varvec{\nabla }p + \mu \varvec{\nabla }^{2} \varvec{u} + \varvec{\nabla } \cdot \varSigma^{\varvec{M}} $$
(17)

The substrate at the bottom (y = 0) is considered to be rigid and impermeable which allows us to have a no-slip and no-penetration boundary condition as,

$$ u\left( {0,t} \right) = 0,\quad v\left( {0,t} \right) = 0 . $$
(18)

The free surface is initially flat and stationary and is geometrically placed at y = h 0. After the interface is destabilized, it is represented by y = h(x, t). For a perturbation of small amplitude compared to its wavelength, one can express the boundary conditions at y = h(x, t) as a first-order Taylor series expansion of the base state boundary conditions at y = h 0. The deformation of a flat fluid surface generates viscous stresses. The resulting curvature due to a disturbance, introduces a jump in the normal component of the total stress, which is balanced by the surface tension,

$$ \left[ {\varvec{n} \cdot\varvec{\varSigma}^{\varvec{T}} \cdot \varvec{n}} \right]_{{y = h\left( {x,t} \right)}} = 2\kappa \gamma = \gamma \left( {\frac{1}{R} - \frac{1}{\infty }} \right) = \frac{\gamma }{R} $$
(19)

where \( \varvec{n} \) is the normal vector at the free surface, \( \gamma \) is the surface tension coefficient, \( \kappa \) is the mean curvature of the interface, and R is the radius of curvature of the interface. The stress free condition of a free surface is realized by balancing off the total tangential stress, which has the contributions from the electrical and viscous stresses,

$$ \left[ {\varvec{t} \cdot\varvec{\varSigma}^{\varvec{T}} \cdot \varvec{n}} \right] = 0 $$
(20)

where t is the tangential vector at the free surface. The fluid velocity at the free surface satisfies the kinematic constraint as,

$$ \frac{\partial h}{\partial t} + \left( {\varvec{u} \cdot \nabla } \right)h = \left. v \right|_{{y = h\left( {x,t} \right)}} . $$
(21)

The dimensionless conservation equations are written using the scaling parameters as, \( \varTheta = \omega t \), \( U = u/u_{\text{ref}} \), \( V = v/u_{\text{ref}} \), \( P = ph_{0} /\left( {\mu u_{\text{ref}} } \right) \), \( \varPi = p_{d} h_{0} /\left( {\mu u_{\text{ref}} } \right) \) as,

$$ {\text{Continuity:}}\;\;\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0 $$
(22)
$$ {\text{Momentum:}}\;\;Wo^{2} \frac{\partial U}{\partial \varTheta } + Re \left( {U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}} \right) = \frac{\partial \varPi }{\partial X} - \frac{\partial P}{\partial X} + \frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }} + \gamma_{R} E_{R} \frac{\partial \varPhi }{\partial X}\frac{{\partial^{2} \varPhi }}{{\partial Y^{2} }} $$
(23)
$$ Wo^{2} \frac{\partial V}{\partial \varTheta } + Re \left( {U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}} \right) = - \frac{\partial P}{\partial Y} + \frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }} + \gamma_{R} E_{R} \frac{\partial \varPhi }{\partial Y}\frac{{\partial^{2} \varPhi }}{{\partial Y^{2} }} $$
(24)

where \( Wo = \sqrt {\omega h_{0}^{2} /\nu } \) is the Womersley number expressing the relative strength of temporal inertial force over the viscous dissipation force, \( \gamma_{R} = \varepsilon E_{0} \zeta_{b} /\left( {\mu u_{\rm ref} } \right) = - u_{\rm HS} /u_{\rm ref} \) is the relative strength of the electrical body forces over the viscous dissipation force and is henceforth referred to as electroviscous ratio, \( u_{\rm HS} = - \varepsilon E_{0} \zeta_{b} /\mu \) is the Helmholtz–Smoluchowski slip velocity and \( Re = \rho u_{\rm ref} h_{0} /\mu \) is the Reynolds number. The term \( \frac{\partial \varPi }{\partial X} = \frac{A}{{H^{4} }}\frac{\partial H}{\partial X} \) is the contribution from the disjoining pressure where, \( A = a/\left( {2\pi h_{0}^{2} \mu u_{\rm ref} } \right) \) is the dimensionless Hamaker constant and \( H = h/h_{0} \). The dimensionless boundary conditions are,

At the wall, \( Y = 0 \):

$$ U\left( {0,\varTheta } \right) = 0,\;V\left( {0,\varTheta } \right) = 0 $$
(25)

At the free surface, \( Y = H\left( {X,\varTheta } \right) \), the dimensionless continuity of tangential stress and normal stress, respectively, are,

$$ \begin{aligned} & \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)\left( {1 - \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right) - 4\frac{\partial H}{\partial X}\frac{\partial U}{\partial X} \\ & \quad + \gamma_{R} E_{R} \left( {\frac{\partial \varPhi }{\partial X}\frac{\partial \varPhi }{\partial Y}\left( {1 - \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right) - \frac{\partial H}{\partial X}\left( {\left( {\frac{\partial \varPhi }{\partial X}} \right)^{2} - \left( {\frac{\partial \varPhi }{\partial Y}} \right)^{2} } \right)} \right) = 0 \\ \end{aligned} $$
(26)
$$ \begin{aligned} & - \left( {P + \frac{{\gamma_{R} E_{R} }}{2}\left( {\left( {\frac{\partial \varPhi }{\partial X}} \right)^{2} + \left( {\frac{\partial \varPhi }{\partial Y}} \right)^{2} } \right)} \right) \\ & \quad + \frac{2}{{\left( {1 + \left( {{\raise0.7ex\hbox{${\partial H}$} \!\mathord{\left/ {\vphantom {{\partial H} {\partial X}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial X}$}}} \right)^{2} } \right)}}\left( {\frac{\partial U}{\partial X}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} - 1} \right) - \frac{\partial H}{\partial X}\left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)} \right) \\ & \quad + \frac{{\gamma_{R} E_{R} }}{{\left( {1 + \left( {{\raise0.7ex\hbox{${\partial H}$} \!\mathord{\left/ {\vphantom {{\partial H} {\partial X}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial X}$}}} \right)^{2} } \right)}}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} \left( {\frac{\partial \varPhi }{\partial X}} \right)^{2} + \left( {\frac{\partial \varPhi }{\partial Y}} \right)^{2} - 2\frac{\partial H}{\partial X}\frac{\partial \varPhi }{\partial X}\frac{\partial \varPhi }{\partial Y}} \right) \\ & = \frac{1}{{\left( {1 + \left( {{\raise0.7ex\hbox{${\partial H}$} \!\mathord{\left/ {\vphantom {{\partial H} {\partial X}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial X}$}}} \right)^{2} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} Ca}}\frac{{\partial^{2} H}}{{\partial X^{2} }} \\ \end{aligned} $$
(27)

where \( Ca = \mu u_{\rm ref} /\gamma \) is the capillary number. The dimensionless kinematic constraint at the free surface is,

$$ \frac{{Wo^{2} }}{Re}\frac{\partial H}{\partial \varTheta } + U\frac{\partial H}{\partial X} = V. $$
(28)

5 Base state solution

The base state flow is considered to be a laminar flow (\( V = 0 \)) with a planar free surface (H = 1). Hence, in the absence of an external pressure gradient, the dimensionless conservation Eqs. (22)–(24) reduce to,

$$ \frac{{\partial U_{b} }}{\partial X} = 0 $$
(29)
$$ Wo^{2} \frac{{\partial U_{b} }}{\partial \varTheta } = \frac{{\partial^{2} U_{b} }}{{\partial Y^{2} }} + \gamma_{R} E_{R} \frac{{\hbox{d}\varPhi_{app} }}{\hbox{d}X}\frac{{d^{2} \varPhi_{\rm sc} }}{{\hbox{d}Y^{2} }} $$
(30)
$$ 0 = - \frac{{\partial P_{b} }}{\partial Y} + \gamma_{R} E_{R} \frac{{\partial \varPhi_{\rm sc} }}{\partial Y}\frac{{d^{2} \varPhi_{\rm sc} }}{{\hbox{d}Y^{2} }} $$
(31)

The boundary conditions by non-dimensionalizing Eqs. (25) and (26) can be written as,

$$ U_{b} \left( {0,\varTheta } \right) = 0, \left. {\frac{{\partial U_{b} }}{\partial Y}} \right|_{Y = 1} + \gamma_{R} E_{R} \frac{{\partial \varPhi_{app} }}{\partial X}\left. {\frac{{\partial \varPhi_{\rm sc} }}{\partial Y}} \right|_{Y = 1} = 0. $$
(32)

The solution of the system of Eqs. (29)–(32) can be obtained by decomposing the velocity into time and space-dependent functions as,

$$ U_{b} \left( {Y,\varTheta } \right) = \text{Im} \left( {U_{b1} \left( Y \right)e^{i\varTheta } } \right). $$
(33)

Upon substituting Eq. (33) in Eqs. (30) and (32), an ordinary differential equation in U b1(Y) is obtained as,

$$ iWo^{2} U_{b1} = \frac{{\hbox{d}^{2} U_{b1} }}{{\hbox{d}Y^{2} }} - \gamma_{R} \frac{{\hbox{d}^{2} \varPhi_{\rm sc} }}{{\hbox{d}Y^{2} }}. $$
(34)

The corresponding boundary conditions are,

$$ \left. {\frac{{\hbox{d}U_{b1} }}{\hbox{d}Y}} \right|_{Y = 1} - \gamma_{R} \left. {\frac{{\hbox{d}\varPhi_{\rm sc} }}{\hbox{d}Y}} \right|_{Y = 1} = 0,\;\; U_{b1} \left( 0 \right) = 0. $$
(35)

Hence, upon solving Eqs. (34, 35), the resulting velocity profile can be obtained (see Appendix A for the complete expression of the base state velocity profile).

The base state pressure (P b ), henceforth called as the electro-osmotic pressure (P EO), is obtained from Eq. (31) as,

$$ \begin{aligned} P_{b} \left( {Y,\varTheta } \right) & = \frac{{\gamma_{R} E_{R} }}{2}\left( {\frac{{\hbox{d}\varPhi_{\rm sc} }}{\hbox{d}Y}} \right)^{2} - \frac{{\gamma_{R} E_{R} }}{2}\left( {\frac{{\hbox{d}\varPhi_{app} }}{\hbox{d}X}} \right)^{2} \\ & = \frac{{\gamma_{R} E_{R} }}{2}\left( {\frac{{\hbox{d}\varPhi_{\rm sc} }}{\hbox{d}Y}} \right)^{2} - \frac{{\gamma_{R} }}{{2E_{R} }}\text{Im} \left( {e^{i2\varTheta } } \right). \\ \end{aligned} $$
(36)

From the above expression for electro-osmotic pressure (P EO = P b (Y, Θ)) one can see the distinct contributions of EDL potential (Φ sc) and the applied potential bias (Φ app). In other words, the electro-osmotic pressure, P EO, can be written as a sum of the two mentioned contributions as, P EO = P EDL + P EF where \( P_{\rm EDL} = \frac{{\gamma_{R} E_{R} }}{2}\left( {\frac{{\hbox{d}\varPhi_{\rm sc} }}{\hbox{d}Y}} \right)^{2} \) is the EDL pressure and \( P_{EF} = - \frac{{\gamma_{R} }}{{2E_{R} }}\text{Im} \left( {e^{i2\varTheta } } \right) \) is the pressure induced due to the applied electric field. It is interesting to note that P EDL is always positive (repulsive) and hence can have a significant contribution toward stability of thin films with significant EDL size. The detailed contribution of EDL pressure toward film stability is discussed later.

6 Linear stability analysis

The perturbations in the flow variables are introduced as, \( U = U_{b} + \widetilde{U} \), \( V = \widetilde{V} \), \( P = P_{b} + \widetilde{P} \), and \( H = 1 + \widetilde{H} \). At this point, we would like to discuss the non-inclusion of perturbation in the electrostatic potential field in the transport equations. Since in the present work we are proposing a fully analytical approach toward stability prediction of a rather complex system, we are not exploring the temporal evolution of the interface under perturbation. To that end, we have assumed a “perpetual” equipotential gas–liquid interface, where infinitesimal stretching or contraction of the interface will not affect the interfacial charge distribution. Since, we are also considering here that the origin of interfacial charge is due to internal redistribution of charges rather than some chemical reaction as a source or sink of the charges, the former is independent of the superficial extent of the interface (see Sect. 3.1). Further, in the electrolyte bulk, the electrostatic potential distribution is nonexistent due to the electroneutrality condition. The velocity components are converted into stream function using \( \widetilde{U} = \partial \widetilde{\varPsi }/\partial Y \) and \( \widetilde{V} = - \partial \widetilde{\varPsi }/\partial X \). The normal mode perturbations are considered with small amplitude and with long wavelength (\( \lambda_{L} \gg h_{0} \gg \widetilde{H} \)) as,

$$ \begin{aligned} \widetilde{\varPsi }\left( {X,Y,\varTheta } \right) & = \overline{\varPsi } \left( {Y,\varTheta } \right)e^{i\alpha X} \\ \widetilde{P}\left( {X,Y,\varTheta } \right) & = \overline{P} \left( {Y,\varTheta } \right)e^{i\alpha X} \\ \widetilde{H}\left( {X,\varTheta } \right) & = \overline{H} \left( \varTheta \right)e^{i\alpha X} \\ \end{aligned} $$
(37)

where \( \alpha = 2\pi h_{0} /\lambda_{L} \) is the dimensionless wavenumber and λ L is the wavelength of the perturbation. Upon substituting the flow variables with the perturbations mentioned above in the Eqs. (22)–(28), linearizing and eliminating the pressure, the following Orr–Sommerfeld equation is obtained as,

$$ \left( {\frac{{\partial^{2} }}{{\partial Y^{2} }} - \alpha^{2} } \right)^{2} \overline{\varPsi } - \left( {Wo^{2} \frac{\partial }{\partial \varTheta } + i\alpha Re U_{b} } \right)\left( {\frac{{\partial^{2} }}{{\partial Y^{2} }} - \alpha^{2} } \right)\overline{\varPsi } + \,i\alpha Re \frac{{\partial^{2} U_{b} }}{{\partial Y^{2} }}\overline{\varPsi } = 0 . $$
(38)

The boundary conditions using the normal mode representation of the perturbation parameters can be written as,

$$ \overline{\varPsi } (0,\varTheta ) = 0,\frac{{\partial \overline{\varPsi } }}{\partial Y}(0,\varTheta ) = 0 $$
(39)
$$ \begin{aligned} & \left( {\frac{{\partial^{2} }}{{\partial Y^{2} }} + \alpha^{2} } \right)\overline{\varPsi } \left( {1,\varTheta } \right) + \overline{H} \left( \varTheta \right)\frac{{\partial^{2} U_{b} \left( {1,\varTheta } \right)}}{{\partial Y^{2} }} \\ & \quad - i\alpha \gamma_{R} E_{R} \overline{H} \left( \varTheta \right)\left. {\left( {\left( {\frac{\partial \varPhi }{\partial X}} \right)^{2} - \left( {\frac{\partial \varPhi }{\partial Y}} \right)^{2} } \right)} \right|_{Y = 1} = 0 \\ \end{aligned} $$
(40)
$$ \begin{aligned} & \left( {\frac{\partial }{{\partial Y^{2} }} - 3\alpha^{2} } \right)\frac{{\partial \overline{\varPsi } \left( {1,\varTheta } \right)}}{\partial Y} - Wo^{2} \frac{{\partial^{2} \overline{\varPsi } \left( {1,\varTheta } \right)}}{\partial \varTheta \partial Y} \\ & \quad - i\alpha Re \left( {U_{b} \left( {1,\varTheta } \right)\frac{\partial }{\partial Y} - \frac{{\partial U_{b} \left( {1,\varTheta } \right)}}{\partial Y}} \right)\overline{\varPsi } \left( {1,\varTheta } \right) = i\alpha \overline{H} \left( \varTheta \right)\left( {\frac{1}{{\overline{\rm Ca} }} - A} \right) \\ \end{aligned} $$
(41)
$$ \frac{{{Wo}^{2} }}{Re}\frac{{\hbox{d}\overline{H} }}{\hbox{d}\varTheta } + i\alpha U_{b} \left( {1,\varTheta } \right)\overline{H} \left( \varTheta \right) = - i\alpha \overline{\varPsi } \left( {1,\varTheta } \right) $$
(42)

where \( \overline{\rm Ca} = {\text{Ca}}/\alpha^{2} \). For thin film flows with long wavelength perturbations \( {\text{h}}_{0} /\lambda_{L} \ll \) 1 which leads to α ≪ 1 (Oron and Bankoff 1997). Using Floquet theory, \( \overline{\varPsi } \left( {Y,\varTheta } \right) = \widehat{\varPsi }\left( {Y,\varTheta } \right)e^{\sigma \varTheta } \) and \( \overline{H} \left( \varTheta \right) = \widehat{H}\left( \varTheta \right)e^{\sigma \varTheta } \) where σ is the dimensionless Floquet exponent and using asymptotic expansions in small parameter (α ≪ 1), the amplitudes (\( \widehat{\varPsi }\left( {Y,\varTheta } \right),\widehat{H}\left( \varTheta \right) \)) can be expanded as,

$$ \widehat{\varPsi }\left( {Y,\varTheta } \right) = \widehat{\varPsi }_{0} \left( {Y,\varTheta } \right) + \alpha \widehat{\varPsi }_{1} \left( {Y,\varTheta } \right) + \alpha^{2} \widehat{\varPsi }_{2} \left( {Y,\varTheta } \right) + \cdots $$
$$ \widehat{H}\left( \varTheta \right) = \widehat{H}_{0} \left( \varTheta \right) + \alpha \widehat{H}_{1} \left( \varTheta \right) + \alpha^{2} \widehat{H}_{2} \left( \varTheta \right) + \cdots $$
$$ \sigma = \sigma_{0} + \alpha \sigma_{1} + \alpha^{2} \sigma_{2} + \cdots $$
(43)

Upon solving the resulting set of equations for different orders of α (the details of which can be found in Appendix B), the characteristic equation of the system in its simplified form is obtained as,

$$ \sigma = \frac{{\alpha^{2} Re }}{{3Wo^{2} }}\left( {g\left( {Re ,De,Wo,E_{R} ,\gamma_{R} ,Z_{R} } \right) + A - \frac{{\alpha^{2} }}{\rm Ca}} \right) . $$
(44)

The observed form is consistent with the form of growth rate for thin electrolytic films as obtained by some recent works on thin electrolytic film stability (Conroy et al. 2010; Ketelaar and Ajaev 2014). For sake of brevity, the lengthy expression of \( g\left( {Re ,De,Wo,E_{R} ,\gamma_{R} ,Z_{R} } \right) \) is not shown here. The following results are focused on the marginal stability curves showing the critical wave number obtained from Eq. (44) by setting σ = 0 as,

$$ \alpha_{c} = \sqrt {Ca\left[ {g\left( {Re ,De, Wo,E_{R} ,\gamma_{R} ,Z_{R} } \right) + A} \right]} . $$
(45)

7 Results

7.1 System parameters

To estimate the values of the dimensionless parameters used in present study, an aqueous solution is considered as the working fluid where the transport coefficients are taken to be of water at the normal temperature and pressure, viz. \( \rho \sim10^{3} \,{\text{kg}}/{\text{m}}^{3} \), \( \mu \sim10^{ - 3} \,{\text{Pa}}\,{\text{s}} \), \( \varepsilon \sim80\varepsilon_{0} \), where, \( \varepsilon_{0} \) is the permittivity of vacuum, the surface tension between water and air,\( \gamma \) is taken as 0.072 N/m, the Hamaker constant, a as 10−20 J, the substrate zeta potential, \( \zeta_{b} \) as 10 mV (Kirby and Hasselbrink 2004b; Manciu and Ruckenstein 2012a), the applied electric field \( E_{0} \) as 1 kV/cm, and ω ~ 1 MHz is the applied frequency. The ionic concentration in the system is considered to be low (\( {\text{C}}_{0} \sim\,O\left( {10^{ - 4} } \right) M \)) which gives a Debye length \( \lambda_{D} \sim\,O\left( {10^{ - 9} } \right)m \). Such a small ionic concentration helps to consider linearized PBE for estimating the dynamics of ions in the electrolyte film. In this study, upon considering the film thickness of the order of 100 nm, the Debye number can be estimated as \( De\sim\,O\left( {0.1} \right) \). The corresponding characteristic electro-osmotic slip velocity, \( u_{\rm HS} = - \varepsilon \zeta_{b} E_{0} /\mu \), is thus of the order of 1 mm/s. For a film thickness h 0 of 100 nm, the dimensionless parameters can be estimated as, Hamaker constant, \( A\sim\,O\left( {0.1} \right) \), the electroviscous ratio, \( \gamma_{R} \sim\,O\left( 1 \right) \), the relative strength of electric field \( {\text{E}}_{\text{R}} \sim\,O\left( 1 \right) \), Capillary number, \( {\text{Ca}}\sim\,O\left( {10^{ - 5} } \right) \) and Reynolds number, \( {Re}\sim\,O\left( {10^{ - 4} } \right) \). Moreover, the above flow control parameters are varied further in order to illustrate the parametric dependence of the free surface stability of the system.

7.2 Instability mechanism

7.2.1 Contribution of capillary and disjoining pressure

The stability of a thin film under electro-osmotic flow can be attributed to the competing dynamics between the capillary forces through Laplace pressure (P L ), van der Waals forces through disjoining pressure (Π) and electrostatic forces through the electro-osmotic pressure (P EO). The Laplace pressure contribution (via Capillary number, \( {\text{Ca}} \)) and disjoining pressure contribution (via dimensionless Hamaker constant, \( {\text{A}} \)) appear together at the free surface boundary condition in a contrasting sense (see Eq. 41), showing the existence of conflicting forces even when the film is static.

When the film surface is perturbed by a small amplitude disturbance, the induced curvature forces the local Laplace pressure (\( P_{L} \sim\gamma \kappa \)) to become greater (or smaller) than the bulk pressure creating an outflow (or inflow) of liquid restoring the equilibrium configuration of the film (see Fig. 2a). However, the long-range nature of the disjoining pressure has a permanent effect on the film dynamics. A negative disjoining pressure (Π < 0, \( \varPi \sim - \frac{A}{{H^{3} }} \)) between the interfaces leads to an attraction between them forcing a film breakup, while a positive disjoining pressure (Π > 0) leads to a repulsion between the interfaces, causing a film build-up (see Fig. 2a). Moreover, upon application of an oscillating electric field, the stability characteristics of the film can be modified as compared to the static case (see Fig. 2b, c). The details of the effect of oscillating electric field and EDL parameters are discussed in the following sections.

Fig. 2
figure 2

a Schematics which demonstrates qualitatively the influence of disjoining pressure (\( \varPi \)) and Laplace pressure (\( P_{L} \)) under a positive (crest) and negative (trough) perturbation in the interface (black line), direction of fluid movement (arrows), and evolved shape of the interface after stability/instability has set in (blue lines). b Marginal stability curves showing the critical wave number as a function of the dimensionless Hamaker constant, A in the absence of time-periodic electric field with \( De = 0.1 \). c Marginal stability curves showing the critical wave number as a function of the dimensionless Hamaker constant, A in the presence of time-periodic electric field with \( De = 0.1 \), \( Z_{R} = 0.01 \), \( {Re} = 10^{ - 4} \), \( \gamma_{R} = 1 \), \( Wo = 1 \) (color figure online)

Full size image

7.2.2 Contribution of EDL

Within an EDL, two important interactions between ions can be identified, firstly, the repulsive Coulombic interaction between the counter ions, and secondly, the configurational entropy of the counter ion distribution, which resists the configurational change due to the Coulombic repulsion (Israelachvili 2011). Such a competition between the two phenomena manifests itself in terms of a pressure, which has been termed as the EDL pressure (P EDL). The EDL pressure distribution in a thin film has been obtained from the basic state solution of the system (see Eq. 36).

The positive nature of P EDL can be attributed to the entropic origin of the pressure (Israelachvili 2011). The diffused cloud of counter ions in an EDL is maintained in an equilibrium through mutual repulsions which forces them away from the oppositely charged substrate (or interface) and hence leads to a configurational entropy. When two such ordered charged clouds (diffused charges in the EDL) are brought closer through a perturbation, a repulsive force initiates between the two charged clouds, restoring the equilibrium and stabilizing the film. From Fig. 3, one can observe that a charged free surface (\( Z_{R} \ne 0 \)) over a charged substrate (\( \gamma_{R} E_{R} \ne 0 \)) is relatively more stable than an uncharged free surface (\( Z_{R} = 0 \)). The case of a charged free surface over a charged substrate creates two interfaces with diffused charge distribution following the stability dynamics mentioned above. Moreover, the symmetry observed in the marginal stability curves (see Fig. 3) about \( Z_{R} = 0 \) justifies the entropic rather than Coulombic origin of the EDL pressure where the polarity of the free surface charge cloud does not affect the stability of the film.

Fig. 3
figure 3

Marginal stability curves showing the critical wave number as a function of the zeta potential ratio (\( {\text{Z}}_{\text{R}} \)) with stability trends for different values of substrate zeta potential (\( \gamma_{R} E_{R} \)) in the absence of external electric field at a \( De = 0.01 \), b \( {De} = 0.1 \) with \( {\text{Ca}} = 10^{ - 5} \) and \( A = 0.1 \)

Full size image

Another parameter associated with the EDL is the extent of the diffused charge penetration in the bulk. This extent of the diffused charge distribution is characterized by the Debye length (λ D ). The relative extent of the EDL thickness as compared to the film thickness is represented in this work through Debye number, \( {De} \). For thin EDLs (i.e., small \( {De} \)) one can imagine a closer packing of diffused ions leading to a higher configurational entropy and hence greater repulsion between the interfaces, leading to a more stable film. This idea is also observed in Fig. 3 where thinner EDL (\( {De} = 0.01 \)) (see Fig. 3a) is more stable than a thicker EDL (\( {De} = 0.1 \)) (see Fig. 3b).

7.2.3 Contribution of the oscillating electric field

An oscillating electric field acting on a charged interface introduces a time-dependent dispersive field near the interfaces (see Fig. 4a). It can be seen that the maximum magnitude of the vorticity (\( \left|\varvec{\omega}\right| = \left| {\nabla \times \varvec{U}_{\varvec{b}} } \right| = \left| {\partial U_{b} /\partial Y} \right| \)) occurs at the interface. The deformation of the free surface is dependent upon the strength of this vortex which is a function of various parameters like Debye number, which accounts for the diffusive extent of the electrical effects in the bulk, the strength of the applied electric field (\( \gamma_{R} /E_{R} \)) and the strength of the interfacial polarity (\( \gamma_{R} E_{R} \), \( {\text{Z}}_{\text{R}} \)). However, it is also known that any deformation in such an interface is countered by a dissipating viscous stress. The strength of this viscous damping mainly depends upon parameters like the Reynolds and Womersley numbers, which account for the diffusive extent of the viscous effects in the bulk. The two competing mechanisms mentioned above contribute to the neutral stability characteristics of the system. Upon changing the Reynolds number by keeping all the other parameters fixed, which is equivalent to changing the dynamic viscosity, one observes from the marginal stability curves (α c , \( {Wo} \)) that more viscous fluids (smaller \( {Re} \)) are more stable as compared to less viscous fluids (larger \( {Re} \)) (see Fig. 4c). Thin EDLs (smaller \( {De} \)) owing to their smaller spatial extent of charge have high-velocity gradients as compared to thicker EDLs (larger \( {De} \)). This is also observed in Fig. 4a. Hence, for thin EDLs (smaller \( {De} \)) the film is expected to be more unstable as compared to films with thicker EDLs (see Fig. 4b). The electro-osmotic velocity distribution in the film is directly proportional to the strength of the applied electric field. Hence, upon increasing the strength of the applied electric field, the strength of the free surface vortex is enhanced thus leading to a more unstable system (see Fig. 4d).

Fig. 4
figure 4

a Base state vorticity (\( \left|\varvec{\omega}\right| = \left| {\nabla \times \varvec{U}_{\varvec{b}} } \right| \)) distribution over the film thickness at \( \gamma_{R} = 1 \), \( Z_{R} = 1 \). b Marginal stability curves showing the critical wave number as a function of the Debye number (\( {De} \)) with stability trends for different values of Womersley number (\( {Wo} \)). c Marginal stability curves showing the critical wave number as a function of \( {Wo} \) with stability trends for different values of Reynolds number (Re). d Marginal stability curves showing the critical wave number as a function of \( {Wo} \) with stability trends for different values of Electric field strength (\( \gamma_{R} /E_{R} \))

Full size image

7.3 Maximum instability growth rate

From Eq. (44), we can estimate the maximum growth rate (σ max) as,

$$ \sigma_{\hbox{max} } = \frac{Re}{{12Wo^{2} }}Ca\left[ {g\left( {Re ,De, Wo,E_{R} ,\gamma_{R} ,Z_{R} } \right) + A} \right]^{2} $$
(46)

which corresponds to the wavenumber, α max defined by Eq. (47) under the condition, \( g\left( {Re ,De, Wo,E_{R} ,\gamma_{R} ,Z_{R} } \right) \ge - A \). The expression for α max can be written as,

$$ \alpha_{\hbox{max} } = \sqrt {\frac{{Ca\left[ {g\left( {Re ,De, Wo,E_{R} ,\gamma_{R} ,Z_{R} } \right) + A} \right]}}{2}} = \frac{{\alpha_{c} }}{\sqrt 2 } $$
(47)

where we can see that α c  > α max. This suggests that the critical wavelength (\( \frac{1}{{\alpha_{c} }} \)) for instability is smaller than the fastest growing wavelength (\( \frac{1}{{\alpha_{max} }} \)). Moreover, we see that σ max scales linearly with the capillary number. That is upon decreasing surface tension, the instability grows at a faster rate. Similarly, σ max increases with \( {\text{A}} > 0 \) and decreases for \( {\text{A}} < 0 \), which is again consistent with our previous observations. Figure 5 shows the variation in σ max in the phase space of \( {Wo} \) and \( {De} \). We have chosen the representative set of \( {Wo} \) and \( {De} \) phase space as they correspond to, respectively, the dynamic and static parts of electric potential field. One of the most remarkable observations from the plots of σ max is that the high-frequency electrokinetic actuation of the electrolytic film strongly suppresses the growth rate of the instability as compared to the low-frequency actuation regime. Further, for large range of \( {Wo} \), especially at high frequencies, the greater the penetration depth of the diffused charge distribution (\( {De} \uparrow \)), the slower is the instability propagation (σ max↓). Moreover, in the absence or a low strength of net charge or zeta potential (\( {\text{Z}}_{\text{R}} = 0 \)) on the surface of the electrolytic film, the effect of penetration depth of diffuse charge distribution (\( {De} \)) due to the charged solid substrate, is insignificant on the growth rate of the film instability.

Fig. 5
figure 5

Variation in \( \sigma_{\hbox{max} } \) in the phase space of \( {Wo} \) and \( {De} \). Upon using a fixed set of parameters as, \( \gamma_{R} = 1 \), \( {\text{Ca}} = 10^{ - 4} \), \( Re = 10^{ - 2} \), \( E_{R} = 10^{ - 2} \), the distribution in \( \sigma_{\hbox{max} } \) is plotted for a \( A = 0.5 \), \( {\text{Z}}_{\text{R}} = 0.5 \), b \( A = - 0.5 \), \( {\text{Z}}_{\text{R}} = 0.5 \), c \( A = 0.5 \), \( Z_{R} = 0 \), d \( A = - 0.5 \), \( Z_{R} = 0 \). The values of \( \sigma_{\hbox{max} } \) are rounded off to the fifth decimal place

Full size image

8 Conclusions

With the help of linear stability analysis for long wavelength disturbances, stability thresholds of a thin aqueous film under time-periodic electro-osmotic flow are explored with the help of an analytical formulation. It is observed that the stability of a thin electrically conducting aqueous film can be precisely controlled by varying the electrochemistry of the film (Debye length and interfacial zeta potential) and also the frequency and amplitude of the applied electric field. Phenomena that are observed to have a stabilizing effect on the film dynamics are surface tension, repulsive disjoining pressure (\( {\text{A}} < 0 \)), osmotic pressure due to the EDL at the interfaces and viscous dissipation. The phenomena contributing toward the instability of the film are attractive disjoining pressure (\( {\text{A}} > 0 \)), thin EDLs (\( {De} \ll 1 \)), external electric field driving the electro-osmotic flow, and low frequencies. However, due to a complex interaction of all the above phenomena together, the individual stability thresholds overlap, generating interesting stability trends, which are tunable over a wide range of the above, mentioned parameters. Such a generalized analysis helps identifying parametric boundaries for sustaining thin films over a wide range of fluid properties and operating conditions. However, a more detailed understanding of such a complex thin film stability requires an analysis of nonlinear film evolution under various parameter sets of the coupled physical effects and is under investigation.