Long-wave interface instabilities of a two-layer system under periodic excitation for thin films

Abstract

The stability of a system of two thin liquid films under AC electroosmotic flow is studied using linear stability analysis for long-wave disturbances. The system is bounded by two rigid plates which act as substrate. Boltzmann charge distribution is assumed for the two electrolyte solutions. The effect of van der Waals interactions in these thin films is incorporated in the momentum equations through the disjoining pressure. The base-state velocity profile from the present study is compared with simple experiments and other analytical results. Parametric study involving various electrochemical factors is performed and the stability behaviour is analysed using growth rate, marginal stability, critical amplitude and maximum growth rate in phase space. An increase in the disjoining pressure is found to decrease stability of the system. On the other hand, increasing the frequency of the applied electric field is found to stabilize the system. However, the dependence of the stability on parameters such as viscosity ratio, permittivity ratio, interface zeta potential and interface charge depends not only on the value of individual parameters but also on the rest of the parameters. Design of experiments (DOE) is used to observe the general trend of stability with different parameters.

1 Introduction

Microfluidics is finding applications in diverse fields ranging from life science to aerospace and even extending to the development of nanofluidics (Chang et al. 2012; Stone et al. 2004). Its importance is also being recognized in the synthesis of nanoparticles and for simulating in vivo microenvironments (Lim and Karnik 2014). Huge emphasis is being laid on developing micro total analysis system (µTAS) or lab-on-chip (LOC) which can perform as point-of-care (POC) devices with steep reduction in the amount of sample required for the analysis, elimination of artefacts introduced due to mishandling of samples in a laboratory and reduction in time required for analysis (Mairhofer et al. 2009; Toner and Irimia 2005).

These applications require pumping and mixing of reagents. Electroosmosis is one of the basic principles which uses an electric field and can be used for pumping. The applied electric field can be a steady (DC) field which results in plug-type velocity profile for thin Debye layers or time-periodic (AC) field which results in an oscillating velocity profile. However, in case of DC electroosmotic flow (EOF), bubble formation due to electrolysis can cause serious issues if the electrodes are inside the microfluidic channel. These issues can be avoided with the use of an AC field (Wang et al. 2009). Symmetrical electrodes can produce local flow with AC field (Ramos et al. 1999), but when used with a travelling wave, a net bulk flow can be achieved (Ramos et al. 2005). Both these cases use planar microelectrodes placed at the wall of the microchannel. The use of electrokinetic instability induced by a time-periodic electric field with electrodes at the inlet and outlet of microchannel to enhance mixing has also been experimentally observed (Oddy et al. 2001). The base state for AC EOF of a single fluid between two parallel plates has been investigated by assuming a Boltzmann charge distribution (Dutta and Beskok 2001).

However, the use of electric field to generate an EOF is restricted only to conductive fluids. The small levels of conductivity in the biological fluids such as blood, serum and insulin may pose a problem. To address this concern, there have been studies to develop a two-liquid system in which the non-conductive liquid takes a ride on an immiscible conductive liquid (Brask et al. 2003). Enhancement in discrimination of DNA molecules can be achieved by taking multiple measurements using nanopore sensors and requires the polarity of a DC electric field to be switched periodically (Sen et al. 2012). One of the direct applications of the present study can be to replace this DC field with an AC field and to achieve enhanced discrimination of two species without bubble formation at the electrodes, avoiding thus an unstable regime.

Previous studies on AC EOF show interesting results. But, they were either based on a single fluid flow in a channel (Toner and Irimia 2005) or based on thin films with a flat interface (Mayur et al. 2014). Efforts have been made to understand instability in liquid–gas interface for DC field (Ganchenko et al. 2015). Base-state analysis by taking interfacial electrostatics in the two-fluid system into consideration is available (Choi et al. 2011; Gao et al. 2005). Also, the stability analysis by considering the Maxwell stress in the momentum balance can be found in Thaokar and Kumaran (2005) and Shankar and Sharma (2004) for DC field and in Gambhire and Thaokar (2010) for a transverse AC field. Stability for a two-liquid system under DC EOF with Maxwell stress consideration has been studied in Navarkar et al. (2015). Base state for two-liquid AC electroosmotic system has been analysed in Navarkar et al. (2016), but, to our knowledge, the stability analysis for this case has not been considered yet and constitutes the purpose of the present study.

The first section describes the physical system under consideration. In the second section, the electric potential profile developed due to the space charge distribution is derived with the Debye–Hückel approximation. The hydrodynamic governing equations and boundary conditions are described in the third section. The base state is then obtained with suitable assumptions. Linear stability procedure in the long-wave limit is employed in the fourth section wherein small perturbations are added to the hydrodynamic variables and Floquet theory is used to extract the time component from these perturbations. Finally, growth rate and marginal stability curves are presented in the fifth section to analyse the stability of the system.

2 Mathematical formulation

2.1 Electric potential due to ionic charge distribution

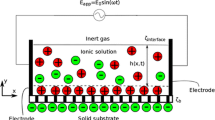
The physical system under consideration consists of two thin films of immiscible liquids having constant density $\rho_{i}$, viscosity $\mu_{i}$ and electric permittivity $\varepsilon_{i}$, where i = 1 and 2 correspond to the lower and upper liquids, respectively. The system is confined between two infinite and rigid parallel plates at $y = 0$ and $y = h_{2}$ (see Fig. 1). The interface is represented by $y = h\left( {x,t} \right)$. A time-periodic electric field $E_{0} { \sin }\left( {\omega t} \right)$ is applied, where $E_{0}$ and $\omega$ are the amplitude and the frequency of the electric field, respectively.

Fig. 1

Schematics of two-liquid AC EOF system

The zeta potential of the substrate at the upper and lower walls is represented by $\zeta_{u}$ and $\zeta_{b}$, respectively; $\zeta_{I}$ and $Q_{I}$ are the zeta potential and the surface charge density present at the interface, respectively (Choi et al. 2011), and are considered as independent parameters. Previous studies of Baygents and Saville (1991) and later that of Schnitzer and Yariv (2015) have shown that the surface charge and potential are closely related to the total adsorption of ions at the interface, for dielectric liquids. This leads to the formation of multiple double layers near the interface, which largely follow the Poisson–Boltzmann description, under weak field and weak advection approximations (Schnitzer and Yariv 2012; Saville 1977). However, in later experimental studies of the interface between two immiscible electrolyte solutions (ITIES), Samec et al. (1985) showed that for a given interface zeta potential ($\zeta_{I}$), the surface charge density ($Q_{I}$) can be varied by varying the electrolyte concentrations. The water/nitrobenzene interface with LiCl in water and TBATPB (tetrabutylammonium tetraphenylborate) in nitrobenzene can be considered as an example of ITIES (Senda et al. 1991).

The liquids are considered to have a low concentration of ions in order to ignore the Joule heating effect (Tang et al. 2004), and hence, it ensures that the properties of the liquids remain constant even if large electric fields are applied. It is also assumed that the ionic distribution is not affected by the liquid flow. For a symmetrical electrolyte, combining the Boltzmann charge distribution,

$$ \rho_{e,i} = - 2z_{i} e\rho_{0,i} {\text{Sinh}}\left( {\frac{{ez_{i} \phi_{{{\text{sc}},i}} }}{{k_{B} T}}} \right) $$

(1)

and the Poisson equation for the potential distribution,

$$ \frac{{{\text{d}}^{2} \phi_{{{\text{sc}},i}} }}{{{\text{dy}}^{2} }} = - \frac{{\rho_{e,i} }}{{\varepsilon_{i} }} $$

(2)

the Poisson–Boltzmann equation for the potential field can be derived as,

$$ \frac{{{\text{d}}^{2} \phi_{{{\text{sc}},i}} }}{{{\text{dy}}^{2} }} = \frac{{2z_{i} e\rho_{0,i} }}{{\varepsilon_{i} }}{\text{Sinh}}\left( {\frac{{ez_{i} \phi_{{{\text{sc}},i}} }}{{k_{B} T}}} \right) $$

(3)

where $\phi_{{{\text{sc}},i}}$ is the electric potential due to the space charge distribution for liquid “i” and $\rho_{0,i}$, $z_{i}$, $k_{B}$, $T$ and e are, respectively, the bulk ionic density (number of ions/m³), the valence of the ions in the aqueous phase for liquid “i”, the Boltzmann constant, the temperature and the electronic charge. Using the non-dimensional parameters $\varPhi_{{{\text{sc}},i}} = \frac{{\phi_{{{\text{sc}},i}} }}{{\zeta_{b} }},\;Y = \frac{y}{{h_{1} }}$, Eq. (3) can be written as,

$$ \frac{{{\text{d}}^{2} \varPhi_{{{\text{sc}},i}} }}{{{\text{d}}Y^{2} }} = \beta \text{Sinh} \left( {\chi \varPhi_{{{\text{sc}},i}} } \right) $$

(4)

where $\beta = \frac{{h_{1}^{2} }}{{\chi \lambda_{{D_{i} }}^{2} }},\;\chi = \frac{{ez_{i} \zeta_{b} }}{{k_{B} T}}$ is the ionic energy parameter and $\lambda_{Di} = \sqrt {\frac{{\varepsilon_{i} k_{B} T}}{{2z_{i}^{2} e^{2} \rho_{0,i} }}}$ is the Debye length. For $\chi < 1$, which corresponds to $\zeta_{b} < 25\;{\text{mV}}$ at 25 °C, the Debye–Hückel linearization can be applied and Eq. (4) can be written as,

$$ \frac{{{\text{d}}^{2} \varPhi_{{{\text{sc}},i}} }}{{{\text{dY}}^{2} }} = \frac{{\varPhi_{{{\text{sc}},i}} }}{{De_{i}^{2} }} $$

(5)

where $De_{i} = \frac{{\lambda_{Di} }}{{h_{1} }}$ is the Debye number which represents the relative extent of the electric double layer with respect to the characteristic length scale $h_{1}$. Note that the electric potential depends on the ionic energy parameter $\left( {\chi = \frac{{ez_{i} \zeta_{b} }}{{k_{B} T}}} \right)$. While using the Debye–Hückel linearization, this parameter is assumed to be less than one and does not appear in the subsequent equations. Equation (5) represents two second-order homogeneous linear differential equations, one for each liquid. The four non-dimensional boundary conditions required to solve this set of equations are,

$$ \varPhi_{{{\text{sc}},1}} \left( 0 \right) = 1 $$

(6)

$$ \varPhi_{{{\text{sc}},2}} \left( {H_{2} } \right) = \bar{\zeta }_{u} $$

(7)

$$ \varPhi_{{{\text{sc}},1}} \left( 1 \right) - \varPhi_{{{\text{sc}},2}} \left( 1 \right) = \bar{\zeta }_{I} $$

(8)

$$ \frac{{{\text{d}}\varPhi_{{{\text{sc}},1}} \left( 1 \right)}}{{{\text{d}}Y}} - \varepsilon_{R} \frac{{{\text{d}}\varPhi_{{{\text{sc}},2}} \left( 1 \right)}}{{{\text{d}}Y}} = \bar{Q}_{I} $$

(9)

where $\bar{\zeta }_{u} = \zeta_{u} /\zeta_{b} , \bar{\zeta }_{I} = \zeta_{I} /\zeta_{b} , \bar{Q}_{I} = \left( {Q_{I} h_{1} } \right)/\left( {\varepsilon_{1} \zeta_{b} } \right), \varepsilon_{R} = \varepsilon_{2} /\varepsilon_{1}$ and $H_{2} = h_{2} /h_{1}$. The expressions for $\varPhi_{{{\text{sc}},1}}$ and $\varPhi_{{{\text{sc}},2}}$ are given in "Appendix 1".

At this stage, it is important to discuss the validity of the Poisson–Boltzmann model applied herein. Note that the charge density, concentration and the potential are governed by the Poisson–Nernst–Planck equations (Saville 1977). The Poisson–Boltzmann model can only be derived by assuming the advection of ions as well as the applied field strength to be small. As Saville (1977) has pointed out, the strength of advection is dictated by ionic Peclet number as follows: ${\text{Pe}} = \varepsilon k_{B}^{2} T^{2} /z^{2} e^{2} \mu D$, where $\mu$ is the fluid viscosity and $D$ is the ionic diffusivity. For field-driven phenomena, this number can be ${\text{O}}\left( 1 \right)$ at most. In the present analysis, we assume the ionic Peclet number to be small enough ($Pe \ll 1$) so that the effects of ionic advection on the charge density and potential can be neglected. Further, one can also define an external field strength variable as follows (Saville 1977; Khair and Squires 2008; Schnitzer and Yariv 2012): $\wp = E_{0} Hze/kT$. For linearized Poisson–Boltzmann model to hold, the applied field strength must be such that $\wp \sim$ $O\left( 1 \right)$ at most.

2.2 Electric potential due to applied electric field

An external electric field ($E_{\text{app}}$) is applied to both the liquids and can be written in terms of the gradient of an externally applied potential $\left( {\phi_{\text{app}} } \right)$ as,

$$ - \frac{{{\text{d}}\phi_{\text{app}} }}{{{\text{d}}x}} = E_{\text{app}} = {\text{Im}}\left( {E_{0} {\text{e}}^{i\omega t} } \right) $$

(10)

Upon using non-dimensional parameters as $\varPhi_{\text{app}} = \phi_{\text{app}} /\zeta_{b} ;X = x/h_{1} , \theta = \omega t$, Eq. (10) can be written as,

$$ \frac{{{\text{d}}\varPhi_{\text{app}} }}{{{\text{d}}X}} = - \frac{1}{{E_{R} }}{\text{Im}}\left( {{\text{e}}^{i\theta } } \right) $$

(11)

where $E_{R} = \zeta_{b} /\left( {E_{0 } h_{1} } \right)$ is the relative strength of the zeta potential to the applied electric field. Therefore, the solution of $\varPhi_{\text{app}} \left( X \right)$ with boundary conditions $\varPhi_{\text{app}} \left( 0 \right) = 0$ is obtained as,

$$ \varPhi_{\text{app}} \left( X \right) = - \frac{X}{{E_{R} }}{\text{Im}}\left( {{\text{e}}^{i\theta } } \right) $$

(12)

The external electric field does not affect the potential due to space charge distribution (Dutta and Beskok 2001), and by applying the superposition principle, the total electric potential for the ith liquid can be written as,

$$ \varPhi_{i} \left( {X,Y,\theta } \right) = \varPhi_{\text{app}} \left( {X,\theta } \right) + \varPhi_{{{\text{sc}},i}} \left( Y \right) $$

(13)

where $\varPhi_{i}$ is the dimensionless total electric potential for $i = 1$ and 2.

3 Hydrodynamic equations

3.1 Governing equations

When subjected to an externally applied electric field, the liquid experiences Maxwell stress ($\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}}$) along with the hydrodynamic stress ($\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}}$). The total stress corresponding to the sum of both stresses can be written as,

$$ \varvec{\varSigma}_{\varvec{i}}^{\varvec{T}} =\varvec{\varSigma}_{\varvec{i}}^{\varvec{H}} +\varvec{\varSigma}_{\varvec{i}}^{\varvec{M}} = - \left( {p_{i} + \frac{{\varepsilon_{i} \left| {\varvec{E}_{\varvec{i}} } \right|^{2} }}{2}} \right)\varvec{I} + \mu_{i} \left( {\nabla \varvec{u}_{\varvec{i}} + \nabla \varvec{u}_{\varvec{i}}^{\varvec{T}} } \right) + \varepsilon_{i} \varvec{E}_{\varvec{i}} \otimes \varvec{E}_{\varvec{i}} $$

(14)

where $\varvec{E}_{\varvec{i}} = - \nabla \varPhi_{i}$ is the electric field vector, $\varvec{u}_{\varvec{i}} = u_{i} \varvec{i} + v_{i} \varvec{j}$ is the liquid velocity vector, $p_{i}$ is hydrostatic pressure in the liquid and $\varvec{I}$ is the unit tensor. In case of thin films, the intermolecular van der Waals interactions cannot be ignored, and it manifests in the form of a disjoining pressure (Mayur et al. 2012) given by,

$$ p_{d,i} = - \frac{{a_{i} }}{{6\pi d_{i}^{3} }} $$

(15)

where $a_{i}$ is the Hamaker’s constant for liquid “i” and $d_{i}$ is the film thickness. Hence, for the lower film $d_{1} = h_{1}$ and for upper film $d_{2} = h_{2} - h_{1}$. For an incompressible flow, the conservation of mass and momentum leads to the following equations,

$$ \nabla \cdot \varvec{u}_{\varvec{i}} = 0 $$

(16)

$$ \rho_{i} \left( {\frac{{\partial \varvec{u}_{\varvec{i}} }}{\partial t} + \left( {\varvec{u}_{\varvec{i}} \cdot \nabla } \right)\varvec{u}_{\varvec{i}} } \right) = \nabla p_{d,i} - \nabla p_{i} + \mu_{i} \nabla^{2} \varvec{u}_{\varvec{i}} + \nabla \cdot\varvec{\varSigma}^{\varvec{M}}_{\varvec{i}} $$

(17)

The substrate plates at $y = 0$ and $y = h_{2}$ are assumed to be rigid and impermeable, and hence, we impose the conditions of no slip and no penetration,

$$ u_{1} \left( 0 \right) = v_{1} \left( 0 \right) = u_{2} \left( {h_{2} } \right) = v_{2} \left( {h_{2} } \right) = 0 $$

(18)

The perturbed form of the interface between the two liquids is represented by $y = h\left( {x,t} \right)$. At the interface, the continuity of tangential and normal components of the velocity leads to the following equations,

$$ \varvec{u}_{1} \cdot\varvec{\tau}= \varvec{u}_{2} \cdot\varvec{\tau}, \quad \varvec{ u}_{1} \cdot \varvec{n} = \varvec{u}_{2} \cdot \varvec{n } $$

(19)

where $\varvec{ n }$ and $\varvec{\tau}$ are unit vectors along the normal and tangential direction, respectively, at the interface:

$$ \varvec{n} = \frac{{\frac{\partial h}{\partial x}\varvec{i} - \varvec{j}}}{{\sqrt {1 + \left( {\frac{\partial h}{\partial x}} \right)^{2} } }}, \quad \varvec{\tau}= - \frac{{\left( {\varvec{i} + \frac{\partial h}{\partial x}\varvec{j}} \right)}}{{\sqrt {1 + \left( {\frac{\partial h}{\partial x}} \right)^{2} } }} $$

Considering the force balance at the interface, there is a continuity of shear stress in the tangential direction and a jump in the normal stress created by the capillary forces,

$$ \left[ {\varvec{\tau}\cdot\varvec{\varSigma}_{\varvec{i}}^{\varvec{T}} \cdot \varvec{n}} \right]_{1}^{2} \,= 0 $$

(20)

$$ \left[ {\varvec{n} \cdot\varvec{\varSigma}_{\varvec{i}}^{\varvec{T}} \cdot \varvec{n}} \right]_{1}^{2} \,= \gamma \kappa $$

(21)

where $\left[ \right]_{1}^{2}$ denotes the jump in variables at the interface and $\kappa = \nabla \cdot \varvec{n}$ is the curvature of the interface. Since the two liquids are immiscible, there is no mass transfer across the interface; hence, the fluid velocity at the interface is equal to the velocity of the interface. This is given by the following kinematic condition,

$$ \frac{\partial h}{\partial t} + u_{i} \frac{\partial h}{\partial x} = v_{i} $$

(22)

By using the non-dimensional parameters, $X = \frac{x}{{h_{1} }}, Y = \frac{y}{{h_{1} }}, U_{i} = \frac{{u_{i} }}{{U_{\text{ref}} }}, \theta = \omega t, P_{i} = \frac{{p_{i} h_{1} }}{{\mu_{1} U_{\text{ref}} }}, H\left( {x,t} \right) = \frac{{h\left( {x, t} \right)}}{{h_{1} }} , H_{i} = \frac{{h_{i} }}{{h_{1} }}, \mu_{R} = \frac{{\mu_{2} }}{{\mu_{1} }}$, the corresponding non-dimensional conservation of mass and momentum equations can be written as,

$$ \frac{{\partial U_{i} }}{\partial X} + \frac{{\partial V_{i} }}{\partial Y} = 0 $$

(23)

For liquid 1,

$$ Wo_{1}^{2} \frac{{\partial U_{1} }}{\partial \theta } + Re_{1} \left( {U_{1} \frac{{\partial U_{1} }}{\partial X} + V_{1} \frac{{\partial U_{1} }}{\partial Y}} \right) = - \frac{{\partial P_{1} }}{\partial X} + \frac{{3A_{1} }}{{H^{4} }}\frac{\partial H}{\partial X} + \frac{{\partial^{2} U_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} U_{1} }}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \frac{{\partial \varPhi_{1} }}{\partial X}\left( {\frac{{\partial^{2} \varPhi_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}} \right) $$

(24)

$$ Wo_{1}^{2} \frac{{\partial V_{1} }}{\partial \theta } + Re_{1} \left( {U_{1} \frac{{\partial V_{1} }}{\partial X} + V_{1} \frac{{\partial V_{1} }}{\partial Y}} \right) = - \frac{{\partial P_{1} }}{\partial Y} + \frac{{\partial^{2} V_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} V_{1} }}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \frac{{\partial \varPhi_{1} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}} \right) $$

(25)

For liquid 2,

$$ Wo_{2}^{2} \frac{{\partial U_{2} }}{\partial \theta } + Re_{2} \left( {U_{2} \frac{{\partial U_{2} }}{\partial X} + V_{2} \frac{{\partial U_{2} }}{\partial Y}} \right) = \frac{ - 1}{{\mu_{R} }}\frac{{\partial P_{2} }}{\partial X} - \frac{{3A_{2} }}{{\left( {H_{2} - H} \right)^{4} }}\frac{\partial H}{\partial X} + \frac{{\partial^{2} U_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} U_{2} }}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \frac{{\partial \varPhi_{2} }}{\partial X}\left( {\frac{{\partial^{2} \varPhi_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}} \right) $$

(26)

$$ Wo_{2}^{2} \frac{{\partial V_{2} }}{\partial \theta } + Re_{2} \left( {U_{2} \frac{{\partial V_{2} }}{\partial X} + V_{2} \frac{{\partial V_{2} }}{\partial Y}} \right) = \frac{ - 1}{{\mu_{R} }}\frac{{\partial P_{2} }}{\partial Y} + \frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \frac{{\partial \varPhi_{2} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}} \right) $$

(27)

where ${{Wo}}_{i}^{2} = \frac{{\omega h_{1}^{2} }}{{\nu_{i} }}$ is the Womersley number and $\nu_{i}$ is the kinematic viscosity for liquid “i”. The dimensionless boundary conditions are as follows: no slip and no penetration at the two walls:

$$ \left. {U_{1} (0} \right) = \left. {U_{2} (H_{2} } \right) = \left. {V_{1} (0} \right) = \left. {V_{2} (H_{2} } \right) = 0 $$

(28)

And at the interface, the continuity of normal velocity,

$$ \left( {U_{1} - U_{2} } \right)\frac{\partial H}{\partial X} - \left( {V_{1} - V_{2} } \right) = 0 $$

(29)

and the continuity of tangential velocity,

$$ \left( {U_{1} - U_{2} } \right) + \left( {V_{1} - V_{2} } \right)\frac{\partial H}{\partial X} = 0 $$

(30)

The kinematic condition can be written as,

$$ \frac{{Wo_{i}^{2} }}{{Re_{i} }}\frac{\partial H}{\partial \theta } + U_{i} \frac{\partial H}{\partial X} = V_{i} $$

(31)

And finally, the continuity of shear stress,

$$ \begin{aligned} & \left( {\frac{{\partial U_{1} }}{{\partial Y}} + \frac{{\partial V_{1} }}{{\partial X}}} \right)\left( {1 - \left( {\frac{{\partial H}}{{\partial X}}} \right)^{2} } \right) - 4\frac{{\partial H}}{{\partial X}}\frac{{\partial U_{1} }}{{\partial X}} \\ & \qquad + \gamma _{{R,1}} E_{R} \left( {\frac{{\partial \Phi _{1} }}{{\partial X}}\frac{{\partial \Phi _{1} }}{{\partial Y}}\left( {1 - \left( {\frac{{\partial H}}{{\partial X}}} \right)^{2} } \right)} \right) \\ & \qquad - \frac{{\partial H}}{{\partial X}}\left( {\left( {\frac{{\partial \Phi _{1} }}{{\partial X}}} \right)^{2} - \left( {\frac{{\partial \Phi _{1} }}{{\partial Y}}} \right)^{2} } \right) \\ & \quad = \mu _{R} \left\{ {\left( {\frac{{\partial U_{2} }}{{\partial Y}} + \frac{{\partial V_{2} }}{{\partial X}}} \right)\left( {1 - \left( {\frac{{\partial H}}{{\partial X}}} \right)^{2} } \right) - 4\frac{{\partial H}}{{\partial X}}\frac{{\partial U_{2} }}{{\partial X}}} \right. \\ & \quad \quad + \gamma _{{R,2}} E_{R} \left( {\frac{{\partial \Phi _{2} }}{{\partial X}}\frac{{\partial \Phi _{2} }}{{\partial Y}}\left( {1 - \left( {\frac{{\partial H}}{{\partial X}}} \right)^{2} } \right)} \right. \\ & \quad \quad - \left. { \frac{{\partial H}}{{\partial X}}\left( {\left( {\frac{{\partial \Phi _{2} }}{{\partial X}}} \right)^{2} - \left( {\frac{{\partial \Phi _{2} }}{{\partial Y}}} \right)^{2} } \right)} \right\} \\ \end{aligned} $$

(32)

and normal stress balance,

$$ \begin{aligned} \left\{ { - \left( {P_{1} + \frac{{\gamma_{R,1} E_{R} }}{2}\left( {\left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)^{2} } \right)} \right) + \frac{2}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\frac{{\partial U_{1} }}{\partial X}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} - 1} \right) - \frac{\partial H}{\partial X}\left( {\frac{{\partial U_{1} }}{\partial Y} + \frac{{\partial V_{1} }}{\partial X}} \right)} \right)} \right. \hfill \\ \left. { + \frac{{\gamma_{R,1} E_{R} }}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} \left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)^{2} - 2\frac{\partial H}{\partial X}\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial \varPhi_{1} }}{\partial Y}} \right)} \right\} \hfill \\ - \left\{ { - \left( {P_{2} + \frac{{\mu_{R} \gamma_{R,2} E_{R} }}{2}\left( {\left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{2} }}{\partial Y}} \right)^{2} } \right)} \right)} \right. + \frac{{2\mu_{R} }}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\frac{{\partial U_{2} }}{\partial X}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} - 1} \right) - \frac{\partial H}{\partial X}\left( {\frac{{\partial U_{2} }}{\partial Y} + \frac{{\partial V_{2} }}{\partial X}} \right)} \right) \hfill \\ \left. { + \frac{{\mu_{R} \gamma_{R,2} E_{R} }}{{\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)}}\left( {\left( {\frac{\partial H}{\partial X}} \right)^{2} \left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \varPhi_{2} }}{\partial Y}} \right)^{2} - 2\frac{\partial H}{\partial X}\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial \varPhi_{2} }}{\partial Y}} \right)} \right\} = \frac{{\frac{{\partial^{2} H}}{{\partial X^{2} }}}}{{Ca\left( {1 + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right)^{{\frac{3}{2}}} }} \hfill \\ \end{aligned} $$

(33)

In addition to the above-mentioned control parameters ($\mu_{R} , \varepsilon_{R} ,\nu_{R} = \frac{{\nu_{2} }}{{\nu_{1} }}, H_{2} , De_{i} , \bar{Q}_{I} , \bar{\zeta }_{I} , \bar{\zeta }_{u}$), the problem is now described by the following additional ten control parameters,

$$ \gamma_{R,i} = \frac{{\varepsilon_{i} \zeta_{b} E_{0} }}{{\mu_{i} U_{\text{ref}} }}, \;{Re}_{i} = \frac{{\rho_{i} U_{\text{ref}} h_{1} }}{{\mu_{i} }}, A_{i} = \frac{{a_{i} }}{{6\mu_{i} \pi h_{1}^{2} U_{\text{ref}} }}, E_{R} = \frac{{\zeta_{b} }}{{E_{0} h_{1} }}, {{Ca}} = \frac{{\mu_{1} U_{ref} }}{\gamma }, {{Wo}}_{i} = \frac{{\omega h_{1}^{2} }}{{\nu_{i} }} $$

Here, $\gamma_{R,i}$ is the electroosmotic number, ${{Re}}_{i}$ is the Reynolds number, $A_{i}$ is the disjoining pressure parameter, $E_{R}$ is the relative strength of the zeta potential to the applied electric field and Ca is the capillary number.

3.2 Base-state solution

The base-state solution is obtained by assuming the flow to be uniform and only in the X-direction ($V_{i} = 0$) without a pressure-driven component. Hence, there is no velocity gradient in the X-direction. Initially, the interface is flat and is represented by the equation $Y = 1$. These assumptions result in the following base-state equations for $i = 1$ and $2$,

$$ \frac{{\partial U_{i,b} }}{\partial X} = 0 $$

(34)

$$ {{Wo}}_{i}^{2} \frac{{\partial U_{i,b} }}{\partial \theta } = \frac{{\partial^{2} U_{i,b} }}{{\partial Y^{2} }} + \gamma_{R,i} E_{R} \frac{{\partial \varPhi_{i} }}{\partial X}\left( {\frac{{\partial^{2} \varPhi_{i} }}{{\partial Y^{2} }}} \right) $$

(35)

$$ 0 = - \frac{{\partial P_{1} }}{\partial Y} + \gamma_{R,1} E_{R} \frac{{\partial \varPhi_{1} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}} \right) $$

(36)

$$ 0 = - \frac{1}{{\mu_{R} }}\frac{{\partial P_{2} }}{\partial Y} + \gamma_{R,2} E_{R} \frac{{\partial \varPhi_{2} }}{\partial Y}\left( {\frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}} \right) $$

(37)

The corresponding boundary conditions to the base state take the following form,

$$ U_{1,b} \left( {0,\theta } \right) = 0, \quad U_{2,b} \left( {H_{2} ,\theta } \right) = 0 $$

(38)

$$ U_{1,b} \left( {1,\theta } \right) = U_{2,b} \left( {1,\theta } \right) $$

(39)

$$ \frac{{\partial U_{1,b} }}{\partial Y}\left( {1,\theta } \right) - \gamma_{R,1} { \sin }\left( \theta \right)\frac{{\partial \varPhi_{1} }}{\partial Y}\left( {1,\theta } \right) = \mu_{R} \left\{ {\frac{{\partial U_{2,b} }}{\partial Y}\left( {1,\theta } \right) - \gamma_{R,2} { \sin }\left( \theta \right)\frac{{\partial \varPhi_{2} }}{\partial Y}\left( {1,\theta } \right)} \right\} $$

(40)

Equation (35) represents a set of two linear partial differential equations, and the solution can be obtained by decomposing the velocity into time- and space-dependent functions as,

$$ U_{i,b} \left( {Y,\theta } \right) = {\text{Im}}\left( {F_{i} \left( Y \right){\text{e}}^{i\theta } } \right) $$

(41)

With this form of the velocity, Eq. (35) reduces to a set of two non-homogeneous ordinary differential equations:

$$ {{iWo}}_{i}^{2} F_{i} \left( Y \right) = \frac{{{\text{d}}^{2} F_{i} \left( Y \right)}}{{{\text{d}}Y^{2} }} - \gamma_{R,i} \left( {\frac{{{\text{d}}^{2} \varPhi_{{{\text{sc}},i}} }}{{{\text{d}}Y^{2} }}} \right) $$

(42)

with the following four boundary conditions,

$$ F_{1} \left( 0 \right) = 0, F_{2} \left( {H_{2} } \right) = 0, F_{1} \left( 1 \right) = F_{2} \left( 1 \right) $$

(43)

$$ \frac{{{\text{d}}F_{1} }}{{{\text{d}}Y}}\left( 1 \right) - \gamma_{R,1} \frac{{{\text{d}}\varPhi_{{{\text{sc}},1}} }}{{{\text{d}}Y}}\left( 1 \right) = \mu_{R} \left\{ {\frac{{{\text{d}}F_{2} }}{{{\text{d}}Y}}\left( 1 \right) - \gamma_{R,2} \frac{{{\text{d}}\varPhi_{{{\text{sc}},2}} }}{{{\text{d}}Y}}\left( 1 \right)} \right\} $$

(44)

The solution to Eqs. (42–44) is found as a superposition of the general solution of the homogeneous equation and the particular solution of the full equation.

The general solution can be written as,

$$ F_{i} \left( Y \right) = F_{{{\text{CF}},i}} \left( Y \right) + F_{{{\text{CP}},i}} \left( Y \right) $$

The complementary function can be written as,

$$ F_{{{\text{CF}},i}} \left( Y \right) = C_{i} {\text{e}}^{{\sqrt {\text{i}} {{Wo}}_{i} Y}} + D_{i} {\text{e}}^{{ - \sqrt {\text{i}} {{Wo}}_{i} Y}} $$

where $C_{i}$ and $D_{i}$ are the constants of integration. The particular integral can be obtained as,

$$ F_{{{\text{PI}},i}} \left( Y \right) = \frac{{\gamma_{R,i} }}{{2\sqrt {\text{i}} {{Wo}}_{i} }}\left( {{\text{e}}^{{\sqrt {\text{i}} {{Wo}}_{i} Y}} \int {\text{e}}^{{ - \sqrt {\text{i}} {{Wo}}_{i} Y}} \left( {\frac{{{\text{d}}^{2} \varPhi_{{{\text{sc}},i}} }}{{{\text{d}}Y^{2} }}} \right){\text{d}}Y - {\text{e}}^{{ - \sqrt {\text{i}} {{Wo}}_{i} Y}} \int {\text{e}}^{{\sqrt {\text{i}} {{Wo}}_{i} Y}} \left( {\frac{{{\text{d}}^{2} \varPhi_{{{\text{sc}},i}} }}{{{\text{d}}Y^{2} }}} \right){\text{d}}Y} \right) $$

After superposition,

$$ F_{i} \left( Y \right) = C_{i} {\text{e}}^{{\sqrt {\text{i}} {{Wo}}_{i} Y}} + D_{i} {\text{e}}^{{ - \sqrt {\text{i}} {{Wo}}_{i} Y}} + \frac{{\gamma_{R,i} }}{{2\sqrt {\text{i}} {{Wo}}_{i} }}\left( {\frac{{A_{i} }}{{M_{i} }}{\text{e}}^{{Y\left( {\frac{1}{{{\text{De}}_{i} }}} \right)}} - \frac{{B_{i} }}{{N_{i} }}{\text{e}}^{{ - Y\left( {\frac{1}{{{\text{De}}_{i} }}} \right)}} - \frac{{A_{i} }}{{N_{i} }}{\text{e}}^{{Y\left( {\frac{1}{{{\text{De}}_{i} }}} \right)}} + \frac{{B_{i} }}{{M_{i} }}{\text{e}}^{{ - Y\left( {\frac{1}{{{\text{De}}_{i} }}} \right)}} } \right) $$

(45)

where $N_{i} = \left( {{\text{De}}_{i} + {\text{De}}_{i}^{2} \sqrt {\text{i}} {{Wo}}_{i} } \right)$ and $M_{i} = \left( {{\text{De}}_{i} - {\text{De}}_{i}^{2} \sqrt {\text{i}} {{Wo}}_{i} } \right)$. The coefficients $C_{i}$ and $D_{i}$ can be found by using the boundary conditions (43–44) and using Mathematica’s simultaneous equations solver package, and $A_{i}$ and $B_{i}$ are the same constants defined for the potential $\varPhi_{{{\text{sc}},i}}$ (see "Appendix 1"). The solution for $U_{i,b}$ can then be found by taking the imaginary part of $F_{i} \left( Y \right){\text{e}}^{i\theta }$.

4 Linear stability analysis

The system is subjected to small perturbations,

$$ U_{i} = U_{i,b} + \widetilde{{U_{i} }}, V_{i} = \widetilde{{V_{i} }}, P_{i} = P_{i,b} + \widetilde{{P_{i} }}, H = 1 + \tilde{H} $$

(46)

where the variables with a tilde correspond to perturbation variables. Velocity components are converted to their corresponding stream function representation as $\widetilde{{U_{i} }} = \frac{{\partial \widetilde{{\varPsi_{i} }}}}{\partial Y}$ and $\widetilde{{V_{i} }} = - \frac{{\partial \tilde{\varPsi }_{i} }}{\partial X}$ to reduce the number of variables. The normal modes approach is then used to represent the perturbations,

$$ \widetilde{{\varPsi_{i} }}\left( {X,Y,\theta } \right) = \bar{\varPsi }_{i} \left( {Y,\theta } \right){\text{e}}^{i\alpha X} , \tilde{H}\left( {X,\theta } \right) = \bar{H}\left( \theta \right){\text{e}}^{i\alpha X} , \tilde{P}_{i} \left( {X,Y,\theta } \right) = \bar{P}_{i} \left( {Y,\theta } \right){\text{e}}^{i\alpha X} $$

(47)

where $\alpha$ is the wave number. Upon substitution of the perturbed variables and linearization, the base-state equations are subtracted from the perturbed equations. The pressure term is eliminated by taking derivative of X-momentum and Y-momentum equations with respect to Y and X, respectively, and subtracting one from the other. Using Floquet theory, the stream function and the interface height can be written as,

$$ \bar{\varPsi }_{i} \left( {Y,\theta } \right) = \hat{\varPsi }_{i} \left( {Y,\theta } \right){\text{e}}^{\sigma \theta } , \quad \bar{H}\left( \theta \right) = \hat{H}\left( \theta \right){\text{e}}^{\sigma \theta } $$

(48)

where $\hat{\varPsi }_{i} \left( {Y,\theta } \right),\;\hat{H}\left( \theta \right)$ are periodic functions and $\sigma$ is the Floquet exponent. This Floquet exponent will be used to comment on the stability of the system. The following equation for the stream function is then obtained,

$$ \left( {\frac{{\partial^{2} }}{{\partial Y^{2} }} - \alpha^{2} } \right)^{2} \hat{\varPsi }_{i} \left( {Y,\theta } \right) - \left( {{{Wo}}_{i}^{2} \frac{\partial }{\partial \theta } + {\text{i}}\alpha {{Re}}_{i} U_{i,b} } \right)\left( {\frac{{\partial^{2} }}{{\partial Y^{2} }} - \alpha^{2} } \right)\hat{\varPsi }_{i} \left( {Y,\theta } \right) + {\text{i}}\alpha {{Re}}_{i} \frac{{\partial^{2} U_{i,b} }}{{\partial Y^{2} }}\hat{\varPsi }_{i} \left( {Y,\theta } \right) = \sigma {{Wo}}_{i}^{2} \left( {\frac{{\partial^{2} }}{{\partial Y^{2} }} - \alpha^{2} } \right)\hat{\varPsi }_{i} \left( {Y,\theta } \right) $$

(49)

The boundary conditions at the interface are to be applied at $Y = 1 + \tilde{H}$ and can be written as Taylor series expansion around $Y = 1$ as follows:

$$ \frac{{\partial \hat{\varPsi }_{1} }}{\partial Y}\left( {0,\theta } \right) = 0, \hat{\varPsi }_{1} \left( {0,\theta } \right) = 0, \frac{{\partial \hat{\varPsi }_{2} }}{\partial Y}\left( {H_{2} ,\theta } \right) = 0, \hat{\varPsi }_{2} \left( {H_{2} ,\theta } \right) = 0 $$

(50)

$$ \hat{\varPsi }_{1} \left( {1,\theta } \right) = \hat{\varPsi }_{2} \left( {1,\theta } \right) $$

(51)

$$ \hat{H}\left( \theta \right)\left( {\frac{{\partial U_{1,b} \left( {1,\theta } \right)}}{\partial Y} - \frac{{\partial U_{2,b} \left( {1,\theta } \right)}}{\partial Y}} \right) + \frac{\partial }{\partial Y}\left( {\hat{\varPsi }_{1} \left( {1,\theta } \right) - \hat{\varPsi }_{2} \left( {1,\theta } \right)} \right) = 0 $$

(52)

$$ {\text{i}}\alpha \hat{\varPsi }_{1} \frac{{Wo_{1}^{2} }}{{Re_{1} }}\frac{{\partial \hat{H}\left( \theta \right)}}{\partial \theta } + \sigma \hat{H}\left( \theta \right)\frac{{Wo_{1}^{2} }}{{Re_{1} }} + \hat{H}\left( \theta \right)U_{1,b} \left( {1,\theta } \right){\text{i}}\alpha = 0 $$

(53)

$$ \begin{aligned} \left( {\frac{{\partial^{2} }}{{\partial^{2} Y^{2} }} + \alpha^{2} } \right)\hat{\varPsi }_{1} \left( {1,\theta } \right) + \hat{H}\left( \theta \right)\frac{{\partial^{2} U_{1,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \hat{H}\left( \theta \right)\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} \hfill \\ - {\text{i}}\alpha \gamma_{R,1} E_{R} \hat{H}\left( \theta \right)\left( {\left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right) \hfill \\ = \mu_{R} \left( {\left( {\frac{{\partial^{2} }}{{\partial^{2} Y^{2} }} + \alpha^{2} } \right)\hat{\varPsi }_{2} \left( {1,\theta } \right) + \hat{H}\left( \theta \right)\frac{{\partial^{2} U_{2,b} \left( 1 \right)}}{{\partial Y^{2} }}} \right. \hfill \\ \left. { + \gamma_{R,2} E_{R} \hat{H}\left( {1,\theta } \right)\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }} - {\text{i}}\alpha \gamma_{R,2} E_{R} \hat{H}\left( \theta \right)\left( {\left( {\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right)} \right) \hfill \\ \end{aligned} $$

(54)

$$ \begin{aligned} & {{Wo}}_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1} \left( {1,\theta } \right)}}{\partial \theta \partial Y} + \sigma Wo_{1}^{2} \frac{{\partial \hat{\varPsi }_{1} \left( {1,\theta } \right)}}{\partial Y} + i\alpha {Re}_{1} \left( {U_{1,b} \left( {1,\theta } \right)\frac{{\partial \hat{\varPsi }_{1} \left( {1,\theta } \right)}}{\partial Y} - \hat{\varPsi }_{1} \left( {1,\theta } \right)\frac{{\partial U_{1,b} }}{\partial Y}} \right) \\ & \quad \quad + \left( {3\alpha^{2} - \frac{{\partial^{2} }}{{\partial Y^{2} }}} \right)\frac{{\partial \hat{\varPsi }_{1} \left( {1,\theta } \right)}}{\partial Y} \\ & \quad = i\alpha \hat{H}\left( \theta \right)\left( { - \frac{{\alpha^{2} }}{{Ca}} + \frac{{3A_{1} }}{{H_{1} }} + \mu_{R} \frac{{3A_{2} }}{{\left( {H_{2} - H_{1} } \right)}}} \right) \\ & \quad \quad + \mu_{R} \left\{ {{{Wo}}_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2} \left( {1,\theta } \right)}}{\partial \theta \partial Y} + \sigma {{Wo}}_{2}^{2} \frac{{\partial \hat{\varPsi }_{2} \left( {1,\theta } \right)}}{\partial Y}} \right. \\ & \quad \quad \left. { + i\alpha {Re}_{2} \left( {U_{2,b} \frac{{\partial \hat{\varPsi }_{2} \left( {1,\theta } \right)}}{\partial Y} - \hat{\varPsi }_{2} \frac{{\partial U_{2,b} \left( {1,\theta } \right)}}{\partial Y}} \right) + \left( {3\alpha^{2} - \frac{{\partial^{2} }}{{\partial Y^{2} }}} \right)\frac{{\partial \hat{\varPsi }_{2} \left( {1,\theta } \right)}}{\partial Y}} \right\} \\ \end{aligned} $$

(55)

The stability information of thin film systems can be recovered without solving the complete set of equations. Yih’s method (Yih 1963) (long-wave expansion method) can be used to expand the dependent variables $\hat{\varPsi }_{i} \left( {Y,\theta } \right),\hat{H}_{0} \left( \theta \right)$ and $\sigma$ in powers of $\alpha$,

$$ \hat{\varPsi }_{i} \sim \hat{\varPsi }_{i,0} + \alpha \hat{\varPsi }_{i,1} + \alpha^{2} \hat{\varPsi }_{i,2} ,\;\hat{H}_{0} \left( \theta \right)\sim\hat{H}_{0} + \alpha \hat{H}_{1} + \alpha^{2} \hat{H}_{2} ,\;\sigma \sim\sigma_{0} + \alpha \sigma_{1} + \alpha^{2} \sigma_{2} $$

(56)

The lengthy equations corresponding to zero, first and second order in $\alpha$ are given in "Appendix 2". An additional assumption is made that the capillary forces are large, i.e. $\alpha^{2} /Ca \sim O\left( 1 \right)$ (Mayur et al. 2012). The expression for the real part of the growth rate, $\sigma_{R}$, is found by calculating the real part of $\sigma_{2}$, and the critical wave number can then be obtained by equating the growth rate to zero which in turn gives the marginal stability curves for the system.

5 Results

5.1 Base-state profiles

In the following results, we have assumed that the two-liquid layers are of same thickness which implies $H_{2} = 2$. By assuming the electroosmotic number, the Womersley number and the Reynolds number for the lower liquid ($i = 1$), as $\gamma_{R}$, ${Wo}$ and Re, respectively, these numbers for the upper liquid turn out to be $\frac{{\varepsilon_{R} }}{{\mu_{R} }}\gamma_{R} ,\;\frac{{Wo}}{{\sqrt {\nu_{R} } }}$ and $\frac{{Re}}{{\nu_{R} }}$, respectively, where $\nu_{R} = \frac{{\nu_{2} }}{{\nu_{1} }}$ corresponds to the kinematic viscosity ratio. Also, the disjoining pressure parameters are assumed to be the same: $A_{1} = A_{2} = A$. The quantity $\frac{{\gamma_{R} }}{{E_{R} }}$ represents the applied electric field and $\gamma_{R} E_{R}$ represents the wall zeta potential (at $y = 0$). The zeta potential of the wall in contact with liquid 2 ($\zeta_{u}$) is assumed to be same as the zeta potential of the wall in contact with liquid 1 ($\zeta_{b}$). Therefore, $\bar{\zeta }_{u} = 1$. The relaxation time of ionic species in a homogeneous dielectric media is given by the Maxwell–Wagner–O’Konski relaxation time (Delgado et al. 2007), and the corresponding frequency can be written as,

$$ \omega_{\text{MWO}} = \frac{1}{{\tau_{\text{WMO}} }} \approx \frac{{2 D_{i} }}{{\lambda_{D}^{2} }} $$

where $\lambda_{D}$ is the Debye length. In the limit of $\omega < \omega_{\text{MWO}}$, charges relax to the equilibrium distribution faster than the time-dependent external perturbation and hence polarization effects are negligible and the permittivity can be assumed constant as $\varepsilon \left( \omega \right) \approx \varepsilon$ (Mayur et al. 2014). Consequently, for $\lambda_{D}$ ranging from 1 to 100 nm and with reference length ($h_{1}$) equal to 100 nm, the ${{Wo}}$ number has an approximate range of 0.05 to 5.

The dimensional electric potential depends on the ionic energy parameter $\left( {\chi = \frac{{ez_{i} \zeta_{b} }}{{k_{B} T}}} \right)$. While using the Debye–Hückel linearization, this parameter is assumed to be less than one and does not appear in the subsequent equations. Dutta and Beskok (2001) derived the electric potential without applying the Debye–Hückel linearization but with constraints of thin EDL which entails a zero centre-line potential.

The accuracy of the obtained velocity profile in this study is validated with the work from Dutta and Beskok (2001) on AC EOF in a channel. The two-liquid system can be converted to a single liquid system by assuming that there is no jump in the parameters such as permittivity, kinematic viscosity and density ($\varepsilon_{R} = 1,\;\nu_{R} = 1$ and $\mu_{R} = 1$). The interface is also free from any interface zeta potential and charge. Figure 2a shows the velocity profile ($U_{b}$) for two values of the Womersley number (${{Wo}} = 1$ and ${{Wo}} = 10$) for the present case and the one reported by Dutta and Beskok (2001). There is a small difference between the half-channel velocity profile extracted from the work of Dutta and Beskok (2001) and the velocity profile in our case, particularly for high frequency (${{Wo}} = 10$) due to the values of the ionic energy parameter $\chi$ considered in the two studies.

Fig. 2

a Comparison of velocity profile with Dutta and Beskok (2001), for ${\text{De}}_{1} = {\text{De}}_{2} = {\text{De}} = 0.01,\;\bar{\zeta }_{u} = 1,\;\bar{\zeta }_{I} = 0, \;\bar{Q}_{I} = 0, \mu_{R} = 1,\;\varepsilon_{R} = 1, \nu_{R} = 1,\;\gamma_{R} = 1$, $\theta = \pi /2$, $\chi = 5$ for (Dutta and Beskok 2001) and $\chi < 1$ in the present study. b Experiments (Mayur 2013), for ${\text{De}}_{1} = {\text{De}}_{2} = 0.01,\;\bar{\zeta }_{u} = 1, \bar{\zeta }_{I} = 0, \;\bar{Q}_{I} = 0, \mu_{R} = 1,\;\varepsilon_{R} = 1, \nu_{R} = 1,\;\gamma_{R} = 1$, ${{Wo}} = 0.01, \;\theta = 3\pi /2$ and for two values of $E_{0}$ and $\zeta_{b}$

In addition to the above comparison, the results from the present work are also compared with experimental results for DC EOF (Mayur 2013). In Fig. 2b, small value for ${{Wo}}$ is chosen which corresponds to small value of the excitation frequency so as to consider a DC case with reversing polarity. The reference length ($h_{1}$) is equal to the half-channel height, i.e. 50 µm. In this figure, the reference velocity is taken as $U_{\text{ref}} = - U_{\text{HS}}$, where $U_{\text{HS}} = - \varepsilon_{1} \zeta_{b} E_{0} /\mu_{1}$ is the Helmholtz–Smoluchowsky velocity. With this assumption, $\gamma_{R} = \varepsilon_{1} \zeta_{b} E_{0} /\mu_{1} U_{\text{ref}} = - U_{\text{HS}} /U_{\text{ref}} = 1$. For the two values of the magnitude of applied electric field considered, 50 and 70 V/cm, the reference velocity is 0.0885 and 0.198 mm/s, respectively. Also, since the Debye length is small, a plug-type velocity profile is observed. A quite well agreement with the experimental results is observed in Fig. 2b except very close to the solid boundary where the experimental velocity vanishes a bit far from the boundary. This could be due to the experimental accuracy of the images of the tracer particle near the boundary (see Mayur 2013). But in the bulk, our theoretical results are perfectly matching to the experimental data.

Figure 3a represents the base-state velocity profile at different time instances for ${{Wo}} = 0.1$. Except the dynamic viscosity, all other parameters are assumed to be same for both liquids. Liquid 2 has higher viscosity and hence shows lower magnitude of velocity as compared to liquid 1. As the Womersley number is increased, the wavy nature of the velocity profile increases (see Fig. 3b). At certain time instances, the velocity is not completely unidirectional. For example, at $\theta = \pi /8$ in Fig. 3b, the lower liquid has negative velocity, whereas a major portion of the upper liquid has positive velocity.

Fig. 3

a Velocity profile, $U_{b}$, at different values of non-dimensional time, $\theta$, and for ${\text{De}}_{1} = {\text{De}}_{2} = 0.1,\;\bar{\zeta }_{u} = 1, \bar{\zeta }_{I} = 1, \;\bar{Q}_{I} = 0, \mu_{R} = 2,\;\varepsilon_{R} = 1,\;\nu_{R} = 1,\;\gamma_{R} = 1$ and a ${{Wo}} = 0.1$. b ${{Wo}} = 1$

5.2 Growth rate

The stability behaviour of this system depends on complex interplay of various parameters defined in this study. For instance, the way the viscosity ratio affects the stability depends on interface charge when all other parameters are fixed. Figure 4 shows the variation of the real part of the growth rate for different values of viscosity ratio, $\mu_{R}$. Stability in this case is governed by the difference in the forces experienced by the upper and the lower liquid. The greater is this difference, the greater will be the instability. The interface charge and potential contribute in the momentum equation through $\gamma_{R,i} E_{R} \frac{{\partial^{2} \varPhi_{i} }}{{\partial Y^{2} }}$ (for i = 1, 2) which, in this example, is equal to $\frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}$ and $\frac{{\varepsilon_{R} }}{{\mu_{R} }}\frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}$ for lower and upper liquids, respectively. In these expressions, since rest of the parameters are held constant, $\frac{{\partial^{2} \varPhi_{i} }}{{\partial Y^{2} }}$ may be thought of as representing the net charge.

Fig. 4

Variation of the real part of growth rate with the wave number for different values of viscosity ratio and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \bar{\zeta }_{I} = 1, \varepsilon_{R} = 1,\;\nu_{R} = 1, {{Re}} = 0.001,\;{{Wo}} = 0.1,\;{{Ca}} = 0.01, A = 0.1, E_{R} = 1,\;\gamma_{R} = 1,$ and for two values of the electric field: a ${Q}_{I} = 1$ and b $Q_{I} = 0$. c Velocity profile, $U_{b}$, for different values of viscosity ratio, and for ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \bar{\zeta }_{I} = 1, \varepsilon_{R} = 1,\nu_{R} = 1, {{Re}} = 0.001,Wo = 0.1,{{Ca}} = 0.01, A = 0.1,\gamma_{R} = 1 {\text{and Q}}_{\text{I}} = 0$

In Fig. 4a, the interface charge (${\bar{{Q}}}_{{I}}$) is assumed to be nonzero and the instability increases as $\mu_{R}$ increases. Since the rest of the parameters are held constant, an increase in $\mu_{R}$ actually implies that $\mu_{1}$ is fixed and $\mu_{2}$ is increased. At the interface, $\frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }} = 55$ for the lower liquid and $\frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }} = - 45$ for the upper liquid. For $\mu_{R} > 1$, the difference between $\frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}$ and $\frac{{\varepsilon_{R} }}{{\mu_{R} }}\frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}$ increases even further which leads to instability. Physically, as the upper liquid is experiencing less electric force, an increase in its viscosity enhances the force difference experienced by the two liquids and hence leads to instability. However, for ${\bar{\text{Q}}}_{\text{I}} = 0$, stability trend gets twisted and is shown in Fig. 4b. In this case, $\frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }} = 50.0091$ for the lower liquid and $\frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }} = - 49.9909$ for the upper liquid. As the value of $\frac{{\partial^{2} \varPhi_{i} }}{{\partial Y^{2} }}$ is almost same for the two liquids, for the extreme values of viscosity ratio ($\mu_{R} = 0.1$ and $\mu_{R} = 10$) the difference between $\frac{{\partial^{2} \varPhi_{1} }}{{\partial Y^{2} }}$ and $\frac{{\varepsilon_{R} }}{{\mu_{R} }}\frac{{\partial^{2} \varPhi_{2} }}{{\partial Y^{2} }}$ increases as $\varepsilon_{R} = 1$. This makes the system more unstable as compared to $\mu_{R} = 1$. This can also be concluded by observing the high velocity gradient at the interface which is highlighted in Fig. 4c. For $\mu_{R} = 1$, the growth rate curve is same for both ${\bar{\text{Q}}}_{\text{I}} = 1$ and ${\bar{\text{Q}}}_{\text{I}} = 0$. Hence, the effect of ${\bar{\text{Q}}}_{\text{I}}$ is significant only when $\mu_{R}$ is away from 1.

In Fig. 5, the applied electric field represented by $\frac{{\gamma_{R} }}{{E_{R} }} = \frac{{\varepsilon_{1} E_{0}^{2} d}}{{\mu_{1} U_{\text{ref}} }}$ is varied, with the rest of the parameters being same as in Fig. 4a. The system is unstable even for very low values of $\frac{{\gamma_{R} }}{{E_{R} }}$, and the growth rate behaviour remains the same even for $\frac{{\gamma_{R} }}{{E_{R} }}$ equal to unity. For very large values of $\frac{{\gamma_{R} }}{{E_{R} }}$, there is a significant increase in the instability of the system. This points out a threshold value of $\frac{{\gamma_{R} }}{{E_{R} }}$ above which the applied electric field starts affecting the system significantly.

Fig. 5

Variation of the real part of growth rate with the wave number for different values of applied electric field and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \bar{\zeta }_{I} = 1, \varepsilon_{R} = 1,\;\mu_{R} = 2,\;\nu_{R} = 1, {{Re}} = 0.001,\;{{Wo}} = 0.1,\;{{Ca}} = 0.01, A = 0.1, Q_{I} = 0$

In Fig. 6, increasing the permittivity ratio $\left( {\varepsilon_{R} } \right)$ decreases the stability of the system. The lower liquid is less viscous than the upper liquid. When $\varepsilon_{R}$ is increased, the permittivity of the upper liquid ($\varepsilon_{2}$) is increased, thus the upper liquid experiences greater Maxwell stress as compared to the lower liquid. This can be expressed in terms of electroosmotic (EO) number which is $\frac{{\varepsilon_{R} }}{{\mu_{R} }}\gamma_{R}$ for the upper liquid and $\gamma_{R}$ for the lower liquid and corresponds to the coefficient of the Maxwell stress term in the momentum equation (see Eqs. 24, 26). So, when $\varepsilon_{R}$ is increased the EO number for liquid 1 remains the same while that of liquid 2 increases. Because of this disparity, i.e. the difference in the forces experienced by the two liquids, the instability of the system increases. Figure 6 also shows very small effect of $\varepsilon_{R}$ on stability of the system when $\varepsilon_{R}$ is raised from 0.1 to 1. This indicates that, for the given set of parameters, the effect $\varepsilon_{R}$ saturates below a certain value. Stability of the system is also greatly influenced by electrostatics at the interface. The negative charge present at the interface is stabilizing the system in Fig. 6a, while the positive charge in Fig. 6b has a destabilizing effect. This can be better understood with the help of marginal stability curves.

Fig. 6

Variation of the real part of growth rate with the wave number for different values of permittivity ratio and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \mu_{R} = 2, \nu_{R} = 1, {\text{Re}} = 0.001,\;{{Wo}} = 0.1,\;A = 0.1,\;E_{R} = 1,\;\gamma_{R} = 1, {{Ca}} = 0.01,\;\bar{\zeta }_{I} = 1$ and a $Q_{I} = - 1$, b $Q_{I} = 1$

5.3 Marginal stability

Marginal stability curves provide insight to the stability behaviour through critical wave number. Large critical wave number implies that all the wave numbers below it are unstable. Hence, the larger is the critical wave number, the greater is the instability of the system. The region below the marginal stability curve marks the unstable region and vice versa.

The effect of the interface charge $\left( {\bar{Q}_{I} } \right)$ depends not only on the polarity of the charge itself but also on the polarity of the interface zeta potential ($\bar{\zeta }_{I}$). With zero $\bar{\zeta }_{I}$, the effect of $\bar{Q}_{I}$ on the critical wave number is negligible as compared to the case with nonzero $\bar{\zeta }_{I}$ (see Fig. 7). The critical wave number increases with magnitude of $\bar{Q}_{I}$ when $\bar{\zeta }_{I}$ and $\bar{Q}_{I}$ are of the same polarity and decreases when $\bar{\zeta }_{I}$ and $\bar{Q}_{I}$ are of opposite polarity. This is true for the given set of parameters. There is also a threshold value of $\bar{Q}_{I}$ at which the instability sets in or the point at which the critical wave number becomes nonzero. In this case, the magnitude of the threshold value is around |0.18| for both $\bar{\zeta }_{I} = 1$ and $\bar{\zeta }_{I} = - 1$. It can be noted that, in this case and for $\bar{\zeta }_{I} = 1$, a negative charge of magnitude greater than 0.18 at the interface will stabilize the system as it happened in Fig. 6 for $\bar{Q}_{I} = - 1$. Similarly for $\bar{\zeta }_{I} = - 1$, with the given parameters, positive charge of magnitude greater than 0.18 will also stabilize the system.

Fig. 7

Marginal stability curve showing the critical wave number as a function of interface charge for different values of interface zeta potential and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, { }\mu_{R} = 2, \varepsilon_{R} = 1, \nu_{R} = 1, {{Re}} = 0.001,\;{{Wo}} = 0.1,\;A = 0.1,\;E_{R} = 1,\;\gamma_{R} = 1 , {{Ca}} = 0.01$

Figure 8 shows the critical wave number plotted against the interface zeta potential $\left( {\bar{\zeta }_{I} } \right)$. The permittivity and kinematic viscosity are same for both liquids. For the given set of parameters, the system shows similar tendency as for DC field (Navarkar et al. 2015). When the two liquids have the same viscosity, instability escalates with increment in $\bar{\zeta }_{I}$ (with polarity).

Fig. 8

Marginal stability curve showing the critical wave number as a function of interface zeta potential for different values of viscosity ratio and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, Q_{I} = 0,\;\nu_{R} = 1,\;\varepsilon_{R} = 1,\;{{Re}} = 0.001,\;{{Wo}} = 0.1,\;A = 0.1,\;E_{R} = 1,\;\gamma_{R} = 1,\;{{Ca}} = 0.01$

Figure 9 shows dependence of the critical wave number on the capillary number $\left( {{Ca}} \right)$. As the capillary number increases, the surface tension force decreases. Hence, the stability of the system decreases with an increase in Ca. Also raising the value of the applied electric field further pushes the marginal stability curve upwards thereby enlarging the unstable region. But the change is negligible when the $\frac{{\gamma_{R} }}{{E_{R} }}$ is raised from 0.01 to 1. As observed in Fig. 5, this also points out the possibility that there exists a threshold value for the applied electric field above which it starts to make significant changes in the behaviour of the system.

Fig. 9

Marginal stability curve showing the critical wave number as a function of the capillary number for different values of applied electric field and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1,\;\bar{\zeta }_{I} = 1,\;Q_{I} = 0,\;\varepsilon_{R} = 2,\;\mu_{R} = 2,\;\nu_{R} = 1, {{Re}} = 0.001,\;A = 0.1,\;{{Wo}} = 0.1$ $\left( {\text{assuming the applied wall zeta potential to be constant}} \right)$

Similarly, there exists a threshold value for dimensionless Hamaker constant $\left( A \right)$ and can be observed in Fig. 10. A large value of the Hamaker constant is needed and in this case the critical value is 8.5 for the lowest value of $\mu_{R}$. The threshold values for a particular case are dependent on the rest of the parameters of the system. For the other value of $\mu_{R}$ considered, the threshold value is zero, i.e. the system will be unstable even with zero disjoining pressure. The disjoining pressure $A$ constitutes a destabilizing force, i.e. a decrease in stability is observed with an increase in $A$.

Fig. 10

Marginal stability curve showing the critical wave number as a function of the dimensionless Hamaker constant for different values of viscosity ratio and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1,\;\bar{\zeta }_{I} = 1,\;Q_{I} = 0,\;\varepsilon_{R} = 2,\;\nu_{R} = 1, {{Re}} = 0.001,\;{{Wo}} = 0.1,\;\gamma_{R} = 1,\;{\text{E}}_{R} = 1, {{Ca}} = 0.01$

Figure 11 shows the marginal stability curve for different values of applied electric field. As the electric field is increased, the system becomes more unstable as the Maxwell stress experienced by the liquid increases. The same was experimentally observed by Oddy et al. (2001). But the effect of the applied electric field is negligible as it is raised from 0 to 2. This is also noted in Fig. 9 (note that the curves in Fig. 9 for $\frac{{\gamma_{R} }}{{E_{R} }} = 0.01$ and $\frac{{\gamma_{R} }}{{E_{R} }} = 1$ are very close). Increasing the frequency of oscillation has a stabilizing effect. For very large frequency, the liquids are not able to cope up with the rapid change in direction of the electric field and hence lose their momentum. The system becomes static except near the Debye layer where there is a higher concentration of net charge. Also the charge at the interface is assumed to be zero. These factors lead to increased stability for the case of ${{Wo}} = 2$.

Fig. 11

Marginal stability curve showing the critical wave number as a function of the electroosmotic number for different values of Womersley number and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1,\;\bar{\zeta }_{I} = 1,\;Q_{I} = 0,\;\varepsilon_{R} = 1, \mu_{R} = 2 ,\;\nu_{R} = 1, {{Re}} = 0.001,\;A = 0.1,\;E_{R} = 1/\gamma_{R} , {{Ca}} = 0.01$ $\left( {{\text{assuming the applied wall zeta potential to be constant, i}} . {\text{e }}E_{R} \gamma_{R} { = 1}} \right)$

In Fig. 12, the system responds in a slightly complicated way to the changes in viscosity ratio. As expected, the system becomes more unstable as the applied electric field ($\frac{{\gamma_{R} }}{{E_{R} }}$) is increased. And as the viscosity ratio increases, the stability of the system decreases for small values of applied electric field. Even though the critical wave number can be seen to increase with the applied electric field, the increment is small with a maximum change in the order of 0.05. Also there is jump in the potential at the interface due to space charge distribution $\left( {\bar{\zeta }_{I} = 1} \right)$. Since the electric permittivity of both liquids is same, they experience the same amount of electric force. For small values of electric field, viscous forces dominate. So, as the viscosity ratio is increased, the viscosity of the upper liquid gets increased, and it becomes difficult for the upper liquid to keep up with lower liquid. This leads to the decrease in the stability. On the other hand, for very strong electric field, the system is more stable when the two liquids share the same viscosity as compared to the extreme values of the viscosity ratios.

Fig. 12

Marginal stability curve showing the critical wave number as a function of the electroosmotic number for different values of viscosity ratio and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1,\;\bar{\zeta }_{I} = 1,\;Q_{I} = 0,\;\varepsilon_{R} = 1, \nu_{R} = 1, {{Re}} = 0.001,\;A = 0.1,\;E_{R} = 1/\gamma_{R} , {{Ca}} = 0.01,\;{{Wo}} = 0.1$ $\left( {{\text{assuming the applied wall zeta potential to be constant, i}} . {\text{e }}E_{R} \gamma_{R} { = 1}} \right)$

It is difficult to predict how the system will behave when one of the parameters is changed without knowing the values for the rest of the parameters. Figure 13 is an example which shows the complex interplay of the parameters. The critical wave number is plotted against the applied electric field for different values of interface zeta potential ($\bar{\zeta }_{I}$). The interface charge is assumed to be zero. The upper liquid is twice as viscous as the lower liquid, and the rest of the parameters are same for both the liquids. When $\bar{\zeta }_{I} = - 5$, the system is highly stable and the transition to instability occurs only when the applied electric field is raised beyond the threshold value ($\gamma_{R} = 52.8$ in this case). When $\bar{\zeta }_{I} = - 1$, the applied electric field switches role and stabilizes the system. Its effect gets saturated beyond $\gamma_{R} = 44$. For $\bar{\zeta }_{I} = 0,$ and $\bar{\zeta }_{I} = 1$, the electric field has a classical effect of destabilizing the system as a function of electroosmotic number.

Fig. 13

Marginal stability curve showing the critical wave number as a function of the electroosmotic number for different values of interface zeta potential and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, Q_{I} = 0,\;\varepsilon_{R} = 1,\; \mu_{R} = 2, \;\nu_{R} = 1, {{Re}} = 0.001,\;A = 0.1,E_{R} = 1/\gamma_{R} , {{Ca}} = 0.01,\;{{Wo}} = 0.1$ $\left( {{\text{assuming the applied wall zeta potential to be constant, i}} . {\text{e }}E_{R} \gamma_{R} { = 1}} \right)$

Figure 14a shows the neutral curve obtained by setting the real part of growth rate equal to zero, i.e. $\sigma_{R} = 0$, and the critical value of $\gamma_{R}$ is plotted against the critical wave number. This plot shows the value of $\gamma_{R}$ required to achieve a particular critical wave number and whether it is possible to achieve it. It is similar to the marginal stability curve which is also obtained by setting $\sigma_{R} = 0$. Figure 14a shows that for $\mu_{R} = 0.1$ and $\mu_{R} = 0.5$, with the given set of parameters, the system becomes unstable only above a nonzero threshold value of $\gamma_{R}$, whereas, for $\mu_{R} > 1$, this threshold value is equal to zero. This is verified using the growth rate curves in Fig. 14b, c.

Fig. 14

a Neutral curves showing the critical electroosmotic number as a function of the critical wave number for different values of interface viscosity ratio and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, {\text{Q}}_{\text{I}} = 1,\bar{\zeta }_{I} = 1,\varepsilon_{R} = 1, \nu_{R} = 1, {{Re}} = 0.001,\;A = 0.1,\;E_{R} = 1/\gamma_{R} , {{Ca}} = 0.01,\;{{Wo}} = 0.1$ $\left( {\text{assuming the applied wall zeta potential to be constant}} \right)$. Variation of the real part of growth rate with the wave number for different values of applied electric field and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \bar{\zeta }_{I} = 1, \varepsilon_{R} = 1,\nu_{R} = 1, {{Re}} = 0.001,\;{{Wo}} = 0.1,E_{R} = 1/\gamma_{R}, {{Ca}} = 0.01, A = 0.1, Q_{I} = 1,\;{\mathbf{b}}\;\mu_{R} = 0.1, \;{\mathbf{c}}\;\mu_{R} = 10$

As observed in Fig. 7, the effect of interface zeta potential and charge on the stability of the system is closely interlinked. Figure 15 shows a clearer picture of this interaction through a plot of maximum growth rate $\left( {\sigma_{ \hbox{max} } } \right)$ in the $\bar{Q}_{I} - \bar{\zeta }_{I}$ plane. For $\mu_{R} < 1$, the system is unstable when $\bar{Q}_{I}$ and $\bar{\zeta }_{I}$ are of opposite polarity, whereas, for $\mu_{R} > 1$, the system is unstable when $\bar{Q}_{I}$ and $\bar{\zeta }_{I}$ are of the same polarity. This can be attributed to the force difference mentioned in the explanation of Fig. 4a.

Fig. 15

a Variation $\sigma_{ \hbox{max} }$ in the phase space of $\bar{Q}_{I} - \bar{\zeta }_{I}$ and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \varepsilon_{R} = 1,\nu_{R} = 1, {{Re}} = 0.001,\;{{Ca}} = 0.01, A = 0.1, {{Wo}} = 0.1, \mu_{R} = 0.5,\gamma_{R} = 1,E_{R} = 1$. b Variation $\sigma_{ \hbox{max} }$ in the phase space of $\bar{Q}_{I} - \bar{\zeta }_{I}$ and with ${\text{De}}_{1} = {\text{De}}_{2} = 0.1, \varepsilon_{R} = 1,\nu_{R} = 1, {{Re}} = 0.001,\;{{Ca}} = 0.01, A = 0.1, {{Wo}} = 0.1 , \mu_{R} = 2,\gamma_{R} = 1,E_{R} = 1$

5.4 Design of experiments (DOE)

In the results discussed above, the stability behaviour is observed by changing one of the parameters while keeping all other parameters constant. Marginal stability curves and maximum growth rates in phase space aided in studying the stability behaviour while considering two factors simultaneously. However, the way a particular parameter affects the system depends not only on its value but also on the rest of the parameters. So, if the system is stable for $\bar{\zeta }_{I} = 1$ with a particular set of parameters, the same may not be true if the value of this set is changed. Even if only five of the control parameters mentioned after Eq. (33) are considered at five levels, then in order to study the entire solution behaviour 5⁵ iterations will be needed. This is a common issue in design and optimization problems and can be dealt with using Taguchi’s design of experiments (DOE).

Using DOE, an orthogonal array is obtained (see "Appendix 3") using the fact that which of the solution space mentioned above can be covered with 25 iterations. It also helps in identifying how the system output (in our case max growth rate, $\sigma_{ \hbox{max} }$) changes when one of the parameters is changed. For example, to find the variation with $\bar{\zeta }_{I}$, the mean value of $\sigma_{ \hbox{max} }$ is taken for each level of $\bar{\zeta }_{I}$. Figure 16 shows the results using DOE. The variation with Wo is monotonic and has a stabilizing effect. However, its effect is negligible beyond ${{Wo}} = 0.5$. The effect of $\bar{\zeta }_{I}$ is also monotonic till 0.5 and saturates beyond this value. ${\bar{\text{Q}}}_{\text{I}} , \mu_{R}$ and $\gamma_{R}$ have non-monotonic variation, which suggests strong interaction between these parameters. The system is more unstable when $- 0.5 < \bar{Q}_{I} < 0.5$ and $0.5 < \mu_{R} < 1$. However, it must be noted that these results were obtained using a statistical method and gives only a general idea about the stability variation.

Fig. 16

DOE by means of the maximum growth rate for the five control parameters

6 Conclusion

Stability of a system of two thin liquid films under AC electroosmotic flow is a result of complex interplay between the viscous forces, electric forces, disjoining pressure and capillary forces. The greater is the difference between the forces experienced by the two liquids, the greater will be the instability. Interfacial electrostatics also plays an important role in determining the stability of the system. Disjoining pressure has a destabilizing effect, and capillary forces have stabilizing effect. But the effect of a particular parameter on the stability of the system depends not only on its own value but also on the rest of the parameters. According to the results obtained using design of experiments, the system is relatively unstable when ${{Wo}} < 0.5, - 0.5 < \bar{Q}_{I} < 0.5$, $0.5 < \mu_{R} < 1$ and $\bar{\zeta }_{I} > 0.5$. The applied electric field can have a stabilizing or destabilizing effect depending on its operating range. However, these are approximate ranges and can be used to arrive at a preliminary set of parameters based on application requirements and can be further fine-tuned by analysing the actual stability behaviour using growth rate curves.

Appendices

Appendix 1

The electric potential $\varPhi_{{{\text{sc}},i}}$ (i = 1, 2) due the space charge distribution can be written as follows:

$$ 0 < Y < 1: \varPhi_{{{\text{sc}},1}} = A_{1} {\text{e}}^{{\frac{Y}{{{\text{De}}_{1} }}}} + B_{1} {\text{e}}^{{ - \frac{Y}{{{\text{De}}_{1} }}}} $$

(57)

$$ 1 < Y < H_{2} : \varPhi_{{{\text{sc}},2}} = A_{2} {\text{e}}^{{\frac{Y}{{{\text{De}}_{2} }}}} + B_{2} {\text{e}}^{{ - \frac{Y}{{{\text{De}}_{2} }}}} $$

(58)

$$ A_{1} = \frac{{\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} \left( {1 + e^{{\frac{1}{{De_{1} }}}} De_{1} \bar{Q}_{I} } \right) + De_{1} \varepsilon_{R} \left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} - 2e^{{\frac{1}{{De_{1} }} + \frac{{1 + H_{2} }}{{De_{2} }}}} \left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\bar{\zeta }_{I} + \bar{\zeta }_{u} } \right)} \right)}}{{\left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

$$ B_{1} = \frac{{e^{{\frac{1}{{De_{1} }}}} \left( {\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} \left( {e^{{\frac{1}{{De_{1} }}}} - De_{1} \bar{Q}_{I} } \right) - De_{1} \varepsilon_{R} \left( {e^{{\frac{1}{{De_{1} }}}} \left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right) - 2e^{{\frac{{1 + H_{2} }}{{De_{2} }}}} \left( {\text{Cosh} \left[ {\frac{{1 - H_{2} }}{{De_{2} }}} \right]\bar{\zeta }_{I} + \bar{\zeta }_{u} } \right)} \right)} \right)}}{{\left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

$$ A_{2} = \frac{{2{\text{e}}^{{\left( {\frac{1}{{De_{1} }} + \frac{1}{{De_{2} }}} \right)}} De_{2} \left( {1 + {\text{Sinh}}\left[ {\frac{1}{{De_{1} }}} \right]De_{1} \bar{Q}_{I} - {\text{Cosh}}\left[ {\frac{1}{{De_{1} }}} \right]\bar{\zeta }_{I} } \right) - {\text{e}}^{{\frac{{H_{2} }}{{De_{2} }}}} \left( {De_{2} - De_{1} \varepsilon_{R} + {\text{e}}^{{\frac{2}{{De_{1} }}}} \left( {De_{2} + De_{1} \varepsilon_{R} } \right)} \right)\bar{\zeta }_{u} }}{{\left( {1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} - {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} - \left( { - 1 + {\text{e}}^{{\frac{2}{{De_{1} }}}} } \right)\left( {{\text{e}}^{{\frac{2}{{De_{2} }}}} + {\text{e}}^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

$$ B_{2} = \frac{{e^{{\frac{{1 + H_{2} }}{{De_{2} }}}} \left( {2e^{{\frac{1}{{De_{1} }} + \frac{{H_{2} }}{{De_{2} }}}} De_{2} \left( {1 + \text{Sinh} \left[ {\frac{1}{{De_{1} }}} \right]De_{1} \bar{Q}_{I} - \text{Cosh} \left[ {\frac{1}{{De_{1} }}} \right]\bar{\zeta }_{I} } \right) - e^{{\frac{1}{{De_{2} }}}} \left( {De_{2} + De_{1} \varepsilon_{R} + e^{{\frac{2}{{De_{1} }}}} \left( {De_{2} - De_{1} \varepsilon_{R} } \right)} \right)\bar{\zeta }_{u} } \right)}}{{ - \left( {1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} - e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{2} + \left( { - 1 + e^{{\frac{2}{{De_{1} }}}} } \right)\left( {e^{{\frac{2}{{De_{2} }}}} + e^{{\frac{{2H_{2} }}{{De_{2} }}}} } \right)De_{1} \varepsilon_{R} }} $$

Appendix 2

The set of equations with $\alpha^{0}$ order is as follows:

$$ \frac{{\partial^{4} \hat{\varPsi }_{1,0} }}{{\partial Y^{4} }} - {{Wo}}_{1}^{2} \frac{{\partial^{3} \hat{\varPsi }_{1,0} }}{{\partial \theta \partial Y^{2} }} = \sigma_{0} {{Wo}}_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1,0} }}{{\partial Y^{2} }} $$

(59)

$$ \frac{{\partial^{4} \hat{\varPsi }_{2,0} }}{{\partial Y^{4} }} - {{Wo}}_{2}^{2} \frac{{\partial^{3} \hat{\varPsi }_{2,0} }}{{\partial \theta \partial Y^{2} }} = \sigma_{0} {{Wo}}_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }} $$

(60)

with the corresponding boundary conditions,

No slip and no penetration:

$$ \frac{{\partial \hat{\varPsi }_{1,0} }}{\partial Y}\left( {0,\theta } \right) = 0, \quad \hat{\varPsi }_{1,0} \left( {0,\theta } \right) = 0, \quad \frac{{\partial \hat{\varPsi }_{2,0} }}{\partial Y}\left( {H_{2} ,\theta } \right) = 0, \hat{\varPsi }_{2,0} \left( {H_{2} ,\theta } \right) = 0 $$

(61)

Shear stress balance:

$$ \begin{aligned} &\frac{{\partial^{2} \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \hat{H}_{0} \left( \theta \right)\frac{{\partial^{2} U_{1,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \hat{H}_{0} \left( \theta \right)\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} \hfill \\ &\quad = \mu_{R} \left( {\frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }}\left( {1,\theta } \right) + \hat{H}_{0} \left( \theta \right)\frac{{\partial^{2} U_{2,b} \left( 1 \right)}}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \hat{H}_{0} \left( \theta \right)\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }}} \right) \hfill \\ \end{aligned} $$

(62)

Normal stress balance:

$$ \begin{aligned} &\frac{{\partial^{3} \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial \theta \partial Y} - \sigma_{0} Wo_{1}^{2} \frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y} \hfill \\ & \quad = \mu_{R} \left( {\frac{{\partial^{3} \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial \theta \partial Y} - \sigma_{0} Wo_{2}^{2} \frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y}} \right) \hfill \\ \end{aligned} $$

(63)

Continuity of normal and tangential velocity:

$$ \hat{\varPsi }_{1,0} \left( {H_{1} ,\theta } \right) = \hat{\varPsi }_{2,0} \left( {H_{1} ,\theta } \right) $$

(64)

$$ \hat{H}_{0} \left( \theta \right)\left( {\frac{{\partial U_{1,b} \left( {1,\theta } \right)}}{\partial Y} - \frac{{\partial U_{2,b} \left( {1,\theta } \right)}}{\partial Y}} \right) + \left( {\frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y} - \frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y}} \right) = 0 $$

(65)

Kinematic conditions:

$$ \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }}\frac{{\partial \hat{H}_{0} \left( \theta \right)}}{\partial \theta } + \sigma_{0} \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }}\hat{H}_{0} \left( \theta \right) = 0 $$

(66)

The set of equations with $\alpha^{1}$ order with $\sigma_{0} = 0$ and $\hat{H}_{0} = 1$ is as follows:

$$ \frac{{\partial^{4} \hat{\varPsi }_{1,1} }}{{\partial Y^{4} }} - {{Wo}}_{1}^{2} \frac{{\partial^{3} \hat{\varPsi }_{1,1} }}{{\partial \theta \partial Y^{2} }} - {{iRe}}_{1} U_{1,b} \frac{{\partial^{2} \hat{\varPsi }_{1,0} }}{{\partial Y^{2} }} + {{iRe}}_{1} \frac{{\partial^{2} U_{1,b} }}{{\partial Y^{2} }}\hat{\varPsi }_{1,0} = \sigma_{1} {{Wo}}_{1}^{2} \frac{{\partial^{2} \hat{\varPsi }_{1,0} }}{{\partial Y^{2} }} $$

(67)

$$ \frac{{\partial^{4} \hat{\varPsi }_{2,1} }}{{\partial Y^{4} }} - {{Wo}}_{2}^{2} \frac{{\partial^{3} \hat{\varPsi }_{2,1} }}{{\partial \theta \partial Y^{2} }} - {{iRe}}_{2} U_{2,b} \frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }} + {{iRe}}_{2} \frac{{\partial^{2} U_{2,b} }}{{\partial Y^{2} }}\hat{\varPsi }_{2,0} = \sigma_{1} {{Wo}}_{2}^{2} \frac{{\partial^{2} \hat{\varPsi }_{2,0} }}{{\partial Y^{2} }} $$

(68)

with the following boundary conditions:

No slip and no penetration:

$$ \frac{{\partial \hat{\varPsi }_{1,1} }}{\partial Y}\left( {0,\theta } \right) = 0, \hat{\varPsi }_{1,1} \left( {0,\theta } \right) = 0, \frac{{\partial \hat{\varPsi }_{2,1} }}{\partial Y}\left( {H_{2} ,\theta } \right) = 0, \hat{\varPsi }_{2,1} \left( {H_{2} ,\theta } \right) = 0 $$

(69)

Shear stress balance:

$$ \begin{aligned} &\frac{{\partial^{2} \hat{\varPsi }_{1,1} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \hat{H}_{1} \left( \theta \right)\frac{{\partial^{2} U_{1,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,1} E_{R} \hat{H}_{1} \left( \theta \right)\frac{{\partial \varPhi_{1} }}{\partial X}\frac{{\partial^{2} \varPhi_{1} \left( 1 \right)}}{{\partial Y^{2} }} \hfill \\ & \qquad - {\text{i}}\gamma_{R,1} E_{R} \hat{H}_{0} \left( \theta \right)\left( {\left( {\frac{{\partial \varPhi_{1} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{1} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right) \hfill \\ & \quad = \mu_{R} \left( {\frac{{\partial^{2} \hat{\varPsi }_{2,1} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \hat{H}_{1} \frac{{\partial^{2} U_{2,b} \left( {1,\theta } \right)}}{{\partial Y^{2} }} + \gamma_{R,2} E_{R} \hat{H}_{1} \left( \theta \right)\frac{{\partial \varPhi_{2} }}{\partial X}\frac{{\partial^{2} \varPhi_{2} \left( 1 \right)}}{{\partial Y^{2} }} - {\text{i}}\gamma_{R,2} E_{R} \hat{H}_{0} \left( \theta \right)\left( {\left( {\frac{{\partial \varPhi_{2} }}{\partial X}} \right)^{2} - \left( {\frac{{\partial \varPhi_{2} \left( 1 \right)}}{\partial Y}} \right)^{2} } \right)} \right) \hfill \\ \end{aligned} $$

(70)

Normal stress balance:

$$ \begin{aligned} & \frac{{\partial^{3} \hat{\varPsi }_{1,1} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{1}^{2} \left( {\frac{{\partial^{2} \hat{\varPsi }_{1,1} \left( {1,\theta } \right)}}{\partial \theta \partial Y} + \sigma_{1} \frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y}} \right) \hfill \\ &\qquad- iRe_{1} \left( {U_{1,b} \left( {1,\theta } \right)\frac{{\partial \hat{\varPsi }_{1,0} \left( {1,\theta } \right)}}{\partial Y} - \hat{\varPsi }_{1,0} \left( {1,\theta } \right)\frac{{\partial U_{1,b} \left( {1,\theta } \right)}}{\partial Y}} \right) \hfill \\ &\quad = i\left( {\frac{{\alpha^{2} }}{Ca} - \frac{{3A_{1} }}{{H_{1} }} - \mu_{R} \frac{{3A_{2} }}{{\left( {H_{2} - H_{1} } \right)}}} \right) \hfill \\ &\mu_{R} \left\{ {\frac{{\partial^{3} \hat{\varPsi }_{2,1} \left( {1,\theta } \right)}}{{\partial Y^{3} }} - Wo_{2}^{2} \left( {\frac{{\partial^{2} \hat{\varPsi }_{2,1} \left( {1,\theta } \right)}}{\partial \theta \partial Y} + \sigma_{1} \frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y}} \right)} \right. \hfill \\ &\qquad -\left. { \,iRe_{2} \left( {U_{2,b} \left( {1,\theta } \right)\frac{{\partial \hat{\varPsi }_{2,0} \left( {1,\theta } \right)}}{\partial Y} - \hat{\varPsi }_{2,0} \left( {H_{1} ,\theta } \right)\frac{{\partial U_{2,b} \left( {1,\theta } \right)}}{\partial Y}} \right)} \right\} \hfill \\ \end{aligned} $$

(71)

Continuity of normal and tangential velocity:

$$ \hat{\varPsi }_{1,1} \left( {1,\theta } \right) = \hat{\varPsi }_{2,1} \left( {1,\theta } \right) $$

(72)

Kinematic conditions:

$$ \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }}\frac{{\partial \hat{H}_{1} \left( \theta \right)}}{\partial \theta } + \sigma_{1} \frac{{{{Wo}}_{1}^{2} }}{{{{Re}}_{1} }} + {\text{i}}U_{1,b} \left( {1,\theta } \right) = - {\text{i}}\hat{\varPsi }_{1,0} \left( {1,\theta } \right) $$

(73)

The kinematic condition in the first and second set of equations entails $\sigma_{0} = 0$ and $\sigma_{1} = 0$, respectively. Without loss of generality, $\hat{H}_{0} \left( \theta \right) = 1$ (Kamachi and Honji 1982). The periodic function $\hat{\varPsi }_{i,0}$ can be found by representing it as ${\text{Im}}\left( {G_{i,0} \left( Y \right){\text{e}}^{i\theta } } \right)$.

Kinematic condition corresponding to $\alpha^{2}$ order with $\sigma_{0} = 0$ and $\hat{H}_{0} = 1$:

$$ {{Wo}}_{1}^{2} \frac{{\partial \hat{H}_{2} \left( \theta \right)}}{\partial \theta } + \sigma_{2} {{Wo}}_{1}^{2} + {{iRe}}_{1} \left( {\hat{H}_{1} U_{1,b} \left( {1,\theta } \right) + \hat{\varPsi }_{1,1} \left( {1, \theta } \right)} \right) = 0 $$

(74)

Since $\hat{H}_{2} \left( \theta \right)$ must be periodic in time, $\sigma_{2}$ can be derived using only the steady part of $\hat{\varPsi }_{1,1}$. A set of time-independent equations is hence obtained from the second set (equations corresponding to $\alpha^{1}$). Since the two sets of equations are complicated owing to the number of parameters involved, they are solved by substituting the numerical values of the parameters with Mathematica’s differential equation solver package.

Considering the steady part of the above equation, expression for growth rate:

$$ \sigma_{2} = - \frac{{{{iRe}}_{1} }}{{{{Wo}}_{1}^{2} }}\left( { - H_{11} \frac{{\bar{F}_{1} \left( 1 \right)}}{{2{\text{i}}}} + H_{12} \frac{{F_{1} \left( 1 \right)}}{{2{\text{i}}}} + \hat{\varPsi }_{1,1s} \left( 1 \right)} \right) $$

(75)

$\hat{\varPsi }_{1,1s}$ is the steady part of $\hat{\varPsi }_{1,1}$. $H_{11}$ and $H_{12}$ are defined as follows:

$$ H_{11} = \frac{{{{iRe}}_{1} }}{{2{{Wo}}_{1}^{2} }}\left( {F_{1} \left( {H_{1} } \right) + G_{1,0} \left( {H_{1} } \right)} \right);H_{12} = \frac{{{{iRe}}_{1} }}{{2{{Wo}}_{1}^{2} }}\left( {\left( {\overline{{F_{1} }} \left( {H_{1} } \right) + \bar{G}_{1,0} \left( {H_{1} } \right)} \right)} \right) $$

G _1,0 (Y)is defined for $\hat{\varPsi }_{i,0} \left( {Y,\theta } \right)$ as follows:

$$ \hat{\varPsi }_{1,0} \left( {Y,\theta } \right) = {\text{Im}}\left( {G_{1,0} \left( Y \right){\text{e}}^{{{\text{i}}\theta }} } \right) $$

And $F_{1} \left( Y \right)$ is same as defined for the base state:

$$ U_{1,b} \left( {Y,\theta } \right) = {\text{Im}}\left( {F_{1} \left( Y \right){\text{e}}^{i\theta } } \right) $$

and $\bar{F}_{1} \left( Y \right)$ and $\bar{G}_{1,0} \left( Y \right)$ are the complex conjugates of $F_{1} \left( Y \right)$ and $G_{1,0} \left( Y \right)$, respectively.

Appendix 3

Table 1