1 Introduction

Nowadays, lithium-ion batteries (LIBs) stand as a new class of most promising candidates of energy-storage materials which have been widely used in sophisticated electronics and energy-storage devices since the excellent electrochemical properties and high-efficient ability of storaging or discharging ions. When nanobattery works in rapid charging/discharging condition, the abrupt changes of ionic concentration will give rise to ions diffusion and local diffusion-induced stresses [1]. In such a case, the classical linear [1] and nonlinear [2] mechanical-diffusion coupling theories fail to characterize inherent diffusion-wave feature at the micro/nanotemporal scale. To eliminate such paradox, the non-Fick diffusion–elasticity model [3] was put forward by introducing diffusive wave mass transfer model. Following this theory, the transient mechanical-diffusion responses of elastic solids subjected to shock loadings of molar concentration have been investigated [4,5,6,7]. With flourishing development of electrode nanomaterials [8,9,10] and ultrafast charging/discharging technology [11], the mechanical-diffusion coupling analysis at micro/nanotemporal and spatial scale appears to be particularly important [12,13,14]. However, the above-mentioned models and predictions merely consider temporal nonlocal effect of mass transport, whereas the spatial nonlocal effects of elastic deformation and mass transport are neglected.

Firstly, the classical Fick’s mass diffusion (CFMD) model will be not applicable if fast mass transfer occurs at very small time and length scales, and spatial and temporal nonlocal effects of mass transport [15] remarkably increase. In such cases, mass transport is an inherently nonlocal phenomenon; that is, the diffusion flux at reference point depends on carriers of diffusion from other points and the history of mass carriers reaching at the point. The spatial nonlocal effect of mass transport should be seriously considered if the mean free path of diffusing particle approaches to (or longer than) the characteristic length of the system. This effect is ruled by the ratio of the mean free path to the characteristic length of the system (i.e., the Knudsen number.). Additionally, the temporal nonlocal effect is often referred to the phase lagging of local diffusion flux if diffusion relaxation time approaches to characteristic time of mass transport process under consideration. To shed light on the mass transport mechanism at micro/nanotemporal and spatial scale, the nonlocal mass transfer models [15] have been developed by introducing additional material characteristic length parameters, such as two-concentration model, discrete model, Jeffreys-type model, and diffusion-stress coupling model. Sobolev [15] concluded that existing nonlocal mass transfer models are mainly developed by extended irreversible thermodynamics, phenomenological approach, discrete approach, and fluctuation theory. As discussed by Sobolev, it is clearly that these models are only capable of characterizing spatial nonlocal effect of mass transport and phase lagging of diffusion flux. However, these models fail to characterize inherent phase lagging of molar concentration gradient [16,17,18]. Chen and his colleagues [16,17,18] emphasized that both phase laggings of diffusion flux and molar concentration gradient should be considered for transient process of mass transport, and a dual-phase-lag diffusion model was developed. Nevertheless, this model cannot depict the spatial nonlocal effect of mass transport. As a consequence, a new dual-phase-lag diffusion model involving nonlocality of mass transfer is imperatively to be established.

Secondly, the spatial nonlocal effect of elastic deformation is also an important factor that cannot be ignored in mechanical-diffusion coupling analysis at micro/nanotemporal and spatial scale. In such a case, the additional material characteristic parameter must be introduced into the classical elasticity theory. So far, the nonlocal elasticity theories have been put forward to characterize mechanical response of nanostructures by incorporating information about material microstructure (e.g., lattice spacing between individual atoms, etc.), such as stress gradient elasticity [19, 20], strain gradient elasticity [21], couple stress elasticity [22], and nonlocal strain gradient elasticity [23, 24]. Recently, it was also found that Eringen’s nonlocal differential elasticity model may be ill-posed in some specific conditions and some new nonlocal elasticity models [25,26,27]. Surely it cannot be denied that this model is still widely applied in size-dependent mechanical behavior of bending, vibration, and buckling of nanobeams [28, 29].

As the above literature survey and further examination of other available works reveal, the current generalizations for non-Fick diffusion–elasticity are mainly made by considering phase lagging behavior of mass transport [3]. However, the existing theoretical models and transient shock responses on this topic will be questionable at micro/nanotemporal and spatial scale. Firstly, the spatial nonlocal effects of mass transfer and elastic deformation as well as the influences of phase lagging of molar concentration gradient are still not fully considered in non-Fick diffusion–elasticity problems. Secondly, the spatial nonlocal effect of mass transport is also not involved in current dual-phase-lag diffusion model. To address these problems, the present work aims to develop a non-Fick diffusion–elasticity theory based on a new nonlocal dual-phase-lag diffusion model, considering spatial nonlocal effects of mass transfer and elastic deformation as well as the influences of temporal nonlocal effects of mass transport (i.e., the phase laggings of diffusion flux vector and molar concentration gradient). Based on nonlocal continuum mechanics, the new constitutive and field equations are strictly derived. The proposed model is then applied to investigate structural dynamic mechanical-diffusion responses of a one-dimensional layered structure subjected to transient shock loadings of molar concentration by Laplace transformation method. The influences of temporal and spatial nonlocal parameters the dimensionless results of structural dynamic responses are also analyzed and discussed in detail.

2 Thermodynamic-based constitutive model

This subsection is mainly contributed to develop the theoretical framework of the thermodynamic-based constitutive model of nonlocal mechanical-diffusion coupling at micro/nanotemporal and spatial scale. In the context of linear theory of elasticity, the motion equation is:

$$\sigma_{ij,j} + f_{i} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}.$$
(1)

The relation of strain and displacement is:

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),$$
(2)

where \(\sigma_{ij}\) are the components of stress tensor, \(f_{i}\) are the components of body force vector, \(\varepsilon_{ij}\) are the components of strain tensor, \(u_{i}\) are the components of displacement vector, and \(\rho\) is the mass density. The strain energy function \(\psi\) will be introduced as:

$$2\psi = c_{ijkl} \varepsilon_{ij} \left( {\mathbf{x}} \right)\varepsilon_{ij} \left( {{\mathbf{x^{\prime}}}} \right) + \beta C\left( {\mathbf{x}} \right)C\left( {{\mathbf{x^{\prime}}}} \right) + \alpha_{ij} \left[ {\varepsilon_{ij} \left( {\mathbf{x}} \right)C\left( {{\mathbf{x^{\prime}}}} \right) + \varepsilon_{ij} \left( {{\mathbf{x^{\prime}}}} \right)C\left( {\mathbf{x}} \right)} \right],$$
(3)

where the elastic modulus tensor \(c_{ijkl}\), mechanical-diffusion coefficients \(\alpha_{ij}\), and chemical potential constant \(\beta\) are prescribed functions of \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\). The constitutive coefficients satisfy the following symmetry conditions:

$$c_{ijkl} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = c_{klij} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = c_{jikl} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right),\quad \alpha_{ij} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) = \alpha_{ji} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right).$$
(4)

Following Eringen’s nonlocal theory [19], the constitutive relations are given by:

$$\Pi = \int_{\upsilon } {\left[ {\frac{\partial \psi }{{\partial \Gamma }} + \left( {\frac{\partial \psi }{{\partial \Gamma^{\prime}}}} \right)^{{{\text{Sym}}}} } \right]} \;{\text{d}}\upsilon \left( {{\mathbf{x^{\prime}}}} \right),$$
(5)

where the superscript indicating symmetrization. The nonlocal medium is initially assumed to be traction free. The strain tensor and molar concentration at two neighboring points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\) are:

$$\Gamma = \left\{ {\varepsilon_{ij} \left( {\mathbf{x}} \right),\;\;C\left( {\mathbf{x}} \right)} \right\},\quad \Gamma^{\prime} = \left\{ {\varepsilon_{ij} \left( {{\mathbf{x^{\prime}}}} \right),C\left( {{\mathbf{x^{\prime}}}} \right)} \right\}.$$
(6)

which are assumed to be the ordered set of \(\Pi = \left\{ {\sigma_{ij} ,\mu } \right\}\). In view of Eqs. (3) and (5), the constitutive equations of \(\sigma_{ij}\) and \(\mu\) are derived as below:

$$\sigma_{ij} = \int_{\upsilon } {\left[ {c_{ijkl} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)\varepsilon_{ij} \left( {{\mathbf{x^{\prime}}}} \right) - \alpha_{ij} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)C\left( {{\mathbf{x^{\prime}}}} \right)} \right]{\text{d}}\upsilon \left( {{\mathbf{x^{\prime}}}} \right)} ,$$
(7)
$$\mu = \int_{\upsilon } {\left[ {\alpha_{ij} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)\varepsilon_{ij} \left( {{\mathbf{x^{\prime}}}} \right) + \beta \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)C\left( {{\mathbf{x^{\prime}}}} \right)} \right]{\text{d}}\upsilon \left( {{\mathbf{x^{\prime}}}} \right)} ,$$
(8)

where \(\mu\) is the chemical potential. The constitutive coefficients of \(c_{ijkl} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)\), \(\alpha_{ij} \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)\) and \(\beta \left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right)\) are the attenuation functions with distance \(\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|\), that is:

$$\mathop {\lim }\limits_{{\left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right| \to \infty } \right)}} c_{ijkl} \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right) = \mathop {\lim }\limits_{{\left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right| \to \infty } \right)}} \alpha_{ij} \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right) = \mathop {\lim }\limits_{{\left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right| \to \infty } \right)}} \beta \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right) \to 0.$$
(9)

In the context of Ref. [19], the local and nonlocal constitutive coefficients satisfy the following relations:

$$\frac{{c_{ijkl} \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right)}}{{c_{ijkl} }} = \frac{{\alpha_{ij} \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right)}}{{\alpha_{ij} }} = \frac{{\beta \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right)}}{\beta } = \Psi \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right),$$
(10)

where the attenuating function \(\Psi \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right)\) is a nonlocal kernel representing the influence of distant interactions of material points between \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\), and it can be viewed as a Dirac delta function over the domain of influence. This function attains peak value at \(\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|\) and decays with increasing \(\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|\). Eringen [19] also pointed out that the nonlocal kernel function \(\Psi \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right)\) satisfies following relations:

$$\int_{\upsilon } {\Psi \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right){\text{d}}\upsilon \left( {{\mathbf{x^{\prime}}}} \right)} = 1,\quad \left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\Psi \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right) = \delta \left( {\left| {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right|} \right),$$
(11)

where the elastic nonlocal parameter \(ea\) has been widely used to predict spatial nonlocal effect of elastic deformation for mechanical behavior of nanobeam [28]. Applying the operator \(\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\) and formula \(\int {f\left( x \right)\delta \left( {x - a} \right){\text{d}}x} = f\left( a \right)\) on the constitutive Eqs. (7) and (8), the following equations are derived:

$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\sigma_{ij} = \sigma_{ij}^{{{\text{Local}}}} = c_{ijkl} \varepsilon_{ij} - \alpha_{ij} C,$$
(12)
$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\mu = \mu^{{{\text{Local}}}} = \alpha_{ij} \varepsilon_{ij} + \beta C,$$
(13)

by using Eqs. (10) and (11), where \(\sigma_{ij}^{{{\text{Local}}}}\) and \(\mu^{{{\text{Local}}}}\) are the local stress tensor and local chemical potential. The dual-phase-lag diffusion model proposed by Chen and his colleagues [16,17,18] is extended as:

$${\mathbf{J}}\left( {{\mathbf{x}} + {{\varvec{\upchi}}}_{{\mathbf{D}}} ,t + \tau_{D} } \right) = - D_{0} {\mathbf{\nabla }}C\left( {{\mathbf{x}},t + \tau_{C} } \right)$$
(14)

by considering spatial nonlocal effect of mass transport, where \({\mathbf{J}}\) is the diffusion flux vector, \(C\) is the molar concentration of diffusing substance, and \(D_{0}\) is the diffusion coefficient. In Eq. (14), the diffusive nonlocal vector \({{\varvec{\upchi}}}_{{\mathbf{D}}}\) represents the spatial nonlocal effect of mass transport, the diffusion relaxation time \(\tau_{D}\) represents the phase lagging of diffusion flux, and the molar concentration lag \(\tau_{C}\) represents phase lagging of molar concentration gradient. The relation (14) is similar to that in the studies of [30, 31], and it provides a simple and user-friendly macroscopic formulation of nonlocal dual-phase-lag diffusion at microscopic levels, which enables engineering analyses with sufficient accuracy. By applying first-order Taylor’s series expansion of \(\chi_{D}\), \(\tau_{D}\) and \(\tau_{C}\), the extension of Eq. (14) is given as below:

$$\left( {1 + {{\varvec{\upchi}}}_{{\mathbf{D}}} \cdot {\mathbf{\nabla }}} \right)\left[ {{\mathbf{J}}\left( {{\mathbf{x}},t} \right) + \tau_{D} {\dot{\mathbf{J}}}\left( {{\mathbf{x}},t} \right)} \right] = - D_{0} \left[ {\nabla C\left( {{\mathbf{x}},t} \right) + \tau_{C} \nabla \dot{C}\left( {{\mathbf{x}},t} \right)} \right]$$
(15)

which is defined as a refined nonlocal dual-phase-lag mass transfer (R-NDPL-MT) model. Additionally, if the mixed-derivative term of \(\tau_{D} \left( {{{\varvec{\upchi}}}_{{\mathbf{D}}} \cdot {\mathbf{\nabla }}} \right){\dot{\mathbf{J}}}\left( {{\mathbf{x}},t} \right)\) is neglected, the following nonlocal dual-phase-lag mass transfer (NDPL-MT) model is obtained:

$${\mathbf{J}}\left( {{\mathbf{x}},t} \right) + \left( {{{\varvec{\upchi}}}_{{\mathbf{D}}} \cdot {\mathbf{\nabla }}} \right){\mathbf{J}}\left( {{\mathbf{x}},t} \right) + \tau_{D} {\dot{\mathbf{J}}}\left( {{\mathbf{x}},t} \right) = - D_{0} \left[ {\nabla C\left( {{\mathbf{x}},t} \right) + \tau_{C} \nabla \dot{C}\left( {{\mathbf{x}},t} \right)} \right]$$
(16)

which will degenerate into dual-phase-lag mass transfer (DPL-MT) model:

$${\mathbf{J}}\left( {{\mathbf{x}},t} \right) + \tau_{D} {\dot{\mathbf{J}}}\left( {{\mathbf{x}},t} \right) = - D_{0} \left[ {\nabla C\left( {{\mathbf{x}},t} \right) + \tau_{C} \nabla \dot{C}\left( {{\mathbf{x}},t} \right)} \right]$$
(17)

if the spatial nonlocal effect of mass transport is ignored. Furthermore, if the phase lagging of molar concentration gradient is neglected, the damped wave mass transfer DW-MT model will be derived. Following Bachher et al. [32] and Challamel et al. [33], Sharma and his colleagues [34] proposed an Eringen-type differential nonlocal model of Cattaneo–Maxwell heat conduction equation. Enlightened by this, a refined Eringen-type nonlocal dual-phase-lag mass transfer (RE-NDPL-MT) model is further extended as:

$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\left( {1 + {{\varvec{\upchi}}}_{{\mathbf{D}}} \cdot {\mathbf{\nabla }}} \right)\left[ {{\mathbf{J}}\left( {{\mathbf{x}},t} \right) + \tau_{D} {\dot{\mathbf{J}}}\left( {{\mathbf{x}},t} \right)} \right] = - D_{0} \left[ {\nabla C\left( {{\mathbf{x}},t} \right) + \tau_{C} \nabla \dot{C}\left( {{\mathbf{x}},t} \right)} \right].$$
(18)

As shown in Table 1, a comparison of RE-NDPL-MT model adopted in this work and DW-MT model, DPL-MT model, NDPL-MT model, R-NDPL-MT model is made. Additionally, the Fick diffusion equation has the form:

$$\dot{\mu } = \frac{I}{{C_{0} }} - \beta \nabla J_{i} ,$$
(19)

where \(I\) and \(C_{0}\) are the diffusion source and initial reference molar concentration.

Table 1 Comparison of nonlocal mass transfer models
Full size table

3 Structural transient mechanical-diffusion responses analysis

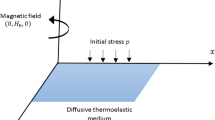
In this section, the newly developed model in Sect. 2 is adopted to investigate structural transient mechanical-diffusion responses of an isotropic homogeneous thin layer of finite thickness \(L\). The coordinate system is so chosen that the z-axis is taken perpendicularly to the thin layer, and the x- and y-axis is parallel to the layer. The structure is initially unstrained and unstressed, and its traction-free bounding surface (\(z = 0\)) is subjected to transient shock loadings of molar concentration. Additionally, a thin layer by definition has its thickness small compared to the other lengths in other directions. During the analysis, it is also assumed that neither elastic nor diffusive wave reaches the lower bounding surface of the thin layer (i.e., \(z = L\)), and dynamic responses along z-axis will be analyzed. The problem can be simplified as one-dimensional case, and all physical variables depend only on \(z\) and \(t\). Consequently, the components of displacement and molar concentration are given by:

$$u_{x} = 0,\quad u_{y} = 0,\quad u_{z} = w\left( {z,t} \right),\quad C = C\left( {z,t} \right).$$
(20)

Initial conditions are:

$$w\left( {z,0} \right) = \frac{{\partial \left( {z,0} \right)}}{\partial t} = 0,\;\;\sigma_{zz} \left( {z,0} \right) = \frac{{\partial \sigma_{zz} \left( {z,0} \right)}}{\partial t} = 0,\;\;C\left( {z,0} \right) = \frac{{\partial C\left( {z,0} \right)}}{\partial t} = 0.$$
(21)

The boundary conditions are:

$$C\left( {0,t} \right) = C_{0} H\left( t \right),\quad C\left( {L,t} \right) = 0,$$
(22)
$$w\left( {L,t} \right) = 0,\quad \sigma_{zz} \left( {0,t} \right) = 0.$$
(23)

Similar to Ref. [35], the influence of strain field on chemical potential is ignored for simplicity. Neglecting body force and diffusion source, the fundamental equations of one-dimensional nonlocal mechanical-diffusion coupling problem for an isotropic homogeneous layer by adopting the developed model in Sect. 2 are given as below:

  1. (i)

    Motion and diffusion equations:

    $$\frac{{\partial \sigma_{zz} }}{\partial z} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }},\quad \frac{\partial \mu }{{\partial t}} = - \beta \frac{{\partial J_{z} }}{\partial z}.$$
    (24)
  2. (ii)

    Strain components:

    $$\varepsilon_{xx} = 0,\;\;\varepsilon_{yy} = 0,\;\;\varepsilon_{zz} = \frac{\partial w}{{\partial z}},\;\;\varepsilon_{xy} = 0,\;\;\varepsilon_{xz} = 0,\;\;\varepsilon_{yz} = 0.$$
    (25)
  3. (iii)

    Constitutive equations of stress and chemical potential:

    $$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\sigma_{zz} = \left( {\lambda + 2\nu } \right)\frac{\partial w}{{\partial z}} - \alpha C,$$
    (26)
    $$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\sigma_{xx} = \left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\sigma_{yy} = \lambda \frac{\partial w}{{\partial z}} - \alpha C,$$
    (27)
    $$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\mu = \beta C.$$
    (28)

    where \(\lambda\) and \(\nu\) are Lame’s constants.

  4. (iv)

    Evolution equation of RE-NDPL-MT model:

    $$\left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right]\left( {1 + \chi_{D} \frac{\partial }{\partial z}} \right)\left( {1 + \tau_{D} \frac{\partial }{\partial t}} \right)J_{z} = - D_{0} \left( {\frac{\partial C}{{\partial z}} + \tau_{C} \frac{{\partial^{2} C}}{\partial z\partial t}} \right).$$
    (29)

Substitution of Eqs. (25) and (26) into Eq. (24)1 yields the governing equation of displacement field:

$$\left( {\lambda + 2\nu } \right)\frac{{\partial^{2} w}}{{\partial z^{2} }} - \alpha \frac{\partial C}{{\partial z}} = \rho \left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial z^{2} }}} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }}.$$
(30)

Substitution of Eqs. (28) and (29) into Eq. (24)2 yields the governing equation of molar concentration:

$$\left( {1 + \chi_{D} \frac{\partial }{\partial z}} \right)\left( {1 + \tau_{D} \frac{\partial }{\partial t}} \right)\frac{\partial C}{{\partial t}} = D_{0} \left( {1 + \tau_{C} \frac{\partial }{\partial t}} \right)\frac{{\partial^{2} C}}{{\partial z^{2} }}.$$
(31)

For convenience, the dimensionless quantities are introduced as:

$$\begin{gathered} \left[ {\overline{z},\overline{w},\left( {\overline{ea} } \right),\overline{\chi }_{D} } \right] = \sqrt {\frac{\lambda + 2\nu }{\rho }} \frac{1}{{D_{0} }}\left[ {z,w,\left( {ea} \right),\chi_{D} } \right],\;\;\overline{\mu } = \frac{\mu }{{\beta C_{0} }}, \hfill \\ \left( {\overline{t},\overline{\tau }_{C} ,\overline{\tau }_{D} } \right) = \frac{\lambda + 2\nu }{\rho }\frac{1}{{D_{0} }}\left( {t,\tau_{C} ,\tau_{D} } \right),\;\;\overline{C} = \frac{C}{{C_{0} }},\;\;\overline{J}_{z} = \sqrt {\frac{\lambda + 2\nu }{\rho }} \frac{1}{{C_{0} }}J_{z} ,\;\;\overline{\sigma }_{ij} = \frac{{\sigma_{ij} }}{\nu }. \hfill \\ \end{gathered}$$
(32)

which are introduced into (26)–(31), and it is obtained that:

$$\gamma \frac{{\partial^{2} \overline{w}}}{{\partial \overline{z}^{2} }} - \varphi \frac{{\partial \overline{C}}}{{\partial \overline{z}}} = \gamma \left[ {1 - \left( {\overline{ea} } \right)^{2} \nabla^{2} } \right]\frac{{\partial^{2} \overline{w}}}{{\partial \overline{t}^{2} }},$$
(33)
$$\left( {1 + \overline{\chi }_{D} \frac{\partial }{{\partial \overline{z}}}} \right)\left( {1 + \overline{\tau }_{D} \frac{\partial }{{\partial \overline{t}}}} \right)\frac{{\partial \overline{C}}}{{\partial \overline{t}}} = \left( {1 + \overline{\tau }_{C} \frac{\partial }{{\partial \overline{t}}}} \right)\frac{{\partial^{2} \overline{C}}}{{\partial \overline{z}^{2} }},$$
(34)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} \nabla^{2} } \right]\;\overline{\sigma }_{zz} = \gamma \frac{{\partial \overline{w}}}{{\partial \overline{z}}} - \varphi \overline{C},$$
(35)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} \nabla^{2} } \right]\;\overline{\sigma }_{xx} = \left[ {1 - \left( {\overline{ea} } \right)^{2} \nabla^{2} } \right]\;\overline{\sigma }_{yy} = \left( {\gamma - 2} \right)\frac{{\partial \overline{w}}}{{\partial \overline{z}}} - \varphi \overline{C},$$
(36)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} \nabla^{2} } \right]\;\overline{\mu } = \overline{C},$$
(37)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} \nabla^{2} } \right]\left( {1 + \overline{\chi }_{D} \frac{\partial }{{\partial \overline{z}}}} \right)\left( {1 + \overline{\tau }_{D} \frac{\partial }{{\partial \overline{t}}}} \right)\overline{J}_{z} = - \left( {1 + \overline{\tau }_{C} \frac{\partial }{{\partial \overline{t}}}} \right)\frac{{\partial \overline{C}}}{{\partial \overline{z}}}.$$
(38)

where \(\gamma = \frac{{\lambda + 2\nu }}{\nu },\;\varphi = \frac{{\alpha C_{0} }}{\nu }\) Applying Laplace transformation:

$$f^{\prime}\left( s \right) = L\left[ {f\left( t \right)} \right] = \int_{0}^{\infty } {f\left( t \right)e^{ - st} {\text{d}}t} ,{\text{Re}} \left( s \right) > 0,$$
(39)

to Eqs. (33)–(36) with Eq. (23) yields:

$$\gamma D^{2} \overline{w}^{\prime} - \varphi D\overline{C}^{\prime} = \gamma \left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\;s^{2} \overline{w}^{\prime},$$
(40)
$$s\left( {1 + \overline{\chi }_{D} D} \right)\left( {1 + \overline{\tau }_{D} s} \right)\overline{C}^{\prime} = \left( {1 + \overline{\tau }_{C} s} \right)D^{2} \overline{C}^{\prime},$$
(41)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\;\overline{\sigma }^{\prime}_{zz} = \gamma D\overline{w}^{\prime} - \varphi \overline{C}^{\prime},$$
(42)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\;\overline{\sigma }^{\prime}_{xx} = \left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\;\overline{\sigma }^{\prime}_{yy} = \left( {\gamma - 2} \right)D\overline{w}^{\prime} - \varphi \overline{C}^{\prime},$$
(43)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\;\overline{\mu }^{\prime} = \overline{C}^{\prime},$$
(44)
$$\left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\left( {1 + \overline{\chi }_{D} D} \right)\left( {1 + \overline{\tau }_{D} s} \right)\overline{J}^{\prime}_{z} = - \left( {1 + \overline{\tau }_{C} s} \right)D\overline{C}^{\prime},$$
(45)

where \(D = \frac{{\text{d}}}{{{\text{d}}\overline{z}}}\). In view of Eq. (39), Eqs. (22) and (23) are:

$$\overline{C}^{\prime}\left( {0,s} \right) = \frac{1}{s},\quad \overline{C}^{\prime}\left( {L,s} \right) = 0,\;\;\overline{w}^{\prime}\left( {L,s} \right) = 0,\quad \overline{\sigma }^{\prime}_{zz} \left( {0,s} \right) = 0.$$
(46)

The solution of Eq. (41) is given by:

$$\overline{C}^{\prime}\left( s \right) = \sum\limits_{i = 1}^{2} {C_{i} e^{{k_{i} \overline{z}}} } ,$$
(47)

where

$$k_{1,2} = \frac{{\overline{\chi }_{D} s\left( {1 + \overline{\tau }_{D} s} \right) \pm \sqrt {\left[ {\overline{\chi }_{D} s\left( {1 + \overline{\tau }_{D} s} \right)} \right]^{2} + 4s\left( {1 + \overline{\tau }_{D} s} \right)\left( {1 + \overline{\tau }_{C} s} \right)} }}{{2\left( {1 + \overline{\tau }_{C} s} \right)}},$$
(48)
$$C_{1} = \frac{1}{s} - \frac{1}{s}\frac{{e^{{k_{1} L}} }}{{e^{{k_{1} L}} - e^{{k_{2} L}} }},\quad C_{2} = \frac{1}{s}\frac{{e^{{k_{1} L}} }}{{e^{{k_{1} L}} - e^{{k_{2} L}} }}.$$
(49)

Substituting Eq. (47) into Eq. (40) yields the solution of displacement field:

$$\overline{w}^{\prime}\left( s \right) = \sum\limits_{i = 1}^{4} {w_{i} e^{{k_{i} \overline{z}}} } ,$$
(50)

where \(k_{3,4} = \pm \frac{s}{{\sqrt {1 + s^{2} \left( {\overline{ea} } \right)^{2} } }}\), and \(w_{i} \left( {i = 1,2} \right)\) is given as below:

$$w_{1} = \frac{{\varphi C_{1} k_{1} }}{{\gamma \left[ {1 + s^{2} \left( {\overline{ea} } \right)^{2} } \right]\left( {k_{1} } \right)^{2} - \gamma s^{2} }},\quad w_{2} = \frac{{\varphi C_{2} k_{2} }}{{\gamma \left[ {1 + s^{2} \left( {\overline{ea} } \right)^{2} } \right]\left( {k_{2} } \right)^{2} - \gamma s^{2} }}.$$
(51)

The unknown parameters of \(w_{3}\) and \(w_{4}\) will be determined by associating with boundary conditions. Substituting Eqs. (47) and (50) into Eq. (42) yields:

$$\left[ {1 - \left( {\overline{ea} } \right)^{2} D^{2} } \right]\;\overline{\sigma }_{zz} = \gamma \sum\limits_{i = 1}^{4} {w_{i} k_{i} e^{{k_{i} \overline{z}}} } - \varphi \sum\limits_{i = 1}^{2} {C_{i} e^{{k_{i} \overline{z}}} } ,$$
(52)

The solution of Eq. (52) is:

$$\overline{\sigma }^{\prime}_{zz} \left( s \right) = \sum\limits_{i = 1}^{4} {\sigma_{zzi} e^{{k_{i} \overline{z}}} } ,$$
(53)

where \(\sigma_{zzi} = \frac{{\gamma w_{i} k_{i} - \varphi C_{i} }}{{1 - \left( {\overline{ea} } \right)^{2} \left( {k_{i} } \right)^{2} }}\). The following algebraic equations will be obtained:

$$w_{1} e^{{k_{1} \overline{L}}} + w_{2} e^{{k_{2} \overline{L}}} + w_{3} e^{{k_{3} \overline{L}}} + w_{4} e^{{k_{4} \overline{L}}} = 0,\quad \sigma_{zz1} + \sigma_{zz2} + \sigma_{zz3} + \sigma_{zz4} = 0.$$
(54)

by boundary conditions \(\overline{w}\left( {L,s} \right) = 0\) and \(\overline{\sigma }_{zz} \left( {0,s} \right) = 0\). Then, the unknown parameters will be obtained by solving Eq. (54). In addition, the expressions of \(\overline{\sigma }^{\prime}_{xx} \left( s \right)\), \(\overline{\sigma }_{yy} \left( s \right)\), \(\overline{\mu }^{\prime}\left( s \right)\), and \(\overline{J}^{\prime}_{zz} \left( s \right)\) are:

$$\overline{\sigma }^{\prime}_{xx} \left( s \right) = \overline{\sigma }_{yy} \left( s \right) = \sum\limits_{i = 1}^{4} {\sigma_{i} e^{{k_{i} \overline{z}}} } ,\quad \overline{\mu }^{\prime}\left( s \right) = \sum\limits_{i = 1}^{2} {\mu_{i} e^{{k_{i} \overline{z}}} } ,\quad \overline{J}^{\prime}_{z} \left( s \right) = \sum\limits_{i = 1}^{2} {J_{zi} e^{{k_{i} \overline{z}}} } .$$
(55)

where

$$\begin{gathered} \sigma_{i} = \frac{{\left( {\gamma - 2} \right)w_{1} k_{i} - \varphi C_{i} }}{{1 - \left( {\overline{ea} } \right)^{2} \left( {k_{i} } \right)^{2} }},\quad \mu_{i} = \frac{{C_{i} }}{{1 - \left( {\overline{ea} } \right)^{2} \left( {k_{i} } \right)^{2} }}, \hfill \\ J_{zi} = - \frac{{\left( {1 + \overline{\tau }_{C} s} \right)k_{i} C_{i} }}{{\left( {1 + \overline{\tau }_{D} s} \right)\left( {1 + \overline{\chi }_{D} k_{i} } \right)\left[ {1 - \left( {\overline{ea} } \right)^{2} \left( {k_{i} } \right)^{2} } \right]}}. \hfill \\ \end{gathered}$$

Thus far, the analytical solutions are obtained in the Laplace domain. To capture time-domain solutions, a numerical inversion Laplace-transform (NILT) algorithm [36] will be adopted.

4 Results and discussion

In this section, the parametric investigations are conducted to analyze and discuss the effects of both nonlocal mass transfer and nonlocal elasticity on diffusive wave propagation and mechanical-diffusion responses. The material parameters [5] listed in Table 2 will be adopted for numerical evaluations. The evaluation of the derivation in Sect. 3 and NILT algorithm is conducted to examine the validity. Clearly, if the nonlocal parameters of \(\overline{\chi }_{D} ,\,\overline{ea} ,\,\overline{\tau }_{C}\) are valued as \(10^{ - 10}\), the newly developed model in Sect. 2 degenerates into non-Fick diffusion–elasticity model [4]. Figure 1 shows that the dimensionless responses of concentration by NILT algorithm agree well with those from Ref. [7], implying that the numerical algorithm adopted in this work is reliable. In the following, the dimensionless results of dynamic mechanical-diffusion responses for \(\overline{t} = 0.05\) are graphically presented.

Table 2 Material constants [5]
Full size table
Fig. 1
figure 1

Dimensionless response of concentration by present model and Ref. [7]

Full size image

4.1 Comparison study

This subsection mainly contributes to a comparison of RE-NDPL-MT model and the models of DW-MT, DPL-MT, NDPL-MT, and R-NDPL-MT for \(\overline{\tau }_{D} = 0.04\). Figure 2 shows dimensionless responses of molar concentration, displacement, compressive stress, chemical potential, and diffusion flux for different nonlocal mass transfer models. It is clearly observed that there exists an abrupt jump of molar concentration around diffusive wave front for DW-MT model, while the displacement will also suddenly jump from a higher value to a lower one around elastic wave front. In such a case, \(\overline{\sigma }_{zz}\) or \(\overline{\sigma }_{xx}\) (\(\overline{\sigma }_{yy}\)) suddenly jumps to lower (higher) value at elastic (diffusive) wave front. Additionally, the chemical potential and diffusion flux also sharply jump from higher values to lower ones around diffusive front. Additionally, if \(\overline{\tau }_{C}\) is valued as 0.02, all the sharp jumps of mechanical-diffusion responses around diffusive wave front will vanish for DPL-MT model. Furthermore, the deformation of thin layer becomes smaller around elastic wave front, and the absolute value of diffusion flux is reduced at \(\overline{z} = 0\). A common feature of NDPL-MT and R-NDPL-MT models is that the spatial nonlocal effect of mass transport is considered, whereas the R-NDPL-MT model involves additional mixed-derivative term of \(\tau_{D} \left( {{{\varvec{\upchi}}}_{{\mathbf{D}}} \cdot {\mathbf{\nabla }}} \right){\dot{\mathbf{J}}}\left( {{\mathbf{x}},t} \right)\). If \(\overline{\chi }_{D}\) is valued as 0.05, the distribution of molar concentration predicted by R-NDPL-MT model is smoother than that from DPL-MT model. This suggests that R-NDPL-MT model predicts faster diffusive wave. In such a case, the compressive stress, chemical potential, and diffusion flux become smoother around diffusive wave front. As consequence, the mechanical-diffusion response region is also enlarged. As to RE-NDPL-MT model, Fig. 2 also shows that the dimensionless results of molar concentration, chemical potential, and diffusion flux for \(\overline{ea} = 0.05\) match well with that for \(\overline{ea} = 0.00\), implying that the parameter \(\overline{ea}\) have no effects on them. However, the magnitudes of displacement greatly decrease nearby \(\overline{z} = 0\), and abrupt change of deformation around elastic wave front is totally removed. Consequently, the abrupt jumps of \(\overline{\sigma }_{zz}\) and \(\overline{\sigma }_{xx}\) (\(\overline{\sigma }_{yy}\)) are also eliminated. Figure 3 displays time histories of dimensionless structural dynamic responses at \(\overline{z} = 0.50\). From Fig. 3a, e and f, it is shown that the abrupt jumps of molar concentration, chemical potential, and diffusion flux will vanish for DPL-MT, NDPL-MT, R-NDPL-MT, and RE-NDPL-MT models. If \(\overline{\chi }_{D} \ne 0\), the diffusive wave will travel faster. Figure 3b and c also displays that the distribution of displacement and stress will become smoother, while the sharp jump of displacement (or stress) at elastic wave is eliminated.

Fig. 2
figure 2

Comparisons of RE-NDPL-MT model and the models of DW-MT, DPL-MT, NDPL-MT, and R-NDPL-MT

Full size image
Fig. 3
figure 3

Time histories of dimensionless structural dynamic responses at \(\overline{z} = 0.50\)

Full size image

4.2 Effects of spatial nonlocal parameters of \(\overline{ea}\) and \(\overline{\chi }_{D}\)

In this subsection, the effects of spatial nonlocal parameters of \(\overline{e}\overline{a}\) and \(\overline{\chi }_{D}\) on structural mechanical-diffusion responses are evaluated and discussed for \(\overline{\tau }_{D} = 0.04\) and \(\overline{\tau }_{C} = 0.02\). As shown in Fig. 4 a, if \(\overline{\chi }_{D}\) increases, the distribution of molar concentration becomes smoother and its magnitudes are also improved. This suggests that diffusive wave travels faster for larger \(\overline{\chi }_{D}\). However, the dimensionless results of molar concentration for \(\overline{ea} = 0.00\) agree well that for \(\overline{e}\overline{a} = 0.04\) or \(\overline{ea} = 0.08\), suggesting that \(\overline{ea}\) has no effect on its profile. Figure 4b also presents the deformation of thin layer around elastic wave front if \(\overline{\chi }_{D}\) becomes larger. Additionally, if \(\overline{ea}\) increases from 0.00 to 0.08, a clear elimination of displacement sharp jump around elastic wave front is observed, while its peak values around \(\overline{z} = 0\) are also greatly reduced. Consequently, Fig. 4c and d shows that the compressive stress \(\overline{\sigma }_{zz}\) or \(\overline{\sigma }_{xx}\) (\(\overline{\sigma }_{yy}\)) suddenly jumps from higher value to lower one, while its distribution becomes smoother. Furthermore, the distribution of compressive stress becomes smoother if \(\overline{\chi }_{D}\) increases. In such a case, Fig. 4e and f indicates that the distribution of chemical potential and diffusion flux is even smoother. If \(\overline{ea}\) increases, the peak magnitudes of diffusion flux are clearly reduced, while its distribution is slightly smoothed. Figure 5 illustrates the time histories of dimensionless responses for different parameters of \(\overline{ea}\) and \(\overline{\chi }_{D}\) at \(\overline{z} = 0.50\). If \(\overline{\chi }_{D}\) increases, the diffusive wave travels faster, while the distribution of displacement and compressive stress will become smoother beyond elastic wave front. Additionally, it is also found that the dimensionless responses of molar concentration, chemical potential, and diffusion flux are not changed for larger \(\overline{ea}\), but the sudden jumps of displacement and compressive stress will vanish.

Fig. 4
figure 4

Dimensionless responses for \(\overline{\tau }_{D} = 0.04\) and \(\overline{\tau }_{C} = 0.02\)

Full size image
Fig. 5
figure 5

Time histories of dimensionless structural dynamic responses at \(\overline{z} = 0.50\) for \(\overline{\tau }_{D} = 0.04\) and \(\overline{\tau }_{C} = 0.02\)

Full size image

4.3 Effects of temporal nonlocal parameters of \(\overline{\tau }_{D}\) and \(\overline{\tau }_{C}\)

This subsection is contributed to analyze and discuss the effects of temporal nonlocal parameters of \(\overline{\tau }_{D}\) and \(\overline{\tau }_{C}\) for \(\overline{ea} = 0.02\) and \(\overline{\chi }_{D} = 0.05\). As displayed in Fig. 6a, if \(\overline{\tau }_{D}\) increases, the absolute values of molar concentration become smaller. And its distribution for \(\overline{\tau }_{D} = 0.02\) is smoother than that for \(\overline{\tau }_{D} = 0.04\). This indicates that the diffusive wave travels slower for increasing \(\overline{\tau }_{D}\). In addition, when \(\overline{\tau }_{C}\) becomes larger, the magnitudes of molar concentration are clearly improved to higher levels and its distribution becomes smoother. Figure 6b shows that the deformation of the thin layer increases around elastic wave front if \(\overline{\tau }_{D}\) (\(\overline{\tau }_{C}\)) becomes larger. Additionally, the peak value of compressive stress \(\overline{\sigma }_{zz}\) or \(\overline{\sigma }_{xx}\) (\(\overline{\sigma }_{yy}\)) is improved (see Fig. 6c and d). Figure 6e and f shows that the distribution of chemical potential and diffusion flux will become smoother if \(\overline{\tau }_{C}\) (\(\overline{\tau }_{D}\)) increases (decreases). Figure 7 presents time histories of dimensionless responses for different parameters of \(\overline{\tau }_{D}\) and \(\overline{\tau }_{C}\) at \(\overline{z} = 0.50\). If \(\overline{\tau }_{D}\) (\(\overline{\tau }_{C}\)) increases, it is shown that the diffusive wave will travel slower and the displacement is not changed, while the peak values of \(\overline{\sigma }_{zz}\) or \(\overline{\sigma }_{xx}\) (\(\overline{\sigma }_{yy}\)) increase slightly.

Fig. 6
figure 6

Dimensionless responses for \(\overline{ea} = 0.02\) and \(\overline{\chi }_{D} = 0.05\)

Full size image
Fig. 7
figure 7

Time histories of dimensionless structural dynamic responses at \(\overline{z} = 0.50\) for \(\overline{ea} = 0.02\) and \(\overline{\chi }_{D} = 0.05\)

Full size image

5 Concluding remarks

The main contributions of this paper can be summarized as follows. Firstly, the current dual-phase-lag diffusion model is extended into RE-NDPL-MT model, which fully considered the spatial nonlocal effect of mass transfer as well as the influences of temporal nonlocal effects of mass transport (i.e., the phase laggings of diffusion flux vector and molar concentration gradient). Secondly, a new theoretical framework of non-Fick diffusion–elasticity based on RE-NDPL-MT model is developed via nonlocal continuum mechanics. The newly proposed model is applied to investigate transient mechanical-diffusion responses of a one-dimensional isotropic homogeneous thin layer of finite thickness subjected to transient shock loadings of molar concentration. Dimensionless results reveal that the newly developed RE-NDPL-MT model can characterize a faster propagation speed of diffusive wave, and abrupt sharp jumps of molar concentration, compressive stress, chemical potential, and diffusion flux around diffusive wave front will be eliminated. Additionally, the deformation of the structure and the higher peak values of diffusion-induced stresses are greatly reduced. The newly model developed in this work is expected to provide a thorough and comprehensive understanding on mechanical-diffusion coupling at micro/nanotemporal and spatial scale.