Introduction

The Lord–Shulman theory of thermoelasticity [1] with one relaxation time is based on the modification of the equation of heat conduction proposed by Maxwell [2] and later by Cattaneo [3]. This modification takes into account the time needed for the acceleration of heat flow. The theory ensures the finite speed of wave propagation of heat and displacement distributions. The remaining governing equations and constitutive relations for this theory are the same as those for the classical theory of thermoelasticity [4, 5].

In contrast, the DPL heat conduction equation includes two phase-lags in Fourier's law of heat conduction. This is done to account for microstructural effects that occur in high-rate heat transfer. The DPL model has been confirmed by experimental results [6] and has been shown to have physical meanings and applicability. Researchers such as Mukhopadhyay et al. [7], Othman and Eraki [8], and Abouelregal et al. [9] have further studied the effects of different fields on thermoelastic materials using the DPL model. These studies have looked at potential-temperature disturbances, gravity influence, and the inclusion of higher-order time-fractional derivatives in the equations. Overall, both the L-S theory and the DPL model provide valuable insights into thermoelasticity and have been utilized in various research studies on micro-elongated thermoelastic medium [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]

The Thomson effect is a significant phenomenon in the field of thermal power generation, particularly in electrical circuits and sensors. It occurs when an electric current flows through a circuit made of a single material that has a temperature difference along its length. This results in the evolution or absorption of heat. The transfer of heat due to the Thomson effect is in addition to the heat produced from the electrical resistance in conductors. It plays a crucial role in understanding and designing thermal power generation systems. Abouelregal and Abo-Dahab [26] conducted a study on the electro-magneto-thermoelastic problem in an infinitely solid cylinder using the dual-phase-lag model. This research aimed to analyze the Thomson effect in this specific context. Abd-Elaziz et al. [27, 28] also investigated multiple problems related to the Thomson effect and other effects on voids using the Green-Naghdi theories. Marin et al. [29] conducted research on mixed problems in thermoelasticity of type III for Cosserat media. These studies aimed to gain a deeper understanding of the Thomson effect’s characteristics and its implications in various scenarios.

The diffusion phenomenon is of significant interest due to its numerous applications in geophysics and industries. Currently, the thermal diffusion process is being explored by oil companies for more efficient oil extraction from deposits. Kumar and Kansal [30] conducted research on the propagation of plane waves in a diffusive medium that is both isotropic and generalized thermoelastic. Recently, Othman et al. [31] examined the impact of fractional parameters on plane waves in a diffusive medium that is both generalized magneto-thermoelastic and dependent on reference temperature for elasticity. Othman et al. [32] also investigated the effect of magnetic field and thermal relaxation on the 2-D problem of generalized thermoelastic diffusion. Diffusion phenomena have many applications in geophysical and industrial (petroleum) areas. For instance, oil corporations have an interest in the thermo-diffusion technique to extract oil from oil resources with greater efficiency. Diffusion is employed in the manufacture of integrated circuits to introduce “dopants” into the semiconductor substrate in precise proportions. Diffusion is used in particular to dope polysilicon gates in MOS transistors, form integrated resistors, form the source/drain domains in MOS transistors, and form the base and emitter in bipolar transistors. The concentration in most of these applications is estimated using Fick’s law.

The initial stresses present in solids have a significant impact on how the material responds mechanically in situations where it is already stressed. These initial stresses are relevant in various fields including geophysics, engineering structures, and the behavior of soft biological tissues. These initial stresses occur as a result of processes like manufacturing or growth, and they exist even in the absence of external forces. Abd-Elaziz et al. [33] developed a formulation for initial stress in a thermo-porous elastic solid. Other researchers, such as Othman et al. [34,35,36,37], Singh et al. [38], Singh [39] and Ailawalia et al. [40], have applied this theory [33] to investigate plane harmonic waves within the framework of generalized thermoelasticity.

In this study, as a novelty of the previous works, we analyze the influence of the Thomson effect on diffusive media in the presence of initial stress, using the normal mode analysis method within the context of the DPL model.

Formulation of the Problem and Basic Equations

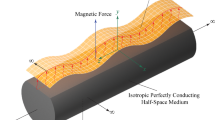
For two dimensional problem, assume the displacement vector as \({\varvec{u}} = (u,0,w),\) All quantities considered will be a function of the time variable \(t\), and of the coordinates \(x\) and \(z.\) Consider a magnetic field with components \({\varvec{H}} = (0,H_{0} ,0)\), having a constant intensity, which acts parallel to the direction of the \(y\)-axis, as shown in the schematic configuration of the problem (Fig. 1). The magnetic field of the for \({\varvec{H}} \equiv (0,H_{0} + h(x,z,t),0)\) produces an induced electric field of components \({\varvec{E}} \equiv (E_{1} ,0,E_{3} ),\) and an induced magnetic field, as denoted by \({\varvec{h}}\), and these satisfy the electromagnetism equations, in the linearized form.

Fig. 1
figure 1

The schematic configuration of the problem

Full size image

The variation of magnetic and electric fields inside the medium is given by Maxwell’s equations as follows Abd-Elaziz et al. [28]:

$${\mathbf{\nabla }} \times {\varvec{h}} = {\varvec{J}} + {\varvec{D}}_{,t} ,$$
(1)
$${\mathbf{\nabla }} \times {\varvec{E}} = - \;{\varvec{B}}_{,t} ,$$
(2)
$${\mathbf{\nabla }}.\;{\varvec{B}} = 0,\quad {\mathbf{\nabla }}.\;{\varvec{D}} = \rho_{e} ,$$
(3)
$${\varvec{B}} = \mu_{0} ({\varvec{H}} + {\varvec{h}}),\quad {\varvec{D}} = \varepsilon_{0} {\varvec{E}}.$$
(4)

The modified Ohm’s law for a medium with finite conductivity supplements the above system of coupled equations, namely

$${\varvec{J}} = \sigma_{0} [{\varvec{E}} + \mu_{0} \;({\varvec{u}}_{,t} \times {\mathbf{H}})].$$
(5)

The constitutive relations in a homogeneous, isotropic thermoelastic solid can be written as Othman and Eraki [23]:

$$\sigma_{ij} = 2\mu \varepsilon_{ij} + (\lambda e - \beta_{1} \,T - \beta_{2} \,C)\delta_{ij} - p\,(\delta_{ij} + \omega_{ij} ),$$
(6)
$$e_{ij} = \frac{1}{2}(u_{i,j} + u_{j,i} ),\quad \omega_{ij} = \frac{1}{2}(u_{j,i} - u_{i,j} ),$$
(7)
$$P = - \;\beta_{2} \,e + b\,C - a\,T.$$
(8)

The heat conduction equation (DPL) model can be written in the form (Othman and Eraki [35])

$$k\left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right)\nabla^{2} T = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{{\tau_{q}^{2} }}{2}\frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left[ {\rho \;C_{E} T_{,t} + \left( {\beta {}_{1}\;T_{0} + M} \right)e_{,t} + a\,T_{0} \;C_{,t} } \right]\;.$$
(9)

where the term \(M\,e_{,t}\) represents the Thomson effect.

The equation of mass diffusion is

$$d\,\beta_{2} \,\nabla^{2} e + d\,a\,\nabla^{2} T - d\,b\,\nabla^{2} C + \left( {1 + \tau \,\frac{\partial }{\partial t}} \right)\,C_{,t} = 0.$$
(10)

The equations of motion, taking into consideration the Lorentz force, are

$$\sigma_{ji,j\;\;} + \,\;F_{i\;} = \rho \;u_{i,tt} .$$
(11)

The Lorentz force is given by [22,23,24,25]

$${\varvec{F}}_{i\;} = \mu_{0} ({\varvec{J}} \times {\varvec{H}})_{,i}.$$
(12)

The current density vector \({\varvec{J}}\) is parallel to the electric intensity vector \({\varvec{E}}\), thus \({\varvec{J}} = (J_{1} ,0,J_{3} )\;\)

The Ohm’s law (5) after linearization gives (Abd-Elaziz et al. [33])

$${\varvec{J}} \equiv \sigma_{0} (E_{1} - \mu_{0} H_{0} w_{,t} ,\;0,\;E_{3} + \mu_{0} H_{0} u_{,t} ).$$
(13)

Equations (1), (4) and (13) give

$$\frac{\partial h}{{\partial z}} = - \;\sigma_{0} \,(E_{1} - \mu_{0} \,H_{0} \,w_{,t} ) - \varepsilon_{0} \,E_{1,t} \;,$$
(14)
$$\frac{\partial h}{{\partial x}} = \sigma_{0} \,(E_{3} + \mu_{0} H_{0} u_{,t} ) + \varepsilon_{0} E_{3,t} .$$
(15)

From Eqs. (2) and (4), we get

$$\frac{{\partial E_{3} }}{\partial x} - \frac{{\partial E_{1} }}{\partial z} = \mu_{0} \,h_{,t} .$$
(16)

Using Eqs. (12) and (13), Lorentz force becomes

$${\varvec{F}} \equiv \mu_{0} H_{0} \sigma_{0} ( - \,E_{3} + \mu_{0} H_{0} u_{,t} ,\;0,\,E_{1} - \mu_{0} H_{0} w_{,t} )\;,$$
(17)

From Eqs. (6), (7) and (17) in Eq. (11), equations of motion become

$$\left( {\mu - \frac{p}{2}} \right)\nabla^{2} u + \left( {\lambda + \mu + \frac{p}{2}} \right)\;e_{,x} - \beta_{1} T_{,x} - \beta_{2} C_{,x} - \mu_{0} H_{0} \sigma_{0} (E_{3} + \mu_{0} H_{0} u_{,t} ) = \rho \;u_{,tt} ,$$
(18)
$$\left( {\mu - \frac{p}{2}} \right)\nabla^{2} w + \left( {\lambda + \mu + \frac{p}{2}} \right)\;e_{,z} - \beta_{1} T_{,z} - \beta_{2} C_{,z} + \mu_{0} H_{0} \sigma_{0} (E_{1} - \mu_{0} H_{0} w_{,t} ) = \rho \;w_{,tt} .$$
(19)

For simplifying the governing equations, the following dimensionless quantities are proposed:

$$\begin{gathered} (x^{\prime},\,z^{\prime},\,u^{\prime},\,w^{\prime}) = c_{1} \;\eta \;(x,\,z,\,u,\,w)\;,\;\;T^{\prime} = \frac{{\beta_{1} }}{{\left( {\lambda + 2\,\mu } \right)}}\;T,\;\;C^{\prime} = \frac{{\beta_{2} }}{{\left( {\lambda + 2\,\mu } \right)}}\;C,\;\;\{ \sigma^{\prime}_{ij} ,\;p^{\prime}\} = \frac{{\{ \sigma_{ij} ,\;p\} }}{{\left( {\lambda + 2\,\mu } \right)}}\;, \hfill \\ (t^{\prime},\,\tau^{\prime},\,\tau^{\prime}_{\theta } ,\,\tau^{\prime}_{q} ) = c_{1}^{2} \;\eta \;(t,\,\tau ,\;\tau_{\theta } ,\,\tau_{q} ),\;\;h^{\prime} = \frac{\eta }{{\sigma_{0} \,\mu_{0} \,H_{0} }}h\;,\;P^{\prime} = \frac{P}{{\beta_{2} }},c_{1}^{2} = \frac{\lambda + 2\mu }{\rho }\;,\;\eta = \frac{{\rho \;C_{E} }}{k}\;. \hfill \\ \end{gathered}$$
(20)

For dimensionless sizes that are defined in Eq. (31), we can write the above basic equations in the following from, with dropping the dashed, for convenience

$$\left( {{\mathbf{\nabla }}^{2} - a_{1} \frac{\partial }{\partial t} - \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\;e - \nabla^{2} T - \nabla^{2} C - a_{2} h_{,t} = 0,$$
(21)
$$\left( {{\mathbf{\nabla }}^{2} - a_{3} \frac{\partial }{\partial t} - a_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\;h - e_{,t} = 0,$$
(22)
$$\left( {1 + \tau_{\theta } \frac{\partial }{\partial t}} \right){\mathbf{\nabla }}^{2} T = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{{\tau_{q}^{2} }}{2}\frac{{\partial^{2} }}{{\partial t^{2} }}} \right)(T_{,t} + a_{5} \,C_{,t} + a_{6} \,e_{,t} ),$$
(23)
$${\mathbf{\nabla }}^{2} e + a_{7} \,{\mathbf{\nabla }}^{2} T - a_{8} \,{\mathbf{\nabla }}^{2} C + a_{9} \,\left( {1 + \tau \,\frac{\partial }{\partial t}} \right)\,C_{,t} = 0,$$
(24)

where \(a_{i} ,\;\left( {i = 1:9} \right)\) are defined in the Appendix.

Normal Mode Analysis

The solution of physical variable may be analyzed modes as the following from

$$[e,\;T,\;h,\;C,\;\sigma_{ij} ](x,z,t) = [e^{*} ,\;T^{*} ,\;h^{*} ,\;C^{*} ,\;\sigma_{ij}^{*} ](z)\;e^{{i(a_{0} \;x - \omega \;t)}} ,$$
(25)

where \(\omega\) is a complex constant, \(i = \sqrt { - 1} \;,\;a_{0}\) is wave number in \(x\)-direction.

Using Eq. (25) into Eqs. (21)–(24), then we get

$$(D^{2} - b_{1} )\;e^{*} - (D^{2} - a_{0}^{2} )\,T^{*} - (D^{2} - a_{0}^{2} )\;C^{*} + b_{2} h^{*} = 0,$$
(26)
$$b_{3} \;e^{*} + (D^{2} - b_{4} )\;h^{*} = 0\;,$$
(27)
$$- \;b_{6} e^{*} + (D^{2} - b_{7} )\;T^{*} - b_{8} C^{*} = 0\;,$$
(28)
$$(D^{2} - a_{0}^{2} )\;e^{*} + a_{7} (D^{2} - a_{0}^{2} )T^{*} - (a_{8} D^{2} - b_{9} )\;C^{*} = 0\;.$$
(29)

Equations (26)–(29) have a non-trivial solution if the physical quantities determinant coefficients equal to zero, then we get:

$$(D^{8} - A_{1} \,D^{6} + A_{2} \,D^{4} - A_{3} \,D^{2} + A_{4} )\{ e^{*} ,h^{*} ,T^{*} ,\,C^{*} \} = 0\;.$$
(30)

Equation (30) can be factorized as

$$(D^{2} - K_{1}^{2} )(D^{2} - K_{2}^{2} )(D^{2} - K_{3}^{2} )(D^{2} - K_{4}^{2} )\,\{ e^{*} ,\,h^{*} ,\,T^{*} ,\,C^{*} \} = 0\;,$$
(31)

where, \(K_{n}^{2} ,(n = 1,\,2,\,3,4)\) are roots of Eq. (31).

The general solution of Eq. (40) bounded as \(z \to \infty\) is given by

$$(e^{*} ,\;h^{*} ,\,\;T^{*} ,\;C^{*} )(z) = \sum\limits_{n = 1}^{4} {(1,\;H_{1n} ,\;H_{2n} ,\;H_{3n} )R_{n} \;e^{{ - k_{n} z}} .}$$
(32)

Substituting from Eqs. (20), (25) and (32) into Eq. (6), we get

$$\sigma = \sum\limits_{n = 1}^{4} {H_{4n} \;R_{n} \;e^{{\left( { - k_{n} z + i\,a_{0} \,x - i\,\omega \,t} \right)}} } - p,$$
(33)
$$P^{*} = \sum\limits_{n = 1}^{4} {H_{5n} \;R_{n} \;e^{{ - k_{n} z}} } .$$
(34)

where \(b_{i} ,\;(i = 1 - 9)\) and \(H_{jn} ,\;(j = 1 - 5)\) are defined in Appendix.

The Boundary Conditions

The parameters \(R_{n} ,(n = 1,2,3,4)\) have to be selected such that boundary conditions at the surface \(z = 0\) are

$$e^{*} = 0,\;\quad h^{*} = h_{0} \;,\;\quad T^{*} = 0\;,\quad \frac{{\partial C^{*} }}{\partial z} = 0.$$
(35)

Applying boundary conditions (35), using Eq. (32), we obtain a system of equations, by solving this system using matrix inverse, the constants \(R_{n} ,(n = 1,2,3,4)\) are obtained as follows

$$\left( \begin{gathered} R_{1} \hfill \\ R_{2} \hfill \\ R_{3} \hfill \\ R_{4} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \begin{array}{*{20}c} {1\quad } & {\quad 1\;\quad } & {1\quad \quad \quad \quad 1} \\ {H_{11} \quad } & {\quad \;H_{12} \;\quad } & {\,\quad H_{13} \quad \quad \quad H_{14} } \\ {H_{21} \quad \quad } & {\quad H_{22} \quad } & {\quad H_{23} \quad \quad \quad H_{24} } \\ \end{array} \hfill \\ - k_{1} \,H_{31} \quad - k_{2} \,H_{32} \quad - k_{3} \,H_{33} \quad - k_{4} \,H_{34} \hfill \\ \end{gathered} \right)^{ - 1} \left( \begin{gathered} 0 \hfill \\ h_{0} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right)\;.$$
(36)

Numerical Analysis and Discussion

The copper substance was selected for numerical evaluations. The problem's material constants were then taken as (Abd-Elaziz et al. [28]).

\(\lambda = 7.76 \times 10^{10\,} {\text{N}}.\,{\text{m}}^{ - 2} ,\)\(\mu = 3.86 \times 10^{10} \,{\text{kg}}.\,{\text{m}}^{ - 1} .\,{\text{s}}^{ - 2} \,,\)\(K = 386\,{\text{w}}.\,{\text{m}}^{ - 1} .\,{\text{k}}^{ - 1} ,\)\(T_{0} = 293\;{\text{K}}\),

\(\alpha_{t} = 1.78 \times 10^{ - 5} \,{\text{k}}^{ - 1} ,\)\(\alpha_{c} = 1.98 \times 10^{ - 4} \,{\text{k}}^{ - 1} ,\)\(\rho = 8954\;{\text{kg}}.\,{\text{m}}^{ - 3} ,\)\(C_{e} = 383.1\;{\text{J}}{\text{.kg}}^{ - 1} .{\text{k}}^{ - 1}\), \(\sigma_{0} = 9.36 \times 10^{5} \,{\text{siemens}}\,{\text{m}}^{ - 1} .\)

The comparisons were carried out for:

$$\begin{gathered} x = 0.83\,\,{\text{m}},\,\quad t = 0.05\,{\text{s}},\quad \tau_{T} = 0.0001\,{\text{s}},\quad \tau_{q} = 0.015\,{\text{s}},\quad \omega = \omega_{0} + i\;\omega_{1} ,\quad \omega_{0} = 0.1\,{\text{s}}^{ - 1} , \hfill \\ \quad \omega_{1} = 0.000\,{\text{s}}^{ - 1} ,\,\,H_{0} = 55{\text{A}}\,{\text{m}}^{ - 1} ,\;M = 2\,{\text{N}}\,{\text{m}}^{ - 2} . \hfill \\ \end{gathered}$$

The numerical values, outlined above, were used for the distribution of the physical quantities \(T\,,h\,,\sigma \,,e\,,c\,,p\,,\) for the problem have established in the context of DPL model and L-S theory, in the absence and presence of Thomson effect parameter \((M = 0,\,2\,).\)

In these figures, the dotted line represents the solution in the DPL model in the presence of Thomson effect parameter, the dashed-dotted line represents the solution derived using DPL model in the absence of Thomson effect parameter, the solid line indicates the (L-S) theory in the presence of Thomson effect parameter and finally the dashed line refers to (L-S) theory when Thomson effect parameter equals zero. Here all variables are taken in non-dimensional form. The results were obtained by using MATLAB 2021a.

Figures 2, 3 and 4 depict that the distribution of the strain distribution \(e\), temperature \(T\) and the stress distribution \(\sigma ,\) they show that they have the same behavior, they are noticed that their values increases to a maximum value in the range \(0 \le z \le 1,\) then decreases until become constant in the range \(1 \le z \le 12,\) this results for L-S theory and DPL model. The values of these physical quantities in the presence of the Thomson effect parameter \((M = 2)\) for L-S theory are greater than in the absence of it \((M = 0),\) but the reversed behavior is found for DPL model. Farther more the values in the context of L-S theory are higher than those for DPL model. Figure 5 illustrates the dispersion of the generated magnetic field \(h.\) It shows that the impact of the Thomson parameter on the induced magnetic field is insignificant. Figures 6 and 7 show the distribution of concentration \(C\) and chemical potential \(P.\) Then value of \(C\) decrease to a minimum value in the interval \(0 \le z \le 7,\) and finally up to zero in \(7 \le z \le 12,\) while the values of \(P\) decrease to a minimum value in the interval \(0 \le z \le 5,\) and finally remains constant and up to zero in \(5 \le z \le 12.\) In the context of L-S theory, the values of concentration and chemical potential are higher in the presence of the Thomson effect parameter \((M = 2)\) compared to its absence \((M = 0).\) However, the behavior is reversed for the DPL model when compared to L-S theory. Additionally, the values in the context of L-S theory are higher than those for the DPL model. Figures 8, 9, and 10 demonstrate the distribution of strain \(e,\) temperature \(T,\) and stress \(\sigma\) in the presence of the Thomson effect parameter \((M = 2)\) and at different values of the phase lag of heat flux \(\tau_{q}\)\((\tau_{q} = 0.015\,,\)\(0.04).\) They show the same behavior for both L-S theory and DPL model, with values increasing to a maximum in the range \(0 \le z \le 1,\) and then decreasing until they become constant in the range \(1 \le z \le 12.\) It show that the values of those quantities at \(\tau_{q} = 0.04\) are higher than the previous distributions at \(\tau_{q} = 0.015.\) Additionally, the values in the context of L-S theory are higher than those for the DPL model. Figure 11 shows that the induced magnetic field almost does not change from \(\tau_{q} = 0.015\) to \(\tau_{q} = 0.04.\) Figures 12 and 13 explain the distributions of the chemical potential \(P\) and the concentration \(C\) in the context of the two theories for \((\tau_{q} = 0.015\,,0.04)\) and in the presence of the Thomson effect parameter \((M = 2).\) The values of \(C\) are decreased to a minimum value in the interval \(0 \le z \le 7,\) and finally up to zero in \(7 \le z \le 12,\) while the values of \(P\) are decreased to a minimum value in the interval \(0 \le z \le 5,\) and finally remains constant and up to zero in \(5 \le z \le 12.\) It disappear that the values of those quantities at \(\tau_{q} = 0.04\) are greater than those at \(\tau_{q} = 0.015.\) Also, the values in the context of L-S theory are higher than those for DPL model for \((\tau_{q} = 0.015\,,0.04)\).

3D curves in Figs. 14, 15 and 16 demonstrate the relationship between physical quantities and both distance components \((x,\,z)\) in the context of the DPL model. These figures are.

important for studying the dependence of physical quantities on the vertical component of distance. The curves show wave propagation and indicate a strong dependence on the vertical distance.

Conclusion

By comparing the figures that were obtained, important phenomena are observed:

  1. 1.

    The phenomenon of finite speeds of propagation is manifested in all figures.

  2. 2.

    All physical quantities satisfied the boundary conditions.

  3. 3.

    The Thomson effect parameter has a noticeable influence on all physical quantities (except the induced magnetic field). It decreases them under both DPL model and L-S theory.

  4. 4.

    The values of most physical quantities in the context of L-S theory are higher than those for the DPL model, in the presence and absence of the Thomson effect parameter as well as at different values of the phase lag of the heat flux.