Development of a 3D Hybrid Finite-Discrete Element Simulator Based on GPGPU-Parallelized Computation for Modelling Rock Fracturing Under Quasi-Static and Dynamic Loading Conditions

Abstract

As a state-of-the-art computational method for simulating rock fracturing and fragmentation, the combined finite-discrete element method (FDEM) has become widely accepted since Munjiza (2004) published his comprehensive book of FDEM. This study developed a general-purpose graphic-processing-unit (GPGPU)-parallelized FDEM using the compute unified device architecture C/C ++ based on the authors’ former sequential two-dimensional (2D) and three-dimensional (3D) Y-HFDEM IDE (integrated development environment) code. The theory and algorithm of the GPGPU-parallelized 3D Y-HFDEM IDE code are first introduced by focusing on the implementation of the contact detection algorithm, which is different from that in the sequential code, contact damping and contact friction. 3D modelling of the failure process of limestone under quasi-static loading conditions in uniaxial compressive strength (UCS) tests and Brazilian tensile strength (BTS) tests are then conducted using the GPGPU-parallelized 3D Y-HFDEM IDE code. The 3D FDEM modelling results show that mixed-mode I–II failures are the dominant failure mechanisms along the shear and splitting failure planes in the UCS and BTS models, respectively, with unstructured meshes. Pure mode I splitting failure planes and pure mode II shear failure planes are only possible in the UCS and BTS models, respectively, with structured meshes. Subsequently, 3D modelling of the dynamic fracturing of marble in dynamic Brazilian tests with a split Hopkinson pressure bar (SHPB) apparatus is conducted using the GPGPU-parallelized 3D HFDEM IDE code considering the entire SHPB testing system. The modelled failure process, final fracture pattern and time histories of the dynamic compressive wave, reflective tensile wave and transmitted compressive wave are compared quantitatively and qualitatively with those from experiments, and good agreements are achieved between them. The computing performance analysis shows the GPGPU-parallelized 3D HFDEM IDE code is 284 times faster than its sequential version and can achieve the computational complexity of O(N). The results demonstrate that the GPGPU-parallelized 3D Y-HFDEM IDE code is a valuable and powerful numerical tool for investigating rock fracturing under quasi-static and dynamic loading conditions in rock engineering applications although very fine elements with maximum element size no bigger than the length of the fracture process zone must be used in the area where fracturing process is modelled.

1 Introduction

Understanding the mechanism of the fracturing process in rocks is important in civil and mining engineering and several other fields, such as geothermal, hydraulic, and oil and gas engineering, in which rock fractures play an important role. Numerical methods have been increasingly applied to analyze the fracturing process of rocks (e.g., Mohammadnejad et al. 2018). Due to the limitations of computing power/environments and the difficulty in extending some numerical techniques to three-dimension, numerous previous studies of rock fracture modelling using various numerical methods have been limited to two-dimensional (2D) analyses. However, successful simulation of the three-dimensional (3D) fracturing process is essential for better understanding and solving many practical rock engineering problems because rock fracturing essentially involves complex 3D processes. Moreover, meaningful developments and applications of 3D numerical methods for 3D rock fracture modelling have been limited in the past, except those that had full access to the most advanced high-performance-computing (HPC) environments, such as supercomputers. This situation has been dramatically improved due to the recent advancements in computer technology, such as general-purpose graphic-processing-unit (GPGPU) accelerators and the many integrated cores architecture, which can be installed even in a personal computer (PC) or a workstation and can achieve HPC environments in ordinary computer environments with relatively low costs. These improvements have allowed scientists and engineers to apply and develop 3D rock fracture computational methods that were not tractable previously.

Recent advances in computational mechanics have resulted in modelling complex rock fracturing processes using various numerical approaches. Generally, these approaches can be classified mainly into continuous and discontinuous methods. In the framework of rock fracture process analysis, the continuum-based methods include the finite element method (FEM), finite difference method (FDM), boundary element method (BEM), scaled boundary finite element method (SBFEM), extended finite element method (XFEM), several mesh-less/mesh-free methods, such as smoothed particle hydrodynamics (SPH), and those based on peridynamics and phase-field method. The discontinuum-based methods include the distinct element method (DEM), discontinuous deformation analysis (DDA), lattice model and molecular dynamics. Comprehensive reviews of recent advances in computational fracture mechanics of rocks can be found in recent review articles (Lisjak and Grasselli 2014; Mohammadnejad et al. 2018). For a realistic simulation of the rock fracturing process, numerical techniques must be capable of capturing the transition of rock from a continuum to a discontinuum through crack initiation, growth and coalescence. Therefore, increasing attention has been paid in recent years to these techniques, which can combine/couple the advantages of the aforementioned continuum-based and discontinuum-based methods while overcoming the disadvantages of each method (Lisjak and Grasselli 2014; Mohammadnejad et al. 2018).

The combined finite-discrete element method (FDEM) proposed by Munjiza et al. (1995) has recently attracted the attention of many engineers and researchers in the field of rock engineering which deals with rock fracturing and fragmentation. The method incorporates the advantages of both continuous and discontinuous methods and is able to simulate the transition from a continuum to a discontinuum caused by rock fracturing. The two main implementations of the FDEM include the open-source research code, Y code (Munjiza 2004), and the commercial code, ELFEN (Rockfield 2005). Due to the open-source nature of the Y code, several attempts have been made to actively extend it, such as Y-Geo (Mahabadi et al. 2014), Y-Flow (Yan and Jiao 2018; Yan and Zheng 2017), Irazu (Lisjak et al. 2018; Mahabadi et al. 2016), Solidity (Guo 2014; Solidity 2017) and HOSS with MUNROU (Rougier et al. 2011, 2014). Moreover, the authors have developed Y-HFDEM IDE (An et al. 2017; Liu et al. 2015, 2016; Mohammadnejad et al. 2017). In addition, using user-defined subroutines in the explicit module of the commercial software ABAQUS, Ma et al. (2018) recently implemented the FDEM to investigate the effects of different fracture mechanisms on impact fragmentation of brittle rock-like materials. The principles of all of the FDEM codes are based on continuum mechanics, the cohesive zone model (CZM) and contact mechanics, which make the FDEM extremely computationally expensive. Thus, few practical rock engineering problems can be solved using the 3D FDEM based on sequential central-processing-unit (CPU)-based implementations. Therefore, it is imperative to develop robust parallel computation schemes to handle large-scale 3D FDEM simulations with massive numbers of nodes, elements and contact interactions.

To date, several successful parallel implementations of FDEM codes have been reported using the message-passing interface (MPI) (Elmo and Stead 2010; Hamdi et al. 2014; Lei et al. 2014; Lukas et al. 2014; Rockfield 2005; Rogers et al. 2015; Rougier et al. 2014) and shared memory programming, such as OpenMP (Xiang et al. 2016). Among these, Lukas et al. (2014) proposed a novel approach for the parallelization of 2D FDEM using MPI and dynamic domain decomposition-based parallelization solvers, and they successfully applied the parallelized Y code to a large-scale 2D problem on a PC cluster, which should be able to be applied to practical 3D problems, although future developments are needed. In addition, Lei et al. (2014) successfully developed the concept of the virtual parallel machine for the FDEM using MPI, which can be adapted to different computer architectures ranging from several to thousands of CPU cores. Rougier et al. (2014) introduced the HOSS with MUNROU code, in which they used 208 processors for parallel computation controlled by MPI and developed novel contact detection and contact force calculation algorithms (Munjiza et al. 2011). The MUNROU code was then successfully applied to perform 3D simulations of a dynamic Brazilian tensile test of rock with a SHPB apparatus. ELFEN (Elmo and Stead 2010; Hamdi et al. 2014; Rockfield 2005; Rogers et al. 2015) uses MPI in its parallelization scheme and has been employed successfully in 2D and 3D simulations of rock fracturing process. For example, analyses of the 3D fracturing process in conventional laboratory tests using up to 3 million elements have been reported (Hamdi et al. 2014). Xiang et al. (2016) optimized the contact detection algorithm in their Solidity code and parallelized the code using OpenMP. Although they modelled a packing system with 288 rock-like boulders and achieved a speedup of 9 times on 12 CPU threads, the details of the applied algorithm and its implementation were not given. In general, MPI requires large and expensive CPU clusters to achieve the best performance. In addition, the application of shared memory programming such as OpenMP is limited by the total number of multiprocessors that can reside in a single computer; thus, MPI is still required for large-scale problems, in which each computer uses both OpenMP and MPI to transfer the data between multiple computers. This means that the hybrid MPI/OpenMP is necessary. In all of these approaches, more than 100 CPUs are necessary to achieve a speed-up of more than 100 times compared with sequential CPU-based FDEM simulations, which results in the need for a larger space or expensive HPC environments.

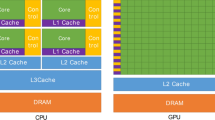
In addition to the CPU-based parallelization schemes, a GPGPU accelerator controlled by either the Open Computing Language (OpenCL) (Munshi et al. 2011) or the Compute Unified Device Architecture (CUDA) (NVIDIA 2018) can be considered as another promising method for the parallelization of FDEM codes. Hundreds and thousands of GPU-core processors can reside and concurrently work in a small GPGPU accelerator within an ordinary laptop/desktop PC or a workstation, which also has lower energy consumption than CPU-based clusters. Zhang et al. (2013) developed a CUDA-based GPGPU parallel version of the Y code (2D) without considering the fracturing process and contact friction. Batinić et al. (2018) implemented a GPGPU-based parallel FEM/DEM that is based on the Y code to analyze cable structures using CUDA. However, none of these implementations have been employed to simulate rock fracturing. In this regard, a GPGPU-based FDEM commercial code, namely Irazu (Lisjak et al. 2017, 2018), has just been developed with OpenCL and used successfully in rock fracture simulations. Irazu is the only available commercial GPGPU-based FDEM code with OpenCL that is currently capable of modelling the rock fracturing process (Lisjak et al. 2017, 2018). In addition, the authors have developed a free FDEM research code, Y-HFDEM IDE (An et al. 2017; Liu et al. 2015, 2016; Mohammadnejad et al. 2017), and parallelized its 2D implementation using GPGPU with CUDA C/C ++ (Fukuda et al. 2019). This paper focuses on parallelizing the 3D implementation of the Y-HFDEM IDE code using GPGPU with CUDA C/C ++, which is completely different from Irazu’s GPGPU parallelization using OpenCL. Additional studies are required to verify and validate the GPGPU-based 3D FDEM code. Furthermore, for any newly implemented GPGPU-based codes, it is desirable to describe their complete details because the implementation of any GPGPU-based code is generally different from that of CPU-based sequential codes. Most importantly, there are no freely available GPGPU-based FDEM codes, whereas the GPGPU-based Y-HFDEM IDE is free to use, and the freely available GPGPU-parallelized 2D/3D Y-HFDEM IDE software may significantly contribute to researches in the field of rock engineering.

To validate and calibrate newly developed codes in the field of rock mechanics, two standard rock mechanics laboratory tests, the uniaxial compressive strength (UCS) tests and Brazilian tensile strength (BTS) tests, have often been modelled to simulate the fracturing process and associated failure mechanisms of rock materials under quasi-static loading conditions. Although the UCS and BTS tests have been actively modelled using 2D FDEM, their modelling in the framework of 3D FDEM has been very limited and less well explained. For example, UCS and BTS tests were three-dimensionally simulated using Y-Geo (Mahabadi et al. 2014) with a relatively large element size (2 mm for both tests) and a very high loading velocity (1 m/s) resulting in the appearance of dynamic effects in the model, such as multi-fracture propagation around the center of the BTS models, which is also shown in the dynamic BTS simulation discussed in Sect. 3.3. Moreover, although Mahabadi et al. (2014) observed splitting fractures in their BTS modelling, the post-peak behavior of the stress–strain curve was not well demonstrated. Later, Lisjak et al. (2018) introduced IRAZU based on GPGPU parallelization and three-dimensionally simulated UCS and BTS tests using a finer element size (1.5 mm for both tests) and slower loading rate (0.1 m/s). In comparison with the aforementioned simulations by Mahabadi et al. (2014), many reasonable results were achieved by Lisjak et al. (2018). Mahabadi et al. (2014) may have chosen the relatively high loading rate because 3D FDEM modelling using Y-Geo is computationally demanding, which may have required them to find ways to reduce the running time and accordingly the time required for calibration, although any remedies should not significantly affect the obtained results. Moreover, Lisjak et al. (2018) claimed that the effect of their high loading rates was compensated for by the critical damping scheme. However, it should be noted that the critical damping scheme implemented in almost all FDEM simulations is intended to model the quasi-static loading conditions using the dynamic relaxation method, which cannot reduce the effect of the loading rate, unlike what was claimed by Lisjak et al. (2018). Guo (2014) investigated 3D FDEM modelling of BTS tests at different loading rates using the critical damping scheme and showed that both the fracture pattern and obtained peak load were affected by the loading rate when the velocity of the loading platens is higher than 0.01 m/s (i.e., loading rate = 0.02 m/s). Correspondingly, the findings of Guo (2014) support the statement that “the critical damping scheme used in almost all FDEM simulations cannot reduce the effect of the loading rate”. Therefore, for an accurate simulation with quasi-static loading conditions in the framework of the FDEM, the loading rate should be selected correctly to avoid the dynamic effects of the loading rate before selecting any input parameters, which is another strong motivation for this study to conduct 3D simulations of UCS and BTS tests using the GPGPU-parallelized 3D Y-HFDEM IDE.

Furthermore, 3D FDEM simulations of dynamic fracturing processes of rock materials under dynamic loads, such as SHPB tests (e.g. Zhang and Zhao 2014), have been much more limited; in particular, 3D FDEM simulations of the full system of the SHPB test are rare. However, for any qualitative and quantitative discussion, accurate modelling and reasonable calibration of the SHPB test are paramount for any meaningful numerical simulations of the dynamic fracturing process in rock such as blasting. In fact, to date, only four peer-reviewed international journal papers have been reported for modelling SHPB tests in the framework of the 2D/3D FDEM. Using the 2D FDEM, Mahabadi et al. (2010) modelled the dynamic fracturing process of Barre granite in a dynamic BTS test with an SHPB apparatus and found good agreement between the numerical simulations and experiments. In their modelling, each of the SHPB bars was modelled as a large single triangular element, and not only was the element assigned mechanical properties, but velocities were prescribed to all nodes. This may cause the given mechanical properties except for the contact penalty and contact friction to have no meaning and the element used to model the SHPB bar to become rigid. Moreover, the mode I and mode II fracture energies cannot be distinguished, which has generally been recognized as important for reasonable simulations of rock fracturing by the current FDEM community. Using the 3D FDEM (HOSS), Rougier et al. (2014) modelled the dynamic BTS tests of weathered granite documented in Broome et al. (2012) by explicitly considering elastically deformable SHPB bars. The results showed remarkably good agreement with those from the experiment. Subsequently, although 2D HOSS was applied, Osthus et al. (2018) proposed a novel and detailed calibration procedure based on a general and probabilistic approach for numerical simulations of dynamic BTS tests of the weathered granite modelled by Rougier et al. (2014) with the SHPB apparatus. Furthermore, by targeting the same SHPB-based dynamic BTS tests of the same weathered granite, Godinez et al. (2018) conducted several sensitivity analyses with different combinations of input parameters using 2D HOSS. They showed that the simulation results are most sensitive to the parameters related to the tensile and shear strengths and the fracture energies, which are valuable information. In this way, additional knowledge has gradually been accumulated for the realistic modelling of dynamic BTS tests with the SHPB apparatus in the FDEM community. However, although the target rock in previous studies (Mahabadi et al. 2010; Osthus et al. 2018; Rougier et al. 2014) was granite, in which heterogeneity and anisotropy generally play important roles, none of the studies considered or discussed these important characteristics. In light of these results, further investigation of FDEM modelling is needed, especially for 3D modelling of dynamic fracturing of rocks of various types, because only one case of the 3D dynamic fracturing of granite in a dynamic BTS test has been modelled using the FDEM to date.

Based on this background, this paper aims to first explain the theory and algorithm of the recently developed GPGPU-parallelized FDEM implemented in the 3D Y-HFDEM IDE code. The capability of the 3D Y-HFDEM IDE code in rock engineering applications is then demonstrated by modelling the fracturing process of rocks and the movements of the resultant rock fragments under a series of quasi-static and dynamic loading conditions. Thus, this paper may provide a basis for further improvement and development of the FDEM codes based on GPGPU parallelization for modelling rock fracturing, especially the dynamic fracturing of rock. Many previous publications have focused on the advantages of the FDEM. However, although the FDEM is very useful, there is currently no universal/perfect method to simulate rock fracturing/fragmentation processes, so the disadvantages of this method other than the high computational burden must also be carefully addressed. In fact, the calibration of the FDEM, which is the most fundamental procedure for any meaningful numerical simulation, tends to be more complex than in non-combined methods. Although the calibration method for the 2D FDEM has been reported in the literature (e.g., Tatone and Grasselli 2015), it was found during the development of the 3D FEM/DEM code that the calibration of 3D simulations requires more careful treatment and is more sensitive to the input parameters than the 2D counterparts. Especially in 3D simulations of the fracturing process of rocks due to dynamic loading involving significant fragmentation of hard rock, special care must be paid to avoid spurious fracture modes, which have sometimes been misunderstood or omitted/hidden in the literature.

This paper is organized as follows. The theory used in the 3D FDEM, i.e., Y-HFDEM IDE code, is first introduced, and its implementation in the framework of the GPGPU parallel computation is then explained in detail. Subsequently, the accuracy and capability of the developed code are investigated by modelling several common examples in rock mechanics, including modelling the 3D fracturing process of rocks in BTS and UCS tests, which have been used to benchmark new computational methods for rock fracturing. The entire SHPB testing system of 3D dynamic BTS tests is then simulated using the newly developed GPGPU-parallelized hybrid FDEM, and the numerical results are compared with those from SHPB experiments by focusing on the dynamic fracturing process of rock in the 3D dynamic Brazilian tests. Finally, conclusions are drawn from this study.

2 GPGPU-Parallelized 3D FDEM

The FDEM code “Y-HFDEM 2D/3D IDE” was originally developed using object-oriented programming with visual C++ (Liu et al. 2015) based on the CPU-based sequential open-source Y 2D/3D libraries (Munjiza 2004; Munjiza et al. 2010) and OpenGL. The Y-HFDEM 2D/3D IDE code can significantly simplify the process of building and manipulating the input models and greatly reduce the possibility of erroneous model setup, and it can also display the calculated results graphically in real time with OpenGL. The code has been successfully employed in simulations of rock fracturing in various geotechnical engineering problems (An et al. 2017; Liu et al. 2015, 2016; Mohammadnejad et al. 2017). Because of the nature of sequential programming, it has mainly been applied to small-scale 2D problems using relatively rough meshes. To overcome this limitation, the parallel programming scheme using the GPGPU controlled by CUDA C/C++ was implemented in the code in a recent study by the authors (Fukuda et al. 2019) for 2D modelling and in this study for 3D modelling. Because the various FDEM-based codes reviewed in Sect. 1 were independently developed by each research institute/organization and have different features, the fundamental features of the 3D Y-HFDEM IDE code and its GPGPU-based parallelization scheme are explained in detail in the following subsections.

2.1 Fundamental Theory of 3D Y-HFDEM IDE

The principles of the FDEM are based on continuum mechanics, nonlinear fracture mechanics based on the CZM and contact mechanics, all of which are formulated in the framework of explicit FEM (Munjiza 2004). Therefore, this section focuses on introducing the features of 3D Y-HFDEM IDE unavailable in other FDEMs such as the hyperelastic model, the irreversible damage during unloading, and the extrinsic cohesive zone model. Of course, these features need to be introduced in context and some of the fundamental FDEM theory is reviewed here to provide the context, which is also motivated by the fact that there are some poor, unclear and even incorrect descriptions in some literatures of the FDEM community.

The continuum behavior of materials, including rocks, is modelled in 3D by an assembly of continuum 4-node tetrahedral finite elements (TET4s) (Fig. 1a). Two types of isotropic elastic constitutive models have been implemented. In the first type, which was implemented in the original Y-code and has been widely used, the isotropic elastic solid obeys Eq. (1) of the neo-Hookean elastic model:

$$\sigma_{ij} = \frac{\lambda }{2}\left( {J - \frac{1}{J}} \right)\delta_{ij} + \frac{\mu }{J}\left( {B_{ij} - \delta_{ij} } \right) + \eta D_{ij} \quad (i,j \, = 1, \, 2, \, 3),$$

(1)

where σ_ij denotes the Cauchy stress tensor, B_ij is the left Cauchy–Green strain, λ and µ are the Lame constants, J is the determinant of the deformation gradient, η is the viscous damping coefficient, δ_ij is the Kronecker delta, and D_ij is the rate of deformation tensor. However, Eq. (1) cannot model anisotropic elasticity, which is important in the field of rock engineering. Thus, in the second type, a hyperelastic solid obeying Eqs. (2) and (3) is also implemented:

$$S_{KL} = C_{KLMN} E_{MN} (K,L,M,N \, = 1, \, 2, \, 3),$$

(2)

$$\sigma_{ij} = \frac{1}{J}F_{iK} S_{KL} F_{jL} + \eta D_{ij} \quad (i,j,K,L \, = 1, \, 2, \, 3),$$

(3)

where S_KL denotes the second Piola–Kirchhoff stress tensor, C_KLMN is the effective elastic stiffness tensor, E_MN is the Green–Lagrange strain tensor, and F_iK is the deformation gradient. The Einstein’s summation convention applies to Eqs. (2) and (3). By properly setting C_KLMN in Eq. (2), both isotropic and anisotropic elastic behaviors can be simulated although only isotropic behavior is considered in this study since the rocks used in this study are better modelled as isotropic materials. The small strain tensor is not used in Eqs. (1) and (2); therefore, large displacements and large rotations can be simulated. Equation (1) is used for the 3D UCS and BTS modellings presented in Sect. 3.2 while both Eq. (1) and Eqs. (2, 3) are used for the 3D dynamic BTS modelling presented in Sect. 3.3 and no noticeable differences between Eq. (1) and Eqs. (2, 3) are observed since rock deformation is small. To simulate the deformation process of materials under quasi-static loading, η = η_crit = 2 h√(ρE) is used to achieve critical damping (Munjiza 2004), where h, ρ, and E are the element length, density and Young’s modulus, respectively, of the target material. The value of σ_ij within each TET4 is converted to the equivalent nodal force f_int (e.g., Munjiza et al. 2015).

Fig. 1

Two types of finite elements (TET4 and CE6) and the mechanical behaviors of CE6 during the failure process: a two TET4s surrounding a CE6, b tensile/shear softening curves in the ICZM

Fracturing of rock under mode I and mode II loading conditions (i.e., opening and sliding cracks, respectively) is modelled using the CZM with the concept of a smeared crack (Munjiza et al. 1999). To model the behavior of the fracture process zone (FPZ) in front of the crack tips, tensile and shear softening is applied using an assembly of 6-node initially zero-thickness cohesive elements (CE6s) (Fig. 1a) as a function of the crack opening and sliding displacements, (o, s), respectively (Fig. 1b). Two methods can be used for the insertion of the CE6s. One is to insert the CE6s into all of the boundaries of the TET4s at the beginning of the analysis, which is known as the intrinsic cohesive zone model (ICZM), and the second is to adaptively insert the CE6s into particular boundaries of the TET4s with the help of adaptive remeshing techniques where a given failure criterion is met, which is referred to as the extrinsic cohesive zone model (ECZM) (Zhang et al. 2007; Fukuda et al. 2017). Many existing FDEM codes, such as the family of Y codes that includes 3D Y-HFDEM IDE, have employed the ICZM, whereas some codes, such as ELFEN, use the ECZM. One of the advantages of the ICZM is that the implementation and application of parallel computing algorithms is straightforward, but an “artificial” intact and elastic behavior of CE6s before the onset of fracturing must be specified, which requires the introduction and correct estimation of penalty terms for CE6s and the careful selection of the time step increment, Δt, to avoid numerical instability. In the GPGPU-based 3D Y-HFDEM IDE, the normal and shear cohesive tractions, (σ^coh and τ^coh, respectively), acting on each face of the CE6s are computed using Eqs. (4) and (5) assuming tensile and shear softening behaviors, respectively:

$$\sigma^{\text{coh}} = \left\{{\begin{array}{*{20}c} {\frac{2o}{{o_{\text{overlap}} }}T_{\text{s}} } & {{\text{if }}o < 0} \\ {\left[ {\frac{2o}{{o_{\text{p}} }} - \left( {\frac{o}{{o_{\text{p}} }}} \right)^{2} } \right]f(D)T_{\text{s}} } & {{\text{if }}0 \le o \le o_{\text{p}} } \\ {f(D)T_{\text{s}} } & {{\text{if }}o_{\text{p}} < o} \\ \end{array} } \right.,$$

(4)

$$\tau^{\text{coh}} = \left\{ {\begin{array}{*{20}c} {\left[ {\frac{2\left| s \right|}{{s_{\text{p}} }} - \left( {\frac{\left| s \right|}{{s_{\text{p}} }}} \right)^{2} } \right]\left( { - \sigma^{\text{coh}} \tan (\phi ) + f(D)c} \right) \, } & {{\text{if }}0 \le \left| s \right| \le s_{\text{p}} } \\ {-\sigma^{\text{coh}} \tan (\phi ) + f(D)c} & {{\text{if }}s_{\text{p}} < \left| s \right|} \\ \end{array} } \right.,$$

(5)

where o_p and s_p are the “artificial” elastic limits of o and s, respectively, o_overlap is the representative overlap when o is negative, T_s is the tensile strength of a CE6, c is the cohesion of a CE6, and ϕ is the internal friction angle of a CE6. Positive o and σ^coh values indicate crack opening and a tensile cohesive traction, respectively. Equation (5) corresponds to the Mohr–Coulomb shear strength model with a tension cutoff. The cohesive tractions σ^coh and τ^coh are applied to the opposite directions of the relative opening and sliding in a CE6, respectively. The artificial elastic behavior of each CE6 characterized by o_p and s_p along with o_overlap is necessary when the ICZM is used to connect the TET4s to express the intact deformation process, which is given as follows and has been used in most FDEM codes (Munjiza et al. 1999):

$$o_{\text{p}} = 2hT_{\text{s}} /P_{\text{open}} ,$$

(6)

$$s_{\text{p}} = 2hc/P_{\tan } ,$$

(7)

$$o_{\text{overlap}} = 2hT_{\text{s}} /P_{\text{overlap}} ,$$

(8)

where P_open, P_tan, and P_overlap are the artificial penalty terms of the CE6 for opening in the normal direction, sliding in the tangential direction and overlapping in the normal direction, respectively, and h is the element length. In this paper, the terminologies “fracture penalties” for P_open, P_tan, and P_overlap used in previous publications are intentionally avoided because they should not be considered as penalties for the fracturing behavior but rather as those for controlling the artificial elastic (intact) regime of CE6. The values of P_open, P_tan, and P_overlap can be considered as the artificial stiffnesses of the CE6 for opening, sliding and overlapping, respectively. Ideally, their values should be infinity to satisfy the elastic (intact) behavior of rocks according to Eqs. (1) or (2), resulting in the requirement of the infinitesimal Δt. Therefore, reasonably large values of the artificial penalty terms of CE6s compared to the Young’s modulus or Lame constants are required because it is impossible to use infinity in actual numerical simulations. Otherwise, the intact behavior of the bulk rock shows significantly different (i.e., softer) behavior from that specified by Eqs. (1) or (2), and the elastic constants used in these elastic constitutive equations completely lose their meanings. In addition, during the development of the 3D Y-HFDEM IDE code, the authors found that the sufficiently large values for the penalty terms (10 times the Young’s modulus of rock, E_rock, in most cases) recommended in many previous studies that applied the FDEM are not sufficient to satisfy the continuum elastic behavior of Eqs. (1) or (2); this topic is investigated and discussed in Sect. 3 for both quasi-static and dynamic loading problems. Some studies argue that the artificial penalty terms are mechanical properties. However, in that case, the CE6s must be considered as joint elements, and the artificial penalty terms of the CE6s should be called joint stiffnesses to describe discontinuous media, such as preexisting joints. The function, f(D), in Eqs. (4) and (5) is the characteristic function for the tensile and shear softening curves (Fig. 1b) and depends on a damage value D of the CE6. When 0 < D < 1 or D = 1 for a CE6, the CE6 can be considered to be a microscopic or macroscopic crack, respectively. The following definitions of D and f(D) are used to consider not only the mode I and II fracturing modes but also a mixed-mode I–II fracturing mode (Mahabadi et al. 2012; Munjiza et al. 1999):

$$D = {\text{Minimum}}\left( {1,\sqrt {\left( {\frac{{o - o_{\text{p}} }}{{o_{\text{t}} }}} \right)^{2} + \left( {\frac{{\left| s \right| - s_{\text{p}} }}{{s_{\text{t}} }}} \right)^{2} } \, } \right){\text{ if }}o \ge o_{\text{p}} {\text{ or }}\left| s \right| > s_{\text{p}} {\text{ , otherwise }}0,$$

(9)

$$f\left( D \right) = \left[ {1 - \frac{A + B - 1}{A + B}\exp \left( {D\frac{A + CB}{{\left( {A + B} \right)\left( {1 - A - B} \right)}}} \right)} \right]\left[ {A\left( {1 - D} \right) + B(1 - D)^{C} } \right]{ (0} \le D \le 1 ) ,$$

(10)

where A, B and C are intrinsic rock properties that determine the shapes of the softening curves, and o_t and s_t are the critical values of o and s, respectively, at which a CE6 breaks and becomes a macroscopic fracture. To avoid unrealistic damage recovery (i.e., an increase of f), the following treatment has been implemented in the code. If the trial f computed from Eq. (10) at the current time step becomes larger than that at the previous time step, f_pre, a condition of f = f_pre is assigned to avoid unrealistic damage recovery. The o_t and s_t in Eq. (9) satisfy the mode I and II fracture energies G_fI and G_fII (Fig. 1b) specified in Eqs. (11) and (12), respectively:

$$G_{\text{fI}} = \int\limits_{{o_{\text{p}} }}^{{o_{\text{t}} }} {\sigma^{\text{coh}} (o){\text{d}}o} ,$$

(11)

$$G_{\text{fII}} + W_{E} = \int\limits_{{s_{\text{p}} }}^{{s_{\text{t}} }} {\left\{ {\tau^{\text{coh}} (|s|)} \right\}{\text{d}}\left| s \right|} ,$$

(12)

where W_res is the amount of work per area of a CE6 done by the residual stress term in the Mohr–Coulomb shear strength model. Note that in the current formulation, mode II and III fracturing modes are not distinguished, and it is assumed that in-plane (mode II) and out-plane (mode III) responses of the micro cracks (i.e., CE6s) are simply described by the parameter G_fII because the clear definition of crack tips and conducting reproducible/reliable mode II and Mode III fracture toughness tests are challenging. This paper uses the same f(D) with A, B and C equal to 0.63, 1.8, and 6.0, respectively (Munjiza et al. 1999), for both mode I and II fracture processes because of the lack of experimental data. However, it is worth mentioning that the recent studies by Osthus et al. (2018) and Godinez et al. (2018) using the FDEM code “2D HOSS” showed that the shape of the softening curve had minor influences on the obtained results and that the tensile and shear strengths and fracture energies are the main affecting factors. Unloading (i.e., a decrease of o or |s|) can also occur during the softening regime (i.e., o > o_p or |s| > s_p) (see Fig. 1b), which is modelled based on Eqs. (13) and (14) (Camacho and Ortiz 1996):

$$\sigma^{\text{coh}} = f(D_{\text{max} } )T_{\text{s}} \frac{o}{{o_{\text{max} } }}{\text{ if }}0 < o < o_{\text{max} } {\text{ and }}o_{\text{max} } > o_{\text{p}} ,$$

(13)

$$\tau^{\text{coh}} = \left\{ { - \sigma^{\text{coh}} \tan (\phi ) + f(D_{\text{max} } )c} \right\}\frac{\left| s \right|}{{s_{\text{max} } }}{\text{ if }}\left| s \right| < s_{\text{max} } {\text{ and s}}_{\text{max} } > s_{\text{p}} .$$

(14)

In each CE6, the computed σ^coh and τ^coh are converted to the equivalent nodal force f_coh using a 3-point or 7-point Gaussian integration scheme depending on the required precision of the simulation. When either o_t or s_t is achieved in a CE6, the CE6 is deactivated, and its surfaces are considered as new macroscopic fracture surfaces that are subjected to contact processes.

The contact processes between the material surfaces, including the new macroscopic fractures created by the separation of each CE6, are modelled by the penalty method (Munjiza 2004); a complete and excellent explanation of the method is given in the literature (Munjiza 2004). As a brief explanation, when any two TET4s subjected to contact detection (see Sect. 2.2 for the implementation of contact detection in the framework of GPGPU) are found to overlap each other, the contact potential due to the overlapping of the two TET4s (i.e., the contacting couple) is exactly computed. The normal contact force, f_{con_n}, is then computed for each contacting couple, which acts normally to the contact surface and is proportional to the contact potential. The proportional factor is called the normal “contact penalty”, P_{n_con}. After the normal contact force, f_{con_n}, and its acting point are obtained, the nominal normal overlap, o_n, and relative displacement vector, Δu_slide, at the acting point of f_{con_n} are readily computed. The contact damping model proposed by An and Tannant (2007) (Fig. 2) can also be applied if the role of contact damping is very important. When this scheme is applied, the normal contact force, f_{con_n}, described above is regarded as a trial contact force, (f_{con_n})^try, and a trial contact stress (σ_{con_n})^try is then computed by dividing (f_{con_n})^try by the contact area, A_con. Equation (15) is then used to determine the contact stress σ_{con_n}:

$$\sigma_{{{\text{con\_n}}}} = \left\{ {\begin{array}{*{20}c} {{\text{Minimum}}\left( {\left( {\sigma_{{{\text{con\_n}}}} } \right)^{\text{try}} ,T} \right){\text{ during the increase of }}o_{\text{n}} ({\text{Loading}})} \\ {T\left( {o_{\text{n}} /o_{n\_\hbox{max} } } \right)^{b} {\text{during the decrease of }}o_{\text{n}} ({\text{Unloading}})} \\ \end{array} ,} \right.$$

(15)

where T is the transition force, b is the exponent, and o_{n_max} is the maximum value of o_n experienced during the loading process at the contact. T limits σ_{con_n} and defines the transition between a linearly elastic stress–displacement relationship and a ‘recoverable’ displacement at a constant contact stress. The values of T may be related to the physical properties of rocks, such as the uniaxial compressive strength. The exponent b adjusts the power of the damping function that is applied to the rebound or extension phase of the contact. The value of the exponent has an effect on the energy loss during an impact event. A similar contact damping model is implemented in the 2D Y-Geo code in the framework of the FDEM, in which only b is considered (Mahabadi et al. 2012). After σ_{con_n} is computed using Eq. (15), it is converted to f_{con_n} (= A_con × σ_{con_n}). The verification of the implemented contact damping is discussed in Sect. 3.1. After f_{con_n} is determined, the magnitude of the tangential contact force vector, |f_{con_tan}|, is computed according to the classical Coulomb friction law. The |f_{con_tan}| is computed based on Eq. (16):

$$\left\| {{\mathbf{f}}_{{{\text{con\_tan}}}} } \right\| = \mu_{\text{fric}} f_{{{\text{con\_n}}}} ,$$

(16)

where μ_fric is the friction coefficient between the contact surfaces. The tangential contact force, f_{con_tan}, is applied parallel to the contact surface in the opposite direction to Δu_slide. The verification of the implementation of the contact friction, which is important in any simulation of fracturing due to quasi-static loading, is discussed in Sect. 3.1. In each contacting couple, the contact force is converted to the equivalent nodal force f_con (Munjiza 2004).

Fig. 2

[modified after An and Tannant (2007)]

Elastic–inelastic power function model for contact damping

By computing the nodal forces described above, the following equation of motion, Eq. (17), is obtained and solved in the framework of the explicit FEM (Munjiza 2004):

$${\mathbf{M}}\frac{{\partial^{2} {\mathbf{u}}}}{{\partial t^{2} }} = {\mathbf{f}}_{\text{ext}} + {\mathbf{f}}_{\text{int}} + {\mathbf{f}}_{\text{coh}} + {\mathbf{f}}_{\text{con}}$$

(17)

where M is a lumped nodal mass computed from the initial TET4 volume and element mass density ρ, u is the nodal displacement, and f_ext is the nodal force corresponding to the external load. The central difference scheme is employed for the explicit time integration to solve Eq. (17). A careful selection of the time step, Δt, is necessary to avoid numerical instability and spurious fracture modes. An excellent explanation of the reasonable selection of Δt in the ordinary FDEM can be found in Guo (2014).

2.2 GPGPU-Based Parallelization of 3D Y-HFDEM IDE by CUDA C/C++

To speed up the simulation process of the 3D Y-HFDEM IDE code, a parallel computation scheme based on the NVIDIA^® GPGPU accelerator is incorporated. In our case, the computation on the GPGPU device is controlled through NVIDIA’s CUDA C/C++ (NVIDIA 2018), which is essentially an ordinary C/C++ programming language with several extensions that make it possible to leverage the power of the GPGPU in the computations. The CUDA programming model uses abstractions of “threads”, “blocks” and “grids” (Fig. 3). A greater degree of parallelism occurs within the GPGPU device itself. Functions, also known as “kernels”, are launched on the GPGPU device and are executed by many “threads” in parallel. A “thread” is just an execution of a “kernel” with a given “thread index” within a particular “block”. As shown in Fig. 3, a “block” is a group of threads, and a unique “block index” is given to each “block”. The “block index” and “thread index” enable each thread to use its unique “index” to globally access elements in the GPGPU data array such that the collection of all threads processes the entire data set in massively parallel manner. The “grid” is just a group of “blocks”. Only a single “grid” system is used in this study. The concept of a GPGPU cluster with a massive number of GPGPU accelerators is also possible, although this is beyond the scope of this paper. The “blocks” can execute concurrently or serially depending on the number of streaming processors available in a GPGPU accelerator. Synchronization between “threads” within the same “block” is possible, but no synchronization is possible between the “blocks”. In each “thread” level, the corresponding code that the “threads” execute is very similar to the CPU-based sequential code (see Fukuda et al. 2019), which is one of the advantages of the application of CUDA C/C++. For example, the Quadro GP100 accelerator (in Pascal generation) used in this paper contains 56 and 3584 streaming processors and CUDA cores (NVIDIA 2018), respectively. Higher computational performance of the GPGPU-parallelized code running on the same GPU accelerator can be achieved than that of ordinary CPU-based sequential codes. The number of “blocks” per “grid” (N_BpG) and the number of “threads” per “block” (N_TpB) can be changed to speed up the GPGPU (Fig. 3). The current version of 3D Y-HFDEM IDE normally sets N_TpB to either 256 or 512, and N_BpG is automatically computed by dividing the total number of threads (N_thread) in each “kernel” by N_TpB, in which an additional block is needed if N_thread/N_TpB is not a multiple of N_TpB. The value of N_thread is set to be equal to the total number of TET4s, CE6s, contact couples or nodes depending on the purpose of each “kernel”.

Fig. 3

Concept of the CUDA programming model using the abstractions of “threads”, “blocks” and “grid”

In the GPGPU implementation of 3D Y-HFDEM IDE, the computations for each TET4 (f_int and M), CE6 (f_coh), contact couple (f_con) or nodal equation of motion (Eq. (17)) are assigned to each GPGPU “kernel” as shown in Fig. 4 and processed in a massively parallel manner. The CUDA code used in each “kernel” is similar to the functions/subroutines in CPU-based sequential codes, which also holds true for the computations shown in Fig. 4. Thus, most parts of the original sequential CPU-based code can be used with minimum modifications. For the computation of the contact force, f_con, “TET4 to TET4 (TtoT)” contact interaction kinematics are used in the earliest versions of the Y3D code (Munjiza 2004). This TtoT approach exactly considers the geometries of both the contactor and target TET4s, and the integration of the contact force distributed along the surfaces of the TET4s is performed analytically. Because this approach integrates the contact forces exactly, it is precise although quite time consuming. As pointed out in the literature (Lei et al. 2014), the contact interaction in 3D can be further simplified by “TET4 to point (TtoP)” contact interaction kinematics, which make the implementation simpler and more time efficient. However, the precision of the computed contact force using the TtoP approach is less accurate unless a sufficient number of target points per TET4 are used. Thus, the TtoT approach is intentionally applied for all of the numerical simulations in this paper instead of the TtoP approach to ensure the precision of the computed contact force.

Fig. 4

Concept of massively parallel computation for each CUDA “kernel” for particular computational purposes

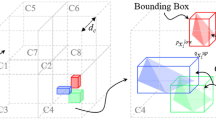
A flowchart of the GPGPU-based 3D Y-HFDEM IDE is shown in Fig. 5. One of the challenging tasks in Fig. 5 is the implementation of contact detection to identify each contacting couple only through the GPGPU without a sequential computational procedure. For sequential CPU implementation, powerful and efficient contact detection algorithms, such as No Binary Search and Munjiza–Rougier contact detection algorithms, have been proposed (Munjiza 2004; Munjiza et al. 2011), and these can achieve the fastest (i.e., linear) neighbor searches with the computational complexity of O(N), in which N is the number of elements and the required computation for the contact detection is proportional to the number of TET4 candidates subjected to contact detection. However, these contact detection algorithms are not straightforward to be implemented in the GPGPU-based code. In the GPGPU-based 3D Y-HFDEM IDE code, because the FDEM modelling requires a fine mesh that often consists of TET4s with similar sizes, the following contact detection algorithm is implemented. In this algorithm, the analysis domain comprising a massive number of TET4s is subdivided into multiple equal-sized (n_x, n_y, n_z) cubic sub-cells (Fig. 6) along each direction, so the largest TET4 in the analysis domain is completely included in a single sub-cell. In this way, the center point of every TET4 can always belong to a unique sub-cell. Using integer coordinates (ix, iy, iz) (ix  = 0,…, n_x−1, iy  = 0,…, n_y−1, iz  = 0,…, n_z−1) for the location of each sub-cell (Fig. 6), unique hash values, h (= iz × n_x + i_yx n_y +  iy × n_x +  ix), are assigned to each sub-cell. The subsequent contact detection procedure is explained using a simplified example, as shown in Fig. 7, where ten TET4 candidates with similar sizes are subjected to contact detection. First, all of the TET4s are mapped into integer coordinates (ix  = 0, 1 and 2, iy  = 0, 1 and 2, and iz  = 0, 1 and 2) with n_x =  n_y =  n_z = 3 along with the computation of the hash values in each sub-cell. In this way, the list L-1 is readily constructed using the massively parallel computation based on the similar concept shown in Fig. 4 by assigning the computation of each TET4 to each CUDA “thread”. The IDs of the TET4s in the list L-1 in Fig. 7 are then sorted from the smallest to largest according to the hash values h as keys, which generates the list L-2 in Fig. 7. The radix sorting algorithm optimized for CUDA (Satish et al. 2009) and implemented in the open-source “thrust” library is used for the key-sorting by the hash values; therefore, this procedure can also be processed in a massively parallel manner. Utilizing the list L-2 and the GPGPU device’s shared memory (NVIDIA 2018), the list L-3 in Fig. 7 is further constructed in a GPGPU “kernel”, which makes it possible to identify the first and last indices for the particular hash value in the list L-2. Therefore, with the lists L-2 and L-3, the IDs of all the TET4s included in a particular sub-cell with its unique hash value are readily available. Finally, for a particular TET4 with its sub-cell position, it is sufficient to only search its adjacent 27 sub-cells [or 14 sub-cells using the concept of a contact mask (Munjiza 2004)] for contact detection, which makes it possible to achieve efficient contact detection using only the GPGPU device and without a sequential CPU procedure. When the sizes of the TET4s are completely different, the size of the cubic sub-cell is very large, resulting in very inefficient contact detection; thus, other parallel neighbor search schemes, such as the Barnes–Hut tree algorithm (Burtscher and Pingali 2011), should be used for efficient contact detection. The contact detection algorithm used in the GPGPU-based 3D Y-HFDEM IDE is similar to that applied by Lisjak et al. (2018) in terms of the applied hash-based contact detection algorithm. However, Lisjak et al. (2018) further incorporated the hyperplane separation theorem as the second step of contact detection. Unfortunately, Lisjak et al. (2018) did not discuss the algorithm used to generate the hash-table in the framework of OpenCL, which is also one of very important aspects of the performance gain, and the effect of introducing the second step. Furthermore, no discussion was given for the sped up performance of Irazu for the 3D simulation. Instead, the computing performance of our GPGPU-parallelized 3D Y-HFDEM IDE is discussed in Sect. 3.4 of this study proving that the GPGPU-parallelized 3D Y-HFDEM IDE is very efficient in terms of contact detection and has the computational complexity of O(N).

Fig. 5

Flowchart of the GPGPU-parallelized 3D Y-HFDEM IDE code

Fig. 6

Concept of hash values assigned to each cubic sub-cell (left) and a TET4 included in a particular sub-cell (right)

Fig. 7

GPGPU-based contact detection algorithm implemented in the GPGPU-parallelized 3D Y-HFDEM IDE code

Therefore, the GPGPU-parallelized 3D Y-HFDEM IDE code can run in a completely parallel manner on the GPGPU device, and no sequential processing is necessary, except for the input and output procedures. The data transfer from the GPGPU device to the host computer is always necessary to output the analysis results, the time of which is often negligible compared to the entire simulation time for most Y-HFDEM IDE simulations. The results can be visualized in either OpenGL implemented in the 3D Y-HFDEM IDE code (Liu et al. 2015) or in the open-source visualization software Paraview (Ayachit 2015).

Finally, it should be noted that an efficient contact calculation activation approach has been applied in some publications about the FDEM in the framework of ICZM [e.g., Section 2.3.3.2 along with Fig. 2.14 in Guo (2014)]. In this approach, only the TET4s in the vicinity of newly broken/failed CE6s become contact candidates and are added to the contact detection list. One advantage of this approach is that the contact detection and contact force calculations are necessary only for the initial material surfaces by the time when the broken/failed CE6s are generated; thus, dramatic savings in the computational time for the contact detection are possible. This approach is called an efficient contact detection activation (ECDA) approach hereafter. However, in the ICZM-based FDEM simulation of hard rocks under compressive loading conditions, most of the TET4s can overlap during the progress of compression even before the generation of broken/failed CE6s. In this case, if the amount of overlap is not negligible when broken CE6s are generated, this ECDA approach generally results in the sudden application of the contact force like a step-function, which can easily cause numerical instability and result in unrealistic/spurious fragmentation. To avoid the numerical instability and spurious fracturing modes, an infinitesimally small Δt must be used, which makes the simulation intractable. One way to avoid this instability is to monitor the overlapping of the CE6s. If a significant overlap is detected in a CE6, the TET4s in the vicinity of the CE6 are immediately considered as new candidates for the contact detection although the threshold of this “significant overlap” is problem-dependent. Another simple remedy is to add all of the TET4s as contact candidates. This approach is called the brute-force contact detection activation approach. Although it is too time consuming, the brute-force contact detection activation approach can work as a remedy for a wide range of rock conditions, including very hard rock, which is used for the 3D dynamic BTS modelling of marble with the split Hopkinson pressure bar (SHPB) testing system. It should be noted that all FDEM simulations must deal with this problem carefully to avoid inaccurate simulation results, although it has not been reported in the literature. Otherwise the obtained fracture patterns may be spurious.

3 Numerical Tests and Code Validation

This section aims to verify and validate the GPGPU-parallelized 3D Y-HFDEM IDE code by conducting several numerical simulations. All of the numerical simulations in this section are conducted using the GPGPU-based code.

3.1 Verifications of Contact Damping and Contact Friction

To assess the accuracy of the contact damping model implemented in Sect. 2.1, a simple impact test is modelled (Fig. 8a) using the GPGPU-parallelized 3D Y-HFDEM IDE. The model is the extension of the 2D model reported by Mahabadi et al. (2012) to 3D, and the obtained results are discussed. The model consists of a spherical elastic body with a radius of 0.1 m impacting a fixed rigid surface vertically. The elastic body is not allowed to fracture in this model. Following the study (Mahabadi et al. 2012), gravitational acceleration is neglected, the density of the elastic body is 2700 kg/m³, and the initial total kinetic energy of the elastic body, $E_{\text{kin}}^{0}$, before the impact event is 565.5 J. Because the Lame constants λ and µ for the elastic body are not available in that study (Mahabadi et al. 2012), it is simply assumed that λ = µ = 5.0 GPa and that the viscous damping coefficient η = 0 for internal viscous damping. Contact friction is also neglected. Thus, energy dissipation is only due to the contact damping to make it simple to discuss the effect of the contact damping. Parametric analyses are conducted by changing the exponent b, the transition force T in Eq. (15) and the normal contact penalty P_{con_n} between the elastic body and the rigid surface. The normalized total kinetic energy of the elastic body by $E_{\text{kin}}^{0}$ as a function of time is monitored during the parametric analyses.

Fig. 8

Contact damping verification: a 3D model configuration [modified after Mahabadi et al. (2012)], b comparison between numerical and theoretical results

Figure 8b compares five cases with b values equal to 1, 2, 5, 20, and 30 when T = ∞ (very large value, i.e., 1.0e+30 Pa) and P_{con_n} = 0.1 GPa. The case with b = 1 corresponds to an elastic contact; thus, no energy dissipation occurs due to the contact, although a very small decrease in the kinetic energy actually occurs after the impact because a small amount of the kinetic energy is converted to the strain energy of the elastic body. As the value of b increases, the amount of kinetic energy dissipates from the system increases. This behavior is similar to that reported in the literature (Mahabadi et al. 2012) using a sequential 2D FDEM. The cases with different values of P_{con_n} (= 0.1 GPa and 10 GPa) but constant b = 2 and T = ∞ show that the same b does not result in the same energy dissipation when P_{con_n} is different. This is a reasonable outcome because the maximum value of the nominal normal overlap o_{n_max} in Eq. (15) during the impact event changes for different values of P_{con_n} (Munjiza 2004). However, this important fact has not been reported in the literature (Mahabadi et al. 2012). Likewise, the two cases with different values of T (= ∞ and 1 MPa) but constant b = 2 and P_{con_n} = 0.1 GPa show different amounts of energy dissipation, which can be also explained by the change in o_{n_max}. These expected results verify that the contact detection and computation of f_con are properly processed in the GPGPU-based code, although this paper does not consider contact damping in the following numerical simulations because the calibration of these parameters against rock fall experiments is beyond the scope of this paper.

To assess the accuracy of the contact friction model implemented in Sect. 2.1, a simple sliding test, which was originally suggested by Xiang et al. (2009) as a 2D problem, is modelled as a 3D problem, and the obtained results are compared with those from theoretical analyses. The model consists of a simple cube sliding along a fixed plane with a friction coefficient of μ_fric = 0.5. The cube is assigned an initial velocity, which varies from 1 m/s to 6 m/s. With each initial velocity, the cube slows and stops due to the friction between the sliding cube and the rigid base. Theoretically, the sliding distance can be defined as a function of the initial velocity (v_i), gravitational acceleration (g) and the friction coefficient (μ_fric) through Eq. (18).

$$L = v_{\text{i}}^{2} /\left( {2\mu_{\text{fric}} g} \right).$$

(18)

Figure 9 shows an excellent agreement between the numerical simulation and the theoretical solution from Eq. (18), which validates the accuracy of the implemented contact friction model.

Fig. 9

Contact friction verification: a 3D model configuration [modified after Xiang et al. (2009)], b comparison between numerical and theoretical results

3.2 3D FDEM Modelling of the Failure Process of Rock Under Quasi-Static Loading Conditions

In this subsection, two standard rock mechanics laboratory tests, the UCS test and BTS test, of a relatively homogeneous limestone are modelled to investigate the capabilities of the GPGPU-parallelized 3D Y-HFDEM IDE for simulating the fracturing process and associated failure mechanism of the rock under quasi-static loading conditions.

The numerical models for the 3D FDEM simulations of the UCS and BTS tests are shown in Fig. 10, in which the diameter of both specimens is 51.7 mm, and the height and thickness of the specimens are 129.5 mm and 25.95 mm, respectively. The rock specimens are placed between two moving rigid loading platens. Flat rigid loading platens are used in the UCS model, whereas curved rigid loading platens are used in the BTS model, whose curvature is 1.5 times the diameter of the BTS disk, as suggested by the International Society for Rock Mechanics (ISRM). It is important to note that in the FDEM simulation with the CZM, it is essential to use an unstructured mesh to obtain reasonable rock fracture patterns because the FDEM only allows the fractures to initiate and propagate along the boundaries of the solid elements. Moreover, the use of a very fine mesh is the key to reducing the mesh dependency of the crack propagation paths, which is why most 2D FDEM simulations in previous studies used very fine meshes. However, if very fine meshes are used in 3D models, the number of TET4s and CE6s can easily exceed several million, which makes the 3D modelling become intractable in terms of memory limitations and the simulation time required for the calibration process using FDEM codes parallelized by a single GPGPU accelerator. Thus, fine meshes comparable to those investigated by Lisjak et al. (2018) are used in the 3D FDEM models. Accordingly, the average edge length of the TET4s in both models is set to 1.5 mm, and the UCS and BTS models contain 695,428 TET4s and 1,298,343 CE6s and 187,852 TET4s and 348,152 CE6s, respectively. According to a recent study on 2D FDEM modelling conducted by Liu and Deng (2019), the effect of the element size can be negligible if there are not less than 27–28 meshes in the length corresponding to the diameter of the specimen and the maximum element size should not be longer than the length of fracture process zone of the CZM. The UCS and BTS models used in this study satisfy these requirements. Based on the review of the effects of the loading rate presented above, a constant velocity of 0.01 m/s is applied on the loading platens to satisfy the quasi-static loading conditions, as suggested by Guo (2014). Moreover, our preliminary sensitivity study of 3D UCS and BTS modellings under various loading rates confirms the quasi-static loading conditions can be achieved with the platen velocity of 0.01 m/s, which further shows little difference can be noticed from 3D UCS modelling even if the platen velocity is increased to 0.05 m/s although slightly higher peak loads and spurious fragmentations around the loading areas are observed from 3D BTS modelling with the platen velocity increasing.

Fig. 10

3D numerical models for analysis of the fracturing process of rock under quasi-static loading. (a) UCS test, (b) BTS test

The physical/mechanical properties of the limestone are obtained from laboratory measurements, which are used to determine the input parameters for the numerical modelling (Table 1). As introduced in Sect. 2, the intact behavior of the numerical model follows Eq. (1), and the elastic parameters are determined in such a way that the elastic region of the stress–strain curve from the 3D FDEM simulation of the UCS test agrees well with that of the laboratory experiment. Our preliminary investigation showed that the experimentally obtained elastic parameters can be directly used as the input parameters if sufficiently large artificial penalty terms of the CE6s are used. The penalty terms for the contacts and CE6s are determined as multiples of the elastic modulus of the rock (i.e., E_rock). The value of the contact penalty (P_{n_con}) is set as 10 E_rock. However, higher values are required for the artificial penalty terms of the CE6s (i.e., 100 E_rock for P_open and P_tan and 1000 E_rock for P_overlap) to allow the artificial increase in the compliance of the bulk rock to become negligible. Because the artificial elastic regime of the CE6 in Eqs. (6)–(8) can also be influenced by the strength parameters, an artificial increase in the bulk compliance of the rock becomes non-negligible if the artificial penalty terms for the CE6s are not set to be sufficiently large. In other words, smaller artificial penalty terms for the CE6s can result in non-negligible changes in the artificial elastic response of the CE6s during the calibration process, in which the strength parameters are also varied. This fact has not been pointed out by any studies of the development and/or application of the FDEM. Then, after setting the penalty terms of the CE6s, the strength parameters (i.e., tensile strength T_{s_rock}, cohesion c_rock and internal friction angle ϕ_rock) and the fracture energies, G_{fI_rock} and G_{fI_rock}, of the numerical model are calibrated by trial and error. To do this, a series of FDEM simulations was conducted to achieve a reasonable match between the numerical and experimental results so the peak load and fracture patterns from the numerical simulations agree well with those from the experiments. The same input parameters shown in Table 1 are also used for the numerical modelling of the BTS test. The friction coefficients, μ_fric, of the contact between the platens and the rock, and, that between rock surfaces generated by broken CE6s are assumed to be 0.1 and 0.5, respectively, as in Mahabadi (2012). The ECDA approach introduced in Sect. 2.2 is used in these simulations because the rock can be considered to be relatively soft, and no spurious modes are observed in this case. The concept of mass scaling (Heinze et al. 2016) with the mass-scaling factor = 5 is applied to increase Δt in such a way that the quasi-static loading condition is still satisfied. Thus, Δt = 4.5 and 9 ns are used for the simulations of the BTS and UCS tests, respectively. Further details about the mass-scaling concept can be found in the literature (Heinze et al. 2016). The critical damping scheme [η = η_crit = 2 h√(ρE) in Eq. (1)] is also used in all of the FDEM simulations in this section. Hereafter, compressive stresses are considered negative (cold colors), whereas tensile stresses are regarded as positive (warm colors).

Table 1 Physical–mechanical properties of rock and computational parameters used in the FDEM simulations of the UCS and BTS tests (Sect. 3.2)

Figure 11a–c shows the modelled 3D progressive rock failure process in terms of the distributions of the minor principal (mostly compressive) stress (upper row) and the damage variable [i.e., D in Eq. (9); lower row] at different loading stages (points A, B and C in Fig. 11d) in the FDEM simulation of the UCS test. Figure 11d shows the obtained axial stress versus axial strain curve. Figure 11a shows the stress and damage distribution in the sample at the stage before the onset of nonlinearity in the axial stress versus axial strain curve (point A in Fig. 11d). As the loading displacement continues, the growth of unstable microscopic cracks commences and continues until the peak stress of the stress–strain curve is reached (point B in Fig. 11d). Subsequently, the microscopic cracks coalesce to form macroscopic cracks, which results in the loss of bearing capacity of the bulk rock, and the axial stress begins to decrease with increasing strain. Finally, the formed macroscopic cracks propagate further, resulting in the complete loss of the bearing capacity of the rock (point C in Fig. 11d). Figure 12a compares the final fracture patterns obtained from the FDEM simulation and the laboratory experiment. The resulting fracture patterns (Fig. 12a) and the peak loads (Fig. 11d) from the numerical simulation and laboratory experiment are in good agreement. Although the formation of the shearing planes is evident in Fig. 12b, it must be noted that mixed-mode I–II fractures are the dominant mechanism of rock fracturing, as shown in Fig. 12c, which will be explained in detail later. Therefore, the obtained results demonstrate that the developed GPGPU-parallelized 3D Y-HFDEM IDE is able to reasonably model the fracturing process of rock in UCS tests.

Fig. 11

3D modelling of the UCS test under quasi-static loading. a Initiation and propagation of microscopic cracks before the peak stress, b unstable crack propagation at the peak stress, c post-failure fracture pattern, and d axial stress versus axial strain curve

Fig. 12

Comparison of the final rock fracture patterns in the UCS test from the numerical simulation and experiment: a comparison of the final fracture patterns, b final fracture pattern with pure mode II damages highlighted, c final fracture pattern with mixed-mode I–II damages highlighted

Figure 13a–c illustrates the modelled 3D progressive rock failure process in terms of the distributions of the horizontal stress, σ_xx, (upper row) and the damage variable D in Eq. (9) (lower row) at different stages (points A, B, and C in Fig. 13d) in the FDEM simulation of the BTS test. Figure 13d shows the obtained indirect tensile stress versus axial strain curve. As the loading displacement gradually increases, a uniform horizontal (tensile) stress (σ_xx) field gradually builds up around the central line of the rock disk. Figure 13a shows that although some microscopic damage, D < <1, appears in the rock disk near the loading platens due to stress concentrations, there is no macroscopic crack (i.e., CE6s with D = 1). Once the peak indirect tensile strength of the rock (point B in Fig. 13d) is reached, macroscopic cracks form around the central diametrical line of the rock disk due to the coalescence and propagation of microscopic cracks. As shown in Fig. 13b, the macroscopic crack that causes the splitting failure of the rock disk nucleates slightly away from the exact center of the disk. The reason for the nucleation of this vertically off-center macroscopic crack is that the curved loading platens provide a relatively narrow contact strip; accordingly, an off-center horizontal stress concentration first develops within the rock disk, which is consistent with the location of the macroscopic crack nucleation in Fig. 13b. This phenomenon was also addressed by Fairhurst (1964) and Erarslan et al. (2012), who further pointed out that a wider contact strip was required to ensure near-center crack initiation in a BTS test with curved loading platens. Moreover, Li and Wong (2013) conducted strain–stress analyses of a 50-mm-diameter rock disk in BTS tests using FLAC3D and pointed out that the maximum indirect tensile stress and strain were located approximately 5 mm away from the two loading points along the central loading diametrical line of the rock disk. Nearly the same results are observed in Fig. 13b; most importantly, the vertically off-center macroscopic cracks are captured explicitly. Moreover, following Lisjak et al. (2018), Fig. 13e compares the simulated stress distributions along the diameter of the rock disk in the middle and on the surface (i.e., lines AB and CD, respectively) with the analytical solution of Hondros (1959), where y and r represent the vertical distance from the center and the radius of the rock disk, respectively. It can be seen from Fig. 13e that the stress distribution on the surface of the rock disk differs from that in the middle plane, which is consistent with Hondros’ solution based on the plane-strain assumption. In other words, Hondros’ solution is invalid for the stress distributions on the surface of the rock disk, especially for the tensile stress concentrations in the regions near the loading platens, which are clearly depicted in Fig. 13e. The local tensile stress concentrations in the regions near the loading platens on the surface of the rock disk explain the nucleation of the off-center macroscopic cracks modelled in Fig. 13b, which will not be possible if 2D plane-strain modelling is conducted. As the loading platens continue to move toward each other, the resultant macroscopic cracks propagate and coalesce to split the rock disk into two halves (Fig. 13c), and the stress–strain curve decreases toward zero during the post-peak stage (i.e., line BC in Fig. 13d). These results show that mixed-mode I–II failure is the dominant mechanism during the nucleation, propagation and coalescence of the splitting macroscopic cracks (Fig. 14a), which is due to the unstructured mesh used in the FDEM modelling. To clarify this point, Fig. 14b shows the modelled failure pattern of the rock disk using the FDEM simulation with a structured mesh, in which the loading diametrical line aligns with the boundaries of the TET4 elemental mesh. The splitting fracture forms exactly along the loading diametrical line, and the mode I failure is the only failure mechanism. Figure 14c and d show the topological relationships between the horizontal indirect tensile stress (blue arrows in the x direction) and the TET4s in the cases of the unstructured and structured meshes used in Fig. 14a and b, respectively. In Fig. 14d, the normal directions of the planes A and A′ of the CE6 located between the two TET4s exactly aligns with the direction of the indirect tensile stress (i.e., the x direction). Therefore, pure mode I cracks preferably develop along the CE6s on the loading diametrical line in terms of the most efficient energy release due to fracturing. On the other hand, when the unstructured mesh in Fig. 14a is used, few CE6s have planes exactly on the loading diametrical line, as illustrated in Fig. 14c, in which two CE6s (i.e., planes A–A′ and B–B′) contributing to the fracturing process are depicted, and none of their normal directions are aligned with that of the indirect tensile stress (blue arrows in the x direction). In this case, it is obvious that a pure mode I crack cannot form due to the topological restriction, and a combination of mode I (opening) and mode II (sliding) cracks can always form resulting in a macroscopic fracture. This is why mixed-mode I–II fracturing is the main failure mechanism in the FDEM simulations of the BTS tests with unstructured meshes. Tijssens et al. (2000) conducted a comprehensive mesh sensitivity analysis for the CZM and concluded that the fractures tended to propagate along dominant directions of local mesh alignment. Guo (2014) further commented that unstructured meshes should be used in the numerical simulation using the CZM to reduce mesh dependency but fracture paths were still dependent on local mesh orientation in the unstructured meshes. Accordingly, when the CZM is applied to model material failure, it is unrealistic to pursue a pure mode I splitting fracture in the simulation of the BTS test with an unstructured mesh regardless of the numerical approach and 2D/3D modelling. In this sense, any intentional reduction of the mode I fracture energy G_{fI_rock} and tensile strength T_{s_rock} to capture the unreasonable pure mode I fracture pattern prevalent in studies of the FDEM should be considered a manipulation of the input parameters. The same explanation is valid for the dominant mixed-mode I–II failures along the macroscopic shear fracture plane modelled in the UCS test. The boundaries of the TET4s will not exactly align with the macroscopic shear stress direction at each location; thus, mixed-mode I–II failure along the macroscopic shear fracture plane, rather than pure mode II failure, is the natural consequence.

Fig. 13

3D simulation of the fracturing process of rock in the BTS test under quasi-static loading: a distributions of the horizontal stress and microscopic damage before the peak stress, b distributions of the horizontal stress, microscopic damage and macroscopic cracks at the peak stress, c distributions of the horizontal stress and macroscopic fracture pattern in the post-failure stage, d Brazilian indirect tensile stress versus axial strain curve and e comparison between the simulated stress distributions and those from Hondros’ solution along the loading diametrical line in the middle plane and on the surface of the disk

Fig. 14

Modelled fracture patterns of rock in the BTS tests with unstructured and structured meshes. a Dominant mixed-mode I–II fractures in the BTS test with an unstructured mesh, b dominant pure-mode I fracture in the BTS test with a structured mesh, c schematic sketch of the tensile fracturing mechanism in a structured mesh, d schematic sketch of the tensile fracturing mechanism in an unstructured mesh

3.3 Full 3D Modelling of the Fracturing Process of Rock Under Dynamic Loads in SHPB Tests

In this subsection, the GPGPU-parallelized Y-HFDEM IDE is applied to model the dynamic fracturing of Fangshan marble, which is much more isotropic and homogeneous than granite, in dynamic BTS tests while considering the entire SHPB testing system.

The 4th and 5th authors of this paper conducted dynamic BTS tests of Fangshan marble with a SHPB apparatus (Zhang and Zhao 2013). The marble consists of dolomite (98%) and quartz (2%), and the size of the minerals ranges from 10 to 200 μm with an average dolomite size of 100 μm and an average quartz size of 200 μm (Zhang and Zhao 2013). The marble can be considered as a homogeneous and isotropic rock, which is ideal to avoid the complexity intrinsic to highly anisotropic rocks such as granite. The detailed procedure of the dynamic BTS test can be found in the literature (Zhang and Zhao 2013), and the test is briefly summarized here. As illustrated in Fig. 15a, a metal projectile called a striker is first accelerated by a gas gun, and the striker impacts one end of a long cylindrical metal bar called an incident bar (IB). Upon the impact of the striker on the IB, a dynamic compressive strain wave (ε_inci) is induced in the IB. The ε_inci propagates toward the other end of the IB, on which the target marble disk is placed. When the ε_inci arrives at the interface between the IB and the marble disk, some portion is reflected as a tensile strain wave (ε_refl), and remaining portion is transmitted into the marble disk as a compressive strain wave (ε_{tans_rock}). The ε_{tans_rock} then propagates toward the interface between the marble disk and one end of another long cylindrical metal bar called a transmission bar (TB). When the ε_{tans_rock} arrives at the interface, the marble disk is subjected to dynamic loading (i.e., compressed by the IB and the TB). In addition, a compressive strain wave (ε_tans) generated in the TB propagates toward the other end of the TB. The diameter and thickness of the marble disk used in the experiment were 50 mm and 20 mm, respectively. The lengths of the IB and the TB were 2 m and 1.5 m, respectively, and the diameter of both the IB and the TB was 50 mm. Strain gauges are attached on the surfaces of the IB and TB at 1 m from the interfaces between the marble disk and each bar to measure the time history of the axial strain in the IB (to measure ε_inci and ε_refl) and the TB (to measure ε_trans). Assuming one-dimensional (1D) stress wave propagation in each bar without wave attenuation, the axial stresses on the metal bars (i.e., σ_inci, σ_refl and σ_tans) are calculated by multiplication of the measured axial strains (ε_inci, ε_refl and ε_trans) by the Young’s modulus of each bar. In practice, the axial compressive force f_IB in the IB is calculated from the superposition of the wave shapes corresponding to σ_inci and σ_refl, whereas the axial compressive force f_TB in the TB is directly calculated from σ_tans (Fig. 15b). Thus, the axial compressive forces f_IB and f_TB can be obtained by multiplication of (σ_inci–σ_refl) and σ_tans by the cross-sectional areas of each bar. By ensuring that the time histories of the axial compressive forces f_IB and f_TB are nearly equal up to the peak, the dynamic indirect tensile stress can be defined at the center of the marble disk using the theory applied to the BTS test due to quasi-static loading conditions. Satisfying these conditions is equivalent to achieving dynamic stress equilibrium in the marble disk. The experimental results in Fig. 15b satisfy the dynamic stress equilibrium state, and the corresponding loading rate is approximately 830 GPa/s (Zhang and Zhao 2013). The peak value of the dynamic indirect tensile stress is called the dynamic indirect tensile strength. Due to this dynamic indirect tensile stress, the marble disk is dynamically split into two halves due to the formation of blocky fragments near the diametrical center line and numerous shear fractures near the impact region by the IB and the TB. The dynamic indirect tensile strength calculated under these conditions was 32 MPa, which was significantly higher than the quasi-static indirect tensile strength of 9.5 MPa (Zhang and Zhao 2013). The fracture pattern obtained after the test is shown in Fig. 15c. This paper attempts to model the test condition.

Fig. 15

Overview of the SHPB-based dynamic BTS test simulated by the GPGPU-parallelized 3D Y-HFDEM IDE code. a Configuration of the SHPB system [after Fig. 3 in Zhang and Zhao (2013) with minor additions], b achievement of dynamic stress equilibrium between the axial forces in the IB and the TB [after Fig. 11d in Zhang and Zhao (2013) with minor additions] and c failure patterns of the marble specimen at a dynamic loading rate of 830 GPa/s [after Fig. 12b in Zhang and Zhao (2013)]

Figure 16 shows the 3D FDEM numerical model for the dynamic BTS test of the marble with the entire SHPB testing apparatus modelled explicitly, which consists of 647,456 nodes, 179,022 TET4s and 314,689 CE6s. The average edge length of the mesh for the rock disk is 1.3 mm. The experimental evaluation by Brooks et al. (2012) indicates that the sizes of the FPZs for Carrara marble (typical grain size 300 μm) and Danby marble (typical grain size 520 μm) are approximately 2–3 mm and 6 mm, respectively, based on nanomechanical and environmental scanning electron microscopic observations. In other words, the size of the FPZ is correlated well with the typical grain size. Thus, it can be estimated that the FPZ size of Fangshan marble is on the order of 1 mm because the grain size of the dominant mineral (i.e., dolomite) is approximately 100 μm, as described above. Thus, the FDEM mesh with an average edge length of 1.3 mm used to simulate the Fangshan marble should be fine. Moreover, it should be noted that this mesh is finer than the 90,000 TET4s used by Rougier et al. (2014) in a 3D numerical simulation of SHPB-based dynamic BTS tests, and the size of the rock disk is similar. In the model, the striker is not explicitly modelled, and the prescribed velocity corresponding to the impact of the striker is instead applied to the nodes on the left end of the IB (Fig. 16). Once the prescribed velocity reaches zero after the peak, the corresponding nodes are considered to be free nodes; otherwise, an unrealistic stress wave is generated in the IB. The shape of the prescribed velocity profile is determined by the time history of the measured axial strain profile, ε_inci, of the strain gauge on the IB. Based on the measured density (7697 kg/m³) and dilatational wave speed (5600 m/s) of the SHPB bars, the dynamic Young’s modulus used for the simulation is determined assuming that 1D stress wave theory (i.e., zero Poisson’s ratio) is approximately applicable for stress propagation in the IB and the TB. This assumption should be acceptable to the first approximation; otherwise, all of the previous publications on dynamic rock experiments using the SHPB lose their meanings. For the elastic parameters of the marble, homogeneous and isotropic elasticity is assumed in Eq. (2); therefore, the effective elastic stiffness C_IJKL in Eq. (2) is merely given by the Lame constants λ and μ. The measured wave speeds of the dilatational wave (6000 m/s) and shear wave (2800 m/s) of the marble along with its measured mass density (2800 kg/m³) are used to determine λ and μ. Thus, the approach for the determination of the elastodynamic parameters is clearly different from that used by Mahabadi et al. (2010) and Rougier et al. (2014), who used the Young’s modulus and Poisson’s ratio of rock obtained from the quasi-static tests reported by Iqbal and Mohanty (2006) and Broome et al. (2012), respectively, as the input parameters for their FDEM simulations. In the case of dynamic simulations, the intact stress wave and its wave speed are the most important, and it must be emphasized that the dynamic fracturing is just the outcome of the intact stress wave propagation. Thus, the most reasonable approach to determine the input elastic parameters should be based on the measured wave speeds of the target rock instead of quasi-statically obtained elastic parameters, which often result in incorrect wave speeds. In addition, the values of the artificial penalty terms used for the CE6s are not explicitly given in the publications described above. As mentioned in Sects. 2 and 3.2, the artificial penalty terms P_f, P_tan, and P_overlap of the CE6s must be set reasonably high; otherwise, the input elastic properties lose their meaning. Based on a recent study conducted by the authors (Fukuda et al. 2019), the conditions of P_overlap = 100 E_dyn and P_f = P_tan =50 E_dyn (E_dyn is the dynamic Young’s modulus of the marble calculated from the aforementioned measured wave speeds of the marble) are used. The reason for using the smaller penalty terms of the CE6s than those used for the case of quasi-static loading discussed in Sect. 3.2 is that using the high values can cause spurious modes in dynamic fracturing simulations, whereas the adopted penalty values of the CE6s here ensure that the aforementioned measured wave speeds of the marble result in a negligible numerical error. Following Mahabadi (2012), the contact penalty P_{con_n}= 10E_dyn is used for the rock surfaces generated by broken CE6s and the surfaces between rocks and loading platens. The damping factor η in Eq. (3) is assumed to be 10⁴ Pa∙s to filter out waves with excessively high frequencies that result in spurious modes. It should be noted that even η =η_crit does not result in significant damping in the time range of interest in the current dynamic simulation, and the effect of η can be considered as a filtering function of high-frequency noise that results in spurious modes. Similar to Rougier et al. (2014), a dynamic Coulomb type friction law is used for the contact friction. The dynamic friction coefficients μ_{fric_dyn} on the rock surfaces generated by broken CE6s and the surfaces between rocks and loading platens are assumed to be 0.6 and 0.1, respectively, according to Mahabadi et al. (2010) and Rougier et al. (2014).

Fig. 16

3D FDEM model for the SHPB-based dynamic BTS test with velocity boundary conditions applied on the one end of the IB

In the FDEM simulation of dynamic fracturing, the most challenging task is to correctly set the parameters governing the rock fracturing process, and the lack of experimental evidence is still significant, especially for the Mode II parameters. The approach used in some previous studies (Mahabadi et al. 2010; Rougier et al. 2014) for modelling the dynamic fracturing of rock using the FDEM, in which the input parameters such as strengths were obtained from quasi-static tests, should be reviewed carefully. In fact, a significant amount of experimental evidence (e.g., Zhang 2016) clearly shows that with increasing loading rate, both inter-grain fractures (weaker portions of the rock) and intra-grain fractures (stronger portions of the rock) occur, which indicates that the nominal input strengths for the FDEM simulation should be increased. On the other hand, increasing the values of the critical opening and sliding displacements o_t and s_t in Eqs. (11) and (12) too much can result in physically unrealistic situations in which cohesive tractions still act on the macroscopic (i.e., almost visible) fracture surfaces, whereas the CZM is mainly for the modelling of the micro-cracking in the FPZ of rocks. In fact, the experimental evidence reported by Sato and Hashida (2006) showed that o_t is roughly 100 μm in the case of Iidate granite. For marble, the linear elastic fracture mechanics relation G_fI =(K_IC)²/E_static can be used to estimate the value of G_fI to be 26.5 J/m² considering its quasi-static Young’s modulus (85 MPa) and quasi-static mode I fracture toughness K_IC (1.5 MPa∙m^1/2). Hence, with the aforementioned quasi-static tensile strength (9.5 MPa), a rough estimate of o_t in Eq. (11) is 10 µm in the quasi-static loading case. Then, it is simply assumed that the range of o_t is expected to be on the order of 10–100 µm in the calibration. Because no experimental evidence is available for the value of s_t in Eq. (12) to the best of the authors’ knowledge, the relation o_t = s_t is assumed following Rougier et al. (2014). Based on the loading rate independence of φ (e.g., Yao et al. (2017)), the internal friction angle φ is set to 59° from the quasi-static test. Finally, we varied the values of the tensile strength T_s and cohesion c under the conditions of various o_t (= s_t = 10–100 µm) so the values of ε_inci, ε_refl and ε_trans in the SHPB bars obtained from the FDEM simulation reasonably match those in the experiment (Zhang and Zhao 2013). For the initial guesses of T_s and c, we started from T_s = 32 MPa from the dynamic BTS (Zhang and Zhao 2013) and c = 42.5 MPa from the dynamic shear strength (Yao et al. 2017), both of which correspond to a loading rate of 830 GPa/s. Here, the experimental evidence is used, in which the dynamic shear strength shows a similar loading rate dependency to the dynamic BTS (i.e., dynamic shear strength ≈ 0.025 × loading rate × static shear strength (= 21.7 MPa)). By trial and error, we found that the calibrated conditions of T_s = 30 MPa and c  = 65 MPa with o_t = s_t = 10 µm results in a good match, including the obtained fracture pattern between the FDEM simulation and the experiment; therefore, only the simulation results for these conditions are presented. The ECDA approach described in Sect. 2.2 is not used because it can easily result in spurious modes, as shown in the following paragraphs. Thus, the brute-force contact detection activation approach is used instead; i.e., all of the TET4s corresponding to the marble disk are added to the contact list from the beginning of the simulation. In this case, approximately 8,242,000 contact couples (i.e., a tremendous number of contact force calculations) must be processed in each time step due to the GPGPU parallelization.

Figure 17 shows the modelled dynamic fracturing process of Fangshan marble in the SHPB-based dynamic BTS test using the GPGPU-based 3D Y-HFDEM IDE with the calibrated input parameters. The stress wave propagation in the bars is not shown here to save space. In Fig. 17, the spatial distribution of σ_zz (left column), the macroscopic fracture pattern (damage D = 1; middle column) and the spatial distribution of D (right column) in the rock disk are shown, in which t = 0 is set when the non-negligible strain/stress waves in the IB arrive at the interface between the IB and the rock disk. The warmer and colder colors of σ_zz correspond to tensile and compressive stresses, respectively. The impact between the IB and the rock disk results in stress propagation from the IB side of the rock disk toward the TB side (t = 35 μs). After the arrival of the stress wave at the interface between the rock disk and the TB, the dynamic indirect tensile stress field begins to develop due to the dynamically increasing loads from both the IB and TB sides, and the stress field shows approximate symmetries with respect to the y and z directions across the center of the disk (t = 70 μs). It is notable that the micro-cracking is initiated at this stage in the vicinity of the IB and TB. Then, due to the dynamically induced indirect tensile stress field, macroscopic fractures (tension-dominant mode I–II fractures) begin to nucleate away from the center of the disk (i.e., the IB side) and propagate approximately in the y-direction (t = 83 μs). In fact, using the digital image correlation technique, Zhang and Zhao (2013) evaluated the dynamic strain field that developed on one surface of a marble disk, which showed that the large strains (i.e., a macroscopic crack) began to develop not from the exact center of the disk but rather slightly away from the center toward the IB side [see Fig. 11f for the result of the digital image correlation data at 48 μs in Zhang and Zhao (2013)]. The FDEM modelling shows a similar trend to the experimental observations. Local crack branching also occurred during microscopic crack propagation from the IB and TB sides (t = 83 μs) along with the commencement of macroscopic crack propagation from the TB side. It can be seen that the front of the propagating cracks from the IB and TB are far from flat which shows another importance of the 3D modelling. In the 2D dynamic simulation conducted by Mahabadi et al. (2010), Osthus et al. (2018) and Godinez et al. (2018), all the surface waves on the positive and negative x-planes in Fig. 17 cannot be considered, which makes the interpretation of the 2D simulations very difficult. Finally, these microscopic and macroscopic cracks coalesced and formed the resultant splitting macroscopic fracture plane (t = 98 μs). Furthermore, in contrast to the BTS test under quasi-static loading, in which stress can be released through the opening of splitting fractures, the induced stress in the dynamic BTS test cannot be released completely in such a short time due to the high-speed loading by the IB and TB. In addition, the shear-dominant mixed-mode I–II fractures result in the formation of crushed zones near the IB and TB, which contribute to the stress release process. The reason for the formations of shear-dominant mixed-mode I–II fractures in the unstructured mesh was discussed in Sect. 3.2. With the splitting fractures interacting with the crushed zones, a blocky rock fragment is also generated (t = 98 μs), which was not found in the BTS test under quasi-static loading conditions. The comparison of the resultant fracture pattern at t = 98 μs with the experimental pattern in Fig. 15c indicates that the FDEM modelling shows a good correspondence with the experiment in terms of the formation of the splitting central cracks, the crushed zones near the IB and TB and the blocky rock fragments along the centerline.

Fig. 17

3D modelling of the dynamic fracturing process of marble in the SHPB-based dynamic BTS test: distribution of σ_zz (left column), distribution of macroscopic cracks (damage D = 1) (middle column) and distribution of damage D (right column). Note that t = 0 is set when the stress wave in the IB arrives at the interface between the IB and the rock disk

Figures 18a, b compare the time histories of ε_inci and ε_refl in the IB and ε_trans in the TB obtained from the experiment and the calibrated FDEM simulation. Because the momentum bar is not modelled in the FDEM simulation, the profile of ε_trans in the TB is only shown at the time when ε_trans drops to zero after the 1st peak; a comparison between the FDEM simulation and the experiment after this time has no meaning. The calibration and comparison are performed using the axial strains instead of the axial stress/force because the authors have difficulty in interpreting the Young’s modulus used for the conversion from the strain to stress in the IB and TB. In the FDEM, the elastodynamic parameters (i.e., the Lame constants) that satisfy the wave speed of the SHPB bars are used; thus, the stress should be interpreted as the dynamic stress. In contrast, the quasi-statically obtained Young’s moduli of the IB and the TB have conventionally been used for the most SHPB experiments to convert the measured axial strain to the axial stress. However, if we use the quasi-statically obtained Young’s moduli of the IB and the TB for the FDEM simulation, the wave speed in the FDEM simulation becomes incorrect. Therefore, the axial strains in the IB and the TB are used for the calibration. The results show that the FDEM simulation is well calibrated against the measured strain profile, which demonstrates that the modelled results of the SHPB-based dynamic BTS test from the GPGPU-parallelized Y-HFDEM agree well with those from the experiment.

Fig. 18

Comparison between numerically simulated and experimentally measured axial strains (ε_inci, ε_refl and ε_trans) in the IB and the TB

Finally, Fig. 19 shows the results of applying the ECDA approach (Guo 2014) described in Sect. 2.2 to model the SHPB-based dynamic BTS test. In this model, only the TET4s corresponding to the surfaces of the IB and the TB as well as the rock disk surface in the vicinity of the IB and TB are registered as contact candidates at the onset of the FDEM simulation (red regions in Fig. 19a). Then, with the generation of macroscopic cracks, the TET4s in the vicinity of the macroscopic cracks are adaptively registered as contact candidates. This approach is much faster in terms of the total run time compared with the case using the brute-force contact detection activation approach. However, when the same mesh with the same input parameters except for the ECDA approach is applied, the simulation can easily result in spurious modes, as shown in Fig. 19b, in which too many unrealistic fragmentations are generated. Using a smaller time step Δt may solve this problem. However, the authors could not find a time step Δt in which the total run time of the ECDA approach is less than that for the brute-force contact detection activation approach. This spurious mode (i.e., numerical instability) could be due to the use of a very high value of the internal friction angle as well as the target loading rate being very high. In fact, our quasi-static simulation presented in Sect. 3.2 used the ECDA approach, but no unstable results were obtained. Interestingly, this finding has not been pointed out in any previous studies that used the 3D FDEM and can be regarded as the most valuable information. For example, in the case of the FDEM simulation of the “penetration problem”, which is important in impact engineering to understand the dynamic fracturing of rock, the aforementioned spurious mode can easily occur if the ECDA approach is used. One of the most serious problems is that the fragmentation due to penetration always occurs in this kind of simulation; therefore, judicious judgement must be used in evaluating whether the obtained fragmentation is an artificial fracture due to the spurious mode or not. In this sense, the brute-force contact detection activation approach can solve or alleviate the spurious mode.

Fig. 19

Spurious fracture caused when the ECDA approach is used instead of the brute-force contact detection activation approach. a Highlighted contact candidates from the onset of the simulation for the ECDA, b unrealistic fragmentation due to the ECDA approach

3.4 Computing Performance of the GPGPU-Parallelized 3D FDEM

This section discusses the computing performance of the GPGPU-parallelized 3D Y-HFDEM IDE, mainly in terms of its improvement compared with the sequential implementation of the 3D Y-HFDEM IDE and its performance on several GPGPU accelerators. To accomplish this goal, the modelling of the rock failure process in the 3D UCS test, as discussed in Sect. 3.2, is selected as a benchmark because it is a computationally demanding simulation. To make the computation become further intensive, the brute-force contact detection activation approach introduced in Sect. 2.2 is used in the 3D modelling of the UCS test to evaluate the computing performance of the GPGPU-parallelized 3D Y-HFDEM IDE. Moreover, since the performance of GPGPU-parallelized code is significantly dependent on the applied GPGPU accelerators, the GPGPU-parallelized 3D Y-HFDEM IDE is run using several NVIDIA^® GPGPU accelerators, i.e., Quadro GV100, Titan V and Quadro GP100 to investigate its performance. The developed GPGPU-parallelized 3D Y-HFDEM IDE can be run in all these GPGPU accelerators without any modifications. At the same time, an Intel^® Xeon^® Silver 4112 processor (2.60 GHz and 32.0 RAM) is used to run our sequential CPU-based 3D Y-HFDEM IDE. Table 2 shows the number of TET4s, CE4s and nodes, and the initial number of contact couples in each model. It is evident that the mesh discretization with the average element size h_ave = 1.3 mm results in tremendously massive computation. The list of actual runtimes required for 500 calculation time steps is shown at the bottom of Table 2 for several values of h_ave, in the cases of the GPGPU-based code using the Quadro GV100 accelerator and the sequential CPU-based code (i.e. the original Y3D code). The results show that 134,943 s (37.5 h) are required to solve the 500 time steps in the sequential CPU-based code for h_ave = 1.3 mm, which means that solving the problem with this level of fine discretization is too computationally expensive using the sequential code. Figure 20 shows the speed-up times of the GPGPU-parallelized 3D Y-HFDEM IDE relative to the CPU sequential code running on a single thread for the 3D modelling of the UCS test with 695,428 TET4s and 187,852 CE6s. In Fig. 20, the vertical axis shows the quotients of the total run time using each GPGPU accelerator divided by that using the CPU sequential code, which, thus, correspond to the speed-up times of the GPGPU-parallelized 3D Y-HFDEM IDE relative to the CPU sequential code. Clearly, the GPGPU-parallelized 3D Y-HFDEM IDE run on all GPU accelerators has achieved significant speed-up times compared with the CPU sequential code, and the Quadro GV100 accelerator shows the maximum speed-up times of 284, which is even better than the maximum speed-up times of 128.6 achieved by the authors’ GPGPU-parallelized 2D Y-HFDEM IDE (Fukuda et al. 2019) and much higher than the maximum speed-up times of 100 achieved by Irazu’s parallelization using OpenCL (Lisjak et al. 2018). Moreover, the relative speed-up times between the GPGPU-parallelized code and the CPU sequential code depend on the number of TET4s used in the numerical model, which are illustrated in Fig. 21a. As can be seen from Fig. 21a, the relative speed-up times initially increase with the number of TET4s increasing, which reveals that, in this case, keeping all the GPGPU cores busy is the most important factor in achieving the best performance of the GPGPU-parallelized code. However, after the number of TET4s increases to a certain value, which is about 430,000 TET4s in this study, the relative speed-up times slightly decrease with the number of TET4s increasing. In other words, there is a model limit of the maximum speed-up times for a single GPU accelerator to achieve the best performance and multiple GPU accelerators may be needed to lift the limit. Compared with the limit of the model size of 294,840 TET4s in Irazu’s parallelization using OpenCL (Lisjak et al. 2018), the limit of the model size for the maximum speed-up times of the GPGPU-parallelized 3D FDEM increases significantly. Therefore, as long as currently available publications are concerned, our 3D GPGPU-parallelized FDEM using CUDA has much better performance than Irazu’s parallelization using OpenCL in terms of both the maximum speed-up times and the limits of the model sizes. Furthermore, no performance report of CUDA version of Irazu-software is unavailable in any publications. In addition, as illustrated in Fig. 21b, the computation time of the GPGPU-parallelized 3D Y-HFDEM IDE linearly increases with respect to the number of TET4s. Therefore, the computational complexity of the GPGPU-parallelized 3D Y-HFDEM IDE is O(N), i.e. the amount of computation is proportional to the number of elements, which proves the high computational efficiency of the GPGPU-parallelized 3D Y-HFDEM IDE. The implementation of the hyper separating theorem into the contact detection algorithm (e.g. Lisjak et al. 2018) may be able to further enhance the computational performance of the GPGPU-parallelized 3D Y-HFDEM IDE.

Table 2 Model details for several h_ave values

Fig. 20

Relative speed-up of the GPGPU-parallelized 3D Y-HFDEM IDE compared with the sequential CPU-based code

Fig. 21

Computing performance of the GPGPU-parallelized 3D Y-HFDEM IDE: a Variation of relative speed-up with the increase of the number of TET4s and b variation of computation time with the increase of the number of TET4s

4 Conclusion and Future Work

This paper developed a general-purpose graphics-processing-unit (GPGPU)—parallelized combined finite-discrete element method (FDEM) based on the authors’ former sequential two-dimensional (2D) and three-dimensional (3D) Y-HFDEM IDE codes using compute unified device architecture (CUDA) C/C++. The algorithm of the developed 3D GPGPU-parallelized code was first presented in detail, which can provide a basis for further improvement and progress of the FDEM codes reviewed in the introduction section based on GPGPU parallelization. It should be noted that a different contact detection algorithm from that used in the sequential code was implemented in the 3D GPGPU-parallelized code because the algorithm in the sequential code is not suitable for GPGPU parallelization. Contact damping and contact friction were then implemented and verified although further verification may be needed. After that, the GPGPU-parallelized 3D Y-HFDEM IDE code was applied to 3D modelling of the failure process of limestone in a uniaxial compression strength (UCS) test and a Brazilian tensile strength (BTS) test to demonstrate its capability in modelling rock engineering applications under quasi-static loading conditions. The 3D modelling results demonstrate that for the FDEM simulations with the cohesive zone model (CZM) using unstructured meshes, mixed-mode I–II failures are the dominant failure mechanisms along the shear and splitting failure planes in the UCS and BTS tests, respectively, whereas pure mode I failure along the splitting failure plane in the BTS test and pure mode II failure along the shear failure in the UCS test are only possible in models with structured meshes. Moreover, compared with 2D models of the BTS test, new insights about the nucleation locations of macroscopic tensile splitting cracks were gained from the 3D model of the BTS test. Moreover, the GPGPU-parallelized 3D Y-HFDEM IDE code was implemented to model dynamic fracturing of a relatively isotropic and homogeneous marble in a split Hopkinson pressure bar (SHPB)—based dynamic Brazilian test to investigate its applicability in modelling rock engineering problems under dynamic loading conditions. Thanks to the GPGPU parallelization, the entire SHPB system was modelled using the 3D Y-HFDEM IDE code. The physical–mechanical parameters and computing parameters, including the penalty terms and dynamic strengths, were carefully selected for the 3D FDEM simulation, and the limitations of previous studies in the parameter selection were discussed. The modelled failure process, final fracture pattern and time histories of the dynamic compressive strain wave, reflective tensile strain wave and transmitted compressive strain wave were compared with those from experiments, and good agreements were achieved between them. In addition, the spurious fracturing mode in the form of unrealistic fragmentation, which can occur when the efficient contact detection activation approach is used, is highlighted because it has not been pointed out in previous FDEM studies. Finally, the computing performance of the GPGPU-parallelized 3D Y-HFDEM IDE run on various GPGPU accelerators was discussed against that of the sequential CPU-based 3D Y-HFDEM and other GPGPU parallelization of 2D FDEM using OpenCL since the computing performance of the GPGPU parallelization of 3D FDEM using OpenCL is not available in any publications.

The following conclusions can be drawn from this study:

• A GPGPU-parallelized 3D Y-HFDEM IDE code was developed to model the fracturing process of rock under quasi-static and dynamic loading conditions. In addition to GPGPU parallelization, robust contact detection, contact damping and contact friction were implemented in the 3D Y-HFDEM IDE code and were verified and validated through a series of numerical simulations under quasi-static and dynamic loading conditions. The computing performance analysis shows the GPGPU-parallelized 3D HFDEM IDE code is 284 times faster than its sequential version and can achieve the computational complexity of O(N).

• The 3D models of the failure processes of limestone in UCS and BTS tests demonstrated the capability of the GPGPU-parallelized 3D HFDEM IDE code in simulating rock engineering applications under quasi-static loading conditions. Moreover, important findings and new insights were obtained from the 3D modelling: (1) the selection of penalty terms for cohesive elements in any FDEM simulation with the intrinsic cohesive zone model (ICZM) is crucial to reasonably model rock continuous behavior before fracturing, which has been overlooked in the literature. (2) For all FDEM simulations with the CZM using unstructured meshes, mixed-mode I–II failures are the dominant failure mechanisms along the shear and splitting failure planes in the UCS and BTS tests, respectively, whereas pure mode I failure along the splitting failure plane in the BTS test and pure mode II failure with shear failure in the UCS test are only possible with structured meshes. Because rock is a collection of mineral grains, whose structure generally corresponds to that of an unstructured mesh in FDEM simulations, the results indicated that the mixed-mode I–II failures may be the possible failure mechanisms in experiments of the UCS and BTS tests. (3) Compared with 2D models of the BTS test, the 3D model of the BTS test results in different stress distributions along the loading diametrical lines in the middle plane and on the surface of the Brazilian disk as well as different nucleation locations of macroscopic tensile splitting cracks.

• The GPGPU-parallelized 3D Y-HFDEM IDE code can consider the entire SHPB testing system and successfully model the dynamic fracturing of marble in the SHPB-based dynamic BTS test. The modelled failure process, final fracture pattern and time histories of the dynamic compressive strain wave, reflective tensile strain wave and transmitted compressive strain wave are compared with those from experiments, and good agreements are achieved between them. Therefore, the 3D modelling of dynamic fracturing of marble in the SHPB-based dynamic BTS test demonstrates the capability of the GPGPU-parallelized 3D Y-HFDEM IDE code in simulating rock engineering applications under dynamic loading conditions.

Therefore, with careful calibration and insights, the FDEM, including the newly developed GPGPU-parallelized 3D Y-HFDEM IDE code in this study, is a valuable and powerful numerical tool for investigating the failure process of rock under quasi-static and dynamic loading conditions in rock engineering applications although very fine elements with maximum element size no bigger than the length of the fracture process zone must be used in the area where fracturing process is modelled.