1 Introduction

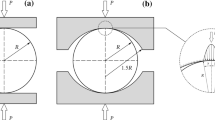
The Brazilian test is a simple indirect testing method to obtain the tensile strength of brittle material such as concrete, rock, and rock-like materials. In this test, a thin circular disc is diametrically compressed to failure. Four typical loading configurations are shown in Fig. 1.

Fig. 1
figure 1

Typical Brazilian tensile test loading configurations: a flat loading platens, b flat loading platens with two small-diameter steel rods, c flat loading platens with cushion, and d curved loading jaws

Full size image

The compression induces tensile stresses normal to the vertical diameter, which are essentially constant over a region around the center. The indirect tensile strength is typically calculated based on the assumption that failure occurs at the point of maximum tensile stress, i.e., at the center of the disc. The suggested formula for calculating the splitting tensile strength σ t (MPa) based on the Brazilian test is (ASTM 2008; ISRM 1978)

$$ \sigma_{\text{t}} = \frac{2P}{\pi Dt} = 0.636\frac{P}{Dt}, $$
(1)

where P is the load at failure (N), D is the diameter of the test specimen (mm), and t is the thickness of the test specimen measured at the center (mm). Since it was introduced independently by Carneiro and Akazawa in 1943 (Carneiro 1943; Akazawa 1943; Fairbairn and Ulm 2002), the Brazilian tensile test has received considerable attention even until nowadays (Erarslan and Williams 2012).

In this paper, we present a review of and some new insights into the intact Brazilian test for rock mechanics applications. Firstly, we discuss the background of the Brazilian test from the viewpoint of assumptions, perceptions, and debates related to the test in Sect. 2. The three major developmental stages of the Brazilian test for rock mechanics applications are presented in Sect. 3 based on a comprehensive literature review. One of the key issues of the Brazilian test related to the crack initiation position of rocks or rock-like materials obtained from the test is discussed in Sect. 4, where the applicability of the critical extension strain criterion is discussed. In Sect. 5, we present numerical modeling using FLAC3D to obtain the stress and strain distributions in the Brazilian disc test. Both the maximum tensile stress and the maximum tensile strain in the Brazilian disc are studied by numerical modeling to determine the crack initiation positions. Finally, some conclusions are drawn in Sect. 6. It should be pointed out that the present review and study only focus on the intact Brazilian disc test. The cracked Brazilian disc test and the dynamic loading problems of the Brazilian disc test are not covered.

2 Background

2.1 Assumptions

In the Brazilian test, a thin disc specimen is assumed to be loaded by a uniform pressure, which is radially applied over a short strip of the circumference at each end of a diameter. The frictional stresses between loading platens and specimen are neglected. The failure of the Brazilian specimen follows the Griffith criterion. The intermediate principal stress (σ 2) is assumed to have no influence on the disc fracture (Fairhurst 1964). An important and basic assumption for the determination of the tensile strength of rocks and rock-like materials by the Brazilian test is that the material is regarded as homogeneous, isotropic, and linearly elastic before brittle failure occurs (Mellor and Hawkes 1971).

2.2 Perceptions

Because of the difficulty of performing direct uniaxial tensile tests, Brazilian tests are widely used to measure the indirect tensile strength of rocks and rock-like materials. As pointed out by the ISRM-suggested Brazilian test method, the justification for the test is based on the experimental fact that most rocks in biaxial stress fields fail in tension at their uniaxial tensile strength, when one principal stress is tensile and the other principal stress is compressive with a magnitude not exceeding three times that of the tensile principal stress (ISRM 1978). Some perceptions regarding the Brazilian test have developed over the years; for example, the Brazilian test specimen should split along the compressive diametral line, or else is regarded as exhibiting an invalid failure mode. In other words, the fracture should initiate from the central part of the Brazilian disc, where the maximum tensile stress induces the rock failure (Colback 1966). Another perception is that, since the Brazilian test may overestimate the tensile strength of rocks because of its biaxial stress instead of uniaxial tension condition, the Brazilian test can never replace uniaxial tensile testing of rocks. In addition, the compressive stress concentration near the loading platen has been recognized as having a significant influence on the results of Brazilian tests. Specially designed curved loading platens or cardboard cushions between a flat loading platen and the specimen are suggested for using in the Brazilian test (ISRM 1978; ASTM 2008).

2.3 Debates

The validity of the Brazilian test has been debated for a long time, ever since it was introduced to measure the tensile strength of rock and rock-like materials; For example, as early as 1964, Fairhurst (1964) had already pointed out that failure may occur away from the center of the test disc for small angles of loading contact area for materials with low compression–tension ratios. In such cases, the “tensile strength” as usually calculated from test results was lower than the true value. After that, Hudson et al. (1972) found that failure always initiated directly under the loading points in the Brazilian test if only flat steel platens were used to load the specimens in a servo-controlled testing machine. They concluded that neither the Brazilian test nor the ring test could be recommended as a proper method for measuring the “tensile strength” as a material property. Based on three-dimensional (3D) finite element method (FEM) numerical analysis, Yu (2005) pointed out that the Brazilian test was not suitable to measure the tensile strength of rock-like materials, because the largest equivalent stress was not at the center of the end surface of the disc but always at the loading point of the end surface.

The crack initiation point should be located at the center of the Brazilian disc based on the Griffith fracture criterion, which is evidently supported by experimental and numerical studies (Yanagidani et al. 1978; Chen et al. 2004a). However, crack initiation at points away from the center of the disc have also been frequently observed (Fairhurst 1964; Hooper 1971; Hudson et al. 1972; Swab et al. 2011). The discrepancy between the theoretical analysis and laboratory observations may be the result of both the assumptions and the criteria for fracturing, and also the inherent defects and heterogeneity of the tested rocks.

3 Development of the Brazilian Test in Rock Mechanics Applications

The Brazilian tensile test for rock mechanics applications is like a work of art, drawing the research interest of a number of outstanding scholars over the past 70 years. Table 1 presents the developmental timeline of the Brazilian test from 1943 to 2012. The review focuses on the various milestones and the research approaches over the years.

Table 1 Developmental timeline of the Brazilian test on rocks and rock-like materials (1943–2011)
Full size table

Based on the comprehensive review presented in Table 1, three research stages for the development of the Brazilian test in the field of rock mechanics can be observed.

Stage 1 (1943–1978) This stage began with the publications by Carneiro (1943) and Akazawa (1943). Research focused on 2D stress analysis of the Brazilian disc and comparisons with other indirect tensile testing methods and uniaxial tensile tests (Hobbs 1965; Hiramatsu and Oka 1966; Jaeger and Hoskins 1966a, b; Jaeger 1967; Hudson 1969; Mellor and Hawkes 1971; Hudson et al. 1972; Peng 1976), as well as the validity of the tensile strength of rocks and rock-like materials obtained by the Brazilian test (Fairhurst 1964; Colback 1966; Hudson et al. 1972; Wijk 1978). Indirect tensile tests (the Brazilian test and the ring test) of anisotropic rocks were experimentally and theoretically investigated by Barla and Innaurato (1973). Analytical and experimental studies, which were the main research approaches, provided the groundwork for the preparation of the suggested testing method by ISRM (1978).

Stage 2 (1979–1991) The release of the ISRM-suggested method for determination of tensile strength of rock materials marked the beginning of this application stage. The Brazilian test had become very popular to measure the tensile strength of rocks all over the world. Relatively fewer references related to the Brazilian test were found. The anisotropy, nonlinear deformation characteristics under compression and tension, and the size effect of rock specimens drew attention from some scholars in this stage (Lajtai 1980; Sundaram and Corrales 1980; Pandey and Singh 1986; Satoh 1987; Newman and Bennett 1990; Bazant et al. 1991). The end of this stage is marked by the publication of the review articles by Andreev (1991a, b).

Stage 3 (1992–present) The improvement and modification of the traditional Brazilian test have been extensively studied and discussed during this stage. Researchers attempted to take into consideration all the influencing factors in the Brazilian test of rocks; for example, the influence of intermediate principal stress (σ 2) on the Brazilian test was considered using the 3D numerical modeling technique (Yu and Meng 2005; Yu et al. 2006, 2009). The effects of the anisotropic (transverse isotropic) nature of rocks in the Brazilian test have been analytically, numerically, and experimentally studied (Chen et al. 1998; Exadaktylos and Kaklis 2001; Claesson and Bohloli 2002; Cai and Kaiser 2004; Chou and Chen 2008; Tavallali and Vervoort 2010a, b). The assumption of homogeneous material in the Brazilian test has been extended to heterogeneous rock materials by numerical modeling techniques (Yue et al. 2003; Chen et al. 2004a, b; Zhu and Tang 2006). The influence of the frictional force between the loading platen and the Brazilian specimen on the stress distribution and failure modes of the Brazilian disc has been theoretically, experimentally, and numerically studied (Lavrov and Vervoort 2002; Xu et al. 2006; Markides et al. 2011; Dorogoy and Banks-Sills 2005). Closed analytical solutions for the stress field of the Brazilian disc have been given by considering the influence of material anisotropy (Claesson and Bohloli 2002), tangential friction along the loading rims (Lavrov and Vervoort 2002; Markides et al. 2012), and the distribution of applied load (Markides et al. 2010; Markides and Kourkoulis 2012). The crack patterns (including crack initiation and propagation) in the Brazilian test are still a hot issue. Different numerical analysis methods and experimental observations have been undertaken to study this problem (Lavrov et al. 2002; Van De Steen et al. 2005; Zhu and Tang 2006; Lanaro et al. 2009; Erarslan et al. 2011). Researchers have attempted to obtain more information besides the indirect tensile strength of rocks from the Brazilian test, e.g., the tensile elastic modulus of rocks (Ye et al. 2009; Gong et al. 2010). A flattened Brazilian disc test and some relevant modifications of the traditional Brazilian test were put forward and studied during this stage (Wang et al. 2004; Yu et al. 2009). Research on the Brazilian test in the field of rock mechanics became rejuvenated, as reflected by an increasing number of related publications.

To summarize, research on the Brazilian test of rock mechanics has been centered around the following five questions over the past 70 years:

  • Why can the Brazilian test be used to determine the tensile strength of rocks?

  • What is the stress distribution inside a Brazilian disc of rock?

  • Where is the crack initiation point of a Brazilian disc of rock?

  • Which criterion can be used to describe crack propagation in a Brazilian disc?

  • How can we improve the Brazilian test to obtain more accurate testing results and other useful information for rocks?

These questions are extensively discussed, and their answers can be found, in the related references. In general, almost all of the previous studies are based on stress analysis of the Brazilian test of rocks. Only a few experimental studies recorded and analyzed the strain distribution of the Brazilian disc for the purpose of measuring the extension strain or lateral deformation of rock specimens under diametral compressive loading (Yanagidani et al. 1978; Exadaktylos and Kaklis 2001; Ye et al. 2009; Gong et al. 2010). Despite the simple extension strain criterion for fracture of brittle rock put forward by Stacey (1981) three decades ago, most of the studies assumed that the splitting fracture of rocks in the Brazilian test was caused by the maximum tensile stress along the diametral loading line. The extension strain criterion has not been widely used to account for rock fracturing in the Brazilian test.

On the other hand, contradictory conclusions about the relationship between the tensile strength of rocks obtained by indirect Brazilian tests and that observed by direct uniaxial tensile tests exist in the literatures; for example, some researchers concluded that the Brazilian test may underestimate the tensile strength for rock with low ratio of compressive to tensile strength (Fairhurst 1964; Coviello et al. 2005), while some researchers concluded that the Brazilian disc results appeared to give a reasonable value for the tensile strength of rocks (Mellor and Hawkes 1971; Andreev 1991a, b). However, a significant number of researchers showed that the Brazilian test overestimated the tensile strength of rocks (Pandey and Singh 1986; Efimov 2009; Fuenkajorn and Klanphumeesri 2011). In view of these, some researchers have suggested that the tensile strength should not be considered as a material property but rather an experimental property (Hudson et al. 1972; Pandey and Singh 1986). Table 2 compiles some tensile strengths of rocks determined by direct and indirect tensile testing methods available in literatures. Compared with the ring tensile test, the Brazilian tensile test usually yields testing results much closer to those determined from the uniaxial tensile test. Normally, the Brazilian test may overestimate the tensile strength of rocks. Despite such deviation, the Brazilian test is still a popular means to determine the tensile strength of rocks, since the specimen preparation and experimental procedures for the Brazilian test are much easier than those for the direct uniaxial tensile test.

Table 2 Comparison of the measured tensile strength of rocks and rock-like materials obtained by direct and indirect tensile testing methods
Full size table

4 Crack Initiation Points of Rocks in the Brazilian Test

It is reasonable to expect that, in uniaxial tension, fracture preferentially initiates from the tips of microcracks lying perpendicular to the direction of principal tensile stress. The resulting crack would propagate in a plane normal to the loading direction, and the specimen would finally separate into two halves. Hawkes and Mellor (1970) pointed out that the final fracture surface, even in very precise tests, was neither perfectly flat nor exactly normal to the loading direction under uniaxial tension. Some direct pull tests showed that the rock fracture surface could not be planar and might be inclined to the loading direction (Nova and Zaninetti 1990; Okubo and Fukui 1996; Li et al. 2010). For homogeneous rocks subjected to the Brazilian test, it is quite common for the fracture surface to be parallel to the compressive loading direction, leading to splitting of the cylindrical disc into two halves. However, the generation of a central diametral crack provides no information regarding the crack initiation position. Researchers have long been curious to know where the first crack initiates and how the crack propagates.

A complete stress solution along the load diameter for the case of a load distributed over finite arcs (for instance, 2α in Fig. 2), valid for conditions of both plane stress (discs) and plane strain (cylinders), was given by Hondros (1959) as

$$ \sigma_{\theta } = + \frac{P}{\pi Rt\alpha }\left\{ {\frac{{\left[ {1 - \left( {r/R} \right)^{2} } \right]\sin 2\alpha }}{{1 - 2\left( {r/R} \right)^{2} \cos 2\alpha + \left( {r/R} \right)^{4} }} - \tan^{ - 1} \left[ {\frac{{1 + \left( {r/R} \right)^{2} }}{{1 - \left( {r/R} \right)^{2} }}\tan \alpha } \right]} \right\}, $$
(2a)
$$ \sigma_{r} = - \frac{P}{\pi Rt\alpha }\left\{ {\frac{{\left[ {1 - \left( {r/R} \right)^{2} } \right]\sin 2\alpha }}{{1 - 2\left( {r/R} \right)^{2} \cos 2\alpha + \left( {r/R} \right)^{4} }} + \tan^{ - 1} \left[ {\frac{{1 + \left( {r/R} \right)^{2} }}{{1 - \left( {r/R} \right)^{2} }}\tan \alpha } \right]} \right\}, $$
(2b)

where P is the applied load, R is the disc radius, t is the disc thickness, 2α is the angular distance over which P is assumed to be distributed radially (usually ≤15°), and r is the distance from the center of the disc. Tensile stress is taken positive.

Fig. 2
figure 2

Sketch of the Brazilian disc test under a uniformly distributed load over finite arcs

Full size image

Theoretically, according to the Griffith criterion, the exact center of the disc is the only crack initiation point at which the conditions for tensile failure at a value equal to the uniaxial strength are met. The principal stresses there are

$$ \sigma_{\theta } = + \frac{P}{\pi Rt}\left\{ {\frac{\sin 2\alpha }{\alpha } - 1} \right\} \approx + \frac{P}{\pi Rt}, $$
(3a)
$$ \sigma_{r} = - \frac{P}{\pi Rt}\left\{ {\frac{\sin 2\alpha }{\alpha } + 1} \right\} \approx - \frac{3P}{\pi Rt}. $$
(3b)

With a 15° contact arc, the error introduced by using the approximate expression for σ θ is 2 %. For the ISRM standardized device, two steel loading jaws are designed to create a contact with a disc-shaped rock sample over a finite arc of approximately 10° (ISRM 1978) or even within 5° (depending on the relative deformability of the disc and the jaw material) (Markides and Kourkoulis 2012) at the failure of the specimen. However, in some laboratory Brazilian tests, the crack initiation points have been observed to be located away from the center of the test disc. In addition, the stress concentration near the loading platen occasionally leads to an early shear failure fracture in the rock (Fairhurst 1964; Hudson et al. 1972). Yue et al. (2003) used a novel FEM analysis to demonstrate that material inhomogeneity had significant effects on the tensile stress distribution along the vertical loading diameter in the classical Brazilian test. They pointed out that the tensile cracks might not initiate at the center because of material inhomogeneity. Based on closed full-field solutions for stresses and displacements in the Brazilian disc under a distributed load, Markides et al. (2010) found that “discontinuity” of stress and displacement fields occurred at the edges of the load contact. They pointed out that the fracture might start at these points rather than at the specimen center. This observation could explain the fact that, for relatively hard materials, which do not permit smooth transition from the loaded rim to the unloaded portion of the specimens, the fracture indeed starts from the perimeter of the disk. On the other hand, based on experimental and numerical studies of rocks, some authors have shown that the failure of the Brazilian disc begins as an extension fracture in the center (interior) of the disk and then propagates to the top and bottom surfaces (Yanagidani et al. 1978; Van De Steen et al. 2005; Zhu and Tang 2006; Cai and Kaiser 2004). It should be pointed out that these numerical studies are all based on stress analysis of the Brazilian disc, which assumes that tensile cracks will occur if the maximum tensile stress exceeds its tensile strength.

It is rather strange that few studies use the critical extension strain criterion to assess crack initiation and propagation in the Brazilian test of rocks, even though the criterion is particularly applicable in areas of low confining stress. This criterion states that “a fracture of brittle rock will initiate when the total extension strain (ε) in the rock exceeds a critical value which is characteristic of that rock type” (Stacey 1981). In other words, fracture initiates when the following condition is satisfied:

$$ \varepsilon \ge \varepsilon_{\text{c}}, $$
(4)

where ε c is the critical value of extension strain. The fractures will form in planes normal to the direction of the extension strain, which corresponds to the direction of the minimum principal stress (the least compressive principal stress). For material that shows ideal linear deformation behavior, the strain in this direction is related to the three principal stresses (σ 1, σ 2, σ 3) by the following equation:

$$ \varepsilon_{3} = \frac{1}{E}\left[ {\sigma_{3} - \nu \left( {\sigma_{1} + \sigma_{2} } \right)} \right], $$
(5)

where E is the Young’s modulus and v is Poisson’s ratio.

At the center of the Brazilian disc surface, σ 3 = σ θ  ≈ +P/πRt and σ 1 = σ r  ≈ −3P/πRt. If we neglect the intermediate principal stress (σ 2) on the Brazilian disc surface and substitute σ 3 and σ 1 in Eq. (5), we can obtain

$$ \varepsilon_{3} = \frac{1 + 3\nu }{E}\frac{P}{\pi Rt} = \frac{{\sigma_{\theta } }}{E}\left( {1 + 3\nu } \right), $$
(6)

where ε 3 is the extension strain normal to the compressed diameter. This shows that the extension strain at the center of the Brazilian disc is larger than the value of σ θ /E, and it is related to the Poisson’s ratio of the rock. According to the critical extension strain criterion, the extension crack will initiate at the disc point when ε 3 ≥ ε c. Table 3 lists the critical magnitudes of extension strain for various rock types obtained from the laboratory tests by Stacey (1981).

Table 3 Critical magnitudes of extension strain for various rock types, obtained from the laboratory tests by Stacey (1981)
Full size table

It can be seen from Table 3 that the magnitudes of the critical extension strain of rocks are very low. Taking quartzite as an example, the critical extension strain is about 110 × 10−6. Considering a typical Young’s modulus of 55 GPa and a Poisson’s ratio of 0.10 for quartzite (Goodman 1989; Christensen 1996), the required tensile stress (σ θ ) for crack initiation in the rock will be about 4.65 MPa according to Eq. (6). This value is obviously less than the tensile strength of quartzite, which is reported to be larger than 10 MPa (Goodman 1989). The difference between the required tensile stress based on the critical extension strain criterion and the measured tensile strength indicates that the tensile cracks might have first initiated at the place where the tensile strain equals the critical extension strain for rock specimens subjected to the Brazilian test.

5 Numerical Modeling of the Brazilian Test by FLAC3D

Existing numerical analyses of the Brazilian test mostly consider the tensile stress distribution along the diametral loading line, while ignoring the tensile strain distribution. In this work, the commercial software FLAC3D was used to analyze both the stress and strain distributions of a Brazilian disc. The material is assumed to be homogeneous and linear elastic. The studied Brazilian disc specimen is 50 mm in diameter and 25 mm in thickness. For a more even distribution of elements, brick- and wedge-shaped mesh instead of cylindrical-shaped mesh were built using the FEM software ANSYS and then imported into FLAC3D. The size of the brick-shaped mesh is 1.00 mm in the thickness direction (Y-direction) and 1.25 mm in both the diametrical loading direction (Z-direction) and the horizontal direction (X-direction). The 3D model contains 33,375 zones and 36,348 grid points (Fig. 3).

Fig. 3
figure 3

The model of a Brazilian disc specimen: a 3D model and b a vertical plane view (note: arrows represent the applied loading direction at grid points; X, Y, and Z represent the coordinate axes)

Full size image

The material properties assigned to the specimen are: Young’s modulus (E) = 50 GPa, Poisson’s ratio (ν) = 0.24, and density (ρ) = 2.70 g/cm3. The displacements of the grid points in the loading parts are restricted in the X- and Y-directions at both the top and bottom locations. A vertical distributed load (Z-direction) is applied to the specimen along and parallel to the diametral line (AB) incrementally with the calculation steps. The uniform load is applied vertically to each grid point in the loading strip (three grid points in the vertical plane view shown in Fig. 2b) at loading rate of 0.2 N/step for 2,000 steps, then being kept constant until reaching a final mechanical equilibrium in the model. Therefore, the final vertical loading force (P) is equal to 31.2 kN (0.2 × 3 × 26 × 2,000 = 31,200 N). It should be noted that the load applied in the model (uniformly distributed and parallel to the diameter AB) is slightly different from the radial load distribution considered by Hondros (1959). For small contact arcs, this difference is not expected to play a crucial role, especially in disc regions far from the loaded rim. The loading angle (2α) in the model can be calculated by

$$ 2\alpha = 2 \times \sin^{ - 1} \frac{1.25}{25} = 5.73^{ \circ } \approx 6^{ \circ }. $$
(7)

After 3,402 calculation steps, the maximum unbalanced force reaches a very small value (about 0.005 N) and the mechanical ratio falls below the default limit of 1.0 × 10−5 in the model. This implies that mechanical equilibrium has been reached (Itasca 2006). Figure 4 shows the variation of the maximum unbalanced force and the total applied axial load in the model.

Fig. 4
figure 4

Maximum unbalanced force and total applied load in the Brazilian disc specimen

Full size image

According to Eq. (3a), the tensile stress at the center of the disc specimen is about 15.90 MPa. To better understand the principal stress distribution along the compressed diameter AB, both the tangential stress (σ xx , tensile stress) and the radial stress (σ zz , compressive stress) were obtained from the numerical modeling. Meanwhile, the principal stresses along the diameter AB were calculated according to the Hondros solution using Eqs. (2a) and (2b) for comparison. The principal stresses obtained on the mid-plane of the specimen (Y = 12.5 mm), normalized by 2P/πDt, are plotted against the Z-coordinate of the specimen along the line AB in Fig. 5. It can be seen that the numerical results for both σ xx and σ zz agree well with the Hondros solution except near the two loading points. The tensile stresses (σ xx ) in the middle section (−20 mm < Z < 20 mm) are almost uniformly distributed and almost equal to the value of 2P/πDt. However, the compressive stresses (σ zz ) are not uniformly distributed along the diameter AB; they increase from the center of the diameter to the two loading points.

Fig. 5
figure 5

Comparison of normalized principal stresses along the middle part of the compressed diametral line (AB) between the numerical modeling results and Hondros’ solutions. The dashed circle represents the Brazilian disc specimen

Full size image

In order to show the difference of the principal stress distribution caused by the 3D effect of the Brazilian disc specimen, Fig. 6 shows the normalized principal stresses along the diameter AB obtained on the surface plane and the middle plane of the disc. It can be seen that the tensile stress (σ xx ) distribution on the surface plane is different from that on the middle plane, while the compressive stress (σ zz ) distribution is almost the same on the two planes. Along the diameter AB the tensile stress in the range of −18 mm < Z < 18 mm is about 8–25 % larger than the value of 2P/πDt on the disc surface, while it is about 10–22 % less than the value of 2P/πDt on the middle cross-section plane (Y = 12.5 mm). In addition, on the specimen’s surface, the maximum tensile stress value occurs near the two loading points (about 5–6 mm away from points A and B).

Fig. 6
figure 6

Comparison of normalized principal stresses along the compressive diametral line between the surface and the middle part of a Brazilian disc specimen in numerical modeling results. The dashed circle represents the Brazilian disc specimen

Full size image

The influence of triaxiality on the failure of glass cylinders under diametral compression was discussed analytically by Hooper (1971). Numerical analyses were later carried out by Yu et al. (2006) using 3D FEM modeling, where uniform line loading was applied on the disc specimen instead of the uniformly distributed loading presented here. A revised formula to calculate the tensile strength to account for the 3D size effect of the Brazilian disc specimen was put forward by Yu et al. (2006):

$$ \sigma_{\text{t}} = \left( {0.2621k + 1} \right)\frac{2P}{\pi Dt}, $$
(8)

where k is the ratio of the thickness to the diameter (t/D) of the disc specimen. However, they did not consider the distribution of tensile strain, or its effect on crack initiation and propagation in the Brazilian specimen. The distribution of tensile strain in the Brazilian specimen obtained numerically is further described and discussed below.

The strain distribution of the Brazilian specimen was obtained by a FISH program in FLAC3D. The contour diagrams of either the tensile stress (σ xx ) or tensile strain (ε xx ) along with the outline of the Brazilian disc specimen are shown in Fig. 7 on the specimen surface zones (Y = 1.00 mm), and in Fig. 8 on the middle cross-section zones (Y = 12.5 mm) of the specimen.

Fig. 7
figure 7

Contour plots of tensile stress and tensile strain on the Brazilian disc surface zones (Y = 1.0 mm): a tensile stress (σ xx ) and b tensile strain (ε xx )

Full size image
Fig. 8
figure 8

Contour plots of tensile stress and tensile strain on the middle cross-section plane zones (Y = 12.5 mm): a tensile stress (σ xx ) and b tensile strain (ε xx )

Full size image

It can be seen that both the tensile stress and strain have local concentrations on the Brazilian disc surface, which occur at some distance away from the two loading points (Fig. 7a, b). However, such a bimodal tensile stress distribution is absent in the middle cross-section (Fig. 8a), while the bimodal tensile strain distribution still exists in the middle cross-section (Fig. 8b). The results thus show the 3D effect on the nonuniform stress distribution along the thickness (Y-direction) in the Brazilian disc. In addition, the maximum tensile strain is found to be located neither in the center of the disc nor at the two loading points. It occurs at some distance away from the two loading points, being about 5 mm away from the loading points on the Brazilian specimen surface for a 50-mm-diameter disc. As shown in Fig. 7b for the specimen surface, the maximum tensile strain is approximately 900 × 10−6, while it gradually decreases to about 550 × 10−6 in the central portion. Similar strain distribution results along the compressive diametral line have been observed by using a 3D digital image correlation (DIC) system in the Brazilian test of polymethylmethacrylate (PMMA) material and also by analytical solutions (Markides and Kourkoulis 2012). Figure 9 shows the experimentally measured and the theoretically calculated radial and transverse strains along the compressive radius of a PMMA disc subjected to the Brazilian test by Markides and Kourkoulis (2012), where the maximum tangential tensile strain occurs at about r = 0.80R; for example, in our numerical model where R = 25 mm, then r = 20 mm, which is the same as the presented numerical modeling results (5 mm away from the loading points).

Fig. 9
figure 9

Experimentally measured and theoretically calculated radial and transverse strains along the compressive radius of a PMMA disc subjected to the Brazilian test, redrawn from Markides and Kourkoulis (2012)

Full size image

The location where the maximum tensile strain occurs is usually described as corresponding to a failure mode transition between shear failure and tensile failure (Fig. 10), as observed for many rock types in the solid Brazilian disc test (Hobbs 1964). The central splitting fracture line GH should be associated with a tensile failure mode. However, it is difficult to judge whether the tensile fracture initiates and propagates from the point G (H) to the center or from the center to the point G (H) during experimental study.

Fig. 10
figure 10

Transition between shear and tensile failure modes in a solid disk in the Brazilian test, modified from the illustration by Hobbs (1964)

Full size image

As indicated in Eq. (6), the tensile strain developed in the Brazilian specimen is related to the Poisson’s ratio. To investigate the influence of the Poisson’s ratio, the numerical calculations were repeated with Poisson’s ratio of 0.12, 0.16, 0.30, and 0.36, while keeping the other parameters the same as before. The maximum tensile strain (ε xx-max) along the central diametral line and the tensile strain at the center of the disc surface (ε xx-center) determined from the numerical calculations were obtained and plotted against the Poisson’s ratio, as shown in Fig. 11.

Fig. 11
figure 11

Influence of Poisson’s ratio on the maximum tensile strain and the tensile strain at the center of the Brazilian disc surface

Full size image

As shown in Fig. 11, both ε xx-max and ε xx-center increase with the Poisson’s ratio. The former increases nonlinearly, while the latter increases almost linearly with the Poisson’s ratio. It can be observed from Fig. 11 that, the larger the value of the Poisson’s ratio, the greater the difference between the maximum tensile strain and the tensile strain at the disc center. Since the numerically investigated Poisson’s ratios span from 0.12 to 0.36 in Fig. 11, covering the values for most rock types, it can be used as a reference for different rock types under the Brazilian test.

In addition, if the loading condition changes to line loading or uniform diametrically distributed radial loading in the numerical modeling, similar distributions of tensile stress and tensile strain can be obtained except for a small difference occurring near the two loading points. This difference has been analytically solved and reported by Markides and Kourkoulis (2012) under different distributions of applied load, including diametral point load, uniform, sinusoidal, and parabolic loading conditions. They pointed out that the stress field in the major part of the disc was rather insensitive to the exact loading application mode, but critical differences were detected in the vicinity of the loaded arc of the disc. Further work can be carried out to model the influence of loading conditions and the frictional stresses between the loading platens and the specimen in the Brazilian test. The purpose of the numerical modeling part of this work is to reveal and highlight that the maximum tensile strain does not occur at the center of the Brazilian specimen surface but in the vicinity of the loading points.

Although the present numerical modeling of the Brazilian disc is based on an elastic analysis, the local concentration of tensile strain has been shown to be associated with a first crack initiation position near the loading points, instead of at the center of the specimen where the maximum extension strain criterion is satisfied. This means that the splitting fracture of a Brazilian disc may not be controlled only by the maximum tensile stress, but also by the maximum tensile strain. In previous numerical studies of fracture propagation in the Brazilian test using the boundary element code DIGS (Van De Steen et al. 2005) and the FRACOD2D code (Lanaro et al. 2009), the material failure criteria are all based on the Mohr–Coulomb criterion with a tension cut-off, while the critical extension strain criterion has not been adopted. Assessing the suitability of the strain criterion in modeling 3D crack initiation and propagation of a Brazilian rock disc is an important research task for the future. Application of the strain criterion can be helpful to explain the splitting fracture not only in the Brazilian test but also extension slabbing fractures under uniaxial compression testing of hard rock; for example, Li et al. (2011) observed that slabbing fractures parallel to the loading direction initiate at a critical extension strain which is about equal to the maximum tensile strain of the rock as measured by lateral strain gages on the specimen surface when subjected to the Brazilian test.

6 Conclusions

The development and applications of the intact Brazilian disc test in rock mechanics have been reviewed and investigated. Based on the history of research on the Brazilian test by analytical, experimental, and numerical approaches, three main research stages have been identified: before 1978 (the stage of groundwork for the preparation of the standard suggested Brazilian test method for rock and rock-like materials), 1979–1991 (the stage of widespread application of the Brazilian test in rock mechanics), and 1992–present (the stage of application, modification, and improvement of the Brazilian test in rock mechanics).

The Brazilian test is found to usually overestimate the tensile strength of rocks. Despite this deviation, the Brazilian test is still a popular means to determine the tensile strength of rocks due to its much easier specimen preparation and experimental procedure as compared with the direct uniaxial tensile test. The crack initiation point of the Brazilian disc has been intensively investigated, since different experimental results have been obtained. The critical extension strain criterion (Stacey 1981), which is seldom used, appears to be promising to explain crack initiation and propagation in the Brazilian test.

A numerical analysis has been conducted using a linear elastic model by FLAC3D to study the stress and strain distributions in a 50-mm-diameter Brazilian disc. The maximum tensile stress and the maximum tensile strain are both found to occur about 5 mm away from the two loading points along the central loading diameter of the disc, instead of at the center of the disc surface. The crack initiation point of the Brazilian test for rocks may be located near the loading point when the tensile strain meets the critical extension strain criterion, and it may also be located at the surface center when the tensile stress meets the maximum tensile strength criterion.