1 Introduction

A number of researches have attempted in the recent years to simulate high-strain rate loading laboratory tests and in particular dynamic indirect tensile tests. Hughes et al. (1993) used the finite element method (FEM) to model splitting tests of concrete samples at high-strain rates. Galvez et al. (1997) also used FEM to model split Hopkinson pressure bar (SHPB) tests. Brara et al. (2001) used the discrete element method (DEM) to study concrete at high-strain rates in tension. Yu et al. (2004) studied dynamic behaviour of ceramics by the application of FEM. Zhu and Tang (2006) utilised FEM to model both static and dynamic failure mechanisms of rocks. Dong et al. (2006) also used FEM to model SHPB tests of Brazilian discs to model dynamic fracture of brittle polymers. Zhou and Hao (2008) modelled concrete at high-strain rates under tension by the use of FEM. However, none of these works is fully able to properly model the entire loading and failure process and in particular the transition from continuum to discontinuum and the interaction of the generated fragments that is typical of fracturing and fragmentation processes in rock.

Rock heterogeneity together with fracture and fragmentation processes limit the applicability of continuum-based models to address rock engineering problems and in particular those that involve a dynamic failure of the rock. To overcome these limitations Munjiza (2004) formalised the idea of using a new hybrid finite-discrete element method (FEM/DEM). In FEM/DEM each discrete element is discretised into finite elements meaning that there is a finite element mesh associated with each discrete element. Thus, continuum behaviour is modelled through finite elements while discontinuum behaviour is analysed by discrete elements. In the context of the combined finite-discrete element method, transition from continua to discontinua is done through fracture and fragmentation processes (Munjiza 2004). A combined single and smeared crack model is implemented in the FEM/DEM code used for this study. In this model, a typical stress–strain curve is divided into two sections. The first part, corresponding to strain hardening prior to reaching the peak stress (i.e. tensile strength), is implemented through constitutive laws as in any standard finite element method. The second part, related to the post-peak behaviour, refers to strain-softening and is formulated in terms of stress and displacements (Munjiza et al. 1999). The softening stress-displacement relationship is modelled through a single crack model. A bonding stress is generated by the separation of the edges, and this stress is assumed to be a function of the size of separation (or crack opening). Further details can be found in the book “The combined finite-discrete element method” (Munjiza 2004).

In this work, we present the results of an exercise conducted to numerically simulate the failure of Brazilian disc specimens as observed in the laboratory under dynamic, high-strain rate, indirect tensile stress using the FEM/DEM code, based on Y-code of Munjiza (2004), currently being researched and developed by the Geomechanics Group at the University of Toronto. The results of the numerical simulations are compared and verified against our SHPB experiments.

2 Experimental Work: Split Hopkinson Pressure Bar (SHPB) tests on Barre Granite Discs

In general, for the assessment of critical failure stresses in rock, various load rates can be utilised to simulate low-strain rate loading under quasi-static conditions, or high-strain rate loading such as those imparted by shock or blast stress waves. Dynamic testing of rock refers to high-strain rate, low-duration application of stresses into the sample. In a dynamic laboratory test, the stress wave is imparted to the rock through dynamic processes, such as an explosive or percussive tool.

The experimental data used in this study as a basis for the numerical models stems from our laboratory experiments which utilised a split Hopkinson pressure bar (SHPB) apparatus to carry out dynamic testing on Brazilian disc specimens for the measurement of indirect tensile stress at failure. The obtained experimental data were later used in this study as a basis for the numerical models. The SHPB system has been used by various researchers for the dynamic testing of rock specimens (Cai et al. 2007; Iqbal et al. 2008; Xia et al. 2008; Zhang et al. 2000). Using the SHPB, rock samples can be tested under various configurations, such as compression, indirect tensile, direct tensile, or fracture toughness modes of failure. The apparatus consists of two long and thin steel bars, termed the incident and transmission bar, and a short striker bar used to produce the impact loading; the rock sample is maintained in contact between the incident and transmission bars (Fig. 1). During each test, the striker bar is projected at the incident bar at various velocities generated through a gas gun pressure burst. The impact between the striker bar and incident bar results in a stress wave which propagates through the incident bar, rock sample, and transmission bar (see Xia et al. (2008) for a more detailed explanation of the SHPB procedure).

Fig. 1
figure 1

Loading configuration for SHPB Brazilian tests

Full size image

For this study SHPB testing was performed on four Barre Granite disc specimens at gas gun pressures of 34, 48, 69, and 103 kPa. As described above, the test specimens, placed in the SHPB system between the incident and transmission bars, were loaded through a stress pulse generated by the impact of the striker bar against the long incident bar (Fig. 1). The strain gauges attached to the incident and transmission bars recorded the strain amplitude (converted from voltage) and time duration of the passing stress waves at 0.2 μs increments. The measured strains and modulus of the steel bars were used in calculating the incident (σ i ), reflected (σ r ), and transmitted (σ t ) stresses (Fig. 2). It should be noted that a pulse-shaping technique was used to reduce the loading rate on the samples in order to slow down the load ramp-up, helping the sample to better reach stress equilibrium during loading (see Xia et al. 2008).

Fig. 2
figure 2

Incident, Reflected, Transmitted and Incident + Reflected stress wave components measured for a Test 1 (467 GPa/s), b Test 2 (276 GPa/s), c Test 3 (772 GPa/s), and d Test 5 (1,150 GPa/s)

Full size image

Under dynamic loading in the SHPB system, the load (P) imparted to the rock is assessed from the transmitted stress wave (σ t ) and incident bar area (A b ) according to the following:

$$ P(t) = \sigma_{t} A_{b} $$
(1)

For assessment of the Brazilian indirect tensile strength, the peak tensile stress at failure (σ T ) is calculated from the external load applied to the sample (International Society of Rock Mechanics (ISRM) 1978). The relationship between compressive loads and peak tensile stress at failure in the SHPB Brazilian test, as confirmed in work by Dai and Xia (2009), can be assessed directly from the following equation under quasi-static loading conditions:

$$ \sigma_{T} = {\frac{2P(t)}{\pi DB}} $$
(2)

Where P(t) is the load on the specimen, and D and B are the specimen diameter and width, respectively. In the present study the four tested specimens had an average diameter and width of 39.7 and 16.8 mm, respectively. The calculated tensile (σ t ) stresses and peak tensile stresses (σ T ) at failure are shown in Fig. 3. Loading rates are shown to vary between 276 GPa/s for Test 2 and 1,150 GPa/s for Test 5. The approximate time to failure, between the contact of the incident stress wave to the sample, and the peak tensile stress (critical stress) at failure, ranged between 116 and 55 μs, decreasing with increased load rate. The peak calculated tensile stress at failure (Eq. 2) was shown to increase from 23.7 to 37.4 MPa with the increased load rate. The tensile strength of Barre granite tested under quasi-static conditions was measured at 12.7 MPa by previous researchers (Iqbal and Mohanty 2006).

Fig. 3
figure 3

Indirect tensile stresses calculated from the SHPB testing of four Barre granite Brazilian discs

Full size image

3 The Combined Finite-Discrete Element Method

The data obtained during our laboratory work has been modelled using a finite-discrete element code based on Munjiza’s Y-code (2004). A combined finite-discrete element method simulation comprises a large number of interacting distinct bodies, each associated with a separate finite element mesh. These meshes define the shape and boundaries of discrete elements, contact between them, and their deformability. Continuous deformations are modelled through finite elements while discontinuous behaviour is analysed by discrete elements. In order to assure that at any time no body overlap occurs it is fundamental to have an efficient treatment of contact impact. From an algorithmic point of view, this is taken care of by two processes: contact detection and contact interaction. The other key processes in FEM/DEM are deformability of continuum bodies, and fracture propagation. Each of these processes, but deformability, is discussed briefly in the coming sections. Deformability is implemented as in any standard explicit finite element analysis and thus is not discussed any further here.

3.1 Contact Detection And Interaction

A contact detection algorithm has to detect all the couples that are in contact and also remove couples that are too far apart to be contacting. In the FEM/DEM code a Munjiza-NBS (no binary search) contact detection algorithm (Munjiza 2004; Munjiza and Andrews 1998) is implemented. The NBS algorithm, being characterised by an O(N) complexity, is one of the most efficient algorithms developed to date. The total CPU time, needed to detect all contacting couples, of this algorithm is indeed proportional to the total number of discrete elements.

Contact interaction has a fundamental importance in FEM/DEM since it defines the behaviour of the system formed by a very large number of interacting distinct elements. As soon as contacting couples are detected by the contact detection algorithm, contact interaction is performed to calculate forces between discrete bodies. A potential function method is used for the interaction algorithm. This method is based on the assumption that contacting couples tend to penetrate into each other, generating distributed contact forces. Using this concept, the contact function is given as:

$$ U_{C} = \int\limits_{{\Upgamma_{C} }} {\frac{1}{2}p\left( {{\mathbf{r}}_{t} - {\mathbf{r}}_{c} } \right)^{T} \left( {{\mathbf{r}}_{t} - {\mathbf{r}}_{c} } \right)} {\text{d}}\Upgamma $$
(3)

in which p is the penalty term, Γ c boundary of the contactor element, r t and r c the position vectors of the points falling on the target and contactor elements, respectively. A distributed contact force is generated according to the shape and size of the overlap between the contactor and target elements. As the contactor penetrates an area dA into the target (Fig. 4), an infinitesimal contact force (df) is generated:

Fig. 4
figure 4

Schematic of a contacting couple showing the infinitesimal contact force due to overlap, after Munjiza (2004)

Full size image
$$ {\text{d}}{\mathbf{f}} = [{\text{grad}}\varphi_{c} ({\text{P}}_{c} ) - {\text{grad}}\varphi_{t} ({\text{P}}_{t} )]{\text{d}}A $$
(4)

where P c and P t are overlapping points of the contactor and target, respectively, and φ is the corresponding potential function.

The potential function formulation shows that for the penetration of any point P c of the contactor into the target specified by end points A and B, the work done by contact force only depends on the end points and is independent of the path taken. To preserve the energy during interaction:

$$ \begin{aligned} \varphi_{t} (A) & = \varphi_{t} (B) \\ \varphi_{c} (A) & = \varphi_{c} (B) \\ \end{aligned} $$
(5)

Therefore, if the potentials are chosen to be constant on the boundaries of both contactor and target elements, energy balance is preserved by the contact force of Eq. 4 independent on the penalty term, geometry and shape of elements, and magnitude of penetration.

3.2 Fracture Model

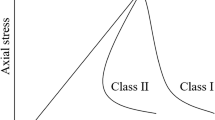
The transition from continua to discontinua is done through fracture and fragmentation processes. A combined single and smeared crack model also known as the discrete crack model has been implemented in the FEM/DEM code. In such a model, a typical stress–strain curve for rock (in direct tension) is divided into two sections (Fig. 5a): strain-hardening prior to reaching the peak stress (f t ), which is easily implemented in FEM/DEM through the constitutive law; and strain-softening for which the stress decreases with an increase in strain. There are several issues related to the latter including localisation of strains, loss of ellipticity (or hyperbolicity) of the governing equations, and sensitivity to mesh size and mesh orientation. Formulation of the strain-softening branch in terms of stress and displacements, as shown in Fig. 5b, helps deal with these problems. Note that the area under the stress-displacement curve corresponds to the energy release rate, G f  = 2γ where the energy required for a crack surface expansion of unit area, known as the surface energy, is denoted as γ.

Fig. 5
figure 5

a Stress–strain curve divided into the hardening and softening branches; b strain softening defined in terms of displacements, after Munjiza (2004)

Full size image

The softening stress-displacement relationship is modelled through a single crack model (Fig. 6). When the size of separation is zero (δ = δ t  = 0) the bonding stress is equal to the tensile strength f t , meaning that the separation begins only after reaching the tensile strength. Once that the separation increases (δ > δ c ), there will be a decrease in the bonding stress and right at δ = δ c the bonding stress tends to zero. Therefore, the bonding stress for separation δ t  < δ < δ c is expressed as a scaled tensile strength by:

Fig. 6
figure 6

Representation of a single crack model. After Munjiza et al. (1999)

Full size image
$$ \sigma = zf_{t} $$
(6)

where z is a heuristic scaling function representing an approximation of the experimental stress-displacement curves obtained from literature (Evans and Marathe 1968) defined as:

$$ z = \left[ {1 - {\frac{a + b - 1}{a + b}}\exp \left( {D{\frac{a + cb}{{\left( {a + b} \right)\left( {1 - a - b} \right)}}}} \right)} \right]\left[ {a\left( {1 - D} \right) + b\left( {1 - D} \right)^{c} } \right] $$
(7)

with

$$ {\text{D}} = \left\{ {\begin{array}{*{20}l} {0,} & {{\text{if}}\;\delta \le \delta_{t} } \\ {1,} & {{\text{if}}\;\delta > \delta_{c} } \\ {{\frac{{\delta - \delta_{t} }}{{\delta_{c} - \delta_{t} }}},} & {\text{otherwise}} \\ \end{array} } \right. $$
(8)

where a, b, and c are used for fitting the experimental stress-displacement curves.

4 Numerical Modelling of SHPB Dynamic Testing on Brazilian Disc Specimens

The numerical modelling was carried out using a time-explicit FEM/DEM research code, currently under development by the Geomechanics Group at the University of Toronto, based on Munjiza’s Y-code (2004). The input file was created using the pre-processor Y-GUI (Mahabadi et al. 2010). See http://www.geogroup.utoronto.ca/femdem.html for more information on the code. The model configuration showing the nodal and element distribution for the Brazilian disc, and arrangement of loading platens is shown in Fig. 7. The model was scaled to the approximate true dimensions of the SHPB disc (40 mm diameter) and transmission bar diameter (25 mm). The average element size ranged between 0.5 and 1.0 mm, which resembles the average grain size of Barre Granite (approximately 0.9 mm) (Nasseri et al. 2006).

Fig. 7
figure 7

Schematic of the model

Full size image

A Mohr–Coulomb type material with maximum tensile strength cut-off was used in the models. The material properties of the rock are given in Table 1. Note that a friction coefficient of 0.1 (equivalent to 5.71°) is assumed between the rock sample and the loading platens. The penalty term used in the penalty function method for contact interaction of the code is assumed to be equal to Young’s modulus of elasticity (Munjiza 2004). Fracture energy, needed for the fracture criterion of the code, was estimated from published fracture toughness data in accordance with the experimental observations of Chen and Xia (2009) and Chen et al. (2009). A value of 2500 J/m2 was used for all the models except for Test 2, which has a lower loading rate of 276 GPa/s and falls into the transition zone between quasi-static and dynamic behaviour (Dai and Xia 2009). Following their experience, fracture energy of 1,500 J/m2 was adopted as model input for modelling Test 2. Iqbal et al. (2008) also reported five to eight times increase in fracture toughness of Barre granite at high-strain rates. Using the relationship between fracture energy and fracture toughness, G f  = K 2IC /E (G f fracture energy, K IC mode I fracture toughness, and E elastic modulus) a 25–64 times increase in fracture energy between the quasi-static and dynamic state could be anticipated, which is in agreement with the values used for this study.

Table 1 Material properties of the rock sample and the loading platens
Full size table

The particle velocities measured at the bar/sample interface were used in the numerical simulations as a loading condition applied to the steel platens. The particle velocity imparted to the sample was calculated from the measured strains in the incident and transmission bars. The velocity at interface 1 (V 1 incident bar) and interface 2 (V 2 transmission bar) is assessed from the following:

$$ V_{1} = C_{0} \left( {\varepsilon_{i} - \varepsilon_{r} } \right) $$
(9)
$$ V_{2} = C_{0} \varepsilon_{t} $$
(10)

where C 0 is the elastic wave velocity in the bar (4,970 m/s), and ɛ i , ɛ r , and ɛ t are the incident, reflected, and transmitted wave strains, respectively. Since the reflected wave strain is in the opposite direction to the incident wave strain, the sign convention results in the addition of the two wave strains resulting in a substantially higher resulting velocity at interface 1 (V 1) compared to interface 2 (V 2). The recorded velocities of the four SHPB tests are shown in Fig. 8.

Fig. 8
figure 8

Recorded velocities at the SHPB tests bar/sample interface (V1 incident bar and V2 transmission bar) for a Test 1 (467 GPa/s), b Test 2 (276 GPa/s), c Test 3 (772 GPa/s), and d Test 5 (1,150 GPa/s). Note that the scales on the four graphs are different

Full size image

5 Results and Discussion

The results of the numerical simulations are herein discussed and compared with the experimental findings. Time history of indirect tensile stresses, as calculated by Eq. 2 is shown in Fig. 9. While the peak tensile stresses for Test 2 (276 GPa/s) and Test 5 (1,150 GPa/s) are almost equal in the simulation and experiment, those of Test 1 (467 GPa/s) and Test 3 (772 GPa/s) are underestimated by the numerical simulations. Physically, under dynamic loading, the presence of flaws and defects in the intact specimen may be fundamental on how cracks nucleate and grow. Moreover, dynamic crack growth is a process that depends on inertial effects and rate-dependent fracture processes. Therefore, the difference in values between simulations and experiments might be explained by the absence of micro-cracks and flaws in the numerical model versus the real rock samples. The time needed to reach the peak stress is approximately estimated accurately for Tests 1, 2 and 3, while Test 5 needs more time to reach the peak stress. The slopes of the curves indirectly representative of the loading rates are approximated appropriately by the numerical simulations.

Fig. 9
figure 9

Time histories of tensile stress for the four samples obtained in the laboratory experiments and numerical simulations

Full size image

5.1 Fracture Pattern

The fractured disc specimens obtained in the laboratory (Fig. 10, top) showed a major tensile splitting along the loaded axis of the sample and substantial damage at the loading points of the samples, possibly related to crushing or shearing of the rock. This local damage was more dominant for higher strain rates (e.g. Test 5). Radial cracking, likely caused by the presence of pre-existent micro-cracks in the sample, was visible in one test (Test 5). Interestingly, the FEM/DEM simulations (Fig. 10, bottom) were able to reproduce the observed fracture patterns including tensile splitting and crushing at the loading points. Micro-CT X-ray image of sample Test 3 (Fig. 11) clearly shows the presence of crack branching close to the loading points that is not otherwise visible. A similar feature can be seen in the numerical simulation. However, no propagation of radial cracking was obtained numerically since the numerical simulations use average rock parameters and do not account for material heterogeneity and presence of micro-cracks and material flaws. Preliminary attempts using heterogeneous material and mechanical properties measured at grain level show promising results to numerically reproduce experimental observations. However, those types of micro-mechanical models are out of the scope of the present work which is to demonstrate the validity of FEM/DEM to model dynamic failures in rock.

Fig. 10
figure 10

Fracture pattern of the samples failed in experiments (top) and simulated (bottom); a Test 1 (467 GPa/s), b Test 2 (276 GPa/s), c Test 3 (772 GPa/s), and d Test 5 (1,150 GPa/s)

Full size image
Fig. 11
figure 11

Micro-CT image of Test 3 sample obtained using Phoenix|X-ray v-tome|x scanner at a resolution of 80 μm voxel size

Full size image

To further investigate cracking process of the samples, fracture propagation of Test 3 (772 GPa/s) is presented in Fig. 12. The model reproduces the main failure mechanism observed in the experiments, including tensile splitting from the centre of the disc along the loading axis and shear failure near the loading platens. A close look at the model at 42 and 63 μs simulation time illustrates that an adequate load balance at the two sides of the disc is achieved prior to failure of the rock.

Fig. 12
figure 12

Fracture propagation of Test 3 (772 GPa/s) at different time steps during the simulation

Full size image

5.2 Tensile Strength Versus Loading Rate

It is known that the mechanical behaviour of materials depends on the applied loading rate. In a general sense, materials exhibit more strength as the loading rate increases (for instance see Brara et al. (2001); Cho et al. (2003); Zhao and Li (2000)). As proposed by Dai and Xia (2009), a linear relationship between tensile strength and loading rate can be observed in the dynamic range. In order to investigate this effect in the FEM/DEM simulations, indirect tensile strength calculated by Eq. 2 for the four test cases is compared. Figure 13 shows a linear relationship between calculated tensile strength and loading rate (note that loading rates are higher than 200 GPa/s). Quantitatively, all tensile strength values calculated in FEM/DEM simulations are satisfactorily close to those obtained in the laboratory experiments. To compare the experimental and numerical results from the present study to published data, results of tests by Dai and Xia (2009) for tensile strength anisotropy of Barre granite are also included in Fig. 13. In their tests, Dai and Xia (2009) studied the tensile strength of the samples in three directions (i.e. X-plane, Y-plane and Z-plane) corresponding to preferential micro-crack orientations inherent in Barre granite (Nasseri and Mohanty 2008). The simulation results of the present study fall within acceptable range of Y-plane data of Dai and Xia (2009) (shaded area of Fig. 13).

Fig. 13
figure 13

Tensile strength versus loading rate obtained in the laboratory and FEM/DEM simulations. X-plane, Y-plane and Z-plane data are taken from Dai and Xia (2009)

Full size image

Overall, by using only measured material properties, with minimal calibration of the parameters, FEM/DEM models show a reasonable proximity between simulation results and laboratory experiments. The relatively simple modelling exercise presented in this text shows good agreement between simulation results and laboratory observations. There is shown to be considerable potential in using FEM/DEM to both qualitatively and quantitatively simulate the dynamic response of rocks and geomaterials.

6 Conclusions

The results presented in this contribution show the capability of the FEM/DEM hybrid method to realistically reproduce SHPB dynamic testing on Brazilian disc specimens for the measurement of indirect tensile stress at failure. In the near future the FEM/DEM code will likely be applied to quantitatively model large-scale complex engineering processes such as mass mining, or complex slope stability problems. Currently the major limiting factors for the FEM/DEM code are the computational power required for solving large models (with tens of millions of elements), as well as the additional computational power required for modelling rock engineering problems in three dimensions. It is envisaged that the development of a cluster version of the FEM/DEM code will likely overcome several of those limitations and provide engineers with a reliable predictive tool ready to be used in practice.