1 Introduction

Due to successful applications, the master–slave synchronization introduced by Pecora and Carroll [1] has attracted a great deal of attention recently [2, 3]. Secure communication is considered as one of the most important applications of chaos synchronization [4, 5]. For this purpose, two chaotic systems are employed as transmitter and receiver. The transmitter produces chaotic signals and combines them with information signal. Then, the receiver, which is also a chaotic system, is synchronized with the transmitter and recovers the information signal [6]. Of all previously utilized methods in synchronization, sliding mode control [7, 8], impulsive control [9, 10], auxiliary system approach [11], active control [12], and adaptive passive method [13] can be mentioned. One of the challenges occurring in the synchronization problem is the fact that the master and slave systems have mostly uncertain dynamics. Such uncertainties can appear in the form of unmodeled dynamics and/or unknown parameters. As a result, adopting strategies to cope with such uncertainties is of prime importance. Thus, the necessity and practicality of adaptive methods for the synchronization of uncertain chaotic systems are accentuated [14, 15].

Combination of chaotic behavior and uncertain dynamics makes the synchronization problem both interesting and multifaceted. Therefore, the problem is divided into several classifications, and researchers have contrived different methods to tackle these categories separately. As examples of these cases, synchronization of nonidentical chaotic systems [16], synchronization and anti-synchronization of stochastic chaotic systems [17, 18], synchronization of chaotic systems with time-varying parameters [19], synchronization of growing chaotic network models [20], and intelligent approaches to the synchronization problem [21, 22] can be stated.

To simplify the challenging problem of synchronization, it has been commonly assumed that all states of the systems are measurable [23, 24]. Therefore, the need for designing observers is obviated. However, due to unavailability of all states in practical applications, observer design becomes important in the synchronization problem. The complexity of designing observers for the synchronization problem stems from the fact that the master and slave systems are mostly uncertain. Coupling unknown dynamics and unknown states requires a combination of adaptive and/or robust controllers and observers, which is still an open problem.

Several different observer-based strategies have been proposed for the synchronization problem in the literature [25, 26]. Nijmeijer and Mareels [27] have reviewed several observer design methods, utilized for the synchronization problem of chaotic systems. The nonlinear nature of chaotic dynamics makes design of observers difficult for such complex systems. There is no systematic approach for designing nonlinear observers, as opposed to linear ones [27]. In addition, existence of uncertainties in such systems adds to the complication of observer design. Nevertheless, to reduce the problem complexity, it is assumed in many cases that uncertainties are not coupled with unmeasured states [28]. However, such an assumption is not valid in practical applications. Another approach to address the complications of observer design for the synchronization problem of uncertain chaotic systems is to impose some structural assumptions on systems dynamics. Considering merely parametric uncertainties, and requiring dynamic equations of the systems to satisfy some specific conditions are of main examples of such assumptions [29, 30]. Nonetheless, such assumptions are restrictive, and their fulfillment cannot be always guaranteed.

When the systems have uncertain dynamics and all states are not measured, the synchronization problem becomes complicated. As mentioned earlier, the existing methods in the literature impose restrictive assumptions on the dynamics of the systems, in order to synchronize uncertain chaotic systems with unknown parameters. The contribution of this paper is proposing a novel synthesis of neural network-based observer and adaptive controller to synchronize uncertain chaotic systems with unknown states. The proposed scheme relaxes the previously imposed assumptions on system dynamics. As a result, the proposed method can be applied to a wider range of systems. Further, the proposed scheme can cope with a more general form of uncertainties such as unmodeled dynamics, and parametric and nonparametric uncertainties, instead of merely parametric uncertainties. In addition, we extended an existing observer design method for linear systems [31] to nonlinear systems. In this study, an adaptive neural network-based observer and an adaptive controller are designed to tackle the synchronization problem of uncertain chaotic systems. Two chaotic systems are considered as the master and slave. It is assumed that the parameters of the master system are unknown. Furthermore, a general form of uncertainty has been considered for the slave system. It is also assumed that the slave system states are not measured. Finally, the stability of the closed-loop system in the presence of observer dynamics has been established.

2 Problem statement

In this section, an adaptive controller along with an adaptive neural network-based observer is designed to synchronize two chaotic systems. One of the systems is considered as the master, generating chaotic signals. The other one is considered as the slave system, which is forced to follow the master signals. Both systems have uncertainties. In addition, it is assumed that states of the slave system are not fully measured. The equations governing the dynamics of the master and slave systems are given below, respectively.

$$\dot{x} = f(x) + F(x)P$$
(1)
$$\begin{aligned} & \dot{y} = g(y) + S(y)\beta + U \\ & z = Cy \\ \end{aligned}$$
(2)

where \(x \in {\mathbb{R}}^{n}\) and \(y \in {\mathbb{R}}^{n}\) are the state vectors; \(f(x),\,g(y):{\mathbb{R}}^{n} \to {\mathbb{R}}^{n}\) are two known continuously differentiable nonlinear vector functions; \(F(x):{\mathbb{R}}^{n} \to {\mathbb{R}}^{n \times n}\) is a known continuously differentiable nonlinear function; \(S(y):{\mathbb{R}}^{n} \to {\mathbb{R}}^{n \times n}\) is an unknown nonlinear vector function; and \(P,\,\beta \in {\mathbb{R}}^{n}\) are vectors of the master and slave parameters, respectively, which are unknown. \(U \in {\mathbb{R}}^{n}\) is the input vector, employed to synchronize the master and slave systems; \(z \in {\mathbb{R}}^{m}\) is the output vector of the slave system; and \(C \in {\mathbb{R}}^{m \times n}\) is a constant matrix. It is assumed that all the states of the master system are available, while the sates of the slave system are not measured.

3 Observer and controller design

In this section, the equations of the master and slave systems given by (1–2) are used to design a controller and an observer for the synchronization purpose. First, in Sect. 3.1, an adaptive neural network-based observer and controller are deigned, and their stabilities in the sense of Lyapunov are established by the use of the Lyapunov stability analysis. Next, in Sect. 3.2, the asymptotic stability of the tracking error for the designed controller is demonstrated.

3.1 Designing adaptive neural network-based observer and controller

Without the loss of generality, (2) can be rewritten as

$$\begin{aligned} & \dot{y} = Ay + s(y) + U \\ & z = Cy \\ \end{aligned}$$
(3)

where \(A \in {\mathbb{R}}^{n \times n}\) is a constant matrix, and the pair (A, C) is observable, that is, for a positive definite matrix L, there exists a unique symmetric positive definite matrix H such that \((A - KC)^{\text{T}} H + H(A - KC) = - L.\) It is also assumed that \(s(y):{\mathbb{R}}^{n} \to {\mathbb{R}}^{n}\) is an unknown nonlinear vector function.

Unknown nonlinear function s(y) can be approximated by a combination of some radial basis functions and unknown parameters as

$$s(y) = R(y)\bar{Q} + \bar{d}$$
(4)

where \(R(y):{\mathbb{R}}^{n} \to {\mathbb{R}}^{n \times np}\) is a matrix of radial basis functions of the form \(r_{ij} (y) = {\text{e}}^{{ - \frac{{\left\| {y - c_{ij} } \right\|}}{{\upsilon_{ij} }}}}\); c ij is the center of the receptive field; \(\upsilon_{ij}\) is the width of the basis functions; and \(\bar{d}\) is a bounded error where \(\left\| {\bar{d}} \right\|\,\le\,\bar{\gamma },\) and \(\left\| . \right\|\) denotes the Euclidean norm of a vector. \(\bar{Q}\) is the optimal vector of the weight parameters, which minimizes \(\bar{d}.\). As specified earlier, it is assumed that the states of the slave system are not available. Therefore, y cannot be used to approximate s(y). Since it is assumed that the slave system is observable, its states can be also recovered from the outputs. Thus, it is proposed to use the outputs to approximate s(y) as

$$s(y) = R(z)Q + d$$
(5a)

where Q and d are similar to \(\bar{Q}\) and \(\bar{d},\) which have been previously defined; z represents the output vector of the slave system. The proposed neural network which approximates the unknown dynamics of the slave system is presented as

$$s(y) = \left[ {\begin{array}{*{20}c} {r_{1} (z)} & {r_{2} (z)} & . & . & . & 0 \\ 0 & . & {r_{3} (z)} & {r_{4} (z)} & . & 0 \\ . & . & {} & . & {} & . \\ . & {} & . & {} & . & . \\ . & {} & {} & . & {} & . \\ 0 & . & . & . & {r_{n \times p - 1} (z)} & {r_{n \times p} (z)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {Q_{1} } \\ {Q_{2} } \\ . \\ . \\ . \\ {Q_{n \times p} } \\ \end{array} } \right] + d$$
(5b)

where n denotes the number of the slave system states; p stands for the number of the basis functions. \(Q^{\text{T}} = [\begin{array}{*{20}c} {Q_{1} } & {Q_{2} } & \ldots & {Q_{n \times p} } \\ \end{array} ]^{\text{T}}\) is the vector of the weight parameters.

Due to unavailability of the slave system states, the following adaptive observer is proposed as

$$\begin{aligned} & \dot{\hat{y}} = A\hat{y} + \hat{s}(\hat{y}) + U + K(z - \hat{z}) \\ & \hat{z} = C\hat{y} \\ \end{aligned}$$
(6)

where \(\hat{y} \in {\mathbb{R}}^{n}\) is the estimate of the state vector; \(\hat{z} \in {\mathbb{R}}^{m}\) is the output vector of the observer; K is a gain matrix yet to be determined. In addition, tracking error e, observation error \(\varepsilon ,\) and parameters estimation error \(\tilde{P}\) are defined below

$$e = \hat{y} - x$$
(7)
$$\varepsilon = y - \hat{y}$$
(8)
$$\tilde{P} = \hat{P} - P$$
(9)

where \(\hat{P} \in {\mathbb{R}}^{n}\) is the parameters estimation vector.

In order to design an observer, the dynamic equation of the slave system can be written as:

$$\dot{y} = (A - KC)y + Kz + U + s(y)$$
(10)

The above equation can be broken into two parts as [31]

$$\dot{y}_{u} = (A - KC)y_{u} + Kz + U$$
(11)
$$\dot{y}_{Q} = (A - KC)y_{Q} + s(y)$$
(12)
$$y = y_{u} + y_{Q}$$
(13)

where (11) can be construed as the part of the slave system, which does not contain any unknown dynamics. On the other hand, (12) contains the unknown dynamics of the slave system.

Similarly, the observer equation can be split as

$$\dot{\hat{y}}_{u} = (A - KC)\hat{y}_{u} + Kz + U$$
(14)
$$\dot{\hat{y}}_{Q} = (A - KC)\hat{y}_{Q} + R(z)\hat{Q} + w(t)$$
(15)
$$\hat{y} = \hat{y}_{u} + \hat{y}_{Q}$$
(16)

where w(t) is a compensating term to cope with the estimation error, and \(\hat{Q}\) is the unknown vector of the weight parameters.

An auxiliary matrix \(\gamma (t),\) which relates the observer states to the unknown weight vector, is defined by the following equation

$$\hat{y}_{Q} = \gamma \hat{Q}$$
(17)

It is worth mentioning that the main challenge of designing adaptive observers is the coupling between unknown dynamics and unknown states. To tackle this problem, \(\gamma\) is defined to relate these two unknown parts. Moreover, the unknown dynamics and unknown sates have time-varying natures. As a result, \(\gamma\) becomes time-varying as well. Thus, it is desired to obtain an adaptive law for updating \(\gamma\) such that (17) holds for all times. Taking time derivative of (17) gives

$$\dot{\hat{y}}_{Q} = \dot{\gamma }\hat{Q} + \gamma \dot{\hat{Q}}$$
(18)

Using (15) in (18) gives

$$\dot{\gamma }\hat{Q} + \gamma \dot{\hat{Q}} = (A - KC)\gamma \hat{Q} + R(z)\hat{Q} + w(t)$$
(19)

By selecting \(w(t) = \gamma \dot{\hat{Q}},\) (19) becomes

$$\dot{\gamma } = (A - KC)\gamma + R(z)$$
(20)

The above equation is utilized to update \(\gamma .\) As a result, (17) can be used to link \(\hat{y}_{Q}\) to \(\hat{Q}.\) Note that the final goal is to prove the convergence of the tracking error to zero, as well as establishing the stability of the observer. To demonstrate the stability of the observer, \(\gamma\) is used in the observer equations to compensate for the system uncertainties. Selecting \(w(t) = \gamma \dot{\hat{Q}},\) (15) yields to

$$\dot{\hat{y}}_{Q} = (A - KC)\hat{y}_{Q} + \hat{s}(z)\hat{Q} + \gamma \dot{\hat{Q}}$$
(21)

To establish the stability of the proposed observer, the following vector is defined as

$$\mu (t) = \varepsilon - \gamma \tilde{Q}$$
(22)

where \(\tilde{Q}\) is the estimation error of the weight parameters vector, defined as \(\tilde{Q} = Q - \hat{Q}.\) Taking time derivative of (22) results in

$$\dot{\mu }(t) = \dot{\varepsilon } - \dot{\gamma }\tilde{Q} - \gamma \dot{\tilde{Q}}$$
(23)

Employing (5a), (8), (10), and (14–16), \(\dot{\varepsilon }\) can be written as

$$\dot{\varepsilon } = (A - KC)y + R(z)Q - (A - KC)\hat{y} - R(z)\hat{Q} - w(t) + d$$
(24)

Employing w(t) which was defined earlier (i.e., \(w(t) = \gamma \dot{\hat{Q}}\)), (24) becomes

$$\dot{\varepsilon } = (A - KC)\varepsilon + R(z)\tilde{Q} - \gamma \dot{\hat{Q}} + d$$
(25)

Using (20) and (25) in (23) gives

$$\dot{\mu }(t) = (A - KC)\varepsilon + R(z)\tilde{Q} - \gamma \dot{\hat{Q}} - ((A - KC)\gamma + R(z))\tilde{Q} - \gamma \dot{\tilde{Q}} + d$$
(26)

Utilizing (22) in (26) and noting that \(\tilde{Q} = Q - \hat{Q},\) (26) can be written as

$$\dot{\mu }(t) = (A - KC)\mu (t) + d$$
(27)

Since d is a bounded vector and the pair (A, C) is observable, by appropriate selection of gain matrix K, vector \(\mu (t)\) remains bounded.

The following Lyapunov function is proposed to obtain the control law, required for the synchronization purpose, and also to establish the stability of the proposed observer

$$V = \frac{1}{2}e^{\text{T}} e + \bar{e}^{\text{T}} H\bar{e} + \frac{1}{2}\tilde{P}^{\text{T}} \tilde{P} + \frac{1}{2}\mu^{\text{T}} \mu$$
(28)

where \(\bar{e} = y_{u} - \hat{y}_{u} .\) Using (7), (9), and (27), the time derivative of (28) is obtained as

$$\begin{aligned} \dot{V} & = \left[ { - \left( {\hat{P} - \tilde{P}} \right)^{\text{T}} F(x)^{\text{T}} - f(x)^{\text{T}} + U^{\text{T}} + \hat{y}^{\text{T}} \left( {A^{\text{T}} - C^{\text{T}} K^{\text{T}} } \right) + z^{\text{T}} K^{\text{T}} } \right. \\ & \quad \left. { + \hat{Q}^{\text{T}} R(z)^{\text{T}} + w^{\text{T}} (t)} \right]e + \dot{\tilde{P}}^{\text{T}} \tilde{P} + \bar{e}^{\text{T}} H(A - KC)\bar{e} + \bar{e}^{\text{T}} (A - KC)^{\text{T}} H\bar{e} + \mu^{\text{T}} \dot{\mu } \\ \end{aligned}$$
(29)

To make (29) negative semidefinite, the following control and adaptive laws are proposed

$$\dot{\tilde{P}} = \dot{\hat{P}} = - F(x)^{\text{T}} e$$
(30)
$$U = - \varLambda_{1} e + F(x)\hat{P} + f(x) - (A - KC)\hat{y} - Kz - R(z)\hat{Q} - w(t)$$
(31)

where \(\varLambda_{1}\) is a symmetric positive definite matrix of appropriate size.

Substituting (27), (30), and (31) into (29) results in

$$\dot{V} = - e^{\text{T}} \varLambda_{2} e - \bar{e}^{\text{T}} L\bar{e} + \mu^{\text{T}} \left[ {(A - KC)\mu (t) - w(t) - \gamma \dot{\tilde{Q}} + d} \right]$$
(32)

where L is a symmetric positive definite matrix. Choosing \(w(t) = \gamma \dot{\hat{Q}}\) and recalling the definition of \(\tilde{Q},\) (32) can be written as

$$\dot{V} \le - e^{\text{T}} \varLambda_{2} e - \bar{e}^{\text{T}} L\bar{e} + \lambda_{\hbox{max} } \left( {(A - KC)} \right)\left\| {\mu (t)} \right\|^{2} + \left\| {\mu (t)} \right\|\sigma$$
(33)

where \(\left\| d \right\| \le \sigma ,\) and \(\sigma\) is unknown. \(\lambda_{\hbox{max} } ( \cdot )\) denotes the maximum eigenvalue of a matrix. (33) can be rewritten as

$$\dot{V} \le - e^{\text{T}} \varLambda_{2} e - \bar{e}^{\text{T}} L\bar{e} + \left\| {\mu (t)} \right\|\left[ {\lambda_{\hbox{max} } \left( {(A - KC)} \right)\left\| {\mu (t)} \right\| + \sigma } \right]$$
(34)

It follows directly that the first two elements of (34) are negative. Additionally, for a region where \(\left\| {\mu (t)} \right\| \ge \frac{ - \sigma }{{\lambda_{\hbox{max} } \left( {(A - KC)} \right)}},\) the last term becomes negative as well. Therefore, the rate of the Lyapunov function is negative inside this region. Thus, using the proposed control and adaptive laws, the Lyapunov function remains ultimately uniformly bounded. As a result, it implies that signals e, \(\bar{e}\), and \(\mu\) belong to \(L_{\infty }\) and are bounded. In addition, it is concluded that the above signals converge to a sphere-like region with the radius of \(\left\| {\mu (t)} \right\| = \frac{ - \sigma }{{\lambda_{\hbox{max} } \left( {(A - KC)} \right)}}.\) It is worth noting that the radius of this region depends on the eigenvalues of the matrix (A − KC), which can be determined by the designer as a part of the observer design. Consequently, the radius can be made arbitrarily small.

So far, a control law has been extracted to synchronize the slave and master systems, as well as designing a stable observer to estimate the states. However, the proposed control law given by (31) employs the estimation of the weight parameters of the neural network (i.e., \(\hat{Q}\)). Therefore, the next step is to provide an adaptive law to estimate \(\hat{Q}\). In addition, such an adaptive law should be stable and guarantee boundedness of \(\hat{Q}.\)

Motivated by the chaotic nature of the systems, it is postulated that the persistently exciting condition holds. It means that there exist positive constants \(\alpha ,\beta ,T\), and a bounded symmetric positive definite matrix S such that

$$\alpha I \le \int_{t}^{t + T} {\gamma^{\text{T}} (\tau )C^{\text{T}} SC\gamma (\tau ){\text{d}}\tau \le \beta I}$$
(35)

As mentioned earlier, the chaotic behavior of the systems makes sure that the richness condition is satisfied.

The following adaptive law is proposed as

$$\dot{\tilde{Q}} = - \eta \gamma^{\text{T}} C^{\text{T}} S\left( {z - C\hat{y}} \right)$$
(36)

Employing (8), (36) becomes

$$\dot{\tilde{Q}} = - \eta \gamma^{\text{T}} C^{\text{T}} SC\varepsilon$$
(37)

Substituting (22) into (37) leads to

$$\dot{\tilde{Q}} = - \eta \gamma^{\text{T}} C^{\text{T}} SC\left( {\mu + \gamma \tilde{Q}} \right)$$
(38)

Or

$$\dot{\tilde{Q}} = - \eta \gamma^{\text{T}} C^{\text{T}} SC\gamma \tilde{Q} - \eta \gamma^{\text{T}} C^{\text{T}} SC\mu$$
(39)

Lemma

The differential equation given by (39) is stable and has a bounded solution.

Proof

It is concluded from the richness condition, given by (35), that the first term on the right side of (39) is negative definite. For notation convenience, (39) is rewritten as

$$\dot{\tilde{Q}} = - M\tilde{Q} - \alpha$$
(40)

where \(M = \eta \gamma^{\text{T}} C^{\text{T}} SC\gamma\), \(\alpha = \eta \gamma^{\text{T}} C^{\text{T}} SC\mu ,\) and are time-varying. Considering the observability of the pair (A, C), along with boundedness of R(z), it can be concluded from (20) that \(\gamma\) is bounded. Further, (27) implies that \(\mu (t)\) is also bounded. Therefore, it is deduced that M and \(\alpha\) are bounded as well. To prove the stability of the differential equation given by (40), the following Lyapunov function is proposed as

$$V = \frac{1}{2}\tilde{Q}^{\text{T}} \tilde{Q}$$
(41)

Taking time derivative of (41) and using (40) lead to

$$\begin{aligned} \dot{V} & = \tilde{Q}^{\text{T}} \dot{\tilde{Q}} \\ & = \tilde{Q}^{\text{T}} \left( { - M\tilde{Q} - \alpha } \right) \\ & = - \tilde{Q}^{\text{T}} M\tilde{Q} - \tilde{Q}^{\text{T}} \alpha \\ \end{aligned}$$
(42)

By definition, M is symmetric and positive definite, thus

$$\begin{aligned} \dot{V} & \le {-} \lambda_{\hbox{min} } (M)\tilde{Q}^{T} \tilde{Q} - \tilde{Q}^{\text{T}} \alpha \\ & \le {-} \lambda_{\hbox{min} } (M)\left\| {\tilde{Q}} \right\|^{2} + \left\| {\tilde{Q}} \right\|\left\| \alpha \right\| \\ & \le {-} \left\| {\tilde{Q}} \right\|\left( {\lambda_{\hbox{min} } (M)\left\| {\tilde{Q}} \right\| - \left\| \alpha \right\|} \right) \\ \end{aligned}$$
(43)

It follows from (43) that in a region where \(\tilde{Q} > \frac{\left\| \alpha \right\|}{{\lambda_{\hbox{min} } (M)}},\) \(\dot{V}\) becomes negative definite. Therefore, \(\tilde{Q}\) remains in a sphere-like region with a radius of \(\frac{\left\| \alpha \right\|}{{\lambda_{\hbox{min} } (M)}}.\) As a result, it can be deduced that \(\tilde{Q}\) is bounded, that is, \(\tilde{Q} \in L_{\infty } .\) Therefore, it is learnt that using the derived control law (31) and adaptive laws (30) and (36) guarantees the stability of the designed observer and satisfies the synchronization purpose.

3.2 Asymptotic stability of the tracking error

So far, it has been demonstrated that all the signals, including the tracking and observation errors, remain bounded. However, to show the asymptotic stability of the tracking error, the equation governing the dynamics of the tracking error is investigated separately. Consider the following Lyapunov function

$$V_{e} = \frac{1}{2}e^{\text{T}} e + \frac{1}{2}\tilde{P}^{\text{T}} \tilde{P}$$
(44)

As observed from (44), the new Lyapunov function merely contains the tracking and parameter estimation errors. Taking time derivative of (44) and using (7) and (9) lead to the following

$$\begin{aligned} \dot{V}_{e} & = \left[ { - \left( {\hat{P} - \tilde{P}} \right)^{\text{T}} F(x)^{\text{T}} - f(x)^{\text{T}} + U^{\text{T}} + \hat{y}^{\text{T}} \left( {A^{\text{T}} - C^{\text{T}} K^{\text{T}} } \right) + z^{\text{T}} K^{\text{T}} } \right. \\ & \quad \left. +\, {\hat{Q}^{\text{T}} R(z)^{\text{T}} + w^{\text{T}} (t)} \right]e + \dot{\tilde{P}}^{\text{T}} \tilde{P} \\ \end{aligned}$$
(45)

Using (30) and (31), (45) becomes

$$\dot{V}_{e} = - e^{\text{T}} \varLambda_{2} e$$
(46)

where \(\varLambda_{2}\) is a symmetric positive definite matrix. Hence, \(\dot{V}_{e}\) is negative semidefinite. Since \(\varLambda_{2}\) is symmetric, it is concluded that \(\dot{V}_{e} \le {-}\lambda_{\hbox{min} } (\varLambda_{2} )\left\| e \right\|^{2} ,\) where \(\uplambda_{\hbox{min} } (\cdot)\) denotes the minimum eigenvalue of a matrix. Taking integral from both sides leads to \(\lambda_{\hbox{min} } (\varLambda_{2} )\int_{0}^{\infty } {\left\| e \right\|^{2} {\text{d}}t\, \le V(0) - V(\infty )} .\) Since the Lyapunov function given by (44) is decreasing, it is deduced that \(e \in L_{2} .\) Moreover, it follows from (35) that \(\dot{e} \in L_{\infty } .\) Thus, according to Barbalat's lemma \(\lim_{t \to \infty } e(t) = 0.\) Hence, the proposed scheme guarantees the asymptotic stability of the tracking error.

4 Simulation results

In this section, utilizing the proposed controller and observer, a simulation is conducted to investigate the behavior of two chaotic systems as the master and slave. The governing equations of the master and slaves systems are as follows:

$$\dot{x} = \left[ {\begin{array}{*{20}c} {x_{2} - x_{1} } & 0 & 0 \\ { - x_{1} } & 0 & {x_{1} + x_{2} } \\ 0 & { - x_{3} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {p_{1} } \\ {p_{2} } \\ {p_{3} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ { - x_{1} x_{3} } \\ {x_{1} x_{2} } \\ \end{array} } \right]$$
(47)
$$\begin{aligned} & \dot{y} = \left[ {\begin{array}{*{20}c} { - 10} & {10} & 0 \\ {28} & { - 1} & 0 \\ 0 & 0 & {2.67} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ {y_{3} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ { - y_{1} y_{3} } \\ {y_{1} y_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \end{array} } \right] \\ & z = y_{1} + y_{2} + y_{3} \\ \end{aligned}$$
(48)

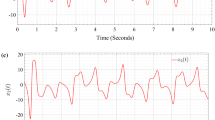
where \(p^{\text{T}} = [\begin{array}{*{20}c} {p_{1} } & {p_{2} } & {p_{3} } \\ \end{array} ]^{\text{T}}\) is the unknown parameters vector of the master system, and its actual values are \(p^{\text{T}} = [\begin{array}{*{20}c} {35} & 3 & {28} \\ \end{array} ]^{\text{T}}\); z is the measurable output of the slave system. It is assumed that the nonlinear part of the slave system \(\left[ {\begin{array}{*{20}c} 0 \\ { - y_{1} y_{3} } \\ {y_{1} y_{2} } \\ \end{array} } \right]\) is unknown. Therefore, as explained in the previous section in detail, a neural network is designed to approximate it. The neural network uses six basis functions for each element of the unknown nonlinear vector function. The basis functions are as follows: \([\begin{array}{*{20}c} {e^{{ - \left\| {z - c_{1} } \right\|}} } & {e^{{ - \left\| {z - c_{2} } \right\|}} } & {e^{{ - \left\| {z - c_{3} } \right\|}} } & {e^{{ - \left\| {z - c_{4} } \right\|}} } & {e^{{ - \left\| {z - c_{5} } \right\|}} } & {e^{{ - \left\| {z - c_{6} } \right\|}} } \\ \end{array} ]\) where \(c_{1} = 0,\,c_{2} = 5,\,c_{3} = 10,\,c_{4} = 15,\,c_{4} = 25,\,c_{4} = 35.\) Using the designed controller and observer, the synchronization results are shown in Figs. 1, 2, 3, 4, 5, and 6. Figures 1 and 2 depict the phase plane plots of the master and observer systems, respectively. As can be seen from Figs. 1 and 2, the master and observer systems exhibit chaotic behavior. As shown in Fig. 3, the synchronization tracking errors converge to zero successfully. As demonstrated analytically, the tracking error is expected to converge to zero, which is also verified by Fig. 3. Figure 4 shows the observation errors. As proven analytically, the observation errors remain bounded. Moreover, by adjusting the observer gain, the observation errors can be made arbitrarily small. However, the asymptotic convergence of the observation error is not guaranteed, as it was expected. The estimations of the unknown parameters of the master system are depicted in Fig. 5. As shown in Fig. 5, the estimated values converge to their actual values. The convergence of the estimated parameters of the master system to their actual values indicates that the richness condition has been satisfied, which stems from the chaotic nature of the systems. Finally, Fig. 6 exhibits the weight parameter estimates of the designed RBNN.

Fig. 1
figure 1

Phase plane of the master system

Full size image
Fig. 2
figure 2

Phase plane of the observer

Full size image
Fig. 3
figure 3

Tracking errors. a First state error, b second state error, c third state error

Full size image
Fig. 4
figure 4

Observation errors. a First state error, b second state error, c third state error

Full size image
Fig. 5
figure 5

Parameter estimates of master system. a First parameter estimate, b second parameter estimate, c third parameter estimate

Full size image
Fig. 6
figure 6

Weight parameter estimations of RBNN

Full size image

5 Future work

The proposed scheme guarantees the stability of the designed observer in the sense of Lyapunov. Designing an observer which can establish the asymptotic stability of the observation error can be considered as a future work.

6 Conclusion

To address the challenging problem of designing adaptive observers for uncertain chaotic systems, a novel synthesis of neural network-based observer and an adaptive controller was proposed. The goal was to synchronize two chaotic master–slave systems, where the master system has unknown parameters, and the slave system has unknown nonlinear dynamics. In addition, it was assumed that the states of the slave system were not measurable. A novel neural network-based observer, employing the outputs of the slave system, was proposed to estimate the unavailable states and approximate the unknown nonlinear dynamics of the slave system. Moreover, an adaptive controller was designed to satisfy the synchronization objective. It is worth noting that the proposed scheme can relax some of the assumptions, made in the existing methods in the literature. Further, a more general kind of uncertainty in the master system was considered. Consequently, the proposed method can be applied to a wider range of systems. Further, an existing observer for linear systems was extended to nonlinear systems. The extended observer can be used to estimate states of a broad range of nonlinear systems with uncertain dynamics of the form given by (2). Finally, the stability of the entire closed-loop system was proven, and the conducted simulation demonstrated the effectiveness of the proposed scheme. It was shown both analytically and numerically that the tracking error converges to zero, and the observation error remains bounded. In addition, the bound of observation error can be made arbitrarily small by increasing the observer gain.