A concept of coupled chaotic synchronous observers for nonlinear and adaptive observers-based chaos synchronization

Abstract

In this paper, new control approaches for synchronization the master and the slave chaotic systems is established by means of novel coupled chaotic synchronous observers and coupled chaotic adaptive synchronous observers. The simultaneous estimation of the master and the slave systems’ states is accomplished, by means of the proposed observers for each of the master and the slave systems, to produce error signals between these estimated states. This estimated synchronization error signal and the state-estimation errors converge to the origin by means of a specific observers-based feedback control signal to ensure synchronization as well as state estimation. Using Lyapunov stability theory, nonadaptive and adaptive control laws and properties of nonlinearities, a convergence condition for the state-estimation errors and the estimated synchronization error is developed in the form of nonlinear matrix inequalities. Solution of the resulted inequality constraints using a two-step approach is presented, which provides the necessary and sufficient condition to obtain values of the observer gain and controller gain matrices. Further, a method requiring less computational efforts for solving the matrix inequalities for obtaining the observer and the controller gain matrices using decoupling technique is also proposed. Numerical simulation of the proposed synchronization technique for FitzHugh–Nagumo neuronal systems is illustrated to elaborate efficaciousness of the proposed observers-based control methodologies.

1 Introduction

One of the earliest physicists known in the field of chaos, Edward Ott [1], made marvelous contribution in developing chaos theory that can be applied to many natural phenomenon and synthetic systems. Chaos is an interesting aperiodic long-time oscillatory behavior of dynamical nonlinear systems that can demonstrate a sensitive dependence on the initial condition [2]. Since the development of chaos theory, the control and synchronization of chaotic systems flourished as an emerging topic of research. Synchronization is a dynamic progression during which the driven system becomes in line with the driving system so that the synchronized or slave system, in a certain manner, tracks the trajectory of the synchronizing or master system [3, 4]. Carroll and Pecora made first successful attempt to present an experimental setup for synchronization of chaotic systems with different initial conditions and published a seminal paper [5] that acted as a catalyst in the field of chaos synchronization. Since then, many chaos synchronization techniques have been witnessed by the researchers.

The literature review reveals that different approaches such as linear feedback control [6], full-order and reduced-order output-affine observers [7], Runge–Kutta model-based nonlinear observer [8], synchronization with Huygens’ coupling [9], delay-range-dependent methodologies [10, 11], adaptive schemas using fuzzy disturbance observers [12], back-stepping techniques [13], robust adaptive methodologies [14, 15], step-by-step sliding-mode observer-based techniques [16], Chaos synchronization of unknown inputs Takagi-Sugeno fuzzy [3], adaptive generalized projective synchronization (GPS) [17] and evolutionary algorithms [18] are exercised for synchronization of the chaotic systems. All of these techniques for synchronization of the chaotic systems exhibit their strengths in variety of applications such as secure communication [19–21], chemical reactions [22], neural networks [23], optics and lasers [24], biological systems [25], robotics [26] and information science [27].

The observer-based synchronization techniques are more relevant to the situation where all the states of the master as well as the slave systems are unknown [28]. Researchers are continuously exploring such techniques with different types of observers for different applications. For instance, synchronous chaos in coupled systems [29], chaos-based secure communications by employing reduced-order and step-by-step sliding-mode observers [16], and generalized projective synchronization technique based on state estimation of hyperchaotic systems without calculating Lyapunov exponent [18] are presented. Active sliding-mode observer-based synchronization, where an active observer increased the attraction strength of the sliding surface, is elaborated in [30]. Similarly, adaptive observer-based synchronization of two nonidentical chaotic systems with unknown parameters is described recently in [31]. Further, a robust adaptive control approach for synchronization of the uncertain chaotic networks in the presence of mixed time-delays is described in [32]. In addition, output-affine observers to estimate the system states and to identify the message signal simultaneously, based on synchronization of the uncertain chaotic systems, for establishing secure communication modules are developed in [8]. Some other observer-based synchronization techniques include observers for unknown inputs in Takagi-Sugeno fuzzy models with application to the secure communication [3] and observer-based synchronization methodology in a cascade connection of hyperchaotic systems [33]. However, the above-mentioned observer-based synchronization techniques are not dealing with the coupled chaotic synchronous (CCS) and coupled chaotic adaptive synchronous (CCAS) observers-based control methodologies demonstrated in this paper. The main drawback of the aforementioned techniques, in contrast to the CCS and CCAS observers-based control methods, is their applicability to a lesser extent to synchronize two chaotic systems with unavailable state vectors.

In this paper, a novel technique for synchronization of the master and the slave chaotic systems based on two observers for estimating states of both of the systems is presented, through which complete synchronization of the master–slave networks is achieved via utilizing their outputs rather than the exact states. In the recent work [34], an error convergent observer-based synchronization technique was proposed by employing estimation of the synchronization error. However, the approach only deals with the chaotic systems for which the overall error system is transformable into a linear combination of various error dynamics. In this paper, a more generic technique based on CCS observers and control input using estimated states is accomplished that can deal with the nonlinear error dynamics for complete synchronization of the master–slave oscillators. Development of the proposed CCS observers-based control method is a nontrivial problem as compared to the existing observer-based techniques for synchronization because the present approach simultaneously estimates the states of both the master and the slave systems using CCS observers and controls the dynamics of the error system using a control input. Hence, the proposed synchronization technique is capable for two automations, that is, estimation of the states of the chaotic systems and synchronization of the chaotic systems. Another contribution of this paper is the adaptation of uncertain parameters present in the nonlinear dynamics by suggesting simple adaptation laws which are employed along with the proposed control signal based on CCAS observers for complete synchronization of the master–slave systems. The CCS and CCAS observers-based synchronization schemes with the static and adaptive controllers to simultaneously estimate and synchronize states of two chaotic systems are not fully elaborated in the literature. Additionally, a two-step approach and a decoupling methodology to determine the controller and the observer gain matrices using linear matrix inequalities (LMIs) are provided herein.

The scope of the proposed observers-based synchronization methodologies differs from the conventional synchronization schemes such as [3, 6, 8–11, 16, 18] and [29–34]. The conventional observer-based approaches are used to estimate the state vector of a chaotic system and can be employed to specific scenarios like secure communication. The proposed methodologies are useful for monitoring through state estimation as well as controlled synchronization of the two master–slave systems and have versatile applications. It is worth mentioning that the proposed observers are different from the conventional Luenberger-type and adaptive observers owing to the presence of coupling terms employed to achieve chaos synchronization. It should be noted that these CCS and CCAS observers are specifically designed for synchronization of chaos. Therefore, coupling terms are introduced to aid the synchronization. The application area of the proposed methodologies is broader than the conventional chaos synchronization approaches, which require exact states of the master–slave systems for feedback control. The proposed chaos synchronization approaches can be applied to the chaotic systems using information of their outputs, when states are not available, and synchronization is achieved using feedback of the estimated states (as well as the parametric estimates in the adaptive synchronization case). Numerical simulation results are demonstrated for synchronization of FitzHugh–Nagumo neurons by estimating states of the neurons and taking feedback of the estimated states under both the known and the unknown parametric information cases.

This paper is organized as follows: Sect. 2 introduces the systems under consideration. Sections 3 and 4 illustrate the proposed nonlinear and adaptive nonlinear observers-based synchronization methods, respectively. Convex routines for computing gains of the controller and the observers are provided in Sect. 5. Simulation results for synchronization of neurons are detailed in Sect. 6. Section 7 concludes the article.

2 System description

Consider the master and the slave chaotic systems, defined by the state-space representations

$$\begin{aligned} \dot{x}_\mathrm{m} (t)= & {} Ax_\mathrm{m} (t) + f(x_\mathrm{m} (t)) + Bg(x_\mathrm{m} (t))\theta _\mathrm{m}, \nonumber \\ y_\mathrm{m} (t)= & {} Cx_\mathrm{m} (t),\end{aligned}$$

(1)

$$\begin{aligned} \dot{x}_\mathrm{s} (t)= & {} Ax_\mathrm{s} (t) + f(x_\mathrm{s} (t)) + Bg(x_\mathrm{s} (t))\theta _\mathrm{s} + Bu(t), \nonumber \\ y_\mathrm{s} (t)= & {} Cx_\mathrm{s} (t), \end{aligned}$$

(2)

where $x_\mathrm{m} (t)\in R^{n}$ and $x_\mathrm{s} (t)\in R^{n}$ are the state vectors for the master and the slave systems, respectively, and $y_\mathrm{m} (t)\in R^{m}$ and $y_\mathrm{s} (t)\in R^{m}$ are the output vectors. $A\in R^{n \times n}$,$B\in R^{n \times l}$ and $C\in R^{m\times n}$ are the real constant matrices. The vector functions $f(x(t)) \in R^{n}$ and $g(x(t))\in R^{l \times p}$ are the nonlinear functions, $\theta _\mathrm{m} \in R^{p}$ and $\theta _\mathrm{s} \in R^{p}$ are the unknown parameters in the dynamics of the chaotic oscillators, and $u(t)\in R^{l}$ is the control input.

Assumption 1

The nonlinear functions f(x(t)) and g(x(t)) in both the master and the slave systems satisfy

$$\begin{aligned}&\left\| {f(x(t))-f(\bar{{x}}(t))} \right\| \le L_f \left\| {x(t)-\bar{{x}}(t)} \right\| ,\nonumber \\&\quad \forall x(t), \bar{{x}}(t)\in R^{n}, \end{aligned}$$

(3)

$$\begin{aligned}&\left\| {g_\mathrm{m} (x_\mathrm{m} (t))-g_\mathrm{m} (\bar{{x}}_\mathrm{m} (t))} \right\| \le L_{g\mathrm{m}} \left\| {x_\mathrm{m} (t)-\bar{{x}}_\mathrm{m} (t)} \right\| ,\nonumber \\&\quad \forall x_\mathrm{m} (t), \bar{{x}}_\mathrm{m} (t)\in R^{n}, \end{aligned}$$

(4)

$$\begin{aligned}&\left\| {g_\mathrm{s} (x_\mathrm{s} (t))-g_\mathrm{s} (\bar{{x}}_\mathrm{s} (t))} \right\| \le L_{g\mathrm{s}} \left\| x_\mathrm{s} (t)-\bar{{x}}_\mathrm{s} (t) \right\| ,\nonumber \\&\quad \forall x_\mathrm{s} (t), \bar{{x}}_\mathrm{s} (t)\in R^{n}, \end{aligned}$$

(5)

where $g_\mathrm{m} (x_\mathrm{m} (t))=Bg(x_\mathrm{m} (t))\theta _\mathrm{m}$ and $g_\mathrm{s} (x_\mathrm{s} (t))=Bg(x_\mathrm{s} (t))\theta _\mathrm{s}$. $L_f >0, L_{g\mathrm{m}} >0$ and $L_{g\mathrm{s}} >0$ are the constant matrices of appropriate dimensions.

A lot of work has been devoted to the synchronization of chaotic systems using state-feedback control approach. However, in many cases, the exact states are not available. Therefore, only estimated states of both the drive and the response systems (1)–(2) can be used for synchronization. The proposed control signal has the form

$$\begin{aligned} u(t)=\Psi (\hat{{x}}_\mathrm{m} (t),\hat{{x}}_\mathrm{s} (t)), \end{aligned}$$

(6)

where $\hat{{x}}_\mathrm{m} (t)\in R^{n}$ and $\hat{{x}}_\mathrm{s} (t)\in R^{n}$ are the estimates of $x_\mathrm{m} (t)$ and $x_\mathrm{s} (t)$, respectively. The purpose of the present study is to device static and adaptive feedback control strategies using the control signal (6) for synchronization of the master and the slave systems (1)–(2) by employing the estimated states. For this reason, appropriate approaches for the state estimation of the master and the slave systems using nonlinear and adaptive nonlinear observers are explored for an efficient synchronization remedy.

3 Observers-based synchronization

This section discusses observers-based control for synchronization of the chaotic systems (1) and (2) under known dynamics, that is, by assuming $\theta _\mathrm{m} =\theta _\mathrm{s} =0$. The vector function $\Psi (\hat{{x}}_\mathrm{m} (t),\hat{{x}}_\mathrm{s} (t))$ of the proposed controller (6) is selected as

$$\begin{aligned} \Psi (\hat{{x}}_\mathrm{m} (t),\hat{{x}}_\mathrm{s} (t))=F(\hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t)), \end{aligned}$$

(7)

where $F\in R^{l\times n}$ is the controller gain matrix. Observers are intended for both the master and the slave systems for estimation of their states. The proposed nonlinear observers for the master–slave systems are given by

$$\begin{aligned} \dot{\hat{{x}}}_\mathrm{m} (t)= & {} A\hat{{x}}_\mathrm{m} (t)+f(\hat{{x}}_\mathrm{m} (t))+L_\mathrm{m} (y_\mathrm{m} (t)-\hat{{y}}_\mathrm{m} (t))\nonumber \\&-\,\frac{1}{2}{} { BF}(\hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t)), \nonumber \\ \hat{{y}}_\mathrm{m} (t)= & {} C\hat{{x}}_\mathrm{m} (t), \end{aligned}$$

(8)

$$\begin{aligned} \dot{\hat{{x}}}_\mathrm{s} (t)= & {} A\hat{{x}}_\mathrm{s} (t)+f(\hat{{x}}_\mathrm{s} (t))+L_\mathrm{s} (y_\mathrm{s} (t)-\hat{{y}}_\mathrm{s} (t))\nonumber \\&-\,\frac{1}{2}{} { BF}(\hat{{x}}_\mathrm{s} (t)-\hat{{x}}_\mathrm{m} (t)),\nonumber \\ \hat{{y}}_\mathrm{s} (t)= & {} Cx_\mathrm{s} (t), \end{aligned}$$

(9)

where $L_\mathrm{m} \in R^{n\times m}$ and $L_\mathrm{s} \in R^{n\times m}$ are the gain matrices of the observers.

Defining the errors

$$\begin{aligned} e_\mathrm{m} (t)= & {} x_\mathrm{m} (t)-\hat{{x}}_\mathrm{m} (t), \end{aligned}$$

(10)

$$\begin{aligned} e_\mathrm{s} (t)= & {} x_\mathrm{s} (t)-\hat{{x}}_\mathrm{s} (t), \end{aligned}$$

(11)

$$\begin{aligned} e_\mathrm{o} (t)= & {} \hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t). \end{aligned}$$

(12)

Synchronization of the master–slave observers (8)–(9) is established by means of convergence of the estimated synchronization error $e_\mathrm{o} (t)$ to the origin, while convergence of state-estimation errors $e_\mathrm{m} (t)$ and $e_\mathrm{s} (t)$ to the origin ensures that the estimated states $\hat{{x}}_\mathrm{m} (t)$ and $\hat{{x}}_\mathrm{s} (t)$ approach to the actual states $x_\mathrm{m} (t)$ and $x_\mathrm{s} (t)$, respectively. Note that synchronization of the master and the slave chaotic systems is ensured by convergence of all the error signals (10)–(12) to the zero. The problem to be addressed herein is to determine the gain matrices $L_\mathrm{m}, L_\mathrm{s}$ and F such that the master and the slave chaotic networks demonstrate the identical behavior by employing information of output vectors without using the actual states for feedback. The complete closed-loop architecture for synchronization of the master and the slave systems with their observers is shown in Fig. 1.

Fig. 1

Block diagram to show the coupling architecture for the master and the slave systems with their respective observers in nonadaptive case

Remark 1

Novelty of this paper lies in the idea that the master and the slave chaotic systems can be made coherent by application of their respective observers. Both estimates of the master and the slave systems are enforced to catch up the same behavior such that the estimated synchronization error $e_\mathrm{o} (t)=\hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t)$ approaches to the zero. Once it happens, it is obvious that the states of the master and the slave observers are synchronized; consequently, these observers are called as synchronous observers.

Remark 2

The proposed observers (8)–(9), deliberately designed with the specific structures, are different from the traditional Luenberger-oriented observers owing to the specific coupling terms $-0.5{ BF}(\hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t))$ and $-0.5{ BF}(\hat{{x}}_\mathrm{s} (t)-\hat{{x}}_\mathrm{m} (t))$. For a specific selection of F, the coupling strength can be increased enough so that the coupled observers achieve synchronization. Consequently, the proposed observers are explicitly called as coupled chaotic synchronous observers.

Now, we provide a synchronization condition for systems (1)–(2) using CCS observers.

Theorem 1

For the given controller and observer gain matrices $F\in R^{l\times n}, L_\mathrm{m} \in R^{n\times m}$ and $L_\mathrm{s} \in R^{n\times m}$, a sufficient condition for the synchronization of the master–slave networks (1) and (2), subject to Assumption 1, using the control law (6)–(7) and CCS observers (8)–(9) is that there exist positive-definite symmetric matrices $P_\mathrm{m}, P_\mathrm{s}$ and $P_\mathrm{o}$ of appropriate dimensions and scalars $\alpha _1 >0, \alpha _2 >0$ and $\alpha _3 >0$ such that the matrix inequality

$$\begin{aligned} \Omega _1 =\left[ {{\begin{array}{cccccc} {\Gamma _1 }&{} 0&{} {0.5P_\mathrm{m} { BF}+C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{o} }&{} {P_\mathrm{m} }&{} 0&{} 0 \\ {*}&{} {\Gamma _2 }&{} {0.5P_\mathrm{s} { BF}-C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{o} }&{} 0&{} {P_\mathrm{s} }&{} 0 \\ {*}&{} {*}&{} {\Gamma _3 }&{} 0&{} 0&{} {P_\mathrm{o} } \\ {*}&{} {*}&{} {*}&{} {-\alpha _1 I_n }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {-\alpha _2 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {-\alpha _3 I_n } \\ \end{array} }} \right] <0 \end{aligned}$$

(13)

is satisfied, where

$$\begin{aligned} \Gamma _1= & {} A^\mathrm{T}P_\mathrm{m} +P_\mathrm{m} A-C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{m} -P_\mathrm{m} L_\mathrm{m} C+\alpha _1 L_f^2 I_n, \\ \Gamma _2= & {} A^\mathrm{T}P_\mathrm{s} +P_\mathrm{s} A-C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{s} -P_\mathrm{s} L_\mathrm{s} C+\alpha _2 L_f^2 I_n ,\\ \Gamma _3= & {} A^\mathrm{T}P_\mathrm{o} +P_\mathrm{o} A-F^\mathrm{T}B^\mathrm{T}P_\mathrm{o} -P_\mathrm{o} { BF}+\alpha _3 L_f^2 I_n. \end{aligned}$$

Proof

Consider the Lyapunov function

$$\begin{aligned} V(t)=e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} e_\mathrm{m} (t)+e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} e_\mathrm{s} (t)+e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} e_\mathrm{o} (t). \end{aligned}$$

(14)

The time derivative of the Lyapunov function is given as

$$\begin{aligned} \dot{V}(t)= & {} \dot{e}_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} e_\mathrm{m} (t)+ e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} \dot{e}_\mathrm{m} (t) \nonumber \\&+\, \dot{e}_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} e_\mathrm{s} (t)\nonumber + e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} \dot{e}_\mathrm{s} (t) \nonumber \\&+\,\dot{e}_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} e_\mathrm{o} (t)\, + e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} \dot{e}_\mathrm{o} (t). \end{aligned}$$

(15)

Using the systems (1)–(2), employing the observers (8)–(9) and incorporating the error equations (10)–(12) reveal

$$\begin{aligned} \dot{e}_\mathrm{m} (t)= & {} (A - L_\mathrm{m} C)e_\mathrm{m} (t) + f(x_\mathrm{m} (t))\nonumber \\&-\, f(\hat{x}_\mathrm{m} (t)) + \frac{1}{2}{} { BF}e_\mathrm{o} (t), \end{aligned}$$

(16)

$$\begin{aligned} \dot{e}_\mathrm{s} (t)= & {} (A - L_\mathrm{s} C)e_\mathrm{s} (t) + f(x_\mathrm{s} (t))\nonumber \\&-\, f(\hat{x}_\mathrm{s} (t)) + \frac{1}{2}{} { BF}e_\mathrm{o} (t) , \end{aligned}$$

(17)

$$\begin{aligned} \dot{e}_\mathrm{o} (t)= & {} (A - { BF})e_\mathrm{o} (t) + f(\hat{x}_\mathrm{m} (t))\nonumber \\&-\, f(\hat{x}_\mathrm{s} (t)) + L_\mathrm{m} Ce_\mathrm{m} (t) - L_\mathrm{s} Ce_\mathrm{s} (t). \end{aligned}$$

(18)

From Assumption 1, we can write

$$\begin{aligned}&-\alpha _1 \left[ {f(x_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{m} (t))} \right] ^\mathrm{T}\left[ {f(x_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{m} (t))} \right] \\&\quad +\,\alpha _1 L_f^2 e_\mathrm{m}^\mathrm{T} (t)e_\mathrm{m} (t)>0,\\&-\,\alpha _2 \left[ {f(x_\mathrm{s} (t))-f(\hat{{x}}_\mathrm{s} (t))} \right] ^\mathrm{T}\left[ {f(x_\mathrm{s} (t))-f(x_\mathrm{s} (t))} \right] \\&\quad +\,\alpha _2 L_f^2 e_\mathrm{s}^\mathrm{T} (t)e_\mathrm{s} (t)>0,\\&-\,\alpha _3 \left[ {f(\hat{{x}}_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{s} (t))} \right] ^\mathrm{T}\left[ {f(\hat{{x}}_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{s} (t))} \right] \\&\quad +\,\alpha _3 L_f^2 e_\mathrm{o}^\mathrm{T} (t)e_\mathrm{o} (t)>0. \end{aligned}$$

It is imperative to mention that the above-mentioned inequalities, derived from the Lipschitz condition for f(x(t)), contain scalars $\alpha _1 >0, \alpha _2 >0$ and $\alpha _3 >0$ as free variables that can be useful for feasibility of the design constraints. By utilizing (16)–(18) into (15) and, subsequently, incorporating the above-mentioned inequalities, one can obtain

$$\begin{aligned} \dot{V}\left( t \right)\le & {} \left[ e_\mathrm{m}^\mathrm{T} (t)(A^\mathrm{T} - C^\mathrm{T} L_\mathrm{m}^\mathrm{T} ) + \left[ {f(x_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{m} (t))} \right] ^\mathrm{T}\right. \nonumber \\&\left. +\, 0.5e_\mathrm{o}^\mathrm{T} (t)F^\mathrm{T} B^\mathrm{T} \right] P_\mathrm{m} e_\mathrm{m} (t) \nonumber \\&+\, e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} \,\left[ (A - L_\mathrm{m} C)e_\mathrm{m} (t) \right. \nonumber \\&\left. + \left[ f(x_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{m} (t)) \right] + 0.5{ BF}e_\mathrm{o} (t)\right] \nonumber \\&+\,\left[ e_\mathrm{s}^\mathrm{T} (t)(A^\mathrm{T} - C^\mathrm{T} L_\mathrm{s}^\mathrm{T} ) +\left[ {f(x_\mathrm{s} (t)) - f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T}\right. \nonumber \\&\left. +\,0.5e_\mathrm{o}^\mathrm{T} (t)F^\mathrm{T} B^\mathrm{T} \right] P_\mathrm{s} e_\mathrm{s} (t) \nonumber \\&+\,e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} \,\,\left[ (A - L_\mathrm{s} C)e_\mathrm{s} (t) + f(x_\mathrm{s} (t)) \right. \nonumber \\&\left. -\, f(\hat{x}_\mathrm{s} (t))+ 0.5{ BF}e_\mathrm{o} (t) \right] \nonumber \\&+\, \left[ e_\mathrm{o}^\mathrm{T} (t)(A^\mathrm{T} - F^\mathrm{T} B^\mathrm{T} )\right. \nonumber \\&\left. + \,\left[ {f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T} \right] \,P_\mathrm{o} e_\mathrm{o} (t) \nonumber \\&+\, \left[ {e_\mathrm{m}^\mathrm{T} (t)C^\mathrm{T} L_\mathrm{m}^\mathrm{T} - e_\mathrm{s}^\mathrm{T} (t)C^\mathrm{T} L_\mathrm{s}^\mathrm{T} } \right] P_\mathrm{o} e_\mathrm{o} (t) \nonumber \\&+\, e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} \left[ (A - { BF})e_\mathrm{o} (t)\right. \nonumber \\&+\, \left. \left[ {f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] \right] \nonumber \\&+\, e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} \left[ {L_\mathrm{m} Ce_\mathrm{m} (t) - L_\mathrm{s} Ce_\mathrm{s} (t)} \right] \nonumber \\&-\, \alpha _{1} \left[ {f(x_\mathrm{m} (t))-f(\hat{x}_\mathrm{m} (t))} \right] ^\mathrm{T} \left[ {f(x_\mathrm{m} (t))-f(\hat{x}_\mathrm{m} (t))} \right] \nonumber \\&+\, \alpha _{1} L_{f}^{2} e_\mathrm{m}^\mathrm{T} (t)e_\mathrm{m} (t)\nonumber \\&-\, \alpha _{2} \left[ {f(x_\mathrm{s} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T} \left[ {f(x_\mathrm{s} (t)){-}f(x_\mathrm{s} (t))} \right] \nonumber \\&+\, \alpha _{2} L_{f}^{2} e_\mathrm{s}^\mathrm{T} (t)e_\mathrm{s} (t)\nonumber \\&-\, \alpha _{3} \left[ {f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T}\nonumber \\&\left[ {f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] + \alpha _{3} L_{f}^{2} e_\mathrm{o}^\mathrm{T} (t)e_\mathrm{o} (t), \end{aligned}$$

(19)

which further produces

$$\begin{aligned}&\dot{V}\left( t \right) \le E_{1}^\mathrm{T} (t)\Omega _{1} E_{1} (t),\nonumber \\&E_{1}^\mathrm{T} (t) = \Big [ {\begin{array}{*{20}c} {e_\mathrm{m}^\mathrm{T} (t)} &{} {e_\mathrm{s}^\mathrm{T} (t)} &{} {e_\mathrm{o}^\mathrm{T} (t)} &{} {\Delta f_{{m\hat{m}}}^\mathrm{T} (t)} &{} {\Delta f_{{s\hat{s}}}^\mathrm{T} (t)} &{} {\Delta f_{{\hat{m}\hat{s}}}^\mathrm{T} (t)} \\ \end{array} } \Big ]\nonumber \\&\Delta f_{{m\hat{m}}} (t) = f(x_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{m} (t)) \nonumber \nonumber \\&\Delta f_{{s\hat{s}}} (t) = f(x_\mathrm{s} (t)){-}f(\hat{x}_\mathrm{s} (t)) \nonumber \nonumber \\&\Delta f_{{\hat{m}\hat{s}}} (t) = f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t)) \end{aligned}$$

(20)

From (20), it is obvious that $\dot{V}(t) < 0$ is ensured if $\Omega _1 <0$ is satisfied. Hence, the error signals $e_\mathrm{m} (t), e_\mathrm{s} (t)$ and $e_\mathrm{o} (t)$ are asymptotically stable. Subsequently, the master and the slave systems (1)–(2) are synchronized, which completes the proof. $\square$

Remark 3

Several observer-based synchronization approaches are available in the literature, in which an observer is used to estimate states of a single chaotic oscillator (see, for instance, [3, 8, 16, 18] and [28–30]). These so-called observer-based synchronization methodologies are very helpful for secure communication and image processing. However, these synchronization approaches are inapplicable to two chaotic oscillators because there theme is to estimate states of a single oscillator rather than to synchronize two independent oscillators. The proposed observers-based synchronization methodology, contrastingly, addresses a relatively different synchronization perplexity, that is, synchronization of the two chaotic oscillators, and has broad applications.

Remark 4

Compared to the traditional observer-based synchronization approaches [3, 8, 16, 18] and [28–30], based on estimation of the unknown state vector of a single chaotic entity, CCS observers can be applied to synchronize the master–slave networks. The estimated states using CCS observers are utilitarian to synchronize the states of the master and the slave oscillators using a control signal (6). By virtue of the proposed CCS observers-based chaos synchronization scheme, exact state vectors are not required in contrast to the conventional methods (such as [6, 9, 10], and [11]) and output measurements can be employed for a static feedback control. It is notable that such an observers-based chaos synchronization approach for two independent chaotic entities (1)–(2) is lacking in the literature.

Remark 5

Recently, an observer-based synchronization approach is developed in [34] for synchronization of two chaotic oscillators by employing estimation of error between the master and the slave states by means of a linear state estimation error dynamics. This approach is developed for a specific class of memristive systems, while the proposed CCS observers-based synchronization method is applicable to a broad class of systems. In addition, observer design for estimation of state errors becomes unmanageable in the present case because the estimation error dynamics is nonlinear. In contrast to [34] and similar Luenberger observers in [35–37], the proposed methodology demonstrates that synchronization of a broad class of chaotic systems resulting nonlinear state error dynamics can be achieved by application of CCS observers-based control strategy employing estimation of states of both oscillators. For autonomous dynamical systems, both the proposed approach and the methodology in [34] can be employed for synchronization. However, the proposed approach can be used for a large operational range, as the results in [34] are specific to consider some particular linear modes of operation.

4 Adaptive observers-based synchronization

If the dynamics of the master and the slave chaotic systems contain unknown parameters (that is, $\theta _\mathrm{m} ,\theta _\mathrm{s} \in R^{p})$, the synchronization of both systems cannot be achieved by the control law (6)–(7). Rather, we have to use adaptation laws along with the specific selection of control law $u(t)=\Psi (\hat{{x}}_\mathrm{m} (t),\hat{{x}}_\mathrm{s} (t))$ as

$$\begin{aligned}&\Psi (\hat{{x}}_\mathrm{m} (t),\hat{{x}}_\mathrm{s} (t))=F(\hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t))\nonumber \\&\quad +\,g(\hat{{x}}_\mathrm{m} (t))\hat{{\theta }}_\mathrm{m} (t)-g\left( {\hat{{x}}_\mathrm{s} (t)} \right) \hat{{\theta }}_\mathrm{s} (t), \end{aligned}$$

(21)

where $\hat{{\theta }}_\mathrm{m} \in R^{p}$ and $\hat{{\theta }}_\mathrm{s} \in R^{p}$ are the estimates of the unknown parameters $\theta _\mathrm{m}$ and $\theta _\mathrm{s}$, respectively. Coupled adaptive observers are aimed for both the master and the slave systems for estimation of their states under unknown parameters.

$$\begin{aligned} \dot{\hat{{x}}}_\mathrm{m} (t)= & {} A\hat{{x}}_\mathrm{m} (t)+\left[ {f(\hat{{x}}_\mathrm{m} (t))+Bg\left( {\hat{{x}}_\mathrm{m} (t)} \right) \hat{{\theta }}_\mathrm{m} (t)} \right] \nonumber \\&+\,L_\mathrm{m} \left( {y_\mathrm{m} (t)-\hat{{y}}_\mathrm{m} (t)} \right) \nonumber \\&-\,\frac{1}{2}{} { BF}(\hat{{x}}_\mathrm{m} (t)-\hat{{x}}_\mathrm{s} (t)), \end{aligned}$$

(22)

$$\begin{aligned} \dot{\hat{{x}}}_\mathrm{s} (t)= & {} A\hat{{x}}_\mathrm{s} (t)+\left[ {f(\hat{{x}}_\mathrm{s} (t))+Bg(\hat{{x}}_\mathrm{s} (t))\hat{{\theta }}_\mathrm{s} (t)} \right] \nonumber \\&+\,L_\mathrm{s} (y_\mathrm{s} (t)-\hat{{y}}_\mathrm{s} (t))\nonumber \\&-\,\frac{1}{2}{} { BF}(\hat{{x}}_\mathrm{s} (t)-\hat{{x}}_\mathrm{m} (t))+Bu_{g} , \end{aligned}$$

(23)

where $u_g (t)=g(\hat{{x}}_\mathrm{m} (t))\hat{{\theta }}_\mathrm{m} (t)-g\left( {\hat{{x}}_\mathrm{s} (t)} \right) \hat{{\theta }}_\mathrm{s} (t)$ is the nonlinear component of u(t). The proposed nonlinear adaptive observers-based control methodology for synchronization the master–slave systems is shown in Fig. 2.

Fig. 2

Block diagram to show the coupling architecture for the master and the slave systems with their respective observers along with adaptation laws and control block in adaptive case

Remark 6

Unequivocally, it is worth noting that CCAS observers are more generic than the CCS observers developed in the previous section because these CCAS observers can deal with the nonlinearities of two types, that is, nonlinearities with the known parameters and nonlinearities with the unknown parameters. However, the main snag of the CCAS observers is their slow response because of adaptation of parameters $\hat{{\theta }}_\mathrm{m} (t)$ and $\hat{{\theta }}_\mathrm{s} (t)$. If all the parameters are known, it is better to use CCS observers for a fast convergence. However, CCAS observers are utilitarian for adaptive synchronization of chaos due to practical limitations in parametric measurements.

Let us introduce the following assumption for adaptive observers-based control.

Assumption 2

Let $B^\mathrm{T}P_\mathrm{m} C^{\bot }=0$ and $B^\mathrm{T}P_\mathrm{s} C^{\bot }=0$, where $C^{\bot }$ denotes the orthogonal projection on to the null of C.

If Assumption 2 holds, matrices $R_\mathrm{m}$ and $R_\mathrm{s}$ can be selected by solving $B^\mathrm{T}P_\mathrm{m} -R_\mathrm{m} C=0$ and $B^\mathrm{T}P_\mathrm{s} -R_\mathrm{s} C=0$. Now, we provide an adaptive controller design condition using CCAS observers.

Theorem 2

For the given controller and observer gain matrices $F\in R^{l\times n}, L_\mathrm{m} \in R^{n\times m}$ and $L_\mathrm{s} \in R^{n\times m}$, a sufficient condition for the synchronization of the master–slave networks (1) and (2) with unknown parameters $\theta _\mathrm{m} \in R^{p}$ and $\theta _\mathrm{s} \in R^{p}$, subject to Assumptions 1– 2, using the control law in (6) and (21), and CCAS observers (22)–(23) along with the adaptation laws, given by

$$\begin{aligned} \dot{\hat{{\theta }}}_\mathrm{m} (t)= & {} -\Theta _\mathrm{m} g^\mathrm{T}(\hat{{x}}_\mathrm{m} (t))R_\mathrm{m} (y_\mathrm{m} (t)-C\hat{{x}}_\mathrm{m} (t)),\Theta _\mathrm{m} >0,\nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} \dot{\hat{{\theta }}}_\mathrm{s} (t)= & {} -\Theta _\mathrm{s} g^\mathrm{T}(\hat{{x}}_\mathrm{s} (t))R_\mathrm{s} (y_\mathrm{s} (t)-C\hat{{x}}_\mathrm{s} (t)),\Theta _\mathrm{s} >0,\nonumber \\ \end{aligned}$$

(25)

where $\Theta _\mathrm{m}$ and $\Theta _\mathrm{s}$ are the adaptation rates of appropriate dimensions, is that there exist positive-definite matrices $P_\mathrm{m}$, $P_\mathrm{s}$, and $P_\mathrm{o}$ and scalars $\alpha _1 >0, \quad \alpha _2 >0, \quad \alpha _3 >0, \quad \beta _1 >0$ and $\beta _2 >0$, such that matrix inequality

$$\begin{aligned} \Omega _2 =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\Upsilon _1 }&{} 0&{} {0.5P_\mathrm{m} { BF}+C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{o} }&{} {P_\mathrm{m} }&{} 0&{} 0&{} {P_\mathrm{m} }&{} 0 \\ {*}&{} {\Upsilon _2 }&{} {0.5P_\mathrm{s} { BF}-C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{o} }&{} 0&{} {P_\mathrm{s} }&{} 0&{} 0&{} {P_\mathrm{s} } \\ {*}&{} {*}&{} {\Upsilon _3 }&{} 0&{} 0&{} {P_\mathrm{o} }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\alpha _1 I_n }&{} 0&{} 0&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {-\alpha _2 I_n }&{} 0&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {-\alpha _3 I_n }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {-\beta _1 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {*}&{} {-\beta _2 I_n } \\ \end{array} }} \right] <0 \end{aligned}$$

(26)

holds, where

$$\begin{aligned} \Upsilon _1= & {} A^\mathrm{T}P_\mathrm{m} +P_\mathrm{m} A-C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{m}\\&-\,P_\mathrm{m} L_\mathrm{m} C+\alpha _1 L_f^2 I_n +\beta _1 L_{g\mathrm{m}}^2 I,\\ \Upsilon _2= & {} A^\mathrm{T}P_\mathrm{s} +P_\mathrm{s} A-C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{s} -P_\mathrm{s} L_\mathrm{s} C\\&+\,\alpha _2 L_f^2 I_n +\beta _2 L_{g\mathrm{s}}^2 I,\\ \Upsilon _3= & {} A^\mathrm{T}P_\mathrm{o} +P_\mathrm{o} A-F^\mathrm{T}B^\mathrm{T}P_\mathrm{o} -P_\mathrm{o} { BF}\\&+\,\alpha _3 L_f^2 I_n . \end{aligned}$$

Proof

The stability condition (26) for synchronization of the master and the slave systems is derived in “Appendix 1”. $\square$

5 Convex routines for observers-based control

The above-mentioned Theorems 1–2 provide solutions of the synchronization problems for the master–slave chaotic systems under the constraint that the controller gain matrix F and the observer gain matrices $L_\mathrm{m}$ and $L_\mathrm{s}$ are imparted. To get rid of this limitation, we have proposed two procedures in Theorems 3–4 to evaluate the possible values of F, $L_\mathrm{m}$ and $L_\mathrm{s}$ through convex routines. First, we provide a two-step LMI-based approach for solving the matrix inequalities in Theorem 2.

Theorem 3

A solution to the matrix inequalities presented in Theorem 2 is achievable, if and only if there exist positive-definite matrices $P_\mathrm{m} , P_\mathrm{s}$ and $P_\mathrm{o}$, scalars $\alpha _1 >0, \quad \alpha _2 >0, \quad \alpha _3 >0, \quad \beta _1 >0$, and $\beta _2 >0$ and a matrix $Z<0$ that can be partitioned as

$$\begin{aligned} Z=\left[ {{\begin{array}{ccc} {Z_{11} }&{} {Z_{12} }&{} {Z_{13} } \\ {*}&{} {Z_{22} }&{} {Z_{23} } \\ {*}&{} {*}&{} {Z_{33} } \\ \end{array} }} \right] , \end{aligned}$$

(27)

such that the inequalities

$$\begin{aligned} \left[ {{\begin{array}{cc} {{\begin{array}{ccc} {\hbox {Z}_{11} }&{} {\hbox {Z}_{12} }&{} {\hbox {Z}_{13} } \\ {*}&{} {\hbox {Z}_{22} }&{} {\hbox {Z}_{23} } \\ {*}&{} {*}&{} {\hbox {Z}_{33} } \\ {*}&{} {*}&{} {*} \\ {*}&{} {*}&{} {*} \\ {*}&{} {*}&{} {*} \\ {*}&{} {*}&{} {*} \\ {*}&{} {*}&{} {*} \\ \end{array} }}&{} {{\begin{array}{ccccc} {P_\mathrm{m} }&{} 0&{} 0&{} {P_\mathrm{m} }&{} 0 \\ 0&{} {P_\mathrm{s} }&{} 0&{} 0&{} {P_\mathrm{s} } \\ 0&{} 0&{} {P_\mathrm{o} }&{} 0&{} 0 \\ {-\alpha _1 I_n }&{} 0&{} 0&{} 0&{} 0 \\ {*}&{} {-\alpha _2 I_n }&{} 0&{} 0&{} 0 \\ *&{} {*}&{} {-\alpha _3 I_n }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\beta _1 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {-\beta _2 I_n } \\ \end{array} }} \\ \end{array} }} \right] <0, \nonumber \\\end{aligned}$$

(28)

$$\begin{aligned} \left[ {{\begin{array}{ccc} {Z_{11} -\Upsilon _1 }&{} {Z_{12} }&{} {Z_{13} -0.5P_\mathrm{m} { BF}-C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{o}} \\ {*}&{} {Z_{22} -\Upsilon _2 }&{} {Z_{23} -0.5P_\mathrm{s} { BF}+C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{o} } \\ {*}&{} {*}&{} {Z_{33} -\Upsilon _3 } \\ \end{array} }} \right] \ge 0\nonumber \\ \end{aligned}$$

(29)

are satisfied.

Proof

Sufficiency: Let $\Omega _2 \hbox {=} \Phi \hbox {<} \hbox {0}$ represent the matrix inequality (26). It can be partitioned as

$$\begin{aligned} \Phi= & {} \left[ {{\begin{array}{cc} {\Phi _{11} }&{} {\Phi _{12} } \\ {\Phi _{12}^\mathrm{T} }&{} {-\mathrm{diag}\{\alpha _1 \hbox {I}_\mathrm{n} ,\alpha _2 \hbox {I}_\mathrm{n} ,\alpha _3 \hbox {I}_\mathrm{n} ,\beta _1 \hbox {I}_\mathrm{n} ,\beta _2 \hbox {I}_\mathrm{n} \}} \\ \end{array} }} \right] <0, \nonumber \\ \Phi _{11}= & {} \left[ {{\begin{array}{ccc} {\Upsilon _1 }&{} 0&{} {0.5P_\mathrm{m} { BF}+C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{o} } \\ {*}&{} {\Upsilon _2 }&{} {0.5P_\mathrm{s} { BF}-C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{o} } \\ {*}&{} {*}&{} {\Upsilon _3 } \\ \end{array} }} \right] , \end{aligned}$$

(30)

$$\begin{aligned} \Phi _{12}= & {} \left[ {{\begin{array}{ccccc} {P_\mathrm{m} }&{} 0&{} 0&{} {P_\mathrm{m} }&{} 0 \\ 0&{} {P_\mathrm{s} }&{} 0&{} 0&{} {P_\mathrm{s} } \\ 0&{} 0&{} {P_\mathrm{o} }&{} 0&{} 0 \\ \end{array} }} \right] . \end{aligned}$$

(31)

Let us introduce a matrix $Z<0$ such that $Z\ge \Phi _{11}$. Note that if

$$\begin{aligned} \left[ {{\begin{array}{cc} Z&{} {\Phi _{12} } \\ {\Phi _{12}^\mathrm{T} }&{} {-\mathrm{diag}\{\alpha _1 \hbox {I}_\mathrm{n} ,\alpha _2 \hbox {I}_\mathrm{n} ,\alpha _3 \hbox {I}_\mathrm{n} ,\beta _1 \hbox {I}_\mathrm{n} ,\beta _2 \hbox {I}_\mathrm{n} \}} \\ \end{array} }} \right] <0 \end{aligned}$$

(32)

remains valid, $\Omega _2 =\Phi <0$ is ensured. One can also witness the inequality (28) by substituting (27) and (31) into (32). The matrix inequality $Z\ge \Phi _{11}$ can be written as (29) by putting the value of Z and $\Phi _{11}$ from (27) and (30), respectively. Therefore, the inequalities in Theorem 3 provide a sufficient condition to establish a solution of matrix inequalities in Theorem 2.

Necessity: If the inequality (26) is verified, there always exists a negative-definite matrix Z such that the inequalities $Z\ge \Phi _{11}$ and (32) are satisfied. At least, we can always choose a matrix Z validating $Z=\Phi _{11}$ (and thus ensuring $Z\ge \Phi _{11} )$, through which Z can be replaced by $\Phi _{11}$ to obtain (32). $Z\ge \Phi _{11}$ and (32) can be written as (27)–(28). Hence, the condition in Theorem 3 is necessary for the statement in Theorem 2, which completes the proof. $\square$

Remark 7

Obtainment of a solution to the matrix inequality (26) can be a difficult task. Notwithstanding, we provided a technique in Theorem 3 for the solution of the controller and the observer gain matrices. It is significant to note that the whole procedure discussed in Theorem 3 can be arranged into a two-step LMI-based approach. In the step-1, LMI (28) along with $Z<0$ can be solved. The solution of this LMI in the form of $Z, P_\mathrm{m} , P_\mathrm{s}$ and $P_\mathrm{o}$ can be utilitarian for solving the step-2. In the step-2, LMI (29) can be resolved for obtaining the controller and the observer gain matrices.

In the following theorem, an alternative method for obtaining the LMI-based solution of the nonlinear constraint (26) is proposed based on the decoupling technique [38].

Theorem 4

A sufficient condition for the solution of the constraints in Theorem 2 is that there exist positive-definite matrices $\tilde{P}_\mathrm{m} ,\tilde{P}_\mathrm{s}$ and $\bar{{P}}_\mathrm{o}$, matrices $H_1 , H_2$ and $H_3$ of appropriate dimensions, and scalars $\bar{{\alpha }}_1 >0, \quad \bar{{\alpha }}_2 >0, \quad \bar{{\alpha }}_3 >0, \quad \bar{{\beta }}_1 >0$, $\bar{{\beta }}_2 >0, \eta _1 >0$ and $\eta _2 >0$ such that the following LMIs are satisfied:

$$\begin{aligned}&\left[ {{\begin{array}{ccccc} {\Theta _1 }&{} {\tilde{P}_\mathrm{m} }&{} {\tilde{P}_\mathrm{m} }&{} {\bar{{\beta }}_1 L_{g\mathrm{m}} }&{} {\bar{{\alpha }}_1 L_f } \\ {*}&{} {-\bar{{\alpha }}_1 I_n }&{} 0&{} 0&{} 0 \\ {*}&{} {*}&{} {-\bar{{\beta }}_1 I_n }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\bar{{\beta }}_1 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {-\bar{{\alpha }}_1 I_n } \\ \end{array} }} \right] <0, \end{aligned}$$

(33)

$$\begin{aligned}&\left[ {{\begin{array}{ccccc} {\Theta _2 }&{} {\tilde{P}_\mathrm{s} }&{} {\tilde{P}_\mathrm{s} }&{} {\bar{{\beta }}_2 L_{g\mathrm{s}} }&{} {\bar{{\alpha }}_2 L_f } \\ {*}&{} {-\bar{{\alpha }}_2 I_n }&{} 0&{} 0&{} 0 \\ {*}&{} {*}&{} {-\bar{{\beta }}_2 I_n }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\bar{{\beta }}_2 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {-\bar{{\alpha }}_2 I_n } \\ \end{array} }} \right] <0, \end{aligned}$$

(34)

$$\begin{aligned}&\left[ {{\begin{array}{ccccc} {\Theta _3 }&{} {\bar{{P}}_\mathrm{o} }&{} 0&{} {\bar{{\alpha }}_3 L_f } \\ {*}&{} {-2\bar{{P}}_\mathrm{o} }&{} {\bar{{\alpha }}_3 I_n }&{} 0 \\ {*}&{} {*}&{} {-\bar{{\alpha }}_3 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\bar{{\alpha }}_3 I_n } \\ \end{array} }} \right] <0,\\&\Theta _1 =A^\mathrm{T}\tilde{P}_\mathrm{m} +\tilde{P}_\mathrm{m} A-C^\mathrm{T}H_1^\mathrm{T} -H_1 C,\nonumber \\&\Theta _2 =A^\mathrm{T}\tilde{P}_\mathrm{s} +\tilde{P}_\mathrm{s} A-C^\mathrm{T}H_2^\mathrm{T} -H_2 C,\nonumber \\&\Theta _3 =\bar{{P}}_\mathrm{o} A_\mathrm{o}^\mathrm{T} +A\bar{{P}}_\mathrm{o} -H_3^\mathrm{T} B^\mathrm{T}-BH_3\nonumber . \end{aligned}$$

(35)

The observer and controller gain matrices can be obtained by solving $L_\mathrm{m} =\tilde{P}_\mathrm{m}^{-1} H_1$, $L_\mathrm{s} =\tilde{P}_\mathrm{s}^{-1} H_2$ and $F=H_3 \bar{{P}}_\mathrm{o}^{-1}$.

Proof

To elaborate the agreement of Theorem 4 with Theorem 2, we can regenerate the matrix inequality (26) as presented in “Appendix 2”. $\square$

Remark 8

Analysis of Theorems 3 and 4 reveals that Theorem 3 provides a necessary and sufficient condition for the solution of Theorem 2, while Theorem 4 describes only a sufficient condition. The retrieval of the matrices $L_\mathrm{m} , L_\mathrm{s}$ and F using Theorem 3 may be comparatively difficult, as the value of Z achieved in the step-1 may not be suitable to attain feasible values of $L_\mathrm{m}, L_\mathrm{s}$ and F in the step-2. In contrast, Theorem 4 requires less effort for computation of the gains.

Similar to Theorems 3 and 4, convex conditions can be established for solving the inequalities in Theorem 1. However, the conditions are omitted here and left for the reader due to their analogous derivation nature to the constraints in Theorems 3–4.

6 Simulation results

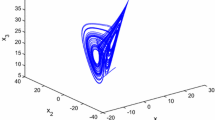
The validity of the proposed techniques for the synchronization of the master and the slave systems, proposed in Theorems 1–2, is illustrated by a corroborating simulation study for FitzHugh–Nagumo (FHN) master–slave architectures. The FHN systems are utilized to understand behavior of multiple neurons under external electrical stimulation current, such as deep brain stimulation therapy (see [10, 39] and [40]). Such therapies are used to overcome the symptoms such as tremor caused by neuronal disorders in the brain (such as Parkinson’s disease and Huntington disorder) because of malfunctioning of different parts of the brain. The FHN systems are described as follows:

$$\begin{aligned} \begin{array}{l} \dot{x}_\mathrm{m1} =x_\mathrm{m1} (x_\mathrm{m1} -1)(1-r_1 x_\mathrm{m1} )-x_\mathrm{m2} +I_\mathrm{o} , \\ \dot{x}_\mathrm{m2} =bx_\mathrm{m2} , \\ \dot{x}_{\mathrm{s}1} =x_{\mathrm{s}1} (x_{\mathrm{s}1} -1)(1-r_2 x_{\mathrm{s}1} )-x_{\mathrm{s}2} +I_\mathrm{o} , \\ \dot{x}_{\mathrm{s}2} =bx_{\mathrm{s}2}. \\ \end{array} \end{aligned}$$

Let the stimulation current is $I_\mathrm{o} =\left( {m/\omega } \right) \cos (\omega t)$ and the parameters are selected as $r_1 =10.1, r_2 =9.9, b=1, m=0.1, \omega =2\pi f$ and $f=0.129$. The initial conditions of both states, that is, normalized membrane potentials for the master and the slave systems, are assumed to be $x_{\mathrm{m},1} (0)=0.2$ and $x_{\mathrm{m},2} (0)=0.5$, while recovery variables has initial state as $x_\mathrm{s,1} (0)=\hbox {0.4 }$ and $x_\mathrm{s,2} (0)=\hbox {0.1}$. Phase portraits of both the master and slave systems are shown in Fig. 3a, b, respectively, to endorse the chaotic behavior of FHN drive and response systems. These initial conditions show that there is a difference between the corresponding states (membrane potentials) of the master and the slave FHN system. The time series for both states of the master and the slave systems and the corresponding errors are plotted in Fig. 3c–e.

Fig. 3

Phase portraits of the master and the slave FHN systems and time evolutions of the normalized membrane potentials, recovery variables and membrane potential errors: a phase portrait of the master system, b phase portrait of the slave system, c time evolution of membrane potentials, d time evolution of recovery variables e time evolution of errors between corresponding states of master and slave systems

It should be noted that the simulation results provided herein for both nonadaptive and adaptive control techniques are based on normalized membrane potentials for FHN systems because of the following three reasons. First, the above-mentioned mathematical representation of FHN systems inherently supports the normalized membrane potential as seen in the literature [10, 39] and [40]. Second, the normalized potential for the FHN system can demonstrate a generalized behavior of a neuron. The ranges of voltages for the membrane potentials of neurons for different species are not alike; however, these membrane potentials can be normalized to the same ranges by employing different scaling factors. Consequently, the normalized membrane potentials provide an overall behavior of neurons, applicable to a large number of species. Third, normalized variables are useful from control point of view due to conversion of the variable ranges to desirable values as it allows calculation of a reasonable controller gain for simulation and implementation purpose and simplifies the numerical calculation handling. As a result, we took advantage of the normalized membrane potential for the synchronization control simulation purpose.

6.1 Simulation results for nonadaptive control

If the nonlinear chaotic master and slave systems have all the parameters known, FHN system dynamics, in accordance with (1)–(2), can be written as

$$\begin{aligned}&A=\left[ {{\begin{array}{cc} {-1}&{} {-1} \\ 1&{} 0 \\ \end{array} }} \right] , \quad B=\left[ {{\begin{array}{c} 1 \\ 0 \\ \end{array} }} \right] ,\quad C=\left[ {{\begin{array}{cc} 1&{} 0 \\ \end{array} }} \right] ,\\&\quad f(x(t))=\left[ {{\begin{array}{c} {11x_1^2 -10x_1^3 +\frac{m}{\omega }\cos (\omega t)} \\ 0 \\ \end{array} }} \right] . \end{aligned}$$

The synchronization problem can be resolved by employing nonadaptive approach propounded in Theorem 1. The observer gain matrices $L_\mathrm{m}$ and $L_\mathrm{s}$ and the controller gain matrix Fcan be selected by using a similar two-step procedure discussed in Theorem 3. By selecting

$$\begin{aligned} L_\mathrm{m} =\left[ {{\begin{array}{c} {1.3} \\ 0 \\ \end{array} }} \right] ,L_\mathrm{s} =\left[ {{\begin{array}{c} {1.3} \\ 0 \\ \end{array} }} \right] ,F=\left[ {{\begin{array}{cc} 1&{} 0 \\ \end{array} }} \right] \end{aligned}$$

and applying the control law $u=F(\hat{{x}}_\mathrm{m} -\hat{{x}}_\mathrm{s} )$, simulation results are shown in Fig. 4. The plots affirm the validity of the proposed scheme for synchronization of the master–slave chaotic systems by elaborating complete synchronization. Figure 4a, b shows phase portraits of the FHN master and the slave networks, respectively. Figure 4c, d displays the phase portraits of observed states of the master and the slave systems, respectively. Similarly, Fig. 4e, f represents the temporal evolution of both states of the master–slave architectures with their respective observers. Figure 5 witnesses the fact that by application of the proposed control law, various synchronization errors $e_{\mathrm{m}1} ,e_{\mathrm{m}2} , e_{\mathrm{s}1} ,e_{\mathrm{s}2} , e_{\mathrm{o}1}$, and $e_{\mathrm{o}2}$ asymptotically converge to the zero.

Fig. 4

Phase portraits of the master and the slave FHN systems, phase portraits of their corresponding observers using the approach provided in Theorem 1, the time evolutions of the membrane potentials and the recovery variables: a phase portrait of the master system, b phase portrait of the slave system, c phase portrait of the master observer, d phase portrait of the slave observer, e time evolution of membrane potentials of the master and slave systems and their corresponding observers, f time evolution of recovery variables of the master and slave systems and their corresponding observer

Fig. 5

Synchronization errors between the master–slave systems and their corresponding observers, the synchronization errors between the observers of the master–slave systems using the approach provided in Theorem 1 and the errors between the corresponding states of the master and the slave systems

From (16) and (17), it is clear that the values of observer gain matrices $L_\mathrm{m}$ and $L_\mathrm{s}$ have explicit effects on the $e_\mathrm{m} (t)$ and $e_\mathrm{s} (t)$. Similarly, from (18), we can mention the value of F has an explicit effect on $e_\mathrm{o} (t)$. That is why, with the change in the gains, the trend of synchronization for the nonlinear control scheme is elaborated in Figs. 6 and 7. These figures show the time evolution of $e_{\mathrm{m}1} (t)$ and $e_{\mathrm{o}1} (t)$ only because the second terms of the observer gain and input matrices are zero and the effects on $e_{\mathrm{m}2} (t)$ and $e_{\mathrm{o}2} (t)$ may not have any relation with the current selections of the observer and controller gains. Additionally, the behavior of $e_{\mathrm{s}1} (t)$ is similar to that of $e_{\mathrm{m}1} (t)$; therefore, it is not plotted here.

Fig. 6

Synchronization error $e_{\mathrm{m}1}$ for different values of observer gains and fixed value of controller gain

Fig. 7

Synchronization error $e_{\mathrm{o}1}$ for different values of controller gains and fixed values of observer gains

To show the degree of synchronization (DOS) quantitatively, we define error-based DOS criteria as follows:

$$\begin{aligned} \hbox {DOS}(\tilde{e})=1-\frac{\left\| {\tilde{e}} \right\| _{2 } }{\left\| {\tilde{e}} \right\| _{2,\max } }=1-\frac{\sqrt{\int \nolimits _0^t {\tilde{e}^{2}\mathrm{d}t} }}{\left. {\sqrt{\int \nolimits _0^t {\tilde{e}^{2}\mathrm{d}t} }} \right| _{\max } }, \end{aligned}$$

where $\left\| {\tilde{e}} \right\| _{2 }$ is the 2-norm of any error $\tilde{e}$ and $\left\| {\tilde{e}} \right\| _{2,\max }$is the maximum value of the norm over a range of the observer or the controller gain. Note that the minimum and maximum values of $\hbox {DOS(}\tilde{e}\hbox {)}$ are 0 and 1, respectively. The minima occur for $\left\| {\tilde{e}} \right\| _2 =\left\| {\tilde{e}} \right\| _{2,\max }$, when synchronization error is maximum, while the maxima occur for the minimum synchronization error, that is, $\left\| {\tilde{e}} \right\| _2 =0$. It is important to mention that the maximum value $\left\| {\tilde{e}} \right\| _{2,\max }$ is obtained by choosing either $L_\mathrm{m} =L_\mathrm{s} =[ {{\begin{array}{cc} 0&{} 0 \\ \end{array} }}]^\mathrm{T}$ for any fixed value of F or by using $F=[ {{\begin{array}{cc} 0&{} 0 \\ \end{array} }}]$ with some fixed value of $L_\mathrm{m}$ and $L_\mathrm{s}$. Degree of synchronization is calculated for nonadaptive case to show the effect of variations in $L_\mathrm{m}$, $L_\mathrm{s}$ and F. Tables 1 and 2 demonstrate the effect of $L_\mathrm{m} =L_\mathrm{s}$ and Fon the DOS, respectively. It can be concluded that increase in the entries of $L_\mathrm{m}$ and F can increase degree of synchronization errors $e_{\mathrm{m}1} (t)$ and $e_{\mathrm{o}1} (t)$, respectively.

Table 1 DOS for different values of $L_\mathrm{m} =L_\mathrm{s}$ and fixed $F=[1\; 0]$

Table 2 DOS for different values of F and fixed $L_\mathrm{m} =L_\mathrm{s} =[1.3 0]^\mathrm{T}$

6.2 Simulation results for adaptive control

If the value of the parameters $r_1$ and $r_2$ is unknown, we can assign $\theta _\mathrm{m} =r_1$ and $\theta _\mathrm{s} =r_2$. The FHN systems can be represented by

$$\begin{aligned}&A=\left[ {{\begin{array}{cc} {-1}&{} {-1} \\ 1&{} 0 \\ \end{array} }} \right] ,\quad B=\left[ {{\begin{array}{cc} 1 \\ 0 \\ \end{array} }} \right] ,\quad C=\left[ {{\begin{array}{cc} 1&{} 0 \\ \end{array} }} \right] ,\\&\quad f(x(t))=\left[ {{\begin{array}{c} {x_1^2 +\frac{m}{\omega }\cos (\omega t)} \\ 0 \\ \end{array} }} \right] \\&\quad g(x(t))=x_1^2 (t)-x_1^3 (t). \end{aligned}$$

It is important to mention that to increase the feasibility of the design constraints, the matrix A and the nonlinearity f(x(t)) of the FHN system are modified as

$$\begin{aligned} A=\left[ {{\begin{array}{cc} {-1}&{} {-1} \\ 1&{} {-0.3} \\ \end{array} }} \right] ,\quad f(x(t))=\left[ {{\begin{array}{c} {x_1^2 +\frac{m}{\omega }\cos (\omega t)} \\ {0.3x_2 } \\ \end{array} }} \right] , \end{aligned}$$

without loss of generality. By application of Theorem 3, we obtain

$$\begin{aligned} L_\mathrm{m} =\left[ {{\begin{array}{c} {\hbox {3.286}} \\ 0 \\ \end{array} }} \right] ,\quad L_\mathrm{s} =\left[ {{\begin{array}{c} {\hbox {3.286}} \\ 0 \\ \end{array} }} \right] ,\quad F=\left[ {{\begin{array}{cc} {\hbox {1.409}}&{} {0.7} \\ \end{array} }} \right] . \end{aligned}$$

By applying the control and adaptation laws in (21) and (24)–(25), simulation results are presented in Fig. 8 to uphold the validity of proposed scheme for adaptive synchronization of the master and the slave chaotic systems under unknown parameters. Fig. 8a, b shows phase portraits of the master and the slave FHN systems. Figure 8c, d characterizes the phase portraits of observed states of the master and the slave systems. Similarly, Fig. 8e, f demonstrates the temporal evolution of both states of the master–slave systems and their observers. Figure 9 demonstrates that by application of the proposed control and adaptation laws, complete synchronization of the master observer and the slave observer is attained and the errors $e_{\mathrm{m}1} ,e_{\mathrm{m}2} , e_{\mathrm{s}1} ,e_{\mathrm{s}2} , e_{\mathrm{o}1}$ and $e_{\mathrm{o}2}$ converge to the origin. Simulation results for the adaptation of the unknown parameters are plotted in Fig. 10, which shows convergence of the adaptive parameters to their true values, that is, $\theta _\mathrm{m} =r_1 =10.1$ and $\theta _\mathrm{s} =r_2 =9.9$.

Fig. 8

Phase portraits of the master and the slave FHN systems, phase portraits of their corresponding observers using the approach provided in Theorem 3, the time evolutions of the normalized membrane potentials and the recovery variables: a phase portrait of the master system, b phase portrait of the slave system, c phase portrait of the master observer, d phase portrait of the slave observer, e time evolution of membrane potentials of the master and slave systems and their corresponding observers, f time evolution of recovery variables of the master and slave systems and their corresponding observer

Fig. 9

Synchronization errors between the master–slave systems and their corresponding observers, the synchronization errors between the observers of the master–slave systems using the approach provided in Theorem 3 and the errors between the corresponding states of the master and the slave systems

Fig. 10

Graphical representation of convergence of the adaptation parameters to their true values using the approach provided in Theorem 3

It is noteworthy that synchronization behavior varies with the change in the observer gain matrices $L_\mathrm{m}$ and $L_\mathrm{s}$ and the controller gain matrix F. Figure 11 shows dependency of synchronization behavior on the observer gain matrices $L_\mathrm{m}$ and $L_\mathrm{s}$, by keeping the controller gain matrix as $F=\left[ {{\begin{array}{cc} {\hbox {1.409}}&{} {0.7} \\ \end{array} }} \right]$, while Fig. 12 shows dependency of synchronization behavior on the controller gain matrix F for $L_\mathrm{m} =L_\mathrm{s} =\left[ {{\begin{array}{cc} {\hbox {3.286}}&{} 0 \\ \end{array} }} \right] ^\mathrm{T}$. Tables 3 and 4 show the effects of $L_\mathrm{m} =L_\mathrm{s}$ and Fon the DOS, respectively, for the adaptive mechanism, which are similar as for the case of the nonadaptive control discussed in the previous subsection.

Table 3 DOS for different values of $L_\mathrm{m} =L_\mathrm{s}$ and fixed $F=[1.5 0.7]$

Table 4 DOS for different values of F and fixed $L_\mathrm{m} =L_\mathrm{s} =[3.286 0]^\mathrm{T}$

Fig. 11

Synchronization error $e_{\mathrm{m}1}$ for different values of observer gains and fixed value of controller gain for proposed adaptive controller

Fig. 12

Synchronization error $e_{\mathrm{o}1}$ for different values of controller gains and fixed values of observer gains for proposed adaptive control

7 Conclusions

A new approach for the synchronization of the master–slave chaotic systems by means of CCS and CCAS observers-based control schemes was propounded in this paper. The proposed techniques are applicable to attain multi-objectives, that is, estimation of states of chaotic systems and control of the synchronization errors in the absence and the presence of unknown parameters. The novel CCAS observers presented are more generic than the CCS observers but with a snag of slow response because of adaptation of the unknown parameters. By means of Lyapunov stability theory, a convergence condition for the synchronization errors was developed in the form of nonlinear matrix inequalities. The evaluation of controller and observer gain matrices from the resulted nonlinear matrix inequalities using a two-step approach was described, and further, a decoupling methodology to attain LMI-based solution was presented. The two-step technique is more generic, and the decoupling method requires less computational efforts for the design of the controller and the observer. The recommended methodologies for synchronization are dissimilar with the conventional chaos synchronization approaches, requiring exact states of the master–slave systems for feedback control. In future, robust nonlinear and robust adaptive control approaches for the synchronization of the nonlinear systems using nonlinear and adaptive observers can be considered against noises and disturbances. Numerical simulation for synchronization of FitzHugh–Nagumo neuronal systems was illustrated to demonstrate effectiveness of the proposed observers-based chaos synchronization control methodologies.

Appendices

Appendix 1: Proof of Theorem 2

Using (10)–(12), CCAS observers (22)–(23) and systems (1)–(2) reveal the error systems as

$$\begin{aligned} \dot{e}_\mathrm{m} (t)= & {} Ae_\mathrm{m} (t)+\left[ {f(x_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{m} (t))} \right] \nonumber \\&+\,Bg(x_\mathrm{m} (t))\theta _\mathrm{m} -Bg(\hat{{x}}_\mathrm{m} (t))\widehat{\theta }_\mathrm{m} (t) \nonumber \\&-\,L_\mathrm{m} Ce_\mathrm{m} (t)+\frac{1}{2}{} { BF}e_\mathrm{o} (t), \end{aligned}$$

(36)

$$\begin{aligned} \dot{e}_\mathrm{s} (t)= & {} Ae_\mathrm{s} (t)+\left[ {f(x_\mathrm{s} (t))-f(\hat{{x}}_\mathrm{s} (t))} \right] \nonumber \\&+\,Bg(x_\mathrm{s} (t))\theta _\mathrm{s} -Bg(\hat{{x}}_\mathrm{s} (t))\widehat{\theta }_\mathrm{s} (t) \nonumber \\&-\,L_\mathrm{s} Ce_\mathrm{s} (t)+\frac{1}{2}{} { BF}e_\mathrm{o} (t),\end{aligned}$$

(37)

$$\begin{aligned} \dot{e}_\mathrm{o} (t)= & {} Ae_\mathrm{o} (t)+\left[ {f(\hat{{x}}_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{s} (t))} \right] \nonumber \\&+\,Bg(\hat{{x}}_\mathrm{m} (t))\hat{{\theta }}_\mathrm{m}(t)-Bg(\hat{{x}}_\mathrm{s} (t))\hat{{\theta }}_\mathrm{s} (t) \nonumber \\&+\,L_\mathrm{m} Ce_\mathrm{m} (t)-L_\mathrm{s} Ce_\mathrm{s} (t)-{ BF}e_\mathrm{o} (t)-Bu_g.\nonumber \\ \end{aligned}$$

(38)

Applying $\tilde{\theta }_\mathrm{m} (t)=\theta _\mathrm{m} -\hat{{\theta }}_\mathrm{m} (t)$ and $g_\mathrm{m} (x_\mathrm{m} (t))=Bg(x_\mathrm{m} (t))\theta _\mathrm{m}$ and, further, employing the mathematical fact

$$\begin{aligned}&Bg(x_\mathrm{m} (t))\theta _\mathrm{m} -Bg(\hat{{x}}_\mathrm{m} (t))\hat{{\theta }}_\mathrm{m} (t)=g_\mathrm{m} (x_\mathrm{m} (t))\\&\quad -\,g_\mathrm{m} (\hat{{x}}_\mathrm{m} (t))+Bg(\hat{{x}}_\mathrm{m} (t))\tilde{\theta }_\mathrm{m} (t), \end{aligned}$$

we obtain

$$\begin{aligned} \dot{e}_\mathrm{m} (t)= & {} (A-L_\mathrm{m} C)e_\mathrm{m} (t)+\left[ {f(x_\mathrm{m} (t))-f(\hat{{x}}_\mathrm{m} (t))} \right] \nonumber \\&+\,\frac{1}{2}{} { BF}e_\mathrm{o} (t) +g_\mathrm{m} (x_\mathrm{m} (t))-g_\mathrm{m} (\hat{{x}}_\mathrm{m} (t)) \nonumber \\&+\,Bg(\hat{{x}}_\mathrm{m} (t))\widetilde{\theta }_\mathrm{m} (t). \end{aligned}$$

(39)

Similarly, it is implicit to obtain

$$\begin{aligned} \dot{e}_\mathrm{s} (t)= & {} (A-L_\mathrm{s} C)e_\mathrm{s} (t)+\left[ {f(x_\mathrm{s} (t))-f(\hat{{x}}_\mathrm{s} (t))} \right] \nonumber \\&+\,\frac{1}{2}{} { BF}e_\mathrm{o} (t) +g(x_\mathrm{s} (t))-g(\hat{{x}}_\mathrm{s} (t))\nonumber \\&+\,Bg(\hat{{x}}_\mathrm{s} (t))\widetilde{\theta }_\mathrm{s} (t). \end{aligned}$$

(40)

Using $u_g =g(\hat{{x}}_\mathrm{m} (t))\hat{{\theta }}_\mathrm{m} -g\left( {\hat{{x}}_\mathrm{s} (t)} \right) \hat{{\theta }}_\mathrm{s}$, we have

$$\begin{aligned} \dot{e}_\mathrm{o} (t)= & {} (A - { BF})e_\mathrm{o} (t) + \left[ {f(\hat{x}_\mathrm{m} (t)) - f(\hat{x}_\mathrm{s} (t))} \right] \nonumber \\&+\, L_\mathrm{m} Ce_\mathrm{m} (t) - L_\mathrm{s} Ce_\mathrm{s} (t) \end{aligned}$$

(41)

Consider the Lyapunov function

$$\begin{aligned} V(t)= & {} e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} e_\mathrm{m} (t)+e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} e_\mathrm{s} (t)+e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} e_\mathrm{o} (t) \nonumber \\&+\,\tilde{\theta }_\mathrm{m}^\mathrm{T} (t)\Theta _\mathrm{m}^{-1} \tilde{\theta }_\mathrm{m} (t)+\tilde{\theta }_\mathrm{s}^\mathrm{T} (t)\Theta _\mathrm{s}^{-1} \tilde{\theta }_\mathrm{s} (t). \end{aligned}$$

(42)

Its time derivative along (39)–(41), by employing $B^\mathrm{T}P_\mathrm{m} -R_\mathrm{m} C=0$ and $B^\mathrm{T}P_\mathrm{s} -R_\mathrm{s} C=0$, is given by

$$\begin{aligned} \dot{V}(t)= & {} e_\mathrm{m}^\mathrm{T} (t)(A^\mathrm{T} - C^\mathrm{T} L_\mathrm{m}^\mathrm{T} )P_\mathrm{m} e_\mathrm{m} (t) + \left[ f(x_\mathrm{m} (t))\right. \nonumber \\&\left. - f(\hat{x}_\mathrm{m} (t)) \right] ^\mathrm{T} P_\mathrm{m}e_\mathrm{m} (t) \nonumber \\&+\, 0.5e_\mathrm{o}^\mathrm{T} (t)F^\mathrm{T} B^\mathrm{T} P_\mathrm{m} e_\mathrm{m} (t) + \left[ g_\mathrm{m} (x_\mathrm{m} (t))\right. \nonumber \\&\left. -\, g_\mathrm{m} (\hat{x}_\mathrm{m} (t)) \right] ^\mathrm{T}P_\mathrm{m} e_\mathrm{m} (t)\nonumber \\&+\, \widetilde{\theta }_\mathrm{m}^\mathrm{T} (t)g^\mathrm{T}(\hat{x}_\mathrm{m} (t))R_\mathrm{m} (y_\mathrm{m} (t)\nonumber \\&-\, C\hat{x}_\mathrm{m} (t)) + e_\mathrm{m}^\mathrm{T}(t)P_\mathrm{m} \left( {A - L_\mathrm{m} C} \right) e_\mathrm{m} (t)\nonumber \\&+\,e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} \left[ {f(x_\mathrm{m} (t)) - f(\hat{x}_\mathrm{m} (t))}\right] \nonumber \\&+\, 0.5e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} { BF}e_\mathrm{o} (t) \nonumber \\&+\, e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} \left[ {g_\mathrm{m} (x_\mathrm{m} (t)) - g_\mathrm{m}(\hat{x}_\mathrm{m} (t))}\right] \nonumber \\&+\, (y_\mathrm{m} (t) - C\hat{x}_\mathrm{m} (t))^\mathrm{T} R_\mathrm{m}^\mathrm{T} g(\hat{x}_\mathrm{m}(t))\tilde{\theta }_\mathrm{m} (t) \nonumber \\&+\,e_\mathrm{s}^\mathrm{T} (t)(A^\mathrm{T} -C^\mathrm{T} L_\mathrm{s}^\mathrm{T} )P_\mathrm{s} e_\mathrm{s} (t) + \left[ f(x_\mathrm{m} (t)) \right. \nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned}&\left. -\,f(\hat{x}_\mathrm{m} (t)) \right] ^\mathrm{T} P_\mathrm{s} e_\mathrm{s} (t)\nonumber \\&+\,0.5e_\mathrm{o}^\mathrm{T} (t)F^\mathrm{T} B^\mathrm{T} P_\mathrm{s} e_\mathrm{s} (t) + \,\left[ g_\mathrm{s} (x_\mathrm{s}(t))\right. \nonumber \\&\left. -\, g_\mathrm{s} (\hat{x}_\mathrm{s} (t)) \right] ^\mathrm{T} P_\mathrm{s} e_\mathrm{s} (t) \nonumber \\&+\,\tilde{\theta }_\mathrm{s}^\mathrm{T} (t)g^\mathrm{T} (\hat{x}_\mathrm{s} (t))R_\mathrm{s} (y_\mathrm{s} (t)\nonumber \\&-\,C\hat{x}_\mathrm{s} (t)) + \,e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} (A - L_\mathrm{s} C)e_\mathrm{s} (t) \nonumber \\&+\, e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} \left[ {f(x_\mathrm{s} (t)) - f(\hat{x}_\mathrm{s} (t))}\right] \nonumber \\&+\, 0.5e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} { BF}e_\mathrm{o} (t)\nonumber \\&+\, e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} \left[ {g_\mathrm{s} (x_\mathrm{s} (t)) - g_\mathrm{s} (\hat{x}_\mathrm{s} (t))} \right] + (y_\mathrm{m} (t)\nonumber \\&-\, C\hat{x}_\mathrm{m} (t))^\mathrm{T}R_\mathrm{s}^\mathrm{T} g(\hat{x}_\mathrm{s} (t))\tilde{\theta }_\mathrm{s} (t)\nonumber \\&+\,e_\mathrm{o}^\mathrm{T} (t)(A^\mathrm{T} - F^\mathrm{T} B^\mathrm{T} )P_\mathrm{o} e_\mathrm{o} (t)+\left[ f(\hat{x}_\mathrm{m} (t))\right. \nonumber \\&\left. -\, f(\hat{x}_\mathrm{s} (t)) \right] ^\mathrm{T}P_\mathrm{o} e_\mathrm{o} (t) \nonumber \\&+\, e_\mathrm{m}^\mathrm{T} (t)C^\mathrm{T} L_\mathrm{m}^\mathrm{T} P_\mathrm{o} e_\mathrm{o}(t) - e_\mathrm{s}^\mathrm{T} (t)C^\mathrm{T} L_\mathrm{s}^\mathrm{T} P_\mathrm{o} e_\mathrm{o} (t)\nonumber \\&+\, e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} (A - { BF})e_\mathrm{o} (t) \end{aligned}$$

Using Assumption 1 for positive scaling factors $\beta _1$ and $\beta _2$, we have

$$\begin{aligned}&-\,\beta _1 \left[ {g_\mathrm{m} (x_\mathrm{m} (t))-g(\hat{{x}}_\mathrm{m} (t))} \right] ^\mathrm{T}\left[ {g_\mathrm{m} (x_\mathrm{m} (t))-g_\mathrm{m} (\hat{{x}}_\mathrm{m} (t))} \right] \nonumber \\&\quad +\,\beta _1 L_{g\mathrm{m}}^2 e_\mathrm{m}^\mathrm{T} \left( t \right) e_\mathrm{m} \left( t \right) >0,\\&-\,\beta _2 \left[ {g_\mathrm{s} (x_\mathrm{s} (t))-g_\mathrm{s} (\hat{{x}}_\mathrm{s} (t))} \right] ^\mathrm{T}\left[ {g_\mathrm{s} (x_\mathrm{s} (t))-g_\mathrm{s} (\hat{{x}}_\mathrm{s} (t))} \right] \nonumber \\&\quad +\,\beta _2 L_{g\mathrm{s}}^2 e_\mathrm{s}^\mathrm{T} \left( t \right) e_\mathrm{s} \left( t \right) >0, \end{aligned}$$

Employing the above inequalities, using (43), $\dot{\tilde{\theta }}_\mathrm{m} (t)=-\dot{\hat{{\theta }}}_\mathrm{m} (t)$ and $\dot{\tilde{\theta }}_\mathrm{s} (t)=-\dot{\hat{{\theta }}}_\mathrm{s} (t)$ and incorporating the adaptation laws (24)–(25) under Assumption 2, it implies that

$$\begin{aligned} \dot{V}\left( t \right)\le & {} e_\mathrm{m}^\mathrm{T} (t)(A^\mathrm{T} - C^\mathrm{T} L_\mathrm{m}^\mathrm{T} )P_\mathrm{m} e_\mathrm{m} (t)\\&+\, \left[ {f(x_\mathrm{m} (t)) - f(\hat{x}_\mathrm{m} (t))} \right] ^\mathrm{T} P_\mathrm{m} e_\mathrm{m} (t) \\&+\, 0.5e_\mathrm{o}^\mathrm{T} (t)F^\mathrm{T} B^\mathrm{T} P_\mathrm{m} e_\mathrm{m} (t) + \left[ g_\mathrm{m} (x_\mathrm{m} (t))\right. \nonumber \\&\left. -\, g(\hat{x}_\mathrm{m} (t)) \right] ^\mathrm{T} P_\mathrm{m} e_\mathrm{m} (t)\\&+\, e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} (A- L_\mathrm{m} C)e_\mathrm{m} (t)\\&+\,e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} \left[ {f(x_\mathrm{m}(t)) - f(\hat{x}_\mathrm{m} (t))} \right] \\&+\,0.5e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m}{} { BF}e_\mathrm{o} (t) + e_\mathrm{m}^\mathrm{T} (t)P_\mathrm{m} \left[ g(x_\mathrm{m} (t),\theta _\mathrm{m} )\right. \\&\left. -\,g(\hat{x}_\mathrm{m} (t),\theta _\mathrm{m} ) \right] \\&+\, e_\mathrm{s}^\mathrm{T}(t)(A^\mathrm{T} - C^\mathrm{T} L_\mathrm{s}^\mathrm{T} )P_\mathrm{s} e_\mathrm{s} (t) + \left[ f(x_\mathrm{m} (t))\right. \\&\left. -\, f(\hat{x}_\mathrm{m} (t)) \right] ^\mathrm{T} P_\mathrm{s} e_\mathrm{s} (t) \\&+\,0.5e_\mathrm{o}^\mathrm{T} (t)F^\mathrm{T} B^\mathrm{T} P_\mathrm{s} e_\mathrm{s} (t) + \,\left[ g(x_\mathrm{s} (t),\theta _\mathrm{s} )\right. \nonumber \\&\left. -\, g(\hat{x}_\mathrm{s} (t),\theta _\mathrm{s} ) \right] ^\mathrm{T}P_\mathrm{s} e_\mathrm{s} (t) \\ \end{aligned}$$

$$\begin{aligned}&+\,e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} (A - L_\mathrm{s} C)e_\mathrm{s} (t)+ e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s}\\&\times \,\left[ {f(x_\mathrm{s} (t)) - f(\hat{x}_\mathrm{s} (t))} \right] \\&+\, 0.5e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} { BF}e_\mathrm{o} (t)\\&+\,e_\mathrm{s}^\mathrm{T} (t)P_\mathrm{s} \left[ {g(x_\mathrm{s} (t),\theta _\mathrm{s} ) - g(\hat{x}_\mathrm{s} (t),\theta _\mathrm{s} )} \right] \\&+\, e_\mathrm{o}^\mathrm{T}(t)(A^\mathrm{T} - F^\mathrm{T} B^\mathrm{T} )P_\mathrm{o} e_\mathrm{o} (t)\\&+\,\left[ {f(\hat{x}_\mathrm{m} (t)) - f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T} P_\mathrm{o} e_\mathrm{o}(t) \\&+\, e_\mathrm{m}^\mathrm{T} (t)C^\mathrm{T} L_\mathrm{m}^\mathrm{T} P_\mathrm{o} e_\mathrm{o} (t) \\&-\,e_\mathrm{s}^\mathrm{T} (t)C^\mathrm{T} L_\mathrm{s}^\mathrm{T} P_\mathrm{o} e_\mathrm{o} (t)\\&+\,e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} (A - { BF})e_\mathrm{o} (t)\\&+\, e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} \left[ f(\hat{x}_\mathrm{m} (t) - f(\hat{x}_\mathrm{s} (t) \right] \\&+\, e_\mathrm{o}^\mathrm{T}(t)P_\mathrm{o} L_\mathrm{m} Ce_\mathrm{m} (t) - e_\mathrm{o}^\mathrm{T} (t)P_\mathrm{o} L_\mathrm{s} Ce_\mathrm{s} (t) \\ \end{aligned}$$

$$\begin{aligned}&-\, \alpha _{1} \left[ {f(x_\mathrm{m} (t))-f(\hat{x}_\mathrm{m} (t))} \right] ^\mathrm{T}\\&\times \,\left[ {f(x_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{m} (t))} \right] + \alpha _{1} L_{f}^{2} e_\mathrm{m}^\mathrm{T} (t)e_\mathrm{m} (t) \\&-\, \alpha _{2} \left[ {f(x_\mathrm{s} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T} \left[ f(x_\mathrm{s}(t))\right. \\&\left. -\,f(\hat{x}_\mathrm{s} (t)) \right] + \alpha _{2} L_{f}^{2} e_\mathrm{s}^\mathrm{T}(t)e_\mathrm{s} (t)\\&-\, \alpha _{3} \left[ {f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T}\\&\times \,\left[ {f(\hat{x}_\mathrm{m} (t)){-}f(\hat{x}_\mathrm{s} (t))} \right] \\&+\, \alpha _{3} L_{f}^{2} e_\mathrm{o}^\mathrm{T} (t)e_\mathrm{o} (t) \\&-\, \beta _{1} \left[ g_\mathrm{m} (x_\mathrm{m} (t))\right. \\&\left. -\,g(\hat{x}_\mathrm{m} (t)) \right] ^\mathrm{T} \left[ {g_\mathrm{m} (x_\mathrm{m} (t)){-}g_\mathrm{m} (\hat{x}_\mathrm{m} (t))} \right] \nonumber \\&+\, \beta _{1} L_{{gm}}^{2} e_\mathrm{m}^\mathrm{T} \left( t \right) e_\mathrm{m} \left( t \right) \\&-\, \beta _{2} \left[ {g_\mathrm{s} (x_\mathrm{s} (t)){-}g_\mathrm{s} (\hat{x}_\mathrm{s} (t))} \right] ^\mathrm{T}\\&\times \left[ {g_\mathrm{s} (x_\mathrm{s} (t)){-}g_\mathrm{s} (\hat{x}_\mathrm{s} (t))} \right] + \beta _{2} L_{{gs}}^{2} e_\mathrm{s}^\mathrm{T} \left( t \right) e_\mathrm{s} \left( t \right) , \end{aligned}$$

which further reveals

$$\begin{aligned}&\dot{V}\left( t \right) \le E_{2}^\mathrm{T} (t)\Omega _{2} E_{2} (t)\\&E_2^\mathrm{T} (t)=\left[ {e_\mathrm{m}^\mathrm{T} (t)}\quad {e_\mathrm{s}^\mathrm{T} (t)}\quad {e_\mathrm{o}^\mathrm{T} (t)}\quad {\Delta f_{\mathrm{m}\hat{{m}}}^\mathrm{T} (t)}\quad {\Delta f_{\mathrm{s}\hat{{s}}}^\mathrm{T} (t)}\right. \nonumber \\&\left. \quad {\Delta f_{\hat{{m}}\hat{{s}}}^\mathrm{T} (t)}\quad {\Delta g_{\mathrm{m}\hat{{m}}}^\mathrm{T} (t)}\quad {\Delta g_{\mathrm{s}\hat{{s}}}^\mathrm{T} (t)} \right] ,\nonumber \\&\Delta g_{\mathrm{m}\hat{{m}}} (t)=\left[ {g_\mathrm{m} (x_\mathrm{m} (t))-g_\mathrm{m} (\hat{{x}}_\mathrm{m} (t))} \right] ,\nonumber \\&\Delta g_{\mathrm{s}\hat{{s}}} (t)=\left[ {g_\mathrm{s} (x_\mathrm{s} (t))-g_\mathrm{s} (\hat{{x}}_\mathrm{s} (t))} \right] .\nonumber \end{aligned}$$

(44)

If (26) is satisfied, the above inequality (44) implies $\dot{V}(t) < 0$. Hence, the errors $e_\mathrm{m} (t), e_\mathrm{s} (t)$ and $e_\mathrm{o} (t)$ converge to the origin, which entails synchronization of the master and the slave chaotic oscillators. $\square$

Appendix 2: Proof of Theorem 4

Applying the congruence transformation, that is, by pre- and post- multiplying (33) by $\mathrm{diag} (I_n , I_n ,I_n ,\beta _1 I_n ,\alpha _1 I_n ,)$, where $\beta _1 =1/{\eta _1 \bar{{\beta }}_1 }$ and $\alpha _1 =1/{\eta _1 \bar{{\alpha }}_1 }$ for an appropriate number $\eta _1$, the resultant matrix inequality

$$\begin{aligned} \left[ {{\begin{array}{ccccc} {\Theta _1 }&{} {\tilde{P}_\mathrm{m} }&{} {\tilde{P}_\mathrm{m} }&{} {\frac{L_{g\mathrm{m}} }{\eta _1 }}&{} {\frac{L_f }{\eta _1 }} \\ {*}&{} {-\bar{{\alpha }}_1 I_n }&{} 0&{} 0&{} 0 \\ {*}&{} {*}&{} {-\bar{{\beta }}_1 I_n }&{} 0&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\frac{1}{\eta _1 }\beta _1 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {*}&{} {-\frac{1}{\eta _1 }\alpha _1 I_n } \\ \end{array} }} \right] <0 \end{aligned}$$

(45)

is obtained. Employing Schur complement obtains

$$\begin{aligned} \zeta _{_1 }= & {} \left[ {{\begin{array}{ccc} {\Delta _1 }&{} {\tilde{P}_\mathrm{m} }&{} {\tilde{P}_\mathrm{m} } \\ {*}&{} {-\bar{{\alpha }}_1 I_n }&{} 0 \\ {*}&{} {*}&{} {-\bar{{\beta }}_1 I_n } \\ \end{array} }} \right] <0,\\ \Delta _1= & {} A^\mathrm{T}\tilde{P}_\mathrm{m} +\tilde{P}_\mathrm{m} A-C^\mathrm{T}H_1^\mathrm{T}\nonumber \\&-\,H_1 C+\bar{{\alpha }}_1 L_f^2 +\bar{{\beta }}_1 L_{g\mathrm{m}}^2.\nonumber \end{aligned}$$

(46)

Similarly, by using $\beta _2 =1/{\eta _2 \bar{{\beta }}_2 }$, and $\alpha _2 =1/{\eta _2 \bar{{\alpha }}_2 }$ for a scalar $\eta _2$, and following the same procedure as above, the matrix inequality (34) can be modified as

$$\begin{aligned} \zeta _{_2 }= & {} \left[ {{\begin{array}{ccc} {\Delta _2 }&{} {\tilde{P}_\mathrm{s} }&{} {\tilde{P}_\mathrm{s} } \\ {*}&{} {-\bar{{\alpha }}_2 I_n }&{} 0 \\ {*}&{} {*}&{} {-\bar{{\beta }}_2 I_n } \\ \end{array} }} \right] <0,\\ \Delta _2= & {} A^\mathrm{T}\tilde{P}_\mathrm{s} +\tilde{P}_\mathrm{s} A-C^\mathrm{T}H_2^\mathrm{T} -H_2 C+\bar{{\alpha }}_2 L_f^2 +\bar{{\beta }}_2 L_{g\mathrm{m}}^2.\nonumber \end{aligned}$$

(47)

By application of congruence transformation to (35) using $\mathrm{diag}(I_n ,I_n ,\alpha _3 I_n ,\alpha _3 I_n ,)$, where $\alpha _3 =1/{\bar{{\alpha }}_3 }$, the resultant inequality is obtained as

$$\begin{aligned} \left[ {{\begin{array}{cccc} {\Theta _3 }&{} {\bar{{P}}_\mathrm{o} }&{} 0&{} {L_f } \\ {*}&{} {-2\bar{{P}}_\mathrm{o} }&{} {I_n }&{} 0 \\ {*}&{} {*}&{} {-\alpha _3 I_n }&{} 0 \\ {*}&{} {*}&{} {*}&{} {-\alpha _3 I_n } \\ \end{array} }} \right] <0. \end{aligned}$$

By applying Schur complement, we achieve

$$\begin{aligned} \left[ {{\begin{array}{cc} {\Theta _3 +\bar{{\alpha }}_3 L_f^2 }&{} {\bar{{P}}_\mathrm{o} } \\ {*}&{} {-2\bar{{P}}_\mathrm{o} +\bar{{\alpha }}_3 I_n } \\ \end{array} }} \right] <0. \end{aligned}$$

Since we have

$$\begin{aligned}&\frac{1}{\bar{{\alpha }}_3 }\bar{{P}}_\mathrm{o} \bar{{P}}_\mathrm{o} -2\bar{{P}}_\mathrm{o} +\bar{{\alpha }}_3 I_n =(\bar{{P}}_\mathrm{o} -\bar{{\alpha }}_3 I_n )(\bar{{\alpha }}_3 I_n )^{-1} \\&(\bar{{P}}_\mathrm{o}-\bar{{\alpha }}_3 I_n )\ge 0,-\frac{1}{\bar{{\alpha }}_3 }\bar{{P}}_\mathrm{o} \bar{{P}}_\mathrm{o} \le -2\bar{{P}}_\mathrm{o} +\bar{{\alpha }}_3 I_n. \end{aligned}$$

Consequently, we obtain

$$\begin{aligned} \left[ {{\begin{array}{cc} {\Theta _3 +\bar{{\alpha }}_3 L_f^2 }&{} {\bar{{P}}_\mathrm{o} } \\ {*}&{} {-\frac{1}{\bar{{\alpha }}_3 }\bar{{P}}_\mathrm{o} \bar{{P}}_\mathrm{o} } \\ \end{array} }} \right] <0. \end{aligned}$$

By considering $H_3 =F\bar{{P}}_\mathrm{o}$ and applying congruence transformation by $\mathrm{diag}(P_\mathrm{o} , P_\mathrm{o} )$, it results into

$$\begin{aligned} \zeta _{3 }= & {} \left[ {{\begin{array}{cc} {\Delta _3 }&{} {P_\mathrm{o} } \\ {*}&{} {-\frac{1}{\bar{{\alpha }}_3 }I_n } \\ \end{array} }} \right] <0,\\ \Delta _3= & {} A^\mathrm{T}_\mathrm{o} P_\mathrm{o} +P_\mathrm{o} A-F^\mathrm{T}B^\mathrm{T}P_\mathrm{o} -P_\mathrm{o} { BF}+\bar{{\alpha }}_3 L_f^2.\nonumber \end{aligned}$$

(48)

By lumping together the linear matrix inequalities (46), (47), and (48) and, further, using $H_1 =\tilde{P}_\mathrm{m} L_\mathrm{m}$ and $H_2 =\tilde{P}_\mathrm{s} L_\mathrm{s}$, it produces

$$\begin{aligned}&\left[ {{\begin{array}{ccc} {\eta _1 \zeta _1 }&{} {\zeta _4 }&{} {\zeta _5 } \\ {*}&{} {\eta _2 \zeta _2 }&{} {\zeta _6 } \\ {*}&{} {*}&{} {\zeta _3 } \\ \end{array} }} \right] <0,\\&\zeta _{_4 } =\left[ {{\begin{array}{ccc} 0&{} 0&{} 0 \\ 0&{} 0&{} 0 \\ 0&{} 0&{} 0 \\ \end{array} }} \right] , \zeta _{_5 } =\left[ {{\begin{array}{cc} {0.5P_\mathrm{m} { BF}+C^\mathrm{T}L_\mathrm{m}^\mathrm{T} P_\mathrm{o} }&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ \end{array} }} \right] ,\nonumber \\&\zeta _{_6 } =\left[ {{\begin{array}{cc} {0.5P_\mathrm{s} { BF}-C^\mathrm{T}L_\mathrm{s}^\mathrm{T} P_\mathrm{o} }&{} 0 \\ 0&{} 0 \\ 0&{} 0 \\ \end{array} }} \right] .\nonumber \end{aligned}$$

(49)

We can regenerate the matrix inequality (26), by pre- and post-multiplying (49) by $[\mathbb {I}_1^\mathrm{T} , \mathbb {I}_4^\mathrm{T} , \mathbb {I}_7^\mathrm{T} , \mathbb {I}_2^\mathrm{T} , \mathbb {I}_5^\mathrm{T} , \mathbb {I}_8^\mathrm{T} , \mathbb {I}_3^\mathrm{T} , \mathbb {I}_6^\mathrm{T} ]^\mathrm{T}$ and its transpose, respectively, where $\mathbb {I}_{\alpha }$ is the matrix generated by replacing the ith $0_{n\times n}$ with $I_n$ in $0_{n\times 8n}$ matrix (for example $\mathbb {I}_2 = [0_{n\times n} , I_n, 0_{n\times n} , 0_{n\times n} , 0_{n\times n}, 0_{n\times n},0_{n\times n} ,0_{n\times n} ])$ and substituting $\tilde{P}_\mathrm{m} =\eta _1 ^{-1}P_\mathrm{m}$,$\tilde{P}_\mathrm{s} \,{=}\,\eta _1 ^{-1}P_\mathrm{s}$, $\bar{{P}}_\mathrm{o} \,{=}\,P_\mathrm{o}^{-1}$, $\bar{{\alpha }}_1 \,{=}\,1/{(\eta _1 \alpha _1 )}$, $\bar{{\alpha }}_2 =1/{(\eta _2 \alpha _2 )}$, $\bar{{\alpha }}_3 \,{=}\,\alpha _3 ^{-1}$, $\bar{{\beta }}_1 \,{=}\,1/{(\eta _1 \beta _1 })$, and $\bar{{\beta }}_2 \,{=}\,1/{(\eta _2 \beta _2 })$.