1 Introduction

During the previous two decades, the synchronization study of chaotic systems has always been a hot topic in the research field of nonlinear science. This is motivated by its potential application in many areas such as secure communication. In the common framework of chaos synchronization, one system serves as the drive system and the other the response system. The main task for the synchronization problem is to design effective controllers so that the response state would finally track the drive trajectory. In many practical situations, there exist partially or even fully uncertain parameters in either/both drive system and/or response system. The conventional control approaches are not applicable in such case, as the desired synchronization would be destroyed by these uncertainties. Hence, the synchronization design for chaotic systems with unknown parameters is an interesting problem that has attracted great attention recently.

The pioneer paper that deals with the adaptive synchronization of uncertain chaotic systems is [1]. In [1], Parlitz firstly proposed the synchronization-based identification method to estimate the unknown parameters in uncertain Lorenz system. Later, this method has been applied and extended to synchronize other uncertain chaotic (or hyperchaotic) systems. For example, in [2], the adaptive synchronization of uncertain Chen system was studied. In [3], the authors investigated the synchronization design of hyperchaotic Rössler systems with unknown parameters via the parameter identification method. From the literature, there are abundant articles discussing the adaptive synchronization or parameter identification of other specific dynamical systems. An elaborate collection of such articles can be found in a recent paper [4], in which the authors have reviewed and compared many adaptive synchronization schemes reported in the literature before the year 2010.

Nevertheless, the synchronization design for uncertain chaotic systems continues to be a significant topic among the researchers. Many other research articles have been published in the recent two years, and some more specific cases and more general synchronization forms have been studied in the literature. In [5], a general method was proposed for the Q–S synchronization between different chaotic systems with uncertain parameters and double scaling functions. In [6], Zheng et al. studied the so-called adaptive modified function projective synchronization for uncertain hyperchaotic systems and then presented two numerical simulations to verify the effectiveness of the proposed scheme. A recent article by Wu and Li [7] considered a new chaotic system and designed controllers and updating laws to realize the hybrid function projective synchronization of that newly found chaotic system with unknown parameters. Another recent article by Yang [8] reported an interesting result that the adaptive synchronization of uncertain Lü hyperchaotic system can be achieved via single-input controller. Via this similar single-input controller method, Yang in [9] further investigated the exponential synchronization of a new Lorenz-like attractor. In [10], Wang and Sun designed the adaptive controllers to achieve the adaptive multi-switching synchronization of chaotic systems with unknown parameters. Wu and Lu in [11] introduced a new synchronization form, i.e. the generalized projective lag synchronization (GPLS), and designed controllers to achieve the GPLS between Lorenz hyperchaotic system and Lü hyperchaotic system, and between Lorenz–Stenflo hyperchaotic system and Lorenz hyperchaotic system, all with unknown parameters. However, the article [11] only studied the GPLS of specific uncertain hyperchaotic systems and did not present a general scheme. Later, this issue was addressed by the same authors in [12], in which they presented a detailed analysis to derive the general method for achieving the adaptive GFPLS of different chaotic systems with fully unknown parameters. Another article worth mentioning is [13]. Based on the pragmatical asymptotical stability theory and the nonlinear control method, Li and Ge [13] proposed the pragmatical adaptive scheme for the synchronization of different orders chaotic systems with all uncertain parameters.

The above articles [1–13] have addressed the problem of synchronization design for chaotic systems with unknown parameters. Recently, some researchers have generalized the parameter identification method to the synchronization and estimation of chaotic systems with unknown delays. The basic idea is to treat the unknown delays as kinds of special system parameters. In [14], Ma and Lin have proposed a systematic synchronization-based method to adaptively identify the unknown delays in nonlinear dynamical systems. Furthermore, this adaptive synchronization concept have been employed in [15] to estimate the unknown communication delays between coupled systems. Another direction of the adaptive synchronization research that should be mentioned is that there have already been some attempts on identifying uncertain real-world systems instead of toy models. In [16], the authors used the parameter-estimation-based synchronization method to gain the biological insights of the tuberculosis in Cameroon. In [17], the adaptive synchronization problem of two coupled chaotic Hindmarsh–Rose neurons with unknown parameters was investigated and the authors proposed a novel method by only controlling the membrane potential in the slave neuron. Also reported in [18] is the feasibility analysis of multi-parameter identification from scalar outputs of chaotic systems. The authors in [18] further applied this method to identify multiple unknown parameters in the so-called Malkus–Lorenz water wheel model. Note that the above mentioned articles are far from a complete list of the recent literature concerning the adaptive synchronization design, as many other novel and interesting concepts and schemes have been reported which have enhanced our understanding and knowledge for controlling uncertain dynamical systems.

This paper is inspired by a previous review article [4] published recently in Nonlinear Dynamics. In [4], after reviewing a collection of related articles published before 2010 on the adaptive chaos synchronization, the authors concluded that those articles suffered from research novelty as many reported schemes can be categorized by a union form. In this paper we will go some extra miles further. We will focus on reviewing and revisiting other adaptive synchronization schemes from recent literature (mainly from the year 2010 to the present year 2012). It is found that some articles have reported imperfect or incorrect results regarding this topic. One typical problem is the misapplication of adaptive control method in the designing procedure of adaptive synchronization scheme, resulting in that the unknown parameters are wrongly involved in the parameter identification process. Another issue that receives less consideration in those articles is the deduction of the sufficient condition for successful parameter convergence, while this condition has been unfortunately neglected in many articles. We have noticed that recently there have been some comment articles aiming to point out the errors reported in the current literature, see e.g. [19–21]. Generally speaking, however, the existing problems appearing in these articles have not received adequate attention. Hence, we intend to present a detailed review and analysis to those problems, and this is the prime motivation of this article.

The objectives of this review article are three-fold. First, we will revisit the proposed synchronization schemes reported in some recent articles [5–13, 27–31, 33–39] and will point out that some recent articles have proposed problematic results for the adaptive synchronization deign. The designing problems are categorized into five cases (see Sect. 2 for detailed analysis). Among the five cases, the infeasible updating laws and the neglect of important Linear Independence (LI) condition for parameter estimation are listed as the top two scenarios. In fact, these two defects have been slightly mentioned in several previous articles [22–24]. However, these problems have not attracted enough attention in the literature and we feel the need to present hereby a comprehensive revisit in the current article. Meanwhile, we will present detailed analysis and discussion on why these schemes are problematic. Second, we will further propose modified synchronization schemes to correct the imperfect schemes reported in these articles while this issue has not been addressed in the previous articles. This part constitutes the main content of Sect. 3 of this article. Third, we will emphasize the important LI condition for the parameter identification, while this condition has been regretfully neglected in a series of articles. It is worth noting that the LI condition has been analyzed and established in [22, 25]. Furthermore, in some recent articles [23, 26] the authors have proposed another more practical criterion, the finite-time LI condition, for synchronization-based parameter identification. In this paper we do not attempt to go further about this condition. Instead, we intend to draw a list of the defective articles in order to gain more attention as well as to present a systematic study to deal with the cases of the linear dependence scenario. Hence, in Sect. 4, we will elaborate three cases when this condition does not hold and then propose four feasible approaches to guarantee the successful identification. Typical examples and numerical simulations are also provided in each part of Sect. 4 to show the effectiveness of those approaches. To the best of our knowledge, there are few articles that have discussed this significant subject. Hence, the content of Sect. 4 serves as another contribution presented in this review article.

This article mainly consists of five parts, and the main content of this article follows similarly as mentioned in the above paragraph.

2 Review and comment on some reported schemes with defects

In the literature there are many adaptive schemes reported for the synchronization design of dynamical systems with uncertain parameters. The designing task in this topic has two simultaneous objectives: one is to design the controller functions to achieve the adaptive synchronization and the other is to design updating laws to identify the unknown system parameters. The reported results from the recent literature have enriched our knowledge on the control of uncertain chaotic systems. However, it is regretfully found that some proposed schemes are questionable. In this section, we will review several recent articles and analyze why the adaptive schemes proposed in these articles are questionable or incorrect.

2.1 Case I: infeasible parameter updating laws

This problem is the most commonly seen one in the literature. By collecting the relevant data or time series from the dynamical systems, the aim of the parameter updating process is to use the collected time series to identify the unknown parameters. Note that the parameters, before successful identification, are unknown to us. However, in many adaptive schemes reported in the literature, the unknown parameters are directly employed in the parameter updating laws. This causes an apparent contradiction which implies that the proposed updating methods are not applicable. In the following, we will take the result of [5] as an illustrative example, as the Q–S synchronization studied in [5] is a general one which can cover many other synchronization forms.

In a recent paper [5] the authors studied the Q–S synchronization between two non-identical chaotic systems with unknown parameters. Consider the following dynamical systems:

(1)

where P and Θ are system parameter vectors which are unknown before identification. The readers are referred to Sect. 2 of [5] for detailed definitions of x,y,f(x),F(x),g(y), and G(y).

According to the definition of Q–S synchronization, the synchronization errors are defined as

$$ e(t)=\alpha (t)Q(x)-\beta(t)S(y) $$
(2)

where α(t) and β(t) are the scaling factors. The main theoretical result of [5] is that the authors proposed the following controller functions and updating laws to achieve the Q–S synchronization between systems (1):

(3)

where \(\hat{P}\) and \(\hat{\varTheta}\) are the estimation vectors of unknown parameters.

The updating laws of the estimated parameters are given as

$$ \begin{cases} \dot{\hat{P}}=(\alpha(t)\cdot DQ\cdot F(x))^T\cdot e-\tilde{P}\\ \dot{\hat{\varTheta}}=-(\beta(t)\cdot DS\cdot G(y))^T\cdot e-\tilde{\varTheta} \end{cases} $$
(4)

where DQ and DS are the Jacobian matrices of the vector functions Q(x) and \(S(y), \tilde{P}\) and \(\tilde{\varTheta}\) are the estimation errors defined as \(\tilde{P} = \hat{P} - P\) and \(\tilde{\varTheta} = \hat{\varTheta} - \varTheta\). Clearly, by inserting the definition of \(\tilde{P}\) and \(\tilde{\varTheta}\) into Eq. (4), one can find that the true values of the unknown parameters appear in the updating process. Hence, the updating laws designed in Eq. (4) are infeasible in practice.

We should mention that in another article [27] concerning the Q–S synchronization by the same authors, this problem still exists.

Remark 1

Other articles with similar defective results include [6, 7, 28–31] (see Eq. (13) of [28], Eq. (10) and Eq. (11) of [6], Theorem 1 of [29], Eq. (4.7) in [30], Eq. (11) in [7], etc.). Note that this list is not complete. In Sect. 3 of this paper, we will give feasible and general schemes to correct such defects appeared in these articles.

Remark 2

Some infeasible schemes have been detected in several comment articles, e.g. [19, 21]. We should note that the modified scheme in the comment [19] is still incorrect, as an important condition for the parameter identification is neglected. For details, see Sects. 2.2 and 4 below.

2.2 Case II: the neglect of the linear independence (LI) condition for the parameter identification

To start, we would like to re-investigate the result in a recent paper [10], in which the authors investigated the multi-switching synchronization of chaotic system with adaptive controllers and unknown parameters. In Sect. 3 of [10], the multi-switching synchronization of Lorenz system and Chen system with unknown parameters was studied and the controllers were designed. For the convenience of analysis, we restate the theoretical results of [10] as follows.

Consider the adaptive synchronization problem between the drive Lorenz system and the controlled response Chen system. Those two systems are written as

$$ \begin{cases} \dot{x}_1=a_1(x_2-x_1)\\ \dot{x}_2=c_1x_1-x_1x_3-x_2\\ \dot{x}_3=x_1x_2-b_1x_3 \end{cases} $$
(5)

and

$$ \begin{cases} \dot{y}_1=a_2(y_2-y_1)+u_{i1}(t)\\ \dot{y}_2=(c_2-a_2)y_1-y_1y_3+c_2y_2+u_{i2}(t)\\ \dot{y}_3=y_1y_2-b_2y_3+u_{i3}(t) \end{cases} $$
(6)

In the case i=1, the error signal is defined as e 11=y 1−x 1, e 12=y 2−x 2, e 13=y 3−x 3. According to Eqs. (5) and (6), the error dynamics was obtained as

$$ \begin{cases} \dot{e}_{11}=a_2(y_2-y_1)-a_1(x_2-x_1)+u_{11}(t)\\ \dot{e}_{12}=(c_2-a_2)y_1-y_1y_3+c_2y_2 - c_1 x_1\\ \phantom{\dot{e}_{12}=}{}+x_1x_3+x_2+u_{12}(t)\\ \dot{e}_{13}=y_1y_2-b_2y_3-x_1x_2+b_1x_3+u_{13}(t) \end{cases} $$
(7)

Then the controller functions and update laws were designed asFootnote 1

$$ \begin{cases} u_{11}(t)=-e_{11}-\bar{a}_2(y_2-y_1)+\bar{a}_1(x_2-x_1)\\ u_{12}(t)=-e_{12}-(\bar{c}_2-\bar{a}_2)y_1+y_1y_3\\ \phantom{u_{12}(t)=}-\bar{c}_2y_2+\bar{c}_1x_1-x_1x_3-x_2\\ u_{13}(t)=-e_{13}-y_1y_2+\bar{b}_2y_3+x_1x_2-\bar{b}_1x_3 \end{cases} $$
(8)

and

$$ \begin{cases} \dot{\bar{a}}_1=-(x_2-x_1)e_{11}\\ \dot{\bar{b}}_1=x_3e_{13}\\ \dot{\bar{c}}_1=-x_1e_{12}\\ \dot{\bar{a}}_2=(y_2-y_1)e_{11}-y_1e_{12}\\ \dot{\bar{b}}_2=-y_3e_{13}\\ \dot{\bar{c}}_2=y_1e_{12}+y_2e_{12}\\ \end{cases} $$
(9)

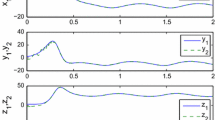
where \(\bar{a}_{1}\sim\bar{c}_{2}\) are the estimated values of the unknown parameters a 1∼c 2. We adopt the same initial conditions as those in [10] for variable states x 1(0)∼y 3(0) and estimated parameters \(\bar{a}_{1}(0)\sim\bar{c}_{2}(0)\) to replicate the numerical results. The time evolutions of parameter identifications for the unknown parameters a 1∼c 2 are depicted in Fig. 1. For clarity, the dashed lines are added in each subfigure to indicate the real values of each unknown parameter.

Fig. 1
figure 1

Parameter identification of system (5) and system (6) with the controller function Eq. (8) and the updating laws Eq. (9) designed in Ref. [10]

Full size image

Figure 1 clearly shows that, except for the unknown parameter c 2, the remaining five unknown parameters a 1∼b 2 have been estimated to false values with the controllers (8) and updating laws (9). Hence, the authors’ statement that “as predicated, we observe that the unknown parameters in system (15) and system (16) have been identified using the parameters updating laws (20)” (see the last paragraph of Sect. 3.1 of [10]) does not hold.

Next we will analyze the reasons for the identification failure of the unknown parameters a 1∼b 2. For t→∞, we have e 1,i →0 and \(\dot{e}_{1,i} \to 0\). By inserting the controller functions (8) and updating laws (9) into Eq. (7), we can obtain

(10)

With the realization of synchronization between system (5) and system (6), it is clear that x 1(t)=y 1(t)| t→∞, x 2(t)=y 2(t)| t→∞ and x 3(t)=y 3(t)| t→∞, and also y 2(t)−y 1(t)=x 2(t)−x 1(t)| t→∞. For the linear equation (10), when the synchronization is achieved between corresponding states, the vector signals x 1,x 2,x 3 will be linearly dependent to y 1,y 2,y 3, respectively. Thus the solutions of (10) should be

$$ \begin{cases} (a_2- \bar{a}_2 )- (a_1 -\bar{a}_1 )=\mathit{const}_1\\ (a_2- \bar{a}_2 )- (c_1 -\bar{c}_1 )=\mathit{const}_2\\ (b_1- \bar{b}_1 )- (b_2 -\bar{b}_2 )=\mathit{const}_3\\ (c_2-\bar{c}_2 )=0 \end{cases} $$
(11)

where the constant numbers const i (i=1,2,3) can be arbitrary values. Hence, with the updating laws (9), only the estimated parameter \(\bar{c}_{2}\) can be successfully identified to the true value c 2.

Note that the above analysis indicates that synchronization is an obstacle for parameter identification, which confirms the conclusion drawn by a previous study [32]. When the synchronization-based method is employed to identify the system parameters or network topologies, the LI condition should be carefully checked for a successful identification [21, 24, 25].

Remark 3

Other articles which neglect the important LI condition include [33–38]. In fact, in the recent review article [4] this condition has not been taken into consideration either. In those studies, since this essential condition is not derived, the theoretical analysis is incomplete and the true convergence of the estimated parameters cannot be guaranteed. For the same reason, the comment letter [19] did not provide a complete correction to the commented article [39]. If the LI condition (or more specifically, the finite-time LI condition) is not satisfied in the adaptive synchronization process, the parameter estimation would be in trouble. Thus, another significant concern is how to guarantee the true identification of the unknown parameters. This topic will be discussed in detail in Sects. 4.2–4.5.

2.3 Case III: wrongly designed controller functions

Recently in [11], Wu and Lu investigated the GPLS between different hyperchaotic systems with uncertain parameters. In Sect. 4 of [11], the authors studied the GPLS between Lorenz hyperchaotic system and uncertain Lü hyperchaotic system, which are described as

$$ \begin{cases} \dot{x}_1=a(y_1-x_1)\\ \dot{y}_1=bx_1+y_1-x_1z_1-w_1\\ \dot{z}_1=x_1y_1-cz_1\\ \dot{w}_1=dy_1z_1 \end{cases} $$
(12)

and

$$ \begin{cases} \dot{x}_2=\tilde{l}(y_2-x_2)+w_2+u_1(t)\\ \dot{y}_2=-x_2z_2+\tilde{h}y_2+u_2(t)\\ \dot{z}_2=x_2y_2-\tilde{p}z_2+u_3(t)\\ \dot{w}_2=x_2z_2+\tilde{r}w_2+u_4(t)\\ \end{cases} $$
(13)

where \(\tilde{l}\), \(\tilde{h}\), \(\tilde{p}\) and \(\tilde{r}\) are unknown parameters to be identified in the response system.

The authors designed the following controller function to achieve the GPLS:

$$ \begin{cases} u_1(t )=-l (y_2 (t )-x_2 ( t))-w_2 (t )-ax_2 (t )\\ \phantom{u_1(t )=}{}+am_1y_1 (t-\tau_1 )-k_1e_1 ( t)\\ u_2(t )=x_2 (t ) z_2(t )- (h- 1)y_2 (t )\\ \phantom{u_2(t )=} {}+bm_2x_1(t-\tau_2 )-m_2w_1 (t-\tau_2 )\\ \phantom{u_2(t )=} {} +(k_2+ 1)e (t )\\ u_3(t)=-x_2 (t)y_2 (t) -(c-p )z_2 (t)\\ \phantom{u_3(t)=}{}+m_3x_1 (t-\tau_3 )y_1 (t-\tau_3 )-k_3e_3 (t)\\ u_4(t)=-x_2 (t)z_2 (t) -rw_2(t)\\ \phantom{u_4(t)=}{}+dm_4y_1 (t-\tau_4 )z_1 (t-\tau_4 )-k_4e_4 (t) \end{cases} $$
(14)

and

$$ \begin{cases} \dot{\tilde{l}}=-(y_2-x_2)e_1\\ \dot{\tilde{h}}=-y_2e_2\\ \dot{\tilde{p}}=z_2e_3\\ \dot{\tilde{r}}=-w_2e_4 \end{cases} $$
(15)

where τ i (i=1,2,3,4) is the time delay and m i (i=1,2,3,4) is the scaling factor. Clearly, we observe that the true values l, h, p and r, which require identification in the process of synchronization, have been used in advance in the controllers of Eq. (14) in order to achieve the synchronization.

Despite the errors appeared in the controller function of Eq. (14), it is not very difficult to correct this wrong scheme. In system (13), the parameters should be written without the hat “∼” to indicate that they are true values of system parameters. In the designed controller function of Eq. (14), all the parameter terms should add the hat “∼” implying that they are the estimations for each unknown parameter, while the estimation process are governed by Eq. (15) and the update laws remain the same.

Another erroneous result of [11] that should be mentioned is that the parameter update laws designed by Eq. (20) in [11] are not applicable either, and this error is same as the above-mentioned case in Sect. 2.1. In Sect. 3 of this paper, we will present a general and correct method to deal with this problem.

2.4 Case IV: adaptive synchronization or parametric synchronization?

In a recently published article [8], the author discussed a very interesting topic: using the single-input controller to adaptively synchronize hyperchaotic systems with uncertain parameters. To avoid lengthy statements, the same symbols and notations in [8] are employed here.

In Sect. 3 of [8], the following theoretical results were reported. For the specified hyperchaotic Lü system, the adaptive single-input controller was designed as

$$ \begin{cases} U_2(t)=-\tilde{k}_2(t)e_2(t)\\ U_1(t)=U_3(t)=U_4(t)=0 \end{cases} $$
(16)

The adaptive algorithm for the feedback gain \(\tilde{k}_{2}(t)\) was proposed as

$$ \dot{\tilde{k}}_2=\gamma_1e^2_2, \qquad \tilde{k}_2(0)=0 $$
(17)

In addition, the adaptive update laws of system parameters were suggested as

$$ \begin{cases} \dot{e}_a=-\gamma_2e_a+\lambda(e^2_1-e_1e_2-(x_2-x_1)e_1)\\ \dot{e}_b=-\gamma_3e_b+(e^2_3+x_3e_3)\\ \dot{e}_c=-\gamma_4e_c+(-e^2_2-x_2e_2)\\ \dot{e}_d=-\gamma_5e_d+(e^2_4+x_4e_4) \end{cases} $$
(18)

In Eqs. (16)–(18), e i =y i −x i (i=1,2,3,4) are the state errors and e a , e b , e c , e d are the parameter errors which are defined as e a =a r −a and so on. The author stated that a r , b r , c r , d r were uncertain parameters in response system and they should be identified via update laws (18) to their true values a,b,c,d respectively. By expanding the expression of e a ,e b ,e c ,e d , we can find that each update laws involves the true values, which leads to an obvious irrationality. To be more specific, the reported scheme is for parametric synchronization, but not for adaptive synchronization. The concept of parametric synchronization, which is proposed in [40], is obviously different from the concept of adaptive synchronization. In the research of adaptive synchronization, we know the structures of the systems and the time series of system states, but we have no a priori knowledge about the true values of the system parameters. What we have to do is to design effective controllers to achieve the synchronization and parameter identification based on the measured time series of the states. The definition of adaptive synchronization implies that no direct information about the system parameters is available for designing the controller functions and update laws. However, things are much different for parametric synchronization. A premise of the parametric synchronization scheme is that the system parameters, either in drive system or in response system, should be known in advance. Based on this premise the controllers then can be designed to synchronize the unknown parameters with the known parameters. In fact, parametric synchronization is the same as the conventional synchronization scheme if we treat the system parameters as the system states with unchangeable or constant values.

In order to obtain adaptive synchronization of the systems studied in [8], those terms e a , e b , e c , e d should be canceled in the updating laws (18). We should mention that the same problem occurs in another article [9] by the same author.

2.5 Case V: the impracticability of a pragmatical adaptive synchronization scheme

Recently Li and Ge [13] reported a pragmatical adaptive synchronization scheme. In this section, we briefly introduce the main theoretical results of [13], and then analyze why this scheme is not practical.

Consider the adaptive synchronization between master chaotic system and slave chaotic system as

$$ \begin{cases} \dot{x}=Ax+Bf(x)\\ \dot{y}=\hat{A}x+\hat{B}f(y)+u(t) \end{cases} $$
(19)

The main contribution of [13] is that it proposed the following controllers and updating laws to realize the synchronization of systems (19) (see Theorem 1 of [13]).

The parametric update laws were designed as

$$ \dot{\hat{a}}_m = -\tilde{a}_m e,\quad m= 1\sim p $$
(20)

where e=x−y are the synchronization errors, p is the number of parameters, a m are the unknown parameters in the master system, \(\hat{a}_{m}\) are the estimated parameters in the slave system and \(\tilde{a}_{m} = a_{m} - \hat{a}_{m}\) are the estimation errors of unknown parameters.

The controller functions were designed as

(21)

where \(\dot{y}_{out}\) is \(\dot{y}\) without controllers, gain K should satisfy the following constant:

$$ \min(K )> \Biggl(L\|B\|+\|A\| +\max\Biggl(\sum ^p_{i=1} \tilde{a}^2_i \Biggr)\Biggr) $$
(22)

The authors proved that, via the above synchronization design, the master and slave systems could achieve adaptive synchronization. However, we will argue that this pragmatical scheme has some defects which make it unsuitable for practical applications.

  1. (I)

    The authors stated that “by applying this new relation formula, an appropriate feedback gain K can be decided easily to obtain controllers achieving adaptive synchronization” (see Sect. 4 of the Conclusions of [13]). However, by re-considering that relation formula (i.e., Eq. (22)), it is clearly shown that B,A and \(\tilde{a}_{m} = a_{m} - \bar{a}_{m}\) are all unknown to us. Also, the determination of the Lipschitz constant L for a specified nonlinear system is a tough task (we note that in [13] the Lipschitz constants for different systems were arbitrarily chosen as L=1). Hence, it is not the question whether it is easy or not for such a task, but it is almost practically impossible to determine the minimum values for the feedback gain K.

  2. (II)

    The controller functions (21) involve the unknown parameters A and \(a_{m}^{2}\), which indicate that it is impractical for real applications

  3. (III)

    The parameter update laws (20) can be rewritten as \(\dot{\hat{a}}_{m} = - \tilde{a}_{m}e = - (a_{m} - \hat{a}_{m})e\). Note that a m is the unknown parameter that needs identification, but it is involved in the identification process. This again results in the same problem as described in Case I of Sect. 3.1. Thus, the updating laws are infeasible either. This error has also been pointed out in a recent comment [20].

As a conclusion, the pragmatical scheme proposed in [13] cannot be used in practical situations. It is worth mentioning that in a recent article [41] the above problems (II) and (III) still exist. Note that in the comment [20], a modified scheme is provided to correct the erroneous results in [13].

3 The corrections

In this section we would like to propose several modified schemes to correct the defective schemes listed in Sect. 2. We firstly provide a general theorem for the adaptive synchronization design. Then this theorem will be extended to other specific synchronization cases in order to present the corresponding corrections.

3.1 General theorem

Consider the driving and response systems described by

$$ \begin{cases} \dot{x}=f(x)+F(x)P\\ \dot{y}=g(y)+G(y)Q+U \end{cases} $$
(23)

where x∈R n,y∈R n are the state vectors in drive system and response system, respectively; f(x) is an n×1 matrix and F(x) is an n×p matrix in drive system. Similarly, in response system, g(y) is an n×1 matrix and G(y) is an n×q matrix. Note that P∈R p and Q∈R q are uncertain parameter vectors.

Firstly we introduce the following useful lemma which will be used for the stability analysis in our designing process.

Lemma 1

(See p. 76 of [42])

If \(f,\dot{f} \in L_{\infty }\), and f∈L p for some p∈[1,∞), then f(t)→0 as t→∞.

The result of Lemma 1 is actually a special case of the well-known Barbalat lemma.

Define the synchronization error as e(t)=y(t)−x(t), further define the parameter estimation error as \(\tilde{Q} = Q - \hat{Q}\) and \(\tilde{P} = P - \hat{P}\). Then the error dynamical system is obtained as

(24)

where \(\bar{U} = (U + g(y) - f(x) + G(y)\hat{Q} - F(x)\hat{P})\). Our aim is to achieve the synchronization as well as the identification of the unknown parameters. Thus we construct the following positive definite Lyapunov function with the common quadratic form:

(25)

and V=V 1(e)+V 2(P,Q). Differentiating V along the error trajectory (24) yields

(26)

Further, if we choose

$$ \begin{cases} \bar{U}=-Ke\\ \dot{\tilde{Q}}= -\dot{\hat{Q}}=-G^T(y)e\\ \dot{\tilde{P}}=-\dot{\hat{P}}=F^T(x)e \end{cases} $$
(27)

Then we can obtain \(\dot{V} = - Ke^{2} \le 0\), where K are the predefined positive controlling gains. Since V(0) is bounded, V(t) is also bounded. Consequently, from dynamical systems (23), the state trajectories and parameter estimates are also bounded, i.e., \(x,y,e,\hat{P},\allowbreak \hat{Q} \in L_{\infty }\). From (24) we know that \(\dot{e}(t)\) exists and is bounded for t∈[0,+∞). From \(\dot{V} = - Ke^{2} \le 0\), one gets

$$ \int^{\infty}_0e^2(\tau)\,d\tau=- \frac{1}{K}\int^{\infty}_0\dot{V}\,d\tau= \frac{1}{K} (V_0-V_{\infty}) $$
(28)

where \(V_{0} = V(e(0),\tilde{P}(0),\tilde{Q}(0))\). The above equation indicates that e∈L 2. According to the result of Lemma 1, we can conclude that e(t)→0 as t→∞, which means that the synchronization would be finally attained. In addition, this in turn also implies that \(\dot{\tilde{Q}}(t),\dot{\tilde{P}}(t) \to 0\) as t→∞.

Despite the fact that \(e(t),\dot{\tilde{Q}}(t),\dot{\tilde{P}}(t) \to 0\) as t→∞, it should be noticed that \(\tilde{Q}(t), \tilde{P}(t)\) does not necessarily converge to zero (and it may not converge at all). This point shows that the reported results in [33, 34, 43] etc. are incorrect. Additional conditions should be imposed to establish the convergence of the parameter estimation errors, while this condition has unfortunately been neglected in those papers [33–38].

When the synchronization has been achieved between the dynamical systems (23) with bounded state signals, we have e=0 and \(\dot{e} \to 0\) as t→∞. By inserting e=0 (or y=x) into Eq. (24), we notice that as t→∞ Eq. (24) actually becomes

$$ G(y)\tilde{Q}-F(x)\tilde{P}=0 $$
(29)

Equation (29) is analogue to a linear algebraic equation group if we consider the function groups G(y) and F(x) as the common constant matrices. Hence, we can apply the well-known concept of linear independence in linear algebra to derive the important condition for the identification problem. Denote

$$ \begin{cases} G(y)=\{ G^{(1)}(y), G^{(2)}(y), \ldots, G^{(p)}(y)\}\\ F(x)=\{ F^{(1)}(x), F^{(2)}(x), \ldots, F^{(q)}(x)\} \end{cases} $$
(30)

where G (i)(y)∈R n for i=1,2,…,p and F (j)(x)∈R n for j=1,2,…,q. Thus Eq. (29) can be rewritten as

$$ \sum^{p}_{i=1}G^{(i)}(y) (Q_i-\hat{Q}_i)-\sum^{q}_{i=1}F^{(j)}(x) (P_j-\hat{P}_j)=0 $$
(31)

To ensure that the above equation has the unique solution of \(Q_{i} = \hat{Q}_{i}\) and \(P_{j} = \hat{P}_{j}\), the function elements {G (i)(y)| i=1,2,…,p ,F (j)(x)| j=1,2,…,q } should be linearly independent on the orbit y(t)=x(t) of the synchronization manifold. Otherwise, there would exist many nonzero constants α and β such that \(Q_{i} - \hat{Q}_{i} = \alpha\ne 0\) and \(P_{j} - \hat{P}_{j} = \beta\ne 0\), which means that the unknown parameters would be estimated to some other false values. This is exactly the case that has not been considered by [10].

3.2 Corrections to some defective synchronization schemes

Based on the above general result, the theoretical error in [5] should be corrected as

$$ \begin{cases} U=-g(y)-G(y)\hat{\varTheta}+\frac{1}{\beta(t)}DS^{-1}\\ \phantom{U=}{}\cdot (H(x,y,t)+\alpha(t)\cdot DQ\cdot F(x)\hat{P})\\ \dot{\hat{P}}=(\alpha(t)\cdot DQ\cdot F(x))^T\cdot e\\ \dot{\hat{\varTheta}}=- (\beta(t)\cdot DS\cdot G(y))^T\cdot e \end{cases} $$
(32)

Note that to achieve successful identification, the LI property of the function groups (α(t)⋅DQ⋅F(x))T and −(β(t)⋅DS⋅G(y))T on the synchronization manifold should be checked.

The theoretical result of [11] should be corrected as

$$ \begin{cases} U(t)=\theta f(x(t-\tau))-g(y(t))\\ \phantom{U(t)=}{}+\theta F(x(t-\tau))\hat{P}\\ \phantom{U(t)=}{}-G(y(t))\hat{Q}-Ke\\ \dot{\hat{P}}=\theta F(x(t-\tau))^Te\\ \dot{\hat{Q}}=-G(y(t))^Te \end{cases} $$
(33)

Equation (33) is a general formula to achieve the GPLS of uncertain dynamical systems, however, this formula was not derived in [11]. Similarly, the LI property of the function group θF(x(t−τ))T and −G(y(t))T on the synchronization is important for successful identification. Note that the imperfect result of [12] which deals with the adaptive GFPLS should be corrected in a similar way as described by Eq. (33).

Similarly, the errors appearing in Theorem 1 of [29] should be modified as

$$ \begin{cases} u=f_2(y)+g_2(y)\tilde{\alpha}-h(t)f_1(x)\\ \phantom{u=}{}-h(t)g_1(x)\tilde{\beta}\\ \dot{\tilde{\beta}}=-h(t)(g_1(x))^Te\\ \dot{\tilde{\alpha}}=(g_2(y))^Te\\ \dot{h}(t) = x^T e \end{cases} $$
(34)

The proofs of the above modified schemes follow the same procedures of Sect. 3.1, hence we omit them here.

The defective results in some other articles [6, 7, 28, 30] can be fixed up in a similar manner.

Note that for successful parameter identification, the LI condition should always be tested and guaranteed. However, in some cases, the vector terms would be linearly dependent on the synchronization manifold in the process of adaptive synchronization, which may lead to failures of the parameter identification. In Sect. 4, we will present detailed discussion on the avoidance or elimination of the linear dependence of the relevant vector terms.

Remark 4

The LI condition is conceptually the same as the persistence excitation condition, which is an established concept in the area of adaptive control [44]. We have shown that, if the system model can be exactly known and the time series of the system states can be sampled properly, the unknown parameters could be recovered according to the adaptive synchronization method. On one hand, the complicated chaotic signals are favorable for the potential application of secure communication. On the other hand, the property of the chaotic signals (or the sensitivity to initial data) leads to that the LI condition can be easily satisfied. As a result, the unknown parameters would be hopefully extracted from the sampled chaotic signals. In fact, some reported secure communications (e.g. [45, 46]) have been cracked by the adaptive synchronization method (see the cryptanalysis in [47, 48]). The research motivation for the adaptive synchronization of chaotic systems is that the synchronization scheme is expected to be adopted in the secure communication domains. However, the claimed advantage of the chaotic signals in communication schemes would also be used in the parameter identification purposes. This indicates that people should be very cautious in designing the chaos-based secure communication scheme in the context of uncertain chaotic systems via the adaptive method. Some detailed analysis on the identifiability of uncertain dynamical systems can be found in an early paper [49].

Remark 5

As a conclusion of this section, we have presented several modified schemes with rigorous proofs to correct the defective schemes that have been reported in several previous papers [5–7, 11, 12, 28, 30]. As mentioned above, the main defect in those articles is that the unknown knowledge of the uncertain parameters is used in the parameter updating laws. By removing the parameter terms in the updating laws, the defective results can be corrected accordingly. By employing Barbalat’s Lemma and/or LaSalle’s invariance principle, the stability of the synchronization error system, as well as the sufficient LI condition, can be rigorously obtained. This is actually the proving strategy adopted in [23, 24, 50]. In fact, these papers [23, 24, 50] present correct schemes for the adaptive synchronization design.

4 On avoiding the linear dependence in identifying unknown parameters

As stated in the above analysis in Sect. 3, the LI property of the related function terms is important for successful identification. However, in practical situations, the identification functions might become linearly dependent, which will probably cause identification failures. Hence, how to avoid the linear dependence in such cases is a significant issue for parameter identification. To the best of our knowledge, the only literature that has clearly discussed this topic is [51] (see Sect. 4 of [51]). The basic concept of the proposed method in [51] is to check the angles between the subspaces of the function terms and then determine which parameter index should be eliminated from the overall index set. However, that method is somewhat complex and difficult to understand, and the calculation of the angle between the subspaces might result in a heavy computation burden. In this section, we will present a systematic study for this significant topic and propose several feasible solutions to this problem.

4.1 There typical cases when the LI condition would be violated

Generally speaking, there are three cases when the LI condition would not be satisfied.

  1. (I)

    The function elements \(F_{i}^{T}(x)\) (or \(G_{i}^{T}(y)\)) finally converge to zero and, accordingly, these function elements would be linearly dependent. If this happens in a quite short time, the identification of the unknown parameters P i (or Q i ) would probably be unsuccessful since the stable state could not provide sufficient information for the true convergence of the parameter estimations.

  2. (II)

    Some states in drive system (or response system) might reach inner synchronization, i.e. x i (t)→x j(j≠i)(t) (or y i (t)→y j(j≠i)(t)) as t→∞. Then there exists the possibility that either

    1. (a)

      \(F_{i}^{T}(x(t)) \to 0\) (or \(G_{i}^{T}(y(t)) \to 0\)), or

    2. (b)

      \(F_{i}^{T}(x(t)) \to F_{j}^{T}(x(t))\) (or \(G_{i}^{T}(y(t)) \to G_{j}^{T}(y(t))\)).

    For case (a), it is essentially the same as Case (I) mentioned above. For case (b), the function element \(F_{i}^{T}(\bullet)\) (or \(G_{i}^{T}(\bullet)\)) would be linearly dependent with \(F_{j}^{T}(\bullet)\) (or \(G_{j}^{T}(\bullet)\)) on the inner synchronized trajectory x i (t)→x j (t) (or y i (t)→y j (t)). If this happens in a short time, the identification of the unknown parameters P i and P j (or Q i and Q j ) would probably be failed. The concept of finite-time linear independence condition, proposed in [23, 26], are applicable for the convergence analysis in such case. One should carefully check the transient process of the function elements to ensure that they have provided enough persistent time for the parameter estimation before the driving functions converge to the synchronous states. In Sect. 4.5, we will consider a concrete example to illustrate this particular case. Note that the concept inner synchronization refers to the synchronization between different states of the same system.

  3. (III)

    When the synchronization between the drive system \(\dot{x}\) and the response system \(\dot{y}\) is achieved, there exists the possibility that \(F_{i}^{T}(x(t)) \to G_{j}^{T}(y(t))\) on the synchronization trajectory y j →x i as t→∞. If this happens in a short time before the parameter estimations converge to their true values, the identification of the unknown parameters P i and Q j would be failed by a strong possibility. We call this synchronization outer synchronization, in order to distinguish it with the above mentioned inner synchronization. In Sect. 4.4, we will present a simple and feasible approach to deal with this case.

Based on the above analysis, in the following sections, four methods are proposed to avoid the linear dependence of the functions to ensure successful identification.

4.2 Method I: changing the structures of the function groups F T(x) (or G T(y))

In the identification process, if the linear dependence of the function element \(F_{i}^{T}(x(t))\) is predicted due to \(F_{i}^{T}(x(t)) \to 0\) or \(F_{i}^{T}(x(t)) \to F_{j}^{T}(x(t))\) (or \((F_{i}^{T}(x(t)) \to G_{j}^{T}(y(t)))\) on the synchronization orbit x i (t)→x j (t) (or y j (t)→x i (t)), then we can simply change its structure as \({\stackrel{\frown}{F}}{_{i}^{T}}(x(t))\) and re-examine its LI property. If that there cases discussed in Sect. 4.1 are avoided for the new function \({\stackrel{\frown}{F}}{_{i}^{T}}(x(t))\), then the unknown parameter P i can be truly estimated.

The same strategy can be applied to function groups G T(y) if the linear dependence of \(G_{i}^{T}(y(t))\) is predicted. In the following, we will illustrate this method by giving a typical example.

Consider the following system [25]:

$$ \begin{cases} \dot{x}_1=a_1(x_2-x_1)+a_2(x_4-x_1)\\ \dot{x}_2=cx_1-x_2-x_1x_3\\ \dot{x}_3=-bx_3+x_1x_2\\ \dot{x}_4=-(x_4-x_1)+a_3(x_2-x_1) \end{cases} $$
(35)

This system is artificially constructed in [25] based on the classical Lorenz system with the aim to demonstrate the reason of the identification failure. System (35) is chaotic when parameters are set as a 1=a 3=10,b=8/3,c=28,a 2=6. It has been shown in [25] that, despite the successful identification of a 1,a 3,b,c, the identification of a 2 cannot be achieved via the synchronization-based method. In fact, since \(\dot{x}_{4} - \dot{x}_{1} = - (1 + a_{2})(x_{4} - x_{1})\), it is obvious that x 4(t)→x 1(t) as t→∞. Hence, the inner synchronization between state x 4 and state x 1 leads to (x 4−x 1)→0, which means that the function element F 1(x)=x 4−x 1 is linearly dependent to other functions.

There are many options for the changing of \(\stackrel{\frown}{F}_{1}(x)\). Here we simply change the function structure as \(\stackrel{\frown}{F}_{1}(x) = x_{4} - x_{1} + x_{2}\). Then the updating law for parameter a 2 becomes

$$ \dot{\hat{a}}_2=(y_4-y_1+y_2)e_1 $$
(36)

Obviously, the new function \(\stackrel{\frown}{F}_{1}(x)\) is LI to other function elements. With this modification, the identification of a 2 is successful now, which is shown in the right part of Fig. 2.

Fig. 2
figure 2

Parameter identification of system (35). Left: identification result with the original updating laws designed in Ref. [25]. Right: identification result with the modified updating laws Eq. (36)

Full size image

4.3 Method II: adding extra signals to the state function

In many real situations the structures of the system is fixed and it is not so convenient (or even not allowed) to change the function structures. In such cases, Method I described in Sect. 4.2 would not be applicable. To tackle the identification problem in such a situation, we suggest adding auxiliary signals to the system state equation while the structures of the function groups F T(•) (or G T(•)) should remain unchanged.

Suppose that in the state x i the function element F i (x) is detected to be linearly dependent. We shall modify the evolution equation of the state x i as

$$ \dot{x}_i=f_i(x)+F_i(x)P_i+ \omega_i $$
(37)

where ω i is the additive signal. This approach is especially useful in two cases:

  1. (I)

    If the state x i originally converges to stable zero point, then the additive signal ω i would inject extra energy to the evolution of x i and thus activate the LI property of F i (x).

  2. (II)

    If the function term F i (x) is linearly dependent due to the inner synchronization between state x i and some other states x j(j≠i), via adding the extra signal ω i we may break this undesired synchronization and thus re-gain the LI condition of F i (x).

It is worth noting that the concept of adding auxiliary signals was also mentioned in [52]. The authors of [52] remarked that by adding supplement signals the dynamical system would be driven out of the stable state. In fact, the added signals can be regarded as additional information or injected energy which could be used not only to break the stable state but also to disturb the undesirable synchronous orbits. Furthermore, in practice, the extra signal can also be added to other states rather than the sole state x i .

In the following, we will present a concrete example. Again, we consider the above example employed in Sect. 4.2. The reason for the identification failure is due to the fact that F 1(x(t))=x 4(t)−x 1(t)→0 as t→∞. We suggest two schemes, i.e., adding extra signals to either the state x 1 or the state x 4,

$$ \dot{x}_1=a_1(x_2-x_1)+a_2(x_4-x_1)+ \omega_1 $$
(38)

or

$$ \dot{x}_4=-(x_4-x_1)+a_3(x_2-x_1)+ \omega_4 $$
(39)

By doing this, the inner synchronization between x 1 and x 4 could be eliminated. Two numerical simulations are performed: one is to add the time-varying signal ω 1=−x 3 to state x 1, the other is to add a constant ω 4=15 to the state x 4. As predicted, the LI property of the function F 1(x(t)) is satisfied and the identification of the unknown parameter a 2 has been successfully attained (for details, see Fig. 3).

Fig. 3
figure 3

Parameter identification of system (35) by adding extra signals to the state function. Left: identification result with the modified updating laws Eq. (38). Right: identification result with the modified updating laws Eq. (39)

Full size image

4.4 Method III: altering the synchronization orbits

In some practical situations we may confront the situations that the driving system and response system both involve unknown parameters. It would be a tough task to estimate all the unknown parameters as well as to achieve the synchronization. As discussed in Case III of Sect. 4.1, the synchronization between drive state and the corresponding response state would result in the linear dependence of relevant function on the synchronization manifold. In other words, as the synchronization becomes the major hindrance for parameter identification, it would become difficult to achieve the system synchronization and parameter identification simultaneously.

Inspired by the so-called switching synchronization scheme [53], we propose a simple method of changing the synchronization orbits to tackle the problem in this case. By examining the different combination of drive state and the synchronized response system, we can finally find one feasible combination of the synchronization orbits that can maximize the number of the function elements which are linearly independent on the synchronization orbit. By doing this, the number of the unknown parameters that can be identified can also be optimized.

We choose the most commonly used Lorenz chaotic system as an illustrative example. The drive Lorenz system and the controlled response Lorenz system are given, respectively, as

$$ \begin{cases} \dot{x}_1=a_1(x_2-x_1)\\ \dot{x}_2=c_1x_1-x_2-x_1x_3\\ \dot{x}_3=x_1x_2-b_1x_3 \end{cases} $$
(40)

and

$$ \begin{cases} \dot{y}_1=a_2(y_2-y_1)+u_1\\ \dot{y}_2=c_2y_1-y_2-y_1y_3+u_2\\ \dot{y}_3=y_1y_2-b_2y_3+u_3 \end{cases} $$
(41)

The true values of system parameters in driving Lorenz system are a 1=10,c 1=28 and b 1=8/3. We assume that the parameters in response Lorenz system are not identical to those in drive system, and their values are a 2=9,c 2=27 and b 2=8/3+0.2, respectively. Note that with the specified parameter values the driving and response systems both possess chaotic attractors. We further suppose that the parameters a 1,b 1,c 1 in drive system (40) and the parameters a 2,b 2,c 2 in response system (41) are all unknown which need to be identified via the synchronization method.

If we consider the conventional synchronization mode that the states in response system are synchronized to the corresponding states in drive system, that is, \(y_{1} \mathop{\to}\limits^{\mathrm{syn}} x_{1}, y_{2} \mathop{\to}\limits^{\mathrm{syn}} x_{2}\) and \(y_{3} \mathop{\to}\limits^{\mathrm{syn}} x_{3}\), then the synchronization errors should be defined as

$$ e_1=y_1-x_1,\qquad e_2=y_2-x_2, \qquad e_3=y_3-x_3 $$
(42)

The controller functions can be derived directly according to Eq. (27). The parameter update laws are designed as

$$ \left \{ \begin{array}{l} \dot{\hat{a}}_{1} = - (x_{2} - x_{1})e_{1} \\ \dot{\hat{b}}_{1} = x_{3}e_{3} \\ \dot{\hat{c}}_{1} = - x_{1}e_{2} \\ \end{array} \right .\quad \mbox{and}\quad \left \{ \begin{array}{l} \dot{\hat{a}}_{2} = (y_{2} - y_{1})e_{1} \\ \dot{\hat{b}}_{2} = - y_{3}e_{3} \\ \dot{\hat{c}}_{2} = y_{1}e_{2} \end{array} \right . $$
(43)

Obviously, on the synchronization orbits y 1(t)=x 1(t),y 3(t)=x 3(t) and y 2(t)=x 2(t), the function terms −(x 2−x 1),x 3,−x 1 are linearly dependent to (y 2−y 1),−y 3,y 1, respectively. Under such case all the six unknown parameters a 1∼c 2 would be failed to be identified. We have also performed some numerical simulations to verify our analysis. The initial values for the parameter estimations are \(\hat{a}_{1}(0) = \hat{a}_{2}(0) = 3, \hat{b}_{1}(0) = \hat{b}_{2}(0) = - 6\) and \(\hat{c}_{1}(0) = \hat{c}_{2}(0) = - 2\). The initial conditions for the drive states and response states are [x 1(0),x 2(0),x 3(0)]T=[2,−5,−1]T,[y 1(0),y 2(0),y 3(0)]T=[−2,5,1]T, respectively. The simulation results are shown in Fig. 4. It can be clearly seen from the figures that none of the six unknown parameters have been successfully identified to their true values.

Fig. 4
figure 4

Identification failures for all of the unknown parameters in drive Lorenz system (40) and response Lorenz system (41) with the original updating laws Eq. (43)

Full size image

Actually, the failures of the identification are caused by the linear dependence of the function terms. Let us recall the expressions of the system structures described in Eq. (43). It is obvious that the term x 1 is always linearly independent with the term (y 2−y 1); hence, if we let the state y 1 synchronize with the state x 2, then the synchronization orbit y 1(t)=x 2(t) is created and, as a result, the two unknown parameters a 2 and c 1 would be identified. Similarly, if we choose the states y 3 and x 1 as the synchronizing couples, as the function terms −y 3 and (x 2−x 1) are linearly independent on the synchronization orbit y 3(t)=x 1(t), the unknown parameters b 2 and a 1 can also be identified. For the rest two states y 2 and x 3, if they are synchronized, the function terms y 1 and −x 3 are apparently linearly independent on the created orbit y 2(t)=x 3(t), which indicates that it is possible to identify the last two unknown parameters c 2 and b 1. As a conclusion, all the unknown parameters can be correctly identified by changing synchronization orbits.

To verify the correctness of the theoretical analysis, some simulations are also performed to provide intuitive explanations. Based on the above analysis, the synchronization modes should be designed as \(y_{1}\mathop{\to}\limits^{\mathrm{syn}}x_{2}\), \(y_{3}\mathop{\to}\limits^{\mathrm{syn}}x_{1}\) and \(y_{2}\mathop{\to}\limits^{\mathrm{syn}}x_{3}\), and the synchronization errors are now modified as

(44)

The controller functions are designed as

$$ \begin{cases} u_1=-(x_2+x_1x_3)+\hat{c}_1x_1-\hat{a}_2(y_2-y_1)-k_1e_1\\ u_2=x_1x_2+y_2+y_1y_3-\hat{b}_1x_3-\hat{c}_2y_1-k_2e_2\\ u_1=-y_1y_2+\hat{a}_1(x_2-x_1)+\hat{b}_2y_3-k_3e_3 \end{cases} $$
(45)

The parameter update laws should be modified as

$$ \left \{ \begin{array}{l} \dot{\hat{a}}_{1} = - (x_{2} - x_{1})e_{3} \\ \dot{\hat{b}}_{1} = x_{3}e_{2} \\ \dot{\hat{c}}_{1} = - x_{1}e_{1} \\ \end{array} \right .\quad \mbox{and}\quad \left \{ \begin{array}{l} \dot{\hat{a}}_{2} = (y_{2} - y_{1})e_{1} \\ \dot{\hat{b}}_{2} = - y_{3}e_{3} \\ \dot{\hat{c}}_{2} = y_{1}e_{2} \end{array} \right . $$
(46)

We employ the same initial conditions for parameter estimations and system states used in the above simulations. The controlling gains are chosen as K=diag(k 1,k 2,k 3)=diag(2,2,2). The numerical results, which are shown in Fig. 5, clearly indicate that all the unknown parameters have been accurately estimated. Thus the effectiveness of this method is verified.

Fig. 5
figure 5

Identification success for all of the unknown parameters in drive Lorenz system (40) and response Lorenz system (41) by altering the synchronization orbits with the modified updating laws Eq. (46)

Full size image

Remark 6

The defective scheme reported in [10, 33–38] can be resolved in a similar manner via this method introduced in this section. For example, in the recent paper [38] the authors studied the reduced-order anti-synchronization between uncertain hyperchaotic Chen system and Lü system. However, via the designed updating laws Eq. (15) of [38], none of the unknown parameters except for d 1 could be precisely estimated (we should mention that Fig. 2 presented in [38] is inaccurate). A feasible remedy to this problem is to alter the synchronization orbits as \(x_{1} \mathop{\to}\limits^{\mathrm{syn}} - y_{3}, x_{2} \mathop{\to}\limits^{\mathrm{syn}} - y_{1}\), and \(x_{3} \mathop{\to}\limits^{\mathrm{syn}} - y_{2}\) such that all the function terms in the updating laws can be linearly independent to each other. Detailed numerical results are omitted here.

4.5 Method IV: adjusting the persistent time and transient time

The above schemes in Sects. 4.1–4.3 are quite applicable to ensure the long-time LI condition. However, as mentioned in [23, 26], the concept of the finite-time LI condition is more desirable for some cases when the long-time LI condition is not applicable. The basic idea for the finite-time LI condition is to guarantee that the persistent time is larger than the parameter transient time such that the unknown parameters can be estimated to their true values. Intuitively, two directions can be considered, i.e., by shortening the transient time of the estimation process, or by extending the persistent time of the function elements before they converge to the stable states or synchronous states. In this section we shall present a typical example to show how to adjust the persistent time and transient time simultaneously such that the parameter identification can be achieved at a high accuracy even if the long-time LI condition is not met.

Let us consider the well known Lorenz system (40) as the drive system. But here we assume that the unknown parameters only exist in the drive system and we need to construct a response system to achieve the synchronization as well as to estimate the unknown parameters. Hence, we rewrite the response system as

$$ \begin{cases} \dot{y}_1=\hat{a}_1(y_2-y_1)+u_1\\ \dot{y}_2=\hat{c}_1y_1-y_2-y_1y_3+u_2\\ \dot{y}_3=y_1y_2-\hat{b}_1y_3+u_3 \end{cases} $$
(47)

Note that in comparison with (41), here the parameters \(\hat{a}_{1}, \hat{b}_{1}\), and \(\hat{c}_{1}\) in (47) are time-varying estimates for the unknown parameters a 1,b 1, and c 1. We design the feedback controllers as u i =−10(y i −x i ) for i=1,2,3. The updating laws for the unknown parameters are designed as

$$ \begin{cases} \dot{\hat{a}}_1=-k_1(y_2-y_1)e_1\\ \dot{\hat{b}}_1=k_2y_3e_3\\ \dot{\hat{c}}_1=-k_3y_1e_2 \end{cases} $$
(48)

where k i are the control gains for the parameter updating laws. According to [23], we assume that the true values of the unknown parameters are a 1=1,b 1=8/3 and c 1=28. With these parameter settings the Lorenz system will display steady states rather than the typical chaotic attractor. The time evolutions for the driving states are shown in Fig. 6, where one can find that as y 2→y 1, the parameter estimation for a 1=1 would be in doubt (also see Sect. III of [23] which presents a curve for the false convergence of a 1).

Fig. 6
figure 6

Time evolutions of the states of the Lorenz system with parameters a 1=1,b 1=8/3 and c 1=28. (Initial conditions: [x 1(0),x 2(0),x 3(0)]T=[1,5,4]T)

Full size image

To achieve the estimation of a 1 with high accuracy, we must guarantee that the persistent time of the driving function should be long enough, or at least longer than the transient time for the estimation process of a 1. By analyzing the above example, we can fix the initial conditions for the unrelated states and parameter estimations such that the transient time for the synchronization process is much less influenced. The desired persistent time and the transient time for estimating a 1 can be adjusted by varying the initial conditions for x 1(0),x 2(0), and \(\hat{a}_{1}(0)\). The gap between the initial conditions for x 1(0) and x 2(0) would affect the persistent time (i.e., the larger gap between the initial conditions of x 1(0) and x 2(0), the longer process it would be for x 1(t) converging to x 2(t)). Also, the transient time for estimating a 1 would be partially determined by the gap between the initial condition \(\hat{a}_{1}(0)\) and its true value a 1=1 (i.e., larger gap from its true value would lead to longer transient time for the parameter estimation). Hence, in order to achieve a better estimation, the initial conditions for x 1(0) and x 2(0) should be selected with a large enough gap and the initial conditions for the estimation \(\hat{a}_{1}(0)\) should be chosen sufficiently close to its true value. According to the above analysis, we have performed several numerical simulations to present an intuitive observation of this method. In the simulations, we set the updating gains as k 1,2,3=1 and fix the initial conditions as \([x_{1}(0),x_{3}(0)]^{T} = [1,4]^{T}, [y_{1}(0),y_{2}(0),y_{3}(0)]^{T} = [ - 1,1,6]^{T}, \hat{b}_{1}(0) = 20\), and \(\hat{c}_{1}(0) = 5\). These initial values remain unchanged and the initial conditions for x 2(0) and \(\hat{a}_{1}(0)\) are varying in each simulation. The simulation results are shown in Fig. 7. For the sake of presentation, the y axis in Fig. 7, which represents the estimation error \(\tilde{a}_{1}\), is depicted in a logarithmic manner. As can be found in Fig. 7, the numerical results confirm the feasibility of this conceptual method. If we choose x 2(0)=100 and \(\hat{a}_{1}(0) = 2\), the time difference between the persistent time and the transient time is large enough and the identification result is quite favorable.

Fig. 7
figure 7

Parameter identification of a 1 by adjusting the persistent time and the transient time via selecting different initial conditions

Full size image

When we implement the above method, another problem would arise: since we have little information about the true values for the unknown parameters, we cannot judge whether the initial conditions for parameter estimators are chosen sufficiently close their true values. To deal with this issue, here we present another scheme to address this problem. Motivated by the concept of iterative algorithm, we could run the parameter estimation process for several times and update the initial conditions for the estimated parameters in each round with the latest values in the last round. As proved in Sect. 3, the parameter identification method features global asymptotical stability and the estimators would not be trapped in any local equilibrium. Instead, after each estimation round, the unknown parameters would converge better to their true values.

We have also performed numerical simulations to demonstrate the effectiveness of this scheme by using the same example in this section. The initial conditions are chosen as \([x_{1}(0),x_{2}(0),x_{3}(0)]^{T} = [1,5,4]^{T}, [y_{1}(0),y_{2}(0),y_{3}(0)]^{T} = [ - 1,1,6]^{T}, \hat{b}_{1}(0) = 20, \hat{c}_{1}(0) = 5\) and they will remain unchanged in each round. We assume that after every 20 second we shall initialize a new estimation round. In the first round, we select \(\hat{a}_{1}(0) = 10\). The numerical results are shown in Fig. 8. In the third round, the accuracy has only been slightly improved from 0.9864 to 0.9884 and it could be predicted that, if without additional measures, in the following rounds the estimations could be attained with limited improvement. Thus, in the fourth round, we not only choose the initial condition as \(\hat{a}_{1}(0) = 0.9884\) but also magnify the updating gain as k 1=10. By doing this the transient time can be further shortened and the estimation result in the fourth round is quite satisfactory.

Fig. 8
figure 8

Parameter identification of a 1 by using an iterative estimation scheme

Full size image

Remark 7

The idea in this section is inspired by the concept of the finite-time LI condition studied in [23, 26]. When the finite-time LI period is over, the parameter estimations would remain unchanged. Hence, we should enlarge the time gap between the persistent time and the transient time. In practical cases, one can combine the above mentioned strategies to achieve a better performance for the parameter estimation. For example, one can choose larger parameter updating gains, closer initial conditions for the estimated parameters, more unparallel values for the system states, and run the estimations with desirable rounds.

5 Conclusions

In this paper, several adaptive synchronization schemes reported in a series of recent articles have been carefully reviewed and revisited, and it is found that some proposed adaptive schemes are defective. The major defects in these studies are that the unknown parameters were inappropriately involved in the designed updating laws or the controller functions. Based on a general theorem for the adaptive synchronization design, several modified answers have been provided to correct these synchronization schemes.

In addition to addressing and correcting these imperfect results, we also point out that the important LI condition has been neglected in several articles. We have analyzed three cases in which the LI condition would not hold and accordingly we have proposed several methods to avoid the linear dependence of the identification functions such that the successful parameter identification can be achieved during the synchronization process. In addition, typical examples and numerical results are also presented to validate the feasibility of the proposed methods. Finally, we hope this article can provide insightful guidance for the synchronization and identification design of chaotic (or hyperchaotic) systems with unknown parameters.