1 Introduction

Currently, the term catalysis isolates the connections loosening progression through which chemical fusions are occurred mutually. Catalysis advances materializes via heterogeneous–homogeneous expansions. The mass transport phenomenon considering the aspects of chemical processes (heterogeneous/homogeneous) has an essential use in biological structure. Numerous multifaceted relations can arise between homogeneous–heterogeneous processes. These processes progress gradually or not all collectively deprived of any catalyst. However, these reactions have competence to respond much hurriedly with catalyst. Furthermore, a quantity of collective uses of chemical processes comprises porcelains, fog materialization and diffusion, unindustrialized and industrialized regions, etc. Few studies based on influence of these processes were conferred via Refs. (Chaudhary and Merkin 1995; Merkin 1996; Khan et al. 2018; Xu et al. 2018; Irfan et al. 2018; Hayat et al. 2018). The chemical processes properties in micropolar fluid in cone reported by Mahdy (2019). In curved surface, the influence of chemical species with radiative second-grade fluid was examined by Imtiaz et al. (2019). Recently, numerically study on ferromagnetic chemically reactive flow was scrutinized by Waqas (2020). He established that the homogeneous–heterogeneous parameters fall off the concentration of micropolar fluid. He noted that the ferro-hydro-dynamic interaction parameter has conflicted performance on thermal and velocity field.

Recent advances clarify that owing to widespread and developing uses the non-Newtonian fluids have attained noteworthy thought in engineering (Zhao et al. 2016; Deng et al. 2017a, b, c; Zhao et al. 2017; Deng et al. 2019; Zhao et al. 2019a, b; Zhao et al. 2020; Hei et al. 2019; Zhang et al. 2019) bio-chemical and genetic properties for instance pharmacological substances, polymer waters, synovial liquefied, etc. The auspicious sorts of non-Newtonian liquids (Khan et al. 2017; Mahanthesh et al. 2018; Soomro et al. 2018; Anwar and Rasheed 2018; Rashid et al. 2019; Asghar et al. 2019; Waqas et al. 2019; Khan et al. 2019) and unpredictability of flow in natural surroundings, innumerable nonlinear associations have been proposed by scientists to explore the physical aspects of these non-Newtonian liquids. The Sisko fluid model is the sort of generalized Newtonian fluids which associate the species of power law and viscous models, respectively. Khan et al. (2016) reported numerically the performance of non-Fourierís and Fickís laws on Sisko liquid model. Shen et al. (2018) studied transient Sisko nanomaterial with Cattaneo heat transport. Their assessment established that to explore the augmentation of abnormal thermal conductivity Caputo time fractional derivatives are additional proficient. The chemical species aspects on Sisko fluid was analyzed by Malik and Khan (2018). They scrutinized that concentration of Sisko fluid fall off for heterogeneous parameter. Currently, in diverse veins the blood flow considering nonlinear Sisko fluid was examined by Toghraie et al. (2020). Their theory identified that in the dominant vein area the heat fluxes impact is deserted.

Here, we scrutinize the properties of chemical species on radiated Sisko curved surface via bvp4c approach (Khan et al. 2019a, b; Sultan et al. 2019; Muhammad et al. 2019; Haq et al. 2019; Ali et al. 2019a, b, 2020; Sultan et al. 2019; Shahzad et al. 2020). The convective phenomenon, magnetic and non-uniform heat sink/source aspects are incorporated. Outcomes of influential parameters are conferred via graphs.

2 Problem formulation

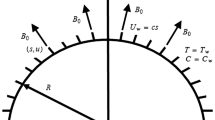
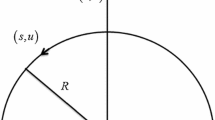
Here, an electrically conducting Sisko material in curved configuration is considered. Geometry of presented physical model in curvilinear coordinate is presented through Fig. 1. Features of viscous dissipation are retained. Characteristics of homogeneous–heterogeneous processes are accounted. The geometry of the presented problem depends on R. Moreover, heated liquid behind sheet is operated to heat up the stretched surface by convective mode of heat transport.

Fig. 1
figure 1

Flow geometry

Full size image

The quartic autocatalysis for isothermal reaction is given by

$$ E + 2F \to 3F,\quad {\text{rate}} = k_{1} G_{a} G_{b}^{2} , $$
(1)

While on catalytic surface the isothermal reaction is single reaction and first order is

$$ E \to F,\quad {\text{rate}} = k_{s} G_{a} , $$
(2)

Note that the relationship of Eq. (1) specifies reaction rate at far field is zero, so does it at the external edge of related layer. By employing overhead assumptions, the governing the physical problem is written as:

$$ \frac{\partial }{\partial r}\left( {rv} \right) + \frac{\partial }{\partial r}\left( {Rv} \right) + R\frac{\partial u}{\partial s} = 0, $$
(3)
$$ \frac{\partial p}{\partial r} = \rho_{\text{f}} \left( {\frac{{u^{2} }}{r + R}} \right), $$
(4)
$$ \begin{aligned} \frac{\partial u}{\partial t} + v\frac{\partial u}{\partial r} + u\left( {\frac{R}{r + R}} \right)\,\frac{\partial u}{\partial s} + uv\left( {\frac{1}{r + R}} \right) & = - \frac{1}{{\rho_{\text{f}} }}\left( {\frac{R}{r + R}} \right)\,\frac{\partial p}{\partial s} + \frac{a}{{\rho_{\text{f}} \left( {r + R} \right)^{2} }} \\ & \quad \times \frac{\partial }{\partial r}\left[ {\left( {r + R} \right)^{2} \frac{\partial u}{\partial r} - u\left( {r + R} \right)^{2} \left( {\frac{1}{r + R}} \right)} \right] \\ & \quad + \frac{b}{{\rho_{\text{f}} \left( {r + R} \right)^{2} }}\frac{\partial }{\partial r}\left[ {\left( {r + R} \right)^{2} \times \left( {\frac{\partial u}{\partial r} - \frac{u}{r + R}} \right)^{n} } \right] - \frac{{\sigma B_{0}^{2} }}{{\rho_{\text{f}} }}u, \\ \end{aligned} $$
(5)
$$ \frac{\partial T}{\partial t} + v\frac{\partial T}{\partial r} + u\left( {\frac{R}{r + R}} \right)\,\frac{\partial T}{\partial s} = \alpha_{1} \frac{{\partial^{2} T}}{{\partial r^{2} }} + \alpha_{1} \left( {\frac{1}{r + R}} \right)\,\frac{\partial T}{\partial r} - \frac{1}{{\left( {r + R} \right)}}\frac{\partial }{\partial r}\left( {r + R} \right)\,q_{\text{r}} + q^{\prime \prime \prime } , $$
(6)
$$ \frac{{\partial G_{a} }}{\partial t} + v\frac{{\partial G_{a} }}{\partial r} + \frac{Ru}{r + R}\frac{{\partial G_{a} }}{\partial s} = D_{A} \left( {\frac{{\partial^{2} G_{a} }}{{\partial r^{2} }} + \frac{1}{r + R}\frac{{\partial G_{a} }}{\partial r}} \right) - k_{1} G_{a} G_{b}^{2} , $$
(7)
$$ \frac{{\partial G_{b} }}{\partial t} + v\frac{{\partial G_{b} }}{\partial r} + u\left( {\frac{R}{r + R}} \right)\,\frac{{\partial G_{b} }}{\partial s} = D_{B} \left( {\frac{{\partial^{2} G_{b} }}{{\partial r^{2} }} + \frac{1}{r + R}\frac{{\partial G_{b} }}{\partial r}} \right) + k_{1} G_{a} G_{b}^{2} , $$
(8)

with

$$ u = U_{w} \left( s \right) = \frac{as}{1 - \alpha t},\,v = 0,\quad k_{\text{f}} \frac{\partial T}{\partial r} = h\left( {T_{\text{f}} - T} \right),\quad D_{A} \frac{{\partial G_{b} }}{\partial r} = - D_{B} \frac{{\partial G_{b} }}{\partial r} = k_{s} G_{a} {\text{ at }}r = 0, $$
(9)
$$ u \to 0,\,\frac{\partial u}{\partial r} \to 0,\,T \to T_{\infty } ,\,G_{a} \to G_{0} ,\,G_{b} \to 0\quad {\text{as}}\quad \, r \to \infty . $$
(10)

Non-uniform heat sink/source and radiative heat flux are estimated as

$$ q^{\prime \prime \prime } = \frac{{kU_{s} \left( {s,\,t} \right)}}{sv}\left[ {A^{ * } \left( {T_{w} - T_{\infty } } \right)\,f^{{^{\prime } }} + \left( {T - T_{\infty } } \right)\,B^{ * } } \right], $$
(11)
$$ q_{r} = - \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}\frac{\partial T}{\partial r}, $$
(12)

invoking Eqs. (11) and (12) into Eq. (6), we get

$$ \begin{aligned} \frac{\partial T}{\partial t} + v\frac{\partial T}{\partial r} + u\left( {\frac{R}{r + R}} \right)\,\frac{\partial T}{\partial s} & = \frac{k}{{\left( {\rho c} \right)_{\text{f}} }}\left( {1 + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3kk^{ * } }}} \right)\,\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r + R}\frac{\partial T}{\partial r}} \right) \\ & \quad + \frac{{kU_{s} \left( {s,\,t} \right)}}{sv}\left[ {A^{ * } \left( {T_{w} - T_{\infty } } \right)\,f^{{^{\prime } }} + \left( {T - T_{\infty } } \right)\,B^{ * } } \right]. \\ \end{aligned} $$
(13)

Considering

$$ \begin{aligned} u & = U_{w} f^{\prime } \left( \eta \right),\,v = - U_{w} \left( {\frac{R}{r + R}} \right)\,Re_{b}^{{ - \tfrac{1}{n + 1}}} \left[ {\frac{2n}{n + 1} + \left( {\frac{1 - n}{1 + n}} \right)\,\eta f^{\prime } \left( \eta \right)} \right], \\ \varPsi & = sU_{w} Re_{b}^{{ - \tfrac{1}{n + 1}}} f\left( \eta \right),\,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\,G_{a} = G_{\infty } \varphi \left( \eta \right),\,G_{b} = G_{\infty } \vartheta \left( \eta \right), \\ p & = \frac{{\rho a^{2} s^{2} }}{{\left( {1 - \alpha t} \right)^{2} }}P\left( \eta \right),\,\eta = \frac{r}{s}Re_{b}^{{\tfrac{1}{n + 1}}} . \\ \end{aligned} $$
(14)

Utilizing the overhead transformations, the requirement of Eq. (1) is automatically fulfilled and Eqs. (4) and (5) take the form

$$ \frac{\partial P}{\partial \eta } = \frac{{f^{\prime 2} }}{\eta + K}, $$
(15)
$$ \begin{aligned} \frac{2K}{\eta + K}P & = \frac{K}{\eta + K}\left( {\frac{2n}{n + 1}} \right)\,\left( {ff^{\prime \prime } + \frac{1}{\eta + K}ff^{\prime } } \right) - \frac{K}{\eta + K}f^{\prime 2} \\ & \quad + A\left[ {f^{\prime \prime \prime } - \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime } + \frac{1}{\eta + K}f^{\prime \prime } } \right] + n\left( {f^{\prime \prime } - \frac{1}{\eta + K}f^{\prime } } \right)^{n - 1} \left( {f^{\prime \prime \prime } + \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime } - \frac{1}{\eta + K}f^{\prime \prime } } \right)\, \\ & \quad + \frac{2}{\eta + K}\left( {f^{\prime \prime } - \frac{1}{\eta + K}f^{\prime } } \right)^{n} - Mf^{\prime } - \delta \left[ {f^{\prime } + \left( {\frac{2 - n}{n + 1}} \right)\,\eta f^{\prime \prime } } \right], \\ \end{aligned} $$
(16)

Eliminating contribution of pressure from Eqs. (15) and (16), then governing boundary layer expression of Sisko fluid with heat and mass transfer is expressed as follows

$$ \begin{aligned} & A\left[ {f^{\prime \prime \prime \prime } + \frac{2}{\eta + K}f^{\prime \prime \prime } - \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime } + \frac{1}{{\left( {\eta + K} \right)^{3} }}f^{\prime } } \right] + \left( {\frac{2n}{n + 1}} \right)\,\left[ {\frac{K}{\eta + K}\left( {ff^{\prime \prime } + f^{\prime } f^{\prime \prime } } \right)} \right. \\ & \quad \left. { + \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {ff^{\prime \prime } + f^{\prime 2} } \right) - \frac{K}{{\left( {\eta + K} \right)^{2} }}ff^{\prime } } \right] - \frac{2K}{\eta + K}f^{\prime } f^{\prime \prime } - \frac{2K}{{\left( {\eta + K} \right)^{2} }}f^{\prime 2} \\ & \quad + n\left( {f^{\prime \prime } - \frac{1}{\eta + K}f^{\prime } } \right)^{n - 1} \times \left( {f^{\prime \prime \prime \prime } + \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime \prime } - \frac{1}{{\left( {\eta + K} \right)^{3} }}f^{{^{\prime } }} } \right) \\ & \quad + n\left( {n - 1} \right)\,\left( {f^{\prime \prime } - \frac{1}{\eta + K}f^{\prime } } \right)^{n - 2} \left( {f^{\prime \prime \prime } - \frac{1}{\eta + K}f^{\prime \prime } + \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime } } \right)^{2} \\ & \quad + 2n\left( {f^{\prime \prime } - \frac{1}{\eta + K}f^{\prime } } \right)^{n - 1} \left( {\frac{1}{\eta + K}f^{\prime \prime \prime } - \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime \prime } + \frac{1}{{\left( {\eta + K} \right)^{3} }}f^{\prime } } \right) \\ & \quad - M\left( {f^{\prime \prime } + \frac{1}{\eta + K}f^{\prime } } \right) - \frac{\delta }{\eta + K}\left[ {f^{\prime } + \frac{2 - n}{n + 1}\eta f^{\prime \prime } } \right] - \delta \left[ {\frac{2 - n}{n + 1}\eta f^{\prime \prime \prime } + \frac{3}{n + 1}f^{\prime \prime } } \right] = 0, \\ \end{aligned} $$
(17)
$$ \theta^{\prime \prime } + \frac{1}{\eta + K}\theta^{\prime } + \mathop {\Pr }\limits Nr \times \left( {\frac{K}{\eta + K}} \right)\,\left( {\frac{2n}{n + 1}} \right)\,f\theta^{\prime } - \mathop {\Pr }\limits Nr\delta \left( {\frac{n - 2}{n + 1}} \right)\,\eta \theta^{\prime } = 0, $$
(18)
$$ \varphi^{\prime \prime } + \left( {\frac{1}{\eta + K}} \right)\,\varphi^{\prime } + {\text{Sc}}\left[ {\frac{K}{\eta + K}f\varphi^{\prime } - \delta \left( {\frac{n - 2}{n + 1}} \right)\,\eta \varphi^{\prime } + k_{2} \varphi \vartheta^{2} } \right] = 0, $$
(19)
$$ \vartheta^{\prime \prime } + \left( {\frac{1}{\eta + K}} \right)\,\vartheta^{\prime } + \frac{\text{Sc}}{\varepsilon }\left[ {\frac{K}{\eta + K}f\vartheta^{\prime } - \delta \left( {\frac{n - 2}{n + 1}} \right)\,\eta \vartheta^{\prime \prime } - k_{2} \varphi \vartheta^{2} } \right] = 0, $$
(20)
$$ f\left( 0 \right) = 0,\,f^{\prime } \left( 0 \right) = 1,\,\theta^{\prime \prime } \left( 0 \right) = \gamma \left( {1 - \theta^{\prime } \left( 0 \right)} \right),\,\varphi^{\prime } \left( 0 \right) = - \varepsilon \varphi^{\prime } \left( 0 \right) = k_{s} \vartheta \left( 0 \right), $$
(21)
$$ f^{\prime } \left( \infty \right) = 0,\,f^{\prime \prime } \left( \infty \right) = 0,\,\theta \left( \infty \right) = 0,\,\varphi \left( \infty \right) = 1, $$
(22)

physical parameters involved in the problem are represented as follows

$$ \begin{aligned} Re_{a} & = \frac{{U_{w} s\rho_{\text{f}} }}{a},\,Re_{b} = \frac{{U_{w}^{2 - n} s^{n} \rho_{\text{f}} }}{b},\,A = \frac{{Re_{b}^{{\tfrac{2}{n + 1}}} }}{{Re_{a} }},\,M = \frac{{\sigma B_{0}^{2} }}{{\left( {\rho c} \right)_{\text{f}} }}\left( {1 - \alpha t} \right), \\ K & = \frac{R}{{s\left( {1 - \alpha t} \right)}}Re_{b}^{{\tfrac{1}{n + 1}}} ,\,\delta = \frac{\alpha }{a},\,{\text{Nr}} = \frac{{3R_{d} }}{{4 + 3R_{d} }},\,R_{d} = \frac{{kk^{ * } }}{{4\sigma^{ * } T_{\infty }^{3} }}, \\ \alpha_{1} & = \frac{k}{{\left( {\rho c_{p} } \right)_{\text{f}} }},\,\mathop {\Pr }\limits = \frac{{sU_{w} }}{{\alpha_{1} }}Re_{b}^{{ - \tfrac{2}{n + 1}}} ,\,Sc = \frac{{sU_{w} }}{{D_{B} }}Re_{b}^{{ - \tfrac{2}{n + 1}}} ,\,k_{2} = \frac{{k_{1} G_{\infty } \left( {1 - \alpha t} \right)}}{a}. \\ \end{aligned} $$
(23)

For simplicity, we assume

$$ \vartheta \left( \eta \right) + \varphi \left( \eta \right) = 1. $$
(24)

By utilizing Eq. (18), one obtains

$$ \varphi^{\prime \prime } + \left( {\frac{1}{\eta + K}} \right)\,\varphi^{\prime } + {\text{Sc}}\left[ {\frac{K}{\eta + K}f\varphi^{\prime } - \delta \left( {\frac{n - 2}{n + 1}} \right)\,\eta \varphi^{\prime } + k_{2} \varphi \left( {1 - \varphi } \right)^{2} } \right] = 0, $$
(25)

2.1 Drag force and rate of heat–mass transport

Mathematically

$$ C_{\text{f}} = \frac{{\tau_{w} }}{{\tfrac{1}{2}\rho_{\text{f}} U_{w}^{2} }},\,{\text{with }}\tau_{w} = \left. {\mu \left( {\frac{\partial u}{\partial r} - \frac{u}{{\left( {r + R} \right)}}} \right)} \right|_{r = 0} , $$
(26)
$$ {\text{Nu}}_{s} = \frac{{q_{m} s}}{{k\left( {T_{\text{f}} - T_{\infty } } \right)}},\,{\text{with }}q_{m} = \left. { - k\left( {1 + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3kk^{ * } }}} \right)\,\frac{\partial T}{\partial r}} \right|_{r = 0} . $$
(27)

Utilizing the non-dimensional variables, we obtain

$$ \frac{1}{2}Re_{b}^{{\tfrac{1}{n + 1}}} C_{\text{f}} = A\left[ {f^{\prime \prime } \left( 0 \right) - \frac{{f^{\prime \prime } \left( 0 \right)}}{K}} \right] + \left[ {f^{\prime \prime } \left( 0 \right) - \frac{{f^{\prime } \left( 0 \right)}}{K}} \right]^{n} , $$
(28)
$$ Re_{b}^{{ - \tfrac{1}{n + 1}}} {\text{Nu}}_{s} = - \frac{{\theta^{\prime } \left( 0 \right)}}{Nr}. $$
(29)

3 Numerical solutions

Set of Eqs. (17)–(22) along with associated conditions are tackled numerically via MATLAB tool bvp4c. For this scheme boundary value problem is rehabilitated into initial value problem and MATLAB software bvp4c is implemented for step by step integrated.

4 Discussion

Main theme of this research work is to mark the physical interpretation of behavior of various physical parameters which arise in flow, heat and mass transport of Sisko magneto-fluid past a curved stretched surface. Numerical technique namely bvp4v is employed to integrate. Main motivation behind current research work is to investigate the aspect of all arising physical parameters on velocity, temperature and concentration profiles. Moreover, flow and heat transport mechanisms are probed by computing the value of drag forces and Nusselt number.

4.1 Velocity profiles

Features of \( A \), \( \delta \), \( K \) and \( M \) via Figs. 2, 3, 4 and 5 are communicated in this subsection for \( n < 1 \) and \( n > 1 \). Figure 2a and b represents the significant effect \( A \) on velocity of Sisko fluid for curved stretched surface. Through graphical data, outcomes are substantial in case of \( n < 1 \). Physical enhancement conducts with \( A \) due to low shear rate and high shear rate for low viscosity regarding Sisko fluid flow. The non-dimensional velocity of Sisko fluid for \( \delta \) is sketched through Fig. 3a and b with raising values of time-dependent parameter \( \delta \). As revealed from graphical data, \( \delta \) has great impact on velocity of magneto-fluid, i.e., velocity of magneto-fluid deteriorates by raise in \( \delta \). Figure 4a and b visualizes that augmented values of \( K \) has a great impact on velocity for \( n < 1 \) as well as for \( n > 1 \). It is observed that Sisko fluid and its momentum boundary layer enhances for augmented values of \( K \). Moreover, we can detect from our graphical data that results are more prominent for shear thinning fluid as compared to shear thickening fluid. Figures 5a and b demarcates the inspiration of \( M \) on velocity of Sisko fluid. One can explicitly observe that momentum boundary layer declines for incrementing values of \( M \).

Fig. 2
figure 2

a, b \( f^{{^{\prime } }} \left( \eta \right) \) via \( A \) for \( n < 1 \) and \( n > 1 \)

Full size image
Fig. 3
figure 3

a, b \( f^{{^{\prime } }} \left( \eta \right) \) via \( \delta \) for \( n < 1 \) and \( n > 1 \)

Full size image
Fig. 4
figure 4

a, b \( f^{{^{\prime } }} \left( \eta \right) \) via \( K \) for \( n < 1 \) and \( n > 1 \)

Full size image
Fig. 5
figure 5

a, b \( f^{{^{\prime } }} \left( \eta \right) \) via \( M \) for \( n < 1 \) and \( n > 1 \)

Full size image

4.2 Pressure profile

Figures 6 and 7 illustrate the aspects of various physical parameter on pressure profile inside the boundary region for \( n > 1 \). Figure 6a is devoted to illuminate the bearing of \( A \) on Sisko fluid. One can detect from these pressure profiles that inside the boundary layer region pressure profile raises with boosts values of \( A \). Moreover, pressure profile inside boundary layer enhances with raising values of \( K \) and is detected through Fig. 6b. We also observed from our data that curved surface become planner surface for augmented values of \( K \) and pressure inside boundary layer approaches to zero. Curved surface becomes more curved for smaller value of \( K \). This behavior of \( K \) can explained on basis that curvature of surface raises due to curvilinear nature of flow. Furthermore, variation of pressure distribution for different values of unsteady parameters \( \delta \) and magnetic parameter \( M \) is demonstrated through Fig. 7a and b. We can perceive from our data that pressure profile inside the boundary layer deteriorate with boosts values of \( \delta \) and \( M \).

Fig. 6
figure 6

a, b \( P\left( \eta \right) \) via \( A \) for \( n < 1 \) and \( K \) for \( n > 1 \)

Full size image
Fig. 7
figure 7

a, b \( P\left( \eta \right) \) via \( \delta \) for \( n < 1 \) and \( M \) for \( n < 1 \)

Full size image

4.3 Temperature profile

Figures 8 and 9 illustrate the aspects of various physical on the temperature of Sisko fluid for \( n < 1 \) and \( n > 1 \). Figures 8a and b and 9a and b scrutinize the pivotal effect of nonlinear heat source/sink parameter \( A^{ * } \left( {\text{space dependent}} \right) \) and \( B^{ * } \left( {\text{temperature dependent}} \right) \) on temperature of fluid. It is engrossed that there is considerable raise in temperature of Sisko fluid for growing values of \( A^{ * } \) and \( B^{ * } \).

Fig. 8
figure 8

a, b \( \theta \left( \eta \right) \) via \( A^{ * } \) for \( n < 1 \) and \( n > 1 \)

Full size image
Fig. 9
figure 9

a, b \( \theta \left( \eta \right) \) via \( B^{ * } \) for \( n < 1 \) and \( n > 1 \)

Full size image

4.4 Concentration profile

Figures 10 and 11 display the features of \( k_{2} \) and \( k_{s} \) on concentration of Sisko fluid. Impact of \( k_{2} \) on concentration profile is presented through 10a and b. It is appraised from obtained data that concentration of Sisko fluid is rising function of \( k_{2} \). Figure 11a and b reflects the behavior of concentration profile in response to variation in \( k_{s} \). It elucidates that concentration profile deteriorates with the escalation in \( k_{s} \).

Fig. 10
figure 10

a, b \( \phi \left( \eta \right) \) via \( k_{2} \) for \( n < 1 \) and \( n > 1 \)

Full size image
Fig. 11
figure 11

a, b \( \phi \left( \eta \right) \) via \( k_{s} \) for \( n < 1 \) and \( n > 1 \)

Full size image

4.5 Quantities of physical interest

Tables 1 and 2 are presented to demonstrate the impact of achieved outcomes for surface drag forces \( \tfrac{1}{2}Re_{b}^{{ - \tfrac{1}{n + 1}}} C_{\text{f}} \) and heat transfer rate \( \text{Re}_{b}^{{ - \frac{1}{n + 1}}} {\text{Nu}}_{s} \). It is noticed from Table 1 that magnitude of surface drag forces is greater for larger estimation of \( \delta ,\, \, M, \, \,A \) while opposite trend is observed for \( K \). Table 2 reveals that magnitude of heat transport rate deteriorates for augmented values of \( K,\, \, N_{r} , \, \,A^{ * } \;{\text{and}}\;B^{ * } \) while it rises for \( \delta \).

Table 1 Numerical outcomes of \( \tfrac{1}{2}Re_{b}^{{ - \tfrac{1}{n + 1}}} C_{\text{f}} \) for various physical parameters
Full size table
Table 2 Numerical outcomes of \( {\text{Re}}_{b}^{{ - \frac{1}{n + 1}}} {\text{Nu}}_{s} \) for various physical parameters when \( A = M = 2, \)\( \Pr = 2.5, \)\( {\text{Sc}} = 3.0, \)\( k_{\text{s}} = 0.2, \)\( k_{2} = 1 \) and \( N_{\text{r}} = 2.5 \)
Full size table

5 Main outcome

A detailed characterization of boundary layer flow and heat transport of Sisko fluid is studied here in order to elucidate the aspects of chemical process. Moreover, heat sink/source is utilized to describe the heat–mass transport mechanism. Numerical computation is employed for the modeled equations. Outcomes of current paper are presented in form of graphical and tabular data. The finding can be summarized as follows:

  • Larger \( M \) and \( \delta \) yield reduction in \( f^{\prime } \left( \eta \right) \).

  • Pressure profile inside boundary region is increased when \( A \) and \( K \) are enhanced.

  • Dimensionless curvature \( K \) and \( \tfrac{1}{2}Re_{b}^{{ - \tfrac{1}{n + 1}}} C_{\text{f}} \) are inversely proportional.

  • An increment in heat source/sink parameters \( A^{ * } \) and \( B^{ * } \) corresponds to rise up temperature and decreases heat transfer rate.

  • The homogeneous reaction and isothermal cubic autocatalator kinetics, govern by first-order kinetics occurring ambient fluid.

  • The model of chemical reaction is involved for mass transfer.