Theoretical aspects of thermophoresis and Brownian motion for three-dimensional flow of the cross fluid with activation energy

Abstract

The current review proclaims the forced convective flow and heat–mass transfer characteristics of cross nanofluid past a bidirectional stretched surface. The most significant aim of the current review is to incorporate the features of Buongiorno relation, activation energy, nonlinear thermal radiation and heat sink–source for a three-dimensional flow of the cross fluid. Appropriate transformations are employed to transform the modelled partial differential equations (PDEs) of momentum, temperature and concentration into coupled nonlinear ordinary differential equations (ODEs). The governing boundary value problem is numerically integrated with the help of bvp4c scheme. The obtained numerical data are plotted for the temperature and concentration profiles of nanofluid for various converging values of physical parameters. The dependence of increasing thermophysical parameters on temperature and concentration profiles of the cross nanofluid is graphically demonstrated. Furthermore, detailed study reveals that the concentration of the cross nanofluid decreases for increasing values of Brownian motion parameter. It is also perceived from the sketches that the concentration of the cross nanofluid decreases for higher values of chemical reaction parameter. The validity of the achieved numerical outcomes is ensured by making a comparison with the existing work as special cases.

1 Introduction

Nowadays, the notion of nanoscience has been comprehensively exploited in problems attributing the conventional heat transfer in order to rise the heat transfer features of numerous fluids. The low thermal conductivity of fluids is a principal obstacle to raise the heat transport in engineering frameworks. Therefore, it is necessary to have liquids that possess high thermal conductivity. Nanoliquids are significant for this purpose. Nanoliquids are very stable and composed of nanometre-sized particles, which have substantially large surface area. On account of outstanding rise in the thermal conductivity, nanoliquids found practical utility in several technological and pharmaceutical processes. Nanoliquids are mostly used as coolants in many electronic devices. Furthermore, nanotechnology is proficiently applied in treating numerous diseases such as cancer and in designing numerous military devices. The concept of nanoliquid was initially conceived by Choi [1] who intended to increase the rate of heat transfer. Oztop and Abu-Nada [2] investigated the natural convective flow of partially heated surface by utilising the nanoparticle aspects. Khan et al [3] established the mathematical relation for three-dimensional (3D) flow of an Oldroyd-B fluid by considering the aspects of nanoparticles and heat source / sink mechanisms. Sheikholeslami and Ellahi [4] deliberated the 3D flow of natural convective flow of magnetonanofluids by utilising the cubic cavity. Akbar et al [5] scrutinised the characteristics of induced magnetohydrodynamics (MHD) for carbon nanotubes in peristaltic flow. Khan and Khan [6] devoted their research work to explore the impact of nanoparticles on the generalised Burgers fluid flow. Sandeep et al [7] inspected the impact of convective heat–mass transfer mechanisms on non-Newtonian magnetonanofluids. Rehman et al [8] considered the aspects of entropy generation for nanofluids by utilising the revised and more realistic relation of nanofluids. Khan et al [9] worked on the 3D forced convective flow of Burgers fluid in the presence of newly suggested relation for nanoparticles. Haq et al [10] investigated the impact of $\hbox {H}_2\mathrm{O}$ and $\hbox {C}_2\hbox {H}_6\hbox {O}_2$-based $\hbox {Cu}$ nanoparticles by utilising two parallel disks. Khan and Khan [11] utilised the revised mass flux conditions to investigate the impact of nanoparticles on power-law fluids. Hayat et al [12] deliberated the characteristics of Carreau nanofluid in the presence of convective boundary conditions. Khan and Khan [13] computed the analytical solution of Burgers nanofluid in the presence of heat sink–source aspects. Rahman et al [14] investigated the impact of slip on non-Newtonian and nanoparticles in a tapered artery with stenosis. Hayat et al [15] provided the characteristics of chemical processes of nanofluids utilising the rotating disk. Bhatti et al [16] summarised the impact of thermal radiation on nanofluid suspension induced by metachronal waves. Shirvan et al [17] explored the properties of wavy surface characteristics on natural convection heat transfer with nanofluids. Hayat et al [18] inspected the characteristics of magnetonanofluids by utilising the variable rotating disc. Sandeep [19] deliberated the impact of aligned MHD on nanofluids by utilising the thin film. Shirvan et al [20] analysed the numerical investigation of heat exchanger effectiveness in a pipe filled with nanofluid. Ellahi et al [21] contemplated the development of a boundary layer of nano–ferro liquid flow by utilising the low oscillating stretchable rotating disk. Rashidi et al [22] surveyed the consequence of convective heat transport mechanism by utilising obstructed duct for particle motion. Some latest research work on nanfluids includes [23,24,25,26,27,28,29,30,31,32,33,34].

The mass transfer phenomena in the chemical process depend on the behaviour of variable concentration of chemically reacting species. The species varies from a low concentrated area to a high concentrated region. Chemical processes play vital roles in advancement in culture. The categorisation of a chemical reaction can be in specific ways: among them the two major categorisations are homogeneous and heterogeneous reactions. Homogeneous reactions require the same phase or medium while the heterogeneous reactions require different phase spaces. A homogeneous reaction may be affected by temperature, volume and composition while the heterogeneous reactions are more complex in nature due to different phase spaces. A chemical reaction can be identified based on the variety and number of kinetic equations used to draw the progress of the reaction. When a single stoichiometry number and a single kinetic equation are used to complete the chemical progress, then we need a single reaction. Contrary to this, when we have applied more than one stoichiometry equation, then more than one kinetic equation is required to watch the changing composition and we have multiple answers. Multiple reactions can be classified into two types: the series reactions and the parallel reactions. Furthermore, the term activation energy has a significant role in chemical reactions. Arrhenius firstly presented the idea of activation energy in 1889. It is the least required amount of energy for the species, which changes the reactants into products. It can be in the form of potential energy or kinetic energy. In the absence of activation energy, reactants cannot form products. Conversely, a reaction occurs when the movement of the particles is rapid due to the activation energy. The applications of activation energy are very wide in chemical engineering, geothermal and mechanics of water and oil emulsions. Ramzan et al [35] presented the mathematical relation to examine the impact of binary reactions and activation energy on the magnetonanofluids. Ramzan et al [36] studied the characteristics of chemical processes and double stratification on the radiative flow of Powell–Eyring magnetonanofluids. Shafique et al [37] investigated the aspects of activation energy and rotating frame for the Maxwell fluid. Khan et al [38] analysed the effects of chemical processes on the 3D flow of Burgers fluid. Khan et al [27] inspected the impact of chemical reactions on the generalised Burgers fluid by utilising nanoparticles. Mustafa et al [39] examined the characteristics of activation energy and chemical mechanisms of magnetonanofluids.

The main emphasis of our study is to investigate the aspects of activation energy of 3D flow of the cross fluid with combined effects of thermal radiation. Moreover, we have considered the aspects of heat source–sink in this research. The novelty of this research is that it provides a comprehensive mathematical detail about the 3D flow of cross magnetonanofluid and activation energy. Graphical results are utilised to elaborate on the impacts of various variables. We have compared our results with available literature (see table 1). Furthermore, the temperature gradient is deliberated and scrutinised in table 2.

Table 1 A comparison of $-{f}''( 0 )$ and $-{g}''( 0)$ for Newtonian liquid $\left( {\hbox {We}_1 =\hbox {We}_2 =M=0} \right)$.

Table 2 Numerical values of local Nusselt number $\left( {\hbox {Re}_x } \right) ^{-1/2}\hbox {Nu}_x$ for distinct values of escalating parameters when $M=0.8, \hbox {We}_1 =\hbox {We}_2 =2.2, \hbox {Le}=2.0, R_{\mathrm{d}} =0.5, \theta _f =0.3, N_b =0.2$ and $\alpha =0.3$.

2 Mathematical descriptions

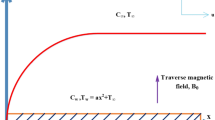
A steady, 3D MHD flow of cross nanofluid flow in the presence of heat sink–source is considered. The heat transport mechanism is carried out in the presence of nonlinear thermal radiation. Furthermore, the combined features of destructive–constructive chemical reactions and activation energy are taken in this investigation. The magnetic field is applied normal to the stretched surface. Reynolds number is supposed to be small neglecting the impact of induced magnetic field on the cross nanofluid. The temperature and concentration of magnetonanoliquid at the sheet are, respectively, $({T_w , C_w })$ which are kept constant while the nanofluid outside the boundary is maintained at uniform temperature and concentration $({T_\infty , C_\infty })$, respectively. In areas such as geothermal, the governing equations are (see [40])

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\nonumber \\&\quad ={-}\frac{1}{\rho _f }\frac{\partial P}{\partial x}+\nu \dfrac{\partial }{\partial z}\left[ {\dfrac{{\partial u}/{\partial z}}{1+\left\{ {\Gamma \left( {{\partial u}/{\partial z}} \right) } \right\} ^{n}}} \right] -\frac{\sigma ^{{1}}B_0^2 u}{\rho _f }, \nonumber \\\end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\nonumber \\&\quad ={-}\frac{1}{\rho _f }\frac{\partial P}{\partial y}+\nu \dfrac{\partial }{\partial z}\left[ {\dfrac{{\partial v}/{\partial z}}{1+\left\{ {\Gamma \left( {{\partial v}/{\partial z}} \right) } \right\} ^{n}}} \right] \nonumber \\&\qquad -\frac{\sigma ^{{1}}B_0^2 v}{\rho _f }, \end{aligned}$$

(3)

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\&\quad = \alpha _1 \frac{\partial ^{2}T}{\partial z^{2}}+\tau \left[ {D_B \frac{\partial C}{\partial z}\frac{\partial T}{\partial z}+\frac{D_T }{T_\infty }\left( {\frac{\partial T}{\partial z}} \right) ^{2}} \right] \nonumber \\&\qquad -\,\frac{1}{(\rho c)_f }\frac{\partial q_r }{\partial z}+\frac{Q_0 }{(\rho c)_f }(T-T_\infty ), \end{aligned}$$

(4)

$$\begin{aligned}&u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}= D_B \frac{\partial ^{2}C}{\partial z^{2}}+\frac{D_T }{T_\infty }\frac{\partial ^{2}T}{\partial z^{2}} \nonumber \\&\qquad -\,k_c^2 \left( {C-C_\infty } \right) \left( {\frac{T}{T_\infty }} \right) ^{m}\exp \left( {-\frac{E_a }{KT}} \right) . \end{aligned}$$

(5)

The boundary conditions for the present flow analysis are

$$\begin{aligned}&u=U_w =ax,\quad v=V_w =by,\quad w=0,\quad T=T_w ,\nonumber \\&C=C_w\quad \hbox { at } z=0, \end{aligned}$$

(6)

$$\begin{aligned}&u\rightarrow 0,\quad v\rightarrow 0,\quad T\rightarrow T_\infty ,\quad C\rightarrow C_\infty \hbox { as } z\rightarrow \infty {,}\nonumber \\ \end{aligned}$$

(7)

where $u, v, w, T, C, \nu , \Gamma , n, \rho _{_f } , \alpha _1 , \tau , D_B , D_T , q_r , k_c , E_a , K, m$ are, respectively, the velocity components, temperature, concentration, kinematic viscosity, cross time constant, flow behaviour index, fluid density, thermal diffusivity of the base liquid, ratio of heat capacities of nanoparticle to cross magnetofluid, Brownian diffusion coefficient, thermophoresis diffusion coefficient, radiative heat flux, chemical reaction constant, activation energy parameter, Boltzmann constant and fitted rate constant. The radiative heat flux $q_r$ is given by

$$\begin{aligned} q_r =-\frac{4\sigma ^{{*}}}{3k^{{*}}}\frac{\partial T^{4}}{\partial z}=-\frac{16\sigma ^{{*}}}{3k^{{*}}}\frac{\partial }{\partial z}\left( {T^{3}\frac{\partial T}{\partial z}} \right) , \end{aligned}$$

(8)

where $\left( {k^{{*}}, \sigma ^{{*}}} \right)$ are, respectively, the mean absorption coefficient and Stefan–Boltzmann constant.

Substituting eq. (8) into eq. (4), we have the following energy equation:

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\&\quad = \alpha _1 \frac{\partial ^{2}T}{\partial z^{2}}+\tau \left[ {D_B \frac{\partial C}{\partial z}\frac{\partial T}{\partial z}+\frac{D_T }{T_\infty }\left( {\frac{\partial T}{\partial z}} \right) ^{2}} \right] \nonumber \\&\qquad +\,\frac{1}{(\rho c)_f }\frac{16\sigma ^{{*}}}{3k^{{*}}}\frac{\partial }{\partial z}\left( {T^{3}\frac{\partial T}{\partial z}} \right) \nonumber \\&\qquad +\frac{Q_0 }{(\rho c)_f }(T-T_\infty ). \end{aligned}$$

(9)

Utilise the following suitable conversions:

$$\begin{aligned}&u= ax{f}'(\eta ),\quad v=ay{g}'(\eta ),\nonumber \\&w=-(a\nu )^{1/2}\left[ {f(\eta )+g(\eta )} \right] , \nonumber \\&\theta (\eta )= \frac{T-T_\infty }{T_w -T_\infty },\quad \varphi (\eta )=\frac{C-C_\infty }{C_w -C_\infty },\nonumber \\&\eta =z\sqrt{\frac{a}{\nu }}. \end{aligned}$$

(10)

Equation (1) is automatically satisfied and eqs (2)–(7) and (9) yield

$$\begin{aligned}&\left[ {1+(1-n)\left( {\hbox {We}_1 {f}''} \right) ^{n}} \right] {f}'''\nonumber \\&\quad -\,\left[ {1+\left( {\hbox {We}_1 {f}''} \right) ^{n}} \right] ^{2}\left[ {{f}'^{2}-\left( {f+g} \right) {f}''} \right] \nonumber \\&\quad -\,M^{2}{f}'=0, \end{aligned}$$

(11)

$$\begin{aligned}&\left[ {1+(1-n)\left( {\hbox {We}_2 {g}''} \right) ^{n}} \right] {g}'''\nonumber \\&\quad -\,\left[ {1+\left( {\hbox {We}_2 {g}''} \right) ^{n}} \right] ^{2}\left[ {{g}'^{2}-\left( {f+g} \right) {g}''} \right] \nonumber \\&\quad -\,M^{2}{g}'=0, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}\eta }[\{1+R_d (1+(\theta _f -1)\theta ) ^{3}\}{\theta }']\nonumber \\&\quad +\,\mathop {\Pr }\limits [(f+g){\theta }'+N_b {\theta }'{\varphi }'+N_t {\theta }'^{2}]+\mathop {\Pr }\limits \lambda \theta =0, \end{aligned}$$

(13)

$$\begin{aligned}&{\varphi }''+\hbox {Le}\mathop {\Pr }\limits (f+g){\varphi }'-\hbox {Le}\mathop {\Pr }\limits \sigma \left( {1+\delta \theta } \right) ^{m}\varphi \nonumber \\&\quad \times \exp \left( {-\frac{E}{1+\delta \theta }} \right) +\frac{N_t }{N_b }{\theta }''=0, \end{aligned}$$

(14)

$$\begin{aligned}&f( 0)=0,\quad g( 0 )=0,\quad {f}'( 0 )=1,\nonumber \\&{g}'( 0 )=\alpha ,\quad \theta ( 0 )=1,\quad \varphi (0 )=1, \end{aligned}$$

(15)

$$\begin{aligned}&{f}'\rightarrow 0,\quad {g}'\rightarrow 0,\quad \theta \rightarrow 0,\quad \varphi \rightarrow 0\quad \hbox {as } \eta \rightarrow \infty .\nonumber \\ \end{aligned}$$

(16)

Fig. 1

Profiles of temperature $\theta (\eta )$ for various values of $\alpha$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 2

Profiles of temperature $\theta (\eta )$ for various values of $N_b$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 3

Profiles of temperature $\theta (\eta )$ for various values of $N_t$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 4

Profiles of temperature $\theta (\eta )$ for various values of $\theta _f$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 5

Profiles of concentration $\varphi (\eta )$ for various values of E for (a) shear-thinning liquids and (b) shear-thickening liquids.

In the above expressions, $\hbox {We}_1 , \hbox {We}_2 , M, \alpha , R_d , \theta _f , \Pr , N_b , N_t , \lambda , \hbox {Le}, \sigma , \delta , E$ are, respectively, the local Weissenberg numbers, magnetic parameter, the ratio of stretching rate parameter, radiation parameter, temperature ratio parameter, Prandtl number, Brownian motion parameter, thermophoresis parameter, heat source–sink parameter, Lewis number, chemical reaction parameter, temperature difference parameter and activation energy. Mathematically, these parameters are expressed in the following manner:

$$\begin{aligned}&\hbox {We}_1 = \Gamma ax\sqrt{\frac{a}{\nu }}, \quad \hbox {We}_2 =\Gamma ay\sqrt{\frac{a}{\nu }},\quad R_d =\frac{16\sigma ^{{*}}T_\infty ^3 }{3kk^{{*}}},\nonumber \\&\alpha =\frac{b}{a},\quad \theta _f =\frac{T_w }{T_\infty }, \nonumber \\&M= \frac{\sigma ^1 B_0^2 }{\rho _f a},\quad N_b =\frac{\tau D_B ( {C_w -C_\infty } )}{\nu },\nonumber \\&N_t =\frac{\tau D_T (T_w -T_\infty )}{\nu T_\infty },\quad \lambda =\frac{Q_0 }{a(\rho c)_f }, \nonumber \\&\mathop {\Pr }\limits = \frac{\nu }{\alpha _1 },\quad \hbox {Le}=\frac{\alpha _1 }{D_B },\quad \sigma =\frac{k_c^2 }{a},\nonumber \\&E=\frac{E_a }{K_{\infty }T_{\infty }},\quad \delta =\frac{T_w -T_\infty }{T_\infty }. \end{aligned}$$

(17)

2.1 Skin friction and rate of heat–mass transfer

The definitions of skin friction and rate of heat–mass transfer are

$$\begin{aligned}&C_{f_x } = \frac{2\tau _{xz} }{\rho _f U_w^2 },\quad C_{f_y } =\frac{2\tau _{yz} }{\rho _f U_w^2 }, \nonumber \\&\hbox {Nu}_x = -\frac{x}{\left( {T_w -T_\infty } \right) }\left. {\left( {\frac{\partial T}{\partial z}} \right) } \right| _{z=0} +\frac{xq_r }{k\left( {T_w -T_\infty } \right) }.\nonumber \\ \end{aligned}$$

(18)

The above quantities are reduced to the following dimensionless form:

$$\begin{aligned}&C_{f_x } \left( {\hbox {Re}_x } \right) ^{1/2}= \frac{2{f}''( 0 )}{\left[ {1+\left( {\hbox {We}_2 {f}''( 0 )} \right) ^{n}} \right] },\; \nonumber \\&C_{f_y } \left( {\hbox {Re}_y } \right) ^{1/2} =\frac{2V_w {g}''( 0 )}{U_w \left[ {1+\left( {\hbox {We}_1 {g}''( 0 )} \right) ^{n}} \right] }, \nonumber \\&\left( {\hbox {Re}_x } \right) ^{-1/2}\hbox {Nu}_x\nonumber \\&\quad = -\left[ {1+R_d \{1 +(\theta _f-1 )\theta \}^{3}} \right] {\theta }'(0), \end{aligned}$$

(19)

where $\hbox {Re}_x ={ax^{2}}/\nu$ is the local Reynolds number.

3 Solution procedure

3.1 Numerical scheme

The governing ODEs for the flow and heat–mass transport of the cross nanofluid are numerically handled with the help of bvp4c scheme. The resultant problem is converted to the corresponding initial value problem. The procedure is given as follows:

$$\begin{aligned}&f=Q_1 ,\quad {f}'=Q_2 ,\quad {f}''=Q_3 ,\quad {f}'''=Q_3^\prime , \end{aligned}$$

(20)

$$\begin{aligned}&g=Q_4 ,\quad {g}'=Q_5 ,\quad {g}''=Q_6 ,\quad {g}'''=Q_6^\prime , \end{aligned}$$

(21)

$$\begin{aligned}&\theta =Q_7 ,\quad {\theta }'=Q_8 ,\quad {\theta }''=Q_8^\prime , \end{aligned}$$

(22)

$$\begin{aligned}&\varphi =Q_9 ,\quad {\varphi }'=Q_{10} ,\quad {\varphi }''=Q_{10}^\prime , \end{aligned}$$

(23)

where

$$\begin{aligned} Q_3^\prime =\frac{\left[ {\left[ {1+\left( {\hbox {We}_1 Q_3 } \right) ^{n}} \right] ^{2}\left[ {Q_2^2 -( {Q_1 +Q_4 } ) Q_3 } \right] +\left[ {1+\left( {\hbox {We}_1 Q_3 } \right) ^{n}} \right] ^{2}M^{2}Q_2 } \right] }{A_1 }, \end{aligned}$$

(24)

$$\begin{aligned} Q_6^\prime =\frac{\left[ {\left[ {1+\left( {\hbox {We}_2 Q_6 } \right) ^{n}} \right] ^{2}\left[ {Q_5^2 -\left( {Q_1 +Q_4 } \right) Q_6 } \right] +\left[ {1+\left( {\hbox {We}_2 Q_6 } \right) ^{n}} \right] ^{2}M^{2}Q_5 } \right] }{A_2 }. \end{aligned}$$

(25)

Fig. 6

Profiles of concentration $\varphi (\eta )$ for various values of m for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 7

Profiles of concentration $\varphi (\eta )$ for various values of $N_b$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 8

Profiles of concentration $\varphi (\eta )$ for various values of $N_t$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Fig. 9

Profiles of concentration $\varphi (\eta )$ for various values of $\sigma$ for (a) shear-thinning liquids and (b) shear-thickening liquids.

Here

$$\begin{aligned}&A_1 =\left[ {1+(1-n)\left( {\hbox {We}_1 Q_3 } \right) ^{n}} \right] \nonumber \\&\quad \hbox {and\quad }\nonumber \\&A_2 =\left[ {1+(1-n)\left( {\hbox {We}_2 Q_6 } \right) ^{n}} \right] , \end{aligned}$$

(26)

$$\begin{aligned}&Q_8^\prime =\frac{\mathop {-\Pr }\limits [(Q_1+Q_4)Q_8+N_b Q_8Q_{10}+N_t Q_8^{2}]-\mathop {\Pr }\limits \lambda Q_7 -3R_d (1+(\theta _f -1)Q_7 )^{2}((\theta _f -1)Q_8^2 )}{A_3 }, \end{aligned}$$

(27)

$$\begin{aligned}&A_3 =(1+R_\mathrm{d} (1+(\theta _f -1)Q_7 )^{3}), \end{aligned}$$

(28)

$$\begin{aligned}&Q_{10}^\prime =-\hbox {Le} \mathop {\Pr }\limits \sigma \left( {1+\delta Q_7 } \right) ^{m}\nonumber \\&\qquad \qquad \times \exp \left( {-\frac{E}{1+\delta Q_7 }} \right) Q_9\nonumber \\&\qquad \qquad -\,\hbox {Le} \mathop {\Pr }\limits (Q_1 +Q_4 )Q_{10} -\frac{N_t }{N_b }Q_8^\prime , \end{aligned}$$

(29)

with

$$\begin{aligned}&Q_1 ( 0 )=0,\quad Q_4 ( 0 )=0,\quad Q_2 ( 0 )=1,\quad Q_5 ( 0 )=\alpha , \nonumber \\&Q_7 ( 0 )=1,\quad Q_9\left( 0 \right) =1, \end{aligned}$$

(30)

$$\begin{aligned}&Q_2 \rightarrow 0,\quad Q_5 \rightarrow 0,\quad Q_7 \rightarrow 0,\nonumber \\&Q_9 \rightarrow 0\; \hbox {as}\; \eta \rightarrow \infty . \end{aligned}$$

(31)

3.2 Verification of numerical outcomes

The accuracy of the numerical technique is verified in table 1 by making a comparison in the absence of nonlinear mechanisms with the results tabulated by Ariel [41]. The numerical outcomes of $-{f}''( 0 )$ and $-{g}''( 0 )$ are computed and the legitimacy of our results is ensured.

4 Discussion

The foremost emphasis of the current research is to explore the features of constructive–destructive reactions and activation energy effects for MHD 3D forced convective flow of cross nanofluid. Heat sink–source and nonlinear radiation effects are taken into consideration. Detailed graphical analysis has been made for the temperature and concentration fields and discussed for various parameters of interest. Additionally, the heat transfer rate of various fluctuating parameters is included in table 2. From table 2, we perceived that the heat transfer rate increases for accumulative values of $\Pr , E, n$ and $\sigma$ while it decreases for $\delta , m$ and $N_t$.

The dependence of various parameters on the temperature of cross nanofluid is exhibited graphically in figures 1–4. Figures 1a and 1b are sketched to perceive the dependence of 3D flow of cross nanofluid on $\alpha$ for $n<1$ and $n>1$. The exploration of these plots shows that nanofluid temperature decreases for argumented values of alpha. This behaviour of cross magnetonanoliquid appears to be due to the fact that as we increase $\alpha$, stretching at infinity is higher when compared to the stretching rate at $\eta =0$. Furthermore, a careful analysis of these sketches shows that the decaying behaviour of the cross nanofluid is more prominent for $n>1$. Figures 2a, 2b and 3a, 3b present the impact of $N_b$ and $N_t$ on the temperature profile of the cross nanofluid. These figures show that the augmented values of $N_b$ and $N_t$ affect the heat transfer strongly. The rise in the temperature of cross nanofluid is detected for increasing values of $N_b$ and $N_t$. Physically, $N_t$ demonstrates the temperature difference of cross nanofluid between the hot fluid behind the sheet and temperature of the liquid at infinity. Therefore, as we raise the values of $N_t ,$ the difference of temperature at infinity and at $\eta =0$ increases due to which the temperature of the cross nanoliquid enhances. The influence of $\theta _{f}$ on the temperature profile of the cross fluid is displayed in figures 4a and 4b. It can be seen from these figures that the temperature profile enhances with an increment in $\theta _{f}$. Physically, as $\theta _{f}$ strengthens, the temperature of the wall increases compared to the temperature of the nanoliquid at infinity. Thus, the temperature of the nanofluid increases.

The concentration profiles of the cross nanofluid exhibit remarkable changes with the variation of $E, m, N_b , N_t$ and $\sigma$ for $n<1$ and $n>1$. Concentration profiles of the cross nanofluid for different values of activation energy E are shown in figures 5a and 5b. The increasing values of E result in an augmentation in the concentration of cross nanofluid. From eq. (1), we detected that high activation energy and low temperature reduce the reaction rate due to which chemical reaction mechanisms slow down. Therefore, the concentration of cross nanofluid increases. Figures 6a and 6b are plotted to detect the characteristics of the fitted rate constant m on the concentration of cross nanofluid. Chemically, as we boost the values of m destructive chemical mechanisms enhance due to the decline in the concentration of the cross nanofluid. Figures 7a, 7b and 8a, 8b show the concentration profile of the cross nanofluid for various values of $N_b$ and $N_t$. These figures show that the concentration of cross nanofluid decreases with elevation in $N_t$ while the reverse trend is observed for $N_b$. Additionally, it is detected that physically, an increase in the magnitude of $N_b$ corresponds to an increase in the rate at which nanoparticles in the base liquid move in random directions with different velocities. This movement of nanoparticles augments transfer of heat and therefore, decreases the concentration profile. The influence of $\sigma$ on the concentration profile of the cross fluid is shown in figures 9a and 9b. These figures show that the concentration profile deceases with an increment in $\sigma$.

5 Concluding remarks

The intent of the present work was to develop a physical model and to provide a better understanding of 3D flow of cross magnetonanofluid under the aspects of heat source–sink. Furthermore, the impacts of activation energy and destructive–constructive chemical reactions for magnetonanofluid were considered here. Modelled equations of cross magnetonanofluid were simplified by applying suitable similarity transformations and the numerical solutions of these equations were found with the help of bvp4c scheme. The main findings can be listed as:

• Temperature field and thermal layer structures exhibited descending trend for increasing values of heat sink parameter.

• The increasing values of $N_t$ resulted in the elevation of the liquid temperature.

• $N_t$ and $N_b$ have opposite effects on the concentration profile of the nanofluid.

• There was an increase in concentration of 3D flow of cross magnetonanofluid for increasing values of E.

• There was a decrease in concentration of the cross fluid with increase in m and $\sigma$.