Chemically reactive flow of thixotropic nanofluid with thermal radiation

Abstract

This article addresses the flow of a thixotropic liquid with nanomaterials due to a stretching sheet of variable thickness. The stimulus effects of the heat source / sink and first-order chemical reaction are retained. Convective conditions of heat and mass transfer are also considered at the boundary. Unlike the classical consideration, the linear thermal radiation aspect is examined. The influence of emergent flow, heat and mass parameters on velocity, concentration and temperature fields are shown graphically. It is also noted that the velocity of the fluid significantly favours the non-Newtonian parameters. For higher values of radiation and heat source / sink parameter, the temperature rises. Moreover, a novel investigation on heat and mass transfer rates subject to nanomaterials (i.e. Brownian motion and thermophoresis) in the liquid has been carried out. Nonlinear systems are solved by the optimal homotopy analysis method (OHAM). Convergence analysis has been executed and the optimal values are computed. The main advantage of the proposed technique is that it can be directly utilised in highly nonlinear systems without using discretisation, linearisation and round-off errors. The table shows the results of the error analysis.

1 Introduction

Nanofluid is a uniform suspension of ultrafine nanosized particles (metallic / non-metallic / nanofibres) with the typical size less than 100 nm of diameter in base fluids, such as water, ethylene, toluene and oil. Some common nanoparticles are copper, aluminium, silver [1], silicon [2], diamond [3], titanium [4] and carbon nanotubes [5] which tend to enhance thermal conductivity. Experimental investigation revealed that the thermal performance of nanofluids depends on particle material, particle shape, particle volume fraction, temperature, particle size and base fluid material. Nanofluids have attained great importance in many engineering and biological fields such as catalysis, electronics, solar cells, medicines, glass industry, material manufacturing, laser cutting, plasma, etc. Choi [6] initiated the basic mechanism of nanofluids to enhance their thermal characteristics. Buongiorno [7] observed enhanced thermal conductivities with the insertion of Brownian motion and thermophoresis properties in a flow. Babu and Sandeep [8] worked on nanofluids with thermophoresis and Brownian motion aspects due to stretching sheets. A review of the thermal conductivity of various nanofluids was done by Ahmadi et al [9]. Uddin et al [10] studied the convective flow of nanofluids. For further details, see refs [1,2,3,4,5, 11, 12].

Nowadays, the boundary layer flow of non-Newtonian fluids is a hot topic of research and such fluids can be used in fibre technology, coating of wires, ketchup, slurries, drilling muds, shampoo, apple sauce, synovial fluid and heather honey. Non-Newtonian fluids exhibit a nonlinear relationship between shear stress and strain rate. The thixotropic fluid model is one of these models. The thixotropic fluid exhibits a reduction in viscosity over time at a constant shear rate. Sadeqi et al [13] elaborated the Blasius flow of thixotropic materials. Deus and Dupim [14] investigated the behaviour of thixotropic fluids. Shehzad et al [15] worked on the chemically reactive flow of thixotropic fluids subject to stretching sheets. In a doubly stratified medium, the flow analysis of thixotropic nanomaterials with magnetic field effects is discussed by Hayat et al [16]. Zubair et al [17] elaborated the flow of thixotropic fluid with the Cattaneo–Christov heat flux model. A comparison of non-thixotropic and thixotropic materials in a tube is presented by Abedi et al [18]. Qayyum et al [19] presented the flow of thixotropic nanofluids subject to a stretched surface of variable thickness.

Heat and mass transport in the flow of an incompressible fluid due to the stretching surface has been extensively investigated by many researchers. Recently, an attempt has been made to introduce variable thicknesses on stretching surfaces. Due to the acceleration or deceleration of the surface, the thickness of the stretched surface may decrease or increase depending on the value of the power index of velocity. Presently, fluid flow subject to stretching surfaces with variable thicknesses is an important area of research. This is due to its relevance in the industrial and engineering sectors, particularly in civil, marine, aeronautical and architectural engineering. It also helps in refining the utilisation of the material. Fang et al [20] introduced flow due to a stretched sheet of variable thickness. The flow of the thixotropic fluid with nanomaterials subject to a nonlinear stretching surface of variable thickness is modelled by Hayat et al [21]. Daniel et al [22] studied the radiative flow of nanofluids towards a nonlinear stretching sheet with variable thickness. A fragment’s mass distribution scaling relation with variable thickness is elaborated by Zhang et al [23]. Hayat et al [24] described the MHD effects on the $\hbox {Al}_{2} \hbox {O}_{3}-$water nanofluid due to the rotating disk with variable thickness. The flow of the Maxwell fluid by a stretching sheet with variable thickness is studied by Liu and Liu [25].

The main aim of this study is to explore the flow of thixotropic nanofluid by a stretching sheet of variable thickness with a heat source / sink. The effects of thermal radiation and chemical reaction are also highlighted. The relevant problems are formulated. The governing nonlinear framework is solved by the optimal homotopy analysis method (OHAM) [26,27,28,29,30,31,32]. Based on the aforementioned literature survey, the flow of the thixotropic nanofluid on a stretching surface with variable thickness is discussed for the first time. The immediate applications are in the melting of plastics, engine cooling and paper production.

Fig. 1

Flow geometry.

2 Modelling

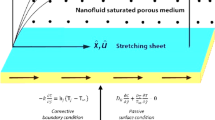
Consider the chemically reactive flow of a thixotropic nanofluid due to a stretching surface of variable thickness. The flow caused by the nonlinear stretching surface is restricted to the domain $y>0$. The stretching velocity of the sheet is ${{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} _w \left( x \right) =a(x+b)^{n}$ (n being the power-law index). The flow fills the porous medium. In this analysis, contributions due to thermophoresis and Brownian movements are studied. Heat transfer analysis is performed in the presence of thermal radiation and heat generation / absorption effects. Figure 1 plots the physical description.

The problem statements are:

$$\begin{aligned}&\frac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial x}+\frac{\partial {{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\left. {{\begin{array}{l} {\rho \left( {{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial x}+{{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) {=}\mu \left( {\dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) {-}6R_a \left( {\dfrac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) ^{2}\dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}{-}\dfrac{\mu }{K}u} \\ +4R_b \left[ {{\begin{array}{l} {\left( {\dfrac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) \left( {\dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) \left( {\hat{{u}}\dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial x\partial y}+{{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) } \\ \quad +\left( {\dfrac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) ^{2}\left( {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial ^{3}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial x\partial y^{2}}+{{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial ^{3}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{3}}{+}\dfrac{\partial \hat{{u}}}{\partial y}\dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial x\partial y}\right. \\ \quad \left. {+}\dfrac{\partial {{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}\dfrac{\partial ^{2}{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}} \right) \\ \end{array} }} \right] , \\ \end{array} }} \right\} \end{aligned}$$

(2)

$$\begin{aligned}&\left. {{\begin{array}{l} {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial x}+{{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}=\alpha \left( {\dfrac{\partial ^{2}{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) \\ \quad +\tau \left[ {D_\mathrm{B} \left( {\dfrac{\partial {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}\dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) +\dfrac{D_{{{\mathop {{T}}\limits ^{\scriptscriptstyle \smile }}} } }{{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty }\left( {\dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) ^{2}} \right] \\ {\quad -\dfrac{1}{\left( {\rho C_p } \right) _f }\dfrac{\partial q}{\partial y}+\dfrac{Q_h }{\left( {\rho C_p } \right) _f }({{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ),} \\ \end{array} }} \right\} \end{aligned}$$

(3)

$$\begin{aligned} {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} \frac{\partial {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial x}+{{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} \frac{\partial {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}&=D_\mathrm{B} \left( {\frac{\partial ^{2}{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) +\frac{D_\mathrm{T} }{T_\infty }\left( {\frac{\partial ^{2}{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) \nonumber \\&\quad \,\, -K_{\mathrm{C}} ({{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} -{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _\infty ), \end{aligned}$$

(4)

$$\begin{aligned}&\left. {{\begin{array}{l} {{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} ={{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} _w =a\left( {x{+}b} \right) ^{n},~ {{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} =0,~ -k\dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}=h\big ( {{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _{f} -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} } \big ),} \\ {-D_m \dfrac{\partial {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}=k_{\mathrm{m}} \big ( {{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _{f} -{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} } \big )\quad \hbox { at }y=\delta \left( {x+b} \right) ^{(1-n)/2},} \\ {{{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} \rightarrow 0,~ {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} ={{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ,~ {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} ={{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _\infty \quad \hbox { as }y\rightarrow \infty ,} \\ \end{array} }} \right\} \end{aligned}$$

(5)

where ${{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} , {{\mathop {v}\limits ^{\scriptscriptstyle \smile }}}$ are the velocity components parallel to the x and y directions, respectively, ${{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} _w$ is the stretching velocity, ${{\mathop {C}\limits ^{\scriptscriptstyle \smile }}}$ is the volume fraction of the nanoparticles, ${{\mathop {T}\limits ^{\scriptscriptstyle \smile }}}$ is the temperature, $\rho$ is the fluid density, $R_a$ and $R_b$ are the material constants, $\alpha ={k}/{(\rho {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} )_p }$ is the thermal diffusivity, k is the thermal conductivity, $(\rho {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} )_p$ is the specific heat, $k_{\mathrm{m}}$ is the mass transfer coefficient, $D_{{{\mathop {{T}}\limits ^{\scriptscriptstyle \smile }}} }$ is the thermophoresis diffusion coefficient, $\tau ={(\rho {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} )_p }/{(\rho {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} )_f }$ is the heat capacity ratio, K is the permeability of porous space, h is the heat transfer coefficient, $D_\mathrm{B}$ is the Brownian diffusion coefficient and $K_{\mathrm{C}}$ is the chemical reaction rate coefficient. By utilising Rosseland’s concept, the radiative heat flux q is

$$\begin{aligned} q=-\frac{4\sigma ^{{*}}\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}}^{4} }{3k^{{*}}\partial y}, \end{aligned}$$

(6)

where $\sigma ^{{*}}$ and $k^{{*}}$ are Stefan–Boltzmann and Rosseland’s mean absorption coefficients. Temperature is expanded about ${{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty$ into the Taylor series

$$\begin{aligned} {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} ^{4}\cong 4{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ^3 {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} -3{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ^4 . \end{aligned}$$

(7)

Now eq. (3) is reduced to

$$\begin{aligned} \left. {{\begin{array}{l} {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial x}+{{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} \dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}=\alpha \left( {\dfrac{\partial ^{2}{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}} \right) \\ \quad +\tau \left[ {D_\mathrm{B} \left( {\dfrac{\partial {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}\dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) +\dfrac{D_{{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} } }{{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty }\left( {\dfrac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) ^{2}} \right] \\ \times {\dfrac{1}{\left( {\rho C_p } \right) _{f} }\dfrac{16\sigma ^{{*}}{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ^3 }{3^{{*}}}\dfrac{\partial ^{2}{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y^{2}}+\dfrac{Q_h }{\left( {\rho C_p } \right) _{f} }({{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ).} \\ \end{array} }} \right\} \end{aligned}$$

(8)

Considering

$$\begin{aligned} \left. {{\begin{array}{l} {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} =a\left( {x+b} \right) ^{n}{\tilde{F}}^{\prime }(\xi ), \hbox { }\\ {{\mathop {v}\limits ^{\scriptscriptstyle \smile }}} =-\sqrt{\left( {\dfrac{n+1}{2}} \right) \nu a\left( {x+b} \right) ^{n-1}}\\ \qquad \,\, \times \left[ {{\tilde{F}}(\xi )+\dfrac{n-1}{n+1}\xi {\tilde{F}}^{\prime } (\xi )} \right] , \\ \xi =y\sqrt{\left( {\dfrac{n+1}{2}} \right) \dfrac{a}{\nu }\left( {x+b} \right) ^{n-1}}, \hbox { }{\tilde{\Theta }}(\xi )=\dfrac{{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty }{{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _f -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty },\\ \hbox { }{\tilde{\phi }}(\xi )=\dfrac{{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} -{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _\infty }{{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _f -{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _\infty }, \\ \end{array} }} \right\} \end{aligned}$$

(9)

eq. (1) is trivially satisfied while eqs (2), (4), (5) and (8) give

$$\begin{aligned}&\left. {{\begin{array}{l} {\tilde{F}}^{\prime \prime \prime }-\dfrac{2n}{n+1}{\tilde{F}}^{\prime 2}+{\tilde{F}}{\tilde{F}}^{\prime \prime }\\ \quad +{Ka}\left( x \right) \left[ {\dfrac{n+1}{2}{\tilde{F}}^{\prime \prime {2}} {\tilde{F}}^{\prime \prime \prime }} \right] -\dfrac{2}{n+1} {Da}{\tilde{F}}^{\prime } \\ {+{Kb}\left( x \right) \left[ {{\begin{array}{l} \left( {\dfrac{n+1}{2}} \right) \left( {\dfrac{3n-1}{2}} \right) {\tilde{F}}^{\prime \prime {4}}\\ \quad -\dfrac{n+1}{2}{\tilde{F}} {\tilde{F}}^{\prime \prime {2}}{\tilde{F}}^{iv} \\ \quad -\left( {\dfrac{n+1}{2}} \right) ^{2}{\tilde{F}}{\tilde{F}}^{\prime \prime } {\tilde{F}}^{\prime \prime \prime {2}}\\ \quad +\left( {\dfrac{n+1}{2}} \right) \left( {\dfrac{5n-3}{2}} \right) {\tilde{F}}^{\prime }{\tilde{F}}^{\prime \prime {2}}{\tilde{F}}^{\prime \prime \prime } \\ \end{array} }} \right] \!\!=0,} \\ \end{array} }} \right\} \end{aligned}$$

(10)

$$\begin{aligned}&\frac{1}{\Pr }\left( {1+R} \right) \tilde{\Theta }^{\prime \prime }+{Nb}{\tilde{\Theta }}^{\prime } {\tilde{\phi }}^{\prime }+{Nt}{\tilde{\Theta }}^{\prime 2}\nonumber \\&\quad +{\tilde{F}}{\tilde{\Theta }}^{\prime }+Q{\tilde{\Theta }}=0, \end{aligned}$$

(11)

$$\begin{aligned}&{\tilde{\phi }}^{\prime \prime }+\left( {\frac{{Nt}}{{Nb}}} \right) {\tilde{\Theta }}^{\prime \prime }+\hbox {Sc}{\tilde{F}}{\tilde{\phi }}^{\prime }-Lc \hbox {Sc}{\tilde{\phi }}=0, \end{aligned}$$

(12)

$$\begin{aligned}&\left. {{\begin{array}{l} {{\tilde{F}}(\lambda )=\lambda \dfrac{1-n}{1+n}, \hbox { }{\tilde{F}}^{\prime }(\lambda )=1,\quad \hbox { }{\tilde{F}}^{\prime }(\infty )=0,} \\ {{\tilde{\Theta }}^{\prime }(\lambda )=-\gamma _1 [1-\tilde{\Theta }\left( \lambda \right) ],\quad \hbox { }{\tilde{\Theta }}(\infty )=0,} \\ {{\tilde{\phi }}^{\prime }\left( \lambda \right) =-\gamma _2 [1-{\tilde{\phi }}\left( \lambda \right) ],\quad \hbox { }\tilde{\phi }\left( \infty \right) =0.} \end{array} }} \right\} \end{aligned}$$

(13)

Letting

$$\begin{aligned}&{\tilde{F}}={\tilde{f}}(\xi -\lambda )={\tilde{f}}(\eta ),\quad \tilde{\Theta }={\tilde{\theta }}(\xi - \lambda )=\tilde{\theta }({\eta }), \nonumber \\&{\tilde{\phi }}={\tilde{\varphi }}(\xi -\lambda )={\tilde{\varphi }}({\eta } ). \end{aligned}$$

(14)

we have

$$\begin{aligned}&\left. {{\begin{array}{l} {\tilde{f}}^{\prime \prime \prime }-\dfrac{2n}{n+1}{\tilde{f}}^{\prime 2}+{\tilde{f}}{\tilde{f}}^{\prime \prime }+{Ka}\left( x \right) \left[ {\dfrac{n+1}{2}{\tilde{f}}^{\prime \prime {2}}{\tilde{f}}^{\prime \prime \prime }} \right] \\ \quad -\dfrac{2}{n+1}{Da}{\tilde{f}}^{\prime } \\ +{Kb}\left( x \right) \left[ {{\begin{array}{l} \left( {\dfrac{n+1}{2}} \right) \left( {\dfrac{3n-1}{2}} \right) {\tilde{f}}^{\prime \prime {4}}\\ \quad -\dfrac{n+1}{2}{\tilde{f}}{\tilde{f}}^{\prime \prime {2}}{\tilde{f}}^{iv} \\ \quad -\left( {\dfrac{n+1}{2}} \right) ^{2}{\tilde{f}}{\tilde{f}}^{\prime \prime }{\tilde{f}}^{\prime \prime \prime {2}}\\ \quad +\left( {\dfrac{n+1}{2}} \right) \left( {\dfrac{5n-3}{2}} \right) {\tilde{f}}^{\prime }{\tilde{f}}^{\prime \prime {2}}{\tilde{f}}^{\prime \prime \prime } \\ \end{array} }} \right] =0, \\ \end{array} }} \right\} \end{aligned}$$

(15)

$$\begin{aligned}&\left. {\frac{1}{\Pr }\left( {1+R} \right) \tilde{\theta }^{\prime \prime }+{Nb}{\tilde{\theta }}^{\prime }\tilde{\varphi }^{\prime }+{Nt}{\tilde{\theta }}^{\prime 2}+{\tilde{f}}{\tilde{\theta }}^{\prime }+Q{\tilde{\theta }}=0,} \right\} \end{aligned}$$

(16)

$$\begin{aligned}&{\tilde{\phi }}^{\prime \prime }+\left( {\frac{{Nt}}{{Nb}}} \right) {\tilde{\theta }}^{\prime \prime }+\hbox {Sc}{\tilde{f}}{\tilde{\varphi }}^{\prime }-Lc \hbox {Sc}{\tilde{\varphi }}=0, \end{aligned}$$

(17)

$$\begin{aligned}&\left. {{\begin{array}{l} {{\tilde{f}}(0)=\lambda \left( {\dfrac{1-n}{1+n}} \right) ,\;\hbox { }{\tilde{f}}^{\prime }(0)=1,\;\hbox { }{\tilde{f}}^{\prime }(\infty )=0,\hbox { }} \\ {{\tilde{\theta }}^{\prime }(0)=-\gamma _1 [1-{\tilde{\theta }}\left( 0 \right) ],\;\hbox { }{\tilde{\theta }}(\infty )=0,} \\ {{\tilde{\varphi }}^{\prime }\left( 0 \right) =-\gamma _2 [1-\tilde{\varphi }\left( 0 \right) ],\;\hbox { }{\tilde{\varphi }}\left( \infty \right) =0.} \\ \end{array} }} \right\} \end{aligned}$$

(18)

Here Ka and Kb are the non-Newtonian parameters, $\gamma _1$ is the thermal Biot number, $\gamma _2$ is the concentration Biot number, $\Pr$ is the Prandtl number, Da is the porosity parameter, Sc is the Schmidt number, R is the radiation parameter, Nb is the Brownian motion parameter, Q is the heat generation / absorption parameter, Nt is the thermophoresis parameter, Lc is the reaction-rate parameter and $\lambda$ is the variable thickness index. These values are

$$\begin{aligned} \left. {{\begin{array}{l} {Ka}=\dfrac{6a^{3}R_a \left( {x+b} \right) ^{3n-1}}{\rho \nu ^{2}},\;\\ {Kb}=\dfrac{-4a^{4}R_b \left( {x+b} \right) ^{4n-2}}{\rho \nu ^{2}},\;\\ \gamma _1 =\dfrac{h}{k\sqrt{\left( {{(n+1)}/{2}} \right) {(a/\nu )}\left( {x+b} \right) ^{n-1}}}, \\ \gamma _2 =\dfrac{k_m }{D_m \sqrt{\left( {{(n+1)}/{2}} \right) ({a}/{\nu })\left( {x+b} \right) ^{n-1}}},\\ \Pr =\dfrac{\left( {\mu {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _p } \right) _f }{k_f },\\ { Da}=\dfrac{\upsilon }{aK\left( {x+b} \right) ^{n-1}},\;\hbox { Sc}=\dfrac{\nu }{D_{\mathrm{B}} }, \\ R=\dfrac{4\sigma ^{{*}} {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ^3 }{k_f k^{{*}}}, { Nb}=\dfrac{\tau D_{\mathrm{B}} ({{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _f -{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _\infty )}{\nu },\;\\ Q=\dfrac{Q_h }{a\left( {x+b} \right) ^{n-1}\left( {\rho C_p } \right) _f },\; { Nt}=\dfrac{\tau D_{\mathrm{T}} ({{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _f -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty )}{\nu {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty }, \\ {Lc =\dfrac{K_{\mathrm{C}} }{a\left( {x+b} \right) ^{n-1}},\;\hbox { } \lambda =\delta \sqrt{\dfrac{a\left( {x+b} \right) ^{(1-n)/2}}{2\nu }}.} \\ \end{array} }} \right\} \end{aligned}$$

(19)

3 Physical quantities of curiosity

3.1 Skin friction coefficient

Mathematically, the coefficient of skin friction is defined as

$$\begin{aligned} C_{f_x } =\frac{\tau _{\mathrm{w}} }{\frac{1}{2}\rho {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} _{\mathrm{w}}^2 }, \end{aligned}$$

(20)

where wall shear stress $(\tau _{\mathrm{w}} )$ is expressed as

$$\begin{aligned}&\tau _{\mathrm{w}} =\left[ {\left( {\mu -2R_a \left( {\frac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) ^{2}} \right) \frac{\partial {{\mathop {u}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right] _{y=\lambda \left( {x+b} \right) ^{(1-n)/2}} . \end{aligned}$$

(21)

$$\begin{aligned} \hbox {Re}_x^{1/2} C_f&=\sqrt{\frac{n+1}{2}}\nonumber \\&\quad \times \left[ {{\tilde{f}}^{\prime \prime }(0)+\left( {\frac{n+1}{2}} \right) \frac{Ka}{3}( {{\tilde{f}}^{\prime \prime }(0)})^{3}} \right] . \end{aligned}$$

(22)

3.2 Local Nusselt number

Mathematically,

$$\begin{aligned} \hbox {Nu}=\frac{\left( {x+b} \right) q_{\mathrm{w}} }{k_f ( {{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _f -{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty })}, \end{aligned}$$

(23)

where the wall heat flux $(q_{\mathrm{w}} )$ is expressed as

$$\begin{aligned}&q_{\mathrm{w}} =-k_f \left( {1+\frac{16\sigma ^{{*}}{{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} _\infty ^3 }{3k_f k^{{*}}}} \right) \left( {\frac{\partial {{\mathop {T}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) _{y=\lambda \left( {x+b} \right) ^{(1-n)/2}} , \end{aligned}$$

(24)

$$\begin{aligned}&\hbox {Re}_x^{-1/2} \hbox {Nu}=-\sqrt{\frac{n+1}{2}}(1+R)\tilde{\theta }^{\prime }(0). \end{aligned}$$

(25)

3.3 Sherwood number

Mathematically, the ratio of convective mass transfer to diffusive mass transport rate is portrayed as

$$\begin{aligned} \hbox {Sh}=\frac{\left( {x+b} \right) q_{\mathrm{m}} }{D_\mathrm{B} ( {{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _f -{{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} _\infty } )}, \end{aligned}$$

(26)

where the mass flux $(q_{\mathrm{m}} )$ is expressed as

$$\begin{aligned}&j_w =-D_{\mathrm{B}} \left( {\frac{\partial {{\mathop {C}\limits ^{\scriptscriptstyle \smile }}} }{\partial y}} \right) _{y=\lambda \left( {x+b} \right) ^{(1-n)/2}} , \end{aligned}$$

(27)

$$\begin{aligned}&\hbox {Re}_x^{-1/2} \hbox {Sh}=-\sqrt{\frac{n+1}{2}}{\tilde{\varphi }}^{\prime }(0). \end{aligned}$$

(28)

In the above expressions $\hbox {Re}_x =U_0 (x+b)^{n+1}/\nu _f$ is the local Reynolds number.

4 Solution methodology

4.1 Optimal homotopic solutions

With the aim of computing the solutions, the optimal values are determined using OHAM. We select suitable operators and initial guesses as follows:

$$\begin{aligned} {{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{f}}} ={\tilde{f}}^{\prime \prime \prime }-{\tilde{f}}^{\prime },\quad {{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\theta }}} =\tilde{\theta }^{\prime \prime }-{\tilde{\theta }},\quad {{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\varphi }}} ={\tilde{\varphi }}^{\prime \prime }-{\tilde{\varphi }} \end{aligned}$$

(29)

with

$$\begin{aligned} {\tilde{f}}_0 ({\eta } )= & {} \lambda \left( {\frac{1-n}{1+n}} \right) +(1-\exp (-{\eta } )), \nonumber \\ {\tilde{\theta }}_0 ({\eta } )= & {} \frac{\gamma _1 }{1+\gamma _1 }\exp (-{\eta } ),\quad {\tilde{\varphi }}=\frac{\gamma _2 }{1+\gamma _2 }\exp (-{\eta } ), \end{aligned}$$

(30)

and

$$\begin{aligned}&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{f}}} \left[ d_1 +d_2 \exp ({\eta } )+d_3 \exp (-{\eta } ) \right] = 0, \nonumber \\&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\theta }}} \left[ d_4 \exp ({\eta } )+d_5 \exp (-{\eta } ) \right] = 0, \nonumber \\&{{{\mathbf {\mathtt{{L}}}}}}_{{\tilde{\varphi }}} \left[ d_6 \exp ({\eta } )+d_7 \exp (-{\eta } ) \right] = 0, \end{aligned}$$

(31)

where $d_i$ ($i=1\hbox {--}7)$ are arbitrary constants.

4.2 Convergence analysis

In homotopic solutions, convergence is obtained by setting the non-zero auxiliary variables $\hbar _{{{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} }$, $\hbar _{{\tilde{\theta }}}$ and $\hbar _{{\tilde{\varphi }}}$. The best optimal values of the convergence control parameters are $\hbar _{{{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} } =-1.2617,\quad \hbar _{{\tilde{\theta }}} =-1.22107$ and $\hbar _{{\tilde{\varphi }}} =-1.04927.$ Following

$$\begin{aligned}&e_m^t =e_m^{{{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} } +e_m^{{\tilde{\theta }}} +e_m^{{\tilde{\varphi }}} , \end{aligned}$$

(32)

$$\begin{aligned}&e_m^{{{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} } =\frac{1}{k+1}\mathop \sum \limits _{l=0}^k \left[ {{{\mathbf {\mathtt{{N}}}}}}_{{{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} } \left( \mathop \sum \limits _{i=0}^m {{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} \left( {\eta } \right) , \mathop \sum \limits _{i=0}^m {\tilde{\theta }}\left( \eta \right) \right) _{\eta =l\delta \eta } \right] ^{2}, \end{aligned}$$

(33)

$$\begin{aligned}&e_m^{{\tilde{\theta }}} =\frac{1}{k+1}\nonumber \\&\quad \times \mathop \sum \limits _{l=0}^k \left[ {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\theta }}} \left( \mathop \sum \limits _{i=0}^m {{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} \left( {\eta } \right) , \mathop \sum \limits _{i=0}^m {\tilde{\theta }}\left( {\eta } \right) , \mathop \sum \limits _{i=0}^m {\tilde{\varphi }}\left( {\eta } \right) \right) _{\eta =l\delta \eta } \right] ^{2}, \end{aligned}$$

(34)

$$\begin{aligned}&e_m^{{\tilde{\varphi }}} =\frac{1}{k+1}\nonumber \\&\quad \times \mathop \sum \limits _{l=0}^k \left[ {{{\mathbf {\mathtt{{N}}}}}}_{{\tilde{\varphi }}} \left( \mathop \sum \limits _{i=0}^m {{\mathop {f}\limits ^{\scriptscriptstyle \smile }}} \left( \eta \right) , \mathop \sum \limits _{i=0}^m {\tilde{\theta }}\left( \eta \right) ,\mathop \sum \limits _{i=0}^m {\tilde{\varphi }}\left( \eta \right) \right) _{\eta =l\delta \eta } \right] ^{2}, \end{aligned}$$

(35)

where $e_m^t$ represents the total squared residual error, $\delta \eta =0.5$ and $k=20.$ Total average squared residual error is $e_m^t =0.0284356$ (see figure 2 and table 1).

Fig. 2

Total residual error for thixotropic nanofluid.

Table 1 Magnitudes of error with optimal parameter $m=2$.

Fig. 3

${\tilde{f}}^{\prime }({{\eta }} )$ against Ka.

Fig. 4

${\tilde{f}}^{\prime }({{\eta }} )$ against Kb.

Fig. 5

${\tilde{f}}^{\prime }({{\eta }} )$ against Da.

Fig. 6

${\tilde{f}}^{\prime }({{\eta }} )$ against n.

Fig. 7

$\tilde{\theta }({{\eta }} )$ against Nb.

Fig. 8

$\tilde{\theta }({{\eta }} )$ against Nt.

Fig. 9

$\tilde{\theta }({{\eta }} )$ against $\gamma _1$.

Fig. 10

$\tilde{\theta }({{\eta }} )$ against $\Pr$.

Fig. 11

$\tilde{\theta }({{\eta }} )$ when ${Q>0}$.

Fig. 12

$\tilde{\theta }({{\eta }} )$ when ${Q<0}$.

Fig. 13

$\tilde{\phi }({{\eta }} )$ against Nt.

Fig. 14

$\tilde{\phi }({{\eta }} )$ against Nb.

Fig. 15

$\tilde{\phi }({{\eta }} )$ against $\gamma _2$.

Fig. 16

$\tilde{\phi }({{\eta }} )$ against Lc.

Fig. 17

$\tilde{\phi }({{\eta }} )$ against $\hbox {Sc}$.

Fig. 18

$\left( {\hbox {Re}_x } \right) ^{1/2}C_f$ against Ka.

Fig. 19

$\left( {\hbox {Re}_x } \right) ^{1/2}C_f$ against Kb.

Fig. 20

$\left( {\hbox {Re}_x } \right) ^{-1/2}\hbox {Nu}$ against Nb.

5 Discussion

5.1 Velocity

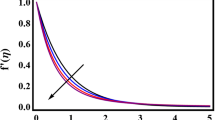
Figures 3 and 4 are plotted to analyse the behaviour of ${{Ka}=0.0, 0.2, 0.4, 0.6}$ and ${{Kb}=0.0, 1.4, 0.7, 1.0}$ for velocity ${\tilde{f}}^{\prime }({{\eta }} ).$ Here thixotropic parameters Ka and Kb significantly favour the velocity ${\tilde{f}}^{\prime }({{\eta }} ).$ Physically, ${{Ka,} {Kb}<1}$ leads to a shear thinning case in which the viscosity varies with time. A reduction in fluid viscosity is noted for larger Ka and Kb. Hence fluid velocity increases. From figure 5, it can be seen that the velocity field diminishes for larger local porosity parameters $\left( {{Da}=0.2, 0.7, 1.3, 2.2} \right)$. Due to the presence of porous space, resistance is produced in the liquid flow which is the reason for the reduced fluid velocity. Multiple values of n for the velocity profile ${\tilde{f}}^{\prime }({{\eta }} )$ are depicted in figure 6. Velocity is enhanced for $n>1$ near the surface.

Fig. 21

$\left( {\hbox {Re}_x } \right) ^{-1/2}\hbox {Nu}$ against Nt.

5.2 Temperature profile

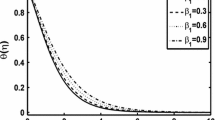
The influence of the Brownian motion parameter Nb $\left( {{Nb}=0.1, 0.4, 0.8, 1.1} \right)$ on $\tilde{\theta }({{\eta }} )$ is plotted in figure 7. Temperature and thermal layer thickness show an increasing trend for Brownian motion (Nb). Physically, collision of particles occurs for increasing values of the Brownian motion parameter which enhances the irregular motion of nanoparticles. As a consequence, kinetic energy is transformed into heat energy, resulting in temperature enhancement. Figure 8 depicts an enhancement in temperature for the thermophoresis motion Nt $\left( {{Nt}=0.1, 0.3, 0.5, 0.7} \right) .$ It is due to the thermophoresis phenomenon that the temperature of the fluid increases, in which heated particles are pulled away from a hot region to a cold surface. The effect of the thermal Biot number $\gamma _1$ $\left( {\gamma _1 =0.2, 0.4, 0.6, 0.8} \right)$ for temperature $\theta ({{\eta }} )$ is plotted in figure 9. An increase in ${\gamma _1}$ causes a stronger convection which shows a higher temperature profile $\theta ({{\eta }} )$. The impact of Prandtl number Pr $\left( {\Pr =1.0, 1.5, 2.0, 2.5} \right)$ on temperature $\tilde{\theta }({{\eta }} )$ is plotted in figure 10. It is noted that temperature $\tilde{\theta }({{\eta }} )$ shows a decreasing trend for Prandtl number $\left( {\Pr } \right) .$ Physically, bigger values of Pr yield weaker thermal diffusivity which corresponds to a decay in temperature. The impact of the heat generation / absorption parameter ($Q>0\hbox { or }Q<0)$ on temperature is plotted in figures 11 and 12. A rise in temperature is observed for higher $Q \quad \left( {Q>0} \right)$. Physically, the internal energy of liquid particles rises for higher values of Q. Therefore, the temperature increases. A reverse trend is noticed for ${Q<0}$.

Fig. 22

$\left( {\hbox {Re}_x } \right) ^{1/2}\hbox {Sh}$ against $\gamma _2$.

5.3 Concentration field

Figure 13 depicts the effect of thermophoresis motion parameter Nt $\left( {{Nt}=0.1, 0.3, 0.5, 0.7} \right)$ on concentration $\tilde{\varphi }({{\eta }} )$. It is noted that the concentration enhances for larger values of Nt. There is no doubt that thermal conductivity increases in the presence of nanoparticles. Higher values of Nt enhance fluid thermal conductivity. Larger thermal conductivity leads to high concentration. Figure 14 elucidates the variation of Nb $\left( {{Nb}=0.1, 0.4, 0.8, 1.1} \right)$ for $\tilde{\varphi }({{\eta }} ).$ Physically, for larger Nb, collision among the fluid particles rises and the corresponding concentration decreases. Figure 15 shows the results of the plot to study the variation of concentration $\tilde{\varphi }({{\eta }} )$ for larger $\gamma _2$ $(\gamma _2 =0.1, 0.3, 0.5, 0.7)$. With an increment in solutal Biot number $\left( {\gamma _2 } \right)$, the resulting coefficient of mass transfer increases. It gives an enhancement in concentration $\tilde{\varphi }({{\eta }} )$. Higher values of $L{c}~\left( {{Lc}=0.1, 0.3, 0.5, 0.7} \right)$ on concentration $\tilde{\varphi }({{\eta }} )$ are depicted in figure 16. A larger chemical reaction parameter $\left( {{Lc}} \right)$ shows a decay in concentration $\tilde{\varphi }({{\eta }} )$ because the chemical reaction parameter depends on the reaction rate which produces a decay in concentration $\tilde{\varphi }({{\eta }} )$. The impact of Schmidt number $\left( \hbox {Sc}=0.5, 1.0, 1.5, 2.0 \right)$ on concentration $\tilde{\varphi }({{\eta }} )$ is shown in figure 17. Physically, Schmidt number (Sc) has an inverse relation with Brownian diffusivity. So a larger Schmidt number $\left( {\hbox {Sc}} \right)$ yields a weaker Brownian diffusivity leading to lower concentration $\tilde{\varphi }({{\eta }} )$.

Fig. 23

$\left( {\hbox {Re}_x } \right) ^{1/2}\hbox {Sh}$ against Nb.

5.4 Skin friction coefficient and local Nusselt and Sherwood numbers

Figures 18 and 19 depict the impacts of Ka and Kb on surface drag force. The magnitude of the skin friction coefficient shows increasing behaviour for larger values of Ka while decreasing behaviour for Kb. For Nb and Nt, the heat transfer reduces (see figures 20 and 21). Figures 22 and 23 show that the magnitude of Sherwood number increases for larger $\gamma _2$ and Nb.

6 Conclusions

In this paper, the use of a thixotropic nanomaterial towards a nonlinear stretching surface of variable thickness is addressed. In our view, no attempt at analysing the chemically reactive flow of a thixotropic nanofluid through nonlinear thermal radiation under convective conditions has been made. The velocity of fluid particles enhances the variable thickness index and the non-Newtonian parameters Ka and Kb, while it decays the porosity parameter Da. The temperature and concentration are enhanced through the thermophoresis variable and heat generation parameter. The skin friction coefficient strongly depends on the non-Newtonian parameter Ka. The Nusselt number decreases through the Brownian motion parameter and the thermophoresis parameter, respectively. The magnitude of the Sherwood number is enhanced by the Brownian motion parameter and the concentration Biot number.