1 Introduction

In recent times, because of countless applications in engineering and industrial progressions, the mechanism of heat transfer phenomenon has exposed various concerns for the entire world. Certainly, this phenomenon happened due to temperature difference between two dissimilar bodies. Heat transfer appliance plays essential roles in cooling nuclear vessel, biomedical solicitations, conduction of heat in the muscles and prescription targeting. Fourier [1] was the first one to propose a relation for heat transfer appliance. Fourier law has been extremely efficacious in a widespread assortment of trade applications. However, one unphysical property is that it disputes an infinite velocity of propagation, i.e., the entire structure is instantaneously exaggerated by the initial disturbance. To overcome this obstacle, Cattaneo [2] improved the Fourier law by inserting relaxation time to heat flux. This additional term in the energy equation turns the parabolic diffusion equation into a hyperbolic one. Later on, Christov [3] established Maxwell–Cattaneo relation by considering the frame in different formulation. After this, numerous researchers worked on heat transfer with diverse norms (see refs [4,5,6,7,8,9,10,11]). Hayat et al [12] investigated the second-grade fluid flow by utilising the improved heat conduction theory. The flow is thermally stratified in the existence of variable properties. This exploration exposes that the temperature distribution is an augmenting function of thermal stratified parameter. Hashim and Khan [13] explored the features of Carreau liquid flow by using advanced heat conduction relation. The results showed that the heat transfer rate was pointedly enhanced by advanced wall thickness parameter while for thermal relaxation parameter, conflicting behaviour was initiated. Aspects of advanced heat flux relation and chemical processes on third-grade fluid flow was studied by Imtiaz et al [14]. They concluded from their observations that the liquid velocity augments by increasing third-grade liquid parameters and Reynolds number.

An analysis of non-Newtonian (refs [15,16,17,18,19,20]) flow behaviour owing to the chemical processes has attracted the attention of numerous investigators. Chemical processes can be catogorised as homogeneous and heterogeneous chemical processes. This discrepancy is interrelated to the circumstance that whether they arise in liquid substance or transpire in some catalytic exteriors. A homogeneous process occurs consistently in the entire phase, whereas the heterogeneous process proceeds in a circumscribed region or inside the phase boundary. The prominence of chemical processes is more apparent in diverse trade solicitations, for example, dispensation of foods, hydrometallurgical production, plantations of fruit plants, destruction of yields via freezing. Additionally, the homogeneous and heterogeneous processes allied with the improvement and consumption of the reactant sort at numerous rates both inside the fluid and on the catalytic exteriors are extremely sophisticated. For the exploration of homogeneous–heterogeneous processes on the flow of viscous liquids, Merkin [21] proposed an isothermal relation. This scrutiny exposes that because of the surface reaction this utilisation is dominant. Further, by considering both sorts of identical diffusivities, Chaudhary and Merkin [22] studied the properties of homogeneous–heterogeneous reaction in viscous fluid flow. Khan et al [23] scrutinised the 3D Burgers liquid in the existence of homogenous–heterogeneous procedure. They noticed that by enriching the values of homogeneous process parameter the concentration profile reduces whereas it augments for Schmidt number. Rana et al [24] explored the features of the heterogeneous–homogeneous process on mixed convection Casson fluid. They established that with a rise in the slip parameter the concentration of chemical species on the surface declines. Numerous studies pertinent to the chemical reaction in different liquid models can be seen in refs [25,26,27,28,29,30]. Recently, impact of Cattaneo–Christov heat flux relation with heterogeneous–homogeneous chemical reaction on 3D Sisko fluid was reported by Khan et al [31]. Their analysis reveals that there is a decay in the liquid temperature and thickness of thermal boundary layer for enlargement in the thermal relaxation parameter.

In all the above quoted literatures, the foremost attention of the current exertion is to scrutinise the features of homogeneous–heterogeneous reaction for steady 3D flow of Carreau fluid over a bidirectional stretching surface. Additionally, heat transfer phenomenon is established by utilising the advanced heat flux relation. By means of proper conversion, a set of combined non-linear PDEs are transformed into coupled non-linear ODEs and then resolved numerically by utilising the bvp4c function in Matlab. The impact of scheming parameters on temperature and concentration fields are exposed graphically and conferred in details. Furthermore, a tabular comparison between bvp4c (refs [32,33,34,35]) and HAM (refs [36,37,38]) with existing studies are also presented in limiting cases.

2 Problem formulation

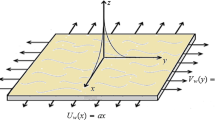
Consider the steady, 3D incompressible forced convective flow of a Carreau fluid over a bidirectional stretched surface. The sheet is stretched with linear velocity \(u=ax\) and \(v=by,\) respectively, in which \(a, b>0\) are taken as constants and the flow occupies the domain \(z>0\) (see figure 1). The heat transfer phenomenon is established in the presence of an improved heat conduction relation. Additionally, the influence of heterogeneous–homogeneous reactions is presented. Homogeneous response for cubic autocatalysis is of the form

$$\begin{aligned} G+2H\rightarrow 3H,\hbox { rate}=k_c gh^{2}, \end{aligned}$$
(1)

whereas on the catalyst surface, the isothermal response of the first-order is of the form

$$\begin{aligned} G\rightarrow H,\hbox { rate}=k_s g, \end{aligned}$$
(2)

where the chemical species \(\left( {G, H} \right) \) have the concentration \(\left( {g, h} \right) \) and rate constants \(\left( {k_c , k_s } \right) \), respectively. Moreover, it is supposed that both processes are isothermal and far away from the sheet at the ambient fluid, there is a uniform concentration \(g_0 \) of reactant G and there is no autocatalyst H.

Fig. 1
figure 1

Flow configuration.

Full size image
Fig. 2
figure 2

Temperature distribution \(\theta (\eta )\) for different values of thermal relaxation parameter \(\beta \) when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 3
figure 3

Temperature distribution \(\theta (\eta )\) for different values of Prandtl number Pr when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 4
figure 4

Concentration distribution \(l(\eta )\) for different values of local Weissenberg number \(\mathrm{We}_1\) when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 5
figure 5

Concentration distribution \(l(\eta )\) for different values of local Weissenberg number \(\mathrm{We}_2\) when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 6
figure 6

Concentration distribution \(l(\eta )\) for different values of ratio of stretching rate parameter \(\alpha \) when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 7
figure 7

Concentration distribution \(l(\eta )\) for different values of Schmidt number Sc when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 8
figure 8

Concentration distribution \(l(\eta )\) for different values of homogeneous reaction parameter \(k_1\) when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 9
figure 9

Concentration distribution \(l(\eta )\) for different values of heterogeneous reaction parameter \(k_2\) when (a) \(n=0.5\) and (b) \(n=1.5\).

Full size image
Fig. 10
figure 10

A comparison of Prandtl number (a) and thermal relaxation time parameter \(\beta \) (b) on temperature distribution \(\theta {(\eta )}\) for two different techniques.

Full size image
Table 1 A comparison of local skin friction coefficient with two different techniques in limiting cases when \(\mathrm{We}_1 =\mathrm{We}_2 =0\) and \(n=3\).
Full size table
Table 2 A comparison of local skin friction coefficient with two different techniques in limiting cases when \(\mathrm{We}_1 =\mathrm{We}_2 =0\) and \(n=3\).
Full size table
Table 3 A comparison of local Nusselt number with two different techniques in limiting cases when \(\mathrm{We}_1 =\mathrm{We}_2 =\beta =0\) and \(n=3\).
Full size table
Table 4 A comparison of local Nusselt number with two different techniques for different values of Prandtl number when \(\mathrm{We}_1 =\mathrm{We}_2 =\beta =0\) and \(n=3\).
Full size table

Under these considerations, the governing flow problem with boundary conditions [39, 40] can be written as

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$
(3)
$$\begin{aligned}&u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z}=\nu \frac{\partial ^{2}u}{\partial z^{2}}\left[ {1 + \Gamma ^{2}\left( {\frac{\partial u}{\partial z}} \right) ^{2}} \right] ^{\left( \frac{n-1}{2}\right) }\nonumber \\&\quad +\nu (n-1)\Gamma ^{2}\frac{\partial ^{2}u}{\partial z^{2}}\left( {\frac{\partial u}{\partial z}} \right) ^{2}\left[ {1+\Gamma ^{2}\left( {\frac{\partial u}{\partial z}} \right) ^{2}} \right] ^{\left( \frac{n-3}{2}\right) },\nonumber \\\end{aligned}$$
(4)
$$\begin{aligned}&u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=\nu \frac{\partial ^{2}v}{\partial z^{2}}\left[ {1+\Gamma ^{2}\left( {\frac{\partial v}{\partial z}} \right) ^{2}} \right] ^{\left( \frac{n-1}{2}\right) } \nonumber \\&\quad +\nu (n-1)\Gamma ^{2}\frac{\partial ^{2}v}{\partial z^{2}}\left( {\frac{\partial v}{\partial z}} \right) ^{2}\left[ {1+\Gamma ^{2}\left( {\frac{\partial v}{\partial z}} \right) ^{2}} \right] ^{\left( \frac{n-3}{2}\right) },\nonumber \\ \end{aligned}$$
(5)
$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}=\alpha _1 \frac{\partial ^{2}T}{\partial z^{2}} -\lambda \left[ {{\begin{array}{l} {u^{2}\dfrac{\partial ^{2}T}{\partial x^{2}}+v^{2}\dfrac{\partial ^{2}T}{\partial y^{2}}+w^{2}\dfrac{\partial ^{2}T}{\partial z^{2}}+2uv\dfrac{\partial ^{2}T}{\partial x\partial y}} \\ {+2vw\dfrac{\partial ^{2}T}{\partial y\partial z}+2uw\dfrac{\partial ^{2}T}{\partial x\partial z}+\left( {u\dfrac{\partial u}{\partial x}+v\dfrac{\partial u}{\partial y}+w\dfrac{\partial u}{\partial z}} \right) \frac{\partial T}{\partial x}} \\ {+\left( {u\dfrac{\partial v}{\partial x}+v\dfrac{\partial v}{\partial y}+w\dfrac{\partial v}{\partial z}} \right) \dfrac{\partial T}{\partial y}+\left( {u\dfrac{\partial w}{\partial x}+v\dfrac{\partial w}{\partial y}+w\dfrac{\partial w}{\partial z}} \right) \dfrac{\partial T}{\partial z}} \\ \end{array} }} \right] ,\qquad \nonumber \\ \end{aligned}$$
(6)
$$\begin{aligned}&u\frac{\partial g}{\partial x}+v\frac{\partial g}{\partial y}+w\frac{\partial g}{\partial z}=D_G \frac{\partial ^{2}g}{\partial z^{2}}-k_c gh^{2}, \end{aligned}$$
(7)
$$\begin{aligned}&u\frac{\partial h}{\partial x}+v\frac{\partial h}{\partial y}+w\frac{\partial h}{\partial z}=D_H \frac{\partial ^{2}h}{\partial z^{2}}+k_c gh^{2}, \end{aligned}$$
(8)
$$\begin{aligned}&u= U_w (x)=ax, \hbox { }v=V_w (y)=by, \hbox { }w=0,\nonumber \\&T = T_w , \hbox { }\;\hbox { }D_G \frac{\partial g}{\partial z}=k_s g, \hbox { }D_H \frac{\partial h}{\partial z}=-k_s g\hbox { at }z=0,\end{aligned}$$
(9)
$$\begin{aligned}&u{\rightarrow } 0, \hbox { }v{\rightarrow } 0, \hbox { }T{\rightarrow } T_\infty , \hbox { }g{\rightarrow } g_0 , \hbox { }h{\rightarrow } 0\hbox { as }z{\rightarrow } \infty ,\nonumber \\ \end{aligned}$$
(10)

where (u, v, w) represent the velocity components along x-,y- and z-directions, respectively, \(\nu \) is the kinematic viscosity, \(\Gamma \) is the material rate constant, n is the power law index, T is the liquid temperature, \(\alpha _1 \) is the thermal diffusivity of the liquid, \(\lambda \) is the thermal relaxation time and \((D_G , D_H )\) are the diffusion species coefficients of G and H,  respectively.

The transformations are as follows:

$$\begin{aligned}&u= ax{f}'(\eta ),\nonumber \\&v=ay{g}'(\eta ),\nonumber \\&w=-\sqrt{a\nu }[f(\eta )+g(\eta )],\nonumber \\&\theta \left( \eta \right) = \frac{T-T_\infty }{T_w -T_\infty }, \nonumber \\&g=g_0 l(\eta ),\quad h=h_0 m(\eta ), \quad \eta =z\sqrt{\frac{a}{\nu }}. \end{aligned}$$
(11)

In view of overhead transformations, the incompressibility condition is satisfied identically and eqs (4)–(10) yield

$$\begin{aligned}&{f}'''[1+\mathrm{We}_1^2 f^{\prime \prime 2}]^{({n-3})/{2}}[1+n\mathrm{We}_1^2 f^{\prime \prime 2}]\nonumber \\&\quad -f^{\prime 2}+{f}''(f+g)=0, \end{aligned}$$
(12)
$$\begin{aligned}&{g}'''[1+\mathrm{We}_2^2 g^{\prime \prime 2}]^{({n-3})/{2}}[1+n\mathrm{We}_2^2 g^{\prime \prime 2}]\nonumber \\&\quad -g^{\prime 2}+{g}''(f+g)=0, \end{aligned}$$
(13)
$$\begin{aligned}&{\theta }''+\mathop {\Pr }{(f+g)}{\theta }'-\mathop {\Pr }{\beta } [(f+g)(f^{{\prime }}+{g}'){\theta }'\nonumber \\&\quad +(f+g)^{2}{\theta }'']=0, \end{aligned}$$
(14)
$$\begin{aligned}&\frac{1}{\mathrm{Sc}}{l}''+(f+g){l}'-k_1 lm^{2}=0, \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\lambda _1 }{\mathrm{Sc}}{m}''+(f+g){m}'+k_1 lm^{2}=0,\end{aligned}$$
(16)
$$\begin{aligned}&f(0)=0, \hbox { }g(0)=0, \hbox { }{f}'(0)=1, \hbox { }{g}'(0)=\alpha ,\nonumber \\&\theta (0)=1, \hbox { }{l}'(0)=k_2 l(0), \hbox { }\lambda _1 {m}'(0)=-k_2 l(0), \end{aligned}$$
(17)
$$\begin{aligned}&{f}'\rightarrow 0, \hbox { }{g}'\rightarrow 0, \hbox { }\theta \rightarrow 0, \hbox { }l\rightarrow 1, \hbox { }m\rightarrow 0\hbox { as }\eta \nonumber \\&\quad \rightarrow \infty . \end{aligned}$$
(18)

In the above expressions, \(\mathrm{We}_1 \left( {=\sqrt{\frac{\Gamma ^{2}aU_w^2 }{\nu }}} \right) \) and \(\mathrm{We}_2 \left( {=\sqrt{\frac{\Gamma ^{2}aV_w^2 }{\nu }}} \right) \) are the local Weissenberg numbers, \(\Pr \left( {=\frac{\nu }{\alpha _1 }} \right) \) is the Prandtl number, \(\beta \left( {=\lambda a} \right) \) is the thermal relaxation time parameter, \(\lambda _1 \left( {=\frac{D_H }{D_G }} \right) \) is the ratio of diffusion coefficient, \(\mathrm{Sc}\left( {=\frac{\nu }{D_G }} \right) \) is the Schmidt number, \(\alpha \left( {=\frac{b}{a}} \right) \) is the ratio of stretching rates parameter and \((k_2 , k_1 )\) are the measures of the strength of heterogeneous–homogeneous processes.

In physical circumstances, the diffusion coefficients \(D_G \) and \(D_H \) are taken to be equivalent, i.e. \(\lambda _1 =1,\) which will provide us

$$\begin{aligned} l(\eta )+m(\eta )=1. \end{aligned}$$
(19)

Subsequently, eqs (15) and (16) yield

$$\begin{aligned} \frac{1}{\mathrm{Sc}}{l}''+(f+g){l}'-k_1 (1-l)^{2}l=0, \end{aligned}$$
(20)

with boundary conditions

$$\begin{aligned} {l}'(0)=k_2 l(0), \hbox { }l\rightarrow 1\hbox { as }\eta \rightarrow \infty . \end{aligned}$$
(21)

3 Physical quantities

3.1 The skin friction coefficients

Essential features of flow are the local skin friction coefficients \(C_{fx} \) and \(C_{fy} \) which are defined as

$$\begin{aligned} C_{fx} =\frac{\tau _{xz} }{\frac{1}{2}\rho U_w^2 }\quad \hbox { and }\quad C_{fy} =\frac{\tau _{yz} }{\frac{1}{2}\rho U_w^2 }, \end{aligned}$$
(22)

and in the dimensionless forms, we have

$$\begin{aligned}&\frac{1}{2}C_{fx} \mathrm{Re}_x^{{1}/{2}} = {f}''(0)[1+\mathrm{We}_1^2 f^{\prime \prime 2}(0)]^{({n-1})/{2}},\nonumber \\&\frac{1}{2}\left( {\frac{U_w }{V_w }} \right) C_{fy} \mathrm{Re}_x^{{1}/{2}} ={g}''(0)[1+\mathrm{We}_2^2 g^{\prime \prime 2}(0)]^{({n-1})/{2}},\nonumber \\ \end{aligned}$$
(23)

in which \(\mathrm{Re}_{x}=ax^{2}/\nu \) is the local Reynolds number.

4 Numerical results and discussion

This section predominantly emphasises the somatic features of heterogeneous–homogeneous responses on the non-Fourier’s heat conduction relation by utilising 3D Carreau fluid flow past a stretched surface. The set of eqs (12)–(14) and (20) with boundary restrictions (17),    (18) and (21) are established and resolved via bvp4c scheme. The main purpose of the following discussion is to showcase the influence of emergent parameters such as the local Weissenberg numbers \((\mathrm{We}_1 ,\mathrm{We}_2 )\), ratio of stretching rate parameter \(\alpha \), Prandtl number Pr, thermal relaxation time parameter \(\beta \), heterogeneous–homogeneous reaction parameters \((k_2 ,k_1 )\) and Schmidt number Sc on the temperature and concentration fields in both circumstances (i.e. shear thinning / thickening) liquids. Additionally, the numerical and analytical outcomes in comparison of some former existing literature are available for diverse values of ratio of stretching rate parameter \(\alpha \) and Prandtl number Pr.

4.1 Temperature field

Figures 2a, 2b, 3a and 3b are portrayed to visualise the impact of thermal relaxation parameter \(\beta \) and Prandtl number Pr on the temperature of the Carreau liquid for both shear thinning and shear thickening liquids, respectively. From these plots, we see that the liquid temperature and thickness of the thermal boundary layer decrease for increasing values of Prandtl number and thermal relaxation parameter for both cases. Physically, this happen because, for increased values of thermal relaxation parameter, the liquid needs extra time to transfer heat to its adjacent elements which raises the temperature gradient and hence decreases the temperature distribution. Moreover, for the case of Fourier’s law the temperature field is better when compared with Cattaneo–Christov heat flux relation. This coincides with that of ref. [41]. Moreover, it can be noticed that \(\theta (\eta )\) and related thickness of the layer decrease when Pr increases. An increase in Pr causes a decrease in thermal diffusion and temperature field.

4.2 Concentration field

Figures 4a, 4b, 5a and 5b are plotted to interpret the features of the local Weissenberg numbers \(\mathrm{We}_1 \) and \(\mathrm{We}_2\) on the concentration profile of the Carreau liquid. The result shows that with the enlargement of the local Weissenberg numbers, the concentration distribution increases whereas the thickness of the concentration boundary layer reduces for shear thinning liquid. Shear thickening liquid’s moderately conflicting behaviour is identified for the increased values of local Weissenberg numbers.

The impact of increasing values of the ratio of stretching rate parameter \(\alpha \) and the Schmidt number Sc on the concentration of the Carreau fluid for both instances \((n<1)\) and \((n>1)\) are shown in figures 6a, 6b, 7a and 7b respectively. From these plots, the analogous behaviours for the emergent values of the ratio of stretching rate parameter and the Schmidt number for shear thinning / thickening liquids are perceived. Increase in values of these parameters results in enhanced concentration field while thickness of concentration boundary layer reduces. For physical point of vision advance values of ratio of the stretching rates parameter, stretching beside the y-direction growths which reasons the escalation of the concentration of the Carreau liquid. Moreover, as the Schmidt number is the relation of the viscous diffusion rate to the molecular diffusion rate. However, higher values of Schmidt number cause greater viscous diffusion rate, which is fit to intensify the liquid concentration.

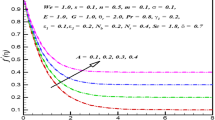
Figures 8a, 8b, 9a and 9b respectively explore the properties of homogeneous and heterogeneous response parameters for the shear thinning and shear thickening situations on the concentration scattering. The concentration field is moderate for both conditions \((n{<}1)\) and \((n{>}1)\) for increased values of homogeneous / heterogeneous parameters. However, for larger values of homogeneous–heterogeneous parameters there is a decline in the concentration and allied thickness of concentration boundary layer. Physically, from these plots, this behaviour occurs because of the fact that throughout the homogeneous reaction the reactants are disbursed. Instead, one can notice from figures 9a and 9b that the advanced values of the heterogeneous response parameter \(k_2 \) results in the decline of the concentration distribution. This coincides with the overall physical behaviour of homogeneous and heterogeneous reactions. Hence, the concentration field decays for \(k_2\).

4.3 Tabular and graphical comparisons

Figures 10a and 10b depict the impact of Pr and \(\beta \) for two dissimilar schemes namely, the homotopy analysis method (HAM) and bvp4c approach. From these plots, we can see that plots for both techniques agree quite brilliantly. The authenticity of the numerical consequences is also established by assessing the analytical outcomes achieved by the HAM as shown in tables 1–3. Moreover, these results are compared with former available literature as an exceptional instance of the problem and outstanding settlement is noticed. The discrepancy of the Nusselt number for different values of Prandtl number are presented in table 4. A comparison between HAM and numerical scheme (bvp4c) with some former studies is also presented in this table. Consequently, we assure that the present outcomes are very accurate.

5 Concluding remarks

The features of homogenous–heterogeneous reaction on 3D Carreau fluid flow induced by a stretched surface was examined in this paper. The improved heat conduction model is executed to reveal the heat transfer phenomenon of Carreau liquid. From the present examination, the following inferences are summarised:

  • Both the Prandtl number and thermal relaxation parameter diminished the temperature field and the boundary layer thickness in both instances for increased values of these parameters.

  • The impact of Weissenberg numbers for shear thinning \((n<1)\) liquid was quite reverse to the thinning \((n>1)\) liquid for larger values of these numbers.

  • Conflicting behaviours for \(n<1\) and \(n>1\) of homogeneous response parameter and Schmidt number were detected for the concentration distribution.