1 Introduction

BY assembling the stiff face sheets and the low-density core layer, a light-weight sandwich structure can be designed for the weight-sensitive engineering field, such as aerospace, ships and civil engineering. Structural weight can be reduced efficiently by selecting the well-matched face sheets and the core layer. Nevertheless, analysis of mechanical behaviors in such structures will confront a rigorous challenge, as the large transverse shear deformations have to be deliberated attributing to the sudden change of transverse shear modulus at the interlayer between the face sheet and the core layer. As a result, the classical plate theory (CPT) [1] discarding transverse shear deformation is no longer adaptable to analysis of the mechanical behaviors of sandwich structures. Therefore, numerous investigators have paid more attention to the models deliberating transverse shear deformation.

In the early stage of exploration on the shear deformation theory, Reissner [2] attempted to research the impact of transverse shear deformation on static response of plates. Mindlin [3] assumed transverse shear deformation to be linear distribution along the thickness of plate, so that the first-order shear deformation theory (FSDT) can be established by utilizing such assumption. The FSDT has been utilized to deliberate mechanical behaviors of isotropic, functionally graded material (FGM) and orthotropic plates attributing to its flexibility and efficiency. For the sandwich plates with low-density core, transverse shear deformation will suddenly change at the adjacent laminates attributing to large diversion of transverse shear moduli between the face sheets and the core. Evidently, the FSDT is not adaptable to simulation of such large transverse shear deformation, so that the correction factor has to be selected to elevate prediction of transverse shear deformation. Nonetheless, reasonable selection of the correction factors severely depends on material characteristics. For the sake of conquering limitation of the FSDT, the inspiration deriving from three-dimensional (3D) elasticity theory [4, 5] inspired investigators to establish the higher-order shear deformation theory (HSDT).

Whitney and Sun [6] attempted to establish a HSDT for analysis of layered plates. Reddy [7] developed a delicate higher-order theory with five independent unknowns, which can simulate the parabolic distributions of transverse shear deformation across thickness of plate. Furthermore, the free condition of transverse shear stresses on surfaces can be met in advance. Reddy’s model can yield the more precise results contracted to those acquired from the FSDT. Advantages of HSDT contrasting to FSDT motivate researchers to construct various HSDTs [8, 9]. Meiche et al. [10] established a hyperbolic-type HSDT with four unknowns to calculate natural frequencies and buckling loads of FGM sandwich plates subjected to four simply-supported edges. Matsunaga [11,12,13] established a series of HSDTs to explore an impact of higher-order shear deformation on dynamic and buckling behaviors of layered and sandwich plates. In the light of Reddy’s HSDT [7], Nayak et al. [14] constructed a plate element to produce natural frequencies of layered and sandwich plates. Taking advantage of Reddy’s HSDT, Jin et al. [15] deliberated influence of boundary conditions on dynamic response of sandwich structures. What’s more, Tomar and Talha [16] made use of Reddy’s HSDT to research the bending and vibration problems of the FGM sandwich plates by deliberating the influence of material uncertainties. Bennoun et al. [17] established a five-unknown theory to deal with free vibration problems of FGM sandwich plates. However, the existing investigations [18, 19] indicated that the HSDTs neglecting continuity conditions of transverse shear stresses at the interfaces will encounter difficulty to produce accurately natural frequencies of the sandwich plate made up of soft core.

What’s more, layerwise theories in conjunction with finite element method have been established to yield accurate results [20]. Even so, the displacement variables in layerwise model augment with increase of layer number, so that tedious and complex calculation is to be needed. According to three-dimensional elasticity [4], in-plane displacements are required to be the zig-zag distribution through the thickness direction. By drawing a linear zig-zag function in the in-plane displacement of FSDT, Murakami [21] established a zig-zag model to describe the zig-zag distribution of in-plane displacements. However, such zig-zag model [21] will meet trouble to produce precisely transverse shear stresses directly from constitutive relation. Accurate transverse shear stresses impact largely prediction of natural frequencies of sandwich plates [22]. Based on Kirchhoff–Love plate theory, Orakdögen et al. [23] constructed two quadrilateral elements to study the coupling effect of extension and bending for the functionally graded plates. Making use of the first-order shell theory and Donnell kinematics assumption, Sofiyev and Osmancelebioglu [24] investigated carefully influence of functionally graded coatings on dynamic behaviors of sandwich-truncated conical shells, and some valuable conclusions have been drawn. Subsequently, buckling behaviors of sandwich-truncated conical shells composed of functionally graded materials have been investigated in detail by Sofiyev [25] via utilizing the first-order theory. Haciyev et al. [26] researched the vibration behaviors of functionally graded (FG) rectangular plates resting on elastic foundations, where effects of material parameters including material gradient and orthotropy on dynamic response have been analyzed in detail. In order to propose the methodological solutions of the pure FG structures and the FG sandwich constructions, Sofiyev [27] presented an exhaustive review on the published theories and models for the FG conical shells, FG-layered conical shells and the FG sandwich conical shells, which can provide a valuable reference for other investigators. Recently, based on the shear deformation theory, Sofiyev and Fantuzzi [28] proposed a novel approach to investigate vibration and stability behaviors of clamped sandwich cylindrical shells with the FG coatings.

By means of the hyperbolic shear deformation model, Avcar et al. [29] analyzed dynamic response of sigmoid FG sandwich beams, and influence of layup schemes of the FG sandwich beams on natural frequencies has been explored in detail. Hadji and Avcar [30] further utilized the hyperbolic shear displacement theory to study influence of boundary conditions, porosity volume fraction and layup scheme on free vibration of the FG sandwich plates. Based on the layerwise model, Belarbi et al. [31] constructed a new element to analyze free vibration of multilayered sandwich plates, and the good performance of the proposed model has been verified by several examples. On the basis of the third-order model, Hadji et al. [32] investigated dynamic behaviors of the imperfect FG sandwich plates resting on elastic foundation, and the instructive conclusions have been presented. In addition, Hirane et al. [33] proposed a novel higher-order finite element model to investigate static and dynamic behaviors of FG sandwich plates. Based on the higher-order zig-zag model, Garg et al. [34] constructed a finite element formulation to study vibration and buckling response of the FG sandwich plates. In terms of a new hyperbolic theory, Vinh and Huy [35] proposed a four-node quadrilateral element to research the bending, buckling and dynamic behaviors of the FG plates. Moreover, impact of porosity distribution on mechanical response of FG sandwich plates has been evaluated carefully. Making use of the improved first-order theory and the mixed finite element formulation, Vinh et al. [36] developed a four-node plate element to study the buckling and the bending behaviors of bi-directional FG plates, and some remarkable conclusions have been presented. In addition, the advancement of theory, new design and application trend for sandwich structures are summarized by Birman and Kardomateas [37].

As it is clear, most researches by means of the different models have been limited to rectangular plates. In fact, the mechanical characteristics of circular and elliptic plates utilized in repairment are extremely important as well. Ebrahimi and Rastgo [38] explored the free vibration behaviors of FGM piezoelectric sandwich circular plate by utilizing analytical method relying on the CPT. In the light of the FSDT, a mathematical derivation of free flexural vibration for the three-layer piezoelectric circular plate was made by Liu et al. [39]. Qiu et al. [40] established an analytical model to research dynamic behaviors of circular sandwich plates under shocking loads. Du and Ma [41] attempted to study impact of diverse loads on the nonlinear vibration characteristics of sandwich circular plates. In the light of the Reddy’s HSDT [7], Hashemi et al. [42] explored the dynamic behaviors of the piezoelectric FGM annular plates with diverse thickness-radius ratios and boundary conditions. What’s more, Sharma and Parashar [43] and Jandaghian et al. [44] also made an exhausive analysis on the dynamic behaviors of FGM piezoelectric circular plates. Furthermore, vibration regulation of circular piezolaminated and sandwich plates was investigated relying on the nonfragile control strategy [45]. For the vibration of annular sandwich plates, other researchers have also carried out a series of studies which can be seen in literature [46, 47]. Recently, Shishehsaz et al. [48] predicted stress distribution in the circular plate by means of layerwise theory and the hyperbolic HSDT. Shahrokhi et al. [49] attempted to investigate effect of length scale and electric field on the vibrational behaviors of circular sandwich micro-plates.

Survey of literature shows that numerous theories and the finite element methods have been established for the analysis of rectangular sandwich plates and shells. However, investigations on dynamic characteristic of the circular and ellipse sandwich structures made up of aluminum/composite face sheets and PMI core are less reported. In order to accurately predict dynamic response of the circular and ellipse sandwich structures, a higher-order model with five independent unknowns will be established. The proposed model can fulfill in advance continuity conditions of transverse shear stresses at the interfaces between adjacent layers, which can improve accuracy in predicting natural frequencies. For the free vibration of sandwich circular and ellipse plates with clamped boundaries, it is hard to present an analytical solution. In the light of the present model, a three-node triangular element in conjunction with the refined-element method [50] is to be developed for dynamic analysis of sandwich circular and ellipse plates. For the sake of appraising capability of the five-unknown higher-order models for free vibration of circular and ellipse sandwich plates, the present work tries to implement three types of five-unknown higher-order models proposed by Shi et al. [51], Kumar et al. [52] and Shukla et al. [53] by utilizing the same finite element method. In addition, results acquired from the three-dimensional finite element method (3D-FEM) are also selected as the reference solutions to appraise the present model as well as other models. This work establishes an alternative method to elevate the capability yielding accurately natural frequencies of sandwich circular and ellipse plates without augment of any additional displacement variables.

2 A novel finite element formulation (RFEF)

2.1 A higher-order model with five independent variables

It is well known that Reddy’s model [7] has been widely utilized for mechanical analysis of composite and sandwich plates attributing to its efficiency and accuracy. In the Reddy’s model, rotation of the normal is divided into the transverse shear components and the derivatives of deflection with respect to x and y, so that it is convenient to construct reasonably transverse shear components for accurate analysis of composite plates with hybridized laminates. In the light of such assumption, a Reddy-type higher-order model with five unknowns is to be presented in present work. Compared to the classical Reddy’s model, the compatible conditions of transverse shear stresses at the adjacent laminates will be enforced in advance.

To acquire the improved Reddy’s model, the classical Reddy’s model should be recalled, which can be presented by

$$\begin{gathered} u\left( {x,y,z} \right) = u_{0} \left( {x,y} \right) + f\left( z \right)\gamma_{x} \left( {x,y} \right) - zw_{x} \left( {x,y} \right) \hfill \\ v\left( {x,y,z} \right) = v_{0} \left( {x,y} \right) + f\left( z \right)\gamma_{y} \left( {x,y} \right) - zw_{y} \left( {x,y} \right) \hfill \\ w\left( {x,y,z} \right) = w_{0} \left( {x,y} \right) \hfill \\ \end{gathered}$$
(1)

in which u0, v0 and w0 represent the displacements on the mid-plane of plate along x and y directions; γx and γy signify the transverse shear components; wx and wy denote separately the derivatives of deflection with respect to y and x axes.

According to three-dimensional elasticity theory [4], transverse shear stress components should be compatible at the interfaces of adjacent laminates. For a sandwich plate with form core, transverse shear modulus suddenly changes at common surface of adjacent laminates, which will induce a large transverse shear deformation. Thereby, it is required to construct a transverse shear deformation function f(z) with a good performance. To achieve this goal, local displacement functions will be utilized at each laminate. By inserting the second-order local functions into displacement field, the displacements at arbitrary point of plate can be described as

$$\begin{gathered} u\left( {x,y,z} \right) = u_{0} \left( {x,y} \right) + f\left( z \right)\gamma_{x} \left( {x,y} \right) - zw_{x} \left( {x,y} \right) + \varsigma_{k} u_{1}^{k} \left( {x,y} \right) + \varsigma_{k}^{2} u_{2}^{k} \left( {x,y} \right) \hfill \\ v\left( {x,y,z} \right) = v_{0} \left( {x,y} \right) + f\left( z \right)\gamma_{y} \left( {x,y} \right) - zw_{y} \left( {x,y} \right) + \varsigma_{k} v_{1}^{k} \left( {x,y} \right) + \varsigma_{k}^{2} v_{2}^{k} \left( {x,y} \right) \hfill \\ w\left( {x,y,z} \right) = w_{0} \left( {x,y} \right) \hfill \\ \end{gathered}$$
(2)

where transverse shear function developed by Reddy [7] f (z) = z(1 − 4z2/3h2), in which h denotes whole thickness of plate; \(\varsigma_{k}\) signifies the thickness coordinate at the kth laminate. Relationship between the local coordinate \(\varsigma_{k}\) and the global coordinate z can be expressed as

$$\varsigma_{k} { = }c_{1}^{k} z - c_{2}^{k}$$
(3)

in which \(c_{1}^{k} { = }2/\left( {z_{k + 1} - z_{k} } \right)\), \(c_{2}^{k} { = }\left( {z_{k + 1} + z_{k} } \right)/\left( {z_{k + 1} - z_{k} } \right)\), where zk+1 signifies the thickness coordinate at the interface between the kth layer and (k + 1)th layer.

In Eq. (2), it is found that four displacement parameters \(u_{1}^{k}\), \(u_{2}^{k}\), \(v_{1}^{k}\) and \(v_{2}^{k}\) are involved in the kth laminate. For a composite plate made up of N laminates, 4 N additional displacement variables will be introduced. In order to decrease calculational cost, these additional variables should be reduced without compromising accuracy. As a result, making use of compatible conditions of displacements at the common interfaces between adjacent laminates, the variables at each laminate can be reduced, which can be expressed as

$$\begin{gathered} u_{2}^{k} \left( {x,y} \right){ = }u_{1}^{k} \left( {x,y} \right) + u_{1}^{{k{ - }1}} \left( {x,y} \right) + u_{2}^{{k{ - }1}} \left( {x,y} \right) \hfill \\ v_{2}^{k} \left( {x,y} \right){ = }v_{1}^{k} \left( {x,y} \right) + v_{1}^{{k{ - }1}} \left( {x,y} \right) + v_{2}^{{k{ - }1}} \left( {x,y} \right) \hfill \\ \end{gathered}$$
(4)

where k is always more than one.

To further reduce displacement parameters, the compatible conditions of transverse shear stresses between the kth laminate and (k-1)th laminate will be enforced, which may be given by

$$\begin{gathered} \tau_{xz}^{k} \left( {x,y,z_{k} } \right){ = }\tau_{xz}^{k - 1} \left( {x,y,z_{k} } \right) \hfill \\ \tau_{yz}^{k} \left( {x,y,z_{k} } \right){ = }\tau_{yz}^{k - 1} \left( {x,y,z_{k} } \right) \hfill \\ \end{gathered}$$
(5)

For free vibration problems, the lower and upper surfaces of sandwich plates do not subject to any loadings. Therefore, transverse shear stresses on the lower and upper surfaces should be equal to be zero, so the following equation can be given by

$$\begin{gathered} \tau_{xz}^{1} \left( {x,y,z_{1} } \right){ = }\tau_{xz}^{N} \left( {x,y,z_{N + 1} } \right) = 0 \hfill \\ \tau_{yz}^{1} \left( {x,y,z_{1} } \right){ = }\tau_{yz}^{N} \left( {x,y,z_{N + 1} } \right) = 0 \hfill \\ \end{gathered}$$
(6)

where N denotes the total number of layers.

Once the constrained conditions above mentioned are fulfilled, all displacement parameters depending on laminates can be completely removed from the initial displacement field. As a result, the proposed Reddy-type higher-order model can be presented by

$$\begin{gathered} u\left( {x,y,z} \right) = u_{0} \left( {x,y} \right) + f_{u}^{k} \left( z \right)\gamma_{x} \left( {x,y} \right) - zw_{x} \left( {x,y} \right) \hfill \\ v\left( {x,y,z} \right) = v_{0} \left( {x,y} \right) + f_{v}^{k} \left( z \right)\gamma_{y} \left( {x,y} \right) - zw_{y} \left( {x,y} \right) \hfill \\ w\left( {x,y,z} \right) = w_{0} \left( {x,y} \right) \hfill \\ \end{gathered}$$
(7)

In Eq. (7), it can be found that the form of the present model is nearly the same as that of Reddy’s model [7], and transverse shear functions through thickness direction \(f_{u}^{k} \left( z \right)\) and \(f_{v}^{k} \left( z \right)\) only differ from those of Reddy’s model. Furthermore, the proposed model can meet compatible conditions of transverse shear stresses at the interfaces, which can elevate accuracy predicting natural frequencies of sandwich plates. In addition, the zig-zag effect of in-plane displacements has been also taken into account in the proposed model, which is induced by the mismatching material properties at the adjacent layers.

Transverse shear functions \(f_{u}^{k} \left( z \right)\) and \(f_{v}^{k} \left( z \right)\) can be determined by utilizing the constrained conditions of displacements and stresses, which can be explicitly shown as follows

$$\begin{gathered} f_{u}^{k} \left( z \right) = \lambda_{1}^{k} \varsigma_{k} + \lambda_{2}^{k} \varsigma_{k}^{2} + f\left( z \right) \hfill \\ f_{v}^{k} \left( z \right) = \kappa_{1}^{k} \varsigma_{k} + \kappa_{2}^{k} \varsigma_{k}^{2} + f\left( z \right) \hfill \\ \end{gathered}$$
(8)

where f (z) is the transverse shear function proposed by Reddy [7].

$$\begin{gathered} \lambda \,_{i}^{k} = F_{i1}^{k} L + F_{i2}^{k} \hfill \\ \kappa_{i}^{k} = H_{i1}^{k} M + H_{i2}^{k} \hfill \\ \end{gathered}$$
(9)

where coefficients \(F_{i1}^{k}\), \(F_{i2}^{k}\), \(H_{i1}^{k}\) and \(H_{i2}^{k}\) can be determined by using the compatible conditions of transverse shear stresses.

In the light of the compatible conditions of transverse shear stresses at the interfaces, the following equations can be presented by

$$\begin{gathered} F_{11}^{k} = - \left( {2 + \alpha_{1}^{k} } \right)F_{11}^{k - 1} - 2\left( {1 + \alpha_{1}^{k} } \right)F_{21}^{k - 1} \hfill \\ F_{12}^{k} = - \left( {2 + \alpha_{1}^{k} } \right)F_{12}^{k - 1} - 2\left( {1 + \alpha_{1}^{k} } \right)F_{22}^{k - 1} + \alpha_{2}^{k} \hfill \\ F_{21}^{k} = F_{11}^{k} + F_{11}^{k - 1} + F_{21}^{k - 1} \hfill \\ F_{22}^{k} = F_{12}^{k} + F_{12}^{k - 1} + F_{22}^{k - 1} \hfill \\ H_{11}^{k} = - \left( {2 + \beta_{1}^{k} } \right)H_{11}^{k - 1} - 2\left( {1 + \beta_{1}^{k} } \right)H_{21}^{k - 1} \hfill \\ H_{12}^{k} = - \left( {2 + \beta_{1}^{k} } \right)H_{12}^{k - 1} - 2\left( {1 + \beta_{1}^{k} } \right)H_{22}^{k - 1} + \beta_{2}^{k} \hfill \\ H_{21}^{k} = H_{11}^{k} + H_{11}^{k - 1} + H_{21}^{k - 1} \hfill \\ H_{22}^{k} = H_{12}^{k} + H_{12}^{k - 1} + H_{22}^{k - 1} \hfill \\ \end{gathered}$$
(10)

whereas k = 1, \(F_{11}^{k} = H_{11}^{k} = 1\), \(F_{12}^{k} = H_{12}^{k} = 0\); \(F_{21}^{k} = H_{21}^{k} = 1/2\), \(F_{22}^{k} = H_{22}^{k} = \left( {1 - 4z_{k}^{2} /h^{2} } \right)/\left( {2c_{1}^{k} } \right)\); as k is more than one, \(F_{ij}^{k}\) and \(H_{ij}^{k}\) can be obtained by Eq. (10).

$$\begin{gathered} \alpha_{1}^{k} = \left( {c_{1}^{k - 1} Q_{44}^{k - 1} } \right)/\left( {c_{1}^{k} Q_{44}^{k} } \right) \hfill \\ \alpha_{2}^{k} = \left( {Q_{44}^{k} - Q_{44}^{k - 1} } \right)\left( {1 - 4z_{k}^{2} /h^{2} } \right)/\left( {c_{1}^{k} Q_{44}^{k} } \right) \hfill \\ \beta_{1}^{k} = \left( {c_{1}^{k - 1} Q_{55}^{k - 1} } \right)/\left( {c_{1}^{k} Q_{55}^{k} } \right) \hfill \\ \beta_{2}^{k} = \left( {Q_{55}^{k} - Q_{55}^{k - 1} } \right)\left( {1 - 4z_{k}^{2} /h^{2} } \right)/\left( {c_{1}^{k} Q_{55}^{k} } \right) \hfill \\ \end{gathered}$$
(11)

in which \(Q_{44}^{k} { = }G_{13}^{k}\) and \(Q_{55}^{k} { = }G_{23}^{k}\), where \(G_{13}^{k}\) and \(G_{23}^{k}\) denote the shear moduli in 1–3 plane and 2–3 plane, respectively.

Coefficients L and M can be determined by using the free-surface conditions of transverse shear stresses on the upper surfaces, which are presented by

$$\begin{gathered} L = - \left( {c_{1}^{N} F_{12}^{N} + 2c_{1}^{N} F_{22}^{N} + \left( {1 - 4z_{N + 1}^{2} /h^{2} } \right)} \right)/\left( {c_{1}^{N} F_{11}^{N} + 2c_{1}^{N} F_{21}^{N} } \right) \hfill \\ M = - \left( {c_{1}^{N} G_{12}^{N} + 2c_{1}^{N} G_{22}^{N} + \left( {1 - 4z_{N + 1}^{2} /h^{2} } \right)} \right)/\left( {c_{1}^{N} G_{11}^{N} + 2c_{1}^{N} G_{21}^{N} } \right) \hfill \\ \end{gathered}$$
(12)

In order to appraise the proposed model, several Reddy-type higher-order models [51,52,53] recently reported in the literature will be selected for comparison.

2.2 Finite element formulation based on the proposed model

In present work, free vibration of sandwich circular and ellipse plates with clamped boundaries will be investigated, so that it is hard to present an analytical solution. To extend the proposed model for dynamic analysis of circular and ellipse sandwich plates, the finite element formulation of a three-node triangular element by means of the present model is to be established.

Displacement parameters in the plane can be expressed by using the area coordinates and nodal displacements, so that the displacement parameters u0, v0, γx and γy within one element can be presented by

$$\begin{gathered} u_{0} = \sum\limits_{i = 1}^{3} {L_{i} } u_{0i} ,\quad \gamma_{x} = \sum\limits_{i = 1}^{3} {L_{i} } \gamma_{xi} \hfill \\ v_{0} = \sum\limits_{i = 1}^{3} {L_{i} } v_{0i} ,\quad \gamma_{y} = \sum\limits_{i = 1}^{3} {L_{i} } \gamma_{yi} \hfill \\ \end{gathered}$$
(13)

where \(L_{i}\) represents the area coordinate, and i = 1 ~ 3.

For the present model, the first partial derivatives of transverse displacement are contained in the displacement field, so in-plane strains will contain the second partial derivatives of transverse displacement. As a result, the first partial derivatives of transverse displacement are required to be compatible on the common edges of elements. For the sake of such requirement, the refined-element method proposed by Cheung and Chen [50] will be recalled. According to the refined-element approach, transverse displacement can be discretized as follows

$$w_{0} = \sum\limits_{i = 1}^{3} {({\text{N}}_{i}^{1} w_{i} + {\text{N}}_{xi}^{1} w_{xi} + {\text{N}}_{yi}^{1} w_{yi} )}$$
(14)

Shape functions in Eq. (14) can be explicitly expressed as

$${\mathbf{N}}^{1} { = }\left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{1}^{1} } & {{\mathbf{N}}_{2}^{1} } & {{\mathbf{N}}_{3}^{1} } \\ \end{array} } \right] = {\mathbf{N}}^{0} + {\mathbf{\rm P}}\left( {{\mathbf{B}}^{c} - {\mathbf{B}}^{0} } \right)$$
(15)

where \({\mathbf{P}} = \left[ {\begin{array}{*{20}c} {0.5x^{2} } & {0.5y^{2} } & {xy} \\ \end{array} } \right]\).

N0 denotes the shape function of the element BCIZ [54], which only satisfies the compatible conditions of transverse displacement on the common edge of adjacent elements. Transverse shear strains in the present model merely include the partial first derivatives of transverse displacement, so the shape function of BCIZ will be used to discretize transverse displacement in transverse shear strain, which can be given as

$${\mathbf{N}}^{0} { = }\left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{1}^{0} } & {{\mathbf{N}}_{2}^{0} } & {{\mathbf{N}}_{3}^{0} } \\ \end{array} } \right]$$
(16)

where

$$\begin{gathered} {\text{N}}_{i}^{0} { = }L_{i} + L_{i}^{2} L_{j} + L_{i}^{2} L_{k} - L_{i} L_{j}^{2} - L_{i} L_{k}^{2} \hfill \\ {\text{N}}_{xi}^{0} = c_{x}^{k} L_{i}^{2} L_{j} - c_{x}^{j} L_{i}^{2} L_{k} + 0.5\left( {c_{x}^{k} - c_{x}^{j} } \right)L_{i} L_{j} L_{k} \hfill \\ {\text{N}}_{yi}^{0} = c_{y}^{j} L_{i}^{2} L_{k} - c_{y}^{k} L_{i}^{2} L_{j} + 0.5\left( {c_{y}^{j} - c_{y}^{k} } \right)L_{i} L_{j} L_{k} \hfill \\ \end{gathered}$$
(17)

in which\(c_{x}^{i} = x_{k} - x_{j}\), \(c_{y}^{i} = y_{j} - y_{k}\), where xj, yj, xk and yk signify, respectively, coordinates at the jth and kth nodes.

In terms of refined-element approach, strain matrix Bc can be given by

$${\mathbf{B}}^{c} { = }\left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{1}^{c} } & {{\mathbf{B}}_{2}^{c} } & {{\mathbf{B}}_{3}^{c} } \\ \end{array} } \right]$$
(18)

where

$$B_{1}^{c} = \left[ {\begin{array}{*{20}c} {l_{1} m_{1} - l_{3} m_{3} } & {0.5(l_{1}^{2} y_{21} + l_{3}^{2} y_{13} )} & {0.5(l_{1}^{2} x_{12} + l_{3}^{2} x_{31} )} \\ {l_{3} m_{3} - l_{1} m_{1} } & {0.5(m_{1}^{2} y_{21} + m_{3}^{2} y_{13} )} & {0.5(m_{1}^{2} x_{12} + m_{3}^{2} x_{31} )} \\ {m_{1}^{2} - m_{3}^{2} } & {0.5(l_{1}^{2} x_{12} + l_{3}^{2} x_{31} )} & {0.5(m_{1}^{2} y_{21} + m_{3}^{2} y_{13} )} \\ \end{array} } \right]$$
(19)

in which li and mi signify the cosines of vector normal to the ith edge; \(x_{ij} = x_{i} - x_{j} ,\quad y_{ij} = y_{i} - y_{j}\). Further rotating the subscript, matrices \({\mathbf{B}}_{2}^{c}\) and \({\mathbf{B}}_{3}^{c}\) can be acquired.

In addition, the matrix B0 can be expressed as follows

$${\mathbf{B}}^{0} = \frac{1}{A}\iint {{\overline{\mathbf{B}}}dxdy}$$
(20)

where A signifies the area of one element, and \({\overline{\mathbf{B}}}\) represents the strain matrix of BCIZ.

By means of relationship between displacements and strains, the strain vector at the kth ply can be presented by

$${{\varvec{\upvarepsilon}}}^{k} = {\mathbf{Bu}}^{e}$$
(21)

in which \({\mathbf{B}} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{1} } & {{\mathbf{B}}_{2} } & {{\mathbf{B}}_{3} } \\ \end{array} } \right]\), \({\mathbf{u}}^{e} = \left[ {\begin{array}{*{20}c} {{\mathbf{u}}_{1}^{{}} } & {{\mathbf{u}}_{2}^{{}} } & {{\mathbf{u}}_{3}^{{}} } \\ \end{array} } \right]^{T}\), ui = [u0i, v0i, w0i, γxi, wxi, γyi, wyi], i = 1, 2, 3.

By means of the present model, strain matrix Bi at the ith node can be written as follows

$${\mathbf{B}}_{i} = \left[ {\begin{array}{*{20}c} {\frac{{\partial L_{i} }}{\partial x}} & 0 & {{\text{B}}_{1,3} } & {\Phi_{1}^{k} \frac{{\partial L_{i} }}{\partial x}} & {{\text{B}}_{1,5} } & 0 & {{\text{B}}_{1,7} } \\ 0 & {\frac{{\partial L_{i} }}{\partial y}} & {{\text{B}}_{2,3} } & 0 & {{\text{B}}_{2,5} } & {\Psi_{1}^{k} \frac{{\partial L_{i} }}{\partial y}} & {{\text{B}}_{2,7} } \\ {\frac{{\partial L_{i} }}{\partial y}} & {\frac{{\partial L_{i} }}{\partial x}} & {{\text{B}}_{3,3} } & {\Phi_{1}^{k} \frac{{\partial L_{i} }}{\partial y}} & {{\text{B}}_{3,5} } & {\Psi_{1}^{k} \frac{{\partial L_{i} }}{\partial x}} & {{\text{B}}_{3,7} } \\ 0 & 0 & {{\text{B}}_{4,3} } & {\frac{{\partial \Phi_{1}^{k} }}{\partial z}L_{i} } & {{\text{B}}_{4,5} } & 0 & {{\text{B}}_{4,7} } \\ 0 & 0 & {{\text{B}}_{5,3} } & 0 & {{\text{B}}_{5,5} } & {\frac{{\partial \Psi_{1}^{k} }}{\partial z}L_{i} } & {{\text{B}}_{5,7} } \\ \end{array} } \right]$$
(22)

where

$$\begin{gathered} {\text{B}}_{1,3} = \Phi_{2}^{k} \frac{{\partial^{2} {\text{N}}_{i}^{1} }}{{\partial x^{2} }},{\text{B}}_{1,5} = \Phi_{2}^{k} \frac{{\partial^{2} {\text{N}}_{xi}^{1} }}{{\partial x^{2} }},{\text{B}}_{1,7} = \Phi_{2}^{k} \frac{{\partial^{2} {\text{N}}_{yi}^{1} }}{{\partial x^{2} }} \hfill \\ {\text{B}}_{2,3} = \Psi_{2}^{k} \frac{{\partial^{2} {\text{N}}_{i}^{1} }}{{\partial y^{2} }},{\text{B}}_{2,5} = \Psi_{2}^{k} \frac{{\partial^{2} {\text{N}}_{yi}^{1} }}{{\partial y^{2} }}{\text{,B}}_{2,7} = \Psi_{2}^{k} \frac{{\partial^{2} {\text{N}}_{yi}^{1} }}{{\partial y^{2} }} \hfill \\ {\text{B}}_{3,3} = \left( {\Phi_{2}^{k} + \Psi_{2}^{k} } \right)\frac{{\partial^{2} {\text{N}}_{i}^{{1}} }}{\partial x\partial y},{\text{B}}_{3,5} = \left( {\Phi_{2}^{k} + \Psi_{2}^{k} } \right)\frac{{\partial^{2} {\text{N}}_{xi}^{1} }}{\partial x\partial y},{\text{B}}_{3,7} = \left( {\Phi_{2}^{k} + \Psi_{2}^{k} } \right)\frac{{\partial^{2} {\text{N}}_{yi}^{1} }}{\partial x\partial y} \hfill \\ {\text{B}}_{4,3} = \left( {1 + \frac{{\partial \Phi_{2}^{k} }}{\partial z}} \right)\frac{{\partial {\text{N}}_{i}^{0} }}{\partial x},{\text{B}}_{4,5} = \left( {1 + \frac{{\partial \Phi_{2}^{k} }}{\partial z}} \right)\frac{{\partial {\text{N}}_{xi}^{0} }}{\partial x},{\text{B}}_{4,7} = \left( {1 + \frac{{\partial \Phi_{2}^{k} }}{\partial z}} \right)\frac{{\partial {\text{N}}_{yi}^{0} }}{\partial x} \hfill \\ {\text{B}}_{5,3} = \left( {1 + \frac{{\partial \Psi_{2}^{k} }}{\partial z}} \right)\frac{{\partial {\text{N}}_{i}^{0} }}{\partial y},{\text{B}}_{5,5} = \left( {1 + \frac{{\partial \Psi_{2}^{k} }}{\partial z}} \right)\frac{{\partial {\text{N}}_{xi}^{0} }}{\partial y},{\text{B}}_{5,7} = \left( {1 + \frac{{\partial \Psi_{2}^{k} }}{\partial z}} \right)\frac{{\partial {\text{N}}_{yi}^{0} }}{\partial y} \hfill \\ \end{gathered}$$

It should be shown that the coefficients \(\Phi_{i}^{k}\) and \(\Psi_{i}^{k}\) can be given by

$$\begin{gathered} \Phi_{1}^{k} = f_{u}^{k} \left( z \right) \hfill \\ \Psi_{1}^{k} = f_{v}^{k} \left( z \right) \hfill \\ \Phi_{2}^{k} = \Psi_{2}^{k} = z \hfill \\ \end{gathered}$$
(23)

Once stain matrix can be acquired, the stiffness matrix within one element can be presented by using the following equation.

$${\mathbf{K}}^{e} = \sum\limits_{i = 1}^{N} {\int_{{z_{i} }}^{{z_{i + 1} }} {\left( {\iint {{\mathbf{B}}^{T} {\mathbf{QB}}dxdy}} \right)} } dz$$
(24)

Utilizing the Hamilton’s principle, equation of motion within one element may be written as

$${\mathbf{M}}^{e} {\dot{\mathbf{u}}} + {\mathbf{K}}^{e} {\mathbf{u}} = 0$$
(25)

In Eq. (25), the mass matrix \({\mathbf{M}}^{e}\) within one element can be presented by

$${\mathbf{M}}^{e} = \int_{{A_{e} }} {\sum\limits_{i = 1}^{N} {\int_{{z_{i} }}^{{z_{i + 1} }} {{\overline{\mathbf{N}}}^{T} {{\varvec{\uprho}}}_{i} } {\overline{\mathbf{N}}}dz} } dA$$
(26)

In Eq. (26), the matrices \({\overline{\mathbf{N}}}\) and \({{\varvec{\uprho}}}_{i}\) can be, respectively, expressed as

$${\overline{\mathbf{N}}} = \left[ {\begin{array}{*{20}c} {{\overline{\mathbf{N}}}_{1} } & {{\overline{\mathbf{N}}}_{2} } & {{\overline{\mathbf{N}}}_{3} } \\ \end{array} } \right]$$
(27)

in which

$${\overline{\mathbf{N}}}_{i} = \left[ {\begin{array}{*{20}c} {L_{i} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {L_{i} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {{\text{N}}_{i}^{0} } & 0 & {{\text{N}}_{xi}^{0} } & 0 & {{\text{N}}_{yi}^{0} } \\ 0 & 0 & 0 & {L_{i} } & 0 & 0 & 0 \\ 0 & 0 & {{\text{N}}_{i,x}^{0} } & 0 & {{\text{N}}_{xi,x}^{0} } & 0 & {{\text{N}}_{yi,x}^{0} } \\ 0 & 0 & 0 & 0 & 0 & {L_{i} } & 0 \\ 0 & 0 & {{\text{N}}_{i,y}^{0} } & 0 & {{\text{N}}_{xi,y}^{0} } & 0 & {{\text{N}}_{yi,y}^{0} } \\ \end{array} } \right]$$
(28)
$${{\varvec{\uprho}}}_{i} = \rho_{i} \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {\Phi_{1}^{k} } & {\Phi_{2}^{k} } & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & {\Psi_{1}^{k} } & {\Psi_{2}^{k} } \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ {\Phi_{1}^{k} } & 0 & 0 & {\Phi_{1}^{k} \Phi_{1}^{k} } & {\Phi_{1}^{k} \Phi_{2}^{k} } & 0 & 0 \\ {\Phi_{2}^{k} } & 0 & 0 & {\Phi_{2}^{k} \Phi_{1}^{k} } & {\Phi_{2}^{k} \Phi_{2}^{k} } & 0 & 0 \\ 0 & {\Psi_{1}^{k} } & 0 & 0 & 0 & {\Psi_{1}^{k} \Psi_{1}^{k} } & {\Psi_{1}^{k} \Psi_{2}^{k} } \\ 0 & {\Psi_{2}^{k} } & 0 & 0 & 0 & {\Psi_{2}^{k} \Psi_{1}^{k} } & {\Psi_{2}^{k} \Psi_{2}^{k} } \\ \end{array} } \right]$$
(29)

where \(\rho_{i}\) signifies the density at the ith laminate.

Putting all the element mass and stiffness matrices into the global mass and stiffness matrices according to the order of nodes, the dynamic equation may be presented as

$${\mathbf{M}}\ddot{\mathbf{U}} + {\mathbf{KU}} = 0$$
(30)

In Eq. (30), M and K represent the global mass and stiffness matrices. Natural frequencies of composite and sandwich plates can be acquired by solving the following eigenvalue equation.

$$\left( {{\mathbf{K}} - \omega^{2} {\mathbf{M}}} \right){\mathbf{U}} = 0$$
(31)

where ω denotes frequency of plate.

3 Numerical examples

Free vibration of an isotropic plate with clamped boundaries will be firstly investigated, where present results are compared with the published results [55,56,57]. Subsequently, free vibration analysis of a sandwich circular plate made up of aluminum (Al) sheets and polymethacrylimide (PMI) core is further carried out, which is utilized to account for the performance of the proposed model. In addition, influence of the ratios of major axis to minor axis of ellipse on natural frequencies will be investigated. To improve the stiffness of sandwich plates, we attempt to utilize the composite face sheets to replace the aluminum face sheets. Furthermore, impact of lamination sequence on stiffness of sandwich plate is also investigated.

Example 1

Free vibration analysis of the sandwich circular and ellipse plates with clamped boundaries is carried out to appraise the capability of the proposed model.

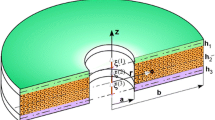
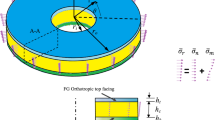
In Fig. 1, a, b and h denote length of semimajor axis, length of semiminor axis and height of the sandwich ellipse plate, respectively. In addition, tc and tf represent thicknesses of the core layer and face sheets, respectively. As a is equal to b, radius of a circular plate is written as R = a = b.

Fig. 1
figure 1

Geometry and structure of a sandwich ellipse plate

Full size image

To evaluate performance of the present finite element formulation, free vibration of an isotropic plate with clamped boundaries will be firstly analyzed, in which Young modulus, Poisson ratio and density of material properties are 71 GPa, 0.3 and 2700 kg/m3, respectively. Dimensionless frequencies are defined as \(\varpi = \omega R^{2} \sqrt {\rho h/D}\), where \(D = \frac{{Eh^{3} }}{{12\left( {1 - \upsilon^{2} } \right)}}\). In Table 1, results obtained from the present model using 1027 elements, 2013 elements and 3278 elements are compared with those presented by Qin et al. [55], Civalek and Ersoy [56], and Liew and Yang [57]. In addition, 3D-FEM results using 43,910 elements are also presented for comparison. Numerical results show that the present results using 2013 elements agree well with the 3D-FEM results, which can verify accuracy of the present model.

Table 1 Dimensionless frequencies of the clamped circular plate (h/R = 0.3)
Full size table

Subsequently, free vibration of the sandwich circular and ellipse plates with clamped boundary will be studied. Young modulus, Poisson ratio and density of face sheets made up of the aluminum are 71 GPa, 0.3 and 2700 kg/m3, respectively. For the core layer of PMI, Young modulus, Poisson ratio and density are 92 MPa, 0.375 and 75 kg/m3, respectively. The natural frequencies are normalized as \(\varpi = \omega d^{2} \sqrt {\rho_{s} /E_{s} } /h\), in which d = 2R signifies diameter of circular plate, and d = 2a for an ellipse plate, where a denotes the length of major axis of ellipse; \(\rho_{s}\) and \(E_{s}\), respectively, denote the density and elastic modulus of face sheets.

It requires to be indicated that three-dimensional elasticity solutions of natural frequencies for the sandwich circular and ellipse plates are less reported in the published literature. Thus, the results acquired from 3D-FEM will be selected for a reference to appraise the present model as well as the chosen models. Firstly, variation of 3D-FEM results with refinement of meshes is depicted in Fig. 2, which shows that the converged results can be obtained by using the 3D-FEM with 29,505 elements.

Fig. 2
figure 2

Variation of natural frequencies acquired from 3D-FEM with increase of elements

Full size image

In order to explore the capability of the proposed model predicting the higher-order frequencies, the first twenty frequencies of sandwich circular plate are compared with the 3D-FEM results in Table 2, where four kinds of Reddy-type higher-order models recently proposed by Shi et al. [51], Kumar et al. [52], Shukla et al. [53] and Babu et al. [58] are also selected for comparison. Differing from the present model, the shear deformation functions of the selected models can be written as f(z) = (h/2)tanh(2z/h) − z/cosh2(1) [51], f(z) = sin(2pπz/h) − (2pπz/h)cos(pπ) where p = 0.6 [52], f(z) = sin(2pπz/h) − (2pπz/h) cos(pπ) where p = 0.4 [53], and f(z) = g(z) + zΩ where g(z) = sinh−1(rz/h), Ω = − 2r/(h \(\sqrt {r^{2} + 4}\)) and r = 3 [58]. Typical finite element mesh configuration with 2027 elements has been depicted in Fig. 3. In Fig. 4, displacement modes corresponding to the higher-order frequencies are depicted, which can help to understand well the vibration modes of sandwich circular plate.

Table 2 Comparison of natural frequencies obtained from various models for a three-layer sandwich circular plate (tc/tf = 8, d/h = 100)
Full size table
Fig. 3
figure 3

Typical finite element mesh configuration with 2027 elements

Full size image
Fig. 4
figure 4

Displacement modes of a three-ply sandwich circular plate with clamped boundaries (tc/tf = 8, d/h = 100)

Full size image

In addition, all results in Table 2 are plotted in Fig. 5a. It can be noted that curved line of the results acquired from present model RFEF nearly covers that of 3D-FEM results. With increase of mode number, complex deformation of sandwich plate will occur, so that the zig-zag effect plays the more important rule in structural deformation. Thus, natural frequencies acquired from the selected models discarding the zig-zag effect [51,52,53, 58] rapidly deviate the 3D-FEM results. Furthermore, it can be observed that when mode number is more than 17, divergence between these results and 3D-FEM results is rapidly aggravated. For the sake of accounting for such appearance, the percentage errors of results acquired from the selected models relative to 3D-FEM results are depicted in Fig. 5b. Numerical results indicate that the maximum error of the present model is less than 2.5%. However, the maximum errors of other models are more than 80%.

Fig. 5
figure 5

Comparison of natural frequencies acquired from various models for a three-layer sandwich circular plate (tc/tf = 8, d/h = 100)

Full size image

To extend range of application of the proposed model, natural frequencies of the sandwich ellipse plate with major axis a along x direction and minor axis b along y direction are analyzed, which are shown in Table 3. The first twenty displacement modes corresponding to diverse frequencies are depicted in Fig. 6. Variation of displacement modes in the ellipse plate evidently differs from those of the circular plate attributing to dissimilar stiffness along x and y directions. In fact, bending stiffness along the long axis is smaller than that of short axis, so that bending deformation along the long axis more easily occurs in comparison with deformation along the short axis. All results in Table 3 are plotted in Fig. 7 in conjunction with 3D-FEM results. Again, curved line of the results acquired from the present model RFEF covers exactly the curved line of 3D-FEM results, which may illustrate well the capability of the proposed model for a sandwich ellipse plate.

Table 3 Comparison of natural frequencies obtained from various models for a three-layer sandwich ellipse plate (tc/tf = 8, a/h = 50, a/b = 0.5)
Full size table
Fig. 6
figure 6

Displacement modes of a three-ply sandwich ellipse plate with clamped boundaries (tc/tf = 8, a/h = 50, a/b = 0.5)

Full size image
Fig. 7
figure 7

Comparison of natural frequencies obtained from various models for a three-layer sandwich ellipse plate (tc/tf = 8, a/h = 50, a/b = 0.5)

Full size image

In addition, impact of the ratios of major axis a to minor axis b on natural frequencies is to be researched. Natural frequencies of sandwich ellipse plates with diverse ratios of a/b are shown in Table 4. In order to explicitly illustrate performance of different models, results in Table 4 are depicted in Fig. 8. In Fig. 8a, results acquired from the present model RFEF are consistent well with the 3D-FEM results, but a slight divergence from 3D-FEM can be noted with increase of the ratios of major axis a and minor axis b. Furthermore, the maximum error of present model RFEF reaches at 6.43% for a/b = 3, which can be found in Fig. 8b.

Table 4 Effect of the chosen parameters on the first natural frequencies of the three-layer sandwich plates (a/h = 50, tc/tf = 8)
Full size table
Fig. 8
figure 8

Effect of the chosen parameters on the first natural frequencies of the three-layer sandwich plates (a/h = 50, tc/tf = 8)

Full size image

Example 2

Free vibration of the clamped sandwich circular plate with composite face sheets and PMI core is analyzed.

In this case, material properties of face sheets [59] are \(E_{1} = 181\;{\text{GPa}}\), \(E_{2} = 10.3\;{\text{GPa}}\), \(E_{3} = E_{2}\), \(G_{12} = 7.17\;{\text{GPa}}\), \(G_{13} = G_{12}\), \(G_{23} = 2.87\;{\text{GPa}}\), \(\nu_{12} = 0.25\), \(\nu_{13} = 0.25\) and \(v_{23} = 0.33\), where subscripts ‘1’ and ‘2’ denote the direction parallel to the fibers and the direction vertical to the fibers in the 1–2 plane, respectively; subscript ‘3’ denotes the direction vertical to the 1–2 plane. Material properties of PMI core can be found in example 1. The natural frequencies are normalized as \(\varpi = \omega d^{2} \sqrt {\rho_{s} /E_{2s} } /h\), where the density of face sheet \(\rho_{s} = 1578\;{\text{kg}}/{\text{m}}^{3}\), and elastic modulus \(E_{2s} { = }10.3\;{\text{GPa}}\).

Firstly, performance of the proposed model predicting natural frequencies of the sandwich circular plate with composite face sheets and PMI core will be researched, which is the foundations studying an impact of face sheets on frequencies. In Table 5, results acquired from the higher-order models are compared with the 3D-FEM results. It can be noted that present results are in good agreement with the 3D-FEM results. Nevertheless, the results obtained from the selected higher-order models [51,52,53, 58] are largely more than the 3D-FEM results, as these models are unable to fulfill continuity conditions of interlaminar stresses. In order to illustrate the relationships between the results obtained from the five-unknown higher-order models and the 3D-FEM results, all results in Table 5 have been plotted in Fig. 9, and it is found that several frequencies acquired from the present model corresponding to displacement modes 13, 16 and 20 are slight diverse from the 3D-FEM results. However, present results corresponding to other displacement modes are in exact agreement with the 3D-FEM results.

Table 5 Comparison of natural frequencies obtained from various models for a three-layer sandwich circle plate with composite face sheets (tc/tf = 8, d/h = 100)
Full size table
Fig. 9
figure 9

Comparison of natural frequencies obtained from various models for a three-layer sandwich circle plate with composite face sheets (tc/tf = 8, d/h = 100)

Full size image

In addition, natural frequencies of the same size sandwich plate made up of composite face sheets and PMI core are compared with those of the sandwich plate composed of aluminum face sheets and PMI core in Fig. 10. Numerical comparison reveals that the natural frequencies of sandwich circular plate made up of composite face sheets have been significantly improved, which imply that relative stiffness of sandwich circular plate can be largely elevated by utilizing the composite face sheets to replace aluminum face sheets.

Fig. 10
figure 10

Comparison of natural frequencies for the three-layer sandwich circle plates with aluminum face sheet and composite face sheets (tc/tf = 8, d/h = 100)

Full size image

In the above study, it can be observed that if aluminum face sheets are replaced by composite face sheets, the stiffness of sandwich circular plate can be significantly elevated, so an approach increasing the stiffness of sandwich circular plate should be explored. Therefore, configuration of face sheets will be designed to improve stiffness of such structure. As a result, three groups of sandwich plates containing aluminum face sheets [Al/C/Al] (Sandwich-1), composite face sheets [0°/C/0°] (Sandwich-2) and composite face sheets [0°/90°/C/90°/0°] (Sandwich-3) will be analyzed, and all results have been shown in Table 6 in conjunction with 3D-FEM results.

Table 6 Comparison of natural frequencies obtained from various models for the sandwich circle plates with different face sheets (tc/tf = 18, d/h = 100)
Full size table

To find out variation of natural frequencies, all results in Table 6 have been plotted in Fig. 11. Numerical results imply that relative stiffness of sandwich circular plate can be surely elevated by using the composite face sheets. In addition, the relative stiffness of sandwich circular plate can be further elevated by changing the laminated configuration. For example, stiffness of sandwich plate [0°/90°/C/90°/0°] is explicitly more than that of sandwich plate [0°/C/0°], which can show that composite face sheets possess the designability.

Fig. 11
figure 11

Comparison of natural frequencies obtained from various models for the sandwich circle plates with different face sheets (tc/tf = 18, d/h = 100)

Full size image

4 Conclusions

IN this work, a finite element formulation is developed for free vibration analysis of sandwich circular and ellipse plates. Compared to the existing five-variable theories, the present model can fulfill in advance compatible conditions of transverse shear stresses at the adjacent laminates, but they possess the same displacement parameters. Strain components of present model have the second derivatives, so the refined-element method is utilized to overcome the compatible requirement of the first derivatives of transverse displacement at the shared edge of the adjacent elements. In order to appraise capability of the proposed model, free vibration analysis of sandwich circular plate with aluminum face sheets and PMI core is firstly carried out. Subsequently, effect of ratios of major axis to minor axis for an ellipse plate on natural frequencies is further studied. An approach improving the stiffness of sandwich plates is also discussed by changing the face sheets. By means of the outcome of analysis, the following conclusions will be drawn:

  1. (1)

    Possessing the same expression of displacements, the proposed model can more precisely produce natural frequencies of sandwich circular and ellipse plates than the existing five-variable higher-order models.

  2. (2)

    Variation of displacement modes in the ellipse plate evidently differs from those of the circular plate attributing to dissimilar stiffness along x and y directions. Moreover, the ratios of major axis a to minor axis b influence the capability of the models predicting natural frequencies.

  3. (3)

    The relative stiffness of sandwich circular plate can be surely elevated by using the composite face sheets. Moreover, the relative stiffness of sandwich circular plate can be further elevated by changing the lamination configuration, which can account for the designability of sandwich plate with composite face sheets.