On the layerwise finite element formulation for static and free vibration analysis of functionally graded sandwich plates

Abstract

This paper presents a novel C⁰ higher-order layerwise finite element model for static and free vibration analysis of functionally graded materials (FGM) sandwich plates. The proposed layerwise model, which is developed for multilayer composite plates, supposes higher-order displacement field for the core and first-order displacement field for the face sheets maintaining a continuity of displacement at layer. Unlike the conventional layerwise models, the present one has an important feature that the number of variables is fixed and does not increase when increasing the number of layers. Thus, based on the suggested model, a computationally efficient C⁰ eight-node quadrilateral element is developed. Indeed, the new element is free of shear locking phenomenon without requiring any shear correction factors. Three common types of FGM plates, namely, (i) isotropic FGM plates; (ii) sandwich plates with FGM face sheets and homogeneous core and (iii) sandwich plates with homogeneous face sheets and FGM core, are considered in the present work. Material properties are assumed graded in the thickness direction according to a simple power law distribution in terms of the volume power laws of the constituents. The equations of motion of the FGM sandwich plate are obtained via the classical Hamilton’s principle. Numerical results of present model are compared with 2D, quasi-3D, and 3D analytical solutions and other predicted by advanced finite element models reported in the literature. The results indicate that the developed finite element model is promising in terms of accuracy and fast rate of convergence for both thin and thick FGM sandwich plates. Finally, it can be concluded that the proposed model is accurate and efficient in predicting the bending and free vibration responses of FGM sandwich plates.

1 Introduction

Sandwich structures are one of the most functional forms of advanced composite structures developed by engineers. They have been ubiquitously applied in modern engineering especially in the civil constructions, marine industry, automobile, aerospace applications and other industrial applications due to their excellent mechanical performances, i.e., high bending rigidity and vibration characteristics, high ratio of stiffness to weight, excellent durability. Sandwich constructions consist of two outer strong layers and an inner relatively thick, lightweight core material [1]. Sandwich structure has become even more attractive to the introduction of advanced composite materials for the face sheets like functionally graded ceramic–metal materials [2]. The considerable advantages offered by FGM over conventional composite materials are to eliminates the interface problems and thus the stress distribution becomes smooth [3]. Subsequently, a number of studies have been performed to studies the static, vibration, and buckling of functionally graded structures due to the increased relevance of the FGM structural components in the design of engineering structures [4].

For a design purpose, it is necessary to understand the mechanical behavior of FGM sandwich plates. Several computational models, both analytically and numerically, have been proposed by researchers to predict accurately the vibrational characteristics of FGM structures. Anderson [5] presented a three-dimensional (3D) analytical elasticity solution for a sandwich plates with a functionally graded (FG) core subjected to transverse loading using a rigid spherical indentor. Vel and Batra [6] proposed an exact elasticity solution using the power series expansion method to study the free and forced vibrations behaviour of simply supported FGM rectangular plates. The authors used Mori–Tanaka method to estimate the effective material properties. Li, Iu et al. [3] presented a 3D analytical elasticity solutions based on Ritz method, in conjunction with Chebhyshev polynomial series, for free vibration analysis of FGM sandwich rectangular plates. They considered two types of FGM sandwich plates with simply supported and clamped boundary conditions. Similarly, Kashtalyan and Menshykova [7] developed a 3D analytical elasticity solutions based on Plevako method for simply supported sandwich plates with a FG core. They concluded from their results that use of functionally graded core eliminates discontinuity of the in-plane normal stress across the face sheet/core interface, and reduces the magnitude of stresses in the face sheets and deflection of panels.

From the review paper of Swaminathan et al. [8], the 3D analytical elasticity solution are becomes difficult and tedious when a power law is used for the gradation of material properties. In addition, boundary value and eigenvalue problems of 3D elasticity equations are hard to solve. Hence, the development of accurate two-dimensional (2D) models has drawn a considerable amount of attention from researchers to represent accurately the behavior of FGM sandwich structures.

In the framework of 2D approaches, Equivalent Single-Layer (ESL) theories of different orders [Classical Plate Theory (CPT), First-order Shear Deformation Theory (FSDT) and Higher order Shear Deformation Theories (HSDT)] have been used. The classical plate theory based on the Kirchhoff’s assumptions ignores the transverse shear strain and is suitable only to studies thin plates/shells [9,10,11,12,13,14]. However, it is not appropriate for the moderately thick and thick plates, which require that the transverse and normal strain should be taken into account. First-order shear deformation theory considers a constant transverse shear deformation effects and gives acceptable results for thick and thin plates [15,16,17,18,19], but needs a shear correction factor which is hard to find as it depends on the geometries, material properties and boundary conditions of each problem [20]. To overcome the limitation of CLPT and FSDT, various HSDT (sinusoidal, exponential, hyperbolic, inverse-hyperbolic, and third-order shear deformation theory) were developed for a better representation of transverse shear stresses without the use of correction factors [21,22,23,24,25,26,27,28,29,30]. These theories include higher-order terms in the approximation of the in-plane displacement fields and satisfy zero shear stress conditions at top and bottom surfaces of plates.

Recently, several 2D analytical models, based on HSDT, have been performed to examine the realistic structural behavior of FGM sandwichs plates/shells. Zenkour [23, 31] investigated the static response, buckling and free vibration of a simply supported sandwich plates with FG face sheets and homogeneous core using sinusoidal shear deformation plate theory (SSDPT). Hadji et al. [32] employed a four-variable refined plate theory (RPT) to study the free vibration analysis of FGM sandwich rectangular plates. The closed form solutions are obtained by using the Navier technique. Neves et al. [33,34,35] investigated the static, free vibration and buckling analyses of FGM isotropic and sandwich plates by using various non-polynomial functions. Ye et al. [36] presented a new higher-order refined model for the static and free vibration analysis of sandwich plate with FGM soft core. Meziane et al. [37] developed an efficient and simple refined shear deformation theory for the vibration and buckling of sandwich plate resting on elastic foundations under various boundary conditions. The core layer is considered as a homogeneous material and the face sheets is assumed as FGM. The researchers used a new exponential law distribution to estimate the material properties of the sandwich plate. Nguyen et al. [38] proposed a new inverse trigonometric shear deformation theory for the static, buckling and free vibration analyses of simply supported FGM isotropic and sandwich plates. In a later study, Bennoun et al. [39] made an attempt to analyze the free vibration behavior of simply supported square FGM sandwich plates using a new five-variable refined plate theory. Recently, Meksi et al. [40] proposed a new four-variable shear deformation plate theory for the bending, buckling and free vibration responses of FGM sandwich plates. Similarly, Sayyad and Ghugal [41] presented a unified five-variable shear deformation theory for the bending analysis of a simply supported softcore and hardcore functionally graded sandwich beams and plates. More recently, a novel displacement field based on exponential-trigonometric HSDT was developed by Belkhodja et al. [42] to study the bending, free vibration, and buckling analysis of FGM plates. The material properties of the plate are estimated as power (P-FGM) and exponential (E-FGM) function. Saini and Lal [43] studied a free vibration analysis of bi-directional functionally graded circular plates subjected to two-dimensional temperature variation using FSDT.

From the previous literature review, we found that the majority of researchers used analytical models to study the behavior of FGM sandwichs plates/shells. However, the analytical approaches were limited to simple geometries, certain types of gradation of material properties (e.g., exponential or power law distribution), special loading cases and specific types of boundary conditions [44, 45]. Therefore, the numerical methods have been chosen to analyze the complex behavior of FGM structures. Among them, the finite element method (FEM) is the most popular one. The FEM has several advantages in terms of ease in implementation of complex loading, arbitrary grading properties, varying boundary conditions and ease of solution process [46, 47].

Das et al. [48] developed a C¹ triangular plate element based on HSDT for modelling thick sandwich panels with or without FG core subjected to thermo‐mechanical loading. Talha and Singh [49] developed a C⁰ continuous nine-node quadrilateral isoparametric plate element with 13 degrees-of-freedom (DOFs) for the bending and vibration analysis of FGM plates using HSDT. With a similar effort, Natarajan and Manickam [50] carried-out the static deflection and free vibration analysis of thick/thin FGM sandwich plates using a C⁰ eight nodes quadrilateral element with 13 DOFs per node on the basis of HSDT. Nguyen et al. [51] developed a new C⁰ three-node triangular element having 7 DOFs for static and vibration analysis of FGM isotropic and sandwich plates using HSDT. The formulation of this element is based on the Mixed Interpolation of Tensorial Components (MITC) approach. In the same year, a C⁰ nine-node quadrilateral plate element based on HSDT is developed by Gupta et al. [52] to determine the natural frequencies of FGM plate with various boundary conditions. The influences of volume fraction indices, geometry, material inhomogeneity and various boundary conditions on the free vibration of FGM plates were demonstrated. In another study, A hybrid-mixed, four-node, quadrilateral element for the 3D stress analysis of FGM plates is developed by Kulikov et al. [53] using the method of sampling surfaces (SaS).

Based on the above discussed literature review, it appears that a considerable number of finite element models, based on ESL theories, were used in the analysis of FGM structures. The main advantages of ESL models are their inherent simplicity and their low computational cost, due to the number of variables is independent of the number of layers. However, ESL approach fails to capture precisely the local behavior of FGM sandwich structures [54, 55]. Therefore, the use of layerwise (LW) theory, in which the DOFs are linked to specific layers, is important for accurate analyses of thin and thick FGM structures [46, 56,57,58,59,60,61,62,63]. The LW theory provides a kinematically correct representation of the strain field in discrete layers [64, 65]. Liu et al. [66] studied the free vibration analysis of FGMs sandwich plates by using a refined higher-order layerwise model with ANSYS software. The authors adopted a FSDT for the face sheets and a 3D-elasticity solution for the core. The FGM face sheets is modeled using the solid46 element, whereas the homogeneous flexible core is modeled using the solid45 element. Pandey and Pradyumna [46] presented a new high-order layerwise plate formulation for static and free vibration analyses of symmetric FGM sandwich plates. A high order displacement field is used for the middle layer and a first-order displacement field for top and bottom layers. The authors used an eight-node isoparametric element containing 104 DOFs to model the plate. The effective material properties of the FGM are computed using rule of mixture (ROM).

From the best knowledge of authors, the literature on the analysis of free vibration response of FGM sandwichs plates using LW finite element formulation is very few. Therefore, combining the advantage of ESL theories, LW theory and finite element formulation, an efficient layerwise C⁰ finite element model is presented to investigate the bending and free vibration responses of thick/thin FGM sandwichs plates. The presented model is an extension of the authors' earlier model presented in [58]. The face sheets and the core are modeled individually using, respectively, the FSDT and the HSDT. Compatibility conditions are imposed at face sheets/core interfaces to satisfy the interlaminar displacement continuity. Moreover, an eight-node quadrilateral isoparametric element with 13 DOFs per node is developed based on the proposed model. Three common types of functionally graded plates are studied: (i) isotropic FGM plates; (ii) sandwich plates with FGM face sheets and homogeneous core; (iii) sandwich plates with homogeneous face sheets and FGM core. The material properties of FGM sandwich plates are varied according to a power-law function. To assess the performance and reliability of the present layerwise FE model, several examples covering the various features such as effects of material distribution, side to-thickness ratio, aspect ratios, core-to-face thickness ratio, boundary conditions, volume fraction index, are solved for symmetric and non-symmetric FGM sandwich plates. Effects of hardcore and softcore on the non-dimensional natural frequencies are discussed as well. The author’s results are compared with those obtained using the 3D exact elasticity theory, refined analytical solutions and other advanced finite element models. Finally, the new results obtained from this study are provided as a benchmark for future investigations.

2 Theoretical formulation

2.1 Geometrical configuration

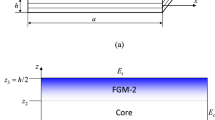
A rectangular isotropic FGM plates is considered as shown in Fig. 1. The plate has length a, width b, and thickness h. The mid-plane of the plate (z = 0) is considered as the reference plane. In the present study, three types of FGM plates are studied: (A) isotropic FGM plates; (B) sandwich plates with homogeneous face sheets and FGM core; (C) sandwich plates with FGM face sheets and homogeneous core.

Fig. 1

Geometry of a typical FGM plate (Type A)

2.1.1 Type A: isotropic FGM plates

The plate is graded from a mixture of metal and ceramic, in which the composition is varied from the top to the bottom surface (see Fig. 1). The volume fraction of the FGM plate vary along the thickness direction via a power-law function as follows [67]:

$$V_{c} {(}z{)} = \left( {\frac{2z + h}{{2h}}} \right)^{k} , \, z \in \left[ {{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2},{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right]$$

(1)

where the volume fractions of the ceramic (V_c) and the metal (V_m) phases are related by V_c + V_m = 1. k is the volume fraction index ${(}0 \le k \le + \infty {)}$ that allows the user to define gradation of material properties through the thickness direction. The value of ‘k’ equal to 0 and + ∞ represents a fully ceramic and metal plate, respectively.

2.1.2 Type B: sandwich plates with homogeneous face sheets and FGM core.

In this type, the top and bottom face sheet, of thickness (h_t) and (h_b), are made of pure ceramic and metal, respectively, while the FGM core layer, of thickness (h_c), is graded from metal to ceramic (see Fig. 2). Thus, there are no interfaces between core and face sheets.

Fig. 2

Geometry of the sandwich plate with FGM core and homogenous face sheets (Type B)

The vertical positions of the bottom surface, the two interfaces between the layers, and the top surface are denoted by h₁ = h/2, h₂, h₃, and h₄ =− h/2, respectively. The volume fraction of each component material is defined as:

$$\begin{gathered} V_{1} {(}z{)} = 1{\text{ for }}z \in \left[ {h_{3} ,h_{4} } \right],{\text{ Top face sheet;}} \hfill \\ V_{2} {(}z{)} = \left( {\frac{{z - h_{2} }}{{h_{3} - h_{2} }}} \right)^{k} {\text{ for }}z \in \left[ {h_{2} ,h_{3} } \right],{\text{ Core;}} \hfill \\ V_{3} {(}z{)} = 0{\text{ for }}z \in \left[ {h_{1} ,h_{2} } \right],{\text{ Bottom face sheet}} \hfill \\ \end{gathered}$$

(2)

Here $h_{1} = \, - \left( {h_{c} /2 \, + h_{b} } \right), \, h_{2} = \, - h_{c} /2, \, h_{3} = h_{c} /2, \, h_{4} = \, \left( {h_{t} + \, h_{c} /2} \right)$ as shown in Fig. 2.

2.1.3 Type C: sandwich plates with FGM face sheets and homogeneous core

As shown in Fig. 3, the top and bottom face sheets are assumed as FGM through the thickness direction, whereas the core is made of an isotropic homogeneous material. In this case, the volume fraction of the FGM sandwich plate can be expressed as [3, 23]:

$$\begin{gathered} V_{1} {(}z{)} = \left( {\frac{{z - h_{4} }}{{h_{3} - h_{4} }}} \right)^{k} {\text{ for }}z \in \left[ {h_{3} ,h_{4} } \right],{\text{ Top face sheet;}} \hfill \\ V_{2} {(}z{)} = 1{\text{ for }}z \in \left[ {h_{2} ,h_{3} } \right],{\text{ Core;}} \hfill \\ V_{3} {(}z{)} = \left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{k} {\text{ for }}z \in \left[ {h_{1} ,h_{2} } \right],{\text{ Bottom face sheet}} \hfill \\ \end{gathered}$$

(3)

Fig. 3

Geometry of the sandwich plate with FGM face sheets and homogenous core (Type C)

Figure 4 show the through thickness variation of the volume fraction function of the mentioned three cases of FGM plates for various values of the power law index k.

Fig. 4

Variation of volume fraction of the ceramic constituent through the thickness of three types of FGM plates for various values of the power law index k: a Type (A), b Type (B) and c Type C

2.2 Estimation of mechanical properties

The effective material properties of the plate, which are assumed to varying smoothly across the thickness direction due to a power-law distribution, are calculated using the following rule of mixture [68]:

$$P^{\left( n \right)} \left( z \right) = P_{2} + \left( {P_{1} - P_{2} } \right)V^{\left( n \right)}$$

(4)

where P⁽ⁿ⁾ (z) represents the effective material properties for each layer n (n = 1, 2, 3), viz., Young’s modulus E, Poisson’s ratio ν, and mass density $\rho$. V⁽ⁿ⁾ is the volume fraction of each layer depends on the type of FGM plate. For type B, P₁ and P₂ are the properties of the top and bottom faces of layer 1 $\left( {h_{1} \le z \le h_{2} } \right)$, respectively, and vice versa for layer 3 $\left( {h_{3} \le z \le h_{4} } \right)$ depending on the volume fraction. For type C, P₁ and P₂ are the properties of layer 3 and layer 1, respectively. For simplicity, Poisson’s ratio of plate is assumed to be constant in this study for that the effect of Poisson’s ratio on deformation is much less than that of Young’s modulus [69].

2.3 Kinematics of the present layerwise model

2.3.1 Displacement field

In the present layerwise model, the HSDT is adopted for the core layer. Hence, the displacements fields are written as a cubic pattern for the in-plane displacements, and as a constant one for the transverse displacement:

$$\begin{gathered} u_{c} = u_{0} + z\psi_{x}^{c} + z^{2} \eta_{x}^{c} + z^{3} \zeta_{x}^{c} \hfill \\ v_{c} = v_{0} + z\psi_{y}^{c} + z^{2} \eta_{y}^{c} + z^{3} \zeta_{y}^{c} \hfill \\ w_{c} = w_{0} \hfill \\ \end{gathered}$$

(5)

where u₀, v₀ and w₀ are respectively, in-plane and transverse displacement components at the mid-plane of the sandwich plate. $\psi_{x}^{c}$, $\psi_{y}^{c}$ represent normal rotations about the x and y axis, respectively. The parameters $\eta_{x}^{c}$, $\eta_{y}^{c}$, $\zeta_{x}^{c}$ and $\zeta_{y}^{c}$ are higher order terms.

The FSDT is adopted to model the top and bottom face sheet. The compatibility conditions as well as the displacement continuity between the face sheets and the core, which is assumed to be perfect, leads to the following improved displacement fields (Fig. 5):

Fig. 5

Representation of layerwise kinematics and coordinate system

• Top face sheet

$$\begin{gathered} u_{t} = u_{0} + \left( {\frac{{h_{c} }}{2}} \right)\psi_{x}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{x}^{c} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{x}^{c} + \left( {z - \frac{{h_{c} }}{2}} \right)\psi_{x}^{t} \hfill \\ v_{t} = v_{0} + \left( {\frac{{h_{c} }}{2}} \right)\psi_{y}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{y}^{c} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{y}^{c} + \left( {z - \frac{{h_{c} }}{2}} \right)\psi_{y}^{t} \hfill \\ w_{t} = w_{0} \hfill \\ \end{gathered}$$

(6)

where $\psi_{x}^{t}$ and $\psi_{y}^{t}$ are the rotations of the top face-sheet cross section about the y and x axis, respectively.

• Bottom face sheet

$$\begin{gathered} u_{b} = u_{0} - \left( {\frac{{h_{c} }}{2}} \right)\psi_{x}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{x}^{c} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{x}^{c} + \left( {z + \frac{{h_{c} }}{2}} \right)\psi_{x}^{b} \hfill \\ v_{b} = v_{0} - \left( {\frac{{h_{c} }}{2}} \right)\psi_{y}^{c} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\eta_{y}^{c} - \left( {\frac{{h_{c}^{3} }}{8}} \right)\zeta_{y}^{c} + \left( {z + \frac{{h_{c} }}{2}} \right)\psi_{y}^{b} \hfill \\ w_{b} = w_{0} \hfill \\ \end{gathered}$$

(7)

where $\psi_{x}^{b}$ and $\psi_{y}^{b}$ are the rotations of the bottom face-sheet cross section about the y and x axis, respectively.

2.3.2 Strain–displacement relations

The strain–displacement relations corresponding to any ith (i = 1, 2, 3) layer of FGM sandwich plate are given as follows:

For the core layer,

$$\begin{gathered} \varepsilon_{xx}^{c} = \frac{{\partial u_{0} }}{\partial x} + z\frac{{\partial \psi_{x}^{c} }}{\partial x} + z^{2} \frac{{\partial \eta_{x}^{c} }}{\partial x} + z^{3} \frac{{\partial \zeta_{x}^{c} }}{\partial x} \hfill \\ \varepsilon_{yy}^{c} = \frac{{\partial v_{0} }}{\partial y} + z\frac{{\partial \psi_{y}^{c} }}{\partial y} + z^{2} \frac{{\partial \eta_{y}^{c} }}{\partial y} + z^{3} \frac{{\partial \zeta_{y}^{c} }}{\partial y} \hfill \\ \gamma_{xy}^{c} = \left( {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right) + z\left( {\frac{{\partial \psi_{x}^{c} }}{\partial y} + \frac{{\partial \psi_{y}^{c} }}{\partial x}} \right) + z^{2} \left( {\frac{{\partial \eta_{x}^{c} }}{\partial y} + \frac{{\partial \eta_{y}^{c} }}{\partial x}} \right) + z^{3} \left( {\frac{{\partial \zeta_{x}^{c} }}{\partial y} + \frac{{\partial \zeta_{y}^{c} }}{\partial x}} \right) \hfill \\ \gamma_{yz}^{c} = \psi_{y}^{c} + \frac{{\partial w_{0} }}{\partial y} + 2z\eta_{y}^{c} + 3z^{2} \zeta_{y}^{c} \hfill \\ \gamma_{xz}^{c} = \psi_{x}^{c} + \frac{{\partial w_{0} }}{\partial x} + 2z\eta_{x}^{c} + 3z^{2} \zeta_{x}^{c} \hfill \\ \end{gathered}$$

(8)

For the top face sheet,

$$\begin{gathered} \varepsilon_{xx}^{t} = \frac{{\partial u_{t} }}{\partial x} = \frac{{\partial u_{0} }}{\partial x} + \left( {\frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{x}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\frac{{\partial \eta_{x}^{c} }}{\partial x} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\frac{{\partial \zeta_{x}^{c} }}{\partial x} + (z - \frac{{h_{c} }}{2})\frac{{\partial \psi_{x}^{t} }}{\partial x} \hfill \\ \varepsilon_{yy}^{t} = \frac{{\partial v_{t} }}{\partial y} = \frac{{\partial v_{0} }}{\partial x} + \left( {\frac{{h_{c} }}{2}} \right)\frac{{\partial \psi_{y}^{c} }}{\partial y} + \left( {\frac{{h_{c}^{2} }}{4}} \right)\frac{{\partial \eta_{y}^{c} }}{\partial y} + \left( {\frac{{h_{c}^{3} }}{8}} \right)\frac{{\partial \zeta_{y}^{c} }}{\partial y} + (z - \frac{{h_{c} }}{2})\frac{{\partial \psi_{y}^{t} }}{\partial y} \hfill \\ \gamma_{xy}^{t} = \frac{{\partial u_{t} }}{\partial y} + \frac{{\partial v_{t} }}{\partial x} = \left( {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right) + \frac{{h_{c} }}{2}\left( {\frac{{\partial \psi_{x}^{c} }}{\partial y} + \frac{{\partial \psi_{y}^{c} }}{\partial x}} \right) + \frac{{h_{c}^{2} }}{4}\left( {\frac{{\partial \eta_{x}^{c} }}{\partial y} + \frac{{\partial \eta_{y}^{c} }}{\partial x}} \right) \hfill \\ \, + \frac{{h_{c}^{3} }}{8}\left( {\frac{{\partial \zeta_{x}^{c} }}{\partial y} + \frac{{\partial \zeta_{y}^{c} }}{\partial x}} \right) + (z - \frac{{h_{c} }}{2})\left( {\frac{{\partial \psi_{x}^{t} }}{\partial y} + \frac{{\partial \psi_{y}^{t} }}{\partial x}} \right) \hfill \\ \gamma_{yz}^{t} = \frac{{\partial w_{0} }}{\partial y} + \psi_{y}^{t} \hfill \\ \gamma_{xz}^{t} = \frac{{\partial w_{0} }}{\partial x} + \psi_{x}^{t} \hfill \\ \end{gathered}$$

(9)

We follow the same procedure for strain–displacement relations of the bottom face sheet.

2.4 Constitutive equations

The stress–strain relationship of FGM sandwich plate, for three layers (n = 1, 2, 3), is given by:

$$\left\{ \begin{gathered} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{yz} \hfill \\ \sigma_{xz} \hfill \\ \sigma_{xy} \hfill \\ \end{gathered} \right\}^{\left( n \right)} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{21} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{44} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right]^{\left( n \right)} \left\{ \begin{gathered} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \gamma_{yz} \hfill \\ \gamma_{xz} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right\}^{\left( n \right)}$$

(10)

where Q_ij is the stiffness coefficient matrix, which are functions of coordinate z, defined as:

$$Q_{11} = Q_{22} = \frac{E\left( z \right)}{{1 - \nu^{2} \left( z \right)}}, \, Q_{12} = Q_{21} = \nu \left( z \right)Q_{11} , \, Q_{44} = Q_{55} = Q_{66} = \frac{E\left( z \right)}{{2\left( {1 - \nu \left( z \right)} \right)}}$$

For the core layer, the efforts resultants are obtained by integration of the stresses through the thickness direction of laminated plate.

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {N_{x} } & {M_{x} } & {\overline{{N_{x} }} } & {\overline{{M_{x} }} } \\ {N_{y} } & {M_{y} } & {\overline{{N_{y} }} } & {\overline{{M_{y} }} } \\ {N_{xy} } & {M_{xy} } & {\overline{{N_{xy} }} } & {\overline{{M_{xy} }} } \\ \end{array} } \right] = \int\limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\tau_{xy} } \\ \end{array} } \right\}} \left( {1,z,z^{2} ,z^{3} } \right)dz \hfill \\ \left[ {\begin{array}{*{20}c} {V_{x} } & {S_{x} } & {R_{x} } \\ {V_{y} } & {S_{y} } & {R_{y} } \\ \end{array} } \right] = \int\limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} {\left\{ {\begin{array}{*{20}c} {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right\}} \left( {1,z,z^{2} } \right)dz \hfill \\ \end{gathered}$$

(11)

where N and M denote membrane and bending moment, respectively, and $\overline{N} {\text{ and }}\overline{M}$ are the higher order moment resultants. V is the shear resultant; S and R are the higher order shear resultant.

Substituting Eq. (10) into Eq. (11) and integrating through the thickness of the plate, the stress resultants of the core are given as:

$$\left\{ {\begin{array}{*{20}c} N \\ M \\ {\overline{N} } \\ {\overline{M}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left[ A \right]} & {\left[ B \right]} & {\left[ D \right]} & {\left[ E \right]} \\ {\left[ B \right]} & {\left[ D \right]} & {\left[ E \right]} & {\left[ F \right]} \\ {\left[ D \right]} & {\left[ E \right]} & {\left[ F \right]} & {\left[ G \right]} \\ {\left[ E \right]} & {\left[ F \right]} & {\left[ G \right]} & {\left[ H \right]} \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\varepsilon^{\left( 0 \right)} } \\ {\chi^{\left( 1 \right)} } \\ {\chi^{\left( 2 \right)} } \\ {\chi^{\left( 3 \right)} } \\ \end{array} } \right\}$$

(12a)

$$\left\{ {\begin{array}{*{20}c} V \\ S \\ R \\ \end{array} } \right\} = \left[ { \begin{array}{*{20}c} {\left[ {A^{s} } \right]\left[ {B^{s} } \right]\left[ {D^{s} } \right]} \\ {\left[ {B^{s} } \right]\left[ {D^{s} } \right]\left[ {E^{s} } \right]} \\ {\left[ {D^{s} } \right]\left[ {E^{s} } \right]\left[ {F^{s} } \right]} \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\gamma_{s}^{\left( 0 \right)} } \\ {\chi_{s}^{\left( 1 \right)} } \\ {\chi_{s}^{\left( 2 \right)} } \\ \end{array} } \right\}$$

(12b)

where $\left[ {A_{ij} } \right],\, \left[ {B_{ij} } \right]$ are the elements of the reduced stiffness matrices of the core, defined by:

$$\begin{gathered} \left( {A_{ij} , B_{ij} , D_{ij } ,E_{ij} ,F_{ij} ,G_{ij} ,H_{ij} } \right) = \mathop \smallint \limits_{{\frac{{ - h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} Q_{ij} (z)\left( {1,z, z^{2} ,z^{3} ,z^{4} ,z^{5} ,z^{6} } \right)dz (i,j = 1,2,6) \hfill \\ \left( {A_{ij}^{s} , B_{ij}^{s} , D_{ij}^{s} , E_{ij}^{s} , F_{ij}^{s} } \right) = \mathop \smallint \limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} Q_{ij} (z)\left( {1,z, z^{2} ,z^{3} ,z^{4} } \right)dz (i,j = 4,5) \hfill \\ \end{gathered}$$

(13)

According to the FSDT, the constitutive equations for the two face sheets are:

$$\left\{ {\begin{array}{*{20}c} {N^{f} } \\ {M^{f} } \\ {T^{f} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A^{f} } & {B^{f} } & 0 \\ {B^{f} } & {D^{f} } & 0 \\ 0 & 0 & {A_{c}^{f} } \\ \end{array} } \right] \left\{ {\begin{array}{*{20}c} {\varepsilon_{m}^{f} } \\ {\varepsilon_{f}^{f} } \\ {\gamma_{c}^{f} } \\ \end{array} } \right\}$$

(14)

where the elements of reduced stiffness matrices of the face sheets are given by:

• Top face sheet

$$\begin{gathered} \left( {A_{ij}^{t} , B_{ij}^{t} , D_{ij}^{t} } \right) = \mathop \smallint \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{t} }} Q_{ij} (z)\left( {1,z, z^{2} } \right) \, dz (i,j = 1,2,6) \hfill \\ \left( {\overline{A}_{ij}^{t} } \right) = \mathop \smallint \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{t} }} Q_{ij} (z) \, dz \, \, (i,j = 4,5) \hfill \\ \end{gathered}$$

(15)

• Bottom face sheet

$$\begin{gathered} \left( {A_{ij}^{b} , B_{ij}^{b} , D_{ij}^{b} } \right) = \mathop \smallint \limits_{{ - \left( {\frac{{h_{c} }}{2} + h_{b} } \right)}}^{{ - \frac{{h_{c} }}{2}}} Q_{ij} (z)\left( {1,z, z^{2} } \right)dz (i,j = 1,2,6) \hfill \\ \left( {\overline{A}_{ij}^{b} } \right) = \mathop \smallint \limits_{{ - \left( {\frac{{h_{c} }}{2} + h_{b} } \right)}}^{{ - \frac{{h_{c} }}{2}}} Q_{ij} (z) \, dz \, (i,j = 4,5) \hfill \\ \end{gathered}$$

(16)

3 Finite element formulation

In the present work, a C^o eight-node isoparametric element, denoted FEM-Q8-LW, with 13 DOFs per node is developed for free vibration of functionally graded sandwich plates. This new element is formulated based on recently proposed layerwise model. Each node contains: two rotational DOFs for each face sheet, six rotational DOFs for the core, while the three translations DOFs are common for sandwich layers (Fig. 6). One of the characteristic features of the element is imposed the same transverse displacement of each layer. Hence, the number of variables is fixed and does not increase when increasing the number of layers. The proposed model can provide more accurate results for symmetric and non-symmetric thin/thick FGM sandwich plate with various boundary conditions and arbitrary FG material distribution. Further, the numerical results show that the present finite element model is free of shear locking and have a high accuracy and fast rate of convergence.

Fig. 6

Geometry and corresponding DOFs of the present element

The displacements vectors at any point of coordinates (x, y) of the plate are given by:

$$\delta \left( {x,y} \right) = \sum\limits_{i = 1}^{8} {N_{i } } \delta_{i }$$

(17)

where $\delta _{i} = \left\{ {u_{{0i}} ~~v_{{0i}} ~~~w_{{0i}} ~~~\psi _{{xi}}^{c} ~~~\psi _{{yi}}^{c} ~~~\eta _{{xi}}^{c} ~~\eta _{{yi~}}^{c} ~\zeta _{{xi}}^{c} ~~\zeta _{{yi}}^{c} ~~~\psi _{{xi}}^{t} ~~~\psi _{{yi}}^{t} ~~~\psi _{{xi}}^{b} ~~~\psi _{{yi}}^{b} } \right\}^{T}$ is the displacement vector corresponding to node i (i = 1–8). N_i are the classical serendipity interpolation functions which given as:

$$\begin{gathered} N_{1} \left( {\xi ,\eta } \right) = \frac{1}{4}\left( {1 - \xi } \right)\left( {\eta - 1} \right)\left( {\xi + \eta + 1} \right), \, N_{2} \left( {\xi ,\eta } \right) = \frac{1}{4}\left( {1 + \xi } \right)\left( {\eta - 1} \right)\left( { - \xi + \eta + 1} \right) \hfill \\ N_{3} \left( {\xi ,\eta } \right) = \frac{1}{4}\left( {1 + \xi } \right)\left( {\eta + 1} \right)\left( {\xi + \eta - 1} \right), \, N_{4} \left( {\xi ,\eta } \right) = \frac{1}{4}\left( { - 1 + \xi } \right)\left( {\eta + 1} \right)\left( {\xi - \eta + 1} \right) \hfill \\ N_{5} \left( {\xi ,\eta } \right) = \frac{1}{2}\left( {1 - \eta } \right)\left( {1 - \xi^{2} } \right), \, N_{6} \left( {\xi ,\eta } \right) = \frac{1}{2}\left( {1 - \eta^{2} } \right)\left( {1 + \xi } \right) \hfill \\ N_{7} \left( {\xi ,\eta } \right) = \frac{1}{2}\left( {1 + \eta } \right)\left( {1 - \xi^{2} } \right), \, N_{8} \left( {\xi ,\eta } \right) = \frac{1}{2}\left( {1 - \eta^{2} } \right)\left( {1 - \xi } \right) \hfill \\ \end{gathered}$$

(18)

The generalized strain vector for three layers can be expressed in terms of nodal displacements vector as follows:

$$\left\{ {\varepsilon^{(k)} } \right\} = \left[ {B_{i}^{(k)} } \right]\left\{ {\delta_{i } } \right\}$$

(19)

where the matrices $\left[ {B_{i}^{(k)} } \right]$ relate the strains to nodal displacements.

4 Governing differential equation

In this work, Hamilton’s principle is applied to formulate governing equation for the bending and free vibration analyses of FGM sandwich plate, which is given as:

$$\delta \Pi = \int\limits_{{t_{1} }}^{{t_{2} }} {\delta \left( {U + W - T} \right)dt = 0}$$

(20)

where t is the time, U is the strain energy, W is the work done due to external force and T is the kinetic energy.

The variation of strain energy of FGM sandwich plate is the summation of contribution from the two face sheets and from the core as:

$$\begin{gathered} \delta U = \int_{{A_{c} }} {\mathop \smallint \limits_{{\frac{{ - h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} \left( {\sigma_{xx}^{c} \delta \varepsilon_{xx}^{c} + \sigma_{yy}^{c} \delta \varepsilon_{yy}^{c} + \sigma_{xy}^{c} \delta \varepsilon_{xy}^{c} + \sigma_{xz}^{c} \delta \varepsilon_{xz}^{c} + \sigma_{yz}^{c} \delta \varepsilon_{yz}^{c} } \right)} \, dV_{c} \hfill \\ \, + \int_{{A_{t} }} {\mathop \smallint \limits_{{\frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2} + h_{t} }} \left( {\sigma_{xx}^{t} \delta \varepsilon_{xx}^{t} + \sigma_{yy}^{t} \delta \varepsilon_{yy}^{t} + \sigma_{xy}^{t} \delta \varepsilon_{xy}^{t} + \sigma_{xz}^{t} \delta \varepsilon_{xz}^{t} + \sigma_{yz}^{t} \delta \varepsilon_{yz}^{t} } \right)} \, dV_{t} \hfill \\ \, + \int_{{A_{b} }} {\mathop \smallint \limits_{{ - \left( {\frac{{h_{c} }}{2} + h_{b} } \right)}}^{{ - \frac{{h_{c} }}{2}}} \left( {\sigma_{xx}^{b} \delta \varepsilon_{xx}^{b} + \sigma_{yy}^{b} \delta \varepsilon_{yy}^{b} + \sigma_{xy}^{b} \delta \varepsilon_{xy}^{b} + \sigma_{xz}^{b} \delta \varepsilon_{xz}^{b} + \sigma_{yz}^{b} \delta \varepsilon_{yz}^{b} } \right)} \, dV_{b} \hfill \\ \end{gathered}$$

(21)

The work done by external transverse static load of intensity f(x, y) on j^th element is

$$\delta W = \int\limits_{A} {f(x,y)_{j} } \delta wdA$$

(22)

where f_j is the nodal load vector corresponding to jth element.

The variation of kinetic energy for an ith layer of a FGM sandwich plate can be expressed as:

$$\begin{gathered} \delta T = \int_{{V_{t} }} {\rho_{t} \left( z \right)} \left( {\ddot{u}_{t} \delta u_{t} + \ddot{v}_{t} \delta v_{t} + \ddot{w}_{t} \delta w_{t} } \right)dV_{t} \hfill \\ \, + \int_{{V_{c} }} {\rho_{c} } \left( z \right)\left( {\ddot{u}_{c} \delta u_{c} + \ddot{v}_{c} \delta v_{c} + \ddot{w}_{c} \delta w_{c} } \right)dV_{c} \hfill \\ \, + \int_{{V_{b} }} {\rho_{b} } \left( z \right)\left( {\ddot{u}_{b} \delta u_{b} + \ddot{v}_{b} \delta v_{b} + \ddot{w}_{b} \delta w_{b} } \right)dV_{b} \hfill \\ \end{gathered}$$

(23)

where u_i, v_i and w_i are the displacement in x, y and z directions, respectively, of the three-layered sandwich (i = t, c, b), ρ_i (z) are the effective density of the FGM sandwich plate, and (..) is a second derivative with respect to time.

• Kinetic energy of the core

From the displacement field of the core, defined by Eq. (5), the kinetic energy of the core can be expressed as:

$$\begin{gathered} \delta T_{c} = \int\limits_{{\Omega_{0} }} {\left[ {I_{0} \left( {\ddot{u}_{0} \delta u_{0} + \ddot{v}_{0} \delta v_{0} + \ddot{w}_{0} \delta w_{0} } \right) + I_{1} \left( {\ddot{u}_{0} \delta \psi_{x}^{c} + \ddot{\psi }_{x}^{c} \delta u_{0} + \ddot{v}_{0} \delta \psi_{y}^{c} + \ddot{\psi }_{y}^{c} \delta v_{0} } \right)} \right.} \hfill \\ \, + I_{2} \left( {\ddot{u}_{0} \delta \eta_{x}^{c} + \ddot{\psi }_{x}^{c} \delta \psi_{x}^{c} + \ddot{\eta }_{x}^{c} \delta u_{0} + \ddot{v}_{0} \delta \eta_{y}^{c} + \ddot{\psi }_{y}^{c} \delta \psi_{y}^{c} + \ddot{\eta }_{y}^{c} \delta v_{0} } \right) \hfill \\ \, + I_{3} \left( {\ddot{u}_{0} \delta \zeta_{x}^{c} + \ddot{\psi }_{x}^{c} \delta \eta_{x}^{c} + \ddot{\eta }_{x}^{c} \delta \psi_{x}^{c} + \ddot{\zeta }_{x}^{c} \delta u_{0} + \ddot{v}_{0} \delta \zeta_{y}^{c} + \ddot{\psi }_{y}^{c} \delta \eta_{y}^{c} + \ddot{\eta }_{y}^{c} \delta \psi_{y}^{c} + \ddot{\zeta }_{y}^{c} \delta v_{0} } \right) \hfill \\ \, + I_{4} \left( {\ddot{\psi }_{x}^{c} \delta \zeta_{x}^{c} + \ddot{\eta }_{x}^{c} \delta \eta_{x}^{c} + \ddot{\zeta }_{x}^{c} \delta \psi_{x}^{c} + \ddot{\psi }_{y}^{c} \delta \zeta_{y}^{c} + \ddot{\eta }_{y}^{c} \delta \eta_{y}^{c} + \ddot{\zeta }_{y}^{c} \delta \psi_{y}^{c} } \right) \hfill \\ \, + I_{5} \left( {\ddot{\eta }_{x}^{c} \delta \zeta_{x}^{c} + \ddot{\zeta }_{x}^{c} \delta \eta_{x}^{c} + \ddot{\eta }_{y}^{c} \delta \zeta_{y}^{c} + \ddot{\zeta }_{y}^{c} \delta \eta_{y}^{c} } \right) + I_{6} \left. {\left( {\ddot{\zeta }_{x}^{c} \delta \zeta_{x}^{c} + \ddot{\zeta }_{y}^{c} \delta \zeta_{y}^{c} } \right)} \right]dxdy \hfill \\ \end{gathered}$$

(24)

where the inertia moments of the core I_i = (i = 0–6) are defined by:

$$\left( {I_{0} , I_{1} , I_{2} ,I_{3} ,I_{4} ,I_{5} ,I_{6} } \right) = \mathop \smallint \limits_{{\frac{{ - h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} \rho_{c} \left( z \right)\left( {1,z, z^{2} ,z^{3} ,z^{4} ,z^{5} ,z^{6} } \right)dz$$

(25)

We follow the same procedure for kinetic energy of the face sheets.

For linear static analysis, the equilibrium equation can be expressed as follows:

$$\left[ K \right] = \left\{ \delta \right\}\left\{ F \right\}$$

(26)

where {F} and [K_e] are the load vector and the element stiffness matrix of the plate, respectively.

For free vibration problem, the work done by external forces and the damping are neglected. The Hamilton’s principle (Eq. 20) leads to the following dynamic equilibrium equation of a system.

$$\left[ {M_{e} } \right]\left\{ {\ddot{\delta }} \right\} + \left[ {K_{e} } \right]\left\{ \delta \right\} = 0$$

(27)

where [M_e] and [K_e] denote the total element mass matrix and the total element stiffness matrix respectively, which are computed using the Gauss numerical integration.

The total element stiffness matrix is the summation of contribution from the two face sheets and from the core as:

$$\left[ {K_{e} } \right] = \left[ {K_{e}^{\left( t \right)} } \right] + \left[ {K_{e}^{\left( c \right)} } \right] + \left[ {K_{e}^{\left( b \right)} } \right]$$

(28)

where the element stiffness matrix of the two face sheet is given by:

• a. Top face sheet:

$$\begin{gathered} \left[ {K_{e}^{\left( t \right)} } \right] = \iint {\left( {\underbrace {{\left[ {B_{m}^{t} } \right]^{T} \left[ {A^{\left( t \right)} } \right]\left[ {B_{m}^{t} } \right]}}_{{\text{ membrane}}}} \right.} + \underbrace {{\left[ {B_{m}^{t} } \right]^{T} \left[ {B^{\left( t \right)} } \right]\left[ {B_{f}^{t} } \right]}}_{{\text{coupling membrane - bending}}} + \underbrace {{\left[ {B_{f}^{t} } \right]^{T} \left[ {B^{\left( t \right)} } \right]\left[ {B_{m}^{t} } \right]}}_{{\text{coupling bending - membrane}}} \hfill \\ { + }\underbrace {{\left[ {B_{f}^{t} } \right]^{T} \left[ {D^{\left( t \right)} } \right]\left[ {B_{f}^{t} } \right]}}_{{{\text{bending}}}} + \left. {\underbrace {{\left[ {B_{s}^{t} } \right]^{T} \left[ {A_{c}^{\left( t \right)} } \right]\left[ {B_{s}^{t} } \right]}}_{{{\text{shear}}}}} \right)dA \hfill \\ \end{gathered}$$

(29)

• b. Bottom face sheet:

$$\begin{gathered} \left[ {K_{e}^{\left( b \right)} } \right] = \iint {\left( {\underbrace {{\left[ {B_{m}^{b} } \right]^{T} \left[ {A^{\left( b \right)} } \right]\left[ {B_{m}^{b} } \right]}}_{{\text{ membrane}}}} \right.} + \underbrace {{\left[ {B_{m}^{b} } \right]^{T} \left[ {B^{\left( b \right)} } \right]\left[ {B_{f}^{b} } \right]}}_{{\text{coupling membrane - bending}}} + \underbrace {{\left[ {B_{f}^{b} } \right]^{T} \left[ {B^{\left( b \right)} } \right]\left[ {B_{m}^{b} } \right]}}_{{\text{coupling bending - membrane}}} \hfill \\ { + }\underbrace {{\left[ {B_{f}^{b} } \right]^{T} \left[ {D^{\left( b \right)} } \right]\left[ {B_{f}^{b} } \right]}}_{{{\text{bending}}}} + \left. {\underbrace {{\left[ {B_{s}^{b} } \right]^{T} \left[ {A_{c}^{\left( b \right)} } \right]\left[ {B_{s}^{b} } \right]}}_{{{\text{shear}}}}} \right)dA \hfill \\ \end{gathered}$$

(30)

For the core, the element stiffness matrix can be written as:

$$\begin{gathered} \left[ {K_{e}^{\left( c \right)} } \right] = \iint {\left( {\left[ {B_{\varepsilon }^{\left( 0 \right)} } \right]^{T} \left[ A \right]\left[ {B_{\varepsilon }^{\left( 0 \right)} } \right]} \right. + \left[ {B_{\varepsilon }^{\left( 0 \right)} } \right]^{T} \left[ B \right]\left[ {B_{\chi }^{\left( 1 \right)} } \right] + \left[ {B_{\varepsilon }^{\left( 0 \right)} } \right]^{T} \left[ D \right]\left[ {B_{\chi }^{\left( 2 \right)} } \right]} \hfill \\ \, + \left[ {B_{\varepsilon }^{\left( 0 \right)} } \right]^{T} \left[ E \right]\left[ {B_{\chi }^{\left( 3 \right)} } \right] + \left[ {B_{\chi }^{\left( 1 \right)} } \right]^{T} \left[ B \right]\left[ {B_{\varepsilon }^{\left( 0 \right)} } \right] + \left[ {B_{\chi }^{\left( 1 \right)} } \right]^{T} \left[ D \right]\left[ {B_{\chi }^{\left( 1 \right)} } \right] \hfill \\ \, + \left[ {B_{\chi }^{\left( 1 \right)} } \right]^{T} \left[ E \right]\left[ {B_{\chi }^{\left( 2 \right)} } \right] + \left[ {B_{\chi }^{\left( 1 \right)} } \right]^{T} \left[ F \right]\left[ {B_{\chi }^{\left( 3 \right)} } \right] + \left[ {B_{\chi }^{\left( 2 \right)} } \right]^{T} \left[ D \right]\left[ {B_{\varepsilon }^{\left( 0 \right)} } \right] \hfill \\ \, + \left[ {B_{\chi }^{\left( 2 \right)} } \right]^{T} \left[ E \right]\left[ {B_{\chi }^{\left( 1 \right)} } \right] + \left[ {B_{\chi }^{\left( 2 \right)} } \right]^{T} \left[ F \right]\left[ {B_{\chi }^{\left( 2 \right)} } \right] + \left[ {B_{\chi }^{\left( 2 \right)} } \right]^{T} \left[ L \right]\left[ {B_{\chi }^{\left( 3 \right)} } \right] \hfill \\ \, + \left[ {B_{\chi }^{\left( 3 \right)} } \right]^{T} \left[ E \right]\left[ {B_{\varepsilon }^{\left( 0 \right)} } \right] + \left[ {B_{\chi }^{\left( 3 \right)} } \right]^{T} \left[ F \right]\left[ {B_{\chi }^{\left( 1 \right)} } \right] + \left[ {B_{\chi }^{\left( 3 \right)} } \right]^{T} \left[ L \right]\left[ {B_{\chi }^{\left( 2 \right)} } \right] \hfill \\ \, + \left[ {B_{\chi }^{\left( 3 \right)} } \right]^{T} \left[ H \right]\left[ {B_{\chi }^{\left( 3 \right)} } \right] + \left[ {B_{{\gamma_{s} }}^{\left( 0 \right)} } \right]^{T} \left[ {A^{s} } \right]\left[ {B_{{\gamma_{s} }}^{\left( 0 \right)} } \right] + \left[ {B_{{\gamma_{s} }}^{\left( 0 \right)} } \right]^{T} \left[ {B^{s} } \right]\left[ {B_{{\chi_{s} }}^{\left( 1 \right)} } \right] \hfill \\ \, + \left[ {B_{{\gamma_{s} }}^{\left( 0 \right)} } \right]^{T} \left[ {D^{s} } \right]\left[ {B_{{\chi_{s} }}^{\left( 2 \right)} } \right] + \left[ {B_{{\chi_{s} }}^{\left( 1 \right)} } \right]^{T} \left[ {B^{s} } \right]\left[ {B_{{\gamma_{s} }}^{\left( 0 \right)} } \right] + \left[ {B_{{\chi_{s} }}^{\left( 1 \right)} } \right]^{T} \left[ {D^{s} } \right]\left[ {B_{{\chi_{s} }}^{\left( 1 \right)} } \right] \hfill \\ \, + \left[ {B_{{\chi_{s} }}^{\left( 1 \right)} } \right]^{T} \left[ {E^{s} } \right]\left[ {B_{{\chi_{s} }}^{\left( 2 \right)} } \right] + \left[ {B_{{\chi_{s} }}^{\left( 2 \right)} } \right]^{T} \left[ {D^{s} } \right]\left[ {B_{{\gamma_{s} }}^{\left( 0 \right)} } \right] + \left[ {B_{{\chi_{s} }}^{\left( 2 \right)} } \right]^{T} \left[ {E^{s} } \right]\left[ {B_{{\chi_{s} }}^{\left( 1 \right)} } \right] \hfill \\ \, + \left. {\left[ {B_{{\chi_{s} }}^{\left( 2 \right)} } \right]^{T} \left[ {F^{s} } \right]\left[ {B_{{\chi_{s} }}^{\left( 2 \right)} } \right]} \right)dA \hfill \\ \end{gathered}$$

(31)

The total element mass matrix, for the three-layer sandwich plate, can be written as

$$\left[ {M_{e} } \right] = \iint {\left( {\left[ N \right]^{T} \left[ {m^{(t)} } \right]\left[ N \right] + \left[ N \right]^{T} \left[ {m^{(c)} } \right]\left[ N \right]{ + }\left. {\left[ N \right]^{T} \left[ {m^{(b)} } \right]\left[ N \right]} \right)} \right. \, dA}$$

(32)

where $\left[ {m^{(t)} } \right]$, $\left[ {m^{(c)} } \right]$ and $\left[ {m^{(b)} } \right]$ are the consistent mass matrices of the top face sheet, core and the bottom face sheet, respectively, containing inertia terms.

Now, after evaluating the stiffness and mass matrices for all elements, the governing equations for free vibration analysis of FGM sandwich plate can be stated in the form of generalized eigenvalue problem.

$$\left[ K \right]\left\{ \chi \right\} - \omega^{2} \left[ M \right]\left\{ \chi \right\} = 0$$

(33)

where, ω denote the natural frequency, [K] is he global stiffness matrix, [M] is the global mass matrix, $\left\{ \chi \right\}$ are the vectors defining the mode shapes.

5 Numerical results and discussions

In this section, several numerical examples are presented and discussed to demonstrate the accuracy and robustness of the developed layerwise FE model in predicting the bending and free vibration responses of functionally graded sandwich plates. A wide range of comparison and convergence studies are presented with 2D/3D elasticity solutions and others finite elements numerical results found in the literature. The effect of different materials and geometric parameters with arbitrary boundary conditions are carried-out in the present study. The applied boundary conditions and the material properties of FGM plates, considered for all examples, are illustrated in Tables 1 and 2, respectively.

Table 1 Boundary conditions used in the present study

Table 2 Material properties used in the FG plate

Several kinds of FGM sandwich plates are considered for presenting the numerical results.

• The (1-1-1) FGM sandwich plate: the plate is symmetric and made of three equal-thickness layers.

• The (1-0-1) FGM sandwich plate: the plate is symmetric and made of two layers of equal thickness without a core.

• The (2-1-2) FGM sandwich plate: the core has half the thickness of the functionally graded face sheets.

• The (1-2-1) FGM sandwich plate: the functionally graded face sheets have half the thickness of the core.

• The (2-1-1) FGM sandwich plate: the plate is non-symmetric and here the core thickness equals the top face thickness while it is half the bottom face thickness.

• The (1-8-1) FGM sandwich plate: the core is eight times thicker than the individual face sheets.

5.1 Bending analysis

To verify the robustness and the accuracy of the proposed layerwise finite element formulation, it is necessary to validate it in the static analysis.

Example 1

In the first example, the convergence test of the developed finite element is carried out for a square isotropic FGM plate subjected to uniformly distributed load. The single layered is made of aluminum and zirconia (Al/ZrO₂) and their corresponding material properties are provided in Table 1. The top surface of FGM plate is ceramic-rich and the bottom surface is metal-rich. The study is performed for different volume fraction index (k) and boundary conditions with side-to-thickness ratio a/h = 5. The convergence of non-dimensional center deflections is reported in Table 3 for different mesh sizes (4 × 4, 6 × 6 and 8 × 8). The obtained results are compared with moving kriging (MK) meshfree methods based on HSDT [70], such as third shear deformation plate theory (TSDT), exponential shear deformation plate theory (ESDT) and inverse trigonometric shear deformation plate theory (ITSDT); and another HSDT model [71] using more variables (18 DOFs/node). It is clear, for all the boundary conditions and the volume fraction index (k), that the present results are in good agreement with the existing solutions, as shown in Table 3. Thus, the performance of present finite element formulation is confirmed in terms of both accuracy and rate of convergence. Moreover, it can be clear, for all the applied boundary conditions (SFSF, SSSS and CCCC) that increasing the volume fraction index (k) results in an increase the central deflection (see Fig. 7). This behaviour is expected because the larger volume fraction index means the plate has a smaller ceramic component whose Young's modulus is greater than that of metal and hence, the stiffness is reduced. In addition, it is evident that the central deflection decreases as the rigidity of boundary restraint is increased.

Table 3 Non-dimensional center deflections ($\overline{w}$) of Al/ZrO₂ FGM square plate subjected to uniformly distributed load with different boundary conditions and volume fraction index (k)

Fig. 7

Effects of volume fraction index (k) with different boundary conditions on the non-dimensional center deflexion of Al/ZrO₂ FGM square plate subjected to uniformly distributed load (a/h = 5)

Example 2.

This example is performed for symmetric and non-symmetric square FGM sandwich plate of type C. The face sheets are assumed to be made of FGM layers. The bottom face sheet are graded from metal to ceramic (Al/ZrO₂) and the core layer is made of pure ceramic (ZrO₂). The plate is fully clamped along their sides (CCCC) and subjected to sinusoidal load, q = q₀ sin (πx/a) sin (πy/b). For the current study, five different core-to-face sheets thickness ratio h_b-h_c-h_t (1–0-1, 2–1-2, 1–1-1, 2–2-1, 1–2-1), three side-to-thickness ratio a/h (5, 10, 100) and four volume fraction index k (0, 1, 5, 10) are considered. From the previous example, it is evident that a (6 × 6) mesh has been found to give good convergence for this type of plates. Therefore, this mesh size is employed in the present analysis. The non-dimensional center deflections are presented in Table 4. The present results are compared with triangular element model (MITC3) of Nguyen et al. [40] using HSDT and those obtained by Pluciński and Jaśkowiec [61] using 3D finite elements models (FEM23-1, ABAQUS). A good agreement between the results is obtained for all schemes, volume fraction index and both thin and thick FGM sandwich plates. Further, it should be noted that the developed element is free from shear locking phenomena where it is able to provide excellent results for thin FGM sandwich plate (a/h = 100). Figure 8 show the variation of the non-dimensional deflection with varying volume fraction index (k). In addition, the effect of volume fraction index (k) on the non-dimensional central deflection for different core-to-face sheets thickness ratio (h_c/h_f) is illustrated in Fig. 9. It can be seen that the lowest and highest values of deflection correspond to the (1-0-1) and (1-2-1) FGM sandwich plate, respectively. For the case of (1-2-1) plate, it is observed that as the core thickness increases, the deflection value decreases. This is due to high proportion of ceramic which leads the plate to be more rigid.

Table 4 Non-dimensional center deflections ($\overline{w}$) of clamped square sandwich plates with Al/ZrO₂ FGM face sheets subjected to sinusoidally distributed load

Fig. 8

Variation of the non-dimensional deflection of clamped square 1-0-1 FGM sandwich plate of type C subjected to sinusoidal load for different volume fraction index (k)

Fig. 9

Effect of volume fraction index (k) with different core-to-face sheets thickness ratio on the non-dimensional center deflexion of clamped square sandwich plates with FGM face sheets (a/h = 10)

5.2 Free vibration analysis

The robustness of the present layerwise finite element formulation is also verified for free vibration analysis of functionally graded sandwich plates.

Example 3

For the verification purpose, the convergence of developed finite element model is examined for thin and thick square isotropic FGM (Al^*/ZrO₂) plate. The plate is simply supported on all four sides. In the present analysis, different side-to-thickness ratio (a/h) and volume fraction index (k) are considered. The non-dimensional natural frequencies is reported in Table 5 using different mesh sizes (4 × 4, 6 × 6 and 8 × 8). The present results are compared with the 3D-elasticity solutions [72], the analytical results based on HSDT [42] as well as finite element solutions [51]. The comparison shows that the performance of the present finite element formulation, for both thin and thick FGM plates, is very good in terms of the efficiency and the rate of convergence with mesh refinement. Indeed, for moderately thick plate (a/h = 10), the maximum percentage error predicted by present element in comparison with 3D-Exact elasticity solution of Uymaz and Aydogdu [72], is 0.0287%, 0.0181%, 0.0939%, 0.0000% with respect to the volume fraction index (k) of 0.5, 1, 2 and 5. For thin plate (a/h = 100) with k = 0.1, the maximum percentage error is about 0.0773% for the present model and 0.7417% for Nguyen model [40] when compared with the exact 3D dimensional solution [72]. Furthermore, the effect of side-to-thickness ratio (a/h) and volume fraction index (k) on the fundamental natural frequency is illustrated in Fig. 10. It can be seen that the fundamental natural frequency increases with increased side-to-thickness ratio (a/h) up to a/h = 20 and then varies constantly in all cases. This probably can be explained by the effect of shear deformation which is less significant when the thickness decreases (a/h > 20). To conclude, the non-dimensional fundamental frequency of thick FGM sandwich plates is more sensitive side-to-thickness ratio than that of thin ones. Besides, by increasing the volume fraction index (k), the fundamental natural frequency decreases. This is due to the reduction of the rigidity of plate because of the high proportion of metal. This latter having a Young's modulus lower than that of ceramic.

Table 5 Non-dimensional fundamental frequency ($\overline{\omega }$) of simply supported square Al^∗/ZrO₂ FGM plates

Fig. 10

Effect of side-to-thickness ratio (a/h) with volume fraction index (k) on the non-dimensional fundamental frequency of clamped square sandwich plates with FGM face sheets

Example 4

In the 4th example, a rectangular FGM plate made of aluminum (Al) and alumina (Al₂O₃) is studied for different volume fraction index and side-to-thickness ratio. Both square (b = a) and rectangular (b = 2a) plates are considered. Numerical results have been obtained for six different combinations of symmetric (SSSS, SCSC, SFSF) and asymmetric (SCSF, SSSC, SSSF), boundary conditions. Based on the convergence study, a mesh size with 6 × 6 elements is sufficient to obtain an accurate results. The comparison results presented in Table 6 and in Fig. 11 show the accuracy of the developed element where one can see clearly, for all types of boundary conditions, that the present results are in excellent agreement with the 3D-Exact elasticity solutions of Jin et al. [73]. Indeed, for b/a = 2, a/h = 10 and k = 5, the maximum percentage error of fundamental frequency under boundary conditions SSSS, SCSC, SFSF, SCSF, SSSC, and SSSF when compared with the 3D-Exact elasticity solution [73] is 0.2335, 0.5395, 0.0538, 0.1759, 0.3862 and 0.0000, respectively. Further, the excellent accuracy of the new element is insensitive to boundary conditions. In addition, it can be observed, for both square and rectangular FGM plates, that the lowest fundamental natural frequency is observed for SSSF, SFSF and SCSF boundary conditions, while the highest fundamental natural frequency is seen for SCSC and SSSC boundary conditions, as shown in Fig. 11. Generally speaking, the natural frequencies increase as the rigidity of boundary restraint is increased.

Table 6 Non-dimensional fundamental frequency ($\overline{\omega }$) of rectangular Al/Al₂O₃ FGM plates with different boundary conditions

Fig. 11

Effect of aspect ratio (b/a) with different boundary conditions on the non-dimensional fundamental frequency of Al/ Al₂O₃ FGM plate (a/h = 10, k = 5)

Example 5

After establishing the performance of present model for isotropic FGM plates, the free vibration analysis of square sandwich plates with FGM face sheets and homogenous core (Type C) is examined in this example. The plate is simply supported on all four sides. The present study is performed for two cases of FGM sandwich plates, namely, hardcore and softcore. In the case of hardcore, the bottom face sheet is graded from ceramic to metal (Al₂O₃/Al) and the core layer is made of pure metal (Al). For the case of softcore, the plate is made of pure ceramic core (Al₂O₃) and the upper and lower surfaces of the bottom face sheet are rich in metal and ceramic (Al/Al₂O₃), respectively. The computed results are obtained for five different core-to-face sheets thickness ratio h_b-h_c-h_t (1-0-1, 2-1-2, 1-1-1, 1-2-1, 1-8-1), three side-to-thickness ratio a/h (5, 10, 100) and five volume fraction index k (0, 0.5, 1, 5, 10). A mesh size of 6 × 6 is considered for the analysis. The accuracy of the developed finite element, for both hardcore and softcore, can be seen, respectively, in Table 7 and 8. One can see clearly that the present results are very close to those of 3D-elasticity solutions of Li, Iu et al. [3], the finite element model of Pandey and Pradyumna [37] and the meshless solution based on spline radial basis function by Xiang et al. [74]. It can be clearly seen, from these results, that the non-dimensional fundamental frequencies for hardcore FGM sandwich plates decreased with an increase in volume fraction index (see Fig. 12), whereas the opposite nature of variation in non-dimensional fundamental frequencies is observed for softcore FGM sandwich plates (see Fig. 13). This is due to the difference in stiffness parameters due to change in material properties. It is also pointed out that, for hardcore FGM sandwich plates, the non-dimensional fundamental frequencies is maximum for (1-8-1) plate and minimum for (1-0-1) plate, whereas for softcore FGM sandwich plates, the non-dimensional fundamental frequencies reaches its maximum for (1-0-1) plate and minimum for (1-8-1) plate.

Table 7 Non-dimensional fundamental frequency ($\overline{\omega }$) of simply supported square FGM sandwich plates with homogeneous hardcore

Table 8 Non-dimensional fundamental frequency ($\overline{\omega }$) of simply supported square FGM sandwich plates with homogeneous softcore

Fig. 12

Effect of volume fraction index (k) with different core-to-face sheets thickness ratio on the non-dimensional fundamental frequency of hardcore FGM sandwich plates (a/h = 10)

Fig. 13

Effect of volume fraction index (k) with different core-to-face sheets thickness ratio on the non-dimensional fundamental frequency of softcore FGM sandwich plates (a/h = 10)

Example 6

To check the higher order modes of vibration, a square FGM sandwich plate of type C is invistigated with ℎ_t-ℎ_c-ℎ_b = 2-1-2. The bottom face sheet iso graded from metal to ceramic (Al/Al₂O₃) and the core is made a fully ceramic material (Al₂O₃). Two different boundary conditions (SSSS and CCCC) with two side-to-thickness ratio (a/h = 10 and 100) and volume fraction index (k = 1 and 10) are considered in the present study. The non-dimensional natural frequencies of the first-five mode shapes are shown in Table 9. Based on the convergence study, a mesh size with 8 × 8 elements is sufficient to obtain good results. The obtained results are compared with the 3D-elasticity solutions [3] and various numerical results found in the literature, such as, the eight nodes quadrilateral finite element model based on HSDT [50], the meshfree solution based on TSDT [70] and the isogeometric results (IGA) based on four-unknown shear and normal deformations theory (SNDT) [22]. It is evident from the results of comparison that the proposed finite element model agree very well with both the 3D-elasticity solutions [52] and the numerical models available in the literature. Further, the developed element is free from transverse shear locking, and its excellent accuracy is insensitive to thin FGM sandwich plates. The first six flexural mode shapes of a simply supported FGM sandwich plates of type C, are plotted in Fig. 14 for a/h = 10 and k = 1.

Fig. 14

First six flexural mode shapes of a simply supported FGM sandwich plates of type C. (a/h = 10 and k = 1)

Table 9 First five non-dimensional fundamental frequency ($\overline{\omega }$) of square 2-1-2 FGM sandwich plates (Al/Al₂O₃) of type C with two different boundary conditions

Example 7

After studying the free vibration of sandwich plate with FGM face sheets, a simply supported square sandwich plate with FGM core and homogenous face sheets (Type B) is analyzed with ℎ_t-ℎ_c-ℎ_b = 1-8-1 (h₂ = 0.8 h and h₁ = h₃ = 0.1). The top and bottom face sheets are made of pure metal (Al) and ceramic (Al₂O₃), respectively, whereas the FGM core layer is graded from ceramic to metal (Al₂O₃/Al). Three values of side-to-thickness ratio (a/h = 5, 10, 100) with five different volume fraction index (k = 0.5, 1, 2, 5, 10) are considered for the investigation. The non-dimensional fundamental frequencies predicted by the present layerwise model are listed in Table 10 with different mesh size (4 × 4, 6 × 6 and 8 × 8). For comparison purposes, 3D-elasticity solutions derived by Li et al. [3], hyperbolic higher order shear deformation theory (HHSDT) computed by Bennoun, Houari et al. [39], semi analytical solutions based on differential quadrature method (DQM) given by Alibeigloo and Alizadeh [75] as well as those obtained by Pandey and Pradyumna [46] using layerwise finite element solutions, are carried out. According the Table 9, it can be observed that the obtained result, for all cases presented, are in excellent agreement with reported literature values and even more accurate than those predicted by the analytical solutions of Bennoun, Houari et al. [39] using HHSDT. For example, with a/h = 100, the maximum error predicted by present model, when compared with exact 3D-elasticity solutions [3], is only 0.0223%, 0.0288%, 0.0069%, 0.0391%, 0.0000%, with respect to the volume fraction index (k) of 0.5, 1, 2, 5,10, whereas the maximum error of the HHSDT model [39] is 2.3146%, 2.1779%, 1.6956%, 0.9599%, 0.5971%. As expected, the comparison confirms the high accuracy of the developed layerwise model. It can be concluded that the proposed finite element formulation is not only accurate but also simple in predicting the natural frequencies of FGM sandwich plates. Moreover, it can be clear from Table 10 that the fundamental natural frequency of FGM sandwich plate of type B increase when the values of volume fraction index (k) changes from 0.5 to 10.

Table 10 Non-dimensional natural frequency ($\overline{\omega }$) of simply supported sandwich plate 1-8-1 with FGM core (Type B, Al₂O₃/Al)

6 Conclusion

In the current study, for the first time, the original layerwise formulation has been generalized to predict accurately the deflection and natural frequency of functionally graded sandwich plates. The proposed model assumes a first-order shear deformation theory in the face sheets and a higher-order displacement field in the core maintaining a continuity of displacement at layer. Three common types of FGM plates have been taken into consideration: (i) isotropic FGM plates; (ii) sandwich plates with FGM face sheets and homogeneous core and (iii) sandwich plates with homogeneous face sheets and FGM core. Based on the suggested model, an improved C⁰ eight-node quadrilateral element has been successfully developed. Several numerical examples have been performed to assess the performance and reliability of the developed layerwise finite element model. The obtained results have been compared with 3D, quasi-3D, and 2D analytical solutions and those predicted by advanced finite element models available in the literature. The comparison showed that the result accuracy, fast rate of convergence and broad range of applicability of the proposed finite element model, for both thin and thick FGM isotropic and sandwich plates, are excellent. Furthermore, the effects of volume fraction index, material distribution, side-to-thickness ratio, aspect ratios, core-to-face thickness ratio, type of core (hard/soft), frequency modes, and boundary conditions on the natural frequency have been all investigated and reported. From the numerical illustration, the key points of the present study are the following:

• The combination between both equivalent single layer approach and layerwise approach is very advantageous, because the result of present model combines the features of both approaches, which are the simplicity and the accuracy. Thus, the plate theory enjoys the advantage of a single-layer plate theory, even though it is based on the concept of a layerwise plate approach.

• From a computational cost point of view, it is important to mention here that the proposed layerwise finite element formulation needs only C⁰ shape functions that contributes to a noticeable decrease of computational efforts.

• The developed finite element is free of shear locking phenomenon without requiring any shear correction factors.

• The non-dimensional deflection increases with the increase of the volume fraction index (k).

• The natural frequency increases with the increase of side-to-thickness ratio (a/h) up to a/h ≤ 20 while further increasing this ratio (a/h > 20) has no remarkable effect on the natural frequency.

• The natural frequency of thick FGM sandwich plates is more sensitive side-to-thickness ratio (a/h) than that of thin ones.

• For all types of boundary conditions, the natural frequency decreases by increasing the volume fraction index (k) and the plate’s aspect ratio (b/a).

• The lowest natural frequency is observed for SSSF, SFSF and SCSF boundary conditions, while the highest fundamental natural frequency is seen for SCSC and SSSC boundary conditions. Hence, the natural frequency increases as the rigidity of boundary restraint is increased.

• The natural frequency for hardcore FGM sandwich plates decreased with an increase in volume fraction index (k), whereas the opposite nature of variation in natural frequency is observed for softcore FGM sandwich plates.

• For hardcore FGM sandwich plates, the natural frequency is maximum for (1-8-1) plate and minimum for (1-0-1) plate, whereas for softcore FGM sandwich plates, the natural frequency reaches its maximum for (1-0-1) plate and minimum for (1-8-1) plate.

• In the case of sandwich plate with FGM core, the natural frequency increases when the values of volume fraction index (k) changes from 0.5 to 10.

It is concluded that the present layerwise finite element model is not only accurate, but also simple in solving the free vibration problems for all types of FGM sandwich plates.