Analytical layerwise free vibration analysis of circular/annular composite sandwich plates with auxetic cores

Abstract

In the present research, free vibration of circular and annular sandwich plates with auxetic (negative Poisson’s ratio) cores and isotropic/orthotropic face sheets is investigated for different combinations of the boundary conditions. To ensure that the results are accurate and reliable, a global–local layerwise plate theory is employed instead of the traditional equivalent single-layer theories. The governing equations are derived based on Hamilton’s principle and solved using a Taylor transform whose center is located at the outer radius of the plate. Due to this hint, the resulting semi-analytical solution can be employed for both circular and annular sandwich plates. After investigation of vibration behavior of a single-layer annular auxetic plate, a comprehensive parametric study including evaluation of effects of the auxeticity for sandwich plates with isotropic and orthotropic face sheets, symmetric and asymmetric layups, different core to sheet thickness, radius to thickness, and inner to outer radius ratios, and various boundary conditions, is carried out. Results show that unlike the single-layer auxetic plates that exhibit a transition state, the auxeticity may considerably increase the natural frequencies and rigidities of the circular/annular sandwich plates, especially when the boundary conditions induce higher rigidity in the plate or when the fibers are along the radial direction. Accuracy of results of the employed layerwise theory and the proposed semi-analytical solution is verified by comparing the results with those of the three-dimensional theory of elasticity extracted from the ABAQUS software.

1 Introduction

While rectangular plates have commonly been used for relatively fixed structural components, plates with circular or annular configurations have been the most appropriate choice for plates with continuous (e.g., power train transmission plates or discs) or partial (e.g., supporting or rotating tables) rotations or when less energy dissipation (e.g., heat transfer) is of concern. These types of plates may be fabricated in three-layer sandwich constructions with different layer material properties to satisfy a diversity of purposes; so that depending on the design requirements, the core may be either more rigid or more compliant than the isotropic/orthotropic face sheets. Various studies have been performed on annular single layer and sandwich plates based on the three-dimensional theory of elasticity and plate theories, using different solution procedures (So and Leissa 1998; Tornabene et al. 2009; Malekzadeh et al. 2010a, b; Tajeddini et al. 2011; Zhou et al. 2003).

Apart from the researches that have been accomplished based on the traditional equivalent single-layer plate theories, some more accurate researches have been developed for the single-layer circular and annular plates. Zhou et al. (2003) and Dong (2008) investigated three-dimensional free vibration of annular plates with different boundary conditions using Chebyshev-Ritz method. Liew and Yang (2000) and Hosseini Hashemi et al. (2008) employed Ritz method for three-dimensional free vibration analysis of thick annular plates with different edge conditions. Malekzadeh et al. (2010a, b) studied free vibration of thick laminated circular and annular plates supported by elastic foundations, using a three-dimensional layerwise-finite element method.

Very limited researches have been presented so far on vibration of the sandwich circular or annular plates. Lee et al. (1998) analyzed free vibration and transient dynamic responses of a rotating multi-layer annular plate using the finite element method. The governing equations of motion were derived using a zigzag theory with a higher-order shear-deformation global and a linear local displacement fields. Alipour and Shariyat have presented numerous studied on the sandwich circular and annular plates. Alipour and Shariyat (2012, 2013a, 2014a) and Shariyat and Alipour (2013) have shown that results of the traditional single-layer plate theories may be erroneous, even for the simple cases. For this reason, they proposed zigzag and layerwise theories with local and global components for static and dynamic deformation and stress distributions of the sandwich plates, using corrections based on the three-dimensional theory of elasticity. Alipour and Shariyat (2014b) studied vibration of annular functionally graded sandwich plates supported by non-uniform elastic foundations. Finally, Shariyat and Alipour (2012, 2014, 2015) proposed the concept of local correction factors for functionally graded viscoelastic circular, functionally graded annular, and functionally graded sandwich plates.

Power series solutions were employed by some researchers for different analyses of the circular plates (Alipour et al. 2010). On the basis of the power series solutions, Alipour and Shariyat investigated buckling loads and stresses (2010, 2011, 2013b) of heterogeneous/viscoelastic variable thickness circular plates resting on elastic foundations and axisymmetric bending of the functionally graded circular/annular sandwich plates (Alipour et al. 2010; Alipour and Shariyat 2012, 2013a, 2014a; Shariyat and Alipour 2013) based on the differential transform method. Moreover, the differential transform method was employed by Shariyat and Alipour (2011) for free vibration and modal analyses of circular plates made of bidirectional functionally graded materials. Using the differential transform technique, Lal and Ahlawat (2015) have recently studied vibration and buckling of the functionally graded circular plates.

Auxetic materials are solids with negative Poisson’s ratios (Alipour and Shariyat 2015). Unlike the conventional solids, auxetic rods expand laterally when stretched axially while auxetic plates transform into synclastic domes when a bending moment is applied on two opposite sides. Through buckling and vibration analyses of circular plates under various boundary conditions, Lim (2014) deduced that as the Poisson’s ratio of the plate becomes more negative, the critical bucking loads and the natural frequencies diminish. Recently, Azoti et al. (2013) studied free vibration of rectangular composite sandwich plates with viscoelastic and auxetic layers, using equivalent single-layer theories.

Vibration analysis of the single layer and sandwich circular and annular plates with auxetic cores has not been accomplished so far. In the present study, the mentioned task is accomplished, including the following novelties:

• 1. Assessment of effects of using the auxetic cores on the behavior of the sandwich plates, for the first time.

• 2. Free vibration analysis of circular and annular sandwich plates with auxetic cores and orthotropic face sheets for the whole practical range of the auxeticity, for the first time.

• 3. The analysis is performed using a layerwise theory rather than the traditional equivalent single-layer theories whose results may encounter serious accuracy problems in analyzing the sandwich plates.

• 4. The resulting equations are solved using a finite Taylor’s transform whose center is located at the outer radius of the plate. Due to this hint, the resulting semi-analytical solution can be employed for both solid and annular sandwich plates.

• 5. A comprehensive parametric study including evaluation of effects of the auxeticity for sandwich plates with symmetric and asymmetric layups, different core to sheet thickness, radius to thickness, and inner to outer radius ratios, and various boundary conditions, is carried out.

• 6. The presented conclusions extend the available published information regarding the single-layer isotropic auxetic circular plates and provide more accurate results for the more complicated sandwich circular and annular plates with orthotropic face sheets and auxetic cores.

• 7. Present results are verified by the results of the three-dimensional theory of elasticity extracted from ABAQUS software.

2 The layerwise constitutive laws and displacement fields of the annular sandwich plate with auxetic core and orthotropic face sheets

Unlike the conventional materials, the auxetic (with negative Poisson ratios) annular layers expand laterally when they are subjected to radial tensions, e.g., due to tensile bending stresses, and the opposite is true as well. Therefore, the tensile regions of the thickness expand and the compressive regions shrink laterally. The auxetic materials may be manufactured in various forms, among them, the fiber and foam shapes.

The traditional equivalent single-layer plate theories are generally not proper for the sandwich plates and may lead to unreliable and sometimes, erroneous results (Carrera et al. 2011; Carrera and Brischetto 2009; Di Sciuva et al. 2009; Maturi et al. 2014). Indeed, this shortcoming stems from the fact that the traditional equivalent single-layer theories assume an identical and unique section rotation for all the layers of the sandwich plate. The available results of the 3D elasticity and zigzag theories (Di Sciuva et al. 1999, 2015; Iurlaro et al. 2015; Carrera et al. 2011; Carrera and Brischetto 2009; Shariyat 2010; Alipour and Shariyat 2012) reveal that not only rotations of the adjacent layers are different, but also rotation of the core may be even opposite (with different sign) to those of the face sheets. On the other hand, the continuity condition of the in-plane displacements has to be satisfied at the interfaces between layers. Therefore, if the assumption of the equivalent single-layer theories regarding the identical rotations is employed, erroneous in-plane displacements will be predicted at the interfaces between layers; a fact that completely alters the resulting responses.

The layerwise or zigzag theories may be used for the sandwich plates. At the early years of evolution of the layerwise theories, some authors have proposed higher-order layerwise theories. Di Sciuva et al. (1999) presented a third-order generalized zigzag theory that fulfilled a priori the shear traction continuity conditions at each interface of the laminated plates. Although this condition is generally suitable for investigation of the local effects, e.g., the resulting stresses, it may not affect the global responses (e.g., lateral deflection and vibration responses) remarkably (Reddy 2004; Di Sciuva et al. 2015). Eslami et al. (1998) presented an mth-order layerwise theory whose results where compatible to those of the three-dimensional theory of elasticity (Shariyat and Eslami 1999). However, later investigations of Di Sciuva and his co-authors and Shariyat and his co-authors have proven that using higher-order local functions (e.g., zigzag function) within all the individual layer, leads to a compliant and sometime, numerically instable systems of equations. For this reason, they continued their later researchers by using efficient but piecewise linear zigzag functions (Di Sciuva et al. 2015; Shariyat et al. 2015) releasing or retaining the continuity condition of the transverse stresses, especially, the normal transverse stress, at the interfaces between layers. This approach was proven to be more efficient and leads to numerically more robust results. For this reason, they called these first-order zigzag theories as Refined Zigzag Theories (Iurlaro et al. 2015; Di Sciuva et al. 2015; Shariyat et al. 2015; Khalili et al. 2014).

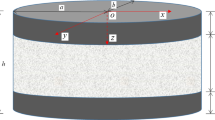
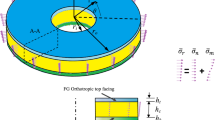
The considered plate is shown in Fig. 1 along with the considered global (radial, r, and transverse, z) and local ($\xi$) coordinates. The inner and outer radii are denoted respectively, by a and b and thickness of the top, core, and bottom layers are indicated by $h_{1}$, $h_{2}$, and $h_{3}$, respectively. Based on the aforementioned brief introduction, to present a sandwich plate theory with a best compromise between the accuracy and computational costs, a layerwise theory with piecewise-defined linear local and linear global components may be proposed in the present research. This piecewise linear layerwise theory is sufficient for accurately prediction of not only the global behaviors (such as the present vibration behaviors) but also the local responses (e.g., the resulting stresses).

Fig. 1

Geometric parameters of the considered annular sandwich plate with orthotropic face sheets and auxetic core

Present theory is a variant of the first-order global–local layerwise theories of Di Sciuva et al. (2015) and Shariyat et al. (2015). According to this theory, the displacement field within each individual layer may be described as:

$$ \left\{ \begin{aligned} &u_{k} (x,y,z) = u_{1}^{g} + u_{1}^{l} = u_{0} (x,y) + z\varphi_{r} (x,y) + \sum\limits_{k = 1}^{N - 1} {\left[ {z - Z^{(k)} } \right]\chi_{r}^{(k)} (x,y,z)H(z - Z^{(k)} )} \hfill \\& w_{k} (x,y,z) = w_{0} (x,y) \hfill \\ \end{aligned} \right. $$

(1)

where $u_{0}$ and $w_{0}$ are the radial and lateral displacement components of the reference surface of the whole sandwich plate, $\varphi_{r}$ and $\chi_{r}^{(k)}$ are global and local rotations of the kth layer of the plate, H is the Heaviside unit step function, $Z^{(k)}$ is the z coordinate of the bottom surfaces of the kth layer, the superscripts g and l denote the global and local displacement components respectively, and N = 3 is number of the layers. After some manipulations and incorporating the continuity of the displacement components at the interfaces between layers, the following description may be introduced for the displacement field of the entire sandwich plate:

$$ \left\{ \begin{aligned} u_{1} & = u_{0} + \frac{1}{2}(h_{1} + h_{2} + 2\xi^{(1)} )\varphi_{r} + \frac{{h_{2} }}{2}\chi_{r}^{(2)} + \left( {\xi^{(1)} + \frac{{h_{1} }}{2}} \right)\chi_{r}^{(1)} \\ & = u_{0} + \left( {\xi^{(1)} + \frac{{h_{1} }}{2}} \right)\psi_{r}^{(1)} + \frac{{h_{2} }}{2}\psi_{r}^{(2)} ; - \frac{{h_{1} }}{2}\, \le \xi^{(1)} \le \frac{{h_{1} }}{2} \\ u_{2} & = u_{0} + \xi^{(2)} (\varphi_{r} + \chi_{r}^{(2)} ) = u_{0} + \xi^{(2)} \psi_{r}^{(2)} ; - \frac{{h_{2} }}{2}\, \le \xi^{(2)} \le \frac{{h_{2} }}{2} \\ u_{3} & = u_{0} - \frac{1}{2}(h_{1} + h_{2} - 2\xi^{(3)} )\varphi - \frac{{h_{2} }}{2}\chi_{r}^{(2)} + \left( {\xi^{(3)} - \frac{{h_{3} }}{2}} \right)\chi_{r}^{(3)} \\ & = u_{0} - \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(3)} - \frac{{h_{3} }}{2}} \right)\psi_{r}^{(3)} ; - \frac{{h_{3} }}{2} \le \xi^{(3)} \le \frac{{h_{3} }}{2} \\ w & = w_{0} \\ \end{aligned} \right. $$

(2)

where and $\psi_{r}^{(k)}$ is the total rotation (sum of the global $\varphi_{r}$ and local $\chi_{r}^{(k)}$ rotations) of the kth layer of the plate. The transverse global and local coordinates are measured from their relevant mid-planes.

Cauchy’s strain–displacement relations are:

$$ \varepsilon_{r} = u_{,r} \quad \varepsilon_{\theta } = \frac{u}{r}\quad \varepsilon_{rz} = u_{,z} + w_{,r} $$

(3)

where the symbol “,” stands for the partial derivative. On the other hand, based on Hooke’s generalized stress–strain law:

$$ \begin{aligned} \left\{ \begin{aligned} \sigma_{r}^{(k)} \hfill \\ \sigma_{\theta }^{(k)} \hfill \\ \tau_{rz}^{(k)} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {C_{11}^{(k)} } & {C_{12}^{(k)} } & 0 \\ {C_{21}^{(k)} } & {C_{22}^{(k)} } & 0 \\ 0 & 0 & {C_{44}^{(k)} } \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon_{r}^{(k)} \hfill \\ \varepsilon_{\theta }^{(k)} \hfill \\ \gamma_{rz}^{(k)} \hfill \\ \end{aligned} \right\}, \hfill \\ C_{11}^{(k)} = \frac{{E_{r}^{(k)} }}{{1 - v_{r\theta }^{(k)} v_{\theta r}^{(k)} }},\quad C_{12}^{(k)} = C_{21}^{(k)} = \frac{{v_{\theta r}^{(k)} E_{r}^{(k)} }}{{1 - v_{r\theta }^{(k)} v_{\theta r}^{(k)} }},\quad C_{22}^{(k)} = \frac{{E_{\theta }^{(k)} }}{{1 - v_{r\theta }^{(k)} v_{\theta r}^{(k)} }},\quad C_{44}^{(k)} = G_{rz}^{(k)} \hfill \\ \end{aligned} $$

(4)

where the C, E, G, and $v$ symbols denote the elasticity coefficients, Young’s modulus, shear modulus, and Poisson’s ratio, respectively.

3 The governing equations of motion of the plate

The governing equations of motion of the sandwich plate are derived based on Hamilton’s principle:

$$ \int\limits_{{t_{1} }}^{{t_{2} }} {(\delta K - \delta U)dt} = 0 $$

(5)

where K and U are the kinetic and potential energies of the plate, respectively.

$$ K = \frac{1}{2}\int\limits_{V} {\rho (\dot{u}^{2} + \dot{w}^{2} )dV} , $$

(6)

$$ \,U = \frac{1}{2}\int\limits_{V} {(\sigma_{r} \varepsilon_{r} + \sigma_{\theta } \varepsilon_{\theta } + \tau_{rz} \gamma_{rz} )dV} $$

(7)

According to Eqs. (2), (3), (6), and (7), one may write:

$$ \delta K = \int\limits_{V} {\rho (\dot{u}\delta \dot{u} + \dot{w}\delta \dot{w})dV} , $$

(8)

$$ \delta U = \int\limits_{V} {\delta {\varvec{\upvarepsilon}}^{T} {\varvec{\upsigma}}dV} = \int\limits_{V} {\left\{ {\sigma_{r} \delta \left( {\frac{\partial u}{\partial r}} \right) + \sigma_{\theta } \delta \left( {\frac{u}{r}} \right) + \tau_{rz} \delta \left( {\frac{\partial u}{\partial z} + \frac{\partial w}{\partial r}} \right)} \right\}} dV $$

(9)

Integrating Eqs. (8) and (9) by parts, leads to:

$$ \delta K = - \int\limits_{A} {\rho \left( {\textit{\"{u}}\delta u + \textit{\"{w}}\delta w} \right)dA} $$

(10)

$$ \delta U = \int\limits_{V} {\left\{ { - \left( {\sigma_{r,r} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r}} \right)\delta u + \tau_{rz} \delta u,_{z} } \right.} \left. { - \left( {\tau_{rz,r} + \frac{{\tau_{rz} }}{r}} \right)\delta w} \right\}dV + \int\limits_{\varGamma } {\int\limits_{ - h/2}^{h/2} {(\sigma_{r} \delta u + \tau_{rz} \delta w)dz} }\;\;d\varGamma = 0 $$

(11)

Substituting Eqs. (10) and (11) into Eq. (5) yields:

$$ \begin{aligned} & \int\limits_{t} {\int\limits_{A} {\int\limits_{ - h/2}^{h/2} {\left\{ {\left( {\frac{{\sigma_{r} - \sigma_{\theta } }}{r} + \sigma_{r,r} } \right)\delta u - \tau_{rz} \delta u,_{z} + \left( {\tau_{rz,r} + \frac{{\tau_{rz} }}{r}} \right)\delta w - \rho (\textit{\"{u}}\delta u + \textit{\"{w}}\delta w)} \right\}dz\,dA\,dt} } } \\ & \quad - \int\limits_{t} {\int\limits_{\varGamma } {\int\limits_{ - h/2}^{h/2} {(\sigma_{r} \delta u + \tau_{rz} \delta w)} } } r\,d\theta\,dz\,dt = 0 \\ \end{aligned} $$

(12)

where $\varGamma$ is the boundary of the plate, i.e., the edges. The governing equations have to be valid for any arbitrary time interval. Therefore, the integrand of the time integral has to be zero for the entire time interval. Using this evidence and expanding the integrand of Eq. (12) based on the layers quantities gives the following result:

$$ \begin{aligned} & \int\limits_{A} {\left\{ {\int\limits_{{ - h_{1} /2}}^{{h_{1} /2}} {\left[ {\left( {\frac{{\sigma_{r}^{(1)} - \sigma_{\theta }^{(1)} }}{r} + \sigma_{r,r}^{(1)} } \right)\delta u_{1} - \tau_{rz}^{(1)} \delta u_{{1,\xi^{(1)} }} + \left( {\tau_{rz,r}^{(1)} + \frac{{\tau_{rz}^{(1)} }}{r}} \right)\delta w - \rho^{(1)} \textit{\"{u}}_{1} \delta u_{1} - \rho^{(1)} \textit{\"{w}}\delta w} \right]d\xi^{(1)} } } \right.} \\ & \quad + \int\limits_{{ - h_{2} /2}}^{{h_{2} /2}} {\left[ {\left( {\frac{{\sigma_{r}^{(2)} - \sigma_{\theta }^{(2)} }}{r} + \sigma_{r,r}^{(2)} } \right)\delta u_{2} - \tau_{rz}^{(2)} \delta u_{{2,\xi^{(2)} }} + \left( {\tau_{rz,r}^{(2)} + \frac{{\tau_{rz}^{(2)} }}{r}} \right)\delta w - \rho^{(2)} \textit{\"{u}}_{2} \delta u_{2} - \rho^{(2)} \textit{\"{w}}\delta w} \right]d\xi^{(2)} } \\ & \quad + \left. {\int\limits_{{ - h_{3} /2}}^{{h_{3} /2}} {\left[ {\left( {\frac{{\sigma_{r}^{(3)} - \sigma_{\theta }^{(3)} }}{r} + \sigma_{r,r}^{(3)} } \right)\delta u_{3} - \tau_{rz}^{(3)} \delta u_{{3,\xi^{(3)} }} + \left( {\tau_{rz,r}^{(3)} + \frac{{\tau_{rz}^{(3)} }}{r}} \right)\delta w - \rho^{(3)} \textit{\"{u}}_{3} \delta u_{3} - \rho^{(3)} \textit{\"{w}}\delta w} \right]d\xi^{(3)} } } \right\}dA \\ & \quad - \int\limits_{\varGamma } {\left\{ {\int\limits_{{ - h_{1} /2}}^{{h_{1} /2}} {\left( {\tau_{rz}^{(1)} \delta w + \sigma_{r}^{(1)} \delta u_{1} } \right)d\xi^{(1)} } + \int\limits_{{ - h_{2} /2}}^{{h_{2} /2}} {\left( {\tau_{rz}^{(2)} \delta w + \sigma_{r}^{(2)} \delta u_{2} } \right)d\xi^{(2)} } + \int\limits_{{ - h_{3} /2}}^{{h_{3} /2}} {\left( {\tau_{rz}^{(3)} \delta w + \sigma_{r}^{(3)} \delta u_{3} } \right)d\xi^{(3)} } } \right\}} = 0 \\ \end{aligned} $$

(13)

The displacement components may be substituted according to Eq. (2). Therefore, Eq. (13) becomes:

$$ \begin{aligned} & \int\limits_{A} {\left\{ {\int\limits_{{ - h_{1} /2}}^{{h_{1} /2}} {\left[ {\left( {\frac{{\sigma_{r}^{(1)} - \sigma_{\theta }^{(1)} }}{r} + \sigma_{r,r}^{(1)} } \right)\delta \left( {u_{0} + \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(1)} + \frac{{h_{1} }}{2}} \right)\psi_{r}^{(1)} } \right) - \tau_{rz}^{(1)} \delta \psi_{r}^{(1)} } \right.} } \right.} + \left( {\tau_{rz,r}^{(1)} + \frac{{\tau_{rz}^{(1)} }}{r}} \right)\delta w \\ & \quad \left. { - \rho^{(1)} \left( {\textit{\"{u}}_{0} + \frac{{h_{2} }}{2}\ddot{\psi }_{r}^{(2)} + \left( {\xi^{(1)} + \frac{{h_{1} }}{2}} \right)\ddot{\psi }_{r}^{(1)} } \right)\delta \left( {u_{0} + \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(1)} + \frac{{h_{1} }}{2}} \right)\psi_{r}^{(1)} } \right) - \rho^{(1)} \textit{\"{w}}\delta w} \right]d\xi^{(1)} \\ & \quad + \int\limits_{{ - h_{2} /2}}^{{h_{2} /2}} {\left[ {\left( {\frac{{\sigma_{r}^{(2)} - \sigma_{\theta }^{(2)} }}{r} + \sigma_{r,r}^{(2)} } \right)\delta \left( {u_{0} + \xi^{(2)} \psi_{r}^{(2)} } \right) - \tau_{rz}^{(2)} \delta \psi_{r}^{(2)} + \left( {\tau_{rz,r}^{(2)} + \frac{{\tau_{rz}^{(2)} }}{r}} \right)\delta w} \right.} \\ & \quad \left. { - \rho^{(2)} \left( {\textit{\"{u}}_{0} + \xi^{(2)} \ddot{\psi }_{r}^{(2)} } \right)\delta \left( {u_{0} + \xi^{(2)} \psi_{r}^{(2)} } \right) - \rho^{(2)} \textit{\"{w}}\delta w} \right]d\xi^{(2)} \\ & \quad + \int\limits_{{ - h_{3} /2}}^{{h_{3} /2}} {\left[ {\left( {\frac{{\sigma_{r}^{(3)} - \sigma_{\theta }^{(3)} }}{r} + \sigma_{r,r}^{(3)} } \right)\delta \left( {u_{0} - \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(3)} - \frac{{h_{3} }}{2}} \right)\psi_{r}^{(3)} } \right) - \tau_{rz}^{(3)} \delta \psi_{r}^{(3)} + } \right.} \left( {\tau_{rz,r}^{(3)} + \frac{{\tau_{rz}^{(3)} }}{r}} \right)\delta w \\ & \left. {\quad \left. { - \rho^{(3)} \left( {\textit{\"{u}}_{0} - \frac{{h_{2} }}{2}\ddot{\psi }_{r}^{(2)} + \left( {\xi^{(3)} - \frac{{h_{3} }}{2}} \right)\ddot{\psi }_{r}^{(3)} } \right)\delta \left( {u_{0} - \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(3)} - \frac{{h_{3} }}{2}} \right)\psi_{r}^{(3)} } \right) - \rho^{(3)} \textit{\"{w}}\delta w} \right]d\xi^{(3)} } \right\}dA \\ & \quad - \int\limits_{\varGamma } {\left\{ {\int\limits_{{ - h_{1} /2}}^{{h_{1} /2}} {\left[ {\tau_{rz}^{(1)} \delta w + \sigma_{r}^{(1)} \delta \left( {u_{0} + \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(1)} + \frac{{h_{1} }}{2}} \right)\psi_{r}^{(1)} } \right)} \right]d\xi^{(1)} } } \right.} \\ & \quad + \int\limits_{{ - h_{2} /2}}^{{h_{2} /2}} {\left[ {\tau_{rz}^{(2)} \delta w + \sigma_{r}^{(2)} \delta \left( {u_{0} + \xi^{(2)} \psi_{r}^{(2)} } \right)} \right]d\xi^{(2)} } \\ & \quad + \int\limits_{{ - h_{3} /2}}^{{h_{3} /2}} {\left[ {\tau_{rz}^{(3)} \delta w + \sigma_{r}^{(3)} \delta \left( {u_{0} - \frac{{h_{2} }}{2}\psi_{r}^{(2)} + \left( {\xi^{(3)} - \frac{{h_{3} }}{2}} \right)\psi_{r}^{(3)} } \right)} \right]d\xi^{(3)} } = 0 \\ \end{aligned} $$

(14)

Equation (14) may be rewritten by performing the integrations in the thickness direction to achieve:

$$ \begin{aligned} & \int\limits_{A} {\left\{ {\left[ {\frac{{N_{r}^{(1)} - N_{\theta }^{(1)} }}{r} + N_{r,r}^{(1)} + \frac{{N_{r}^{(2)} - N_{\theta }^{(2)} }}{r} + N_{r,r}^{(2)} + \frac{{N_{r}^{(3)} - N_{\theta }^{(3)} }}{r} + N_{r,r}^{(3)} - \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\textit{\"{u}}_{0} } \right.} \right.} \\ & \left. {\quad - \left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} - \left( {\frac{{h_{2} }}{2}\left( {I_{0}^{(1)} - I_{0}^{(3)} } \right) + I_{1}^{(2)} } \right)\ddot{\psi }_{r}^{(2)} - \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} } \right]\delta u_{0} \\ & \quad + \left[ {\frac{{h_{1} }}{2}\left( {\frac{{N_{r}^{(1)} - N_{\theta }^{(1)} }}{r} + N_{r,r}^{(1)} } \right) + \frac{{M_{r}^{(1)} - M_{\theta }^{(1)} }}{r} + M_{r,r}^{(1)} - Q_{rz}^{(1)} - \left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\textit{\"{u}}_{0} - \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\ddot{\psi }_{r}^{(2)} } \right. \\ & \quad \left. { - \left( {I_{2}^{(1)} + h_{1} I_{1}^{(1)} + \frac{{h_{1}^{2} }}{4}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} } \right]\delta \psi_{r}^{(1)} \\ & \quad + \left[ {\frac{{h_{2} }}{2}\left( {\frac{{N_{r}^{(1)} - N_{\theta }^{(1)} }}{r} + N_{r,r}^{(1)} } \right) - \frac{{h_{2} }}{2}\left( {\frac{{N_{r}^{(3)} - N_{\theta }^{(3)} }}{r} + N_{r,r}^{(3)} } \right) + \frac{{M_{r}^{(2)} - M_{\theta }^{(2)} }}{r} + M_{r,r}^{(2)} - Q_{rz}^{(2)} } \right. \\ & \quad - \left( {\frac{{h_{2} }}{2}I_{0}^{(1)} + I_{1}^{(2)} - \frac{{h_{2} }}{2}I_{0}^{(3)} } \right)\textit{\"{u}}_{0} - \frac{{h_{2} }}{2}\left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} - \left[ {\left( {\frac{{h_{2} }}{2}} \right)^{2} \left( {I_{0}^{(1)} + I_{0}^{(3)} } \right) + I_{2}^{(2)} } \right]\ddot{\psi }_{r}^{(2)} \\ & \quad \left. { + \frac{{h_{2} }}{2}\left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} } \right]\delta \psi_{r}^{(2)} \\ & \quad + \left[ { - \frac{{h_{3} }}{2}\left( {\frac{{N_{r}^{(3)} - N_{\theta }^{(3)} }}{r} + N_{r,r}^{(3)} } \right) + \frac{{M_{r}^{(3)} - M_{\theta }^{(3)} }}{r} + M_{r,r}^{(3)} - Q_{rz}^{(3)} - \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\textit{\"{u}}_{0} } \right. \\ & \quad \left. { - \left( {I_{2}^{(3)} - h_{3} I_{1}^{(3)} + \frac{{h_{3}^{2} }}{4}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} - \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}I_{0}^{(3)} - I_{1}^{(3)} } \right)\ddot{\psi }_{r}^{(2)} } \right]\delta \psi_{r}^{(3)} \\ & \left. {\quad + \left[ {Q_{rz,r}^{(1)} + \frac{{Q_{rz}^{(1)} }}{r} + Q_{rz,r}^{(2)} + \frac{{Q_{rz}^{(2)} }}{r} + Q_{rz,r}^{(3)} + \frac{{Q_{rz}^{(3)} }}{r} - \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\textit{\"{w}}} \right]\delta w} \right\}dA \\ & \quad - \int\limits_{\varGamma } {\left[ {(N_{r}^{(1)} + N_{r}^{(2)} + N_{r}^{(3)} )\delta u_{0} + \left( {\frac{{h_{1} }}{2}N_{r}^{(1)} + M_{r}^{(1)} } \right)\delta \psi_{r}^{(1)} + \left( {\frac{{h_{2} }}{2}N_{r}^{(1)} + M_{r}^{(2)} - \frac{{h_{2} }}{2}N_{r}^{(3)} } \right)\delta \psi_{r}^{(2)} } \right.} \\ & \quad \left. { + \left( { - \frac{{h_{3} }}{2}N_{r}^{(3} + M_{r}^{(3)} } \right)\delta \psi_{r}^{(3)} + \left( {Q_{r}^{(1)} + Q_{r}^{(2)} + Q_{r}^{(3)} } \right)\delta w} \right]d\varGamma = 0 \\ \end{aligned} $$

(15)

While the governing equations may be derived based on the first integral, the essential and natural boundary conditions of the plate may be defined based on the last (boundary) integral.

Since increments of the displacement parameters of the interior points of the plate are generally, nonzero values (especially, in vibration), the following five coupled governing equations are resulted from the first integral of Eq. (15):

$$ \begin{aligned} & \delta u_{0} \ne 0{:} \\ & \quad \frac{{N_{r}^{(1)} - N_{\theta }^{(1)} }}{r} + N_{r,r}^{(1)} + \frac{{N_{r}^{(2)} - N_{\theta }^{(2)} }}{r} + N_{r,r}^{(2)} + \frac{{N_{r}^{(3)} - N_{\theta }^{(3)} }}{r} + N_{r,r}^{(3)} = \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\textit{\"{u}}_{0} + \left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} \\ & \quad + \left( {\frac{{h_{2} }}{2}(I_{0}^{(1)} - I_{0}^{(3)} ) + I_{1}^{(2)} } \right)\ddot{\psi }_{r}^{(2)} + \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} \\ \end{aligned} $$

(16)

$$ \begin{aligned} &\delta \psi_{r}^{(1)} \ne 0{:} \hfill \\ &\quad \frac{{h_{1} }}{2}\left( {\frac{{N_{r}^{(1)} - N_{\theta }^{(1)} }}{r} + N_{r,r}^{(1)} } \right) + \frac{{M_{r}^{(1)} - M_{\theta }^{(1)} }}{r} + M_{r,r}^{(1)} - Q_{rz}^{(1)} = \left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\textit{\"{u}}_{0} + \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\ddot{\psi }_{r}^{(2)} \hfill \\ &\quad + \left[ {I_{2}^{(1)} + h_{1} I_{1}^{(1)} + \left( {\frac{{h_{1} }}{2}} \right)^{2} I_{0}^{(1)} } \right]\ddot{\psi }_{r}^{(1)} \hfill \\ \end{aligned} $$

(17)

$$ \begin{aligned} & \delta \psi_{r}^{(2)} \ne 0{:} \\ & \quad \frac{{h_{2} }}{2}\left( {\frac{{N_{r}^{(1)} - N_{\theta }^{(1)} }}{r} + N_{r,r}^{(1)} } \right) - \frac{{h_{2} }}{2}\left( {\frac{{N_{r}^{(3)} - N_{\theta }^{(3)} }}{r} + N_{r,r}^{(3)} } \right) + \frac{{M_{r}^{(2)} - M_{\theta }^{(2)} }}{r} + M_{r,r}^{(2)} - Q_{r}^{(2)} = \\ & \quad \left( {\frac{{h_{2} }}{2}I_{0}^{(1)} + I_{1}^{(2)} - \frac{{h_{2} }}{2}I_{0}^{(3)} } \right)\textit{\"{u}}_{0} + \frac{{h_{2} }}{2}\left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} + \left[ {\left( {\frac{{h_{2} }}{2}} \right)^{2} \left( {I_{0}^{(1)} + I_{0}^{(3)} } \right) + I_{2}^{(2)} } \right]\ddot{\psi }_{r}^{(2)} \\ & \quad - \frac{{h_{2} }}{2}\left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} \\ \end{aligned} $$

(18)

$$ \begin{aligned} & \delta \psi_{r}^{(3)} \ne 0{:} \\ & \quad - \frac{{h_{3} }}{2}\left( {\frac{{N_{r}^{(3)} - N_{\theta }^{(3)} }}{r} + N_{r,r}^{(3)} } \right) + \frac{{M_{r}^{(3)} - M_{\theta }^{(3)} }}{r} + M_{r,r}^{(3)} - Q_{rz}^{(3)} = \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\textit{\"{u}}_{0} \\ & \quad + \left[ {I_{2}^{(3)} - h_{3} I_{1}^{(3)} + \left( {\frac{{h_{3} }}{2}} \right)^{2} I_{0}^{(3)} } \right]\ddot{\psi }_{r}^{(3)} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}I_{0}^{(3)} - I_{1}^{(3)} } \right)\ddot{\psi }_{r}^{(2)} \\ \end{aligned} $$

(19)

$$ \begin{aligned} & \delta w \ne 0{:} \\ & \quad Q_{r,r}^{(1)} + \frac{{Q_{r}^{(1)} }}{r} + Q_{r,r}^{(2)} + \frac{{Q_{r}^{(2)} }}{r} + Q_{r,r}^{(3)} + \frac{{Q_{r}^{(3)} }}{r} = \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\textit{\"{w}} \\ \end{aligned} $$

(20)

where:

$$ \left\{ \begin{aligned} N_{ij}^{(k)} \hfill \\ M_{ij}^{(k)} \hfill \\ \end{aligned} \right\} = \int\limits_{{ - \frac{{h_{k} }}{2}}}^{{\frac{{h_{k} }}{2}}} {\sigma_{ij}^{(k)} } \left\{ \begin{aligned} 1 \hfill \\ z^{(k)} \hfill \\ \end{aligned} \right\}d\xi^{(k)} ,Q_{r}^{(k)} = \int\limits_{{ - \frac{{h_{k} }}{2}}}^{{\frac{{h_{k} }}{2}}} {\tau_{rz}^{(k)} } d\xi^{(k)} ,\quad i = 1,2,3;\quad i,j = r,\theta $$

(21)

$$ I_{j}^{(k)} = \int\limits_{{ - \frac{{h_{k} }}{2}}}^{{\frac{{h_{k} }}{2}}} {\rho^{(k)} \xi^{(k)j} } d\xi^{(k)} ,\quad k = 1,2,3;\quad j = 0,1,2 $$

(22)

Based on Eqs. (2)–(4), (21) may be rewritten in the following form:

$$ \begin{aligned} \left\{ \begin{aligned} N_{r}^{(1)} \hfill \\ M_{r}^{(1)} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} A_{11}^{(1)} \hfill \\ B_{11}^{(1)} \hfill \\ \end{aligned} \right\}\left( {u_{0,r} + \frac{{h_{1} }}{2}\psi_{r,r}^{(1)} + \frac{{h_{2} }}{2}\psi_{r,r}^{(2)} } \right) + \frac{1}{r}\,\left\{ \begin{aligned} A_{12}^{(1)} \hfill \\ B_{12}^{(1)} \hfill \\ \end{aligned} \right\}\left( {\,u_{0} + \frac{{h_{1} }}{2}\,\psi_{r}^{(1)} + \frac{{h_{2} }}{2}\psi_{r}^{(2)} } \right) + \left\{ \begin{aligned} B_{11}^{(1)} \hfill \\ D_{11}^{(1)} \hfill \\ \end{aligned} \right\}\psi_{r,r}^{(1)} \\ & \quad + \frac{1}{r}\left\{ \begin{aligned} B_{12}^{(1)} \hfill \\ D_{12}^{(1)} \hfill \\ \end{aligned} \right\}\psi_{r}^{(1)} , \\ \left\{ \begin{aligned} N_{r}^{(2)} \hfill \\ M_{r}^{(2)} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} A_{11}^{(2)} \hfill \\ B_{11}^{(2)} \hfill \\ \end{aligned} \right\}u_{0,r} + \frac{1}{r}\left\{ \begin{aligned} A_{12}^{(1)} \hfill \\ B_{12}^{(1)} \hfill \\ \end{aligned} \right\}u_{0} + \left\{ \begin{aligned} B_{11}^{(2)} \hfill \\ D_{11}^{(2)} \hfill \\ \end{aligned} \right\}\psi_{r,r}^{(2)} + \frac{1}{r}\left\{ \begin{aligned} B_{12}^{(2)} \hfill \\ D_{12}^{(2)} \hfill \\ \end{aligned} \right\}\psi_{r}^{(2)} , \\ \left\{ \begin{aligned} N_{r}^{(3)} \hfill \\ M_{r}^{(3)} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} A_{11}^{(3)} \hfill \\ B_{11}^{(3)} \hfill \\ \end{aligned} \right\}\left( {u_{0,r} - \frac{{h_{3} }}{2}\psi_{r,r}^{(3)} - \frac{{h_{2} }}{2}\psi_{r,r}^{(2)} } \right) + \frac{1}{r}\left\{ \begin{aligned} A_{12}^{(3)} \hfill \\ B_{12}^{(3)} \hfill \\ \end{aligned} \right\}\left( {u_{0} - \frac{{h_{3} }}{2}\psi_{r}^{(3)} - \frac{{h_{2} }}{2}\psi_{r}^{(2)} } \right) + \left\{ \begin{aligned} B_{11}^{(3)} \hfill \\ D_{11}^{(3)} \hfill \\ \end{aligned} \right\}\psi_{r,r}^{(3)} \\ & \quad + \frac{1}{r}\left\{ \begin{aligned} B_{12}^{(3)} \hfill \\ D_{12}^{(3)} \hfill \\ \end{aligned} \right\}\psi_{r}^{(3)} , \\ \left\{ \begin{aligned} N_{\theta }^{(1)} \hfill \\ M_{\theta }^{(1)} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} A_{12}^{(1)} \hfill \\ B_{12}^{(1)} \hfill \\ \end{aligned} \right\}\left( {u_{0,r} + \frac{{h_{1} }}{2}\psi_{r,r}^{(1)} + \frac{{h_{2} }}{2}\psi_{r,r}^{(2)} } \right) + \frac{1}{r}\,\left\{ \begin{aligned} A_{22}^{(1)} \hfill \\ B_{22}^{(1)} \hfill \\ \end{aligned} \right\}\left( {\,u_{0} + \frac{{h_{1} }}{2}\,\psi_{r}^{(1)} + \frac{{h_{2} }}{2}\psi_{r}^{(2)} } \right) + \left\{ \begin{aligned} B_{12}^{(1)} \hfill \\ D_{12}^{(1)} \hfill \\ \end{aligned} \right\}\psi_{r,r}^{(1)} \\ & \quad + \frac{1}{r}\left\{ \begin{aligned} B_{22}^{(1)} \hfill \\ D_{22}^{(1)} \hfill \\ \end{aligned} \right\}\,\psi_{r}^{(1)} , \\ \left\{ \begin{aligned} N_{\theta }^{(2)} \hfill \\ M_{\theta }^{(2)} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} A_{12}^{(2)} \hfill \\ B_{12}^{(2)} \hfill \\ \end{aligned} \right\}u_{0,r} + \frac{1}{r}\left\{ \begin{aligned} A_{22}^{(2)} \hfill \\ B_{22}^{(2)} \hfill \\ \end{aligned} \right\}u_{0} + \left\{ \begin{aligned} B_{12}^{(2)} \hfill \\ D_{12}^{(2)} \hfill \\ \end{aligned} \right\}\psi_{r,r}^{(2)} + \frac{1}{r}\left\{ \begin{aligned} B_{22}^{(2)} \hfill \\ D_{22}^{(2)} \hfill \\ \end{aligned} \right\}\psi_{r}^{(2)} , \\ \left\{ \begin{aligned} N_{\theta }^{(3)} \hfill \\ M_{\theta }^{(3)} \hfill \\ \end{aligned} \right\} & = \left\{ \begin{aligned} A_{12}^{(3)} \hfill \\ B_{12}^{(3)} \hfill \\ \end{aligned} \right\}\left( {u_{0,r} - \frac{{h_{3} }}{2}\psi_{r,r}^{(3)} - \frac{{h_{2} }}{2}\psi_{r,r}^{(2)} } \right) + \frac{1}{r}\left\{ \begin{aligned} A_{22}^{(3)} \hfill \\ B_{22}^{(3)} \hfill \\ \end{aligned} \right\}\left( {u_{0} - \frac{{h_{3} }}{2}\psi_{r}^{(3)} - \frac{{h_{2} }}{2}\psi_{r}^{(2)} } \right)\left\{ \begin{aligned} B_{12}^{(3)} \hfill \\ D_{12}^{(3)} \hfill \\ \end{aligned} \right\}\psi_{r,r}^{(3)} \\ & \quad + \frac{1}{r}\left\{ \begin{aligned} B_{22}^{(3)} \hfill \\ D_{22}^{(3)} \hfill \\ \end{aligned} \right\}\psi_{r}^{(3)} , \\ \end{aligned} $$

(23)

$$ Q_{r}^{(1)} = A_{44}^{(1)} \left( {\psi_{r}^{(1)} + w_{,r} } \right),\quad Q_{r}^{(2)} = A_{44}^{(2)} \left( {\psi_{r}^{(2)} + w_{,r} } \right),\quad Q_{r}^{(3)} = A_{44}^{(3)} \left( {\psi_{r}^{(3)} + w_{,r} } \right) $$

(24)

where

$$ \left\{ \begin{gathered} A_{{ij}}^{{(k)}} \hfill \\ B_{{ij}}^{{(k)}} \hfill \\ D_{{ij}}^{{(k)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{k} }}{2}}}^{{\frac{{h_{k} }}{2}}} {C_{{ij}}^{{(k)}} } \left\{ {\begin{array}{l} 1 \\ {z^{{(k)}} } \\ {z^{{(k^{2} )}} } \\ \end{array} } \right\}dz^{{(k)}} \quad k = 1,2,3;\quad i,j = 1,2,4 $$

(25)

Based on Eqs. (23) and (24), the governing Eqs. (16)–(20) may be rewritten as:

$$ \begin{aligned} & \delta u_{0} \ne 0{:} \\ & \quad \left( {A_{11}^{(1)} + A_{11}^{(2)} + A_{11}^{(3)} } \right)\left( {u_{0,rr} + \frac{{u_{0,r} }}{r}} \right) - \left( {A_{22}^{(1)} + A_{22}^{(2)} + A_{22}^{(3)} } \right)\frac{{u_{0} }}{{r^{2} }} + \left( {\frac{{h_{1} }}{2}A_{11}^{(1)} + B_{11}^{(1)} } \right)\left( {\psi_{r,rr}^{(1)} + \,\frac{{\psi_{r,r}^{(1)} }}{r}} \right) \\ & \quad - \left( {\frac{{h_{1} }}{2}A_{22}^{(1)} + B_{22}^{(1)} } \right)\frac{{\psi_{r}^{(1)} }}{{r^{2} }} + \left( {\frac{{h_{2} }}{2}A_{11}^{(1)} + B_{11}^{(2)} - \frac{{h_{2} }}{2}A_{11}^{(3)} } \right)\left( {\psi_{r,rr}^{(2)} + \frac{{\psi_{r,r}^{(2)} }}{r}} \right) \\ & \quad - \left( {\frac{{h_{2} }}{2}A_{22}^{(1)} + B_{22}^{(2)} - \frac{{h_{2} }}{2}A_{22}^{(3)} } \right)\frac{{\psi_{r}^{(2)} }}{{r^{2} }} + \left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)\left( {\psi_{r,rr}^{(3)} + \,\frac{{\psi_{r,r}^{(3)} }}{r}} \right) - \left( {B_{22}^{(3)} - \frac{{h_{3} }}{2}A_{22}^{(3)} } \right)\frac{{\psi_{r}^{(3)} }}{{r^{2} }} \\ & \quad = \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\textit{\"{u}}_{0} + \left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} + \left( {\frac{{h_{2} }}{2}(I_{0}^{(1)} - I_{0}^{(3)} ) + I_{1}^{(2)} } \right)\ddot{\psi }_{r}^{(2)} + \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} \\ \end{aligned} $$

(26)

$$ \begin{aligned} & \delta \psi_{r}^{(1)} \ne 0{:} \\ & \quad \left( {B_{11}^{(1)} + \frac{{h_{1} }}{2}A_{11}^{(1)} } \right)\left( {u_{0,rr} + \frac{{u_{0,r} }}{r}} \right) - \left( {B_{22}^{(1)} + \frac{{h_{1} }}{2}A_{22}^{(1)} } \right)\frac{{u_{0} }}{{r^{2} }} + \left( {\frac{{h_{1}^{2} }}{4}A_{11}^{(1)} + h_{1} B_{11}^{(1)} + D_{11}^{(1)} } \right)\left( {\psi_{r,rr}^{(1)} + \frac{{\psi_{r,r}^{(1)} }}{r}} \right) \\ & \quad - \left( {\frac{{h_{1}^{2} }}{4}A_{22}^{(1)} + h_{1} B_{22}^{(1)} + D_{22}^{(1)} } \right)\frac{{\psi_{r}^{(1)} }}{{r^{2} }} + \frac{{h_{2} }}{2}\left( {B_{11}^{(1)} + \frac{{h_{1} }}{2}A_{11}^{(1)} } \right)\left( {\psi_{r,rr}^{(2)} + \frac{{\psi_{r,r}^{(2)} }}{r}} \right) - \frac{{h_{2} }}{2}\left( {B_{22}^{(1)} + \frac{{h_{1} }}{2}A_{22}^{(1)} } \right)\frac{{\psi_{r}^{(2)} }}{{r^{2} }} \\ & \quad - A_{44}^{(1)} (\psi_{r}^{(1)} + w_{,r} ) = \left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\textit{\"{u}}_{0} + \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\ddot{\psi }_{r}^{(2)} + \left( {I_{2}^{(1)} + h_{1} I_{1}^{(1)} + \frac{{h_{1}^{2} }}{4}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} \\ \end{aligned} $$

(27)

$$ \begin{aligned} & \delta \psi_{r}^{(2)} \ne 0{:} \\ & \quad \left( {\frac{{h_{2} }}{2}A_{11}^{(1)} + B_{11}^{(2)} - \frac{{h_{2} }}{2}A_{11}^{(3)} } \right)\left( {u_{0,rr} + \frac{{u_{0,r} }}{r}} \right) - \left( {\frac{{h_{2} }}{2}A_{22}^{(1)} + B_{22}^{(2)} - \frac{{h_{2} }}{2}A_{22}^{(3)} } \right)\frac{{u_{0} }}{{r^{2} }} + \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}A_{11}^{(1)} + B_{11}^{(1)} } \right) \\ & \quad \left( {\psi_{r,rr}^{(1)} + \frac{{\psi_{r,r}^{(1)} }}{r}} \right) - \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}A_{22}^{(1)} + B_{22}^{(1)} } \right)\frac{{\psi_{r}^{(1)} }}{{r^{2} }} + \left( {\frac{{h_{2}^{2} }}{4}A_{11}^{(1)} + D_{11}^{(2)} + \frac{{h_{2}^{2} }}{4}A_{11}^{(3)} } \right)\left( {\psi_{r,rr}^{(2)} + \frac{{\psi_{r,r}^{(2)} }}{r}} \right) \\ & \quad - \left( {\frac{{h_{2}^{2} }}{4}A_{22}^{(1)} + D_{22}^{(2)} + \frac{{h_{2}^{2} }}{4}A_{22}^{(3)} } \right)\frac{{\psi_{r}^{(2)} }}{{r^{2} }} - \frac{{h_{2} }}{2}\left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)\left( {\psi_{r,rr}^{(3)} + \,\frac{{\psi_{r,r}^{(3)} }}{r}} \right) + \frac{{h_{2} }}{2}\left( {B_{22}^{(3)} - \frac{{h_{3} }}{2}A_{22}^{(3)} } \right)\frac{{\psi_{r}^{(3)} }}{{r^{2} }}\, \\ & \quad - A_{44}^{(2)} (\psi_{r}^{(2)} + w_{,r} ) = \left( {\frac{{h_{2} }}{2}I_{0}^{(1)} + I_{1}^{(2)} - \frac{{h_{2} }}{2}I_{0}^{(3)} } \right)\textit{\"{u}}_{0} + \frac{{h_{2} }}{2}\left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\ddot{\psi }_{r}^{(1)} \\ & \quad + \left( {\frac{{h_{2}^{2} }}{4}I_{0}^{(1)} + I_{2}^{(2)} + \frac{{h_{2}^{2} }}{4}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(2)} - \frac{{h_{2} }}{2}\left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} \\ \end{aligned} $$

(28)

$$ \begin{aligned} & \delta \psi_{r}^{(3)} \ne 0{:} \\ & \quad \left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)\left( {u_{0,rr} + \frac{{u_{0,r} }}{r}} \right) - \left( {B_{22}^{(3)} - \frac{{h_{3} }}{2}A_{22}^{(3)} } \right)\frac{{u_{0} }}{{r^{2} }} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}A_{11}^{(3)} - B_{11}^{(3)} } \right)\left( {\psi_{r,rr}^{(2)} + \frac{{\psi_{r,r}^{(2)} }}{r}} \right) \\ & \quad - \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}A_{22}^{(3)} - B_{22}^{(3)} } \right)\frac{{\psi_{r}^{(2)} }}{{r^{2} }} + \left( {D_{11}^{(3)} - h_{3} B_{11}^{(3)} + \frac{{h_{3}^{2} }}{4}A_{11}^{(3)} } \right)\left( {\psi_{r,rr}^{(3)} + \,\frac{{\psi_{r,r}^{(3)} }}{r}} \right) - \left( {D_{22}^{(3)} - h_{3} B_{22}^{(3)} + \frac{{h_{3}^{2} }}{4}A_{22}^{(3)} } \right)\frac{{\psi_{r}^{(3)} }}{{r^{2} }} \\ & \quad - A_{44}^{(3)} (\psi_{r}^{(3)} + w_{,r} ) = \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\textit{\"{u}}_{0} + \left( {I_{2}^{(3)} - h_{3} I_{1}^{(3)} + \frac{{h_{3}^{2} }}{4}I_{0}^{(3)} } \right)\ddot{\psi }_{r}^{(3)} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}I_{0}^{(3)} - I_{1}^{(3)} } \right)\ddot{\psi }_{r}^{(2)} \\ \end{aligned} $$

(29)

$$ \begin{aligned} & \delta w \ne 0{:} \\ & \quad (A_{44}^{(1)} + A_{44}^{(2)} + A_{44}^{(3)} )\left( {w_{,rr} + \frac{{w,_{r} }}{r}} \right) + A_{44}^{(1)} \left( {\psi_{r,r}^{(1)} + \frac{{\psi_{r}^{(1)} }}{r}} \right) + A_{44}^{(2)} \left( {\psi_{r,r}^{(2)} + \frac{{\psi_{r}^{(2)} }}{r}} \right) + A_{44}^{(3)} \left( {\psi_{r,r}^{(3)} + \frac{{\psi_{r}^{(3)} }}{r}} \right) \\ & \quad = (I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} )\textit{\"{w}} \\ \end{aligned} $$

(30)

4 The mathematical forms of the edge conditions

The governing Eqs. (26)–(30) have to be solved along with the boundary conditions. As mentioned in Sect. 3, the essential (kinematic) and natural boundary conditions may be defined based on the second integral of Eq. (15). In this regard, the following combinations of the edge conditions may be defined:

• Clamped immovable edge:

  $$ \left\{ {\begin{array}{l} {u_{0} = 0} \hfill \\ {\psi _{r}^{{(1)}} = 0} \hfill \\ {\psi _{r}^{{(2)}} = 0} \hfill \\ {\psi _{r}^{{(3)}} = 0} \hfill \\ {w = 0} \hfill \\ \end{array} } \right. $$

  (31)

• Simply-supported immovable edge:

  $$ \left\{ {\begin{array}{l} {u_{0} = 0} \hfill \\ {\frac{{h_{1} }}{2}N_{r}^{{(1)}} + M_{r}^{{(1)}} = 0} \hfill \\ {\frac{{h_{2} }}{2}N_{r}^{{(1)}} + M_{r}^{{(2)}} - \frac{{h_{2} }}{2}N_{r}^{{(3)}} = 0} \hfill \\ { - \frac{{h_{3} }}{2}N_{r}^{{(3)}} + M_{r}^{{(3)}} = 0} \hfill \\ {w = 0} \hfill \\ \end{array} } \right. $$

  (32)

• Roller-supported movable edge:

  $$ \left\{ {\begin{array}{l} {N_{r}^{{(1)}} + N_{r}^{{(2)}} + N_{r}^{{(3)}} = 0} \hfill \\ {\frac{{h_{1} }}{2}N_{r}^{{(1)}} + M_{r}^{{(1)}} = 0} \hfill \\ {\frac{{h_{2} }}{2}N_{r}^{{(1)}} + M_{r}^{{(2)}} - \frac{{h_{2} }}{2}N_{r}^{{(3)}} = 0} \hfill \\ { - \frac{{h_{3} }}{2}N_{r}^{{(3)}} + M_{r}^{{(3)}} = 0} \hfill \\ {w = 0} \hfill \\ \end{array} } \right. $$

  (33)

• Free edge:

  $$ \left\{ {\begin{array}{l} {N_{r}^{{(1)}} + N_{r}^{{(2)}} + N_{r}^{{(3)}} = 0} \hfill \\ {\frac{{h_{1} }}{2}N_{r}^{{(1)}} + M_{r}^{{(1)}} = 0} \hfill \\ {\frac{{h_{2} }}{2}N_{r}^{{(1)}} + M_{r}^{{(2)}} - \frac{{h_{2} }}{2}N_{r}^{{(3)}} = 0} \hfill \\ { - \frac{{h_{3} }}{2}N_{r}^{{(3)}} + M_{r}^{{(3)}} = 0} \hfill \\ {Q_{r}^{{(1)}} + Q_{r}^{{(2)}} + Q_{r}^{{(3)}} = 0} \hfill \\ \end{array} } \right. $$

  (34)

5 The differential (Taylor’s) transform solution of the resulting eigenvalue problem

The governing Eqs. (26)–(30) may be solved using finite Taylor transformation of the displacement parameters [i.e., $u_{0} (r),\,\,w(r),\,\,\psi (r),\,\,\psi_{r}^{(1)} (r),\,\,\psi_{r}^{(2)} (r),\,\,{\text{and}}\,\,\psi_{r}^{(3)} (r)$]. In contrast to the conventional transformations, since present plate is mainly an annular one, the transformation cannot be expressed in terms of series about the central point of the plate. The displacement parameters are assumed to be analytical functions. Using finite Taylor series transformation about the outer radius of the sandwich plate, i.e., $r = b$, and a Kantorovich-type separation of variables, these functions may be expressed as follows:

$$ \begin{aligned} u_{0} & = \sum\limits_{j = 0}^{\infty } {U_{j} (r - b)^{j} } e^{i\omega t},\,\psi_{r}^{(1)} = \sum\limits_{k = 0}^{\infty } {\vartheta_{j}^{(1)} (r - b)^{j} } e^{i\omega t},\,\psi_{r}^{(2)} = \sum\limits_{k = 0}^{\infty } {\vartheta_{j}^{(2)} (r - b)^{j} e^{i\omega t} }, \\ \psi_{r}^{(3)} & = \sum\limits_{j = 0}^{\infty } {\vartheta_{j}^{(3)} (r - b)^{j} e^{i\omega t} },\quad w = \sum\limits_{k = 0}^{\infty } {W_{j} (r - b)^{j} e^{i\omega t} } \\ \end{aligned} $$

(35)

where i is the unit imaginary number. Based on Taylor’s series expansion, the $\frac{1}{r}$ and $\frac{1}{{r^{2} }}$ terms appeared in Eqs. (26) to (30) may be expressed by the following power series whose centers are located at $r = b$.

$$ \begin{aligned} \frac{1}{r} & = - \sum\limits_{k = 0}^{\infty } {\varsigma^{i + 1} (r - b)^{k} } \\ \frac{1}{{r^{2} }} & = \sum\limits_{k = 0}^{\infty } {(k + 1)\varsigma^{k + 2} (r - b)^{k} } \\ \end{aligned} $$

(36)

where $\varsigma = - \frac{1}{b}$. Substituting Eqs. (35) and (36) into the governing Eqs. (26) to (30) and performing some manipulations, the transformed form of the governing equations may be obtained as:

$$ \begin{aligned} & \delta u_{0} \ne 0{:} \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {A_{11}^{(1)} + A_{11}^{(2)} + A_{11}^{(3)} } \right)\left( {(j + 2)(j + 1)U_{j + 2} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{i + 1} (j - k + 1)U_{j - k + 1} } } \right)} \right.} - \left( {A_{22}^{(1)} + A_{22}^{(2)} + A_{22}^{(3)} } \right) \\ & \quad \sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{i + 2} } U_{j - k} + \left( {\frac{{h_{1} }}{2}A_{11}^{(1)} + B_{11}^{(1)} } \right)\left( {(j + 2)(j + 1)\vartheta_{k + 2}^{(1)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(1)} } } \right) \\ & \quad - \left( {\frac{{h_{1} }}{2}A_{22}^{(1)} + B_{22}^{(1)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(1)} + \left( {\frac{{h_{2} }}{2}A_{11}^{(1)} + B_{11}^{(2)} - \frac{{h_{2} }}{2}A_{11}^{(3)} } \right) \\ & \quad \left( {(j + 2)(j + 1)\vartheta_{j + 2}^{(2)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(2)} } } \right) - \left( {\frac{{h_{2} }}{2}A_{22}^{(1)} + B_{22}^{(2)} - \frac{{h_{2} }}{2}A_{22}^{(3)} } \right) \\ & \quad \sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{i + 2} } \vartheta_{j - i}^{(2)} + \left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)\left( {(j + 2)(j + 1)\vartheta_{j + 2}^{(3)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(3)} } } \right) \\ & \quad - \left( {B_{22}^{(3)} - \frac{{h_{3} }}{2}A_{22}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(3)} + \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\omega^{2} U_{j} + \left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\omega^{2} \vartheta_{j}^{(1)} \\ & \quad \left. { + \left( {\frac{{h_{2} }}{2}I_{0}^{(1)} + I_{1}^{(2)} - \frac{{h_{2} }}{2}I_{0}^{(3)} } \right)\omega^{2} \vartheta_{j}^{(2)} + \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\omega^{2} \vartheta_{j}^{(3)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(37)

$$ \begin{aligned} & \delta \psi_{r}^{(1)} \ne 0{:} \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {B_{11}^{(1)} + \frac{{h_{1} }}{2}A_{11}^{(1)} } \right)\left[ {(j + 2)(j + 1)U_{k + 2} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)U_{j - k + 1} } } \right]} \right.} \\ & \quad - \left( {B_{22}^{(1)} + \frac{{h_{1} }}{2}A_{22}^{(1)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{i + 2} } U_{j - i} + \left( {\frac{{h_{1}^{2} }}{4}A_{11}^{(1)} + h_{1} B_{11}^{(1)} + D_{11}^{(1)} } \right) \\ & \quad \left[ {(j + 2)(j + 1)\vartheta_{j + 2}^{(1)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - i + 1}^{(1)} } } \right] - \left( {\frac{{h_{1}^{2} }}{4}A_{22}^{(1)} + h_{1} B_{22}^{(1)} + D_{22}^{(1)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(1)} \, \\ & \quad + \frac{{h_{2} }}{2}\left( {B_{11}^{(1)} + \frac{{h_{1} }}{2}A_{11}^{(1)} } \right)\left[ {(j + 2)(j + 1)\vartheta_{j + 2}^{(2)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(2)} } } \right] \\ & \quad - \frac{{h_{2} }}{2}\left( {B_{22}^{(1)} + \frac{{h_{1} }}{2}A_{22}^{(1)} } \right)\sum\limits_{i = 0}^{j} {(i + 1)\varsigma^{i + 2} } \vartheta_{j - i}^{(2)} - A_{44}^{(1)} \left[ {\vartheta_{j}^{(1)} + (j + 1)W_{j + 1} } \right] + \left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\omega^{2} U_{j} \\ & \left. {\quad + \left( {I_{2}^{(1)} + h_{1} I_{1}^{(1)} + \frac{{h_{1}^{2} }}{4}I_{0}^{(1)} } \right)\omega^{2} \vartheta_{j}^{(1)} + \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}I_{0}^{(1)} + I_{1}^{(1)} } \right)\omega^{2} \vartheta_{j}^{(2)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(38)

$$ \begin{aligned} & \delta \psi_{r}^{(2)} \ne 0{:} \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {\frac{{h_{2} }}{2}A_{11}^{(1)} + B_{11}^{(2)} - \frac{{h_{2} }}{2}A_{11}^{(3)} } \right)\left[ {(j + 2)(j + 1)U_{j + 2} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)U_{j - k + 1} } } \right]} \right.} \\ & \quad - \left( {\frac{{h_{2} }}{2}A_{22}^{(1)} + B_{22}^{(2)} - \frac{{h_{2} }}{2}A_{22}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } U_{j - k} + \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}A_{11}^{(1)} + B_{11}^{(1)} } \right) \\ & \quad \left[ {(j + 2)(j + 1)\vartheta_{k + 2}^{(1)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(1)} } } \right] - \frac{{h_{2} }}{2}\left( {\frac{{h_{1} }}{2}A_{22}^{(1)} + B_{22}^{(1)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(1)} \\ & \quad + \left( {\frac{{h_{2}^{2} }}{4}A_{11}^{(1)} + D_{11}^{(2)} + \frac{{h_{2}^{2} }}{4}A_{11}^{(3)} } \right)\left[ {(j + 2)(j + 1)\vartheta_{j + 2}^{(2)} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(2)} } } \right] \\ & \quad - \left( {\frac{{h_{2}^{2} }}{4}A_{22}^{(1)} + D_{22}^{(2)} + \frac{{h_{2}^{2} }}{4}A_{22}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(2)} - \frac{{h_{2} }}{2}\left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right) \\ & \quad \left[ {(j + 2)(j + 1)\vartheta_{j + 2}^{(3)} - \sum\limits_{k = 0}^{k + 1} {\varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(3)} } } \right] + \frac{{h_{2} }}{2}\left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(3)} \\ & \quad - A_{44}^{(2)} \left[ {\vartheta_{j}^{(2)} + (j + 1)W_{j + 1} } \right] + \left( {\frac{{h_{2} }}{2}I_{0}^{(1)} + I_{1}^{(2)} - \frac{{h_{2} }}{2}I_{0}^{(3)} } \right)\omega^{2} U_{j} + \frac{{h_{2} }}{2}\left( {I_{1}^{(1)} + \frac{{h_{1} }}{2}I_{0}^{(1)} } \right)\omega^{2} \vartheta_{j}^{(1)} \\ & \left. {\quad + \left( {\frac{{h_{2}^{2} }}{4}I_{0}^{(1)} + I_{2}^{(2)} + \frac{{h_{2}^{2} }}{4}I_{0}^{(3)} } \right)\omega^{2} \vartheta_{j}^{(2)} - \frac{{h_{2} }}{2}\left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\omega^{2} \vartheta_{j}^{(3)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(39)

$$ \begin{aligned} & \delta \psi_{r}^{(3)} \ne 0{:} \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)\left[ {(j + 2)(j + 1)U_{j + 2} + \sum\limits_{k = 0}^{j + 1} { - \varsigma^{k + 1} (j - k + 1)U_{j - k + 1} } } \right]} \right.} \\ & \quad - \left( {B_{22}^{(3)} - \frac{{h_{3} }}{2}A_{22}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } U_{j - k} + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}A_{11}^{(3)} - B_{11}^{(3)} } \right) \\ & \quad \left[ {(j + 2)(j + 1)\vartheta_{k + 2}^{(2)} + \sum\limits_{k = 0}^{j + 1} { - \varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(2)} } } \right] - \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}A_{22}^{(3)} - B_{22}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(2)} \\ & \quad + \left( {D_{11}^{(3)} - h_{3} B_{11}^{(3)} + \frac{{h_{3}^{2} }}{4}A_{11}^{(3)} } \right)\left[ {(j + 2)(j + 1)\vartheta_{j + 2}^{(3)} + \sum\limits_{k = 0}^{j + 1} { - \varsigma^{k + 1} (j - k + 1)\vartheta_{j - k + 1}^{(3)} } } \right] \\ & \quad - \left( {D_{22}^{(3)} - h_{3} B_{22}^{(3)} + \frac{{h_{3}^{2} }}{4}A_{22}^{(3)} } \right)\sum\limits_{k = 0}^{j} {(k + 1)\varsigma^{k + 2} } \vartheta_{j - k}^{(3)} - A_{44}^{(3)} \left[ {\vartheta_{j}^{(3)} + (j + 1)W_{j + 1} } \right] + \left( {I_{1}^{(3)} - \frac{{h_{3} }}{2}I_{0}^{(3)} } \right)\omega^{2} U_{j} \\ & \quad \left. { + \frac{{h_{2} }}{2}\left( {\frac{{h_{3} }}{2}I_{0}^{(3)} - I_{1}^{(3)} } \right)\omega^{2} \vartheta_{j}^{(2)} + \left( {I_{2}^{(3)} - h_{3} I_{1}^{(3)} + \frac{{h_{3}^{2} }}{4}I_{0}^{(3)} } \right)\omega^{2} \vartheta_{j}^{(3)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(40)

$$ \begin{aligned} & \delta w \ne 0{:} \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {A_{44}^{(1)} + A_{44}^{(2)} + A_{44}^{(3)} } \right)\left[ {(j + 2)(j + 1)W_{j + 2} - \sum\limits_{k = 0}^{j + 1} {\varsigma^{k + 1} (j - k + 1)W_{j - k + 1} } } \right]} \right.} + A_{44}^{(1)} (j + 1)F_{j + 1}^{(1)} \\ & \quad - A_{44}^{(1)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} F_{j - k}^{(1)} } + A_{44}^{(2)} (j + 1)F_{j + 1}^{(2)} - A_{44}^{(2)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} F_{j - k}^{(2)} } + A_{44}^{(3)} (j + 1)F_{j + 1}^{(3)} \\ & \quad \left. { - A_{44}^{(3)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} F_{j - k}^{(3)} } + \left( {I_{0}^{(1)} + I_{0}^{(2)} + I_{0}^{(3)} } \right)\omega^{2} W_{j} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(41)

By solving Eqs. (37)–(41), an algebraic homogeneous system of equations including the unknown displacement parameters $U_{j + 2} ,\,\,\,\vartheta_{j + 2}^{(1)} ,\,\,\,\vartheta_{j + 2}^{(2)} ,\,\,\,\vartheta_{j + 2}^{(3)}$ and $W_{j + 2}$ (j = 0, 1, 2,…) is obtained. These equations have to be solved with the transformed form of the edge conditions, e.g., the transformed form of Eqs. (31) to (34) that are as follows:

$$ \begin{aligned} & \triangleright \quad u = 0 \Rightarrow \sum\limits_{j = 0}^{\infty } {U_{j} } (r - b)^{j} = 0, \\ & {\text{or}} \\ & \triangleright \quad N_{r}^{(1)} + N_{r}^{(2)} + N_{r}^{(3)} = 0 \Rightarrow \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {A_{11}^{(1)} + A_{11}^{(2)} + A_{11}^{(3)} } \right)(j + 1)U_{j + 1} - \left( {A_{12}^{(1)} + A_{12}^{(2)} + A_{12}^{(3)} } \right)\sum\limits_{k = 0}^{\infty } {\varsigma^{k + 1} } U_{j - k} } \right.} \\ & \quad + \left( {\frac{{h_{1} }}{2}A_{11}^{(1)} + B_{11}^{(1)} } \right)(j + 1)\vartheta_{j + 1}^{(1)} - \left( {\frac{{h_{1} }}{2}A_{12}^{(1)} + B_{12}^{(1)} } \right)\sum\limits_{i = 0}^{\infty } {\varsigma^{k + 1} } \vartheta_{j - k}^{(1)} \\ & \quad + \left( {\frac{{h_{2} }}{2}A_{11}^{(1)} + B_{11}^{(2)} - \frac{{h_{2} }}{2}A_{11}^{(3)} } \right)(j + 1)\vartheta_{j + 1}^{(2)} - \left( {\frac{{h_{2} }}{2}A_{12}^{(1)} + B_{12}^{(2)} - \frac{{h_{2} }}{2}A_{12}^{(3)} } \right)\sum\limits_{k = 0}^{\infty } {\varsigma^{k + 1} } \vartheta_{j - k}^{(2)} \\ & \quad \left. { + \left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)(j + 1)\vartheta_{j + 1}^{(3)} - \left( {B_{12}^{(3)} - \frac{{h_{3} }}{2}A_{12}^{(3)} } \right)\sum\limits_{k = 0}^{\infty } {\varsigma^{k + 1} } \vartheta_{j - k}^{(3)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(42)

$$ \begin{aligned} & \triangleright \quad \psi_{r}^{(1)} = 0 \Rightarrow \sum\limits_{j = 0}^{\infty } {\vartheta_{j}^{(1)} (r - b)^{j} } = 0, \\ & {\text{or}} \\ & \triangleright \quad \frac{{h_{1} }}{2}N_{r}^{(1)} + M_{r}^{(1)} = 0 \Rightarrow \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\left( {\frac{{h_{1} }}{2}A_{11}^{(1)} + B_{11}^{(1)} } \right)(j + 1)\left( {U_{j + 1} + \frac{{h_{1} }}{2}\vartheta_{j + 1}^{(1)} + \frac{{h_{2} }}{2}\vartheta_{j + 1}^{(2)} } \right) + \left( {\frac{{h_{1} }}{2}B_{11}^{(1)} + D_{11}^{(1)} } \right)(j + 1)\vartheta_{j + 1}^{(1)} } \right.} \\ & \quad - \left( {\frac{{h_{1} }}{2}A_{12}^{(1)} + B_{12}^{(1)} } \right)\sum\limits_{k = 0}^{\infty } {\varsigma^{k + 1} } \left( {U_{j - k} + \frac{{h_{1} }}{2}\vartheta_{j - k}^{(1)} + \frac{{h_{2} }}{2}\vartheta_{j - k}^{(2)} } \right) \\ & \quad \left. { - \left( {\frac{{h_{1} }}{2}B_{12}^{(1)} + D_{12}^{(1)} } \right)\sum\limits_{k = 0}^{\infty } {\varsigma^{k + 1} } \vartheta_{j - k}^{(1)} ,} \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(43)

$$ \begin{aligned} & \triangleright \quad \psi_{r}^{(2)} = 0 \Rightarrow \sum\limits_{j = 0}^{\infty } {\vartheta_{j}^{(2)} (r - b)^{j} } = 0, \\ & {\text{or}} \\ & \triangleright \quad \frac{{h_{2} }}{2}N_{r}^{(1)} + M_{r}^{(2)} - \frac{{h_{2} }}{2}N_{r}^{(3)} = 0 \Rightarrow \\ & \quad \sum\limits_{j = 0}^{\infty } {\left\{ {\frac{{h_{2} }}{2}A_{11}^{(1)} (j + 1)\left( {U_{j + 1} + \frac{{h_{1} }}{2}\vartheta_{j + 1}^{(1)} + \frac{{h_{2} }}{2}\vartheta_{j + 1}^{(2)} } \right) - \frac{{h_{2} }}{2}A_{12}^{(1)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \left( {U_{j - k} + \frac{{h_{1} }}{2}\vartheta_{j - k}^{(1)} + \frac{{h_{2} }}{2}\vartheta_{j - k}^{(2)} } \right)} \right.} \\ & \quad + \frac{{h_{2} }}{2}B_{11}^{(1)} (j + 1)\vartheta_{j + 1}^{(1)} - \frac{{h_{2} }}{2}B_{12}^{(1)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \vartheta_{j - k}^{(1)} + B_{11}^{(2)} (j + 1)U_{j + 1} - \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } B_{12}^{(2)} U_{j - k} \\ & \quad + D_{11}^{(2)} (j + 1)\vartheta_{j + 1}^{(2)} + D_{12}^{(2)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \vartheta_{j - k}^{(2)} - \frac{{h_{2} }}{2}A_{11}^{(3)} (j + 1)\left( {U_{j + 1} - \frac{{h_{3} }}{2}\vartheta_{j + 1}^{(3)} - \frac{{h_{2} }}{2}\vartheta_{j + 1}^{(2)} } \right) \\ & \quad + \frac{{h_{2} }}{2}A_{12}^{(3)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \left( {U_{j - k} - \frac{{h_{3} }}{2}\vartheta_{j - k}^{(3)} - \frac{{h_{2} }}{2}\vartheta_{j - k}^{(2)} } \right) \\ & \quad \left. { - \frac{{h_{2} }}{2}B_{11}^{(3)} (j + 1)\vartheta_{j + 1}^{(3)} + \frac{{h_{2} }}{2}B_{12}^{(3)} \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \vartheta_{j - k}^{(3)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(44)

$$ \begin{aligned} & \triangleright \quad \psi_{r}^{(3)} = 0 \Rightarrow \sum\limits_{j = 0}^{\infty } {\vartheta_{j}^{(3)} (r - b)^{j} } = 0, \\ & {\text{or}} \\ & \triangleright \quad - \frac{{h_{3} }}{2}N_{r}^{(3} + M_{r}^{(3)} = 0 \Rightarrow \\ & \quad \sum\limits_{j = 0}^{N} {\left\{ {\left( {B_{11}^{(3)} - \frac{{h_{3} }}{2}A_{11}^{(3)} } \right)(j + 1)\left( {U_{j + 1} - \frac{{h_{3} }}{2}\vartheta_{j + 1}^{(3)} - \frac{{h_{2} }}{2}\vartheta_{j + 1}^{(2)} } \right) + \left( {D_{11}^{(3)} - \frac{{h_{3} }}{2}B_{11}^{(3)} } \right)(j + 1)\vartheta_{j + 1}^{(3)} } \right.} \\ & \quad - \left( {B_{12}^{(3)} - \frac{{h_{3} }}{2}A_{12}^{(3)} } \right)\sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \left( {U_{j - k} - \frac{{h_{3} }}{2}\vartheta_{j - k}^{(3)} - \frac{{h_{2} }}{2}\vartheta_{j - k}^{(2)} } \right) \\ & \quad \left. { - \sum\limits_{k = 0}^{j} {\varsigma^{k + 1} } \left( {D_{12}^{(3)} - \frac{{h_{3} }}{2}B_{12}^{(3)} } \right)\vartheta_{j - k}^{(3)} } \right\}(r - b)^{j} = 0 \\ \end{aligned} $$

(45)

$$ \begin{aligned} & \triangleright \quad w = 0 \Rightarrow \sum\limits_{j = 0}^{\infty } {W_{j} } (r - b)^{j} = 0, \\ & {\text{or}} \\ & \triangleright \quad Q_{r}^{(1)} + Q_{r}^{(2)} + Q_{r}^{(3)} = 0 \Rightarrow \\ & \quad \sum\limits_{j = 0}^{N} {\left[ {\left( {A_{44}^{(1)} + A_{44}^{(2)} + A_{44}^{(3)} } \right)(j + 1)W_{j + 1} + A_{44}^{(1)} \vartheta_{j}^{(1)} + A_{44}^{(2)} \vartheta_{j}^{(2)} + A_{44}^{(3)} \vartheta_{j}^{(3)} } \right]} (r - b)^{j} = 0 \\ \end{aligned} $$

(46)

Substituting $U_{j + 2} ,\,\,\,\vartheta_{j + 2}^{(1)} ,\,\,\,\vartheta_{j + 2}^{(2)} ,\,\,\,\vartheta_{j + 2}^{(3)}$ and $W_{j + 2}$(j = 2…n + 2) from Eqs. (37) to (41) into the appropriate transformed form of the boundary conditions appeared in Eqs. (42) to (46), leads to the following system of equations:

$$ \left[ {\begin{array}{*{20}c} {\Phi (\omega )_{{1,1}} } & {\Phi (\omega )_{{1,2}} } & \cdots & \cdots & {\Phi (\omega )_{{1,9}} } & {\Phi (\omega )_{{1,10}} } \\ {\Phi (\omega )_{{2,1}} } & {\Phi (\omega )_{{2,2}} } & \cdots & \cdots & {\Phi (\omega )_{{2,9}} } & {\Phi (\omega )_{{2,10}} } \\ {\Phi (\omega )_{{3,1}} } & {\Phi (\omega )_{{3,2}} } & \cdots & \cdots & {\Phi (\omega )_{{3,9}} } & {\Phi (\omega )_{{3,10}} } \\ {\Phi (\omega )_{{4,1}} } & {\Phi (\omega )_{{4,2}} } & \cdots & \cdots & {\Phi (\omega )_{{4,9}} } & {\Phi (\omega )_{{4,10}} } \\ {\Phi (\omega )_{{5,1}} } & {\Phi (\omega )_{{5,2}} } & \cdots & \cdots & {\Phi (\omega )_{{5,9}} } & {\Phi (\omega )_{{5,10}} } \\ {\Phi (\omega )_{{6,1}} } & {\Phi (\omega )_{{6,2}} } & \cdots & \cdots & {\Phi (\omega )_{{6,9}} } & {\Phi (\omega )_{{6,10}} } \\ {\Phi (\omega )_{{7,1}} } & {\Phi (\omega )_{{7,2}} } & \cdots & \cdots & {\Phi (\omega )_{{7,9}} } & {\Phi (\omega )_{{7,10}} } \\ {\Phi (\omega )_{{8,1}} } & {\Phi (\omega )_{{8,2}} } & \cdots & \cdots & {\Phi (\omega )_{{8,9}} } & {\Phi (\omega )_{{8,10}} } \\ {\Phi (\omega )_{{9,1}} } & {\Phi (\omega )_{{9,2}} } & \cdots & \cdots & {\Phi (\omega )_{{9,9}} } & {\Phi (\omega )_{{9,10}} } \\ {\Phi (\omega )_{{10,1}} } & {\Phi (\omega )_{{10,2}} } & \cdots & \cdots & {\Phi (\omega )_{{10,9}} } & {\Phi (\omega )_{{10,10}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {U_{0} } \hfill \\ {U_{1} } \hfill \\ {\vartheta _{0}^{{(1)}} } \hfill \\ {\vartheta _{1}^{{(1)}} } \hfill \\ {\vartheta _{0}^{{(2)}} } \hfill \\ {\vartheta _{1}^{{(2)}} } \hfill \\ {\vartheta _{0}^{{(3)}} } \hfill \\ {\vartheta _{1}^{{(3)}} } \hfill \\ {W_{0} } \hfill \\ {W_{1} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right\} $$

(47)

Existence of non-trivial solutions for the resulting system of equations requires that:

$$ \left| {\begin{array}{*{20}c} {\varPhi (\omega )_{1,1} } & {\varPhi (\omega )_{1,2} } & \cdots & \cdots & {\varPhi (\omega )_{1,9} } & {\varPhi (\omega )_{1,10} } \\ {\varPhi (\omega )_{2,1} } & {\varPhi (\omega )_{2,2} } & \cdots & \cdots & {\varPhi (\omega )_{2,9} } & {\varPhi (\omega )_{2,10} } \\ {\varPhi (\omega )_{3,1} } & {\varPhi (\omega )_{3,2} } & \cdots & \cdots & {\varPhi (\omega )_{3,9} } & {\varPhi (\omega )_{3,10} } \\ {\varPhi (\omega )_{4,1} } & {\varPhi (\omega )_{4,2} } & \cdots & \cdots & {\varPhi (\omega )_{4,9} } & {\varPhi (\omega )_{4,10} } \\ {\varPhi (\omega )_{5,1} } & {\varPhi (\omega )_{5,2} } & \cdots & \cdots & {\varPhi (\omega )_{5,9} } & {\varPhi (\omega )_{5,10} } \\ {\varPhi (\omega )_{6,1} } & {\varPhi (\omega )_{6,2} } & \cdots & \cdots & {\varPhi (\omega )_{6,9} } & {\varPhi (\omega )_{6,10} } \\ {\varPhi (\omega )_{7,1} } & {\varPhi (\omega )_{7,2} } & \cdots & \cdots & {\varPhi (\omega )_{7,9} } & {\varPhi (\omega )_{7,10} } \\ {\varPhi (\omega )_{8,1} } & {\varPhi (\omega )_{8,2} } & \cdots & \cdots & {\varPhi (\omega )_{8,9} } & {\varPhi (\omega )_{8,10} } \\ {\varPhi (\omega )_{9,1} } & {\varPhi (\omega )_{9,2} } & \cdots & \cdots & {\varPhi (\omega )_{9,9} } & {\varPhi (\omega )_{9,10} } \\ {\varPhi (\omega )_{10,1} } & {\varPhi (\omega )_{10,2} } & \cdots & \cdots & {\varPhi (\omega )_{10,9} } & {\varPhi (\omega )_{10,10} } \\ \end{array} } \right| = 0 $$

(48)

Solution of Eq. (48) gives the natural frequencies of the annular/circular sandwich plate with auxetic core.

6 Results and discussions

Effects of the core auxeticity on the resulting natural frequencies of the sandwich plates with isotropic or orthotropic face sheets are evaluated in the present section. Moreover, both symmetric and asymmetric lamination schemes are examined. After presenting results of the single-layer auxetic plates, for the first time, results of the circular and annular sandwich plates are reported for various boundary conditions. Since the present results are the first reported results for the circular/annular sandwich plates, no available results may be found in literature to be used for comparison purposes. For this reason, present results are verified by results of the three dimensional theory of elasticity extracted from ABAQUS finite element analysis software. The results presented for the simple single-layer circular auxetic plates by Lim (2014) for the first time, show discrepancies with respect to ABAQUS results. For this reason, they have not been used here for the verification purposes.

Results of ABAQUS finite element analysis code for the circular and annular sandwich plates are derived using axisymmetric quadratic (eight-node) CAX8R solid elements with reduced integration (Fig. 2). To ensure that the resulting nodes of the successive layers are coincident at the interfaces between layers, all the layers are constructed by partitioning a single hollow or solid cylinder. For this reason, they appeared integrated in a single solid, in Fig. 3 which has been depicted for sandwich plates with $h_{1} /b = h_{3} /b = 0.1\,,h_{2} /b = 0.15$. The convergence analysis (whose results are not included here for the brevity sake) shows that even choosing two elements (five nodal points) along the thickness of the individual layers may lead to convergent results. However, more elements are used to guarantee convergence in all situations. Results of Tables 1, 2, 3, 4, 5 and 6 are derived based on 900, 1800, 3500, 4000, 3150, and 2800 axisymmetric quadratic element (in the radial section), respectively.

Fig. 2

Discretization of a the circular and b the annular sandwich plates, in ABAQUS software

Fig. 3

Trends of variations of the a first and b second natural frequencies of a clamped sandwich plate with an auxetic core

Table 1 A comparison among the first two dimensionless natural frequencies ($\varOmega = \omega a\sqrt {\rho /E}$) of the single-layer annular auxetic plate predicted by the present formulations and ABAQUS software, for various Poisson’s ratios and boundary conditions ($h/b = 0.1,\,\,a/b = 0.1$)

Table 2 A comparison among the first two dimensionless natural frequencies ($\varOmega = \omega a\sqrt {\rho /E}$) of the single-layer annular auxetic plate predicted by the present formulations and ABAQUS software, for various Poisson’s ratios and boundary conditions ($h/b = 0.2,\,\,a/b = 0.1$)

Table 3 A comparison among the natural frequencies predicted by present theory for aluminium/auxetic core/alumina sandwich circular plates and those predicted based on the three-dimensional theory of elasticity (ABAQUS software) ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.15$)

Table 4 A comparison among the natural frequencies predicted by present theory for aluminium/auxetic core/alumina sandwich circular plates and those predicted based on the three-dimensional theory of elasticity (ABAQUS software) ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.2$)

Table 5 Influences of the auxeticity and boundary conditions on the first two natural frequencies of the aluminium/auxetic core/alumina sandwich annular plates (a/b = 0.1, $h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.15$)

Table 6 Influences of the auxeticity and boundary conditions on the first two natural frequencies of the aluminium/auxetic core/steel sandwich annular plates ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.15$)

The extracted ABAQUS results may be considered as 3D elasticity results. Indeed, merely using ABAQUS software, cannot lead to “3D elasticity” results. For example, if one models the sandwich plate by using shell/plate elements of the ABAQUS software, the results will surely not be “3D elasticity” ones but they will be associated with the classical or Mindlin plate theories. Present results of ABAQUS software correspond to 3D elasticity theory only because “Solid 3D elements” are used and not due to using the ABAQUS code itself (plate theories are 2D ones). The formulation used by ABAQYS for the solid elements, is derived based on the energy-version of the 3D elasticity theory. Washizu (1975), has proven that minimization of the functional of the total potential energy of the structure is equivalent to directly solving the equilibrium equations in terms the stress components, i.e., equations of the 3D elasticity.

The material properties chosen for the isotropic top, core, and bottom layers are as follows:

$$ \begin{array}{*{20}l} {{\text{Aluminium}}:} \hfill & {E = 70\,{\text{GPa,}}} \hfill & {\rho = 2700\,{\text{kg/m}}^{3} ,} \hfill & {v = 0.33} \hfill \\ {{\text{Core}}:} \hfill & {E = 10\,{\text{GPa,}}} \hfill & {\rho = 950\,{\text{kg/m}}^{3} } \hfill & {} \hfill \\ {{\text{Steel}}:} \hfill & {E = 210\,{\text{GPa,}}} \hfill & {\rho = 7850\,{\text{kg/m}}^{3} ,} \hfill & {v = 0.3} \hfill \\ {{\text{Alumina}}:} \hfill & {E = 380\,{\text{GPa,}}} \hfill & {\rho = 3800\,{\text{kg/m}}^{3} ,} \hfill & {v = 0.26} \hfill \\ \end{array} $$

Material properties of the orthotropic face sheets are mentioned in Sect. 6.4 along with the relevant discussions.

6.1 Results of a single-layer auxetic annular plate

As a first verification and investigation example, effects of the auxetic nature of the material properties on the first two dimensionless natural frequencies ($\varOmega = \omega a\sqrt {\rho /E}$) of the single-layer auxetic annular plate (a/b = 0.1) are assessed. The results are extracted for various Poisson’s ratios and boundary conditions and given for moderately thick ($h/b = 0.1$) and thick ($h/b = 0.2$) plates in Tables 1 and 2, respectively. Results show that by decreasing the Poisson’s ratio from 0.5 to −0.9, the natural frequencies first decrease but then grow as the Poisson’s ratio becomes more negative. The same trend has been observed for the solid circular plate; for this reason, the relevant results are not included, to save space. The trend may be observed for all of the considered boundary conditions of the moderately thick and thick plates. However, ABAQUS results that show a good agreement with the present results (the maximum relative discrepancy is less than 2 %), confirm accuracy of the present conclusions. It should be mentioned that since in the present study, the plate is a single-layer one, present layerwise theory becomes a first-order shear-deformation theory for which Hutchinson’s (1984) $\kappa = 5/(6 - v)$ shear correction factor is selected. Results show that the trend transition is a complicated phenomenon and depends on many factors, among them: thickness to radius ratio, radius ratio, material properties of the plate, boundary conditions, and some other factors.

6.2 Effects of the core auxeticity on free vibration of circular sandwich plates with various boundary conditions

In the present section, a comprehensive sensitivity analysis for evaluation of the auxeticity, boundary conditions, thickness ratio, and lamination scheme effects is presented. In this regard, sandwich plates with the isotropic layers mentioned in Sect. 6.1 are considered, for verification and investigation purposes.

Results of the first two natural frequencies of aluminium/auxetic core/alumina sandwich plates with thick isotropic face sheets ($h_{1} /b = h_{3} /b = 0.1\,$) are extracted and compared respectively, in Tables 3 and 4 for two core thickness to outer radius ratios ($\,h_{2} /b = 0.15$ and 0.2) with the results of the three-dimensional theory of elasticity extracted from ABAQUS. Results are extracted for various edge conditions and the practical range of the Poisson ratio to present an adequate sensitivity analysis. It is known that the auxeticity extent (value of the Poisson’s ratio) depends on the employed manufacturing process. Present results are derived using as much as twenty series terms to ensure that significantly high accurate results are achieved. Results of even the present thick sandwich plates are in excellent agreement (the maximum relative discrepancy is about 2.5 %), even though an asymmetric lamination scheme (that leads to a tension-bending coupling) is used. However, part of this discrepancy stems from the approximate nature of the finite element method (ABAQUS); so that, the actual differences may be much smaller. Both types of results, i.e., present layerwise results and results of the ABAQUS software reveal that unlike the single-layer auxetic plates, the auxeticity generally increases the rigidities of the sandwich plates, and consequently, leads to higher natural frequencies. Results given in Tables 3 and 4 reveal that the auxeticity affects the natural frequencies of the clamped sandwich plates more considerably than the free (or even the roller supported) plates. For positive Poisson’s ratios, natural frequencies of the sandwich plate with free edge are higher whereas natural frequencies of the clamped plate become higher for the more negative Poisson’s ratios.

To present a better imagination of the trend of variations of the first two natural frequencies of the aluminium/auxetic core/steel plate, results of the clamped, roller supported, and free sandwich plates are plotted in Figs. 3, 4 and 5, respectively ($h_{1} /b = h_{3} /b = 0.1\,$).

Fig. 4

Trends of variations of the a first and b second natural frequencies of a sandwich plate with a roller supported edge

Fig. 5

Trends of variations of the a first and b second natural frequencies of a sandwich plate with a free edge

Recalling from Eq. (4) that the denominator of the elastic coefficients is a parabolic (even) function of the Poisson ratio, it may be expected that an absolute extremum occurs at $\nu = 0$, e.g., in Fig. 3. However, effect of the elasticity constants C₁₂ = C₂₁ of the core material, that are directly affected by magnitude and especially, sign of the Poisson ratio, cannot be ignored. For this reason, the mentioned transition point has not appeared in Figs. 3, 4 and 5.

Results presented in Figs. 3, 4 and 5 for the fundamental (first) natural frequency belong to the first lateral vibration and increase with the Poisson’s ratio with a higher rate for the plate with clamped edge. The second natural frequency of the clamped plate is associated with the second lateral (or radial) vibration mode. However, the second natural frequencies of the roller supported plate are associated with the second lateral (or radial) vibration mode for Poisson ratios larger than −0.75. The vibration mode associated with the Poisson’s ratios that are smaller than −0.75, is an axial one. This issue may be checked through investigation of the radial vibration modes depicted for the three edge conditions, in Figs. 6, 7 and 8, respectively. Therefore, for this range of Poisson’s ratio, the axial vibration mode occurs before the second lateral vibration mode. The Poisson ratio does not affect the mode shapes of the lateral vibration considerably. For this reason, the lateral vibration modes are not depicted here. Similarly, for the plate with free edge, the second vibration mode corresponds to Poisson ratios higher than $\nu_{2} = - 0.25$ are lateral (or radial) ones and the vibrations modes associated with the smaller Poisson ratios are axial ones.

Fig. 6

Variations of the radial vibration modes of the clamped sandwich plate, for a first and b second natural frequencies ($\nu_{c} \equiv \nu_{2} \,$)

Fig. 7

Variations of the radial vibration modes of the roller supported sandwich plate, for a first natural frequency, b second natural frequency with $\nu_{2} = - 0.5, \ldots ,0.5$, and c second natural frequency with $\nu_{2} = - 0.75$ and 0.9 ($\nu_{c} \equiv \nu_{2} \,$)

Fig. 8

Variations of the radial vibration modes of the sandwich plate with free edge, for a first natural frequency, b second natural frequency and positive Poisson ratios, and c second natural frequency and negative Poisson ratios ($\nu_{c} \equiv \nu_{2} \,$)

6.3 Effects of the core auxeticity for annular sandwich plates with various boundary conditions

Now, a comprehensive sensitivity analysis is performed for some annular sandwich plates having different lamination schemes and edge conditions. As before, the annular (a/b = 0.1) sandwich plate is considered to be thick to use advantages of the layerwise theory proposed in the present research ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.15$). In this regard, sandwich plates with aluminium/auxetic core/alumina and aluminium/auxetic core/steel are considered and the relevant results are given in Tables 5 and 6, respectively. Results of Table 6 are derived for two inner to outer radii ratios, i.e., a/b = 0.1 and 0.2. In Tables 5 and 6, the edge conditions are denoted by two terms phrases wherein the first one corresponds to the inner edge. The conclusions made in the preceding section for the circular sandwich plates are also confirmed by results of Tables 5 and 6; e.g., the natural frequencies increase monotonically as Poisson ratio decreases. Furthermore, influence of the auxeticity is more remarkable for the more rigid plate, i.e., the roller supported and the free-clamped sandwich plates. The discrepancies between present results and results of the 3D elasticity theory are still small and in many cases, ignorable.

6.4 Sandwich annular plates with orthotropic face sheets

Finally, influence of the core auxeticity on natural frequencies of annular sandwich plates with orthotropic face sheets is investigated for various radius ratios (a/b = 0.1 and 0.2), various lamination schemes, and various combinations of the edge conditions. The results are given in Tables 7 and 8 for moderately thick ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.15$) and thick ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.2$) plates, respectively. The face sheets are assumed to be fabricated from an ultra-high modulus graphite-epoxy material with the following material properties and types:

Table 7 A comparison among natural frequencies of moderately thick sandwich annular plates with orthotropic face sheets and auxetic cores ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.15$)

Table 8 A comparison among natural frequencies of thick sandwich annular plates with orthotropic face sheets and auxetic cores ($h_{1} /b = h_{3} /b = 0.1\,,\,\,h_{2} /b = 0.2$)

Material	$E_{r}$ (GPa)	$E_{\theta }$ (GPa)	$G_{rz}$ (GPa)	$v_{r\theta }$	$\rho$ (kg/m3)
Mat I	310	6.2	4.1	0.26	1613
Mat II	6.2	310	1.35	0.0052	1613

Materials indicated by Mat I and Mat II are identical with the exception of the fiber orientation that is radial and circumferential, in the first and second materials, respectively. Results of Tables 7 and 8 reveal that although Young modulus of the core is significantly lower than those of the face sheets, a trend similar to that observed in the preceding sections may be noticed; so that the natural frequencies grow monotonically with the decrease in the Poisson’s ratio. Moreover, effect of the core auxeticity is more remarkable for the more rigid plates (i.e., roller supported-clamped plates), higher radius ratios, and radial orientation of the fibers (i.e., for the Mat I/auxetic core/Mat I lamination scheme).

Investigation of the discrepancies between the 3D elasticity and present results in Tables 1, 2, 3, 4, 5 and 6 show that generally, the errors have not shown a robust trend and in some cases, this trend is an oscillatory one. Moreover, the relative errors are small. However, the main source of discrepancy may be attributed to natures of the employed solution techniques in derivation of the two categories of results; as ABAQUS uses the relatively accurate but approximate finite element method and present method uses a series solution that is sensitive to number of the terms of the series (although number of the terms is adopted based on an accurate convergence study).

7 Conclusions

In the present research, influences of using the core auxeticity on the free vibration of circular and annular sandwich plates with isotropic or orthotropic face sheets is investigated for the practical range of auxeticity and for different combinations of the boundary conditions, using a layerwise plate theory. The resulting equations are solved using Taylor’s transform whose center is located at the outer radius of the plate. After investigation of vibration behavior of a single-layer annular auxetic plate, a comprehensive parametric study including evaluation of effects of the auxeticity for sandwich plates with isotropic and orthotropic face sheets, symmetric and asymmetric layups, different core to sheet thickness, radius to thickness, and inner to outer radius ratios, and various boundary conditions is carried out. Novelties of the present research are listed at the end of the introduction section. The main practical conclusions may be summarized as:

• Present results are accurate and in an excellent agreement with results of the 3D theory of elasticity extracted from ABAQUS.

• The single-layer auxetic plates exhibit a trend with a transition state that begins by reductions in the natural frequencies by decreasing the Poisson’s ratio and ends by an opposite trend.

• Decreasing the Poisson’s ratio, considerably and monotonically increase the natural frequencies and rigidities of the circular/annular sandwich plates.

• The axeticity may affect the order of the mode shapes of the lateral vibration.

• The trend transition is dependent on many factors, among them: lamination scheme, thickness to radius ratio, radius ratio, material properties of the core, and boundary conditions.

• Influence of the core auxeticity is more remarkable for plates with more rigid edges, higher radius ratios, and plates with radially oriented fibers.