Natural frequency and bending analysis of heterogeneous polar orthotropic-faced sandwich panels in the existence of in-plane pre-stress

Abstract

In this paper, the effects of plane pre-stresses on the free vibration and static analyses of circular and annular sandwich panels are examined based on an accurate formulation, as first time. It is assumed that initially pre-stresses consist of in-plane normal (tensile/compressive) and pure bending stresses. New first-order shear deformation theory together with a layerwise approach for sandwich panel is utilized. The sandwich panels are made up of either orthotropic or heterogeneous polar orthotropic materials. Furthermore, piecewise-defined linear local in-plane displacements are adopted based on zigzag theory. The governing partial differential equations are extracted by implementing principle of minimum total potential energy. A unified analytical solution procedure is developed based on power series method for the analysis of heterogeneous initially stressed annular and circular sandwich panels with arbitrary boundary conditions. The transverse shear stress is precisely calculated by considering three-dimensional theory of elasticity. To validate the proposed formulation, the obtained results are compared with those of finite element method. After numerically demonstrating the accuracy of the method, the effects of different geometrical and material parameters, boundary conditions and in-plane pre-stresses on the free vibration and static behavior of circular and annular sandwich panels are investigated.

1 Introduction

Heterogeneous orthotropic materials have been used extensively in various and modern marine, nuclear and military industries. Nowadays, in some industries, heterogeneous functionally graded (FG) materials are just now becoming a primary choice for material. On the other hand, due to manufacturing process, initial stresses are presented in the structures which cannot be neglected. The initial stress may have some advantageous or disadvantages for some applications of laminated composite and/or sandwich panel. As a result, it is important to consider the effect of initial stress on the static and vibration behavior of laminated composite and sandwich panels.

Most of the presented studies on the initially stressed structures were carried out using equivalent single layer theories. Based on the first-order shear deformation theory (FSDT), some researchers investigated the vibration and buckling behavior of initially stressed plates with simply supported edges [1,2,3,4,5,6,7,8,9,10,11]. Brunelle and Robertso studied free vibration of thick plates by considering bending and extensional stresses [1]. The random vibration of an initially stressed simply supported plate on elastic foundation was studied by Chonan [2]. He obtained lowest buckling load for uniformly stressed rectangular plates. Yang [3] considered buckling and bending behavior of antisymmetric cross-ply laminates. He solved the governing equations analytically for simply supported boundary conditions. Nayar et al. [4] studied axisymmetric free vibration analysis of initially stressed annular plates by using the finite element method (FEM). Chen and Doong [5] considered effect of non-uniform initial stress in large amplitude analysis of transversely isotropic moderately thick plate. Chen et al. [6] investigated vibration behavior of transversely isotropic circular thick plates in the presence of initial stress based on the FSDT. In other work, Chen et al. [7] used Runge–Kutta method to analyze nonlinear large vibration of rectangular cross-ply laminated plates. Yang and Shieh [8] investigated vibration of orthotropic circular thick plate with initial by considering transverse shear and rotary inertia effects. Fung and his co-workers [9]– [12] studied the large amplitude vibration of initially stressed rectangular plates. They used Galerkin method to transform the partial differential equations to ordinary differential equations. Furthermore, they implemented the Runge–Kutta method to obtain the ratio of nonlinear to linear frequency. Chen [13] studied the buckling and vibration of composite plates. The effects of initial stresses on the natural frequencies and buckling loads of simply supported functionally graded plates were performed by Doong et al. [14] and Chen et al. [15] based on higher order deformation theory. Nayak et al. [16] studied the dynamic response of composite sandwich plates subjected to initial stresses based on a higher order deformation theory and using finite element method. Natural frequencies and mode shapes of in-plane pre-stressed sandwich panels with a viscoelastic core were investigated by Malekzadeh et al. [17]. Malekzadeh and Farajpour [18] investigated the initial radial stress effects on the axisymmetric free and forced vibrations of circular single- and double-layered nano-plates based on the nonlocal constitutive equations in conjunction with the classical plate theory and using Galerkin’s method. According to the classical plate theory, Khalili et al. [19] studied the static indentation response of an in-plane pre-stressed composite sandwich plate subjected to a rigid blunted indenter. Pichal et al. [20] determined critical buckling load and post-buckling path in pre-stressed columns using two- and three-dimensional FEM. Rahmani [21] derived governing equations of initially pre-stressed beam using Hamilton principle and presented analytical solution for vibration of nanobeam. Li [22] considered pre-stressed beams and determined natural frequency of them using Fast Fourier Transformation (FFT) and Hilbert–Huang Transform (HHT). Wu et al. [23] studied the instability behavior of beam–columns subjected to pre-stressed loads analytically and verified their model with FE solution.

On the other hand, structures made of heterogeneous materials have been extensively used in many engineering fields. So, investigation of these structures and development of the mathematical modeling for accurate analysis are essential. The effect of material non-homogeneity on the mechanical behaviors of a thick-walled sandwich cylindrical structure embedded with a FG interlayer was investigated by Wang and Wei [24]. Aragh et al. [25] studied the free vibration and obtained vibrational displacements of two-dimensional (2-D) FG fiber-reinforced curved panels with six-parameter power-law distribution using the 2-D generalized differential quadrature method (DQM). Nie et al. [26] analyzed an orthotropic FG beam with different material distribution along the thickness direction. Based on the exponential variation of material properties, Shariyat and Asemi [27] investigated buckling of rectangular orthotropic FGM plates. Thai et al. [28] analyzed the bending, buckling and free vibration of sandwich plates composed of FG face sheets and isotropic homogeneous core, based on a new FSDT. Fazzolari and Carrera [29] examined free vibration of anisotropic composite plates and isotropic/sandwich FGM plates by combining refined hierarchical plate models and a trigonometric Ritz method. Using state space differential quadrature method, static and free vibration analyses of functionally graded sandwich plates were performed by Alibeigloo and Alizadeh [30]. Pandey and Pradyumna [31] used a layerwise finite element formulation for free vibration analysis of FG sandwich plates in thermal environment. The non-linear free vibration and static deformations of FG orthotropic cylindrical shells with exponential variation of material properties were analyzed by Sofiyev [32, 33], Nie and Batra [34], respectively. Based on the modified strain gradient theory and the spline finite strip method, buckling and free vibrations of the FGM thin micro-plate were studied by Mirsalehi et al. [35]. Free vibration and damping analyses of viscoelastic two-directional functionally graded plates were performed by Shariyat and Alipour [36]. Alipour and Shariyat [37] developed the power series solution for axisymmetric bending and stress analysis of circular functionally graded sandwich plates. Alipour presented new analytical method for bending and stress analysis of elastically restrained sandwich circular [38] and annular [39] plates with FG face sheets and core. Alipour [40] investigated transient bending analysis of a sandwich plate with viscoelastic edge that sandwich plate is fabricated from heterogeneous face sheets. Akbarov et al. [41] investigated the effect of initial stresses in the natural frequency of sphere. They considered that the sphere is made from FGM and filled with compressive fluid.

According to the above literature survey, a few works dedicated to the effect of initial pre-stresses in static and vibration of laminated sandwich panels. In this regard, the presented study investigates effect of in-plane pre-stresses on the static and free vibration response of sandwich circular and annular plates with FG polar orthotropic face sheets. The main novelties or superiorities of this study can be mentioned as follows:

• Free vibration and static analyses of initially stressed circular and annular sandwich panels are examined. It is assumed that initially pre-stresses consist of in-plane normal (tensile/compressive) and pure bending stresses.

• Using the presented formulation, sandwich panels with heterogeneous polar orthotropic materials layers can be analyzed. The variations of the material properties of each layer can be described by a general function in the radial direction. Using the applied coefficients of the radial variations, the presented procedure enables a more accurate monitoring of the material properties.

• For analysis of multi-layered structures, equivalent single-layer theories are inaccurate or erroneous in most circumstances. To overcome these shortcomings, The governing differential equations are derived based on the layerwise-zigzag theory and using the minimum total potential energy principle.

• In contrast to the displacement discontinuity, continuity of the transverse shear stress is satisfied.

• The power series method is developed for the analysis of heterogeneous plates, and a unified solution procedure was proposed for the analysis of annular and circular sandwich plates.

2 Governing differential equations of initially stressed heterogeneous polar orthotropic sandwich panels

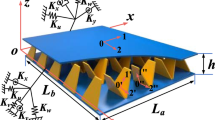
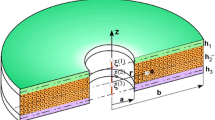
In this section, the governing differential equations are derived based on the principle of minimum total potential energy in conjugation with the layerwise-zigzag theory. As shown in Fig. 1, top and bottom face sheets and core thickness are denoted by h_t, h_b and h_c, respectively. The core is subjected to initially in-plane normal stress (tensile /compressive)$\overline{\sigma }_{n}$ and bending $\overline{\sigma }_{m}$ stress.

$$\begin{aligned} {\overline{\sigma }}_{r} &= {\overline{\sigma }_{n}} + \frac{2}{{h_{c} }}z^{(c)} {\overline{\sigma }}_{m} \\ \delta &= \frac{{\overline{\sigma }_{m} }}{{\overline{\sigma }_{n} }}, \\ \end{aligned}$$

(1)

Fig. 1 

Annular sandwich panels subjected to the in-plane pre-stresses

where δ is the initial stress ratio that considered ratio of bending to normal stress. If the transverse normal strain can be neglected, the Hooke's generalized stress–strain law in polar coordinate system, (r, θ, z), may be expressed as

$$\begin{gathered} \left\{ \begin{gathered} \sigma_{r}^{(i)} \hfill \\ \sigma_{\theta }^{(i)} \hfill \\ \tau_{rz}^{(i)} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {C_{11}^{(i)} (r)} & {C_{12}^{(i)} (r)} & 0 \\ {C_{12}^{(i)} (r)} & {C_{22}^{(i)} (r)} & 0 \\ 0 & 0 & {C_{33}^{(i)} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{r}^{(i)} \hfill \\ \varepsilon_{\theta }^{(i)} \hfill \\ \gamma_{rz}^{(i)} \hfill \\ \end{gathered} \right\} \hfill \\ C_{11}^{(i)} (r) = \frac{{E_{r}^{(i)} }}{{1 - v_{r\theta }^{(i)} v_{\theta r}^{(i)} }}P^{(i)} (r), \hfill \\ C_{12}^{(i)} (r) = \frac{{v_{\theta r}^{(i)} E_{r}^{(i)} }}{{1 - v_{r\theta }^{(i)} v_{\theta r}^{(i)} }}P^{(i)} (r), \hfill \\ C_{22}^{(i)} (r) = \frac{{E_{\theta }^{(i)} }}{{1 - v_{r\theta }^{(k)} v_{\theta r}^{(k)} }}P^{(i)} (r)\, \hfill \\ C_{33}^{(i)} (r) = G_{rz}^{(i)} \,\,P^{(i)} (r),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ P^{(i)} (r) = \left[ {1 + \gamma_{i} \left( {r - b} \right)^{{\lambda_{i} }} } \right],\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = t,b. \hfill \\ \end{gathered}$$

(2)

C_kl, E_k, G_kl, and ν_kl symbols denote the elasticity coefficients, Young’s modulus, shear modulus, and Poisson’s ratio, respectively. The superscript (i) represents the layer, i.e. top and bottom face sheets, respectively. P^(t)(r) and P^(b)(r) are the coefficient of radial variation of Young’s modulus and shear modulus for top and bottom face sheets, respectively. The compatibility relation is as follows:

$$\frac{{v_{r\theta } }}{{E_{r} }} = \frac{{v_{\theta \,r} }}{{E_{\theta } }}.$$

(3)

The density of face sheets are varied along the radial direction as the following form:

$$\rho^{(i)} (r) = \overline{\rho }^{(i)} L^{(i)} (r)\,\,\,\,\,\,\,L^{(i)} (r) = \left[ {1 + \mu^{(i)} \left( {r - b} \right)^{{\eta^{(i)} }} } \right]\,\,\,\,\,\,\,\,\,\,\,\,i = t,b.$$

(4)

In the above relation, γ_i, λ_i, μ⁽ⁱ⁾ and η⁽ⁱ,⁾ i = t,b are the face sheets inhomogeneity parameters. Indeed, E_r⁽ⁱ⁾ and $\overline{\rho }^{(i)}$ are the material properties at the outer radius of face sheets. Based on the layerwise-zigzag theory with the linear variation of the displacement fields, the in-plane displacement of each layer may be expressed as

$$u_{i} = u_{0}^{(i)} + z^{(i)} \phi_{r}^{(i)} \,\,\,\,\,\,\,\,\,\,\,\,\,\,i = t,c,b,$$

(5)

where c denotes the core parameter, u₀⁽ⁱ⁾ is the radial displacement component of the mid plane, φ_r⁽ⁱ⁾ is the local rotation and $z^{(i)} \,\left( { - h_{i} /2 \le z^{(i)} \le h_{i} /2} \right)$ is the transverse local coordinate of each layer. By incorporating the continuity of the displacement components at the interfaces between the layers, u₀^(t) and u₀^(b) may be expressed as

$$\begin{aligned} u_{0}^{(t)} = & u_{0}^{(c)} + \frac{{h_{c} }}{2}\phi_{r}^{(c)} + \frac{{h_{t} }}{2}\phi_{r}^{(t)} \\ u_{0}^{(b)} = & u_{0}^{(c)} - \frac{{h_{c} }}{2}\phi_{r}^{(c)} - \frac{{h_{b} }}{2}\phi_{r}^{(b)} . \\ \end{aligned}$$

(6)

The Cauchy’s strain–displacement relations for each layer are

$$\varepsilon_{r}^{(i)} = \frac{{\partial u^{(i)} }}{\partial r},\,\,\,\,\,\,\,\,\,\varepsilon_{\theta }^{(i)} = \frac{{u^{(i)} }}{r},\,\,\,\,\,\,\,\,\,\varepsilon_{rz}^{(i)} = \frac{{\partial u^{(i)} }}{\partial z} + \frac{\partial w}{{\partial r}}.$$

(7)

For the free vibration analysis, the equations of motion can be derived using minimum total potential energy principle, as follows:

$$\delta \Pi = \delta U + \delta K - \delta W = 0,$$

(8)

where δU, δK and δW are increments of the strain energy, kinetic energy and work done by external applied loads, respectively:

$$\delta U = \int\limits_{V} {\left( {\sigma_{r}^{(i)} \delta \varepsilon_{r}^{(i)} + \sigma_{\theta }^{(i)} \delta \varepsilon_{\theta }^{(i)} + \tau_{rz}^{(i)} \delta \gamma_{rz}^{(i)} } \right)dV + \int {\overline{\sigma }_{r} \left( {u_{c,r}^{2} + w_{,r}^{2} } \right)dV} } ,$$

(9)

$$\delta K = \int\limits_{V} {\rho \left( {\ddot{u}_{i} \delta u_{i} + \ddot{w}\delta w} \right)dV} ,$$

(10)

$$\delta W = \int\limits_{A} {q\delta w\,\,dA} .$$

(11)

Substituting Eqs. (9) to (11) into Eq. (8) and using Eqs. (5) to (7), and performing the integration by parts, the following governing differential equations are extracted after some manipulations:

$$\begin{aligned} & \frac{1}{r}\frac{\partial }{\partial r}\left( {rN_{r}^{(t)} + rN_{r}^{(c)} + rN_{r}^{(b)} } \right) - \frac{1}{r}\left( {N_{\theta }^{(t)} + N_{\theta }^{(c)} + N_{\theta }^{(b)} } \right) + h_{c} \overline{\sigma }_{n} \nabla^{2} u_{0}^{(c)} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \nabla^{2} \phi_{r} \hfill \\ & \quad = \left( {I_{0}^{(t)} + I_{0}^{(c)} + I_{0}^{(b)} } \right)\ddot{u}_{0}^{(c)} + \frac{{h_{t} }}{2}I_{0}^{(t)} \ddot{\phi }_{r}^{(t)} + \frac{{h_{c} }}{2}\left( {I_{0}^{(t)} - I_{0}^{(b)} } \right)\ddot{\phi }_{r}^{(c)} - \frac{{h_{b} }}{2}I_{0}^{(b)} \ddot{\phi }_{r}^{(b)} , \hfill \end{aligned}$$

(12)

$$\begin{aligned} & \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{h_{t} }}{2}N_{r}^{(t)} + rM_{r}^{(t)} } \right) - \frac{1}{r}\left( {\frac{{h_{t} }}{2}N_{\theta }^{(t)} + M_{\theta }^{(t)} } \right) - Q_{rz}^{(t)} \hfill \\ & \quad = \frac{{h_{t} }}{2}I_{0}^{(t)} \ddot{u}_{0}^{(c)} + \frac{{h_{t} h_{c} }}{4}I_{0}^{(t)} \ddot{\phi }_{r}^{(c)} + \left( {I_{2}^{(t)} + \frac{{h_{t}^{2} }}{4}I_{0}^{(t)} } \right)\ddot{\phi }_{r}^{(t)} , \hfill \end{aligned}$$

(13)

$$\begin{aligned} & \frac{1}{r}\frac{\partial }{\partial r}\left[ {r\frac{{h_{c} }}{2}\left( {N_{r}^{(t)} - N_{r}^{(b)} } \right) + rM_{r}^{(c)} } \right] - \frac{{h_{c} }}{2}\frac{1}{r}\left( {N_{\theta }^{(t)} - N_{\theta }^{(b)} } \right) - \frac{{M_{\theta }^{(2)} }}{r} - Q_{rz}^{(c)} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \nabla^{2} u_{0}^{(c)} + \frac{{h_{c}^{3} }}{12}\overline{\sigma }_{n} \nabla^{2} \phi_{r}^{(c)} \hfill \\ & \quad = \frac{{h_{c} }}{2}\left( {I_{0}^{(t)} - I_{0}^{(b)} } \right)\ddot{u}_{0}^{(c)} + \frac{{h_{t} h_{c} }}{4}I_{0}^{(t)} \ddot{\phi }_{r}^{(t)} + \left( {\frac{{h_{c}^{2} }}{4}I_{0}^{(t)} + I_{2}^{(c)} + \frac{{h_{c}^{2} }}{4}I_{0}^{(b)} } \right)\ddot{\phi }_{r}^{(2)} + \frac{{h_{c} h_{b} }}{4}I_{0}^{(b)} \ddot{\phi }_{r}^{(b)} , \hfill \end{aligned}$$

(14)

$$\begin{aligned} \frac{1}{r}\frac{\partial }{\partial r}&\left( { - \frac{{h_{b} }}{2}rN_{r}^{(b)} + rM_{r}^{(b)} } \right) + \frac{1}{r}\left( {\frac{{h_{b} }}{2}N_{\theta }^{(b)} - M_{\theta }^{(b)} } \right) - Q_{rz}^{(b)} \\ &= - \frac{{h_{b} }}{2}I_{0}^{(b)} \ddot{u}_{0}^{(c)} + \frac{{h_{c} h_{b} }}{4}I_{0}^{(b)} \ddot{\phi }_{r}^{(c)} + \left( {I_{2}^{(b)} + \frac{{h_{b}^{2} }}{4}I_{0}^{(b)} } \right)\ddot{\phi }_{r}^{(b)} , \hfill \\ \end{aligned}$$

(15)

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {rQ_{r}^{(t)} + rQ_{r}^{(c)} + rQ_{r}^{(b)} } \right) + h_{c} \overline{\sigma }_{n} \nabla^{2} w = q + \left( {I_{0}^{(t)} + I_{0}^{(c)} + I_{0}^{(b)} } \right)\ddot{w},$$

(16)

where $\nabla^{2} = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}} \right)$ is the Laplacian operator in the radial direction. M, N and Q are stress resultants that are defined in appendix.

The higher order mass inertia, I_k, are defined as

$$I_{k}^{{(i)}} = \int\limits_{{ - \tfrac{{h_{i} }}{{2}}}}^{{\tfrac{{h_{i} }}{2}}} {\rho ^{{(i)}} (r)z^{{(i)^{k} }} dz^{{(i)}} = \bar{I}_{k}^{{(i)}} L^{{(i)}} (r), \,\, \left\{ {\begin{array}{*{20}l} {\bar{I}_{0}^{{(i)}} } \\ {\bar{I}_{2}^{{(i)}} } \\ \end{array} } \right\}} = \left\{ {\begin{array}{*{20}c} {h_{i} } \\ {\tfrac{{h_{i}^{3} }}{{12}}} \\ \end{array} } \right\}\bar{\rho }^{{(i)}} \quad i = t,b \,\, k = 0,2$$

(17)

Using the above relations, the governing Eqs. (12) to (16) may be rewritten in terms of displacement field components as

$$\begin{aligned}& \left[ {\overline{A}_{11}^{(t)} P^{(t)} (r) + A_{11}^{(c)} + \overline{A}_{11}^{(b)} P^{(b)} (r) + h_{2} \overline{\sigma }_{n} } \right]\nabla^{2} u_{0}^{(c)} - \left[ {\overline{A}_{22}^{(t)} P^{(t)} (r) + A_{22}^{(c)} + \overline{A}_{22}^{(b)} P^{(b)} (r)} \right]\frac{{u_{0}^{(c)} }}{{r^{2} }} \hfill \\& \quad + \frac{{h_{c} }}{2}\left[ {\overline{A}_{11}^{(t)} P^{(t)} (r) - \overline{A}_{11}^{(b)} P^{(b)} (r) + \frac{{h_{2}^{2} }}{6}\overline{\sigma }_{m} } \right]\nabla^{2} \phi_{r}^{(c)} - \frac{{h_{c} }}{2}\left[ {\overline{A}_{22}^{(t)} P^{(t)} (r) - \overline{A}_{22}^{(b)} P^{(b)} (r)} \right]\frac{{\phi_{r}^{(c)} }}{{r^{2} }} \hfill \\ & \quad+ \frac{{h_{t} }}{2}P^{(t)} (r)\left( {\overline{A}_{11}^{(t)} \nabla^{2} - \overline{A}_{22}^{(t)} \frac{1}{{r^{2} }}} \right)\phi_{r}^{(t)} + \frac{{\partial P^{(t)} (r)}}{\partial r}\left( {\overline{A}_{11}^{(t)} \frac{\partial }{\partial r} + \frac{{\overline{A}_{12}^{(t)} }}{r}\,} \right)\left( {u_{0}^{(c)} + \frac{{h_{t} }}{2}\phi_{r}^{(t)} + \frac{{h_{c} }}{2}\phi_{r}^{(c)} } \right) \hfill \\ & \quad- \frac{{h_{b} }}{2}P^{(b)} (r)\left( {\overline{A}_{11}^{(b)} \nabla^{2} - \overline{A}_{22}^{(b)} \frac{1}{{r^{2} }}} \right)\phi_{r}^{(b)} + \frac{{\partial P^{(b)} (r)}}{\partial r}\left( {\overline{A}_{11}^{(b)} \frac{\partial }{\partial r} + \frac{{\overline{A}_{12}^{(b)} }}{r}\,} \right)\left( {u_{0}^{(c)} - \frac{{h_{b} }}{2}\phi_{r}^{(b)} - \frac{{h_{c} }}{2}\phi_{r}^{(c)} } \right) \hfill \\ & \,\,\,= \left[ {\overline{I}_{0}^{(t)} \,\,L^{(t)} (r) + \overline{I}_{0}^{(c)} + \overline{I}_{0}^{(b)} \,\,L^{(b)} (r)} \right]\ddot{u}_{0}^{(c)} + \frac{{h_{t} }}{2}\overline{I}_{0}^{(t)} \,\,L^{(t)} (r)\ddot{\phi }_{r}^{(t)} + \frac{{h_{c} }}{2}\left[ {\overline{I}_{0}^{(t)} L^{(t)} (r) - \overline{I}_{0}^{(b)} L^{(b)} (r)} \right]\ddot{\psi }_{r}^{(2)} \hfill \\ & \quad - \frac{{h_{b} }}{2}\overline{I}_{0}^{(b)} \,L^{(b)} (r)\ddot{\phi }_{r}^{(b)} , \hfill \end{aligned}$$

(18)

$$\begin{aligned} & \frac{{h_{t} }}{2}P^{(t)} (r)\left( {\overline{A}_{11}^{(t)} \nabla^{2} - \overline{A}_{22}^{(t)} \frac{1}{{r^{2} }}} \right)u_{0}^{(c)} + \left( {\frac{{h_{t}^{2} }}{4}\overline{A}_{11}^{(t)} + \overline{D}_{11}^{(t)} } \right)P^{(t)} (r)\nabla^{2} \phi_{r}^{(t)} - \left( {\frac{{h_{t}^{2} }}{4}\overline{A}_{22}^{(t)} + \overline{D}_{22}^{(t)} } \right)P^{(t)} (r)\frac{{\phi_{r}^{(t)} }}{{r^{2} }} \hfill \\ & \quad + \frac{{h_{t} h_{c} }}{4}P^{(t)} (r)\left( {\overline{A}_{11}^{(t)} \nabla^{2} - \overline{A}_{22}^{(t)} \frac{1}{{r^{2} }}} \right)\phi_{r}^{(c)} - \overline{A}_{33}^{(t)} P^{(t)} (r)\left( {\phi_{r}^{(1)} + \frac{\partial w}{{\partial r}}} \right) + \frac{{\partial P^{(t)} (r)}}{\partial r}\left( {\overline{D}_{11}^{(t)} \frac{\partial }{\partial r} + \frac{{\overline{D}_{12}^{(t)} }}{r}} \right)\phi_{r}^{(t)} \hfill \\ & \quad + \frac{{h_{t} }}{2}\frac{{\partial P^{(t)} (r)}}{\partial r}\left( {\overline{A}_{11}^{(t)} \frac{\partial }{\partial r} + \frac{{\overline{A}_{12}^{(t)} }}{r}} \right)\left( {u_{0}^{(c)} + \frac{{h_{t} }}{2}\phi_{r}^{(t)} + \frac{{h_{c} }}{2}\phi_{r}^{(c)} } \right) \hfill \\ & \,\, = \frac{{h_{t} }}{2}\overline{I}_{0}^{(t)} L^{(t)} (r)\left( {\ddot{u}_{0}^{(c)} + \frac{{h_{t} }}{2}\ddot{\phi }_{r}^{(t)} + \frac{{h_{c} }}{2}\ddot{\phi }_{r}^{(c)} } \right) + \overline{I}_{2}^{(t)} L^{(t)} (r)\ddot{\phi }_{r}^{(t)} , \hfill \end{aligned}$$

(19)

$$\begin{aligned} & \frac{{h_{c} }}{2}\left[ {\overline{A}_{11}^{(t)} P^{(t)} (r) - \overline{A}_{11}^{(b)} P^{(b)} (r) + \frac{{h_{c} }}{3}\overline{\sigma }_{m} } \right]\nabla^{2} u_{0}^{(c)} - \frac{{h_{c} }}{2}\left[ {\overline{A}_{22}^{(t)} P^{(t)} (r) - \overline{A}_{22}^{(b)} P^{(b)} (r)} \right]\frac{{u_{0}^{(c)} }}{{r^{2} }} \hfill \\ & \quad + \frac{{h_{t} h_{c} }}{4}\overline{A}_{11}^{(t)} P^{(t)} (r)\nabla^{2} \phi_{r}^{(t)} - \frac{{h_{t} h_{c} }}{4}\overline{A}_{22}^{(t)} P^{(t)} (r)\frac{{\phi_{r}^{(t)} }}{{r^{2} }} + \frac{{h_{2} h_{3} }}{4}\overline{A}_{11}^{(b)} P^{(b)} (r)\nabla^{2} \phi_{r}^{(b)} \, \hfill \\ & \quad- \frac{{h_{c} h_{b} }}{4}\overline{A}_{22}^{(b)} P^{b)} (r)\frac{{\phi_{r}^{(b)} }}{{r^{2} }} + \left[ {\frac{{h_{t}^{2} }}{4}\overline{A}_{11}^{(t)} P^{(t)} (r) + D_{11}^{(c)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{11}^{(b)} P^{(b)} (r) + \frac{{h_{c}^{3} }}{12}\overline{\sigma }_{n} } \right]\nabla^{2} \phi_{r}^{(c)} - A_{33}^{(c)} \left( {\phi_{r}^{(c)} + \frac{\partial w}{{\partial r}}} \right) \hfill \\ & \quad- \left[ {\frac{{h_{c}^{2} }}{4}\overline{A}_{22}^{(t)} P^{(t)} (r) + D_{22}^{(c)} + \frac{{h_{c}^{2} }}{4}\overline{A}_{22}^{(b)} P^{(b)} (r)} \right]\frac{{\phi_{r}^{(c)} }}{{r^{2} }} + \frac{{h_{c} }}{2}\frac{{\partial P^{(t)} (r)}}{\partial r}\left( {\overline{A}_{11}^{(t)} \frac{\partial }{\partial r} + \frac{{\overline{A}_{12}^{(t)} }}{r}} \right)\left( {u_{0}^{(c)} + \frac{{h_{t} }}{2}\phi_{r}^{(t)} + \frac{{h_{c} }}{2}\phi_{r}^{(c)} } \right) \hfill \\ & \quad - \frac{{h_{c} }}{2}\frac{{\partial P^{(b)} (r)}}{\partial r}\left( {\overline{A}_{11}^{(b)} \frac{\partial }{\partial r} + \frac{{\overline{A}_{12}^{(b)} }}{r}\,} \right)\left( {u_{0}^{(c)} - \frac{{h_{b} }}{2}\psi_{r}^{(b)} - \frac{{h_{c} }}{2}\psi_{r}^{(c)} } \right) = \frac{{h_{c} }}{2}\overline{I}_{0}^{(t)} L^{(t)} (r)\left( {\ddot{u}_{0}^{(c)} + \frac{{h_{t} }}{2}\ddot{\phi }_{r}^{(t)} + \frac{{h_{c} }}{2}\ddot{\phi }_{r}^{(c)} } \right) \hfill \\ &\quad + \overline{I}_{2}^{(c)} \ddot{\phi }_{r}^{(c)} - \frac{{h_{c} }}{2}\overline{I}_{0}^{(b)} L^{(b)} (r)\left( {\ddot{u}_{0}^{(c)} - \frac{{h_{c} }}{2}\ddot{\phi }_{r}^{(c)} - \frac{{h_{b} }}{2}\ddot{\phi }_{r}^{(b)} } \right), \hfill \end{aligned}$$

(20)

$$\begin{aligned} & - \frac{{h_{b} }}{2}P^{(b)} (r)\left( {\overline{A}_{11}^{(b)} \nabla^{2} - \overline{A}_{22}^{(b)} \frac{1}{{r^{2} }}} \right)u_{0}^{(c)} + \left( {\overline{D}_{11}^{(b)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{11}^{(b)} } \right)P^{(b)} (r)\nabla^{2} \phi_{r}^{(b)} - \left( {\overline{D}_{22}^{(b)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{22}^{(b)} } \right)P^{(b)} (r)\frac{{\phi_{r}^{(b)} }}{{r^{2} }} \hfill \\ & \quad + \frac{{h_{c} h_{b} }}{4}P^{(b)} (r)\left( {\overline{A}_{11}^{(b)} \nabla^{2} - \overline{A}_{22}^{(b)} \frac{1}{{r^{2} }}} \right)\phi_{r}^{(c)} - \overline{A}_{33}^{(b)} P^{(b)} (r)\left( {\phi_{r}^{(b)} + \frac{\partial w}{{\partial r}}} \right) + \frac{{\partial P^{(b)} (r)}}{\partial r}\left( {\overline{D}_{11}^{(b)} \frac{\partial }{\partial r} + \frac{{\overline{D}_{12}^{(b)} }}{r}} \right)\phi_{r}^{(b)} \hfill \\ & \quad - \frac{{h_{b} }}{2}\frac{{\partial P^{(b)} (r)}}{\partial r}\left[ {\overline{A}_{11}^{(b)} \frac{\partial }{\partial r} + \frac{{\overline{A}_{12}^{(b)} }}{r}} \right]\,\left( {u_{0}^{(c)} - \frac{{h_{b} }}{2}\phi_{r}^{(b)} - \frac{{h_{c} }}{2}\psi_{r}^{(c)} } \right) = - \frac{{h_{b} }}{2}\overline{I}_{0}^{(b)} L^{(b)} (r)\left( {\ddot{u}_{0}^{(c)} - \frac{{h_{c} }}{2}\ddot{\phi }_{r}^{(c)} - \frac{{h_{b} }}{2}\ddot{\phi }_{r}^{(b)} } \right) \hfill \\ & \quad + \overline{I}_{2}^{(b)} L^{(b)} (r)\ddot{\phi }_{r}^{(b)} , \hfill \end{aligned}$$

(21)

$$\begin{aligned} & \left[ {\overline{A}_{33}^{(t)} P^{(t)} (r) + A_{33}^{(c)} + \overline{A}_{33}^{(b)} P^{(b)} (r) + h_{c} \overline{\sigma }_{n} } \right]\nabla^{2} w + \overline{A}_{33}^{(t)} P^{(t)} (r)\left( {\frac{\partial }{\partial r} + \frac{1}{r}} \right)\phi_{r}^{(t)} + A_{33}^{(c)} \left( {\frac{\partial }{\partial r} + \frac{1}{r}} \right)\phi_{r}^{(c)} \hfill \\ & \quad + \overline{A}_{33}^{(b)} P^{(b)} (r)\left( {\frac{\partial }{\partial r} + \frac{1}{r}} \right)\phi_{r}^{(b)} + \overline{A}_{33}^{(t)} \frac{{\partial P^{(t)} (r)}}{\partial r}\left( {\phi_{r}^{(t)} + \frac{\partial w}{{\partial r}}} \right) + \overline{A}_{33}^{(b)} \frac{{\partial P^{(b)} (r)}}{\partial r}\left( {\phi_{r}^{(b)} + \frac{\partial w}{{\partial r}}} \right) \hfill \\ & \,\,= - q + \left[ {\overline{I}_{0}^{(t)} P^{(t)} (r) + \overline{I}_{0}^{(c)} + \overline{I}_{0}^{(b)} P^{(b)} (r)} \right]\ddot{w}. \hfill \end{aligned}$$

(22)

3 Mathematical form of edge conditions and regularity conditions

There are different types of boundary conditions which can be applied at the outer edges of annular plate. These conditions are

Clamped immovable edge:

$$u_{0}^{(c)} = \phi_{r}^{(t)} = \phi_{r}^{(c)} = \phi_{r}^{(b)} = w = 0$$

(23)

Simply supported immovable edge:

$$\left\{ \begin{gathered} u_{0}^{(c)} = 0 \hfill \\ \frac{{h_{t} }}{2}N_{r}^{(t)} + M_{r}^{(t)} = 0 \hfill \\ \frac{{h_{c} }}{2}N_{r}^{(t)} + M_{r}^{(c)} - \frac{{h_{c} }}{2}N_{r}^{(b)} + \frac{{h_{c}^{3} }}{12}\overline{\sigma }_{n} \frac{{\partial \phi_{r}^{(c)} }}{\partial r} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \frac{{\partial u_{0}^{(c)} }}{\partial r} = 0 \hfill \\ - \frac{{h_{b} }}{2}N_{r}^{(b)} + M_{r}^{(b)} = 0 \hfill \\ w = 0 \hfill \\ \end{gathered} \right.$$

(24)

Roller-supported movable edge:

$$\left\{ \begin{gathered} N_{r}^{(t)} + N_{r}^{(c)} + N_{r}^{(b)} + h_{c} \overline{\sigma }_{n} \frac{{\partial u_{0}^{(c)} }}{\partial r} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \frac{{\partial \phi_{r}^{(c)} }}{\partial r} = 0 \hfill \\ \frac{{h_{t} }}{2}N_{r}^{(t)} + M_{r}^{(t)} = 0 \hfill \\ \frac{{h_{c} }}{2}N_{r}^{(t)} + M_{r}^{(c)} - \frac{{h_{c} }}{2}N_{r}^{(b)} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \frac{{\partial u_{0}^{(c)} }}{\partial r} + \frac{{h_{c}^{3} }}{12}\overline{\sigma }_{n} \frac{{\partial \phi_{r}^{(c)} }}{\partial r} = 0 \hfill \\ - \frac{{h_{b} }}{2}N_{r}^{(b)} + M_{r}^{(b)} = 0 \hfill \\ w = 0 \hfill \\ \end{gathered} \right..$$

(25)

Free edge:

$$\left\{ \begin{gathered} N_{r}^{(t)} + N_{r}^{(c)} + N_{r}^{(b)} + h_{c} \overline{\sigma }_{n} \frac{{\partial u_{0}^{(c)} }}{\partial r} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \frac{{\partial \phi_{r}^{(c)} }}{\partial r} = 0 \hfill \\ \frac{{h_{t} }}{2}N_{r}^{(t)} + M_{r}^{(t)} = 0 \hfill \\ \frac{{h_{c} }}{2}N_{r}^{(t)} + M_{r}^{(c)} - \frac{{h_{c} }}{2}N_{r}^{(b)} + \frac{{h_{c}^{2} }}{6}\overline{\sigma }_{m} \frac{{\partial u_{0}^{(c)} }}{\partial r} + \frac{{h_{c}^{3} }}{12}\overline{\sigma }_{n} \frac{{\partial \phi_{r}^{(c)} }}{\partial r} = 0 \hfill \\ - \frac{{h_{b} }}{2}N_{r}^{(b)} + M_{r}^{(b)} = 0 \hfill \\ Q_{r}^{(t)} + Q_{r}^{(c)} + Q_{r}^{(b)} + h_{c} \overline{\sigma }_{n} \frac{\partial w}{{\partial r}} = 0 \hfill \\ \end{gathered} \right..$$

(26)

Moreover, at the center of axisymmetric circular plate, the regularity conditions should be satisfied

$$u_{0}^{(c)} = \phi_{r}^{(t)} = \phi_{r}^{(c)} = \phi_{r}^{(b)} = \frac{\partial w}{{\partial r}} = 0.$$

(27)

4 Power series procedure for static and free vibration analyses

To utilized power series solution, Kantorovich-type separation of variables are applied in this study. Using finite Taylor series transformation about the outer radius of the sandwich plate, the unknown displacement functions may be expressed as follows:

$$\begin{gathered} u_{0}^{(c)} (r,t) = \sum\limits_{n = 0}^{N} {F_{n}^{(1)} \left( {r - b} \right)^{n} } e^{i\omega t} ,\,\,\,\,\,\,\,\,\,\,\phi_{r}^{(t)} = \sum\limits_{n = 0}^{N} {F_{n}^{(2)} \left( {r - b} \right)^{n} } e^{i\omega t} ,\,\,\,\,\,\,\,\,\phi_{r}^{(c)} = \sum\limits_{n = 0}^{N} {F_{n}^{(3)} \left( {r - b} \right)^{n} e^{i\omega t} } , \hfill \\ \phi_{r}^{(b)} = \sum\limits_{n = 0}^{N} {F_{n}^{(4)} \left( {r - b} \right)^{n} e^{i\omega t} } ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,w = \sum\limits_{n = 0}^{N} {F_{n}^{(5)} \left( {r - b} \right)^{n} e^{i\omega t} } . \hfill \\ \end{gathered}$$

(28)

It should be noted that the external applied load, q, or natural frequency, ω, should be set equal to zero either for free vibration or static analysis.

Inserting for the displacement components from Eq. (28) into the governing Eqs. (18) to (22) and considering Taylor’s series expansion of $\frac{1}{r}$ and $\frac{1}{{r^{2} }}$ and performing some manipulations, the transformed form of the governing differential equations may be extracted as

$$\begin{gathered} \sum\limits_{{n = 0}}^{N} {\left\{ {\left( {\bar{A}_{{11}}^{{(t)}} + A_{{11}}^{{(c)}} + \bar{A}_{{11}}^{{(b)}} } \right)\left[ {\left( {n + 2} \right)\left( {n + 1} \right)F_{{n + 2}}^{{(1)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} \left( {n - m + 1} \right)F_{{n + 2 - m}}^{{(1)}} } } \right]} \right.} \hfill \\ \bar{A}_{{11}}^{{(t)}} \gamma ^{{(t)}} \left[ {(n - \lambda ^{{(t)}} + 2)(n - \lambda ^{{(t)}} + 1)F_{{n + 2 - \lambda ^{{(t)}} }}^{{(1)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(t)}} - m + 1)F_{{n - \lambda ^{{(t)}} - m + 1}}^{{(1)}} } } \right] \hfill \\ + \bar{A}_{{11}}^{{(b)}} \gamma ^{{(b)}} \left( {(n - \lambda ^{{(b)}} + 2)(n - \lambda ^{{(b)}} + 1)F_{{n + 2 - \lambda ^{{(b)}} }}^{{(1)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(b)}} - m + 1)F_{{n - \lambda ^{{(b)}} - m + 1}}^{{(1)}} } } \right) + \hfill \\ - \left( {\bar{A}_{{22}}^{{(t)}} + A_{{22}}^{{(c)}} + \bar{A}_{{22}}^{{(b)}} } \right)\sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} F_{{n - m}}^{{(1)}} } - \bar{A}_{{22}}^{{(t)}} \gamma ^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} F_{{n - \lambda ^{{(t)}} - m}}^{{(1)}} } \hfill \\ - \bar{A}_{{22}}^{{(3)}} \gamma ^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{s + 2}} } U_{{n - \lambda ^{{(b)}} - m}} + \frac{{h_{t} }}{2}\bar{A}_{{11}}^{{(1)}} \left( {(n + 2)(n + 1)F_{{n + 2}}^{{(2)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{s + 1}} (n - m + 1)F_{{n - m + 1}}^{{(2)}} } } \right) \hfill \\ + \frac{{h_{t} }}{2}\bar{A}_{{11}}^{{(t)}} \gamma ^{{(t)}} \left( {(n - \lambda ^{{(t)}} + 2)(n - \lambda ^{{(t)}} + 1)F_{{n - \lambda ^{{(t)}} + 2}}^{{(2)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(t)}} - m + 1)F_{{n - \lambda ^{{(t)}} - m + 1}}^{{(2)}} } } \right) \hfill \\ - \frac{{h_{t} }}{2}\bar{A}_{{22}}^{{(t)}} \sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - m}}^{{(2)}} - \frac{{h_{1} }}{2}\bar{A}_{{22}}^{{(t)}} \gamma ^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(t)}} - m}}^{{(2)}} \hfill \\ + \frac{{h_{c} }}{2}\left( {\bar{A}_{{11}}^{{(t)}} - \bar{A}_{{11}}^{{(b)}} } \right)\left( {(n + 2)(n + 1)F_{{n + 2}}^{{(3)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - m + 1)F_{{n - m + 1}}^{{(3)}} } } \right) \hfill \\ + \frac{{h_{c} }}{2}\bar{A}_{{11}}^{{(t)}} \gamma ^{{(t)}} \left( {(n - \lambda ^{{(t)}} + 2)(n - \lambda ^{{(t)}} + 1)F_{{n - \lambda ^{{(t)}} + 2}}^{{(3)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(t)}} - m + 1)F_{{n - \lambda ^{{(t)}} - m + 1}}^{{(3)}} } } \right) \hfill \\ - \frac{{h_{c} }}{2}\bar{A}_{{11}}^{{(b)}} \gamma ^{{(b)}} \left( {(n - \lambda ^{{(b)}} + 2)(n - \lambda ^{{(b)}} + 1)F_{{n - \lambda ^{{(b)}} + 2}}^{{(3)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(b)}} - m + 1)F_{{n - \lambda ^{{(b)}} - m + 1}}^{{(3)}} } } \right) \hfill \\ - \frac{{h_{c} }}{2}\left( {\bar{A}_{{22}}^{{(t)}} - \bar{A}_{{22}}^{{(b)}} } \right)\sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - m}}^{{(3)}} - \frac{{h_{c} }}{2}\bar{A}_{{22}}^{{(t)}} \gamma ^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(t)}} - m}}^{{(3)}} \hfill \\ + \frac{{h_{c} }}{2}\bar{A}_{{22}}^{{(b)}} \gamma ^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{n + 2}} } F_{{n - \lambda ^{{(b)}} - m}}^{{(b)}} - \frac{{h_{b} }}{2}\bar{A}_{{11}}^{{(b)}} \left( {(n + 2)(n + 1)F_{{n + 2}}^{{(4)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - m + 1)F_{{n - m + 1}}^{{(4)}} } } \right) \hfill \\ - \frac{{h_{b} }}{2}\bar{A}_{{11}}^{{(b)}} \gamma ^{{(b)}} \left( {(n - \lambda ^{{(b)}} + 2)(n - \lambda ^{{(b)}} + 1)F_{{n - \lambda ^{{(b)}} + 2}}^{{(4)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(b)}} - m + 1)F_{{n - \lambda ^{{(b)}} - m + 1}}^{{(4)}} } } \right) \hfill \\ + \frac{{h_{b} }}{2}\bar{A}_{{22}}^{{(b)}} \sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - m}}^{{(4)}} + \frac{{h_{b} }}{2}\bar{A}_{{22}}^{{(b)}} \gamma ^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(b)}} - m}}^{{(4)}} \hfill \\ + \gamma ^{{(t)}} \lambda ^{{(t)}} \bar{A}_{{11}}^{{(t)}} (n - \lambda ^{{(t)}} + 2)\left( {F_{{n - \lambda ^{{(t)}} + 2}}^{{(1)}} + \frac{{h_{t} }}{2}F_{{n - \lambda ^{{(t)}} + 2}}^{{(2)}} + \frac{{h_{c} }}{2}F_{{n - \lambda ^{{(t)}} + 2}}^{{(3)}} } \right) \hfill \\ - \gamma ^{{(t)}} \lambda ^{{(t)}} \bar{A}_{{12}}^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} + 1}} {\left( { - \frac{1}{b}} \right)^{{m + 1}} } \left( {F_{{n - m - \lambda ^{{(t)}} + 1}}^{{(1)}} + \frac{{h_{t} }}{2}F_{{n - m - \lambda ^{{(t)}} + 1}}^{{(2)}} + \frac{{h_{c} }}{2}F_{{n - m - \lambda ^{{(t)}} + 1}}^{{(3)}} } \right) \hfill \\ + \gamma ^{{(b)}} \lambda ^{{(b)}} \bar{A}_{{11}}^{{(b)}} (n - \lambda ^{{(b)}} + 2)\left( {F_{{n - \lambda ^{{(b)}} + 2}}^{{(1)}} - \frac{{h_{b} }}{2}F_{{n - \lambda ^{{(b)}} + 2}}^{{(4)}} - \frac{{h_{c} }}{2}F_{{n - \lambda ^{{(b)}} + 2}}^{{(3)}} } \right) \hfill \\ - \gamma ^{{(b)}} \lambda ^{{(b)}} \bar{A}_{{12}}^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} + 1}} {\left( { - \frac{1}{b}} \right)^{{m + 1}} } \left( {F_{{n - m - \lambda ^{{(b)}} + 1}}^{{(1)}} - \frac{{h_{b} }}{2}F_{{n - m - \lambda ^{{(b)}} + 1}}^{{(4)}} - \frac{{h_{c} }}{2}F_{{n - m - \lambda ^{{(b)}} + 1}}^{{(3)}} } \right) \hfill \\ + \left( {\bar{I}_{0}^{{(t)}} + I_{0}^{{(c)}} + \bar{I}_{0}^{{(b)}} } \right)\omega ^{2} F_{n}^{{(1)}} + \mu ^{{(t)}} \bar{I}_{0}^{{(t)}} \omega ^{2} F_{{n - \eta ^{{(t)}} }}^{{(1)}} + \mu ^{{(b)}} \bar{I}_{0}^{{(b)}} \omega ^{2} F_{{n - \eta ^{{(b)}} }}^{{(1)}} \hfill \\ + \frac{{h_{t} }}{2}\bar{I}_{0}^{{(t)}} \omega ^{2} F_{n}^{{(2)}} + \frac{{h_{c} }}{2}\left( {\bar{I}_{0}^{{(t)}} - \bar{I}_{0}^{{(b)}} } \right)\omega ^{2} F_{n}^{{(3)}} - \frac{{h_{b} }}{2}\bar{I}_{0}^{{(b)}} \omega ^{2} F_{n}^{{(4)}} + \mu ^{{(t)}} \bar{I}_{0}^{{(t)}} \omega ^{2} \left( {\frac{{h_{t} }}{2}F_{{n - \eta ^{{(t)}} }}^{{(2)}} + \frac{{h_{c} }}{2}F_{{n - \eta ^{{(t)}} }}^{{(3)}} } \right) \hfill \\ \left. { - \mu ^{{(b)}} \bar{I}_{0}^{{(b)}} \omega ^{2} \left( {\frac{{h_{c} }}{2}F_{{n - \eta ^{{(b)}} }}^{{(3)}} + \frac{{h_{b} }}{2}F_{{n - \eta ^{{(b)}} }}^{{(4)}} } \right)} \right\}(r - b)^{n} = 0 \hfill \\ \end{gathered}$$

(29)

$$\begin{gathered} \sum\limits_{n = 0}^{N} {\left\{ {\frac{{h_{t} }}{2}\overline{A}_{11}^{(t)} \left[ {(n + 2)(n + 1)F_{n + 2}^{(1)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n + 2}^{(1)} U_{n - m + 1} } } \right]} \right.} \hfill \\ + \frac{{h_{t} }}{2}\overline{A}_{11}^{(t)} \gamma^{(t)} \left[ {(n - \lambda^{(t)} + 2)(n - \lambda^{(t)} + 1)F_{{n - \lambda^{(t)} + 2}}^{(1)} - \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(t)} - m + 1)F_{{n - \lambda^{(t)} - m + 1}}^{(1)} } } \right] \hfill \\ - \frac{{h_{t} }}{2}\overline{A}_{22}^{(t)} \sum\limits_{m = 0}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} F_{n - m}^{(1)} } - \frac{{h_{t} }}{2}\overline{A}_{22}^{(t)} \gamma^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{{n - \lambda^{(t)} - m}}^{(1)} \hfill \\ + \left( {\frac{{h_{t}^{2} }}{4}\overline{A}_{11}^{(t)} + \overline{D}_{11}^{(t)} } \right)\left[ {(n + 2)(n + 1)F_{n + 2}^{(2)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n - m + 1}^{(2)} } } \right] \hfill \\ + \left( {\frac{{h_{t}^{2} }}{4}\overline{A}_{11}^{(t)} + \overline{D}_{11}^{(t)} } \right)\gamma^{(t)} \left[ {(n - \lambda^{(t)} + 2)(n - \lambda^{(t)} + 1)F_{{n - \lambda^{(t)} + 2}}^{(2)} - \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(t)} - m + 1)F_{{n - \lambda^{(t)} - m + 1}}^{(2)} } } \right] \hfill \\ - \left( {\frac{{h_{t}^{2} }}{4}\overline{A}_{22}^{(t)} + \overline{D}_{22}^{(t)} } \right)\sum\limits_{m = 0}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{n - m}^{(2)} - \left( {\frac{{h_{t}^{2} }}{4}\overline{A}_{22}^{(t)} + \overline{D}_{22}^{(t)} } \right)\gamma^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{{n - \lambda^{(t)} - m}}^{(2)} \hfill \\ + \frac{{h_{t} h_{c} }}{4}\overline{A}_{11}^{(t)} \left[ {(n + 2)(n + 1)F_{n + 2}^{(3)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n - m + 1}^{(3)} } } \right] \hfill \\ + \frac{{h_{t} h_{c} }}{4}\gamma^{(t)} \overline{A}_{11}^{(t)} \left[ {(n - \lambda^{(t)} + 2)(n - \lambda^{(t)} + 1)F_{{n - \lambda^{(t)} + 2}}^{(3)} - \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(t)} - m + 1)F_{{n - \lambda^{(t)} - m + 1}}^{(3)} } } \right] \hfill \\ - \frac{{h_{t} h_{c} }}{4}\overline{A}_{22}^{(t)} \sum\limits_{m = 0}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{n - m}^{(3)} - \frac{{h_{1} h_{2} }}{4}\gamma^{(t)} \overline{A}_{22}^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{{n - \lambda^{(t)} - m}}^{(3)} \hfill \\ - \overline{A}_{33}^{(t)} \left[ {F_{n}^{(2)} + (n + 1)F_{n + 1}^{(5)} } \right] - \overline{A}_{33}^{(t)} \gamma^{(t)} \left[ {F_{{n - \lambda^{(t)} }}^{(2)} + (n - \lambda^{(t)} + 1)F_{{n - \lambda^{(t)} + 1}}^{(5)} } \right] \hfill \\ + \gamma^{(t)} \lambda^{(t)} \overline{D}_{11}^{(t)} (n - \lambda^{(t)} + 2)F_{{n - \lambda^{(t)} + 2}}^{(2)} - \gamma^{(t)} \lambda^{(t)} \overline{D}_{12}^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} + 1}} {\left( { - \frac{1}{b}} \right)^{m + 1} } F_{{n - m - \lambda^{(t)} + 1}}^{(2)} \hfill \\ + \frac{{h_{t} }}{2}\gamma^{(t)} \lambda^{(t)} \overline{A}_{11}^{(1)} (n - \lambda^{(t)} + 2)\left( {F_{{n - \lambda^{(t)} + 2}}^{(1)} + \frac{{h_{t} }}{2}F_{{n - \lambda^{(t)} + 2}}^{(2)} + \frac{{h_{c} }}{2}F_{{n - \lambda^{(t)} + 2}}^{(3)} } \right) \hfill \\ - \frac{{h_{t} }}{2}\gamma^{(t)} \lambda^{(t)} \overline{A}_{12}^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} + 1}} {\left( { - \frac{1}{b}} \right)^{m + 1} } \left( {\,F_{{n - m - \lambda^{(t)} + 1}}^{(1)} + \frac{{h_{t} }}{2}\,F_{{n - m - \lambda^{(t)} + 1}}^{(2)} + \frac{{h_{c} }}{2}F_{{n - m - \lambda^{(t)} + 1}}^{(3)} } \right) \hfill \\ + \frac{{h_{t} }}{2}\overline{I}_{0}^{(t)} \omega^{2} \left( {F_{n}^{(1)} + \frac{{h_{t} }}{2}F_{n}^{(2)} + \frac{{h_{c} }}{2}F_{n}^{(3)} } \right) + \frac{{h_{1} }}{2}\overline{I}_{0}^{(t)} \mu^{(t)} \omega^{2} \left( {F_{{n - \eta^{(t)} }}^{(1)} + \frac{{h_{t} }}{2}F_{{n - \eta^{(t)} }}^{(2)} + \frac{{h_{c} }}{2}F_{{n - \eta^{(t)} }}^{(3)} } \right) \hfill \\ \left. { + \overline{I}_{2}^{(t)} \omega^{2} F_{n}^{(2)} + \overline{I}_{2}^{(t)} \mu^{(t)} \omega^{2} F_{{n - \eta^{(t)} }}^{(2)} } \right\}(r - b)^{n} = 0. \hfill \\ \end{gathered}$$

(30)

$$\begin{gathered} \sum\limits_{{n = 0}}^{N} {\left\{ {\frac{{h_{c} }}{2}\left( {\bar{A}_{{11}}^{{(t)}} - \bar{A}_{{11}}^{{(b)}} } \right)\left( {(n + 2)(n + 1)F_{{n + 2}}^{{(1)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - m + 1)F_{{b - m + 1}}^{{(1)}} } } \right)} \right.} \hfill \\ + \frac{{h_{c} }}{2}\bar{A}_{{11}}^{{(t)}} \gamma ^{{(t)}} \left( {(n - \lambda ^{{(t)}} + 2)(n - \lambda ^{{(t)}} + 1)F_{{n - \lambda ^{{(t)}} + 2}}^{{(1)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {\left( { - \frac{1}{b}} \right)^{{s + 1}} (n - \lambda ^{{(t)}} - m + 1)F_{{n - \lambda ^{{(t)}} - m + 1}}^{{(1)}} } } \right) \hfill \\ - \frac{{h_{c} }}{2}\bar{A}_{{11}}^{{(b)}} \gamma ^{{(b)}} \left( {(n - \lambda ^{{(b)}} + 2)(n - \lambda ^{{(b)}} + 1)F_{{n - \lambda ^{{(b)}} + 2}}^{{(1)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} + 1}} {\left( { - \frac{1}{b}} \right)^{{s + 1}} (n - \lambda ^{{(b)}} - m + 1)F_{{n - \lambda ^{{(b)}} - m + 1}}^{{(1)}} } } \right) \hfill \\ - \frac{{h_{c} }}{2}\left( {\bar{A}_{{22}}^{{(t)}} - \bar{A}_{{22}}^{{(b)}} } \right)\sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} F_{{n - m}}^{{(1)}} } - \frac{{h_{c} }}{2}\bar{A}_{{22}}^{{(t)}} \gamma ^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} F_{{n - \lambda ^{{(t)}} - m}}^{{(1)}} } \hfill \\ + \frac{{h_{c} }}{2}\bar{A}_{{22}}^{{(b)}} \gamma ^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} F_{{n - \lambda ^{{(b)}} - m}}^{{(1)}} } + \frac{{h_{t} h_{c} }}{4}\bar{A}_{{11}}^{{(t)}} \left( {(n + 2)(n + 1)F_{{n + 2}}^{{(2)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - m + 1)F_{{n - m + 1}}^{{(2)}} } } \right) \hfill \\ + \frac{{h_{t} h_{c} }}{4}\bar{A}_{{11}}^{{(t)}} \gamma ^{{(t)}} \left( {(n - \lambda ^{{(t)}} + 2)(n - \lambda ^{{(t)}} + 1)F_{{n - \lambda ^{{(t)}} + 2}}^{{(2)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(t)}} - m + 1)F_{{n - \lambda ^{{(t)}} - m + 1}}^{{(2)}} } } \right) \hfill \\ - \frac{{h_{t} h_{c} }}{4}\bar{A}_{{22}}^{{(t)}} \sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - m}}^{{(2)}} - \frac{{h_{t} h_{c} }}{4}\bar{A}_{{22}}^{{(t)}} \gamma ^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(t)}} - m}}^{{(2)}} \hfill \\ + \left( {\frac{{h_{c}^{2} }}{4}\bar{A}_{{11}}^{{(t)}} + D_{{11}}^{{(c)}} + \frac{{h_{c}^{2} }}{4}\bar{A}_{{11}}^{{(b)}} } \right)\left( {(n + 2)(n + 1)F_{{n + 2}}^{{(3)}} - \sum\limits_{{m = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - m + 1)F_{{n - m + 1}}^{{(3)}} } } \right) \hfill \\ + \frac{{h_{c}^{2} }}{4}\bar{A}_{{11}}^{{(t)}} \gamma ^{{(t)}} \left( {(n - \lambda ^{{(t)}} + 2)(n - \lambda ^{{(t)}} + 1)F_{{n - \lambda ^{{(t)}} + 2}}^{{(3)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(t)}} - m + 1)F_{{n - \lambda ^{{(t)}} - m + 1}}^{{(3)}} } } \right) \hfill \\ + \frac{{h_{c}^{2} }}{4}\bar{A}_{{11}}^{{(b)}} \gamma ^{{(b)}} \left( {(n - \lambda ^{{(b)}} + 2)(n - \lambda ^{{(b)}} + 1)F_{{n - \lambda ^{{(b)}} + 2}}^{{(3)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {\left( { - \frac{1}{b}} \right)^{{s + 1}} (n - \lambda ^{{(b)}} - m + 1)F_{{n - \lambda ^{{(b)}} - m + 1}}^{{(3)}} } } \right) \hfill \\ - \left( {\frac{{h_{c}^{2} }}{4}\bar{A}_{{22}}^{{(t)}} + D_{{22}}^{{(c)}} + \frac{{h_{c}^{2} }}{4}\bar{A}_{{22}}^{{(b)}} } \right)\sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - m}}^{{(3)}} - \frac{{h_{c}^{2} }}{4}\bar{A}_{{22}}^{{(t)}} \gamma ^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(t)}} - m}}^{{(3)}} \hfill \\ - \frac{{h_{c}^{2} }}{4}\bar{A}_{{22}}^{{(b)}} \gamma ^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(b)}} - m}}^{{(3)}} + \frac{{h_{c} h_{b} }}{4}\bar{A}_{{11}}^{{(b)}} \left( {(n + 2)(n + 1)F_{{n + 2}}^{{(4)}} - \sum\limits_{{s = 0}}^{n} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - m + 1)F_{{n - m + 1}}^{{(4)}} } } \right) \hfill \\ \, + \frac{{h_{c} h_{b} }}{4}\bar{A}_{{11}}^{{(b)}} \gamma ^{{(b)}} \left( {(n - \lambda ^{{(b)}} + 2)(n - \lambda ^{{(b)}} + 1)F_{{n - \lambda ^{{(b)}} + 2}}^{{(4)}} - \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {\left( { - \frac{1}{b}} \right)^{{m + 1}} (n - \lambda ^{{(b)}} - m + 1)F_{{n - \lambda ^{{(b)}} - m + 1}}^{{(4)}} } } \right) \hfill \\ - \frac{{h_{c} h_{b} }}{4}\bar{A}_{{22}}^{{(b)}} \sum\limits_{{m = 0}}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - m}}^{{(4)}} - \frac{{h_{c} h_{b} }}{4}\bar{A}_{{22}}^{{(b)}} \gamma ^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{{m + 2}} } F_{{n - \lambda ^{{(b)}} - m}}^{{(4)}} \hfill \\ - A_{{33}}^{{(c)}} \left[ {F_{n}^{{(3)}} + (n + 1)F_{{n + 1}}^{{(5)}} } \right] + \frac{{h_{c} }}{2}\gamma ^{{(t)}} \lambda ^{{(t)}} \bar{A}_{{11}}^{{(t)}} (n - \lambda ^{{(t)}} + 2)\left( {F_{{n - \lambda ^{{(t)}} + 2}}^{{(1)}} + \frac{{h_{t} }}{2}F_{{n - \lambda ^{{(t)}} + 2}}^{{(2)}} + \frac{{h_{c} }}{2}F_{{n - \lambda ^{{(t)}} + 2}}^{{(3)}} } \right) \hfill \\ - \frac{{h_{c} }}{2}\gamma ^{{(t)}} \lambda ^{{(t)}} \bar{A}_{{12}}^{{(t)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(t)}} + 1}} {\left( { - \frac{1}{b}} \right)^{{m + 1}} } \left( {\,F_{{n - m - \lambda ^{{(t)}} + 1}}^{{(1)}} + \frac{{h_{t} }}{2}F_{{n - m - \lambda ^{{(t)}} + 1}}^{{(2)}} + \frac{{h_{c} }}{2}F_{{n - m - \lambda ^{{(t)}} + 1}}^{{(3)}} } \right) \hfill \\ - \frac{{h_{c} }}{2}\gamma ^{{(b)}} \lambda ^{{(b)}} \bar{A}_{{11}}^{{(b)}} (n - \lambda ^{{(b)}} + 2)\left( {F_{{n - \lambda ^{{(b)}} + 2}}^{{(1)}} - \frac{{h_{b} }}{2}F_{{n - \lambda ^{{(b)}} + 2}}^{{(4)}} - \frac{{h_{c} }}{2}F_{{n - \lambda ^{{(b)}} + 2}}^{{(3)}} } \right) + \bar{I}_{2}^{{(c)}} \omega ^{2} F_{n}^{{(3)}} \hfill \\ + \frac{{h_{c} }}{2}\gamma ^{{(b)}} \lambda ^{{(b)}} \bar{A}_{{12}}^{{(b)}} \sum\limits_{{m = 0}}^{{n - \lambda ^{{(b)}} + 1}} {\left( { - \frac{1}{b}} \right)^{{m + 1}} } \,\left( {F_{{n - m - \lambda ^{{(b)}} + 1}}^{{(1)}} - \frac{{h_{b} }}{2}F_{{n - m - \lambda ^{{(b)}} + 1}}^{{(4)}} - \frac{{h_{c} }}{2}F_{{n - m - \lambda ^{{(b)}} + 1}}^{{(3)}} } \right) \hfill \\ + \frac{{h_{c} }}{2}\bar{I}_{0}^{{(t)}} \mu ^{{(t)}} \omega ^{2} \left( {F_{{n - \eta ^{{(t)}} }}^{{(1)}} + \frac{{h_{t} }}{2}F_{{n - \eta ^{{(t)}} }}^{{(2)}} + \frac{{h_{c} }}{2}F_{{n - \eta ^{{(t)}} }}^{{(3)}} } \right) - \frac{{h_{c} }}{2}\bar{I}_{0}^{{(b)}} \omega ^{2} \left( {F_{n}^{{(1)}} - \frac{{h_{c} }}{2}F_{n}^{{(3)}} - \frac{{h_{b} }}{2}F_{n}^{{(4)}} } \right) \hfill \\ \left. { - \frac{{h_{c} }}{2}\bar{I}_{0}^{{(b)}} \mu ^{{(b)}} \omega ^{2} \left( {F_{{n - \eta ^{{(b)}} }}^{{(1)}} - \frac{{h_{c} }}{2}F_{{n - \eta ^{{(t)}} }}^{{(3)}} - \frac{{h_{b} }}{2}F_{{n - \eta ^{{(t)}} }}^{{(4)}} } \right) + \frac{{h_{c} }}{2}\bar{I}_{0}^{{(t)}} \omega ^{2} \left( {F_{n}^{{(1)}} + \frac{{h_{t} }}{2}F_{n}^{{(2)}} + \frac{{h_{c} }}{2}F_{n}^{{(3)}} } \right)} \right\}(r - b)^{n} = 0 \hfill \\ \end{gathered}$$

(31)

$$\begin{gathered} \sum\limits_{n = 0}^{N} {\left\{ { - \frac{{h_{b} }}{2}\overline{A}_{11}^{(b)} \left[ {(n + 2)(n + 1)F_{n + 2}^{(1)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n - m + 1}^{(1)} } } \right]} \right.} \hfill \\ - \frac{{h_{b} }}{2}\overline{A}_{11}^{(b)} \gamma^{(b)} \left[ {(n - \lambda^{(b)} + 2)(n - \lambda^{(b)} + 1)F_{{n - \lambda^{(b)} + 2}}^{(1)} - \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(b)} - m + 1)F_{{n - \lambda^{(b)} - m + 1}}^{(1)} } } \right] \hfill \\ + \frac{{h_{b} }}{2}\overline{A}_{22}^{(b)} \sum\limits_{m = 0}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{n - m}^{(1)} + \frac{{h_{b} }}{2}\overline{A}_{22}^{(b)} \gamma^{(b)} \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} F_{{n - \lambda^{(b)} - m}}^{(1)} } \hfill \\ + \frac{{h_{c} h_{b} }}{4}\overline{A}_{11}^{(b)} \left[ {(n + 2)(n + 1)F_{n + 2}^{(3)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n - m + 1}^{(3)} } } \right] \hfill \\ + \frac{{h_{c} h_{b} }}{4}\overline{A}_{11}^{(b)} \gamma^{(b)} \left[ {(n - \lambda^{(b)} + 2)(n - \lambda^{(b)} + 1)F_{{n - \lambda^{(b)} + 2}}^{(3)} - \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(b)} - m + 1)F_{{n - \lambda^{(b)} - m + 1}}^{(3)} } } \right] \hfill \\ - \frac{{h_{c} h_{b} }}{4}\overline{A}_{22}^{(b)} \sum\limits_{m = 0}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{n - m}^{(3)} - \frac{{h_{c} h_{b} }}{4}\overline{A}_{22}^{(b)} \gamma^{(b)} \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{{n - \lambda^{(b)} - m}}^{(3)} \hfill \\ + \left( {\overline{D}_{11}^{(b)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{11}^{(b)} } \right)\left[ {(n + 2)(n + 1)F_{n + 2}^{(4)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n - m + 1}^{(4)} } } \right] \hfill \\ + \left( {\overline{D}_{11}^{(b)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{11}^{(b)} } \right)\gamma^{(b)} \left[ {(n - \lambda^{(b)} + 2)(n - \lambda^{(b)} + 1)F_{{n - \lambda^{(b)} + 2}}^{(4)} - \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(b)} - m + 1)F_{{n - \lambda^{(b)} - m + 1}}^{(4)} } } \right] \hfill \\ - \left( {\overline{D}_{22}^{(b)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{22}^{(b)} } \right)\sum\limits_{m = 0}^{n} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{n - m}^{(4)} - \left( {\overline{D}_{22}^{(b)} + \frac{{h_{b}^{2} }}{4}\overline{A}_{22}^{(b)} } \right)\gamma^{(b)} \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {(m + 1)\left( { - \frac{1}{b}} \right)^{m + 2} } F_{{n - \lambda^{(b)} - m}}^{(4)} \hfill \\ - \overline{A}_{33}^{(b)} \left[ {F_{n}^{(4)} + (n + 1)F_{n + 1}^{(5)} } \right] - \overline{A}_{33}^{(b)} \gamma^{(b)} \left( {F_{{n - \lambda^{(b)} }}^{(4)} + (n - \lambda^{(b)} + 1)F_{{n - \lambda^{(b)} + 1}}^{(5)} } \right) + \gamma^{(b)} \lambda^{(b)} \overline{D}_{11}^{(b)} (n - \lambda^{(b)} + 2)F_{{n - \lambda^{(b)} + 2}}^{(4)} \hfill \\ - \gamma^{(b)} \lambda^{(b)} \overline{D}_{12}^{(b)} \sum\limits_{m = 0}^{{n - \lambda^{(b)} + 1}} {\left( { - \frac{1}{b}} \right)^{m + 1} } F_{{n - m - \lambda^{(b)} + 1}}^{(4)} - \frac{{h_{b} }}{2}\gamma^{(b)} \lambda^{(b)} \overline{A}_{11}^{(b)} (n - \lambda^{(b)} + 2)\left( {F_{{n - \lambda^{(b)} + 2}}^{(1)} - \frac{{h_{b} }}{2}F_{{n - \lambda^{(b)} + 2}}^{(4)} - \frac{{h_{c} }}{2}F_{{n - \lambda^{(b)} + 2}}^{(3)} } \right) + \hfill \\ \frac{{h_{b} }}{2}\gamma^{(b)} \lambda^{(b)} \overline{A}_{12}^{(b)} \sum\limits_{m = 0}^{{n - \lambda^{(b)} + 1}} {\left( { - \frac{1}{b}} \right)^{m + 1} } \,\left( {F_{{n - m - \lambda^{(b)} + 1}}^{(1)} - \frac{{h_{b} }}{2}F_{{n - m - \lambda^{(b)} + 1}}^{(4)} - \frac{{h_{c} }}{2}F_{{n - m - \lambda^{(b)} + 1}}^{(3)} } \right) + \overline{I}_{2}^{(b)} \omega^{2} F_{n}^{(4)} + \overline{I}_{2}^{(b)} \mu^{(b)} \omega^{2} F_{{n - \eta^{(b)} }}^{(4)} \hfill \\ \left. { - \frac{{h_{b} }}{2}\overline{I}_{0}^{(b)} \omega^{2} \left( {F_{n}^{(1)} - \frac{{h_{b} }}{2}F_{n}^{(4)} - \frac{{h_{c} }}{2}F_{n}^{(3)} } \right) - \frac{{h_{b} }}{2}\overline{I}_{0}^{(b)} \mu^{(b)} \omega^{2} \left( {F_{{n - \eta^{(b)} }}^{(1)} - \frac{{h_{b} }}{2}F_{{n - \eta^{(b)} }}^{(4)} - \frac{{h_{c} }}{2}F_{{n - \eta^{(b)} }}^{(3)} } \right)} \right\}(r - b)^{n} = 0 \hfill \\ \end{gathered}$$

(32)

$$\begin{gathered} \sum\limits_{n = 0}^{N} {\left\{ {\left( {\overline{A}_{33}^{(t)} + A_{33}^{(c)} + \overline{A}_{33}^{(b)} } \right)\left[ {(n + 2)(n + 1)F_{n + 2}^{(5)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - m + 1)F_{n - m + 1}^{(5)} } } \right]} \right.} \hfill \\ + \overline{A}_{33}^{(t)} \gamma^{(t)} \left[ {(n - \lambda^{(t)} + 2)(n - \lambda^{(t)} + 1)F_{{n - \lambda^{(t)} + 2}}^{(5)} - \sum\limits_{m = 0}^{{n - \lambda^{(t)} + 1}} {\left( { - \frac{1}{b}} \right)^{m + 1} (m - \lambda^{(t)} - m + 1)F_{{n - \lambda^{(t)} - m + 1}}^{(5)} } } \right] \hfill \\ + \overline{A}_{33}^{(b)} \gamma^{(b)} \left[ {(n - \lambda^{(b)} + 2)(n - \lambda^{(b)} + 1)F_{{n - \lambda^{(b)} + 2}}^{(5)} - \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} (n - \lambda^{(b)} - m + 1)F_{{n - \lambda^{(b)} - m + 1}}^{(5)} } } \right] \hfill \\ + \overline{A}_{33}^{(t)} (n + 1)F_{n + 1}^{(2)} + \overline{A}_{33}^{(t)} \gamma^{(t)} (n - \lambda^{(t)} + 1)F_{{n - \lambda^{(t)} + 1}}^{(2)} - \overline{A}_{33}^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} \,} F_{n - m}^{(2)} - \overline{A}_{33}^{(t)} \gamma^{(t)} \sum\limits_{m = 0}^{{n - \lambda^{(t)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} } F_{{n - m - \lambda^{(t)} }}^{(2)} \hfill \\ + A_{33}^{(c)} \left[ {(n + 1)F_{n + 1}^{(3)} - \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} } F_{n - m}^{(3)} } \right] + \overline{A}_{33}^{(b)} (n + 1)F_{x + 1}^{(4)} + \overline{A}_{33}^{(b)} \gamma^{(b)} (n - \lambda^{(b)} + 1)F_{{n - \lambda^{(b)} + 1}}^{(4)} \hfill \\ - \overline{A}_{33}^{(b)} \sum\limits_{m = 0}^{n} {\left( { - \frac{1}{b}} \right)^{m + 1} } F_{n - m}^{(4)} - \overline{A}_{33}^{(3)} \gamma^{(b)} \sum\limits_{m = 0}^{{n - \lambda^{(b)} }} {\left( { - \frac{1}{b}} \right)^{m + 1} } F_{{n - \lambda^{(b)} - m}}^{(4)} + \overline{A}_{33}^{(t)} \gamma^{(t)} \lambda^{(t)} F_{{n - \beta^{(t)} + 1}}^{(2)} + q\delta (n) \hfill \\ \overline{A}_{33}^{(t)} \gamma^{(t)} \lambda^{(t)} (n - \lambda^{(t)} + 2)F_{{n - \lambda^{(t)} + 2}}^{(5)} + \overline{A}_{33}^{(b)} \gamma^{(b)} \lambda^{(b)} F_{{n - \lambda^{(b)} + 1}}^{(4)} + \overline{A}_{33}^{(b)} \gamma^{(b)} \lambda^{(b)} (n - \lambda^{(b)} + 2)F_{{n - \lambda^{(b)} + 2}}^{(5)} \hfill \\ \left. { + \left( {\overline{I}_{0}^{(t)} + \overline{I}_{0}^{(c)} + \overline{I}_{0}^{(b)} } \right)\omega^{2} F_{n}^{(5)} + \mu^{(t)} \overline{I}_{0}^{(t)} \omega^{2} F_{{n - \eta^{(t)} }}^{(5)} + \mu^{(c)} \overline{I}_{0}^{(c)} \omega^{2} F_{{n - \eta^{(c)} }}^{(5)} + \mu^{(b)} \overline{I}_{0}^{(b)} \omega^{2} F_{{n - \eta^{(b)} }}^{(5)} } \right\}(r - b)^{n} = 0 \hfill \\ \end{gathered}$$

(33)

By solving Eqs. (29)-(33) for n = 0,1,2,…N, the unknown displacement parameters $F_{n + 2}^{(1)} ,\,\,F_{n + 2}^{(2)} ,\,\,F_{n + 2}^{(3)} ,\,\,F_{n + 2}^{(4)}$ and $F_{n + 2}^{(5)}$ will be obtained in terms of first ten parameters $F_{0}^{(1)} ,\,\,F_{1}^{(1)} ,F_{0}^{(2)} ,\,\,F_{1}^{(2)} ,F_{0}^{(3)} ,\,\,F_{1}^{(3)} ,$$F_{0}^{(4)} ,\,\,F_{1}^{(4)} ,\,\,F_{0}^{(5)}$ and $F_{1}^{(5)}$. Besides, the transformed form of the edge conditions at the outer edge (r = r_o) will be as

$$\begin{gathered} \bullet \,\,\,\,u_{0}^{{(c)}} = \left. {\sum\limits_{{n = 0}}^{N} {F_{n}^{{(1)}} \left( {r - b} \right)^{n} } } \right|_{{r = b}} = 0 \to F_{0}^{{(1)}} = 0 \hfill \\ \bullet \,\,\,\,\phi _{r}^{{(t)}} = \left. {\sum\limits_{{n = 0}}^{N} {F_{n}^{{(2)}} \left( {r - b} \right)^{n} } } \right|_{{r = b}} = 0 \to F_{0}^{{(2)}} = 0 \hfill \\ \bullet \,\,\,\,\phi _{r}^{{(c)}} = \left. {\sum\limits_{{n = 0}}^{N} {F_{n}^{{(3)}} \left( {r - b} \right)^{n} } } \right|_{{r = b}} = 0 \to F_{0}^{{(3)}} = 0 \hfill \\ \bullet \,\,\,\,\phi _{r}^{{(b)}} = \left. {\sum\limits_{{n = 0}}^{N} {F_{n}^{{(4)}} \left( {r - b} \right)^{n} } } \right|_{{r = b}} = 0 \to F_{0}^{{(4)}} = 0 \hfill \\ \bullet \,\,\,\,w = \left. {\sum\limits_{{n = 0}}^{N} {F_{n}^{{(5)}} \left( {r - b} \right)^{n} } } \right|_{{r = b}} = 0 \to F_{0}^{{(5)}} = 0 \hfill \\ \bullet \,\,\,\,N_{r}^{{(t)}} + N_{r}^{{(c)}} + N_{r}^{{(b)}} = 0 \to \hfill \\ \bar{A}_{{11}}^{{(t)}} \left( {F_{1}^{{(1)}} + \frac{{h_{t} }}{2}F_{1}^{{(2)}} + \frac{{h_{c} }}{2}F_{1}^{{(3)}} } \right) - \frac{{\bar{A}_{{12}}^{{(t)}} }}{b}\left( {F_{0}^{{(1)}} + \frac{{h_{t} }}{2}F_{0}^{{(2)}} + \frac{{h_{c} }}{2}F_{0}^{{(3)}} } \right) + \bar{A}_{{11}}^{{(b)}} \left( {F_{1}^{{(1)}} - \frac{{h_{c} }}{2}F_{1}^{{(3)}} - \frac{{h_{b} }}{2}F_{1}^{{(4)}} } \right) \hfill \\ - \frac{{\bar{A}_{{12}}^{{(b)}} }}{b}\left( {F_{0}^{{(1)}} - \frac{{h_{c} }}{2}F_{0}^{{(3)}} - \frac{{h_{b} }}{2}F_{0}^{{(4)}} } \right) + A_{{11}}^{{(c)}} F_{1}^{{(1)}} - \bar{A}_{{12}}^{{(c)}} \frac{{F_{0}^{{(1)}} }}{b} = 0 \hfill \\ \bullet \,\,\,\,\frac{{h_{t} }}{2}N_{r}^{{(t)}} + M_{r}^{{(t)}} = 0 \Rightarrow \hfill \\ \,\,\,\,\,\,\frac{{h_{t} }}{2}\bar{A}_{{11}}^{{(t)}} \left( {F_{1}^{{(1)}} + \frac{{h_{t} }}{2}F_{1}^{{(2)}} + \frac{{h_{c} }}{2}F_{1}^{{(3)}} } \right) - \frac{{h_{t} }}{2}\frac{{\bar{A}_{{12}}^{{(t)}} }}{b}\left( {F_{0}^{{(1)}} + \frac{{h_{t} }}{2}F_{0}^{{(2)}} + \frac{{h_{c} }}{2}F_{0}^{{(3)}} } \right) + \bar{D}_{{11}}^{{(t)}} F_{1}^{{(2)}} + \frac{1}{b}\bar{D}_{{12}}^{{(t)}} F_{0}^{{(2)}} \hfill \\ \bullet \,\,\,\,\frac{{h_{c} }}{2}N_{r}^{{(t)}} + M_{r}^{{(c)}} - \frac{{h_{c} }}{2}N_{r}^{{(b)}} = 0 \Rightarrow \hfill \\ \,\,\,\,\frac{{h_{c} }}{2}\bar{A}_{{11}}^{{(t)}} \left( {F_{1}^{{(1)}} + \frac{{h_{t} }}{2}F_{1}^{{(2)}} + \frac{{h_{c} }}{2}F_{1}^{{(3)}} } \right) - \frac{{h_{c} }}{2}\frac{{\bar{A}_{{12}}^{{(t)}} }}{b}\left( {F_{0}^{{(1)}} + \frac{{h_{t} }}{2}F_{0}^{{(2)}} + \frac{{h_{c} }}{2}F_{0}^{{(3)}} } \right) - \frac{{h_{c} }}{2}\bar{A}_{{11}}^{{(b)}} \left( {F_{1}^{{(1)}} - \frac{{h_{c} }}{2}F_{1}^{{(3)}} - \frac{{h_{b} }}{2}F_{1}^{{(4)}} } \right) \hfill \\ + \frac{{h_{c} }}{2}\frac{{\bar{A}_{{12}}^{{(b)}} }}{b}\left( {F_{0}^{{(1)}} - \frac{{h_{c} }}{2}F_{0}^{{(3)}} - \frac{{h_{b} }}{2}F_{0}^{{(4)}} } \right) + D_{{11}}^{{(c)}} (n + 1)F_{{n + 1}}^{{(3)}} + \frac{1}{b}D_{{12}}^{{(c)}} F_{0}^{{(3)}} = 0 \hfill \\ \bullet \,\,\,\,\, - \frac{{h_{b} }}{2}N_{r}^{{(b)}} + M_{r}^{{(b)}} = 0 \Rightarrow \hfill \\ - \frac{{h_{b} }}{2}\bar{A}_{{11}}^{{(b)}} \left( {F_{1}^{{(1)}} - \frac{{h_{c} }}{2}F_{1}^{{(3)}} - \frac{{h_{b} }}{2}F_{1}^{{(4)}} } \right) + \frac{{h_{b} }}{2}\frac{{\bar{A}_{{12}}^{{(b)}} }}{b}\left( {F_{0}^{{(1)}} - \frac{{h_{c} }}{2}F_{0}^{{(3)}} - \frac{{h_{b} }}{2}F_{0}^{{(4)}} } \right) + \left( {\bar{D}_{{11}}^{{(b)}} (n + 1)F_{{n + 1}}^{{(4)}} + \frac{1}{b}\bar{D}_{{12}}^{{(b)}} F_{n}^{{(4)}} } \right) \hfill \\ \bullet \,\,\,\,\,Q_{r}^{{(t)}} + Q_{r}^{{(c)}} + Q_{r}^{{(b)}} = 0 \Rightarrow \hfill \\ \,\,\,\,\,\,\,\bar{A}_{{33}}^{{(t)}} \left( {F_{0}^{{(2)}} + F_{1}^{{(5)}} } \right) + A_{{33}}^{{(c)}} \left( {F_{0}^{{(3)}} + F_{1}^{{(5)}} } \right) + \bar{A}_{{33}}^{{(b)}} \left( {F_{0}^{{(4)}} + F_{1}^{{(5)}} } \right) = 0 \hfill \\ \end{gathered}$$

(34)

It is noted that various boundary conditions can be applied using Eqs. (34). Of the unknown parameters, five of them will be determined by employing the boundary condition at the outer edge.

• Outer clamped edge: $F_{0}^{(1)} = F_{0}^{(2)} = F_{0}^{(3)} = F_{0}^{(4)} = F_{0}^{(5)} = 0$.

• Outer simply supported edge: $F_{0}^{(5)} = 0$ and $F_{0}^{(1)} ,\,\,F_{0}^{(2)} ,\,\,F_{0}^{(3)}$ and $F_{0}^{(4)}$ are obtained in terms of $F_{1}^{(1)} ,\,\,\,F_{1}^{(2)} ,\,\,\,F_{1}^{(3)}$ and $F_{1}^{(4)}$.

• Outer free edge: m and $F_{1}^{(5)}$ are obtained in terms of $F_{1}^{(1)} ,\,\,\,F_{1}^{(2)} ,\,\,\,F_{1}^{(3)} ,\,\,\,F_{1}^{(4)}$ and $F_{0}^{(5)}$.

The other unknown displacement parameters $F_{n}^{(1)} ,\,\,F_{n}^{(2)} ,\,\,F_{n}^{(3)} ,\,\,F_{n}^{(4)}$ and $F_{n}^{(5)}$ (n = 0, 1, 2, …N + 2) are determined in terms of five unknown parameters depending on the type of boundary condition.

The transformed form of the boundary conditions at the inner edge (r = r_i) of annular sandwich panel and the regularity conditions at the center of the axisymmetric circular plate can be expressed as

$$\begin{gathered} \bullet \,\,\,\,\,Q_{r}^{(t)} + Q_{r}^{(c)} + Q_{r}^{(b)} = 0\,\,\, \Rightarrow \,\,\, \hfill \\ \,\,\,\,\,\,\,\sum\limits_{n = 0}^{N + 1} {\left\{ {\overline{A}_{33}^{(t)} \left[ {1 + \gamma^{(t)} \left( {r - r_{o} } \right)^{{\lambda^{(t)} }} } \right]\left[ {F_{n}^{(2)} + (n + 1)\,F_{n + 1}^{(5)} } \right] + } \right.} \,A_{33}^{(c)} \left[ {F_{n}^{(3)} + (n + 1)\,F_{n + 1}^{(5)} } \right] + \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overline{A}_{33}^{(b)} \left. {\left[ {1 + \gamma^{(b)} \left( {r - r_{o} } \right)^{{\lambda^{(b)} }} } \right]\left[ {F_{n}^{(4)} + (n + 1)\,F_{n + 1}^{(5)} } \right]} \right\}\left( {a - b} \right)^{n} = 0 \hfill \\ \end{gathered}$$

(35)

Also, at the center of the axisymmetric circular plate, the regularity conditions can be expressed as

$$\begin{gathered} \bullet \,\,\,\,u_{0}^{(c)} = \sum\limits_{n = 0}^{N + 2} {F_{n}^{(1)} \left( {0 - b} \right)^{n} } = 0 \hfill \\ \bullet \,\,\,\,\phi_{r}^{(t)} = \sum\limits_{n = 0}^{N + 2} {F_{n}^{(2)} \left( {0 - b} \right)^{n} = 0} \hfill \\ \bullet \,\,\,\,\phi_{r}^{(c)} = \sum\limits_{n = 0}^{N + 2} {F_{n}^{(3)} \left( {0 - b} \right)^{n} = 0} \hfill \\ \bullet \,\,\,\,\phi_{r}^{(b)} = \sum\limits_{n = 0}^{N + 2} {F_{n}^{(4)} \left( {0 - b} \right)^{n} = 0} \hfill \\ \bullet \,\,\,\,w = \sum\limits_{n = 0}^{N + 1} {(n + 1)F_{n + 1}^{(5)} \left( {0 - b} \right)^{n} = 0} \hfill \\ \end{gathered}$$

(36)

Substitution of displacement parameters $F_{n}^{(1)} ,\,\,F_{n}^{(2)} ,\,\,F_{n}^{(3)} ,\,\,F_{n}^{(4)}$ and $F_{n}^{(5)}$ (n = 0,1,2,…N + 2) into the corresponding transformed form of the inner boundary conditions for annular panels or the regularity center conditions for axisymmetric circular ones leads to the following system of equations:

$$\left[ {\begin{array}{*{20}c} {{\rm X}_{11} (\omega )} & {{\rm X}_{12} (\omega )} & {{\rm X}_{13} (\omega )} & {{\rm X}_{14} (\omega )} & {{\rm X}_{15} (\omega )} \\ {{\rm X}_{21} (\omega )} & {{\rm X}_{22} (\omega )} & {{\rm X}_{23} (\omega )} & {{\rm X}_{24} (\omega )} & {{\rm X}_{25} (\omega )} \\ {{\rm X}_{31} (\omega )} & {{\rm X}_{32} (\omega )} & {{\rm X}_{33} (\omega )} & {{\rm X}_{34} (\omega )} & {{\rm X}_{35} (\omega )} \\ {{\rm X}_{41} (\omega )} & {{\rm X}_{42} (\omega )} & {{\rm X}_{43} (\omega )} & {{\rm X}_{44} (\omega )} & {{\rm X}_{45} (\omega )} \\ {{\rm X}_{51} (\omega )} & {{\rm X}_{52} (\omega )} & {{\rm X}_{53} (\omega )} & {{\rm X}_{54} (\omega )} & {{\rm X}_{55} (\omega )} \\ \end{array} } \right]\left\{ \begin{gathered} \,\,\,\,\,\,\,\,F_{1}^{(1)} \hfill \\ \,\,\,\,\,\,\,\,F_{1}^{(2)} \hfill \\ \,\,\,\,\,\,\,\,F_{1}^{(3)} \hfill \\ \,\,\,\,\,\,\,\,\,F_{1}^{(4)} \hfill \\ F_{0}^{(5)} \,or\,F_{1}^{(5)} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} Y_{1} \hfill \\ Y_{2} \hfill \\ Y_{3} \hfill \\ Y_{4} \hfill \\ Y_{5} \hfill \\ \end{gathered} \right\}$$

(37)

• Free vibration analysis:

By setting $Y_{1} = Y_{2} = Y_{3} = Y_{4} = Y_{5} = 0$, free vibration analysis of annular or circular sandwich panels can be performed. Existence of non-trivial solutions requires that

$$\left| {\begin{array}{*{20}c} {{\rm X}_{11} (\omega )} & {{\rm X}_{12} (\omega )} & {{\rm X}_{13} (\omega )} & {{\rm X}_{14} (\omega )} & {{\rm X}_{15} (\omega )} \\ {{\rm X}_{21} (\omega )} & {{\rm X}_{22} (\omega )} & {{\rm X}_{23} (\omega )} & {{\rm X}_{24} (\omega )} & {{\rm X}_{25} (\omega )} \\ {{\rm X}_{31} (\omega )} & {{\rm X}_{32} (\omega )} & {{\rm X}_{33} (\omega )} & {{\rm X}_{34} (\omega )} & {{\rm X}_{35} (\omega )} \\ {{\rm X}_{41} (\omega )} & {{\rm X}_{42} (\omega )} & {{\rm X}_{43} (\omega )} & {{\rm X}_{44} (\omega )} & {{\rm X}_{45} (\omega )} \\ {{\rm X}_{51} (\omega )} & {{\rm X}_{52} (\omega )} & {{\rm X}_{53} (\omega )} & {{\rm X}_{54} (\omega )} & {{\rm X}_{55} (\omega )} \\ \end{array} } \right| = 0$$

(38)

• Static analysis:

The static analysis can be examined by setting ω = 0 and by solving Eq. (37),$\,F_{1}^{(1)} ,\,\,F_{1}^{(2)} ,\,\,\,F_{1}^{(3)} ,\,\,F_{1}^{(4)}$ and $F_{0}^{(5)} \,or\,F_{1}^{(5)}$ will be achieved.

5 Extracting the transverse shear stress based on theory of elasticity

To determine the transverse shear stress, the equilibrium equation based on theory of elasticity is considered:

$$\begin{gathered} \frac{{\partial \sigma_{r}^{(i)} }}{\partial r} + \frac{{\sigma_{r}^{(i)} - \sigma_{\theta }^{(i)} }}{r} + \frac{{\partial \tau_{rz}^{(i)} }}{{\partial z^{(i)} }} = 0\, \hfill \\ \tau_{rz}^{(i)} = - \int {\left( {\frac{{\partial \sigma_{r}^{(i)} }}{\partial r} + \frac{{\sigma_{r}^{(i)} - \sigma_{\theta }^{(i)} }}{r}} \right)} dz^{(i)} ,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{h_{i} }}{2}\, \le z^{(t)} \le \frac{{h_{i} }}{2}\,\,\,\,\,\,\,\,i = t,c,b \hfill \\ \end{gathered}$$

(39)

By using Eqs. (2)–(7), the stress-displacement may be expressed as:

$$\begin{gathered} \left\{ {\begin{array}{*{20}l} {\sigma _{r}^{{(t)}} = \left( {C_{{11}}^{{(t)}} (r)\frac{\partial }{{\partial r}} + C_{{12}}^{{(t)}} (r)\frac{1}{r}} \right)\left( {u_{0}^{{(c)}} + \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} + \frac{{h_{t} }}{2}\phi _{r}^{{(t)}} + z^{{(t)}} \phi _{r}^{{(t)}} } \right)} \hfill \\ {\sigma _{\theta }^{{(t)}} = \left( {C_{{12}}^{{(t)}} (r)\frac{\partial }{{\partial r}} + C_{{22}}^{{(t)}} (r)\frac{1}{r}} \right)\left( {u_{0}^{{(c)}} + \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} + \frac{{h_{t} }}{2}\phi _{r}^{{(t)}} + z^{{(t)}} \phi _{r}^{{(t)}} } \right)} \hfill \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}l} {\sigma _{r}^{{(c)}} = \left( {C_{{11}}^{{(c)}} \frac{\partial }{{\partial r}} + C_{{12}}^{{(c)}} \frac{1}{r}} \right)\left( {u_{0}^{{(c)}} + z^{{(c)}} \phi _{r}^{{(c)}} } \right)} \hfill \\ {\sigma _{\theta }^{{(c)}} = \left( {C_{{12}}^{{(c)}} \frac{\partial }{{\partial r}} + C_{{22}}^{{(c)}} \frac{1}{r}} \right)\left( {u_{0}^{{(c)}} + z^{{(c)}} \phi _{r}^{{(c)}} } \right)} \hfill \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}l} {\sigma _{r}^{{(b)}} = \left( {C_{{11}}^{{(b)}} (r)\frac{\partial }{{\partial r}} + C_{{12}}^{{(b)}} (r)\frac{1}{r}} \right)\left( {u_{0}^{{(c)}} - \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} - \frac{{h_{b} }}{2}\phi _{r}^{{(b)}} + z^{{(b)}} \phi _{r}^{{(b)}} } \right)} \hfill \\ {\sigma _{\theta }^{{(b)}} = \left( {C_{{12}}^{{(b)}} (r)\frac{\partial }{{\partial r}} + C_{{22}}^{{(b)}} (r)\frac{1}{r}} \right)\left( {u_{0}^{{(c)}} - \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} - \frac{{h_{b} }}{2}\phi _{r}^{{(b)}} + z^{{(b)}} \phi _{r}^{{(b)}} } \right)} \hfill \\ \end{array} .} \right. \hfill \\ \end{gathered}$$

(40)

By substituting Eq. (40) into Eq. (39), the transverse shear stress can be expressed as:

$$\begin{gathered} \tau _{{rz}}^{{(t)}} = - \int\limits_{{\frac{{h_{1} }}{2}}}^{{z^{{(t)}} }} {\left\{ {\left( {C_{{11}}^{{(t)}} (r)\frac{\partial }{{\partial r^{2} }} + \frac{{\partial C_{{11}}^{{(t)}} (r)}}{{\partial r}}\frac{\partial }{{\partial r}} + \frac{{\partial C_{{12}}^{{(t)}} (r)}}{{\partial r}}\frac{1}{r} - C_{{12}}^{{(t)}} (r)\frac{1}{{r^{2} }}} \right)\left( {u_{0}^{{(c)}} + \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} + \frac{{h_{t} }}{2}\phi _{r}^{{(t)}} + z^{{(t)}} \phi _{r}^{{(t)}} } \right)} \right.} \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{r}\left[ {\left( {C_{{11}}^{{(t)}} (r) - C_{{12}}^{{(t)}} (r)} \right)\frac{\partial }{{\partial r}} + \frac{1}{r}\left( {C_{{12}}^{{(t)}} (r) - C_{{22}}^{{(t)}} (r)} \right)} \right]\left( {u_{0}^{{(c)}} + \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} + \frac{{h_{t} }}{2}\phi _{r}^{{(t)}} + z^{{(t)}} \phi _{r}^{{(t)}} } \right)} \right\}dz^{{(b)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{h_{t} }}{2} \le z^{{(t)}} \le \frac{{h_{t} }}{2} \hfill \\ \tau _{{rz}}^{{(c)}} = - \int\limits_{{\tfrac{{h_{c} }}{2}}}^{{z^{{(c)}} }} {\left\{ {\left( {C_{{11}}^{{(c)}} \frac{{\partial ^{2} }}{{\partial r^{2} }} - C_{{12}}^{{(c)}} \frac{1}{{r^{2} }}} \right)\left( {u_{0}^{{(c)}} } \right) + z^{{(c)}} \phi _{r}^{{(c)}} } \right\}} \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{r}\left[ {\left( {C_{{11}}^{{(c)}} - C_{{12}}^{{(c)}} } \right)\frac{\partial }{{\partial r}} + \left( {C_{{12}}^{{(c)}} - C_{{22}}^{{(c)}} } \right)\frac{1}{r}} \right]\left( {u_{0}^{{(c)}} + z^{{(c)}} \phi _{r}^{{(c)}} } \right)} \right\}dz^{{(i)}} + \tau _{{rz(z^{{(t)}} = - \,\frac{{h_{t} }}{2})}}^{{(t)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{h_{c} }}{2} \le z^{{(c)}} \le \frac{{h_{c} }}{2} \hfill \\ \tau _{{rz}}^{{(b)}} = - \int\limits_{{\frac{{h_{b} }}{2}}}^{{z^{{(b)}} }} {\left\{ {\left( {C_{{11}}^{{(b)}} (r)\frac{{\partial ^{2} }}{{\partial r^{2} }} + \frac{{\partial C_{{11}}^{{(b)}} (r)}}{{\partial r}}\frac{\partial }{{\partial r}} + \frac{{\partial C_{{12}}^{{(b)}} (r)}}{{\partial r}}\frac{1}{r} - C_{{12}}^{{(b)}} (r)\frac{1}{{r^{2} }}} \right)\left( {u_{0}^{{(c)}} - \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} - \frac{{h_{b} }}{2}\phi _{r}^{{(b)}} + z^{{(b)}} \phi _{r}^{{(b)}} } \right)} \right.} \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{r}\left[ {\left( {C_{{11}}^{{(b)}} (r) - C_{{12}}^{{(b)}} (r)} \right)\frac{\partial }{{\partial r}} + \frac{1}{r}\left( {C_{{12}}^{{(b)}} (r) - C_{{22}}^{{(b)}} (r)} \right)} \right]\left( {u_{0}^{{(c)}} - \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} - \frac{{h_{b} }}{2}\phi _{r}^{{(b)}} + z^{{(b)}} \phi _{r}^{{(b)}} } \right)} \right\}dz^{{(b)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{h_{b} }}{2} \le z^{{(b)}} \le \frac{{h_{b} }}{2} \hfill \\ \end{gathered}$$

(41)

6 Results and discussion

In this section, numerical results for free vibration, bending and stress analyses of sandwich circular/annular plates with heterogeneous polar orthotropic face sheets are presented and the effects of initial in-plane stresses are examined. In this regard, numerical examples of sandwich panels with asymmetric lamination schemes and various combinations of boundary conditions, core and facings thickness, inner and outer radius and several material variation patterns for top and bottom face-sheets are introduced.

Since results of the heterogeneous polar orthotropic-faced sandwich panels have not been reported yet, to demonstrate the efficiency and accuracy of the proposed approach, the obtained results are compared with finite element (FE) ones extracted from the ABAQUS software based on the 3D theory of elasticity. By discretization of the sandwich panel into 4800 eight-node biquadratic axisymmetric quadrilateral elements with reduced integration (CAX8R). Results are reported for the sandwich panels with face-sheets thickness h_t = h_b = 0.1 and the following material properties of core: E^(c) = 20 GPa, ρ^(c) = 950 kg/m³, ν^(c) = 0.25.

As a verification example and examination of the results accuracy, results of proposed method for the fundamental natural frequency of circular and annular sandwich panels are compared with FE results in Tables 1 and 2. The material parameters of sandwich panel are defined as ρ_b = ρ_t = 1631, ν_t = 0.26, ν_b = 0.23, E_r^(t) = E_t^(t) = E_r^(b) = E_t^(b) = 310 GPa, G_rz^(t) = 123 GPa, G_rz^(b) = 126 GPa.

Table 1 Comparison of the fundamental natural frequencies of the circular sandwich plate with heterogeneous face-sheets for various thickness and different boundary condition (α^(t) = γ^(t) = − 1, α^(b) = γ^(b) = 0.5, β^(t) = η^(t) = 2, β^(b) = η^(b) = 1) ρ_b = ρ_t = 1631, ν_t = 0.26, ν_b = 0.23, E_r^(t) = E_t^(t) = E_r^(b) = E_t^(b) = 310 GPa, G_rz^(t) = 123 GPa, G_rz^(b) = 126 GPa

Table 2 Comparison of the fundamental natural frequencies of the annular sandwich plate with heterogeneous face-sheets for various thickness and different boundary condition (α^(t) = γ^(t) = − 1, α^(b) = γ^(b) = 0.5, β^(t) = η^(t) = 2, β^(b) = η^(b) = 1) t_c = 0.2, ρ_b = ρ_t = 1631, ν_t = 0.26, ν_b = 0.23, E_r^(t) = E_t^(t) = E_r^(b) = E_t^(b) = 310 GPa, G_rz^(t) = 123 GPa, G_rz^(b) = 126 GPa

The material variation pattern parameters in the radial and circumferential directions are as follows:α^(t) = γ^(t) =  − 1, α^(b) = γ^(b) = 0.5, β^(t) = η^(t) = 2, β^(b) = η^(b) = 1.

The fundamental natural frequencies of the circular sandwich panels with different boundary conditions, core thickness (h_c = 0.1, 0.15 and 0.2) and outer radius (b = 0.7 and 0.8) are presented in Table 1. Also fundamental natural frequencies of the annular sandwich panels with core thickness h_c = 0.2, inner radius a = 0.2 and 0.3, outer radius b = 1 and various combination of the boundary conditions are presented in Table 2. These tables reveal that even for sandwich plates with radial non-homogeneous material and soft core, there is an excellent agreement between the obtained results based on the layerwise-zigzag theory and results of the three-dimensional theory of elasticity extracted from FE analysis. Based on Table 1 for sandwich circular plate, the global average errors for the prediction of the natural frequency when E_c = 100, 60 and 20 GPa are 0.45%, 0.5% and 1.04%, respectively (relative error (%) = $\left( {100/N} \right)\sum\nolimits_{i = 1}^{N} {\left| {\left( {\omega_{3D} - \omega_{{{\text{layerwise}}}} } \right)/\omega_{3D} } \right|}$). Also based on Table 2 for sandwich annular plate, the global average errors for E_c = 100, 60 and 20 GPa are 0.59%, 0.70% and 0.93%, respectively. It can be seen that the natural frequency of sandwich plate increases by increasing the core thickness but it is interesting to note that for clamped sandwich plate with soft core (E = 20 GPa), the frequency decreases by increasing the core thickness. Indeed for clamped plate with soft core, increasing the thickness of core decreases the rigidity of boundary conditions and the frequency becomes lower. Furthermore, either increasing the outer radius of circular sandwich panel or inner radius (increasing the R_i/R_o ratio), leads to the smaller frequencies.

After validating the current formulation and the solution method, some numerical results are prepared.

In Table 3, the influence of outer radius and material parameters on the fundamental frequency of sandwich annular plate with initially stressed core are studied. Also, effect of inner radius on the fundamental frequency of sandwich annular plate are investigated in Table 4. The results are prepared for heterogeneous orthotropic face sheets and also for four different material parameters. In these two tables, δ indicates the presence of initially bending pre-stresses in the core. The parameter χ is defined as $\chi = \left( {R_{o}^{2} \overline{\sigma }_{n} } \right)/D_{11}^{\left( c \right)}$. For δ = 0, i.e. when only in-plane normal pre-stress is applied to core, five value for K is considered: − 100, − 50, 10, 50 and 100. The negative value of δ shows compressive pre-stresses. According to these tables, one can observe that fundamental frequency increase by increasing the in-plane normal stress. As seen from results of Tables 3 and 4, the bending pre-stress cause a few decrease in frequencies (δ ≠ 0) and the in-plane pre-stress have more significant effect. For sandwich circular plate, the inhomogeneity material parameters can play important role in controlling natural frequencies. It is clear that the parameters α and γ are more pronounced compared to β and η. In fact, the frequency parameter enhances as the parameters α and γ decreased. In the case of sandwich annular plate (Table 4), it cannot found similar trend for material parameters like circular one, and combination of these parameters with initial pre-stress parameters can control the frequency of annular plate.

Table 3 influence of outer radius and material parameters on the fundamental natural frequency of sandwich circular plate with functionally graded orthotropic face sheets and initially stressed core (t_b = t_t = 0.1,t_c = 0.2, ρ_b = ρ_t = 1631, ν_t = 0.26, ν_b = 0.0052, E_r^(t) = 310 GPa, E_t^(t) = 6.2 GPa, E_r^(b) = 6.2 GPa, E_t^(b) = 310 GPa, G_rz^(t) = 4.1 GPa, G_rz^(b) = 1.35 GPa)

Table 4 influence of inner radius on the fundamental natural frequency of sandwich annular plate with functionally graded orthotropic face sheets and initially stressed core t_b = t_t = 0.1,t_c = 0.2, ρ_b = ρ_t = 1631, ν_t = 0.26, ν_b = 0.0052, E_r^(t) = 310 GPa, E_t^(t) = 6.2 GPa, E_r^(b) = 6.2 GPa, E_t^(b) = 310 GPa, G_rz^(t) = 4.1 GPa, G_rz^(b) = 1.35 GPa

In Figs. 2 and 3, variation of the transverse displacement, w, with respect to the radial direction, and transverse shear and radial stress, τ_rz and σ_r along thickness direction (at r = 0.4) are exhibited for static analysis of circular and annular sandwich panel having fully clamped boundary condition, respectively. As expected, continuity condition of transverse deflection and transverse shear stress is satisfied. It is observed that the absolute maximum values of transverse deflection and transverse shear stress decrease as the pre-stress parameter, χ, decreases. These figures also illustrate that bending initial stress significantly increased the transverse deflection in contrast of τ_rz. According to zigzag theory, the radial stress has jumps in layer interfaces and the absolute value of it decreases in the core by increasing χ.

Fig. 2

Variation of the displacement and stresses of the circular sandwich panel with clamped edge for different values of initial pre-stresses. a Transverse displacement distribution along radial direction, b, c transverse shear and radial stress distribution along thickness direction (α^(t) = γ^(t) = 1, α^(b) = γ^(b) = 1, β^(t) = η^(t) = 1, β^(b) = η^(b) = 1)

Fig. 3

Variation of the displacement and stresses of the annular sandwich panel with clamped edges for different values of the material property gradient index. a Transverse displacement distribution along radial direction, b, c transverse shear and radial stress distribution along thickness direction (α^(t) = γ^(t) = − 0.5, α^(b) = γ^(b) = 2, β^(t) = η^(t) = 0.5, β^(b) = η^(b) = 3)

Figure 4 provides the transverse shear and radial stress distribution along thickness direction for annular sandwich panel at two radii, i.e. r = 0.6, 0.8. It can be concluded from Fig. 4 that the influence of initial pre-stress in outer radius (larger r) has less effect on the absolute values of stresses and distribution patterns.

Fig. 4

Transverse shear and radial stress distribution along thickness direction for a, b r = 0.6, c, d r = 0.8 (α^(t) = γ^(t) = − 0.5, α^(b) = γ^(b) = 2, β^(t) = η^(t) = 0.5, β^(b) = η^(b) = 3)

7 Conclusion

Static and free vibration analyses of the circular and annular sandwich panels subjected to the in-plane pre-stresses were performed in this paper, as first time. In the presented analyses, the sandwich panels are fabricated from heterogeneous polar orthotropic face sheets and core is subjected to initially in-plane normal (tensile/compressive) and pure bending stresses. Moreover, both symmetric and asymmetric lamination schemes are examined.

Using the layerwise-zigzag theory with linear local displacements, the governing differential equations are extracted based on principle of minimum total potential energy. An analytical solution method is developed and a unified solution procedure is proposed for analysis of heterogeneous initially stressed annular and circular sandwich panels. The effects of in-plane stresses were investigated for sandwich plates with various thickness, material variations, and boundary conditions.

Appendix

$$\begin{gathered} \left\{ \begin{gathered} N_{r}^{{(t)}} \hfill \\ N_{\theta }^{{(t)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{t} }}{2}}}^{{\frac{{h_{t} }}{2}}} {\left\{ \begin{gathered} \sigma _{r}^{{(t)}} \hfill \\ \sigma _{\theta }^{{(t)}} \hfill \\ \end{gathered} \right\}} dz^{{(t)}} = \left[ {\begin{array}{*{20}l} {A_{{11}}^{{(t)}} (r)} & {A_{{12}}^{{(t)}} (r)} \\ {A_{{12}}^{{(t)}} (r)} & {A_{{22}}^{{(t)}} (r)} \\ \end{array} } \right]\left\{ \begin{gathered} \frac{\partial }{{\partial r}} \hfill \\ \frac{1}{r} \hfill \\ \end{gathered} \right\}\left( {u_{0}^{{(c)}} + \frac{{h_{t} }}{2}\phi _{r}^{{(t)}} + \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} } \right), \hfill \\ \left\{ \begin{gathered} N_{r}^{{(c)}} \hfill \\ N_{\theta }^{{(c)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} {\left\{ \begin{gathered} \sigma _{r}^{{(c)}} \hfill \\ \sigma _{\theta }^{{(c)}} \hfill \\ \end{gathered} \right\}} dz^{{(c)}} = \left[ {\begin{array}{*{20}l} {A_{{11}}^{{(c)}} } & {A_{{12}}^{{(c)}} } \\ {A_{{12}}^{{(c)}} } & {A_{{22}}^{{(c)}} } \\ \end{array} } \right]\left\{ \begin{gathered} \frac{\partial }{{\partial r}} \hfill \\ \frac{1}{r} \hfill \\ \end{gathered} \right\}u_{0}^{{(c)}} , \hfill \\ \left\{ \begin{gathered} N_{r}^{{(b)}} \hfill \\ N_{\theta }^{{(b)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{b} }}{2}}}^{{\frac{{h_{b} }}{2}}} {\left\{ \begin{gathered} \sigma _{r}^{{(b)}} \hfill \\ \sigma _{\theta }^{{(b)}} \hfill \\ \end{gathered} \right\}} dz^{{(b)}} = \left[ {\begin{array}{*{20}l} {A_{{11}}^{{(b)}} (r)} & {A_{{12}}^{{(b)}} (r)} \\ {A_{{12}}^{{(b)}} (r)} & {A_{{22}}^{{(b)}} (r)} \\ \end{array} } \right]\left\{ \begin{gathered} \frac{\partial }{{\partial r}} \hfill \\ \frac{1}{r} \hfill \\ \end{gathered} \right\}\left( {u_{0}^{{(c)}} - \frac{{h_{b} }}{2}\phi _{r}^{{(b)}} - \frac{{h_{c} }}{2}\phi _{r}^{{(c)}} } \right) \hfill \\ \left\{ \begin{gathered} M_{r}^{{(t)}} \hfill \\ M_{\theta }^{{(t)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{t} }}{2}}}^{{\frac{{h_{t} }}{2}}} {\left\{ \begin{gathered} \sigma _{r}^{{(t)}} \hfill \\ \sigma _{\theta }^{{(t)}} \hfill \\ \end{gathered} \right\}z^{{(t)}} \,} dz^{{(t)}} = \left[ {\begin{array}{*{20}l} {D_{{11}}^{{(t)}} (r)} & {D_{{12}}^{{(t)}} (r)} \\ {D_{{12}}^{{(t)}} (r)} & {D_{{22}}^{{(t)}} (r)} \\ \end{array} } \right]\left\{ \begin{gathered} \frac{\partial }{{\partial r}} \hfill \\ \frac{1}{r} \hfill \\ \end{gathered} \right\}\phi _{r}^{{(t)}} , \hfill \\ \left\{ \begin{gathered} M_{r}^{{(c)}} \hfill \\ M_{\theta }^{{(c)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{c} }}{2}}}^{{\frac{{h_{c} }}{2}}} {\left\{ \begin{gathered} \sigma _{r}^{{(c)}} \hfill \\ \sigma _{\theta }^{{(c)}} \hfill \\ \end{gathered} \right\}z^{{(c)}} \,} dz^{{(c)}} = \left[ {\begin{array}{*{20}l} {D_{{11}}^{{(c)}} } & {D_{{12}}^{{(c)}} } \\ {D_{{12}}^{{(c)}} } & {D_{{22}}^{{(c)}} } \\ \end{array} } \right]\left\{ \begin{gathered} \frac{\partial }{{\partial r}} \hfill \\ \frac{1}{r} \hfill \\ \end{gathered} \right\}\phi _{r}^{{(c)}} , \hfill \\ \left\{ \begin{gathered} M_{r}^{{(b)}} \hfill \\ M_{\theta }^{{(b)}} \hfill \\ \end{gathered} \right\} = \int\limits_{{ - \frac{{h_{b} }}{2}}}^{{\frac{{h_{b} }}{2}}} {\left\{ \begin{gathered} \sigma _{r}^{{(b)}} \hfill \\ \sigma _{\theta }^{{(b)}} \hfill \\ \end{gathered} \right\}z^{{(b)}} \,} dz^{{(b)}} = \left[ {\begin{array}{*{20}l} {D_{{11}}^{{(b)}} (r)} & {D_{{12}}^{{(b)}} (r)} \\ {D_{{12}}^{{(b)}} (r)} & {D_{{22}}^{{(b)}} (r)} \\ \end{array} } \right]\left\{ \begin{gathered} \frac{\partial }{{\partial r}} \hfill \\ \frac{1}{r} \hfill \\ \end{gathered} \right\}\phi _{r}^{{(b)}} , \hfill \\ Q_{r}^{{(t)}} = A_{{33}}^{{(t)}} (r)\left( {\phi _{r}^{{(t)}} + \frac{{\partial w}}{{\partial r}}} \right) \hfill \\ Q_{r}^{{(c)}} = A_{{33}}^{{(c)}} (r)\left( {\phi _{r}^{{(c)}} + \frac{{\partial w}}{{\partial r}}} \right) \hfill \\ Q_{r}^{{(b)}} = A_{{33}}^{{(b)}} (r)\left( {\phi _{r}^{{(b)}} + \frac{{\partial w}}{{\partial r}}} \right) \hfill \\ \end{gathered}$$

(42)

Furthermore, the stiffness coefficients are

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {A_{{11}}^{{(i)}} (r)} & {A_{{12}}^{{(i)}} (r)} \\ {A_{{12}}^{{(i)}} (r)} & {A_{{22}}^{{(i)}} (r)} \\ \end{array} } \right] = \int\limits_{{ - \frac{{h_{i} }}{2}}}^{{\frac{{h_{i} }}{2}}} {\left[ {\begin{array}{*{20}c} {C_{{11}}^{{(i)}} (r)} & {C_{{12}}^{{(i)}} (r)} \\ {C_{{12}}^{{(i)}} (r)} & {C_{{22}}^{{(i)}} (r)} \\ \end{array} } \right]} dz^{{(i)}} = \left[ {\begin{array}{*{20}c} {\bar{A}_{{11}}^{{(i)}} } & {\bar{A}_{{12}}^{{(i)}} } \\ {\bar{A}_{{12}}^{{(i)}} } & {\bar{A}_{{22}}^{{(i)}} } \\ \end{array} } \right]P^{{(i)}} (r), \hfill \\ \left[ {\begin{array}{*{20}c} {\bar{A}_{{11}}^{{(i)}} } & {\bar{A}_{{12}}^{{(i)}} } \\ {\bar{A}_{{12}}^{{(i)}} } & {\bar{A}_{{22}}^{{(i)}} } \\ \end{array} } \right] = \frac{{h_{i} }}{{1 - v_{{r\theta }}^{{(i)}} v_{{\theta r}}^{{(i)}} }}\left[ {\begin{array}{*{20}c} {E_{r}^{{(i)}} } & {v_{{\theta r}}^{{(i)}} E_{r}^{{(i)}} } \\ {v_{{\theta r}}^{{(i)}} E_{r}^{{(i)}} } & {E_{\theta }^{{(i)}} } \\ \end{array} } \right],\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = t,b \hfill \\ A_{{11}}^{{(c)}} = A_{{22}}^{{(c)}} = \frac{{h_{c} E^{{(c)}} }}{{1 - v^{{(c)2}} }},\,\,\,\,A_{{12}}^{{(c)}} = v^{{(c)}} A_{{11}}^{{(c)}} \hfill \\ \end{gathered}$$

(43)

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {D_{{11}}^{{(i)}} (r)} & {D_{{12}}^{{(i)}} (r)} \\ {D_{{12}}^{{(i)}} (r)} & {D_{{22}}^{{(i)}} (r)} \\ \end{array} } \right] = \int\limits_{{ - \frac{{h_{i} }}{2}}}^{{\frac{{h_{i} }}{2}}} {\left[ {\begin{array}{*{20}c} {C_{{11}}^{{(i)}} (r)} & {C_{{12}}^{{(i)}} (r)} \\ {C_{{12}}^{{(i)}} (r)} & {C_{{22}}^{{(i)}} (r)} \\ \end{array} } \right]} z^{{(i)2}} dz^{{(i)}} = \left[ {\begin{array}{*{20}c} {\bar{D}_{{11}}^{{(i)}} } & {\bar{D}_{{12}}^{{(i)}} } \\ {\bar{D}_{{12}}^{{(i)}} } & {\bar{D}_{{22}}^{{(i)}} } \\ \end{array} } \right]P^{{(i)}} (r) \hfill \\ \left[ {\begin{array}{*{20}c} {\bar{D}_{{11}}^{{(i)}} } & {\bar{D}_{{12}}^{{(i)}} } \\ {\bar{D}_{{12}}^{{(i)}} } & {\bar{D}_{{22}}^{{(i)}} } \\ \end{array} } \right] = \frac{{h_{i}^{3} }}{{12\left( {1 - v_{{r\theta }}^{{(i)}} v_{{\theta r}}^{{(i)}} } \right)}}\left[ {\begin{array}{*{20}c} {E_{r}^{{(i)}} } & {v_{{\theta r}}^{{(i)}} E_{r}^{{(i)}} } \\ {v_{{\theta r}}^{{(i)}} E_{r}^{{(i)}} } & {E_{\theta }^{{(i)}} } \\ \end{array} } \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = t,b \hfill \\ D_{{11}}^{{(c)}} = D_{{22}}^{{(c)}} = \frac{{h_{c}^{3} E^{{(c)}} }}{{12\left( {1 - v^{{(c)2}} } \right)}}, \hfill \\ \end{gathered}$$

(44)

$$\begin{gathered} A_{33}^{(i)} = \int\limits_{{ - \frac{{h_{i} }}{2}}}^{{\frac{{h_{i} }}{2}}} {C_{33}^{(i)} } dz^{(t)} = \overline{A}_{33}^{(i)} P^{(i)} (r)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overline{A}_{33}^{(i)} = h_{i} G_{rz}^{(i)} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = t,b\,\, \hfill \\ A_{33}^{(c)} = \frac{{h_{c} E^{(c)} }}{{2\left( {1 + v^{(c)} } \right)}}\, \hfill \\ \end{gathered}$$

(45)