Enforcing local boundary conditions in peridynamic models of diffusion with singularities and on arbitrary domains

Abstract

Imposing local boundary conditions and mitigating the surface effect at free surfaces in peridynamic (PD) models are often desired. The fictitious nodes method (FNM) “extends” the domain with a thin fictitious layer of thickness equal to the PD horizon size, and is a commonly used technique for these purposes. The FNM, however, is limited, in general, to domains with simple geometries. Here we introduce an algorithm for the mirror-based FNM that can be applied to arbitrary domain geometries. The algorithm automatically determines mirror nodes (in the given domain) of all fictitious nodes based on approximating, at each fictitious node, the “generalized” (or nonlocal) normal vector to the domain boundary. We tested the new algorithm for a peridynamic model of a classical diffusion problem with a flux singularity on the boundary. We show that other types of FNMs exhibit “pollution” of the solution far from the singularity point, while the mirror-based FNM does not and, in addition, shows a significantly faster rate of convergence to the classical solution in the limit of the horizon going to zero. The new algorithm is then used for mirror-based FNM solutions of diffusion problems in domains with curvilinear boundaries and with intersecting cracks. The proposed algorithm significantly improves the accuracy near boundaries of domains of arbitrary shapes, including those with corners, notches, and crack tips.

Graphical Abstract

1 Introduction

The peridynamic (PD) theory [1], as a nonlocal extension of classical continuum mechanics, allows for the natural treatment of discontinuities/singularities (such as cracks/damages [2,3,4,5]) by employing integration, over a nonlocal region called the horizon region, rather than differentiation. While the PD method has been primarily used to deal with mechanical behaviors [2, 4, 6,7,8,9], it has also been employed in diffusion-type problems involving cracks and damage, including thermal diffusion [10,11,12,13] and mass transport (e.g. corrosion) [14,15,16,17,18,19,20]. For a nonlocal formulation, associated BCs are of nonlocal type as well, and they are sometimes referred to as “nonlocal volume constraints” [21, 22]. In reality, however, conditions to be imposed (on values and/or derivatives of the unknown function) are known (measurable) only at the surface of a body, not through a finite thickness layer at the surface. The natural representation of such measurement-based conditions is via local boundary conditions. Therefore, imposing local BCs in nonlocal/peridynamic models is often desired/needed. Another issue caused by nonlocality is the “peridynamic surface effect” [23] which appears because, unlike in the bulk, points near the free surface/boundary do not have a full horizon region. The PD surface effect leads to the slightly different behavior of material points near the surface compared with those in the bulk.

A few strategies have been introduced to tackle these issues in the literature. One is to get rid of the nonlocality at boundaries, either by decomposing the domain into local and nonlocal subdomains where the former is placed in the neighborhood of the boundary [24] or via using a variable horizon which decreases from a constant value in the interior of the domain to zero at the boundary [25]. These approaches, however, do not work for problems in which nonlocality/discontinuity plays an important role near the boundary (e.g., in problems with interfaces), increase complexity since the coupling of local and nonlocal models is not trivial, or lead to imbalances in bond force/flux between material points caused by using variable-size horizons [26]. A different concept has been recently introduced in [27] to improve results in dynamic brittle/quasi-brittle fracture in samples with complex geometries, like perforated plates, by using non-uniform grids near a boundary. Another strategy is explored by Aksoylu et al. [28,29,30,31] who proposed new operators that agree with the original PD operator in the bulk of the domain and simultaneously enforce local BCs. However, this approach, to the best of our understanding, appears to be limited to rectangular/box domains.

Another popular strategy for reducing the PD surface effect and to impose local BCs is to extend the solution domain by a fictitious layer with the thickness of the PD horizon so that each point in the solution domain has a full horizon region. Then the local BCs (including traction-free BCs) are converted into nonlocal volume constraints to be imposed on this fictitious region. This strategy is called the fictitious nodes method (FNM), or the extended domain method (EDM), and can be further classified into several categories based on the rule of conversion [11, 12, 32,33,34,35,36]. Similar ideas have been used in other nonlocal numerical models [37, 38]. Some of these FNMs require the reformulation of governing equations for each type of problem [33, 36] and thus may not be suitable for general applications. Others do not involve modifying the governing equations and have been proven to work efficiently for problems set on domains with simple geometry (e.g. rectangular) [39, 40], but applying them to problems with irregular geometries (e.g. curved boundaries, kinks, corners, and cracks) is not possible. Specifically, for the mirror-based FNM which determines the volume constraint at each fictitious node based on the value of its mirror node in the solution domain [34, 35, 41], the absence of a general algorithm that can find the mirror nodes (of all fictitious nodes) required by the method makes it inapplicable to problems defined on arbitrary-shape domains.

In this work, we introduce a new algorithm that automatically finds mirror nodes for the mirror-based FNM for domains of arbitrary geometries, including those with cracks. The algorithm approximates, at each fictitious node, a “generalized” normal vector (the “nonlocal normal”) to the boundary of the given domain if the boundary satisfies 1st-order smoothness conditions. We select the PD diffusion model to test the new algorithm. With small modifications, the algorithm presented here can easily be applied to PD models solving other types of problems, such as fracture and corrosion damage. We also investigate two other types of FNMs and compare their results with those from the mirror-based FNM: the “naive” version [42], and the Taylor FNM [32, 37, 43]. We compare the performance of different FNMs in enforcing local boundary conditions using two problems: one set on a simple domain with no singularities, and the other with a flux singularity (in the corresponding local model) along a boundary where Dirichlet and Neumann boundary conditions meet, the Motz problem [44, 45]. We show that the new algorithm can let us use the mirror-based FNM to solve diffusion problems in domains with cracks and curved boundaries.

It should be noted that the main focus of this work is methodology and algorithm development, accompanied by verification via several important and relatively difficult examples. A practical algorithm is described in detail and possible extensions are discussed. While numerical experiments may offer insight into the well-posedness of the problems we investigated here, proofs on existence, uniqueness, and well-posedness are outside of the scope of our manuscript.

This paper is organized as follows: in Sect. 2 we review the PD method for diffusion-type problems; in Sect. 3 we discuss the fictitious nodes method and introduce the autonomous algorithm to generalize the mirror-based FNM for arbitrary geometries; in Sect. 4 we compare the performance of three different types of FNMs using examples with and without local singularities, then test the generality and capability of the algorithm introduced here on the mirror-based FNM for more complicated problems with cracks and in domains with curved boundaries; conclusions are given in Sect. 5.

2 The peridynamic model for diffusion

Consider the diffusion of a scalar quantity $u$ (e.g., temperature, mass, concentration, etc.) in a homogeneous and isotropic body occupying the domain $\Omega \in {\mathbb{R}}^{d}$, $d=1, 2$, or $3$, with constant diffusivity $\nu$. The classical local model describes the diffusion by using the following PDE-based formulation:

$$\left\{\begin{array}{c}\frac{\partial u({\varvec{x}},t)}{\partial t}=\nu {\nabla }^{2}u\left({\varvec{x}},t\right)+s\left({\varvec{x}},t\right) \quad \forall (x, t)\in \Omega \times [0, T] \\ G\left(u\left({\varvec{x}},t\right)\right)=0 \quad \forall (x, t)\in \partial \Omega \times [0, T]\end{array}\right.$$

(1)

where $s\in {\mathbb{R}}$ is the source/sink term and $G(u\left({\varvec{x}},t\right))$ defines the BCs (which could be Dirichlet, Neumann, Robin, or mixed).

The peridynamic (PD) bond-based diffusion model [10, 21, 46], on the other hand, is written as:

$$\frac{\partial u({\varvec{x}},t)}{\partial t}=\nu {\mathcal{L}}_{\omega }u\left({\varvec{x}},t\right)+s\left({\varvec{x}},t\right) \quad \forall ({\varvec{x}}, t) \in \Omega \times [0, T]$$

(2)

where ${\mathcal{L}}_{\omega }$ is the PD Laplacian operator which can be expressed as:

$${\mathcal{L}}_{\omega }u\left({\varvec{x}},t\right)={\int}_{{\mathcal{H}}_{{\varvec{x}}}}\omega \left({\varvec{x}},{\varvec{y}}\right)\left(u\left({\varvec{y}}, t\right)-u({\varvec{x}}, t)\right)d{\varvec{y}} ,$$

(3)

Here ${\mathcal{H}}_{{\varvec{x}}}$ is the (nonlocal) horizon region of ${\varvec{x}}$ and is usually selected to be a disk in 2D (a line segment in 1D or a sphere in 3D) centered at ${\varvec{x}}$, with the radius denoted by $\delta$ (the horizon size, or simply the “horizon”, when it is clear from the context that we refer to the radius or the region, not the region itself). Figure 1 schematically shows a 2D PD body with a generic point ${\varvec{x}}$, its family, and its horizon region. Objects that carry pairwise nonlocal interactions between points are called bonds. In the more generalized state-based formulation, diffusion in a bond is directly influenced by other bonds which connect to the same point [12]. This setting may be beneficial for certain problems but is not considered here.

Fig. 1

A peridynamic body with a generic point ${\varvec{x}}$ and its horizon region, ${\mathcal{H}}_{{\varvec{x}}}$. Nonlocal interactions exist through the bond between point ${\varvec{x}}$ and an arbitrary point ${\varvec{y}}$ located in its horizon

The kernel function $\omega \left({\varvec{x}},{\varvec{y}}\right):\Omega \times\Omega \to {\mathbb{R}}$ in Eq. (3) denotes a nonnegative symmetric mapping, i.e., $\omega \left({\varvec{x}},{\varvec{y}}\right)=\omega \left({\varvec{y}},{\varvec{x}}\right)\ge 0$. It has been shown that for $u\in {C}^{2}(\Omega ),$ ${\mathcal{L}}_{\omega }u\to \Delta u$ as $\delta \to 0$, under certain conditions [42, 47]. A kernel function that leads to good convergence properties with the one-point Gaussian quadrature discretization of the spatial domain is [42]:

$$\omega \left({\varvec{x}},{\varvec{y}}\right)=\frac{A}{{\Vert {\varvec{y}}-{\varvec{x}}\Vert }^{2}}$$

(4)

where $A$ is a constant which can be calibrated by matching PD flux to classical flux for a linearly distributed field, as shown in [11]. One can also determine $A$ by enforcing that Eq. (2) recovers the classical diffusion equation as $\delta \to 0$ using the approach first provided in [25] for 1D linear elasticity, as shown below for 2D diffusion.

Suppose $u({\varvec{x}})$ is sufficiently smooth, one can write, for all ${\varvec{x}}\in {\Omega }_{I}$ and ${\varvec{y}}\in {\mathcal{H}}_{{\varvec{x}}}$:

$$u\left( y \right) = u\left( x \right) + \xi_{x} \frac{\partial u}{{\partial x}}\left( x \right) + \xi_{y} \frac{\partial u}{{\partial y}}\left( x \right) + \frac{1}{2!}\left(\xi_{x}^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }}\left( x \right) + 2\xi_{x} \xi_{y} \frac{{\partial^{2} u}}{\partial x\partial y}\left( x \right) + \xi_{y}^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left( x \right)\right) + \frac{1}{3!}\left( {\xi_{x}^{3} \frac{{\partial^{3} u}}{{\partial x^{3} }}\left( x \right) + 3\xi_{x}^{2} \xi_{y} \frac{{\partial^{3} u}}{{\partial x^{2} \partial y }}\left( x \right) + 3\xi_{x} \xi_{y}^{2} \frac{{\partial^{3} u}}{{\partial x\partial y^{2} }}\left( x \right) + \xi_{y}^{3} \frac{{\partial^{3} u}}{{\partial y^{3} }}\left( x \right)} \right) + 0\left( {\left( {\xi_{x}^{2} + \xi_{y}^{2} } \right)^{2} } \right)$$

(5)

where ${\varvec{\xi}}={\varvec{y}}-{\varvec{x}}={\left[ \begin{array}{cc}{\xi }_{x}& {\xi }_{y}\end{array}\right]}^{T}$. Substitute Eq. (5) into Eq. (3) and consider symmetry, we get:

$${\mathcal{L}}_{\omega }u\left({\varvec{x}},t\right)=\frac{A}{2}{\int}_{{\mathcal{H}}_{{\varvec{x}}}}\frac{{\xi }_{x}^{2}\frac{{\partial }^{2}u}{\partial {x}^{2}}+{\xi }_{y}^{2}\frac{{\partial }^{2}u}{\partial {y}^{2}}+O\left( {\left({\xi }_{x}^{2}+{\xi }_{y}^{2}\right)}^{2}\right)}{{\xi }_{x}^{2}+{\xi }_{y}^{2}}d\widehat{{\varvec{x}}}=\frac{A}{2}\left(\frac{{\partial }^{2}u}{\partial {x}^{2}}{\int}_{0}^{\delta }\rho d\rho {\int}_{0}^{2\pi }{\mathit{cos}}^{2}\theta d\theta +\frac{{\partial }^{2}u}{\partial {y}^{2}}{\int}_{0}^{\delta }\rho d\rho {\int}_{0}^{2\pi }{\mathit{sin}}^{2}\theta d\theta +{\delta }^{2}O\left( {\delta }^{2}\right)\right)=\frac{\pi {\delta }^{2}A}{4}\left(\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}u}{\partial {y}^{2}}+O\left( {\delta }^{2}\right)\right)$$

(6)

One recovers the 2D classical diffusion equation as $\delta \to 0$ when we have:

$$A=\frac{4}{\pi {\delta }^{2}}$$

(7)

Equation (7) agrees with the calibrated values given in [10, 11]. With this value, the PD model converges to the classical model of order two for ${\varvec{x}}$ with a full horizon. However, using Eq. (7) for ${\varvec{x}}$ which does not have a full horizon region would lead to lower diffusivity (or a lower stiffness for problems in elasticity (see [23, 25])). Moreover, BCs for PD equations (e.g., Eq. (2)) should be nonlocal (sometimes called “volume-constraints” [21, 22]), but usually, only the local BCs are available. In the next section, we discuss the FNMs which allow us to enforce local BCs in PD models.

3 Fictitious nodes methods

Unlike classical local methods, the boundary conditions in peridynamics are nonlocal. However, when solving practical problems, imposing local-type boundary conditions in nonlocal/peridynamic models is usually desired/needed because, in reality, conditions (on the unknown function values or its flux) are imposed at the surfaces of a body, not through a finite layer near the surface. The natural representation of such conditions (based on measurements) is via local boundary conditions. Various methods to impose local boundary conditions in PD models have been investigated in [12, 22, 48]. One such method is the fictitious nodes method (FNM) [12, 34, 48].

In FNM for peridynamics, certain volume constraints $c\left(\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)\right)=0$ are specified on the extended fictitious region $\widetilde{\Omega }=\left\{\widetilde{{\varvec{x}}}\notin\Omega |{\text{dist}}\left(\widetilde{{\varvec{x}}}, \partial \Omega \right)<\delta \right\}$ (e.g., the “collar” of the domain $\Omega$ shown in Fig. 2), so that desired local boundary conditions on $\partial\Omega$ (which includes crack surfaces) are satisfied or approximately satisfied. The domain consists of material points, while the fictitious domain is the collection of fictitious points, which are not material points but may occupy the same spatial location with material points, for example when constructing the fictitious domain around a crack (see Fig. 2). If fictitious points “coincide” with material points, that only means that they share the same location, but they are independent of each other.

Fig. 2

Schematic of a peridynamic domain ($\Omega$), its boundary ($\partial\Omega$, which includes the crack surface), its fictitious layer ($\widetilde{\Omega }$, which includes the region around the crack surface overlayed on $\Omega$), and the regular-shaped region $\widehat{\Omega }$ within which $\widetilde{\Omega }$ is determined

Such volume-constrained PD problems are defined analogously to boundary value problems for PDEs in the local theory according to nonlocal vector calculus [22]. Volume-constrained PD steady-state diffusion (or Laplace) problem can be expressed as [22]:

$$\left\{\begin{array}{c}{\mathcal{L}}_{\omega }u\left({\varvec{x}}\right)=0 \quad x\in \Omega \\ c\left(\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)\right)=0 \quad \widetilde{{\varvec{x}}}\in \widetilde{\Omega }\end{array}\right.$$

(8)

When applied to free boundaries (or traction-free crack surfaces), the FNM mitigates the peridynamic surface effect [34]. Surface effect is a common issue for numerical models using nonlocal formulations [22, 38]. The PD surface effect appears because, unlike in the bulk, material points near the free boundary/surface do not have a full non-local neighborhood. The PD surface effect leads to the slightly different behavior of material points near the surface compared with those in the bulk. This could mean a lower diffusivity near the surface for diffusion problems, and a lower stiffness for problems in elasticity (see [23]). These effects are reduced as one decreases $\delta$, and become “exact” when $\delta$ is the same as the physical nonlocal interaction range, which could be atomistically small. In practical modeling, $\delta$ is usually set to match observable physical length scales (see discussion in [49]), and not larger than relevant geometrical features of the domain (notch widths, etc.).

Before implementing FNMs, the explicit $\partial\Omega$ at the initial time is needed to determine the initial configuration of discretized $\Omega$ and $\widetilde{\Omega }$ (see Appendix A). Note that $\Omega$ is considered as a closed set, i.e., if a node ${\varvec{x}}$ sits on $\partial\Omega$, then ${\varvec{x}}\in\Omega$. Then the boundary $\partial\Omega$ will be implicitly tracked by bonds connecting points in $\Omega$ and those in $\widetilde{\Omega }$, or by broken bonds. A regular-shaped region $\widehat{\Omega }$ is usually placed outside $\Omega$ in which $\widetilde{\Omega }$ is determined, and the $\widetilde{\Omega }$ determined after discretization is usually larger than the one before discretization to assure ${\mathcal{H}}_{{\varvec{x}}}$ is complete $\forall {\varvec{x}}\in\Omega$ in the discretized configuration. In this section, we review three different types of FNM from the literature.

3.1 Naïve FNM

The “naïve”-type FNM is often used in the literature to impose local Dirichlet and homogeneous Neumann (no flux) BCs because of its simplicity. This method enforces Dirichlet BCs by assigning the same values to all fictitious points corresponding to a boundary point, while homogeneous Neumann BCs (insulated BCs in diffusion problems) are enforced by simply neglecting all corresponding fictitious points [42]. See Fig. 3 for an illustration of how a Dirichlet BC $u\left({{\varvec{x}}}_{b}\right)={u}_{b}$ at ${{\varvec{x}}}_{b}\in \partial {\Omega }_{{\text{D}}}$ (boundary subjected to Dirichlet BC) is enforced at $\widetilde{{\varvec{x}}}\in {\widetilde{\Omega }}_{{\text{D}}}$ (fictitious region subjected to Dirichlet volume-constraint). An even simpler version of “enforcing” local Dirichlet BCs in the nonlocal model is to dispense entirely with the fictitious points and subject only the surface points to the values of local boundary conditions [10]. Previous work has shown that results by both versions converge to local solutions as the horizon size approaches zero [13, 42].

Fig. 3

Illustration of using the naïve FNM to enforce the local Dirichlet (a) and homogeneous Neumann (b) BCs

Remark:

The naïve FNM has the advantage of featuring the simplest implementation and is the most efficient (see Sect. 4.1). However, a jump-discontinuity in the solution at the boundary may be generated, leading to possible errors in fluxes near the boundary (see Sect. 4.1).

3.2 Taylor-based FNM

The second FNM, used in the PD context first in [32], requires a Taylor expansion (to linear terms) for ${\varvec{x}}\in \widetilde{\Omega }\cup {\Omega }_{\delta }$, in which ${\Omega }_{\delta }=\{{\varvec{x}}\in \Omega |{\text{dist}}({\varvec{x}}, \partial\Omega )<\delta \}$. We call it Taylor-based FNM or simply Taylor FNM. To impose the local Dirichlet BC $u\left({\varvec{x}}\right)={u}_{{\text{D}}}({\varvec{x}})$ for ${\varvec{x}}\in \partial {\Omega }_{{\text{D}}}$ using Taylor FNM, for each ${\varvec{x}}\in {\Omega }_{\delta }$, ${\varvec{y}}\in {\widetilde{\Omega }}_{{\text{D}}}\cap {\mathcal{H}}_{{\varvec{x}}}$ and ${{\varvec{x}}}_{b}=\partial {\Omega }_{{\text{D}}}\cap \overrightarrow{{\varvec{x}}{\varvec{y}}}$, $\widetilde{u}({\varvec{y}})$ is extrapolated from $u$(${\varvec{x}})$ as:

$$\widetilde{u}=u+\left(\frac{\partial u}{\partial{\varvec{\xi}}}\right){\varvec{\xi}}+\mathcal{O}\left({\delta }^{2}\right)\approx u+\frac{\left({u}_{b}-u\right)}{d}\left(d+\widetilde{d}\right)={u}_{b}+\frac{\widetilde{d}}{d}\left({u}_{b}-u\right)$$

(9)

where $\widetilde{u}=\widetilde{u}({\varvec{y}})$, $u=u({\varvec{x}})$, ${u}_{b}={u}_{{\text{D}}}({{\varvec{x}}}_{b})$, ${\varvec{\xi}}={\varvec{y}}-{\varvec{x}}$, $d={\text{dist}}({\varvec{x}},{{\varvec{x}}}_{b})$ and $\widetilde{d}={\text{dist}}({\varvec{y}}, {{\varvec{x}}}_{b})$ (“dist” denotes distance).

Note that when ${\varvec{x}}$ approaches the boundary in Eq. (9), a significantly large  $\widetilde{d}/d$ may occur. This situation could cause numerical errors during the simulation. Therefore, a further modification on Eq. (9) may be required as follows [43] to avoid the above issue:

$$\widetilde{u}=u+\left({u}_{b}-u\right)\times {\text{min}}\left\{\lambda ,\left(1+\frac{\widetilde{d}}{d}\right)\right\}$$

(10)

where $\lambda$ is a parameter determined from numerical tests. Normally $\lambda$ =1.5 leads to good results [43].

To impose a local Neumann or Robin BC $\nabla {u}_{b}\bullet {\varvec{n}}=f\left({u}_{b}\right)$ for ${{\varvec{x}}}_{b}\in \partial {\Omega }_{{\text{NR}}}$ (boundary subjected to Neumann or Robin BC), where $f$ is a given function, for each ${\varvec{x}}\in {\Omega }_{\delta }$, ${\varvec{y}}\in {\widetilde{\Omega }}_{{\text{NR}}}\cap {\mathcal{H}}_{{\varvec{x}}}$ and ${{\varvec{x}}}_{b}=\partial {\Omega }_{{\text{NR}}}\cap \overrightarrow{{\varvec{x}}{\varvec{y}}}$, $\widetilde{u}$ can be approximated by $u$ and ${u}_{b}$ by the following Taylor expansion [32]:

$$\widetilde{u}=u+{\varvec{\xi}}\left(\frac{\partial u}{\partial{\varvec{\xi}}}\right)+\mathcal{O}\left({\delta }^{2}\right)\approx u+{\varvec{\xi}}\left(\frac{\partial {u}_{b}}{\partial {\varvec{n}}}\right)=u+\left(d+\widetilde{d}\right)f({u}_{b})$$

(11)

in which ${u}_{b}$ is not given and needs to be approximated from the following equation:

$${u}_{b}\approx u+df\left({u}_{b}\right)$$

(12)

If $f\left({u}_{b}\right)$ is a nonlinear function, a nonlinear equation solver, such as Newton’s method, is needed to solve for ${u}_{b}$ [50].

Remark:

In this Taylor approach,$\widetilde{u}$ at each ${\varvec{y}}\in \widetilde{\Omega }$ changes, even in the same solution step, and needs to be computed anew for each ${\varvec{x}}\in {\Omega }_{\delta }\cap {\mathcal{H}}_{{\varvec{y}}}$ at which an integration over ${\mathcal{H}}_{{\varvec{x}}}$ is performed (see Eqs. (9) & (12)). This is illustrated in Fig. 4, where for ${{\varvec{x}}}_{i}\in {\Omega }_{\delta }$ and ${{\varvec{x}}}_{b}\in \partial {\Omega }_{{\text{D}}}\cap {\mathcal{H}}_{{{\varvec{x}}}_{i}}$, ${\widetilde{u}}_{i}$ is the distribution of $\widetilde{u}({\varvec{y}})$ $\forall {\varvec{y}}\in \left\{{\varvec{y}}\in {\widetilde{\Omega }}_{{\text{D}}}|\partial {\Omega }_{{\text{D}}}\cap \overrightarrow{{{\varvec{x}}}_{i}{\varvec{y}}}={{\varvec{x}}}_{b}\right\}$. The solution step refers to each call to the Conjugate Gradient (CG) solver (see Fig. 24 in Appendix A for the flowchart of the simulation). Moreover, for boundaries with irregular geometries such as corners, those ${\varvec{x}}$ and ${\varvec{y}}$ nearby also have variable $d$ and $\widetilde{d}$ associated with them, because, for each pair of ${\varvec{x}}$ and ${\varvec{y}}$, $\overrightarrow{{\varvec{x}}{\varvec{y}}}$ may intersect different parts of the boundary.

Fig. 4

Illustration of enforcing the local Dirichlet BC by using the Taylor FNM (redrawn from [38])

3.3 Mirror-based FNM

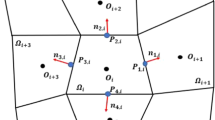
As shown in Fig. 5, the mirror FNM assigns the constraint $\widetilde{u}(\widetilde{{\varvec{x}}})$ at each $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ based on $u\left({{\varvec{x}}}^{R}\right)$ and $u\left({{\varvec{x}}}^{P}\right)$ in which ${{\varvec{x}}}^{P}={{\text{OProj}}}_{\partial\Omega }\left(\widetilde{{\varvec{x}}}\right)$ is the orthogonal projection of $\widetilde{{\varvec{x}}}$ onto $\partial\Omega$ and ${{\varvec{x}}}^{R}={{\text{Ref}}}_{\partial\Omega }\left(\widetilde{{\varvec{x}}}\right)=\widetilde{{\varvec{x}}}+2({{\varvec{x}}}^{P}-\widetilde{{\varvec{x}}})$ is the reflection, or mirror point, of $\widetilde{{\varvec{x}}}$ through/across $\partial\Omega$. For $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$, when $\partial {\Omega }_{\widetilde{{\varvec{x}}}}=\{\partial\Omega \cap {\mathcal{H}}_{\widetilde{{\varvec{x}}}}\}$ is continuous and the normal to $\partial {\Omega }_{\widetilde{{\varvec{x}}}}$ at each point is unique, we have $\overrightarrow{\widetilde{{\varvec{x}}}{{\varvec{x}}}^{P}}=-k{\varvec{n}}({{\varvec{x}}}^{P})$, in which $k\in {\mathbb{R}}^{+}$ and ${\varvec{n}}({{\varvec{x}}}^{P})$ is the outward unit normal vector at ${{\varvec{x}}}^{P}$.

Fig. 5

A schematic of mirror points in mirror-based FNM [12]

In the mirror FNM, to impose the local Dirichlet BC $u\left({\varvec{x}}\right)={u}_{{\text{D}}}({\varvec{x}})$ for ${\varvec{x}}\in \partial {\Omega }_{{\text{D}}}$ and the Neumann BC ${\nabla }_{{\varvec{n}}}u\left({\varvec{x}}\right)=q({\varvec{x}})$ for ${\varvec{x}}\in$ $\partial {\Omega }_{{\text{N}}}$, $\widetilde{u}(\widetilde{{\varvec{x}}})$ at $\widetilde{{\varvec{x}}}\in {\widetilde{\Omega }}_{{\text{D}}}$ is assigned as:

$$\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)=2u({{\varvec{x}}}^{P})- u({{\varvec{x}}}^{R})$$

(13)

and $\widetilde{u}(\widetilde{{\varvec{x}}})$ at $\widetilde{{\varvec{x}}}\in {\widetilde{\Omega }}_{{\text{N}}}$ is assigned as:

$$\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)=u\left({{\varvec{x}}}^{R}\right)+\Vert \widetilde{{\varvec{x}}}-{{\varvec{x}}}^{R}\Vert q({{\varvec{x}}}^{P})$$

(14)

respectively. For the local Robin BC ${\nabla }_{{\varvec{n}}}u\left({\varvec{x}}\right)=f\left(u\left({\varvec{x}}\right)\right)$ for ${\varvec{x}}\in$ $\partial {\Omega }_{{\text{R}}}$, we have, for $\widetilde{{\varvec{x}}}\in {\widetilde{\Omega }}_{{\text{R}}}$:

$$\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)=u\left({{\varvec{x}}}^{R}\right)+\Vert \widetilde{{\varvec{x}}}-{{\varvec{x}}}^{R}\Vert f\left(u\left({{\varvec{x}}}^{P}\right)\right)=u\left({{\varvec{x}}}^{R}\right)+\Vert \widetilde{{\varvec{x}}}-{{\varvec{x}}}^{R}\Vert f\left(\frac{u({{\varvec{x}}}^{R})+\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)}{2}\right)$$

(15)

in which the approximation $u({{\varvec{x}}}^{P})=\frac{u({{\varvec{x}}}^{R})+\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)}{2}$ is made because $u$ should be close to linear between $\widetilde{{\varvec{x}}}$ and ${{\varvec{x}}}^{R}$. Note that $\widetilde{u}\left(\widetilde{{\varvec{x}}}\right)$ requires to be solved using a nonlinear solver if function $f$ is nonlinear.

While the Eq. (9) of Taylor-based FNM with $d=\widetilde{d}$ appears to be similar to Eq. (13) of mirror-based FNM, they are different, except when nodes ${\varvec{x}}$ and ${\varvec{y}}$ (based on which quantities in Eq. (9) are computed) coincide with nodes ${{\varvec{x}}}^{R}$ and $\widetilde{{\varvec{x}}}$ in Eq. (13), respectively.

Remark:

In the mirror FNM, $\widetilde{u}(\widetilde{{\varvec{x}}})$ at each $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ does not change in the same solution step because it only depends on ${{\varvec{x}}}^{R}$ and ${{\varvec{x}}}^{P}$ which can be uniquely determined for each ${\varvec{x}}$. See Fig. 6 for illustrations of how local Dirichlet BCs are enforced in the mirror FNM.

Fig. 6

Illustration of enforcing a local Dirichlet BC in the mirror FNM (redrawn from [12])

Remark:

Note that in the Taylor and mirror FNMs described in this section, all the information for ${\varvec{x}}\in {\Omega }_{\delta }\cup \widetilde{\Omega }$, such as ${\text{dist}}({\varvec{x}}, \partial \Omega )$ or ${{\text{Ref}}}_{\partial\Omega }({\varvec{x}})$, are considered as given, which works for simple geometries. However, for general cases, such information is not straightforward and cannot be provided as input. For example, for shapes with corners of various angles, cusps, crack tips, etc., the tangent line (and normal vector) is not well defined everywhere. While some ad-hoc choices can be made for overcoming this issue, we aim for a general strategy that assures all the information required to implement the FNM can be determined without ambiguity. Moreover, the enforcement of local BCs on surfaces of cracks has not been considered until now, mainly because fictitious regions are not clearly defined for such “inner” surfaces yet. In the next section, we introduce an algorithm for the mirror FNM that automatically enforces local BCs, including those imposed on crack surfaces, in PD models for problems with arbitrary boundary shapes.

3.4 An algorithm to find mirror nodes in mirror-based FNM

Using the mirror FNM for arbitrarily shaped boundaries/surfaces (with corners, cusps, etc.) requires finding both ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R} \forall \widetilde{{\varvec{x}}}\in \widetilde{\Omega }$. Since ${{\varvec{x}}}^{R}=\widetilde{{\varvec{x}}}+2({{\varvec{x}}}^{P}-\widetilde{{\varvec{x}}})$, as shown in Fig. 5, once ${{\varvec{x}}}^{P}$ is known, ${{\varvec{x}}}^{R}$ can be determined. Starting from $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$, one could determine ${{\varvec{x}}}^{P}$ as $\underset{{\varvec{y}}\in {\mathcal{H}}_{\widetilde{{\varvec{x}}}}\cap \partial\Omega }{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},\widetilde{{\varvec{x}}}\right)$. However, the uniqueness of the solution is not guaranteed. Moreover, for $\widetilde{{\varvec{x}}}$ near corners with an angle smaller than $90^\circ$ (see regions ${\widetilde{\Omega }}_{1}$ in Fig. 7), it may lead to ${{\varvec{x}}}^{R}\notin\Omega$.

Fig. 7

Schematic of ${\widetilde{\Omega }}_{1}\subset \widetilde{\Omega }$ near an acute corner where ${{\varvec{x}}}^{R}={{\text{Ref}}}_{\partial\Omega }\left(\widetilde{{\varvec{x}}}\right)\notin\Omega$ for $\widetilde{{\varvec{x}}}\in {\widetilde{\Omega }}_{1}$, when ${{\varvec{x}}}^{P}=\underset{{\varvec{y}}\in {\mathcal{H}}_{\widetilde{{\varvec{x}}}}\cap \partial\Omega }{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},\widetilde{{\varvec{x}}}\right)$

We introduce an algorithm that resolves all these issues. First, following the idea in [36], we define the “generalized” normal vector (or the nonlocal normal) to the boundary at some ${\varvec{x}}\in\Omega$ as:

$$\widehat{{\varvec{n}}}\left({\varvec{x}}\right)=\frac{{\int}_{{\mathcal{H}}_{{\varvec{x}}}}\mu \left({\varvec{x}},{\varvec{y}}\right)({\varvec{x}}-{\varvec{y}})d{\varvec{y}}}{\Vert {\int}_{{\mathcal{H}}_{{\varvec{x}}}}\mu \left({\varvec{x}},{\varvec{y}}\right)({\varvec{x}}-{\varvec{y}})d{\varvec{y}}\Vert }$$

(16)

where $\mu$ is the binary function defined as $\mu \left({\varvec{x}},{\varvec{y}}\right):\Omega \times\Omega \to \{\mathrm{0,1}\}$. $\mu$ takes the value 0 if the bond $\left({\varvec{x}},{\varvec{y}}\right)$ is broken or intersects the boundary (which includes crack surfaces), and 1 otherwise. As we can see in Fig. 8a for a few examples, $\widehat{{\varvec{n}}}$ is nonzero only in the region ${\Omega }_{\updelta }$ near the boundary of $\Omega$, i.e., $\Vert \widehat{{\varvec{n}}}\Vert =0$ for ${\varvec{x}}\notin {\Omega }_{\updelta }$. $\widehat{{\varvec{n}}}$ is a generalization of the corresponding classical external normal vector ${\varvec{n}}({\varvec{x}})$ for ${\varvec{x}}\in \partial\Omega$ if ${\varvec{n}}$ exists, as shown at the point ${{\varvec{x}}}_{1}$ in Fig. 8a, where we have $\widehat{{\varvec{n}}}({{\varvec{x}}}_{1})\to {\varvec{n}}({{\varvec{x}}}_{1})$ as $\delta \to 0$.

Fig. 8

Schematic for the “generalized” (or nonlocal) normal vector when (a) ${\varvec{x}}\in\Omega$ and (b) ${\varvec{x}}\in \widetilde{\Omega }$

The generalized normal vector can be extended to points in the fictitious domain by modifying Eq. (16) to be:

$$\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)=\frac{{\int}_{\begin{array}{c}{\widetilde{\mathcal{H}}}_{\widetilde{{\varvec{x}}}}\\ \end{array}}\left(1-\widetilde{\mu }\left(\widetilde{{\varvec{x}}},{\varvec{y}}\right)\right)({\varvec{y}}-\widetilde{{\varvec{x}}})d{\varvec{y}}}{\Vert {\int}_{{\widetilde{\mathcal{H}}}_{\widetilde{{\varvec{x}}}}}\left(1-\widetilde{\mu }\left(\widetilde{{\varvec{x}}},{\varvec{y}}\right)\right)({\varvec{y}}-\widetilde{{\varvec{x}}})d{\varvec{y}}\Vert } {\text{for}} \widetilde{{\varvec{x}}}\in \widetilde{\Omega }$$

(17)

where $\widetilde{\mu }$ is now defined as $\widetilde{\mu }\left(\widetilde{{\varvec{x}}},{\varvec{y}}\right):\widetilde{\Omega }\times\Omega \to \{\mathrm{0,1}\}$. We also let ${\widetilde{\mathcal{H}}}_{\widetilde{{\varvec{x}}}}={\mathcal{H}}_{\widetilde{{\varvec{x}}}}\cap\Omega$, meaning that fictitious nodes are excluded from ${\widetilde{\mathcal{H}}}_{\widetilde{{\varvec{x}}}}$ and there are no bonds between fictitious nodes. Different from the external nonlocal normal, the nonlocal normal in Eq. (17) points towards the inside of the domain $\Omega$ (because the mirror nodes are to be found inside $\Omega )$. Moreover, in order to find fictitious nodes for regions around cracks, we want to only include bonds that intersect the crack. That is the reason for using the $\widetilde{\mu }$ function which is zero if the bond $\left(\widetilde{{\varvec{x}}},{\varvec{y}}\right)$ intersects the crack. Equation (17) can then be used to find mirror nodes in the solution domain $\Omega$. Since $\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)$ is unique for each $\widetilde{{\varvec{x}}}$, it allows us to locate ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R}$ uniquely. As we can see in Fig. 8b, this works for both regular/smooth boundaries and boundaries with corners, cracks, or cusps.

Note that for $\widetilde{\Omega }$ near sharp (relative to the horizon size) convex corners, Eq. (17) may still lead to ${{\varvec{x}}}^{R}\notin\Omega$ for $\widetilde{{\varvec{x}}}\in$ ${\widetilde{\Omega }}_{2}$ as shown in Fig. 9, although ${\widetilde{\Omega }}_{2}$ covers a much smaller area than that of ${\widetilde{\Omega }}_{1}$ in Fig. 7. This issue can be reduced by using smaller horizon sizes, but not fully resolved. In practice, if ${{\varvec{x}}}^{R}\notin\Omega$ for $\widetilde{{\varvec{x}}}\in$ ${\widetilde{\Omega }}_{2}$, we let ${{\varvec{x}}}^{R}=\underset{{\varvec{y}}\in\Omega }{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},{{\varvec{x}}}^{R}\right)$. Other options include approximating $\widetilde{u}(\widetilde{{\varvec{x}}})$ by $u\left({\varvec{y}}\right)$ at $\underset{{\varvec{y}}\in \widetilde{\Omega }}{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},\widetilde{{\varvec{x}}}\right)$, or using the Naïve FNM, if possible. Since ${\widetilde{\Omega }}_{2}$ only covers a very small fraction of $\widetilde{\Omega }$ around the corner, the error introduced by these approximations should be negligible.

Fig. 9

Schematic of ${\widetilde{\Omega }}_{2}\subset \widetilde{\Omega }$ near an acute corner for which ${{\varvec{x}}}^{R}={{\text{Ref}}}_{\partial\Omega }\left(\widetilde{{\varvec{x}}}\right)\notin\Omega$ for $\widetilde{{\varvec{x}}}\in {\widetilde{\Omega }}_{2}$, when Eq. (17) is used to determine ${{\varvec{x}}}^{R}$

Before implementing the algorithm, the explicit $\partial\Omega$ (including crack surfaces) at the initial time is needed to determine the initial configuration of discretized $\Omega$ and $\widetilde{\Omega }$ (see Appendix A). Note that $\Omega$ is a closed set. Then the boundary $\partial\Omega$ will be implicitly tracked by bonds connecting points in $\Omega$ and those in $\widetilde{\Omega }$ (or by broken bonds). A regular-shaped region $\widehat{\Omega }$ is usually placed outside $\Omega$ in which $\widetilde{\Omega }$ is determined, and the effective $\widetilde{\Omega }$ determined after discretization is usually larger than the one before discretization to ensure ${\mathcal{H}}_{{\varvec{x}}}$ is complete for all ${\varvec{x}}\in\Omega$ in the discretized configuration. Updating ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R}$ is required every time the domain $\Omega$ evolves (which causes $\widetilde{\Omega }$ to evolve as well) in problems such as corrosion or fracture, but only for those $\widetilde{{\varvec{x}}}$ near the evolving portion of the domain.

The algorithm to find mirror nodes for each $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ is as follows:

• (1) Compute $\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)$ using Eq. (17).

• (2) Search for ${{\varvec{x}}}^{P}$:

  • a. if $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$, then search in ${\widetilde{\mathcal{H}}}_{\widetilde{{\varvec{x}}}}$ in the direction of $\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)$ for the node closest to $\widetilde{{\varvec{x}}}$, i.e., ${{\varvec{x}}}^{P}=\underset{{\varvec{y}}\in {\widetilde{\mathcal{H}}}_{\widetilde{{\varvec{x}}}}}{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},\widetilde{{\varvec{x}}}\right)$, subject to $\widetilde{\mu }\left(\widetilde{{\varvec{x}}},{\varvec{y}}\right)=0$ and ${\text{dist}}\left(\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right),{\varvec{y}}\right)<\Delta x/2$. ${\text{dist}}\left(\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right),{\varvec{y}}\right)=\sqrt{\left({\varvec{y}}-\widetilde{{\varvec{x}}}\right)\cdot \left({\varvec{y}}-\widetilde{{\varvec{x}}}\right)-{\left(\left({\varvec{y}}-\widetilde{{\varvec{x}}}\right)\cdot \widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)\right)}^{2}}$ is the perpendicular distance between node ${\varvec{y}}$ and $\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)$;

  • b. if ${{\varvec{x}}}^{P}$ is not found, set ${{\varvec{x}}}^{P}=\underset{{\varvec{y}}\in\Omega }{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},\widetilde{{\varvec{x}}}\right)$, subject to ${\text{dist}}\left(\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right),{\varvec{y}}\right)<\Delta x/2$;

  • c. if two or more ${{\varvec{x}}}^{P}$ are found, selecting either one of them is acceptable.

• (3) Search for ${{\varvec{x}}}^{R}$:

  • a. compute ${{\varvec{x}}}^{\boldsymbol{^{\prime}}}=\widetilde{{\varvec{x}}}+\left(2\Vert {{\varvec{x}}}^{P}-\widetilde{{\varvec{x}}}\Vert -\Delta x\right)\widetilde{{\varvec{n}}}(\widetilde{{\varvec{x}}})$;

  • b. since ${{\varvec{x}}}^{\boldsymbol{^{\prime}}}$ may not coincide with a node’s coordinates in the domain, we have ${{\varvec{x}}}^{R}=\underset{{\varvec{y}}\in {\mathcal{H}}_{{{\varvec{x}}}^{\boldsymbol{^{\prime}}}}\cap\Omega }{{\text{argmin}}}{\text{dist}}\left({\varvec{y}},{{\varvec{x}}}^{\boldsymbol{^{\prime}}}\right)$.

Some examples for this search process are shown in Fig. 10.

Fig. 10

Schematic diagram of determining ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R}$ for a generic $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ given four different $\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)$

Remark:

By using this algorithm, regardless of the smoothness of$\partial\Omega$,${{\varvec{x}}}^{P}$, and ${{\varvec{x}}}^{R}$ will converge, for a certain choice of$\delta$, as the ratio $\delta /\Delta x$ approaches infinity. If the tangent to $\partial\Omega$ is continuous, the converged value will be the analytical one. Until this algorithm, one had to make assumptions (which can vary from one paper to another) about $\overrightarrow{\widetilde{{\varvec{x}}}{{\varvec{x}}}^{P}}$ at sharp corners when using the mirror FNM [12, 34], and the traction-free crack surfaces were usually treated with the naïve FNM. Now, by using this algorithm, ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R}$ are found automatically and consistently for any$\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$. For problems set in domains with complex shapes, the algorithm leads to important time-savings compared to manually determining ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R}$, for all$\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$. Since the number of fictitious nodes usually only accounts for a small portion of the total number of nodes, the computational cost to locate ${{\varvec{x}}}^{P}$ and ${{\varvec{x}}}^{R}\boldsymbol{ }\forall \widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ is negligible compared with the cost of a complete simulation.

Some examples of ${{\varvec{x}}}^{R}$ found with this algorithm are shown in Fig. 11, with arrows starting from $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ and ending at ${{\varvec{x}}}^{R}\in\Omega$. Note that $\overrightarrow{\widetilde{{\varvec{x}}}{{\varvec{x}}}^{R}}\approx$ $k\widetilde{{\varvec{n}}}\left(\widetilde{{\varvec{x}}}\right)$ (with $k\in {\mathbb{R}}^{+}$) and there is a transition of direction for $\overrightarrow{\widetilde{{\varvec{x}}}{{\varvec{x}}}^{R}}$ between that of the normal vectors on two edges of the corner (or inner crack tip). The transition zone will narrow down as the horizon $\delta$ shrinks ($\delta$-convergence) and the transition will be smoother as $m=\delta /\Delta x$ increases (m-convergence). It may be possible that this transition of the $\overrightarrow{\widetilde{{\varvec{x}}}{{\varvec{x}}}^{R}}$ is used to detect/track crack tips, on the fly, but this idea is not pursued here. Although only the 2D implementation using a uniform grid is considered in this work, extending this algorithm to non-uniform grids and the 3D case is straightforward.

Fig. 11

Examples of some $\widetilde{{\varvec{x}}}\in \widetilde{\Omega }$ and their corresponding ${{\varvec{x}}}^{R}\in\Omega$, connected by arrows, computed by the new algorithm: (a) at the corner; (b) at the inner crack tip; (c) at the edge crack tip. Note that the arrow direction for each $\widetilde{{\varvec{x}}}$ is just an approximation of $\widetilde{{\varvec{n}}}(\widetilde{{\varvec{x}}})$ computed by Eq. (16), due to the discretization

Remark:

In this paper, we only treat problems on a fixed domain. For problems in which the crack surfaces open due to deformation, one can use the undeformed configuration to implement the algorithm. For extensions to problems with evolving domains, such as when a crack grows, one would need to update the set of fictitious nodes and create new ones for the newly created surface. Whether the crack stays closed, or it opens, should not affect this procedure. The current algorithm does not cover the growing crack case, but we are planning in the future to address this. One way to easily extend our algorithm to cover such cases could be “detecting” nodes on the growing crack surface based on the information of nodal damage and/or nodal velocity vectors, allowing for the use of existing fictitious nodes and on-the-fly introduction of new mirror nodes.

In the following section, the performance of the mirror FNM will be compared with the naïve and the Taylor FNMs. We will also show the capability of the autonomous mirror FNM using problems with curved geometry and cracks.

4 Results and discussion

In this section, we first show how the previously discussed three different FNMs perform in enforcing local BCs through the steady-state diffusion in a square domain. Then we will show how these FNMs perform in a problem with a singular point on its boundary. Finally, we are going to show the capability of the autonomous mirror FNM in problems with curved geometry and cracks.

4.1 The performance of three different FNMs in enforcing local BCs in peridynamics for diffusion problems without singularities

In the first problem, we consider diffusion in a square domain with its side equal to 0.1, subject to the following local boundary conditions:

$$\left\{\begin{array}{c}u\left(x=-0.05,y\right)=0.1\\ u\left(x=0.05,y\right)=0.6\\ {\nabla }_{{\varvec{n}}}u(x,y=\pm 0.05)=0\end{array}\right.$$

(18)

as shown in Fig. 12. The classical solution to this problem is a linear function:

Fig. 12

The geometry and boundary conditions for diffusion in a square domain used to compare different FNMs’ capabilities in enforcing local BCs in the PD formulation

$$u\left(x,y\right)=5x+0.35$$

(19)

In the PD simulations for this problem, we first take $\delta =0.004$ and $\Delta x=0.001$. This leads to about 10,000 nodes for a uniform discretization.

The solution, obtained with the different FNMs, along the dashed mid-line in Fig. 12 is shown in Fig. 13. All three results match the classical solution very well. However, if we zoom in near the boundary, we can see clearly that the result obtained with the mirror FNM matches the classical analytical solution much better than the results obtained with the other two FNMs. The simulation times for the three FNMs are given in Table 1. The simulation with the naïve FNM is at least 10 times faster than the other two types of FNMs, while the efficiency of Taylor and the mirror FNMs are similar to one another. Therefore, when the accuracy of the solution near the boundary is not critical, the naïve FNM could be the “best” option. If accuracy is needed, then the mirror FNM works better. Certainly, one can use finer grids with the naïve FNM to increase the accuracy near the boundary, but to reach the same accuracy as the mirror FNM, a much finer grid will be required. Considering that the computational cost of PD simulations increases quadratically with grid size (except for the recently introduced convolution-based approximations, see, [35, 51]), this may not be a good option.

Fig. 13

The classical analytical solution and PD solutions with different FNMs for the steady-state diffusion problem seen in Fig. 12, along the dashed line shown there

Table 1 Computational time of the simulation using the three different FNMs, when $\delta =0.004$ and $\Delta x=0.001$

Although the authors in [32] were able to obtain good results using Taylor FNM without Eq. (10), we noticed that the convergence of results is not guaranteed for all the simulations in this work unless we implemented Eq. (10). As pointed out in [43], the discrete arrangement of nodes may permit a node to closely approach the boundary. This could potentially lead to significantly large $\widetilde{d}/d$ in Eq. (9), which may cause numerical issues. Therefore, we recommend consistently employing Eq. (10) to ensure convergence when utilizing Taylor FNM.

The next example has a singular point along a straight boundary, and we will use it to further test the performance of these different FNMs.

4.2 The performance of the three FNMs for the Motz problem

To test the capability of the different FNMs in handling local singularities (singularities present in the classical/local model of diffusion) along the boundary, we choose the Motz problem [44, 45] (see Fig. 14 for the domain geometry). The classical solution (see below) of the Motz problem has a strong singularity $O({\rho }^{-1/2})$ in terms of fluxes at the origin $O$. Here $\rho$ is the polar distance to the origin.

Fig. 14

Domain and boundary conditions for Motz problem

The Motz problem is a classical steady-state diffusion problem with the following boundary conditions:

$$\left\{\begin{array}{c}{\nabla }_{{\varvec{n}}}u\left(x=-1,y\right)=0\\ {\nabla }_{{\varvec{n}}}u\left(x,y=1\right)=0\\ {\nabla }_{{\varvec{n}}}u\left(x>0,y=0\right)=0\\ u\left(x<0,y=0\right)=0\\ u\left(x=1,y\right)=500\end{array}\right.$$

(20)

and its classical solution can be written as [45]:

$$u\left(\rho ,\theta \right)=\sum_{i=0}^{\infty }{D}_{i}{\rho }^{i+1/2}{\text{cos}}\left[\left(i+\frac{1}{2}\right)\theta \right]$$

(21)

where ${D}_{i}$’s are analogous to the stress intensity factors in linear elastic fracture mechanics, sometimes called “generalized flux intensity factors” [52]. Here we choose the first 34 terms in the series to plot our results, as was done in [53].

In Fig. 15a we show the contours for the classical solution. The point-wise relative differences between the PD solutions and the classical solution are given in Fig. 15b–d. For the PD simulations, we used $\delta =$ 0.04 and $\Delta x=0.01$. Notice that for the mirror FNM, the relative difference larger than $5\%$ is restricted to the horizon region of the singular point (point $O$) and the left-bottom corner (point D). As the horizon size approaches zero (with $\delta /\Delta x$ not decreasing), these areas also converge to zero. For the other two types of FNMs, the relative difference is large not only near the point of singularity in fluxes, or near the corner but also at locations far away from them. A quantitative comparison of the solutions along the vertical dash line shown in Fig. 14 between the three types of FNMs is shown in Fig. 16. As we can see in the zoomed-in image, the PD solution obtained with the mirror FNM matches the classical solution significantly better than the PD solutions obtained with the other two FNMs.

Fig. 15

(a) Contours for the classical solution of the Motz problem; Relative difference (Rel. Diff.) to classical solution of the Motz problem using the PD model with the: (b) naïve, (c) Taylor, and (d) mirror FNMs

Fig. 16

The classical solution and PD solutions with different FNMs for the Motz problem along the vertical dashed line at $x=-L/2+\Delta x/2$ shown in Fig. 14

The $\delta$-convergence [54] (with $\delta /\Delta x$ fixed to be $4$) to the classical solution for the three PD solutions at point P (− 0.5, − 0.48) (see Fig. 14), is provided in Fig. 17 in log scale. We do not choose a point on the boundary because the analytical solution there is zero (i.e., the relative difference does not exist). Notice that as the horizon size changes, the grid also changes and there may not exist a node at point P. In such cases, we simply obtain the value at point P by averaging the values at the four nearest nodes around P. Figure 17 demonstrates that, as the horizon size decreases (1/$\delta$ increases), solutions obtained with all three types of FNM approach the classical solution. However, the mirror FNM produces relative differences from the classical solution that are two orders of magnitude smaller than those from the other two FNMs. Moreover, the mirror FNM solution exhibits a convergence rate that is increasing faster than the other two, as the horizon size decreases.

Fig. 17

$\delta$-convergence of PD results (using the different FNMs) to the classical value at point P (− 0.5, − 0.48) in Fig. 14

The above two examples show that the mirror FNM works best at accurately enforcing local boundary conditions in PD models, especially for problems with flux singularities (in local models) along the boundary. In the following section, we will test the algorithm developed for the mirror FNM for problems with more complex geometries.

4.3 Steady-state diffusion in circular disks with cracks

In this subsection, we will apply the autonomous mirror FNM to solve the PD formulation for diffusion in circular disks with cracks on which Dirichlet boundary conditions are to be enforced. Using the algorithm developed in Sect. 3.4, the mirror FNM can be easily implemented for curved boundaries and cracks.

4.3.1 Disk with a single crack

We first consider a circular disk of radius 1 with a 0.5-long vertical crack for which the middle point coincides with the center of the disk which serves as the origin of the coordinate system. The geometry and boundary conditions imposed are shown in Fig. 18. For the simulations, a uniform grid with 40,000 nodes is used in the PD meshfree discretization. The horizon size and m-value are 0.04 and 4, respectively. The mirror node for each fictitious node, required by the mirror FNM, is determined by the algorithm described in Sect. 3.4. See Fig. 11 for how mirror-nodes are found for those nodes near the crack tip.

Fig. 18

Local boundary conditions imposed for diffusion in a disk with a pre-crack at the center

For verification, we also simulate the corresponding PDE-based problem using the steady-state thermal solver in ANSYS Workbench. Details of the ANSYS simulation, including how the “crack” is simulated, can be found in Appendix B. In the PD model, the crack is inserted by cutting all bonds that intersect with the pre-crack segment. The differences between the slightly different approaches in representing the crack in the two models should only have a negligible effect on the results.

Contours of the results obtained by ANSYS and by the PD model, with zoomed-ins around the crack region, are given in Fig. 19. The PD results match the FEM results closely, which shows that the autonomous mirror FNM works very well for problems with a curved boundary and with cracks. The jagged shape in the contours of the PD results appears because no smoothing interpolation technique is used in the visualization, we simply plot the obtained values at each PD node.

Fig. 19

Contours for the solution to the problem shown in Fig. 18, obtained with (a) ANSYS and (b) PD. In (c, d) we show zoomed-in regions around the crack for the corresponding solutions

In practical simulations, the crack surface may have an angle with respect to the (uniform) discretization grid, whether it is a pre-crack or a new crack formed during the simulation. To demonstrate the generality of our algorithm for the mirror FNM, we solve the same problem but we rotate the uniform grid (using the rotation matrix to transform the coordinates of all nodes) in the counterclockwise direction by $30^\circ$ and $45^\circ$ relative to the coordinates shown in Fig. 18, respectively, as shown in Fig. 20. Notice that when the crack is not aligned with the grid, it may intersect with some PD nodes. These nodes are considered to be free nodes (fully damaged) at which the constraint is the average of their family nodes (those not fully damaged). The PD solutions with $30^\circ$-rotated and $45^\circ$-rotated grids are shown in Fig. 21. They match very well the solution obtained with the original grid shown in Fig. 19. Therefore, the autonomous algorithm of generating mirror nodes in FNM can handle arbitrarily-oriented uniform grids effectively.

Fig. 20

Part of the crack (red line) and the PD grid after counterclockwise rotation by (a) $30^\circ$ and (b) $45^\circ$

Fig. 21

Contours of PD solutions for diffusion obtained with the mirror FNM for counterclockwise-rotated grids by (a) $30^\circ$ and (b) $45^\circ$. In (c, d) we show zoomed-in views around the crack for the corresponding solutions

4.3.2 Diffusion in a disk with crossing cracks

To add complexity, we consider the same diffusion problem as the previous one, but with an additional horizontal crack (of the same length as the vertical one) as shown in Fig. 22. We use the same autonomous algorithm introduced in Sect. 3.4 without any changes to treat this case. A contour plot for the PD solution and the zoomed-in picture around the two cracks with imposed Dirichlet BCs are shown in Fig. 23.

Fig. 22

Diffusion in a disk with two intersecting cracks and associated local boundary conditions

Fig. 23

Contour plot for the PD solution obtained with the new mirror FNM algorithm (a) over the disk and (b) over the zoomed-in area around the intersecting cracks. Crack lines are shown superposed on top of the nodal “temperature” plots

The examples shown in this section demonstrated that the autonomous algorithm for the mirror FNM works very well to enforce local BCs for complex geometries, including crack surfaces. The same algorithm could be potentially employed for problems with moving boundaries such as corrosion damage, crack propagation, etc.

5 Conclusions

We introduced a new algorithm for the mirror-based fictitious nodes method (FNM) in peridynamic (PD) models for diffusion problems set in arbitrary geometries, including domains with cracks. Starting from computing, at each fictitious node, the peridynamic “generalized” normal vector to the domain boundary, the algorithm autonomously finds mirror nodes for all fictitious nodes. The algorithm generates the necessary data for mirror-based FNM to correctly impose the desired local BCs in the nonlocal model and reduce/eliminate the surface effect caused by the incomplete nonlocal region near the free boundary/surface in PD diffusion models. The same algorithm, with minor changes, should also work for other types of PD models, including those with moving boundaries and growing cracks.

We compared the mirror-based FNM with the naïve and the Taylor-based FNMs for problems in which the corresponding local models of diffusion have singularities along the boundary and showed that the PD solution with the mirror-based FNM agrees with the classical solution best among the three approaches. The other two methods showed significant “pollution” of the solution far from the location of the singularity. We applied the new algorithm to diffusion problems in domains with curved boundaries and internal cracks. In these cases, the peridynamic solution obtained with the new method matched well with the FE solution obtained in ANSYS.

The new algorithm enables FNM imposition of local BCs in PD models on arbitrary domains and leads to more accurate solutions near the boundaries. High accuracy near arbitrarily-shaped boundaries and material interfaces is crucial in, for example, problems that involve crack initiation and propagation, or evolution of corrosion fronts. In such problems, the new method introduced here will have a great impact.

Future work on the subject includes extending the algorithm to 3D problems as well as problems using irregular grids.

Appendices

Appendix A Numerical implementation of peridynamic diffusion model with the fictitious nodes method

For spatial discretization, we discretize the whole PD interaction region $\Omega \cup \widetilde{\Omega }$ uniformly [2] into cells with nodes in the center of those cells. Figure 

Fig. 24

Uniform discretization for a peridynamic model. The circular region is the horizon region of node ${{\varvec{x}}}_{i}$

24 shows a 2D uniform discretization with grid spacing $\Delta x$ around a node ${{\varvec{x}}}_{i}$. Non-uniform grids are also possible [23, 55, 56], which may conform better to shapes with, for example, rounded boundaries [57], but this is not pursued in this work. Although only 2D problems are considered here, the extension to 3D cases should be straightforward.

To approximate the peridynamic integral operator, we use a meshfree method with one-point Gaussian quadrature [2], with a modification to account for partial nodal volumes covered by the horizon region of a node [4, 58, 59]. Faster numerical methods such as boundary-adapted spectral methods, [35, 51] can be alternative options.

The discretized PD Laplace’s equation (see Eqs. (3) and (4)) for each ${{\varvec{x}}}_{i}\in\Omega$ at ${n}^{{\text{th}}}$ load step becomes:

$$\sum_{\begin{array}{c}j\in {\mathcal{H}}_{i}\\ j\ne i\end{array}}\frac{{u}_{j}^{n}-{u}_{i}^{n}}{{\xi }_{ij}^{2}}\Delta {A}_{ij}=0$$

(22)

where the superscript $n$ means ${n}^{{\text{th}}}$ load step; the subscripts $i$ and $j$ denote the current node ${{\varvec{x}}}_{i}$ and its family node ${{\varvec{x}}}_{j}$ respectively, in the discretized domain; ${\mathcal{H}}_{i}$ is the horizon region of node ${{\varvec{x}}}_{i}$ and $j\in {\mathcal{H}}_{i}$ includes all the nodes covered by ${\mathcal{H}}_{i}$ (fully or partially); ${\xi }_{ij}=\Vert {{\varvec{x}}}_{j}-{{\varvec{x}}}_{i}\Vert$ and $\Delta {A}_{ij}$ is the area of node ${{\varvec{x}}}_{j}$ covered by ${\mathcal{H}}_{i}$. The discretized versions for other equations are similar to Eq. (22).

In Taylor-based and mirror-based fictitious nodes methods, the equilibrium system can be solved iteratively using the linear Conjugate Gradient (CG) solver combined with additional criteria to check for the convergence of the solution. At each iteration or solution step, the CG solver is called and the solution in the domain and fictitious region is updated. To minimize the overall computational cost, the tolerance in the CG solver is set to be ${10}^{-2}$ at first and then decreased with solution steps by a factor until it reaches ${10}^{-6}$. This treatment can lead to simulations that are 50% more efficient than fixing the tolerance in the CG solver to be ${10}^{-6}$ from the start of the simulation. The system converges when the solutions in the domain obtained for two sequential solution steps, differ, in terms of norm-2 of their relative difference, by less than a given tolerance (${10}^{-6}$ was used in this work). The detailed workflow for a complete simulation is shown in Fig. 

Fig. 25

Workflow for the peridynamic simulation with Taylor/mirror FNM

25.

Appendix B FEM modeling of the steady-state diffusion problem in a disk with a crack

To obtain the classical FEM-based solution for the problem shown in Fig. 18, the ANSYS Workbench Steady-State Thermal solver is used. In the FE model, the two crack surfaces are generated by two arcs with the same small curvature and the maximum space between them is $0.01$, which equals the grid size in the corresponding PD model. For the mesh, as shown in Fig. 

Fig. 26

FEM mesh (a) over the whole disk; (b) near the crack tip

26, the element order is selected to be program-controlled and all elements are quadratic triangles with a maximum size equal to 0.05. The total number of nodes and elements are 9312 and 4548, respectively, and reduced integration is selected. All other options in the solver are set to their default values.