Accurate predictions of dynamic fracture in perforated plates

Abstract

Dynamic brittle facture in materials with many pores/perforations has been shown experimentally to feature complex evolution of crack morphologies that include crack branching, micro-branches that arrest, cracks restarting from pores and branching soon after. Computational models of these problems need to accurately account for the dynamic interactions between strain waves and stress concentration zones induced by the perforated geometry. In this paper, we aim to improve the predictive capabilities of computational simulations of dynamic brittle/quasi-brittle fracture in samples with complex geometries, like perforated plates, by introducing a discretization method using non-uniform grids near a boundary (NB-NUG) for 2D peridynamic fracture modeling. The NB-NUG avoids the steps and the corresponding artificial stress concentrations created in PD models when using uniform grids over domains with curved boundaries. The new method also reduces numerical errors compared with general non-uniform grids used for PD models. We apply the model for dynamic fracture of thin PMMA plates with different arrangements of periodic pores/perforations. The results match the experimental observations for all of the cases considered. Fine features observed in the experiments (multiple cracks branching and cracks that arrest soon after splitting, number of branching events, etc.) are captured by the new approach and not by the other PD models with different types of grids. The results show that the high strain energy density regions created around perforations attract a nearby crack tip, deflecting the crack path, altering its propagation velocity, and promoting crack branching in its wake, thus dissipating more energy. Nonlocality of damage helps here in allowing its unrestricted evolution in problems in which complex crack morphology is sensitive to small changes in the geometrical arrangement of pores in the structure.

1 Introduction

Brittle cracks start from defects, inclusions, pores present in the material, or from larger geometrical features like holes, notches, edges, where stress concentrations rise sufficiently to activate small-scale defects or nucleate micro-cracks into growing and propagating macro-cracks. For peridynamic (PD) models of brittle fracture, these holes and notches are regions where accuracy drops, in general, because of the well-known peridynamic surface effect (PDSE) (Le and Bobaru 2018). PDSE’s main source is the size of the nonlocality in the model (the PD horizon size), but the discretization also plays a role (see, e.g., (Li et al. 2018; Mei et al. 2021)). While in some problems the PDSE (due to the nonlocality size) can be used advantageously to capture some real physical material behavior (Li et al. 2018; Jafarzadeh et al. 2019) (for example in atomic-scale systems or in corrosion damage), in other cases, especially those involving fracture it needs to be reduced for correctly predicting the material behavior. The simplest way to sufficiently reduce the influence of the PDSE to the point that it can be neglected is to use a sufficiently small PD horizon size, but this implies costlier computations. Other ways consist of using various strategies to define different PD bond properties for nodes in the boundary layer (of horizon size-thickness) than for points in the bulk (Le and Bobaru 2018). Ref. (Le and Bobaru 2018) summarized and compared all major correction methods for the PDSE, including the volume method (Bobaru, et al. 2016), the force density method (Madenci 2014; Oterkus 2010; Madenci and Oterkus 2014), the energy method (Oterkus 2010; Madenci and Oterkus 2014), the force normalization method (Macek and Silling 2007), and the fictitious nodes method (Madenci and Oterkus 2014; Oterkus et al. 2014; Oterkus 2015). In this paper, we introduce a new method to generate non-uniform grids that conform better to rounded shapes on the boundary with the goal of improving the accuracy of the results produced by peridynamic models of brittle fracture problems.

Using uniform grids for discretizing domains with round boundaries leads to artificial stress concentrations (Li et al. 2018), leading to earlier fracture than expected. Non-uniform grids for PD computations can be generated using, for example, FEM meshers, as done in Bobaru and Ha (2011), so that they conform better to the curved boundaries. However, with the meshfree discretization (the one preferred for problems with cracks), quadrature error is introduced because the mid-point integration used in that method loses accuracy on non-uniform grids and ghost forces can appear. The objective of this paper is to improve the predictive capabilities of computational simulations of dynamic brittle/quasi-brittle fracture in samples with complex geometries, like perforated plates. Such geometries exist in many instances, for example in any system with rivets (airplane structures, bridges, etc.), bolts, or micro-architectured brittle materials (see Barthelat et al. (Mirkhalaf et al. 2014)).

A combination of uniform and non-uniform grids for the meshfree discretization of PD models could reduce the quadrature errors and improve the accuracy around holes if one maintains a uniform grid in the bulk and only uses non-uniform grids near round boundaries, conforming to their shape. In this paper we introduce and test a method for discretizing domains in PD models using “near-boundary non-uniform grids” (NB-NUG).

The paper is organized as follows: in Sect. 2, the bond-based PD theory is briefly reviewed; the near-boundary non-uniform grid (NB-NUG) method is introduced in Sect. 3; in Sect. 4, static linear-elastic deformations and dynamic brittle fracture simulations of 2D perforated plates are used to compared peridynamic results computed using uniform grids, global non-uniform grids, and the NB-NUG method; for linear-elastic deformations we verify the method by comparing with those from corresponding finite element simulations; in Sects. 5 and 6, we use the NB-NUG method to investigate the effect of multi-pores on crack propagation in brittle samples and explain how pores affect the crack propagation speed; conclusions are drawn made in Sect. 7. Appendix 1 contains convergence results for dynamics fracture problems; Appendix 2 describes how the crack tip is track to compute the crack speed; Appendix 3 shows the numerical equivalency between loading conditions; Appendix D gives a detailed of the ANSYS APDL commands used to generate the computational PD grid for the proposed method.

2 Brief review of the bond-based peridynamic model

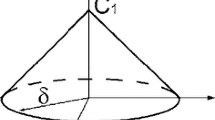
Peridynamics, a nonlocal theory originally introduced in Silling (2000), modifies the classical equations of motion from a spatial-differential equation to a spatial-integral one, thus eliminating singularities at the crack tip present in classical continuum mechanics. In PD, each material point interacts with its surrounding material points through PD bonds, within a finite distance (see Fig. 1). The equation of motion for a material point ${\varvec{x}}$ at time t in Bond-Based PeriDynamics (BB-PD) is:

$$\begin{aligned}\rho \left({\varvec{x}}\right) \ddot{{\varvec{u}}}\left({\varvec{x}},t\right)&={\int }_{{H}_{{\varvec{x}}}}{\varvec{f}}\left({\varvec{u}}\left(\widehat{{\varvec{x}}},t\right)-{\varvec{u}}\left({\varvec{x}},t\right),\widehat{{\varvec{x}}}-{\varvec{x}}\right)d{V}_{\widehat{{\varvec{x}}}}+{\varvec{b}}\left({\varvec{x}},t\right)\\&\qquad\qquad {\varvec{x}}\in \Omega\; and\; t\in \left[{t}_{0},\infty \right]\end{aligned}$$

(1)

where $\Omega$ is the material domain and ${t}_{0}$ is the initial time, ${\varvec{u}}$ represents the displacement vector, and ${\varvec{b}}\left({\varvec{x}},t\right)$ is the body force vector at location x and time t. As shown in Fig. 1, ${H}_{{\varvec{x}}}$ represents the integral region of material point ${\varvec{x}}$, called the horizon region, and $\widehat{{\varvec{x}}}$ denotes a point belonging to the family of ${\varvec{x}}$, inside the horizon region. Generally, the horizon region in 2D is taken as a disk, and the radius of the circle called horizon size (or horizon in short), represented as $\delta$. In some problems it is advantageous to use elliptic horizons with high aspect ratios, see e.g.(Jafarzadeh et al. 2022). ${\varvec{f}}$ is a pairwise force function in the PD bond connecting ${\varvec{x}}$ and $\widehat{{\varvec{x}}}$. If the distance between ${\varvec{x}}$ and $\widehat{{\varvec{x}}}$ in the original configuration is greater than $\delta$, there is no interaction (or PD bond) between them.

Fig. 1

In the horizon region ${H}_{{\varvec{x}}}$ (light blue colored disk) in domain $\Omega$, the central point ${\varvec{x}}$ interacts directly with any point $\widehat{{\varvec{x}}}$

Let ${\varvec{\xi}}=\widehat{{\varvec{x}}}-{\varvec{x}}$ represent the relative position vector between $\widehat{{\varvec{x}}}$ and ${\varvec{x}}$, and ${\varvec{\eta}}=\widehat{{\varvec{u}}}-{\varvec{u}}$ denote the relative displacement, such that:

$${\varvec{f}}\left({\varvec{\xi}},{\varvec{\eta}}\right)=0\;\mathrm{if}\;\Vert {\varvec{\xi}}\Vert >\delta $$

(2)

The pairwise force in a micro-elastic material is derived from the micro-elastic potential ($w$) (Silling 2000):

$${\varvec{f}}\left({\varvec{\xi}},{\varvec{\eta}}\right)=\frac{\partial w\left({\varvec{\xi}},{\varvec{\eta}}\right)}{\partial{\varvec{\eta}}}$$

(3)

For the linear micro-elastic material, we have the micro-elastic potential (Hu et al. 2018; Ni et al. 2018; Rashid 1998):

$$w\left({\varvec{\xi}},{\varvec{\eta}}\right)=\frac{c\left({\varvec{\xi}}\right){s}^{2}\Vert {\varvec{\xi}}\Vert }{2}$$

(4)

where $c\left({\varvec{\xi}}\right)$ is the bond micro-modulus function,$s$ is the relative elongation of the bond connecting $\widehat{{\varvec{x}}}$ and ${\varvec{x}}$, given by:

$$s=\frac{\Vert {\varvec{\xi}}+{\varvec{\eta}}\Vert -\Vert {\varvec{\xi}}\Vert }{\Vert {\varvec{\xi}}\Vert }$$

(5)

Here we only consider the constant-profile micro-modulus function (independent of the bond length), which, when we setup a match of the strain energy density with the classical theory for a homogeneous deformation (Bobaru et al. 2009), leads to the following form:

$$c=\frac{9k}{\pi {\delta }^{3}}$$

(6)

where $k$ is the bulk modulus of material.

The Prototype Micro-elastic Brittle (PMB) model is applied in this work for material damage. In the PMB model, the pairwise force ${\varvec{f}}\left({\varvec{\xi}},{\varvec{\eta}},t\right)$ is given as follows:

$${\varvec{f}}\left({\varvec{\xi}},{\varvec{\eta}},t\right)=\left\{\begin{array}{ll}c\left({\varvec{\xi}}\right)s\left({\varvec{\xi}},{\varvec{\eta}}\right)\mu \left({\varvec{\xi}},{\varvec{\eta}},t\right)\frac{{\varvec{\xi}}+{\varvec{\eta}}}{\Vert {\varvec{\xi}}+{\varvec{\eta}}\Vert} & \quad if \;\Vert {\varvec{\xi}}\Vert \le \delta \\ 0, & \quad otherwise\end{array}\right.$$

(7)

where $\mu$ is used to describe the damage state of bond. If the relative elongation of bond exceeds a critical value, the bond breaks. Value 1 represents an intact bond, while 0 represents a broken bond:

$$\mu \left({\varvec{\xi}},{\varvec{\eta}},t\right)=\left\{\begin{array}{ll}1 \qquad \quad s\left({\varvec{\xi}},{\varvec{\eta}},t\right)\le {s}_{0}\\ 0 \qquad \quad s\left({\varvec{\xi}},{\varvec{\eta}},t\right)>{s}_{0}\end{array}\right.$$

(8)

${s}_{0}$ is the critical relative elongation of a bond, which is obtained from equating the PD strain energy required to break all bonds across a unit fracture area with the critical fracture energy per unit fracture area (Ha and Bobaru 2010). Under plane stress conditions, its form is:

$${s}_{0}=\sqrt{\frac{4\pi {G}_{0}}{9k\delta }}$$

(9)

where ${G}_{0}$ is the critical fracture energy (energy per unit area), a measurable quantity. A way to quantify (useful for visualization of results) the degree of material failure at a point in space and time in a PD model is the damage index(see (Silling and Askari 2004)):

$$D\left({\varvec{x}},t\right)=1-\frac{{\int }_{{H}_{{\varvec{x}}}}\mu \left({\varvec{\xi}},{\varvec{\eta}},t\right)d{V}_{\widehat{{\varvec{x}}}}}{{\int }_{{H}_{{\varvec{x}}}}d{V}_{\widehat{{\varvec{x}}}}}$$

(10)

In PD, material points near the boundaries do not have a full non-local neighborhood. This leads to effective material properties near the surface of a PD model being different from those in the bulk. Several methods/algorithms have been proposed recently to correct this PDSE. Ref. (Le and Bobaru 2018) systematically investigated the efficiency and computational cost of various PD surface correction methods when solving elasticity and fracture problems using PD, and provided practical suggestions for reducing the PDSE. Although the fictitious nodes method can eliminate the PDSE, it is not easy to use for problems defined over domains with complex boundaries. Ref. (Zhao, et al. 2020) introduced a general algorithm that automatically locates mirror nodes for fictitious nodes, without requiring an explicit mathematical description of the boundary. The surface correction method used in this work is the energy method, selected here for its simplicity and efficiency. The specific procedure is as follows (Le and Bobaru 2018; Oterkus 2010; Madenci and Oterkus 2014):

• a) Compute the reference strain energy density ${W}_{0}$ at a point in the bulk (with a full neighborhood) and very fine discretization ($\frac{\updelta }{\Delta x}=25$ in our program) under uniaxial homogeneous deformation (strain of 0.01% selected here).

• b) Set the initial surface correction factor ${\uplambda }_{i}$ (at node ${{\varvec{x}}}_{i}$) as 1, for all nodes.

• c) Apply the same homogeneous deformation as in step a) in the actual domain, and compute the strain energy density ${W}_{i}$ for node ${{\varvec{x}}}_{i}$ by summing up the strain energy density (${w}_{ij}$ for bond connecting node ${{\varvec{x}}}_{i}$ and node ${{\varvec{x}}}_{j}$) of all bonds connecting node ${{\varvec{x}}}_{i}$, corrected by average surface correction factor $\frac{1}{2}\left({\lambda }_{i}+{\lambda }_{j}\right)$: ${W}_{i}=\sum_{j}\frac{1}{2}{w}_{ij}\left({\lambda }_{i}+{\lambda }_{j}\right)$.

• d) Set ${\lambda }_{i}={\lambda }_{i}\frac{{W}_{0}}{{W}_{i}}$ as the updated surface correction factor of node ${{\varvec{x}}}_{i}$ for the next iteration.

• e) Repeat the loop in step c) and step d) for all nodes until all ${\lambda }_{i}$ converge (relative tolerance error used here is 10^–7).

Using the one-point Gaussian integration, the discretization form of PD motion equation can be written as:

$$\rho {\ddot{{\varvec{u}}}}_{i}=\sum_{{{\varvec{x}}}_{j}\in {H}_{{{\varvec{x}}}_{{\varvec{i}}}}}\frac{1}{2}\left({\lambda }_{i}+{\lambda }_{j}\right){{\varvec{f}}}_{ij}{\varphi }_{ij}{V}_{j} +{{\varvec{b}}}_{i}$$

(11)

where ${{\varvec{x}}}_{j}\upepsilon {H}_{{{\varvec{x}}}_{{\varvec{i}}}}$ denotes nodes inside the horizon region of ${{\varvec{x}}}_{i}$, ${V}_{j}$ is the nodal area (volume in 3D) of node ${{\varvec{x}}}_{j}$, ${\lambda }_{i}$ is the surface correction factor for node ${{\varvec{x}}}_{i}$, ${\varphi }_{ij}$ represent the volume correction factor which estimates the partial volume of node ${{\varvec{x}}}_{j}$ covered by the horizon of ${{\varvec{x}}}_{i}$ [see (Seleson 2014)], ${{\varvec{f}}}_{ij}$ is the bond force between ${{\varvec{x}}}_{i}$ and ${{\varvec{x}}}_{j}$, and ${{\varvec{b}}}_{i}$ is the body force exert on node ${{\varvec{x}}}_{i}$. The velocity-Verlet scheme is used to discrete in time to obtain the numerical solution for dynamic problems (see e.g. (Ha and Bobaru 2010) for the details on the velocity-Verlet scheme), and the Nonlinear Conjugated Gradient (NCG) method based on energy minimization is applied for quasi-static simulations (see e.g. (Zhang et al. 2016) for the detail of the NCG method).

When uniform grids are used, a partial-volume correction algorithm (like the HHB method in Hu et al. (2010)) is applied to improve the accuracy of the midpoint quadrature scheme because the nodal area of node ${{\varvec{x}}}_{j}$ may not be fully covered within the horizon of node ${{\varvec{x}}}_{i}$. In the HHB method, the volume correction factor $\varphi$ for uniform grids is:

$$\varphi \left(\Vert {\varvec{\xi}}+{\varvec{\eta}}\Vert \right)=\left\{\begin{array}{ll}1 & \quad if\; \Vert {\varvec{\xi}}\Vert \le \delta -\frac{\Delta x}{2}, \\ \frac{\left(\delta +\frac{\Delta x}{2}-\Vert {\varvec{\xi}}\Vert \right)}{\Delta x} & \quad if\; \delta -\frac{\Delta x}{2}\le \Vert {\varvec{\xi}}\Vert \le \delta +\frac{\Delta x}{2},\\ 0 & \quad if\; \Vert {\varvec{\xi}}\Vert \ge \delta +\frac{\Delta x}{2}\end{array}\right.$$

(12)

To conform to irregular or curved boundaries and avoid the artificial stress concentration induced by the zigzag boundary shape when using uniform grids to discretize domains with curved boundaries, non-uniform grids have been used in peridynamics (Li et al. 2018; Henke and Shanbhag 2014; Mehrmashhadi et al. 2019). Non-uniform grids, however, introduce additional quadrature error as it is difficult to find an algorithm for the volume correction factor like the one used for uniform grids (see Eq. (12)). Obviously, the HHB algorithm is no longer applicable to non-uniform grids, since it is based on areas/volumes of nodes being squares/cubes. It is necessary to find a new characteristic grid spacing to substitute the uniform grid spacing $\Delta x$ (see Eq. (12)). There are two common ways to alter the characteristic spacing and make it useable for non-uniform grids: one is to use the diameter of a circular disk whose area is the same to that of a given PD node (Ni et al. 2018); the other is the length of a square whose area is identical to that of a given PD node (Hu et al. 2018). The latter leads to equivalent results with those from Eq. (12), when using uniform grids. In this work, we adopt this second approach to “correct” the nodal areas and use $\widehat{\varphi }$ to represent the area/volume correction factor for non-uniform grids:

$$\widehat{\varphi }\left(\Vert {\varvec{\xi}}+{\varvec{\eta}}\Vert \right)=\left\{\begin{array}{ll}1 & \quad if \;\Vert {\varvec{\xi}}\Vert \le \delta -\frac{{r}_{j}}{2}, \\ \frac{\left(\delta +\frac{{r}_{j}}{2}-\Vert {\varvec{\xi}}\Vert \right)}{{r}_{j}} & \quad if\; \delta -\frac{{r}_{j}}{2}\le \Vert {\varvec{\xi}}\Vert \le \delta +\frac{{r}_{j}}{2},\\ 0 & \quad if\; \Vert {\varvec{\xi}}\Vert \ge \delta +\frac{{r}_{j}}{2}\end{array}\right.$$

(13)

$${r}_{j}=\sqrt{{V}_{j}}$$

(14)

To reduce quadrature error induced by the use of non-uniform grids (which are needed around round boundaries to reduce the artificial stress concentrations, as discussed before), we introduce a discretization method that is uniform everywhere except around curved boundaries, and the non-uniform nodes have similar areas. Another reason we introduce this semi-uniform grid method is that valid peridynamic failure criteria for irregular spatial discretization are still under development and application of regular uniform grid based failure criteria to problems with irregular non-uniform spatial discretization is debatable (Chen 2019).

To realize the semi-uniform grid method, we obtain local non-uniform grids utilizing the ANSYS Mesh Tool. This is explained in detail in the next section.

3 A near-boundary non-uniform discretization (NB-NUG) method for PD

Artificial stress concentrations can appear around curved boundaries when a domain is discretized using uniform grids. These concentrations are reduced or eliminated by using “fitted” grids, which imply a non-uniform discretization. However, non-uniform grids increase quadrature error. In this section we introduce a method in which non-uniform grids are used only around curved boundaries, while the rest of the domain is discretized uniformly. This mixed-grids discretization method is implemented in ANSYS mesh tool.

For simulation domains containing curved boundaries, such as round boundaries, though the mapping method can be used, the element shape is usually rectangular with a large aspect ratio, which would lead to significant errors when the volume correction algorithm is used.

To reduce the errors caused by non-uniform grids, our approach is to divide the original geometry into several regular rectangular parts (isolate into rectangular shapes regions with rounded boundaries) and use non-uniform grids in those rectangles that contain curved boundaries and uniform grids in the rest of the domain (see Fig. 2). We construct the red edges box (called a “non-uniform box”). The rectangles that do not contain round features are meshed, uniformly, using the mapping method, and the non-uniform box is meshed using the free method. A “padding” of at least one horizon size is recommended around the curved boundaries and the edges of the non-uniform box, to ensure the relative uniformity of the non-uniform grids. The fineness of the non-uniform grids is determined by the size of the features in the geometry (e.g. size of holes, notches, etc.), in other words, the grid has to be fine enough to be able to capture the rough shape of the smallest geometrical features. With the non-uniform grid set like that, the element size used for the uniform grids is determined to match. In the next section we test the method on a variety of quasi-static and dynamic fracture problems.

Fig. 2

Separating regions with curved boundaries (discretized with non-uniform grid) from the rest of the domain (discretized with uniform grids) using rectangular sub-domains

4 Numerical results for the NB-NUG method for static and dynamic brittle fracture

In this section, quasi-static elastic deformation and fracture, as well as dynamic fracture in perforated plates are calculated using peridynamic models with uniform grids, global non-uniform grids, and the NB-NUG, respectively. The results are also compared with the ones from the finite element method (ANSYS and LSDYNA3D), to verify the NB-NUG method for PD.

4.1 Quasi-static elastic deformations in a plate with a central hole

As shown in Fig. 3, a $20\, \mathrm{mm}\times 20\, \mathrm{mm}$ square plate with a circular hole in the center, under uniaxial tension, is considered. A displacement-controlled horizontal tension is applied, with displacement ${U}_{x}=0.0001$ mm (see Fig. 3). The top and bottom boundaries and the inner boundary are traction-free. Discretizations using global non-uniform grids (Fig. 4, bottom panel) and the NB-NUG (Fig. 4, top panel), are obtained with the ANSYS mesh module. To apply the NB-NUG method, the perforated plate is divided into several parts before meshing. For the part containing curved surface or boundaries (the area inside the dashed box shown in Fig. 3), the free mesh type in the ANSYS mesh module is applied for the discretization, while the remaining region is discretized by the mapped mesh method. More specifically, the element size is set to be 0.05 mm and the length of the non-uniform box is 8.4 mm (which is the diameter of the hole plus two horizon sizes, see below). After meshing, we extract the centroid of each element as the nodal point, and the element area serves as the nodal area in PD. With this discretization, elements out of the non-uniform box are all squares. Inside the box, most elements are quads, except for a few around the curved surface that are triangles (Fig. 4, top panel, generated by the built-in algorithm in ANSYS). This processing method can significantly reduce the artificial stress concentrations and improve quadrature accuracy. The parameters used in this example is listed in Table 1.

Fig. 3

Geometry and boundary conditions for a plate with a hole under quasi-static horizontal deformation. The non-uniform box is shown with the red dashed line

Fig. 4

Top: grid obtained by the NB-NUG method. Bottom: global non-uniform grid obtained by free mesh type method. Right figures are zoom-in of the areas in the black squares

Table 1 Parameters used in the simulation of quasi-static elastic deformation

In the PD simulations, the horizon size is set to be 0.2 mm, and the horizon factor (the ratio of horizon size to the grid spacing) is 4. The displacement fields (in the horizontal direction) calculated from FEM, PD with global non-uniform grids, uniform grids, and NB-NUG are shown in Fig. 5a–d, respectively. With the same scalar bar, the displacements’ distributions are all similar. Since uniform grids lead to artificial stress concentrations when applied to curved boundaries, we focus on non-uniform grids which conform to the curved boundaries (the circular boundary for the case shown in Fig. 3), and present the absolute and relative differences between the PD models with non-uniform grids methods and the corresponding FEM results using the same grids as in the PD models (see Fig. 5e–h). The results from the PD model with the NB-NUG method leads to smaller differences from the FEM results, compared with those from the free type generated grid. Note that when calculating the differences, the FEM models adopt the same grids as the global non-uniform grids and the NB-NUG, respectively. The PD nodes’ positions are the centroids of the elements in the ANSYS mesh. We compare the displacement data at the PD nodes. For doing this, we transfer the FEM displacements (calculated at the FEM nodes) to the centroids of each element (the PD nodes) by averaging (see Fig. 5e–h).

Fig. 5

Deformation (maps of horizontal displacements) of a square plate with a hole obtained from a FEM, b PD model using global non-uniform grids, c PD model using uniform grid (zig-zagged grid around the circular hole), and d PD model with the NB-NUG method. Images e and g: the absolute and relative difference of (b) to (a), respectively. Images f and h: the absolute and relative difference of (d) to (a), respectively. The scalar bar in the middle is for (a–d), in meters. The scalar bar on the top-right is for (e) and (f), in meters. The scalar bar on the bottom-right is for (g) and (h)

Note that the relative difference plots in Figs. 5g and h show sharp transition along the vertical symmetry line. These are caused by the very small horizontal displacement values (close to zero), which lead to large round-off errors when computing relative differences.

4.2 Quasi-static fracture in a plate with a central hole

A quasi-static fracture problem for the same structure is investigated in this section. The geometry, grids’ configuration and peridynamic parameters are the same as above. Equal displacements are imposed on both left and right boundaries along the normal directions. Due to the stress concentrations, cracks should initiate from the top and bottom symmetry points on the hole, even in the absence of pre-notches. Three kinds of grids (uniform grids, global non-uniform grids, and NB-NUG) are used, respectively, and we compare their performance in this quasi-static fracture problem only in terms of the morphology of failure and the relative difference for the “strain-at-failure”.

In order to increase computational efficiency, larger displacement steps of 0.01 mm are used for the first eight steps, followed by significantly smaller ones ($1\times {10}^{-4}$, $5\times {10}^{-5}$, or $1\times {10}^{-5}$) until full separation of the sample occurs. We record the boundary displacement when the crack initiates from the hole edge and show these values on the top and bottom of each damage map in Fig. 6. ${\varepsilon }_{x}$ in Fig. 6 is the horizontal strain increment in each step. With uniform grids, due to the stress concentration caused by the artificial zig-zagged boundary, four cracks initiate from the hole, which should not happen. The upper and lower cracks do initiate at the same load–displacement value (as recorded in Fig. 6) because of the symmetry in geometry, discretization, and loading conditions. However, under quasi-static loading, an experimental test of this type in a homogeneous (fine grained) brittle/quasi-brittle material should have cracks initiate from the stress concentration regions (located at the highest and lowest points on the circumference) and grow straight, as shown in Fig. 6, columns 2 and 3.

Fig. 6

Damage maps from PD models of plate with a hole under displacement boundary condition for three different strains increments and using three types of grids. The numbers marked on the damage maps represent the applied displacement values at which the top or bottom cracks crack initiate

With global non-uniform grids, two cracks initiate from the hole (see Fig. 6). We notice that the boundary load-displacements, at which the upper and lower cracks initiate, are close to each other for all three displacement steps considered. The magnitudes of the critical enforced displacements (at which cracks initiate) are slightly greater than those for the case with the uniform grids. With the NB-NUG, also only two cracks are produced. However, the critical imposed displacement value, when the first crack initiates, is slightly smaller than the ones obtained with the global non-uniform grids, but closer to those obtained with the uniform grids. The load–displacement, when the second crack initiates, is very close to ones obtained with the global non-uniform grids.

Note that if we perform an m-convergence for the uniform grid we would, in the limit, eventually obtain single cracks from the top and bottom stress concentration zones. This will happen, however, at a very high computational cost. The NB-NUG gives the correct solution at a significantly reduced computational cost.

Note that with the PMB material model (in which the critical bond-strain is calibrated to the fracture toughness), under quasi-static loading (and for domains without pre-cracks), ones obtains different strength values when using different horizon sizes (Niazi et al. 2021). One of those horizons will eventually match the actual material strength, but its size may be too small to allow for cost-effective computations. For a model that produces the same strength value (and fracture toughness, at the same time) independent of the horizon size, a two-parameter bond-damage model needs to be used, see, e.g. (Niazi et al. 2021). In dynamic fracture problems, however, damage initiation and propagation are controlled primarily by the interactions among elastic waves, and damage evolution (initiation and propagation) predicted by the PMB model (one-parameter bond-damage model) converge, when decreasing the horizon size in the PD model (Zhang et al. 2018; Wu et al. 2021), see Sect. 5. Since the focus of this work is dynamic fracture, the PMB model is used here.

4.3 Dynamic fracture in a plate with an off-center hole

In this subsection we test the method using a dynamic fracture example: as shown in Fig. 7, a plate with a lateral crack and an off-center circular hole is dynamically loaded to fracture. The same problem has been studied in Rashid (1998); Tabiei and Wu 2003), and (Dipasquale et al. 2014). Mechanical properties for the plate are as follows (also see Table 2): $E=71.4\, \mathrm{GPa}, \rho =2700\,\mathrm{kg}/{\mathrm{m}}^{3}, {G}_{0}=\mathrm{1,000}\,\text{J}/{\mathrm{m}}^{2}$. The bottom boundary is clamped and a traction of $2\,0\mathrm{ MPa}$ is suddenly applied on the top boundary and kept constant afterwards. A lateral crack placed a distance $h=15, 10,\,\mathrm{ or }\,5\mathrm{ mm}$ from the bottom boundary is considered, defining Cases A, B, and C, respectively. The plate is discretized with element size $\Delta x=$ 0.1 mm. The plate is discretized with element size 0.1 mm and the length of the non-uniform box is $15.8\,\mathrm{ mm}$. Horizon size and time step is set to $\delta =0.4\,\mathrm{ mm}$ and $\Delta t=0.02\mathrm{ \mu s}$. Thus, the slack between the edge of the non-uniform box and the boundary (the hole) is $\delta$ on each side.

Fig. 7

Geometry and boundary conditions for the plate with a lateral crack and an off-center hole

Table 2 Parameters used in the simulation of dynamic fracture

The crack paths obtained from the PD simulations with the NB-NUG are shown in Fig. 8, and compared with corresponding ones from an explicit FEM code DYNA3D given in Tabiei and Wu (2003). Note that the simulations (cracking in thin plates) in Tabiei and Wu (2003) were in 3D, and the results were shown from the front left view (see Fig. 8), while the PD results shown in Fig. 8 are in 2D under the plane-stress condition. The presence of the hole influences the crack path, attracting it towards it, and this is well captured by both methods. The PD and FEM results show a similar crack-path behavior: with the nearest-to-hole pre-crack, the propagating crack has the largest deflection angle and ends in the hole, while when the pre-crack farthest from the hole, the deflection angle is the smallest.

Fig. 8

Crack paths obtained from PD models with the NB-NUG (top) and from DYNA3D (bottom) (Tabiei and Wu 2003) for different locations of the pre-crack: a h = 15 mm, b h = 10 mm, c h = 5 mm (see Fig. 7)

Figure 9 shows the strain energy density distribution at $20\mathrm{ \mu s}$ for Case A. The corresponding evolution of the strain energy density distribution is shown in Movie 1. High strain energy density is observed at the crack tip and around the hole boundary. During dynamic crack propagation, the crack direction is sensitive to the surrounding strain energy distribution, and moves towards a nearby location with high strain energy density (Chen 2017). As shown in Figs. 8 and 9, the crack tip deviates from the horizontal line due to the influence of the hole. The high strain energy density zone around the hole rotates and attracts the crack tip, and eventually the crack path deflects into the hole in Case A (see Movie 1).

Fig. 9

Strain energy density distribution at $20\,\mathrm{ \mu s}$ for Case A ($h=15\,\mathrm{ mm}$, see Fig. 7)

Figure 9 is taken from the early stages of the deformation. Because of the pre-crack on the left side, it is to be expected that strain energy density will be concentrated at the location where the sample is “held in place”, that would be right bottom corner more than the left bottom corner because of the “weaker” left side where the hole and the pre-crack are present. The loading is dynamic, and the simulation movie shows how the strain energy density evolves in time. Note that the left bottom corner also gets, at times, higher strain energy density than the right bottom corner (see Movie 1), for example at the time when the second crack is just about to nucleate from the right side of the hole, as the loading on top starts to tilt (because of the rotation due to the opening of the crack) and transfer strains to that region.

Note that the DYNA3D simulation for Case A shown in Ref (Tabiei and Wu 2003) (see Fig. 8a) did not consider the crack re-initiation from the right side of the pore. The prediction of crack growth direction in the DYNA3D model (Tabiei and Wu 2003) depends on a function of the stress intensity factors in Mode I and Mode II. Therefore, the DYNA3D model in Ref (Tabiei and Wu 2003) can only predict crack growth (from an existing crack), and cannot be used to model crack initiation or re-initiation from smooth surfaces. PD models can simulate crack initiation. In PD, crack evolution (initiation and propagation) is a representation of the information of all broken bonds, and, in the PMB model used here, bonds break when reaching a critical bond-strain calibrated to the material fracture toughness (see Eqs. (8) and (9)). The PMB model has been successfully applied to simulate many dynamic fracture processes from damage initiation to full failure, for instance, brittle impact fracture in ceramics (Zhang et al. 2018).

In Fig. 10, we compare the crack patterns for Case A ($h=15\mathrm{ mm}$, see Fig. 7) calculated from the PD models with the uniform grids, global non-uniform grids, and NB-NUG, respectively. We focus on three critical moments: crack reaching the hole (left column in Fig. 10), crack re-starting from the side of the hole (middle column in Fig. 10), and the plate fully breaking (right column in Fig. 10). As seen from Fig. 10, with a uniform grid, due to the artificial stress concentrations around the hole, we get a lower resistance to crack re-initiating from the hole, that happens much sooner than in the other two models. The timelines for the results generated from the global non-uniform grids and the NB-NUG are similar: the times for the cracks reaching the hole are very close, while the results from the NB-NUG show a slightly delayed re-initiation from the hole.

Fig. 10

Snapshots of damage maps for Case A obtained from PD models with the uniform grids (a), global non-uniform grids (b), and NB-NUG (c), respectively. Three moments for each case are: crack reaches the hole, crack re-initiates from the hole, and full failure

We have verified the NB-NUG method for PD modeling and showed that the NB-NUG leads to more reliable results than when using uniform grids or global non-uniform grids, for quasi-static elastic deformations and quasi-static fracture, and dynamic fracture in a plate with a hole. In the following sections, we apply the PD model with NB-NUG to investigate the interaction between propagating brittle cracks and various arrangements of arrays of pores, to demonstrate the ability of the new method in obtaining results that match experimental results considerably better than other available options.

5 Dynamic fracture in PMMA plates containing periodic perforations/pores

The benchmark problem is a set of experiments carried out in Carlsson and Isaksson (2019). Figure 11 shows the geometries. Three styles of pores (Cases PMMA-A, PMMA-B and PMMA-C, shown in Fig. 11) are drilled on the plate with the size of $\mathrm{W}\times \mathrm{H}=50 \mathrm{mm} \times 25 \mathrm{mm}$, and an edge crack with the length of $2 \mathrm{mm}$ or $0.75 \mathrm{mm}$ is notched at the middle of the left boundary. The pores have the same radii $R=0.75\mathrm{ mm}$, and the spacing between two adjacent pores is $D=W/9$. The plate is made of PMMA, with the Young’s modulus $E=3.24 \mathrm{GPa}$, density $\rho =1190\mathrm{kg}/{\mathrm{m}}^{3}$, Poisson ratio $\nu =0.35$, and energy release rate at crack initiation ${G}_{0}=200\mathrm{J}/{\mathrm{m}}^{3}$ (see Table 3). State-based peridynamics have been used to simulate this problem and other forms of arresting cracks using holes in Rahimi et al. (2020), but only for the 2 mm pre-crack case, which is the case with crack propagation at lower strain energy in the system. However, uniform grids and relatively large grid spacing used in those simulations inevitably led to low numerical accuracy, which is especially critical for cases with higher strain energy in the system.

Fig. 11

Geometry of plates with different arrangement of arrays of circular pores: a pore array on the midline (Case PMMA-A); b pore array above the midline (Case PMMA-B); c pore arrays symmetrical about the midline (Case PMMA-C)

Table 3 Material properties of PMMA

A ramp-up velocity of $0.3\mathrm{ m}/\mathrm{s}$ (see Appendix 3 and (Rahimi et al. 2020) for using this velocity value) is applied on the top and bottom boundaries (see Fig. 12(a)), and we use a time step of $0.02\,\mathrm{ \mu s}$ for the velocity-Verlet time integration. The ramp-up is employed so as to alleviate the sharp wave that would arise from suddenly enforcing the velocity boundary condition. Over the first $200\mathrm{ \mu s}$ the boundary velocity is linearly increased from 0 to $0.3\,\mathrm{m}/\mathrm{s}$ (see Fig. 12(b)), after which its value is kept constant. The length of the non-uniform box around each pore is 2 mm. We use $0.16\mathrm{ mm}$ as the horizon size (see a convergence study for Cases PMMA-A and PMMA-B with a $2\mathrm{ mm}$ pre-crack in Appendix 1), and select m = 4 (m is the horizon factor, i.e., the ratio between the horizon size and the grid spacing).

Fig. 12

a The loading boundary condition; b Imposed velocity on the top and bottom boundaries use a linear ramp-up stage over the first 200 μs

Note that in the experiments, the top and bottom boundaries of the plate were loaded quasi-statically until a sudden crack occurred, after which a fixed velocity condition is likely present (Carlsson and Isaksson 2019). The specific loading details were not provided in Carlsson and Isaksson (2019). Here, we omit the static loading stage and use the dynamic loading as shown in Fig. 12. To illustrate the feasibility of this simplification in modeling, in Appendix 3, we compute and compare the evolutions of cracking speed in an intact plate (no perforations) with pre-cracks of 0.75 mm and 2 mm, respectively, subjected to static-dynamic loading, and dynamic-only loading, respectively. In Appendix 3, we show that the crack propagation speeds obtained via models with the two schemes are consistent over the entire crack propagation process. The crack patterns obtained from both schemes are also consistent, for both cases with different pre-cracks, respectively. In the following, we use the dynamic-only loading scheme (shown in Fig. 12) to approximate the experimental loading conditions.

Figures 13 and. 14 show the crack paths computed by PD models with different grids, and from the phase-field model and experimental observations in Carlsson and Isaksson (2019). The simulation results from the PD model with the NB-NUG have the best agreement with the experimental results for all 6 scenarios (Cases PMMA-A, PMMA-B, and PMMA-C with both 2 mm and 0.75 mm pre-crack, respectively) considered (see Figs. 13 and 14). In particular, the NB-NUG model-based results captures interesting fine characteristics seen in the experimental results: (a) short branched cracks, that arrest soon after branching, are present in all three cases; and (b) the number of branching events and the crack path morphology.

Fig. 13

Damage maps for the $2\mathrm{ mm}$ pre-cracked sample with different pore styles, for different grids and models. Phase-field results and the experimental results are taken from Carlsson and Isaksson (2019). The red ovals in the right panel of the global non-uniform indicate dispersed damage due to the non-uniform discretization. The yellow rectangles denote some of the locations where cracks arrest soon after branching

Fig. 14

Damage maps for the $0.75\mathrm{ mm}$ pre-cracked sample with different pore styles, for different grids and models. Phase-field results and the experimental results are taken from Carlsson and Isaksson (2019). The yellow rectangles denote some of the locations where cracks arrest soon after branching

Some differences are observed, but, considering that the pores were not perfectly aligned and spaced in the experimental samples (see (Carlsson 2023), and that crack propagation is dynamic under the loading conditions used in the experiments, such differences are to be expected. All of the simulations and the experimental results show that the sample with the shorter pre-crack, features more crack-branching events. This is because before the crack starts to propagate, a higher strain energy density is accumulated around the crack tip (and over the entire structure) for the plate with a shorter pre-crack. Once the crack propagates, the higher strain energy leads to more branching (see Figs. 13 and 14).

Note that the experimental results for the PMMA-B sample (offset row of holes, see middle column of Fig. 14) shows a crack branch getting attracted to the 4th hole but continuing away from the holes. The NB-NUG PD results for that case (see Fig. 14, row 3 column 2) also show the same branch getting attracted to the same 4th hole, but it then continues through the rest of the holes in an undulating crack path. Ref. (Carlsson 2023) confirmed that they also found this behavior in one of the samples they tested with this geometry, not included in Carlsson and Isaksson (2019). This is a great confirmation of the capability of the proposed NB-NUG PD method.

By comparing the crack patterns simulated by using different methods and measured experimentally (see Figs. 13 and  14), we notice: (1) Dispersed damage and discontinuities in the crack path are observed in the results from the PD model with global non-uniform grids. These features are induced by the non-uniform grids-related numerical errors; (2) The damage predicted by the phase field method shows unrealistic thickening, most pronounced near branching locations. The full failure of the samples was not shown in the phase field results in Carlsson and Isaksson (2019). This could be due to the “leaking” of damage around crack lines present in many such models (see discussion in Mehrmashhadi et al. (2020)). The performance of different methods in several aspects is listed in Table 4 to compare them more intuitively.

Table 4 Performance comparison between phase field model from (Carlsson and Isaksson 2019) and PD models with different discretization schemes

Figure 15 shows the crack propagation speed using the PD model with the NB-NUG method. When a crack passes through the pore (see Fig. 15a, d, and f), a slight increment of speed is observed just before the crack reaches the left edge of a pore. One observes that the normalized crack propagation speed at the edge of the first pore is larger than 0.5 in (a) while it is less than 0.5 in (b) and (c). Similarly, the normalized crack propagation speed at the edge of the first pore is about 0.75 in (e) while it is less than 0.75 in (f) and (g). The crack propagation speed returns to its original level rapidly after the crack restarts from the other side of the pore. The same phenomena have been observed in Carlsson and Isaksson (2019). For the cases shown in Fig. 15b, c, and e, in which cracks do not pass through pores (the lower branch in (e)), obvious fluctuations in speed indicate that pores have an effect on crack propagation. Moreover, pores’ locations are exactly aligned with the “valleys” noticed in the crack speed curves (see the dash lines in (b) and (c)), demonstrating their connections.

Fig. 15

Normalized cracking speeds superposed on the damage maps for the long (2 mm, left column) and short (0.75 mm, right column) pre-cracks for cases PMMA-A in (a) and (d), PMMA-B in (b) and (e), and PMMA-C in (c) and (f)

Figure 16 gives the horizontal locations of the crack tips at different time steps. It is evident in the zoom-ins that there is a short flat stage before the crack tip jumps from the left side of a pore to re-initiate on the other side. The time for the crack “trapped” in a pore is the same as the crack propagating in the solid for the distance of the pore diameter. This behavior is as if an “invisible crack” propagates through pores with a constant velocity (see the pink lines shown in the zoom-ins in Fig. 16).

Fig. 16

The evolution of the horizontal coordinate of the crack tip for all six scenarios: PMMA-A, -B, and -C, with long (2 mm) and short (0.75 mm) pre-cracks (see Fig. 11)

To explain why crack speeds are slightly lower when the crack passes right below/above a pore (see the valleys at the yellow dash lines in the left column of Fig. 15b and c), in Fig. 17 we show the strain energy density map for the moment when the crack tip approaches the area right under a pore (at $311\mathrm{ \mu s}$ for Case PMMA-B with the long/2 mm pre-crack). This map shows the mutual attraction of the strain energy density zones around the crack tip and the pore edges. The high strain energy concentration zones around the pores deflect the crack tip and “trap” the crack for a short while, leading to the observed fluctuations in both crack paths and crack propagation speed. The evolution of the strain energy density distribution for NB-NUG PD results are shown in Movies 2–7, respectively.

Fig. 17

The strain energy density map for Case PMMA-B with a long (2 mm) pre-crack at $322\mathrm{ \mu s}$

6 Dynamic fracture in PMMA plates containing random pores

To show the versatility of the PD model with the NB-NUG in simulating fracture of plates with pores, in this section, we simulate dynamic brittle crack propagation in plates with randomly distributed pores of different sizes. The geometry and material properties for the plates in this section are the same as the ones considered in the previous section, and the length of the pre-crack is 2 mm. Pores are randomly generated in the rectangular domains with radii varying from 0.75 mm to 1.5 mm. At this stage, for simplicity, we avoid pores being generated on the boundary by placing their centers at least one diameter away from the boundary. Also, the distance between the centers of any two pores is set to at least 0.3 mm greater than the sum of their two radii to ensure that pores do not overlap. These minor restrictions, however, are not limitations of the discretization technique we introduced here. The examples below use a length of the non-uniform box of 0.15 mm larger than the corresponding radius of the pores they encase. The plate is divided and meshed using APDL commands in ANSYS, as described in Appendix 4.

A 6 MPa tensile load is suddenly applied on the top and bottom boundaries of the plate. Figure 18 displays the snapshots of the crack patterns and the strain energy density maps at the early stages of the cracking processes. The results show that the crack is affected by the pores and turns many times, but the pores’ influence is not apparent at the early propagation stage. With continued loading, strain energy increases. The distribution of strain energy density also depends on the microstructure (hole size and distribution), which causes the different crack responses in the path. A common feature, however, is the attraction of the crack path toward the pores. By comparing the results from the cases where different numbers of pores are implemented, we observe that in Fig. 18a (fewer pores), the crack branches at a location around the center of the plate, and no contact between the crack and pores is observed before branching, while in Fig. 18b and c (more pores) the crack branches after passing through pores (see Movies 8–10).

Fig. 18

Damage maps are all at $120 \mu \mathrm{s}$ (top row) and strain energy density maps (bottom row) at 48 $\mu \mathrm{s}$, 48 $\mu \mathrm{s}$ and 24 $\mu \mathrm{s}$, from left to right, respectively, for cases with a 10 random pores, b 20 random pores, and c 30 random pores. The strain energy density uses the same scalar bar as Fig. 9, while the damage maps use the same color bar as in Fig. 6

To remove the influence of the number of pores in the structure, and study whether the presence of pores along the potential path of a dynamic crack has an effect on when a crack branches, we fix the number of pores to 10 and generate three samples with this configuration. The computed crack paths are shown in Fig. 19. The first snapshot is the same as the case shown in Fig. 18a, in which the crack does not meet a pore before it branches, near the middle of the plate. In the other two configurations, pores happen to be in the path of the growing crack earlier, and we observe that soon after it passes through them, the crack branches, much earlier than in the first configuration. This appears to indicate that pores along a crack path promote crack branching. This earlier branching can also be seen in Fig. 15a and d, and for the same reason.

Fig. 19

Damage maps for three different random distributions of 10 pores (random location and radii). Snapshots taken at 120 $\mu \mathrm{s}$ (a), 112 $\mu \mathrm{s}$ (b), and 122 $\mu \mathrm{s}$ (c) from the start of the simulation

An explanation for why cracks appear to branch “easier” after passing through pores can then be proposed, based also on the simulation movies (see Movies 8–10): when the crack reaches a pore, its propagation is “suspended”, and at the other end of the pore, a much higher strain energy density (stress concentration) builds progressively before a crack can initiate from that location; the crack restarts its growth, but from a higher strain energy density landscape, prompting its branching soon after that (Bobaru and Zhang 2015), therefore leading to more energy dissipation.

7 Conclusions

This paper introduced a strategy to improve the accuracy of peridynamic (PD) fracture simulations in problems with notches, perforations, and other geometrical features that may serve as stress concentration and crack initiation sites. The near-boundary non-uniform grids (NB-NUG) discretization method uses non-uniform grids only in regions close to the curved boundaries, while in the rest of the domain, the discretization is uniform. Nodes in the non-uniform parts have associated volumes/areas similar to the uniform ones. The NB-NUG in PD significantly reduces artificial stress concentrations induced by uniform grids approximating curved boundaries, while minimizing quadrature error over the entire domain.

We performed static and dynamic fracture simulations for plates with a hole, using the PD with NB-NUG and two other types of grids, to show the effectiveness of the NB-NUG. We then applied these models to dynamic fracture in PMMA plates containing periodic pores and investigated the effect of pores on crack propagation. Fine details of the crack path observed in experiments were well captured by the new approach (PD with NB-NUG), including short cracks that spring from pores but soon arrest, the number of crack branching events, and the overall crack morphology. We showed how pores “attract” the crack path, and found that the crack propagation speed is affected as well by the presence of pores. We attributed the influence of the pores to the higher strain energy density around the pores. We also noticed that simulation results from the literature using the phase-field model fail to reproduce significant characteristics seen in the experiments. At the same time, PD models using uniform grids or general non-uniform grids also show features that are not present in the experiments.

We also simulated the crack propagation in plates with randomly distributed pores. The simulation results with different random pores revealed that pores could promote crack branching, meaning that the crack path can be changed artificially. These strategies may be applied in the design of novel metamaterials, mining and geomaterials extraction, nanomaterials processing, and crack shielding.

The comparison between the results obtained with the PD NB-NUG approach and the phase-field corresponding ones taken from the literature explains why having the most general nonlocal model for damage leads to accurate results in these difficult dynamic brittle fracture problems. While phase-field models regularize classical fracture models by introducing a scalar damage variable (the phase-field damage function), the PD model describes damage via an infinitely richer representation: bonds fail at a node in any direction, controlled by the particular loadings in the near vicinity of the node. Nonlocality of damage is critical here in allowing its unrestricted evolution in such problems in which complex crack morphology is sensitive to small changes in the geometrical arrangement of pores in the structure.

The new discretization approach can be easily extended to 3D problems, and this is planned as the next step in this work.

Appendices

Appendix 1. Convergence study

When selecting an appropriate size of the PD horizon, in addition to other factors, one has to take into account the size of the smallest geometrical features, relevant in the problem at hand, and also notice that a relatively large horizon size enhances the nonlocal effect while a small one leads to results that approach the classical solution, for problems that admit a classical solution (Wu et al. 2021; Bobaru and Hu 2012). The smaller the horizon size, however, the costlier the computation. To find a “proper” horizon, $\delta$-convergence analysis is conducted for Cases PMMA-A and PMMA-B (Figs. 11a, b) with a $2\mathrm{ mm}$ pre-crack to study the dependence of the crack propagation speed on the horizon size we selected. We use horizon sizes of 0.24, 0.20 and 0.16 $\mathrm{mm}$, significantly smaller than the pores’ radii, and select m = 4 (m is the horizon factor, i.e., the ratio between the horizon size and the grid spacing).

In Fig. 20, we compared the evolution of the crack propagation speeds (see Appendix 2 for the method used to track the crack tip and computing crack speed) obtained from the PD models with different horizon sizes, in simulating Case PMMA-B with a $2\mathrm{ mm}$ pre-crack (in Fig. 11b, with the boundary conditions shown in Fig. 12). The results shown in Fig. 20 indicate that as the horizon size decreases, the crack initiation time does not change and the crack propagation speed appears to converge. Therefore, for the rest of the simulations, we use $0.16\mathrm{ mm}$ as the horizon size.

Fig. 20

The cracking speed versus time and crack paths for Case PMMA-B (Fig. 11b) and the 2 mm pre-crack for different horizon sizes: $\updelta$ = 0.24, 0.20, and 0.16 mm, respectively. The crack propagation speed is normalized by the Rayleigh wave speed. The corresponding damage maps are in the right panels

We also perform a $\delta$-convergence analysis for Case PMMA-A (Fig. 11a) with a $2\mathrm{ mm}$ pre-crack to study the dependence on the horizon size of the crack re-initiation from pores. Movies 11–13 show the damage evolutions for horizon sizes of 0.24, 0.20 and 0.16 $\mathrm{mm}$, respectively. Figure 21 shows the evolution of the horizontal coordinate of the crack tip (before the cracks pass the third pore) for different horizon sizes. Movies 11–13 show a similar cracking process for the solutions using different horizons. The crack “trapping times” (from arriving at a pore to re-initiating from the other side of the pore) in the pores are also close to each other for the simulations with different horizon sizes.

Fig. 21

The evolution of the horizontal coordinate of the crack tip for PMMA-A (Fig. 11a) and the long (2 mm) pre-cracks for different horizon sizes: $\updelta$ = 0.24, 0.20, and 0.16 mm, respectively. The corresponding damage maps are in the right panels (see Movies 11–13 for the damage evolution)

Appendix 2. Method for tracking the crack tip and computing the crack speed

To calculate the crack speed at a time step, we track the approximate crack tip and compute an average speed for the crack tip moving from the current time step to the next 30 time steps. For time step $i$, the position of crack tip is ${a}_{i}$. We define the average velocity at $i$ step as the ratio of distance between ${a}_{i+30}-{a}_{i}$ and the time period between the $i$ th step and the ($i+30$)th step. Since the time step is a constant $\Delta t$, the computed crack speed is:

2.1 ${v}_{i}=\frac{\left|{a}_{i+30} - {a}_{i}\right|}{30\Delta t}$.

In test defined on simple domains and uniform discretizations that lead to computationally-symmetric problems, the crack tip, used to calculate the crack speed, can be defined as, for example, the most upper right node with a damage index greater than 0.35. For problems considered in this section, the crack may branch and multiple crack tips may appear around pores, leading to a much more complex crack propagation. In addition, when using non-uniform grids, computational symmetry is broken, and the above strategy is bound to fail. In this paper, we simplify the problem of determining the crack tip by splitting a complex crack path into a few simpler paths. We first run the problem once and from the damage map we manually determine the “bounding boxes” for the individual branches (see yellow boxes in Fig. 22) to limit the calculation of crack speed to a single branch at a time and avoid the possible jump between branches. We can then post-process the results, or re-run the problem with the bounding boxes coordinates known to determine the crack propagation speed with confidence.

Fig. 22

Crack-tip tracking is limited to the dashed boxes bounded by coordinates ${x}_{0}$, ${x}_{1}$, ${y}_{0}$, ${y}_{1}$ for branch A, and ${x}_{1}$, ${x}_{2}$, ${y}_{2}$, ${y}_{3}$ for branch B

Appendix 3. Loading condition

To illustrate the feasibility of this simplification in modeling, we compute and compare the evolutions of cracking speed in an intact plate (no perforations) with pre-cracks of 0.75 mm and 2 mm, respectively, subjected to static-dynamic (S + D) loading, and dynamic-only loading (D), respectively. In the modeling with S + D loading condition, through multiple trial calculations, we find the imposed displacements at which the cracks are about to propagate and use these displacements (0.042 mm for the case with a 2 mm pre-crack and 0.074 mm for the case with a 0.75 mm pre-crack) as the loads in a static loading stage; we then switch from the static solver to the dynamic solver, and apply displacement-controlled condition with a fixed velocity of $0.3\mathrm{ m}/\mathrm{s}$ on the bottom and upper boundaries. The comparison between the two loading schemes is shown in Fig. 23. The crack propagation speeds obtained via models with the two schemes are consistent over the entire crack propagation process. The crack patterns obtained from both schemes are also consistent, for both cases with different pre-cracks, respectively. In the following, we use the dynamic-only loading scheme (shown in Fig. 12) to approximate the experimental loading conditions.

Note that the value of 0.3 m/s was from a reference on simulating the same problem (Rahimi et al. 2020). We have also applied other two V values (0.1 m/s, 0.01 m/s) on the unperforated plate with a pre-crack and compared the crack patterns. Under the displacement-control loading with these three V values (loading velocity), all the cracks branched, and the crack patterns are close to each other except for a slight difference in the crack branching locations, as expected.

Fig. 23

Crack propagation speed superposed on damage maps from PD models using the S + D (in white) and the dynamic-only (in red) schemes, respectively: a 2 mm pre-crack, and b 0.75 mm pre-crack. Due to the symmetry, only half of the damage map for each loading is shown in the background (separated by the black dash horizontal midlines)

Appendix 4. APDL code used to generate NB-NUG

/clear /prep7
*set,length,50 *set,width,25 *set,elementsize,0.04	! set the geometry, element size and the non-uniform box length larger than radius(NBLLTR)
*set,NBLLTR,0.15 et,1,plane182
*dim,npores *VREAD,npores,poresfile,TXT,,ijk,1	! read the number of pores from the first line in file “poresfile.txt’’
(F3.0) *dim,pores,array,npores(1),3
*VREAD,pores,poresfile,TXT,,jik,3,npores(1),,1 (3F11.5) *voper,boxlength,pores(1,3),add, NBLLTR	! read coordinates and radii of pores from file “poresfile.txt’’. Note that the format of data should be consistent with the code
*voper,boxlength,boxlength,mult, 2	! compute the length of non-uniform box
blc5,0,0,length,width
*do,i,1,npores(1),1	! create the plate
cyl4,pores(i,1),pores(i,2),pores(i,3)	! create the pores
*enddo *do,i,1,npores(1),1 cyl4,pores(i,1),pores(i,2),pores(i,3) *enddo *do,i,1,npores(1),1
blc5,pores(i,1),pores(i,2),boxlength(i),boxlength(i)	! create the non-uniform box
*enddo asel,s,area,,1,, cm,plate,area asel,s,area,,2,npores(1) + 1 cm,porescm1,area asel,all asel,s,area,,npores(1) + 2, 2*npores(1) + 1 cm,porescm2,area asel,all asel,s,area,,2*npores(1) + 2, 3*npores(1) + 1 cm,boxes,area asel,all asba,boxes,porescm2
asba,plate,porescm1	! obtain the plate with pores
aovlap,all asel,all
asel,s,area,,1,npores(1) asel,inve	! divide the plate to regular area and irregular areas
wprota,0,0,-90 *do,i,1,npores(1) wpave,pores(i,1) + boxlength(i)/2,pores(i,2),0 asbw,all wpave,pores(i,1) − boxlength(i)/2,pores(i,2),0 asbw,all *enddo wprota,0,-90,0 *do,i,1,npores(1) wpave,pores(i,1),pores(i,2) + boxlength(i)/2,0 asbw,all wpave,pores(i,1),pores(i,2) − boxlength(i)/2,0 asbw,all *enddo allsel lesize,all,elementsize,,,,,,0
asel,s,area,,1,npores(1) asel,inve	! mesh the regular areas with mapped meshing method
aesize,all,elementsize mshkey,1 amesh,all allsel asel,s,area,,1,npores(1),,1
aesize,all,elementsize lesize,all,elementsize,,,,,,0	! mesh the irregular areas with free meshing method
mshkey,0 amesh,all allsel
*get,emax,elem,,count	! obtain the total number of elements emax
*dim,nodeid,array,emax,1,1 *vfill,nodeid,ramp,0,1,	! create the nodeid array with the size of emax
*vget,aear1,elem,1,geom,,,2	! obtain the area of each elements
*vget,xelem,elem,1,cent,X,,,2 *vget,yelem,elem,1,cent,Y,,,2	! obtain the x and y coordinates of elements centroid
*cfopen,‘nodes’,‘dat’,” *vwrite,nodeid(1),aear1(1),xelem(1),yelem(1)	! output the node area, x and y coordinates into file “nodes.dat”.
%I%16.6e%16.6e%16.6e *cfclose