Why do cracks branch? A peridynamic investigation of dynamic brittle fracture

Abstract

In this paper we review the peridynamic model for brittle fracture and use it to investigate crack branching in brittle homogeneous and isotropic materials. The peridynamic simulations offer a possible explanation for the generation of dynamic instabilities in dynamic brittle crack growth and crack branching. We focus on two systems, glass and homalite, often used in crack branching experiments. After a brief review of theoretical and computational models on crack branching, we discuss the peridynamic model for dynamic fracture in linear elastic–brittle materials. Three loading types are used to investigate the role of stress waves interactions on crack propagation and branching. We analyze the influence of sample geometry on branching. Simulation results are compared with experimental ones in terms of crack patterns, propagation speed at branching and branching angles. The peridynamic results indicate that as stress intensity around the crack tip increases, stress waves pile-up against the material directly in front of the crack tip that moves against the advancing crack; this process “deflects” the strain energy away from the symmetry line and into the crack surfaces creating damage away from the crack line. This damage “migration”, seen as roughness on the crack surface in experiments, modifies, in turn, the strain energy landscape around the crack tip and leads to preferential crack growth directions that branch from the original crack line. We argue that nonlocality of damage growth is one key feature in modeling of the crack branching phenomenon in brittle fracture. The results show that, at least to first order, no ingredients beyond linear elasticity and a capable damage model are necessary to explain/predict crack branching in brittle homogeneous and isotropic materials.

1 Introduction

As mentioned in Cox et al. (2005), at some scale, all fracture is dynamic. The dynamics of atomic bond rupture plays a role in crack propagation even when a crack at the macroscopic scale appears to be advancing quasi-statically. As the atomic bond rupture is a dynamic process, the authors of the review article (Cox et al. 2005) state that “the dynamic fracture problem is the most fundamental in the science of fracture”. Dynamic fracture covers largely disparate spatial scales: on the smallest scale, dynamic fracture can help us understand how the introduction of nanostructures can affect the ultimate strength of a material, while at the geophysical scale we can understand the conditions required for a fault in the earth’s crust to lose stability and produce a massive earthquake.

Dynamic fracture has been studied from several different angles by researchers from different communities. Two main lines of attack for understanding this problem have been atomistic modeling (classical and quantum) and continuum mechanics modeling.

Atomistic modeling has sometimes produced puzzling results (Zhou et al. 1996). For example, crack branching cannot be reproduced by 2D atomistic models (Procaccia and Zylberg 2013), as branching attempts lead to one of the branches to eventually arrest. Three-dimensionality has been proposed as a potential solution for achieving crack branching in atomistic models of amorphous materials. Further studies that used realistic crystalline potentials have failed to reproduce experimental results (Hauch et al. 1999; Bouchbinder et al. 2014). Somewhat surprisingly, atomistic simulations seem to require quantum mechanical calculations in order to enable an accurate quantitative description for mode I crack propagation (the simplest mode of fracture) at low speeds of a single crack in single crystal silicon (Kermode et al. 2008). The complexity of dynamic fracture in amorphous or polycrystalline materials is significantly enhanced by the physical interplay of multiple length scales due to the presence of microdefects or grain boundaries. For these types of problems, atomistic or quantum calculations cannot yet provide any answers.

In addition to the obstacles in predicting the observed behavior in dynamic brittle fracture with atomistic models mentioned above, such models have some obvious limitations (see Zhou et al. 1996): the small size of the sample modeled (usually micrometer or submicrometer) and the short time scales that can be accessed (usually nanoseconds). Cracks in brittle solids are controlled by waves (Ravi-Chandar and Knauss 1984b) and the influence of elastic waves bouncing from the boundaries of the sample cannot be neglected if one is to predict the behavior of growing cracks in such solids. In trying to predict how cracks propagate in brittle solids it is, therefore, essential to model the entire sample, a feat not achievable by atomistic models. The alternative then remains modeling at a continuum level. Doubts about whether continuum approaches would ever be capable in successfully modeling the evolution of dynamic cracks, through fragmentation, have persisted for decades (Song et al. 2008). One source for these doubts has been attributed to the breaking down of linear fracture mechanics (LEFM) for regions near the crack tip, as is reviewed in Bouchbinder et al. (2014). A number of authors have introduced models that modify the classical picture by introducing a certain region with nonlinear elastic behavior near the crack tip as well of a length-scale (see Bouchbinder et al. 2014). Such models have been successful in correctly representing the opening profile at the crack tip in soft brittle materials (aqueous gels). It is not yet known whether this approach is still valid in more standard brittle materials, like glass or glassy polymers, in which there is no clear separation between nonlinear elastic scales and dissipative ones (Bouchbinder et al. 2014).

The branching of a crack (splitting of a crack in two or more cracks) is one of the characteristics of dynamic brittle fracture (Bowden et al. 1967; Ramulu and Kobayashi 1985). An increase in fracture surface roughness is consistently observed in experiments prior to branching (Ramulu and Kobayashi 1985). The increase in fracture surface roughness is tightly connected to crack path instability. Crack path instabilities, in turn, have been proposed as being responsible for the observed limiting crack speed in amorphous brittle materials. This speed is well below the theoretical limiting speed, rarely reaching above 0.6 of the Rayleigh wave speed (see Ravi-Chandar 2004, p. 191). The source of the observed instabilities has been assigned to a number of potential mechanisms happening in the process zone around the crack tip:

• Ravi-Chandar and Knauss (1984a) suggested that the process zone is significant even in nominally brittle materials, and, in this zone, nucleation, growth, and coalescence of microcracks occurs; the dynamics of evolution of these processes triggers microscopic path instabilities, that eventually lead to crack branching. This mechanism has been observed in glassy polymers like PMMA (see Ravi-Chandar and Yang 1997) and polystyrene (see Hull 1999, p. 141) where conical markings are seen on crack surfaces;

• Hull (1994) suggested that twisting and tilting of the stress vector on the crack front (thus mixed-mode loading around the crack tip) due to microscale variations in the symmetries results in crack path instabilities, surface roughness and eventual crack branching. This mechanism has been suggested for glasses or brittle epoxy resins in which the forming of microcracks around the crack tip has not been observed in experiments, and the stresses required to activate the very small flaws near the crack tip would have to approach the theoretical strength of the material, thus making bond breakage at the tip the more likely scenario (Beauchamp 1996; Hull 1999 p 145).

Crack path instabilities have been addressed in a series of atomistic or theoretical investigations (e.g. Buehler and Gao 2006; Livne et al. 2007). A vast literature on exposing various types of instabilities in dynamic fracture is reviewed in Bouchbinder et al. (2014), Fineberg and Bouchbinder (2015). In our opinion, however, the actual mechanisms that trigger these instabilities has not been clearly identified or satisfactorily explained. Indeed, the authors of the review article Bouchbinder et al. (2014) state: “is it quite likely that the dynamics of the near-tip zone could play an important role in unraveling the physical mechanisms driving instabilities of rapid cracks”. What causes this instability and how is it generated? What is the sequence of events that lead, in one case, to a crack propagating straight, and in another case, instabilities spring up and induce micro-branching and roughening of the crack surface, and eventually macro-branching?

The crack propagation speed has been demonstrated in experiments not to be the main reasons leading to crack branching. The experimental evidence points to the following likely scenario: when a critical stress intensity factor is reached, the crack splits into two of more branches, each propagating with about the same speed as the parent crack but with a smaller process zone (see Ravi-Chandar 2004, p. 214).

In this paper we aim to answer the following questions:

• 1. Is it possible to use a continuum model to predict dynamic brittle fracture, in particular crack branching?

• 2. What is the minimal set of input data that is able to reproduce the most important characteristics observed in crack branching?

• 3. Are quantum calculations the only option for explaining the dynamic instabilities that precede crack branching?

• 4. What are the causes of the dynamic instabilities and how do these lead to crack branching?

• 5. Why do cracks in amorphous materials branch well before reaching propagation speeds close to the Rayleigh wave speed, the theoretical limiting speed of mode I cracks?

• 6. How do stress waves and loading conditions affect crack branching?

As we shall see, a key factor in having a model that reproduces the essential features of crack branching, is being able to capture, at least in some average sense, the evolution of the process zone around the crack tip. The peridynamic model satisfies these requirements. We will also see that, contrary to some recent conclusions that the micro-branching instability is intrinsically a 3D phenomenon and that it “cannot be modeled directly by a 2-dimensional” theory (Bouchbinder et al. 2005), some essential features of crack instabilities are not controlled by the dimensionality, but by how the elastic wave energy flows around the crack tip and by the dynamic evolution of the process zone. Our results confirm previous statements made based on experimental evidence and theoretical considerations that “the process of branching is governed by the inner problem and not the outer problem that is treated by the (classical) continuum elastodynamics” (see Ravi-Chandar 2004, p. 214) and this observation explains why cracks branch well before reaching speeds projected by elastodynamic theories to be required for a crack to branch (Yoffe 1951). The role played by “structural inertia” (see Ožbolt et al. 2011, 2013) has been pointed out in branching of concrete. The results obtained in our paper explain the mechanisms through which the dynamics of strain energy around the crack tip leads to branching.

We will explain the reasons for the angle of branching changing past the branching event (the branched cracks do not grow straight, but may curve after a while). We explain what controls the initial angle of branching, as well as what conditions favor microbranching. We shall see that the peridynamic model explains all these different characteristic features of crack branching without any conditions or extra criteria for crack growth. The fact that only elastic wave propagation and a proper damage model (the nonlocal, peridynamic damage model which only uses fracture energy information) are sufficient to capture all these different features of the dynamic brittle fracture phenomenon, indicates that all other effects or criteria used in earlier models are secondary/not needed to explaining this phenomenon. Results in the present paper also demonstrate that atomistic resolution and quantum calculations are not necessary in order to understand dynamic brittle fracture and, in particular, the crack branching instability.

2 A brief review of literature on crack branching

In this section we provide a brief review of the vast literature dedicated to the subject of dynamic brittle fracture, and in particular to crack branching. This review cannot possibly cover the entire, vast literature dedicated to this subject. Dynamic brittle crack growth remains a challenging problem after almost a century of research dedicated to it (see Cox et al. 2005). To investigate the mechanisms of dynamic brittle fracture, theoretical models, numerical simulations, and experiments have been employed over the years (for a recent review, see Bouchbinder et al. 2014).

2.1 Theoretical models and experimental results on dynamic brittle fracture and crack branching

Various criteria have been proposed to explain crack curving and branching in dynamic brittle fracture. Early on, the crack propagation velocity was thought to control crack branching and a crack branching criterion was proposed based on elastodynamic theoretical results (Yoffe 1951) showing that, for a crack of constant length translating with a constant velocity in an infinite medium, the maximum circumferential stress shifts from the symmetry line to lines that make an angle of 60$^{\circ }$ with the direction of propagation of the crack when the crack speed exceeds the 0.73 fraction of the Rayleigh wave speed. The Rayleigh wave speed is the theoretical limiting velocity for propagating cracks in linear elastic materials (Freund 1990). The limiting crack speed is also discussed in Stroh (1957). In practice, cracks never reach such high speeds in isotropic amorphous brittle materials, loosing stability and branching when they reach fractions of 0.35–0.65 of the Rayleigh wave speed (see Döll 1975; Ravi-Chandar and Knauss 1984a; Ravi-Chandar 2004, Table 11.1). In crystalline materials, in which cracks may become trapped on cleavage planes, the propagation speed can reach close to the Rayleigh wave speed (Field 1971). Another problem with the Yoffe solution is that experimentally observed branching angles (angle between a branch and the original crack line) are between 10$^{\circ }$ and 45$^{\circ }$.

The constant length crack moving with constant velocity under mode II conditions is a physically possible process in seismic events where slip stops after the propagation of the disturbance. Broberg (1999) gave the solution for this mode II Yoffe problem. Crack propagation for semi-infinite cracks has been studied by Freund (1972) and Eshelby (1969) in an infinite 2D linear elastic medium. These models show that cracks propagate smoothly and continuously accelerate until they achieve the limiting velocities. However, in reality, crack path instabilities are triggered well before such speeds are attained and crack surfaces present the “mirror, mist, hackle” patterns before branching takes place (see, e.g. Ravi-Chandar and Knauss 1984a; Ramulu and Kobayashi 1985; Beauchamp 1996; Hull 1999). Noticing the discrepancies between experimental observation and analytical predictions, Gao (1996) indicated that linear elasticity might be inadequate because it misses possible large deformation near the crack tip. The resulting model obtains a local limiting speed that provides an explanation for the onset of mirror-mist transition observed in dynamic fracture experiments.

Crack path instabilities may lead to crack branching. Criteria for crack path curving and crack branching under single or mixed modes were proposed based on, for example, the maximum circumferential-stress or minimal strain energy criteria. The criterion that the crack growth direction is normal to the maximum circumferential-stress was introduced in Erdogan and Sih (1963). Using this model, Streit and Finnie (1980) proposed a directional stability criterion on the hypothesis that the crack instability is caused by an off-axis microcrack, ahead of the crack tip within a critical distance, connecting with the main crack. The crack path kinks or bifurcates once the critical distance is greater than the maximum radius for which the maximum circumferential stress lies on the symmetry axis. Extending Streit and Finnie’s ideas, Ramulu and Kobayashi (1983) put forward a dynamic crack curving criterion by adding the nonsingular stress or remote stress to the directional stability criterion. The dynamic crack curving criterion is capable of predicting the crack angle in both pure Mode I and mixed Mode I and II conditions. Results showed that positive nonsingular stress enhances the instability while the negative one reduces the fracture angle. This work also proposed a “long-range” interaction in dynamic fracture problems, where a sufficient criterion for crack branching is introduced and tested experimentally. The criterion involves a “characteristic distance” $r_{0}$ that depends on the dynamic state of stress near the crack tip. According to Ramulu and Kobayashi (1983), crack branching occurs when $r_{0}\le r_{c}$, where $r_{c}$ is a material property thought to be related to the distance between microvoids and the crack tip. When an off-axis microvoid gets within a critical distance $r_{c}$ from the crack tip, it gets activated by the stress field and directional stability of the propagating crack is lost leading to a deflection of the straight crack path. The loss of directional stability, together with the necessary criterion for crack branching ($K_{I}\ge K_{Ib}$), leads to branching of a propagating straight crack. The role played by microcracks around the crack tip in crack branching has been discussed in, for example, Ravi-Chandar and Knauss (1984a) and Ravi-Chandar and Yang (1997).

Besides the microvoids and microcracks-induced crack path instabilities, the tilting and twisting of the stress vector at the crack front due to mixed-mode loading has been studied as another potential source that can lead to crack branching. The formation of “lances” in glass, as the result of superposition of mode I and mode III, was quantitatively investigated by Sommer (1969). The fracture plane, which is perpendicular to the loading axis in mode I, separates by lances as a result of rotation of the principal stress field at the crack tip. A critical angle of rotation was proposed as a necessary condition for lance formation. Using a modified Sommer’s experiment, Hull (1994) confirmed that a critical rotation angle is needed for “river lines” nucleation. Hull explained the progressive coarsening of river lines and the generation of helicoid surfaces in mixed mode I/III conditions. In inorganic glasses, no evidence of microcracks ahead of the crack tip is found and the source of roughness of the crack surface is placed on local changes in the path of the growing crack arising “from some form of local instability at the tip of the crack related to the dynamical properties of the cracks” (Hull 1999, p. 145). We remark that the specific “dynamic properties” creating these instabilities have not been specified. The picture proposed in Hull (1994), Beauchamp (1996), and Hull (1999) to explain branching in inorganic glasses, involves local tilting of the crack out of the main plane. The tilted cracks grow a short distance. With steps forming between the main crack and the tilted cracks, crack overlapping effects occur. When the dimensions of the tilted elements are comparable to the dimensions of the test sample, macroscopic bifurcation occurs (see Hull 1999).

Reasons of crack surface roughening were also recently investigated by comparing responses of perturbation of growing cracks with shear pulse perturbations (Bonamy and Ravi-Chandar 2005). In this work it was determined that the mode III loading, introduced by the shear waves interacting with the crack front, is responsible for the observed roughening, via local twists that do not produce fragmenting. When a dynamically growing crack running at speeds below 0.4 $C_{\mathrm {R}}$ interacted with a localized heterogeneity (in the form of a groove scratched on the surface of the sample), undulations are produced on the crack surface as a results of the interactions between the crack front and the shear waves radiated from the groove, and not from the crack front waves (acoustic emissions) as suggested by others (Morrissey and Rice 2000). At speeds closer to 0.45 $C_{\mathrm {R}}$, which may be a threshold for developing microbranches, whether emissions of crack front waves induces roughness or not is still unknown and needs to be investigated.

2.2 Computations of dynamic brittle fracture based on FEM

Computational modeling aimed at predicting dynamic brittle fracture has been performed to simulate the crack propagation and crack branching using finite element method (FEM) or various modified versions of the FEM. Existing FEM models are based on the classical continuum mechanics equations, which are described by partial differential equations. In order to solve problems with discontinuities, such as cracks, special techniques need to be devised. Most of these techniques essentially treat every new configuration as a problem in a new domain, since the crack creates new surfaces and the boundaries of the initial domain change. This requires tracking of the crack surface in some way. Other complications relate to describing crack initiation, determining the direction of propagation and the propagation speed. All of these aspects require laws of propagation (or “kinetic relations”) and most of the time they are setup in an ad-hoc manner: they may work for one example, but not for another. These approaches also assume that dynamic crack growth is describable by a surface generally determined by the separation between the elements or tracked by a smooth level-set curve. This excludes capturing roughness on the crack surface that is associated with dynamic brittle fracture.

One of the simplest methods to modeling propagating cracks is the element-deletion (also known as “element-erosion”) method. Such methods suffer from nonconvergence in the limit of the mesh size going to zero. Recent improvements of these approaches have been produced using variational formulations (Pandolfi and Ortiz 2012) or nonlocal averaging of displacement gradients schemes (see Negri 2006) as those employed in the nonlocal models of Eringen (2002). The results in Pandolfi and Ortiz (2012) match well quasi-static type of crack growth under mixed-mode conditions. While a length-scale is introduced in the element erosion model of Pandolfi and Ortiz (2012), Pandolfi et al. (2013) in order to regularize the problem and insure convergence in the limit of the mesh being refined, it is not yet known how this method performs in the crack branching problem.

Alternatives to element-erosion techniques are cohesive zone FEM models (see e.g. Xu et al. 2008; Camacho and Ortiz 1996). Such models remove the need of pre-knowledge of the crack path. The crack path, however, is still forced to follow the particular mesh used, since cracks can only propagate along the element boundaries (see Xu and Needleman 1994; Camacho and Ortiz 1996; Ortiz and Pandolfi 1999). Since the correct, actual crack path (which minimizes the strain energy) of the propagation process may not be computed correctly, there are significant departures from the true energy released during the crack propagation event. In such cases, reliable prediction of strength of brittle ceramics under impact, for example, becomes difficult. The XFEM (see e.g. Dolbow and Belytschko 1999) allows cracks to pass through the finite elements leading to better approximations of the crack path. Interestingly, in dynamic brittle fracture problems, one may need to drastically modify the input fracture energy in the model in order to obtain crack propagation speeds similar to those seen in experiments (see Song et al. 2008). Subdivision of cut elements for numerical integration purposes increases complexity and cost for this method. The method also requires phenomenological damage models and branching criteria as input, and tracking of the crack path using, for example, level sets. A recent review of methods that use tracking of the crack path has been recently provided in Rabczuk (2013).

2.3 Dynamic brittle fracture results based on atomistic modeling

In atomistic models, like molecular dynamics (MD) simulations, under sufficiently high loading conditions that lead to instability of the crack path, cracks can branch without a specific criterion (see Zhou et al. 1996). MD models, however, are not able to capture the crack propagation speed or the angle of crack branching correctly. For instance, MD simulations show instabilities that lead, shortly after the bifurcation of a crack, to the propagation of only one of the two branches, the other being arrested. The limited space and time scales that can be addressed by such models, prevent investigating what could happen if this behavior of branching attempts (followed by the arrest of one of the branches) were monitored over macroscopic scales (perhaps, microns to millimeters and hundreds of microseconds) which are relevant to the crack branching phenomenon (see Ramulu and Kobayashi 1985). Moreover, the initial branching angle computed with MD in Zhou et al. (1996) is greater than 45$^{\circ }$, where experiments show much smaller crack branching angles (see Ramulu and Kobayashi 1985). Ravi-Chandar and Knauss (1984a) showed that the branching angle is influenced by the crack tip stress state, in particular the nonsingular term.

Paradoxically, simulations based on regular arrangement of atoms (crystalline solids) give solutions (see Abraham et al. 1997) that are observed, at much larger scales, in noncrystalline materials! In crystals, cleavage fracture is observed in experiments and crack speed may reach a significant fraction of the Rayleigh wave speed (close to 0.9) without exhibiting branching (see Bowden et al. 1967). Addition of hyperelasticity at the crack tip (see Abraham 2005; Buehler and Gao 2006) does not improve on this, so far, unexplained behavior of atomistic models.

It is important to notice that for MD simulations to correctly predict dynamic brittle fracture one may need to model the entire structure in order to capture, for example, stress wave reflections from the boundaries. Ravi-Chandar and Knauss (1984a) were the first to show that crack branching occurs in “infinite specimens” even in the absence of stress wave reflections from the boundaries, and also showed that elastic stress waves play a major role in the evolution of dynamic brittle cracks. An alternative to modeling the entire structure by MD could be using multiscale models capable of transferring waves between the scales correctly. Whether this is a viable approach is still an open question.

2.4 Dynamic brittle fracture based on particle and lattice-based methods

Particle and lattice-based modeling of brittle fracture has been researched for several decades (see e.g. Cundall and Strack 1979; Marder and Gross 1995). Lattice dynamics models produce ranges of “forbidden velocities” Marder and Gross (1995) which are not observed in experiments. For a band of velocities beginning at zero and proceeding up to around 30 % of the relevant wave speed, steady crack motion is impossible (see Marder and Gross 1995), while in experiments, all such speeds are accessible for a crack (see Ravi-Chandar 2004). Changing from a triangular to a square lattice changes the critical velocities substantially. A phenomenon called “intermittency” is thought to be at the origin of the instability of the crack path (see Marder and Gross 1995).

In Bolander and Saito (1998), rigid-body-spring networks were used to simulate brittle fracture in homogeneous, isotropic materials. In this model, the body is discretized using Voronoi diagrams, and the particles such created are connected via springs. Spring degradation or spring deletion are used to model the fracture initiation and propagation. The random geometry lattice created by the Voronoi structure greatly reduces the preferential direction for crack propagation seen in regular geometry lattice spring networks (see Jirásek and Bazǎnt 1995). Results of a reinforced concrete beam show that fracture patterns obtained by simulation are close to experimental observations.

In the “particle cracking model” introduced in Rabczuk and Belytschko (2004), a crack advances by breaking particles in a sequence. The crack propagation speed in crack branching reaches values of about 0.6$C_{\mathrm {R}}$, which is close to what is observed in experiments. However, the crack patterns obtained after branching appear non-physical, with some unexplained features, like sub-branching in regions which are expected to be unloading. Dynamic failure and fragmentation has also been studied with a semi-Lagrangian reproducing kernel particle method (RKPM) in Guan et al. (2011), where a stabilized non-conforming nodal is introduced. The method is able to show effectiveness for examples of a projectile penetration into a concrete block and bullet into a steel plate. For the brittle damage of the concrete block, not all of the failure features seen in experiments are reproduced by the computations.

2.5 Phase-field models in dynamic fracture

In order to circumvent the problems associated with numerically tracking the propagating discontinuity representing a crack, phase field models (see Aranson et al. 2000; Bhate et al. 2000; Bourdin et al. 2008; Pons and Karma 2010; Spatschek et al. 2011; Bourdin et al. 2011; Borden et al. 2012), approximate the fracture surface by a phase-field: a function of position (and time for dynamic problems) with values in the interval [0, 1], with value 1 away from the crack and 0 inside the crack. By introducing a limiting parameter (in effect a length-scale) into the model, phase-field approaches eliminate the problem with the lack of convergence under grid refinement that classical methods suffer from (Bourdin et al. 2008). Note that the material-point erosion model (Pandolfi et al. 2013) mentioned above uses a similar approach to regularize the problem and achieve convergence.

In phase-field models, one minimizes the free energy functional comprised of the strain energy density and the regularized crack surface density. These models are capable of representing with some success many characteristic of fracture, like crack initiation, propagation, branching, acoustic emissions, and fracture instabilities. Two approaches have been favored in this area: dynamic phase-field fracture models based on Landau–Ginzburg type phase-field evolution equations (e.g., Karma et al. 2001; Spatschek et al. 2011) and phase-field formulations based on Griffith’s theory (see Bourdin et al. 2008, 2011). Some authors (see Borden et al. 2012) prefer the phase-field formulation of the Bourdin-type since the physical properties of Griffith’s theory are well understood and have proven useful in engineering applications. The regularization parameter that defines the width of the failure zone in phase-field models permits (see Borden et al. 2012) obtaining the “crack thickening” before branching that may be a representation of roughening of the crack surface before branching observed in experiments.

Some issues in the Landau-Ginzburg-type formulations related to the evolution of the phase-field away from the crack tip, even when the sample is brought back to equilibrium, are pointed out in Bourdin et al. (2011). The results in Bourdin et al. (2011), however, are not intended to be compared yet with experiments in terms of crack propagation speed and other measures. The phase-field model for dynamic fracture (Borden et al. 2012) used in Hofacker and Miehe (2013) shows branching when one would not expect it (in the KalthoffWinkler test), branching patterns that do not resemble those seen in experiments, and branching angles that are much smaller than those observed in experiments.

In a recent review article (see Spatschek et al. 2011) the authors note that “is not yet clear how to relate quantitatively phase field model predictions of dynamical branching instabilities to experimental observations”, and that “phase field models that incorporate a more realistic description of the process zone are presently needed to make predictions more broadly applicable”. It is not yet clear how one can introduce in phase-field models effects related to the discrete nature of the material, including lattice trapping effects that affect macroscopically observable properties (see Rösch and Trebin 2009), nonlinear elastic effects, post-failure contact between interacting fragments, or severe plastic deformation.

2.6 Results on dynamic brittle fracture from peridynamic models

Peridynamics is a reformulation of the classical continuum mechanics equations that allows a natural treatment of discontinuities in the solution of equation of motion for continua by employing the concept of nonlocal interactions (see Silling 2000). Integration, rather than differentiation, is used to compute the total force-density acting on a certain material volume, and deformation gradients are not used in the formulation. Peridynamics differs from other nonlocal methods such as those described in Eringen (2002), Kunin (1982), and Rogula (1982), or those reviewed in Bažant and Jirásek (2002), for at least two fundamental reasons:

• 1. The deformation gradient and strains (spatial derivatives of displacements) are not used in peridynamics. Other nonlocal methods average strains over the nonlocal region. Spatial derivatives of the displacement field become undefined when discontinuities, like cracks, emerge and this requires special treatment and algorithms in models that employ such derivatives in their formulation.

• 2. Damage is introduced in the peridynamic method at the microlevel in the constitutive model for the peridynamic bonds between material points. When the relative elongation of the bond reaches a failure criterion related to the material’s fracture energy, the bond breaks. Fracture surfaces or diffuse damage result autonomously as a consequence of this definition. Dealing with multiple interacting cracks of arbitrary shapes in complex geometries becomes as easy as dealing with a single straight crack. In this way, peridynamics integrates damage and fracture under a single model for material failure.

In references Ha and Bobaru (2010, 2011a, b), the crack branching problem has been treated using the bond-based version of peridynamics. Convergence results have also been provided there. Peridynamics correctly predicts important elements of dynamic crack propagation: the shape of the crack paths, the general profile of the crack propagation speed (similar to the experimental one reported in Field 1971), attempted and successful branching events [similar to those observed in Ramulu and Kobayashi (1985)], secondary cracks caused by wave reflections from the boundaries, and the relation between the way strain energy is delivered into the fracture zone and the evolution of the fracture process [as reported in the experiments in Ravi-Chandar and Knauss (1984a, b)]. Note that in Ha and Bobaru (2010, 2011a, b) the fracture energy for glass used was that reported in the literature at branching. The fracture energy at crack initiation is significantly lower than that measured at branching. This happens because in measurements, one measures the straight advancement of the crack and cannot account for all of the micro-cracks and roughness of the advancing crack. Therefore, the fracture energy measured at around the branching point appears to be much larger than the energy measured at crack initiation. The results shown in the present contribution use the fracture energy at initiation, and if we were to measure the “apparent” fracture energy in the branching region we would likely obtain values similar to those measure in the experiment because the model allows for the expenditure of fracture energy in autonomously creating damage away from the original crack surface in the form of roughness/microcracks. We notice that one way in which results change when the input fracture energy is changed is the amplitude of the applied loading required to generate crack propagation.

The peridynamic results, in terms of the crack propagation speed and the crack path, converge (see Ha and Bobaru 2010) once the horizon (the nonlocal parameter) reached sub-millimeter values. These values may be related to the characteristic length discussed in Ramulu and Kobayashi (1985, 1983), and further clarifications for this connections are made later in the paper (see Sect. 8).

Peridynamics’ success with modeling the fundamental feature of dynamic fracture, namely crack branching, is perhaps the reason for the excellent results obtained with the peridynamic (PD) model in impact on brittle targets problems, see e.g. Bobaru et al. (2012), Hu et al. (2013).

3 Brief Review of the bond-based Peridynamic model

The peridynamic equations of motion at a point $\mathbf {x}$ and time t are (Silling 2000):

$$\begin{aligned} \rho (\mathbf {x}){\ddot{\mathbf {u}}(\mathbf {x},t)}= & {} \int _{H_{\mathbf {x}}}{ \mathbf {f}( \mathbf {u}( \hat{\mathbf {x}},t ) - \mathbf {u}( \mathbf {x},t), \hat{\mathbf {x}}- \mathbf {x}) \, \mathrm {d} V_{\hat{\mathbf {x}}} }\nonumber \\&+\, \mathbf {b}(\mathbf {x},t) \,\,\, \text{ for } \,\,\, \mathbf {x}\in \varOmega \,\,\, \text{ and } \,\,\, t\in [t_0,\infty )\nonumber \\ \end{aligned}$$

(1)

where $\varOmega$ is the domain occupied by the body, $t_0$ is some initial time, $\mathbf {u}$ is the displacement vector field, $\mathbf {b}$ is the body force vector, and $\mathbf {f}$ is the pairwise force function in the peridynamic bond that connects material points $\mathbf {x}$ and $\hat{\mathbf {x}}$. The integral is defined over a region $H_{\mathbf {x}}$ called the horizon region, or simply the horizon. It is natural to consider the horizon as a small sphere (disk in 2D, interval in 1D) centered at the current point. We will call the radius of the sphere $\delta$ and refer to it also as the horizon. From the context it will always be clear whether we refer to the region or its radius when we mention the word “horizon”. A discussion on the meaning, selection, and use of the peridynamic horizon and its relation to crack branching in brittle materials has appeared in Bobaru and Hu (2012).

For a microelastic material Silling (2000), a pairwise potential exists such that

$$\begin{aligned} \mathbf {f}(\varvec{\xi }, \varvec{\eta }) = \frac{\partial \omega ( \varvec{\xi } , \varvec{\eta })}{ \partial \varvec{\eta } }, \end{aligned}$$

(2)

where $\varvec{\xi } = \hat{\mathbf {x}}- \mathbf {x}$ is the relative position and $\varvec{\eta } = \mathbf {u}( \hat{\mathbf {x}},t ) - \mathbf {u}( \mathbf {x},t )$ is the relative displacement between points $\hat{\mathbf {x}}$ and $\mathbf {x}$. A linear microelastic material is defined by a micropotential $\omega$ as:

$$\begin{aligned} \partial \omega ( \varvec{\eta },\varvec{\xi } ) = \frac{ c( \varvec{\xi }) s^{2} \Vert \varvec{\xi } \Vert }{2}, \end{aligned}$$

(3)

where the $c( \varvec{\xi })$ is the micromodulus function and

$$\begin{aligned} s = \frac{ \Vert \varvec{\eta } + \varvec{\xi } \Vert -\Vert \varvec{\xi } \Vert }{\Vert \varvec{\xi } \Vert } \end{aligned}$$

(4)

is the relative elongation of the bond connecting $\hat{\mathbf {x}}$ and $\mathbf {x}$. For a horizon region with spherical symmetry, the corresponding pairwise force becomes:

$$\begin{aligned} \mathbf {f}(\varvec{\xi },\varvec{\eta }) = \left\{ \begin{array}{l@{\quad }r} \frac{ \varvec{\eta } + \varvec{\xi } }{\Vert \varvec{\eta } + \varvec{\xi } \Vert }c(\xi ) s , &{} \Vert \varvec{\xi } \Vert \le \delta \\ \varvec{0}, &{} \Vert \varvec{\xi } \Vert > \delta \end{array} \right. \end{aligned}$$

(5)

Fig. 1

The conical micromodulus function

Assuming a specific form of the isotropic micromodulus function $c(\varvec{\xi }) = c(\Vert \varvec{\xi } \Vert )$, for example constant over the horizon region or varying linearly with $\Vert \varvec{\xi } \Vert$ (see Fig. 1), one finds the parameters in these representations by calibrating the strain energy density computed with peridynamics to the classical strain energy density for a homogeneous deformation, such as equal bi-axial strain. The calibration is made for a point in the bulk, at least a distance $\delta$ away from the boundaries so that the node has a complete horizon region. Material points close to or on the boundaries of domain $\varOmega$ have horizon regions that are partial disks. If one performs the calibration for these points, the resulting micromodulus value for the bonds connected to such points will be higher than that obtained for the points in the bulk, since the integration area/volume is smaller here. When this special calibration for points within a distance $\delta$ from a boundary is not employed, and the bond stiffness for points near the boundary is assigned to be the same as that for nodes in the bulk, the effective material behavior near the boundaries is slightly softer than in the bulk. As the horizon $\delta$ decrease to zero, the thickness of this softer zone decreases and becomes negligible. More on this “skin effect” is discussed in Ha and Bobaru (2011a). To reduce, or in some cases eliminate, the surface effect, for any horizon size, several options have been proposed in the literature:

• introduce ghost nodes (Gerstle et al. 2005) [also called fictitious nodes, see Oterkus et al. (2014)] outside of the domain. This approach may become cumbersome for bodies with complex geometries.

• compute approximate corrections of the micromoduli for nodes on or near the surface (see, for example, Macek and Silling 2007, and section 4.2 in Madenci and Oterkus 2014). These approaches are exact only for regular boundaries and homogeneous deformations.

A detailed discussion and comparison of the performance of surface-correction methods is given in Le and Bobaru (2015).

In anisotropic materials, the micromodulus function $c(\xi )$ is defined by at least two parameters, and various ways to calibrate the models have been proposed (see Xu et al. 2008; Hu et al. 2011, 2012b, 2014; Ghajari et al. 2014; Oterkus and Madenci 2012).

For examples of micromodulus functions in 3D see Silling and Askari (2005), in 2D see Ha and Bobaru (2010), and in 1D see Bobaru et al. (2009). Because of its faster convergence properties to the classical elasticity solutions (as the horizon goes to zero), in this work we use the 2D conical micromodulus (see Fig. 1) with the plane stress assumptions (since all of the computational tests are done, as in experiments, on thin plates):

$$\begin{aligned} c( \varvec{\xi } ) =C_{1} \left( 1- \frac{\Vert \varvec{\xi } \Vert }{ \delta } \right) =\frac{ 24E }{\pi \delta ^{3}(1-\nu )} \left( 1- \frac{\Vert \varvec{\xi } \Vert }{ \delta } \right) \end{aligned}$$

(6)

where E is Young’s modulus and $\nu$ is the Poisson ratio (fixed to 1/3 in this 2D plane stress case).

To introduce damage, a law for peridynamic bond-failure has to be established. In PD, bonds can break irreversibly (see Silling and Bobaru 2005), or reversibly (see Bobaru 2007) when they are meant to represent Van der Waals-like interactions, for example. Here we assume irreversibility of bond breaking:

$$\begin{aligned}&f (\varvec{\xi },\varvec{\eta }, \mathbf {x}, t)\nonumber \\&\quad = {\left\{ \begin{array}{ll} f(\varvec{\xi },\varvec{\eta }, \mathbf {x}) &{} \text {if } s(\varvec{\xi },\mathbf {x},\tilde{ t})<s_0, \text { for all } 0\le \tilde{t} \le t,\\ 0 &{} \text {otherwise} \end{array}\right. }\nonumber \\ \end{aligned}$$

(7)

where $s_0$ is the critical value of bond relative elongation for breakage. When a bond reaches this critical value, the break is irreversible and the bond no longer sustains a force. This critical value, which could be made to depend on the bond length $\xi = \Vert \varvec{\xi } \Vert$ or on the state of local damage (see Ha and Bobaru 2011a), for example, is defined by matching the fracture energy $G_{0}$ of the material to the energy required by the peridynamic model at a point in the bulk to completely separate a body in two at that point with a fracture surface. This separation requires breaking all bonds that initially connected points on opposite sides of the fracture surface. The value for $s_0$ in 3D is given in Silling and Askari (2005). In 2D, the connection between the critical relative elongation and the material fracture energy is given by (see, e.g. Ha and Bobaru 2010):

$$\begin{aligned} G_{0}=2 \int _0^\delta \int _z^\delta \int _0^{cos^{-1}(z/\xi )} \left[ \frac{cs_{0}^{2}}{2}\right] \xi \, \mathrm {d}\theta \, \mathrm {d}\xi \, \mathrm {d} z \end{aligned}$$

(8)

For the conical micromodulus functions, the critical relative elongation is obtained as:

$$\begin{aligned} s_{0}=\sqrt{ \frac{5\pi G_{0} }{ 9E\delta } }. \end{aligned}$$

(9)

Similar to the “skin effect” discussed above for the computation of the micromodulus function, the critical relative elongation $s_{0}$ value is affected near the boundary of the domain, or in a region where damage is already present. This happens because the above calculation is based on points in the bulk. For points on or near the boundary, the domain of integration is smaller, and when matched to the same $G_0$ value, the resulting critical relative elongation would be higher than in the bulk. Therefore, when a constant $s_0$, computed for a point in the bulk, is used in computations, the peridynamic material model will effectively have slightly weaker bonds for points near the surface than for those in the bulk. The same happens in regions where damage is present, such as on the surface of a propagating crack. As the horizon goes to zero, the weaker “skin” region goes to zero and the effect is minimized. Some attempts to correct this for regions where damage is present have been implemented in the code EMU (Silling 2003) and showed better results in fragmentation problems. The correction, also discussed and used in Ha and Bobaru (2011a), consists in increasing, in an approximate way, the value of the $s_0$ for points with a certain amount of damage, proportional to the damage amount. This model is referred to as the “damage-dependent peridynamic model”. The constant $s_0$ model is used in the present paper.

4 An accurate and efficient quadrature scheme

With the peridynamic formulation introduced in the previous section, we are ready to compute solutions to dynamic fracture problems. Here we will only briefly review on such possible discretization. In principle, the peridynamic equations can be discretized using the finite element method, or any other method appropriate to compute solutions to integro-differential equations. This approach, however, soon hits well-known obstacles and difficulties for problems with evolving topologies, like those in dynamic fracture and fragmentation. Instead, meshfree-types discretizations are preferred in peridynamics simulations of dynamic failure of materials. The discretization proposed in Silling and Askari (2005) uses the mid-point integration scheme (equivalent to a one-point Gaussian integration) for the domain integral.

$$\begin{aligned}&\int _{H_{\mathbf {x}}}{ \mathbf {f}( \mathbf {u}( \hat{\mathbf {x}},t ) - \mathbf {u}( \mathbf {x},t), \hat{\mathbf {x}}- \mathbf {x}) \, \mathrm {d} V_{\hat{\mathbf {x}}} } \nonumber \\&\quad \simeq \sum _{j\in \mathrm {Fam}(i)} c(\xi _{ij}) s_{ij} V_{ij} \end{aligned}$$

(10)

where Fam(i) is the family of nodes j with their area (volume) covered, fully or partially, by the horizon region of nodes i, $\xi _{ij}$ is the bond length between nodes i and j, $s_{ij}$ is the relative elongation for the same bond, and $V_{ij}$ is the area (volume) of node j estimated to be covered by the horizon of node i.

Simple and regular discretization grids are preferable for many reasons and such grids will be used here. When nonuniform grids are used with this type of meshfree discretization approach, special care needs to be taken (see, e.g., Bobaru and Ha 2011). Here, we give a simple algorithm for the numerical integration of the domain integral in Eq. (1), first introduced in Hu et al. (2010) and also shown in Bobaru and Ha (2011) (where the “$-$” sign on line 7 should be a “$+$” sign). The main advantage of this algorithm compared with one that simply checks whether a node is inside (in which case it adds the contribution to the integral as if its entire volume is inside the horizon) or outside the horizon region (in which case it does not add any contribution to the integral, as if its entire volume is outside the horizon) is that as the ratio $m={\delta }/{\varDelta x}$ increases (for a fixed horizon value), the numerical convergence (in terms of strain energy density, for example) is monotonic (Hu et al. 2010).

In the one-point Gauss quadrature method, each node has a certain volume (area in 2D, length in 1D) associated with it. Figure 2a shows nodes covered by horizon $\delta$ of node $\mathbf {p}$. The square indicates the area of an arbitrary node $\mathbf {q}$. The area of the horizon region used in the spatial integration of the peridynamic equations is composed of the nodal areas that are covered, fully or partially, by the horizon region (see Fig. 2b).

Fig. 2

a One-point Gauss quadrature for the spatial integration of the Peridynamic equations; b exact areas of various nodes that participate in the quadrature for node $\mathbf {p}$.

In Hu et al. (2010) several different algorithms have been proposed and tested for approximating the exact nodal areas covered by the horizon. Algorithm 1 adjusts the areas for nodes that are partially covered by the horizon by a certain factor. Note that with this algorithm, the search for the family of nodes needs to consider points that are outside of the horizon, up to a distance $\delta + \varDelta x/2$. This algorithm gives results which do not fluctuate much with respect to variations in $m=\delta /\varDelta x$. Note that when the node’s location is exactly $\delta$ away from the current node, about half of its area is covered by the horizon region, and the algorithm uses half the node’s area.

In computing the quantities in Eq. (10) for the case in which the micromodulus function c depends on the bond length, some adjustments are useful to increase the accuracy of the mid-point quadrature scheme. We distinguish three cases for nodes in the family of nodes of some current node i, shown in Algorithm  2: a node’s area is fully covered by the horizon, the node is inside the horizon but not all of its area is covered, the node is outside the horizon but has some of its area covered by the horizon. For each case, we compute the micromodulus at the node’s actual location or at a slightly modified one (see Algorithm 2).

This algorithm, for the conical micromodulus, produces a close-to-monotonous convergence to the exact classical value in terms of strain energy density for a homogeneous deformation as m increases (see Hu et al. 2010). We note that Seleson (2014) proposed an algorithm based on analytical calculation of the covered areas to perform the numerical spatial integration. This algorithm shows asymptotically monotonic convergence and also demonstrates slight improvements compared with the one shown in Algorithm 2. However, this more “exact” algorithm may be more expensive to use than other approximating algorithms, like Algorithm  2 introduced in Hu et al. (2010).

5 Peridynamic results for dynamic fracture and crack branching

To obtain a more complete understanding of how crack branching is generated and of the factors that influence it, we perform a series of peridynamic computational tests that consider:

• 1. two different material systems, to observe the influence of Young’s modulus, density, and fracture energy on dynamic crack propagation and branching;

• 2. three different loading types, to investigate the role of stress waves interactions with the tip of the advancing crack;

• 3. two different geometries, to analyze how reflected stress waves from the boundaries affect the branching process.

Stress waves have a strong influence on dynamic crack propagation (see e.g. Ravi-Chandar and Knauss 1984b; Ravi-Chandar 2004). Our focus in the computations below is to investigate how stress waves control crack branching. We utilize two material systems, soda–lime glass and homalite, for which substantial experimental results are available in the published literature (e.g. Bowden et al. 1967; Field 1971; Döll 1975; Ramulu and Kobayashi 1985; Ravi-Chandar and Knauss 1984b; Ravi-Chandar 2004). Homalite is a material representative of many other glassy polymers, like PMMA or polycarbonate, on which experimental results have appeared in, for example, Sharon and Fineberg (1996), Bonamy and Ravi-Chandar (2003). One reason more recent experiments have used glassy polymers instead of glass for studies on dynamic brittle fracture is the reduced wave speed (and therefore slower crack propagation speeds) in these materials due to their lower elastic modulus. This allows experimentalists to record the fracture events easier than in the case of glass.

Different loading conditions have been used in experiments on crack branching. A dynamic loading on the boundaries of the sample has been used in Ramulu and Kobayashi (1985), while in Ravi-Chandar (2004), in order to avoid the interaction between the propagating crack and waves reflected from the boundaries of the sample, a sudden loading was applied to the crack surfaces themselves to induce crack propagation and eventual crack branching. The simplest, from the point of view of experimental setup is one of quasi-static loading of samples with sharper or blunter notches used in Bowden et al. (1967). The crack propagates without branching from the sharp notch, but can branch once or multiple times from the blunt notch because of the much higher stress intensity factor reached before propagation. The first two types of loading conditions may, however, be preferred since they do not require changing the sample geometry (the bluntness of the crack tip) as the quasi-static loading conditions do in order to observe cases in which the crack propagates straight and does not branch, and cases when the crack branches. In these types of loading, branching or no branching is produced by higher or lower amplitude applied loadings. We implement three types of loading conditions for a pre-notched sample as follows:

• Load case 1: apply, suddenly, stresses on upper and lower boundaries of the sample (Fig. 3b),

• Load case 2: apply stresses on pre-crack surfaces (Fig. 3c); and

• Load case 3: apply velocity boundary conditions as in Fig. 3d and initial velocity conditions as in Fig. 3e to prevent a strong shock and its reflection from the boundaries. This mimics, to some extent, the quasi-static loading conditions.

We remark that for some quasi-static loading conditions used in experiments, a corresponding explicit-type simulation would be very costly, and solutions for this type of loading require a combination between an implicit solver (up to the point crack growth initiates) and an explicit solver (for the dynamic crack propagation phase). We note that cracks under quasi-static loading can run dynamically, and can branch. On the other hand, quasi-statically growing cracks cannot branch in an isotropic and homogeneous material. Quasi-statically growing cracks do branch in materials with microstructure, as is the case for fatigue-crack growth in materials in which cracks split when encountering tougher inclusions.

Fig. 3

a Sample geometry; three loading conditions: stresses suddenly applied on top and bottom boundaries (b), stress applied on crack surfaces (c), and velocity conditions including (d). In (e) the initial conditions for the case shown in (d)

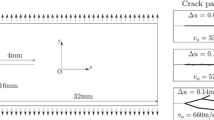
Geometry also has an effect on the crack branching problem since the brittle fracture process is influenced/controlled by stress waves, and wave reflections from the sample’s boundaries, for example, will differ for different geometries. We will consider two sample geometries: one with twice the width but same length as the other. To remove the influence of asymmetries induced rounding errors, we place the coordinate system at the centroid of each sample (see Fig. 3a).

We perform convergence studies for each loading case and material type to justify the selection for the peridynamic horizon size. The aim is to get a crack propagation speed that no longer changes when we change the horizon size. This means that we anticipate that there are no constant material length-scales (induced by the microstructure) that manifest themselves in this problem. This does not preclude existence of length-scales induced by the dynamics of the problem. The meaning of the horizon as a material length-scale is commented in Bobaru and Hu (2012). In peridynamics, one can consider three types of convergence, as introduced in Bobaru et al. (2009). The $\delta$-convergence, which holds the ratio $m={\delta }/{\varDelta x}$ fixed and decreases the magnitude of the horizon, the m-convergence, in which the spatial integration accuracy is increased (for a fixed horizon size), and the combined $\delta -m$ convergence. For a discussion on the form of the kernel under the integral in Eq. (1) that leads, for the 1-point Gaussian quadrature, to a consistent scheme, please see Chen and Bobaru (2015).

Because the m-convergence for dynamic fracture problems has been discussed before (see, e.g. Ha and Bobaru 2010, 2011a) and a value of a least $m=4$ is suggested for crack path independence on the grid, here we focus on the $\delta$-convergence. We select a horizon size, and using a value of $m=4$ we set the nodal spacing $\varDelta x$ for a uniform grid.

The time step for all computations on soda–lime glass samples is the same, $5\times 10^{-3} \upmu$s, while for homalite samples it is $5\times 10^{-2}\,\upmu$s. These time steps sizes insure stability when used with the finest grids (smallest horizons) used in this work.

5.1 Crack branching in soda–lime glass

A soda–lime glass sample with dimensions 10 cm by 4 cm, is used to investigate the role of loading conditions. The sample has Young’s modulus E = 72 GPa, density $\rho = \text {2440 Kg/m}^3$, Poisson ratio $v = 0.22$ (the corresponding 2D plane stress peridynamic model has a Poisson ratio of 1/3) and energy release rate at crack initiation $G_0$ = 3.8 J/$\text {m}^2$ (see Wiederhorn 1969; Fischer-Cripps and Mustafaev 2000). Note that in references Ha and Bobaru (2010, 2011a), a much larger value for the fracture energy $G_{0}$ was used, namely the measured energy release rate at branching, instead of the fracture energy at crack initiation. The main difference between the results shown here and those from Ha and Bobaru (2010, 2011a) is the amplitude of the loading required to generate propagating and branching cracks. A higher fracture energy value requires a larger amplitude loading being applied. The crack will propagate with roughly the same speed, as the propagation is mostly controlled by elastic properties (wave speeds) of the material under consideration.

Fig. 4

$\delta$-convergence study in glass for the crack propagation speed using $\delta$ = 3, 1.5, 0.8 mm, for a suddenly applied tensile stress on the top and bottom boundaries of magnitude $\sigma$ = 2 MPa. Load is maintained constant in time for the duration of the simulation

Fig. 5

Damage maps in glass under suddenly applied tensile stress on the boundaries with different amplitudes. a Damage at 150 $\upmu$s; $\sigma =0.2$ MPa. b Damage at 43 $\upmu$s; $\sigma =2$ MPa. c Damage at 33 $\upmu$s; $\sigma =4$ MPa

5.1.1 Load case 1: stress on boundaries

To perform the $\delta$-convergence study, we use horizon sizes of 3.0, 1.5, and 0.8 mm. With $m={\delta }/{\varDelta x}$, the resulting discretizations have the following number of nodes, respectively: 7236; 28,670; 100,200. The crack propagation speeds for these three different horizon sizes are shown in Fig. 4. The loading amplitude is $\sigma = 2$ MPa, the crack grows straight for a while and branches at some point. The damage profile for this loading and with a horizon of 1 mm is shown in Fig. 5b. The damage profiles, including the time of initiation of branching (which, for this loading amplitude, happens around 20.5 $\upmu$s), are not sensitive to the horizon size (see also Ha and Bobaru 2010, 2011a).

Fig. 6

Crack propagation speed profiles for glass under stress boundary conditions applied on the boundaries of the sample at different amplitudes. a Applied $\sigma =0.2$ MPa. b Applied $\sigma =2$ MPa. c Applied $\sigma =4$ MPa

To calculate the crack velocity, crack tips are tracked by searching the most advanced (right-most) node with a damage index higher than a given threshold (0.3, for example). For each simulation we store outputs from about 200 time steps, and since total simulation times vary, the data-dump period varies between 0.15 to 0.75 $\upmu s$ for soda–lime glass. Crack speed is calculated at each time of the data dump using forward differences approximation. Data points on crack velocity plots are averaged velocities over a time period (usually 1/10 of total simulation time for that particular test), and the abscissa of a data point on these plots is the final time of this time period. For example, the total simulation time for results shown in Fig. 6a is 150 $\upmu$s; each data point shown represents the average velocity over a time interval of 15 $\upmu$s. We normalize velocities by the Rayleigh wave speed $c_{R}$ of the material. For soda–lime glass, $c_{R} \approx 3102$ m/s based on the following equations (see Rahman and Michelitsch 2006):

$$\begin{aligned} c_{R} \equiv \left( 2-M_{2}^{2}\right) ^2 - 4\sqrt{\left( 1-M_{1}^{2}\right) \left( 1-M_{2}^{2}\right) } = 0 \end{aligned}$$

in which,

$$\begin{aligned} M_{1}=\frac{c_{R}}{c_{1}}, M_{2}=\frac{c_{R}}{c_{2}} \end{aligned}$$

and $c_{1}=\sqrt{(\lambda +2\mu )/\rho }, c_{2}=\sqrt{\mu /\rho }$, where $\lambda$, and $\mu$ are Lame’s constants. The Rayleigh wave speed is the real root of this equation in the interval $(0, c_2)$.

In Fig. 4 and similar ones later on, we draw a vertical line to show the branch initiation moment for each computation. Figure 4 shows that this quantity, the time when branching takes place, is independent of the horizon size. Moreover, the difference between crack propagation speed results obtained with the smallest two horizon sizes is minimal. For this reason, the horizon size used in the remaining computations in this section is 1.0 mm, nodal spacing is $\varDelta x=0.25$ mm, and the total number of nodes 64,160 for the grid of $401\times 160$ nodes.

Damage maps for this type of boundary conditions (tensile stress suddenly applied on the boundaries) are shown in Fig. 5. For a load of amplitude $\sigma = 0.2$ MPa applied, we obtain a straight crack. Larger applied load ($\sigma = 2$ MPa) generates one branching event, while multiple branching events develop under stress of 4 MPa magnitude applied suddenly on the top and bottom boundaries. Continued or cascading branching is one cause of fragmentation [see, for example, Chapter 16 in Meyers (1994)]. If the energy dissipated by the formation of the first branching event is overcome by the energy stored in the material, the branching process repeats, eventually leading to fragmentation.

We also observe that the crack branching angle becomes smaller as the magnitude of the applied stress increases. Figure 6 shows the crack propagation speed profiles, normalized by the Rayleigh wave speed $c_{R}$, for these three different loading amplitudes. Some experimental works show that the crack speed decreases slightly after branching (Döll 1975; Ramulu and Kobayashi 1985), and some of our results confirm these observations. This can be observed when the 4 MPa loading amplitude is used (see Fig. 6). At the same time, other experiments [see Fig. 11.12 on page 211 in Ravi-Chandar (2004)] show that the crack speed stays constant or can slightly increased soon after branching. This situation can also be seen in some of the results obtained with peridynamics. Note that, in general, the computations show a crack propagation velocity magnitude that increases as the applied stress increases.

At branching, the crack propagation speed as a fraction of the Rayleigh wave speed, $V/c_{R}$, is 0.51 for the 2 MPa loading, and 0.55 for the 4 MPa loading amplitude. The maximum crack propagation speed approaches $0.6\,c_{R}$. In experiments, the limiting crack speed in glass, as a fraction of the Rayleigh wave speed, ranges from 0.47 to 0.66, depending on the loading conditions [see Table 11.1 in Ravi-Chandar (2004)]. The location of branching moves closer to the starting location (tip of the pre-notch) when the amplitude of the applied stress increases. This is likely due to the increased stress intensity reached when the crack starts to propagate. In experiments conducted using quasi-static loading of glass slides that have blunter and blunter notches, the same behavior is observed, with the location of branching moving closer to the starting point the blunter the notch, and therefore the higher the stress intensity at which the crack starts to propagate, is (see Bowden et al. 1967).

5.1.2 Load case 2: stress on pre-crack surfaces

Electromagnetic loading of crack surfaces has been used in (see also Ravi-Chandar and Knauss 1982) to generate sharp pulses with a rise to peak amplitude of about 25 $\upmu$s and total duration of about 150 $\upmu$s. Such pulses were able to generate surface pressure waves in the range of 1–20 MPa. Until waves reflected from the edges of the plate return to interact with the crack tip, this type of loading can be considered as taking place in an infinite plate. In this section we apply, suddenly, body forces on the nodes located on the crack surfaces to mimic the stress generated by electromagnetic loading conditions and investigate crack branching. These loads, once applied, are maintained constant throughout the simulation. We apply several loading magnitudes and notice that a loading equivalent to 0.5 MPa generates a straight propagating crack in this material, while a load of 3 MPa or higher leads to branching. For this material and sample size, branching still happens after reflected stress waves interact with the tip of the advancing crack. However, as we shall see in Sect. 5.2.2, for a material in which waves speeds are slower than in glass, e.g. homalite, branching can happen in the absence of interactions between the crack tip and waves reflected from the boundaries of the sample. In order to produce this behavior in a soda–lime glass sample, we would have had to consider a much larger sample, resulting in a much larger computation. Nevertheless, we perform a $\delta$-convergence study for the crack propagation velocity with a loading magnitude of 3 MPa and the results are shown in Fig. 7. The damage maps corresponding to these different horizon sizes are identical, and they are given in Fig. 8b. For the remaining of the results shown in this section, we use a horizon size $\delta = 1$ mm and nodal spacing of 0.25 mm, with a grid of $401\times 160$ nodes.

Fig. 7

$\delta$-Convergence study in glass for the crack propagation speed using $\delta$ = 1.5 and 0.8 mm, with a suddenly applied tensile stress on crack surfaces of magnitude $\sigma$ = 3 MPa. The load is maintained constant in time for the duration of the simulation

Damage maps obtained under different stress levels (0.5, 3, and 6 MPa, respectively) applied on crack surfaces are shown in Fig. 8. The stress waves reflected from the boundaries return and meet the crack tip after about 7.36 $\upmu$s from the moment the loading is applied on the crack surfaces, therefore crack propagation and branching is, in these cases, influenced by reflected stress waves. Continued reflections from the boundaries and reinforcement of stress waves interact with the propagating crack, but branching occurs only when the dynamic conditions around the tip of the advancing crack are favorable it. This point is discussed further in Sect. 7.

Fig. 8

Damage maps for glass under stress on pre-crack surface with different stress amplitudes applied. a Damage at 113 $\upmu$s; $\sigma =0.5$ MPa. b Damage at 35 $\upmu$s; $\sigma =3$ MPa. c Damage at 30 $\upmu$s; $\sigma =6$ MPa

Increasing the loading magnitude further did not cause multiple branching events, but rather created fracture at the corners due to reinforcement of the waves bouncing from the boundaries. We note that under these loading conditions, the crack propagation velocity at branching is $V = 0.40\,c_{R}, 0.44\,c_{R}$ for the 3 and 6 MPa applied stresses, respectively. The maximum crack speed is around $0.6\,c_{R}$, even with the larger loading amplitude. It is interesting to observe the significant change in the crack branching angle between the 3 and 6 MPa loading conditions. These differences are caused by the particular conditions at which the dynamic interaction between the advancing crack tip and the reflected stress waves (longitudinal, shear, and well as the Rayleigh waves propagation on the crack surfaces) takes place (see Fig. 9b, c). Simulation movies that allow us to visualize these interactions are included in the tests on homalite (see Sect. 5.2).

Fig. 9

Crack propagation speed profiles for glass under stress boundary conditions applied on the pre-crack surfaces: a $\sigma$ = 0.5 MPa, b $\sigma$ = 3 MPa, c $\sigma$ = 6 MPa

5.1.3 Load case 3: velocity boundary conditions

In many experiments on crack branching (e.g. Bowden et al. 1967), the sample is slowly loaded. When a critical stress intensity is reached around the crack tip, a pre-crack starts propagating. The sharpness of the pre-notch determines the elastic energy stored before the propagation starts. At higher elastic strain energy, the crack propagates and can branch once or multiple times (see Bowden et al. 1967). Simulating the slow loading is costly with an explicit time-integration model like the one used in this work. A close simulacrum of this type of loading is one in which the sides of the plate are moving away from each other with constant velocity, with the initial velocity at all point in the plate being a linear interpolation of the values imposed on the sides (see Fig. 3d, e). While different from a quasi-static loading, this dynamic loading avoids, however, the strong shocks that the previous two loading cases generate.

We conduct a $\delta$-convergence study in terms of the crack propagation speed for the case when the sides of the plate are moving apart from each other with constant velocity of 0.02 m/s. The results are shown in Fig. 10 and for this loading condition, for the three different horizon sizes used, the crack propagation speed is the same. The damage map is given in Fig. 11a, the crack propagating straight. We notice that the crack initiation time and the overall trend for the crack propagation speed are essentially the same for the three different horizon sizes used, and especially so for the smallest two horizon sizes. Because of this, for the remaining results in this section a horizon size $\delta =1$ mm is used, along with grid spacing $\varDelta x=0.25$ mm.

Fig. 10

$\delta$-convergence in terms of crack propagation speed in glass for velocity boundary conditions with a loading magnitude of $V_{max}$ = 0.02 m/s, using $\delta$ = 3, 1.5, and 0.8 mm

Damage maps presented in Fig. 11 demonstrate that as the intensity of loading increases, one branching event can take place, or a series of branchings followed by crack arrest can develop into a fish-bone like pattern. The reason for this extreme behavior can be understood given the type of loading used in which the top and bottom sides of the plate are forced apart at a constant rate. One can imagine that when one increases the loading rate, the material eventually exhibits multiple failure points and fragmentation in trying to accommodate the intense strain rates. The fish-bone failure patterns have been observed before in brittle fracture (see Sharon et al. 1995). We also observe that, as the loading intensity increases, the location of the initiation of branching or branching attempts moves closer to the location of the pre-crack tip, similar to what is reported from experiments.

Fig. 11

Damage maps in glass under velocity boundary conditions with different velocity amplitudes applied. a Damage at 83 $\upmu$s; applied $V_{max} = 0.02$ m/s. b Damage at 45 $\upmu$s; applied $V_{max} = 0.06$ m/s. c Damage at 24 $\upmu$s; applied $V_{max} = 0.2$ m/s

Fig. 12

Crack propagation speed profiles for velocity boundary conditions: a $V_{max}$ = 0.02 m/s, b $V_{max}$ = 0.06 m/s

Corresponding to the first two plots in Fig. 11, we give the crack propagation velocity in Fig. 12. For the case in which the fish-bone profile is obtained it is difficult to decide which of the micro-cracks to focus on and we did not compute the crack propagation speed. We observe that, unlike in the previous two loading cases, in this imposed displacement conditions case, the crack velocity in the region of branching reaches beyond $0.6 c_{R}$, and even higher soon after branching (see Fig. 11b). Such high crack propagation speeds in glass have been experimentally observed, for example, in Anthony et al. (1970). The crack slows down slightly immediately after branching, but it then quickly recovers as the two branches propagate with even higher velocities than before the branching event. These results confirm the theories (see Ravi-Chandar 2004, p. 214) that state that branching does not happen because the crack propagation speed reaches a certain threshold value, but rather that branching occurs when the strain energy in the region around the crack tip reaches a critical state. A region with “thicker” damage extends over a significant length and can be easily observed to occur before branching (see Fig. 11b). This could be the signature of roughening of the crack surface reported in all experiments to occur before branching (Ramulu and Kobayashi 1985). After branching, the thicker damage zones subside and the distinct branches propagate as “thin” damage zones, indicating that the roughness on the crack surfaces has disappeared. If the strain energy delivered into the crack tips areas of the two branches is sufficiently high, the process repeat itself and a second branching event can ensue. In Fig. 11b we observe this phenomenon just about to happen as the branches approach the boundary of the sample.

These results support the ideas proposed by Ravi-Chandar (see Ravi-Chandar and Knauss 1984a; Ravi-Chandar 2004, p. 214) and based on experimental evidence: “when a crack reaches a critical stage identified macroscopically by its stress intensity factor, it splits into two or more branches, each propagating with the same speed as the parent crack, but with a much reduced process zone”. A more detailed discussion of the meaning of this thickening of damage ahead of the branching point is given in Sect. 7.

5.2 Crack branching in Homalite

With elastic wave speeds and crack propagation speeds being so fast in glasses, a significant number of experiments on brittle fracture have switched to glassy polymers that allow easier observation of the crack branching phenomenon (Ramulu and Kobayashi 1985; Ravi-Chandar 2004). For example, in Ravi-Chandar (2004), a homalite sample is used with loadings on the crack surfaces (loading case 2) in order to observe crack branching without waves that reflect from the boundaries interfering with the tip of the advancing crack. In glass, such an experiment would require a much larger sample size, which is not practical. In this section we use a two-dimensional pre-cracked homalite sample with dimensions of 20 by 40 cm. Homalite has significantly different stiffness, density, and fracture energy compared with soda–lime glass. This investigation will also give us insight into the role and influence material properties have on crack branching.

The homalite’s Young’s modulus is $E=4.55$ GPa, density is $\rho =1230$ $\text {kg/m}^{3}$, fracture energy $G_0=38.46$ $\text {J/m}^{2}$. We perform $\delta$-convergence studies (with a fixed $m=\frac{\delta }{\varDelta x}=4$) for each of the loading cases mentioned before, and once the crack propagation speed shows little changes when using a smaller horizon size, we select that horizon size to compute the rest of the results in this section. The time-step in all of the computations in this section is the same, 0.05 $\upmu$s, which is stable for the finest grid used here.

5.2.1 Load case 1: stress on boundaries

For a tensile stress amplitude of 1 MPa suddenly applied on the top and bottom boundaries of the sample as in Fig. 3b, the crack propagation speed for three different horizon sizes varies as shown in Fig. 13. The crack branches at around 260 $\upmu$s and damage maps are identical (except for the “thickness” of the crack line, see Ha and Bobaru 2011a) for the three different horizon sizes, looking like the one shown in Fig. 14b. Notice that the crack speed profiles are almost identical for $\delta$ = 4.0 and 3.0 mm. For the remainder of the computations in this section the horizon size is 4 mm, and, with a ratio $m=4$, this leads to a grid spacing of 1 mm and a total number of nodes of 80,200 ($401\times 200$ nodes) for the sample dimensions selected above.

Fig. 13

$\delta$-Convergence study in homalite for crack propagation speed using $\delta = 6.0, 4.0,\, \hbox {and}\, 3.0\,\hbox {mm}$ for a suddenly applied tensile stress ($\sigma = 1\,\hbox {MPa}$) on the top and bottom boundaries. Load is maintained constant in time for the duration of the simulation

Using this horizon size and grid spacing, we now perform calculations for the damage index under different loading magnitudes (see Fig. 14). With a loading of 0.2 MPa the crack propagates straight, while at 1 MPa the crack branches after growing straight for a while. With further increase of the loading amplitude, at 2 MPa, for example, there is an attempt of branching that is arrested almost immediately, after which a successful branching takes place, followed by secondary branching. The particular shape of the crack branches, as well as the location of the branching events, are all controlled by the wave interactions with the advancing crack. Given the different elastic wave speeds in homalite compared with those in soda–lime glass, these interactions happen at different times resulting in the observed differences in the shape of cracks (compare Figs. 5, 14).

Fig. 14

Damage maps for homalite under tensile stresses of various amplitudes applied on the top and bottom boundaries. Load is maintained constant in time. a $\sigma = 0.2$ MPa at 1000 $\upmu$s. b $\sigma$ = 1 MPa at 400 $\upmu$s. c $\sigma$ = 2 MPa at 300 $\upmu$s

The crack propagation speed profiles for the lower two loading cases are given in Fig. 15. The profile for the 2 MPa loading case is not provided because the unsuccessful branching attempt can make interpreting the results more difficult. We note that for the 1 MPa loading amplitude, the crack speed at branching is about $0.5\,c_{R}$, in line with experimental observations. The crack advances straight at this speed (or at even slightly higher speed) for a significant length before branching, again confirming results obtained in experiments (see Ramulu and Kobayashi 1985, Ravi-Chandar (2004)).

Simulation movies for crack propagation and branching in homalite for this type of boundary conditions are shown in Movies 1, 2, and 3 (see Supplemental Materials). In these movies, the color indicates the vertical component of the velocity vector, allowing us to observe the propagation of stress waves and their interaction with the advancing crack. In Sect. 7 we offer a more detailed discussion of what the movies demonstrate.

Fig. 15

Crack propagation speed profiles in homalite with tensile stresses of various amplitudes applied on the top and bottom boundaries: a $\sigma$ = 0.2 MPa, b $\sigma$ = 1 MPa

5.2.2 Load case 2: stress on pre-crack surfaces

With loads applied directly on the crack surface, for homalite material and the sample size chosen here it will be possible to observe crack branching without the interaction between the advancing crack and waves reflected from the boundaries.

We first perform a $\delta$-convergence study in terms of crack propagation speed for a loading amplitude that leads to a single branching event. Results are shown in Fig. 16. The damage maps for the three different horizon sizes used is identical (except for the thickness of damage) to the one shown in Fig. 17b. Because differences in crack propagation speed are negligible between the smallest two horizon sizes used, for the rest of the computations performed for this section we use the horizon size $\delta =4$ mm, and with a ratio $m=4$ this leads to a grid spacing of 1 mm and a total number of nodes of 80,200 ($401\times 200$ nodes) for the sample dimensions mentioned at the beginning of Sect. 5.2.

Fig. 16

$\delta$-Convergence study for crack propagation speed in homalite, using $\delta$ = 6, 4, and 3 mm, and loading magnitude of $\sigma$ = 2 MPa applied on the pre-crack surfaces

Fig. 17

Damage maps for homalite under stress applied on pre-crack surface with different amplitudes. a $\sigma = 0.3$ MPa at 975 $\upmu$s. b $\sigma = 2$ MPa at 480 $\upmu$s. c $\sigma = 4$ MPa at 400 $\upmu$s. d $\sigma = 6$ MPa at 105 $\upmu$s. e $\sigma = 8$ MPa at 105 $\upmu$s

The damage maps for several different loading amplitudes are shown in Fig. 17, at the times listed in the figure captions. With the lower 0.3 MPa loading amplitude, the crack propagates straight without branching. From a sudden load of 2MPa (and maintained constant in time) applied on the crack surfaces, the crack branches at around 135 $\upmu$s, which is after the stress waves return and interact with the propagating crack. When the load is increased to 4 MPa, the crack branches at around 124 $\upmu$s (see Fig. 18), which is still after the reflected waves meet the crack, this event happening at around 107 $\upmu$s. We observe an interesting phenomenon: the loading amplitude is higher (4 MPa versus 2 MPa), but the point of branching is further away from the tip of the pre-crack (center of plate). This appears to contradict the results seen in the previous sections in which the branching location moved closer to the pre-crack tip when the loading amplitude was increased. The paradox is explained as follows: with the higher loading amplitude of 4 MPa, the straight crack moves faster and the reflected waves meet the tip further down the path compared with the 2 MPa loading case. In both of these cases, branching happens after the reflected waves interact with the advancing straight crack. In the 4 MPa loading case, subsequent interactions between the initial branches and stress waves result in a number of attempted branching and a successful secondary branching event over a time span of 400 $\upmu$s (see Fig. 17c).

Fig. 18

Crack propagation speed profiles for homalite with stress applied on pre-crack surfaces at various amplitudes. a Applied $\sigma =0.3$ MPa. b Applied $\sigma =2$ MPa. c Applied $\sigma =4$ MPa. d Applied $\sigma =6$ MPa. e Applied $\sigma =8$ MPa

We now verify that the branching point moves closer to the pre-crack tip by applying higher loading amplitudes, as long as branching is not influenced by stress waves coming in from the boundaries (incident or reflected). With a loading amplitudes of 6 and 8 MPa, respectively, we indeed see that branching moves closer to the pre-crack tip (see Fig. 17d, e). In both of these cases the crack reaches sufficient conditions to branch before the waves return from the boundaries at around 72 and 50 $\upmu$s, for the 6 and 8 MPa loading amplitudes, respectively (see Fig. 18). The waves return to meet the crack after more than 100 $\upmu$s.

We have thus confirmed that, as long as the branching mechanism is not influenced by incoming stress waves interacting with the propagating crack, higher loadings lead to branching taking place closer (as well as sooner) to the pre-crack tip location. This is further discussed in Sect. 7. When branching is caused by waves that meet the advancing crack, two things can happen under applying higher loading amplitudes:

• (a) the location of branching moves closer to the pre-crack tip when conditions for branching are not met at the first interaction between the advancing crack and the incoming stress waves: this was the case in all of the loading cases of the glass sample, and loading cases 1 and 3 (see below); or

• (b) the location of branching is farther from the pre-crack tip when conditions for branching are met at the first interaction between the advancing crack and the incoming stress waves: this was the case for the homalite sample and loading case 2, when the loading amplitude was high enough to cause branching but lower than 6 MPa, since at those value or higher, branching happens before incoming waves interfere with the crack.

Obviously, the differences between the glass sample and the homalite sample are only due to the different wave propagation speeds in these materials. Every type of branching behavior that we see in homalite (like the variation of branching location with the amplitude of applied loading mentioned above), we can see in glass as well for an appropriately sized sample geometry.

When compared with the results for soda–lime glass with the same type of loading, is it interesting to see that the patterns are similar when the branching mechanisms is the same between the two types of materials (see Figs. 9b, c,  17b). The damage pattern changes significantly (in homalite, see Fig. 17c) when branching happens before the reflected wave return to meet the advancing crack paths.

The crack propagation speed profiles in homalite are shown in Fig. 18. The crack speed at branching reaches $0.42\,c_{R}$ when reflected waves induce it (see the 2MPa loading case), and approaches $0.55\,c_{R}$ when branching is the direct result of the loading on the crack surfaces(see the 4 MPa, and 8 MPa loading cases).

Simulations of crack propagation and branching in homalite when the loading is applied on the crack faces are shown in Movies 4–8 (see Supplementary Materials), for various amplitudes of loading. As before, the color in these movies indicate the vertical velocity component. The simulations help us understand the reasons crack branching happens, and a detailed discussion is provided in Sect. 7.

5.2.3 Load case 3: velocity boundary conditions

In the dynamic loading type that reduces the shocks compared with the previous two loading cases, the sides of the plate are moving away from each other with constant velocity enforced at the top and bottom boundaries, with the initial velocity at all points in the plate being a linear interpolation of the values imposed on the sides (see Fig. 3d, e). While different from a quasi-static loading, this dynamic loading is the closest one to it. We conduct a $\delta$-convergence study in terms of the crack propagation speed for the case when the sides of the plate are separated by a constant velocity applied of 0.02m/s on each of the top and bottom boundaries. The crack propagation speed for horizon sizes equal to 4 mm and 3 mm are shown in Fig. 19. The damage patterns obtained with both these horizon values is given in Fig. 20b. With a horizon size $\delta$ = 6.0 mm the damage map, for the same loading amplitude, results in a fish-bone pattern, for which is it difficult to decide the crack propagation speed. The results shown justify using the $\delta =4.0$ mm as the horizon size for the remaining computations in this section.

Fig. 19

$\delta$-convergence study for homalite under velocity boundary conditions using $\delta$ = 4.0, 3.0 mm for a loading magnitude of $V_{max}$ = 0.02 m/s

With this horizon size and $m=4$, we test different loading amplitudes that lead to the pre-crack propagating straight (see Fig. 20a), branching once (see Fig. 20b), or splitting into a multitude of microbranches (see Fig. 20c).The results are similar to those seen in glass, with the only difference being that in homalite the applied velocities need to be higher to reach the similar patterns. This can be easily understood based on the differences in stiffness and fracture energy between the two materials.

Fig. 20

Damage maps in homalite under velocity boundary conditions with different velocity amplitudes applied. a Applied $V_{max}$ = 0.06 m/s at 800 $\upmu$s. b Applied $V_{max}$ = 0.2 m/s at 390 $\upmu$s. c Applied $V_{max}$= 1 m/s at 180 $\upmu$s

We notice again the thickening of the damage area just before the branching point. Once branching happens, the process zones are reduced significantly, only for them to start thickening again for a potential secondary branching event. As in the glass sample, once the material is ripped apart with higher intensity, multiple failure points can initiate simultaneously to accommodate the enforced displacements, leading to the familiar fish-bone failure pattern.

The crack speed profiles under the first two loading conditions is given in Fig. 21. For the loading in which the crack branches, the crack speed at branching is around $0.6\,c_{R}$. The slight drop in crack speed immediately after branching reported in experiments is seen here as well.

Fig. 21

Crack propagation speed profiles for homalite under velocity boundary conditions for different applied amplitudes. a Applied $V_{max}=0.06$ m/s. b Applied $V_{max}=0.2$ m/s

Fig. 22

Damage maps for narrow sample of glass under suddenly applied tensile stress on the top and bottom boundaries conditions with different amplitudes. a Damage at 150 $\upmu$s; applied $\sigma = 0.2$ MPa. b Damage at 30 $\upmu$s; applied $\sigma = 2$ MPa. c Damage at 25 $\upmu$s; applied $\sigma = 4$ MPa

The evolution of crack propagation and branching in homalite are contained Movies 9–11, for the different magnitude of applied velocity boundary conditions. The color indicate the vertical velocity component. The results contained in these movies are commented further in Sect. 7.

Fig. 23

Crack propagation speed profiles for glass under sudden tensile stress applied on the boundaries of the narrower sample at different amplitudes. a Applied $\sigma = 0.2$ MPa. b Applied $\sigma = 2$ MPa. c Applied $\sigma = 4$ MPa

5.3 Influence of sample geometry

In this section, the influence of sample geometry is investigated for the soda-line glass material. The model is the same at in Sect. 5.1, except that we now use a narrower geometry with dimensions of 2 cm by 10 cm, instead of $4\times 10$ cm. We monitor the crack paths/patterns, the crack propagation speed, and the angle of branching for the three different types of loadings used before. Calculations are performed using the same horizon size and discretization as in the case of the wider sample: $\delta =1$ mm, $\varDelta x=0.25$ mm.

5.3.1 Load case 1: stress on boundaries

For this loading case (see Fig. 3b), a tensile stress with amplitude $\sigma =0.2$ MPa applied on the top and bottom boundaries leads to a straight propagating crack, while increasing this amplitude to 2 MPa results in one branching happening at 14 $\upmu$s, see Figs. 22b and 23b. This is sooner than what happened in the wider sample case (see Fig. 6b), because stress waves travel shorter distances and return sooner from the boundaries in the narrower sample to create conditions favorable to branching. A similar behavior is seen in case of loading the sample with a 4 MPa stress amplitude (compare Figs. 6c, 23c). The branching path in the 2 MPa loading amplitude is similar between the wide and narrow samples, but for the 4 MPa amplitude, the second branching attempt arrests one of the branches in the narrow sample, whereas in the wider sample both branches propagate. The cracks arrest because of wave interactions with the advancing crack. The crack opening angles are only slightly modified by the narrower geometry, while the crack speeds attained at branching are lower than in the wider sample. This result confirms that the crack propagation speed cannot be a criterion for branching. The more intense wave reinforcement taking place in the narrower sample (because of wave reflections from the boundaries that are closer to one another than in the wider sample) leads to conditions sufficient for branching when the crack speed is in the $0.4\,c_{R}$–$0.5\,c_{R}$ range.

Fig. 24

Damage maps for narrow sample of glass under stress on pre-crack surface with different stress amplitudes applied. a Damage at 150 $\upmu$s; applied $\sigma = 0.2$ MPa. b Damage at 68 $\upmu$s; applied $\sigma = 1$ MPa. c Damage at 39 $\upmu$s; applied $\sigma = 3$ MPa

Fig. 25

Crack propagation speed in narrow sample of glass under tensile stress applied on the pre-crack surfaces at different amplitudes. a Applied $\sigma = 0.2$ MPa. b Applied $\sigma = 1$ MPa. c Applied $\sigma = 3$ MPa

After branching, we observe large variations in the crack propagation speed, likely induced by the elastic energy flow to the crack tip regions transported by the bouncing of stress waves from the boundaries and from the newly created crack surfaces.

The evolution of crack propagation and branching in glass for this geometry are contained Movies 12–14, for the stress amplitudes applied on the outer boundaries. The color scheme used in these movies represents the vertical velocity component. The results contained in these movies are commented further in Sect. 7.

5.3.2 Load case 2: stress on pre-crack surfaces

When load is applied to the crack surfaces (see Fig. 3c) in the glass sample with a narrower profile, branching is again induced by stress waves bouncing back and forth from the boundaries. Compared with the wider sample, this time we need to applied smaller amplitude loads to get the crack to branch, consistent with the fact that wave reinforcement of reflected waves happens more frequently in the narrower sample. To obtain a straight crack, the previously used loading amplitude of 0.5 MPa (see Fig. 8a) needs to be reduced to around 0.2 MPa (see Fig. 24a), otherwise the crack eventually branches. The stress wave influence on the crack opening angle is clearly visible when the loading amplitude is increased to 1 MPa, as the branching angle becomes very wide (see Fig. 24b). Further increasing the loading amplitude to 3 MPa, leads to the branching point moving closer to the pre-crack tip, as expected (see Fig. 24c). With the 6 MPa load amplitude used in the results in Fig. 8c, the narrower sample gets damaged in multiple places near the boundaries, confirming the expectation that more frequent stress waves reflections that are taking place in the smaller sample have an amplifying effect on stress reinforcements that lead to damage.

We observe that in this narrow sample, branching can happen at surprisingly low crack propagation speeds. As seen from Fig. 25b, c, crack propagation speed at branching only reaches around $0.3\,c_{R}$. These results provide further evidence that crack branching is not controlled by the crack propagation speed, but by how strain energy flows around the tip of the propagating crack. It would be interesting to confirm experimentally the possibility of crack branching in glass at such low crack propagation speeds. On different geometries and loading conditions, experimental results obtained from 1938 to 1970 by different authors list the limiting crack speed in glass (just before branching) in the range $0.47\,c_{R}$–$0.66\,c_{R}$ (see Table 11.1 in Ravi-Chandar 2004).

The reasons for the large angles of branching observed in this case of geometry and loading conditions are clarified by investigating crack propagation and branching in simulation Movies 15–17. The color indicate the vertical velocity component and the stress waves interactions explain the particular branching patters. More comments are given in Sect. 7.

Fig. 26

Damage maps for narrow glass sample under velocity boundary conditions with different applied velocity amplitudes. a damage at 56.0 $\upmu$s; $V_{max} = 0.02$ m/s. b Damage at 34.5 $\upmu$s; $V_{max} = 0.06$ m/s. c Damage at 27.0 $\upmu$s; $V_{max} = 0.1$ m/s

Fig. 27

Crack propagation speed in narrow glass sample under velocity boundary conditions applied with different magnitudes. for applied velocity: a $V_{max}$ = 0.02 m/s, b $V_{max}$ = 0.06 m/s

5.3.3 Load case 3: velocity boundary conditions

Applying the displacement-controlled boundary conditions like in Fig. 3d and initial conditions that attenuate a strong shock as in Fig. 3e on the narrower glass sample, we obtain the results shown in Fig. 26. Two of the applied boundary velocities are identical to those in the wider glass sample case and the corresponding damage profiles are similar (compare Fig. 11a with Fig. 26a, and Fig. 11b with Fig. 26b). However, the corresponding crack propagation speeds are different (compare Fig. 27 with Fig. 12), with the crack speed in the narrower sample being faster than in the wider sample. Because of this, when the crack branches once (see Fig. 26b), branching takes place sooner in the narrow sample than in the wider sample. This is because the applied initial acceleration (thus force) is higher in the narrower sample than in the wider sample. For the same reason, using in the narrow sample the 0.2 m/s velocity boundary conditions employed earlier in the wider sample, leads to cracks forming early near the boundaries of the sample. Lowering the loading amplitude to 0.1 m/s results in the fish-bone failure pattern observed in the wider sample loaded at 0.2 m/s (see Figs. 11c, 26c).

Table 1 Crack propagation speed at branching, computed by peridynamics, as a fraction of the Rayleigh wave speed (V/$c_{R}$)

The thicker damage zone is easily noticeable before branching in Fig. 26b. From the same figure, after branching, the crack paths display a reduced process zone that increases again as the cracks advance with the potential of a secondary branching event. Once the loading rate is sufficiently high (see Fig. 26c), a multitude of crack initiation points develop simultaneously in the material as the loading conditions are ripping the system apart. For this case it is not easy to define a crack propagation speed. While both the wide and narrow glass samples under these boundary conditions branch at around $0.6\,c_{R}$, we observe that in the case when the crack does not branch, the crack speed reaches close to $0.7 \, c_{R}$, close to the measurement data provided by Anthony et al. (1970).

With the material being forced to move apart with a constant velocity imposed at its boundaries, the stress wave interactions are considerably different from the load-controlled cases. The simulations contained in Movies 18–20 further explain the observed behavior. The vertical velocity component is used to observe the waves in the system. The enlarged crack-tip process zones near the branching points are very prominent here, and when the loading reaches some extreme values, the only way the material can accommodate the imposed deformations is via creating a multitude of microcracks. More on this issue is discussed in Sect. 7.

6 Discussion of crack branching results

In this section we summarize the results obtained so far in terms of crack propagation speed at branching and the angle of branching. In Table 1 we show values of crack propagation speed, relative to the Rayleigh wave speed, at the moment of branching. The only cases for which the data is not included are the loading case 3 under high strain rates (when fish-bone like damage is obtained) and for the attempted but unsuccessful branching event in Load case 1 in homalite under the higher loading amplitude (see Fig. 14c). The reason for these omissions is that tracking of branches becomes ambiguous when the main crack continues to propagate along with the branches that eventually arrest. The range of speeds at branching compare well with the limiting crack propagation speeds measured in glass and homalite by various experimentalists and summarized in reference Ravi-Chandar (2004) on page 191. For glass, the experimentally measured limiting velocity (that is, before a single crack branches) ranges from $0.47\,c_{R}$ to $0.66\,c_{R}$, while for homalite the reported spread is between $0.33\,c_{R}$ and $0.45\,c_{R}$.

From the crack propagation speed plots for load cases 1 and 2 (like the ones in Fig. 23b) we observe that branching tends to initiate after a peak in speed, likely due to the energy dissipated by the migration of damage away from the crack line (the expansion of the process zone). A slight drop in propagation speed is observed after branching, but soon after that, individual branches tend to recover the propagation speed from before the expansion of the process zone. In contrast, for loading case 3 the crack propagation speed profile is more monotonous, with some smaller variations in the region where the process zone enlarges prior to branching.

Table 2 Crack branching angles (between the symmetry line and a branch) computed by peridynamics, estimated at the branching location from damage maps

It is not surprising that when the narrower geometry sample is used, for load cases 1 and 2 the crack propagation speed at branching is lower than in the wider geometry: this only confirms the fact that stress waves reflected from the boundaries (which are now closer to the crack tip) can significantly alter the crack propagation speed by slowing it down in this case, and speeding it up in other cases, depending on the angle at which they meet with the propagating crack. Interestingly, in load case 3 the effect is opposite: the crack propagates slightly faster in the narrower geometry than in the wider one. That is because the imposed acceleration inside the sample is larger in the narrower sample than in the wider one, if the constant velocity applied on the boundaries is the same.

Fig. 28

Velocity vector plot at: a 5.5 $\upmu$s, b 15.0 $\upmu$s, c 24.5 $\upmu$s, d 31.5 $\upmu$s, e 45.0 $\upmu$s for the loading on crack surface case with 8 MPa loading amplitude. The color of the arrows represents the damage index, with red being 40 % or more damage

Crack branching angles, measured between the symmetry line (the original direction of propagation of the crack before branching) and one of the branches are shown in Table 2. Another name used for these angles is “bifurcation half angles” (see Freund 1990). Some authors refer to the branching angle as the angle between the branches (see e.g. Ravi-Chandar and Knauss 1984b), which is twice the angle we use here. As crack branches propagate and interact with stress waves, their path can change direction and the angle of branching changes. This is why, in producing the data in Table 2, we use the damage maps close to the branching point. We observe that in the majority of tests presented here, the crack branching angles are between $15^{\circ }$ and $35^{\circ }$. The only cases when the branching angle is around $60^{\circ }$ is when stress waves reflected from the boundaries interact with the advancing crack. This confirms the experimental observations in Ravi-Chandar and Knauss (1984b). We note that smallest branching angles are for loading conditions that mimic quasi-static loading, and these angles are similar to those seen from experiments in Bowden et al. (1967). For loading case 2, in which the applied loading magnitude is sufficiently high to produce crack branching before stress waves reflected from the boundaries return to interact with the advancing crack, crack branching angles are in the $30^{\circ }$ to $35^{\circ }$ range (homalite with 6 and 8 MPa loading amplitudes). These cases are equivalent to modeling branching in an unbounded medium. Note that the analytical result provided by the Yoffe solution for a crack of constant length that translates with a constant velocity in an unbounded medium (therefore, no wave reflections from boundaries) gives an angle of branching of $60^{\circ }$ (see Yoffe 1951), almost double the value from our predictions, as well as what is reported from experiments.

7 Why do cracks branch?

The experimental investigations in Bonamy and Ravi-Chandar (2005) and Sharon et al. (2002) discuss the role of crack front waves in dynamic brittle fracture. The peridynamic simulations in this work show that crack surface and crack front waves may be responsible for the “migration” of damage away from the original crack line (roughening of the crack surface) when the dynamic loading conditions are met for this to happen. The reason, as described below, appears to be a pile-up of stress waves traveling on the crack surfaces near the crack tip.

Loading case 2 (sudden loading on the crack surfaces), with an amplitude large enough that produces crack branching before the waves return from the boundaries to interact with the advancing crack, makes things easier to monitor and understand. The scenario we observe from the velocity vector plots (see Movie 22 and Fig. 28) is as follows:

• Phase I: dynamic crack propagation. Material in front of the advancing crack is pulled towards it, and the larger the loading amplitude is, the faster the material moves against the advancing crack.

• Phase II: stress waves “pile-up” against crack tip. Stress waves generated by the propagating crack are emitted and travel into the body and along the crack surface as Rayleigh waves; the Rayleigh waves on the crack surfaces are responsible for the rotation induced in the velocity vectors for nodes on or near these surfaces. When loading amplitude (strain energy flow into the process zone) is sufficiently high, these waves are generated at a faster rate and they “pile-up” against the material in front of the crack tip, which is pulled even stronger against the advancing crack. This causes waves to be reflected/ deflected at an angle, leading to having bonds that are at different orientation than those perpendicular to the crack line to be stretched beyond their critical stretch.

• Phase III: migration of damage and branching. A bonds that are stretched to their maximum are away from the symmetry line, damage (captured by peridynamics via nonlocal bond-breaking) “spreads” into the crack surfaces. This would induce significant crack surface roughening, observed in experiments. With the perturbed stress profile around the crack tip, bonds that, until now, where breaking due to the mode I loading (bonds that crossed the symmetry line and are perpendicular on it) start to relax as the wave pile-up and reflections stretch other bonds beyond their critical limit. The branching phase is completed when two independent crack branches start advancing at an angle from the symmetry line.

We explain this scenario based on interpreting the plots in Fig. 28, which show the velocity vector for nodes near the pre-crack tip under 8 MPa loading applied on the crack surfaces. The reason for using results with this loading amplitude is because the differences between the nodal velocities are more pronounced here and easier to follow. The length of the vectors shown in Fig. 28 are proportional to their corresponding nodal velocity magnitudes. The color of the arrows indicates the damage index: blue arrow means nodes have zero damage, while red means that at least 40 % bonds of the node are broken. In the discrete model, a crack line leads to nodes on its surface to exhibit damage index values approaching but slightly lower than 50 %. Regions of interests are marked by circles, squares, and rectangles. These regions move as the crack propagates. Because of symmetry, we discuss on the nodes on the upper half of the model.

The propagation initiates soon after the sudden loading is applied (shown in Fig. 28a) and round wave fronts (see square region) are moving away from the crack surface (see also Movie 21). The velocity of nodes ahead of the crack tip (inside the rectangular region) is opposite the crack propagation direction, so material ahead of the crack tip moves towards or against the propagating crack. A small vortex (inside circular region) with close-to-zero material points velocity exists between the two regions mentioned above, as a transition zone.

As the crack propagates (see Fig. 28b, c), the regions mentioned above change location attempting to reach a steady-state. The nodes directly in front of the propagating line move faster against it. As bonds break, waves are emitted from them and of particular interest are crack surface waves identified by the spinning of the velocity vectors’ direction. We recall that Rayleigh waves induce elliptical motion of material points near a surface. In the early stages of crack propagation, nodes which have 40 % damage are observed only on the closest rows to the symmetry line. The pile-up of surface waves against the crack tip and the reflections induced by their interaction with the material ahead of the crack tip which moves against, leads to having a few rows of nodes away from the symmetry line have that type of damage levels (see Fig. 28d). This is the beginning of damage migration or thickening of the process zone. A similar “spread of damage” has been identified by Johnson (1992) using the cell model for damage.

If the strain energy levels are not too large, a steady-state settles in and the crack propagates straight, without branching. When, however, the flow of strain energy is too high, the waves created by the fracturing (breaking of bonds) process reach higher amplitudes and their pile-up near the crack tip leads to bonds along directions other than those perpendicular to the original crack line being stretched beyond their critical level. This makes nodes in the elliptical region in Fig. 28e to start having damage index higher than those on the same “column” and lying on the symmetry line. Once this happens, material along the symmetry line relaxes, and the branching of the crack process is complete, as the two branches continue to grow (see also Movie 22).

Fig. 29

Vertical component of nodal velocity in homalite sample under 0.3 MPa stress applied on pre-crack surfaces: a waves created by the applied load approach the boundaries, b after several reflections and wave reinforcements, the crack starts propagating, c crack continues to propagate in a straight line without branching

Fig. 30

Vertical component of nodal velocity in homalite sample under 2 MPa stress applied on pre-crack surfaces: a waves propagate towards the boundaries, b crack propagation starts before reflected waves interact with the tip (c) interaction of waves reflected from the boundaries with those produced by the crack propagation process leads to crack branching.

Fig. 31

Vertical component of nodal velocity in homalite sample under 6 MPa stress applied on pre-crack surfaces: a waves propagate from pre-crack surface, crack propagation starts almost as soon as the loads are applied, b branching takes place before reflected waves meet the propagating crack, c waves reflected from the sample’s boundaries meet with the two propagating branches and influence their future path growth

The argument that a sufficiently high level of strain energy needs to be flowing into the process zone for crack branching to take place, is based on the following analysis of the results for the loading on the crack surface case with different loading magnitudes. We monitor the vertical component of the nodal velocity for three loading amplitudes: 0.3, 2, and 6 MPa applied suddenly on the crack surfaces (loading case 2). This allows us to see wave interactions and crack propagation clearly. In Figs. 29, 30, and 31, we show snapshot of the crack propagation process (movies containing the entire process are 4, 5, and 7). In these figures, red indicates positive $v_y$-component, blue is negative $v_y$, and green regions have vertical velocities close to zero. In the beginning, waves travel from the pre-crack surface to the boundaries (see Figs. 29a,  30a,  31a). Under the 0.3 MPa applied stress, the crack does not start to propagate until after waves reflect from the boundaries and meet the pre-crack tip twice (see Fig. 29b). In this case, the crack propagates in a straight line, without branching. We observe the wavelets created by the propagation itself, but these are not strong enough to create branching (see Fig. 29c). For the 2 MPa loading amplitude, crack propagation starts before reflected waves return to meet the crack tip (see Fig. 30b). Crack branching, however, takes place only after waves reflected from the boundaries interact with the advancing crack (see Fig. 30c), specifically after these reflected waves bounce off the propagating crack surfaces. To obtain branching without the interference of waves reflected from the boundaries, one has to increase the applied loading amplitude to, for example, 6 MPa or higher. In this case, the crack starts propagating and branching takes place before waves return from the boundaries (see Fig. 31b, c). The wavelets produced by the crack propagation itself are small relative to the large amplitude waves created by the applied loads and a little harder to see now. In the previous cases these were easier to see due to the lower amplitude waves generated by the lower amplitude of applied loading.

We can conclude that two essential factors are needed in dynamic brittle fracture for crack branching:

• (a) a sufficient loading magnitude for crack propagation, and

• (b) pile-up of waves (created by the crack propagation process) in the process zone, or wave reinforcement between waves reflected from the boundaries and those created by the propagating crack.

The certain instability mentioned, in many references before but never fully explained, as being responsible for crack branching, now has a clear explanation. We find that crack branching is not necessarily a three-dimensional phenomenon, as some recent papers have suggested. We see that the dynamic flow of strain energy around the crack tip is responsible for crack branching and that the elastic modulus and the fracture energy (energy release rate) control how waves propagate and how material damage occurs in the sample prior to branching.

Based on observation of simulated results, the macroscopic mechanism of dynamic brittle branching, when there is no interaction between the advancing crack and incoming waves, could be summarized as follows:

• Applied loading on the pre-crack surfaces generates stress waves that travel on the crack surfaces and in the bulk;

• At sufficiently high loading amplitudes, the pre-crack starts propagating;

• When stress intensity is sufficiently high, waves generated by the propagation itself pile-up against the crack-tip region and are deflected away by material just ahead of the crack tip which moves against the direction of crack propagation;

• The resulting wave interactions and reinforcements lead to loading conditions and that create damage away from the crack line (surface), damage migrating into the crack surfaces;

• When the wave pile-up is sufficiently strong, the amount of damage migration becomes sufficiently large most of it happens off of the original direction of the crack, thus the material directly in front of the original crack tip becomes relaxed; at this point crack branching ensues.

We note that the macroscopic mechanism of dynamic brittle branching described here is independent of the particular microscopic conditions of a particular microstructure. Such microscopic mechanisms proposed in the literature (microcracks ahead of the crack tip, or tilting of the stress vector, etc) may exist and can influence the behavior in a given material system, but our results indicate that the larger picture, the macroscopic one described above, is the “driving mechanism” for crack branching.

8 The importance of nonlocal modeling in crack branching

The peridynamic theory is a non-local formulation that extends the classical continuum mechanics formulation by assuming each material point is connected via peridynamics bonds with more than just its nearest neighbors. Damage in peridynamics is defined through keeping track of bond breaks and crack appear/form as a necessary consequence of bond rupture. How does this type of nonlocality affect modeling of crack branching and why is it important for dynamic brittle fracture? We answer these questions in this section.

A peridynamic model of a linear elastic material under homogeneous deformation matches the classical model solution for any horizon size (assuming that the surface effect is taken care of by, for example, fictitious nodes method), and it converges to the classical model in the limit of the horizon size going to zero, for general problems with smooth solutions or with static cracks (see Hu et al. 2012a).

Fig. 32

Two peridynamic models: one with a horizon region with m = 4 shown by the solid circle, and with nearest-node only interactions, with m = 1.45, shown by the dashed-line circle

In problems with dynamic cracks, when the peridynamic discrete model is setup so that bonds are only between a node and its nearest neighbor nodes (small m-ratio), the PD solution (with a sufficiently small horizon size) is similar to what some discretization methods of the classical model produce. In Fig. 32 we show two PD settings: one in which $m=\delta /\varDelta x=1.45$, leading to bonds between the central node with only its nearest neighbors, and the other with $m=4$, used for all of the results presented in this work. The preference is for the second type, as m-convergence results demonstrated in Ha and Bobaru (2010) and Ha and Bobaru (2011a), in order to obtain crack paths that are not influenced by the grid density. Nevertheless, we perform a dynamic fracture test using the model with nearest-neighbor only bonds.

With the sudden tensile loading applied on the top and bottom edges of the homalite sample (load case 1) and a loading magnitude of 3 MPa, we obtain the results shown in Fig. 33 for m = 1.45. For comparison, we also include the results obtained in Rabczuk and Belytschko (2004), that use the “cracking particle model” for discretizing the classical (local) elasticity equations. The results with the PD model with $m=4$ is similar to that shown in Fig. 14c. Here we used the slightly higher loading magnitude because with 2 MPa loading the crack does not branch in the model that uses m = 1.45. In both the cracking particle model and the peridynamic model with n earest- n eighbor- o nly i nteractions (NNOI), a large number of spurious microcracks form, which are not seen in experiments in homalite. The authors of Rabczuk and Belytschko (2004) commented on the presence of these unexpected extra cracks: “This is a rather spurious artefact which is undesirable but we do not know its origin or how to eliminate it at this time”. We have tried velocity loading conditions (load case 3) with our peridynamic model that uses the NNOI and similar spurious cracks are obtained. We also observe spurious cracks in the NNOI peridynamic model for glass.

Fig. 33

Damage maps for load case 1 for a homalite sample under 3 MPa applied loading: a results from the peridynamic model using only nearest-neighbor bonds, and b results from the cracking particle method in Rabczuk and Belytschko (2004)

The main reasons for the formation of spurious cracks in the peridynamic model that uses NNOI is that there are too few directions for bond breaking under a given applied load. The exiting bonds in this model would not likely break for loading that is not perpendicular to them, had we had bonds in all possible directions. With only a small number of different bond-directions available in a NNOI PD model, the crack paths that evolve depart from the real crack path. The strain energy landscape around the crack tip is also significantly different in the NNOI model than in a regular peridynamic model (one that uses a sufficiently large m value). Waves in the NNOI model propagate like in lattice-type models. We note that lattice models are known to produce zones of “forbidden velocities” for crack propagation (see Marder and Gross 1995). Such zones are not observed in experiments (see Ravi-Chandar 2004, pp. 218–220).

The ability of generating damage in arbitrary directions (by the breaking of a bond stretched in a given, but arbitrary direction) is, perhaps, the most important characteristic that allows for the evolution of crack branches from the damage zone (increased process zone) caused by stress waves pile-ups and wave reinforcements of rapidly growing cracks. We recall that the increased process zone was the mechanism postulated by Ravi-Chandar and Knauss (1984a) for crack branching. Methods that are, for example, employing surfaces for describing (and tracking) crack growth will likely fail to correctly capture the crack branching behavior. As we have seen in the previous sections, crack branching does not evolve as a crack surface that suddenly becomes two crack surfaces, but rather as a damage process-zone that widens (mirror-mist-hackles transition) and splits into two damage process-zones that continue to propagate with the narrower profile that the original crack was showing before its thickening prior to branching. This is what is seen in experiments and this is how branching happens in a PD model (which uses a sufficiently large m-ratio).

Remark Several studies (see e.g. Buehler and Gao 2006; Bouchbinder et al. 2010) have proposed the existence of a nonlinear elastic region near the crack tip in order to obtain crack-tip instabilities and branching. While for soft materials, the existence of a hyperelastic region around the crack tip is a reasonable assumption (see Bouchbinder et al. 2010), for stiff, glass-like materials it is not clear that this is true anymore (see Bouchbinder et al. 2014). The results presented here we have shown that the nonlocality introduced by the simplest peridynamic model of a linear micro-elastic brittle material does not require nonlinear elastic behavior near the crack tip to predict crack branching and explain the origin of instabilities that trigger crack branching. In other words, while hyperelastic behavior near the crack tip may be a sufficient condition to produce crack branching, it is not a necessary condition.

9 Conclusions

In this paper we presented some detailed studies of modeling crack branching in dynamic brittle fracture using peridynamics. Without special crack propagation and branching criteria, results show that the peridynamic model is capable of capturing all the details of dynamic crack branching in brittle materials reported in the experimental literature. We were able to propose an explanation for the origin of instabilities that lead to crack branching in brittle materials.

We verified the peridynamic models by comparing crack propagation velocities and crack branching angles with experimental results. The overall trend of speed profiles match the experimental values under similar types of loading conditions. The values obtained from the model for the crack propagation speed at branching ranged between 0.3$c_R$ and 0.66$c_R$ depending on the material (elastic modulus, density, and fracture energy), loading conditions, and sample geometry. A similar range of values is obtained in experiments, with the higher values observed when the loading amplitudes are increased. We revealed how stress waves can trigger crack branching even when the crack propagation speed is relatively low. Stress waves can also modify the crack opening angles. The values we obtained with the peridynamic model are close to those reported in experiments.

We performed convergence studies in terms of the size of the horizon going to zero and chose to use the horizon size under which the crack propagation speed no longer changes significantly when the horizon continues to decrease. From that point of view, the sufficiently small nonlocal region for glass was 1 mm while for homalite was 4 mm. These values are in the same range with the characteristic distance found for crack branching in Ramulu and Kobayashi (1985).

The peridynamic simulations allowed us to uncover a possible mechanism (macroscopic) for crack branching in brittle isotropic and homogeneous materials: under mode-I loading conditions in which waves coming from the boundaries do not interfere with the propagating crack, mixed-mode loading conditions near the crack tip are induced by stress waves (generated by the fracturing process) pile-up around the crack tip due deflection by the material ahead of the crack tip that moves against the direction of propagation of the crack; the wave pile-up leads to “migration” of damage away from the symmetry line, indicating an enlargement of the process zone (possible roughening of the crack surface); when this migration is sufficiently large, material ahead of the crack tip is unloaded, and damage growth no longer happens along the original crack direction, but splits into two separate process zones that continue to propagate with a reduced thickness compared to that just before the branching event. When crack branching is a result of waves traveling towards the propagating crack, the mechanism responsible for branching is wave reinforcement.

We also explained why the peridynamic model is able to capture the crack branching phenomenon correctly. One significant feature of dynamic brittle branching is crack thickening, which is observed as roughing of the crack surface in experiments (the famous mirror-mist-hackle transition). Because the damage model in peridynamics is based on bond breaking, not on crack surface advancement, and since bonds cover virtually every possible direction (as long as the grid is fine relative to the horizon size), we are able to mimic with this model the evolution of the process zone observed by experimentalists in crack branching. The peridynamic model captures the correct amount of energy dissipated via increasing the process zone, reported in experiments to happen just before branching takes place. Without the right amount of energy (determined by the flow of strain energy around the crack tip) dissipated near that critical point, one gets spurious damage paths or the wrong crack propagation speed. In any dynamic simulation, results that follow a “slightly” wrong move, depart further and further from the actual result.

It is noteworthy that the nonlocality introduced by this simplest peridynamic model of a linear micro-elastic brittle material does not require nonlinear elastic behavior near the crack tip to predict crack branching. Such an idea was used in Buehler and Gao (2006) to provide an explanation for crack branching via atomistic modeling. We conclude that, at least to first order, a continuum-level linear elastic model and a capable damage model (the peridynamic model) are the only ingredients necessary to correctly predict crack branching in brittle, homogeneous and isotropic linear elastic materials. The input data for this model (material density, elastic constants, and fracture energy) appears to be the minimal set of input data possible. While more complex models may provide more accurate descriptions of the branching process for particular material types, the principles of crack branching in linear-elastic brittle materials can be reproduced with the proposed peridynamic model. The results answer the question we promised to answer (see Sect. 1), whether quantum or atomistic, or coupled across-scale models are necessary for modeling of the crack branching phenomenon. They are not, as long as the continuum-level model used is one of the type employed here (peridynamic).