1 Introduction

Diffusion processes are ubiquitous in physics, such as heat propagation or flows in porous media encountered in reservoir engineering [1], heat conduction in fusion plasma [2, 3], atmospheric or oceanic flows [4], the radiation hydrodynamics [5]. In some applications, diffusion equation is usually coupled with fluid equations. The meshes are determined by the fluid that can be distorted as time goes on. Accurate and efficient numerical schemes for diffusion equations on distorted meshes are highly desired.

The stationary diffusion equation with tensor diffusion coefficients reads

$$\begin{aligned} \left\{ \begin{array}{ll} -\nabla \cdot (K\nabla u)=f,&{}\text{ in } \, \Omega ,\\ u=u_{\Gamma },&{}\text{ on } \, \partial \Omega , \end{array} \right. \end{aligned}$$
(1)

where \(\Omega \subset R^2\) is the computational domain and \(\partial \Omega \) is the boundary. The solution u(x, y) is the temperature or pressure to be solved. The diffusion tensor K(x, y) is a symmetric positive definite matrix that writes

$$\begin{aligned} K=\left( \begin{array}{ll}K_{11}&{}K_{12}\\ K_{21}&{}K_{22}\end{array}\right) . \end{aligned}$$
(2)

There have been extensive research on developing numerical methods for stationary diffusion equation with tensor diffusion coefficients on general meshes, see reviews in [6,7,8]. Finite volume methods (FVM) are the most popular ones, the most recent FVM are not only stable and accurate for discontinuous and anisotropic diffusion tensors but also satisfying local mass conservation and discrete maximum principle on general distorted meshes [5, 7, 9,10,11,12,13,14,15,16,17]. Different FVM provides different way of constructing numerical fluxes at the cell faces. However, it is not easy to design high order schemes for FVM.

Discontinuous Galerkin methods [18,19,20] and finite element methods [21,22,23,24,25] are developed as well but much less works are available for distorted meshes. The problem of mesh-distortion sensitivity of finite element method, such as bilinear finite element methods on quadrilateral mesh, has been known to researchers for decades [26]. Mesh distortion leads to incorrect results or the interruption of computations. As discussed in [26, 27], various new strategies have been proposed in order to improve the performance and robustness of traditional finite element methods when the meshes are distorted. The authors in [27] claimed that their method possess excellent precision in both regular and severely distorted meshes, even when a quadrilateral element degenerates into triangular or concave quadrangular shapes. That is the meaning of shape-free finite element. However, the analytical understanding of shape-free finite element methods is not clear. In [28] the authors provide the convergence analysis and error estimates for a mixed finite element method on distorted meshes. However, it is assumed that all the cells have comparable sizes, but their configurations may be quite different.

Classical finite difference schemes are only applicable to structured grids and the mimetic finite difference methods (MFDM) pocess excellent robustness in the presence of grid distortions and severe jumps in coefficients [29,30,31,32,33]. In MFDM, it is crucial to find the discrete analog of some differential operators (for example, divergence or gradient) that can preserve some features of the operators at the continuous level. In this paper, we provide a new way of constructing finite difference schemes on distorted meshes. Similar to MFDM, it uses solution properties at the continuous level to bypass the constraints of classical finite difference schemes, but the idea of scheme constructions is different from MFDM.

Tailor finite point method (TFPM) was first proposed by Han, Huang and Kellogg for singular perturbed elliptic Eqs. [34] and has been extended to the non-homogeneous reaction-diffusion, convection-diffusion, convection-diffusion-reaction, neutron transport equations and nonlinear radiation diffusion Eqs. [34,35,36,37,38,39,40,41]. The main idea of TFPM is to firstly approximate the diffusion coefficient near each grid by a constant, then use special solutions that satisfy exactly the diffusion equation with constant coefficients to determine the weights of a finite difference scheme. Since TFPMs make full use of analytical properties of local solutions, it can capture the boundary and interfaces layers with coarse meshes. However, all previous works of TFPM are on regular meshes and in this paper, we extend it to distorted meshes.

The extension is not trivial since the diffusion coefficients are no longer approximated by a constant near each grid, instead, the computational domain are divided into cells and the diffusion coefficients are approximated by piecewise linear functions inside each cell. The key point of the scheme construction is the discretization of the flux across cell edges. The common edge of two adjacent polygonal cells is denoted by \(\Gamma \). The flux continuity on \(\Gamma \) can be written as

$$\begin{aligned} {\mathbf {n}}^+\cdot K^+\nabla u^+={\mathbf {n}}^-\cdot K^-\nabla u^-, \end{aligned}$$

where \(u^\pm \) are localized solutions inside the two cells and \({\mathbf {n}}^{\pm }\) are the out normal direction of \(\Gamma \) for \(u^\pm \). Since \(u^\pm \) are approximated by a linear combination of special solutions, so are \({\mathbf {n}}\cdot K^\pm \nabla u^\pm \). Thus a discrete analog of flux continuity equation can be written down as well, using special solutions.

The main advantages of our proposed approach are that 1) all fluxes are localized, thus is appropriate for discontinuous and anisotropic diffusion tensors; 2) second order convergence with or without material discontinuities for general distorted meshes; 3) It preserves linear solutions for constant diffusion coefficients; 4) easy to code.

The paper is arranged as follows. In Sect. 2, we construct the TFPM on polygonal meshes. Several numerical examples on distorted meshes are presented in Sect. 3 and second order convergence is observed even when there are strong discontinuous diffusion tensors. Finally we conclude with some discussions in Sect. 4. In the appendix, we prove the second order convergence analytically for 1D TFPM. We would like to emphasis that the convergence does not depend on the ratio between the maximum and minimum mesh sizes, while most classical methods require lower bound for this ratio in the convergence proof.

2 The TFPM on General Polygonal Mesh

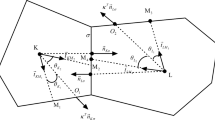
We use stencil as in Fig. 1. \(\Omega _i (i=1,2\cdots ,I)\) are I different polygon and the computational domain \(\Omega =\bigcup _{i=1}^{i=I}\Omega _i\). \({O}_{i}=(x_i,y_i)\) stands for the center of gravity of \(\Omega _i\). The four edges and edge centers of \(\Omega _i\) are respectively denoted by \(\Gamma _{k,i}\) and \(P_{k,i}\), \(k=1,2,3,4\). Assume that the maximum length of \(\Gamma _{k,i}\) (\(k=1,2,3,4\)) is \(h_i\), and \(h=\max \{h_i\}\).

Fig. 1
figure 1

TFPM stencil

Full size image

In the subsequent part, we give details of the scheme construction, in which special solutions are used in each of the cell \(\Omega _i\) and solutions of different cells are pieced together by the continuity of fluxes.

2.1 Approximated Special Solutions

On each \(\Omega _{i}\), we approximate Eq. (1) by

$$\begin{aligned} \left\{ \begin{array}{ll} -\nabla \cdot ({\bar{K}}\nabla {\bar{u}})={\bar{f}},&{}\text{ in } \, \Omega ,\\ {\bar{u}}=u_{\Gamma },&{}\text{ on } \, \partial \Omega , \end{array} \right. \end{aligned}$$
(3)

where

$$\begin{aligned} {\bar{K}}|_{\Omega _i}=A_i(x-x_i)+B_i(y-y_i)+C_i,\qquad {\bar{f}}|_{\Omega _i}=f_i+f_{xi}(x-x_i)+f_{yi}(y-y_i), \end{aligned}$$

with

$$\begin{aligned} A_i=\left( \begin{array}{cc}a_{11,i}&{}a_{12.i}\\ a_{21.i}&{}a_{22,i}\end{array}\right) ,\qquad B_i=\left( \begin{array}{cc}b_{11,i}&{}b_{12,i}\\ b_{21,i}&{}b_{22,i}\end{array}\right) ,\qquad C_i=\left( \begin{array}{cc}c_{11,i}&{}c_{12,i}\\ c_{21,i}&{}c_{22,i}\end{array}\right) , \end{aligned}$$

being constant matrixes, \((x_i,y_i)\) being the gravity center of \(\Omega _i\) and \(f_i\), \(f_{xi}\), \(f_{yi}\) being constants. Here all 12 parameters in \(A_i\), \(B_i\) and \(C_i\) are determined by \(K_i(P_{k,i})\) (\(k=1,2,3,4\)), such that \({\bar{K}}(P_{k,i})=K(P_{k,i})\); The constants \(f_i\), \(f_{xi}\), \(f_{yi}\) are respectively given by \(f(x_i,y_i)\), \(\partial _xf(x_i,y_i)\) and \(\partial _yf(x_i,y_i)\). \({\bar{u}}|_{\Omega _i}\) are pieced together by the continuity of \({\bar{u}}\) and \({\mathbf {n}}\cdot {\bar{K}}\nabla {\bar{u}}\) at cell edges.

From the definitions of \(f_i\) , \(f_{xi}\), \(f_{yi}\), for \(\forall i\in \{1,\cdots , I\}\), when \(f(x,y)|_{\Omega _i}\in C^2(\Omega _i)\),

$$\begin{aligned} f(x,y)|_{\Omega _i}=f(x_i,y_i)+(x-x_i)\partial _xf(x_i,y_i)+(y-y_i)\partial _yf(x_i,y_i)+O(h_i^2)={\bar{f}}_i+O(h_i^2). \end{aligned}$$

Then,

$$\begin{aligned} \begin{aligned} \Vert f-{\bar{f}}\Vert _2^2=\sum _{i=1}^{I}\int _{\Omega _i}(f-{\bar{f}}_i)^2 \, \mathrm{d} x\le \sum _{i=1}^{I} C|\Omega _i| h_i^4\le C|\Omega |h^4. \end{aligned} \end{aligned}$$
(4)

Here \(|\Omega _i|\) and \(|\Omega |\) are the area of \(\Omega _i\) and \(\Omega \). Therefore, \(\Vert f-{\bar{f}}\Vert _2\le C h^2\). Similarly, \(\Vert K-{\bar{K}}\Vert _2<Ch^2\). The difference between u and \({\bar{u}}\) can be given by the following lemma.

Lemma 2.1

Let \({\bar{u}}\in C^1(\Omega )\) and satisfy (3) in each interval \(\Omega _i\). Let \(w=u-{\bar{u}}\), then

$$\begin{aligned} \Vert \nabla w\Vert _2<Ch^2,\quad \quad \Vert w\Vert _2<Ch^2. \end{aligned}$$
(5)

Proof

Since \(w\in C^1(\Omega )\) and \(w|_{\partial \Omega }=u|_{\partial \Omega }-{\bar{u}}|_{\partial \Omega }=u_{\Gamma }-u_{\Gamma }=0\). Multiplying both sides of Eq. (1) by w and integrating over \(\Omega \), noting \(w\in C^1(\Omega )\) and \(w|_{\partial \Omega }=0\), one gets

$$\begin{aligned} \int _\Omega (\nabla w)\cdot K\nabla u d\Omega =\int _\Omega wf d\Omega . \end{aligned}$$
(6)

Similarly, from Eq. (3),

$$\begin{aligned} \int _\Omega (\nabla w)\cdot {\bar{K}}\nabla {\bar{u}} d\Omega =\int _\Omega w{\bar{f}} d\Omega . \end{aligned}$$
(7)

Subtracting (6) from (7), one gets

$$\begin{aligned} \begin{aligned} \int _\Omega (\nabla w)\cdot K\nabla w d\Omega&=- \int _\Omega (\nabla w)\cdot (K-{\bar{K}})\nabla {\bar{u}} d\Omega +\int _\Omega w(f-{\bar{f}}) d\Omega \\&\le \Vert \nabla w\Vert _2\Vert (K-{\bar{K}})\nabla {\bar{u}}\Vert _2+\Vert w\Vert _2 \Vert f-{\bar{f}}\Vert _2, \end{aligned} \end{aligned}$$

where the last inequality is from Holder’s inequality. Since \(w\in C^1(\Omega )\) and \(w|_{\partial \Omega }=0\), from Friedrichs inequality we have \(\Vert w\Vert _2\le C\Vert \nabla w\Vert _2\). Noting that K is positive definite and \(\Vert K-{\bar{K}}\Vert _2<Ch^2\), \(\Vert f-{\bar{f}}\Vert _2<Ch^2\), there exists C that is independent of h and satisfies

$$\begin{aligned} \Vert \nabla w\Vert _2\le Ch^2. \end{aligned}$$

Then Friedrichs inequality gives

$$\begin{aligned} \Vert w\Vert _2\le C\Vert \partial _x w\Vert _2\le Ch^2. \end{aligned}$$

\(\square \)

The key idea of TFPM is to find special solutions inside each cell. However, since \({\bar{K}}|_{\Omega _i}\), \({\bar{f}}|_{\Omega _i}\) are linear functions in x and y, it is not easy to construct functions that satisfy exactly \(-\nabla \cdot ({\bar{K}}\nabla {\bar{u}})|_{\Omega _i}={\bar{f}}|_{\Omega _i}\). We then use some approximations that will not violate the scheme convergence.

Inside \(\Omega _i\), for any function \({\bar{v}}\),

$$\begin{aligned} \begin{aligned} \nabla \cdot ({\bar{K}}\nabla {\bar{v}})=&\big (a_{11,i}\partial _{x}^2 {\bar{v}}+a_{12,i}\partial _{xy}{\bar{v}}+a_{21,i}\partial _{xy}{\bar{v}}+a_{22,i}\partial _{y}^2{\bar{v}}\big )(x-x_i)+ a_{11,i}\partial _x{\bar{v}}+a_{12,i}\partial _y{\bar{v}}\\&+\big (b_{11,i}\partial _{x}^2{\bar{v}}+b_{12,i}\partial _{xy}{\bar{v}}+b_{21,i}\partial _{xy}{\bar{v}}+b_{22,i}\partial _{y}^2{\bar{v}}\big )(y-y_i)+ b_{21,i}\partial _x {\bar{v}}+b_{22,i}\partial _y{\bar{v}}\\&+(c_{11,i}\partial _{x}^2 {\bar{v}}+c_{12,i}\partial _{xy}{\bar{v}}+c_{21,i}\partial _{xy}{\bar{v}}+c_{22,i}\partial _{y}^2 {\bar{v}}) \end{aligned} \end{aligned}$$

We approximate \(\nabla \cdot ({\bar{K}}\nabla {\bar{v}})\mid _{\Omega _i}\) and \({\bar{f}}_i\) by

$$\begin{aligned} \begin{aligned} \nabla \cdot ({\bar{K}}\nabla {\bar{v}})\mid _{\Omega _i}&\approx -r_{1,i} \partial _x^2 {\bar{v}}-r_{2,i} \partial _y^2{\bar{v}}-r_{3,i} \partial _{xy}^2{\bar{v}}-\beta _{1,i} \partial _x{\bar{v}}-\beta _{2,i} \partial _y{\bar{v}},\qquad {\bar{f}}|_{\Omega _i}\approx f_i, \end{aligned} \end{aligned}$$
(8)

where

$$\begin{aligned} r_{1,i}= & {} -c_{11,i},\quad r_{2,i}=-c_{22,i},\quad r_{3,i}=-c_{12,i}-c_{21,i},\\ \beta _{1,i}= & {} -a_{11,i}-b_{21,i}\quad \beta _{2,i}=-a_{12,i}-b_{22,i}. \end{aligned}$$

Here, the terms dropped in Eq. (8) and in \({\bar{f}}|_{\Omega _i}\) are the terms at \(O(h_i)\): \(\big (a_{11,i}\partial _{x}^2 {\bar{v}}+a_{12,i}\partial _{xy}{\bar{v}}+a_{21,i}\partial _{xy}{\bar{v}}+a_{22,i}\partial _{y}^2{\bar{v}}\big )(x-x_i)\), \(\big (b_{11,i}\partial _{x}^2{\bar{v}}+b_{12,i}\partial _{xy}{\bar{v}}+b_{21,i}\partial _{xy}{\bar{v}}+b_{22,i}\partial _{y}^2{\bar{v}}\big )(y-y_i)\), and \(f_{xi}(x-x_i)+f_{yi}(y-y_i)\). Inside \(\Omega _i\), \({\bar{u}}_{h}\) satisfies

$$\begin{aligned} r_{1,i} \partial _x^2{\bar{u}}_h+r_{2,i} \partial _y^2{\bar{u}}_h+r_{3,i} \partial _{xy}^2{\bar{u}}_h+\beta _{1,i} \partial _x {\bar{u}}_h+\beta _{2,i} \partial _y {\bar{u}}_h=f_{i}. \end{aligned}$$
(9)

Then

$$\begin{aligned} \nabla \cdot \big ({\bar{K}}_i\nabla {\bar{u}}_h\big )+{\bar{f}}_i=R.H.S. \end{aligned}$$
(10)

with

$$\begin{aligned} \begin{aligned} R.H.S.=&\big (a_{11}\partial _x^2{\bar{u}}_h+a_{12}\partial _{xy}{\bar{u}}_h+a_{21}\partial _{xy}{\bar{u}}_h+a_{22}\partial _y^2{\bar{u}}_h\big )(x-x_i)\\&+\big (b_{11}\partial _x^2{\bar{u}}_h+b_{12}\partial _{xy}{\bar{u}}_h+b_{21}\partial _{xy}{\bar{u}}_h+b_{22}\partial _y^2{\bar{u}}_h\big )(y-y_i)\\&+f_{xi}(x-x_i)+f_{yi}(y-y_i). \end{aligned} \end{aligned}$$

Since \((x_i,y_i)\) is the center of \(\Omega _i\) such that \(\frac{1}{|\Omega _i|}\int _{\Omega _i}x \, \mathrm{d} x \, \mathrm{d} y=x_i\), \(\frac{1}{|\Omega _i|}\int _{\Omega _i}y \, \mathrm{d} x \, \mathrm{d} y=y_i\), from \({\bar{u}}_h|_{\Omega _i}\in C^\infty (\Omega _i)\), we have

$$\begin{aligned} \int _{\Omega _i}R.H.S. \, \mathrm{d} x \, \mathrm{d} y=O(h_i^4). \end{aligned}$$

We now find special solutions to (9). If \(\beta _{1,i}=\beta _{2,i}=0\), the general solution to Eq. (9) can be written as

$$\begin{aligned} {\bar{u}}_{hi}(x,y)= {\tilde{v}}_i(x,y)+v_i(x,y). \end{aligned}$$
(11)

Let \({\tilde{v}}_i(x,y)=\frac{r_{1,i} (x-x_i)^2+r_{2,i}(y-y_i)^2}{2(r_{1,i}^2+r_{2,i}^2)}f_i\). It is the special solution of Eq. (9) and \(v_i(x,y)\) satisfies the homogenous equation

$$\begin{aligned} r_{1,i}\frac{\partial ^2v_i}{\partial x^2} +r_{2,i}\frac{\partial ^2v_i}{\partial y^2} +r_{3,i}\frac{\partial ^2v_i}{\partial x\partial y}=0. \end{aligned}$$
(12)

Otherwise, when \(\beta _{1,i}^2+\beta _{2,i}^2>0\), the special solution of Eq. (9) becomes \({\tilde{v}}_i(x,y)=\frac{\beta _{1,i} (x-x_i)+\beta _{2,i}(y-y_i)}{(\beta _{1,i}^2+\beta _{2,i}^2)}f_i\) and \(v_i(x,y)\) satisfies the homogenous equation

$$\begin{aligned} r_{1,i}\frac{\partial ^2v_i}{\partial x^2} +r_{2,i}\frac{\partial ^2v_i}{\partial y^2} +r_{3,i}\frac{\partial ^2v_i}{\partial x\partial y} +\beta _{1,i} \frac{\partial v_i}{\partial x}+\beta _{2,i} \frac{\partial v_i}{\partial y}=0. \end{aligned}$$
(13)

We choose 4 linearly independent functions \({W_{k,i}}\) (\(k=1,2,3,4\)) that satisfy the homogeneous equation and approximate \(v(x,y)|_{\Omega _i}\) by a function belonging to the linear space

$$\begin{aligned} \begin{aligned} H_{i}=&\Big \{ \sum _{k=1}^{n}c_{k,i}W_{k,i},\quad c_{k,i}\in {\mathbb {R}} \Big \}. \end{aligned} \end{aligned}$$
(14)

where \(c_{k,i}\) are constant coefficients inside \(\Omega _i\).

In order to find \(W_{k,i}\), suppose \(v_i(x,y)\) is of the special form

$$\begin{aligned} v_i(x,y)=e^{\lambda x+\mu y}. \end{aligned}$$
(15)

Then \(v_i\) of the form as in (15) satisfies (13) when \((\lambda ,\mu )\) is the solution to

$$\begin{aligned} r_{1,i}\lambda ^2+r_{2,i}\mu ^2+r_{3,i}\lambda \mu +\beta _{1,i}\lambda +\beta _{2,i}\mu =0. \end{aligned}$$
(16)

We choose \((\lambda ,\mu )=\) \((-\frac{\beta _{1,i}}{r_{1,i}},0)\), \((0, -\frac{\beta _{2,i}}{r_{2,i}})\). Next, we find solution of the form

$$\begin{aligned} v_i(x,y)=(a_{0,i} x+b_{0,i} y)e^{\lambda x+\mu y}. \end{aligned}$$
(17)

Substituting the above form into (13) yields

$$\begin{aligned} a_{0,i}=-(2 r_{2,i}\mu +r_{3,i}\lambda +{\beta _{2,i}}), \quad b_{0,i}=(2 r_{1,i}\lambda +r_{3,i}\mu +{\beta _{1,i}}). \end{aligned}$$

Therefore, we choose \(W_{k,i}\) are of the following form:

Case 1 \(\beta _{1,i}^2+\beta _{2,i}^2=0\):

$$\begin{aligned} \begin{array}{l} W_{1,i}(x,y)=1,\quad W_{2,i}(x,y)=x,\quad W_{3,i}(x,y)=y,\quad W_{4,i}(x,y)= r_{2,i}x^2-r_{1,i}y^2. \end{array} \end{aligned}$$
(18)

Case 2 \(\beta _{1,i}^2+\beta _{2,i}^2\ne 0\):

$$\begin{aligned} W_{1,i}(x,y)= & {} e^{-\frac{\beta _{1,i}}{r_{1,i}}x},\quad W_{2,i}(x,y)= e^{-\frac{\beta _{2,i}}{r_{2,i}}y}, \nonumber \\ W_{3,i}(x,y)= & {} \left( \left( \frac{r_{3,i}\beta _{1,i}}{r_{1,i}}-{\beta _{2,i}}\right) x-{\beta _{1,i}}y\right) e^{-\frac{\beta _{1,i}}{r_{1,i}}x},\nonumber \\ W_{4,i}(x,y)= & {} \left( {\beta _{2,i}}x+\left( \frac{-r_{3,i}\beta _{2,i}}{r_{2,i}} +{\beta _{1,i}}\right) y\right) e^{-\frac{\beta _{2,i}}{r_{2,i}}y}. \end{aligned}$$
(19)

If \(\beta _{1,i}\rightarrow 0\), \(\beta _{2,i}\ne 0\), then \(W_{1,i}(x,y)\rightarrow 1\), \(W_{3,i}(x,y)\rightarrow -\beta _{2,i} x\). If \(\beta _{2,i}\rightarrow 0\), \(\beta _{1,i}\ne 0\), then \(W_{2,i}(x,y)\rightarrow 1\), \(W_{4,i}(x,y)\rightarrow \beta _{1,i} y\). \({W_{k,i}}\) in (19) are independent functions.

2.2 Construction of TFPM

As discussed in sect. 2.1, the solution to (3) inside each cell \(\Omega _i\) is approximated by

$$\begin{aligned} {\bar{u}}_i(x,y)\approx \sum _{k=1}^{4}c_{k,i}W_{k,i}+{{\tilde{v}}}_{i} \end{aligned}$$
(20)

and the derivatives of \(v_i\) can be obtained analytically such that

$$\begin{aligned} \partial _x {\bar{u}}_i(x,y)\approx \sum _{k=1}^{4}c_{k,i}\partial _x W_{k,i}+\partial _x {{\tilde{v}}}_{i},\qquad \partial _y {\bar{u}}_i(x,y)\approx \sum _{k=1}^{4}c_{k,i}\partial _y W_{k,i}+\partial _y {{\tilde{v}}}_{i}. \end{aligned}$$
(21)

We construct the TFPM by the continuity of fluxes in two adjacent cells. For all cells, denote

$$\begin{aligned} {\bar{u}}|_{\Omega _i}={\bar{u}}_i,\qquad {\bar{K}}|_{\Omega _{i}}={\bar{K}}_{i}. \end{aligned}$$

Assume that \(\Omega _i\) and \(\Omega _{i+1}\) are two adjacent cells and their common edge is \(\Gamma _{1,i}\), then the continuity of \({\bar{u}}\) and \({\mathbf {n}}\cdot {\bar{K}}\nabla {\bar{u}}\) on \(\Gamma _{1,i}\) write

$$\begin{aligned} \left\{ \begin{array}{l} {\bar{u}}_i(x,y)|_{\Gamma _{1,i}}={\bar{u}}_{i+1}(x,y)|_{\Gamma _{1,i}},\\ \\ {\mathbf {n}}_{1,i}\cdot {\bar{K}}_i(x,y) \nabla {\bar{u}}_i(x,y)|_{\Gamma _{1,i}}=-{\mathbf {n}}_{1,i+1}\cdot {\bar{K}}_{i+1}(x,y) \nabla {\bar{u}}_{i+1}(x,y)|_{\Gamma _{1,i}}, \end{array} \right. \end{aligned}$$
(22)

where \({\mathbf {n}}_{1,i}\) (\({\mathbf {n}}_{1,i+1}\)) is out normal direction of \(\Omega _i\) (\(\Omega _{i+1}\)) perpendicular to \(\Gamma _{1,i}\). When \({\bar{u}}_i(x,y)\), \(\partial _x{\bar{u}}_i(x,y)\) and \(\partial _y{\bar{u}}_i(x,y)\) are respectively approximated by \({\bar{v}}_i(x,y)\), \(\partial _x{\bar{v}}_i(x,y)\) and \(\partial _y{\bar{v}}_i(x,y)\) as in (20), (21), the continuity Eq. (22) can no longer be satisfied at all points on \(\Gamma _{1,i}\). Since there exist only a finite number of basis, the solution and fluxes can only be continuous at a finite number of points on \(\Gamma _{1,i}\). Therefore, we piece together \({\bar{v}}_i\) and \({\bar{v}}_{i+1}\) at the center of \(\Gamma _{1,i}\). As in Fig. 1, the middle point of \(\Gamma _{1,i}\) is \(P_{1,i}\) whose coordinates are \((x_{1,i},y_{1,i})\), the continuity conditions at \(P_{1,i}\) write:

$$\begin{aligned} \sum _{k=1}^{4}c_{k,i}W_{k,i}(x_{1,i},y_{1,i})+{\tilde{v}}_{i}= & {} \sum _{k=1}^{4}c_{k,i+1}W_{k,i+1}(x_{1,i},y_{1,i})+{\tilde{v}}_{i+1} \end{aligned}$$
(23a)
$$\begin{aligned}&{\mathbf {n}}_{1,i}\cdot \Big ({\bar{K}}_{i}(\sum _{k=1}^{4}c_{k,i}\nabla W_{k,i}+\nabla {\tilde{v}}_{i})\Big )(x_{1,i},y_{1,i})\nonumber \\&\quad ={\mathbf {n}}_{1,i}\cdot \Big ({\bar{K}}_{i+1}(\sum _{k=1}^{4}c_{k,i+1}\nabla W_{k,i+1}+\nabla {\tilde{v}}_{i+1})\Big )(x_{1,i},y_{1,i}). \nonumber \\ \end{aligned}$$
(23b)

A finite difference scheme can be derived from the above continuity conditions. Assume that there are I polygon cells in the computational domain and J cell edges at the boundary. Then there are \((4I-J)/2\) edges inside the computational domain. Let \(c_{k,i}\) be the unknowns and in order to determine the 4I unknowns, 4I equations are required. (23) gives two equations for each cell edge inside the computational domain, which yields \(4I-J\) equations. For each cell edge \(\Gamma _{bi}\) at the boundary, assume that it belongs to the cell \(\Omega _{i}\). Let \(P_{bi}=(x_{bi},y_{bi})\) be the edge center, Dirichlet boundary conditions write

$$\begin{aligned} \sum _{k=1}^{4}c_{k,i}W_{k,i}(x_{bi},y_{bi})+{\tilde{v}}_{i}(x_{bi},y_{bi})=u(x_{bi},y_{bi}). \end{aligned}$$
(24)

which gives J equations. Therefore, we have a system of 4I linear algebraic equations and the 4I coefficients \(c_{k,i}\) can be determined. The linear system is four times bigger than the FVM and double the size of MFDM, thus is not efficient enough.

Another way of constructing the scheme is to let the unknowns be solution values at all edge centers. There are \(2I+J/2\) edge centers in the computational domain. let \(u_{k,i}\approx u(x_{k,i},y_{k,i})\) (\(k=1,2,3,4\)), when \(u_i(x,y)\) are approximated as in (20), \(u_{k,i}\) can determine the coefficients \(c_{k,i}\) by the following system

$$\begin{aligned} \left\{ \begin{array}{l} \sum _{k=1}^{4}c_{k,i}W_{k,i}(x_{1,i},y_{1,i})+{\tilde{v}}_{i}(x_{1,i},y_{1,i})=u_{1,i}, \\ \sum _{k=1}^{4}c_{k,i}W_{k,i}(x_{2,i},y_{2,i})+{\tilde{v}}_{i}(x_{2,i},y_{2,i})=u_{2,i}, \\ \sum _{k=1}^{4}c_{k,i}W_{k,i}(x_{3,i},y_{3,i})+{\tilde{v}}_{i}(x_{3,i},y_{3,i})=u_{3,i}, \\ \sum _{k=1}^{4}c_{k,i}W_{k,i}(x_{4,i},y_{4,i})+{\tilde{v}}_{i}(x_{4,i},y_{4,i})=u_{4,i}. \end{array} \right. \end{aligned}$$
(25)

Therefore, the continuity of fluxes in (23b) can be expressed by \(u_{k,i}\) and \(u_{k,i+1}\) (\(k=1,2,3,4\)) which yields \(2I-J/2\) equations. Together with the J equations given by Dirichlet boundary conditions, one can get \(2I+J/2\) equations for the \(2I+J/2\) unknowns. In this way, the computational efficiency is the same as MFDM.

3 Numerical Experiments

The performance of the the new TFPM on some highly skewed and highly distorted meshes are presented in this section. Three different kinds of distorted meshes are tested: Kershaw, Shestakov and random. As shown in Figs. 2, 3, 4, a typical Kershaw mesh has a large distortion in vertical direction, a typical Shestakov mesh has three non-convex cells and the random mesh is obtained by randomly disturbing the interior mesh vertices of the uniform mesh. These meshes have been used to test scheme performances on unstructured or highly distorted meshes in the literature [42, 43]. In all examples, let the computational domain be \(\Omega =[0,1]\times [0,1]\). To obtain the convergence order of \(L^2\) error estimates for the first two examples, the number of cells of the three kinds of distorted meshes are displayed on Table 1.

Kershaw, Shestakov meshes are refined in a nested manner. Please see Figs. 2 and 3. For the random meshes, it is constructed from a uniform square mesh of size h and then randomly move the nodes (x, y) to a new position \((x+\omega \xi _x h/2, y +\omega \xi _y h/2)\). Here \(\xi _x\) and \(\xi _y\) are random numbers uniformly distributed in \([-0.5, 0.5]\) and \(\omega \in [0, 1]\) is a constant referred as "the degree of distortion". The meshes are still skewed or even deteriorate as they are refined. As shown in Fig. 4.

Table 1 The number of cells are used to test the convergence order
Full size table
Fig. 2
figure 2

Kershaw meshes. a \(20\times 20\); b \(40\times 40\); c \(80\times 80\)

Full size image
Fig. 3
figure 3

Shestakov meshes. a \(16\times 16\); b \(32\times 32\); c \(64\times 64\)

Full size image
Fig. 4
figure 4

Random meshes with the degree of distortion \(\omega =0.7\) . a \(20\times 20\); b \(40\times 40\); c \(80\times 80\)

Full size image

Example 1

In this example we test the scheme accuracy and convergence order for anisotropic diffusion tensor:

$$\begin{aligned} K=\left( \begin{array}{cc}\cos \theta &{}\sin \theta \\ sin\theta &{}\cos \theta \end{array}\right) \left( \begin{array}{cc}\frac{1}{\epsilon }&{}0\\ 0&{}1\end{array}\right) \left( \begin{array}{cc}\cos \theta &{}-\sin \theta \\ \sin \theta &{}\cos \theta \end{array}\right) , \end{aligned}$$
(26)

with \(\theta =40^\circ \). The exact solution is \(u_{exact}=xy(\sin (\pi x)\sin (\pi y))^{10}\) and the source term f and boundary conditions are chosen according to the exact solution. As shown in Fig. 5, second order convergence can be observed for all three kinds of distorted meshes in Fig. 2.

Fig. 5
figure 5

Example 1. The \(L^2\) norm of errors for different meshes and \(\epsilon \) values of the new TFPM. a Kershaw meshes; b Shestakov meshes c Random meshes

Full size image

Example 2

Space varying diffusion tensor is tested in this example. K is chosen to be an anisotropic rotating tensor such that

$$\begin{aligned} K=\left( \begin{array}{cc}10x^2+ y^2&{}9xy \\ 9xy &{}x^2+10y^2\end{array}\right) , \end{aligned}$$

We impose the following exact solution

$$\begin{aligned} u=\exp {(-20\pi ((x-0.5)^2+(y-0.5)^2))}. \end{aligned}$$

The source term and boundary conditions are determined by substituting u into (1). As shown in Fig. 6, TFPM exhibits second order convergence for all three types of meshes when the diffusion tensors vary in space. We can see from Figs. 3 and 4 that in the Shestakov mesh and Random mesh, some quadrilateral element degenerates into triangular, but the convergence order remains.

Fig. 6
figure 6

Example 2. The \(L^2\) norm of errors for different distorted meshes of TFPM. a Kershaw meshes; b Shestakov meshes; c Random meshes

Full size image

Example 3

In this example we solve an interface problem. The computational domain \(\Omega \) is divided into two subdomains:\([0,0.5] \times [0,1]\) and \([0.5,1]\times [0,1]\). Each has a different diffusion tensor such that

$$\begin{aligned} K(x,y)=\left( \begin{array}{cc}10&{}2\\ 2&{}5\end{array}\right) \,\,\text{ for } \,\,x\le 0.5, \qquad K(x,y)=\left( \begin{array}{cc}10^3&{}0\\ 0&{}1\end{array}\right) \,\,\text{ for }\,\, x>0.5. \end{aligned}$$

Random meshes are used in each subdomain. The analytical solution is defined as follows:

$$\begin{aligned} u(x,y)=\left\{ \begin{array}{ll} [1+(x-0.5)(0.1+8\pi (y-0.5))]e^{-20\pi (y-0.5)^2}\quad x\le 0.5, \\ e^{\frac{x-0.5}{10^3}}e^{-20\pi (y-0.5)^2}\quad x>0.5. \end{array} \right. \end{aligned}$$
(27)

The source term f and boundary conditions are chosen according to the exact solution. The solution is continuous but its derivatives are discontinuous at the interface. For this test problem, two different meshes are tested. Random meshes are refined by the degree of distortion \(\omega =0.7\) and trapezoidal meshes are refined in a self-similar fashion as in [21, 22]. As in Figs. 7, 8, second order convergence in the \(L^2\) norm can be observed numerically for the solution. Different from the bilinear finite element methods, no decreasing of convergence order is observed when trapezoidal meshes are refined.

Fig. 7
figure 7

Example 3. Random meshes with the degree of distortion \(\omega =0.7\). a \(I=16^2\); b \(I=32^2\); c Convergence order of the TFPM for problem with interface on random meshes

Full size image
Fig. 8
figure 8

Example 3. Meshes of self-similar trapezoids. a \(I=16^2\); b \(I=32^2\); c Convergence order of the TFPM for problem with interface on trapezoidal meshes

Full size image
Fig. 9
figure 9

Example 4. An illustration of subdomain together with a synoptic description of the diffusivity tensor

Full size image
Fig. 10
figure 10

Example 4. Random meshes with the degree of distortion \(\omega =0.7\) are used on each side of the interface

Full size image
Fig. 11
figure 11

Example 4. Case 1 a Random meshes \(64\times 64\); b Random meshes \(128\times 128\); c \(256\times 256\); d \(512\times 512\)

Full size image
Fig. 12
figure 12

Example 4. Case 2 a Random meshes \(64\times 64\); b Random meshes \(128\times 128\); c \(256\times 256\); d \(512\times 512\)

Full size image

Example 4

In this example, we consider a more complicate case when the unit square \([0,1]\times [0,1]\) is split into four subdomains: \(\Omega _1=[0,\frac{1}{2}] \times [0,\frac{1}{2}]\), \(\Omega _2=[\frac{1}{2},1]\times [0,\frac{1}{2}]\), \(\Omega _3=[\frac{1}{2}, 1] \times [\frac{1}{2}, 1]\), \(\Omega _4=[0, \frac{1}{2}] \times [\frac{1}{2}, 1]\). The source term is defined by

$$\begin{aligned} f(x,y)=\left\{ \begin{array}{ll} \frac{81}{4}, \quad \text{ for } \, x\in [\frac{7}{18}, \frac{11}{18}]^2, \\ 0,\quad \mathrm {otherwise}. \end{array} \right. \end{aligned}$$
(28)

As in Fig. 9, there are two interfaces along \(x=1/2\) and \(y=1/2\), the diffusion tensors in the subdomains are given by

$$\begin{aligned} K(x,y)=\left( \begin{array}{cc}\cos \theta &{}-\sin \theta \\ \sin \theta &{}\cos \theta \end{array}\right) \left( \begin{array}{cc}\alpha _1&{}0\\ 0&{}\alpha _2\end{array}\right) \left( \begin{array}{cc}\cos \theta &{}\sin \theta \\ sin\theta &{}\cos \theta \end{array}\right) ,\,\,\text{ for } \, (x,y)\in \Omega _1, \Omega _3 \end{aligned}$$
(29)

with \(\theta =\pi /6\) and

$$\begin{aligned} K(x,y)=\left( \begin{array}{cc}\cos \theta &{}-\sin \theta \\ \sin \theta &{}\cos \theta \end{array}\right) \left( \begin{array}{cc}\alpha _1&{}0\\ 0&{}\alpha _2\end{array}\right) \left( \begin{array}{cc}\cos \theta &{}\sin \theta \\ sin\theta &{}\cos \theta \end{array}\right) ,\,\,\text{ for } \, (x,y)\in \Omega _2, \Omega _4 \end{aligned}$$
(30)

with \(\theta =-\pi /6\). Random mesh as in Fig. 10 are tested. Two cases are considered. Case 1: \(\alpha _1=10^3,\alpha _2=10\) in \(\Omega _1,\Omega _3\), \(\alpha _1=10,\alpha _2=1\) in \(\Omega _2,\Omega _4\). Case 2: \(\alpha _1=10^6,\alpha _2=10^3\) in \(\Omega _1,\Omega _3\), \(\alpha _1=10,\alpha _2=1\) in \(\Omega _2,\Omega _4\). To demonstrate the robustness of the proposed TFPM method, we present the numerical results with the resolution of \(64^2\), \(128^2\), \(256^2\) and \(512^2\) in this example. See Figs. 11, 12. The TFPM can capture fast changes at the interfaces. The corresponding CPU time for each resolution also be reported in Table 2.

4 Conclusion

TFPM for anisotropic and strong discontinuous diffusivity problems on distorted meshes is constructed in this paper. First of all, the computational domain is divided into unstructured cells, inside each cell, the diffusion coefficients are approximated by piecewise linear functions. Then special solutions to an approximated constant coefficient advection-diffusion equation are used to construct the discrete analog of flux continuity equation. The local stencil makes it easy to code. The scheme can achieve second order convergence for problems with or without material discontinuities. Compared with MFDM, the number of unknowns are the same, both methods use properties of continuum solutions and seem robust for distorted meshes, it is interesting to investigate the relation between the two approaches, which will be our future work.

The new discrete scheme is an edge-centered scheme. The function values at the cell centers or vertexes or other auxiliary unknowns are not needed to construct the discrete normal flux. The out normal flux of each cell can be expressed by the unknowns at cell edge centers of the local cell, while no information from adjacent cells is needed. So it is suitable for problems with interfaces and for meshes with complex geometry. Numerical examples show that the order of convergence for the TFPM is about 2. No decreasing of convergence order is observed when the skewed meshes and trapezoidal meshes are refined. Since we are considering the distorted meshes, the convergence order analysis is difficult for general 2D case. We give a second order convergence proof for a 1D TFPM in appendix. We would like to emphasize two aspects that the 1D proof may inspire:

  • By letting \(h_i\) be the length of the ith mesh, the convergence order is independent of \(\max \{h_i\} /\min \{h_i\}\). This implies that very non-uniform meshes do not ruin the convergence order. Most classical numerical methods like finite element, finite volume etc., the convergence order depends on the ratio \(\max \{h_i\}/\min \{h_i\}\) [7, 22].

  • It is not easy to construct functions that exactly satisfy \(-\nabla \cdot ({\bar{K}}\nabla {\bar{u}})|_{\Omega _i}={\bar{f}}|_{\Omega _i}\). So we use some approximations to \(\nabla \cdot ({\bar{K}}\nabla {\bar{u}})|_{\Omega _i}\) and \({\bar{f}}|_{\Omega _i}\). The terms dropped in Eq. (8) and in \({\bar{f}}|_{\Omega _i}\) are terms at O(h). We can understand from the 1D convergence order analysis that why second order convergence remains after dropping these terms.

We are not able to prove analytically the second order convergence of TFPM for general 2D distorted meshes in this current paper, but it will be our future work.

Higher order extension of the TFPM is possible, but more unknowns at each cell edge are needed (values at other points or the solution derivatives at the cell edge). The fourth order long-stencil finite difference algorithm has used larger stencil [44, 45] and the higher order version of TFPM would be different from fourth order long-stencil finite difference.

Table 2 Example 4. The CPU time for each resolution
Full size table

5 CRediT Authorship Contribution Statement

Min Tang: Conceptualization, Methodology, Validation, Writing-original draft, Writing -review & editing. Lina Chang: Software, Validation, Writing-review & editing. Yihong Wang: Investigation, Methodology, Validation, Software, Writing-original draft, Writing -review & editing.