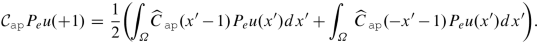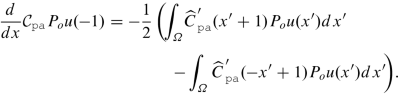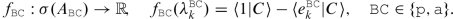Nonlocal Operators with Local Boundary Conditions: An Overview

Abstract

We present novel governing operators in arbitrary dimension for nonlocal diffusion in homogeneous media. The operators are inspired by the theory of peridynamics (PD). They agree with the original PD operator in the bulk of the domain and simultaneously enforce local boundary conditions (BC). The main ingredients are periodic, antiperiodic, and mixed extensions of kernel functions together with even and odd parts of bivariate functions. We present different types of BC in 2D which include pure and mixed combinations of Neumann and Dirichlet BC. Our construction is systematic and easy to follow. We provide numerical experiments that validate our theoretical findings. When our novel operators are extended to vector-valued functions, they will allow the extension of PD to applications that require local BC. Furthermore, we hope that the ability to enforce local BC provides a remedy for surface effects seen in PD.

We recently proved that the nonlocal diffusion operator is a function of the classical operator. This observation opened a gateway to incorporate local BC to nonlocal problems on bounded domains. The main tool we use to define the novel governing operators is functional calculus, in which we replace the classical governing operator by a suitable function of it. We present how to apply functional calculus to general nonlocal problems in a methodical way.

Mathematics Subject Classification (2000): 35L05, 74B99, 47G10.

Introduction

We construct novel governing operators for nonlocal diffusion (Andreu-Vaillo et al. 2010; Du et al. 2012) in arbitrary dimension. The operators are inspired by the theory of peridynamics (PD), a nonlocal extension of continuum mechanics developed by Silling (2000). By suppressing the time variable t, we take the following operator as the original governing operator, and, in 1D, it corresponds to the original bond-based PD operator for homogeneous media. We choose the 2D domain as Ω := [−1, 1] × [−1, 1] and for (x, y) ∈ Ω,

(1)

We define the operator that is closely related to ${\mathcal {L}}_{\text{orig}}$ as

$$\displaystyle \begin{aligned} {\mathcal{L}} u(x,y) := c u(x,y) - \iint \limits_\varOmega {\widehat{C}}({x'}-x,{y'}-y) u({x'},{y'}) d{x'} d{y'}, \quad (x,y) \in \varOmega. \end{aligned} $$

(2)

where $C := {\widehat {C}}|{ }_\varOmega$ and $c := \iint \limits _{\varOmega } C({x'},{y'}) d{x'} d{y'}$. Since ${\widehat {C}}$ enters into the formulation only as a function of (x′− x, y′− y), the operator ${\mathcal {L}}$ also assumes a homogeneous medium. We will show that the two operators agree in the bulk. As the main contribution, we prove that the novel governing operators we construct agree with ${\mathcal {L}}_{\text{orig}}$ in the bulk of Ω and, at the same time, enforce local pure and mixed Neumann, Dirichlet, periodic, and antiperiodic BC.

When PD is considered, the dimension of u must be equal to that of x. In that case, the governing operator in (1) restricted to 1D corresponds to the bond-based linearized PD; see Silling et al. (2003, Eq. 23) and Weckner and Abeyaratne (2005, Eq. 3). For the discussion of PD, it is implied that $u,x \in {\mathbb {R}}$. The case of $u \in {\mathbb {R}}$ and $x \in {\mathbb {R}}^d$ corresponds to nonlocal diffusion (Du et al. 2012; Seleson et al. 2013).

Our approach to nonlocal problems is fundamentally different because we exclusively want to use local BC. In Beyer et al. (2016), one of our major results was the finding that the governing operator of PD equation in ${\mathbb {R}}$ and nonlocal diffusion in ${\mathbb {R}}^d$ are functions of the Laplace operator. This result opened the path to the introduction of local boundary conditions into PD theory. Since PD is a nonlocal theory, one might expect only the appearance of nonlocal BC while employing ${\mathcal {L}}_{\text{orig}}$ as the governing operator. In the original PD formulation, the concept of local BC does not apply to PD. Instead, external forces must be supplied through the loading force density (Silling 2000, p.201). On the other hand, we demonstrate that the anticipation that local BC are incompatible with nonlocal operators is not quite correct. Our novel operators present an alternative to nonlocal BC, and we hope that the ability to enforce local BC will provide a remedy for surface effects seen in PD; see Madenci and Oterkus (2014, Chaps. 4, 5, 7, and 12) and Kilic (2008), Mitchell et al. (2015). Furthermore, our approach will provide us the capability to solve important elasticity problems that require local BC such as contact, shear, and traction.

We studied various aspects of local BC in nonlocal problems (Aksoylu et al. 2017a,b, 2016, 2017, Submitted; Beyer et al. 2016). Building on Beyer et al. (2016), we generalized the results in ${\mathbb {R}}$ to bounded domains (Aksoylu et al. 2017a,b), a critical feature for all practical applications. In Aksoylu et al. (2017b), we laid the theoretical foundations, and in Aksoylu et al. (2017a), we applied the foundations to prominent BC such as Dirichlet and Neumann, as well as presented numerical implementation of the corresponding wave propagation. In Aksoylu et al. (2017), we constructed the first 1D operators that agree with the original bond-based PD operator in the bulk of the domain and simultaneously enforce local Neumann and Dirichlet BC which we denote by ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$, respectively. We carried out numerical experiments by utilizing ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ as governing operators in Aksoylu et al. (2017a). In Aksoylu et al. (2016), we studied other related governing operators. In Aksoylu and Kaya (2018), we study the condition numbers of the novel governing operators. Therein, we prove that the modifications made to the operator ${\mathcal {L}}_{\text{orig}}$ to obtain the novel operators are minor as far as the condition numbers are concerned.

Our approach is not limited to PD; the abstractness of the theoretical methods used allows generalization to other nonlocal theories. Our approach presents a unique way of combining the powers of abstract operator theory with numerical computing (Aksoylu et al. 2017a). Similar classes of operators are used in numerous applications such as nonlocal diffusion (Andreu-Vaillo et al. 2010; Du et al. 2012; Seleson et al. 2013), image processing (Gilboa and Osher 2008), population models, particle systems, phase transition, and coagulation. See the review and news articles Du et al. (2012, 2014), and Silling and Lehoucq (2010) for a comprehensive discussion and the book (Madenci and Oterkus 2014). In addition, see the studies dedicated to conditioning analysis, domain decomposition and variational theory (Aksoylu and Kaya 2018; Aksoylu and Mengesha 2010; Aksoylu and Parks 2011; Aksoylu and Unlu 2014), discretization (Aksoylu and Unlu 2014; Emmrich and Weckner 2007; Tian and Du 2013), and kernel functions (Mengesha and Du 2013; Seleson and Parks 2011).

The rest of the paper is structured as follows. In section “The Novel Operators in 2D,” first we prove that the operators ${\mathcal {L}}_{\text{orig}}$ and ${\mathcal {L}}$ agree in the bulk in 2D. We define the novel operators using orthogonal projections on bivariate functions for which we utilize the periodic, antiperiodic, and mixed extensions of the kernel function C(x). We give the main theorem in 2D. In section “Operators in 1D”, first we prove that the novel operators are self-adjoint. In 1D, we give the main theorem which states they all agree with ${\mathcal {L}}_{\text{orig}}$ in the bulk and simultaneously enforce the corresponding local BC. In section “The Construction of 2D Operators,” we exploit the properties of the operators in 1D to construct the novel operators in 2D. We transfer the agreement in the bulk property established for univariate functions to bivariate ones and eventually prove that the novel operators agree with ${\mathcal {L}}_{\text{orig}}$ in the bulk in 2D. In section “Verifying the Boundary Conditions,” we make use of the Leibniz rule , the Fubini theorem, and the Lebesgue dominated convergence theorem to prove that the novel operators enforce the local BC stated in the main theorem. In section “Operators in Higher Dimensions,” we present the operators in 3D which can be easily extended to arbitrary dimension. In section “Numerical Experiments,” we report the numerical experiments. In section “The Treatment of General Nonlocal Problems Using Functional Calculus,” we present the treatment of general nonlocal problems using functional calculus. We conclude in section “Conclusion.”

The Novel Operators in 2D

For (x, y), (x′, y′) ∈ Ω ¹, it follows that (x′− x, y′− y) ∈ [−2, 2] × [−2, 2]. Hence, in (1), the domain of ${\widehat {C}}({x'}-x,{y'}-y)$ is $\widehat {\varOmega }:= [-2,2] \times [-2,2]$. Furthermore, the kernel function ${\widehat {C}}(x,y)$ is assumed to be even. Namely,

$$\displaystyle \begin{aligned} {\widehat{C}}(-x,-y) = {\widehat{C}}(x,y). \end{aligned}$$

The important choice of ${\widehat {C}}(x,y)$ is the canonical kernel function $\widehat {\chi }_\delta (x,y)$ whose only role is the representation of the nonlocal neighborhood, called the horizon, by a characteristic function. More precisely, for $(x,y) \in \widehat {\varOmega }$,

$$\displaystyle \begin{aligned} \widehat{\chi}_\delta(x,y) := \left\{ \begin{array}{ll} 1, & (x,y) \in (-\delta,\delta) \times (-\delta,\delta) \\ 0, & \mathrm{otherwise.} \end{array} \right. \end{aligned} $$

(3)

The size of nonlocality is determined by δ and we assume δ < 1. Since the horizon is constructed by $\widehat {\chi }_\delta (x,y)$, a kernel function used in practice is in the form

$$\displaystyle \begin{aligned} {\widehat{C}}(x,y) = \widehat{\chi}_\delta(x,y) \widehat{\mu}(x,y), \end{aligned} $$

(4)

where $\widehat {\mu }(x,y) \in L^2(\widehat {\varOmega })$ is even.

Throughout the paper, we assume that

$$\displaystyle \begin{aligned} u(x,y) \in L^2(\varOmega) \cap C^1(\partial \varOmega). \end{aligned} $$

(5)

Inspired by the projections that give the even and odd parts of a univariate function , we define the following operators that act on a bivariate function :

$$\displaystyle \begin{aligned} P_{e,{x'}},P_{o,{x'}},P_{e,{y'}},P_{o,{y'}}: L^2(\varOmega) \rightarrow L^2(\varOmega), \end{aligned}$$

whose definitions are

$$\displaystyle \begin{aligned} P_{e,{x'}} u({x'}{,}{y'}) & := \frac{u({x'}{,}{y'}) {+} u({-}{x'}{,}{y'})}{2}, P_{o,{x'}} u({x'}{,}{y'}) := \frac{u({x'}{,}{y'}) {-} u({-}{x'}{,}{y'})}{2}, {} \end{aligned} $$

(6)

$$\displaystyle \begin{aligned} P_{e,{y'}} u({x'}{,}{y'}) & := \frac{u({x'}{,}{y'}) {+} u({x'}{,}{-}{y'})}{2}, P_{o,{y'}} u({x'}{,}{y'}) := \frac{u({x'}{,}{y'}) {-} u({x'}{,}{-}{y'})}{2}. {} \end{aligned} $$

(7)

Each operator is an orthogonal projection and possesses the following decomposition property :

$$\displaystyle \begin{aligned} P_{e,{x'}} + P_{o,{x'}} = I_{{x'}}, \quad P_{e,{y'}} + P_{o,{y'}} = I_{{y'}}. \end{aligned} $$

(8)

One can easily check that all four orthogonal projections in (6) and (7) commute with each other. We define the following new operators obtained from the products of these projections:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} P_{e,{x'}} P_{e,{y'}} u({x'},{y'}) &\displaystyle := &\displaystyle \frac{1}{4} \big\{ [u({x'},{y'}) + u({x'},-{y'})] + [u(-{x'},{y'}) + u(-{x'},-{y'})] \big\}, \\ P_{e,{x'}} P_{o,{y'}} u({x'},{y'}) &\displaystyle := &\displaystyle \frac{1}{4} \big\{ [u({x'},{y'}) - u({x'},-{y'})] + [u(-{x'},{y'}) - u(-{x'},-{y'})] \big\}, \\ P_{o,{x'}} P_{o,{y'}} u({x'},{y'}) &\displaystyle := &\displaystyle \frac{1}{4} \big\{ [u({x'},{y'}) - u({x'},-{y'})] - [u(-{x'},{y'}) - u(-{x'},-{y'})] \big\}, \\ P_{o,{x'}} P_{e,{y'}} u({x'},{y'}) &\displaystyle := &\displaystyle \frac{1}{4} \big\{ [u({x'},{y'}) + u({x'},-{y'})] - [u(-{x'},{y'}) + u(-{x'},-{y'})] \big\}. \end{array} \end{aligned} $$

Due to the aforementioned commutativity property, these are also orthogonal projections and satisfy the following decomposition property:

$$\displaystyle \begin{aligned} P_{e,{x'}} P_{e,{y'}} + P_{e,{x'}} P_{o,{y'}} + P_{o,{x'}} P_{e,{y'}} + P_{o,{x'}} P_{o,{y'}} = I_{{x'},{y'}}. \end{aligned} $$

(9)

These will be used in the definition of the novel operators in 2D.

Reflecting on the square support of the restricted kernel function χ_δ(x, y), we define the bulk of the domain as follows:

$$\displaystyle \begin{aligned} \text{bulk} = \{ (x,y) \in \varOmega: (x,y) \in (-1+\delta,1-\delta) \times (-1+\delta,1-\delta)\}. \end{aligned}$$

We first prove that the operators ${\mathcal {L}}$ and ${\mathcal {L}}_{\text{orig}}$ agree in the bulk. Throughout the paper, we denote the restriction of a function $\widehat {Z}:\widehat {\varOmega } \rightarrow {\mathbb {R}}$ to Ω as Z, i.e., $Z := \widehat {Z}|{ }_\varOmega$.

Lemma 1

$$\displaystyle \begin{aligned} {\mathcal{L}} u(x,y) = {\mathcal{L}}_{\mathrm{orig}} u(x,y), \quad (x,y) \in \mathit{\text{bulk}}. \end{aligned}$$

Proof

For (x, y) ∈bulk, we have

$$\displaystyle \begin{aligned} (x-\delta,x+\delta) \times (y-\delta,y+\delta) \cap \varOmega = (x-\delta,x+\delta) \times (y-\delta,y+\delta). \end{aligned}$$

Hence,

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} &\iint \limits_{\varOmega} {\widehat{C}}({x'}-x, {y'}-y) d{x'} d{y'} = \iint \limits_{\varOmega} \widehat{\chi}_\delta({x'}-x, {y'}-y) \widehat{\mu}({x'}-x , y -{y'}) d{x'} d{y'} \\ &\quad = \int \limits_{x-\delta}^{x+\delta} \int \limits_{y-\delta}^{y+\delta} \widehat{\mu}({x'}-x, {y'}-y) d{x'} d{y'} = \int \limits_{-\delta}^{\delta} \int \limits_{-\delta}^{\delta} \mu({x'},{y'}) d{x'} d{y'} \\ &\quad = \iint \limits_{\varOmega} \chi_\delta({x'},{y'}) \mu({x'},{y'}) d{x'} d{y'} = \iint \limits_{\varOmega} C({x'},{y'}) d{x'} d{y'}. \end{array}\end{aligned} $$

The result follows. □

In the construction of the novel operators, a crucial ingredient is first restricting ${\widehat {C}}$ to Ω and then suitably extending it back to $\widehat {\varOmega }$. To this end, we define the periodic, antiperiodic, and mixed extensions of C(x) from [−1, 1] to [−2, 2], respectively, as follows:

(10)

We also utilize the following mixed extensions of C(x):

Building on our 1D construction in Aksoylu et al. (2017), in higher dimensions, we discovered the operators that enforce local pure and mixed Neumann and Dirichlet BC. We present the main theorem in 2D with the following 4 types of BC.

Theorem 1 (Main Theorem in 2D)

Let Ω := [−1, 1] × [−1, 1] and the restricted kernel function be separable in the form

$$\displaystyle \begin{aligned} C(x, y) = X(x) Y(y), \end{aligned} $$

(11)

where X and Y are even functions. Then, the operators ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$ , ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}, \, {\mathtt {N}}{\mathtt {D}}}$ , and ${\mathcal {M}}_{{\mathtt {N}}, \, {\mathtt {D}}{\mathtt {N}}}$ defined by

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \big( {\mathcal{M}}_{{\mathtt{N}}} - c \big) u(x,y) := - \iint \limits_{\varOmega} \big[\widehat{X}_{\mathtt{p}}({x'}-x) P_{e,{x'}} + \widehat{X}_{\mathtt{a}}({x'}-x) P_{o,{x'}}\big] &\\ \quad \qquad \big[\widehat{Y}_{\mathtt{p}}({y'}-y) P_{e,{y'}} + \widehat{Y}_{\mathtt{a}}({y'}-y) P_{o,{y'}}\big] u({x'},{y'}) d{x'} \, d{y'}, &\\ \quad \big( {\mathcal{M}}_{{\mathtt{D}}} - c \big) u(x,y) := - \iint \limits_{\varOmega} \big[\widehat{X}_{\mathtt{a}}({x'}-x) P_{e,{x'}} + \widehat{X}_{\mathtt{p}}({x'}-x) P_{o,{x'}}\big]&\\ \quad \qquad \big[\widehat{Y}_{\mathtt{a}}({y'}-y) P_{e,{y'}} + \widehat{Y}_{\mathtt{p}}({y'}-y) P_{o,{y'}}\big] u({x'},{y'}) d{x'} \, d{y'}, &\\ \quad \big( {\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}} , \, {\mathtt{N}}{\mathtt{D}}} - c \big) u(x,y) :=- \iint \limits_{\varOmega} \big[\widehat{X}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x) P_{e,{x'}} + \widehat{X}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) P_{o,{x'}}\big] & \\ \quad \qquad \big[\widehat{Y}_{{\mathtt{a}}{\mathtt{p}}}({y'}-y) P_{e,{y'}} + \widehat{Y}_{{\mathtt{p}}{\mathtt{a}}}({y'}-y) P_{o,{y'}}\big] u({x'},{y'}) d{x'} \, d{y'},& \\ \big( {\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} - c \big) u(x,y) := - \iint \limits_{\varOmega} \big[\widehat{X}_{{\mathtt{p}}}({x'}-x) P_{e,{x'}} + \widehat{X}_{{\mathtt{a}}}({x'}-x) P_{o,{x'}}\big] &\\ \quad \qquad \big[\widehat{Y}_{{\mathtt{p}}{\mathtt{a}}}({y'}-y) P_{e,{y'}} + \widehat{Y}_{{\mathtt{a}}{\mathtt{p}}}({y'}-y) P_{o,{y'}}\big] u({x'},{y'}) d{x'} \, d{y'},& \end{array}\end{aligned} $$

agree with ${\mathcal {L}} u(x,y)$ in the bulk, i.e., for (x, y) ∈ (−1 + δ, 1 − δ) × (−1 + δ, 1 − δ). Furthermore, the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ enforce pure Neumann and Dirichlet BC, respectively:

$$\displaystyle \begin{aligned} \frac{\partial}{\partial n} \big[ \big( {\mathcal{M}}_{\mathtt{N}} -c \big) u \big] (x,\pm 1) = \frac{\partial}{\partial n} \big[ \big( {\mathcal{M}}_{\mathtt{N}} -c \big) u \big] (\pm 1,y) = 0, \end{aligned}$$

$$\displaystyle \begin{aligned} \big({\mathcal{M}}_{\mathtt{D}} -c \big) u(x,\pm 1) = \big({\mathcal{M}}_{\mathtt{D}} -c \big) u(\pm 1,y) = 0. \end{aligned}$$

The operators ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}, \, {\mathtt {N}}{\mathtt {D}}}$ and ${\mathcal {M}}_{{\mathtt {N}}, \, {\mathtt {D}}{\mathtt {N}}}$ enforce mixed Neumann and Dirichlet BC, respectively, in the following way:

$$\displaystyle \begin{aligned} \frac{\partial}{\partial n} \big[ \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) u \big](-1,y) = \frac{\partial}{\partial n} \big[ \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) u \big](x,-1) = 0, \end{aligned}$$

$$\displaystyle \begin{aligned} \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) u(+1,y) = \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) u(x,+1) = 0, \end{aligned}$$

and

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \frac{\partial}{\partial n} \big[ \big({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \big) u \big] (\pm 1,y) & = \frac{\partial}{\partial n} \big[ \big({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \big) u \big] (x,+1) = 0, \\ \big({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \big) u(x,-1) & = 0. \end{array}\end{aligned} $$

Proof

The proofs of agreement in the bulk and the verification of BC are given in sections “The Construction of 2D Operators” and “Verifying the Boundary Conditions,” respectively . □

Remark 1

Although we assume a separable kernel function as in (11), note that we do not impose a separability assumption on the solution u(x, y).

Operators in 1D

The construction in higher dimensions is inspired by the one in 1D. Hence, it is more instructive to provide the construction in 1D. For the convolution present in the governing operators, we use a shorthand notation and define

$$\displaystyle \begin{aligned} {\mathcal{C}} u(x) := \int\nolimits_{\varOmega} {\widehat{C}}({x'}-x) u({x'}) d{x'}. \end{aligned}$$

Furthermore, for each extension type utilized, we define the following operators which will be useful in the exposition. Following the construction in Aksoylu et al. (2017a), we assume that u, C ∈ L ²(Ω) and define

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & {\mathcal{C}}_{\mathtt{p}} u(x) && := \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{p}}({x'}-x) u({x'}) d{x'}, \quad && {\mathcal{C}}_{\mathtt{a}} u(x) && := \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{a}}({x'}-x) u({x'}) d{x'}, {} \end{array}\end{aligned} $$

(12)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} u(x) && := \int\nolimits_\varOmega {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) u({x'}) d{x'}, \quad && {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} u(x) && := \int\nolimits_\varOmega {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x) u({x'}) d{x'}. {} \end{array}\end{aligned} $$

(13)

The only difference in the operators ${\mathcal {C}}_{\mathtt {p}}$, ${\mathcal {C}}_{\mathtt {a}}$, ${\mathcal {C}}_{{\mathtt {p}}{\mathtt {a}}}$, and ${\mathcal {C}}_{{\mathtt {a}}{\mathtt {p}}}$ is the extension utilized for the kernel functions. We prove that the operators agree in the bulk by investigating how the corresponding kernel functions behave in the bulk.

Lemma 2

Let the kernel function ${\widehat {C}}(x)$ be in the form

$$\displaystyle \begin{aligned} {\widehat{C}}(x) = \widehat{\chi}_\delta(x) \widehat{\mu}(x), \end{aligned}$$

where $\widehat {\mu }(x) \in L^2(\widehat {\varOmega })$ is even. Let ${\widehat {C}}_{\mathtt {p}}(x)$ , ${\widehat {C}}_{\mathtt {a}}(x)$ , ${\widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}(x)$ , and ${\widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}(x)$ denote the periodic, antiperiodic, and mixed extensions of C(x) to $\widehat {\varOmega }$ , respectively. Then,

$$\displaystyle \begin{aligned} {\widehat{C}}(x) = {\widehat{C}}_{\mathtt{p}}(x) = {\widehat{C}}_{\mathtt{a}}(x) = {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}(x) = {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}(x), \quad x \in (-2+\delta,2-\delta). \end{aligned}$$

Furthermore, we have the following agreement in the bulk. Namely, for x ∈ (−1 + δ, 1 − δ),

$$\displaystyle \begin{aligned} {\widehat{C}}({x'}-x) = {\widehat{C}}_{\mathtt{p}}({x'}-x) = {\widehat{C}}_{\mathtt{a}}({x'}-x) = {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) = {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x), \quad {x'} \in [-1,1]. \end{aligned} $$

(14)

Proof

Let us study the definition of ${\widehat {C}}_{\mathtt {p}}(x)$ given in (10) by explicitly writing the expression of practical kernel (4) as follows:

$$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}}(x)= \left\{ \begin{array}{ll} \chi_\delta(x+2) \mu(x+2), & x \in [-2,-1), \\ {} \chi_\delta(x) \mu(x), & x \in [-1,1], \\ {} \chi_\delta(x-2) \mu(x-2), & x \in (1,2]. \end{array} \right.\end{aligned} $$

Let us closely look at the first expression in the above definition of ${\widehat {C}}_{\mathtt {p}}(x)$:

$$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}}(x) |{}_{x \in [-2,-1)} = \chi_\delta(x+2) \mu(x+2).\end{aligned} $$

(15)

The expression in (15) is equivalent to

$$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}}(x) |{}_{x \in [-2,-1)} = \left\{ \begin{array}{ll} \mu(x+2), & x+2 \in (-\delta,\delta) ~\text{and}~ x \in [-2,-1), \\ {} 0, & x+2 \notin (-\delta,\delta) ~\text{and}~ x \in [-2,-1). \end{array} \right. \end{aligned} $$

(16)

Due to the following set equivalence

$$\displaystyle \begin{aligned} &\{x: x+2 \in (-\delta,\delta) ~\text{and}~ x \in [-2,-1) \} \\ &\quad =\{x: x \in (-2-\delta,-2+\delta)\cap[-2,-1) = [-2,-2+\delta) \}, \end{aligned} $$

the expression (16) reduces to

$$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}}(x) |{}_{x \in [-2,-1)} = \left\{ \begin{array}{ll} \mu(x+2), & x \in [-2,-2+\delta), \\ 0, & x \in [-2+\delta,-1). \end{array} \right. \end{aligned} $$

(17)

Similar to (17), for x ∈ (1, 2], we have

$$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}}(x) |{}_{x \in (1,2]} = \left\{ \begin{array}{ll} 0, & x \in (1,2-\delta], \\ \mu(x-2), & x \in (2-\delta,2]. \end{array} \right. \end{aligned} $$

(18)

Combining (17) and (18), for x ∈ [−2, 2], we obtain the expression for ${\widehat {C}}_{\mathtt {p}}(x)$. Similarly, we obtain the expressions for the antiperiodic and the mixed extensions. We collect all the expressions in Table 1.

Table 1 The value of each extension of the function C

Clearly, all of the extensions agree for x ∈ [−2 + δ, 2 − δ]. Also, see Figs. 1 and 2. □

Fig. 1

The kernel function ${ \widehat {C}}(x) = \widehat {\chi }_{\delta }(x) \widehat {\mu }(x)$ with δ = 0.4 and $\widehat {\mu }(x) = 0.25 - x^2$. The periodic, antiperiodic, and mixed extensions of $C = { \widehat {C}}|{ }_\varOmega$ are denoted by ${ \widehat {C}}_{\mathtt {p}}$, ${ \widehat {C}}_{\mathtt {a}}$, ${ \widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}$, and ${ \widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}$, respectively. Plots of (a) ${ \widehat {C}}(x)$, (b) ${ \widehat {C}}_{\mathtt {p}}(x)$, (c) ${ \widehat {C}}_{\mathtt {a}}(x)$, (d) ${ \widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}(x)$, (e) ${ \widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}(x)$

Fig. 2

For the same kernel function ${ \widehat {C}}(x)$ in Fig. 1, we employ bivariate versions of ${ \widehat {C}}({x'}-x)$, ${ \widehat {C}}_{\mathtt {p}}({x'}-x)$, ${ \widehat {C}}_{\mathtt {a}}({x'}-x)$, ${ \widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}({x'}-x)$, and ${ \widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}({x'}-x)$ with the definition ${ \widehat {C}}_{\mathtt {BC}}(x,{x'}) := { \widehat {C}}_{\mathtt {BC}}({x'}-x)$. Plots of (a) ${ \widehat {C}}(x,x')$, (b) ${ \widehat {C}}_{\mathtt {p}}(x,x')$, (c) ${ \widehat {C}}_{\mathtt {a}}(x,x')$, (d) ${ \widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}(x,x')$, (e) ${ \widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}(x,x')$

Using (14), we immediately obtain the following equivalence of operators in the bulk:

$$\displaystyle \begin{aligned} {\mathcal{C}} u(x)= {\mathcal{C}}_{\mathtt{p}} u(x) = {\mathcal{C}}_{\mathtt{a}} u(x) = {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} u(x) = {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} u(x), \quad x \in (-1+\delta, 1-\delta). \end{aligned} $$

(19)

Even and odd parts of a univariate function u(x) are used in the governing operators ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$, ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$, and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt { N}}}$. We define the orthogonal projections that give the even and odd parts, respectively, of a univariate function by P_e, P_o : L ²(Ω) → L ²(Ω), whose definitions are

$$\displaystyle \begin{aligned} P_{e} u(x) := \frac{u(x) + u(-x)}{2}, \quad P_{o} u(x) := \frac{u(x) - u(-x)}{2}. \end{aligned}$$

We present a commutativity property that allows us to identify the kernel functions associated with the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$.

Lemma 3

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & {\mathcal{C}}_{\mathtt{p}} P_e && = P_e {\mathcal{C}}_{\mathtt{p}}, \quad && {\mathcal{C}}_{\mathtt{p}} P_o && = P_o {\mathcal{C}}_{\mathtt{p}}, \quad && {\mathcal{C}}_{\mathtt{a}} P_e && = P_e {\mathcal{C}}_{\mathtt{a}}, \quad && {\mathcal{C}}_{\mathtt{a}} P_o && = P_o {\mathcal{C}}_{\mathtt{a}}. {} \end{array}\end{aligned} $$

(20)

Proof

We present the proof for ${\mathcal {C}}_{\mathtt {p}} P_e = P_e {\mathcal {C}}_{\mathtt {p}}$. The other results easily follow. We recall the definition of ${\mathcal {C}}_{\mathtt {p}} u(x)$ in (12). We explicitly write $P_e {\mathcal {C}}_{\mathtt {p}} u(x)$, and the result follows by utilizing the evenness of ${\widehat {C}}_{\mathtt {p}}$ and a change of variable:

$$\displaystyle \begin{aligned} \begin{array}{rcl} P_e {\mathcal{C}}_{\mathtt{p}} u (x) &\displaystyle = &\displaystyle \frac{1}{2} \left( \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{p}}({x'}-x) u({x'}) d{x'} + \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{p}}({x'}+x) u({x'}) d{x'} \right) \\ {} &\displaystyle = &\displaystyle \frac{1}{2} \left( \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{p}}({x'}-x) u({x'}) d{x'} + \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{p}}({x'}-x) u(-{x'}) d{x'} \right) \\ {} &\displaystyle = &\displaystyle \int\nolimits_\varOmega {\widehat{C}}_{\mathtt{p}}({x'}-x) P_e u({x'}) d{x'} \\ {} &\displaystyle = &\displaystyle {\mathcal{C}}_{\mathtt{p}} P_e u (x). \end{array} \end{aligned} $$

□

Remark 2

The above commutativity property plays an important role in determining the spectrum of the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$; see Aksoylu and Kaya (2018). It also helps in identifying the associated kernel functions; see (22) and (23). Note that the above commutativity property does not hold for the operators ${\mathcal {C}}_{{\mathtt {p}}{\mathtt {a}}}$ and ${\mathcal {C}}_{{\mathtt {a}}{\mathtt {p}}}$. Identification of the associated kernel functions can be done by direct manipulation.

Theorem 2 (Main Theorem in 1D)

Let c =∫_ΩC(x′)dx′. The following operators ${\mathcal {M}}_{\mathtt {N}}$ , ${\mathcal {M}}_{\mathtt {D}}$ , ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$ , and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$ defined by

$$\displaystyle \begin{aligned} \begin{array}{rcl} \big( {\mathcal{M}}_{\mathtt{D}} -c \big) u(x) &\displaystyle := &\displaystyle - \int\nolimits_\varOmega \big[ {\widehat{C}}_{\mathtt{a}}({x'}-x) P_e u({x'}) + {\widehat{C}}_{\mathtt{p}}({x'}-x) P_o u({x'}) \big] d{x'}, \\ {} \big( {\mathcal{M}}_{\mathtt{N}} -c \big) u(x) &\displaystyle := &\displaystyle - \int\nolimits_\varOmega \big[ {\widehat{C}}_{\mathtt{p}}({x'}-x) P_e u({x'}) + {\widehat{C}}_{\mathtt{a}}({x'}-x) P_o u({x'}) \big] d{x'}, \\ {} \big( {\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}} -c \big) u(x) &\displaystyle := &\displaystyle - \int\nolimits_\varOmega \big[ {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x) P_e u({x'}) + {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) P_o u({x'}) \big] d{x'}, \\ {} \big( {\mathcal{M}}_{{\mathtt{D}}{\mathtt{N}}} -c \big) u(x) &\displaystyle := &\displaystyle - \int\nolimits_\varOmega \big[ {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) P_e u({x'}) + {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x) P_o u({x'}) \big] d{x'} \end{array} \end{aligned} $$

agree with ${\mathcal {L}} u(x)$ in the bulk, i.e., for x ∈ (−1 + δ, 1 − δ). Furthermore, the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ enforce pure Neumann and Dirichlet BC, respectively:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \frac{d}{dx} \big[ \big({\mathcal{M}}_{{\mathtt{N}}} -c \big) u \big](\pm 1) & = 0, \\ \big({\mathcal{M}}_{{\mathtt{D}}} -c \big) u(\pm 1) & = 0. \end{array}\end{aligned} $$

The operators ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$ and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$ enforce mixed Neumann and Dirichlet BC, respectively:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}} -c \big) u(+1) & = \frac{d}{dx} \big[ \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}} -c \big)u \big](-1) && = 0, \\ \big({\mathcal{M}}_{{\mathtt{D}}{\mathtt{N}}} -c \big) u(-1) & = \frac{d}{dx} \big[ \big({\mathcal{M}}_{{\mathtt{D}}{\mathtt{N}}} -c \big)u \big](+1) && = 0. \end{array}\end{aligned} $$

We define the operators ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$, ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$, and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt { N}}}$ as bounded, linear operators. More precisely, ${\mathcal {M}}_{\mathtt {D}},~ {\mathcal {M}}_{\mathtt {N}}, ~{\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}, ~{\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}} \in L(X,X)$ where X = L ²(Ω) ∩ C ¹(∂Ω). For ${\mathcal {M}}_{\mathtt {D}}$, the choice of X can be relaxed as L ²(Ω) ∩ C ⁰(∂Ω). This choice is implied when we study ${\mathcal {M}}_{\mathtt {D}}$. The assumptions for the operators ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$ and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$ are also implied in a similar way.

Imposing Neumann (also periodic and antiperiodic) BC requires differentiation. For technical details regarding differentiation under the integral sign, see the discussion on the Leibniz rule in Aksoylu et al. (2017) whose proof relies on the Lebesgue dominated convergence theorem . In addition, the limit in the definition of the Dirichlet BC can be interchanged with the integral sign, again by the Lebesgue dominated convergence theorem.

Remark 3

When we assume homogeneous Neumann and Dirichlet BC on u, then the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ enforce homogeneous Dirichlet and Neumann BC, respectively. More precisely, for u(±1) = 0 and u′(±1) = 0, we obtain $\displaystyle \frac {d}{dx}{\mathcal {M}}_{\mathtt {N}} u(\pm 1) = 0$ and ${\mathcal {M}}_{\mathtt {D}} u(\pm 1) = 0$, respectively. The same line of argument applies to the operators ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$ and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$.

Using the operators ${\mathcal {C}}_{\mathtt {p}}$, ${\mathcal {C}}_{\mathtt {a}}$, ${\mathcal {C}}_{{\mathtt {p}}{\mathtt {a}}}$, and ${\mathcal {C}}_{{\mathtt {a}}{\mathtt { p}}}$ given in (12) and (13), we can express the operators ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$, ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$, and ${\mathcal {M}}_{{\mathtt { D}}{\mathtt {N}}}$ in the following way:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & \big( {\mathcal{M}}_{\mathtt{N}} -c \big) && = - \big( {\mathcal{C}}_{\mathtt{p}} P_e + {\mathcal{C}}_{\mathtt{a}} P_o \big), \quad && \big( {\mathcal{M}}_{\mathtt{D}} -c \big) && = - \big( {\mathcal{C}}_{\mathtt{a}} P_e + {\mathcal{C}}_p P_o \big), \\ {} &\big( {\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}} -c \big) && = - \big( {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_e + {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_o \big), \quad && \big( {\mathcal{M}}_{{\mathtt{D}}{\mathtt{N}}} -c \big) && = - \big( {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_e + {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_o \big). \end{array}\end{aligned} $$

Using the commutativity property (20), we arrive at the following representation:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & \big( {\mathcal{M}}_{\mathtt{N}} -c \big) && = - \big( P_e {\mathcal{C}}_{\mathtt{p}} + P_o {\mathcal{C}}_{\mathtt{a}} \big), \quad && \big( {\mathcal{M}}_{\mathtt{D}} -c \big) && = - \big( P_e {\mathcal{C}}_{\mathtt{a}} + P_o {\mathcal{C}}_{\mathtt{p}} \big). \end{array}\end{aligned} $$

Now, we can identify the kernel functions associated with operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$:

(21)

where

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} K_{\mathtt{N}}(x,{x'}) & := \frac{1}{2} \big\{ \big[ {\widehat{C}}_{\mathtt{p}}({x'}-x) && + {\widehat{C}}_{\mathtt{p}}({x'}+x) \big] && + \big[ {\widehat{C}}_{\mathtt{a}}({x'}-x) && - {\widehat{C}}_{\mathtt{a}}({x'}+x) \big] \big\}, {} \end{array}\end{aligned} $$

(22)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} K_{\mathtt{D}}(x,{x'}) & := \frac{1}{2} \big\{ \big[ {\widehat{C}}_{\mathtt{a}}({x'}-x) && + {\widehat{C}}_{\mathtt{a}}({x'}+x) \big] && + \big[ {\widehat{C}}_{\mathtt{p}}({x'}-x) && - {\widehat{C}}_{\mathtt{p}}({x'}+x) \big] \big\}. {} \end{array}\end{aligned} $$

(23)

We also want to identify the integrands associated with the operators ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$ and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$. We proceed by direct manipulation. By writing P_e and P_o explicitly and utilizing a simple change of variable, we arrive at the following expressions:

$$\displaystyle \begin{aligned} \big( {\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}} - c \big) u(x) & = - \int\nolimits_\varOmega K_{{\mathtt{N}}{\mathtt{D}}}(x,{x'}) u({x'})d{x'},\\ \big( {\mathcal{M}}_{{\mathtt{D}}{\mathtt{N}}} - c \big) u(x) & = - \int\nolimits_\varOmega K_{{\mathtt{D}}{\mathtt{N}}}(x,{x'}) u({x'})d{x'}, \end{aligned} $$

where

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} K_{{\mathtt{N}}{\mathtt{D}}}(x,{x'}) & := \frac{1}{2} \big\{ \big[ {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) && \,{+}\, {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}+x) \big] && \,{+}\, \big[ {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x) && \,{-}\, {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}\,{+}\,x) \big] \big\}, \\ K_{{\mathtt{D}}{\mathtt{N}}}(x,{x'}) & := \frac{1}{2} \big\{ \big[ {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-x) && \,{+}\, {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}+x) \big] && \,{+}\, \big[ {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}-x) && \,{-}\, {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}({x'}\,{+}\,x) \big] \big\}. \end{array}\end{aligned} $$

In order to align with the construction given in Aksoylu et al. (2017a), we assume that

$$\displaystyle \begin{aligned} {\widehat{C}}(x),\, {\widehat{C}}_{\mathtt{a}}(x),\, {\widehat{C}}_{\mathtt{p}}(x),\,{\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}(x),\, \text{and}~ {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}(x) \in L^2(\widehat{\varOmega}).\end{aligned} $$

(24)

Remark 4

The boundedness of ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$, ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$, and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt { N}}}$ follow from the choices of (5) and (24). In addition, all of them fall into the class of integral operators ; hence, their self-adjointness follows from the fact that the corresponding kernels are symmetric (due to evenness of C), i.e., K_BC(x, x′) = K_BC(x′, x) and BC ∈{N, D, ND, DN}. The cases of BC ∈{ND, DN} are more involved than the rest. One useful identity is ${\widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}({x'}-x) = {\widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}(-{x'}+x)$.

In the upcoming proofs, we want to report a minor caveat. We use ${\widehat {C}}_{\mathtt {a}}({x'}+1) = -{\widehat {C}}_{\mathtt {a}}({x'}-1)$ which holds for x′≠ 0. For x′ = 0, i.e., ${\widehat {C}}_{\mathtt {a}}({x'}+1) = C(1) \neq - C(-1) = -{\widehat {C}}_{\mathtt {a}}({x'}-1)$. Since x′ = 0 is only a point, it does not change the value of the integral. We choose not to point it out each time we run into this case.

Proof (Proof of Theorem 2)

The key observation that leads to the agreement of the operators ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$, ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$, and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$ with the operator ${\mathcal {L}}$ is the agreement of kernel functions in (14). The property (14) leads to the equivalence (19). Hence, we arrive at the following equivalence for x ∈ (−1 + δ, 1 − δ):

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \big( {\mathcal{L}} - c \big) & = - \, {\mathcal{C}} \\ & = - {\mathcal{C}} (P_e + P_o) && \quad \text{(using }u = P_eu + P_ou) \\ & = - \big( {\mathcal{C}} P_e + {\mathcal{C}} P_o \big) && \\ & = - \big( {\mathcal{C}}_{\mathtt{p}} P_e + {\mathcal{C}}_{\mathtt{a}} P_o \big) {} && \quad \text{(using (19))} \\ & =: \big( {\mathcal{M}}_{\mathtt{N}} - c \big). && \end{array}\end{aligned} $$

(25)

Similar to (25), we can show that the other operators agree in the bulk as well:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \big( {\mathcal{L}} - c \big) & =& - {\mathcal{C}} \\ &=& - \big( {\mathcal{C}}_{\mathtt{a}} P_e + {\mathcal{C}}_{\mathtt{p}} P_o \big) =:\big( {\mathcal{M}}_{\mathtt{D}} - c \big) {} \end{array}\end{aligned} $$

(26)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & = && - \big( {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_e + {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_o \big) && =:\big( {\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}} - c \big) {} \end{array}\end{aligned} $$

(27)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} & = && - \big( {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_e + {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_o \big) && =:\big( {\mathcal{M}}_{{\mathtt{D}}{\mathtt{N}}} - c \big) {} \end{array}\end{aligned} $$

(28)

First, we prove that the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ enforce pure Neumann and Dirichlet BC, respectively. Next, we will prove that the operators ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$ and ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$ enforce mixed Neumann and Dirichlet BC, respectively.

• The operator ${\mathcal {M}}_{\mathtt {N}}$: First we remove the points at which the partial derivative of K_N(x, x′) does not exist from the set of integration. Note that such points form a set of measure zero and, hence, do not affect the value of the integral. We differentiate both sides of (21). In Aksoylu et al. (2017), we had proved that the differentiation in the definition of the Neumann BC can interchange with the integral. We can differentiate the integrand K_N(x, x′) piecewise and obtain

  $$\displaystyle \begin{aligned} \frac{d}{dx} \big[ \big( {\mathcal{M}}_{\mathtt{N}} - c \big) u \big] (x) = - \int_\varOmega \frac{\partial K_{\mathtt{N}}}{\partial x}(x,{x'}) u({x'})d{x'}, \end{aligned} $$

  (29)

  where

  $$\displaystyle \begin{aligned} \frac{\partial K_{\mathtt{N}}}{\partial x}(x,{x'}) = \frac{1}{2} \big\{ \big[ -{\widehat{C}}_{\mathtt{p}}^{\prime}({x'}-x) + {\widehat{C}}_{\mathtt{p}}^{\prime}({x'}+x)\big] + \big[-{\widehat{C}}_{\mathtt{a}}^{\prime}({x'}-x) - {\widehat{C}}_{\mathtt{a}}^{\prime}({x'}+x) \big] \big\}. \end{aligned}$$

  We check the boundary values by plugging x = ±1 in (29).

  $$\displaystyle \begin{aligned} \frac{d}{dx} \big[ \big( {\mathcal{M}}_{\mathtt{N}} - c \big) u \big] (\pm 1) = - \int_\varOmega \frac{\partial K_{\mathtt{N}}}{\partial x}(\pm 1,{x'}) u({x'})d{x'}. \end{aligned} $$

  (30)

  The functions ${\widehat {C}}_{\mathtt {p}}^{\prime }$ and ${\widehat {C}}_{\mathtt {a}}^{\prime }$ are 2-periodic and 2-antiperiodic because they are the derivatives of 2-periodic and 2-antiperiodic functions, respectively. Hence,

  $$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}}^{\prime} ({x'} \mp 1) = {\widehat{C}}_{\mathtt{p}}^{\prime} ({x'} \pm 1) \quad \text{and}\quad {\widehat{C}}_{\mathtt{a}}^{\prime} ({x'} \mp 1) = - {\widehat{C}}_{\mathtt{a}}^{\prime} ({x'} \pm 1). \end{aligned}$$

  Hence, the integrand in (30) vanishes, i.e.,

  $$\displaystyle \begin{aligned} \frac{\partial K_{\mathtt{N}}}{\partial x}(\pm 1,{x'}) = 0. \end{aligned}$$

  Therefore, we arrive at

  $$\displaystyle \begin{aligned} \frac{d}{dx} {\mathcal{M}}_{\mathtt{N}} u(\pm 1) = c u'(\pm 1). \end{aligned}$$

  When we assume that u satisfies homogeneous Neumann BC, i.e., u′(±1) = 0, we conclude that the operator ${\mathcal {M}}_{\mathtt {N}}$ enforces homogeneous Neumann BC as well.

• The operator ${\mathcal {M}}_{\mathtt {D}}$: By the Lebesgue dominated convergence theorem , the limit in the definition of the Dirichlet BC can be interchanged with the integral. Now, we check the boundary values by plugging x = ±1 in (23).

  $$\displaystyle \begin{aligned} \big( {\mathcal{M}}_{\mathtt{D}} - c \big) u(\pm 1) = - \int\nolimits_\varOmega K_{\mathtt{D}}(\pm 1, {x'}) u({x'})d{x'}. \end{aligned} $$

  (31)

  Since ${\widehat {C}}_{\mathtt {p}}$ and ${\widehat {C}}_{\mathtt {a}}$ are 2-periodic and 2-antiperiodic, respectively, we have

  $$\displaystyle \begin{aligned} {\widehat{C}}_{\mathtt{p}} ({x'} \mp 1) = {\widehat{C}}_{\mathtt{p}} ({x'} \pm 1) \quad \text{and}\quad {\widehat{C}}_{\mathtt{a}} ({x'} \mp 1) = - {\widehat{C}}_{\mathtt{a}} ({x'} \pm 1). \end{aligned}$$

  Hence, the integrand in (31) vanishes, i.e., K_D(±1, x′) = 0. Therefore, we arrive at

  $$\displaystyle \begin{aligned} {\mathcal{M}}_{\mathtt{D}} u(\pm 1) = c u(\pm 1). \end{aligned}$$

  When we assume that u satisfies homogeneous Dirichlet BC, i.e., u(±1) = 0, we conclude that the operator ${\mathcal {M}}_{\mathtt {D}}$ enforces homogeneous Dirichlet BC as well.

• The operator ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$: First we prove that ${\mathcal {C}}_{{\mathtt {a}}{\mathtt {p}}} P_e u(+1)=0$. We use a change of variable in the second piece.

  

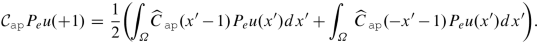
  Then, we split the integrals into two parts as follows:

  $$\displaystyle \begin{aligned} \begin{aligned} {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_e u(+1) & = \frac{1}{2} \int\nolimits_{-1}^0 \big[ {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-1) + {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}(-{x'}-1) \big] P_e u({x'}) d{x'} \\ & \quad + \frac{1}{2} \int_0^1 \big[ {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-1) + {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}(-{x'}-1) \big] P_eu({x'}) d{x'}. \end{aligned} \end{aligned} $$

  (32)

  For x′∈ [−1, 0], we have x′− 1 ∈ [−2, −1]. By using the definition of ${\widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}$ and the evenness of C, we obtain

  $$\displaystyle \begin{aligned} {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-1) = -{\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}+1) = -C({x'}+1) = -C(-{x'}-1) = - {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}(-{x'}-1). \end{aligned} $$

  (33)

  For x′∈ [0, 1], we have x′− 1 ∈ [−1, 0]. By using the definition of ${\widehat {C}}_{{\mathtt {a}}{\mathtt {p}}}$ and the evenness of C, we obtain

  $$\displaystyle \begin{aligned} {\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}({x'}-1) = C({x'}-1) = C(-{x'}+1) = -{\widehat{C}}_{{\mathtt{a}}{\mathtt{p}}}(-{x'}-1). \end{aligned} $$

  (34)

  Combining (33) and (34) with (32), we conclude that ${\mathcal {C}}_{{\mathtt {a}}{\mathtt {p}}} P_e u(+1)=0$. Similarly, we can conclude that ${\mathcal {C}}_{{\mathtt {p}}{\mathtt {a}}} P_o u(+1)=0$. Consequently, we arrive at

  $$\displaystyle \begin{aligned} {\mathcal{C}}_{{\mathtt{N}}{\mathtt{D}}} u(+1) = 0. \end{aligned}$$

  We prove that $\displaystyle \frac {d}{dx} {\mathcal {C}}_{{\mathtt {p}}{\mathtt {a}}} P_o u(-1)=0$. We use a change of variable in the second piece.

  

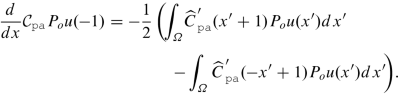
  Then, we split the integrals into two parts as follows:

  $$\displaystyle \begin{aligned} \begin{aligned} \frac{d}{dx} {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_o u(-1) & = - \frac{1}{2} \int_{-1}^0 \big[ {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}({x'}+1) - {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}(-{x'}+1) \big] P_o u({x'}) d{x'} \\ & \quad - \frac{1}{2} \int\nolimits_0^1 \big[ {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}({x'}+1) - {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}(-{x'}+1) \big] P_ou({x'}) d{x'}. \end{aligned} \end{aligned} $$

  (35)

  For x′∈ [−1, 0], we have x′ + 1 ∈ [0, 1]. By using the definition of ${\widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}$ and the oddness of C′, we obtain

  $$\displaystyle \begin{aligned} {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}({x'}+1) = C'({x'}+1) = -C'(-{x'}-1) = -{\widehat{C}}^{\prime}_{{\mathtt{p}}{\mathtt{a}}}(-{x'}-1) = {\widehat{C}}^{\prime}_{{\mathtt{p}}{\mathtt{a}}}(-{x'}+1). \end{aligned} $$

  (36)

  For x′∈ [0, 1], we have x′ + 1 ∈ [1, 2]. By using the definition of ${\widehat {C}}_{{\mathtt {p}}{\mathtt {a}}}$ and the oddness of C′, we obtain

  $$\displaystyle \begin{aligned} {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}({x'}+1) = - {\widehat{C}}_{{\mathtt{p}}{\mathtt{a}}}^{\prime}({x'}-1) = - C'({x'}-1) = C'(-{x'}+1) = {\widehat{C}}^{\prime}_{{\mathtt{p}}{\mathtt{a}}}(-{x'}+1).\end{aligned} $$

  (37)

  Combining (36) and (37) with (35), we conclude that $\frac {d}{dx} {\mathcal {C}}_{{\mathtt {p}}{\mathtt {a}}} P_o u(-1)=0$. Similarly, we can conclude that $\frac {d}{dx} {\mathcal {C}}_{{\mathtt {a}}{\mathtt {p}}} P_e u(-1)=0$. Consequently, we arrive at

  $$\displaystyle \begin{aligned} \frac{d}{dx} {\mathcal{C}}_{{\mathtt{N}}{\mathtt{D}}} u(-1) = 0. \end{aligned}$$

• The operator ${\mathcal {M}}_{{\mathtt {D}}{\mathtt {N}}}$: The proof is similar to the case of ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}}$.

□

Remark 5

As we prepare to construct the operators in 2D, it is useful to explicitly denote the variable x′ on which P_e and P_o act in the following way.

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathcal{C}}_{\mathtt{N}} u(x) &\displaystyle := &\displaystyle \big( {\mathcal{C}}_{\mathtt{p}} P_{e,{x'}} + {\mathcal{C}}_{\mathtt{a}} P_{o,{x'}} \big) u(x) {} \\ {} {\mathcal{C}}_{\mathtt{D}} u(x) &\displaystyle := &\displaystyle \big( {\mathcal{C}}_{\mathtt{a}} P_{e,{x'}} + {\mathcal{C}}_{\mathtt{p}} P_{o,{x'}} \big) u(x) {} \\ {} {\mathcal{C}}_{{\mathtt{N}}{\mathtt{D}}} u(x) &\displaystyle := &\displaystyle \big( {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{x'}} + {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_{o,{x'}} \big) u(x) {} \\ {} {\mathcal{C}}_{{\mathtt{D}}{\mathtt{N}}} u(x) &\displaystyle := &\displaystyle \big( {\mathcal{C}}_{{\mathtt{p}}{\mathtt{a}}} P_{e,{x'}} + {\mathcal{C}}_{{\mathtt{a}}{\mathtt{p}}} P_{o,{x'}} \big) u(x). {} \end{array} \end{aligned} $$

Consequently, checking if the operators enforce the BC reduces to obtaining

$$\displaystyle \begin{aligned} \begin{aligned} \frac{d}{dx} {\mathcal{C}}_{\mathtt{N}} u(\pm 1) & = 0, \quad && {\mathcal{C}}_{\mathtt{D}} u(\pm 1) && = 0 \\ \frac{d}{dx} {\mathcal{C}}_{{\mathtt{N}}{\mathtt{D}}} u(-1) & = 0, \quad && {\mathcal{C}}_{{\mathtt{N}}{\mathtt{D}}} u(+ 1) && = 0 \\ \frac{d}{dx} {\mathcal{C}}_{{\mathtt{D}}{\mathtt{N}}} u(+1) & = 0, \quad && {\mathcal{C}}_{{\mathtt{D}}{\mathtt{N}}} u(- 1) && = 0. \end{aligned} \end{aligned} $$

(38)

The Construction of 2D Operators

For the convolution present in the governing operators, we use a shorthand notation and define the operator

$$\displaystyle \begin{aligned} {\mathcal{C}} u(x,y) := \iint \limits_{\varOmega} {\widehat{C}}({x'}-x,{y'}-y) u({x'},{y'}) d{x'} d{y'}. \end{aligned} $$

(39)

We also define the following auxiliary operators that act on a bivariate function .

where E ∈{p, a, pa, ap}.

Using the separability assumption (11) on the kernel function , we have the following:

$$\displaystyle \begin{aligned} {\widehat{C}}(x,y) = \widehat{X}(x) \widehat{Y}(y). \end{aligned} $$

(40)

The separability of the kernel function leads to the following important property. Using (40) and the Fubini theorem , we rewrite the operator ${\mathcal {C}}$ in (39).

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathcal{C}} u(x,y) &\displaystyle = &\displaystyle \iint \limits_{\varOmega} \widehat{X}({x'}-x) \widehat{Y}({y'}-y) u({x'},{y'}) d{x'} d{y'} \\ &\displaystyle = &\displaystyle \int\nolimits_{\varOmega} \widehat{X}({x'}-x) \Big( \int\nolimits_{\varOmega} \widehat{Y}({y'}-y) u({x'},{y'}) d{y'} \Big) d{x'} \\ &\displaystyle = &\displaystyle \int\nolimits_{\varOmega} \widehat{X}({x'}-x) \Big( {\mathcal{Y}} u({x'},y) \Big) d{x'} \\ &\displaystyle = &\displaystyle {\mathcal{X}} \big( {\mathcal{Y}} u \big) (x,y) {} \end{array} \end{aligned} $$

(41)

In other words, we proved that ${\mathcal {C}}$ can be decomposed into a product of two 1D operators where the action of ${\mathcal {X}}$ and ${\mathcal {Y}}$ is on the variables x and y, respectively. Furthermore, a change in the order of integration leads to

$$\displaystyle \begin{aligned} {\mathcal{C}} u(x,y) = {\mathcal{Y}} {\mathcal{X}} u(x,y). \end{aligned} $$

(42)

Similar to (19), we also obtain the following equivalence of operators in the bulk. For fixed y ₀, we have

$$\displaystyle \begin{aligned} {\mathcal{X}} u(x,y_0) &= {\mathcal{X}}_{\mathtt{p}} u(x,y_0) = {\mathcal{X}}_{\mathtt{a}} u(x,y_0)\\ &= {\mathcal{X}}_{{\mathtt{p}}{\mathtt{a}}} u(x,y_0) = {\mathcal{X}}_{{\mathtt{a}}{\mathtt{p}}} u(x,y_0), x \in (-1+\delta, 1-\delta). \end{aligned} $$

Also, for fixed x ₀, we have

$$\displaystyle \begin{aligned} {\mathcal{Y}} u(x_0,y) &= {\mathcal{Y}}_{\mathtt{p}} u(x_0,y) = {\mathcal{Y}}_{\mathtt{a}} u(x_0,y) = {\mathcal{Y}}_{{\mathtt{p}}{\mathtt{a}}} u(x_0,y)\\ &= {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} u(x_0,y) \quad y \in (-1+\delta, 1-\delta). \end{aligned} $$

The choice made in (25) leads to the construction of the operator that enforces pure Neumann BC in the x- and y-variable as follows:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{X}}_{\mathtt{N}} & := {\mathcal{X}}_{\mathtt{p}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{a}} P_{o,{x'}} && \quad \text{(in the }x\text{-variable)} {} \end{array}\end{aligned} $$

(43)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{Y}}_{\mathtt{N}} & := {\mathcal{Y}}_{\mathtt{p}} P_{e,{y'}} + {\mathcal{Y}}_{\mathtt{a}} P_{o,{y'}} && \quad \text{(in the }y\text{-variable)}. {} \end{array}\end{aligned} $$

(44)

Similarly, the choice made in (26) leads to the construction of the operator that enforces pure Dirichlet BC in the x- and y-variable as follows:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{X}}_{\mathtt{D}} & := {\mathcal{X}}_{\mathtt{a}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{p}} P_{o,{x'}} && \quad \text{(in the }x\text{-variable)} {} \end{array}\end{aligned} $$

(45)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{Y}}_{\mathtt{D}} & := {\mathcal{Y}}_{\mathtt{a}} P_{e,{y'}} + {\mathcal{Y}}_{\mathtt{p}} P_{o,{y'}} && \quad \text{(in the }y\text{-variable)}. {} \end{array}\end{aligned} $$

(46)

Similarly, the choices made in (27) and (28) lead to the construction of the operators that enforce mixed Neumann-Dirichlet and Dirichlet-Neumann BC in the x- and y-variable as follows:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} & := {\mathcal{X}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{x'}} + {\mathcal{X}}_{{\mathtt{p}}{\mathtt{a}}} P_{o,{x'}} && \quad \text{(in the }x\text{-variable)} {} \end{array}\end{aligned} $$

(47)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{Y}}_{{\mathtt{N}}{\mathtt{D}}} & := {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{y'}} + {\mathcal{Y}}_{{\mathtt{p}}{\mathtt{a}}} P_{o,{y'}} && \quad \text{(in the }y\text{-variable)} {} \end{array}\end{aligned} $$

(48)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{X}}_{{\mathtt{D}}{\mathtt{N}}} & := {\mathcal{X}}_{{\mathtt{p}}{\mathtt{a}}} P_{e,{x'}} + {\mathcal{X}}_{{\mathtt{a}}{\mathtt{p}}} P_{o,{x'}} && \quad \text{(in the }x\text{-variable)} {} \end{array}\end{aligned} $$

(49)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} & := {\mathcal{Y}}_{{\mathtt{p}}{\mathtt{a}}} P_{e,{y'}} + {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{o,{y'}} && \quad \text{(in the }y\text{-variable)}. {} \end{array}\end{aligned} $$

(50)

We want to construct an operator that enforces pure Neumann BC on the square. We make the choice that gives the 1D Neumann operator both in x- and y-variables. Hence, combining (43) and (44), we define the 2D pure Neumann operator as

$$\displaystyle \begin{aligned} \big( {\mathcal{M}}_{\mathtt{N}} - c \big) := - {\mathcal{X}}_{\mathtt{N}} {\mathcal{Y}}_{\mathtt{N}} = - \big( {\mathcal{X}}_{\mathtt{p}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{a}} P_{o,{x'}} \big) \big( {\mathcal{Y}}_{\mathtt{p}} P_{e,{y'}} + {\mathcal{Y}}_{\mathtt{a}} P_{o,{y'}} \big). \end{aligned} $$

(51)

Similarly, combining (45) and (46), we define the 2D pure Dirichlet operator as

$$\displaystyle \begin{aligned} \big( {\mathcal{M}}_{\mathtt{D}} - c \big) := - {\mathcal{X}}_{\mathtt{D}} {\mathcal{Y}}_{\mathtt{D}} = - \big( {\mathcal{X}}_{\mathtt{a}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{p}} P_{o,{x'}} \big) \big( {\mathcal{Y}}_{\mathtt{a}} P_{e,{y'}} + {\mathcal{Y}}_{\mathtt{p}} P_{o,{y'}} \big). \end{aligned} $$

(52)

Similarly, combining (47), (48), (49), and (50), we define the 2D mixed operators as follows:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \big( {\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} - c \big) := - {\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}}{\mathcal{Y}}_{{\mathtt{N}}{\mathtt{D}}} = - \big( {\mathcal{X}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{x'}} + {\mathcal{X}}_{{\mathtt{p}}{\mathtt{a}}} P_{o,{x'}} \big) \big( {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{y'}} + {\mathcal{Y}}_{{\mathtt{p}}{\mathtt{a}}} P_{o,{y'}} \big) {} \end{array}\end{aligned} $$

(53)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \big( {\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} - c \big) := - {\mathcal{X}}_{{\mathtt{N}}} \ {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} = - \big( {\mathcal{X}}_{{\mathtt{p}}} P_{e,{x'}} + {\mathcal{X}}_{{\mathtt{a}}} P_{o,{x'}} \big) \ \big( {\mathcal{Y}}_{{\mathtt{p}}{\mathtt{a}}} P_{e,{y'}} + {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{o,{y'}} \big). {} \end{array}\end{aligned} $$

(54)

Recalling (2), we immediately see that the operator ${\mathcal {L}}$ agrees in the bulk with the given operators above. Namely,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \big( {\mathcal{L}} - c \big) &\displaystyle = &\displaystyle - {\mathcal{C}} = \big({\mathcal{M}}_{\mathtt{N}} -c \big) \\ \big( {\mathcal{L}} - c \big) &\displaystyle = &\displaystyle - {\mathcal{C}} = \big({\mathcal{M}}_{\mathtt{D}} -c \big) \\ \big( {\mathcal{L}} - c \big) &\displaystyle = &\displaystyle - {\mathcal{C}} = \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) \\ \big( {\mathcal{L}} - c \big) &\displaystyle = &\displaystyle - {\mathcal{C}} = \big({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \big). \end{array} \end{aligned} $$

Remark 6

The operator ${\mathcal {C}}$ in (2) utilizes a 2D computational domain which is indicated by the integration variable dx′dy′ = d(x′, y′). We can show the construction of each operator by paying attention to the computational domain of each operator and rearranging (41) using the agreement of operators in the bulk in the following way:

$$\displaystyle \begin{aligned} {\mathcal{C}} & = {\mathcal{C}} I_{{x'},{y'}} = {\mathcal{X}} I_{{x'}} \; {\mathcal{Y}} I_{{y'}} \\ & = {\mathcal{X}} (P_{e,{x'}} + P_{o, {x'}}) \; {\mathcal{Y}} ( P_{e,{y'}} + P_{o,{y'}} ) \\ & = \big( {\mathcal{X}} P_{e,{x'}} + {\mathcal{X}} P_{o, {x'}} \big) \; \big( {\mathcal{Y}} P_{e,{y'}} + {\mathcal{Y}} P_{o,{y'}} \big) \\ & = \big( {\mathcal{X}}_{\mathtt{p}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{a}} P_{o, {x'}} \big) \; \big( {\mathcal{Y}}_{\mathtt{p}} P_{e,{y'}} + {\mathcal{Y}}_{\mathtt{a}} P_{o,{y'}} \big) \quad \ \ \, =: - \big({\mathcal{M}}_{\mathtt{N}} -c \big) \\ & = \big( {\mathcal{X}}_{\mathtt{a}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{p}} P_{o, {x'}} \big) \; \big( {\mathcal{Y}}_{\mathtt{a}} P_{e,{y'}} + {\mathcal{Y}}_{\mathtt{p}} P_{o,{y'}} \big) \quad \ \ \, =: - \big({\mathcal{M}}_{\mathtt{D}} -c \big) \\ &= \big( {\mathcal{X}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{x'}} + {\mathcal{X}}_{{\mathtt{a}}{\mathtt{p}}} P_{o, {x'}} \big) \; \big( {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{y'}} + {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{o,{y'}} \big) =: - \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{ D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) {} \end{aligned} $$

(55)

$$\displaystyle \begin{aligned} & = \big( {\mathcal{X}}_{\mathtt{p}} P_{e,{x'}} + {\mathcal{X}}_{\mathtt{a}} P_{o, {x'}} \big) \; \big( {\mathcal{Y}}_{{\mathtt{a}}{\mathtt{p}}} P_{e,{y'}} + {\mathcal{Y}}_{{\mathtt{p}}{\mathtt{a}}} P_{o,{y'}} \big) \ \ \, \, =: - \big({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) {}. \end{aligned} $$

(56)

We construct the operators in higher dimensions by using the corresponding rearrangement; see section “Operators in Higher Dimensions” for the 3D construction. In addition, the 2D decomposition operator $I_{{x'},{y'}}$ given in (9) is indeed the product of the 1D decomposition operators $I_{{x'}}$ and $I_{{y'}}$ given in (8). More precisely ,

$$\displaystyle \begin{aligned} \begin{array}{rcl} I_{{x'},{y'}} &\displaystyle = &\displaystyle I_{{x'}} \; I_{{y'}} \\ &\displaystyle = &\displaystyle \big( P_{e,{x'}} + P_{o,{x'}} \big) \big( P_{e,{y'}} + P_{o,{y'}} \big) \\ &\displaystyle = &\displaystyle P_{e,{x'}} P_{e,{y'}} + P_{e,{x'}} P_{o,{y'}} + P_{o,{x'}} P_{e,{y'}} + P_{o,{x'}} P_{o,{y'}}. \end{array} \end{aligned} $$

Verifying the Boundary Conditions

The operators $\big ({\mathcal {M}}_{\mathtt {N}} - c \big )$, $\big ({\mathcal {M}}_{\mathtt {D}} -c \big )$, $\big ({\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}, \, {\mathtt {N}}{\mathtt {D}}} - c \big )$, and $\big ({\mathcal {M}}_{{\mathtt {N}}, \, {\mathtt {D}}{\mathtt {N}}} - c \big )$ given in (51), (52), (53), and (54), respectively, are the product of two 1D operators. As we mentioned, the limit in the definition of the BC can be interchanged with the integral sign due to the Lebesgue dominated convergence theorem and the Leibniz rule . Then, using the change in the order of integration as in (42) and (38), we can prove that the pure and mixed Neumann and Dirichlet BC are enforced.

First, we prove that the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ enforce pure Neumann and pure Dirichlet BC in 2D:

$$\displaystyle \begin{aligned} \frac{\partial}{\partial n} \big[ \left({\mathcal{M}}_{\mathtt{N}} -c \right) u \big] (x,+1) &= - \left( \frac{\partial}{\partial y} {\mathcal{X}}_{\mathtt{N}} {\mathcal{Y}}_{\mathtt{N}} \right) u(x,+1) \\ {} &= - {\mathcal{X}}_{\mathtt{N}} \left( \frac{d}{dy} {\mathcal{Y}}_{\mathtt{N}} \right) u(x,+1) = 0 \\ {} \frac{\partial}{\partial n} \left[ \left({\mathcal{M}}_{\mathtt{N}} -c \right) u \right] (x,-1) &= \left( \frac{\partial}{\partial y} {\mathcal{X}}_{\mathtt{N}} {\mathcal{Y}}_{\mathtt{N}} \right) u(x,-1)\\ {} & = {\mathcal{X}}_{\mathtt{N}} \left( \frac{d}{dy} {\mathcal{Y}}_{\mathtt{N}} \right) u(x,-1) = 0 \\ {} \frac{\partial}{\partial n} \left[ \left({\mathcal{M}}_{\mathtt{N}} -c \right) u \right] (+1,y) & = - \left( \frac{\partial}{\partial x} {\mathcal{Y}}_{\mathtt{N}} {\mathcal{X}}_{\mathtt{N}} \right) u(+1,y)\\ {} & = - {\mathcal{Y}}_{\mathtt{N}} \left( \frac{d}{dx} {\mathcal{X}}_{\mathtt{N}} \right) u(+1,y) = 0 \\ {} \frac{\partial}{\partial n} \left[ \left({\mathcal{M}}_{\mathtt{N}} -c \right) u \right](-1,y) &= \left( \frac{\partial}{\partial x} {\mathcal{Y}}_{\mathtt{N}} {\mathcal{X}}_{\mathtt{N}} \right) u(-1,y)\\ {} &= {\mathcal{Y}}_{\mathtt{N}} \left( \frac{d}{dx} {\mathcal{X}}_{\mathtt{N}} \right) u(-1,y) = 0.\\ {} \big({\mathcal{M}}_{\mathtt{D}} -c \big) u(x,\pm 1) & = - {\mathcal{X}}_{\mathtt{D}} {\mathcal{Y}}_{\mathtt{D}} u(x, \pm 1) = 0 \\ {} \big({\mathcal{M}}_{\mathtt{D}} -c \big) u(\pm 1,y) & = - {\mathcal{Y}}_{\mathtt{D}} {\mathcal{X}}_{\mathtt{D}} u(\pm 1, y) = 0. \end{aligned} $$

Then, we prove that the operator ${\mathcal {M}}_{{\mathtt {N}}{\mathtt {D}}, \, {\mathtt {N}}{\mathtt {D}}}$ enforces mixed (2+2) Neumann-Dirichlet, i.e., the West and South edges have Neumann and the East and North edges have Dirichlet BC:

$$\displaystyle \begin{aligned} \frac{\partial}{\partial n} \left[ \left({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \right) u \right] (-1,y) &= \left( \frac{\partial}{\partial x} {\mathcal{Y}}_{{\mathtt{N}}{\mathtt{D}}} {\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} \right) u(-1,y) \\ & = {\mathcal{Y}}_{{\mathtt{N}}{\mathtt{D}}} \left( \frac{d}{dx} {\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} \right) u(-1,y) = 0 \\ \frac{\partial}{\partial n} \left[ \left({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \right) u \right] (x,-1) &= \left( \frac{\partial}{\partial y} {\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} {\mathcal{Y}}_{{\mathtt{N}}{\mathtt{D}}} \right) u(x,-1) \\ & = {\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} \left( \frac{d}{dy} {\mathcal{Y}}_{{\mathtt{N}}{\mathtt{D}}} \right) u(x,-1) = 0.\\ \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) u(+1,y) & = -{\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} {\mathcal{Y}}_{{\mathtt{ N}}{\mathtt{D}}} u(+1,y) = 0 \\ \big({\mathcal{M}}_{{\mathtt{N}}{\mathtt{D}}, \, {\mathtt{N}}{\mathtt{D}}} -c \big) u(x,+1) & = -{\mathcal{X}}_{{\mathtt{N}}{\mathtt{D}}} {\mathcal{Y}}_{{\mathtt{ N}}{\mathtt{D}}} u(x,+1) = 0. \end{aligned} $$

Finally, we prove that the operator ${\mathcal {M}}_{{\mathtt {N}}, \, {\mathtt {D}}{\mathtt {N}}}$ enforces mixed Neumann-Dirichlet (3+1), i.e., the East, West, and North edges have Neumann and the South edge have Dirichlet BC :

$$\displaystyle \begin{aligned} \frac{\partial}{\partial n} \big[ \left({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \right) u \big] (+1,y) &= - \left( \frac{\partial}{\partial x} {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} {\mathcal{X}}_{{\mathtt{N}}} \right) u(+1,y) \\ {} & = {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} \left( \frac{d}{dx} {\mathcal{X}}_{\mathtt{N}} \right) u(+1,y) = 0 \\ {} \frac{\partial}{\partial n} \big[ \left({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \right) u \big] (-1,y) &= \left( \frac{\partial}{\partial x} {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} {\mathcal{X}}_{{\mathtt{N}}} \right) u(-1,y) \\ {} &= {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} \big( \frac{d}{dx} {\mathcal{X}}_{\mathtt{N}} \big) u(-1,y) = 0 \\ {} \frac{\partial}{\partial n} \left[ \left({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \right) u \right] (x,+1) & = - \left( \frac{\partial}{\partial y} {\mathcal{X}}_{\mathtt{N}} {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} \right) u(x,+1)\\ {} & = - {\mathcal{X}}_{\mathtt{N}} \left( \frac{d}{dy} {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} \right) u(x,+1) = 0.\\ {} \big({\mathcal{M}}_{{\mathtt{N}}, \, {\mathtt{D}}{\mathtt{N}}} -c \big) u(x,-1) &= -{\mathcal{X}}_{{\mathtt{N}}} {\mathcal{Y}}_{{\mathtt{D}}{\mathtt{N}}} u(x,-1) = 0. \end{aligned} $$

Operators in Higher Dimensions

Let us consider the convolution in 3D and the domain be Ω := [−1, 1] × [−1, 1] × [−1, 1]. We define the convolution in 3D similarly using notation in (39).

$$\displaystyle \begin{aligned} {\mathcal{C}} u(x,y) = \iiint \limits_{\varOmega} {\widehat{C}}({x'}-x,{y'}-y,{z'}-z) u({x'},{y'},{z'}) d{x'} d{y'} d{z'}. \end{aligned}$$

Note that ${\mathcal {C}} = -\big ( {\mathcal {L}} - c \big )$. Hence we concentrate on finding suitable operators that agree with ${\mathcal {C}}$ in the bulk. Assuming a separable restricted kernel function similar to (11),

$$\displaystyle \begin{aligned} C(x, y, z) = X(x) Y(y) Z(z), \end{aligned}$$

the operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ in 3D defined below enforce pure Neumann and Dirichlet BC and simultaneously agree with the operator ${\mathcal {L}}$ in the bulk. The construction process is an extension of the 2D case:

The operators that enforce mixed Neumann and Dirichlet BC can be constructed in a similar fashion to the operators given in (55) and (56). The extension to arbitrary dimension can be performed by the same line of argument .

Numerical Experiments

We numerically solve the following nonlocal wave equation :

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} u_{tt}({\mathbf{x}},t) + {\mathcal{M}}_{\mathtt{BC}} u({\mathbf{x}},t) & = b({\mathbf{x}},t), \quad ({\mathbf{x}},t) \in \varOmega \times [0,T], {} \\ u({\mathbf{x}},0) & = u_0({\mathbf{x}}), \\ u_t({\mathbf{x}},0) & = 0 \end{array}\end{aligned} $$

(57)

by employing the governing operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ in 1D, i.e., BC ∈{N, D}, and the operators ${\mathcal {M}}_{\mathtt {N}}$, ${\mathcal {M}}_{\mathtt {D}}$, ${\mathcal {M}}_{{\mathtt {N}}{\mathtt { D}}, \, {\mathtt {N}}{\mathtt {D}}}$, and ${\mathcal {M}}_{{\mathtt {N}}, \, {\mathtt {D}}{\mathtt {N}}}$ in 2D, i.e., BC ∈{N, D, (ND, ND), (N, DN)}, with discontinuous and continuous initial displacement u ₀(x); see the definition of the governing operators in Theorem 1. For the discretization of the 1D problem, we use the Galerkin projection method with piecewise polynomials. For implementation details and theoretical construction, see Aksoylu et al. (2017a). Note that, for all time, BC are satisfied; see Fig. 3.

Fig. 3

Solution to the nonlocal wave equation on a 1D domain with discontinuous (top) and continuous (bottom) initial solution and vanishing initial velocity with Neumann (left) boundary condition using the governing operator ${\mathcal {M}}_{{\mathtt {N}}}$ and Dirichlet (right) boundary condition using the governing operator ${\mathcal {M}}_{{\mathtt {D}}}$. Note that, for all time, BC are satisfied and discontinuities remain stationary

In 1D, as far as the boundary behavior goes, in nonlocal problems, we observe a similar wave reflection pattern from the boundary as in classical problems. In the classical case, we see that the Neumann and the Dirichlet BC create reflections of same and opposite signs, respectively; for the Neumann BC, see Fig. 4. A parallel behavior is observed for the nonlocal Neumann and Dirichlet cases; see Fig. 3.

Fig. 4

Solution to the classical wave equation with Neumann (left) and Dirichlet (right) boundary conditions with the same continuous initial displacement as in Fig. 3 and vanishing initial velocity

For the discretization of the 2D problem, we use the Nyström method with the quadrature chosen as the trapezoidal rule (Fig. 5). For implementation details, see Aksoylu et al. (Submitted). We depict the solutions to the nonlocal wave equation domain with homogeneous pure Neumann, pure Dirichlet, and mixed Neumann-Dirichlet with vanishing initial velocity and discontinuous initial displacement; see Figs. 6, 7, 8, and 9. Also, for continuous initial displacement, see Fig. 10. The initial solutions are depicted in Fig. 5. Notice that, for all time, local BC are clearly satisfied. Furthermore, for pure Neumann problem, we have numerically verified that ∬_Ωu(x, t)dx remains constant for all t. This is in agreement with the physical implication that homogeneous Neumann BC model insulated boundaries.

Fig. 5

Initial solutions to the nonlocal wave equation on a 2D domain with discontinuous (left) and continuous (right) initial solutions

Fig. 6

Solution to the nonlocal wave equation on a 2D domain with discontinuous initial solution using the governing operator ${\mathcal {M}}_{\mathtt {N}}$

Fig. 7

Solution to the nonlocal wave equation on a 2D domain with discontinuous initial solution using the governing operator ${\mathcal {M}}_{\mathtt {D}}$

Fig. 8

Solution to the nonlocal wave equation on a 2D domain with discontinuous initial solution using the governing operator ${\mathcal {M}}_{{\mathtt {N}}{\mathtt { D}}, \, {\mathtt {N}}{\mathtt {D}}}$

Fig. 9

Solution to the nonlocal wave equation on a 2D domain with discontinuous initial solution using the governing operator ${\mathcal {M}}_{{\mathtt {N}}, \, {\mathtt {D}}{\mathtt {N}}}$

Fig. 10

Solution to the nonlocal wave equation on a 2D domain with continuous initial solution using the governing operator ${\mathcal {M}}_{\mathtt {N}}$

The Treatment of General Nonlocal Problems Using Functional Calculus

Our main tool that allows us to incorporate local BC into nonlocal operators is functional calculus. More precisely, the novel governing operators are obtained by employing the functional calculus of self-adjoint operators, i.e., by replacing the classical governing operator A by a suitable function of A, f(A). We call f the regulating function. Since classical BC is an integral part of the classical operator, these BC are automatically inherited by f(A). One advantage of our approach is that every symmetry that commutes with A also commutes with f(A). As a result, required invariance with respect to classical symmetries such as translation, rotation, and so forth is preserved.

We illustrate the benefit of functional calculus, for instance, by comparing the Laplace operator Δ to the biharmonic operator Δ ². By simply inspecting how the biharmonic operator is connected to the Laplace operator, one can guess that the regulating function would be f(λ) = λ ². Before making a rigorous connection, one has to prescribe the BC for each operator. We choose the Laplace operator with homogeneous Dirichlet and Neumann BC and compare it to the biharmonic operator with simply supported (SS) and Cahn-Hilliard (CH) type BC for plate vibration utilizing the weak formulation of the following eigenvalue problems where the BC used are precisely the following:

$$\displaystyle \begin{aligned} \text{SS-BC:} \quad u = \varDelta u = 0 \text{ on } \partial \varOmega, \quad \text{CH-BC:} \quad \frac{\partial u}{\partial n} = \frac{\partial \varDelta u}{\partial n} = 0 \text{ on } \partial \varOmega. \end{aligned}$$

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l}L(u,v) & := \int\nolimits_\varOmega \nabla u \cdot \nabla v \, dx && = \lambda R(u,v) && := \lambda \int\nolimits_\varOmega u v \, dx, && \quad v \in V_{L,D} \text{ or } V_{L,N} \end{array}\end{aligned} $$

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} B(u,v) & := \int\nolimits_\varOmega \nabla^2 u : \nabla^2 v \, dx && = \lambda R(u,v), && && \quad v \in V_{B,SS} \text{ or } V_{B,CH}, \end{array}\end{aligned} $$

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l}V_{L,D} & := H^1_0(\varOmega), && V_{L,N} && :=\Big\{ v \in H^1(\varOmega): \frac{\partial v}{\partial n} = 0 \Big\}, \\ V_{B,SS} & := H^1_0(\varOmega) \cap H^2(\varOmega), \quad && V_{B,CH} && := \Big\{v \in H^2(\varOmega): \frac{\partial v}{\partial n} = 0 \Big\}. \end{array}\end{aligned} $$

Indeed, the eigenvalues of the biharmonic operator with SS-BC and CH-BC are the squares of those of the Laplace operator with Dirichlet and Neumann BC, respectively. Furthermore, the eigenfunctions are identical for Dirichlet and Neumann BC with SS and CH, respectively. We have provided this example as a proof of concept and, hence, chosen the BC carefully to establish the connection. One may not obtain such connection with arbitrary BC.

The convolution operators in (12) in the form of integrals are derived from their (original) series representation. We defined generalized convolution operators in Aksoylu et al. (2017a,b) in the following series form:

$$\displaystyle \begin{aligned} {\mathcal{C}}_{\mathtt{BC}} u(x) := \sum\limits_{k} \langle{e_k^{\mathtt{BC}}|C}\rangle \langle{e_k^{\mathtt{BC}}|u}\rangle \; e_k^{\mathtt{BC}}, \end{aligned} $$

(58)

where BC = p, a and 〈⋅|⋅〉 denotes the inner product in $L^2_{\mathbb {C}}(\varOmega )$ and is defined by

$$\displaystyle \begin{aligned}\langle {e_k^{\mathtt{BC}} | u}\rangle := \int\nolimits_{\varOmega} \big( e_k^{\mathtt{BC}}\big)^*({x'}) u({x'})d{x'}. \end{aligned}$$

In addition, $\big ( e_k^{\mathtt {BC}} \big )_k$ is chosen to be a basis associated with a multiple of the Laplace operator with appropriate BC, which we call as the classical operator and denote by Δ_BC. The spectrum of Δ_BC with classical BC such as periodic, antiperiodic, Neumann, and Dirichlet is purely discrete. Furthermore, we can explicitly calculate the eigenfunctions $e_k^{\mathtt {BC}}$ corresponding to each BC. These eigenfunctions form a Hilbert (complete and orthonormal) basis for $L^2_{\mathbb {C}}(\varOmega )$ through which the generalized convolution operator is defined. The main reason why we discuss Δ_BC is the fact that the governing operator (1) turns out to be a function of Δ_BC (Aksoylu et al. 2017a,b; Beyer et al. 2016). Since the classical operator A_BC is defined through local BC, the eigenfunctions inherit this information. This observation opened a gateway to incorporate local BC to nonlocal theories on bounded domains (Aksoylu et al. 2017b).

The normalized eigenfunctions of the classical operators are as follows:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} e_{k}^{\mathtt{p}}(x) & := \frac{1}{\sqrt{2}} \, e^{i \pi k x}, \quad k \in {\mathbb{N}}, && e_{k}^{\mathtt{a}}(x) && := \frac{1}{\sqrt{2}} \, e^{i \pi (k + \frac{1}{2}) x}, \quad k \in {\mathbb{N}}, {}\\ e_{k}^{\mathtt{N}}(x) & := \begin{cases} \quad \qquad \frac{1}{\sqrt{2}}, & k = 0, \\ \cos\big(\frac{k \pi}{2}(x+1)\big), & k \in \mathbb{N}^{*}, \end{cases}\quad && e_{k}^{\mathtt{D}}(x) && := \sin\Big(\frac{k \pi}{2}(x+1)\Big), \quad k \in \mathbb{N}^{*}. \end{array}\end{aligned} $$

(59)

Plugging the eigenfunctions in (59) into (58) and after hefty calculation, we proved that the operators ${\mathcal {C}}_{\mathtt {p}}$ and ${\mathcal {C}}_{\mathtt {a}}$ have integral representations given (12). For more details, see Aksoylu et al. (2017a).

Next, we present the steps how to apply functional calculus (FC). We denote a nonlocal operator by NL and its local counterpart by A. Note that both nonlocal diffusion and PD operators are defined initially on ${\mathbb {R}}^d$ and contain convolution. The size of nonlocality is determined by the parameter δ which is encoded in the kernel function .

FC-1. :

Apply limit to the horizon parameter, i.e., δ → 0, to identify a local counterpart A of NL.

FC-2. :

Apply the Fourier transform to “diagonalize” NL and A to obtain the corresponding spectra.

FC-3. :

Read off the regulating function f by comparing the spectra of NL and A. Spectra on ${\mathbb {R}}^d$ are continuous.

We apply the above steps to the concrete example of nonlocal diffusion on ${\mathbb {R}}^d$ where the classical operator A is the Laplace operator $-\varDelta : W^2({\mathbb {R}}^d) \rightarrow L^2({\mathbb {R}}^d)$.

$$\displaystyle \begin{aligned} NL u({\mathbf{x}},t) = f(A) u({\mathbf{x}},t) := \Big( \int\nolimits_{{\mathbb{R}}^d} C({\mathbf{x'}}) d{\mathbf{x'}} \Big) u({\mathbf{x}},t) - \int\nolimits_{{\mathbb{R}}^d} C({\mathbf{x'}}-{\mathbf{x}}) u({\mathbf{x'}},t) d{\mathbf{x'}}.\end{aligned} $$

(60)

We connect the nonlocal operator to A through Fourier transforms. Let $F_1:L^1({\mathbb {R}}^d) \rightarrow C_{\infty }({\mathbb {R}}^d)$, $F_2: L^2({\mathbb {R}}^d) \rightarrow L^2({\mathbb {R}}^d)$ be the Fourier transforms and the kernel function $C \in L^1({\mathbb {R}}^d)$ be even:

$$\displaystyle \begin{aligned} \begin{array}{rcl} A &\displaystyle = &\displaystyle F_2^{-1} \circ T_{\lambda} \circ F_2, \\ {} f(A) &\displaystyle = &\displaystyle F_2^{-1} \circ T_{f(\lambda)} \circ F_2, {} \end{array} \end{aligned} $$

(61)

where T_h(λ) denotes the maximal multiplication operator by h(λ). Then, we directly diagonalize f(A) by using the expression given in (60):

$$\displaystyle \begin{aligned} f(A) = F_2^{-1} \circ T_{F_1 C(0) - F_1 C(\lambda)} \circ F_2.\end{aligned} $$

(62)

Therefore, a comparison of (61) and (62) yields

$$\displaystyle \begin{aligned} f(\lambda) = F_1 C(0) - F_1 C(\lambda). \end{aligned}$$

We explicitly identify to which function of the classical operator the nonlocal operator corresponds:

where the spectral value of the classical operator λ ∈ [0, ∞). Now, we extend the construction on ${\mathbb {R}}^d$ to a bounded domain Ω.

FC-4. :

Restrict A to Ω with a prescribed BC. Denote the new operator by A_BC. Spectrum of A_BC, σ(A_BC) is now discrete. Find the eigenfunctions of A_BC.

FC-5. :

Define a generalized convolution as in (58) by using eigenfunctions of A_BC.

FC-6. :

Rewrite (recycle) the regulating function with discrete spectrum.

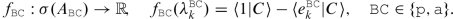(63)

FC-7. :

Construct f_BC(A_BC) using the spectral theorem. Namely, for $u = \sum \nolimits _k \langle {e_k^{\mathtt {BC}}|u}\rangle \; e_k^{\mathtt {BC}}$, we have

$$\displaystyle \begin{aligned} f_{\mathtt{BC}}(A_{\mathtt{BC}}) u = \sum_k f_{\mathtt{BC}}(\lambda_k^{\mathtt{BC}}) \langle{e_k^{\mathtt{BC}}|u}\rangle \; e_k^{\mathtt{BC}}. \end{aligned} $$

(64)

FC-8. :

Find a computationally feasible expression of f_BC(A_BC) such as an integral representation.

Now, we show how we use the FC steps to construct the governing operators ${\mathcal {M}}_{\mathtt {BC}}, ~{\mathtt {BC}} \in \{{\mathtt {p}}, {\mathtt {a}} \}$ in 1D. Namely, we want to verify $f_{\mathtt {BC}}(A_{\mathtt {BC}})u = {\mathcal {M}}_{\mathtt {BC}} u$.

Using (63) and (64), we have the following:

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{\mathtt{BC}}(A_{\mathtt{BC}}) u &\displaystyle = &\displaystyle \sum_k [ \langle{1|C}\rangle - \langle{e_k^{\mathtt{BC}}|C}\rangle ] \langle{e_k^{\mathtt{BC}}|u}\rangle \; e_k^{\mathtt{BC}} \\ &\displaystyle = &\displaystyle \langle{1|C}\rangle \sum_k \langle{e_k^{\mathtt{BC}}|u}\rangle \; e_k^{\mathtt{BC}} - \sum_k \langle{e_k^{\mathtt{BC}}|C}\rangle \langle{e_k^{\mathtt{BC}}|u}\rangle \; e_k^{\mathtt{BC}} \\ &\displaystyle = &\displaystyle c u - {\mathcal{C}}_{\mathtt{BC}} u \\ &\displaystyle = &\displaystyle {\mathcal{M}}_{\mathtt{BC}}, \quad {\mathtt{BC}} \in \{{\mathtt{p}}, {\mathtt{a}} \}. \end{array} \end{aligned} $$

Expressing the regulating function for the case of BC ∈{N, D} requires nontrivial manipulation of series and is more involved than the case of BC ∈{N, D}. We simply report them here:

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} f_{\mathtt{N}}: \sigma(A_{\mathtt{N}}) \rightarrow {\mathbb{R}}, & \quad f_{\mathtt{N}}(\lambda_k^{\mathtt{N}}) && = \langle{1|C}\rangle - \begin{cases} \langle{e_{k/2}^{{\mathtt{p}}}|C}\rangle & \text{if }k \in {\mathbb{N}}\text{ is even,} \\ \langle{e_{(k-1)/2}^{\mathtt{a}}|C}\rangle & \text{if }k \in {\mathbb{N}}\text{ is odd.} \end{cases} \\ f_{\mathtt{D}}: \sigma(A_{\mathtt{D}}) \rightarrow {\mathbb{R}}, & \quad f_{\mathtt{D}}(\lambda_k^{\mathtt{D}}) && = \langle{1|C}\rangle - \begin{cases} \langle{e_{k/2}^{{\mathtt{p}}}|C}\rangle & \text{if }k \in {\mathbb{N}^*}\text{ is even,} \\ \langle{e_{(k-1)/2}^{\mathtt{a}}|C} & \text{if }k \in {\mathbb{N}}\text{ is odd.} \end{cases} \end{array}\end{aligned} $$

In Aksoylu et al. (2017a), we showed that

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} f_{\mathtt{N}} (A_{\mathtt{N}}) u & = \big( c - {\mathcal{C}}_{\mathtt{p}} P_e - {\mathcal{C}}_{\mathtt{a}} P_o \big) u && = {\mathcal{M}}_{\mathtt{N}} u \\ f_{\mathtt{D}} (A_{\mathtt{D}}) u & = \big( c - {\mathcal{C}}_{\mathtt{a}} P_e - {\mathcal{C}}_{\mathtt{p}} P_o \big) u && = {\mathcal{M}}_{\mathtt{D}} u. \end{array}\end{aligned} $$

The operators ${\mathcal {M}}_{\mathtt {N}}$ and ${\mathcal {M}}_{\mathtt {D}}$ were used as governing operator in (57) to perform the numerical experiments in 1D .

Remark 7

Fractional diffusion and fractional PDEs also fall into the class of nonlocal problems; see some of the recent developments (Andreu-Vaillo et al. 2010; Caffarelli et al. 2007; Di Nezza et al. 2012; Nochetto et al. 2015). There is a fundamental difference between these operators and ours: our governing operators are bounded. Note that the regulating function in (63) is bounded and that is why the application of the spectral theorem in (64) is valid. Since our ultimate goal is to capture discontinuities or cracks, we are mainly interested in bounded governing operators. Fractional operators become unbounded for such discontinuities, and hence, we exclude them from our discussion.

Conclusion

We presented novel governing operators in arbitrary dimension for nonlocal diffusion. The operators agree with the original PD operator in the bulk of the domain and simultaneously enforce local BC. We presented methodically how to verify the BC by using a change in the order of integration. We presented different types of BC in 2D which include pure and mixed combinations of Neumann and Dirichlet BC. We presented numerical experiments for the nonlocal wave equation . We verified that the novel operators enforce local BC for all time. We also observed that the property we proved for 1D, namely, discontinuities remain stationary, also holds for 2D.

Our ongoing work aims to extend the novel operators to vector-valued problems which will allow the extension of PD to applications that require local BC. Furthermore, we hope that our novel approach potentially will avoid altogether the surface effects seen in PD.